How Membrane Partitioning Modulates Receptor Activation: Parallel versus Serial Effects of Hydrophobic Ligands

A quantitative understanding of the effects exerted by hydrophobic or amphiphilic drugs and biomolecules on biological membrane function is not possible without parsing the problem into membrane partitioning and the actual trigger that induces the response under study. This problem and its solution are not exactly new, but they have been and continue to be ignored in many cases. In the previous issue of the Biophysical Journal, Collins and Gordon (1) compare the effects on channel proteins such as TRPV1 of water-soluble, short-chain phosphatidylinositol phosphates (PIPs) used in patch-clamp electrophysiology and their membrane-bound, long-chain counterparts found in cells. The authors demonstrate the importance of explicitly accounting for membrane partitioning when studying receptor binding and present a rigorous way to do one’s homework properly. Their results imply the need to revisit previous in vitro data on the activation of membrane channels by water-soluble lipid analogs. But this is only the tip of the iceberg.

The key to interpreting a binding experiment of a hydrophobic or amphiphilic ligand to a membrane protein lies in distinguishing among three states of the ligand, that is, in aqueous solution (aq), in the lipid bilayer (b), and complexed to the protein (c). Thus, it takes two parameters—for example, the membrane–water partition coefficient, K_P, and the dissociation constant of the protein–ligand complex, K_D—to describe the distribution of ligand among the three states:

$$K_{\text{P}}=\frac{R_{\text{b}}}{c_{\text{A}}^{\text{aq}}}=\frac{c_{\text{A}}^{\text{b}}}{c_{\text{L}}{c}_{\text{A}}^{\text{aq}}},$$ (1)

$$K_{\text{D}}=\frac{c_{\text{R}}^{\text{f}}{c}_{\text{A}}^{\text{aq}}}{c_{\text{A}}^{\text{c}}}.$$ (2)

Here, c_A^aq, c_A^b, and c_A^c denote the molar concentrations of the ligand or additive (A) in the aqueous phase, in the bilayer, and complexed to the receptor protein, respectively. The symbol c_L stands for the concentration of lipid (L) accessible to the additive, and c_R^f is the concentration of free binding sites on the receptor (R). In this notation, each concentration refers to the respective molar amount in the total volume of the system; hence, according to Eqs. 1 and 2, K_P and K_D come in units of inverted molarity and molarity, respectively (see Heerklotz (2) for a discussion of various definitions of partition coefficients). K_P is often referred to as an apparent partition coefficient, K_app, to indicate that it comprises the net effects of both hydrophobic and electrostatic interactions and, for ionic additives such as PIPs, will thus vary with the surface charge density of the membrane (1,2). The parameter R_b = c_A^b/c_L denotes the additive/lipid mole ratio within the membrane and, thus, may serve as a measure of membrane composition. Note that, although K_D as defined in Eq. 2 refers to the equilibrium of the additive between the protein site and the aqueous solution, it is unequivocally linked to the composition of the membrane through Eq. 1. Thus, mechanistic details, including the question whether the additive accesses the receptor directly from the aqueous solution or from the membrane, are irrelevant for the following thermodynamic considerations.

For demonstration purposes, we assume simple 1:1 binding, but more complex models may apply. If, for instance, serum albumins or other carriers are used to solubilize the ligand, the model has to be expanded to explicitly account for the presence of the carrier–ligand complex in the aqueous phase. The same holds for other linked equilibria such as micelle formation or adsorption of the ligand to the walls of the measurement chamber, which can be treated implicitly by resorting to nominal rather than actual concentrations or, more satisfyingly, in an explicit manner using an appropriate model (3). However, such refinements needed in specific cases for experimental reasons would not change the general conclusions discussed below. In our simple model, mass conservation requires

$$c_{\text{A}}=c_{\text{A}}^{\text{aq}}+c_{\text{A}}^{\text{b}}+c_{\text{A}}^{\text{c}},$$ (3)

with c_A denoting the total concentration of ligand. Analogously, the total receptor concentration, c_R, comprises free and occupied populations:

$$c_{\text{R}}=c_{\text{R}}^{\text{f}}+c_{\text{A}}^{\text{c}}.$$ (4)

We have solved the system of Eqs. 1−4 to simulate the distribution of additive among the three states as a function of the total concentrations of additive, receptor, and lipid. An example is given in Fig. 1, which depicts the aqueous fraction of additive (blue) and the fractional occupancy of the receptor (red) as functions of the total additive concentration (top) or the membrane composition in terms of R_b (bottom). The figure illustrates three important facts:

• 1.When it comes to equilibrium binding, the membrane actually competes with the receptor for the ligand. Only for low lipid concentrations and weak partitioning (so that K_Pc_L ≪ 1) can the membrane-bound fraction of ligand be neglected. This results from the expression for the membrane-bound fraction (excluding protein-bound ligand) obtained by combining Eqs. 1 and 3 (see Heerklotz (2)):

$$\frac{c_{\text{A}}^{\text{b}}}{c_{\text{A}}^{\text{b}}+c_{\text{A}}^{\text{aq}}}=\frac{K_{\text{P}}{c}_{\text{L}}}{1+K_{\text{P}}{c}_{\text{L}}}.$$ (5)

• 2.The intrinsic, unequivocal abscissa for a protein binding or activation plot is either R_b (Fig. 1, bottom) or c_A^aq. By contrast, a curve given versus total ligand concentration, c_A, depends on the lipid concentration in the assay (Fig. 1, top) and, thus, is not unequivocal and virtually impossible to interpret quantitatively. Trivially, the same applies to additives such as surfactants (4) and peptides (5) that directly act on membranes without involving membrane proteins.
• 3.The membrane has very appropriately been called a catalyst for ligand binding to membrane proteins (for a review, see Vauquelin and Packeu (6)). As a catalyst, it does not change the affinity in terms of K_D. What it might change, however, is the kinetics of binding, which is crucial for response times in signaling or turnover of an enzyme. Note that micellization, serum albumins, or whatever else may help solubilize the ligand in solution (i.e., lowers its chemical potential) has the same effect as the membrane: it may speed up the kinetics of receptor binding but, thermodynamically, competes with the receptor for the ligand.

Figure 1.

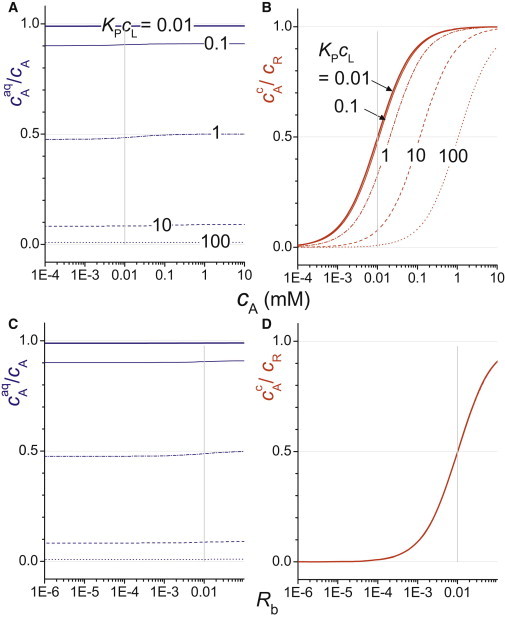
(A and C) Fraction of additive that is in aqueous solution, c_A^aq/c_A (blue), and (B and D) fractional occupancy of the receptor, c_A^c/c_R (red), as functions of the total ligand concentration, c_A (top), and the additive/lipid mole ratio in the membrane, R_b (bottom). Simulations were done for K_P = 1 mM⁻¹, K_D = 10 μM, c_R/c_L = 1:1000, and c_L = 0.01 mM (bold solid), 0.1 mM (thin solid), 1 mM (dash-dot), 10 mM (dashed), or 100 mM (dotted line).

A number of approaches have been developed to deal with these issues. In their binding assay of a ligand to a G-protein-coupled receptor, Seeman et al. (7) explicitly measured both c_A^aq and c_A^c and then modeled the unequivocal plot of c_A^c as a function of c_A^aq. Collins and Gordon (1) make use of the (in their case, very good) approximation that, owing to the low concentration of protein, the protein-bound fraction of ligand is negligible, c_A^c/c_A ≈ 0. Hence, K_P of the ligand to the membrane can be measured in the absence of receptor and may then be used to convert c_A to R_b, the proper abscissa, for the lipid concentration used in the receptor activation experiment. The simplest case is one in which both the receptor concentration (c_A^c/c_A ≈ 0) and the lipid concentration or partition coefficient (K_Pc_L ≪ 1) are low. If both of these conditions are fulfilled, one may assume that virtually all ligand is in solution, and the proper abscissa, c_A^aq, follows from the approximation c_A^aq ≈ c_A.

Let us, on a broader note, have a look into the mechanistic roles of the membrane during the activation of a protein or process by a ligand or, more generally, by a membrane-interacting additive. For the point of the argument, we consider two extreme scenarios, in which membrane partitioning of an additive and the response of the membrane system resemble either a serial or a parallel circuit. In the serial case, the response of the membrane system is a direct consequence of the insertion of the additive into the lipid bilayer, such that membrane partitioning is a prerequisite for the effect under study. In the parallel case, membrane partitioning is an alternative to and, thus, only competes with receptor binding or whatever else evokes the response of the membrane system.

The parallel scenario is applicable to ligands that are able to equilibrate with a high-affinity site on a membrane protein. The activation of TRPV1 by PIPs as discussed by Collins and Gordon (1) exemplifies this case, because PIPs directly bind to TRPV1 and thereby activate the channel. From a thermodynamic viewpoint, membrane partitioning of short-chain PIPs is not a prerequisite for TRPV1 activation, but it nevertheless manifests itself by changing the PIP concentration in the aqueous phase, c_A^aq. However, there is more to this than just correcting for the actual ligand concentration in solution. Water-soluble, short-chain PIPs are used in electrophysiological measurements as proxies of their physiologically relevant long-chain counterparts, whose solubility in aqueous solution is negligibly low. Thus, the latter will be found virtually exclusively in the membrane-bound state, and it is the membrane composition in terms of R_b or the mole fraction within the membrane, X^b = R_b/(1 + R_b), as used by Collins and Gordon (1) that represents the intrinsic, meaningful abscissa for an activation curve characterizing the interaction of PIPs with TRPV1. Unlike the total concentration, c_A, use of R_b enables a quantitative comparison of bilayer concentrations between short-chain PIPs under experimental conditions and long-chain PIPs in the plasma membrane. Similar considerations apply to other association reactions within membranes (8) or membrane-mimetic systems such as detergent micelles (9,10).

In the serial case, the activation of the membrane process is a direct consequence of the incorporation of the additive into the membrane. K_D is not important or not even defined. This is, for example, to be expected if a protein is activated by more or less random collisions of the membrane-bound additive with a low-affinity interaction site. Even without direct contact, additives may activate proteins by changing membrane properties such as mechanical tension, spontaneous curvature, thickness and order, electrostatic potential, etc. (11). Trivially, serial behavior will be found if a process is directly happening in the lipid bilayer. There is no such thing as a protein-bound state in the first place when a surfactant solubilizes a membrane (4), when an antibiotic peptide causes leakage (5), or when a curvature-active additive promotes or inhibits fusion intermediates. Note that serial, that is, bilayer-controlled behavior might also be found in measurements of protein activity rather than equilibrium binding if the rate-limiting step is the kinetics of a ligand to reach a binding site within or beyond the membrane (6). An example is transmembrane pumping of substrates by P-glycoprotein, which shows maximum turnover at a specific balance between K_P and K_D, as discussed by Li-Blatter et al. (12).

More than 100 years ago, Meyer (13) and Overton (14) came up with the classical example of separating the effects of partitioning and activation. They compared the active concentrations of a diverse set of general anesthetics to their oil–water partition coefficients. The very good correlation they found for many compounds implies either that the affinities of all these narcotics from the membrane to specific binding sites on membrane proteins are substantial yet virtually identical (which seems very unlikely) or that anesthesia is—in our words—a serial process to membrane partitioning. The latter interpretation is also supported by the fact that squeezing anesthetics out of the membrane (e.g., by high pressure) does not increase binding to the protein, as would be expected in the parallel scenario, but instead inhibits anesthesia. Part of the controversy seems to result from the misconception that a membrane-controlled process excludes, a priori, direct and to some degree specific interactions of the membrane constituents with proteins.

A similar correlation of biological activity with partitioning has also been found by Ingólfsson and Andersen (11) for amphiphilic additives activating gramicidin channels. They explained this serial effect convincingly by additive-induced alterations of the mechanical properties of the membrane. Stay tuned for an impressive study of the effects of anaesthetics on the critical behaviour of cell membranes by Veatch and coworkers (15) in an upcoming issue of the Biophysical Journal. These authors considered partitioning implicitly (yet elegantly) by correlating the thermodynamic effects with biological function.

In summary, whenever the effect of an additive on a membrane system is concerned, one needs to consider its membrane partitioning—irrespective of whether the additive exerts its effect by changing generic membrane properties or binds specifically to a protein. Even in the latter case, one may neglect the bilayer-bound fraction of additive only if K_Pc_L ≪ 1. Whenever this condition is not met, activation curves should be presented as a function of membrane composition or the actual composition of the aqueous phase after correction for membrane partitioning. Collins and Gordon (1) show in detail how to do this for the case of water-soluble, short-chain PIPs, and they exemplify the drastic consequences this may have for the interpretation of ligand binding studies performed in the presence of a membrane system.