An Explicit Formulation Approach for the Analysis of Calcium Binding to EF-Hand Proteins Using Isothermal Titration Calorimetry

Abstract

We present an improved and extended version of a recently proposed mathematical approach for modeling isotherms of ligand-to-macromolecule binding from isothermal titration calorimetry. Our approach uses ordinary differential equations, solved implicitly and numerically as initial value problems, to provide a quantitative description of the fraction bound of each competing member of a complex mixture of macromolecules from the basis of general binding polynomials. This approach greatly simplifies the formulation of complex binding models. In addition to our generalized, model-free approach, we have introduced a mathematical treatment for the case where ligand is present before the onset of the titration, essential for data analysis when complete removal of the binding partner may disrupt the structural and functional characteristics of the macromolecule. Demonstration programs playable on a freely available software platform are provided. Our method is experimentally validated with classic calcium (Ca²⁺) ion-selective potentiometry and isotherms of Ca²⁺ binding to a mixture of chelators with and without residual ligand present in the reaction vessel. Finally, we simulate and compare experimental data fits for the binding isotherms of Ca²⁺ binding to its canonical binding site (EF-hand domain) of polycystin 2, a Ca²⁺-dependent channel with relevance to polycystic kidney disease.

Introduction

Advances in calorimetric techniques have made isothermal titration calorimetry (ITC) a practical tool in the biophysical laboratory, providing the means for the determination of thermodynamic parameters essential for the elucidation of complex biological processes. The experiment is conducted through the direct measurement of heat released or absorbed during an isothermal titration of a ligand into a solution containing its ligand-binding partner. The utility of this technique is inextricably linked to the experimental design and subsequent data fitting, typically achieved with instrument-bundled commercial software. The mathematical approach employed there is generally inadequate and counterintuitive for modeling higher-order interactions involving multiple interacting species, thus limiting the application of this robust technique in solving the intricate problems typically associated with the function of biological networks.

Traditionally, ITC data have been analyzed using an integrative approach, where the heat from each injection is calculated from the difference in the total heat of the system before and after each injection (1–3), and the data-fitting algorithms based on implementations of the so-called Wiseman isotherm (Wiseman et al. (4), Fisher and Singh (5), and Indyk and Fisher (6)). However, recently, the use of ordinary differential equations (ODEs) has been described as a more natural mathematical basis for modeling isotherms, because the technique is inherently differential in nature (7). The advantages of this alternative approach are multifold:

• 1.It greatly simplifies the binding model, because differentiation lowers polynomial order.
• 2.The integrative approach violates an important principle of nonlinear least-squares fitting: the independence of residuals. With the integrative approach, the error associated with each injection contributes to that of its predecessor, violating this principle of independence. The differential approach considers only the heat associated with each single injection, thus avoiding this complication.
• 3.Both analytical and numerical methods for solving ODEs are well developed and easily implemented.

In this work, we provide improvements to the original proposal to analyze ITC results using ODEs:

• 1.We demonstrate how the inevitable dilution of the reaction cell with each stepwise injection of titrant can be explicitly considered in the ODEs for direct comparison to experimentally derived isotherms.
• 2.We develop a general method for incorporating binding polynomials, as originally described by Robert et al. (8), Gill et al. (9), and Gill (10), into the ODEs.

Equivalent to the partition function used in statistical thermodynamics, the binding polynomial provides a straightforward and easily constructed listing of all the states present in a molecular system in terms of their relative populations. Differential equations describing the change in bound ligand due to each injection are easily derived and incorporated into the expression for measured heat. With a complete description of the state of each molecular component in a system, biophysical models can be further validated through global analysis using measurements from complementary techniques such as NMR or fluorescence spectroscopy. Implementation using the familiar MATHEMATICA software package (Wolfram Research, Champaign, IL) equips the user with a convenient and flexible platform for data visualization, providing starting values for minimization routines when working with complex models.

We apply these techniques to address a common experimental problem when analyzing ion binding by titration calorimetry: the presence of ligand at the onset of the experiment that is not easily quantified by traditional analytical techniques. This can occur when a recombinantly expressed protein binds an endogenous ligand that is retained during the purification protocol or when ligand is added intentionally as part of a strategy to prevent irreversible aggregation or sample degradation. Without accurate quantification of the residual ligand, extraction of the correct thermodynamic parameters from a single isotherm is difficult owing to the interdependence of stoichiometry of binding, ligand and macromolecule concentration, and binding affinities. This is especially true when the binding isotherm is lacking a sigmoidal or similar feature that provides a boundary to define the thermodynamic parameters during data-fitting minimization routines. Here, the concentration of residual ligand and/or macromolecule concentration is experimentally restrained by the addition of a second, well-characterized binding partner to the reaction cell (11,12). We demonstrate this approach in both a model system with multiple Ca²⁺ binding partners and in a recently studied Ca²⁺-binding EF-hand domain of polycystin-2 (13,14).

Most cases of autosomal dominant polycystic kidney disease are caused by mutations in the pkd1 or pkd2 genes, which encode the membrane proteins polycystin-1 (PC1) and polycystin-2 (PC2), and are characterized by life-threatening fluid filled renal cysts (15). The channel activity of PC2 is regulated in part through its cytoplasmic portion (PC2-C), which has been shown to be comprised of an EF-hand domain, a flexible linker region, and a coiled-coil, which promotes oligomerization as an essential part of channel formation (13). The channel activity of PC2 is gated by changes in cytoplasmic Ca²⁺ levels, yet the precise relationship between Ca²⁺ binding and the molecular rearrangement responsible for ion-channel gating has not been fully elucidated (16). The cytoplasmic portion of PC2 binds Ca²⁺ at multiple sites, albeit with different affinities, suggesting a possible cooperativity between Ca²⁺ binding sites of PC2-C (13). Here we reexamine the Ca²⁺ binding properties of the EF-hand motif of PC2 (hPC2-EF), proposed to have a single weak Ca²⁺ binding site, and compare it to that of an ortholog, Sea Urchin PC2 EF-hand domain (suPC2-EF). Like its human ortholog, Sea Urchin PC2 (suPC2) is an integral transmembrane protein with six transmembrane segments and cytoplasmic EF-hand and coiled-coil domain. Sea Urchin PC2 is, however, found exclusively at the plasma membrane of the sperm acrosomal vesicle, implying a role in the sperm acrosomal reaction (17) or as part of the Ca²⁺ gradient detection mechanism of chemotaxis (18,19). In this study, the Ca²⁺ binding of suPC2-EF and hPC2-EF are determined using isothermal titration calorimetry in the presence of competing Ca²⁺ chelators as part of a process to address challenges (20,21) in the quantitative determination of ligand binding in these and similarly behaving biomolecules. This approach will ultimately aid in our understanding of the relationship between channel function and Ca²⁺ binding.

Our mathematical treatment of the ITC data is experimentally validated through simulations of a series of Ca²⁺ binding isotherms of samples composed of combinations of well-characterized Ca²⁺ chelators and known additions of ligand. Ion-binding chelators based on derivatives of BAPTA (1,2-Bis(o-aminophenoxy)ethane-n,n,n′,n′-tetraacetic acid) were developed decades ago as Ca²⁺-sensitive fluorescent indicators and for buffering Ca²⁺ in aqueous solution in the micromolar to nanomolar range (22). The Ca²⁺ affinities of BAPTA and its derivatives range roughly from 100 nM to 100 μM, with the exception of 5,5′ dinitroBAPTA, which has an unusually weak Ca²⁺ affinity of ∼20 mM (23). Unlike EDTA, the apparent Ca²⁺ affinity (K′_Ca) of BAPTA and BAPTA derivatives is generally insensitive to changes in pH in the physiological range and shows greater sensitivity to changes in solution ionic strength when compared to the common chelators EDTA and EGTA (24,25). Our validation experiments were conducted with the high-affinity and commercially available Ca²⁺ chelators 5,5′dimethylBAPTA and EDTA, which bind Ca²⁺ strongly enough to effectively compete with many Ca²⁺ binding proteins.

Materials and Methods

Materials

Buffers for all ITC and matching Ca²⁺-sensitive electrode measurements were prepared from commercially available low-Ca²⁺ 4 M KCl stock (Orion Calcium ISA Cat. No. 932011; Thermo Scientific, Waltham, MA) and 0.1 M Ca²⁺ standard (Orion Calcium Standard Cat. No. 922006; Thermo Scientific). The typical buffer composition was 25 mM TRIS (AB02000; American Bioanalytical, Natick, MA) or HEPES (Cat. No. H9034; Sigma, St. Louis, MO), 150 mM KCl, prepared and pH-adjusted to 7.40 using a calibrated handheld Accumet AP61 pH meter and combination Accumet pH electrode AP50 (Fisher Scientific, Pittsburgh, PA). Calcium chelator stocks were prepared in buffer from 5,5′-dimethyl-BAPTA (5,5′ dimethyl-1,2-bis(o-aminophenoxy)ethane-n,n,n′,n′-tetraacetic acid) (Cat. No. 50008; Biotium, Hayward, CA) or EDTA (Cat. No. E6758; Sigma).

Protein expression and purification

The EF-hand containing domain (Asn⁷²⁰-Pro⁷⁹⁷) of Human PC2 (hPC2-EF) was PCR-amplified from Human PC2 cDNA (obtained from S. Somlo, Yale University, New Haven, CT) cloned into pET-28a vector (EMD Millipore, Billerica, MA) with an N-terminal His tag, and transformed into BL21(DE3) CodonPlus RIL (Agilent Technologies, Santa Clara, CA) for bacterial expression. Similarly, the EF-hand domain of Sea Urchin PC2 (Gly⁶⁵⁰-Glu⁷³⁸) was PCR-amplified from a Sea Urchin cDNA library (gift of Dr. V. Vacquier, University of California at San Diego, La Jolla, CA). Site-directed mutagenesis (QuikChange Kit; Agilent Technologies) was used to generate -X-Z mutations on the first of two purported calcium-binding sites (D678A and E681A or D52A and E55A using the construct numbering used herein). Uniform ¹⁵N protein was prepared and purified as described in Petri et al. (14). Protein-containing chromatographic fractions were further purified by gel filtration chromatography in ITC buffer 25 mM TRIS, 150 mM KCl with 1 mM TCEP with a Superdex 75 HR 10/30 column (GE Healthcare Biosciences, Pittsburgh, PA). Protein concentrations were determined by amino-acid analysis, provided by the Keck Biotechnology Resource Laboratory at the Yale School of Medicine (New Haven, CT) employing a Hitachi L-8900 PH amino-acid analyzer (Hitachi High Technologies America, North Brunswick, NJ).

Ca²⁺ electrode measurements

Calcium-selective electrode measurements were conducted using an Orion Half-Cell Electrode with matching Ca²⁺-specific module (Cat. Nos. 9300BN and 9720BN; Thermo Scientific), Orion Reference Electrode filled with Ag/AgCl reference electrode solution (Cat. Nos. 900100 and 900011; Thermo Scientific), and an Orion 4-Star Benchtop pH/ISE Meter (Thermo Scientific). All sample readings were conducted at 25°C in an insulated polyethylene sample container with stirring and with the ionic strength adjusted to ∼0.155 M for TRIS-containing samples by making slight adjustments to the concentration of KCl in each sample. Fresh stocks of 5,5′-dimethylBAPTA and EDTA at concentrations between 1 and 5 mM were prepared in 25 mM TRIS or HEPES, 150 mM KCl and pH-adjusted with KOH to 7.4 and typically used within a week of ITC and Ca²⁺ electrode measurements.

Electrode calibration standards with 10, 1.0, and 0.10 mM Ca²⁺ were prepared from 0.1 M Ca²⁺ standard stock and buffer using analytical glassware and were subsequently used to prepare a series of chelator samples, each with identical concentrations of individual chelator. The ratio of added Ca²⁺ to chelator concentration were chosen specifically to give electrode readings that fall within the linear performance range of the half-cell electrode combination. Calibration readings were taken on the standard solutions before and after a series of measurements for a particular chelator formulation, with the averaged calibration values used to determine p_Ca of the samples with chelator and used to produce a Scatchard plot for each of the chelators examined. The linear portion of the potentiometric data was used to estimate K′_Ca and extrapolated to the x axis for an estimate of the chelator purity. Samples falling within the linear performance range of the Ca²⁺-selective electrode were then directly analyzed by ITC, with the exception of the chelator samples with no added Ca²⁺ that fell outside that range, for the purpose of modeling their Ca²⁺-free state.

ITC measurements

All calorimetry experiments were conducted on a MicroCal VP-ITC isothermal titration calorimeter (GE Healthcare Life Sciences). Samples were degassed before each experiment. The first injection for each calorimetry experiment was 2 μL and discarded from the dataset with the remaining injection volumes typically 5 or 8 μL. Background heat from dilution of ligand was measured by conducting a titration of ligand into buffer alone. A function for the heat of dilution was generated from the background titration and subsequently subtracted from the raw ITC-derived calorimetry data so as to avoid adding additional noise to the background-corrected ITC data. All baseline corrections were conducted using the software ORIGIN 7.0 (OriginLab, Northampton, MA) with the MICROCAL ITC add-on program provided by the manufacturer (GE Healthcare Life Sciences). Data was exported as comma-delimited ASCII text from the MICROCAL program before being introduced to the analysis in the MATHEMATICA scripts presented herein (MATHEMATICA; Wolfram Research, Champaign, IL).

NMR experiments

All NMR experiments were conducted as described in Petri et al. (14). The two-dimensional ¹H-¹⁵N HSQC experiments were conducted on ¹⁵N uniformly labeled 1.0 mM suPC2-EF-x-z1 or 800 μM suPC2-EF samples in pH 7.4, 25 mM TRIS, 150 mM KC1, 1 mM TCEP and saturating 10–20 mM Ca²⁺ with 5% (v/v) D₂O and 5 mM sodium azide added as a preservative. All NMR spectra were processed using the NMRPIPE (26) software package (BAX Group, National Institutes of Health, Bethesda, MD), with subsequent display and analysis done using the SPARKY (27) program (University of California at San Francisco, La Jolla, CA). Proton chemical shifts were referenced indirectly to 3-(trimethylsilyl)propionic-2,2,3,3-d4 acid at ¹H 0.00 ppm, with indirect dimensions referenced based on their relative gyromagnetic ratios.

Derivation of general differential expressions for molar enthalpy of binding

A general method for the introduction of binding polynomials for defining dX/dL_t, as originally described by Gill et al. (9), is shown in the Supporting Material. We prefer using the site-specific formulation described by Di Cera (28), where molar enthalpy is defined for each individual binding site as would be appropriate for binding in multicomponent reactions. A derivation of the differential expressions to describe the enthalpy of binding for a complex mixture of competing macromolecules as function of total ligand, with a portion of the ligand present and in equilibrium before the onset of the experiment, is described for direct comparison to experimentally derived isotherms. The general expression used to describe the heat per mole of injected titrant in the case where residual ligand is present at the onset is described by

$$NDH=M_0\frac{L_0-L_R}{L_0}{\left(\frac{L_t-L_0}{L_R-L_0}\right)}^2\left(1+\frac{V_{\text{inj}}}{2V_0}\right)\sum _n\text{Δ}{H}_n^{°}\frac{d{X}_n}{d{L}_t},$$

where L₀, L_t, and L_R represent the concentration of ligand as titrant, total concentration, and amount residually present, respectively; V_inj and V₀ represent the injection and cell volume; and M₀ is the macromolecule concentration. In this implementation, L_t is conveniently provided by the bundled ITC software; however, an equivalently derived dilution term could be used as shown in the Supporting Material. For the case where our system can be adequately described by a macromolecule M and competing chelator B, both containing a single class of N-binding sites for the ligand L, we define the relevant binding polynomials by

$$Z_M={\left(1+K_M{L}_f\right)}^{N_M},$$

$$Z_B={\left(1+K_B{L}_f\right)}^{N_B},$$

where L_f represents free ligand. After expressing the polynomials in terms of fraction bound and total ligand, the following are obtained:

$$\frac{d{X}_M}{d{L}_t}=\frac{N_M{K}_M\left(L_0-L_R\right)\left(L_0-L_R+B_0{X}_B+M_0{X}_M-\left(L_0-L_t\right)\left(B_0\raisebox{1ex}{$d{X}_B$}\!\left/ \!\raisebox{-1ex}{$d{L}_t$}\right.+M_0\raisebox{1ex}{$d{X}_M$}\!\left/ \!\raisebox{-1ex}{$d{L}_t$}\right.\right)\right)}{{\left(\left(L_0-L_R\right)\left(1+K_M{L}_t\right)-K_M\left(L_0-L_t\right)\left(B_0{X}_B+M_0{X}_M\right)\right)}^2},$$

$$\frac{d{X}_B}{d{L}_t}=\frac{N_B{K}_B\left(L_0-L_R\right)\left(L_0-L_R+B_0{X}_B+M_0{X}_M-\left(L_0-L_t\right)\left(B_0\raisebox{1ex}{$d{X}_B$}\!\left/ \!\raisebox{-1ex}{$d{L}_t$}\right.+M_0\raisebox{1ex}{$d{X}_M$}\!\left/ \!\raisebox{-1ex}{$d{L}_t$}\right.\right)\right)}{{\left(\left(L_0-L_R\right)\left(1+K_B{L}_t\right)-K_B\left(L_0-L_t\right)\left(B_0{X}_B+M_0{X}_M\right)\right)}^2}.$$

The equations above represent a system of implicit, coupled, ordinary differential equations (ODEs). Instead of seeking an analytical solution, which is likely not possible, we utilize the numerical differential equation solver (NDSOLVE; Wolfram Research) employing the iterative method of Runge-Kutta in the software MATHEMATICA to derive numerical solutions for ITC data based on the above model. Computer-aided data fitting is achieved with built-in minimization routines typically employing the Principal Axis Method of Brent, and subsequent confidence intervals derived from the critical value of the F distribution for a p-value of 0.05. Minimization routines are often best guided by an initial estimate of parameters, which can be obtained by visually examining the dependence of individual parameters on the simulated isotherms.

Binding stoichiometry, purity, and residual ligand

In the customary manner to modeling ligand binding in commercial ITC software, the N parameter incorporates both the binding stoichiometry and, be it from residually bound ligand or structurally nonfunctional sites, the incompetent fraction of the macromolecule. This approach fails to recognize the analytically relevant distinction between chemically unavailable ligand binding sites and occupied, but otherwise in equilibrium, binding sites at the onset of a titration, which can result in incorrect macromolecule concentrations being used in data simulations and a poor interpretation of results. The impact of ignoring residual ligand in computed ITC-derived thermodynamic parameters is significant, with residual ligand concentrations of at least a few percent of the total macromolecule concentration. Under stoichiometric binding conditions, loosely defined as the condition where the product of the binding constant and macromolecule concentration (M₀K) is large and typically >100, and the concentration of residual ligand is significantly less than that of the macromolecule, the ITC-derived macromolecule purity and binding constant will be scaled lower and weaker than their true values by a factor equal to the ratio of free macromolecule relative to total macromolecule at the onset of the titration. Under these sample conditions, it is still possible to obtain an accurate molar enthalpy of binding.

Under the binding conditions where M₀K is small, typically 1–100, the presence of residual ligand would offset the isotherm, potentially obscuring features directly related to the binding model and impact the accuracy of all ITC-derived thermodynamic parameters using the traditional software approach. The degree of inaccuracy is dependent upon many factors in this case, including sample composition, experimental approach, and the employed data-fitting technique. For these reasons, protein macromolecules with nanomolar affinity for common ions present a particular challenge when analyzed using the traditional software approach.

With the addition of an excess of a thermodynamically well-defined competing macromolecule, it becomes possible to statistically distinguish chemically unavailable sites from those with residually bound ligand at the start of a titration because residual ligand has moved to the competing macromolecule at the start of the experiment. Moreover, it becomes necessary to incorporate this distinction in the initial state of macromolecular binding sites when using ITC data as part of a global data-fitting routine, because NMR and other biophysical techniques can provide complementary quantitative structural and functional information. Based on our a priori understanding of the macromolecules studied in this article, we restrict the stoichiometry parameter to integer values and vary the purity and residual ligand parameters during fitting, guided by independent potentiometric measurements.

Other global data and multisite binding ITC programs such as SEDPHAT (http://www.analyticalultracentrifugation.com/sedphat/sedphat.htm), albeit not based on the ODE approach, have incorporated this distinction of parameters in their model formalism (1,29). The quality of the thermodynamic parameters from ITC is directly dependent upon the accurate quantitation of the macromolecule and ligand concentrations. Amino-acid analysis, which is well established as a robust and reproducible method for determining protein concentrations (30), was used for macromolecule quantification in this study owing to a lack of strong UV-absorbing residues in the hPC2-EF protein structure and irreproducible dye-binding properties (C. Keeler, Yale, 2013 unpublished results).

Results

Method validation and comparison to traditional ITC data fitting

The isothermal titration calorimetry of 2.3 mM Ca²⁺ binding to a solution of 1.463 mM EDTA with 1.106 mM residual Ca²⁺ in 25 mM TRIS and 150 mM KCl buffer at pH 7.4 and 25°C is presented in Fig. 1 a. The corresponding baseline-corrected isotherm was fitted using the ODE-based approach with a single binding-site model incorporating a purity and residual ligand parameter (Fig. 1 b). Incorporation of the residual ligand parameter, fixed to 1.106 mM, in the ODE-based model best fits the experimental data with confidence intervals via an F test to a Ca²⁺ affinity of 48.3 nM (95% confidence interval (CI), 46.6–50.0), a purity of 98.5% (95% CI, 98.48–98.51) for the macromolecule, and a favorable enthalpic contribution (ΔH = −12.8 kcal/mol, 95% CI, −12.81 to −12.78). These values match favorably to the potentiometric-based Ca²⁺ binding estimates of a 55.4 nM affinity and purity of 100.3% measured in TRIS buffer (see the Supporting Material). The ODE approach and ORIGIN software analysis report similar and erroneous calcium affinities (207 vs. 188 nM, respectively) and report near-identical stoichiometries (0.230 vs. 0.233, respectively) when residual ligand is not considered in the single binding-site model, which reflects the incorrect presumption of the macromolecule concentration in solution. The ODE-based approach and analytical methodology is further validated through the simultaneous fitting of experimental isotherms of Ca²⁺ binding to the chelator solutions used in the potentiometric measurements, and are shown in the Supporting Material. The best-fit and fixed parameters for each fit are listed in Table 1 along with F-test confidence intervals for parameters allowed to float during minimizations.

Figure 1.

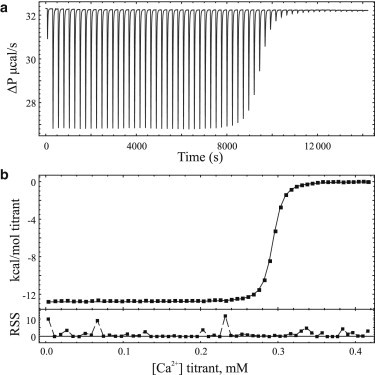
(a) Baseline-corrected titration calorimetry of 5 μL injections of 2.3 mM calcium binding to a solution of 1.463 mM EDTA chelator in pH 7.4, 25 mM TRIS, 150 mM KCl buffer at 25°C with 1.106 mM of added calcium. (b) Fitted isotherm of panel a, using the fitted parameters from the ODE implementation of a single-site binding model with a 1.106-mM residual ligand and purity term. Residual sum-of-squares (RSS; cal/mol) are shown below the fitted isotherm.

Table 1.

Parameters used in simultaneous sum-of-squares best fit of isotherms for a series of separately prepared 5,5′ dimethylBAPTA and EDTA solutions in TRIS buffer with residual calcium present

Sample	Residuala Ca2+ (μM)	Purityb (%)	K′Ca2+ (nM)	ΔH (cal/mol)
5,5′ dimethylBAPTA
0c	0	59.10 (59.05–59.20)d	105e	2155.7 (2148.0–2163.5)
1	563	68.75 (68.67–68.84)
3	663
6	847
EDTA
8	42	97.39 (97.35–97.42)	62.3 (59.0–65.1)	−12,814.3 (−12,785–12,843)
9	975
12	1105

^aAdded Ca²⁺ derived from analytical preparation, with small adjustments made for goodness-of-fit.

^bAn additional 3.5% (95% CI, 3.23–3.79) of the 5,5′ dimethylBAPTA macromolecule described in the simulation is dedicated to a second single-binding site chelator with weak Ca²⁺ affinity (13.1 μM, (95% CI, 9.95–17.85)) and enthalpy of 479 cal/mol to represent an apparent impurity (see the Supporting Material).

^cSample prepared independently without analytical glassware.

^dCa²⁺ apparent dissociation constant derived from potentiometric data analysis.

^eParentheses indicate 95% confidence intervals for floating parameters, computed from sum-of-squares best fit values; they do not reflect propagated experimental errors.

Residual ligand in model system of Ca²⁺-binding chelators

We tested the suitability of our mathematical methods to describe the thermodynamics of binding ligand to multicomponent mixtures of macromolecules and ligand, through comparison of simulated isotherms to experimental isotherms of Ca²⁺ binding to a model system of a mixture of Ca²⁺ chelators. Isotherms of 2.5 mM Ca²⁺ titrated against 589.4 μM EDTA and 1.130 mM 5,5′-dimethylBAPTA, both individually and as a 50:50 v/v mixture with residual ligand present, are shown with ODE-based best-fit simulated isotherms depicted as overlaid traces (Fig. 2 a). All ITC and matching potentiometric experiments for these samples were conducted under identical buffer conditions of 25 mM HEPES at pH 7.4 with 150 mM KCl and at 25°C. Parameters used to generate the simulated isotherms in Fig. 2 a are listed in Table 2 with the Ca²⁺ affinity parameters from potentiometric measurements in HEPES buffer, the residual ligand parameters from the analytical preparation, and the remainder from best-fit data simulations. Simulated isotherms for the EDTA chelator were generated assuming a single, independent Ca²⁺ binding site, whereas the binding behavior of 5,5′-dimethylBAPTA was simulated as described in the Supporting Material. Matching simulations for each sample showing the fraction of macromolecule bound are depicted in Fig. 2, b and c, for 5,5′-dimethylBAPTA and EDTA, respectively.

Figure 2.

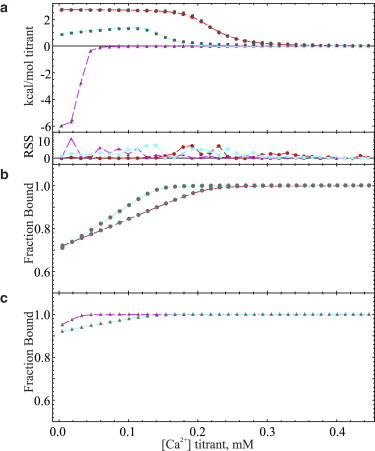
(a) Baseline-corrected titration isotherms (solid symbols) and ODE-based simulations (traces) of calcium binding to solutions of 1.131 mM 5,5′-dimethylBAPTA and 564.7 μM of added Ca²⁺ (solid gray circles with red traces,) 589.4 μM EDTA and 541.2 μM of added Ca²⁺ (solid triangles with magenta traces,) and a 50/50 v/v mixture of each chelator solution with 553 μM of added Ca²⁺ (solid gray squares and cyan traces.) All titration isotherms were conducted in pH 7.4, 25 mM HEPES, 150 mM KCl buffer at 25°C with 8 μL injections of 2.5 mM Ca²⁺ as titrant. Calculated fraction of macromolecule bound versus added Ca²⁺ titrant for (b) 5,5′-dimethylBAPTA-containing samples and (c) EDTA-containing samples using parameters derived from fitted isotherms and denoted by associated symbol shapes and trace color. All fitted isotherms were generated and manually fit using the ordinary differential equation (ODE) approach and a single binding site (EDTA) or a single binding site with a fraction (4.9%) dedicated to a second binding site to represent impurities (5,5′-dimethylBAPTA) and separate parameters to describe residual ligand, macromolecule purity, binding enthalpy, and affinity. A correction of 2.4% was applied to the total macromolecular concentration in the simulation for the sample representing the 50:50 v/v mixture to account for an apparent offset in the independent axis, albeit minor, of the simulated data from the experimental isotherm.

Table 2.

Parameters used in simultaneous fit of isotherms of a series of chelator containing solutions in HEPES buffer with residual ligand present

Sample	Residuala Ca2+ (μM)	Purity (%)	K′Ca2+b (μM)	ΔH(cal/mol)
5,5′ dimethylBAPTAc
16	564.7	69.8	0.129	2723
Mixd	553	69.8	0.129	2723
EDTA
23	541.2	97.1	0.0269	−6075
Mixd	553	97.1	0.0269	−6075

^aAdded Ca²⁺ derived from analytical preparation.

^bCa²⁺ apparent dissociation constant for 5,5′-dimethylBAPTA and EDTA from potentiometric data analysis.

^cA (4.9%) percentage of the macromolecule described in the simulation is dedicated to a second chelator with a weak Ca²⁺ affinity of 18 μM and enthalpy of 1217.8 cal/mol to represent an apparent impurity (see the Supporting Material).

^dSample is a 50:50 v/v mixture of samples 16 and 23.

Careful pH measurements before and after potentiometric and calorimetric experiments showed adequate buffering capacity in our choice of buffers with the exception of the TRIS-based buffer EDTA experiments, where the pH after a Ca²⁺ titration could change by a few tenths of a unit owing to the proton release from EDTA upon Ca²⁺ binding and inadequate buffering capacity under the reported buffer conditions. The 5,5′-dimethylBAPTA does not release a proton upon Ca²⁺ binding at pH 7.4, and hence is not expected to contribute to a solution pH change when reacting with ligand. This makes BAPTA-based chelators more appropriate for certain experimental titrations where pH stability is needed over the course of a titration and conversely, a stable and strong Ca²⁺ affinity over a physiologically relevant pH range. We found that 25 mM HEPES buffer, with a larger buffer capacity at pH 7.4, could sufficiently buffer our EDTA-containing solutions during the Ca²⁺ titrations presented herein. The HEPES buffer has a different ionic strength at pH 7.4 compared to an equimolar TRIS buffer, which may explain the slightly weaker Ca²⁺ affinity for 5,5′-dimethylBAPTA measured in the HEPES buffer (129 vs. 106 nM, respectively) and the differences in Ca²⁺ binding enthalpy observed (2.73 kcal/mol in HEPES vs. 2.16 kcal/mol in TRIS buffer). Similarly for EDTA, the differences in ionic strength and pH stability of TRIS and HEPES buffer likely explain the differences in observed potentiometric-derived Ca²⁺ affinities (55 vs. 26 nM, respectively) while the large difference in ITC-derived enthalpies for Ca²⁺ binding to EDTA in the two buffer systems is primarily due to the different protonation enthalpies for TRIS and HEPES (31).

Ca²⁺ binding to hPC2-EF and suPC2-EF-x-z1 protein with and without 5,5′-dimethylBAPTA chelator

Two site-specific mutations were made in the wild-type suPC2-EF protein construct to disable Ca²⁺ binding at the N-terminal Ca²⁺ binding site. Calcium-coordinating residues in the wild-type construct were predicted based on the sequence alignment with calmodulin and other PC2 proteins, and were mutated in the –x (Asp⁵² to Ala) and –z (Glu⁵⁵ to Ala) positions, guided by previous observations with hPC2-EF where similar mutations were found to disrupt Ca²⁺ binding (13,14). Fig. 3 a shows the sequence alignment of hPC2-EF with the wild-type suPC2-EF and the ortholog suPC2-EF-x-z1, and the relative positions of the helices from the previously reported structure of hPC2-EF (14). The hPC2-EF protein is susceptible to degradation and hence the tertiary structure of the ¹⁵N hPC2-EF protein was confirmed through comparison of a two-dimensional ¹H-¹⁵N HSQC NMR spectrum to previously published data before the start of the ITC experiment. All ITC and matching NMR experiments were conducted in pH 7.4, 25 mM TRIS, 150 mM KCl buffer with 1 mM TCEP as a reducing agent. The addition of TCEP as a reducing agent was necessary to maintain monomeric protein, but did not appear to affect potentiometric measurements when added as a properly buffered stock (C. Keeler, Yale, 2013, unpublished results). Presented in Fig. 3 b are overlaid ¹H-¹⁵N HSQC NMR spectra of the ¹⁵N hPC2-EF, ¹⁵N suPC2-EF-x-z1, and ¹⁵N suPC2-EF (wild-type) proteins in pH 7.4 TRIS buffer with 10 mM Ca²⁺. The spectra show all three proteins to be nominally pure and demonstrate the chemical-shift dispersion consistent with functional, folded protein. The spectrum of the mutant ¹⁵N suPC2-EF-x-z1 protein shows resonant peak shifts primarily at high ¹H chemical shifts (9–10.6 ppm) relative to the wild-type spectrum. This observation is consistent with mutations made to the Ca²⁺ coordinating residues, because these residues tend to have relatively large ¹H shifts, with a dispersion consistent with maintenance of α-helical secondary structure.

Figure 3.

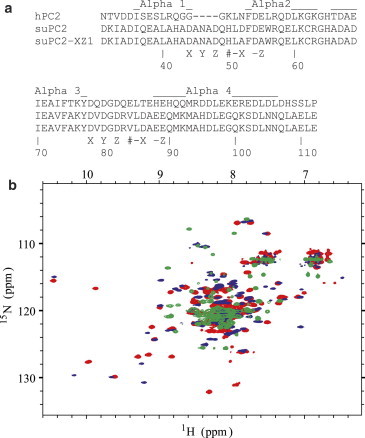
(a) Sequence alignment of Human and Sea Urchin PC2-EF and the suPC2-EF-z-x1 mutant. Relative positions of the structural helices for hPC2-EF are shown above the aligned sequences, with the numbering for the suPC2-EF-x-z1 construct shown at the bottom of the alignment. Sea Urchin constructs are preceded by the N-terminal His-tag sequence MGSSHHHHHHSSGLVPRGSHMASGKINFKR and the Human construct by MGSSHHHHHHSSGLVPRGSHM. (b) Overlaid two-dimensional ¹H-¹⁵N HSQC NMR spectra of calcium-saturated ¹⁵N hPC2-EF (green traces), ¹⁵N suPC2-EF (red traces), and ¹⁵N suPC2-EF-x-z1 (blue traces) proteins in pH 7.4, 25 mM TRIS, 150 mM KCl buffer with 1 mM TCEP and 10 mM Ca²⁺ at 25°C.

The ITC titrations at 25°C for 20 mM Ca²⁺ binding to 97 μM hPC2-EF protein with and without 350 μM of 5,5′-dimethylBAPTA chelator present in pH 7.4, 25 mM TRIS, 150 mM KCl with 1 mM TCEP is depicted in Fig. 4 a. The corresponding baseline-corrected isotherm and chelator-free equivalent is shown in Fig. 4 b, along with their simultaneously fitted synthetic isotherms using sum-of-squared minimized parameters for residual ligand, affinity, and enthalpy of binding. The computed fraction of ligand-bound protein as a function of the titration progress for each sample is presented in Fig. 4 c. Similarly presented data for 1 mM Ca²⁺ binding to 5.8 μM suPC2-EF-x-z1 protein in the same buffer system with 65 μM of 5,5′-dimethylBAPTA chelator present is depicted in Fig. 5, a–c. The fitted parameters and confidence intervals (p value of 0.05) presented in Table 3 were determined assuming a single binding site for the 5,5′-dimethylBAPTA for the sake of computational efficiency, and a single Ca²⁺ binding site for the hPC2-EF or suPC2-EF-x-z1 protein. The fixed thermodynamic parameters for the chelator were chosen based on the potentiometric results and the previous chelator ITC results, with small adjustments made for goodness-of-fit. The calculated fractions of protein bound are shown in Figs. 4 c and 5 c for hPC2-EF and suPC2-EF-x-z1, respectively, and show a strong correlation between Ca²⁺ affinity and bound ligand at the onset of the titration. Alternate fitting results assuming no residual ligand and without a fixed purity term are presented in the Supporting Material.

Figure 4.

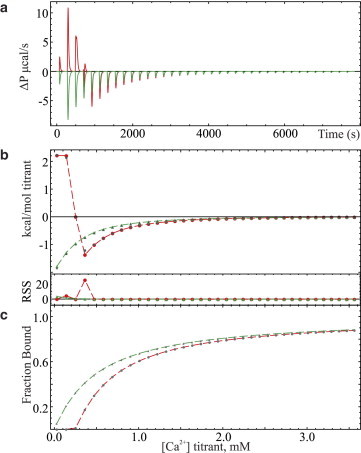
(a) Raw titration calorimetry data of calcium binding to 97 μM hPC2-EF protein with 350 μM 5,5′-dimethylBAPTA (red traces) and without chelator (green traces) in pH 7.4, 25 mM TRIS, 150 mM KCl buffer with 1 mM TCEP at 25°C using 8-μL injections of 20 mM Ca²⁺. (b) Simultaneously fitted, baseline-corrected isotherms of (a) with chelator (red traces) and without chelator (green traces) and with residual sum-of-squares (RSS) error in fitting depicted at the base of the panel. (c) Calculated fraction of ¹⁵N hPC2-EF protein bound to titrant in each sample.

Figure 5.

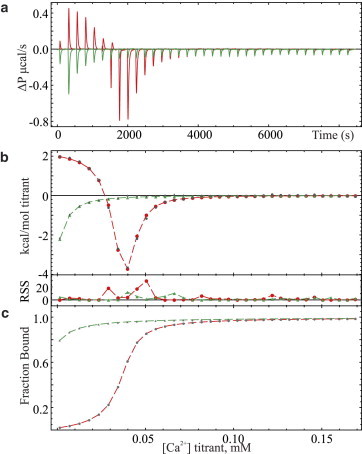
(a) Raw titration calorimetry data of calcium binding to 5.8 μM suPC2-EF-x-z1 protein with 65 μM 5,5′-dimethylBAPTA (red traces) and without chelator (green traces) in pH 7.4, 25 mM TRIS, 150 mM KCl buffer with 1 mM TCEP at 25°C using 8-μL injections of 1 mM Ca²⁺. (b) Simultaneously fitted, baseline-corrected isotherms of (a) with chelator (red traces) and without chelator (green traces) and with residual sum-of-squares (RSS) error in fitting depicted at the base of the panel. (c) Calculated fraction of suPC2-EF-x-z1 protein bound to titrant in each sample.

Table 3.

Fitted parameters and F-test-derived confidence intervals for simultaneously simulated isotherms of calcium binding to EF-hand proteins with and without 5,5′-dimethylBAPTA (P = 0.05)

Macromolecule (trial No.)	5,5′-dimethylBAPTA (fixed parameters)			Purity (%)	ΔH (cal/mol)	KD (μM)	Residual ligand (μM)
	Purity (%)	ΔH (cal/mol)	KD (nM)
15N HuPC2EF (1)	73	2180	125	100 (fixed)	−11,237 (−11,568–10,913)a	461 (437–486)	2.39 (2.01–2.80)
15N SuPC2EF-x-z1 (1)	73	2275	125	100 (fixed)	−20,071 (−19,702–20,442)	1.95 (1.78–2.15)	10.8 (10.5–11.1)

^aParentheses indicate 95% confidence intervals for floating parameters, computed from sum-of-squares best-fit values; they do not reflect propagated experimental errors.

Discussion

We have developed an ODE approach to fitting ITC data obtained with complex mixtures. The primary advantage of the ODE approach employed in our data analysis is in the ease of developing models to describe the thermodynamics of binding in complex mixtures. An inherent limitation in the traditional ITC software treatment is the increasing difficulty in deriving the expressions to describe the thermodynamics of binding in complex mixtures of hetero- and homotropic interacting species as the number and complexity of the interactions increase. In contrast, the foundation of the ODE-based approach is well suited to address these situations, which are relevant in the study of ion-channels where channel activation is commonly triggered by interactions with secondary biomolecules and regulated through ligand binding at a multitude of sites. Comparisons to results from the ORIGIN-based software were carried out to provide part of the mathematical validation of our implementation. We were also able to validate our overall methodology using analytically well-defined binding interactions in a compatible matrix for studying PC2, a known Ca²⁺-binding protein.

The synthetic isotherms of our model system of Ca²⁺ binding to chelators validate our mathematical approach for the treatment of residually bound ligand in the presence of multiple competing reactants in a typical ITC experiment. The discrepancies between fitted and potentiometric-derived parameters are mostly within a few percent, which is generally viewed as a satisfactory agreement on an analytical basis for ITC results. However, there appears to be a significant discrepancy between the potentiometric-determined purity of the 5,5′-dimethylBAPTA chelator and that used for the simulated isotherms, which both deviate from the reported purity by the manufacturer (90%+). There are many potential causes for this mismatch in potentiometric-derived purity, which is observed in all data sets (TRIS and HEPES buffer), and which has been consistently observed in many ITC experiments in our laboratory with this particular chelator. The linearity of the potentiometric data as shown in the Scatchard plots in the Supporting Material suggests the analytical sample preparation is generally sound, and as the same samples, reagents, and buffers were used in the matched ITC experiments, a systematic error in reagent concentration is unlikely to account for the fitting discrepancy in purity between the ITC and potentiometric results. The close agreement in purity terms among the manufacturer-estimated, potentiometric, and ITC-derived values for the samples containing EDTA suggests ITC instrument calibration makes only a minor contribution to this effect. Further discussion regarding the likely nature of the impurities in the 5,5′-dimethylBAPTA can be found in the Supporting Material. The subject of calibration and analytical treatment of ITC experiments has recently been debated in the literature (32,33). We feel a more complete analytical analysis of the ITC performance would require alternate reagent preparations and many additional experimental replications, including those from a survey of protein quantification techniques, and is beyond the scope of this article. However, we believe the techniques presented herein can add to the understanding of using ITC as an analytical tool in the laboratory.

The Human and mutant Sea Urchin EF-hand constructs studied here structurally deviate from most Ca²⁺ binding EF-hand proteins largely due to their unpaired single EF-hand motif, yet possess the characteristic two helix-loop-helix domains in their calcium-saturated secondary structure. Despite the similarity in maintaining a single canonical N-terminal EF-hand motif in these two protein fragments, the hPC2-EF construct displays a dramatically lower Ca²⁺ affinity. Low affinities are also observed in other members of the S100 EF-hand family, and in particular Human S100A16, which also possesses an unpaired EF-hand motif (34,35). In cases where EF-hand motifs are found unpaired, the Ca²⁺ binding proteins often dimerize to produce an EF-hand domain shared within a homo or heterodimer. This dimerization can greatly enhance the apparent Ca²⁺ affinity of the EF-hand motif pair through its cooperative interaction. Neither suPC2-EF (wild-type or mutant) nor hPC2-EF-hand constructs showed evidence of dimerization in their Ca²⁺ saturated state in the presence of a reducing agent, which was necessary due to an unpaired cysteine in the suPC2-EF constructs. SuPC2-EF-x-z1 has homologous residues of a surface-exposed hydrophobic patch identified in hPC2-EF (70I, 73V, 77Y, 93M, 97L residues in suPC2-EF-x-z1), and because exposing a hydrophobic surface upon binding Ca²⁺ can alter its binding affinity, the dramatically stronger Ca²⁺ affinity of the Sea Urchin construct may reflect an alternate structural arrangement of its surface-exposed hydrophobic residues (36).

The sequence alignment of the EF-hand constructs shows deletions in the N-terminal portion of the EF1 (1α-2α) loop of hPC2-EF. Despite this, the protein maintains a fold typical of the EF-hand domain due to maintenance of hydrophobic and hydrogen-bond interactions in a short β-sheet structure involving residues of the 1α-2α and 3α-4α loops. This so-called EF β-scaffold formed between the two loops (L51-L85 in suPC2-EF-x-z1) likely acts to regulate Ca²⁺ binding cooperativity in complete EF-hand domains and functions in concert with coordinating residues to determine the overall conformational response of the domain to calcium binding (37). This is also the site of a key pathogenic mutation in Human PC2 (ΔL736-N737) related to autosomal dominant polycystic kidney disease (14), strongly suggesting a link between Ca²⁺ binding properties of PC2 and pathogenesis. The measured enthalpy of binding of the suPC2-EF-x-z1 construct is unusually large at −20.0 kcal/mol, with a calculated, enthalpically given free energy of formation of −7.78 kcal/mol and with a Ca²⁺ dissociation constant of 1.95 μM. The large difference in enthalpy of binding between the Human and Sea Urchin constructs suggests a more dramatic structural rearrangement of the helices upon Ca²⁺ binding for the latter, and may be a reflection upon alternate function of the suPC2 protein in contrast to the likely mechanosensory role of the human homolog in the context of the PC2 channel.

Based on the results of the minimization trials reported in Table 3 and as can be seen in Fig. 4 c, there is little evidence of a significant population of residually bound ligand at the start of the isothermal Ca²⁺ titration of the hPC2-EF protein. Under the assumption that the amino-acid analysis-derived protein concentration reflects pure, active protein, the Human PC2 protein shows a Ca²⁺ binding affinity of 461 μM and molar enthalpy of −11.2 kcal/mol. The Ca²⁺ binding affinity reported herein is significantly weaker than previously reported values for this motif (Ca²⁺ affinities of 179 μM in pH 6.8 5 mM TRIS, 500 mM NaCl, and 214 μM and ΔH of −8.8 kcal/mol in pH 7.5, 25 mM TRIS, 250 mM NaCl); however, this may reflect the different experimental buffer conditions (13,38) or challenges with protein concentration quantification rather than misinterpretations due to residually bound ligand. It should be emphasized that the buffer used in the Ca²⁺ binding experiments presented in this article has a low Ca²⁺ content, whereas nonanalytical grade NaCl may contain significant Ca²⁺ and other divalent ion impurities, which at 250 mM and greater concentrations would produce a nonnegligible Ca²⁺ background. Moreover, it should be noted that fitting the calcium-binding isotherm of the suPC2-EF-x-z1 protein in the absence of chelator, with the incorrect presumption of no residual calcium and a single binding site, would give an erroneously low molar enthalpy of binding of roughly −5.6 kcal/mol and a slightly weaker 4.0 μM Ca²⁺ binding affinity and demonstrates the importance of modeling ITC data of higher-affinity EF-hand proteins in the presence of a competing macromolecule with consideration for residually bound ligand. The analytical techniques and homologous constructs developed in this article will aid in the elucidation of the extent of the cooperativity in Ca²⁺ binding in the context of PC2 ion channels and help us understand the structural basis of polycystic kidney disease.

The addition of a competing macromolecule, irrespective of residually bound ligand, can act as an enthalpy or affinity standard and establish a baseline for an otherwise featureless isotherm. The addition of chelator to the hPC2-EF protein ITC study partially restrained parameters during minimizations of binding enthalpy and affinity terms. This utility is more clearly demonstrated by the data shown in Fig. 2, where the curvature of the isotherm of the chelator mixture is extremely sensitive to thermodynamic binding properties of the chelators. For a single class of binding sites such as with the individual chelators under stoichiometric binding conditions where M₀K ≫ 1, the enthalpy per mol of added ligand approaches the molar enthalpy of binding as the total ligand approaches zero. In the case where multiple competing macromolecules are present, the curvature of the titration isotherm is dependent on the relative affinities and enthalpies of binding (see the Supporting Material for a mathematical description of this effect). This demonstrates the potential utility of matching competing macromolecules in ligand affinity for quantification of binding affinities, which can be readily exploited in ITC calcium-binding experiments with a range of commercially available BAPTA-based chelators. This is readily apparent when viewing the dependence of input variables on the shape of the synthetic isotherms for fitting the data of Fig. 2, as can be explored using the provided program in the Supporting Material. The explicit formulation approach outlined in this article is well suited for simulating ITC data where the addition of competing ligand-binding chelators increases the complexity of the system beyond the capabilities of traditional ITC software.

The MATHEMATICA 9.0 scripts used to generate the simulations of Fig. 2 are provided in the Supporting Material along with a standalone Computable Document Format (CDF) program (Wolfram Research, Champaign, IL), which can be executed using the freely available Wolfram CDF Player (http://www.wolfram.com/cdf/) provided for popular Windows, Mac, and Linux platforms. A second standalone CDF program is provided for predicting isotherms under a variety of experimental sample and commercial instrument configurations. Scripts for data simulations here have been provided with a convenient parameter input interface that allows the user to adjust parameters and directly observe changes to heat evolved per mole of ligand titrant. These features can give the scientist valuable insight into the sensitive interplay among binding affinities, macromolecule purity, residual ligand, molar enthalpies, and binding cooperativity, and can greatly aid in the design of isothermal calorimetry experiments.