Abstract
Whole-cell patch-clamp measurements of the current, Ip, produced by the Na+,K+-ATPase across the plasma membrane of rabbit cardiac myocytes show an increase in Ip over the extracellular Na+ concentration range 0–50 mM. This is not predicted by the classical Albers-Post scheme of the Na+,K+-ATPase mechanism, where extracellular Na+ should act as a competitive inhibitor of extracellular K+ binding, which is necessary for the stimulation of enzyme dephosphorylation and the pumping of K+ ions into the cytoplasm. The increase in Ip is consistent with Na+ binding to an extracellular allosteric site, independent of the ion transport sites, and an increase in turnover via an acceleration of the rate-determining release of K+ to the cytoplasm, E2(K+)2 → E1 + 2K+. At normal physiological concentrations of extracellular Na+ of 140 mM, it is to be expected that binding of Na+ to the allosteric site would be nearly saturated. Its purpose would seem to be simply to optimize the enzyme’s ion pumping rate under its normal physiological conditions. Based on published crystal structures, a possible location of the allosteric site is within a cleft between the α- and β-subunits of the enzyme.
Introduction
The Na+,K+-ATPase is a crucial enzyme of animal physiology. It is responsible for maintaining Na+ and K+ electrochemical potential gradients across the plasma membrane of the cells of all multicellular animal species. These gradients are essential for the maintenance of cell volume and for a variety of physiological processes, e.g., nerve, muscle, and kidney function.
The mechanism of the enzyme’s complete enzymatic cycle is generally described by the Albers-Post formalism. A simplified version of this cycle is shown in Fig. 1. Within the Albers-Post formalism, Na+ ions bind from the cytoplasm to the E1 conformation of the enzyme and, after phosphorylation by ATP and conformational relaxation of the E1P(Na+)3 state, are released to the extracellular medium from the E2P conformation. K+ ions then bind from the extracellular medium to the E2P conformation, stimulate dephosphorylation, and are transported to the cytoplasm. In the E1P(Na+)3 state, the Na+ ions are enclosed within the protein and have no direct access to either the cytoplasm or the extracellular fluid, whereas in the E2P state the transport sites are open to the extracellular fluid.
Figure 1.
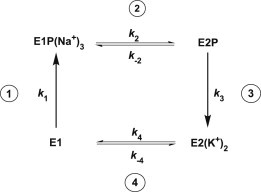
Simplified representation of the Albers-Post scheme describing the Na+,K+-ATPase catalytic cycle. Step 1: Binding of three Na+ ions from the cytoplasm, phosphorylation by ATP, and occlusion of Na+ within the protein. Step 2: Conformational change of the phosphorylated protein releasing the Na+ ions to the extracellular medium. Step 3: Binding of two K+ ions from the extracellular medium, occlusion of K+ within the protein, and dephosphorylation. Step 4: Conformational change of the unphosphorylated protein releasing K+ ions to the cytoplasm.
In the simple scheme outlined in Fig. 1, one would expect cytoplasmic Na+ ions, by promoting phosphorylation, to stimulate pump activity. Extracellular Na+, on the other hand, would be expected to inhibit the release of Na+ to the extracellular medium, drive the enzyme from the E2P conformation back toward the E1P(Na+)3 conformation, and compete with K+ for binding to the E2P state. Because K+ promotes dephosphorylation of the enzyme much more effectively than Na+, any decrease in the occupation of the sites on E2P by K+ would slow down the dephosphorylation step of the cycle. Thus, based on the simple version of the Albers-Post cycle shown in Fig. 1, one would predict that extracellular Na+ ions should inhibit turnover. However, in earlier work on purified Na+,K+-ATPase in native membrane fragments, we discovered (1) a stimulation of the enzyme’s rate-determining E2 → E1 transition by Na+, which could not be explained by this scheme.
The Na+-induced stimulation of the E2 → E1 transition could only be explained by Na+ binding to the E2 state before the enzyme undergoes the transition to the E1 state. Based on steady-state activity studies of the effect of the Na+ concentration on vanadate inhibition, Sachs (2) concluded that cytoplasmic Na+ does not bind to the transport sites of the protein before the release of K+. In the E2(K+)2 state, the K+ ions are occluded within the protein, with no access of the transport sites to the cytoplasm. Therefore, the Na+ ions, which stimulate the E2 → E1 transition, cannot be the same ones that bind in exchange for K+ on the cytoplasmic face of the protein once the enzyme has already undergone its transition to the E1 state.
Although it appeared likely that the acceleration of the E2 → E1 transition was due to Na+ acting from the extracellular face of the protein, no definite conclusion could be reached regarding the side of action, because the experiments were conducted using open membrane fragments with simultaneous access of Na+ to both faces of the protein. Nevertheless, based on kinetic measurements on Na+,K+-ATPase reconstituted into lipid vesicles, a number of authors have supported the presence of a Na+ allosteric site with access from the extracellular medium (3–5). The site appears, however, to not be very specific for Na+, with many buffer cations also exhibiting a Na+-like action in stabilizing the E1 conformation relative to the E2 conformation (5–14).
The purpose of this study was to investigate the effect of the Na+ allosteric site on Na+,K+-ATPase activity in cardiac myocytes. In particular, we aimed to determine from which side of the protein the ions are acting in this cellular system. Furthermore, now that three-dimensional crystal structural information on the Na+,K+-ATPase is available (15–20), it is possible to consider where the Na+ allosteric site within the protein might be.
Materials and Methods
Cells
Ventricular myocytes were isolated from male White New Zealand rabbits. Details of the anesthesia, excision of the heart, and cell isolation techniques have been described previously in Hool et al. (21). Myocytes were used on the day of isolation only and were stored at room temperature in Krebs-Henseleit buffer solution.
Measurement of electrogenic Na+-K+ pump current (Ip)
We measured currents (arising from the 3:2 Na+:K+ exchange ratio) in single myocytes using the whole-cell patch-clamp technique. The composition of the patch-pipette solutions perfusing the intracellular compartment were designed to take into account features of Na+-K+ pump kinetics. The solution included 20 mM Na+, a concentration higher than physiological intracellular levels, to obtain a substantial K+ activated current at 24°C. Wide-tipped patch pipettes (4–5 μm) were filled with solutions containing HEPES 5 mM; MgATP 2; EGTA (ethylene glycol-bis(β-aminoethyl ether)-n,n,n′,n′-tetraacetic acid 5 mM; and TMA-Cl (potassium glutamate 70 mM, sodium glutamate 20 mM, and tetramethylammonium chloride) 70 mM. They were titrated to a pH of 7.2 at 24°C with KOH. In some experiments Na+ and K+ concentrations were varied in the pipette solution, and the concentration of TMA-Cl was adjusted accordingly to maintain a constant osmolarity.
While we were establishing the whole-cell configuration, myocytes were superfused with solution containing NaCl 140 mM; KCl 5.6 mM; CaCl2 2.16 mM; MgCl2 1 mM; glucose 10 mM; NaH2PO4 0.44 mM; and HEPES 10 mM. It was titrated to a pH of 7.4 at 24°C with NaOH. Two-to-three minutes after the whole-cell configuration was established, we switched to a superfusate that was designed to minimize non-pump membrane currents by blocking current arising from transmembrane K+ and Ca2+ gradients. It was nominally Ca2+, K+-free and contained 0.2 mM CdCl2 and 2 mM BaCl2. Unless otherwise indicated, the solution contained 7 mM KCl. The K+-dependent shift in holding current was used to identify Ip. Control experiments using Na+ free patch-pipette solutions to eliminate pump currents indicated that there were no residual K+-induced membrane currents at the holding potential of −40 mV used.
We measured Ip using Na+ concentrations in the superfusate ranging from 0 to 140 mM. We included n-methyl-D-glucamine to compensate for changes in the Na+ concentration and hence maintain the osmolarity of the extracellular solution. In experiments performed to measure the current-voltage (I/V) relationship, Ip was identified as the shift in holding-current induced by Na+-K+ pump blockade with 200 μM ouabain. Holding currents were recorded during voltage steps of 5 s duration in 20-mV increments to test potentials from −100 to +40 mV. Recordings were averaged from three applications of the voltage-clamp protocol and the holding current was taken as the mean value of currents sampled with an electronic cursor.
All experiments were performed at a temperature of 24°C, maintained with automatic temperature controllers and in-line heaters (Warner Instruments, Hamden, CT). TMA-Cl and n-methyl-D-glucamine were purum grade, obtained from Fluka Chemicals (Buchs, Switzerland). All other chemicals used in solutions were analytical grade and obtained from BDH Chemicals (VWR International, Murarrie, Australia).
We used Axoclamp 2A and 2B voltage-clamp amplifiers, supported by pCLAMP Ver. 7 and AxOTAPE Ver. 2 (Axon Instruments, Grand Terrace, CA) to record currents. Currents were identified as the difference between holding currents with and without 7 mM extracellular K+, sampled at 20 Hz before and after Na+-K+ pump activation.
Statistical analysis
The experimental results are expressed as the means ± SD Student’s t-tests for unpaired data, which were used for the comparison of the mean levels of Ip. The Wilcoxon ranked-sum test was used to compare the means of the I/V curves.
Pump current simulations
Computer simulations of the experimental steady-state pump current were performed using the commercially available program Berkeley MADONNA Ver. 8.0 (http://www.berkeleymadonna.com/) and the variable step-size Rosenbrock integration method for stiff systems of differential equations. The simulations yielded the time course of the concentration of each enzyme intermediate involved, the outward current, and the amount of charge transported. For the purposes of the simulations, each enzyme intermediate was normalized to a unitary concentration and the enzyme was assumed arbitrarily to be initially in the E1 state. Each simulation was then carried out until the distribution between the different enzyme states no longer changed and the outward current reached a constant value.
Results
Steady-state pump current measured via the whole-cell patch-clamp technique
Typical whole-cell current recordings are shown in Fig. 2. The steady-state Ip produced by the Na+,K+-ATPase in voltage-clamped myocytes as a function of the extracellular Na+ concentration is shown in Fig. 3. There is an increase in Ip with increasing extracellular Na+ concentration over the range 0–50 mM. With an increase in the Na+ concentration of the pipette solution above 80 mM there was no significant difference in Ip at 0 vs. 50 mM extracellular Na+ (Ip = 0.87 ± 0.1 pA/pF, n = 6, vs. Ip = 0.92 ± 0.12 pA/pF, n = 6, P = 0.76). We also performed experiments in which we maintained the Na+ concentration in pipette solutions at 20 mM but eliminated K+, which was replaced with TMA-Cl. With elimination of K+ in the pipette solution there was no significant difference in Ip at 0 vs. 50 mM extracellular Na+ (Ip = 1.12 ± 0.12 pA/pF, n = 5, vs. Ip = 1.28 ± 0.09 pA/pF, n = 5, P = 0.31).
Figure 2.
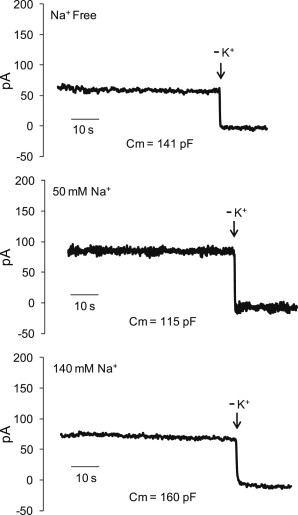
Whole-cell current recordings. K+-sensitive membrane currents recorded in extracellular solutions that were Na+-free or contained 50 or 140 mM Na+. Pipette solutions included 20 mM Na+ and 80 mM K+. The membrane capacitance (Cm) is included for each recording for comparison. (Arrow in each recording) Point at which the cardiomyocyte was exposed to K+-free superfusate; before this point the superfusate included 7 mM K+.
Figure 3.
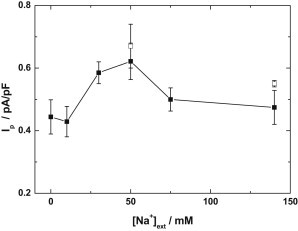
Dependence of the Na+,K+-pump current of cardiac myocytes (Ip) normalized to the membrane capacitance, on the extracellular Na+ concentration. Pipette solutions included 20 mM Na+ and 80 mM K+. Extracellular solutions included 7 (solid symbols) or 15 mM K+ (the latter at 50 and 140 mM extracellular Na+ only). Other experimental conditions were [ATP] = 2 mM, V = −40 mV, and T = 24°C, pH 7.2.
Because the K+-sensitive current that identifies Ip in this work can be affected by competition between K+ and Na+ to pump-binding sites, we performed additional experiments using a high extracellular K+ concentration of 15 mM. Experiments using this K+ concentration were performed using Na+ concentrations of 50 or 140 mM. Because the extracellular transport sites are expected to be completely saturated by K+ at an extracellular K+ concentration of 7 mM (see later in text) in the absence of extracellular Na+, additional experiments at 15 mM extracellular K+ were not performed in the Na+-free superfusates. Mean Ip for experiments using 15 mM K+ have been included in Fig. 3. The K+-dependent increase between currents recorded at 0 and 50 mM extracellular Na+ was also significant when 15 mM K+ was used at the higher Na+ concentration. The decrease in Ip that occurred when the extracellular Na+ concentration was increased further to 140 mM appeared qualitatively similar to the decrease that occurred when 7 mM K+ was used in the superfusate.
We examined whether the difference in Ip recorded in Na+-free extracellular solutions and solutions containing 50 mM Na+ arose from a voltage-dependent step in the pump cycle. Myocytes were voltage-clamped using Na+ and K+ concentrations of 20 and 80 mM, respectively, in the patch-pipette solutions. The extracellular K+ concentration was 7 mM. To eliminate any contamination of the small Na+-K+-pump currents that might arise from voltage-dependent, inwardly rectifying K+-activated K+ channels despite use of 2 mM Ba2+ in the superfusate, we used 200 μM ouabain to inhibit the Na+-K+ pump. Ouabain in this concentration causes near-complete pump blockade in rabbit cardiac myocytes (21). Holding currents were recorded before and after exposure to ouabain (22). An example of holding currents used to derive the voltage dependence of pump currents is shown in Fig. 4 A. Results of all experiments in Na+-free solutions and solutions containing 50 mM Na+ are summarized in Fig. 4 B. The currents recorded in solutions containing 50 mM Na+ were significantly larger than currents in Na+-free solutions (P < 0.01). To examine whether there was a difference in voltage dependence at 0 and 50 mM extracellular Na+, we normalized currents at the different holding potentials to the current recorded at 0 mV (Fig. 4 C). The normalized data did not support the hypothesis that the difference in Ip between 0 and 50 mM extracellular Na+ is voltage-dependent (P = 0.21).
Figure 4.
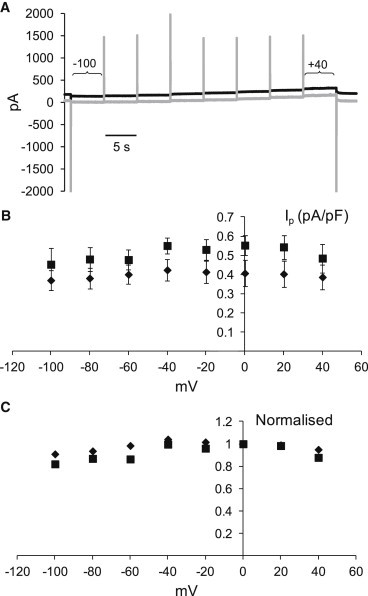
Voltage dependence of the Na+,K+-pump current at 0 and 50 mM extracellular Na+. (A) Examples of holding currents before (solid trace) or after (shaded trace) exposure of a myocyte to 200 μM ouabain. Pipette solutions included 20 mM Na+ and 80 mM K+. The holding potential was stepped from −40 to −100 mV at the beginning of the traces and then in 20-mV increments to +40 mV at the end of the traces before returning to −40 mV. Ip at each potential was identified as the difference in current recorded before and after exposure to ouabain. (B) Voltage dependence of mean Ip at either 50 mM (■) or 0 mM extracellular Na+ (♦). Currents recorded at 0 mM extracellular Na+ were significantly larger than currents at 0 mM Na+ (Wilcoxon’s replicate rank-sum test). (C) Mean Ip normalized to Ip recorded at 0 mV. Voltage dependence of the normalized currents was not statistically significant (P = 0.21, Wilcoxon’s replicate rank-sum test).
The increase in the enzyme’s pump activity with 20 mM Na+ in the patch-pipette solution with an increase in the extracellular Na+ concentration is not predicted by the simple Albers-Post scheme shown in Fig. 1, in which only transport sites for Na+ and K+ are considered. Based on this scheme, the only effect one would expect is an inhibition by extracellular Na+. Extracellular Na+ is expected to compete with extracellular K+ ions at the transport sites on the E2P conformation.
The coupled equilibria describing the competition between extracellular Na+ and K+ ions for the transport sites on the E2P state of the enzyme can be found in Fig. 2 of Garcia et al. (23). This scheme incorporates the generally accepted hypothesis of two transport sites, which can be occupied with different affinities by Na+ and K+, plus a single site that is specific for Na+. To demonstrate the expected dependence of Ip on the extracellular Na+ concentration based on this scheme, we have performed calculations described in the following section, with the mathematical details given in the Appendix.
Modeling of heart Na+,K+-ATPase transported charge-voltage behavior
Under experimental conditions which are not too far removed from physiological conditions, the complex Albers-Post cycle describing the Na+,K+-ATPase’s partial reactions can be reduced to the simpler four-state model shown in Fig. 1. We have used this simple model to describe current-voltage behavior of the Na+,K+-ATPase, as found previously in Hansen et al. (22). The mathematical detail of the model and the assumptions on which it is based are described in detail there. In this work, we describe only the essential points of the model. E1P(Na+)3 and E2(K+)2 here represent occluded states of the protein. In contrast, E1 and E2P represent states in which the ion binding sites have access to the cytoplasm and the extracellular fluid, respectively. In the case of the nonoccluded states, we assume that rapid exchange of Na+ and K+ between the binding sites and either the cytoplasm or the extracellular fluid can occur.
Thus, in the case of the E2P state we assume that there is a rapid exchange of Na+ ions and K+ ions between the extracellular fluid and two of the ion transport binding sites. The stoichiometry of the Na+,K+-ATPase is 3Na+/2K+/ATP. One of the ion binding sites is considered to be specific for Na+, whereas Na+ or K+ can both bind with differing affinities to the other two. Thus, we treat ion binding to E2P as a series of coupled equilibria, as shown in Fig. 2 of Garcia et al. (23). An analogous scheme can be drawn for the E1 state. Only the kinetics of the four major rate-determining reactions shown in Fig. 1 is explicitly considered. We consider that each of the four rate-determining reactions only reaches its maximum observable rate when the reactant state is fully saturated by the appropriate substrates.
Because the enzyme pumps three Na+ ions in exchange for two K+ ions, there is a net transport of one positive charge out of cells. Thus, the overall steady-state turnover of the enzyme equals the outward flux of ions, and can be easily converted to an outward current. The voltage dependence of the charge-translocating reaction steps is taken into account by Boltzmann terms, as previously described in Garcia et al. (23). The numerical simulation procedure of Garcia et al. (23) allows the time dependence of any changes in pump current to be calculated after rapid perturbations, e.g., due to a voltage jump, as well as the steady state.
If one wishes only to calculate the steady-state pump currents, the differential rate equations describing the rate of change of each enzyme intermediate (shown in the Appendix) are all equal to 0. Therefore, in principle, if one makes use of the mass conservation law that the total concentration of the enzyme intermediates is constant, the coupled series of differential equations reduces to a series of simultaneous equations that can be solved analytically to obtain a single equation that allows the pump current to be calculated under varying experimental conditions. However, because of the complex reaction mechanism, the resultant equation for the pump current is unwieldy, and we only present the mathematics for the numerical solution here. Whether one uses a numerical procedure or the analytical solution to the simultaneous equations, the results of the calculations are identical. An advantage of the numerical procedure is that by integration of the time-dependent pump current, the amount of charge transported by the Na+,K+-ATPase can be calculated. We will use this feature of the numerical model to compare with experimental voltage-jump data.
The kinetic and equilibrium parameters used for modeling of the outward sodium pump current, Ip, by Garcia et al. (23) were derived from measurements on purified mammalian kidney enzyme. Significant differences existed between the experimentally observed current-voltage behavior of heart muscle Na+,K+-ATPase in intact cardiac myocytes and the predicted behavior of kidney Na+,K+-ATPase. In particular, the kidney enzyme displayed significantly lower voltage dependence of the pump current at a physiologically relevant extracellular Na+ concentration of 150 mM.
The comparison between the heart and kidney enzymes demonstrates that, if one wishes to simulate the behavior of heart Na+,K+-ATPase, modifications to the rate or equilibrium parameters used in the model must be made. The steep positive slope in the Ip-V curve of the heart enzyme over the membrane-voltage range −120 to 0 mV has its origin in Na+ competition for transport sites on the E2P state. To determine more-reliable values for the equilibrium dissociation constants describing the interaction of Na+ with the E2P state, we have compared the results of simulations of the total charge transported by the Na+,K+-ATPase after a voltage jump with experimental results obtained by Peluffo (24) using rat cardiac myocytes. Because the experiments were performed in the absence of extracellular K+, the comparison allows us to estimate the Na+ dissociation constants without any competition from K+.
Peluffo’s experimental data are reproduced in Fig. 5 together with the simulations based on our kinetic model. Good agreement between the experimental data and the simulations was achieved. To obtain this agreement it was necessary to significantly reduce the Na+ dissociation constants of the E2P state relative to the values previously determined for the kidney enzyme. The microscopic dissociation constant for interaction of Na+ with the two nonspecific sites at a membrane potential of 0 mV, KNo, was reduced from 400 mM (kidney) to 180 mM (heart). Similarly, the dissociation constant for interaction of Na+ with the specific Na+ site, KN1o, was reduced from 100 mM (kidney) to 40 mM (heart).
Figure 5.
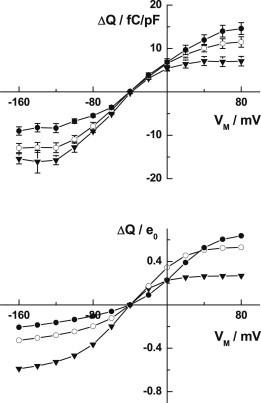
Dependence of the Na+,K+-ATPase transported charge-voltage relationship (ΔQ-V curve) on the extracellular Na+ concentration after voltage jumps from the membrane voltage Vm to −40 mV. Each symbol corresponds to the following Na+ concentrations: 36.3 mM (▾), 72.5 mM (○), and 145 mM (●). (Solid lines between the points have been drawn to aid the eye.) (Upper curve) Experimental results for rat heart myocytes, obtained via the voltage-clamp technique, reproduced from Fig. 3C of Peluffo (24). The transported charge, ΔQ, has been divided by the capacitance of each cell to correct for variations in cell size. The experimental conditions were cytoplasmic [Na+] = 120 mM, cytoplasmic [K+] = extracellular [K+] = 0 mM, and cytoplasmic [ATP] = 15 mM, T = 23°C. (Lower curve) Computer simulations of the ΔQ-V curve for mammalian heart Na+,K+-pump current based on the Albers-Post scheme described by Figs. 1 and 3 and the kinetic and equilibrium parameters given in Table 1 of Garcia et al. (23); however, a microscopic dissociation constant of Na+ for the nonspecific transport sites on E2P state of 180 mM and a dissociation constant of Na+ to the specific site on E2P of 40 mM have been used. The ion concentrations, ATP concentration, and temperature used for the simulations were the same as for the upper curve.
A direct quantitative comparison of the actual amounts of charge transported experimentally and that calculated from the model is not possible, because the total charge transported depends on the number of Na+,K+-ATPase molecules expressed per cell, which depends on the size of the cell. To account for varying cell sizes, Peluffo (24) divided the measured current by the capacitance of each cell, which should be proportional to the cell surface area. Thus, Peluffo’s measured current in units of femto-Coulombs per pico-Farad should be proportional to the current per pump molecule, which is the quantity we calculate in our simulations.
To judge the agreement between the experimental data and the simulated results, it is important to look at the plateaus in charge transported after voltage jumps to very high positive or very low negative potentials. If the magnitudes of these plateaus are equal, at the extracellular Na+ concentration corresponding to this situation the enzyme is half-saturated by Na+ (i.e., the number of bound Na+ ions capable of being released on shifting to inside-positive potentials equals the number of available binding sites, and, hence, the number of free Na+ ions capable of binding on shifting to inside-negative potentials). Although only three different extracellular Na+ concentrations were measured by Peluffo (24), the results indicate that the half-saturating Na+ concentration is in the range 72.5–145 mM, probably closer to 72.5 mM than 145 mM.
Modeling of heart Na+,K+-ATPase current-voltage behavior
We extended the modeling to competition between Na+ and K+ for the transport sites, and thus estimated the E2P microscopic dissociation constant for K+ of the heart enzyme. For this purpose we compare with the experimental steady-state pump current data for heart Na+,K+-ATPase reported by Nakao and Gadsby (25). We showed previously in Garcia et al. (23) that it was not possible to adequately reproduce the current-voltage (I/V) behavior reported by Nakao and Gadsby (25) if we used equilibrium dissociation constants for the E2P state derived from measurements on kidney enzyme. We changed the values of KNo and KN1o from 400 and 100 mM derived from the kidney enzyme to 180 and 40 mM, the values derived from the comparison with Peluffo’s data in the previous section, and have then varied the value of KKo (the microscopic dissociation constant of K+ with the E2P state at a membrane potential of 0 mV) until we obtained the best reproduction of experimental behavior.
The experimental data of Nakao and Gadsby, together with the results of the simulations showing the closest agreement with their data, are shown in Fig. 6. To achieve this agreement, we increased the value of KKo slightly from 1.33 mM (kidney value) to 1.8 mM. The higher value of KKo together with the lower values of KNo and KN1o relative to the values obtained using enzyme derived from mammalian kidney, indicates that Na+ competes with K+ much more strongly for binding to the E2P state in the heart enzyme than the kidney enzyme. Because binding/release of Na+ to the specific site on E2P is the major charge-transporting step of the Na+,K+-ATPase pump cycle, the stronger competition from Na+ ions explains the much greater voltage dependence of the heart enzyme’s steady-state turnover than that predicted for the kidney enzyme.
Figure 6.
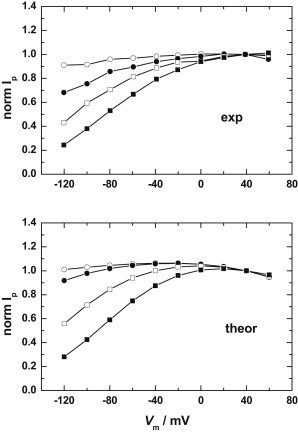
Dependence of the Na+,K+-pump current-voltage relationship (I/V curve) on the extracellular Na+ concentration. Symbols correspond to the Na+ concentrations of 1.5 mM (○), 50 mM (●), 100 mM (□), and 150 mM (▪). (Solid lines between the points have been drawn to aid the eye.) (Upper curve) Experimental results for guinea pig heart ventricular myocytes, obtained via the whole-cell patch-clamp technique, reproduced from Fig. 3 of Nakao and Gadsby (25). The pump current, Ip, of each curve has been normalized to the value at a holding potential of +40 mV. The experimental conditions were cytoplasmic [Na+] = 50 mM, cytoplasmic [K+] = 0 mM, extracellular [K+] = 5.4 mM, and cytoplasmic [ATP] = 10 mM, T = 36°C. (Lower curve) Simulations of the I/V curve for mammalian heart Na+,K+-ATPase pump current based on the Albers-Post scheme described by Figs. 1 and 3 and the kinetic and equilibrium parameters given in Table 1 of Garcia et al. (23); however, a microscopic dissociation constant of K+ for the E2P state of 6.2 mM has been used and the dielectric coefficients of binding of both Na+ and K+ to this state have been reduced to 0.1. The ion concentrations, ATP concentration, and temperature used for the simulations were the same as for the upper curve.
Modeling of the extracellular Na+ concentration dependence of Ip
Now that we have a kinetic model based on the Albers-Post scheme capable of reproducing data from the literature on the transported charge- and current-voltage behavior of heart Na+,K+-ATPase, we can test whether this model explains the experimentally observed dependence of Ip on the extracellular Na+ concentration shown in Fig. 3. Calculations of the expected dependence of the pump current, Ip, per pump molecule on the extracellular Na+ concentration based on the Albers-Post model are shown in Fig. 7 (dotted line).
Figure 7.
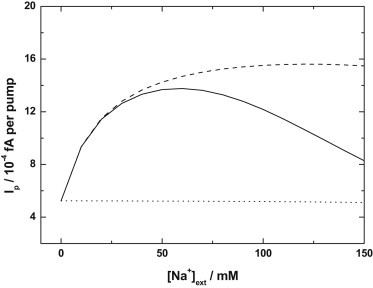
Simulations of expected dependence of Na+,K+-pump current, Ip, per pump molecule on the extracellular Na+ concentration based on the Albers-Post model (dotted line, KKo = 1.8 mM, KNo = 180 mM, and KN1o = 40 mM) and an expanded Albers-Post model incorporating extracellular allosteric Na+ binding (dashed line, KKo = 1.8, KNo = 180 mM, and KN1o = 40 mM). (Solid line) Simulation based on the same model incorporating allosteric Na+ binding, but with reduced dissociation constants for extracellular Na+ interaction with the transport sites (KKo = 1.8 mM, KNo = 68 mM, and KN1o = 15 mM). The experimental conditions used for the simulations were identical to those of the actual experiments (see legend for Fig. 3).
Based on the values of the dissociation constants for extracellular K+ and Na+ interaction with the transport sites derived from the data of Peluffo (24) and Nakao and Gadsby (25) in the previous two sections, it is apparent that the Albers-Post model only predicts a monotonic decrease in steady-state activity of ∼2–3% between 0 and 150 mM Na+ if one only considers interaction of extracellular Na+ with the enzyme’s transport sites. This is not in agreement with the experimental results (Fig. 2), which show an increase in activity between 0 and 50 mM. For these calculations, we have used a value of the rate constant, k4, of the E2(K+)2 → E1 transition of 18 s−1. This value is based on the finding of Humphrey et al. (1) on purified enzyme that Na+ ions cause a roughly fivefold increase in the rate constant of this reaction and the finding of Lüpfert et al. (14) that at physiological levels of Na+, Mg2+, and ATP, the reaction occurs with a rate constant of ∼90 s−1.
To account for the increase in pump current experimentally observed, we have expanded the Albers-Post model to incorporate extracellular Na+ binding to an allosteric site and an associated acceleration of the E2 → E1 conformational transition, as indicated by kinetic experiments on purified enzyme (1). The extensions and changes to the mathematics necessary for these calculations are described in the Appendix. Based on the kinetic results on purified enzyme (1) we have used a dissociation constant for the interaction of Na+ with the allosteric site, Kallo, of 31 mM. The results of the simulations, utilizing the values of KKo = 1.8 mM, KNo = 180 mM, and KN1o = 40 mM, derived from simulations of the data from Peluffo (24) and Nakao and Gadsby (25), are shown in Fig. 7 (dashed line).
The model predicts a roughly hyperbolic increase in the pump current over the 0–50 mM extracellular Na+ concentration range. At Na+ concentrations above 100 mM, there is a very gradual drop in pump current (i.e., qualitatively in agreement with the experimental observations (see Fig. 3)). Therefore, the experimental results are consistent with the existence of an allosteric activating Na+ site with access from the extracellular medium. The drop in Ip at high extracellular Na+ concentrations is, however, much more pronounced than that predicted by the model (see Fig. 7). But if the values of KNo and KN1o are decreased to 68 and 15 mM, respectively, a significant drop in Ip is observed over the Na+ concentration range 50–150 mM (i.e., in much closer agreement with the experimentally observed behavior (see Fig. 3)). Therefore, it appears likely that competition from Na+ for binding to the extracellular transport sites on the E2P state of the enzyme is much stronger in the rabbit cardiac myocytes used in our study, in comparison to the guinea pig myocytes used by Nakao and Gadsby (25).
Discussion
Much information regarding the molecular mechanism of Na+,K+-ATPase has been gained by studies of the purified protein, either in the form of enzyme-containing membrane fragments or protein reconstituted into synthetic lipid vesicles. However, the goal of any mechanistic work on the Na+,K+-ATPase must be to understand how the enzyme works in a living cell, and it is crucial that any discoveries made on purified Na+,K+-ATPase be reconciled with studies on the enzyme in situ in intact cells. Apart from this fundamental point, experiments on cells have the additional advantage over studies of Na+,K+-ATPase-containing membrane fragments in that the cytoplasm and the extracellular medium are separated by the plasma membrane, allowing the side of action of the enzyme’s substrates to be identified. Synthetic vesicles are sided preparations, but, in the case of small unilamellar vesicles generally used for reconstitution, their internal volume is much less than that of cells and it is impossible with vesicles to reproduce the natural membrane composition of a living cell. Therefore, the relevance of results obtained on the Na+,K+-ATPase using lipid vesicles for the enzyme in a cell must always be examined.
Because the Na+,K+-ATPase pumps Na+ ions from the cytoplasm into the extracellular fluid, increased concentrations of extracellular Na+ must inhibit its pumping activity, a simple example of product inhibition. However, studies on purified enzyme have suggested that extracellular Na+ can also stimulate ion pumping by acting at an allosteric site (1,3–14). Our results on whole cells confirm that prediction. This increase cannot be explained by Na+ acting on transport sites alone, and implicates the existence of a separate allosteric Na+ site.
A logical question to ask, however, would be why no evidence for an extracellular allosteric Na+ site was apparent in the results reported by Nakao and Gadsby (25), reproduced in Fig. 6. A likely explanation is that they used a higher Na+ concentration of 50 mM in their patch pipette in comparison to 20 mM in the experiments shown in Fig. 3. In our study on increasing the cytoplasmic Na+ concentration or eliminating the cytoplasmic K+ concentration, there was no longer a statistically significant increase in Ip with increasing extracellular Na+ concentrations from 0 to 50 mM, which we attribute to extracellular allosteric Na+ binding.
If the increase in Ip due to extracellular Na+ is caused by an increase in the flux through the E2(K+)2 → E1 transition, as measurements on purified enzyme suggest (1), then the disappearance of the effect of extracellular allosteric Na+ site at high cytoplasmic Na+ concentrations or low cytoplasmic K+ concentrations implies a decrease in the contribution of the E2(K+)2 → E1 transition to rate-determination of the entire pump cycle. Thus, the E2(K+)2 → E1 transition must already be so fast that any increase in its rate has negligible effect on the enzyme’s turnover. To understand how this might come about, one needs to consider what effects an increase in the cytoplasmic Na+ concentration or a decrease in the cytoplasmic K+ concentration could have on the individual partial reactions of the enzyme.
An increase in the cytoplasmic Na+ concentration would accelerate the phosphorylation reaction, E1 → E1P, but this would tend to increase the contribution of the E2(K+)2 → E1 transition toward an overall rate determination of the pump cycle; hence, one would expect an enhanced effect of extracellular Na+ on Ip rather than the decreased effect experimentally observed. However, an increase in the cytoplasmic Na+ concentration would also increase the degree of competition of Na+ over K+ for binding to the transport sites on E1. This would decrease the rate of the backward reaction E1K+2 → E2(K+)2 and, thus, increase the net flux in the forward direction E2(K+)2 → E1.
A decrease in the cytoplasmic K+ concentration would be expected to have the same effect as an increase in the cytoplasmic Na+ concentration. The result of this would be a decrease in the contribution of the E2-to-E1 transition to overall rate determination and a reduction in the allosteric effect of extracellular Na+. The experimental results that the allosteric effect of extracellular Na+ diminishes either upon increasing the cytoplasmic Na+ level or decreasing the cytoplasmic K+ level indicates that for the heart enzyme, the decrease in the rate of the backward reaction E1K+2 → E2(K+)2 must dominate over the increase in rate of the E1 → E1P reaction by cytoplasmic Na+.
It is in fact likely that in the experiments performed by Nakao and Gadsby (25) there would have been very little competition to Na+ binding to the E1 state, because they replaced K+ with Cs+ ions that compete with Na+ with an ∼10-fold higher K1/2 than K+ (26). Although not quantitatively the same, it is also worth mentioning that the theoretical model predicts the decrease in the allosteric effect of extracellular Na+ at increasing intracellular Na+ concentrations or decreasing intracellular K+ concentrations. At an intracellular Na+ concentration of 20 mM, the model predicts an increase in the relative value of Ip between 0 and 50 mM extracellular Na+ of 172%. If the intracellular Na+ concentration is increased to 80 mM, the model predicts that the increase in Ip over the same extracellular Na+ concentration range should drop to 126%. If the intracellular K+ concentration is decreased to 0, the model predicts that the increase in Ip over the same extracellular Na+ concentration should drop to 93%.
From a consideration of recently published crystal structures of the Na+,K+-ATPase (15–20), we have identified a possible site of allosteric Na+ binding. Based on the sequence numbering of the shark enzyme (PDB:2ZXE), it seems that the Na+ ion could possibly bind to the sequence of acidic amino-acid residues Glu122, Asp123, Glu124, and Asp128. These residues are located in a cleft between the α- and β-subunits of the protein that has access from the extracellular medium. That this cleft has functional importance for the protein is evidenced by the fact that it is also occupied by the specific Na+,K+-ATPase inhibitor ouabain (17,18). It is worth pointing out that, based on x-ray crystallographic data, Ekberg et al. (27) recently identified Asp92 and Asp95 as being involved in cation binding on the extracellular face of the plasma membrane H+-ATPase, another P-type ATPase closely related to the Na+,K+-ATPase. These amino-acid residues are in positions homologous to those which we suggest may be involved in extracellular allosteric Na+ binding in the Na+,K+-ATPase. Based on the effects of mutations on the kinetics of partial reactions, amino-acid residues in homologous positions have also been implicated (28) in extracellular ion binding in the sarcoplasmic reticulum Ca2+-ATPase.
Ip over the 0–50 mM extracellular Na+ concentration range was only weakly voltage-dependent and not significantly different between 0 and 50 mM Na+ (Fig. 4). This is consistent with the expectation that the major voltage-dependent step of extracellular Na+ rebinding to E2P is not rate-limiting under the conditions of these experiments, nor is K+ occlusion by E2P, whose observed rate is dependent on the degree of occupation of the transport sites on E2P by K+. At intracellular Na+ and K+ concentrations of 20 and 80 mM, the forward E2(K+)2 → E1K+2 and backward E1K+2 → E2(K+)2 are major reactions determining the overall forward reaction rate and hence Ip. The absence of significant voltage dependence also indicates that binding of Na+ to the extracellular allosteric site we invoke is not voltage-dependent (i.e., the allosteric site is not buried within the transmembrane domains of the protein).
Finally, it is interesting to speculate whether allosteric Na+ binding has a role in regulation of cell Na+. At a normal physiological extracellular Na+ concentration of ∼140 mM, the Na+ allosteric site should be nearly fully occupied, and hence unlikely to have a regulatory role. It might simply be an evolutionary adaptation of the enzyme to optimize its activity under normal physiological conditions in the presence of a relatively high concentration of extracellular Na+ and to compensate for any inhibition that would arise from extracellular binding to the ion transport sites. However, the allosteric site might also have a role under pathophysiological conditions of low extracellular Na+. Extracellular concentrations as low as ∼100 mM can be encountered in severe hyponatremia in humans. Due to an associated decrease in inward passive Na+ leak, this decreases the intracellular Na+ concentration (29).
The decrease in intracellular concentration arising from the decreased leak would be amplified if the low extracellular Na+ increases the occupation of the transport sites on E2P by K+ and hence increases the forward Na+-K+ pump rate. At an extracellular Na+ concentration of 100 mM and above, the contribution of K+ occlusion by E2P to overall rate determination is expected to be enhanced in cardiac myocytes (21). The allosteric site is expected to reduce such an acceleration of pump rate in hyponatremic states (see Fig. 7), and may therefore serve as a tight control of intracellular Na+ to optimize cell function.
Acknowledgments
The authors acknowledge helpful discussions with Associate Professor Flemming Cornelius, University of Aarhus, Denmark. We also thank Professor Daniel Peluffo, New Jersey Medical School, for providing us with his data for comparison.
H.H.R. acknowledges financial support (under project grant No. 633252) from the National Health and Medical Research Council (Australia). R.J.C. received financial support from the Australian Research Council (under Discovery grant No. DP-120103548).
Contributor Information
Helge H. Rasmussen, Email: helge.rasmussen@sydney.edu.au.
Ronald J. Clarke, Email: r.clarke@chem.usyd.edu.au.
Appendix: Calculation of the Steady-State Pump Current
Simple Albers-Post model
Extracellular Na+ can have two possible effects on the ion pumping activity of the Na+,K+-ATPase:
-
1.
By (re-)binding to the transport sites on the E2P state, Na+ can inhibit pump activity; and
-
2.
By binding to an allosteric site, Na+ can stimulate the E2 → E1 transition and increase pump activity.
Because these two effects involve widely separated reactions of the Albers-Post cycle, the only quantitative way to consider the influences they would both have on the overall steady-state pump current is to carry out calculations of the entire pump cycle.
Based on the four-state Albers-Post model of the Na+,K+-ATPase enzymatic cycle shown in Fig. 1, the differential rate equations describing the changes in concentrations of all the enzyme intermediates are
| (1) |
| (2) |
| (3) |
| (4) |
In these equations, the term f(3Nai) represents the fraction of enzyme in the E1 state occupied by three Na+ ions, which is determined by the current cytoplasmic Na+ and K+ concentrations and the binding affinities of the ion sites. Similarly f(ATPE1) represents the fraction of enzyme in the E1 state occupied by ATP. The significance of these f-terms can be easily understood if we take the phosphorylation reaction as an example. The maximum rate constant for phosphorylation, k1, is only achieved when the E1 state of the enzyme is completely saturated by three Na+ ions and one ATP molecule. Thus the observed rate constant, k1obs, for the reaction is given by k1 multiplied by the probability that E1 has three bound Na+ ions (= f(3Nai)) and by the probability that E1 has a bound ATP molecule (= f(ATPE1)). This simple mathematical formulation of the rates will break down at very low cytoplasmic Na+ and ATP concentrations, when second-order binding of the substrates to the enzyme becomes slower than the following first-order phosphorylation and occlusion of Na+. However, under normal physiological conditions the assumption of rapid binding equilibria, on which Eqs. 1–4 and the four-state scheme shown in Fig. 1 are based, can be considered a good approximation.
Also appearing in Eqs. 1–4 are:
Fraction of enzyme in the E2 state with ATP bound, f(ATPE2);
Fraction of enzyme in the E2P state with three Na+ ions bound, f(3Nao);
Fraction of enzyme in the E2P state with two K+ ions bound, f(2Ko); and
Fraction of enzyme in the E1 state with two K+ ions bound, f(2Ki).
In a similar way to that described for the phosphorylation reaction, these fractions or probabilities modify the observed rate constant for each relevant reaction step, as shown in Eqs. 1–4. Because in our model we consider all of the substrate binding reactions to be equilibria, the f-terms are determined solely by the substrate concentrations and the relevant equilibrium (or dissociation) constants of each substrate. Equations for all of the f-terms are given in Garcia et al. (23).
Based on the model, the transient outward current due to the Na+,K+-ATPase at any moment in time, Ip(t), is given by
| (5) |
Thus, Eqs. 1–4 and 5 represent a coupled series of equations that can be solved numerically to derive the value of Ip(t) at any combination of ion and ATP concentrations.
Once a steady state has been reached, Ip(t) represents the flux through the reaction E1P → E2P, in which Na+ ions are released to the external medium, and is hence equal to the turnover of the enzyme. The amount of charge transported by the Na+,K+-ATPase across the membrane can also be calculated by integrating Ip(t) with respect to time.
Expanded Albers-Post model including extracellular allosteric Na+ binding
To take into account the effect of extracellular allosteric Na+ binding on the steady-state pump current requires some relatively small modifications to the basic model. Because experimental evidence on purified enzyme indicates (1) that extracellular Na+ accelerates the E2(K+)2 → E1 conformational transition, the differential rate equations describing the change in concentrations of the E1 and E2 states, i.e., Eqs. 1 and 4, need to be changed. The modified equations are
| (6) |
| (7) |
In these two equations, k4max represents the maximum value of the rate constant for the E2(K+)2 → E1 transition when the extracellular Na+ allosteric site is fully occupied by Na+ and simultaneously the low-affinity ATP site on E2 is fully occupied by ATP. Similarly, k4min represents the minimum value of the rate constant for the same transition when the extracellular Na+ allosteric site is completely free of Na+ but the low-affinity ATP site on E2 is still fully occupied by ATP. The term f(Naoallo) in Eqs. 6 and 7 represents the fraction of Na+ allosteric sites occupied by Na+. It is given by
| (8) |
Kallo is here the dissociation constant of the extracellular allosteric Na+ site.
References
- 1.Humphrey P.A., Lüpfert C., Clarke R.J. Mechanism of the rate-determining step of the Na+,K+-ATPase pump cycle. Biochemistry. 2002;41:9496–9507. doi: 10.1021/bi025836o. [DOI] [PubMed] [Google Scholar]
- 2.Sachs J.R. The order of addition of sodium and release of potassium at the inside of the sodium pump of the human red cell. J. Physiol. 1986;381:149–168. doi: 10.1113/jphysiol.1986.sp016319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Karlish S.J.D., Stein W.D. Cation activation of the pig kidney sodium pump: transmembrane allosteric effects of sodium. J. Physiol. 1985;359:119–149. doi: 10.1113/jphysiol.1985.sp015578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cornelius F., Skou J.C. The sided action of Na+ on reconstituted shark Na+/K+-ATPase engaged in Na+-Na+ exchange accompanied by ATP hydrolysis. II. Transmembrane allosteric effects on Na+ affinity. Biochim. Biophys. Acta. 1988;944:223–232. doi: 10.1016/0005-2736(88)90435-x. [DOI] [PubMed] [Google Scholar]
- 5.van der Hijden H.T.W.M., de Pont J.J.H.H.M. Cation sidedness in the phosphorylation step of Na+/K+-ATPase. Biochim. Biophys. Acta. 1989;983:142–152. doi: 10.1016/0005-2736(89)90227-7. [DOI] [PubMed] [Google Scholar]
- 6.Karlish S.J.D. Characterization of conformational changes in (Na,K) ATPase labeled with fluorescein at the active site. J. Bioenerg. Biomembr. 1980;12:111–136. doi: 10.1007/BF00744678. [DOI] [PubMed] [Google Scholar]
- 7.Skou J.C., Esmann M. The effects of Na+ and K+ on the conformational transitions of (Na+ + K+)-ATPase. Biochim. Biophys. Acta. 1983;746:101–113. doi: 10.1016/0167-4838(83)90016-x. [DOI] [PubMed] [Google Scholar]
- 8.Schuurmans Stekhoven F.M.A.H., Swarts H.G.P., Bonting S.L. Na+-like effect of imidazole on the phosphorylation of (Na+ + K+)-ATPase. Biochim. Biophys. Acta. 1985;815:16–24. doi: 10.1016/0005-2736(85)90468-7. [DOI] [PubMed] [Google Scholar]
- 9.Schuurmans Stekhoven F.M.A.H., Swarts H.G.P., De Pont J.J.H.H.M. Phosphorylation of (Na+ + K+)-ATPase; stimulation and inhibition by substituted and unsubstituted amines. Biochim. Biophys. Acta. 1988;937:161–176. doi: 10.1016/0005-2736(88)90238-6. [DOI] [PubMed] [Google Scholar]
- 10.Mezele M., Lewitzki E., Grell E. Cation selectivity of membrane proteins. Ber. Bunsenges Phys. Chem. 1988;92:998–1004. [Google Scholar]
- 11.Grell E., Warmuth R., Ruf H. Precision titrations to determine affinity and stoichiometry of alkali, alkaline earth, and buffer cation binding to Na,K-ATPase. In: Kaplan J.H., De Weer P., editors. The Sodium Pump: Recent Developments. Rockefeller University Press; New York: 1991. pp. 441–445. [Google Scholar]
- 12.Doludda M., Lewitzki E., Grell E. Kinetics and mechanism of cation-binding to Na+,K+-ATPase. In: Bamberg E., Schoner W., editors. The Sodium Pump: Structure Mechanism, Hormonal Control and Its Role in Disease. Steinkopff; Darmstadt, Germany: 1994. pp. 629–632. [Google Scholar]
- 13.Grell E., Lewitzki E., Doludda M. Reassignment of cation-induced population of main conformational states of FITC-Na+/K+-ATPase as detected by fluorescence spectroscopy and characterized by equilibrium binding studies. In: Bamberg E., Schoner W., editors. The Sodium Pump: Structure Mechanism, Hormonal Control and Its Role in Disease. Steinkopff; Darmstadt, Germany: 1994. pp. 617–620. [Google Scholar]
- 14.Lüpfert C., Grell E., Clarke R.J. Rate limitation of the Na+,K+-ATPase pump cycle. Biophys. J. 2001;81:2069–2081. doi: 10.1016/S0006-3495(01)75856-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Morth J.P., Pedersen B.P., Nissen P. Crystal structure of the sodium-potassium pump. Nature. 2007;450:1043–1049. doi: 10.1038/nature06419. [DOI] [PubMed] [Google Scholar]
- 16.Shinoda T., Ogawa H., Toyoshima C. Crystal structure of the sodium-potassium pump at 2.4 Å resolution. Nature. 2009;459:446–450. doi: 10.1038/nature07939. [DOI] [PubMed] [Google Scholar]
- 17.Ogawa H., Shinoda T., Toyoshima C. Crystal structure of the sodium-potassium pump (Na+,K+-ATPase) with bound potassium and ouabain. Proc. Natl. Acad. Sci. USA. 2009;106:13742–13747. doi: 10.1073/pnas.0907054106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yatime L., Laursen M., Fedosova N.U. Structural insights into the high affinity binding of cardiotonic steroids to the Na+,K+-ATPase. J. Struct. Biol. 2011;174:296–306. doi: 10.1016/j.jsb.2010.12.004. [DOI] [PubMed] [Google Scholar]
- 19.Kanai R., Ogawa H., Toyoshima C. Crystal structure of a Na+-bound Na+,K+-ATPase preceding the E1P state. Nature. 2013;502:201–206. doi: 10.1038/nature12578. [DOI] [PubMed] [Google Scholar]
- 20.Nyblom M., Poulsen H., Nissen P. Crystal structure of Na+, K+-ATPase in the Na+-bound state. Science. 2013;342:123–127. doi: 10.1126/science.1243352. [DOI] [PubMed] [Google Scholar]
- 21.Hool L.C., Whalley D.W., Rasmussen H.H. Angiotensin-converting enzyme inhibition, intracellular Na+, and Na+-K+ pumping in cardiac myocytes. Am. J. Physiol. 1995;268:C366–C375. doi: 10.1152/ajpcell.1995.268.2.C366. [DOI] [PubMed] [Google Scholar]
- 22.Hansen P.S., Buhagiar K.A., Rasmussen H.H. Dependence of Na+-K+ pump current-voltage relationship on intracellular Na+, K+, and Cs+ in rabbit cardiac myocytes. Am. J. Physiol. Cell Physiol. 2002;283:C1511–C1521. doi: 10.1152/ajpcell.01343.2000. [DOI] [PubMed] [Google Scholar]
- 23.Garcia A., Rasmussen H.H., Clarke R.J. Kinetic comparisons of heart and kidney Na+,K+-ATPases. Biophys. J. 2012;103:677–688. doi: 10.1016/j.bpj.2012.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Peluffo R.D. Effect of ADP on Na+-Na+ exchange reaction kinetics of Na,K-ATPase. Biophys. J. 2004;87:883–898. doi: 10.1529/biophysj.103.030643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nakao M., Gadsby D.C. [Na] and [K] dependence of the Na/K pump current-voltage relationship in guinea pig ventricular myocytes. J. Gen. Physiol. 1989;94:539–565. doi: 10.1085/jgp.94.3.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schneeberger A., Apell H.-J. Ion selectivity of the cytoplasmic binding sites of the Na,K-ATPase: II. Competition of various cations. J. Membr. Biol. 2001;179:263–273. doi: 10.1007/s002320010051. [DOI] [PubMed] [Google Scholar]
- 27.Ekberg K., Pedersen B.P., Buch-Pedersen M.J. Structural identification of cation binding pockets in the plasma membrane proton pump. Proc. Natl. Acad. Sci. USA. 2010;107:21400–21405. doi: 10.1073/pnas.1010416107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Clausen J.D., Andersen J.P. Glutamate 90 at the luminal ion gate of sarcoplasmic reticulum Ca2+-ATPase is critical for Ca2+ binding on both sides of the membrane. J. Biol. Chem. 2010;285:20780–20792. doi: 10.1074/jbc.M110.116459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sheu S.-S., Fozzard H.A. Transmembrane Na+ and Ca2+ electrochemical gradients in cardiac muscle and their relationship to force development. J. Gen. Physiol. 1982;80:325–351. doi: 10.1085/jgp.80.3.325. [DOI] [PMC free article] [PubMed] [Google Scholar]


