Abstract
Data of a large clinical study were used to investigate how much are the QT/RR patterns in healthy subjects curved and whether these curvatures differ between women and men. Daytime drug-free 12-lead Holter recordings were repeated 4 times in each of 176 female healthy subjects and 176 male healthy subjects aged 32.7 ± 9.1 yr. In each of the subjects, up to 1,440 carefully verified QT interval measurements were obtained with QT/RR hysteresis-corrected RR intervals. Individual subject data were used to fit the following regression equation: QT = χ + (δ/γ)(1 − RRγ) + ε, where QT and RR are QT and RR measurements (in s), χ is regression intercept, δ is the QT/RR slope, γ is the QT/RR curvature and provides the lowest regression residual, and ε represents normally distributed zero-centered errors. The bootstrap technique showed the intrasubject reproducibility of QT/RR slopes and curvatures. In women and men, QT/RR curvatures were 0.544 ± 0.661 and 0.797 ± 0.706, respectively (P = 0.0006). The corresponding QT/RR slopes were 0.158 ± 0.030 and 0.139 ± 0.023, respectively (P < 0.0001). QT/RR curvatures were related to QT/RR slopes but not to individually corrected mean QTc intervals or individual QT/RR hysteresis profiles. The individual heart rate correction formula derived from the curvilinear regression provided a significantly lower intrasubject variability of QTc interval than individual optimisation of linear or log-linear QT/RR heart rate corrections. The QT/RR curvature can be reliable measured and expressed numerically. The corresponding heart rate correction formula provides more compact data than the previously proposed approaches. There are substantial sex differences in QT/RR patterns. Women have a QT/RR pattern that is not only steeper than men but also more curved.
Keywords: QT/RR curvature profile, intrasubject stability, intersubject differences, QT heart rate correction
the dependency of the duration of ventricular repolarization on the underlying heart rate is well known. It is also known that it is related to a similar dependency of action potential durations (7) that shows regional differences within the ventricular myocardium (23). Similarly, delayed adaptation of action potential durations after abrupt changes in stimulation rates are well known (8). The intracellular mechanism underlying the repolarization dependency and thus the pattern of the QT/RR relationship are not completely understood and have been subject of both animal and modeling experiments of ionic currents (11, 19, 22). Why the QT/RR relationship and adaptation exhibits substantial intersubject differences with intrasubject stability (3, 27) is not known. Further studies of the phenomenon require appropriate tools for the description of the relationship.
A number of studies (5, 6, 10, 16) assessed the slope of the QT/RR relationship in long-term Holter recordings and investigated its meaning as a clinical characteristic. The majority of these studies investigated the relationship by means of linear regression between simultaneously measured QT and RR intervals; only infrequently was the linear regression applied to logarithmically transformed QT and RR data. However, the pattern of the QT/RR relationship is not necessarily linear (9) and is known to be frequently steeper at faster heart rates compared with slower heart rates. In studies using a linear QT/RR relationship, this possibly creates a systematic bias when the target clinical populations differ or can be expected to differ in heart rate (4, 6), making the observations of the differences between linear QT/RR slopes potentially erroneous.
The nonlinearity of individual-specific as well as population-derived QT/RR patterns has previously been recognized (13) and dealt with mainly in studies requiring accurate heart rate correction of QT intervals (e.g., in studies of drug-induced changes of rate-corrected QT intervals) in which the application of a strictly linear model may lead to noticeable inaccuracy (26). Since the design of accurate individual QT rate corrections depends on accurate mathematical description of baseline QT/RR relationship (9), it has been proposed to fit different nonlinear models to the data of different individuals, which, in essence, means to classify the curvatures of the QT/RR patterns into several distinct categories (10, 12). While this technology has been used successfully in studies of electrocardiographic drug effects (24, 25), it does not deal with the problem of the QT/RR curvature fully (26). Instead of classification into different ad hoc-selected categories, technology is needed to describe the curvatures of QT/RR patterns on a continuous numeric scale.
With this in mind, we used data of a previous study (25) that obtained repeated Holter recordings in hundreds of healthy subjects to propose numeric measurements of the curvatures of QT/RR patterns and to compare them between healthy women and men since many other aspects of normal cardiac electrophysiology are sex dependent (32).
METHODS
Subjects and electrocardiographic recordings.
Data were obtained from a previously published study (25) that enrolled 176 female healthy subjects and 176 male healthy subjects. Table 1 shows the descriptive characteristics of the population. For the purposes of this investigation, only the QT and RR measurements made in the baseline recordings were considered. The baseline 12-lead Holter recordings (SEER MC version 2, GE Healthcare, Milwaukee, WI) were, per the study protocol, obtained during daytime hours (nominal 14-h duration) on predose days −3 and −1 of two different study periods. These pairs of recordings were separated by 25 days. (That is, in each subject, 4 recordings were obtained on days 1, 3, 26, and 28.) Study subjects were not permitted to sleep while the Holter recordings were obtained, and extra care was taken to ensure the adherence to this requirement. During the recordings, subjects were also not on any medication, did not smoke, and did not consume ethanol- or caffeine-containing drinks.
Table 1.
Demographic characteristics of the investigated population
| Women | Men | P Value, Women Compared With Men | |
|---|---|---|---|
| Number of subjects | 176 | 176 | |
| Age, yr | 33.08 ± 9.87 | 33.57 ± 8.42 | NS |
| Range of ages, yr | 18–55 | 18–54 | |
| Body mass index [kg/m2] | 24.78 ± 2.98 | 25.38 ± 2.64 | NS |
| Race, % | |||
| Black or African | 42.6 | 46.6 | NS |
| White | 52.3 | 46.0 | NS |
| Other | 5.1 | 7.4 | NS |
Age is the age at the first recording; The range of ages shows the ages of the youngest and oldest subjects. Other races included Asian, Native American, Native Hawaiian or other Pacific islander, and unspecified other. NS, not significant.
As previously published (25), the clinical study providing the baseline recordings was ethically approved and conformed with the principles outlined in the Declaration of Helsinki. All study subjects gave written informed consent.
Electrocardiographic measurements.
Using previously published quality assurance techniques (12, 24, 25), QT and RR intervals were measured in repeated 10-s ECG segments of each baseline recording. In addition to segments that corresponded to per-protocol study time points, the segments were also selected based on heart rate scans of the entire recording to obtain wide ranges of heart rates (25). For the same purpose, the per-protocol baseline study time points included repeated postural provocation maneuvers (25). Per protocol, 360 ECG segments were measured in each baseline recording, giving a total of 1,440 baseline measurements/subject. In individual subjects, some of these might have been found to be nonmeasurable, resulting in a smaller number of available measurements (see the results).
In each ECG segment with measurable QT intervals, the 5-min history of RR intervals was obtained, and, in each study subject, a QT/RR hysteresis coefficient was calculated, as previously reported (27). QT/RR hysteresis coefficients were used to derive time constants representing the time lag needed to reach 95% of the QT interval adaptation after the RR interval change (these values are reported here and are termed the “QT/RR hysteresis time constant”). Subsequently, the subject-specific hysteresis profile was applied to the heart rate histories of each QT interval measurement to obtain an RR interval value representative of the underlying heart rate to which the QT interval measurement needs to be related. When RR interval or heart rates are referred to in this text, these hysteresis-derived values are used.
Measurement of QT/RR curvatures.
To quantify the curvature of the individual QT/RR patterns, the data of each subject were fitted with nonlinear regression of the following form:
| (1) |
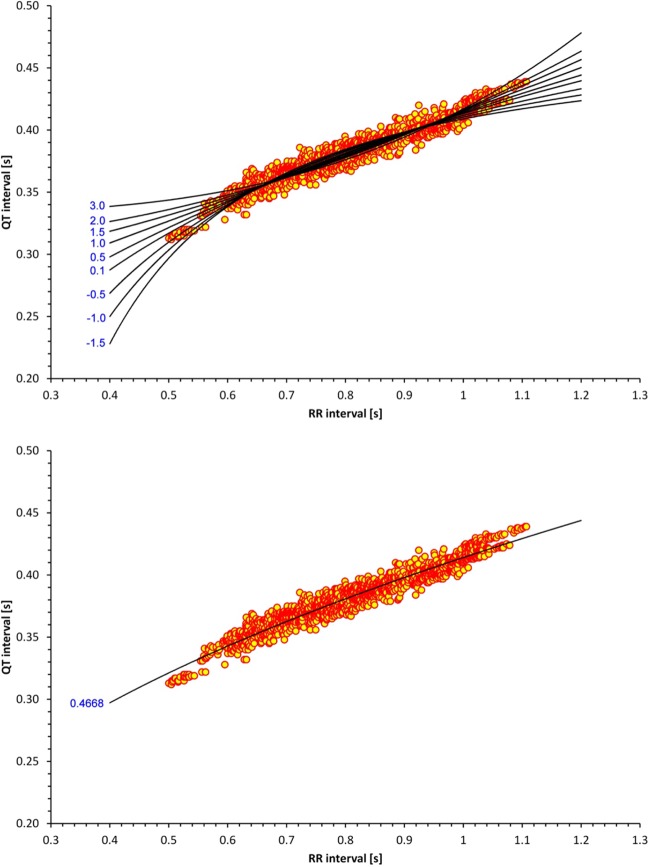
where QTi and RRi are individual QT and RR measurements (in s), respectively, χ and ϕ are derived from linear regression regression analysis, γ is the QT/RR curvature and is derived such that the regression leads to the lowest regression residual, and εi represents normally distributed zero-centered errors. The principle of the methods is shown in Fig. 1. Different values of parameter γ give differently curved regression lines, and the method selects the one that fits the measured data best. The optimum fit was determined by a dedicated software package purpose written in C++ implementing the so-called golden cut algorithm (32).
Fig. 1.
Principle of the nonlinear regression technique. Top: scatter diagram of QT and RR intervals measured in a 30-yr-old woman superimposed by regression lines of different curvatures [the values of the corresponding curvature parameters (γ) are shown on the left]. Of all the different curvatures, the value that fits the data best is selected, i.e., that leads to the lowest regression residual. This is shown in the bottom; γ = 0.4668 was found to be the optimum value in this particular subject.
This nonlinear regression model leads to the following heart rate correction formula:
| (2) |
where QTcI is the individually corrected QT interval, δ is the slope of the QT/RR pattern, and γ is the numeric characteristic of the QT/RR curvature. Note that the fraction δ/γ is needed because the derivative of xγ equals γ at x = 1. That makes the parameter ϕ of Eq. 1 dependent on γ; thus, ϕ equals δ/γ of Eq. 2. When individually corrected QTcI values are referred to in this text, the values calculated according to this formula are shown.
Reproducibility of QT/RR curvatures.
The assessment of QT/RR curvatures and slopes was applied to the QT/RR data of each study subject (merging all the baseline measurements together). To investigate the reproducibility of the curvature and slope measurements, bootstrap technology with repetitions was used (38). In each subject, the bootstrap assessment was repeated 10,000 times to derive intrasubject distributions of QT/RR curvature and slope values. From these distributions, the central values, interquartile ranges (IQRs), and 95% confidence intervals (CIs) of the parameters were derived for each subject.
Comparator heart rate corrections.
To compare the new curve-linear regression analysis with previously proposed approaches, three additional subject-specific heart rate corrections were considered. First, the following linear and log-linear models were used:
with subject-specific optimization (32) of correction parameters αL and αF that guaranteed that in each subject, QTcIL and QTcIF values were uncorrelated to RR interval values. The parameters αL and αF will be referred to as linear and log-linear slopes.
In addition, the previously described battery of 12 different regression models was used selecting a optimum regression formula for each subject (24, 25, 31). QTcI12 values were obtained in this way.
Data comparisons and statistics.
To assess the individuality of QT/RR curvatures and slopes, intrasubject IQRs of these parameters were compared with IQRs of the central values in the population (female and male subjects were assessed separately). Comparisons were made by one-sample two-tailed t-test. The Mann-Whitney test was used to compare numeric differences between women and men as not all measured values were normally distributed. The population distribution of QT/RR curvatures was investigated together with intrasubject 95% CIs. Pearson correlation coefficients were used to investigate the relationship between QT/RR hysteresis time constants, QT/RR curvatures and slopes, individual mean QTcI values, and heart rate ranges and ages of the subjects. To prove that the proposed nonlinear regression model described the individual QT/RR patterns better than the previously proposed approaches, intraindividual SDs of QTcI, QTcIL, QTcIF, and QTcI12 values were compared using a Wincoxon signed-rank test (the variance estimates are not necessarily normally distributed) accompanied by Bland-Altman-like graphs showing the distribution of the differences between the intrasubject SDs of QTcI and of the other QTc values.
Continuous data are presented as means ± SD. Racial proportions of the population were compared by a Fisher exact test. Statistical significance was assumed if P < 0.05. The Statistica software package (StatSoft, Tulsa, OK) was used to perform the statistical tests.
RESULTS
As previously described (25), 21 women (11.9%) and 12 men (6.8%) did not complete the study. However, some of these subjects dropped out only after the baseline recordings of the second period were obtained. Fewer than 1,000 QT/RR measurable baseline readings were available in 13 women (7.4%) and 11 men (6.2%), whereas more that 1,300 QT/RR baseline readings were available in 156 women (88.6%) and 163 men (92.6%).
Table 1 shows that the female and male populations did not differ in age, body mass index, and racial distribution.
Heart rate.
Table 2 shows population data of the slowest and fastest heart rates at which QT intervals were measured as well as the ranges of analyzed heart rates, that is, the differences between the fastest and slowest heart rate at which the QT intervals were measured in the same subject. As expected, both minimum and maximum heart rates were highly significantly higher in women than in men. The ranges of heart rates at which QT intervals were measured were significantly broader in women than in men, but the actual numeric difference was only marginal.
Table 2.
Analyzed heart rates
| Women | Men | P Value, Women Compared With Men | |
|---|---|---|---|
| Maximum heart rate, beats/min | 116.66 ± 13.26 | 109.51 ± 14.30 | <0.0001 |
| Minimum heart rate, beats/min | 53.79 ± 5.91 | 50.35 ± 5.00 | <0.0001 |
| Range of heart rates, beats/min | 62.87 ± 13.52 | 59.16 ± 14.01 | 0.0064 |
The range of heart rates shows within-subject differences between maximum and minimum heart rates at which the QT interval measurements were made.
Individuality of QT/RR patterns.
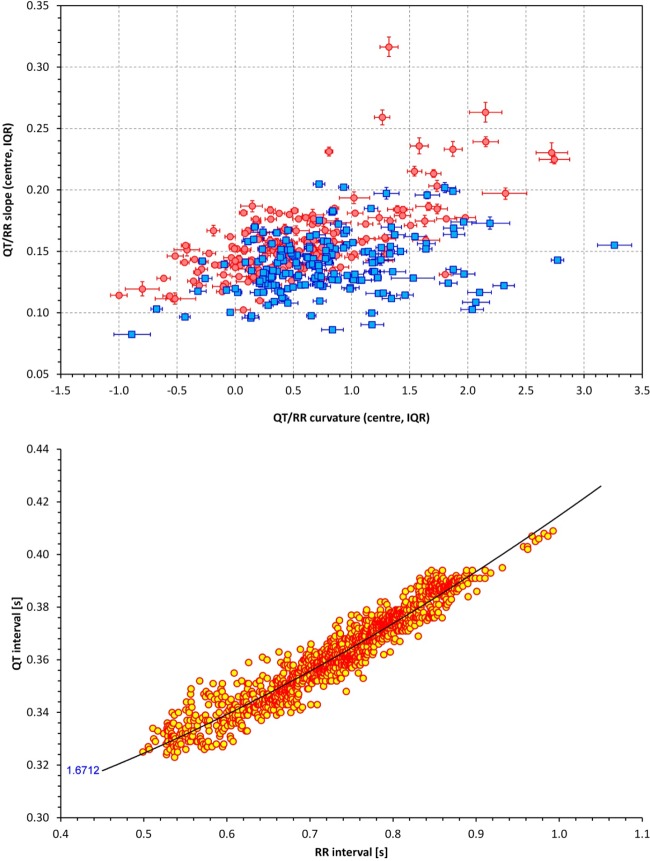
Figure 2, top, shows the scatter diagram of the relationship between QT/RR curvature and slope; intrasubject IQRs are also shown. In women, population IQRs of the central values of QT/RR curvatures and slopes were 0.110–0.839 and 0.139–0.172, respectively. The intrasubject IQRs of these parameters derived from the bootstrap were substantially smaller with IQR widths of 0.127 ± 0.059 for the QT/RR curvature (P < 0.0001 for the comparison with the width of the population IQRs) and 0.0046 ± 0.0030 for the QT/RR slope (P < 0.0001). Similar substantial differences between the population spread and intraindividual spread were found in men, in whom the population IQRs of QT/RR curvatures and slopes were 0.360–1.167 and 0.123–0.152, respectively. The corresponding widths of intraindividual IQRs were 0.117 ± 0.059 (P < 0.0001) and 0.0028 ± 0.0018 (P < 0.0001). Hence, both QT/RR curvatures and QT/RR slopes showed substantial individuality with large differences between different subjects.
Fig. 2.
Top: scatter diagram between QT/RR curvatures and QT/RR slopes, both showing intrasubject interquartile ranges (IQRs; see the text for details). Red/pink circles represent women; blue/cyan squares represent men. Bottom: QT/RR pattern in a 31-yr-old woman in whom the QT/RR pattern was found to be curved upward (curvature measurement of γ = 1.6712).
Surprisingly, in 24 women (13.6%) and 31 men (17.6%), we found the lower 95% CIs of the QT/RR slope to be above 1.0, suggesting that in these individuals, the QT/RR pattern was bent upward. An example of such a situation is shown in Fig. 2, bottom.
Sex differences.
As shown in Table 3, the measured QT/RR characteristics showed substantial sex differences. Compared with men, women adapted their QT interval to heart rate changes faster and had more curved and steeper QT/RR patterns. As expected, the intrasubject mean QTcI interval was much longer in women than in men. The intrasubject variability of QTcI intervals was also significantly larger in women than in men, although this numeric difference between the sex groups was less pronounced.
Table 3.
Measured characteristics of QT/RR profiles
| Women | Men | P Value, Women Compared With Men | |
|---|---|---|---|
| QT/RR hysteresis, s | 113.2 ± 16.6 | 119.1 ± 20.2 | 0.0074 |
| QT/RR curvature | 0.544 ± 0.661 | 0.797 ± 0.706 | <0.0001 |
| QT/RR curvature slope | 0.158 ± 0.030 | 0.139 ± 0.023 | <0.0001 |
| Averaged QTc interval, ms | 418.2 ± 13.0 | 397.0 ± 11.5 | <0.0001 |
| Intrasubject SD of QTc intervals, ms | 5.73 ± 1.14 | 5.37 ± 1.10 | 0.0012 |
QT/RR hysteresis is the calculated time constant needed to reach 95% of QT interval adaptation. SD is ±SD.
Also as expected, log-linear and linear slopes were significantly steeper in women (0.36 ± 0.045, and 0.17 ± 0.028, respectively) than in men (0.33 ± 0.047, P < 0.0001, and 0.14 ± 0.024, P < 0.0001, respectively).
Covariates.
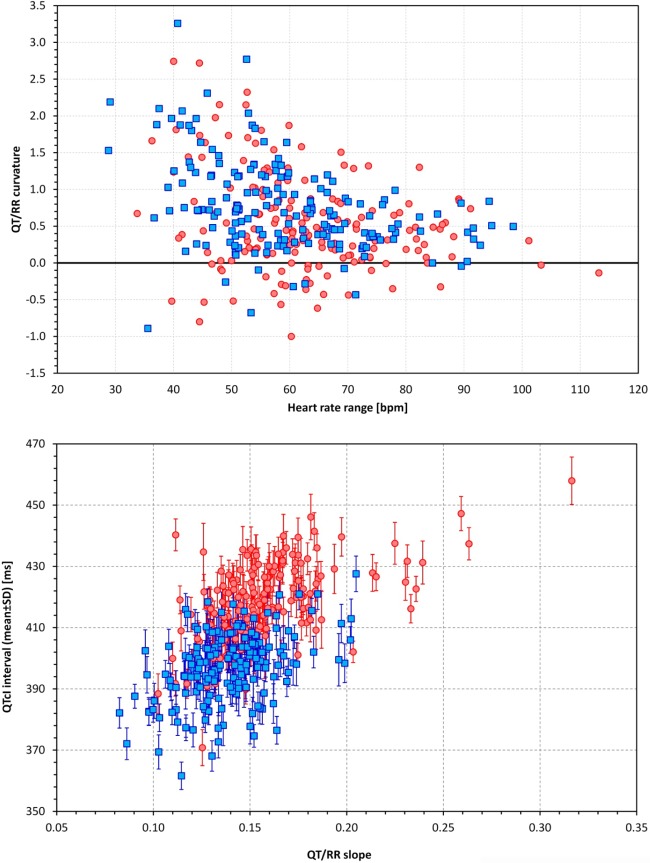
As shown in Fig. 2, top, the QT/RR curvature was correlated to QT/RR slope (r = 0.660 in women and r = 0.266 in men). The curvature was not related to either mean QTcI interval or to the hysteresis time constant. It was, however, correlated to the range of heart rates at which the QT interval was measured (r = −0.267 in women and r = −0.386 in men; Fig. 3, top). On the contrary, QT/RR curvatures were not related to the mean heart rate (calculated over the whole QT/RR pattern).
Fig. 3.
Top: scatter diagram between ranges (differences between maximum and minimum heart rates) at which the QT intervals were measured and QT/RR curvature parameters. Bottom: scatter diagram between QT/RR slopes and intrasubject means of QTcI intervals (QTcI intervals are shown together with their intrasubject SDs). In both graphs, red/pink circles represent women and blue/cyan squares represent men. bpm, beats/min.
The QT/RR slope was not correlated to the hysteresis coefficient, but it was correlated to mean QTcI (r = 0.52 in women and r = 0.43 in men; Fig. 3, bottom). Not surprisingly, the QT/RR slope was also correlated with the linear slope (r = 0.50 in women and r =0.81 in men) and with the log-linear slope (r = 0.44 in women and r = 0.80 in men). However, these slope correlations were not as tight as the correlations between linear and log-linear slopes (r = 0.94 in women and r = 0.93 in men).
The intrasubject QTcI SD was not related to either hysteresis time constants or QT/RR curvature or slope.
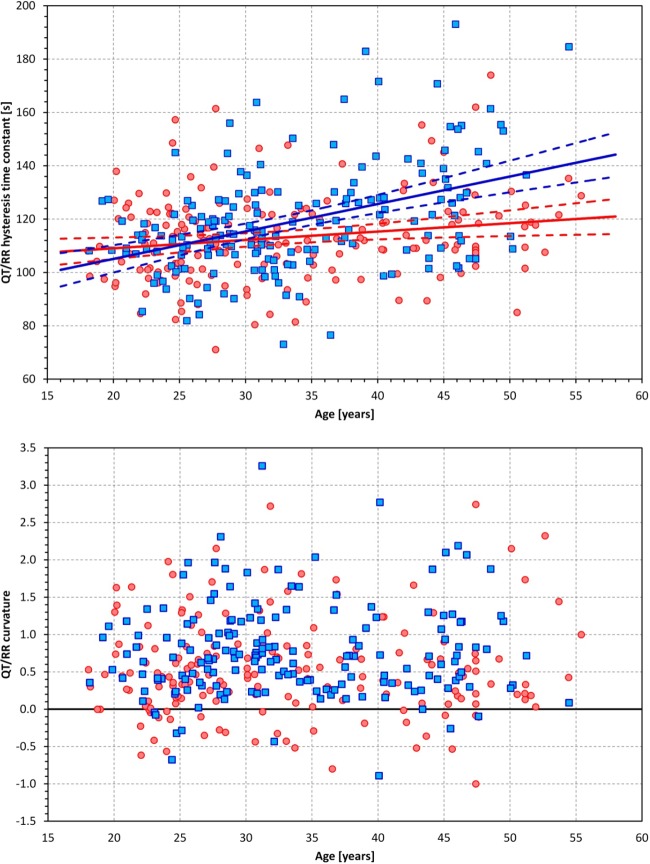
Relationship to age.
Hysteresis time constants were correlated with age (statistically significantly but marginally in women, r = 0.166, and more strongly in men, r = 0.377; Fig. 4, top). Neither QT/RR curvatures (Fig. 4, bottom) nor QT/RR slopes correlated with age. However, the heart rate ranges over which the QT/RR patterns were determined were negatively correlated with age (r = −0.425 in women and r = −0.217 in men). These correlations were caused by age correlations with the maximum heart rate (r = −0.417 in women and r = −0.164 in men), whereas the minimum heart rates were not related to age.
Fig. 4.
Top: scatter diagram between age and the QT/RR hysteresis time constant. The solid and dashed lines show linear regressions together with their 95% confidence intervals. Bottom: scatter diagram of age and QT/RR curvatures. In both graphs, red/pink circles represent women and blue/cyan squares represent men, respectively. The red and blue lines in the top graph correspond to female and male populations, respectively.
Comparison with simpler regressions.
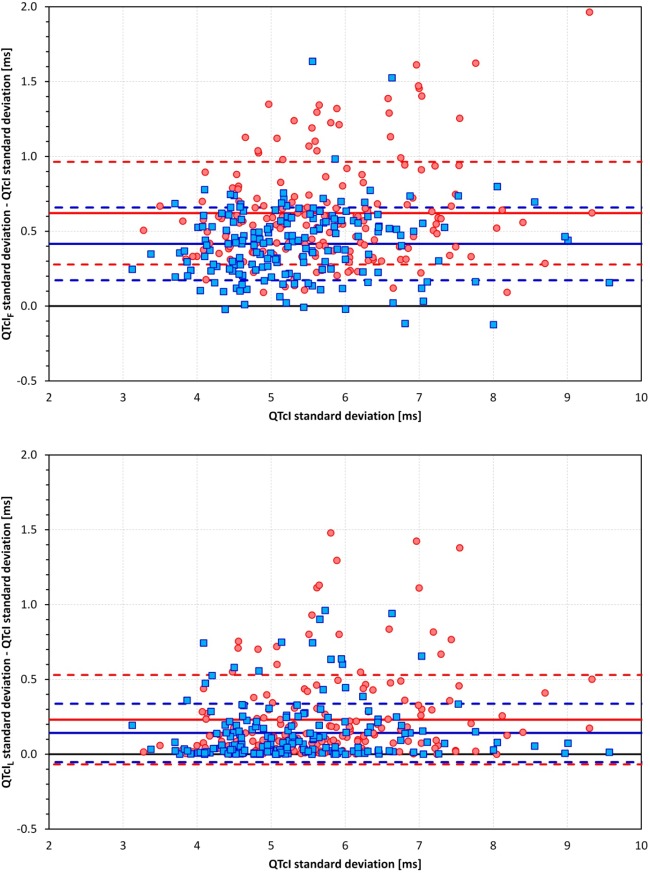
The intrasubject SDs of QTcI were smaller than those of QTcIF, with an averaged reduction of 0.62 ± 0.34 ms (9.71 ± 4.52% of intrasubject SDs of QTcIF, P < 0.0001) and of 0.42 ± 0.24 ms (7.20 ± 3.80%, P < 0.0001) in women and men, respectively. Similar reductions were found for the intrasubject SDs of QTcIL, with averaged reductions of 0.23 ± 0.30 ms (3.61 ± 4.24%, P < 0.0001) in women and 0.14 ± 0.20 ms (2.51 ± 3.26%, P < 0.0001) in men. The corresponding scatter diagrams are shown in Fig. 5.
Fig. 5.
Scatter diagrams between intrasubject SDs of QTcI and differences of intrasubject SDs of QTcIF and SDs of QTcI (top) as well as differences of intrasubject SDs of QTcIL and SDs of QTcI (bottom). In both graphs, red/pink circles represent women and blue/cyan squares represent men, respectively. The full horizontal lines show the mean differences in women (red lines) and men (blue lines). The dashed lines show the corresponding bands of mean ± SD in the population of women (red lines) and men (blue lines).
The reduction of intrasubject SD of QTcI12 was numerically smaller but still highly statistically significant with averaged reductions of 0.029 ± 0.106 ms (0.47 ± 1.74%, P < 0.0001) in women and 0.035 ± 0.145 ms (0.55 ± 2.38%, P < 0.0001) in men.
DISCUSSION
This study shows that the curvature of the QT/RR pattern, i.e., how much nonlinear the pattern is, can be reliably assessed from clinical recordings of good quality. Using the assessment of the curvatures in available data, the study permitted two principal conclusions to be made. First, individual subjects differ not only in the slope of QT/RR patterns but also in the curvatures of the patterns. Second, there are substantial sex differences in QT/RR curvatures, with women having more curved QT/RR patterns than men. In addition, we observed that while the intrasubject curvatures of QT/RR patterns were not related to age, the QT/RR hysteresis appeared to change with age.
The sex differences in the shapes of QT/RR patterns might provide a partial explanation for the clinical differences between women and men (1). Clinical studies in patients are needed to investigate whether the increased curvature of QT/RR patterns (i.e., a lower value of the curvature parameter) indicates an increased propensity to repolarization related proarrhythmia, e.g., drug-induced torsade de pointes.
The curvature measurement by the best-fit regression may seem prone to be influenced by outliers. However, the bootstrap technique showed fairly compact distribution of the results in each subject. There was therefore little influence by a small number of nonrepresentative outliers. Nevertheless, it is not obvious whether the QT/RR pattern in each subject represents a uniform adaptation process or whether it is a mixture of different adaptation processes, e.g., corresponding to different facets of autonomic regulation, each leading to a distinct subset of the overall QT/RR pattern (36, 39).
The observation of the relationship between QT/RR patterns and the range of heart rates at which QT intervals were measured might indicate some technical issues with the data-processing method. However, the lack of correlation with the intrasubject SD of QTcI suggests that the measurements were not influenced by data quality. Since all study subjects underwent the same maneuvers of substantial autonomic provocation, it is more likely that the QT/RR patterns with high values of the curvature parameter appear in subjects in whom the physical provocation leads to a less marked heart rate reaction. (This seems to include subjects in whom the QT/RR pattern is bent upward.) We are unable to speculate on whether this lack of heart rate increase combined with the differently curved QT/RR pattern is an acquired property, e.g., due to physical training or whether it represents a congenital variant.
The relationship between QT/RR slope and intrasubject mean QTc values means that those subjects who show longer QTcI intervals have steeper QT/RR patterns. This observation might be related to the arbitrary convention of correcting the QT interval to the RR interval of 1 s (i.e., heart rate of 60 beats/min). When we attempted to correct the QT interval to different levels of heart rate, we observed a reduction of the intrapopulation spread of QTc values corrected to heart rates around 90 beats/min in both women and men (data not shown here). We are unable to speculate of whether these observations are related to the intrinsic heart rate (2, 17), which was not measured in the study subjects, and whether it would be more physiologically relevant to correct the QT interval for the intrinsic heart rate.
The investigated relationship to age might provide some insights into the mechanistic background of the QT/RR pattern and hysteresis (that is, how much and how quickly the QT interval changes after a change of the underlying heart rate). Although the span of ages in the investigated population was limited, the measured speed of the QT interval adaptation to heart rate appeared to decrease with age. Similar observations of an age-related decline of cardiovascular regulation are well known from heart rate variability and other autonomic regulation studies (21, 28, 33). Indeed, also in this study, we found an age-related decline of cardiovascular reflexes when studying the maximum heart rates captured on the recordings. This likely suggests that QT/RR hysteresis is related to cardiac autonomic reflexes. On the contrary, the lack of an age relationship with QT/RR patterns (both curvature and slope) might suggest that they are determined by cardiac electrophysiology structures such as the geometric distribution of cells with different repolarization properties (15, 30). If islands of cells with different repolarization properties exist in the human myocardium (14, 37), their geometric distribution might easily be individual specific, explaining both the intrasubject stability and intersubject variability of QT/RR patterns.
Apart from these physiological observations, this study has relevant practical implications. Since the measured QTcI values were even less variable in individual subjects than the QTcI12 values, the correction formula for calculating QTcI values may be proposed for investigations in which accurate heart rate-corrected QT values are needed. The problem of forcing a wrong shape of the regression model on individual QT/RR data (26) will be avoided using the formula, whereas QT/RR patterns in all different subjects will be characterized by the same mathematical form. Population risk stratification studies investigating QT/RR patterns would also benefit from this mathematical description avoiding the heart rate influence (note that in our data, the QT/RR curvature was unrelated to mean heart rate).
As far as we know, this is the first study that has measured QT/RR curvatures numerically. We therefore cannot compare our principal results with any previous studies. The sex differences in the mean QTc interval as well as in the linear and log-linear slopes correspond well with previous publications (18, 35). Contrary to a previous report (27), we found statistically significant sex differences in hysteresis time constants (as well as in previously reported hysteresis coefficients; data not shown). This is probably because the present study used a substantially larger data set.
Limitations.
The regression analysis used in the present study assumes that all observations are independent and identically distributed, which is not necessarily the case. With correlated observations, regression slopes might have been underestimated. However, in comparison between women and men, the same bias might be expected. The increased heart rate ranges in our data set have been achieved by postural provocative maneuvers as well as by other uncontrolled provocations to which the study subjects were exposed during the baseline days. As already mentioned, the individual QT/RR patterns are therefore likely a mixture of different regulation processes, which might be different between sexes (34). It has been previously suggested that different autonomic (as well as other) reactions may lead to different QT/RR adaptations (36, 39) and we are unable to separate them. However, the rather small intrasubject SDs of QTcI values (on average around 5 ms in both sexes) suggest that if there are any differences in QT/RR adaptations in response to different reactions, these were either not present in our data or the differences between them are fairly small. The correlation between slope and curvature might be related to the normalization of slope in Eq. 2 at RR of 1 s while averaged heart rates were faster than 60 beats/min, especially in women. Since the QT interval duration is influenced by sleep and sleep stages (20, 29), the original clinical study restricted the Holter recordings to daytime hours. We are therefore unable to comment on the curvature and other properties of QT/RR patterns obtained during the night. However, because of the sleep influence on cardiac repolarization, this limitation poses little practical restriction. Finally, we used a monoparametric exponential decay model of QT/RR hysteresis. All limitations of this approach thus apply (27).
Conclusions.
Despite the limitations, this study permitted us to conclude that QT/RR curvature can be reliable measured and expressed numerically. The corresponding heart rate correction formula provides more compact data than previously proposed approaches. There are substantial sex differences in QT/RR patterns. Women have QT/RR patterns that are not only steeper than men but also more curved. Women also appear to adapt the QT interval duration to changes in RR interval faster than men. In both sexes, the QT interval adaptation to the RR interval changes appears to slow with advancing age.
GRANTS
This work was supported in part by British Heart Foundation Grant PG/12/77/29857.
DISCLOSURES
During the study that provided the data analyzed here, M. Malik was a consultant to Astellas. D. Kowalski, J. J. Keirns, and E. M. van Gelderen are employees of Astellas.
AUTHOR CONTRIBUTIONS
Author contributions: M.M. conception and design of research; M.M., K.H., D.K., and E.M.v.G. analyzed data; M.M., K.H., D.K., J.J.K., and E.M.v.G. interpreted results of experiments; M.M. and K.H. prepared figures; M.M. drafted manuscript; M.M., K.H., D.K., J.J.K., and E.M.v.G. approved final version of manuscript.
REFERENCES
- 1.Abi-Gerges N, Philp K, Pollard C, Wakefield I, Hammond TG, Valentin JP. Sex differences in ventricular repolarization: from cardiac electrophysiology to torsades de pointes. Fundam Clin Pharmacol 18: 139–151, 2004 [DOI] [PubMed] [Google Scholar]
- 2.Alboni P, Malacarne C, Pedroni P, Masoni A, Narula OS. Electrophysiology of normal sinus node with and without autonomic blockade. Circulation 65: 1236–1242, 1982 [DOI] [PubMed] [Google Scholar]
- 3.Batchvarov VN, Ghuran A, Smetana P, Hnatkova K, Harries M, Dilaveris P, Camm AJ, Malik M. QT-RR relationship in healthy subjects exhibits substantial intersubject variability and high intrasubject stability. Am J Physiol Heart Circ Physiol 282: H2356–H2363, 2002 [DOI] [PubMed] [Google Scholar]
- 4.Chevalier P, Burri H, Adeleine P, Kirkorian G, Lopez M, Leizorovicz A, André-Fouët X, Chapon P, Rubel P, Touboul P; Groupe d'Etude du Pronostic de l'Infarctus du Myocarde QT dynamicity and sudden death after myocardial infarction: results of a long-term follow-up study. J Cardiovasc Electrophysiol 14: 227–233, 2003 [DOI] [PubMed] [Google Scholar]
- 5.Couderc JP, Xia X, Denjoy I, Extramiana F, Maison-Blanche P, Moss AJ, Zareba W, Lopes CM. Genotype- and sex-specific QT-RR relationship in the type-1 long-QT syndrome. J Am Heart Assoc 1: e000570, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cygankiewicz I, Zareba W, Vazquez R, Almendral J, Bayes-Genis A, Fiol M, Valdes M, Macaya C, Gonzalez-Juanatey JR, Cinca J, Bayes de Luna A; MUSIC Investigators Prognostic value of QT/RR slope in predicting mortality in patients with congestive heart failure. J Cardiovasc Electrophysiol 19: 1066–1072, 2008 [DOI] [PubMed] [Google Scholar]
- 7.Franz MR, Schaefer J, Schöttler M, Seed WA, Noble MI. Electrical and mechanical restitution of the human heart at different rates of stimulation. Circ Res 53: 815–822, 1983 [DOI] [PubMed] [Google Scholar]
- 8.Franz MR, Swerdlow CD, Liem LB, Schaefer J. Cycle length dependence of human action potential duration in vivo. Effects of single extrastimuli, sudden sustained rate acceleration and deceleration, and different steady-state frequencies. J Clin Invest 82: 972–979, 1988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Garnett CE, Zhu H, Malik M, Fossa AA, Zhang J, Badilini F, Li J, Darpö B, Sager P, Rodriguez I. Methodologies to characterize the QT/corrected QT interval in the presence of drug-induced heart rate changes or other autonomic effects. Am Heart J 163: 912–930, 2012 [DOI] [PubMed] [Google Scholar]
- 10.Genovesi S, Prata Pizzala DM, Pozzi M, Ratti L, Milanese M, Pieruzzi F, Vincenti A, Stella A, Mancia G, Stramba-Badiale M. QT interval prolongation and decreased heart rate variability in cirrhotic patients: relevance of hepatic venous pressure gradient and serum calcium. Clin Sci (Lond) 116: 851–859, 2009 [DOI] [PubMed] [Google Scholar]
- 11.Grandi E, Pasqualini FS, Bers DM. A novel computational model of the human ventricular action potential and Ca transient. J Mol Cell Cardiol 48: 112–121, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hnatkova K, Smetana P, Toman O, Bauer A, Schmidt G, Malik M. Systematic comparisons of electrocardiographic morphology increase the precision of QT interval measurement. Pacing Clin Electrophysiol 32: 119–130, 2009 [DOI] [PubMed] [Google Scholar]
- 13.Jacquemet V, Dubé B, Knight R, Nadeau R, LeBlanc AR, Sturmer M, Becker G, Vinet A, Kuś T. Evaluation of a subject-specific transfer-function-based nonlinear QT interval rate-correction method. Physiol Meas 32: 619–635, 2011 [DOI] [PubMed] [Google Scholar]
- 14.Janse MJ, Coronel R, Opthof T. Counterpoint: M cells do not have a functional role in the ventricular myocardium of the intact heart. Heart Rhythm 8: 934–937, 2011 [DOI] [PubMed] [Google Scholar]
- 15.Janse MJ, Coronel R, Opthof T, Sosunov EA, Anyukhovsky EP, Rosen MR. Repolarization gradients in the intact heart: transmural or apico-basal? Prog Biophys Mol Biol 109: 6–15, 2012 [DOI] [PubMed] [Google Scholar]
- 16.Järvenpää J, Oikarinen L, Korhonen P, Väänänen H, Toivonen L, Viitasalo M. Dynamic QT/RR relationship in post-myocardial infarction patients with and without cardiac arrest. Scand Cardiovasc J 44: 352–358, 2010 [DOI] [PubMed] [Google Scholar]
- 17.Jose AD, Collison D. The normal range and determinants of the intrinsic heart rate in man. Cardiovasc Res 4: 160–167, 1970 [DOI] [PubMed] [Google Scholar]
- 18.Kligfield P, Lax KG, Okin PM. QT interval-heart rate relation during exercise in normal men and women: definition by linear regression analysis. J Am Coll Cardiol 28: 1547–1555, 1996 [DOI] [PubMed] [Google Scholar]
- 19.Knollmann BC, Schober T, Petersen AO, Sirenko SG, Franz MR. Action potential characterization in intact mouse heart: steady-state cycle length dependence and electrical restitution. Am J Physiol Heart Circ Physiol 292: H614–H621, 2007 [DOI] [PubMed] [Google Scholar]
- 20.Krasemann T, Strompen C, Blumenberg J, Gehrmann J, Burkhardtsmaier G, Vogt J. Changes of the corrected QT interval in healthy boys and girls over day and night. Eur Heart J 30: 202–208, 2009 [DOI] [PubMed] [Google Scholar]
- 21.Kuo TB, Lin T, Yang CC, Li CL, Chen CF, Chou P. Effect of aging on gender differences in neural control of heart rate. Am J Physiol Heart Circ Physiol 277: H2233–H2239, 1999 [DOI] [PubMed] [Google Scholar]
- 22.de Lange E, Kucera JP. The transfer functions of cardiac tissue during stochastic pacing. Biophys J 96: 294–311, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Litovsky SH, Antzelevitch C. Rate dependence of action potential duration and refractoriness in canine ventricular endocardium differs from that of epicardium: role of the transient outward current. J Am Coll Cardiol 14: 1053–1066, 1989 [DOI] [PubMed] [Google Scholar]
- 24.Malik M, Andreas JO, Hnatkova K, Hoeckendorff J, Cawello W, Middle M, Horstmann R, Braun M. Thorough QT/QTc study in patients with advanced Parkinson's disease: cardiac safety of rotigotine. Clin Pharmacol Ther 84: 595–603, 2008 [DOI] [PubMed] [Google Scholar]
- 25.Malik M, van Gelderen EM, Lee JH, Kowalski DL, Yen M, Goldwater R, Mujais SK, Schaddelee MP, de Koning P, Kaibara A, Moy SS, Keirns JJ. Proarrhythmic safety of repeat doses of mirabegron in healthy subjects: a randomized, double-blind, placebo-, and active-controlled thorough QT study. Clin Pharmacol Ther 92: 696–706, 2012 [DOI] [PubMed] [Google Scholar]
- 26.Malik M, Hnatkova K, Kowalski D, Keirns JJ, van Gelderen EM. Importance of subject-specific QT/RR curvatures in the design of individual heart rate corrections of the QT interval. J Electrocardiol 45: 571–581, 2012 [DOI] [PubMed] [Google Scholar]
- 27.Malik M, Hnatkova K, Novotny T, Schmidt G. Subject-specific profiles of QT/RR hysteresis. Am J Physiol Heart Circ Physiol 295: H2356–H2363, 2008 [DOI] [PubMed] [Google Scholar]
- 28.Monahan KD, Dinenno FA, Seals DR, Clevenger CM, Desouza CA, Tanaka H. Age-associated changes in cardiovagal baroreflex sensitivity are related to central arterial compliance. Am J Physiol Heart Circ Physiol 281: H284–H289, 2001 [DOI] [PubMed] [Google Scholar]
- 29.Nalivaiko E, Catcheside PG, Adams A, Jordan AS, Eckert DJ, McEvoy RD. Cardiac changes during arousals from non-REM sleep in healthy volunteers. Am J Physiol Regul Integr Comp Physiol 292: R1320–R1327, 2007 [DOI] [PubMed] [Google Scholar]
- 30.Okada J, Washio T, Maehara A, Momomura S, Sugiura S, Hisada T. Transmural and apicobasal gradients in repolarization contribute to T-wave genesis in human surface ECG. Am J Physiol Heart Circ Physiol 301: H200–H208, 2011 [DOI] [PubMed] [Google Scholar]
- 31.Pueyo E, Smetana P, Caminal P, de Luna AB, Malik M, Laguna P. Characterization of QT interval adaptation to RR interval changes and its use as a risk-stratifier of arrhythmic mortality in amiodarone-treated survivors of acute myocardial infarction. IEEE Trans Biomed Eng 51: 1511–1520, 2004 [DOI] [PubMed] [Google Scholar]
- 32.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C. The Art of Scientific Computing. New York, NY: Cambridge Univ. Press, 1992 [Google Scholar]
- 33.Sakata S, Hayano J, Mukai S, Okada A, Fujinami T. Aging and spectral characteristics of the nonharmonic component of 24-h heart rate variability. Am J Physiol Regul Integr Comp Physiol 276: R1724–R1731, 1999 [DOI] [PubMed] [Google Scholar]
- 34.Smetana P, Malik M. Sex differences in cardiac autonomic regulation and in repolarisation electrocardiography. Pflügers Arch 465: 699–717, 2013 [DOI] [PubMed] [Google Scholar]
- 35.Stramba-Badiale M, Locati EH, Martinelli A, Courville J, Schwartz PJ. Gender and the relationship between ventricular repolarization and cardiac cycle length during 24-h Holter recordings. Eur Heart J 18: 1000–1006, 1997 [DOI] [PubMed] [Google Scholar]
- 36.Sundaram S, Carnethon M, Polito K, Kadish AH, Goldberger JJ. Autonomic effects on QT-RR interval dynamics after exercise. Am J Physiol Heart Circ Physiol 294: H490–H497, 2008 [DOI] [PubMed] [Google Scholar]
- 37.Wilson LD, Jennings MM, Rosenbaum DS. Point: M cells are present in the ventricular myocardium. Heart Rhythm 8: 930–933, 2011 [DOI] [PubMed] [Google Scholar]
- 38.Wu CFJ. Jackknife, bootstrap and other resampling methods in regression analysis. Ann Statistics 14: 1261–1350, 1986 [Google Scholar]
- 39.Xhaët O, Argacha JF, Pathak A, Gujic M, Houssiere A, Najem B, Degaute JP, Van de Borne P. Sympathoexcitation increases the QT/RR slope in healthy men: differential effects of hypoxia, dobutamine, and phenylephrine. J Cardiovasc Electrophysiol 19: 178–184, 2008 [DOI] [PubMed] [Google Scholar]