Estimation of Treatment Effect for the Sequential Parallel Design

Summary

The sequential parallel clinical trial is a novel clinical trial design being used in psychiatric diseases which are known to have potentially high placebo response rates. The design consists of an initial parallel trial of placebo versus drug augmented by a second parallel trial of placebo versus drug in the placebo non-responders from the initial trial. Statistical research in the design has focused on hypothesis tests. However, an equally important output from any clinical trial is the estimate of treatment effect and variability around that estimate. In the sequential parallel trial, the most important treatment effect is the effect in the overall population. This effect can be estimated by considering only the first phase of the trial but this ignores useful information from the second phase of the trial. We develop estimates of treatment effect which incorporate data from both phases of the trial. Our simulations and a real data example suggest that there can be substantial gains in precision by incorporating data from both phases. The potential gains appear to be greatest in moderate sized trials which would typically be the case in Phase II trials.

1. Introduction

In psychiatry, randomized, double-blind, placebo controlled clinical trials are necessary to determine the efficacy of a new treatment. However, even for drugs which are known to be effective, such trials have a high failure rate. Khan et al. [1] reviewed the data from nine antidepressants approved by the United States Food and Drug Administration between 1985 and 2000. For these antidepressants, there were 51 randomized, double-blind, placebo-controlled trials and 92 treatment arms with an eventually approved dose; however of these 92 arms, only 45 showed statistically significant separation compared to placebo. Further analysis of the data suggests that high placebo response is the major contributor to the problem of high type II error.

In order to address the placebo response, Fava et al. [2] proposed a novel design aimed at increasing the efficiency of placebo controlled psychiatric clinical trials. The basic idea is that in addition to an initial phase of a standard parallel design, there is a second phase in which patients initially randomized to placebo and who have not responded are randomized to drug or placebo. The inference on treatment is based on a combined analysis of both the initial and second phases of the study. Fava et al. [2,3] called this design the sequential parallel design.

The sequential parallel design is an example of an enrichment design [4] in which the enrichment is the population of placebo non-responders. In contrast to other enrichment designs, however, the primary population of interest in the sequential parallel design is the overall population of depressed patients. This is because in clinical practice, it would be unethical to initiate patients on placebo and wait to observe their response. The null hypothesis of the sequential parallel design is that there is no treatment effect in either the overall population or the subpopulation of placebo non-responders. If it can be assumed that placebo responders are also drug responders, then a significant effect in the subpopulation implies a significant effect in the overall population. Fava et al. [2] proposed a weighted sum of the observed treatment differences over the two phases to test the null hypothesis of no treatment effect in either the overall or the subpopulation of placebo non-responders. Huang and Tamura [5] proposed a score statistic under the assumption of equal treatment effect in the two phases of the study. Ivanova et al. [6] extended the score statistic under the more general assumption that the ratio of treatment effect in the two phases is known. Whichever statistic is chosen, the efficiency of the design can be substantially increased over the traditional parallel design.

In addition to testing of a statistical hypothesis, a second goal of a clinical trial is to yield an estimate of the treatment effect and an associated confidence interval. Although the treatment effect in the population of placebo non-responders may be interesting, the more important treatment effect is the effect in the overall population. How should one estimate the treatment effect in the overall population from a sequential parallel design? One obvious possibility to estimate the treatment effect in the overall population by only considering the data from the first phase of the trial. The usual estimated treatment effect from the first phase will be unbiased and the confidence intervals will have correct coverage if the study is large enough. This approach, however, fails to use any data from the second phase of the study and hence may be inefficient. Standard confidence intervals using only the first phase of the design may result in inconsistencies with the statistical test since the test uses information from both phases. The goal of this manuscript is to explore various options for estimating the treatment effect in the overall population while incorporating information from both phases of the study. We consider binary endpoints and measure the treatment effect as the difference in response rates. In Section 2, we describe the various methods under consideration and in Section 3, we compare the finite sample properties of these estimates and their approximate 95% confidence intervals by simulation. In Section 4, we apply the methods to a recently presented sequential parallel trial of L-methylfolate in the augmentation treatment of depression. We summarize our findings and recommendations in Section 5.

2. Description of Design and Estimators

2.1 Sequential Parallel Design

Assume that the clinical trial consists of a single drug and a placebo. In the sequential parallel design, patients are typically randomized into three groups. The basic idea is that there are two phases of treatment with the duration of each phase sufficiently long for the drug to elicit a response. In trials of major depressive disorder, a four to six week duration for each phase would be reasonable. The three treatment groups are characterized by the choice of placebo or drug in each phase. The first group receives placebo in both phases of the study, the second group receives placebo in the first phase and drug in the second phase, and the third group receive drug in both phases. Patients are randomized to the three groups according to an a : a : (1−2a) ratio where $0<a<\frac{1}{2}$. Typically, a is chosen to initially allocate more patients to placebo yet be easy to implement. For example, a=1/3 leads to 1:1:1, and a=3/8 leads to 3:3:2. All patients in all three groups typically continue through both phases and the blind is maintained throughout the study. When assessing the treatment effect, information is used from all randomized patients in the first phase but only from the first phase placebo non-responders in the second phase. Define p₁ = P (drug response_{first phase}), and q₁ = P (placebo response_{first phase}) as the probabilities of being a drug responder and a placebo responder, in the first phase; define p₂ = P (drug response_{second phase}|placebo non–responder_{first phase}) and q₂ = P (placebo response_{second phase}|placebo non–responder_{first phase}) as the conditional probabilities of being a drug responder and a placebo responder in the second phase given that the patients are placebo non-responders in the first phase; the sequential parallel design is shown in Table 1.

Table 1.

Sequential parallel trial design.

Treatment		Response
First phase	Second phase	First phase	Second phase	Frequency	Probability
Number of patients allocated
Placebo	Placebo	No	Yes	n11	(1 − q1)q2
	na	No	No	n12	(1 − q1)(1 − q2)
		Yes		n13	q1
Placebo	Drug	No	Yes	n21	(1 − q1)p2
	na	No	No	n22	(1 − q1)(1 − p2)
		Yes		n23	q1
Drug	Drug	Yes		n31	p1
	n(1 − 2a)	No		n32	1−p1

The total sample size of the trial is n. In the placebo-placebo treated group, n₁₁ is the observed number of non-responders in the first phase and responders in the second phase, n₁₂ is the observed number of non-responders in both phases, and n₁₃ is the observed number of responders in the first phase. In the placebo-drug treated group, n₂₁ is the observed number of non-responders in first phase and responders in the second phase, n₂₂ is the observed number of non-responders in both phases, and n₂₃ is the observed number of responders in the first phase. In the drug-drug treated group, n₃₁ and n₃₂ are the observed number of responders and non-responders, respectively, in the first phase.

2.2 Maximum Likelihood Estimator

Consider the case where the treatment effect is potentially different in the two phases of the study. The joint likelihood for n₁₁, n₁₂, n₁₃, n₂₁, n₂₂, n₂₃, n₃₁ and n₃₂ is

$$L(p_1,q_1,p_2,q_2)\propto p_1^{n_{31}}{\left(1-p_1\right)}^{n(1-2a)-n_{31}}{q}_1^{n_{13}+n_{23}}{(1-q_1)}^{2na-(n_{13}+n_{23})}{q}_2^{n_{11}}{(1-q_2)}^{n_{12}}{p}_2^{n_{21}}{(1-p_2)}^{n_{22}}$$

The MLE can be obtained by setting the first derivatives of logL(p₁, q₁, p₂, q₂) to 0 and solving, which results in:

$$\begin{array}{llll}{\widehat{p}}_1=\frac{n_{31}}{n(1-2a)},\hfill & {\widehat{q}}_1=\frac{n_{13}+n_{23}}{2na},\hfill & {\widehat{p}}_2=\frac{n_{21}}{n_{21}+n_{22}},\hfill & \hfill \end{array}{\widehat{q}}_2=\frac{n_{11}}{n_{11}+n_{12}}$$

Define

$$\begin{array}{l}\theta =\left(\begin{array}{l}{p}_1\hfill \\ q_1\hfill \\ p_2\hfill \\ q_2\hfill \end{array}\right)\end{array}$$

then the information matrix of θ is $I(\theta )=\frac{1}{n}E\{-\frac{{\partial }^2}{\partial \theta \partial {\theta }^T}\mathit{log}L(p_1,q_1,p_2,q_2)\}$:

$$I(\theta )=\left(\begin{array}{cccc}\frac{1-2a}{p_1(1-p_1)}& 0& 0& 0\\ 0& \frac{2a}{q_1(1-q_1)}& 0& 0\\ 0& 0& \frac{a(1-q_1)}{p_2(1-p_2)}& 0\\ 0& 0& 0& \frac{a(1-q_1)}{q_2(1-q_2)}\end{array}\right)$$

Thus, we expect from the general theory that the MLEs θ̂_MLE = (p̂₁ q̂₁ p̂₂ q̂₂)^T are asymptotically normally distributed with mean θ and covariance matrix

$${\sum }_{{\widehat{\theta }}_{\mathit{\text{MLE}}}}=\frac{1}{n}I{(\theta )}^{-1}=\frac{1}{n}\left(\begin{array}{cccc}\frac{p_1(1-p_1)}{1-2a}& 0& 0& 0\\ 0& \frac{q_1(1-q_1)}{2a}& 0& 0\\ 0& 0& \frac{p_2(1-P_2)}{a(1-q_1)}& 0\\ 0& 0& 0& \frac{q_2(1-q_2)}{a(1-q_1)}\end{array}\right)$$

If we define Δ = p₁ − q₁, then Δ̂_MLE = p̂₁ − q̂₁. This estimator utilizes only data from the first phase and we will refer to it as the Phase 1 estimator.

2.3 Constrained Maximum-Likelihood Estimator

In order to utilize data from the second phase, one needs to make assumptions about the relationship between p₁, q₁, p₂, and q₂. One possibility is to make the assumption of equal treatment effect in the two stages, as was proposed by Huang and Tamura [5] for inferential testing. Define p₁ − q₁ = p₂ − q₂ = Δ. Then the joint likelihood function for n₁₁, n₁₂, n₁₃, n₂₁, n₂₂, n₂₃, n₃₁ and n₃₂ can be written as:

$$L(\mathrm{\Delta },q_1,q_2)\propto {(q_1+\mathrm{\Delta })}^{n_{31}}{(1-(q_1+\mathrm{\Delta }))}^{n(1-2a)-n_{31}}{q}_1^{n_{13}+n_{23}}{(1-q_1)}^{2na-(n_{13}+n_{23})}{q}_2^{n_{11}}{(1-q_2)}^{n_{12}}{(q_2+\mathrm{\Delta })}^{n_{21}}{(1-(q_2+\mathrm{\Delta }))}^{n_{22}}$$

Define

$${\theta }_C=\left(\begin{array}{l}\mathrm{\Delta }\hfill \\ q_1\hfill \\ q_2\hfill \end{array}\right)$$

The first derivatives of logL(Δ, q₁, q₂) are:

$$\begin{gathered} \frac{\partial \mathit{log}L(\mathrm{\Delta },q_1,q_2)}{\partial {\theta }_C}= \\ \left(\begin{array}{l}\begin{array}{c}\frac{n_{31}}{q_1+\mathrm{\Delta }}-\frac{n(1-2a)-n_{31}}{1-(q_1+\mathrm{\Delta })}+\frac{n_{21}}{q_2+\mathrm{\Delta }}-\frac{n_{22}}{1-(q_2+\mathrm{\Delta })}\\ \frac{n_{31}}{q_1+\mathrm{\Delta }}-\frac{n(1-2a)-n_{31}}{1-(q_1+\mathrm{\Delta })}+\frac{n_{13}+n_{23}}{q_1}-\frac{2na-(n_{13}+n_{23})}{1-q_1}\\ \frac{n_{11}}{q_2}-\frac{n_{12}}{1-q_2}+\frac{n_{21}}{q_2+\mathrm{\Delta }}-\frac{n_{22}}{1-(q_2+\mathrm{\Delta })}\end{array}\hfill \end{array}\right) \end{gathered}$$

There is no closed form solution for the MLE of θ_C. The MLE for these parameters have to be obtained via numerical methods. The information matrix of θ is $I({\theta }_C)=\frac{1}{n}E\left\{-\frac{{\partial }^2}{\partial {\theta }_C\partial {\theta }_C^T}\mathit{log}L(\mathrm{\Delta },q_1,q_2)\right\}$ :

$$\left(\begin{array}{ccc}\frac{1-2a}{(q_1+\mathrm{\Delta })(1-(q_1+\mathrm{\Delta }))}+\frac{a(1-q_1)}{(q_2+\mathrm{\Delta })(1-(q_2+\mathrm{\Delta }))}& \frac{1-2a}{(q_1+\mathrm{\Delta })(1-(q_1+\mathrm{\Delta }))}& \frac{a(1-q_1)}{(q_2+\mathrm{\Delta })(1-(q_2+\mathrm{\Delta }))}\\ \frac{1-2a}{(q_1+\mathrm{\Delta })(1-(q_1+\mathrm{\Delta }))}& \frac{1-2a}{(q_1+\mathrm{\Delta })(1-(q_1+\mathrm{\Delta }))}+\frac{2a}{q_1(1-q_1)}& 0\\ \frac{a(1-q_1)}{(q_2+\mathrm{\Delta })(1-(q_2+\mathrm{\Delta }))}& 0& \frac{a(1-q_1)}{(q_2+\mathrm{\Delta })(1-(q_2+\mathrm{\Delta }))}+\frac{a(1-q_1)}{q_2(1-q_2)}\end{array}\right)$$

The constrained MLE (constraint of equal treatment effect) θ̂_CMLE = (Δ̂, q̂₁, q̂₂)^T are approximately normally distributed with mean θ_C and asymptotic covariance matrix ${\sum }_{{\widehat{\theta }}_{\mathit{\text{CMLE}}}}=\frac{1}{n}I{({\theta }_C)}^{-1}$.

2.4 Alternative Treatment Estimator

The assumption of equal treatment effect in the two phases may be clinically debatable because the two populations are different. The overall population however can be envisioned to consist of two subpopulations, the subpopulation of placebo non-responders and the subpopulation of placebo responders. Thus the overall treatment effect Δ can be written as:

$$\mathrm{\Delta }=q_1{\mathrm{\Delta }}_{\mathit{\text{RES}}}+(1-q_1){\mathrm{\Delta }}_{\mathit{\text{NRES}}}$$

where Δ_RES and Δ_NRES represent the treatment effect in responders and non-responders, respectively. Suppose we assume that within the population of placebo responders, all patients also respond to drug. Then Δ_RES = 0. This assumption is referred to as the monotonicity assumption in the causal effects literature and needs to be examined on a case by case basis when considering a sequential parallel design. Without this assumption, the inference from the design becomes problematic because a significant test statistic could arise solely from the population of placebo non-responders.

The quantity p₂−q₂ represents the treatment effect in placebo non-responders after being treated by placebo. If one assumes that the initial placebo treatment does not affect the treatment effect in placebo non-responders, then Δ_NRES = p₂ − q₂. We call this assumption the constancy of treatment effects. Under monotonicity and constancy assumptions, an alternative estimator of the overall treatment effect is:

$${\widehat{\mathrm{\Delta }}}_2=(1-{\widehat{q}}_1)({\widehat{p}}_2-{\widehat{q}}_2)$$

2.5 Linear Combination Estimator

The assumptions of monotonicity and constancy of treatment effect in placebo non-responders would be difficult to verify in practice. Thus, rather than relying on Δ̂₂ alone, we consider linear combinations of the two estimators Δ̂_MLE and Δ̂₂. Serfling [7, p.127] shows that the optimal (minimal variance) linear combination of two estimators that are jointly asymptotically normal is a function of the elements of the asymptotic covariance matrix.

If the covariance matrix of (Δ̂_MLE, Δ̂₂) is denoted:

$$\sum =\left(\begin{array}{cc}{\sum }_{11}& {\sum }_{12}\\ {\sum }_{21}& {\sum }_{22}\end{array}\right)$$

then the linear combination ${\widehat{\mathrm{\Delta }}}_O=w{\widehat{\mathrm{\Delta }}}_{\mathit{\text{MLE}}}+(1-w){\widehat{\mathrm{\Delta }}}_2$ with minimum variance occurs when

$$w=\frac{{\sum }_{22}-{\sum }_{12}}{{\sum }_{11}-2{\sum }_{12}+{\sum }_{22}}.$$

At this value of w, the asymptotic variance of the linear combination times n is

$$({\sum }_{11}{\sum }_{22}-{\sum }_{12}^2)/({\sum }_{11}-2{\sum }_{12}+{\sum }_{22})$$ (1)

For the two estimators Δ̂_MLE and Δ̂₂, the delta method yields the asymptotic covariance matrix

$$\begin{gathered} \sum \\ =\frac{1}{n}\left(\begin{array}{cc}\frac{p_1(1-p_1)}{1-2a}+\frac{q_1(1-q_1)}{2a}& \frac{(p_2-q_2)q_1(1-q_1)}{2a}\\ \frac{(p_2-q_2)q_1(1-q_1)}{2a}& \frac{{(p_2-q_2)}^2{q}_1(1-q_1)}{2a}+\frac{(1-q_1)p_2(1-p_2)}{a}+\frac{(1-q_1)q_2(1-q_2)}{a}\end{array}\right) \end{gathered}$$ (2)

Thus Δ̂_O is asymptotically normal with mean w(p₁ − q₁) + (1 − w)(p₂− q₂) and variance given by (1) with the values of Σ_ij taken from (2). When p₁ − q₁ = (1 − q₁)(p₂− q₂), the asymptotic mean of Δ̂_O is p₁− q₁ and Δ̂_O is asymptotically unbiased.

Table 2 gives the values for the asymptotic variance (×n) of Δ̂_MLE and the optimal linear combination for various values of p₁, q₁, p₂, q₂ and a when the assumptions underlying Δ̂₂ hold. Clearly, substantial reductions in variance are possible when the data from the second phase are combined with the first phase data. The issue of course is that the optimal weight is a function of the unknown parameters. One obvious approach would be to plug in the maximum likelihood estimators for p₁, q₁, p₂, and q₂ into Δ̂_O, and we denote this plug-in estimator as Δ̂_EST. The danger however of using weights with random components and ignoring this randomness, has been discussed by Shuster [8] in the context of meta-analyses.

Table 2.

Asymptotic variances (×n) of the Phase I estimator, Δ̂_MLE, the optimal linear combination estimator, Δ̂_O and the allocation weighted estimator Δ̂_WA.

a	p1	q1	p2	q2	w*	wa**	Var(Δ̂MLE)	Var(Δ̂O)	Var(Δ̂WA)
.25	.6	.5	.5	.3	.488	.522	0.980	0.530	0.532
	.4	.3	.35	.1	.505		0.900	0.506	0.507
.30	.6	.5	.5	.3	.429	.471	1.017	0.483	0.486
	.4	.3	.35	.1	.439		0.950	0.466	0.468
.35	.6	.5	.5	.3	.356	.404	1.157	0.458	0.462
	.4	.3	.35	.1	.361		1.100	0.445	0.448

^*Optimal weight

^**Allocation based weight

An alternative approach to the plug-in estimator is to consider weights that are only a function of the known allocation ratio a. In examining (1) we noticed that the covariance tends to be much smaller in magnitude than the variance quantities. For example, if n = 1, a = .25, p₁ = .6, q₁ = .5, p₂ = .5, and q₂ = .3, the covariance matrix is

$$\left(\begin{array}{cc}.98& .1\\ .1& .94\end{array}\right).$$

Suppose we ignore the covariance in determining the weight. We also somewhat arbitrarily assume q₁ = .4 and p₁(1 − p_l) = p₂(1 − p₂) = q₂(1 − q₂) = .2. Then $w_a=\frac{.24(1-2a)}{.36-.52a}.$ This allocation based weight is compared to the optimal weight in Table 2. It appears that this estimator does a reasonable job as long as the unknown parameters are not too close to zero. For these values of underlying parameters, w_a tends to overweight Δ̂_MLE which may not be unreasonable since Δ̂_MLE is always unbiased. We call this linear combination estimator Δ̂_WA. Note in Table 2 that Var(Δ̂_WA) is close to Var(Δ̂_O). Both Δ̂_EST and Δ̂_WA are asymptotically unbiased when p₁ − q₁ = (1 − q₁)(p₂− q₂).

The monotonicity and constancy of treatment effect assumptions imply that p₁ − q₁ = (1 − q₁)(p₂− q₂). If this does not hold, the linear combination estimator will be biased for estimating p₁ − q₁. The magnitude of the bias compared to the variance depends on the underlying parameters and the sample size n. In the following section, we give results from our simulation study which looks at the various point estimates and their approximate 95% confidence intervals.

3. Simulation Study

The estimators, Δ̂_MLE, Δ̂_CMLE, Δ̂_O, Δ̂_EST, and Δ̂_WA (hereafter referred to as MLE, CMLE, O, EST, and WA respectively) were examined in a simulation study. This section presents the results of a small representative sample from that study. The oracle estimator, Δ̂_O, is not an estimator one can use in practice since it uses the true values of p₁, q₁, p₂, and q₂ in both the weight and the variances of the estimator. However we examined it in the simulations as a benchmark for the other linear combination estimators.

We consider total sample sizes from n = 50 to n = 400. At each sample size and parameter configuration, 1000 realizations were simulated. For all estimators excluding Δ̂_O, we used Wald type confidence intervals obtained by the underlying asymptotic normality of the estimators. The Newton-Raphson method using initial values, q̂₁, q̂₂ and $\frac{1}{2}({\widehat{p}}_1-{\widehat{q}}_1+{\widehat{p}}_2-{\widehat{q}}_2)$ was used to calculate CMLE. If the method failed to converge, a small set of alternative initial values were tested. If nonconvergence was still an issue, then a grid search over allowable values of q₁, q₂ and Δ was used to determine CMLE. Table 3 shows the performance of the estimators in terms of bias, variance, mean squared error (MSE), coverage probability of the nominal 95% confidence interval, and the average length of the 95% confidence interval. At each sample size, we show the range of S.E. across the five estimators for each performance measure. In Table 3, we show two cases for which p₁ − q₁ = (1 − q₁)(p₂ − q₂). These cases represent cases in which the assumptions underlying the linear combination estimators are true and the estimators are asymptotically unbiased. In Table 3, the allocation ratio a is equal to 0.35 which is close to the case where the initial allocation is 1:1:1 for the sequential parallel design. We also examined other a ranging from 0.20 to 0.40 and the results were qualitatively similar. The results show that in all cases, the MSE of the linear combination estimators are smaller than the MLE and CMLE estimators and the lengths of the 95% confidence intervals are smaller than the corresponding lengths for the MLE and CMLE. This indicates that the gains in using a linear combination estimator can be substantial, especially at moderate sample sizes from n = 100 to n = 200. At low sample sizes, the confidence intervals for all of the estimators excluding the benchmark O tend to be liberal, especially for the EST estimator.

Table 3.

Performance of estimators when p₁−q₁ = (1−q₁)(p₂−q₂). Coverage is the empirical coverage of the nominal 95% confidence interval and length is the average length of the 95% confidence interval. Allocation a = 0.35.

		p1 = .6, q1 = .5, p2 = .5, q2 = .3					p1 = .4, q1 = .2, p2 = .35, q2 = .1
n	Estimator	Bias	Variance	MSE	Coverage	Length	Bias	Variance	MSE	Coverage	Length
50	MLE	.001	.023	.023	93	0.590	.002	.021	.021	93	0.557
	CMLE	.032	.016	.017	93	0.483	.023	.011	.012	93	0.395
	O	.003	.009	.009	95	0.374	-.001	.009	.009	96	0.375
	EST	.012	.009	.010	92	0.356	-.002	.010	.010	92	0.358
	WA	.003	.009	.009	94	0.363	-.001	.009	.009	94	0.362
	Range SE	.003-	.0004-	.0004-	.7-	.0000-	.003-	.0004-	.0004-	.6-	.0000-
		.005	.0010	.0010	.9	.0010	.005	.0010	.0009	.9	.0012
100	MLE	.001	.011	.011	95	0.416	.004	.010	.010	94	0.393
	CMLE	.028	.008	.009	93	0.345	.025	.005	.006	94	0.283
	O	-.002	.004	.004	95	0.265	.000	.004	.004	96	0.265
	EST	.002	.005	.005	93	0.259	-.001	.004	.004	94	0.259
	WA	-.001	.004	.004	95	0.261	.000	.004	.004	95	0.260
	Range SE	.002-	.0002-	.0002-	.7-	.0000-	.002-	.0002-	.0002-	.7-	.0000-
		.003	.0005	.0005	.8	.0004	.003	.0004	.0004	.8	.0005
200	MLE	-.003	.006	.006	93	0.296	.003	.005	.005	94	0.279
	CMLE	.028	.004	.005	91	0.246	.025	.003	.003	91	0.202
	O	.000	.002	.002	95	0.188	.001	.002	.002	94	0.188
	EST	.002	.003	.003	94	0.185	.001	.002	.002	94	0.185
	WA	-.001	.002	.002	94	0.187	.001	.002	.002	94	0.186
	Range SE	.002-	.0001-	.0001-	.7-	.0000-	.002-	.0001-	.0001-	.8-	.0000-
		.002	.0003	.0003	.9	.0002	.002	.0002	.0002	.9	.0002
400	MLE	-.004	.003	.003	95	0.210	.000	.002	.002	94	0.198
	CMLE	.026	.002	.003	91	0.175	.025	.001	.002	91	0.144
	O	-.002	.001	.001	95	0.133	.001	.001	.001	96	0.133
	EST	-.001	.001	.001	94	0.132	.001	.001	.001	95	0.132
	WA	-.002	.001	.001	94	0.133	.001	.001	.001	96	0.132
	Range SE	.001-	<.0001-	<.0001-	.7-	.0000-	.001-	<.0001-	<.0001-	.6-	.0000-
		.002	.0001	.0001	.9	.0001	.002	.0001	.0001	.9	.0001

Table 4 shows the same performance measures of the estimators for two cases for which p₁ − q₁ ≠ (1 − q₁)(p₂ − q₂). In these cases, the linear combination estimators will be biased for the true quantity of interest p₁ − q₁ and this is evident in the bias columns of the table. Negative values for bias indicate cases where the estimator underestimates the true quantity of interest. The bias for the linear combination estimators does not go to zero as n increases and thus, as n gets larger, the bias becomes more pronounced in comparison to the variance. This causes the coverage probability to deteriorate as n increases. At moderate values of n, the coverage probability of the linear combination estimators tends to be 90-95% as opposed to the nominal 95%. Even though the estimators are biased, the MSE for the linear combination estimators is still smaller than the MSE for the MLE which suggests that as a point estimate, the linear combination estimator is still competitive with the MLE. The second set of parameters in Table 4 is a case in which the constrained maximum likelihood estimator is asymptotically unbiased since p₁ − q₁ = p₂ − q₂. At small and moderate sample sizes, failure of convergence for the Newton-Raphson method was more pronounced and 5-20% of the time, a grid search was needed to compute CMLE.

Table 4.

Performance of estimators when p₁−q₁ ≠ (1−q₁)(p₂−q₂). Coverage is the empirical coverage of the nominal 95% confidence interval and length is the average length of the 95% confidence interval. Allocation a = 0.35.

		p1 = .4, q1 = .2, p2 = .4, q2 = .1					p1 = .4, q1 = .2, p2 = .3, q2 = .1
n	Estimator	Bias	Variance	MSE	Coverage	Length	Bias	Variance	MSE	Coverage	Length
50	MLE	-.002	.022	.022	92	0.555	.008	.024	.024	93	0.554
	CMLE	.042	.013	.014	89	0.402	.002	.011	.011	92	0.388
	O	.021	.010	.011	94	0.382	-.023	.009	.009	95	0.366
	EST	.019	.011	.012	90	0.366	-.027	.010	.010	90	0.347
	WA	.021	.010	.011	92	0.370	-.022	.009	.009	92	0.353
	Range SE	.003-	.0005-	.0005-	.8-	.0000-	.003-	.0004-	.0004-	.7-	.0000-
		.005	.0010	.0010	.10	.0013	.005	.0011	.0011	1.0	.0013
100	MLE	.001	.010	.010	93	0.391	.001	.010	.010	93	0.391
	CMLE	.043	.006	.008	89	0.287	.000	.006	.006	94	0.279
	O	.021	.005	.005	93	0.270	-.024	.005	.005	93	0.259
	EST	.020	.005	.006	92	0.265	-.025	.005	.005	91	0.253
	WA	.021	.005	.005	93	0.266	-.024	.005	.005	92	0.255
	Range SE	.002-	.0002-	.0002-	.8-	.0000-	.002-	.0002-	.0002-	.7-	.0000-
		.003	.0005	.0004	1.0	.0005	.003	.0005	.0005	.9	.0005
200	MLE	-.002	.005	.005	93	0.279	-.003	.005	.005	95	0.279
	CMLE	.045	.003	.005	85	0.204	.001	.003	.003	94	0.199
	O	.021	.002	.003	93	0.191	-.023	.002	.003	92	0.183
	EST	.021	.003	.003	92	0.189	-.023	.002	.003	91	0.182
	WA	.022	.002	.003	93	0.189	-.023	.002	.003	91	0.182
	Range SE	.002-	.0001-	.0001-	.8-	.0000	.002-	.0001-	.0001-	.7-	.0000-
		.002	.0002	.0002	1.1	.0003	.002	.0002	.0002	.9	.0003
400	MLE	-.001	.003	.003	95	0.198	.000	.002	.002	94	0.198
	CMLE	.044	.001	.003	79	0.145	.000	.001	.001	96	0.141
	O	.021	.001	.002	92	0.135	-.024	.001	.002	89	0.130
	EST	.021	.001	.002	92	0.135	-.025	.001	.002	88	0.129
	WA	.022	.001	.002	92	0.135	-.024	.001	.002	89	0.129
	Range SE	.001-	<.0001-	<.0001-	.7-	.0000-	.001-	<.0001-	<.0001-	.7-	.0000-
		.002	.0001	.0001	1.3	.0001	.002	.0001	.0001	1.0	.0001

When p₁ − q₁ ≠ (1 − q₁)(p₂ − q₂), the bias is a function of how far apart the two estimates are. In general, q₂ < q₁ and thus, as q₁ increases, there is a greater chance that the discrepancy is large. Thus, more caution is needed in using 95% confidence intervals for the linear combination estimators when the placebo response in the first phase is large. Even in cases of large discrepancy, however, we observed that the MSE of the linear combination estimators was lower than the MSE of the MLE.

4. Real Data Example

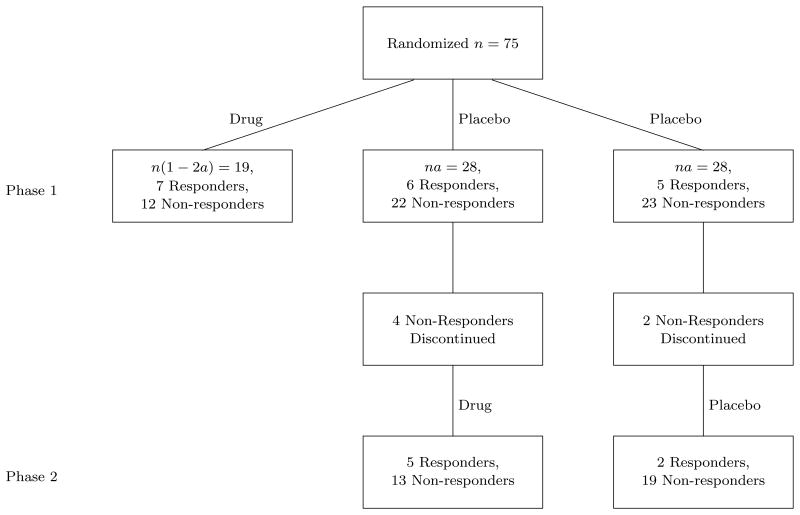
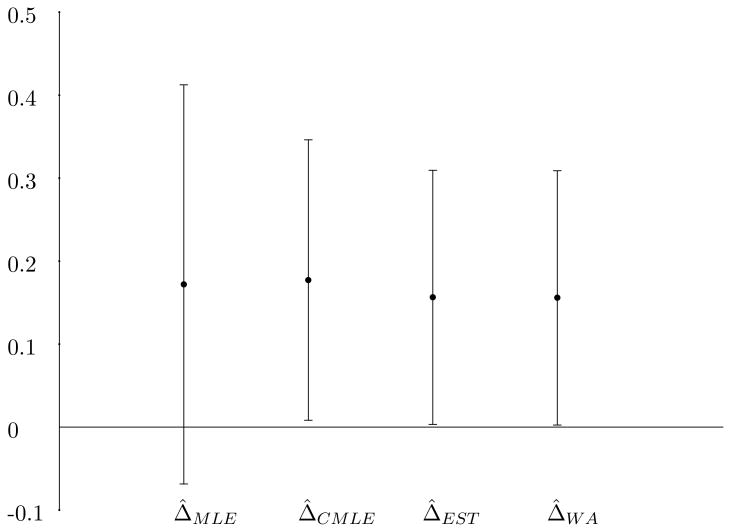
A sequential parallel clinical trial was conducted in Selective Serotonin Reuptake Inhibitor (SSRI) treated patients with Major Depressive Disorder with the test drug being 15 mg of L-methylfolate (ClinicalTrials.gov Identifier: NCT00955955). In this study, the test drug or placebo was augmented to the SSRI which the patient was currently taking. The allocation ratio was 3:3:2 for the groups identified in Table 1 which corresponds to a=0.375. The treatment period for both the first phase and the second phase was 30 days. The primary outcome scale was the change in total scores of the 17 item Hamilton Depression Rating Scale. Response was defined as a 50% reduction from baseline (defined as initiation of the phases) in the total score. Figure 1 illustrates the final response data from the trial (Fava et al. [9]). In this example, p̂₁ = .368, q̂₁ = .196, p̂₂ = .278 and q̂₂ = .095. The dropout of placebo non-responders adds additional multinomial categories in the sequential parallel design (Tamura and Huang [10]). If s is defined as the retention rate of placebo non-responders, then the covariance matrix (1) is modified with the last two terms of the asymptotic variance of Δ̂₂ divided by s. The constrained MLE of s has a closed form solution as the empirical retention rate in placebo non-responders and the constrained MLE of the remaining parameters may be obtained by similar optimization methods as before. With these adjustments, the estimated weight for the plug-in estimator is 0.379, resulting in Δ̂_EST = 0.156 (s.e.=0.078). The weighted estimator Δ̂_WA = 0.156 (s.e.=0.078) and the constrained MLE Δ̂_CMLE = 0.177 (s.e.=0.086). Figure 2 shows the point estimates and the associated 95% confidence limits of the difference in response rates in the overall population. Although all 4 point estimators are very similar, there is a large reduction in the length of the 95% confidence interval for the linear combination estimators and the constrained MLE. The reported p-value for the drug effect was 0.0399 (Fava et al. [9]) which is consistent with the confidence limits which utilize the second phase information.

Figure 1. Response data from sequential parallel clinical trial of 15mg L-methylfolate.

Figure 2.

Point estimates and 95% confidence intervals for the treatment-placebo response rates for the L-methylfolate example.

5. Discussion

Our simulation studies suggest there are substantial gains possible in utilizing information from the second phase of the design in estimating the treatment effect and associated confidence intervals. The linear combination estimators and associated confidence intervals are simple to calculate compared to the constrained maximum likelihood estimator. There appears to be little difference between the two linear combination estimators considered here, however at small sample sizes, we prefer the estimator which weights information only based on the allocation ratio. There are large gains for moderate sample size studies which would be the case in Phase II or proof of concept studies. As the sample size becomes large, bias can cause the coverage probability of the confidence intervals from the linear combination estimators to break down if p₁ − q₁ ≠ (1 − q₁)(p₂ − q₂). This is also true of the CMLE if the treatment effects are not equal in the two phases. If the sequential parallel design is used in a large pivotal Phase III trials where correct coverage is important, it seems reasonable to use the MLE confidence interval widths with a linear combination estimator for the point estimate.

The logic we have used to construct the estimators can be extended to continuous data. In such a case, the important factor is the joint distribution of the estimators of treatment effect from the first phase and the second phase. Once the joint distribution is known, then analogous linear combination estimators to what we have constructed for binary data, can be obtained. The monotonicity assumption in the continuous data case assumes that the quantitative response in placebo responders would be exactly the same whether the patient was administered drug or placebo. Some hint of whether this assumption is tenable can be obtained by examining the data in the second phase from placebo responders. If placebo responders when switched to drug show a significant difference compared to placebo responders who remained on placebo, then the assumption of monotonicity would be questionable.

One of the primary goals of Phase II studies is to get information on the treatment effect in order to design the pivotal Phase III studies. In such studies, exact coverage of the confidence interval is less important. However, analytical methods which reduce the uncertainty of the point estimate are important whether the information is used informally or more formally as was suggested by Chuang-Stein [11] for the design of pivotal Phase III studies. Another important usage of the linear combination estimator and confidence intervals would be in graphical displays involving a number of clinical trials. As an example, suppose a sponsor utilized a sequential parallel design in a Phase II study and subsequently used the traditional parallel design in two Phase III studies. In an integrated summary of efficacy, it would be important to use a linear combination estimator and confidence interval for the sequential parallel design (assuming that there was not a large difference between p̂₁ − q̂₁ and (1 − q̂₁)(p̂₂ − q̂₂)), when graphically representing the results from all three studies. Our results show that if the sequential parallel design is used as a Phase II study, it is important that the treatment effect and variability around that effect be calculated using data from both phases of the study.