Discharge regularity in the turtle posterior crista: comparisons between experiment and theory

Abstract

Intra-axonal recordings were made from bouton fibers near their termination in the turtle posterior crista. Spike discharge, miniature excitatory postsynaptic potentials (mEPSPs), and afterhyperpolarizations (AHPs) were monitored during resting activity in both regularly and irregularly discharging units. Quantal size (qsize) and quantal rate (qrate) were estimated by shot-noise theory. Theoretically, the ratio, σ_V/(dμ_V/dt), between synaptic noise (σ_V) and the slope of the mean voltage trajectory (dμ_V/dt) near threshold crossing should determine discharge regularity. AHPs are deeper and more prolonged in regular units; as a result, dμ_V/dt is larger, the more regular the discharge. The qsize is larger and qrate smaller in irregular units; these oppositely directed trends lead to little variation in σ_V with discharge regularity. Of the two variables, dμ_V/dt is much more influential than the nearly constant σ_V in determining regularity. Sinusoidal canal-duct indentations at 0.3 Hz led to modulations in spike discharge and synaptic voltage. Gain, the ratio between the amplitudes of the two modulations, and phase leads re indentation of both modulations are larger in irregular units. Gain variations parallel the sensitivity of the postsynaptic spike encoder, the set of conductances that converts synaptic input into spike discharge. Phase variations reflect both synaptic inputs to the encoder and postsynaptic processes. Experimental data were interpreted using a stochastic integrate-and-fire model. Advantages of an irregular discharge include an enhanced encoder gain and the prevention of nonlinear phase locking. Regular and irregular units are more efficient, respectively, in the encoding of low- and high-frequency head rotations, respectively.

in most sensory systems, there are distinct sets of afferent nerve fibers, each optimized to encode a different aspect of the sensory world. The vestibular organs are unexceptional in this regard (Goldberg 2000; Goldberg et al. 2012). Some vestibular afferents have a regular spacing of action potentials, while in others the spacing is irregular. Discharge regularity is measured by a normalized coefficient of variation (CV*); the more irregular the discharge, the higher is the CV* (Brichta and Goldberg, 2000a). Regular and irregular units differ in many respects in addition to discharge regularity. This is so in mammals (Goldberg and Fernández 1971; Fernández and Goldberg 1976a, 1976b) and in other vertebrates, including fish (Highstein et al. 2005), amphibians (Honrubia et al. 1989), reptiles (Brichta and Goldberg 2000a; Schessel et al. 1991), and birds (Dickman and Correia 1989a,b) (for review, see Lysakowski and Goldberg 2004).

The more irregular the discharge of a unit, the higher are the gains of its response to natural stimulation (Boyle et al. 1991; Brichta and Goldberg 2000a; Fernández and Goldberg 1976a,b; Goldberg and Fernández 1971), during electrical stimulation of efferent pathways (Boyle et al. 1991; Brichta and Goldberg 2000b; Goldberg and Fernández 1980; McCue and Guinan 1994), and during direct galvanic stimulation of afferent terminals (Ezure et al. 1983; Goldberg et al. 1982, 1984; Kim et al. 2011). The one exception to these trends are so-called low-gain irregular semicircular-canal units, which were shown to be calyx units confined to the central zone of the cristae (Baird et al. 1988); the galvanic and efferent gains of these units are unexceptional, but their responses to natural stimulation are small.

A second difference concerns response dynamics. Regular afferents can be described as tonic because their responses parallel the displacement of the cupula or otoconial membrane; irregular afferents are more phasic in being responsive to the velocity, as well as the displacement, of the cupula or otoconial membrane and in showing a decline or adaptation in response to prolonged stimulation (Boyle et al. 1991; Brichta and Goldberg 2000a; Fernández and Goldberg 1976a,b; Goldberg and Fernández 1971; Highstein et al. 2005).

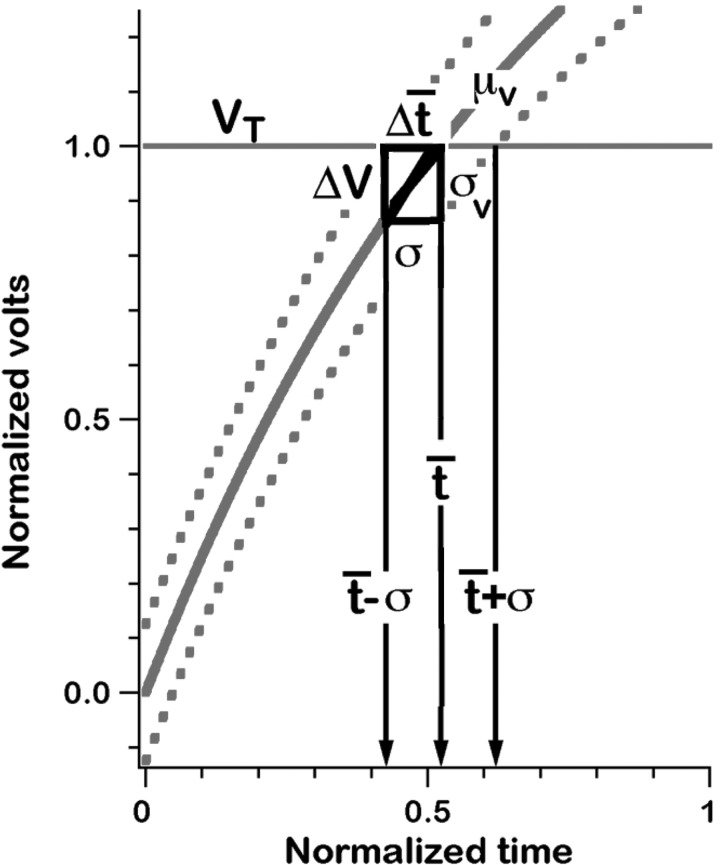
Stein (1967) provided a perspective on the determinants of discharge regularity and gains. The graphical reconstruction (Fig. 1) shows that CV* should be proportional to the ratio, σ_V/(dμ_V/dt), where σ_V is the synaptic noise and dμ_V/dt is the slope of the mean voltage trajectory measured at the mean interval, t̄. As derived in the legend to Fig. 1, sensitivity to depolarizing inputs (β) should be inversely proportional to dμ_V/dt, more or less independent of synaptic noise. The common factor, 1/(dμ_V/dt), provides a rationale for the relation between CV* and β. For the graphical reconstruction to hold requires that the mean voltage trajectory (μ_V) cross threshold (V_T). However, even when threshold crossing does not occur, simulations show that the same two factors determine CV* and β (Smith and Goldberg 1986).

Fig. 1.

A graphical reconstruction, based on Stein (1967), provides approximations between the slope of the interspike voltage trajectory (dμ_V/dt), synaptic noise (σ_V) and interspike interval variability (σ). Shown is the mean trajectory (μ_V) flanked by 2 curves displaced by ± σ_V. A spike occurs when the voltage crosses threshold, V_T. The 2 triangles in the figures have dμ_V/dt as a common slope. From the triangle on the right, CV= σ/t̄ = σ_V/[t̄(dμ_V/dt)] From the triangle at left, change in mean interval with depolarization, dt̄/dv = −1/(dμ_V/dt); expressed in terms of a change in discharge rate, r =1/t̄, so dr/dt̄ = −1/t̄² and β = dr/dV = (dr/dt̄)(dt̄/dv) = 1/[t̄²(dμ/dt)]. The common factor 1/(dμ₁/dt) in the CV and β equations is the basis for a relation between discharge regularity (CV) and depolarization sensitivity (β).

There have been two approaches to the experimental study of discharge regularity in vestibular organs. In the first, recordings from afferent terminals have compared interspike voltage trajectories (AHPs) and synaptic activity (mEPSPs) from regular and irregular afferents in the toadfish (Highstein and Politoff 1978) and a lizard (Schessel et al. 1991). Compared with irregular units, regular units have deeper, slower AHPs and smaller mEPSPs. Differences in AHPs are consistent with the results of Fig. 1; the more prominent AHPs result in larger values of dμ_V/dt and a more regular discharge. What about σ_V? Variations in mEPSP size can alter σ_V and thus might help to determine CV*. However the direct recordings were not used to estimate σ_V, so its impact on discharge regularity could not be evaluated. A second limitation of these studies was that recordings were largely confined to resting activity, so the results did not bear on how discharge regularity was related to gains and phases of the response to natural stimulation.

In the second approach, responses to externally applied galvanic currents (Goldberg et al. 1982, 1984) were combined with a stochastic integrate-and-fire model (Smith and Goldberg 1986). Thresholds of shock-evoked spikes, delivered at selected times after naturally occurring action potentials, were used to compare the postspike recovery of excitability in regular and irregular units. Consistent with the results of direct recordings, regular units were distinguished by their deep, slow recoveries. As shown by the model, differences in galvanic sensitivity (β) and discharge regularity (CV*) could both be explained by variations in postspike recovery and, to a much lesser extent, by differences in σ_V.

To study a possible relation between discharge regularity and response dynamics, responses to sinusoidal rotations and sinusoidal galvanic currents were compared (Goldberg et al. 1982; Kim et al. 2011). Differences in gains but not in response dynamics with CV* were reproduced by the galvanic currents. The currents were shown to act on the postsynaptic spike encoder, the set of ionic conductances that convert synaptic inputs into spike discharge. Combining these results with those of the model, we can conclude that encoder differences are responsible for variations in gain and discharge regularity but not in response dynamics. Stated another way, response dynamics are correlated with, but not determined by, discharge regularity.

This is the third paper in a series in which synaptic activity was recorded with sharp electrodes in the turtle posterior ampullary nerve near the crista. In previous studies (Holt et al. 2006b, 2007), synaptic potentials were characterized after spikes were blocked by tetrodotoxin. Moreover, the studies were confined to irregular units as their large axons facilitated impalement. In the present experiments, spikes and subthreshold events, including mEPSPs and AHPs, were recorded simultaneously, allowing a study of the mechanisms leading to discharge regularity and other aspects of repetitive discharge. Emphasis was placed on intra-axonal recordings from regular, as well as from irregular, units. By applying shot-noise theory to synaptic noise, quantal rate (qrate) and quantal size (qsize) during resting activity could be estimated. Direct measures of mean AHPs and synaptic noise allowed us to compare the influences of dμ_V/dt and σ_V on CV*. Responses to canal-duct indentation (Dickman and Correia 1989a; Rabbitt et al. 1995) were studied to identify the presynaptic and postsynaptic contributions to gains and phases. An improved version of an integrate-and-fire model (Smith and Goldberg 1986) was used to interpret empirical data.

MATERIALS AND METHODS

Preparation

As described previously (Holt et al. 2006a, 2006b, 2007), red-eared slider turtles (Trachemys scripta elegans) of either sex were decapitated and the head was split parasagitally. A half head was mounted in a recording chamber kept at room temperature (21–23°C), viewed with a dissecting microscope, and continually superfused with an oxygenated solution containing (in mM) 105 NaCl, 4 KCl, 0.8 MgCl₂, 2 CaCl₂, 25 NaHCO₃, 2 sodium pyruvate, and 10 glucose, at a pH of 7.2–7.3 after bubbling with 95% O₂-5% CO₂. All procedures were approved by the Institutional Animal Care and Use Committee of the University of Chicago.

The posterior ampullary nerve was exposed as in Holt et al. (2006b) so that recordings could be made as the nerve split into two branches, each destined for a hemicrista. Penetrations took place ∼50 μm from the base of the neuroepithelium. Glass microelectrodes filled with 3 M KCl and having impedances of 40–80 MΩ were connected to the head-stage of a negative-capacitance preamplifier and advanced into the nerve.

To simulate head rotations, the posterior canal duct was deformed by an indenter, the fire-polished, flattened end of a glass tube (contact area, 0.1- 0.2 mm²). The indenter was mounted on an aluminum rod, which in turn was tethered to the center of a trilaminate piezoelectric plate (model Pl-140.10; Polytec PI, Auburn, MA), clamped at its ends so that it bent as a function of the voltage difference between its outer layers. An amplifier (model E-650.00; Polytec PI) controlled the voltage difference. A linear variable differential transformer (LVDT: model DC-75-050, Macrosensors, Pennsauken, NJ), mounted inline along the length of the rod, measured the resulting displacement. The entire assembly was advanced on a three-axis micromanipulator. After contact with the posterior-canal duct was established, the indenter was slowly advanced 150 μm to prevent loss of contact during controlled indenter withdrawals. Maximum displacement was ± 100 μm.

Efferent fibers located in a connecting branch between the superior and inferior vestibular nerves were electrically stimulated (Brichta and Goldberg 2000b; Holt et al. 2006a). Afferents could be distinguished by their efferent responses. Calyx and dimorphic fibers were characterized by large, rapid excitatory responses; irregular bouton fibers by inhibitory responses; and regular bouton fibers by small, slow excitatory responses.

Experiments were controlled by custom Spike2 scripts run on a Pentium IV (386) computer with a Micro1401 interface (Cambridge Electronic Design, Cambridge, UK). The microelectrode signal was low-pass filtered by a 4-pole Bessel filter at a corner frequency of 1 kHz and sampled at 7 kHz by a 12-bit A/D converter; filtering did not distort synaptic activity as the power spectrum of unfiltered mEPSPs was already reduced by >40 dB at the corner frequency of the filter (Holt et al. 2006b). Another A/D converter sampled the inline indenter monitor. Indenter displacement was controlled by the output of a 12-bit D/A converter, which was passed through a three-digit attenuator. A digital-output port controlled the timing of shocks to efferent fibers.

All units were tested with a single trial consisting of a 5-s resting period followed by six cycles of a 0.3-Hz sinusoidal indentation.

Data Processing

Computer files were transferred to Macintosh computers and processed with custom programs written in Igor Pro (Version 6; Wavemetrics, Lake Oswego, OR). Statistical tests were evaluated by Microsoft Excel functions; regressions were calculated in Igor Pro. Unless stated otherwise, results are given as means ± SE.

Discharge regularity.

Discharge regularity was characterized for the 5-s resting period by a coefficient of variation, CV = s/t̄, the ratio of the standard deviation of intervals (s) to the mean interval (t̄), which was transformed by empirical formulas to a normalized CV*, the coefficient of variation appropriate to a mean interval of 50 ms (Brichta and Goldberg 2000a). We calculated correlations between adjacent intervals. Because these were small, only first-order interval statistics were considered.

Afterhyperpolarizations.

Afterhyperpolarizations (AHPs) were studied by splitting the entire resting record into segments synchronized around each action potential at t = 0 and extending from a negative interval of −10 ms to a positive interval chosen so that one-half of the segments were not interrupted by the next spike in the train. The several accepted segments were averaged.

Spike thresholds.

Spike thresholds were determined from phase plots (dV_M/dt vs. V_M) of intracellular voltage (V_M) as the point where the slope increased twofold across adjacent time bins of 0.144 ms. Estimates could be checked, but only in irregular units, by inspecting the amplitudes of ineffective mEPSPs.

Quantal size and quantal rate.

Shot-noise theory was used to estimate the rate of occurrence (qrate) and peak amplitudes of mEPSPs (qsize) during resting activity. The assumptions of the theory are met, viz., that the timing of mEPSPs is random (Poisson distributed) and that mEPSP shape is uniform. These features, which were first established in sharp-electrode recordings (Holt et al. 2006b), were subsequently confirmed in whole cell recordings from calyx endings (Chatlani 2011). Consistent with our previous studies (Holt 2006b, 2007), we refer to mEPSPs as quanta, while recognizing the possibility that these events may be composed of multiple quanta (Keen and Hudspeth 2006; Li et al. 2009; Singer et al. 2004). Because of the validity of shot-noise calculation, neither our estimates of the rate and size of mEPSPs nor their impact on spike discharge in no way depends on their quantal content.

As a first step, intervals including each spike were digitally excluded by having voltages replaced by NANs over a period extending from 7.5 ms before to 15 ms after each spike. The remaining record was then first-order high-pass filtered at a corner frequency of 1 kHz. There are advantages in using high-pass records (Fesce 1990; Holt et al. 2006b; Neher and Sakaba 2001). The most obvious of these is that filtered records reduce the effects of fluctuations in resting membrane potential, both those occurring as a function of postspike time (PST) and those happening over a longer time scale.

Rice's (1944) extension of Campbell's theorem

$${\mu }_n=\lambda \langle h^n\rangle {\text{I}}_n$$ (1)

expresses μ_n, the nth semi-invariant or cumulant, as a function of qrate (λ) and qsize $\langle h^n\rangle$ raised to the nth power; here and elsewhere, angle brackets indicate expected values. The first three cumulants are the corresponding central moments, the mean, variance, and third moment (skew). In using the variance, the contribution of nonquantal components should be subtracted.

There are two nonquantal components, instrumental noise and channel noise, that sum with the quantal contribution to the variance. The problem was treated in Holt et al. 2006b (p. 444). Specifically, instrumental noise was identified by plotting the relation between variance and skew during sinusoidal stimulation and estimating instrumental noise as the variance remaining at zero skew. The rationale for this approach is the realization that synaptic activity, but not instrumental noise, has positive skew. For the method to be reliable, requires that synaptic activity approach zero during inhibitory stimulation. Such estimates could be made in nine units, all of which were irregular and showed large modulations in discharge rate; the mean instrumental noise (σ_V) in these units was 106 ± 18.6 μV with σ_V² amounting to 28.3 ± 5.0% of the total variance. For the other 13 units, which were more regular and showed small modulations, we subtracted the above mean σ_V² from the total variance. In the same paper (Holt et al. 2006b), channel noise was measured by a nonstationary variance analysis applied to the depolarization resulting from the exogenous application of AMPA, a glutamate agonist. Channel noise amounted to 2% of the total variance, a small enough value that it could be ignored.

I_n in Eq. 1 is the definite integral

$$I_n={\displaystyle \underset{0}{\overset{\infty }{\int }}{\left[f(t)\right]}^n\text{d}t}$$ (2)

where f(t) is the shape of the mEPSP normalized to unity amplitude. In evaluating the integrals, the original function, f(t), was first filtered and then normalized before being raised to the nth power and integrated. The values of I_n were calculated from a standard mEPSP of the form, f(t) = (at)² exp(αt), α = 750 s⁻¹, typical of these recordings (Holt et al. 2006b); I₂ = 2.27 × 10⁻³ s and I₃ = 1.14 × 10⁻³ s.

The qsize is estimated from the ratio

$$\begin{array}{c}\langle h\rangle \cong \langle h^3\rangle /\langle h^2\rangle \\ =\frac{{\mu }_3{I}_2}{{\mu }_2{I}_3}\end{array}$$ (3)

The approximation would only be exact were there no variation in h, in which case $\langle h^n\rangle ={\langle h\rangle }^n$. An exact expression can be obtained by the use of two correction factors, D₂ and D₃, defined by the relations, $\langle h^2\rangle =D_2{\langle h\rangle }^2\text{and}\langle h^3\rangle =D_3{\langle h\rangle }^3$, so that Eq. 3 becomes

$$\begin{array}{c}\langle h\rangle =\frac{D_2\langle h^3\rangle }{D_3\langle h^2\rangle }\\ =\frac{D_2{\mu }_3{I}_2}{D_3{\mu }_2{I}_3}\end{array}$$ (4)

The qrate, obtained from Eq. 1 (n = 2) and Eq. 4, is

$$\begin{array}{c}\lambda =\frac{{\mu }_2}{\langle h^2\rangle I_2}\\ =\frac{D_3^2{\mu }_2^3{I}_3^2}{D_2^3{\mu }_3^2{I}_2^3}\end{array}$$ (5)

Values of D₂ and D₃, derived previously (Holt et al. 2006b), lead to

$$\begin{array}{c}{\langle h\rangle }_{\text{TRUE}}=\left[k/(k+2)\right]{\langle h\rangle }_{\text{KON}}\\ =(2/3){\langle h\rangle }_{\text{KON}}\end{array}$$ (6)

and

$$\begin{array}{c}{\langle \lambda \rangle }_{\text{TRUE}}=\left\{{(k+2)}^2/\left[k(k+1)\right]\right\}{\langle \lambda \rangle }_{\text{KON}}\\ =(9/5){\langle \lambda \rangle }_{\text{KON}}\end{array}$$ (7)

where ${\langle h\rangle }_{KON}$ and ${\langle \lambda \rangle }_{KON}$ are the values obtained from Eqs. 4 and 5, respectively, when D₂ = D₃ = 1. The parameter, k = 4, is based on the fourth-order gamma distribution used in the derivation. Note that high-pass filtering does not affect ${\langle \lambda \rangle }_{TRUE}$ but decreases ${\langle h\rangle }_{TRUE}$, which had to be multiplied by 2.306 to get the unfiltered mean mEPSP amplitude.

There is a limitation of shot-noise theory (Fesce 1990; Rice 1944). As quantal rate increases, voltage approaches a normal distribution with the result that the estimate of the third central moment (μ₃) becomes unreliable, as do estimates of qrate and, especially, of qsize.

Sensitivity to indenter stimulation.

Sensitivity to indenter stimulation was evaluated by comparing the modulation in spike discharge and in synaptic potentials during sinusoidal indenter stimulation at a frequency of 0.3 Hz. Each 360° sine-wave period was divided into 40 bins. The bin into which an individual spike fell was determined and a phase histogram constructed as a discharge rate by dividing the count in each bin by its effective time. To determine spike-rate modulation, a Fourier analysis of the phase histogram was calculated using all nonzero bins.

Voltage modulation was measured as a function of sinusoidal phase at one PST following each spike. The PST was chosen so that <50% of the intervals, even those during maximal excitation, were aborted by the next spike in the train.

Stochastic integrate-and-fire model.

A stochastic integrate-and-fire model was improved from a previously published version (Smith and Goldberg 1986). Voltages are stated with respect to a resting potential, V = 0. Quantal mEPSCs were of the form

$$I(t)=\overline{I}{t}^p\exp (-\alpha t)/p!$$ (8)

with α = 2,000 s⁻¹ and p = 3. Ī was adjusted to produce an mEPSP with a specified amplitude, V_MAX, when the current was injected into a single compartment characterized by a rate constant of 625 s⁻¹. The mEPSPs and mEPSCs so obtained resembled those observed in whole cell recordings from calyx endings (Chatlani 2011).

Each mEPSC was represented by a delta function whose timing was obtained from Monte Carlo simulations of a Poisson distribution with a qrate that could be set to a constant or could be sinusoidally modulated. To account for a variable qsize, each delta function was Monte Carlo transformed by a fourth-order gamma distribution (k = 4) having a unity mean and a CV = 1 $\sqrt{k}$ = 0.5; the latter CV was typical of this preparation (Holt et al. 2006b). The variable-sized delta functions were converted to mEPSCs by convolution with I(t) (Eq. 8). The mEPSC record was divided by an equilibrium potential, V_s, yielding a synaptic conductance wave, G_s(t).

The instantaneous voltage, V(t), was obtained by solving the one-compartment ODE

$$C_{\text{M}}\frac{\text{d}V(t)}{\text{d}t}+\frac{1+g_{\text{S}}(t)+g_{\text{K}}(t)}{R_{\text{M}}}V(t)=\frac{g_{\text{S}}(t)V_{\text{S}}+g_{\text{K}}(t)V_{\text{K}}}{R_{\text{M}}}+I_{\text{EXT}}$$ (9)

with a fourth-order Runge-Kutta algorithm. Conductances were normalized by a leak conductance, G_L = 1/R_M, to give g_L = 1, g_S(t) = G_S(t)/G_L and g_K(t) = G_K(t)/G_L. For all simulations, R_M = 40 MΩ and C_M = 40 pF, values that were typical of whole cell recordings from calyx endings (Chatlani 2011). Equilibrium potentials were V_L = 0 for G_L, V_S = 50 mV for synaptic inputs, and V_K = −30 mV for AHPs. Externally applied currents, I_EXT, were delivered to the intracellular compartment. Spikes occurred when V(t) exceeded a threshold, usually set to 2 mV. Each spike triggered an AHP having an exponential conductance,

$$g_{\text{K}}(t)=g_{\text{K}}(0)\cdot \exp (-t/{\tau }_{\text{K}})$$ (10)

The g_K(t) present immediately before each spike was added to the g_K(0) following the spike. This was done to mimic the lengthening of the interspike interval following interposed shock-evoked spikes that were triggered shortly after naturally occurring spikes (Goldberg et al. 1984). Despite the inclusion of this cumulative effect, the correlation between adjacent intervals was small, so higher order interval statistics were not considered.

RESULTS

Conclusions are based on a sample of 22 axons impaled within 250 μm of their entrance into the neuroepithelium of the posterior crista. Responses to efferent stimulation were used to identify units as being bouton (B) and not calyx-bearing (CD) fibers (see materials and methods for details). The posterior crista consists of two triangular-shaped hemicristae, each with an apex near the nonsensory torus and a base abutting the planum semilunatum. Based on the labeling of physiologically characterized units, irregular B units terminate nearer the torus and regular B units nearer the planum (Brichta and Goldberg 2000a). In the present study, consideration was restricted to B units because their activity remained stable after impalement, whereas, for reasons that remain unclear, the activity of CD units declined within a few minutes of penetration (see Holt et al. 2007).

Each unit was presented with a single trial consisting of a 5-s resting period followed by six cycles of a 0.3 Hz sinusoidal canal-duct indentation. Discharge regularity was measured by a normalized coefficient of variation (CV*; see materials and methods for details). The resting period was used to study the factors determining discharge regularity; the responses to sinusoidal indentation provided estimates of depolarization sensitivity as the ratio of the modulation in spike discharge to that in synaptic voltage.

Results will first be presented for two exemplar units, one regular (CV* = 0.106) and the other irregular (CV* = 0.714). Results for the entire sample of 22 units will then be summarized.

Two Exemplar Units

Resting discharge and discharge regularity.

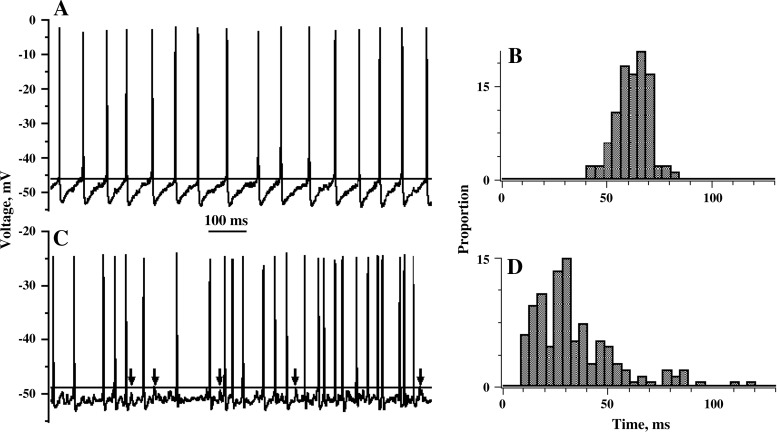
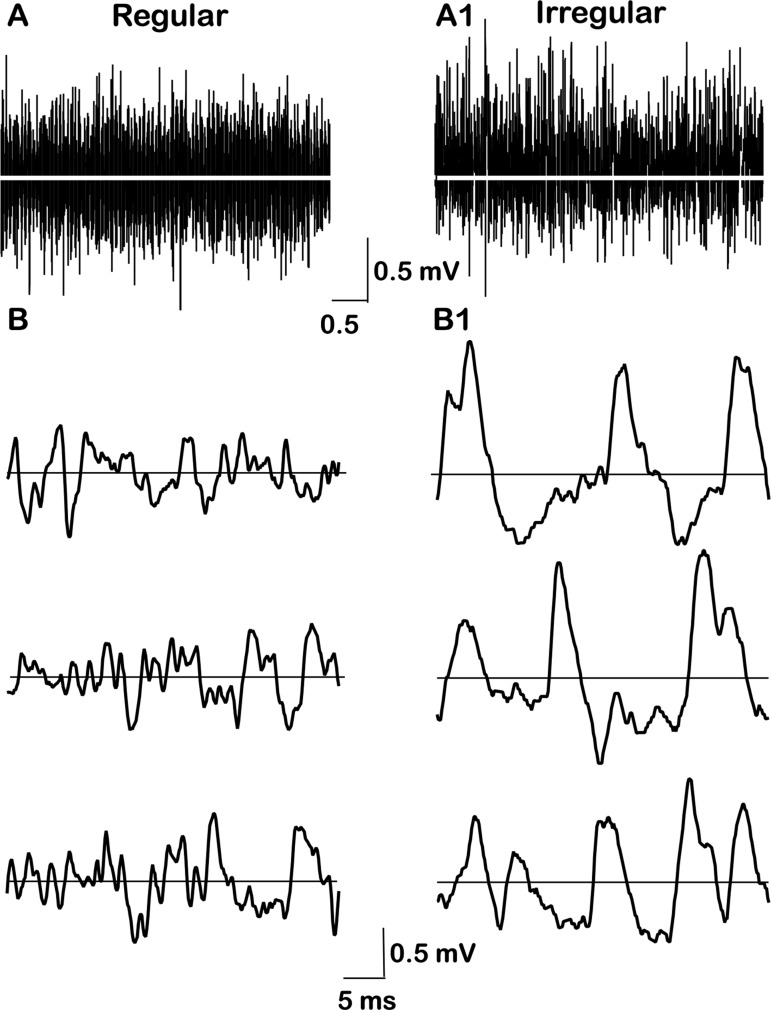
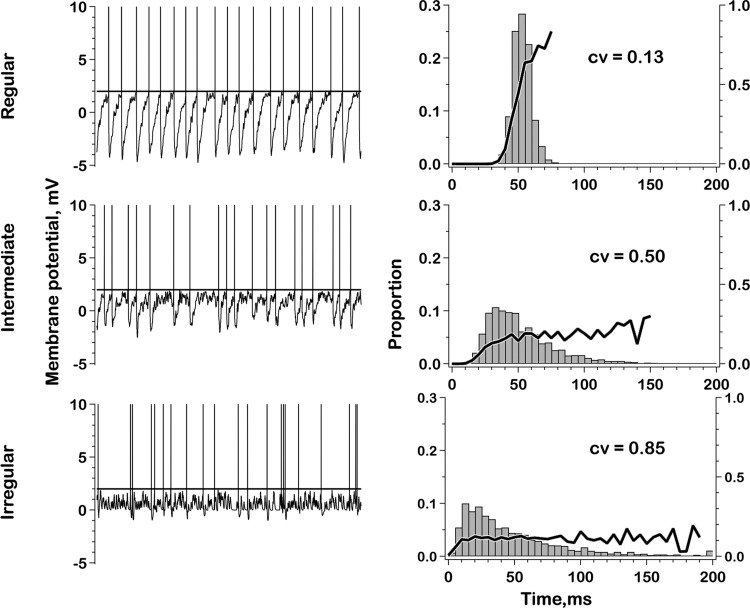
Figure 2 shows samples of the resting activity for the two exemplar units. One unit has a regular spacing of action potentials (Fig. 2A), while the spacing in the other unit is irregular (Fig. 2C). The difference is reflected in the corresponding interspike-interval histograms. That for the regular unit is tightly distributed and symmetric (Fig. 2B), while that for the irregular unit is broadly distributed and skewed to the right (Fig. 2D). Resting firing rates, averaged over the entire 5-s resting period, were 16.1 spikes/s for the regular unit and 28.6 spikes/s for the irregular unit.

Fig. 2.

Voltage traces and interspike-interval histograms for 2 exemplar units, one regular (A and B) and the other irregular (C and D). For the regular unit, the interspike trajectory is characterized by a prominent, prolonged afterhyperpolarization (AHP). The AHP for the irregular unit is shallow and rapid so that the voltage trajectory is flat for much of the interspike interval. Relatively large, easily discerned miniature excitatory postsynaptic potentials (mEPSPs) are seen in the irregular record (C, arrows), but are less evident in the regular record (A). Voltage traces, 1-s duration; interval histograms based on 5-s samples of resting activity; number of intervals; n = 82 (C) and 143 (D).

Two other features can be discerned from the voltage traces. First, the interspike voltage trajectory for the regular unit is dominated by a prominent AHP, consisting of a rapid hyperpolarization after each spike followed by a slower depolarization that leads to the next spike (Fig. 2A). In contrast, the postspike hyperpolarization in the irregular unit is brief and most of the interspike interval is almost flat (Fig. 2C). Second, there are easily discernible, brief depolarizations in the irregular unit (Fig. 2C, arrows). As shown previously (Bonsaquet et al. 2006; Holt et al. 2006b), these are mEPSPs reflecting glutamatergic neurotransmission. Noise-like irregularities are seen between spikes in the regular unit, but individual mEPSPs are difficult to discern (Fig. 2A).

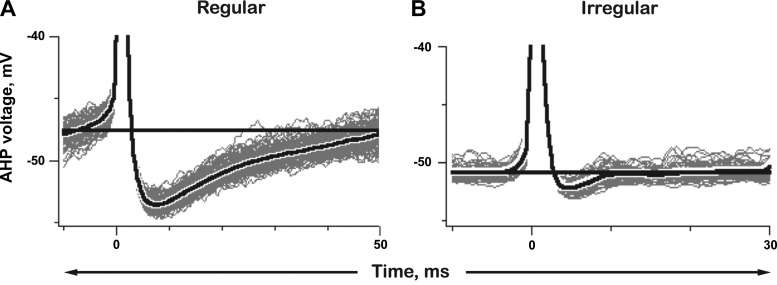
Afterhyperpolarizations.

To characterize AHPs, records were segmented and synchronized on individual spike onsets at t = 0 (Fig. 3). After each spike, the membrane potential rapidly hyperpolarizes. In the regular unit (Fig. 3A), the AHP magnitude measured from the voltage before the spike (Fig. 3A, horizontal line), reaches a peak of −6.8 mV at 7.4 ms after the start of the spike; the AHP then declines exponentially with a time constant, τ = 24 ms. The AHP in the irregular unit is smaller (peak, −1.4 mV), its peak time occurs earlier (4.6 ms postspike), and its exponential time course is considerably faster (τ = 4.3 ms; Fig. 3B).

Fig. 3.

Interspike voltage trajectories for the same 2 exemplar units as in Fig. 2; one regular (A), the other irregular (B). AHPs, individual traces (gray) and mean trajectories (black). Horizontal lines, voltages immediately before prepotentials (cf. Figs. 4C and 5C). In the regular unit, the AHP reaches a −6.8 mV peak, 7.4 ms after spike start and takes 50 ms to return to baseline levels. The AHP in the irregular unit peaks at −1.4 mV in 4.6 ms and returns to baseline in <10 ms. AHP hyperpolarizing peak voltage measured from background voltage (horizontal lines); AHP duration measured from spike start to the time when the AHP returns to the background voltage.

Spike thresholds and prepotentials.

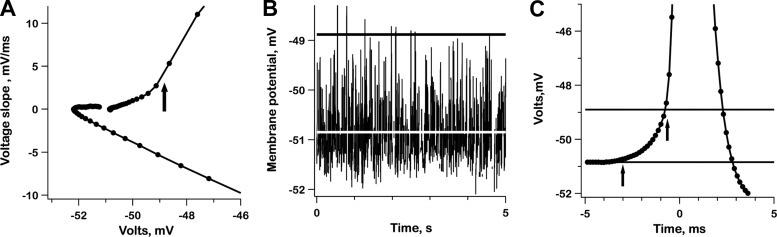
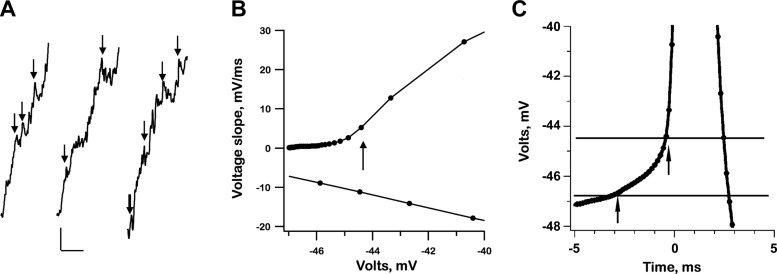
Thresholds were of interest mainly as parameters in integrate-and-fire simulations. We begin with the exemplar irregular unit. As a first step in estimating spike threshold, a phase-plane diagram was constructed by plotting the first derivative of membrane voltage (dV_M/dt) against its magnitude (V_M; Fig. 4A). Threshold was tentatively identified as the first occurrence of a ≥2× increase in slope across adjacent 0.14-ms time bins; the criterion was met when V_M shifted upwards from a baseline of −50.8 to −48.9 mV, resulting in a threshold of 1.9 mV (Fig. 4A, arrow). To investigate whether the criterion actually corresponded to threshold, we removed all the spikes from the resting record, which allowed us to inspect subthreshold mEPSPs (Fig. 4B). Only 8/525 mEPSPs (1.5%) exceeded the estimated 1.9-mV threshold (Fig. 4B, dark line) by 0−0.5 mV. Inspection of a synchronized-spike record (Fig. 4C) indicated that there was a consistent depolarization before threshold was exceeded. This so-called prepotential began ≈3 ms before spike threshold was reached. As indicated by the left-hand arrow in Fig. 4C, the baseline for threshold measurements was taken as the voltage immediately preceding the prepotential.

Fig. 4.

Estimating spike threshold in the exemplar irregular unit. A: threshold is estimated from a phase-plane plot of the voltage slope (dV_M/dt) vs. voltage (V_M) as a 2-fold increase in slope across a single time bin (0.14 ms). B: resting record after spikes are removed, leaving only ineffective mEPSPs. Black line, threshold as determined in A; white line, voltage at 3.0 ms before start of action potential (left-hand vertical arrow in C). Only 8/525 mEPSPs cross the top line. C: mean voltage trajectory. Preceding the action potential is a 2-mV depolarizing prepotential starting 3 ms before the spike. Horizontal lines: bottom, average voltage, 3 ms before each spike; top, spike threshold as in A. Arrows, 3 ms before spike threshold (left) and spike threshold (right). Traces in A and C are based on the average voltage of segments synchronized to the start of spikes at t = 0.

An estimate of threshold, based on large ineffective mEPSPs (Fig. 4B), could be done in irregular units as the records had relatively large mEPSPs superimposed on an almost flat interspike baseline. As can be seen in Fig. 5A, this was not possible in the regular unit because of its small mEPSPs and the steep slopes of its AHPs. Here, thresholds and prepotentials could still be approximated from inspection of the phase-plane diagram (Fig. 5B). In regular units, most of the interspike voltage is dominated by an AHP whose trajectory is concave downward. The prepotential could be identified in favorable cases as beginning when the trajectory changed to concave upward (Fig. 5C, left-hand arrow). Measured relative to the voltage at the start of the prepotential, the threshold of the regular unit was 2.4 mV (Fig. 5C, interval between 2 horizontal lines).

Fig. 5.

Estimating spike threshold in the exemplar regular unit. A: threshold cannot be estimated from the amplitude of mEPSPs because of the small size of mEPSPs and the presence of long-lasting AHPs giving rise to an upward voltage trajectory following each spike. The three segments are from a low-pass record after deletion starting 7.14 ms before and ending 14.28 ms after each spike. Arrows, possible mEPSPs. Calibration, 1 mV, 25 ms. B: phase-plane plot of the voltage slope (dV_M/dt) vs. the voltage magnitude (V_M). Threshold (vertical arrow) based on a rapid increase in slope. C: voltage trajectory. Horizontal lines: bottom: average voltage, 3 ms before each spike; top: spike threshold as in B. Preceding the action potential is a 2.5-mV prepotential starting 3 ms before the spike. Traces in B and C are based on the average voltage of segments synchronized to the start of spikes at t = 0.

Quantal size and quantal rate.

Shot-noise theory provides estimates of qsize and qrate. To accomplish this, the resting record was high-pass filtered and spikes were removed for a period ranging from 7.5 ms before each spike threshold to 15 ms afterwards. Results are presented in Fig. 6. From Eqs. 3–5 in materials and methods, qsize is proportional to μ₃/μ₂, the ratio between the skew (μ₃) and variance (μ₂), whereas qrate is proportional to the ratio, μ₂³/μ₃². Values of μ₂ and μ₃ can be found in Fig. 6, legend. The skew is much larger in the irregular unit (cf. Fig. 6A1 with Fig. 6A); in contrast, the variances are comparable for the two units. This combination leads to the irregular unit having a larger qsize (0.60 vs. 0.040 mV) and a lower qrate (108 vs. 5,870 s⁻¹).

Fig. 6.

Shot-noise theory is used to estimate quantal rate (qrate) and quantal size (qsize). Voltage records of resting activity, 5 s duration, for the 2 exemplar units, one regular (A) and the other irregular (A1). Both records are high-pass filtered and spikes are removed. Horizontal (white) lines, 0 mV. Variances are similar for the 2 units: (0.0533 mV², irregular unit; 0.0401 mV², regular unit); third central moment (skew) is much larger in the irregular unit (7.85 × 10⁻³ mV³ vs. 2.87 × 10⁻⁴ mV³). From this combination of central moments, qsize is estimated to be larger and qrate smaller in the irregular unit. B: expanded time base for low-pass versions of the voltage records, 40-ms duration, 3 samples. Exemplar regular (B) and irregular (B1) units illustrating the higher qrate and smaller qsize for the regular unit. Calibrations: top for A and A1; bottom for B and B1.

Removal of spikes leads to a segmentation of the records. Inspection of individual segments (Fig. 6, B and B1) confirms the conclusion that qsize is smaller and qrate larger in the regular unit.

Response to indenter stimulation: sensitivity to postsynaptic depolarization.

Responses to externally applied galvanic currents have led to the conclusion that the postsynaptic spike encoder is more sensitive to depolarizing inputs, the more irregular is a unit discharge (Ezure et al. 1983; Goldberg et al. 1982, 1984; Kim et al. 2011). The conclusion holds for responses to head rotations and canal-duct indentations, to applied galvanic currents, and to efferent activation (reviewed in Goldberg 2000). In the present study, we compared sinusoidal modulations of spike discharge and synaptic voltage, the latter measured at fixed PST as the phase of a 0.3 Hz sinusoidal canal-duct indentation varied.

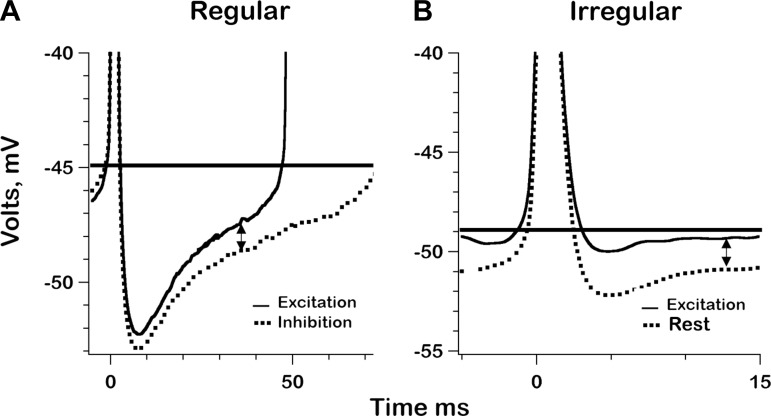
To choose appropriate PSTs, we inspected the AHPs for the regular (Fig. 7A) and irregular units (Fig. 7B) at two times during sinusoidal indentation: 1) maximal excitation, and 2) maximal inhibition or rest. For the regular unit, maximal inhibition could be used. Maximal inhibition in the irregular unit resulted in a silencing of discharge so resting activity was chosen. As was already seen for resting activity (Figs. 2 and 3), AHPs were deeper and slower in the regular unit. Excitation in both units led to a depolarizing shift in the AHP, associated with an increase in qrate. The shift increased with PST in the regular unit, which can be explained by the decrease in a g_K conductance as the AHP declines. The smaller, faster AHP in the irregular unit should be associated with a less striking conductance change, which is consistent with the depolarizing shift remaining nearly constant over much of the interspike interval.

Fig. 7.

Postspike mean voltage trajectories (AHPs) for the 2 exemplar units, one regular (A) and the other irregular (B). In A and B, AHPs are shown for maximal excitation during sinusoidal canal-duct indentation and either maximal inhibition (A) or resting activity (B). Excitation is associated with a depolarization. Spike onset occurs at t = 0; horizontal lines, spike thresholds. Double-headed arrows, time intervals at which 50% of interspike intervals are interrupted by the next spike; this postspike time (PST) is used in Fig. 8 to chart synaptic depolarization as a function of the phase of sinusoidal canal-duct indentations.

The fixed PST chosen for the two units are indicated by double arrows, 35 ms in the regular unit (Fig. 7A) and 12.5 ms in the irregular unit (Fig. 7B). Times had to be chosen sufficiently early so that the second spike of an interval did not abort too many interspike intervals during maximal excitation. For each unit, the time was selected that resulted in the completion of half the excitatory intervals.

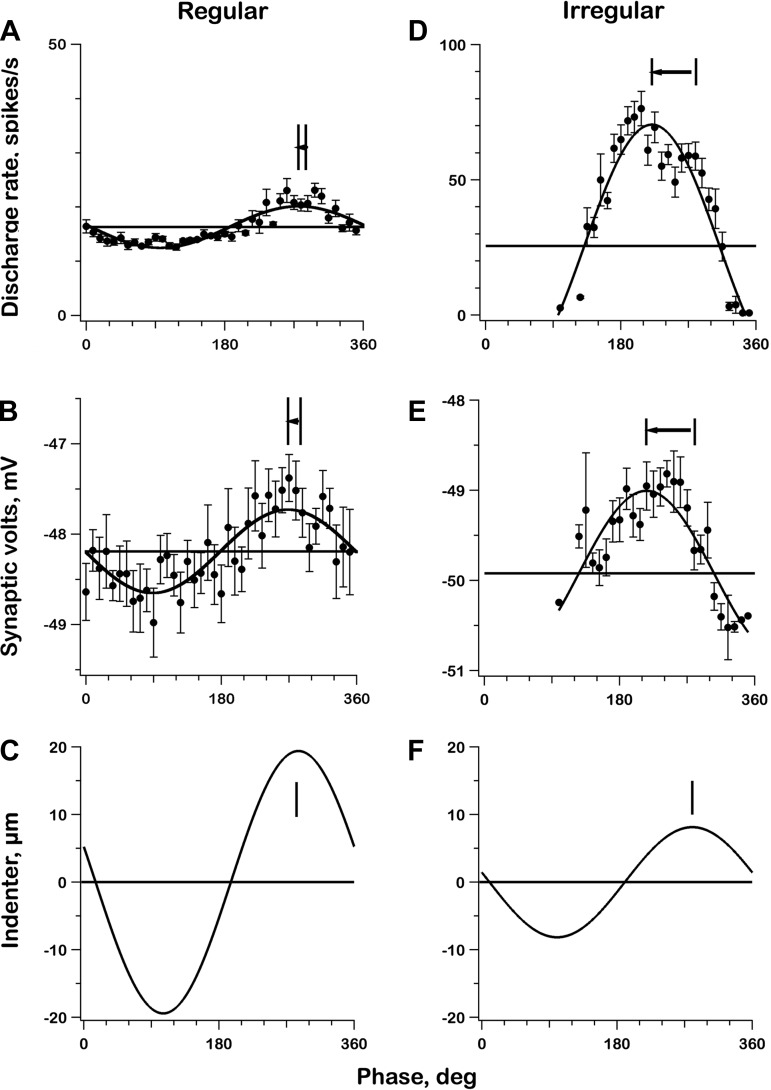
During sinusoidal indentation, there were nearly sinusoidal modulations in spike rate and synaptic voltage provided that periods of inhibitory saturation were excluded in the irregular unit (Fig. 8, D and E). Sensitivity to postsynaptic depolarization was much larger in the irregular unit as indicated by its spike modulation being >10 times larger than that in the regular unit (cf. Fig. 8, A and D), whereas voltage modulation was only twice as large (cf. Fig. 8, B and E). Quantitative measures of sensitivity, based on linear regressions between spike rate and synaptic voltage, were 35.3 ± 4.8 (irregular) vs. 5.5 ± 0.85 spikes·s⁻¹/mV (regular).

Fig. 8.

Phase plots depicting the responses to 0.3-Hz sinusoidal canal-duct indentations for the 2 exemplar units, one regular (left) and the other irregular (right). Each point, mean value for a bin 9° wide averaged over six consecutive sine-wave cycles; error bars, standard errors. A and D: discharge rates calculated from reciprocal interspike intervals. B and E: mean synaptic depolarization calculated at the PSTs illustrated in Fig. 7. C and F: indenter position, withdrawal (excitation) is positive. No error bars for C and F because variability is negligible. Curves are best-fitting sinusoids of nonempty bins. Vertical lines in C and F are times of maximal excitatory indentation; the same vertical lines are plotted in other graphs along with times of peak responses; arrows depict phase leads re indentation. Compared with the regular unit, spike modulation in the irregular unit is much larger (A vs. D), even though the synaptic voltage modulation is only slightly larger (B vs. E) and indentation is smaller (C vs. F). Spike and voltage phase leads are considerably larger in the irregular unit.

The two units also differ in the phase leads of their spike and voltage responses re the indenter stimulus (Fig. 8, vertical lines connected by arrows). As was previously reported (Brichta and Goldberg 2000a; Holt et al. 2006b), phase leads were larger in the irregular unit (spike discharge: 58.7 ± 2.8°; synaptic voltage: 64.4 ± 4.5°) than in the regular unit (spike discharge: 9.6 ± 4.8°; synaptic voltage: 16.6 ± 8.0°). For either unit, the phase difference (Δφ) between synaptic voltage and spike modulation was statistically insignificant (irregular unit: Δφ = 5.7 ± 5.3°; regular unit: Δφ = 7.0 ± 9.4°).

Population Characteristics

Resting potentials and spike heights.

As judged by the resting potentials of individual units, there was considerable variability in the quality of impalements. The mean (±SD) resting potential for the sample of 22 units was −48.6 ± 9.6 mV (range: −36.2 to −72.8 mV). Spikes never overshot 0 mV, reaching a peak voltage with a mean (±SD) value of −14.4 ± 8.4 mV. The deeper the resting potential, the closer to zero was the peak spike voltage; yet there was only a weak correlation between the two variables (r = −0.31, P > 0.1).

Could variations in qsize and AHP magnitude reflect impalement quality, rather than discharge regularity? To examine this possibility, multiple regressions were run with qsize and AHP magnitude as dependent variables plotted against CV* and resting potential as independent variables. Regressions between qsize or AHP magnitude and CV* were significant (P < 0.001 for qsize; P < 0.02 for AHP magnitude); the two regressions with resting potential were not (P > 0.05 for qsize; P > 0.10 for AHP magnitude). While impalement quality as indicated by the resting potential may make marginal contributions to qsize and AHP magnitude, discharge regularity makes a stronger, independent contribution.

Afterhyperpolarizations.

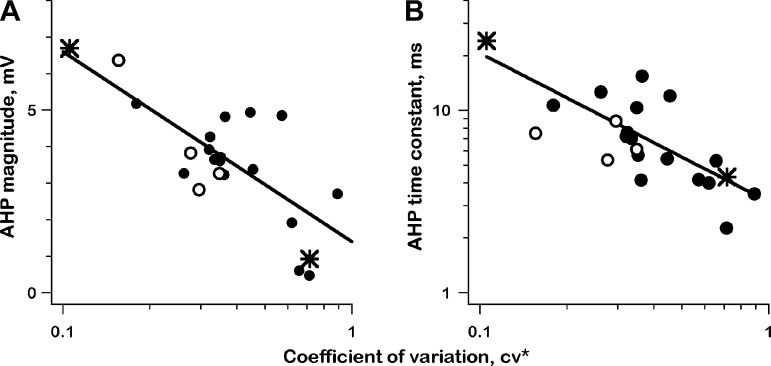
AHPs following each spike are systematically related to discharge regularity. Those of regular units are larger (Fig. 9A) and slower (Fig. 9B) than those of irregular units. Based on regression lines, there is a 3.5 × variation in maximal postspike hyperpolarizations (2 vs. 7 mV) and a 5× variation in exponential time constants (4 vs. 20 ms).

Fig. 9.

Afterhyperpolarization magnitude (A, AHP mag) and time constant (B, AHP tau) are plotted vs. normalized coefficient of variation (CV*) for resting discharge, 22 units; 2 exemplar units (*); 4 units with unreliable qrates (○), >10,000/s. All regressions, df = 20. A: AHP mag vs. log(CV*), t = 5.5, P << 0.001. B: log(AHP tau) vs. log (CV*), t = 4.9, df = 20, P << 0.001.

Spike thresholds.

Spike thresholds determined from phase-plane plots (Figs. 4A and 5B) averaged 2.0 ± 0.24 mV. Units were sorted by CV* into three groups with the following mean (±SD) CV*s: regular, 0.23 ± 0.081, n = 7; intermediate, 0.36 ± 0.037, n = 8; irregular, 0.66 ± 0.14, n = 7. Regular and irregular units had similar thresholds (means ± SE in mV): regular (1.4 ± 0.27) and irregular (1.8 ± 0.20). Values for the intermediate group were higher (2.8 ± 0.50, n = 8). For each of the seven irregular units in which ineffective mEPSPs could be inspected, we compared the biggest such mEPSP falling within the 5-s resting period with phase-plane threshold estimates. The individual mEPSPs exceeded the phase-plane estimate in five of seven cases. Differences between the two measures were small, averaging 0.27 ± 0.14 mV.

The main use of these estimates was as parameters in simulations. Variations of this magnitude require only small adjustments in the other input parameters of the model to produce nearly identical results.

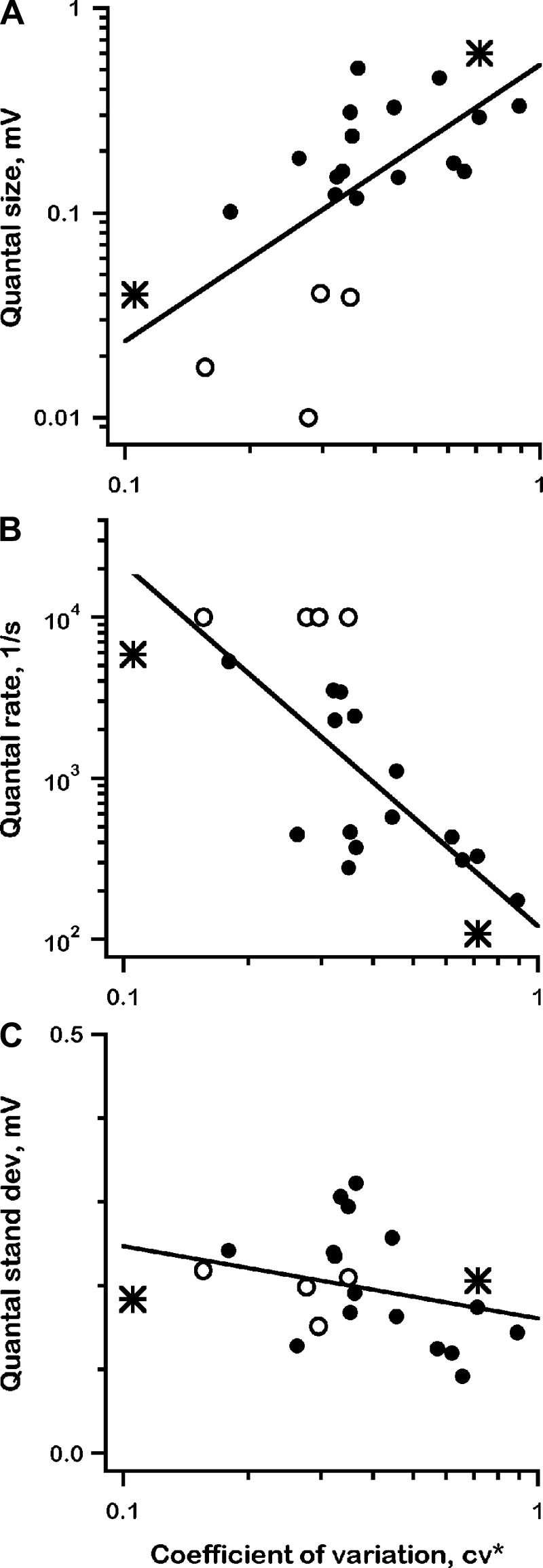
Shot-noise calculations, qsize and qrate.

The variance (μ₂) and skew (μ₃), calculated from high-pass filtered voltage records (e.g., Fig. 6, A and A1) were used to estimate qsize and qrate for all 22 units. As is seen for the two exemplar units (Fig. 10, *), qsize increases (Fig. 10A) and qrate decreases (Fig. 10B) as CV* increases. qrate reaches very high values (>10,000/s) in four units (Fig. 10, open circles), presumably as a result of skew (μ₃) estimates becoming unreliable (see materials and methods). Regressions between quantal variables and CV* are summarized in Fig. 10.

Fig. 10.

Shot-noise estimates, quantal size (A, qsize), quantal rate (B, qrate) and quantal standard deviation (C, qsd) vs. normalized coefficient of variation (CV*) for resting discharge; 2 exemplar units (*); 4 units with unreliable qrates (○), >10,000/s. All regressions, df = 20. A: log(qsize) vs. log (CV*), t = 3.9, P < 0.002; B: log(qrate) vs. log(CV*), t = −4.9, P << 0.001; C: qsd vs. log (CV*), t = 1.5, P > 0.1.

From the graphical reconstruction of Fig. 1, CV* should be related to synaptic noise (σ_V) and inversely related to the slope of the AHP (dμ_V/dt). We have already seen that AHPs vary appropriately to contribute to changes in CV* (Fig. 9). What about σ_V? From shot-noise theory, σ_V is proportional to qsize and the square root of qrate. Because qrate and qsize vary in opposite directions with CV* (Fig. 10, A and B), their effects on σ_V tend to cancel. Estimates of σ_V, measured directly from voltage records, are plotted vs. CV* in Fig. 10C. There is a weak, nonsignificant relation between the two variables, implying that σ_V cannot be a strong determinant of discharge regularity. The conclusion is confirmed by integrate-and fire simulations in the discussion.

Response to indenter stimulation: sensitivity to synaptic depolarization.

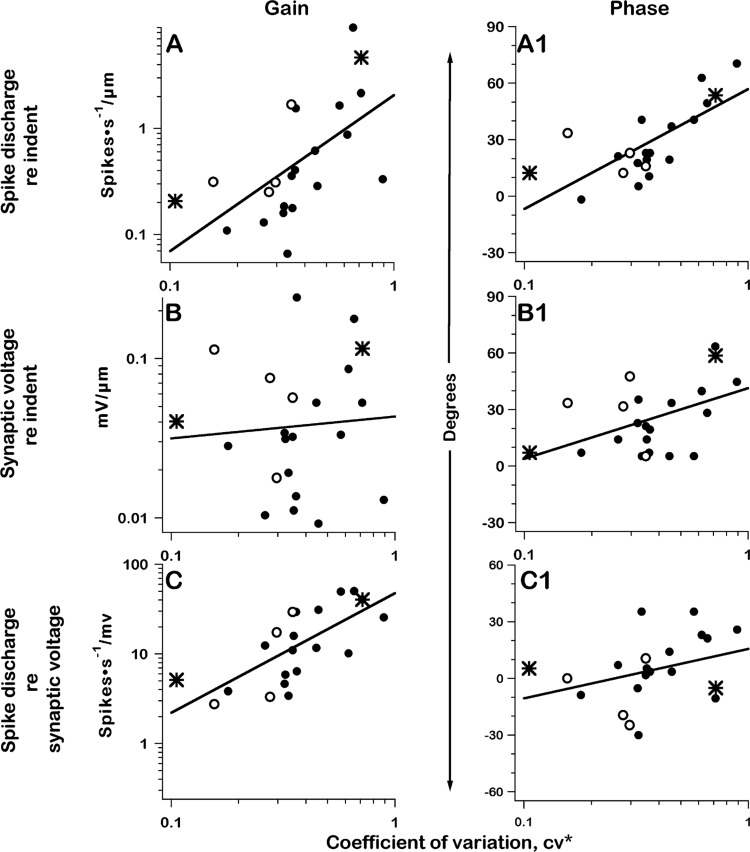
As has been established in a variety of species (review: Lysakowski and Goldberg 2004), including turtles (Brichta and Goldberg 2000a), the rotational responses of irregular units have larger gains and larger phase leads than do the responses of regular units. Reflecting the similar biomechanics governing canal-duct indentation and head rotations (Dickman and Correia 1989a; Rabbitt et al. 1995), such trends are also observed when indentations replace rotations. Regressions with CV* in the present study give a 30-fold increase in spike gain (Fig. 11A) and a nearly 60° increase in spike phase (Fig. 11A1) for a 0.3-Hz indenter stimulus.

Fig. 11.

Gains and phases of response to 0.3-Hz sinusoidal indentations for 22 units are plotted vs. normalized coefficient of variation, CV*. Left: gains; right: phases. Points are mean values. A and A1: spike-rate modulation re indentation. B and B1: postsynaptic voltage re indentation. C and C1: spike-rate modulation re postsynaptic voltage; 2 exemplar units (*); 4 units with unreliable qrates (○), >10,000/s. All regressions, df = 20. A: log (spike gain) vs. log (CV*), t = 3.3, P < 0.01; B: log (synaptic voltage) vs. log(CV*), t = 0.35, P > 0.5; C: log(spike gain re synaptic voltage) vs. log(CV*), t = 4.6, P < 0.001; A1: spike phase vs. log(CV*), t = 4.9, P << 0.001; B1: phase synaptic voltage vs. log(CV*), t = 2.4, P < 0.05; C1: spike phase re synaptic voltage vs. log(CV*), t = 1.6, P > 0.2.

The sinusoidal depolarization recorded postsynaptically in response to canal-duct indentation can be viewed as the synaptic input to the afferent terminal and should reflect presynaptic (hair-cell) factors determining qrate modulation and presynaptic and possibly postsynaptic factors affecting qsize. On the other hand, the relation between discharge rate and sinusoidal depolarization should be determined by the postsynaptic spike encoder. Almost all of the 30-fold variation in gain (Fig. 11A) reflects the spike encoder (Fig. 11C), as there is no systematic variation in the ratio of synaptic voltage to indenter input (Fig. 11B). The phase of sinusoidal depolarization with respect to indentation could reflect the presynaptic kinetics of neurotransmitter release and/or the postsynaptic interaction of excitatory and inhibitory synaptic processes (Fig. 11B1) (Highstein et al. 2005). Any phase difference between postsynaptic voltage and spike discharge is likely to be introduced by postsynaptic ionic conductances, including those involved in spike encoding (Fig. 11C1). Taking the regression coefficients at face value, the two regressions are 59% (Fig. 11B1) and 41% (Fig. 11C1) of the ≈60° total (Fig. 11A1). Only the former regression is statistically significant.

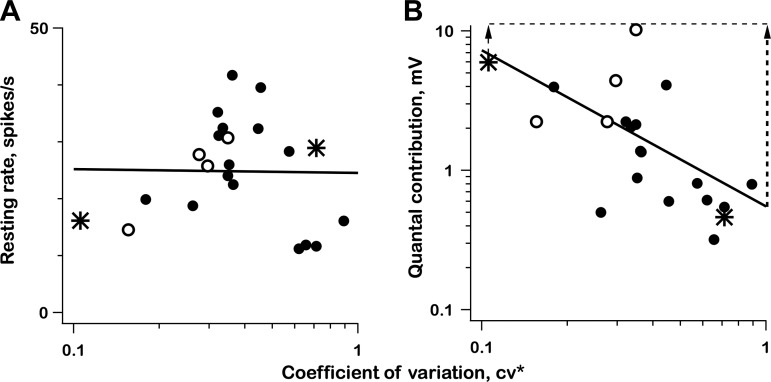
Synaptic contributions to resting discharge.

Figure 12A shows that there is, at most, a weak relation between resting discharge rate (r₀) and CV*. This is in contrast to the large variation with CV* in the gain of sinusoidal spike modulation (Fig. 11A). To see how synaptic inputs could contribute to r₀, we computed the mean synaptic depolarization (v₀) based on shot-noise theory applied to low-pass (original) records, $v_0=\lambda \langle h\rangle I_1,I_1$ = 4.93 × 10⁻³ s. There is a large decline in v₀ with increasing CV* (Fig. 12B), which could lead to a nearly constant r₀ by compensating for an oppositely directed trend in encoder sensitivity.

Fig. 12.

Resting rate (r₀; A) and log resting postsynaptic voltage (v₀; B) both vs. log(CV*); 2 exemplar units (*); 4 units with unreliable qrates (○), > 10,000/s. All regressions, df = 20. A: r₀ vs. log(CV*), t = 0.044, P > 0.9; B: log(v₀) vs. log(CV*), t = 3.2, P < 0.01. Vertical dashed lines in B depict changes needed to transform v₀ from a declining function of CV* during rest (as seen here) to a nearly flat function during 0.3 Hz sinusoidal stimulation (as seen in Fig. 11B).

As CV* increases, the decline in v₀ during rest (Fig. 12B) is replaced by a nearly constant synaptic voltage gain during sinusoidal stimulation (Fig. 11B). The dashed lines in Fig. 12B depict the transition from rest to sinusoidal stimulation as resulting from a larger change in the synaptic voltage of irregular, compared with regular, units. One view of the difference between unit types is that the response dynamics governing synaptic voltage is more phasic in irregular units.

DISCUSSION

In this study, sharp electrodes were inserted into the turtle posterior ampullary nerve near the neuroepithelium to record subthreshold events, including synaptic potentials (mEPSPs) and AHPs, from parent axons. This is the third paper in a series. In previous studies (Holt et al. 2006b, 2007), irregularly discharging units were recorded from almost exclusively. Because of our interest in the determinants of discharge regularity, emphasis in the present study was placed on sampling regularly, as well as irregularly, discharging units even though the thin axons of regular units make even extracellular recordings a challenge (Brichta and Goldberg 2000a). A second, distinctive feature of the present research is that the simultaneous recording of spikes and subthreshold events permitted a study of how synaptic potentials and AHPs regulate the spacing of action potentials. This may be contrasted with previous papers in which spikes were blocked by tetrodotoxin so that synaptic potentials could be recorded in isolation (Holt et al. 2006b, 2007). By extending the observations to include responses to canal-duct indentations, we have been able to characterize the subthreshold events underlying differences in gains and phases.

In this section, we use an improved version of a stochastic integrate-and-fire model (Smith and Goldberg 1986) to explore the role of subthreshold mechanisms in shaping discharge properties. While conclusions are similar to those reached previously (Goldberg et al. 1982, 1984, Smith and Goldberg 1986), they are now based on direct observations of underlying mechanisms, rather than on inferences from the responses to externally applied galvanic currents. Eventually, results with sharp electrodes will have to be extended to whole cell recordings from afferent terminals, but this will require that the synaptic activity in the latter situation be increased to approach physiological levels (Chatlani 2011; Chatlani and Goldberg 2011; Highstein et al. 2012; Songer and Eatock 2013).

Experimental Measures of Synaptic Activity

Shot-noise theory was used to estimate qsize and qrate during resting activity. The calculations required the specification of 1) two adjacent moments measured from synaptic-voltage records; 2) the distribution of quantal sizes; and 3) the shape of individual events. For the moments, the variance and third central moment (skew) were measured from the voltage record after high-pass filtering; in the case of the variance, instrumental noise was subtracted. In a previous study (Holt et al. 2006b), the qsize distribution was shown to resemble a gamma distribution of order k = 4 with a CV = 1$\sqrt{k}$ = 1/2 the shape of individual mEPSPs was inferred in the latter study from the power spectrum of synaptic noise and from the extraction of individual mEPSPs by deconvolution (Wiener filtering) (Holt et al. 2006b). Deconvolution showed that the assumptions of shot-noise theory, viz., the random timing of mEPSPs and the constancy of mEPSP shape, were met.

As was mentioned in materials and methods, there is evidence that individual mEPSPs may be composed of multiple quanta (Keen and Hudspeth 2006; Li et al. 2009; Singer et al. 2004). The possible presence of multiquantal events does not compromise shot-noise estimates of the rate of occurrence and size of mEPSPs, nor does it affect the relation between mEPSPs and spike discharge. A limitation of shot-noise theory is that estimates of qsize (h) and qrate (λ) become unreliable as qrate reaches high values. Fortunately, in deciding on the contribution of quantal parameters to discharge regularity, it is the synaptic noise (σ_V) that is decisive and, because it is directly measured from the voltage record, its estimation remains reliable.

In our analysis of the responses to sinusoidal canal-duct indentation, we were interested in the relation between synaptic voltage and spike discharge. The voltage is directly measured. While much of the voltage modulation can be attributed to quantal synaptic activity (Q), a substantial fraction of the modulation may be due to nonquantal (NQ) transmission, likely the result of the extracellular accumulation of K⁺ ions released from hair cells and/or afferent processes (Goldberg 1996). NQ transmission should be enhanced in CD units, where K⁺ diffusion away from the hair cell is impeded by the presence of the calyx ending (Contini et al. 2012; Goldberg 1996; Lim et al. 2011). However, NQ is also present in B units, presumably the result of K⁺ accumulation in the neuroepithelium (Holt et al. 2006b, 2007).

The presence of NQ should not affect our estimates of qrate and qsize during resting activity as shot-noise calculations were performed on high-pass records that filter out the slow depolarizations resulting from K⁺ accumulation (Contini et al. 2012; Lim et al. 2011). NQ is likely to contribute to indenter-evoked sinusoidal modulation (Holt et al. 2006b). However, here we were mainly interested in the ratio of spike to voltage modulation as a measure of encoder gain. The ratio should be similar regardless of the Q or NQ sources of the voltage modulation, especially since the phase leads for the two kinds of synaptic transmission are similar (Holt et al. 2006b, 2007).

Determinants of Discharge Regularity

Intra-axonal recordings show that the more regular the discharge, the deeper and slower are the AHPs of a unit. The conclusion is consistent with previous studies in which AHPs were directly recorded (Highstein and Politoff 1978; Schessel et al. 1991) or their time course was inferred by measuring thresholds of shock-evoked spikes as a function of PST (Goldberg et al. 1984). Other correlates of CV* include qsize (h) and qrate (λ). Based on the graphical reconstruction of Fig. 1, CV* is proportional to the ratio between synaptic noise (σ_V) and the slope of the mean AHP (dμ_V/dt) at the mean interval, t̄

$${cv}^{*}=\frac{{\sigma }_{\text{V}}}{\overline{t}(\text{d}{\mu }_V/\text{d}t)}$$ (11)

Equation 11 is accurate only when μ_V crosses spike threshold, in which case firing may be termed deterministic; when such crossings do not occur, firing has been called nondeterministic and depends on individual mEPSPs crossing threshold (Smith and Goldberg 1986). Under the latter circumstances, Eq. 11 leads to values that are too high (Table 1) because dμ_V/dt approaches zero; here, simulations are needed to calculate CV*. This is the situation for all except the most regular units in the turtle. In mammals, firing is nondeterministic only for the most irregular units (Smith and Goldberg 1986). The difference between species is the result of the lower resting rates in the turtle (Brichta and Goldberg 2000a) compared with mammals (Goldberg et al. 2012).

Table 1.

Stochastic integrate-and–fire model

	Input				Output		Spike Discharge
Series	qsize, mV	qrate, 1/s	AHP mag, mV	AHP tau, ms	σV, mV	dμV/dt, mV/ms	CV*	Predicted CV*	Galvanic sensitivity, spikes·s−1/mV
1a/reg	0.075	6,000	−6.92	17.5	0.366	0.0526	0.125	0.136	8.26
1b/int	0.2	2,250	−5.00	10.0	0.397	0.0104	0.376	0.767	25.4
1c/irr	0.8	255	−2.73	3.0	0.476	0.00413	0.848	2.305	53.4
2a/reg	0.2	3,450	−6.92	17.5	0.496	0.0457	0.168	0.229	9.39
2b/int	0.2	2,250	−5.00	10.0	0.397	0.0104	0.376	0.483	25.4
2c/irr	0.2	1,940	−2.73	3.0	0.362	0.000856	0.811	8.458	60.4
3a/int	0.075	7,300	−5.00	10.0	0.303	0.00978	0.309	0.620	28.1
3b/int	0.2	2,250	−5.00	10.0	0.397	0.0104	0.376	0.767	25.4
3c/int	0.8	340	−5.00	10.0	0.551	0.00717	0.458	1.537	21.1

Simulation parameters, an integrate-and-fire model for a regular (a/reg), an intermediate (b/int), and an irregular model unit (c/irr). AHP mag, peak afterhyperpolarization (AHP); AHP tau, AHP time constant. Input variables (qsize, qrate, AHP mag, and AHP tau) are set in each simulation to parallel empirical findings (cf. Figs. 9–11) and result in 2 output variables, voltage SD (σ_V) and slope of mean voltage trajectory (dμ_V/dt), both evaluated at the mean interspike interval (50 ms). Spike discharge is characterized by a coefficient of variation (CV)*, the value of CV* predicted from Eq. 11, and the galvanic sensitivity measured as a ratio, spikes·s⁻¹/mV, obtained from regressions between increase in discharge rate and imposed voltage. Series 1 varies both AHPs and qsize so that the 3 units match empirical units differing in discharge regularity. Series 2 varies AHPs but not qsize. Series 3 varies qsize but not AHPs. When qsize or AHP are not varied, they are set to values for the intermediate unit. As a result, series 1b, 2b, and 3b are identical.

How do AHPs and σ_V interact to determine discharge regularity? To explore this issue, the integrate-and-fire model was used to manipulate the two factors independently. As a first step, the model was set up to simulate the discharge of a regular, an intermediate and an irregular unit, each firing at 20 spikes/s, a typical resting rate in the turtle (Fig. 12A) (Brichta and Goldberg 2000a). To obtain the different unit types, inputs to the model, including qsize, qrate and AHP characteristics, were varied consistent with empirical findings (Table. 1, series1a–1c). Specifically, to go from a regular to an irregular discharge, qrate was decreased, qsize increased, and AHPs made shallower and faster.

Simulated voltage traces (Fig. 13, left) and interval histograms (Fig. 13, right) resemble those obtained empirically (Fig. 2). Insight into the etiology of discharge regularity, particularly the role of postspike recovery, is obtained by replotting interval histograms as hazard functions, H(T,T + ΔT) (Cox 1962; Gray 1967; Li and Young 1993), the conditional probability that a spike occurs in the postspike interval, (T,T + ΔT), given that no spike occurs before T, viz.,

$$H(T,T+\Delta T)=\frac{P(T,T+\Delta T)}{P(t\le T)}$$ (12)

H(T,T + ΔT) measures excitability as a function of PST, T. Hazard functions (thick black traces) are superimposed on the interval histograms in Fig. 13, right.

Fig. 13.

Simulations from a stochastic integrate-and-fire model for three units: regular, intermediate and irregular. For each unit, a 1-s voltage trace (left) and interspike-interval histogram based on 20-s smulations (right), including a hazard function (thick black trace). Parameters listed in Table 1, series 1a–1c. Horizontal lines at left: spike thresholds = 2 mV.

In the regular unit, H(T,T + ΔT) remains zero for T ≤ 30 ms, reflecting the deep hyperpolarization at the start of the AHP. H(T,T + ΔT) then grows in parallel with the decline in the AHP and approaches unity as the AHP reaches spike threshold. In contrast, the hazard function for the irregular unit parallels the corresponding AHP in its rapid rise over the first 5–10 ms to reach a nearly constant value, H(T,T + ΔT) ≈ 0.1, whose low value is explainable by the irregular unit AHP remaining below threshold. Because firing is nondeterministic, firing is caused by individual mEPSPs and is irregular as a result of the random timing of mEPSPs. Reflecting an AHP with a more gradual rise than that of the irregular unit, the intermediate unit needs 40–50 ms for its H(T,T + ΔT) to approach a plateau whose value is higher than that of the irregular unit.

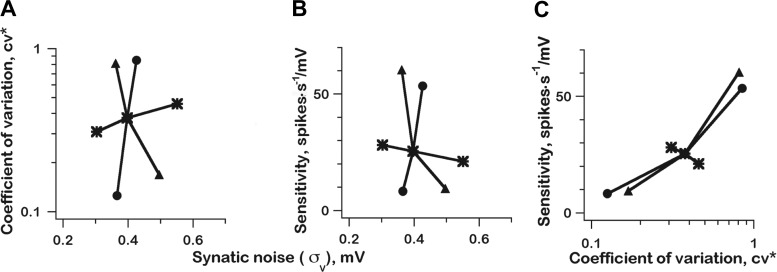
The three units in Fig. 13 differed in both their AHPs and σ_V. Only in the regular unit (Table 1, series 1a) did the AHP (final value, 2.55 mV) cross threshold (2 mV) so that the approximation of Eq. 11 is fairly accurate (estimate, 0.136 vs. actual, 0.125); in the other two, nondeterministic cases, the approximations are too large (Table 1, series 1b and 1c). To estimate the separate influence of dμ_V/dt and σ_V, we compared the parent simulations (Table 1, series 1a–c) with two others, one where AHPs were varied as in the parent simulation, while qsize was kept at 0.2 mV (Table 1, series 2a–2c) and the other where qsize was varied, but AHP parameters were fixed to those of the intermediate unit (Table 1, series 3a–3c). Here, AHPs mainly affects dμ_V/dt, while qsize (and qrate) influence σ_V. In each case, we plotted CV* vs. σ_V (Fig. 14A). In the parent case (Fig. 14A, circles), CV* and σ_V change in the same direction, reflecting the increase in qsize outweighing the decrease in qrate in determining how σ_V varies with CV*. Varying AHP parameters, but not qsize (Fig. 14A, triangles), reverse the σ_V variation with CV*; now σ_V decreases as CV* increases. Yet, the variation in CV* is hardly affected. Finally, keeping the AHP constant while varying qsize leads to a small CV* increase associated with the largest σ_V increase of the three series (Fig. 14A, *). Clearly, there is a dissociation in the changes of CV* and σ_V, indicating that AHP parameters (and thus dμ_V/dt) are much more influential than is σ_V in determining discharge regularity. The small effect of varying σ_V is consistent with the weak relation between σ_V and CV* seen empirically (Fig. 10C).

Fig. 14.

Effect of varying AHP parameters and qsize separately and together, integrate-and-fire model, on discharge regularity (CV*; A) and on galvanic sensitivity (β; B) with both variables plotted against synaptic noise, σ_V. C: galvanic sensitivity (β) vs. CV*. In A–C, 3 series are shown (as listed in Table 1): series 1a–1c, AHP parameters and qsize are varied (●); series 2a–2c, AHP parameters varied, qsize kept constant (▲); series 3a–3c, AHP parameters set at intermediate values, qsize varied (*).

Discharge Regularity and Encoder Sensitivity

Irregularly discharging afferents have much larger responses to externally applied galvanic currents than do regular afferents (Ezure et al. 1983; Goldberg et al. 1982, 1984; Kim et al. 2011). The conclusion that discharge regularity (CV*) and encoder sensitivity (β) are causally related depended on external currents acting in the same way as do physiological inputs. Evidence was presented that this was the case (Goldberg et al. 1984). In the present study, canal-duct indentations produced periodic modulations in synaptic depolarization and discharge rate. Because of the physiological origin of synaptic currents, questions as to their locus of action are effectively eliminated.

The strong relation between encoder sensitivity and discharge regularity suggests that the same factors might determine both discharge properties. Once again, the integrate-and-fire model was used to ascertain the relative roles of AHPs and σ_V. Using the same strategy as for discharge regularity, we varied AHP parameters and qsize separately and together to dissociate AHPs and σ_V (Table 1). AHP variations led to large increases in galvanic sensitivity (β) whether there were simultaneous increases (Fig. 14B, circles) or decreases in σ_V (Fig. 14B, triangles). Varying qsize (and σ_V), while keeping AHP parameters constant resulted in only small changes in β (Fig. 14B, *). As is the case for CV*, we see that AHPs are the major determinant of β. Reflecting their similar dependency on AHPs, there is a strong relation between β and CV* (Fig. 14C), similar to the empirical relation between the indenter gain and CV* (Fig. 11A).

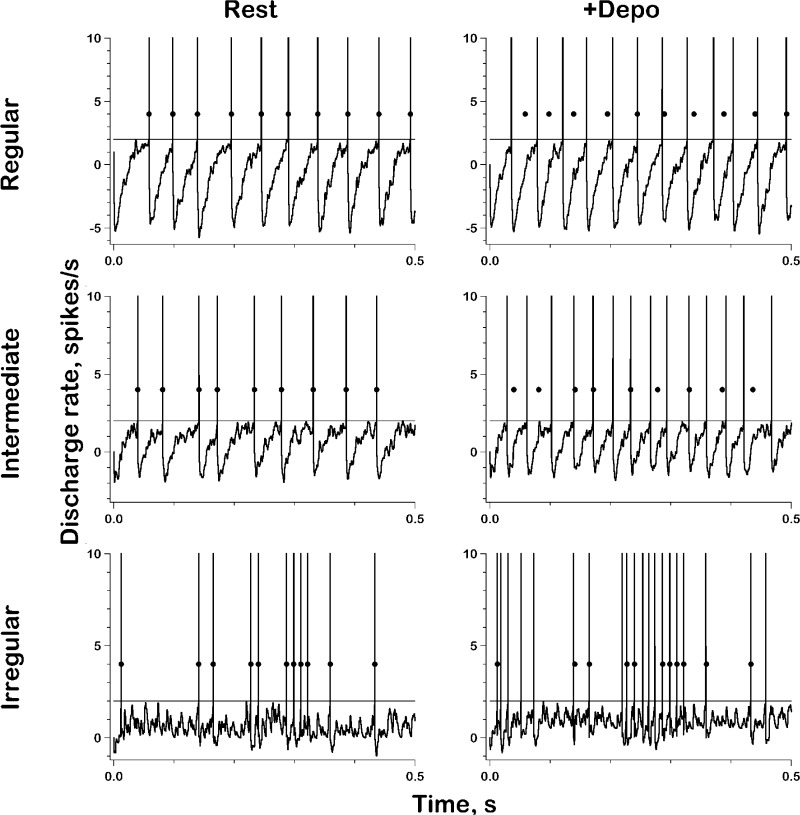
How depolarizing inputs affect the timing of individual spikes bears on the relation between β and CV*. Here, we used galvanic currents rather than synaptic activity so that depolarizations did not lead to the added synaptic noise resulting from increases in qrate. To facilitate the analysis, simulated synaptic activity was identical (frozen) in the presence and absence of the external currents; dots denoting spike times in the absence of imposed depolarization are superimposed on both traces of each pair. In the regular unit (Fig. 15, regular), the added depolarization results in a steeper AHP slope and reduced interspike intervals. There is no synchrony between the timing of spikes in the two conditions; rather, the two spike trains, when superimposed, are seen to beat through each other.

Fig. 15.

Voltage traces in the absence (Rest) and presence of a 0.5-mV depolarization (+Depo) for a regular, an intermediate and an irregular unit. Parameters, see Table 1, series 1a–1c. Dots, indicating timing of spikes occurring during Rest, are superimposed on both traces of each set. Synaptic activity frozen between Rest and +Depo for each set.

The AHP in the irregular unit is nearly flat throughout much of the interspike interval (Fig. 15, irregular). Spikes occur when individual mEPSPs cross threshold; as already noted, the random timing of mEPSPs results in an irregular discharge. Adding the depolarization results in an upward shift of the interspike voltage baseline so that several hitherto ineffective mEPSPs now cross threshold. Because synaptic activity was frozen, almost all of the spikes seen in the original trace are seen during depolarization. In short, a nearly flat interspike trajectory and relatively large mEPSPs provide a common cause for an irregular discharge and enhanced depolarization sensitivity.

In the intermediate unit (Fig. 15, intermediate), only one-third of the spikes present in the control record are found in the depolarized record; here, a fraction of previously effective mEPSPs occur early in the interspike intervals of added spikes and no longer reach threshold.

Discharge Regularity Does Not Determine Response Dynamics

The gain and phase of spike responses to sinusoidal head rotations (and canal-duct indentations) are both correlated with discharge regularity (CV*). Similar results are seen in a variety of species, including fish (Boyle and Highstein 1990; O'Leary et al. 1974), amphibians (Honrubia et al. 1989); reptiles (Brichta and Goldberg 2000a); birds (Dickman and Correia 1989a, 1989b; Si et al. 1997); and mammals (Baird et al. 1988; Fernández and Goldberg 1976a, 1976b; Goldberg and Fernández 1971; Goldberg et al. 1990; Lysakowski et al. 1995; Tomko et al. 1981; Yang and Hullar 2007). In all species studied, regular units have tonic response dynamics, while irregular units are phasic. This almost universal rule raises questions as to how differences in response dynamics arise and whether the processes involved also contribute to the determination of discharge regularity.

There is evidence in mammals, based on the responses to externally applied galvanic currents, that variations in response dynamics across the afferent population are already evident in the synaptic input to the spike encoder. Specifically, sinusoidally modulated, externally applied currents, which engage the encoder, led to only small phase leads and gain enhancements that were similar, independent of discharge regularity (Goldberg et al. 1982, Kim et al. 2011). In mammals, then, response dynamics is already determined by the synaptic inputs to the encoder. Work in turtles (Holt et al. 2006b; the present study) indicates that much of the variation in response dynamics with CV* is present in the synaptic input to the spike encoder (Fig. 11B1) but that the spike encoder or other postsynaptic processes might also be involved (Fig. 11C1). This last observation suggests that discharge regularity and response dynamics might be causally linked, if only partially. Because the integrate-and-fire model can reproduce both regular and irregular firing, it can be used to examine the suggestion that an irregular discharge is associated ipso facto with high-frequency gain enhancements and phase leads.

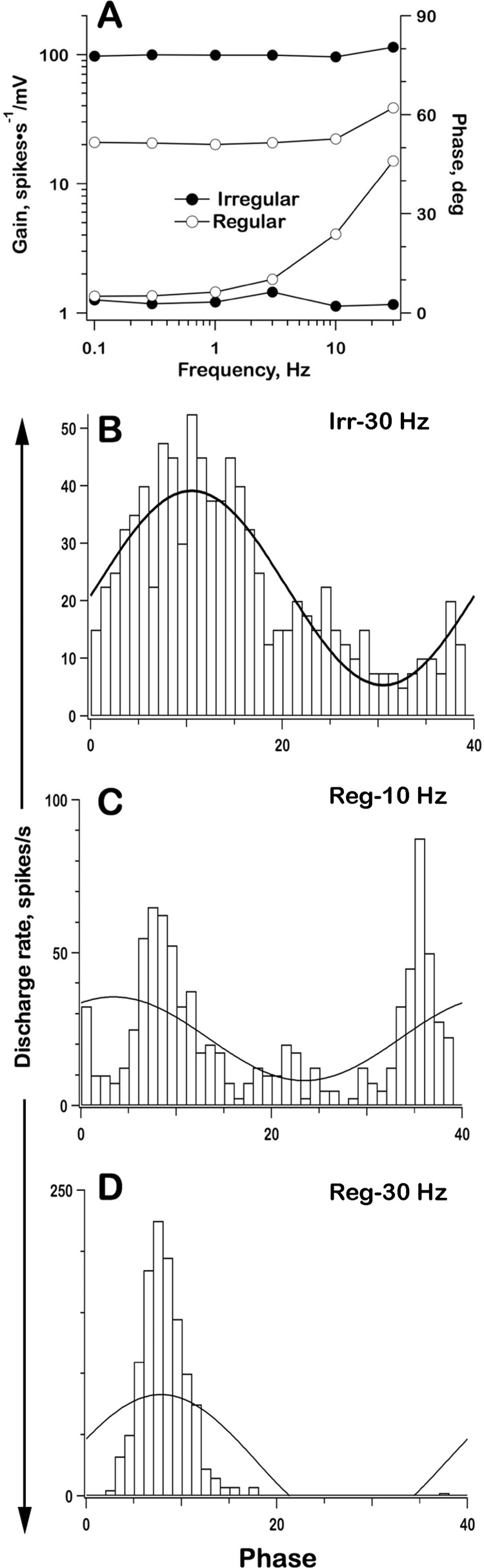
Figure 16A presents Bode plots based on simulations for a regular and an irregular unit. Gains of the irregular unit are almost constant and phases are near zero over the entire frequency range, 0.1–30 Hz. The regular unit has gains, although much lower than those for the irregular unit, that resemble the latter at frequencies of 3 Hz and below in being nearly constant and being associated with near-zero phases. Phases in the regular unit increase at 10 Hz and especially at 30 Hz. To explain the latter effect, we need to examine phase histograms.

Fig. 16.

Responses to sinusoidal modulations in qrate. A: Bode plots, gains (top) and phases (bottom) for a regular (○) and an irregular unit (●), integrate-and-fire model. Gains, ratio between modulations in spike discharge and in synaptic voltage. Phases are re indenter stimulus. B: phase histogram, irregular unit, 30 Hz. Phase histograms, regular unit, 10 Hz (C) and 30 Hz (D). qrate background ± sinusoidal modulation, all frequencies, 8,000 ± 4,000/s (regular), 150 ± 75/s (irregular). Phase histograms, 40 bins, each bin 9° wide; curves, best-fitting sine waves.

Firing in the irregular unit at all frequencies up to 30 Hz was sinusoidally modulated throughout the sine-wave cycle (Fig. 16B). This was also so for the regular unit up to 3 Hz (data not shown). At higher frequencies, the phase histograms of the regular unit were poorly fit by sine waves; rather, firing was at preferred times, twice or occasionally three times during each sine-wave cycle at 10 Hz (Fig. 16C) or once per cycle at 30 Hz (Fig. 16D). Sinusoidal modulation and preferred discharge can be referred to as linear and nonlinear phase locking, respectively. That the regular unit shows nonlinearities, whereas the irregular unit does not, can be explained as follows. In the model, nonlinearities are introduced by the recovery following each spike. The rapid postspike recovery in the irregular unit allows it to respond to sinusoidally modulated quantal traffic shortly after each spike. Recovery in the regular unit is slow; whether there is sinusoidal modulation or preferred firing depends on the relative durations of interspike recovery and the sine-wave period; nonlinear phase locking occurs when the mean interspike recovery is similar to or longer than the sine-wave period.

The simulations for the irregular unit do not show phase leads or frequency-dependent gain enhancements. Hence, an irregular discharge, in and of itself, does not contribute to the phasic response dynamics characteristic of these units. At the same time, an irregular discharge can reduce the incidence of nonlinear phase locking. It should be emphasized that the model is incomplete as it does not include the low-voltage activated (LVA) currents that are likely to be active during repetitive activity (Iwasaki et al. 2008; Kalluri et al. 2010). Postsynaptic LVA currents could contribute to the small phase leads attributable to postsynaptic mechanisms (Fig. 11C1) (Holt et al. 2006b). The participation of postsynaptic mechanisms is also indicated in whole cell recordings from calyx endings in the immature mouse (Songer and Eatock 2013).

Role of Ionic Currents; Etiology of AHPs

Differences in interspike voltage trajectories (AHPs) are responsible for most of the variations in discharge regularity and depolarization sensitivity. What is the ionic basis for the long-lasting, deep AHPs of regular units and the brief, shallow AHPs of irregular units? Most studies of this question have been done in bipolar cells of the vestibular ganglion (reviewed in Eatock et al. 2008).

Ganglion cells can be distinguished by their response to externally applied current steps as phasic or tonic (Iwasaki et al. 2008; Kalluri et al. 2010). Tonic cells discharge throughout current steps, whereas phasic units discharge only once or twice at the beginning and at the end of such steps. The difference in current-step responses is related to the presence of LVA ionic currents only in phasic units. At the onset of a current step, the LVA currents are only slightly activated and the membrane is depolarized to spike threshold. As the step continues, spiking ceases as the LVA currents more fully activate and result in the unit hyperpolarizing below spike threshold. Similarly, LVA currents result in phasic responses in the cochlear nucleus (Rothman and Manis 2003). From a functional perspective, the LVA currents keep the membrane potential below threshold with the result that firing is nondeterministic (Kalluri et al. 2010; the current paper). As shown in previous sections, nondeterministic firing is associated with an irregular discharge, high sensitivity to depolarizing inputs and linear phase locking.

As the present study shows, regularly discharging afferents fire deterministically with the timing of discharge being controlled by long-lasting AHPs. The question arises as to the mechanisms responsible for AHP generation. AHPs can be separated into fast, medium, and slow components (Bean 2007; Fakler and Adelman 2008; Stocker 2004). BK conductances, which are triggered by Ca²⁺ currents occurring during the falling phases of action potentials, can contribute to spike repolarization and to short AHPs. SK channels give rise to medium AHPs, which last for tens to hundreds of milliseconds. Slow AHPs are apparently not seen in vestibular-nerve afferents.

Recordings have documented the presence of BK channels (Limon et al. 2005), SK channels (Limon et al. 2005) and voltage-sensitive Ca²⁺ channels (Chambard et al. 1999; Desmadryl et al. 1997; Limon et al. 2005) in vestibular ganglion cells and SK channels in calyx terminals (Meredith et al. 2011). Despite the presence of BK and SK channels, selective pharmacological blocking has not defined their roles in repetitive discharge (Iwasaki et al. 2008; Limon et al. 2005). It is of interest that in other neurons, where SK channels contribute to medium AHPs, blocking these channels reduces but does not eliminate AHPs (Deister et al. 2009; Wolfart and Roeper 2002). Rapidly inactivating, outward I_A currents can contribute to medium AHPs (Connor and Stevens 1971; Jackson and Bean 2007; Khaliq and Bean 2008) and are present in vestibular afferents (Dhawan et al. 2010; Kalluri et al. 2010). The latter conductances have the advantage over SK currents in allowing the orderly encoding of information down to zero discharge (Connor 1978; Smith and Goldberg 1986). Moreover, consistent with a major theme of the present paper, reducing AHPs by blocking SK channels, can reduce discharge regularity in brain-stem neurons (Deister et al. 2009; Wolfart and Roeper 2002).

Discharge Regularity and Coding Efficiency

As stated in the Introduction, distinct sets of afferent nerve fibers may each be optimized to encode different aspects of the sensory world. Coding efficiency can be measured as the lower-bound mutual information, MI(f), between a band-limited Gaussian stimulus and its spike response

$$\text{MI}(f)=-{\log }_2[1-\text{Co}(f)]$$ (13)

expressed as a function of frequency, f, in bits/s·Hz (Sadeghi et al. 2007). Co(f) is the coherence between stimulus and response (see Bendat and Piersol 2011). When Co(f) << 1, a Taylor-series expansion of Eq. 13 shows that MI(f) is proportional to Co(f).

Calculations of mutual information suggest that regular and irregular units innervating the semicircular canals in turtles are optimized in handling low- and high-frequency head rotations, respectively (Rowe and Nieman 2012). In mammals, the same is true, but the cross-over frequency is different for two groups of irregular units, being <1 Hz in so-called high-gain (central dimorphic) units (Goldberg, In press) and nearer 20 Hz in low-gain (calyx) units (Sadeghi et al. 2007; Goldberg 2013). The superior ability of irregular units to encode higher frequencies depends on their phasic response dynamics, particularly on their frequency-dependent gain increases. Gain increases are important because Co(f) is proportional to the square of the ratio, G(f)/CV where G(f) is the gain (Rowe and Neiman 2012; Goldberg 2013); the cross-over for irregular units occurs when G(f) increases to outweigh the high value of CV. In contrast to irregular units, G(f) and Co(f) of regular units remain almost constant as frequency changes.

We have already emphasized that discharge regularity and response dynamics need not be causally linked. This is so despite the almost universal association of an irregular discharge and phasic response dynamics (review: Lysakowski and Goldberg 2004). The present reasoning suggests that the two attributes are functionally tethered by the need to encode information over a broad frequency range. However, the reasoning would be more persuasive were an irregular discharge to provide unique advantages in the encoding of high-frequency head rotations. A comparison of quantal inputs during rest (Fig. 12B) and sinusoidal stimulation (Fig. 11B) suggests that only the synaptic release machinery of the hair cells innervating irregular units have the phasic response dynamics needed to achieve the requisite gain enhancement. In addition, the highly sensitive spike encoders (Fig. 11C) and large mEPSPs of irregular units (Fig. 10A) minimize the required increase in qrate. The sensitivity to synaptic inputs of irregular spike encoders is 5–10 times higher than that of regular encoders. Furthermore, the qsize of irregular units is 5–10 times larger than that of regular units. Model units series 1a and 1c of Table 1 were used to compare the required qrate increase in a regular and an irregular unit. The qrate increase in the regular unit has to be slightly >50-fold higher than that in the irregular unit. Possibly, the synaptic machinery of regular units and their innervating hair cells is incapable of meeting such a disproportionate demand.

GRANTS

Support was provided by National Institutes of Deafness and Other Communication Disorders Grant DC02508 (“Cellular Mechanisms of the Vestibular System”).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

J.M.G. and J.C.H. conception and design of research; J.C.H. performed experiments; J.M.G. analyzed data; J.M.G. interpreted results of experiments; J.M.G. and J.C.H. prepared figures; J.M.G. drafted manuscript; J.M.G. and J.C.H. edited and revised manuscript; J.M.G. and J.C.H. approved final version of manuscript.