Rare-Variant Extensions of the Transmission Disequilibrium Test: Application to Autism Exome Sequence Data

Abstract

Many population-based rare-variant (RV) association tests, which aggregate variants across a region, have been developed to analyze sequence data. A drawback of analyzing population-based data is that it is difficult to adequately control for population substructure and admixture, and spurious associations can occur. For RVs, this problem can be substantial, because the spectrum of rare variation can differ greatly between populations. A solution is to analyze parent-child trio data, by using the transmission disequilibrium test (TDT), which is robust to population substructure and admixture. We extended the TDT to test for RV associations using four commonly used methods. We demonstrate that for all RV-TDT methods, using proper analysis strategies, type I error is well-controlled even when there are high levels of population substructure or admixture. For trio data, unlike for population-based data, RV allele-counting association methods will lead to inflated type I errors. However type I errors can be properly controlled by obtaining p values empirically through haplotype permutation. The power of the RV-TDT methods was evaluated and compared to the analysis of case-control data with a number of genetic and disease models. The RV-TDT was also used to analyze exome data from 199 Simons Simplex Collection autism trios and an association was observed with variants in ABCA7. Given the problem of adequately controlling for population substructure and admixture in RV association studies and the growing number of sequence-based trio studies, the RV-TDT is extremely beneficial to elucidate the involvement of RVs in the etiology of complex traits.

Introduction

Complex-trait rare-variant association studies of exome or whole-genome sequence data have been facilitated by next-generation sequencing (NGS).¹ The vast majority of NGS association studies of complex traits have been population-based studies of qualitative and quantitative traits. However, these studies are vulnerable to population substructure and admixture, which can greatly increase false-positive rates. The observation of spurious associations due to population substructure has been shown to be an even greater problem for rare variants than for common ones.² Even for European populations, unlike for common variants, there can be considerable differences in the rare allelic spectrum from one European ethnic group to another. These differences can be even more extreme when studying admixed populations such as African-Americans and Hispanics. Although it has been demonstrated for association studies of common variants in European populations that principal components analysis (PCA) can adequately control for population substructure,³ it is debated whether PCA is adequate to control for population substructure when rare variants are analyzed.² For admixed populations, performing PCA to globally control for population admixture can be insufficient, even for the association analysis of common variants.⁴

For population-based studies in the presence of either population substructure or admixture, spurious associations can be detected as a result of sampling artifacts because of differences in allele frequencies between populations. What is desired is to detect an association due to a difference in the genotype frequencies (e.g., between cases and controls, individuals with high and low quantitative trait values) at the causal variant or variants in linkage disequilibrium (LD) with the causal variant. Family-based analysis can avoid the problem of spurious associations due to population substructure and admixture, and significant findings always imply association due to the causal variant or LD with the causal variant. The study of trios is the most basic family-based design for association testing, using genotype data from an affected proband and his parents. Since the trio design was first proposed by Falk and Rubinstein in 1987 to control for population admixture and substructure,⁵ a number of adaptations have been developed including the method that is predominantly used to date, the transmission disequilibrium test (TDT).^6,7 For the TDT, only parents that are heterozygous at the marker locus are informative, and it tests whether or not the frequency of transmitted alleles is the same as the alleles not transmitted to an affected child. The only assumption for the TDT is Mendelian transmission, and an excess of an allele of one type transmitted to the affected offspring indicates a disease-susceptibility locus for the trait that is both linked and associated with the marker.⁸ Both linkage and association between the trait and the marker are required to reject the null hypothesis.⁹ This dual-alternative hypothesis protects the TDT from spurious associations where an association is observed but linkage is not present, which can occur in the presence of population admixture and/or substructure.¹⁰ The cost of recruiting probands and their relatives and performing NGS used to be a bottleneck in performing family-based rare-variant association studies. Currently in order to study the role of de novo mutations in genetic diseases, NGS data are being generated for a large number of trios.¹¹

The traditional TDT can be used to perform rare-variant association analysis by analyzing single variants. However, it has been shown that association analysis of individual rare variants (minor allele frequency [MAF] ≤ 1%) is underpowered,¹² as a result of the small number of observations for a rare variant and a stringent multiple-testing correction. In order to analyze rare variants, many association methods have been developed specifically to enrich the association signal and reduce the multiple-testing penalty. All of these methods group information across multiple variants within a genomic region, which is usually a gene.^13–17 In addition to aggregating rare variants within a region, these methods include (1) weighting each variant by either the frequency in controls¹⁴ or the complete sample¹⁸ or by predicted functionality of the variants¹⁷ and (2) maximizing the test statistic over all variants or variant frequencies.^17–19 These methods can improve power to detect rare-variant associations compared to single variant analysis. Methods that combine the benefits of rare-variant association analysis and family-based tests provide a robust and powerful approach to identify and characterize rare disease-susceptibility variants.

We incorporated four commonly used rare-variant association methods into the TDT framework: Combined Multivariate and Collapsing (CMC),¹³ Weighted Sum Statistic (WSS),¹⁴ Burden of Rare Variants (BRV),²⁰ which is a revised version of Gene- or Region-based Analysis of Variants of Intermediate and Low frequency (GRANVIL),¹⁶ and Variable Threshold (VT).¹⁷ We also compared the power of these methods to the previously described Family Based-Sequence Kernel Association Test (FB-SKAT).²¹ By using simulated genetic data, we demonstrate that type I errors are well-controlled for all extended rare-variant (RV)-TDT methods, even when applied to admixed or substructured populations. However, in the presence of LD between variants, there are some caveats in properly controlling type I errors.

The power of the four RV-TDT methods to detect associations varies only slightly and the most powerful method is dependent on the underlying disease model. However, all RV-TDT methods are more powerful than FB-SKAT. The power of the RV-TDT methods were also compared to population-based rare-variant association methods.

In order to further illustrate the application of the RV-TDT methods with NGS data, 199 autism spectrum disorder (ASD) trios from the Simons Simplex Collection were analyzed.²² ASD, a heterogeneous disorder with substantial heritability, is defined by impaired social communication, deficits in language development, and the presence of restricted interests and/or stereotyped repetitive behaviors.²³ Genome-wide association, de novo mutation, and copy-number-variant studies have reported more than 100 different genes and genomic regions to be associated with this complex trait,²⁴ but for at least 70% of autism cases the underlying genetic component remains unexplained.²⁵ This motivates great interest in investigating the role of low-frequency and rare variants in the etiology of ASD. Application of our RV-TDT methods identified an association with rare variants within ABCA7 (MIM 605414), which encodes ATP-binding cassette subfamily A member 7 protein and might be involved in the etiology of autism.

Material and Methods

Transmission Disequilibrium Test

The TDT was performed in the manner described by Spielman et al.⁷ by using a 2 × 2 table to tally all possible transmission events (Figure 1). For the TDT, only the transmission of alleles from parents who are heterozygous is of interest; for those genotypes where the parent is homozygous the meiosis is uninformative. Transmission events from homozygous parents fall into cells $a$ and $d$, which are not used in the test statistic. The informative meioses from heterozygous parents are where

• (1)the minor allele is transmitted to the proband and the major allele is not transmitted, which we define as a minor-allele-transmitted event. These observations are tallied in cell $c$; and
• (2)the major allele is transmitted to the proband and the minor allele is not transmitted, which we define as a major-allele-transmitted event. These observations are tallied in cell $b$.

Figure 1.

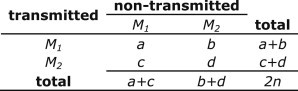
Two-by-Two Table for the McNemar's Test

Displays the manner in which transmission and nontransmission of the parental minor alleles are counted for the transmission disequilibrium test.

The null hypothesis holds when the proportions $b/\left(b+c\right)$ and $c/\left(b+c\right)$ are comparable with probabilities 0.5 and 0.5 (i.e., $b=c$ ). The hypothesis is tested by using a 1-degree of freedom asymptotical ${\chi }^2$ test, McNemar’s test,²⁶ and the ${\chi }^2$ statistic is defined as

$${\chi }^2=\frac{{(b-c)}^2}{(b+c)}.$$ (Equation 1)

For the RV-TDT methods a one-sided test is performed, because only the overtransmission of the minor allele to the affected child is of interest. For all RV-TDT methods, a de novo event is considered to be a minor-allele-transmission event.

Rare-Variant Association Methods

Four commonly used rare-variant association methods are incorporated into the TDT framework to detect the association between rare variants and the phenotype of interest.

TDT-CMC

The CMC method uses an indicator variable to denote the presence or absence of rare variant(s) and tests the association between the phenotype and rare-variant carrier status. For every parent, for each informative variant site we count whether or not a minor-allele-transmitted event occurs. For parent $j$ with variant $i$, we define indicator variables $c_{ij}$ and $b_{ij}$ as

$$c_{ij}=\{\begin{array}{l}1,\text{if}\text{a}\text{minor}\text{-}\text{allele}\text{-}\text{transmitted}\text{event}\text{occurs}\text{for}\text{parent}j\text{with}\text{variant}i\\ 0,\text{otherwise}\end{array}$$

$$b_{ij}=\{\begin{array}{l}1,\text{if}\text{a}\text{major}\text{-}\text{allele}\text{-}\text{transmitted}\text{event}\text{occurs}\text{for}\text{parent}j\text{with}\text{variant}i\\ 0,\text{otherwise}\end{array}$$ (Equation 2)

Then, for a genetic region $L$, the total minor-allele-transmitted events and major-allele-transmitted events for parent $j$ are given by

$$c_j=\sum _{i\in L}{c}_{ij},b_j=\sum _{i\in L}{b}_{ij}.$$ (Equation 3)

For the TDT-CMC method, for a data set with $n$ trios ($2n$ parents), the $c$ and $b$ quadrants in the 2 × 2 table for gene $L$ above are given by

$$c=\sum _{j=1}^{2n}{c}_j/\left(b_j+c_j\right),b=\sum _{j=1}^{2n}{b}_j/\left(b_j+c_j\right).$$ (Equation 4)

Then Equation 1 will be used to attempt to reject the null hypothesis of no linkage or association between the genetic region and the disease. This approach will ensure every informative parent contributes a score of 1 to the McNemar’s test. There are a few rare situations where phasing is required for the TDT-CMC, because each informative parent can only contribute a score of 1, for example, if the proband, mother, and father are all heterozygous at the same rare-variant site and the mother is heterozygous at an additional rare variant site. In this situation, if both of the mother’s rare variants are on the same haplotype, then she is scored 1 for a major-allele-transmitted event (quadrant b) and the father is scored 1 for a minor-allele-transmitted event (quadrant c). On the other hand, if the mother’s rare variants are on different haplotypes, she is scored ½ for a major-allele-transmitted event (quadrant b) and ½ for a minor-allele-transmitted event (quadrant c), whereas the father is scored 1 for a major-allele-transmitted event (quadrant b). Therefore, for the application of the TDT-CMC, haplotypes must be phased.

TDT-BRV

The TDT-BRV method counts the number of minor-allele-transmitted events and major-allele-transmitted events from every informative parent to the affected proband. Therefore unlike the TDT-CMC where each informative parent can only contribute a score of 1 to the McNemar’s test, for the TDT-BRV each informative parent contributes a score that is equivalent to the number of informative sites within the region, e.g., 1, 2, 3.

The same analysis is used as for the TDT-CMC, except Equation 4 above is given in the form of

$$c=\sum _{j=1}^{2n}{c}_j,b=\sum _{j=1}^{2n}{b}_j.$$ (Equation 5)

Because each site within an informative region can be counted independently of the other sites, it is not necessary to phase the data before performing the TDT-BRV, when analytical p values are obtained. However to control type I errors in the presence of LD, empirical p values should be estimated via haplotype permutation, which requires phasing the trio data.

TDT-WSS

For the TDT-WSS, each variant site is weighted by the estimated SD of the number of variants in the parental haplotypes that are not transmitted to the offspring

$${\hat{\omega }}_i=\sqrt{n_i·q_i(1-q_i)},$$ (Equation 6)

where $q_i$ is the allele frequency of variant $i$ in parental haplotypes that are not transmitted to the offspring. The remaining analysis is similar to the TDT-BRV, except the $c$ and $b$ in Equation 4 above are given in the form of

$$c=\sum _{j=1}^{2n}{c}_j=\sum _{j=1}^{2n}\sum _{i\in L}\frac{c_{ij}}{{\hat{\omega }}_i},b=\sum _{j=1}^{2n}{b}_j=\sum _{j=1}^{2n}\sum _{i\in L}\frac{b_{ij}}{{\hat{\omega }}_i}.$$ (Equation 7)

Because internal information is applied to obtain the weights, p values must be obtained empirically by using permutation to avoid spurious associations.

TDT-VT

For the TDT-VT, the test statistic is maximized over allele frequencies and therefore a variable allele frequency threshold is applied, instead of a fixed MAF cut-off. The TDT-VT can be implemented by using either the TDT-CMC or TDT-BRV coding. The TDT-VT avoids the implicit assumption about the relationship between allele frequency and odds ratio. Because the test statistic is maximized over allele frequencies, to correct for multiple testing, p values must be obtained empirically.

We also compared the power of the RV-TDT methods to FB-SKAT. FB-SKAT is an extension of the family-based association test (FBAT) to detect rare-variant associations by using a variance component test. More details about this method can be found in Ionita-Laza et al.²¹

Simulation Based on Population Demographic Models

To evaluate type I error rates and the power of the RV-TDT methods, we generated population genetic data by using forward time simulation.²⁷ Two population demographic models were followed, Kryukov²⁸ and Boyko.²⁹ For the Kryukov model, a conventional four-parameter model was used to describe the demographic history (i.e., bottleneck and exponential expansion) of the European population. Purifying selection, which affects the rare-variant site frequency spectrum, is also modeled for nonsynonymous variants. Details on the population genetic model’s parameters can be found in Kryukov et al.²⁸ For the Boyko model, a simple two-epoch and a six-parameter complex bottleneck models were used to model population demographic changes for Africans and Europeans, respectively. Details for these population genetic models can be found in Boyko et al.,²⁹ and particulars on the choice of parameters have been previously described by Liu and Leal.³⁰ For each population genetic model, 500 haplotype pools were generated, each consisting of 200,000 haplotypes of 1,500 bp in length, which is the average size of a human gene. This 1,500 bp “gene” represents only the coding regions and consists of sites deemed to be either synonymous or nonsynonymous.

Generation of Trio Data

One haplotype pool is randomly selected for each replicate. The genotypes for the proband are obtained by pairing two randomly drawn haplotypes. When genetic data are generated under the alternative hypothesis, a penetrance model is used to determine whether the inherited pair of haplotypes will cause the proband to be “affected.” When an affected proband is obtained, one haplotype is selected to be the maternal haplotype and the other chosen to be the paternal haplotype. The remaining maternal and paternal haplotypes are obtained by randomly selecting two additional haplotypes from the same haplotype pool. When genetic data are generated under the null hypothesis, the same procedure is performed, except that the proband’s genotypes are composed solely from two randomly sampled haplotypes.

To generate African and European admixed trios, we generated haplotype pools by using African and European population demographic models, and the haplotypes were sampled from both the African and European pools. The proportion of African and European admixture is determined by the probability that is used to select from either the African or European haplotype pool. Various degrees of population admixture are examined, i.e., 75% African and 25% European, 50% African and 50% European, and 25% African and 75% European, with the assumption of random mating. By using these probabilities, the two proband haplotypes are either selected both from the African pool, both from the European pool, or one haplotype is selected from the European pool and the other from the African pool. Each one of the proband’s haplotypes is assigned to a parent and then, by using the admixture probabilities, it is determined whether the second haplotype for each parent should be selected from an African or European haplotype pool.

To generate trios in the presence of population substructure, the proband’s haplotypes were constructed by sampling from haplotype pools that were either African or European, and the parents’ haplotypes were drawn from a haplotype pool of the same ancestry. Population substructure was created by analyzing together “African” and “European” trios with the proportions 75% African and 25% European, 50% African and 50% European, and 25% African and 75% European.

To evaluate the effect of intermarker LD on type I error, we generated trio haplotypes with perfect LD. To create a pool, we selected 20 haplotypes that have two or more variant sites and no one variant site could be found on more than one haplotype background. Additionally, to evaluate haplotype reconstruction when there is perfect LD and population substructure, two pools were created each with 20 nonoverlapping haplotypes. Haplotypes were drawn from these two pools with either equal probability or 25% of haplotypes were sampled from one pool and 75% from the other haplotype pool.

Generation of Case-Control Data

In order to compare the power of the RV-TDT methods to the analysis of population-based data by using the original versions of the rare-variant association methods, variant data were generated by the Kryukov model. Two haplotypes were sampled from a haplotype pool and by using the penetrance model described below it was determined whether the haplotype pair should be assigned “case” or “control” status. The process was repeated until the desired numbers of cases and controls were obtained.

Generation of Phenotype Data

The disease status for a pair of haplotypes is assigned based upon their multisite genotypes consisting only of rare nonsynonymous variant sites (MAF ≤ 1%). Power is evaluated when 100%, 75%, and 50% of the nonsynonymous variant sites are causal. Those sites within the gene region that are nonsynonymous were randomly deemed to be causal based upon the predetermined proportions, whereas the remaining rare-variant sites are noncausal with no phenotypic effect. An odds ratio (OR) > 1 is assigned to each causal variant, and the disease probabilities of all variants within a gene are computed based upon an additive mode of inheritance.³¹ Two different disease models were applied, both using a disease prevalence of 1%: the equal-effect model where the ORs of causal variants are constant and the variable-effects model where the ORs of causal variants are inversely correlated with their MAFs. For the equal-effect model, those variant sites that are deemed to be causal were evaluated by using four ORs = 1.8, 2.0, 2.2, and 2.5. For the variable-effects model, those variant sites which were deemed to be causal with the lowest observed allele frequency were assigned OR_max while those variant sites with the highest allele frequency were assigned OR_min. Interpolation was used to obtain the effect size of all causal variants with allele frequency between the highest and lowest MAF. The power was evaluated for four variable-effects models OR_min-OR_max = 1.5–2.5, 1.5–3.0, 1.5–3.5 and 1.5–4.0.

Data Analysis

For the TDT-CMC, TDT-BRV, and FB-SKAT, only rare variants with a MAF ≤ 1% were analyzed, whereas for the TDT-WSS, TDT-VT-CMC, and TDT-VT-BRV both rare and low frequency variants (MAF ≤ 5%) were analyzed. For evaluating the effect of LD on the RV-TDT methods, a MAF of ≤ 5% was used for all tests. All variants meeting the MAF criteria were analyzed whether or not they were deemed to be “causal.” For TDT-CMC and TDT-BRV, p values were obtained both analytically and empirically, whereas for TDT-WSS, TDT-VT-CMC, and TDT-BRV, p values were only obtained empirically through genotype and haplotype permutation. For the FB-SKAT method, p values were obtained by moment matching approach with 10,000 Monte Carlo simulations. For the analysis of population-based data with the rare-variant association methods BRV, WSS, and VT, p values were obtained empirically, whereas for the CMC, p values were obtained both empirically and analytically.

Permutation

Genotype and haplotype permutation methods were evaluated. For genotype permutation, genotypes are shuffled at every variant site between each parental pair, and then a paternal and maternal haplotype were randomly chosen to form the offspring’s genotypes. For haplotype permutation, the haplotypes are phased and then the parental haplotypes within each trio are shuffled, and the offspring’s genotypes are obtained by pairing a randomly selected paternal and maternal haplotype.

Haplotype Phasing

For the TDT-CMC, TDT-VT-CMC and haplotype permutation, haplotypes must be phased. In order to evaluate how well haplotypes could be phased in the presence of African and European population admixture, the phase of the generated data was ignored and phasing was performed with BEAGLE.³² Additionally, haplotype data were generated with perfect LD, and the haplotype phases were ignored and then reconstructed with BEAGLE. By using 10,000 replicates, the proportion of times parental haplotypes could be correctly phased was evaluated.

Evaluating Type I Error and Power

To evaluate type I errors, we generated 20,000 replicates each with 1,500 trios. For RV-TDT methods where p values were obtained empirically, 10,000 permutations were performed. Power was evaluated for an α = 0.05. Two thousand replicates were generated to evaluate power for samples of 800, 1,000, 1,200, 1,500, and 1,800 trios, and to obtain p values empirically, 2,000 permutations were performed. Additionally, to compare power for the RV-TDT methods to the analysis of population-based data, 2,000 replicates were generated for three different scenarios: 1,500 trios, 1,500 cases/1,500 controls, and 1,000 cases/1,000 controls. P values were obtained empirically by performing 2,000 permutations.

Application to Autism Data

From the Simons Simplex Collection, 199 autism spectrum disorder trios were analyzed. Previously, 189 of these trios were analyzed to detect de novo events.²⁵ An additional 10 trios, which have not been described, were also analyzed.

All samples and phenotypic data were collected under the direction of the Simons Simplex Collection by its 12 research clinic sites: Baylor College of Medicine; Children's Hospital Boston and Harvard University; Columbia University; Emory University; McGill University; Vanderbilt University; Yale University; University California Los Angeles (UCLA); University of Illinois at Chicago; University of Michigan; University of Missouri; and University of Washington. Parents consented and children assented as required by each local institutional review board. Participants were de-identified before distribution. Research was also approved by the University of Washington Human Subject Division under nonidentifiable biological specimens/data.

Exome Capture and Genotype-Calling

Genomic DNA was extracted from whole blood.²⁵ Exomes were captured by using NimbleGen EZ Exome V2.0 and reads were mapped to a custom reference genome assembly (GRC build37). All exomes met the completed criteria of ≥8× read depth in 90% of the capture target and ≥20× read depth in 80% of capture target. Additional details on exome sequencing of the autism trio data can be found in O’Roak et al.²⁵

Quality Control

Variants were selected if they passed the following GATK filters:³³ AB (allele balance for hets [ref/(ref+alt)]) ≤ 0.75, HRun (largest contiguous homopolymer run of variant allele in either direction) ≤5.0, QD (variant confidence/quality by depth) ≥5, SB (strand bias) ≤−0.10, QUAL (sequencing quality) >30, and SnpCluster (at least 3 variants clustered within 10 bp).³⁴ Variant Association Tools (VAT) software was used to remove genotypes with a read depth <10× and also to select variants for analysis. Gene regions were assigned based upon RefSeq definition and ANNOVAR³⁵ was used to annotate variant sites. Only variant sites that were either nonsynonymous or putative splice site variants were analyzed.

Phasing Trios Data

Before phasing, Mendelian inconsistencies were identified and removed with the PLINK software.³⁶ Phased genotypes were obtained with BEAGLE software.³² For missing genotype data, BEAGLE imputes missing data and only provides the most likely genotype. We observed that analyzing the most likely genotype can increase false-positive rates for trio data (data not shown). Therefore the imputed variant calls were removed from the analysis. Additionally to avoid spurious associations, those regions of the exome containing copy-number variants or pseudogenes were removed from the analysis. Genes on the autosomal chromosomes with ≥4 variant sites were analyzed, and 8,441 genes were included in the analysis.

Results

Evaluation of Type I Error

Type I error rates were estimated by the proportion of replicates with p values ≤ 0.05 or ≤ 0.005. Additionally, Quantile-Quantile (QQ) plots were generated. When the data were generated without LD, no type I error inflation was observed for any of the RV-TDT methods (Table 1; see Figure S1 available online). For both the TDT-CMC and TDT-BRV when p values were obtained analytically, the type I error is well-controlled and the p values are slightly conservative (Table 1; Figures S1A and S1D). Likewise, when p values were obtained empirically through either genotype or haplotype permutation, type 1 error is well-controlled (Table 1; Figure S1). However, when the haplotypes with perfect intermarker LD, i.e., r² = 1 were analyzed, extreme inflation in type I error was observed (Table 1; Figure 2) under several conditions. For p values that were obtained analytically for the TDT-BRV, type I error is extremely inflated, but for the TDT-CMC, the type I errors are well-controlled and even slightly conservative (Table 1; Figure 2A). For example, for the TDT-BRV when haplotypes with the variants in perfect LD were analyzed, an α level of 0.05 has a type I error rate of 0.20. This inflation of type I error is not resolved through genotype permutation (Figure 2B). Haplotype permutation resolves the problem and type I error is well-controlled (p value = 0.05) (Figure 2C). For the TDT-WSS, TDT-VT-CMC, and TDT-VT-BRV, p values must be obtained empirically to properly control type I errors, and when there is intermarker LD, although genotype permutation leads to inflated type I errors (Table 1; Figure 2B), haplotype permutation properly controls type I error rates (Table 1; Figure 2C).

Table 1.

Type I Error for RV-TDT Methods at α Levels of 0.05 and 0.005

Method		Models
		Kyrukov		Boyko		LD
		α = 0.05	α = 0.005	α = 0.05	α = 0.005	α = 0.05	α = 0.005
TDT-BRV	Analyticala	0.0493	0.0032	0.0468	0.0033	0.1996b	0.0946
	Genotypec	0.0427	0.0042	0.0396	0.0034	0.1992	0.0934
	Haplotyped	0.0432	0.004	0.0396	0.0034	0.051	0.0033
TDT-CMC	Analytical	0.0492	0.0032	0.0467	0.0033	0.0472	0.0034
	Genotype	0.043	0.004	0.0397	0.0035	0.1082	0.0265
	Haplotype	0.0431	0.0039	0.0396	0.0034	0.0519	0.0041
TDT-VT-BRV	Genotype	0.0448	0.0037	0.0423	0.0039	0.2795	0.1269
	Haplotype	0.0445	0.0039	0.0424	0.0038	0.0487	0.004
TDT-VT-CMC	Genotype	0.0447	0.0038	0.0423	0.004	0.1086	0.0188
	Haplotype	0.0442	0.0039	0.0425	0.0039	0.0445	0.0047
TDT-WSS	Genotype	0.0459	0.0042	0.0441	0.0038	0.1846	0.081
	Haplotype	0.0449	0.0041	0.0446	0.0037	0.0509	0.0041

Method		Proportion of African and European Admixture
		0.75/0.25		0.5/0.5		0.25/0.75
		α = 0.05	α = 0.005	α = 0.05	α = 0.005	α = 0.05	α = 0.005
TDT-BRV	Haplotype	0.0509	0.0044	0.0489	0.0047	0.0483	0.0050
TDT-CMC	Analytical	0.0416	0.0040	0.0463	0.0043	0.0481	0.0037
	Haplotype	0.0470	0.0041	0.0483	0.0043	0.0504	0.0047
TDT-VT-BRV	Haplotype	0.0491	0.0058	0.0483	0.0051	0.0518	0.004
TDT-VT-CMC	Haplotype	0.0495	0.0055	0.0489	0.0054	0.0520	0.0042
TDT-WSS	Haplotype	0.0519	0.0050	0.0498	0.0056	0.0527	0.0048

^ap values obtained analytically.

^bInflated type I errors are highlighted in bold font.

^cp values obtained with 10,000 genotype permutations.

^dp values obtained with 10,000 haplotype permutations.

Figure 2.

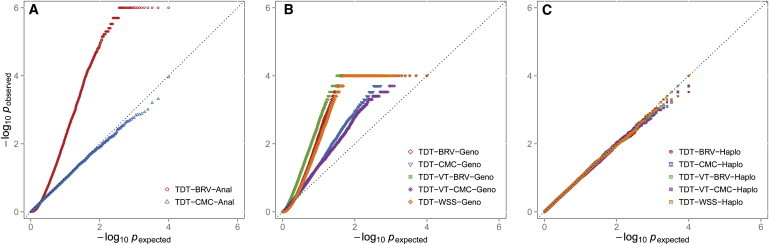
QQ Plot of Negative Natural Log p Values Obtained for Trio Data under the Null Hypothesis of No Association when the Variant Sites that Are Tested Are in Perfect LD

For each scenario, a total of 1,500 trios were analyzed and 20,000 replicates were generated. For the TDT-CMC and TDT-BRV, variants with MAF ≤ 1% were analyzed while for the TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS, variants with MAF ≤ 5% were analyzed.

(A) Displays the results for the TDT-BRV and TDT-CMC when p values were obtained analytically (Anal).

(B) Displays the results for the TDT-BRV, TDT-CMC, TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS. All p values were obtained empirically by performing 10,000 genotype (Geno) permutations for each replicate.

(C) Displays the results for the TDT-BRV, TDT-CMC, TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS. All p values were obtained empirically by performing 10,000 haplotype (Haplo) permutations for each replicate.

To demonstrate that the RV-TDT methods can adequately control for population admixture, admixed African and European populations were generated following the Boyko population demographic models using different ratios of African and European admixture. For all methods, haplotype permutation provided control of type I errors. Also for the TDT-CMC, when p values were obtained analytically, type I error was well-controlled (Table 1; Figure 3). Similar results were obtained for substructured populations (data not shown). These findings strongly support that RV-TDT methods are robust to both population admixture and substructure.

Figure 3.

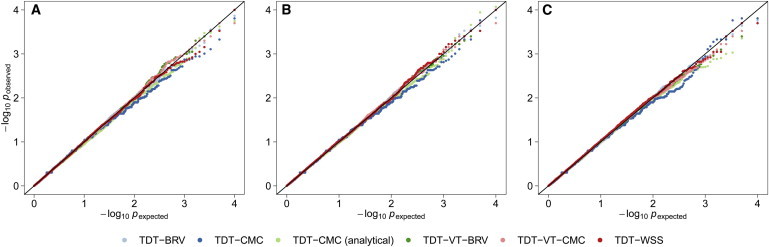
QQ plot of p Values Obtained from the Analysis of African and European Admixed Populations

Genetic variant data for African and European populations were generated under the Boyko model. A total of 1,500 trios were analyzed using 20,000 replicates. Type I error rates were evaluated for the TDT-BRV, TDT-CMC, TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS. For the TDT-CMC and TDT-BRV, variants with a MAF ≤ 1% were analyzed while for the TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS, variants with MAF ≤ 5% were analyzed. All p values were obtained empirically by performing 10,000 haplotype permutations for each replicate, except for the TDT-CMC analytical. The data were generated with different proportions of African and European admixture: in (A) 75% African and 25% European, (B) 50% African and 50% European, and (C) 25% African and 75% European.

For all methods for which type I error is well-controlled, haplotypes need to be reconstructed. We examined the ability to reconstruct haplotypes for trio data, where information from the proband can aid in the reconstruction. In the presence of population admixture, even with no LD, when a ratio of 50% African and 50% European was used, 99.95% (SD 0.12%) of the haplotypes could be reconstructed correctly. Likewise, when the ratio was changed to 75% African and 25% European, 99.93% (SD 0.23%) of the haplotypes were correctly reconstructed. The results were very similar when data were generated under population substructure. For example, for population substructure where 50% of the population was African and 50% European, 99.88% (SD 0.40%) of the haplotypes were correctly reconstructed.

Power of RV-TDT Methods

The power of the RV-TDT methods were evaluated for a variety of sample sizes and effect sizes, and also compared to the power of FB-SKAT. The difference in power between the RV-TDT methods is small, although TDT-BRV and TDT-CMC are slightly more powerful than other methods under the equal-effect model (Figure 4; Figure S2); however, there is a clear difference in power between the RV-TDT methods and FB-SKAT, with the RV-TDT methods being considerably more powerful. The power of the RV-TDT methods, as a function of genetic effect size and sample size, is shown in Figure 4 and Figure S3, respectively. For example, when 75% of all nonsynonymous rare-variant sites were causal and the OR for causal variants is 2.5, the power of TDT-CMC and TDT-BRV is 71.15% and 71.10%, respectively, whereas the power for TDT-WSS, TDT-VT-CMC, and TDT-VT-BRV is 67.25%, 66.00%, and 66.10%, respectively. For the same scenario, the power for FB-SKAT is 53.90% (Figure 4E). When 75% of the variant sites are causal and the OR for causal variant is between 1.5 and 4.0, the power of TDT-CMC, TDT-BRV, TDT-WSS, TDT-VT-CMC, and TDT-VT-BRV is 68.25%, 68.05%, 70.25%, 70.05%, and 70.20%, respectively, while for the same scenario the power for FB-SKAT is 35.88% (Figure 4B).

Figure 4.

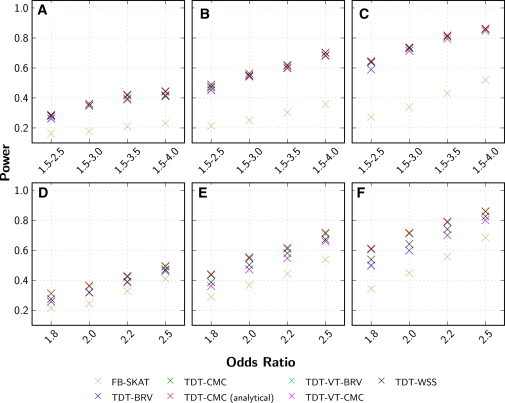
Comparison of Power for the RV-TDT Methods and FB-SKAT

Power was evaluated for an α level of 0.05 for 1,500 trios by generating 2,000 replicates. Analysis was performed with TDT-BRV, TDT-CMC, TDT-VT-BRV, TDT-VT-CMC, TDT-WSS, and FB-SKAT. For the TDT-CMC, TDT-BRV, and FB-SKAT, variants with a MAF ≤ 1% were analyzed while for the TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS, variants with MAF ≤ 5% were analyzed. For the TDT-BRV, TDT-CMC, TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS, p values were obtained empirically by performing 2,000 haplotype permutations for each replicate. For the TDT-CMC, p values were also obtained analytically. For the FB-SKAT, p values were obtained with a moment matching approach by using 10,000 Monte Carlo simulations. Genetic variant data were generated under the Kryukov model and the proband’s affection status was obtained with two different penetrance models: variable-effects model (A, B, C) and equal-effect model (D, E, F). Different proportions of the variant sites were deemed to be causal: (A and D) 50%, (B and E) 75%, and (C and F) 100%.

To further evaluate the power of the RV-TDT methods, we compared their power to the corresponding rare-variant association methods for population-based data. In Figure 5, the comparison of the power between the TDT-BRV and BRV is shown, used to analyze trio and case-control data, respectively. As previously observed for the analysis of common variants per genotyped individuals, the case-control design is slightly more powerful than the trio design. For example, when 75% of all nonsynonymous rare-variant sites are causal with OR = 2.0, the power of BRV when 1,500 cases and 1,500 controls were analyzed is 45.85% and the power of TDT-BRV when 1,000 trios were analyzed is 43.25%. However, if only 1,000 cases and 1,000 controls are analyzed using the BRV, the power is 33.00% (Figure 5B). Similar results were observed for the other TDT extensions (data not shown).

Figure 5.

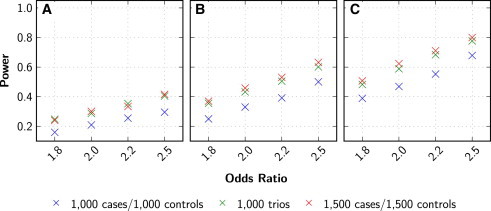
Comparison of Power to Detect Rare-Variant Associations with Population-Based and Trio Data

The BRV was used to analyze samples of size 1,000 cases and 1,000 controls and 1,500 cases and 1,500 controls, and the TDT-BRV was used to analyze 1,000 trios. Power was evaluated for an α level of 0.05 for both case-control and trio data by generating 2,000 replicates. P values were obtained empirically by performing 2,000 haplotype permutations for each replicate. Genetic variant data were generated with Kryukov model. Affection status was determined with an equal-effect penetrance model with ORs varying between 1.8 and 2.5. Different proportions of causal variants were used in the analysis with 50% (A), 75% (B), and 100% (C).

Applications to Autism Data Set

We applied the RV-TDT methods to analyze 199 trios from the Simons Simplex collection that had available whole-exome sequence data. The QQ plots for TDT-CMC, TDT-BRV, TDT-VT-BRV, TDT-VT-CMC, and TDT-WSS indicate that there is no inflation of type I error (Figure S3). None of the detected associations meet exome-wide significance of 5.92 × 10⁻⁶, i.e., an α level of 0.05 Bonferroni corrected for testing 8,441 genes. ABCA7 showed the strongest evidence of being associated with autism (OR = 8.5 ± 0.75 stdev) with all RV-TDT methods.³⁷ Results from the TDT-RV methods were similar: TDT-BRV (p value = 1.4 × 10⁻⁴), TDT-CMC (p value = 1.6 × 10⁻⁴), TDT-CMC (analytical) (p value = 2.9 × 10⁻⁴), TDT-VT-BRV (p value = 1.5 × 10⁻⁴), TDT-VT-CMC (p value = 2.3 × 10⁻⁴), and TDT-WSS (p value = 2.8 × 10⁻⁴). None of the variants that were observed in ABCA7 are de novo events. Ten missense variants in ABCA7 with MAF ≤ 1% were observed in 18 trios with a total of 19 minor alleles observed in the parental generation (Table 2). There were 17 minor-allele-transmitted events and 2 major-allele-transmitted events. For seven missense variants, only a single minor-allele-transmitted event was observed. Three missense variants had multiple transmission events: c.2629G>A (p.Ala877Thr) had a minor-allele-transmitted event in five trios and a major-allele-transmitted event in one trio, c.5435G>A (p.Arg1812His) had a minor-allele-transmitted event in three trios and a major-allele-transmitted in one trio, and c.4795G>A (p.Val1599Met) had a minor-allele-transmitted event in two trios (Table 2). Only in one trio, two transmission events were observed in ABCA7, c.1534C>G (p.Arg512Gly), and c.4795G>A (p.Val1599Met). Of the ten missense variant sites, five occurred at conserved nucleotides (both PhyloP and GERP scores > 1) and were deemed damaging by at least three of four bioinformatics tools, and therefore could be potentially causal (Table 2). Three of the damaging missense variants were observed in the NHLBI GO Exome Sequencing Project (ESP)³⁸ with MAF 0.0002-0.004, while two variants are not previously reported in publically available databases including 1000 Genomes.³⁹ For the additional five ABCA7 variants, only one was not previously reported in publically available databases (Table 2).

Table 2.

Bioinformatic Evaluation and Frequencies of Rare Missense Variants within ABCA7

Chr19 Position	Nucleotide Substitutiona	PhyloPb	GERPc	Amino Acid Substitution	PolyPhen-2	SIFT	MutationTaster	Mutation Assessor	Transmitted/Non-transmitted Events	dbSNP rsID	NHLBI-ESP EA MAFd	NHLBI-ESP AA MAFd
1,043,788e	c.995G>A	2.90	4.33	p.Gly332Glu	Probably damaging	Damaging	Polymorphism	Functional, medium	1/0	NA	NA	NA
1,045,109	c.1324G>A	0.28	2.54	p.Gly442Arg	Possibly damaging	Tolerated	Polymorphism	Nonfunctional, low	1/0	NA	NA	NA
1,046,317	c.1534C>G	−0.04	1.11	p.Arg512Gly	Benign	Tolerated	Polymorphism	Neutral	1/0	NA	0.0001	0
1,050,996	c.2629G>Af	1.18	2.59	p.Ala877Thr	Benign	Tolerated	Polymorphism	Nonfunctional, low	5/1	rs74176364	0.006	0.003
1,051,481	c.2858C>A	4.96	4.43	p.Ala953Asp	Probably damaging	Damaging	Disease-causing	Functional, high	1/0	NA	NA	NA
1,057,343	c.4795G>Af	1.58	3.65	p.Val1599Met	Probably damaging	Damaging	Polymorphism	Functional, medium	2/0	rs117187003	0.004	0.0009
1,058,883	c.5344C>T	1.58	3.14	p.Arg1782Trp	Probably damaging	Damaging	Disease-causing	Functional, medium	1/0	NA	0.0003	0
1,059,056	c.5435G>Af	1.28	0.81	p.Arg1812His	Benign	Damaging	Polymorphism	Neutral	3/1	rs114782266	0.005	0.07
1,062,248	c.5648C>T	4.87	3.61	p.Thr1883Met	Probably damaging	Damaging	Disease-causing	Functional, high	1/0	NA	0	0.0002
1,065,305	c.6322G>Af	2.08	3.73	p.Glu2108Lys	Benign	Tolerated	Polymorphism	Functional, medium	1/0	rs139706726	0.0002	0

^acDNA position is based on reference sequence NM_019112.3.

^bPhyloP scores indicate nucleotide conservation under a null hypothesis of neutral evolution.

^cGERP provides position-specific estimates of evolutionary constraint.

^dMinor allele frequencies (MAF) for European-Americans (EA) and African-Americans(AA) from the NHLBI GO – Exome Sequencing Project (ESP) Exome Variant Server. NA, not available.

^eConserved nucleotides (both PhyloP and GERP with scores > 1) and damaging variants (deemed damaging by at least three of four bioinformatics tools) are highlighted in bold font.

^fIncluded on the Illumina Human Exome BeadChip.

Discussion

In this work, we incorporated rare-variant association analysis into the TDT framework to analyze sequence data, in particular rare variants. The simulation results demonstrate that our RV-TDT methods are robust to both population substructure and admixture, which highlights the potential benefits of their application to the analysis of sequence data. Current methods to control for population substructure and admixture might not be sufficient to avoid spurious associations when analyzing rare variants, in particular for admixed populations such as African-Americans and Hispanics.^2,4 The RV-TDT framework can control for both admixture and substructure and thus avoid spurious associations. Additionally proper control of population substructure and admixture can also decrease type II error and lead to an increase in power.

Although the accuracy of NGS technologies has greatly improved, there is still ∼1% false-positive call rate even for high read-depth sequence data.³⁸ An additional advantage of analyzing trio data is that it is possible to improve the accuracy of variant calls, by using variant callers that make use of family or trio information.^40,41 The increased precision in variant calls can in turn lead to increased power to detect associations.

BEAGLE was used to phase the simulated and autism trio data. Other programs could have been used to accurately phase trio data including PHASE (v2.1)⁴² and Shape-It.⁴³ We demonstrate that phasing is quite accurate for trio data even when “admixed” data were generated. It has also been demonstrated by others that phasing of haplotypes is considerably more accurate for trio data than population-based data.⁴⁴ For example, when PHASE (v2.1) was used, the percentages of genotypes whose phase was correctly inferred was 99.8% for simulated trio data and 99.95% for the HapMap Centre d’Etude du Polymorphisme Humain (CEPH) trio data, whereas for unrelated individuals, haplotype phasing was correctly inferred 94.8% for the simulated data and 94.1% for CEPH data.⁴⁴ Therefore, for trio data it is possible to obtain highly accurate haplotype information.

When p values are analytically obtained for TDT-BRV, it is not necessary to phase the data and additionally for genotype permutation, phasing of the haplotypes is not necessary. We demonstrate that although these methods adequately control type I error when there is no intermarker LD, there can be serious inflation of type I error in the presence of LD. For those methods, which require empirical p values, e.g., TDT-WSS and TDT-VT, haplotypes must be permuted because permuting genotypes leads to an increase in type I errors. When population-based data are analyzed with the BRV method, analytical p values have well-controlled type I errors. Conversely for trio data analyzed with the TDT-BRV, analytical p values have inflated type I errors; however, for empirical p values obtained via haplotype permutation, type I errors are well-controlled.

For rare variants it is usually assumed that there are only low levels of LD, because it is unlikely that rare variants fall on the same haplotype background. However, for the initial analysis of the autism trio data, we detected associations with several genes with TDT-BRV and genotype permutation for which no significant association was discerned by using the TDT-CMC or haplotype permutation. Upon closer inspection we observed that these associations were driven by multiple rare variants that all lay upon the same haplotype. When analytical or empirical p values via genotype permutation are obtained, each variant is treated as an independent event, but in the presence of LD, this is not the case. This led to an additional investigation on the effects of intermarker LD on type I error and the demonstration that analytical p values for the TDT-BRV, and empirical p values obtain through genotype permutation, which breaks down the LD structure, are not robust to intermarker LD and therefore should not be used. Only haplotype permutation retains the LD structure when used to obtain empirical p values and therefore properly controls type I errors.

We demonstrate that the rare-variant case-control design with an equal number of cases and controls is generally slightly more powerful than the trio design if an equal number of individuals are analyzed, e.g., 1,000 trios versus 1,500 cases and 1,500 controls. However, if an equivalent sample size of cases is analyzed, the power for the RV-TDT methods is slightly higher than the population-based design, e.g., 1,000 trios versus 1,000 cases and 1,000 controls. Additionally, for trio design, only the proband must be phenotyped, which is equivalent to one-third of the study participants, whereas for a case-control design, all study participants should be phenotyped.

A disadvantage of the trio design is that it is not usually suitable for late-onset diseases, because parents will often be deceased and no longer available for study. Additionally, nonpaternity can reduce the power to detect associations, because genotype data for the biological fathers will not be available. Its distinct advantages include: control of type I error in the presence of population substructure and admixture and the ability to investigate parent-of-origin effects. These benefits make the family-based design an excellent choice for sequence-based genetic studies, in particular for early-onset diseases. An additional advantage of using the family-based design is that both inherited and de novo events can be studied and tested simultaneously using the RV-TDT methods.

If it is of interest to detect an association with either protective or detrimental variants, although less powerful than a one-sided test, a two-sided test should be performed. If protective variants are involved in disease etiology, there is an undertransmission of minor alleles to the affected proband. In the traditional implementation of the TDT, parents are not phenotyped and some of the parents might manifest the phenotype of interest, thus reducing the power to detect an association with protective variants. If trios have been ascertained to detect de novo events where the parents have been screened to ensure they are unaffected, it could be the case that they harbor protective variants that prevent them from being diseased or they might not have the correct combination of causal variants and\or environmental exposures to induce the phenotype. Another scenario is that both protective and detrimental variants within the same gene are involved in disease etiology. It has been previously shown that in these situations, variance component tests such as SKAT can be more powerful than aggregate rare-variant methods. However, variance-component methods are less powerful when the vast majority of variants within a region are either detrimental or protective.⁴⁵ We also demonstrate here that FB-SKAT is considerably less powerful than the other RV-TDT methods when causal variants within a gene region have an effect that is unidirectional. Additionally, the FB-SKAT did not detect an association between autism and ABCA7 (p = 0.11).

Although the emphasis of this study is performing complex disease association analysis with the proposed RV-TDT methods, the RV-TDT is also suitable for analyzing Mendelian traits. For Mendelian traits, the RV-TDT is particularly beneficial to use when although a family history of disease has been recorded, only the proband and his parents are available for study. The power of the RV-TDT will be dependent on the underlying Mendelian model. Assuming that there is no locus heterogeneity for the disease under study, it is possible to analytically obtain estimates of the necessary sample sizes to detect an association for various Mendelian modes of inheritance. For 80% power, to detect an association for an autosomal recessive trait when α = 0.05, four trios are needed, and if an exome-wide significance criterion of α = 2.5 × 10⁻⁶ (a Bonferroni correction for testing 20,000 genes) is used, then 15 trios are necessary to detect an association with 80% power. For autosomal-dominant traits for α = 0.05 and α = 2.5 × 10⁻⁶, 13 trios and 59 trios, respectively, are required to detect an association with 80% power. It is also possible to use the TDT-RV methods to analyze X-linked traits, although only the mother will provide informative meioses. To detect an association for an X-linked recessive trait with a power of 80% for α = 0.05, seven trios are necessary, but for α = 5 × 10⁻⁵ (Bonferroni correction for testing ∼1,000 genes on the X chromosome) 23 trios are necessary.

By using the RV-TDT methods, we identified variants in ABCA7 (19p13.3) as potentially the underlying cause of autism by analyzing 199 families from the Simons Simplex collection. Previously, an ASD locus was mapped to the 19p13.12 region with a maximum nonparametric LOD (NPL) score of >2.0 in 115 multiplex U.S. families.^46,47 Additionally, by using an extended ASD pedigree consisting of 20 nuclear families from Finland, we obtained an NPL score of 3.57 within chromosome 19p13.3 at marker D19S591,⁴⁸ which is 1.9 Mb away from ABCA7.

The association between rare variants in ABCA7 and autism is consistent with the finding that autistic children display abnormal rates of in vivo lipid metabolism compared with healthy controls.⁴⁹ ABCA7 is an integral transmembrane ATP–binding cassette transporter that involves the translocation of cellular lipid across membrane, such as cholesterol.⁵⁰ Current studies suggest that lipid signaling plays an important role in neuronal processes, such as synaptogenesis and neurotransmitter functions.^51,52 There is increasing evidence suggesting abnormalities of lipid metabolic pathways might affect the nervous system and contribute to autism.^49,53

Common variants in ABCA7 have been associated with Alzheimer disease (AD) through brain expression and genome-wide association studies with samples from patients of both African and European descent.^54–56 It has been shown that, like in AD, plasma levels of β-amyloid or α-precursor protein (APP) are significantly elevated in ASD patients.⁵⁷ While the occurrence of β-amyloid plaques in the brain is well-known as a pathologic hallmark of AD, the accumulation of β-amyloid in the brains of both pediatric and adult ASD patients was demonstrated only recently.⁵⁸ In Abca7^−/− mice, phagocytotic cells have reduced ability to clear amyloid from the brain, which results in decreased memory and capacity to learn new tasks.⁵⁹ The identification of ABCA7 as a gene that is possibly involved in autism etiology suggests the existence of a common pathway for neurodevelopmental and neurodegenerative diseases that might be targeted for prevention and treatment.

The RV-TDT methods were developed to provide a robust and powerful way to identify rare-variant complex disease associations by using trio sequence data. Given the problem of adequately controlling for population substructure and admixture in rare-variant association studies and the growing number of sequence-based trio studies, the RV-TDT is extremely beneficial in elucidating the involvement of rare variants in the etiology of complex traits. The RV-TDT methods can be used to analyze exome and genome sequence data. Additionally, these methods can be applied to analyze rare variants obtained from genotyping arrays including the “exome” chip. To analyze the autism trio data with all five RV-TDT methods, TDT-BRV, TDT-CMC, TDT-WSS, TDT-VT-CMC, and TDT-VT-BRV, obtaining empirical p values based on haplotype permutation took a total of 3.1 hr. To analyze the same data set implementing the TDT-CMC, obtaining analytical p values took 4.5 min. The analysis was performed with a single CPU, however, by using multiple processors for the analysis can greatly decrease the computational time. The RV-TDT software package and documentation are publicly available online.

Web Resource

The URLs for data presented herein are as follows:

• 1000 Genomes, http://browser.1000genomes.org

• BEAGLE, http://faculty.washington.edu/browning/beagle/beagle.html

• dbSNP, http://www.ncbi.nlm.nih.gov/projects/SNP/

• Exome Variant Server (EVS), http://evs.gs.washington.edu/EVS/

• Genome Analysis Toolkit (GATK), http://www.broadinstitute.org/gatk/

• MutationAssessor, http://mutationassessor.org/v1/

• MutationTaster, http://www.mutationtaster.org/

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

• PolyPhen-2, http://www.genetics.bwh.harvard.edu/pph2/

• RV-TDT, http://bioinformatics.org/rv-tdt/

• SIFT, http://sift.jcvi.org/

• Simons Foundation Autism Research Initiative (SFARI), http://sfari.org/sfari-initiatives/simons-simplex-collection

• Variant Association Tools (VAT), http://varianttools.sourceforge.net/Association/

Accession Numbers

The dbGaP accession number for the exome sequences reported in this paper is phs000482.v1.p.