Time-frequency methods and voluntary ramped-frequency breathing: a powerful combination for exploration of human neurophysiological mechanisms

Abstract

We experimentally altered the timing of respiratory motoneuron activity as a means to modulate and better understand otherwise hidden human central neural and hemodynamic oscillatory mechanisms. We recorded the electrocardiogram, finger photoplethysmographic arterial pressure, tidal carbon dioxide concentrations, and muscle sympathetic nerve activity in 13 healthy supine young men who gradually increased or decreased their breathing frequencies between 0.05 and 0.25 Hz over 9-min periods. We analyzed results with traditional time- and frequency-domain methods, and also with time-frequency methods (wavelet transform, wavelet phase coherence, and directional coupling). We determined statistical significance and identified frequency boundaries by comparing measurements with randomly generated surrogates. Our results support several major conclusions. First, respiration causally modulates both sympathetic (weakly) and vagal motoneuron (strongly) oscillations over a wide frequency range—one that extends well below the frequency of actual breaths. Second, breathing frequency broadly modulates vagal baroreflex gain, with peak gains registered in the low frequency range. Third, breathing frequency does not influence median levels of sympathetic or vagal activity over time. Fourth, phase relations between arterial pressure and sympathetic and vagal motoneurons are unaffected by breathing, and are therefore likely secondary to intrinsic responsiveness of these motoneurons to other synaptic inputs. Finally, breathing frequency does not affect phase coherence between diastolic pressure and muscle sympathetic oscillations, but it augments phase coherence between systolic pressure and R-R interval oscillations over a limited portion of the usual breathing frequency range. These results refine understanding of autonomic oscillatory processes and those physiological mechanisms known as the human respiratory gate.

the human central nervous system responds in real time to continually changing external and internal influences by orchestrating patterned neural responses, which in the case of autonomic outflows may be organized as rhythms. Close examination of human autonomic and hemodynamic rhythms may yield insights into central mechanisms that cannot be gained by direct observation. For example, our group recently published a wavelet analysis of simultaneously recorded skin and muscle sympathetic nerve activities (9) and reported that these anatomically and functionally discrete neural outflows oscillate coherently at frequencies and strengths that fluctuate continuously. From this analysis, we posited the existence of time-varying, coupled central sympathetic oscillators in humans.

One easily observed oscillation, respiration, exerts major influences on autonomic function: respiratory periodicities can be discerned in both skin and muscle sympathetic neural outflows (9, 31), and in R-R intervals and hemodynamic parameters. Respiration phasically alters the responsiveness of sympathetic (12, 24) and vagal motoneurons (22, 25, 27, 56) to stimulatory inputs, and mechanically alters arterial pressure (17, 75, 92) and associated baroreceptor nerve activity. The great significance of respiration for physiological research is that humans, unique among research subjects, can alter their central oscillatory milieu simply and precisely by controlling their breathing, apparently at little cost in terms of mental effort (24, 35, 67, 69).

Our simple protocol comprised uncontrolled breathing followed by periods of steadily increasing or decreasing breathing frequencies. This ramped-frequency breathing protocol progressively moved subjects from or to their usual resting breathing frequencies, and thus imposed an external, deterministic rhythm onto their ongoing oscillatory processes. We recorded usual hemodynamic parameters, as well as muscle sympathetic nerve activity, which provided direct information on one central oscillation.

We brought an innovative combination of analytical techniques to tease out and explain the complex, largely hidden neurophysiological mechanisms we studied. Wavelet transforms (14, 41) characterize the magnitudes of oscillations and provide logarithmic frequency resolution of oscillations at usual frequencies, but also at very low and even ultralow frequencies. Wavelet phase and phase coherences (5, 79) identify linkages between two oscillator frequencies and frequency changes, and information theory methods (65) point to causality and indicate which oscillation is driving the other. We divided the breathing range into independent frequencies, generated surrogate signals, and then compared the surrogates with actual measurements to identify statistically significant changes and define their frequency boundaries (76, 91).

METHODS

Participants

We studied 13 healthy nonobese men (age 24–35 years) who were nonsmokers and who took no medications. All volunteers followed moderate exercise routines, but none were endurance athletes. Subjects refrained from imbibing alcohol or caffeine-containing drinks, and did not perform strenuous exercise during the 24 h before the experiment. This study was approved by the human research committees of the Medical College of Virginia at Virginia Commonwealth University and the Hunter Holmes McGuire Department of Veterans Affairs Medical Center, and conformed with guidelines established in the Declaration of Helsinki. Subjects gave their informed, written consent before they participated.

Measurements

We continuously recorded data on digital tape and subsequently redigitized the data at 500 Hz with commercial hardware and software (WINDAQ; Dataq Instruments, Akron, OH). Measurements included the electrocardiogram, integrated tidal volume (Fleisch pneumotachograph), beat-by-beat finger photoplethysmographic arterial pressure (Finapres, Model 2300; Ohmeda, Englewood, CO), tidal CO₂ concentration (Infrared Analyzer; Gambro-Engström, Bromma, Sweden), and sympathetic nerve activity.

Multifiber muscle sympathetic nerve activity was recorded with tungsten microelectrodes inserted transcutaneously into a peroneal nerve. A reference electrode was inserted subcutaneously 1 to 2 cm from the recording electrode. Signals from the two electrodes were processed by a nerve traffic analyzer (Model 662C-1; University of Iowa Bioengineering, Iowa City, IA), where they were led successively into a differential preamplifier and an amplifier (total gain ∼70,000), band-pass filtered (700–2,000 Hz), and integrated (time constant 0.1 s) to obtain mean voltage neurograms. We identified muscle bursts according to their narrow-waisted appearances, pulse synchronicity, augmentation during end-expiratory apnea or Valsalva straining, and failure to respond to unexpected auditory or tactile stimulation.

Breathing Control

At the beginning of the recording session, subjects rested quietly in the supine position and breathed at a comfortable, uncontrolled rate and tidal volume, with a face mask connected to the pneumotachograph and a two-way respiratory valve (Hans Rudolph, St. Louis, MO). Tidal CO₂ was measured from air withdrawn from a port in the face mask. Breathing cues were displayed on a laptop computer positioned in front of the subject. Subjects matched their breathing to target waveforms that scrolled across the computer display. In practice, the ramped-frequency breathing cues were easy for subjects to follow. Breathing frequency changes were gradual and small—almost imperceptible—and subjects were able to breathe according to the signals provided, with high accuracy. An earlier article (11) provides details about the breathing control methods we used.

After a period of spontaneous breathing, subjects followed two breathing protocols in random order, comprising 9 min of breathing at steadily increasing or decreasing frequencies, between 0.05 and 0.25 Hz. The mean duration (± SD) of experiments was 72.3 ± 11.5 min. Each recording began with a period of spontaneous breathing, which lasted 7.9 ± 2.6 min (minimum duration 6 min). For all subjects, the spontaneous breathing period was taken as the last 6 min before the first breathing ramp, a duration that yielded wavelet analyses of frequencies as low as 0.021 Hz. After the initial spontaneous breathing period, subjects breathed according to the ramped protocol. Each breathing ramp was followed by approximately 6-min periods of uncontrolled breathing. These periods were not analyzed to avoid possible carryover influences of preceding ramped-frequency breathing (86). The mean length of breathing ramps was 9.05 min, with an SD of 8.4 s.

Analyses

Analyses were performed with WinCPRS software (Absolute Aliens Ay, Turku, Finland) and MatLab-based algorithms (MathWorks, Boston, MA) developed at Lancaster University (5, 79, 81). One author overread the WinCPRS detection of electrocardiographic R-waves and systolic and diastolic pressures, and corrected errors. We used R-R intervals and R-R interval fluctuations as indices for vagal-cardiac nerve activity and its breath-by-breath changes. In humans, mean R-R intervals increase in proportion to arterial pressure (26), and in anesthetized, spontaneously breathing dogs, respiratory-frequency R-R interval oscillations significantly track directly recorded vagal-cardiac nerve activity (44). We analyzed integrated sympathetic neurograms two ways. First, one author identified sympathetic bursts in each subject and normalized each burst by dividing it by the average burst area recorded during the session. These measurements were used simply to quantitate muscle sympathetic nerve activity. Second, we analyzed entire integrated neurograms without regard to the presence or absence of bursts; these data included baseline voltages between bursts, which may increase during periods of intense sympathetic stimulation (21). We did not attempt to analyze individual sympathetic action potentials.

Vagal baroreflex gain was estimated with a frequency-domain method, the transfer function (73), calculated as the average value of the systolic pressure–(R-R interval cross-spectrum derived by Fourier transform, divided by the systolic pressure spectrum in the low frequency range, 0.04–0.15 Hz. We obtained moving baroreflex gain estimates by iteratively calculating the transfer function in 25-s windows, moved through the measurements by 2-s steps. A very recent study (16) reported a highly significant correlation between this indirect index and baroreflex slopes calculated after large, isolated sympathetic bursts.

Wavelet Transforms

Our methods are based on continuous wavelet transforms, which project signals from the time- to the time-frequency domain. A detailed description of these methods is given in the appendix and in published references (81, 85). Briefly, we resampled signals at 10 Hz and removed the trends below the lowest frequency analyzed (0.021 Hz for spontaneous and ramp breathing periods, and 0.005 Hz for entire experiments) by the standard moving average technique acting as a high-pass filter. Only the residuals above the frequency cutoffs were analyzed; all the frequency content below was filtered out. Our method adjusts the length of the complex Morlet mother wavelet during the calculations, such that low frequency signals are analyzed with long wavelets, and high frequency signals are analyzed with short wavelets. This approach provides excellent frequency resolution, and by allowing time-localization, it improves upon Fourier transforms, which are based on fixed window lengths. The method is particularly valuable for study of very low frequency rhythms, which make important, but not necessarily large contributions to total power.

Wavelet Phase Coherence and Windowed Wavelet Phase Coherence

We calculated wavelet transforms for all signals, instantaneous frequency changes for individual signals, and finally, phase coherence between phase changes of signal pairs [0 = no coherence, and 1 = perfect coherence (5)].

Coupling Between Interacting Oscillators on the Basis of Information Theory

We determined the directionality of couplings with an information theory method proposed by Paluš & Stefanovska (65), which has been used to advantage in a variety of earlier technical and physiological studies (49, 59, 70). This method, based on mutual information theory (13), determines whether information contained in one signal predicts future changes in a second signal. Because thermodynamically open systems (which continuously exchange energy and substances with the environment) and physiologically interacting processes can be mutually (bidirectionally) coupled, we evaluated not only the dominant direction of coupling (defined by which signal more accurately predicts the other), but also coupling in the opposite direction, and their time variations. We resampled time series at 10 Hz in normalized state space and used four equiquantal bins for calculation of entropies (65). Our coupling calculations were performed with 50- to 300-s time based windows, with 5-s time shifts. The windows were overlapped; thus with 50-s windows, all window widths were 50 s, except the first and the last, which were 45 s long.

Statistical Analysis

Many data sets were not distributed normally (Kolmogorov-Smirnov test). Therefore, we used nonparametric statistical tests (SigmaPlot 11.0; Systat, San Jose, CA; and Statistic Toolbox, MatLab) and report individual values, ranges, and medians to identify phase coherences, couplings, and changes provoked by the ramped time-varying breathing protocol. We used linear regression to identify trends in individual subjects, the Wilcoxon rank-sum test to identify differences between two populations, and one-way ANOVA with ranks to identify differences among responses to the three breathing modes.

Wavelet transforms with different window lengths decompose signals into independent observations at each frequency. The large number of independent observations defines the resolution of the continuous wavelet transform, but does not yield measurements that constitute a statistical family. We divided the logarithmic scale for both spontaneous and ramped-frequency breathing periods (0.021–2 Hz) into 100 independent frequency segments for statistical analysis.

We used the nonparametric rank test to identify significant differences at each of these discrete frequencies. Special care must be taken to determine whether wavelets differ significantly from each other; small, nonzero differences can exist between such measurements but may be insignificant. Moreover, with wavelet analyses, low frequency components are represented by fewer periods than high frequency components. Consequentially, fewer variations of phase differences occur at low than high frequencies, and this may translate into higher phase coherence.

To identify significant changes between wavelet phase coherences and coupling directionalities, we used surrogate statistical analysis. Amplitude-adjusted Fourier transform surrogate signals were generated by shuffling the phases of the original time series to create new time series with the same means, variances, and autocorrelation functions (and therefore the same power spectra) as the original sequences, but without their phase relations (91). We averaged 100 measurements (phase coherences or couplings) calculated from 100 surrogate realizations of the signals. Phase coherences and the coupling directions were considered significant if their values were 2 SD above the surrogate means (P ≤ 0.05). [Note that because the sampling frequency used to derive R-R interval and systolic and diastolic pressure time series in our study varied around 1 Hz (according to the cardiac rate), the Nyquist frequency was set to be 0.5 Hz (1 Hz/2); we did not test for statistical significance above this frequency.]

In the figures, significant differences between median and surrogate values in each frequency are denoted by red vertical lines, and significant differences between medians recorded during spontaneous and ramped-frequency breathing are denoted by gold lines. Where many contiguous frequencies show significant effects, these lines are confluent and appear as homogeneous red or gold areas. Additionally, we tested for significance over fixed-frequency ranges of 0.021–0.052, 0.052–0.145, and 0.145–0.5 Hz (81, 84). These ranges were evaluated with logarithmic frequency resolution using wavelet transforms; they correspond coarsely with the very low, low, and respiratory frequency ranges, evaluated with linear frequency resolution reported in other publications, and are referred to as such. For all comparisons, we considered P ≤ 0.05 to be significant.

RESULTS

Figure 1 illustrates the breathing protocol and shows a wavelet transform of the CO₂ signal (taken as an index of breathing) for an entire experiment from one subject. The four breathing ramps are clearly indicated by the diagonal traces. During spontaneous breathing (periods between the diagonal traces), CO₂ wavelet amplitudes varied over a wide frequency range. The main wavelet amplitude was concentrated at ∼0.25 Hz, with an approximate range of 0.15–0.32 Hz. This wavelet band indicates the actual spontaneous breathing frequency and its variability. During ramped-frequency breathing, frequencies steadily increased or decreased according to the deterministic breathing protocol. (Lines parallel to the ramped frequencies represent harmonics caused by the nonsinusoidal shape of the breathing waveform.)

Fig. 1.

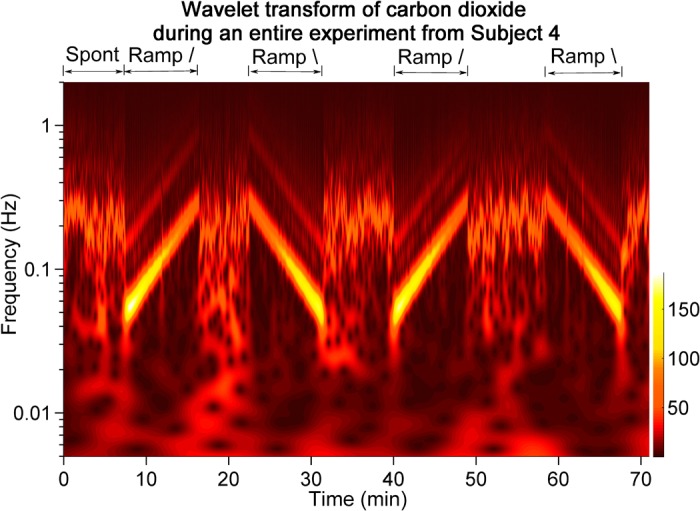
This contour plot shows the wavelet transform of CO₂ taken as an index of respiration for one subject during one entire experiment. Segments between the diagonal ramps illustrate spontaneous breathing frequencies, which aggregated at ∼0.25 Hz, but also could include lower frequencies.

Subjects controlled their breathing frequencies extremely well during ramped-frequency breathing. The median R² for the regression of breathing interval on time was 0.959 (25th and 75th percentiles, 0.933 and 0.97 linear model; and 0.992 (25th and 75th percentiles, 0.972 and 0.997), quadratic model (P = 0.005). We measured the instantaneous frequencies between all breaths during the first spontaneous and the first ramped-frequency breathing periods to further characterize breathing parameters. The total number of breaths during the thirteen 900-s periods (one per subject, comprising 360 s of spontaneous breathing and 540 s of ramped-frequency breathing) was 2,016. The median number of breaths was 76 (range 45–97) during spontaneous breathing, and 73 (range 72–78) during ramped-frequency breathing (P = 0.16). There was a total of 1,054 breaths during spontaneous breathing. Of these, one had an instantaneous frequency of 0.0508 Hz; all other breaths were above the arbitrary very low frequency ceiling of 0.052 Hz. There was a total of 962 breaths during the first ramped-frequency breathing period. Of these, three breaths had instantaneous frequencies of 0.043, 0.045, and 0.046 Hz; all other breaths were above 0.052 Hz. Nine subjects had no breathing frequencies below 0.052 Hz. Breathing frequencies were distributed during spontaneous and ramped-frequency breathing as follows: very low frequency, 0.1 vs. 0.28%; low frequency, 9.5 vs. 37.1%; and respiratory-frequency, 90.3 vs. 62.6%.

Although end-tidal CO₂ concentrations could vary significantly during individual breathing periods, there were no significant median CO₂ group differences among spontaneous and ramped-frequency breathing periods. Repeated-measures ANOVA indicated that the breathing protocol did not significantly alter group median levels of muscle sympathetic nerve activity, R-R intervals, or arterial pressures.

Figure 2 shows median and 25th and 75th percentile transfer function vagal baroreflex gains during the first fast-to-slow (Fig. 2, top) and slow-to-fast (Fig. 2, bottom) breathing ramps for all subjects. These data illustrate several features of human baroreflex physiology. First, baroreflex gain was highly variable, and even median values documented the occurrence of brief, sharp spikes in baroreflex gain. Second, the median baroreflex gain and the 25th to 75th percentile ranges were significantly larger during the fast-to-slow ramp than the slow-to-fast ramp (P < 0.001, rank sum test). This disparity is especially large at the fastest breathing rates shown on the right of the panels. Median baroreflex gains during the first 30 s of each ramp were similar (fast-to-slow, 14.2 vs. slow-to-fast, 14.8 ms/mmHg; P = 0.74, rank sum test). Third, notwithstanding the great variability among subjects, both relations were described well by quadratic functions (black lines), which peaked broadly in the low frequency range.

Fig. 2.

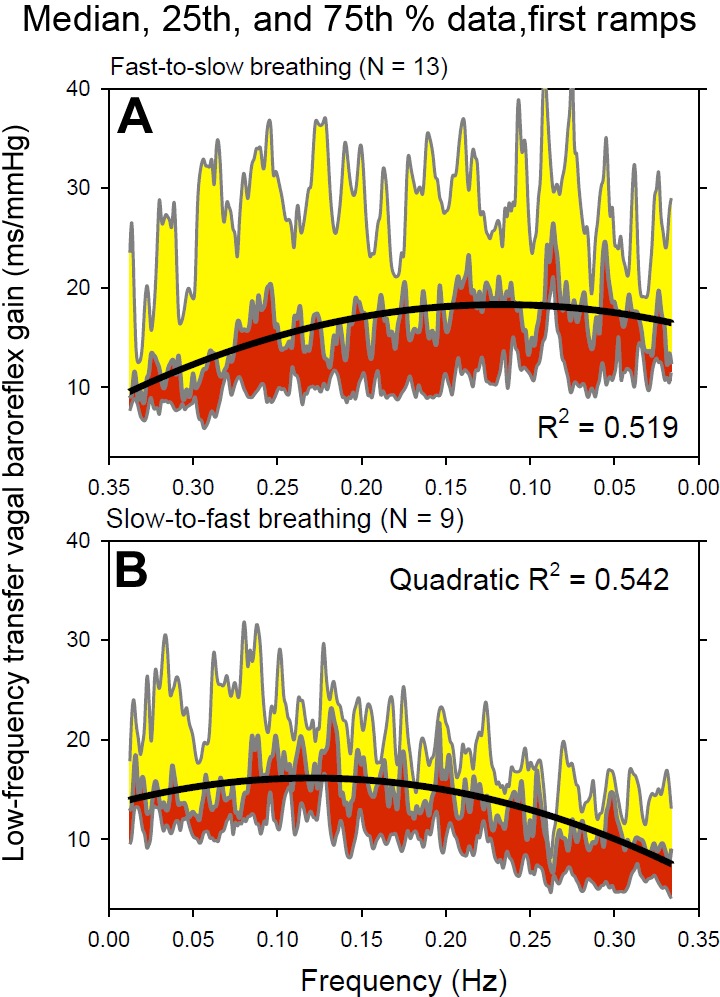
Median, 25th, and 75th percentile low frequency vagal baroreflex transfer functions during the first fast-to-slow and slow-to-fast breathing ramps for all subjects. Heavy black lines indicate quadratic function fits of the data.

As indicated, the breathing mode did not significantly influence most median values. In individual subjects, however, linear regression identified loose but highly significant trends (77% of P values were ≤ 0.001; Table 1). Data obtained during spontaneous breathing (Table 1, left columns) indicated strongly that, as remarked earlier (23, 95), healthy resting human subjects cannot be regarded as being in a steady-state. Baroreflex transfer functions, arterial pressures, and R-R intervals could either increase or decrease significantly. During fast-to-slow breathing (Table 1, middle columns), vagal baroreflex gain increased in most subjects. Remarkably, arterial pressure and R-R intervals could change significantly in either direction, and either increase or decrease. During slow-to-fast breathing (Table 1, right columns) vagal baroreflex transfer functions decreased significantly in 8 of 9 subjects, arterial pressure either increased or decreased, and R-R intervals increased in all subjects who had significant trends. The message conveyed by the significant but small R² values is not necessarily that the changes are physiologically important, but that they document ongoing hemodynamic fluctuations in healthy, resting humans. (Our analyses may also indicate that significant correlations do exist but are not linear.)

Table 1.

Subjects with significant (P ≤ 0.05) linear regressions

	Breathing mode
	Spontaneous (n = 13*)		Fast-to-slow (n = 13*)		Slow-to-fast (n = 9)
	Increasing	Decreasing	Increasing	Decreasing	Increasing	Decreasing
Transfer function baroreflex gain	2 (0.213)	5 (0.212)	8 (0.135)	3 (0.272)		8 (0.281)
Breath periods	1 (0.05)	1 (0.157)	13 (0.764)			9 (0.811)
End-tidal CO2	4 (0.112)	8 (0.042)	5 (0.357)	7 (0.074)	1 (0.209)	8 (0.567)
Sympathetic burst area	1 (0.021)	1 (0.025)	1 (0.020)	1 (0.037)		3 (0.051)
Diastolic pressure	6 (0.081)	7 (0.055)	6 (0.1)	6 (0.092)	4 (0.065)	1 (0.171)
Systolic pressure	7 (0.165)	2 (0.152)	2 (0.6)	7 (0.217)	5 (0.032)	3 (0.041)
R-R interval	2 (0.067)	5 (0.035)	4 (0.012)	6 (0.05)		6 (0.045)

^*n =12. CO₂, end-tidal carbon dioxide. Numbers refer to the number of subjects with significant (P ≤ 0.05) linear correlations during each measurement period. Numbers in parentheses represent median values in those subjects. The period between breaths was measured from thresholds set on the CO₂ recording at the beginning of inspiration.

Carbon dioxide concentrations (which were not controlled) changed significantly during each breathing period in almost all subjects. End-tidal CO₂ either increased or decreased during spontaneous and fast-to-slow breathing, but decreased in eight of nine subjects during slow-to-fast breathing. To further characterize CO₂ changes, we subtracted median measurements made during the last from the first 10% of each breathing period. Median, 25th, and 75th percentile changes were 0.04%, −0.2%, and 0.36%, during normal breathing; 0.04%, −0.21%, and 0.35% during fast-to-slow breathing; and −0.99%, −1.08%, and −0.61%, during slow-to-fast breathing. One-way repeated-measures ANOVA with Holm-Sidak comparisons indicated that end-tidal carbon changes during normal and fast-to-slow breathing were comparable, but were smaller than during slow-to-fast breathing (unadjusted P < 0.001).

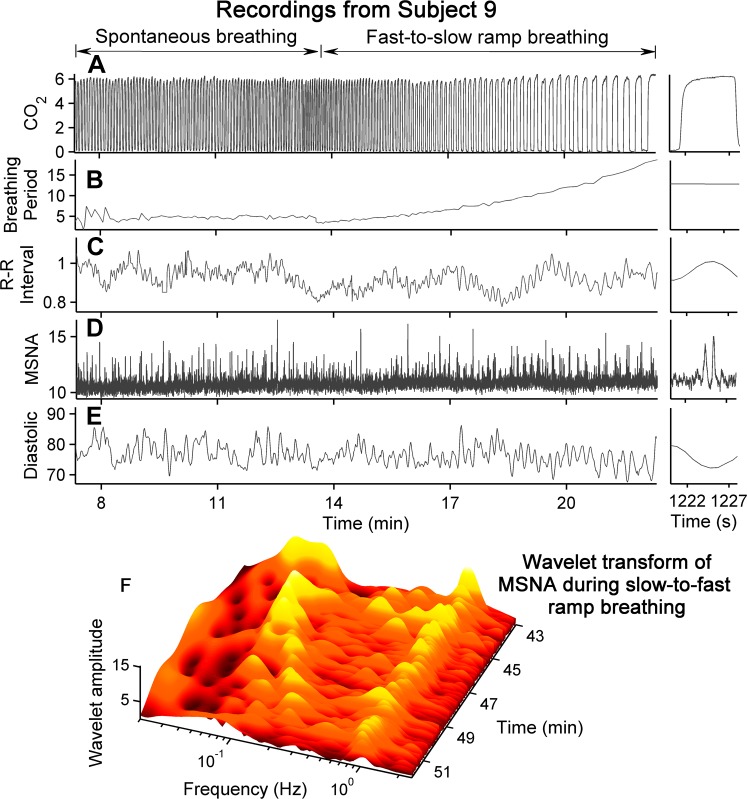
Figure 3, A–E, shows time series from one subject during his spontaneous and first fast-to-slow breathing ramp, and a wavelet transform of muscle sympathetic nerve activity during one slow-to-fast breathing ramp (Fig. 3F). End-tidal CO₂ concentration (peak values; Fig. 3A) increased, but not significantly (R² = 0, P = 0.756) during ramped-frequency breathing (Fig. 3A, right). This subject followed the breathing cues remarkably well: regression of breathing periods on time yielded R² values of 0.944 with linear regression analysis, and 0.997 with quadratic regression analysis. R-R intervals and diastolic pressures fluctuated at the frequencies of breathing and seemed to ride on fluctuations at lower frequencies. R-R interval, muscle sympathetic nerve activity, and diastolic pressure fluctuations appeared to be locked in 1:1 ratios with breathing at the slowest breathing rates (Fig. 3, C–E, right). The muscle sympathetic nerve wavelet transform (Fig. 3) was calculated from data recorded during one slow-to-fast breathing ramp in the same subject. This three-dimensional figure indicates that muscle sympathetic nerve oscillations follow both breathing-frequencies (Fig. 3F, left), and cardiac-frequencies (Fig. 3F, right).

Fig. 3.

Time evolution of measurements during spontaneous breathing and the first ramped-frequency breathing period from one subject. B: steady lengthening of the interval between breaths imposed by the protocol (right). In this subject, both R-R intervals and systolic pressures fluctuated at breathing and lower frequencies. The wavelet contour plot (F) was calculated from the same subject during a slow-to-fast breathing ramp. Sympathetic nerve activity followed the breathing frequency and the cardiac frequency (∼1 Hz). MSNA, muscle sympathetic nerve activity; CO₂, carbon dioxide concentration.

Wavelet Power

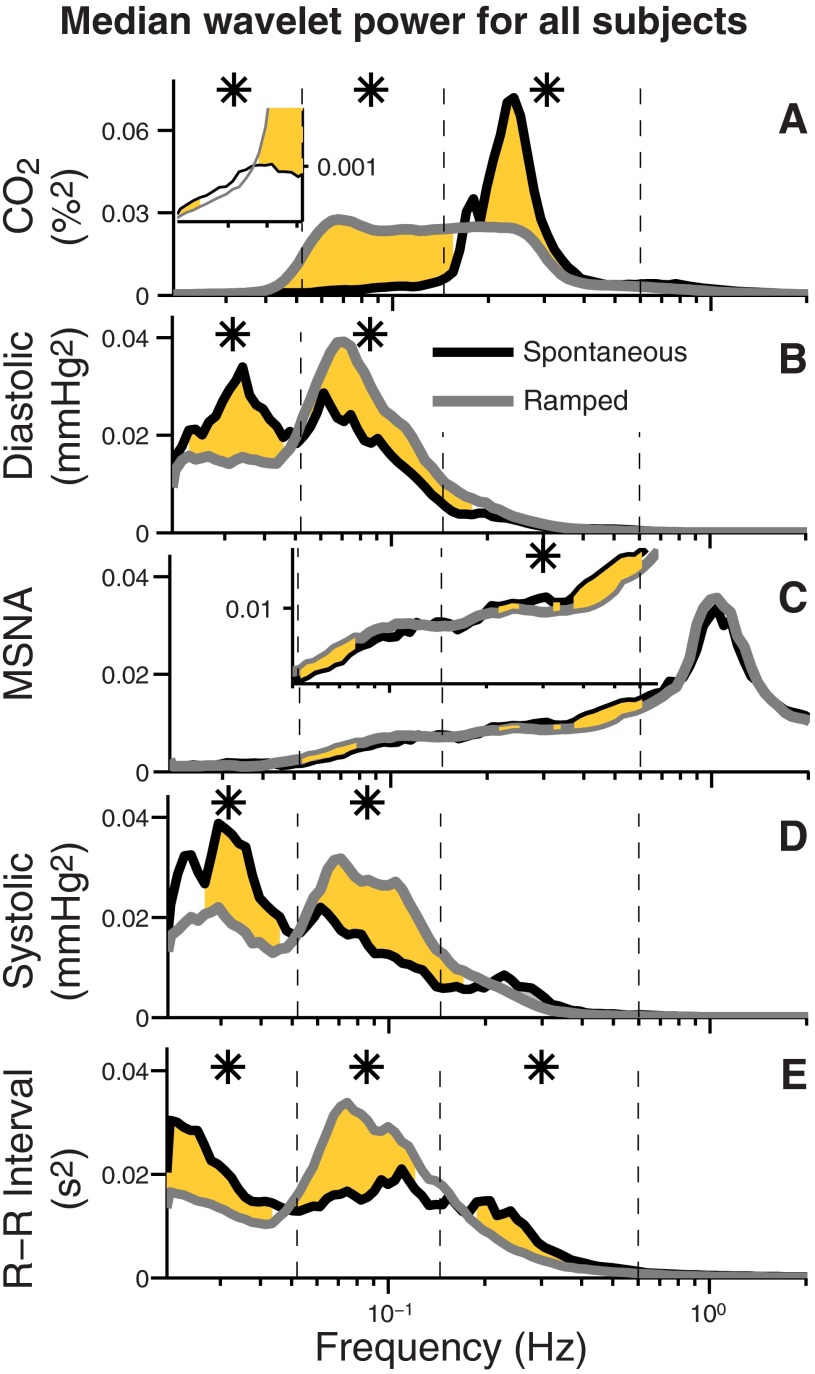
Figure 4 shows median wavelet powers (proportional to the amplitudes of oscillations) for all subjects during spontaneous and ramped-frequency breathing. Because statistical analyses indicated that the direction of breathing changes [slow-to-fast (n = 9), or fast-to-slow (n = 13)] exerted no significant influence on the results, we combined measurements made during the two ramped-frequency breathing directions. In this graph, significant differences between spontaneous and ramped-frequency breathing measurements are indicated by confluent gold areas, and significant differences between these measurements over entire frequency ranges (delimited by the vertical dashed lines) are indicated by asterisks. Figure 4A illustrates the breathing protocol and shows that during spontaneous breathing (black line), CO₂ wavelet power was concentrated over a range centered at about 0.25 Hz; from this peak, wavelet power tapered steeply, and extended at low levels into lower and higher frequency ranges. As expected, ramped-frequency breathing extended respirations through the low frequency range: the time-averaged frequency distribution is nearly rectangular, indicating that our breathing protocol systematically and uniformly yielded breathing frequencies between 0.05 and 0.25 Hz. The inset in Fig. 4A indicates that wavelet power in the very low frequency range was extremely small; statistical significance in this range is not necessarily proof of physiological relevance.

Fig. 4.

Median wavelet power during spontaneous and ramped breathing segments. The gold areas indicate significant differences between measurements made over 100 frequencies during spontaneous (black) and ramped-frequency breathing (gray). Asterisks indicate significant differences between the signals over entire frequency ranges as delimited by the vertical dashed lines. CO₂ wavelet power (A) during ramped-frequency breathing was uniformly distributed between 0.05 and 0.25 Hz. Insets in A and C enlarge frequencies with small but significant differences. The most striking aspects of these data are the almost trivial influence that breathing exerts on muscle sympathetic nerve wavelet power, and the strong diastolic and systolic pressure and R-R interval wavelet powers in the very low frequency range (left columns), at frequencies below those of either breathing mode.

Median wavelet power of muscle sympathetic nerve activity (Fig. 4C) was largest at the cardiac interval, 0.6–2 Hz (Fig. 4C, far right). Sympathetic wavelet power in the respiratory interval (Fig. 4C, third column) was significantly greater during spontaneous than ramped-frequency breathing. The most striking aspect of Fig. 4C, however, is how little respiration influenced the overall distribution of muscle sympathetic nerve wavelet power.

The breathing mode affected other measurements in expected and unexpected ways. At usual breathing frequencies (Fig. 4, third columns), R-R interval wavelet powers were significantly greater during spontaneous than ramped-frequency breathing, but systolic and diastolic pressure powers were similar. At low frequencies (Fig. 4, second columns), diastolic and systolic pressure and R-R interval wavelet powers were significantly greater during ramped-frequency than spontaneous breathing. At very low frequencies (Fig. 4, first column), diastolic and systolic pressure and R-R interval wavelet powers were significantly greater during spontaneous than ramped-frequency breathing. Surprisingly, median systolic pressure wavelet power was greater in the very low frequency interval than in any other interval. These unique and unexpected findings are treated fully in the discussion.

Wavelet Phase Coherence

Figure 5 shows wavelet phase coherences [synchronization of phase changes at each individual frequency (58)] from one subject during his first spontaneous and ramped (fast-to-slow) breathing periods. Fig. 5B visually indicates that both breathing modes modulated diastolic pressure oscillations. Fig. 5, A and C, indicate that time-averaged breathing and diastolic pressure phase coherences were significant during both breathing periods; however, significance was limited almost exclusively to the usual breathing-frequency range (0.145–0.5 Hz). Fig. 5E suggests that although both breathing modes modulated muscle sympathetic nerve oscillations, this influence was small compared with that of breathing on diastolic pressure wavelet power. Fig. 5D indicates that during the spontaneous breathing phase, coherence between breathing and muscle sympathetic nerve oscillations was significant but was limited primarily to a narrow range concentrated at about 0.25 Hz. Fig. 5F shows that during ramped-frequency breathing, time-averaged wavelet phase coherence between breathing and muscle sympathetic nerve activity was not significant at any frequency. Fig. 5, G–I, indicate that diastolic pressure and muscle sympathetic nerve wavelet phase coherences were significant over a wide frequency range, were concentrated in the low frequency range, and were similar during spontaneous and ramped-frequency breathing.

Fig. 5.

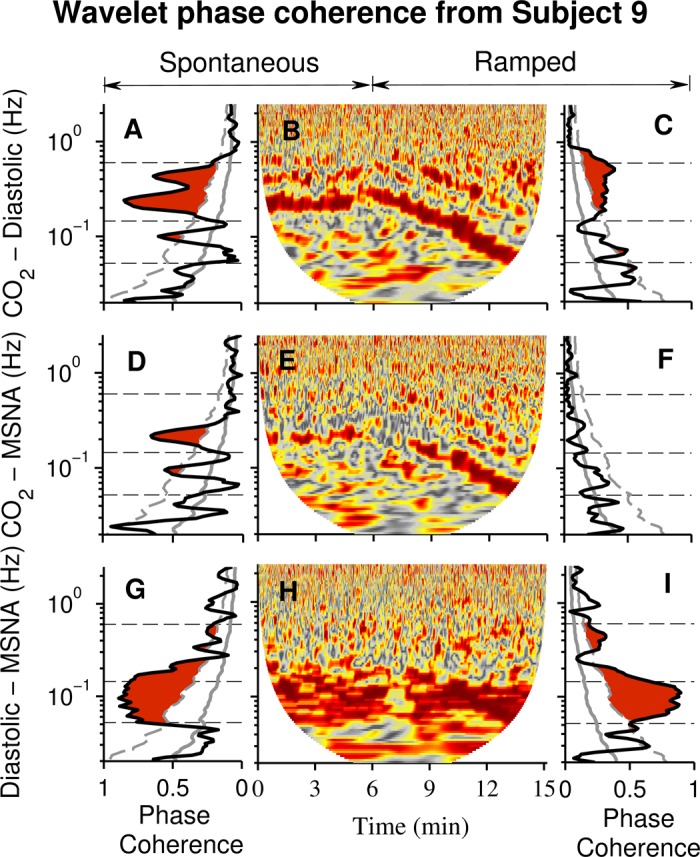
Wavelet phase coherence and windowed wavelet phase coherence from one subject. B: a contour plot documents phase coherence between breathing and diastolic pressure during both spontaneous breathing and the first (fast-to-slow) ramped-frequency breathing period. The time-averaged wavelet phase coherences (A and C) indicated that significant coherence (red) was limited primarily to the usual breathing frequency range. Significant breathing and muscle sympathetic nerve wavelet phase coherence was limited to a narrow frequency range during spontaneous breathing (D). Phase coherence between diastolic pressure and muscle sympathetic nerve oscillations (G and I) was significant over a wide frequency range and seemed to be uninfluenced by the breathing mode. For the analyses depicted in this figure and Fig 6, we did not test for significance above 0.5 Hz (the Nyquist frequency of R-R interval, systolic, and diastolic pressure signals; see methods).

Figure 6 shows data from the same subject whose responses are depicted in Fig. 5. Fig. 6, A and C, indicate that during both spontaneous and ramped-frequency breathing, time-averaged wavelet phase coherence between breathing and systolic pressure oscillations was high; however, significance was limited almost exclusively to the usual breathing frequency interval. Fig. 6, D and F, indicate that during both spontaneous and ramped-frequency breathing, wavelet phase coherence between CO₂ and R-R interval oscillations was high; however, as with systolic pressure, significance was limited almost exclusively to the usual breathing frequency interval. Systolic pressure–R-R interval phase coherences (Fig. 6, G and I) were high during both breathing modes, in both low frequency and respiratory-frequency ranges.

Fig. 6.

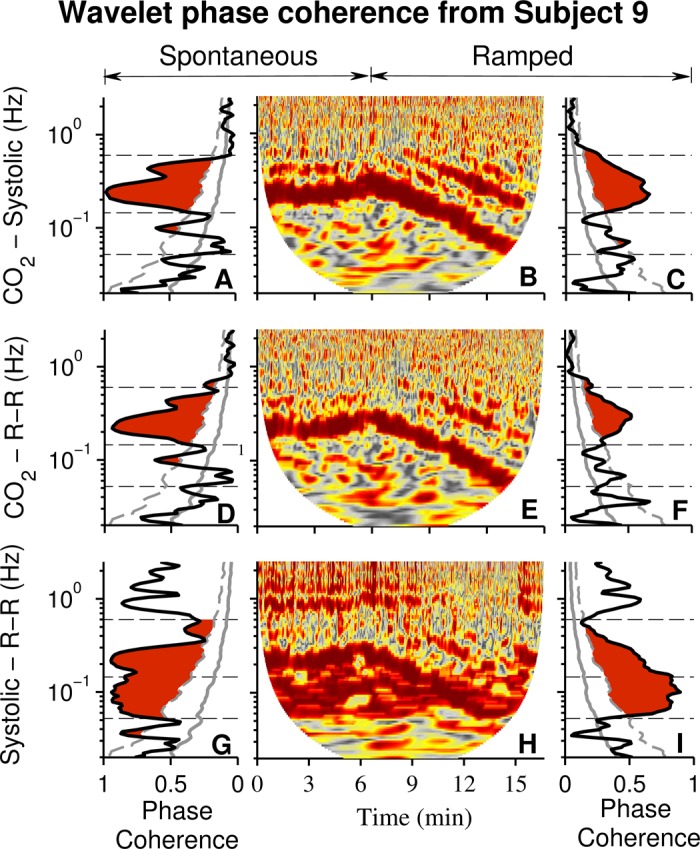
Wavelet phase coherence and windowed wavelet phase coherence from one subject. These data document a much stronger influence of breathing on wavelet phase coherence of systolic pressure and R-R interval than on diastolic pressure and muscle sympathetic nerve oscillations, as shown in Fig. 5. Significant phase coherence between breathing and systolic pressure oscillations was limited primarily to the usual breathing frequency range. Phase coherence between systolic pressure and R-R interval oscillations (G and I) was significant over a wide frequency range, and in the low frequency range it approached 1.0, perfect coherence.

Figure 7 summarizes the influence of breathing on median autonomic and hemodynamic phase coherences for all subjects. As with earlier figures, red shading indicates significant differences from surrogates over 100 frequencies, asterisks indicate significant differences across entire frequency ranges, and gold shading indicates significant differences between breathing modes. Fig. 7, A and E, indicate that both breathing modes significantly influenced wavelet phase coherences between breathing and diastolic pressure. Fig. 7, B and F, show that spontaneous but not ramped-frequency breathing significantly influenced wavelet phase coherence between respiration and muscle sympathetic nerve activity. During spontaneous breathing, wavelet phase coherences between breathing and diastolic and systolic pressures (Fig. 7, C and G), and R-R intervals (Fig. 7, D and H) were significant and tended to be bounded within the usual breathing frequency range. Figure 7, I–L indicates that although breathing modulates autonomic and hemodynamic motoneuron oscillations over a wide frequency range, this influence is strongest in the usual breathing frequency range.

Fig. 7.

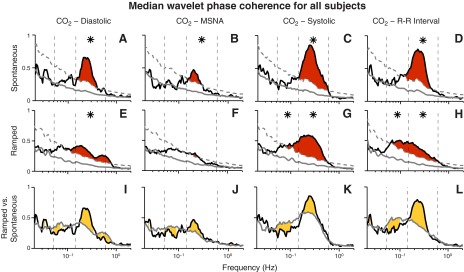
Median diastolic and systolic pressure and sympathetic wavelet phase coherences during spontaneous and ramped-frequency breathing for all subjects. This figure shows the same median coherence values for all subjects (Figs. 5 and 6 show this for one subject). A–H: red areas denote significant coherence over 100 separate frequencies; asterisks denote significant coherence over entire frequency ranges. I–L: gold areas indicate significant differences between the effects of the two breathing modes on measurements. Significant coherence between diastolic pressure and muscle sympathetic nerve oscillations (second columns) exists during spontaneous breathing, but is small compared with other coherence measurements. Of great interest, spontaneous breathing substantially increased coherence between breathing and systolic pressure and R-R interval oscillations (L) within a portion of the usual breathing frequency range.

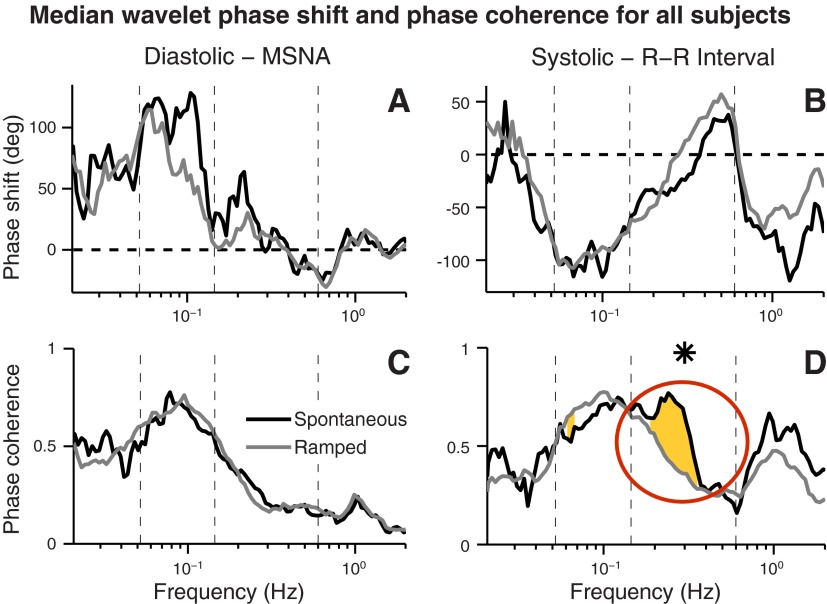
Figure 8 shows median wavelet phase shifts and phase coherences for all subjects during both breathing modes. Neither breathing mode qualitatively altered the phase relations between diastolic pressure and muscle sympathetic nerve, and systolic pressure and R-R interval oscillations (Fig. 8, A and B). Neither breathing mode significantly affected phase coherence between diastolic pressure and muscle sympathetic nerve oscillations (Fig. 8C). Spontaneous breathing, however, substantially increased phase coherence between systolic pressure and R-R interval oscillations within a portion of the usual breathing frequency range (Fig. 8D, circle).

Fig. 8.

Median wavelet phase shift and phase coherence relations for all subjects. Breathing exerted no significant effect on diastolic and systolic pressure, and muscle sympathetic nerve and R-R interval phase relations (A and B). Although neither breathing mode affected coherence between breathing and muscle sympathetic nerve oscillations (C), breathing significantly increased phase coherence between systolic pressure and R-R interval oscillations in a limited portion of the usual breathing frequency range (D, yellow shading, circled).

Information Transfer

Figure 9, top, shows a continuous recording of tidal CO₂ concentrations and muscle sympathetic nerve activity [advanced by this subject's latency, 1.26 s (87)] during one fast-to-slow breathing ramp. In this subject, ramped-frequency breathing did not significantly alter muscle sympathetic nerve burst area or frequency (regression of these measurements on time yielded R² values of 0). Sympathetic bursts tended to occur during expiration, within envelopes inscribed by the CO₂ signal (the highest point in each waveform is the end-tidal CO₂ level, and the steep descent after this point marks the beginning of inspiration).

Fig. 9.

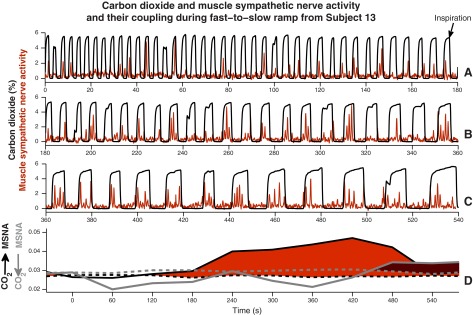
CO₂ concentration and muscle sympathetic nerve activity and their coupling during one fast-to-slow breathing ramp from one subject. Top three rows: continuous recordings of CO₂ (black) and muscle sympathetic nerve activity (red) during one entire fast-to-slow breathing ramp. Almost without exception, muscle sympathetic nerve firing occurred during expiration, the envelope inscribed by the increases and decreases in CO₂. Bottom: red and red-gray shaded areas indicate significant information transfer in the two directions. The large red area documents major information transfer from breathing to muscle sympathetic nerve oscillations and suggests, moreover, that transfer does not begin until a frequency threshold is reached (in this subject, at about 0.2 Hz, a breathing interval of 5 s).

Figure 9, bottom, illustrates the directional coupling between respiration and muscle sympathetic nerve activity. The solid lines indicate directions from breathing to muscle sympathetic nerve oscillations (black), and from muscle sympathetic nerve to breathing oscillations (gray). Median surrogate values are indicated by dashed lines. Statistically significant differences (from surrogate levels) in the direction of breathing to muscle sympathetic nerve oscillations are shown in red, and significant differences in the direction of muscle sympathetic nerve to breathing oscillations are shown in red-gray. Significant information transfer from breathing to muscle sympathetic nerve activity began at about 120 s into the breathing ramp (at a breathing interval of ∼5 s, a breathing rate of ∼0.2 Hz) and increased steadily up to ∼420 s. These data point to the existence of a frequency threshold for the transfer of information from breathing to muscle sympathetic nerve oscillations; when breathing frequency slows beyond this threshold, information transfer begins, and then increases steadily as breathing frequency slows further. As expected, the main directional influence was from breathing to muscle sympathetic nerve (prominent confluent red area). This mathematical analysis also documents a small, unprepossessing (and counterintuitive, because breathing frequency was controlled) influence in the direction from muscle sympathetic nerve to breathing (red-gray; Fig. 9, bottom, extreme right).

Table 2 indicates the strengths and statistical significances (bold typeface) of directional coupling. [Note that coupling strengths are not equivalent to correlation coefficients, which have values between 0 and 1. Coupling strengths are based on statistical properties and the information contained within signals as these relate to surrogate levels (see methods). If a coupling is not significant, its numerical value does not indicate strength or weakness (59); for example, a coupling strength of 0.001 above surrogate levels is meaningful, but a coupling strength of 1 below surrogate levels is not.] Both breathing mode oscillations significantly predicted diastolic and systolic pressure and R-R interval oscillations. Diastolic pressure oscillations during ramped-frequency breathing predicted muscle sympathetic nerve oscillations. Respiration did not significantly affect information transfer from muscle sympathetic nerve to diastolic pressure oscillations, or from systolic pressure to or from R-R interval oscillations.

Table 2.

Coupling strengths and statistical significance

	Breathing mode
	Spontaneous		Ramped-frequency
	strength	P	strength	P
CO2 → Diastolic	0.098	0.011	0.162	0.003
CO2 → MSNA	0.028	0.068*	0.030	0.006
Diastolic → MSNA	0.036	1.000	0.037	0.003
Diastolic ← MSNA	0.026	0.216	0.028	0.759
CO2 → Systolic	0.126	0.006	0.171	0.002
CO2 → R-R Interval	0.127	0.044	0.169	0.009
Systolic → R-R Interval	0.181	0.632	0.197	0.291
Systolic ← R-R Interval	0.105	0.684	0.127	0.132

This table indicates the strength of coupling, derived from an information-theory analysis. Numbers in bold indicate couplings that are significant. Note that the strength of the highly significant coupling from diastolic pressure to muscle sympathetic nerve activity was low, and that phase-coherence analysis (Fig. 6I) indicated that breathing exerted no significant influence on the directional coupling between diastolic pressure and sympathetic nerve activity. The values are obtained for window size of 300 s.

^*See Limitations.

Because our results document influences at frequencies below those of breathing, we considered that respiration might influence even lower frequencies. To test this possibility we examined the influence of the analysis window lengths on results. The statistical results listed in Table 2 are based on measurements made in 300-s windows. In our new analysis (Fig. 10), we used window durations of 50 to 220 s, moved by 10-s steps through all median slow (0 on the time axis)-to-fast-breathing ramp. In Figure 10, the plane at zero coupling delimits 2 SD above surrogate levels; all measurements rising above zero are significant (P ≤ 0.05).

Fig. 10.

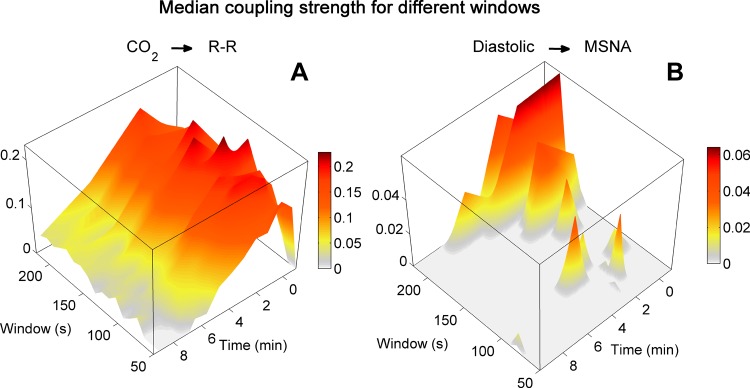
Median coupling strengths calculated with different window lengths during slow-to-fast breathing ramps from all subjects. Statistical analyses of two different couplings were made with window lengths of 50 to 220 s. All measurements rising above the gray floor are ≥2 SD above median surrogate levels (P ≤ 0.05). The length of the analysis window did not materially affect coupling between breathing and R-R interval oscillations (A), which was especially strong toward the beginning of breathing ramps when breathing intervals were longest. In contrast, the length of the analysis window strongly affected coupling between diastolic pressure and muscle sympathetic nerve oscillations (B), which became significant with the longest windows at the longest breathing intervals (apex). Note the difference in scales; coupling between diastolic pressure and muscle sympathetic nerve activity was weak compared with coupling between breathing and R-R intervals.

Coupling between breathing and R-R interval oscillations (Fig. 10A) was time-varying and increased as breathing rate slowed (moving from the bottom to the right). [Stankovski et al. (83) recently described this form of human cardiorespiratory coupling and synchronization mathematically.] This coupling was significant and did not change qualitatively as window durations increased (moving from 50 to 220 s, Fig. 10A, from the bottom to the left). Coupling between diastolic pressure and muscle sympathetic nerve oscillations (Fig. 10B) contrasts dramatically with the coupling between breathing and R-R intervals. First, this coupling was weak (note the smaller vertical scale); most values did not rise above the significance plane. Of greater interest are the concentrations of significant coupling in the longest analysis windows and the longest breaths (Fig. 10B, apex). This observation points to an influence of breathing that extends far below the frequency of actual breaths into the ultralow frequency range [to a frequency as low as 0.005 Hz; 1/220 s)]. This finding does not so much explain (we cannot account for the observation on the basis of known physiological mechanisms) as provoke: studies that focus on ultralow frequency events might yield new perspectives on the organization of human neurophysiological rhythms.

DISCUSSION

Our utterly simple protocol of ramped-frequency breathing imposed a deterministic rhythm on subjects' ongoing rhythms and altered those rhythms in complex ways. Our study yielded five broad new insights into human autonomic physiology. First, respiration causally modulates both sympathetic (weakly) and vagal motoneuron (strongly) oscillations over a wide frequency range—one that extends well below the frequency of actual breaths. Second, breathing frequency broadly modulates vagal baroreflex gain, with peak gains registered in the low frequency range. Third, breathing frequency does not influence median levels of sympathetic or vagal nerve activity over time; therefore, the changes in membrane potential set in motion by individual breaths increase and decrease sympathetic and vagal motoneuron firing in equal measure, and run their courses in 4 s or less. Fourth, phase relations between arterial pressure and sympathetic and vagal motoneurons are unaffected by breathing, and therefore likely reflect intrinsic responsiveness of these motoneurons to other synaptic inputs. Finally, breathing frequency does not affect phase coherence between diastolic pressure and muscle sympathetic oscillations, but augments phase coherence between systolic pressure and R-R interval oscillations over a limited portion of the usual breathing frequency range. We drew these conclusions on the basis of innovative analytical methods, which we discuss first.

Innovative Methodology

Our ramped-frequency breathing protocol yielded continuous rather than discontinuous (11, 18, 35, 89) breathing frequency changes, and uniform rather than nonuniform (11, 28, 75) frequency distributions. Our time-frequency analytical methods are independent of scale and yield precise, logarithmic resolution of wavelet power, phase, and phase shift changes into very low and even ultralow frequencies. Our statistical analyses, based on comparisons between subjects' responses and randomly generated surrogate data confidently identify boundaries over a large, rather than a small number (62) of frequencies. Our use of information theory supports objective mathematical inferences regarding causal relations between oscillations. Finally, our recordings of muscle sympathetic nerve activity tap into one neural outflow directly; only one study cited here (28) involved sympathetic nerve recordings.

Frequency Range of Respiratory Influences

Our most obvious finding is that respiration affects cardiovascular outflows over an astonishingly wide frequency range, from usual breathing frequencies (as expected, Figs. 4 and 7, third columns), to and through very low (first columns), and even ultralow frequencies (Fig. 10B). A major effect of breathing was not expected in very low frequency ranges simply because they lay below actual breathing frequencies (see results). We cannot say whether spontaneous breathing augments very low frequency oscillations or ramped-frequency breathing suppresses them. Neither possibility is supported by our sampling of 2,016 breaths. A corollary of our observation is that strictly speaking, the influence of a breath at any instantaneous frequency on other frequency ranges cannot be known with certainty. It is unlikely that simple breathing rate changes affect other factors known to contribute to very low frequency hemodynamic oscillations, including thermoregulatory (9, 80, 81), renin-aldosterone-angiotensin (3, 88), and endothelial (48) mechanisms. It is more likely that whatever the mechanism(s), breathing imposes its influence upon these other oscillations, which continue apace.

A second finding treats the frequencies of individual breaths. Sympathetic and R-R interval rhythms importantly reflect fluctuations in motoneuron membrane charges imposed by respiratory motoneuron activity, a mechanism commonly referred to as the respiratory gate (19, 53). Animal studies indicate that each breath sets in motion rhythmic increases and decreases in sympathetic (1, 33, 55, 90) and vagal (27, 37, 38, 45, 46, 56) motoneuron firing rates. Human studies suggest that at usual breathing frequencies the waveform of respiration-triggered sympathetic (24, 26) and vagal (22) outflows is broadly sinusoidal and symmetrical (increases of outflows equal decreases). Our new observations extend understanding of the human respiratory gate: because muscle sympathetic nerve and vagal-cardiac nerve activities do not change across a wide range of breathing frequencies, the oscillations in motoneuron membrane potentials set in motion by single breaths increase sympathetic and vagal firing in equal measure, and run their courses within 4 s (the shortest breathing interval we studied).

Hemodynamic Mechanisms

In the usual breathing frequency range, the breathing mode did not significantly affect arterial pressure wavelet power (the strength of oscillations, Fig. 4, B and D, third columns). In the low frequency range (second columns), however, arterial pressure wavelet power was significantly higher during ramped-frequency than spontaneous breathing. [Other studies (11, 62, 75) also indicate that slow breathing augments low frequency arterial pressure oscillations.] Because arterial pressure fluctuations at usual breathing frequencies are mechanically mediated [by changes in left ventricular stroke volume (30, 42, 92)], and because these oscillations largely disappear during apnea (4, 66, 93), we propose that increases in low frequency arterial pressure wavelet power depend upon breathing and are mediated mechanically.

Sympathetic Mechanisms

Our data directly address the question, does breathing rate influence net levels of muscle sympathetic nerve activity? In healthy, spontaneously breathing men, muscle sympathetic nerve burst frequency is proportional to breathing rate (60, 94); in healthy men and women, hyperventilation (which is a complex intervention because it augments the work of breathing) significantly increases muscle sympathetic burst amplitude (77) [but not burst frequency (77, 82)]. In patients with heart failure, muscle sympathetic burst frequency is directly related to respiratory rate (61), and in such patients who also have periodic breathing, brief mechanical ventilator treatments are followed by parallel reductions in spontaneous breathing and muscle sympathetic burst frequencies (32). In patients with obstructive pulmonary disease, slow breathing reduces muscle sympathetic nerve activity (72). These studies support the widely prevalent views (74) that human muscle sympathetic nerve activity is proportional to breathing rate, and that slow breathing reduces muscle sympathetic nerve activity.

We show that breathing frequency exerts no significant effect on median sympathetic nerve activity levels. Moreover, in most individual subjects, linear regression of muscle sympathetic nerve burst areas on breathing frequency identified no significant trends. In the few subjects who had significant trends, sympathetic burst areas could change directly or inversely with breathing frequency (Table 1). We propose that in studies that document significant proportionality between respiratory rate and muscle sympathetic nerve burst frequency or amplitude, this association reflects undefined influences that drive both breathing rate and sympathetic outflow, rather than a simple direct effect of breathing frequency on sympathetic activity.

Although breathing obviously modulates muscle sympathetic nerve oscillations (Fig. 3F), the magnitude of respiratory influences on wavelet power is small; almost trivial (Fig. 4C). This said, muscle sympathetic nerve wavelet power was significantly greater during spontaneous than ramped-frequency breathing in the usual breathing frequency range (Fig. 4C, third column). This effect can be explained economically on the bases of respiratory gating of stimulatory inputs to muscle sympathetic motoneurons (12, 24), and that in our study, spontaneous breathing contributed more breaths in this frequency range than ramped-frequency breathing. A baroreflex mechanism is unlikely: in the usual breathing frequency range, diastolic pressure wavelet power did not change significantly, there was no significant information transfer between diastolic pressure and muscle sympathetic nerve activity (Table 2). Moreover, published studies indicate that respiratory gating of muscle sympathetic nerve activity occurs independent of the direction of arterial pressure changes (24, 54, 77, 78).

We further show that breathing does not significantly affect phase coherence between diastolic pressure and muscle sympathetic nerve oscillations at any frequency (Fig. 8C). This finding has implications for understanding human muscle sympathetic rhythms, which are considered to be due either to baroreflex mechanisms [muscle sympathetic motoneurons fire in response to falling diastolic pressures (16, 87)], or to the firing of a nonlinear sympathetic oscillator, which is episodically entrained by baroreceptor inputs. Barman and her colleagues (6) considered R-waves as fiducial points to mark the timing of baroreceptor inputs, and argued that if sympathetic firing reflects responses to changing levels of baroreceptor input, then R-wave-sympathetic burst intervals should be constant. In their study, these authors relied heavily on observations made in 4 of 32 subjects in whom R-wave-sympathetic burst intervals fluctuated with respiratory periodicities. Our systematic study challenges the observations upon which Barman's conclusions were based: we report that respiration exerts no significant influence on diastolic pressure-muscle sympathetic nerve phase and phase coherence relations at any frequency (Fig. 8, A and C).

Vagal Mechanisms

Vagal tone.

Our data address the surprisingly complex question: does breathing rate influence vagal-cardiac tone? Kollai and Mizsei (47) reported that breathing rate may determine vagal-cardiac tone in individual subjects, depending on their resting levels of vagal activity. Because we did not give autonomic blocking drugs to identify such subjects, we used simple R-R intervals as indices of vagal-cardiac nerve tone (26). On this basis, we report that spontaneous and fast-to-slow ramped breathing do not influence vagal cardiac nerve activity levels (Table 1), and across all median measurements for all subjects, breathing frequency exerts no significant influence on vagal tone. Most (10, 11, 29, 68) but not all (2, 63) systematic studies of respiratory rate–R-R interval relations report similar findings. Wallin et al. (94), however, documented a significant correlation between resting breathing and heart rates in men (but not women). Note that in our study, all six of the nine subjects who had significant R-R interval trends during slow-to-fast breathing (Table 1, right) experienced R-R interval shortening (i.e., vagal tone declined). This indicates that as elaborated below, R-R intervals may be determined in part by the trends in breathing frequency changes; that is, the history prior to the reference breaths.

Vagal oscillations.

In striking contrast to the small influence of breathing on muscle sympathetic nerve oscillations, vagal wavelet power (Fig. 4E) and phase coherence (Fig. 7D) were significantly greater during spontaneous than ramped-frequency breathing at usual breathing frequencies. This observation can be explained by a central effect of respiratory motoneuron activity on vagal motoneurons, a baroreflex effect mediated by respiration-induced fluctuations in arterial pressure, or a combination of these mechanisms. We discuss baroreflex physiology next.

Vagal baroreflex—usual breathing frequencies.

Our results do not favor an arterial baroreflex explanation (15) for R-R interval fluctuations at usual [in this and other studies (60, 94) ∼0.23 Hz] breathing rates. First, as mentioned, arterial pressure wavelet powers in the usual breathing frequency range were not significantly increased during spontaneous breathing, even though there were more spontaneous than ramped-frequency breaths. Second, our analyses (Table 2) did not reveal significant information transfer between systolic pressure and R-R interval wavelet oscillations. Third, the strong phase coherence between systolic pressure and R-R intervals in a portion of the usual breathing frequency range (reflecting the synchronization of oscillations; Fig. 8D) was not associated with a major increase in wavelet power (reflecting the magnitudes of oscillations; Fig. 4E, third column). We refer readers to earlier, in-depth discussions of mechanisms responsible for R-R interval oscillations at usual breathing frequencies (19, 20, 43).

Vagal baroreflex—low frequencies.

Our findings broadly confirm recent physiological (7, 51) and clinical studies (8, 39, 50, 74) showing that slow breathing increases vagal baroreflex gain. In all these studies except two (50, 51), subjects were told to breathe slowly, at a rate of 6 breaths/min. In the last two studies (based on biofeedback), naïve subjects were told to increase their R-R interval excursions as they viewed them on a monitor; they were not told how to do it. The end result of all of these studies was the same: subjects breathed at ∼6 breaths/min (0.1 Hz) and significantly increased their frequency-domain vagal baroreflex gains. [In the studies cited, it is not always clear what baroreflex method is used; the a-coefficient is calculated over two frequency ranges, low and respiratory (64). As we discussed above, R-R interval fluctuations at usual breathing frequencies may not reflect baroreflex physiology.]

Although analyses of our entire material revealed no significant correlation between breathing frequency and vagal baroreflex gain, this finding does not necessarily undermine the belief that slow breathing increases baroreflex gain. First, repetitive breathing protocols with a fixed breathing frequency of ∼0.1 Hz must include more breaths at that frequency than our ramped-frequency protocol. Second, our data provide a mechanism that may underlie the augmentation of vagal baroreflex gain at slow breathing frequencies; as also shown by others (11, 62, 75), slow breathing increases arterial pressure fluctuations in the low frequency range (the range we used to calculate transfer functions), and these presumably translated in some way to increased baroreceptor stimulation. Augmented R-R interval wavelet powers in this range probably reflect in part, a baroreflex mechanism. [Low frequency rhythms are complex and incompletely understood (40); although our analyses inform possible low frequency baroreflex mechanisms, we by no means exclude mechanisms we did not study, including particularly, myogenic rhythms (57).] Third, and most importantly, during slow-to-fast breathing ramps, all subjects with significant trends experienced decreases in vagal outflow (Table 1, right).

On the basis of this last observation, we considered that R-R interval changes during ramped-frequency breathing might reflect underlying changes in baroreflex gain. The data shown in Fig. 2 refine the understanding of the contribution of breathing frequency to vagal baroreflex gain. First, these data confirm earlier observations (36, 95) that vagal baroreflex gain fluctuates hugely in healthy resting, ostensibly steady-state humans. Second, these data confirm in a new way the observation that slow breathing increases vagal baroreflex gain. They show that independent of the direction of breathing frequency changes, vagal baroreflex gain peaks in the low frequency range; however, this augmentation does not occur exclusively as a spike at ∼0.1 Hz, but exists over a wide breathing frequency range. Third, vagal baroreflex gain declines at very low breathing frequencies.

Of greatest interest are the differences in baroreflex gain that result from the direction of breathing frequency changes. Across all breathing frequencies, baroreflex gains were significantly greater during fast-to-slow (Fig. 2A) than slow-to-fast (Fig. 2B) and spontaneous (not shown) breathing. These differences developed after the beginning of ramps, because baroreflex gains during the first 30 s of ramped-frequency breathing were similar. We posit the existence of a memory within human autonomic pathways, such that the history of how breathing frequency changes occur, may be more important than the actual breathing frequency of the moment. We advanced a different formulation of this conclusion earlier (4, 23): profound new insights into human neurophysiological mechanisms might derive from systematic studies designed to explore the importance of the dimension, time, in human autonomic regulation.

Limitations

This study involves muscle sympathetic nerve activity recorded from healthy young men; our results provide no information regarding how breathing frequency might influence other sympathetic outflows or other populations. Our study would have been better had we made longer recordings. This assertion is particularly well borne out by Fig. 10, which points to significant coupling between diastolic pressure and muscle sympathetic nerve oscillations emerging at ultralow frequencies. We cannot exclude the possibility that some of the insignificant correlations we report might have been significant if we had studied more subjects. Sympathetic activity opposes vagally mediated R-R interval oscillations over a wide frequency range (89). Although we report that sympathetic outflow was constant across all breathing frequencies, we are unable to quantitate the degree that sympathetic stimulation opposed vagal inhibition. Because R-R interval fluctuations buffer arterial pressure oscillations in the respiratory-frequency range, the systolic and diastolic pressure wavelet powers we measured in this and possibly lower frequencies (Fig. 4) probably underestimate arterial pressure fluctuations. Our measurements do not allow us to gauge the degree to which vagal R-R interval fluctuations buffer arterial pressure fluctuations. We did not estimate left ventricular stroke volumes; therefore, the likelihood that ramped-frequency breathing modulated left ventricular stroke volumes relies on data published by others (30, 92).

By design, we did not ask subjects to control their inspiratory:expiratory ratios or tidal volumes. Our goal was to understand how physiological breathing rate changes affect neurophysiology. Experimental imposition of fixed inspiratory and expiratory durations would override one physiological response to breathing rate changes: expiratory durations are affected more than inspiratory durations (18).

Major fluctuations of breathing rate occur commonly in resting, healthy humans (52). Respiratory rate changes do not disturb normal alveolar ventilation because they are countered by reciprocal variations in tidal volume (71). These adjustments occur physiologically and automatically, and are not improved by experimental tidal volume control (11). To be sure, in laboratory experiments, tidal volume can be held constant during changes in breathing rate (10, 89). Such experimental control, however, introduces new complexities: CO₂ must be bled into the face masks, and volunteers are required to breathe at tidal volumes that are unphysiologically large, except at the slowest breathing rate.

We did not attempt to control end-tidal CO₂ levels; nonetheless, median levels were comparable during all three breathing modes. During normal and fast-to-slow breathing, changes in end-tidal CO₂ levels could occur in either direction, and differences between median levels at the beginning and end of these breathing periods were very small (<0.05%) and comparable. During slow-to-fast breathing, however, eight of nine subjects reduced their median end-tidal CO₂ levels by a larger amount, −0.99%, which was significantly greater than the changes that occurred during normal and fast-to-slow breathing. We doubt that this CO₂ trend significantly influenced our results for two reasons. First, our wavelet analyses revealed no differences between responses to fast-to-slow and slow-to-fast breathing-frequency changes. Second, an earlier study (34) showed that an average end-tidal CO₂ reduction of 1.04% from normal breathing levels did not significantly alter vagal baroreflex gain, arterial pressure, or R-R intervals.

In conclusion, our study of young men who gradually increased or decreased their breathing frequencies sheds new light on human autonomic neurophysiology. Respiration causally modulates both sympathetic (weakly) and vagal motoneuron (strongly) oscillations, over a wide frequency range, one that extends well below the frequency of actual breaths. Breathing frequency does not influence median levels of sympathetic or vagal activity over time; therefore, the changes in membrane potentials set in motion by individual breaths increase and decrease sympathetic and vagal motoneuron firing in equal measure and run their courses in 4 s or less. Breathing frequency broadly modulates vagal baroreflex gain, with peak gains registered in the low frequency range. This human baroreflex physiology is driven by a memory of past events, such that at any given breathing frequency, baroreflex gain and vagal-cardiac outflow depend more upon the trend in changes leading up to the final breathing frequency than its actual value. Phase relations between arterial pressure and sympathetic and vagal motoneuron oscillations are unaffected by breathing, and therefore likely reflect intrinsic responsiveness of these motoneurons to other synaptic inputs. Finally, breathing frequency does not affect phase coherence between diastolic pressure and muscle sympathetic oscillations, but augments phase coherence between systolic pressure and R-R interval oscillations over a limited portion of the usual breathing frequency range. These results refine the understanding of autonomic and hemodynamic oscillatory processes and physiological mechanisms known as the human respiratory gate.

GRANTS

This research was supported by the National Institutes of Health, Department of Veterans Affairs, and National Aeronautics and Space Administration; and by a Royal Society International Short Visit Grant, the UK Economic and Social Research Council, New Dynamics of Ageing Programme, and Engineering and Physical Sciences Research Council Grant EP/100999X1.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: W.H.C. and D.L.E. conception and design of research; W.H.C., L.R., and D.L.E. performed experiments; T.S., A.S., and D.L.E. analyzed data; T.S., W.H.C., A.S., and D.L.E. interpreted results of experiments; T.S. and D.L.E. prepared figures; D.L.E. drafted manuscript; T.S., W.H.C., A.S., and D.L.E. edited and revised manuscript; T.S., W.H.C., L.R., A.S., and D.L.E. approved final version of manuscript.

Appendix

Wavelet transform.

The wavelet transforms enable us to continuously derive the frequency content in time by use of wavelet windows with variable lengths. A wavelet is shifted along the signal and a coefficient is calculated representing the strength of correlation between the signal and the wavelet. For our analysis we used the Morlet mother wavelet, given by:

$$\psi (u)=\frac{1}{\sqrt[4]{\pi }}\cdot e^{-i2\pi f_{0}u}\cdot e^{-u^2/2}$$

where the central frequency was centered around the cardiac 1-Hz frequency. To create various scales of the wavelet comparable to the original signal, the mother wavelet is stretched and compressed by scaling factor, s:

$${\Psi }_{s,t}={\left|s\right|}^{-p}\cdot \psi \left(\frac{u-t}{s}\right)$$

To reach logarithmic resolution for the frequency, the scale factor s is increased exponentially. The transform itself is then a convolution of the wavelet and the original signal:

$$\tilde{g}(s,t)={\displaystyle {\int }_{-\infty }^{\infty }{\overline{\Psi }}_{s,t}(u)\cdot g(u)du}$$

where Ψ¯_s,t(u) represents the complex conjugate of the mother wavelet, Ψ̄_s,t. Thus any specific scale is avoided and the analysis becomes scale-independent in terms of frequency.

The energy density in the time-scale domain is evaluated from the wavelet transform, and the wavelet power within the f₁:f₂ frequency range can be calculated as:

$$\mathrm{\epsilon }(f_1:f_2)={\displaystyle {\int }_{1/f_2}^{1/f_1}\frac{1}{s^2}{\left|\tilde{g}(s,t)\right|}^2\text{d}s.}$$

Wavelet phase coherence and windowed wavelet phase coherence.

Due to the complex nature of the Morlet wavelet, the wavelet transform for each time t_n, and scale s_k, also consists of complex values:

$$\tilde{g}(s_k,t_n)={\tilde{g}}_{k,n}=a_{k,n}+i\cdot b_{k,n}$$

From here the instantaneous phase can be determined as the angle variable, Φ_k,n = arctan (b_k,n/a_k,n). To evaluate the wavelet phase coherence, the respective phase difference ΔΦ_k,n = Φ_2k,n − Φ_1k,n is calculated. To obtain a normalized measure of coherence between 0 and 1, the sine and cosine of the phase difference are averaged in time, yielding the phase coherence function:

$$C_{\varphi }(f_k)=\sqrt{{\langle \mathit{cos}\Delta {\varphi }_{k,n}\rangle }^2+{\langle \mathit{sin}\Delta {\varphi }_{k,n}\rangle }^2}$$

where the brackets on the righthand side denote the averaging operations. To follow how the phase coherence varies with time we calculated the windowed wavelet phase coherence side. A window is a slide-in-time domain and the phase coherence is evaluated and plotted as a function of both frequency and time, C_wΦ(f_k,t_k), with a window of a given size centered on a particular time, t_k. The window size is varied for low to high frequencies in the same manner as the wavelet transform was calculated. In this way the same logarithmic scale for the frequency is preserved. At the end, each windowing is normalized by the particular window size so that the measure returns to normalized phase coherence between 0 and 1. Due to the finite length of the windows at the end of the sliding is a cutoff of information, and the corresponding plot has a goblet-like shape.

Coupling between interacting oscillators: an information-theoretic approach.

An information-theoretic method for quantifying couplings is based on conditional mutual information between the first X₁(t) and the second X₂(t) signal. The conditional mutual information is estimated as net information about the τ time units in the future of the first signal, X₁(t), contained in the second signal, X₂(t) itself. First the τ increments are defined:

$${\Delta }_{\tau }{X}_1=X_1(t+\tau )-X_1(t).$$

Then the conditional mutual information (i.e., the coupling of the first to second signal) is defined as:

$$I_{21}=I(X_2,{\Delta }_{\tau }{X}_1|X_1)=H(X_2|X_1)+H({\Delta }_{\tau }{X}_1|X_1)-H(X_2,{\Delta }_{\tau }{X}_1|X_1)$$

where H(x|y) + H(x,y|z) are the conditional entropies defined in the usual Shannonian sense. Similarly the coupling I₁₂ from the first to the second signal is defined. The conditional mutual information I₁₂ and I₂₁ can be easily calculated by a simple box-counting algorithm based on equiquantal marginal bins.