Effect of Magnesium on Calcium and Oxalate Ion Binding

Abstract

Background and Purpose: Magnesium (Mg²⁺) has been shown to be a kidney stone inhibitor; however, the exact mechanism of its effect is unknown. Using theoretical models, the interactions of calcium and oxalate were examined in the presence of Mg²⁺.

Methods: Molecular dynamics simulations were performed with NAMD and CHARMM27 force field. The interaction between calcium (Ca²⁺) and oxalate (Ox²⁻) ions was examined with and without magnesium. Concentrations of calcium and oxalate were 0.1 M and 0.03 M, respectively, and placed in a cubic box of length ∼115 Angstrom. Na⁺ and Cl⁻ ions were inserted to meet system electroneutrality. Mg²⁺ was then placed into the box at physiologic concentrations and the interaction between calcium and oxalate was observed. In addition, the effect of citrate and pH were examined in regard to the effect of Mg²⁺ inhibition. Each system was allowed to run until a stable crystalline structure was formed.

Results: The presence of Mg²⁺ reduces the average size of the calcium oxalate and calcium phosphate aggregates. This effect is found to be Mg²⁺ concentration-dependent. It is also found that Mg²⁺ inhibition is synergistic with citrate and continues to be effective at acidic pH levels.

Conclusion: The presence of magnesium ions tends to destabilize calcium oxalate ion pairs and reduce the size of their aggregates. Mg²⁺ inhibitory effect is synergistic with citrate and remains effective in acidic environments. Further studies are needed to see if this can be applied to in vivo models as well as extending this to other stone inhibitors and promoters.

Introduction

The role of magnesium (Mg²⁺) as an inhibitor for calcium oxalate (CaOx) stone formation is controversial because of conflicting results in recent clinical trials.^1–4 Using molecular dynamics and theoretical chemistry modeling, we examine the role of the Mg²⁺ ion in calcium and oxalate binding.

Methods

Using the NAMD program, molecular dynamics (MD) simulations were performed to evaluate the role of Mg²⁺ in calcium and oxalate binding.⁵ NAMD is a molecular dynamics code used in the examination of large systems, including biologic systems. Using CHARMM potential functions, NAMD describes individual particles at a molecular level with force field specifications.⁵ All ions studied used the CHARMM27 force field.^6,7 Force field parameters determined by Yesselman and associates⁸ via MATCH were used for Ox²⁻ and citrate (Cit³⁻), while those for phosphate (PO₄³⁻) and dihydrogen phosphate (H₂PO₄⁻) were determined using CHARMM general force field (CGenFF)⁹ in the CHARMM program. The standard TIP3P potential model was used for water.¹⁰ The short-range repulsion and dispersion (Lennard-Jones interactions) and long-range Coulombic forces were evaluated and the Newton equation of motion was integrated to propagate the dynamics of the system.

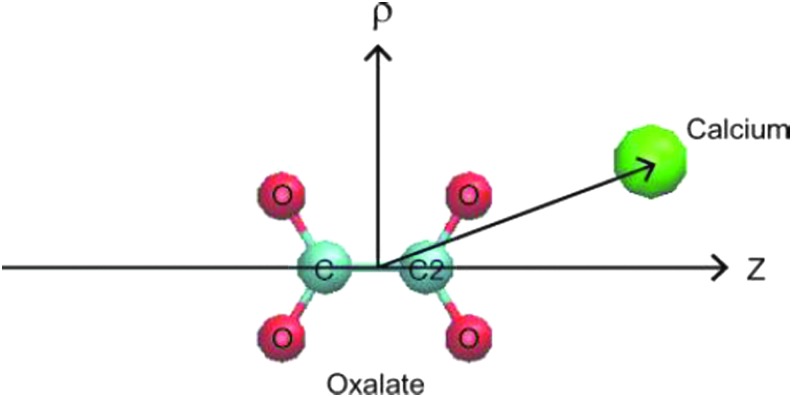
Table 1 outlines the components of each system design. To avoid any confusion, we mention that size of systems 1 and 2 is small; specifically, they are 15 times smaller than systems 4 to 10. We used systems 1 and 2 to simply evaluate the interaction of Ca²⁺ and Ox²⁻ in the absence and presence of Mg²⁺ via the free energy calculations. System 1 consists of one pair of Ca²⁺ and Ox²⁻ and 3330 water molecules. In addition, 10 pairs (∼0.16 M) of Na⁺ and Cl⁻ ions were added, so that its overall salt concentration is close to the physiologic condition. Compared with system 1, one Mg²⁺ and two additional Cl⁻ ions were added to system 2. The latter is to meet the system electroneutrality. The levels of the ions were supraphysiologic to observe any effect within the constraints of the computing power. After equilibration, we computed free energies of systems 1 and 2, using the metadynamics algorithm.¹¹ Two coordinates, 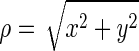and z, of the cylindrical coordinate system were used to describe the position of the calcium ion with respect to oxalate (Fig. 1). For each system, the simulation was performed for 400 ns with a time step of 2 fs, and free energies were obtained by averaging over the azimuthal angle coordinate θ.⁸

Table 1.

Ionic Concentrations in Each System

	Concentrations in mM
		Ca2+	Ox2−	Mg2+	Cit3−	H2PO4−	NH4+	PO43−
System	1	16	16	0	0	0	0	0
	2	16	16	16	0	0	0	0
	3	120	120	0	0	0	0	0
	4	100	33	0	0	0	150	150
	5	100	33	83	0	0	150	150
	6	100	33	150	0	0	150	150
	7	100	33	0	33	0	150	150
	8	100	33	150	33	0	150	150
	9	100	33	0	0	150	150	0
	10	100	33	150	0	150	150	0

FIG. 1.

Coordinates of calcium and oxalate: ρ and z are defined as the displacement of Ca²⁺ from the Ox²⁻ center-of-mass along the carbon–carbon bond in Ox²⁻ and its perpendicular directions, respectively. Ca²⁺ ion is represented in the green sphere and O and C atoms of Ox²⁻ are in red and light blue, respectively. Visual Molecular Ddynamics¹⁸ is used for display.

The free energy results for Ca²⁺ and Ox²⁻, in particular, local minima, provide information on the Ca²⁺-Ox²⁻ binding affinity and structures and their variations with the presence of other ions. Deeper energy minima indicate the formation of a more stable calcium-oxalate ion pair, thereby suggesting that calcium and oxalate ions are more likely to aggregate. Within our model, we are able to determine both the value and location of the free energy minima. We should note, however, that the effect of many urinary ionic species as well as that of heterogeneous biologic environments is ignored in the free energy calculations.

With systems 3 to 10, we investigated aggregation dynamics of CaOx in the absence and presence of various urine ions that are either known stone promoters or inhibitors of low weight.^12–17 System 3 was composed of 22 pairs of Ca²⁺ and Ox²⁻ ions, 30 pairs of Na⁺ and Cl⁻ ions, and 10000 water molecules. For systems 4 to 10, 90 Ca²⁺ and 30 Ox²⁻ were immersed in water consisting of 50,000 water molecules. The salt concentration was adjusted to satisfy the system electroneutrality. Systems 4, 5, and 6 that model a pH neutral/basic environment differ in their magnesium concentration; ie, 0, 83, and 150 mM, respectively (Table 1). For systems 7 and 8, citrate was inserted to evaluate its effect on aggregates. Systems 9 and 10 were generated from systems 4 and 6 by replacing their PO₄³⁻ ions with H₂PO₄⁻ to model an acidic urine environment. This allows us to study how pH influences Ca²⁺-Ox²⁻ aggregation. 100 ns, 80 ns and 40 ns MD simulations were performed for system 3, systems 4 to 8, and systems 9 and 10, respectively.

Results

In system 3, a large aggregate was formed around 30 ns. This structure continued to grow and become stabilized through association and dissociation of Ca²⁺ and Ox²⁻ ions along its edges. After ∼50 ns, a stable structure was formed, and no significant dissociation or association along its edges was observed in the remainder of the simulation. The structure of the aggregate at 100 ns is shown in Figure 2. Its analysis reveals three important configurations for the binding pair. Specifically, Ca²⁺ ions bind to the O-C-O (b1) or the O-C-C-O (b2) pockets of the Ox²⁻ anion. Oxygen atoms (b3) of oxalate can also function as a third cation binding site to form an ion pair with Ca²⁺.⁸

FIG. 2.

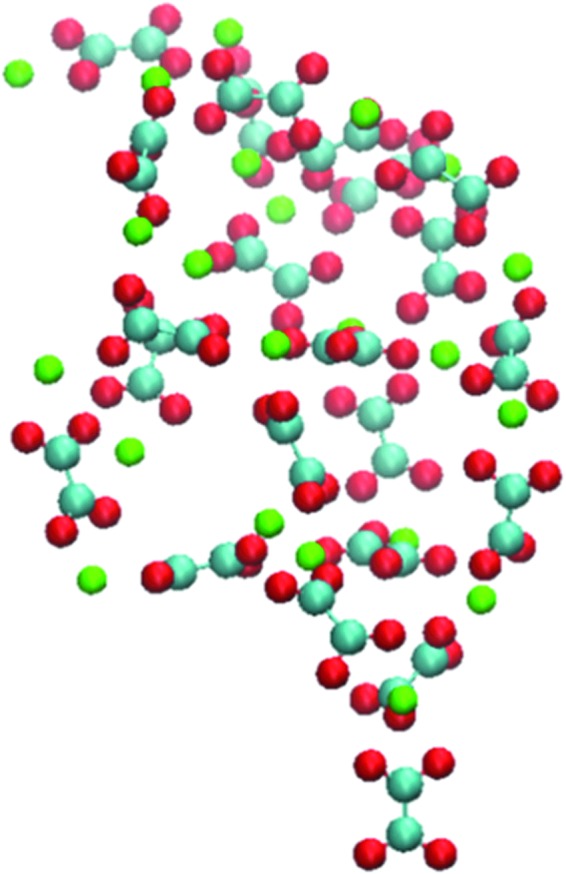
Structure of the calcium-oxalate aggregate obtained from the 100 ns MD simulation of system 3. Ca²⁺ is represented in the green sphere and oxygen and carbon atoms in Ox²⁻ are in red and blue spheres, respectively. Visual Molecular Dynamics was used to display the structure.¹⁸

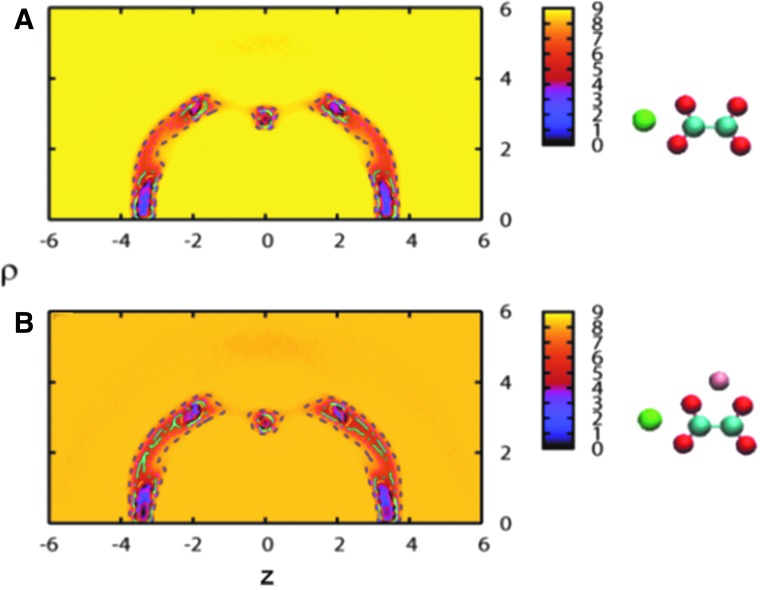
The free energy of a Ca²⁺ and Ox²⁻ complex determined as a function of ρ and z shows that its global minimum is located at the b2 position (viz., ρ∼2.8Å and z=0 Å) of oxalate (Fig. 3A). This means that b2 is the strongest Ca²⁺ binding site of Ox²⁻ when no promoter and/or inhibitor ions are present in the system. Local minima at ρ=0Å and z=∼±3 Å and at ρ∼3.2Å and z=∼±2 Å represent the second and third most stable binding sites, corresponding to b1 and b3, respectively.

FIG. 3.

Two-dimensional free energy map for the Ca²⁺-Ox²⁻ complex in an aqueous solution of NaCl: (A) System 1 and (B) system 2. The free energy is measured in kcal/mol and increases as its color changes from dark purple to light yellow. In each case, pre-equilibrated structure of ions used as an initial configuration in metadynamics simulations is shown next to the contour map. Mg²⁺ ion is represented in the pink sphere. (Units for ρ and z: Å)

Compared with system 1, system 2 shows a slight decrease in the Ca²⁺ and Ox²⁻ binding affinity because of the presence of Mg²⁺ (Fig. 3B). Mg²⁺ initially placed near the b2 site binds to the site during the equilibration (Fig. 3B). In the ensuing 400 ns simulation, it tends to move from one binding site to another and hinder the binding of Ca²⁺. Because Mg²⁺ is smaller, it can “fit” into the binding sites of Ox²⁻ better than Ca²⁺. This can prevent the binding of Ca²⁺ and Ox²⁻ at least at the Mg²⁺ occupied sites and, as a result, slow down the aggregation of Ca²⁺ and Ox²⁻. This paints the picture that Mg²⁺ and Ca²⁺ would compete directly for binding sites on Ox²⁻. The presence of shallow secondary free energy minima for Mg²⁺- Ox²⁻ complexation, however, complicates this picture. As Mg²⁺ ions approach Ox²⁻ from a distance, they can be trapped in these shallow wells. This could decelerate the binding of magnesium and considerably lower its ability to compete with Ca²⁺ to occupy the binding sites of Ox²⁻. To obtain further insight into this issue and the roles of Mg²⁺, we studied the formation of aggregates involving calcium explicitly via MD using systems 4 to 10 (Table 1).

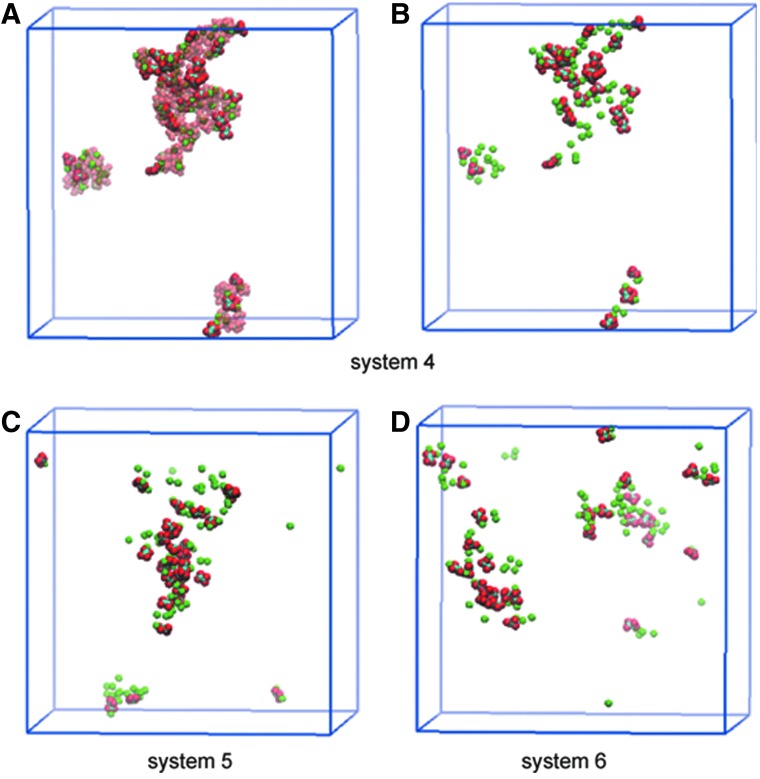
Figure 4 shows the aggregate structures obtained for systems 4 to 6. We notice that Ca²⁺ form aggregates mainly with PO₄³⁻ because of the strong Coulombic interaction of the latter. As a result, aggregates are primarily made up of Ca²⁺- PO₄³⁻ (CaP) binding structure mixed with some CaOx structure (Fig. 4A). The most salient aspect of Figure 4 is that the size of CaOx/CaP aggregates generally decreases as the Mg²⁺ concentration is raised. As shown in Figure 4B–D, however, the difference in the aggregate size between the 0 mM (system 4) to 83 mM (system 5) cases is not significant, compared with the difference of systems 5 (83 mM) and 6 (150 mM). These results indicate that Mg²⁺ has an inhibitory effect on CaOx/CaP aggregation, but this effect is magnesium concentration-dependent.

FIG. 4.

Comparison of Ca²⁺ and Ox²⁻ aggregate in relation to Mg²⁺concentration. In B–D, only Ca²⁺ and Ox²⁻ ions are displayed to clearly expose the difference among systems 4–6, while A also displays PO₄³⁻ ions (transparent) for system 4.¹⁸ System 6, which is the highest in Mg²⁺ concentration among the three systems shown here, yields the smallest calcium phosphate/calcium oxalate aggregates. Although not shown in D, Mg²⁺ ions are located near Ox²⁻ ions instead of directly binding to them.

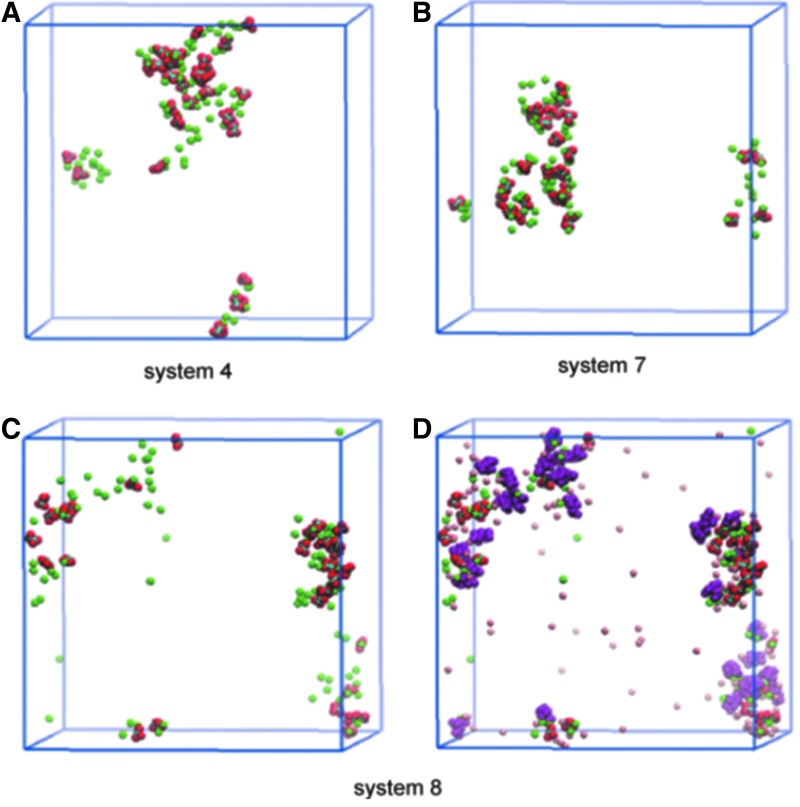
Systems 7 and 8 evaluated the role of citrate in inhibition in the absence and presence of magnesium. Comparison of the results in Figure 5A and B suggests that citrate alone does not have a significant influence on the size of CaP aggregates. We speculate that citrate does not compete with PO₄³⁻ because PO₄³⁻ presents in higher concentration than citrate in the system, although they have the same valency. Because the aggregation is mainly effected via PO₄³⁻ in the present case, citrate therefore tends to show little effect on CaP. The addition of citrate alone, however, can have an inhibitory effect on the formation of CaOx aggregates by directly competing with Ox²⁻ for binding Ca²⁺, which is consistent with our previous free energy result. The role of citrate more clearly appears when both citrate and Mg²⁺ are present (Figs. 5C and D). Interestingly, when citrate was added with Mg²⁺, a synergistic effect was seen, as manifested by the small size of CaOx/CaP aggregates in system 8 (Fig. 5C).

FIG. 5.

Effect of Mg²⁺ and Cit³⁻. In A–C, only Ca²⁺ and Ox²⁻ ions are shown, while Mg²⁺ (pink) and Cit³⁻ (purple) are also displayed in D.¹⁸ There is synergy of the inhibitory effect on Ca²⁺ and Ox²⁻ aggregation.

Finally, the effect of urinary pH and Mg²⁺ was explored in systems 9 and 10 (Figs. 6B and C). H₂PO₄⁻ was used, which would be seen in a weakly acidic urine, as opposed to PO₄³⁻, which would be seen in the more pH neutral and/or basic environment. In this sense, the replacement of PO₄³⁻ by H₂PO₄⁻ effectively represents lowering of pH. This results in the formation of mainly CaOx aggregates, because Ca²⁺ ions are no longer intercepted by trivalent phosphate and thus become more available to interact with Ox²⁻ ions. This demonstrates the expected results of increase in CaOx aggregates in acidic urine. When Mg²⁺ was added to the system, the inhibitory effect as previously shown was maintained within this acidic milieu (Fig. 6C). We should note that Mg²⁺ ions on average do not actively participate in aggregation; ie, in most cases, they do not bind tightly to Ox²⁻. This seems to support our earlier view that Mg²⁺ screens the interactions of Ca²⁺ with Ox²⁻ rather than directly competing with Ca²⁺ for the binding sites on Ox²⁻.

FIG. 6.

Effect of pH. All snapshots were taken at 40 ns of the simulations. The aggregates of system 4 in A have mainly the CaP character while they are primarily CaOx aggregates in a more acidic environment in B and C. Aggregate size difference between the latter two indicates that Mg²⁺ continues to exert its inhibitory effect in the weakly acidic urine environment.

Discussion

Mg²⁺ has been poorly understood within the literature. It is known to be an inhibitor, but the clinical application remains elusive.^1–4 Using MD, theoretical chemistry has allowed us to examine the molecular mechanism of the interaction of Mg²⁺ with Ca²⁺ and Ox²⁻ along with other known promoters and inhibitors. This will ultimately allow for a backbone to begin clinical applications of Mg²⁺ in stone formation.

While theoretical modeling has been used in stone disease, there has not been a previously described application to Mg²⁺ particularly with the obtained calcium oxalate aggregates.

While MD is able to provide information regarding ionic interaction, there are limitations in its use. Primarily, the biggest limitation to date is the inability to run computer experiments at physiologic concentrations. While we have been able to obtain the overall ionic concentrations close to urinary conditions, the concentrations of key ions, such as calcium and oxalate, still remain significantly higher than those seen in normal human urine. Because of the time constraints of the computer simulation, these concentrations were chosen to be significantly high. In addition, these are highly controlled experiments and certainly do not contain all of the species present within human urine. As the technology advances, the experiments have included more constituents but still remain far from physiologic. Finally, this remains theoretical and the application to in vivo studies is unknown.

Further studies are warranted at this time to examine stone formation at physiologic concentrations. In addition, we would like to study Mg²⁺ inhibition within human models.

Conclusion

The ion pair interaction of Ca²⁺ and Ox²⁻ ions is weakened in the presence of magnesium, indicating a shortened contact time. The effect of Mg²⁺ appears to be influenced by its density as well as its positions with respect to Ox²⁻. Mg²⁺ inhibitory effect is synergistic with citrate and remains effective in acidic environments. Further studies are needed to see if this can be applied to in vivo models as well as extending this to other stone inhibitors and promoters.

Abbreviations Used

Ca²⁺

calcium

CaOx

calcium oxalate

CaP

calcium phosphate

Cl⁻

chloride

Cit³⁻

citrate

fs

femtosecond

H₂PO₄⁻

dihydrogen phosphate

MD

molecular dynamics

Mg²⁺

magnesium

Na⁺

sodium

ns

nanosecond

Ox²⁻

oxalate

PO₄³⁻

phosphate

Acknowledgment

We are grateful to the National Institute for Computational Sciences (NICS) for the supercomputing time grant, Kraken TG-MCB100064.

Disclosure Statement

No competing financial interests exist.