Nonlinear estimation of coupling and directionality between signals: Application to uterine EMG propagation

Abstract

Understanding the direction and quantity of information flowing in a complex system is a fundamental task in signal processing. Several measures have been proposed to detect the quantity of synchronization and the directionality between time series and in physiological data. In this paper we use two methods that are widely used in synchronization and directionality analysis: Nonlinear correlation coefficient (h²) and the general synchronization (H). The performances of both methods were tested on four dimensional coupled synthetic nonlinear Rössler models. They were then applied to a single real labor contraction uterine EMG burst with the aim of using them to detect synchronization and to plot the map of direction of information flow between the whole signal channels. The results on synthetic signal show a slight superiority of H over h². The results obtained on a single contraction are encouraging for the future use of these tools for resolving the open question of the directionality of uterine contractions and may provide a way of finding their source loci.

I. Introduction

Multivariate data are often encountered in the study of coupled dynamical systems in many scientific and technical disciplines. The usual problem in the analysis of these data is whether signals are dependent or not [1].

Coupled systems exist in many branches of life, physical and social sciences, but interest for synchronization has also increased in a variety of bio-signals such as EEG [2,3], ECG [4] and uterine EMG [5].

In most coupled systems such as neuronal areas in human body, economic systems, and ecological systems, the intrinsic and internal variants, and the interdependencies among their subsystems are not accessible.

Therefore, in order to quantify the interdependencies among coupled systems, attempts have been made through measuring the synchronization between their outputs represented mostly as time series [6]. Today, much attention has been also paid to the estimation of direction of information flow between the different channels of these multivariate data [7,8]. As the data are practically always nonlinear [9], the application of traditional techniques such as cross-spectrum and cross- correlation analysis [10] has its limitations.

The hypothesis that drives this study is that labor is associated with a great coupling between uterine cells, inducing thus a more synchronized uterus that should generate efficient contractions (the whole uterus contract) in order to push the baby out. This coupling should be evidenced from uterine EMG by using non linear tools [11].

The main objective of this paper is to provide evidence for the usefulness and appropriateness of nonlinear directional coupling analysis for uterine EMG. Two nonlinear methods, one based on nonlinear regression (h²) [12], and the other on synchronization in state space (H) [13] were applied to synthetic four dimensional coupled Rössler model, which is a nonlinear stationary system where the coupling can be controlled. The methods were then applied to real EHG bursts associated to one labor contraction.

Several studies on the applications of synchronization measures have been done on both synthetic and real signals. Most of them are not aimed at studying the directionality between signals [14,11]. The aim of this paper is to compare these two methods on synthetic as well as on real signals, in order to test their power in evidencing properly the direction of information flow between channels.

The results on synthetic signal show a slight superiority of H over h². A demonstration application to an example of real signals shows that both methods result in a synchronization matrix, which is divided into four more or less active (synchronized) regions. According to the analysis the signals propagate in all directions but dominantly towards the cervix.

II. Material and Methods

A. Data

1. Synthetic signals

To evaluate the two synchronization and direction measures, we applied them to a four dimensional coupled Rössler nonlinear stationary model. The non-linear Rössler system with four dimensions is defined as

$$\left(\begin{array}{c}\frac{{dX}_j}{dt}\\ \frac{{dY}_j}{dt}\\ \frac{{dZ}_j}{dt}\end{array}\right)=\left(\begin{array}{c}-{\mathrm{\Omega }}_j{Y}_j-Z_j+[\sum _i{k}_{ji}(X_i-X_j)]+{\eta }_j\\ {\mathrm{\Omega }}_j{X}_j+{aY}_j\\ b+(X_j-c)Z_j\end{array}\right)$$ (1)

With i,j=1,2,3,4 and the frequencies of the four oscillators were shifted using Ω₁=1.01, Ω₂=0.99, Ω₃= 0.97 and Ω₄= 1.03. The parameters of the oscillators were set to a= 0.15, b= 0.2, and c= 10 as in [16]. The stochastic influence is given by a Gaussian distributed white noise η_j.

The interaction between oscillator i and j is modeled by means of a coupling between the X_i and X_j component and the coupling strength is adjusted by the coupling parameters k_ji ≠ 0. In the following, the coupling parameters have been set to k₂₁=0.1, k₃₁=0.5, k₃₂=0.3 and k₄₂= 1. The remaining coupling strengths have been set to zero.

The synthetic signal was generated by using an Euler method with an integration step of 0.04, a sampling step of 0.1 and we generated 30 Monte-carlo trials of each signal with length of N = 5000 points. The time series analysis techniques have been applied to X components of models.

2. Real signals

The methods used here are “bivariate” in that we used all the combination between the 16 monopolar channels of a 4 × 4 recording matrix located on the women’s abdomen (see [17] for details). The signals were recorded on a woman in active labor at the Landspitali University Hospital in Iceland, following a protocol approved by the relevant ethical committee (VSN 02-0006-V2) with sampling frequency of 200 Hz. The EHG signal was segmented manually to extract segments containing uterine activity burst, then filtered using CCA-EMD method developed by our team [18].

B. Methods

1. Nonlinear correlation Coefficient (h²)

The underlying idea is that if the value of X is considered as a function of the value of Y, the value of Y given X can be predicted according to a nonlinear regression curve. The nonlinear correlation coefficient between demeaned signals X and Y is then calculated as follows, for more details see [7]:

$$h_{Y\mid X}^2=\frac{{\sum }_{k=1}^{N}Y{(k)}^2-{\sum }_{k=1}^N{\left(Y(k)-f(X_i)\right)}^2}{{\sum }_{k=1}^{N}Y{(k)}^2}$$ (2)

where f(X_i) is the linear piecewise approximation of the nonlinear regression curve. The estimator h²_Y|X ranges from 0 (Y is independent of X) to 1 (Y is fully determined by X). For a nonlinear relationship, h²_x|y ≠ h²_y|x and the difference Δh² = h²_x|y − h²_y|x indicates the degree of asymmetry of the nonlinear coupling. The delay at which the maximum value for h² is obtained is used as an estimate of the time delay between the signals so we can obtain also the difference Δτ = τ_x|y − τ_y|x.

On combining the information of asymmetry and of time delay in coupling, the following direction index has been recently proposed by [19] to provide a robust measure of the direction of coupling:

$$D_{x\mid y}=\frac{1}{2}\left[sgn\left(\mathrm{\Delta }{h}^2\right)+sgn\left(\mathrm{\Delta }\tau \right)\right]$$ (3)

If D_x|y = +1 (or −1) so X → Y (or Y → X). D_x|y = 0 indicates bidirectional (Y ↔ X) coupling between the signals.

2. General synchronization (H)

From time series measured in two systems X and Y, let us reconstruct delay vectors x_n=(x_n, …, x_{n−(m−1)τ}) and y_n=(y_n, …, y_{n−(m−1)τ}), where n=1, …,N: m is the embedding dimension and τ denotes the time delay. Let r_n,j and s_n,j, j=1, …, k, denote the time indices of the k nearest neighbors of x_n and y_n respectively.

For each x_n, the squared mean Euclidean distance to its k neighbors is defined as:

$$R_n^{(k)}(X)=\frac{1}{k}\sum _{j=1}^k\left(x_n-x_{r_{n,j}}\right)$$ (4)

The Y-conditioned squared mean Euclidean distance is:

$$R_n^{(k)}(X\mid Y)=\frac{1}{k}\sum _{j=1}^k{\left(x_n-x_{s_{n,j}}\right)}^2$$ (5)

Thus, a nonlinear interdependence measure can be defined accordingly [7]:

$$H^{(k)}(X\mid Y)=\frac{1}{N}\sum _{n=1}^{N}log\frac{R_n(X)}{R_n^{(k)}(X\mid Y)}$$ (6)

where R_n(X) is the average distance of a vector x_n to all the other vectors. This measure is close to zero if X and Y are independent, while it is positive if nearness in Y implies also nearness in X for equal time partners.

The nonlinear interdependence is an asymmetric measure, in the sense that H(X|Y) ≠ H(Y|X) so H(X|Y) > H(Y|X), if X → Y.

We should notice that the relation between the coupling degree injected to the model and the coupling measured by these methods is not linear. It is not therefore possible to quantify any error criterion between these two couplings.

III. Results

A. Results on synthetic signals

Figure 1 represents the reference coupling and directionality of the synthetic signal.

Fig. 1.

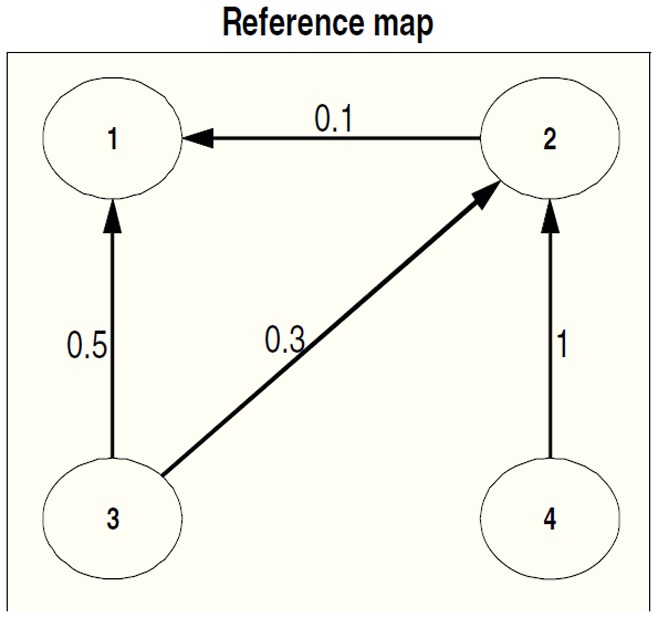
The map of direction using the reference coupling value.

To visualize the results, we plotted the matrix of synchronization (color matrix) between all the combination of the channels for each method applied to the synthetic model, and the corresponding map of direction of signal propagation as nodes with arrows. The colors denote an arbitrary scale of the level of synchronization. The warm colors indicate a higher level of synchronicity and the colder colors indicate a low synchronicity. A dissymmetry in the values across the diagonal line indicates directionality. The stronger this difference, the stronger the directionality. The arrows indicate the directions of the coupling and in figure 1 they indicate the directionality imposed on the Rössler model.

We see in figure 2 the results obtained by the application of the nonlinear correlation coefficient h² to the synthetic signal (Top). It is clear that the warmest colors of the synchronization matrix (highest synchronization) are present in the cells where the coupling values of the model are nonzero. We find also in the map of direction that h² is able to detect three out of four true directions with only one erroneous direction (in red) from node 2 to node 4. We also observe no noticeable asymmetry in the synchronization matrix between the opposite direction in the case of low coupling value, 0.1 between 1 and 2.

Fig. 2.

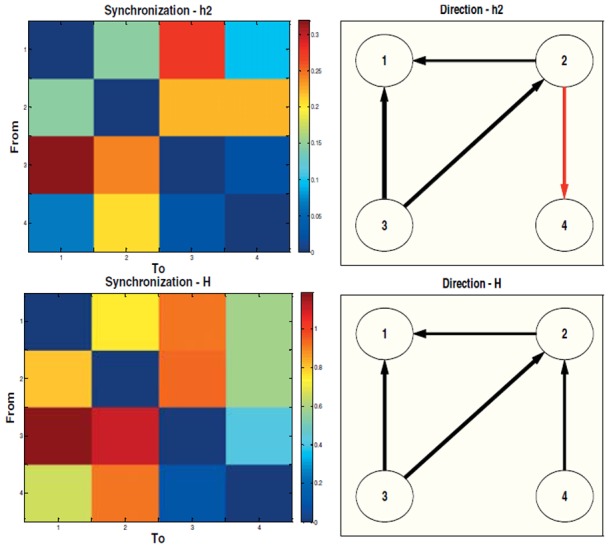
Quantity (left) and direction (right) of information flow using Top: nonlinear correlation coefficient method (h²) applied to the synthetic signal. The red arrow between nodes 2 and 4 indicates erroneous direction detection. Bottom: the index of general synchronization method (H) applied to the synthetic signal.

The application of the index of general synchronization (H) gives essentially the same results as h² in the matrix of synchronization, as seen in figure 2 (bottom). The index of general synchronization correctly detects all the directionalities imposed in the synthetic signal.

B. Application to real EHG signals

Here both methods were applied to real EMG recorded during one uterine contraction during labor. In the following the color matrix represents the synchronization between the 16 channels of the electrode matrix and the map of node and the arrows represent the directions map of the synchronization between these channels. We are not interested in the synchronization between the electrodes and themselves and for this reason we have forced the diagonal of the synchronization matrix to zero. After verification of their Gaussian distribution, the results are thresholded by m+2σ where m is the mean of the synchronization matrix and σ is its standard deviation, in order to remove the least significant couplings between channels and to increase figure readability.

It is clear from the color matrix obtained by h² method (figure 3) that the signal is propagated through the whole matrix of electrode. We note also that the row represented by channel 9 and the column represented by channel 10 divide the matrix in four active regions where we see a high interaction and synchronization between the channels of each region. The map of direction of synchronization confirms what we see in the color matrix since there are arrows in all the directions (propagation in the entire matrix) but with a dominant direction towards the bottom of the matrix (towards the cervix).

Fig. 3.

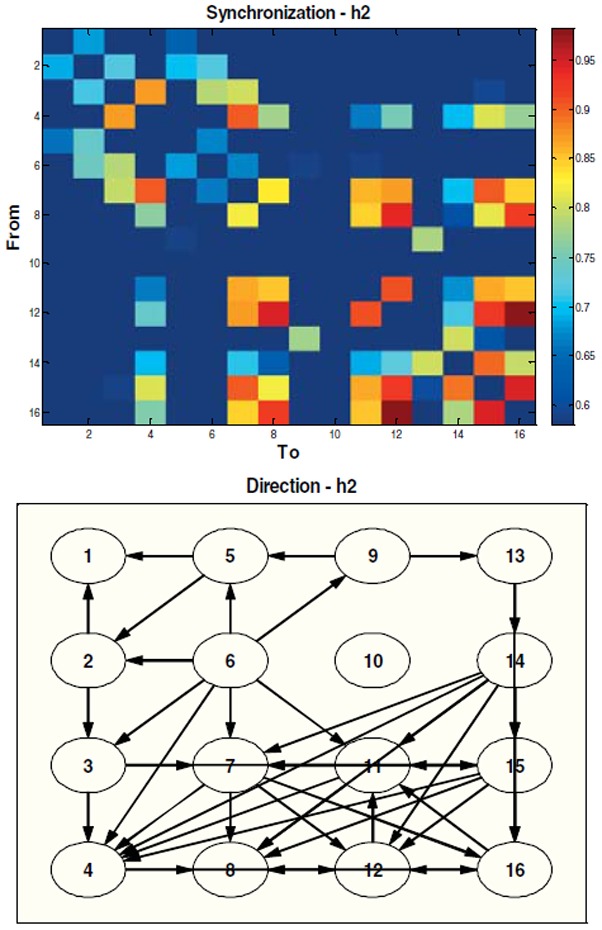
Quantity (top) and direction (bottom) of information flow between the 16 monopolar channels of uterine EMG recorded during a labor contraction using h² method.

From figure 4 obtained by H, method of general synchronization, we can extract the same information about the propagation in the whole matrix and the division of the color matrix in four regions. In the direction map, it is here also clear that there is a multidirectional propagation of signals throughout the channels with more concentration of direction toward cervix.

Fig. 4.

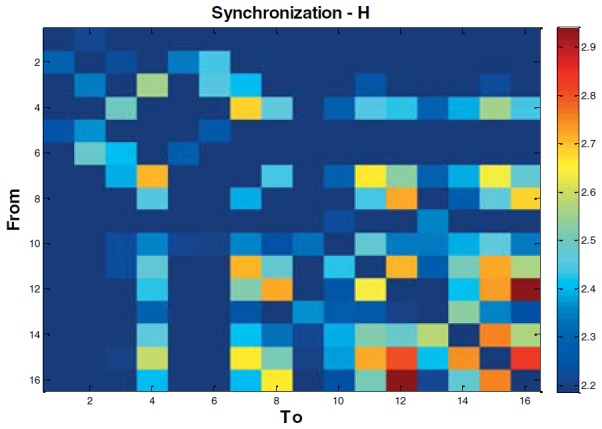
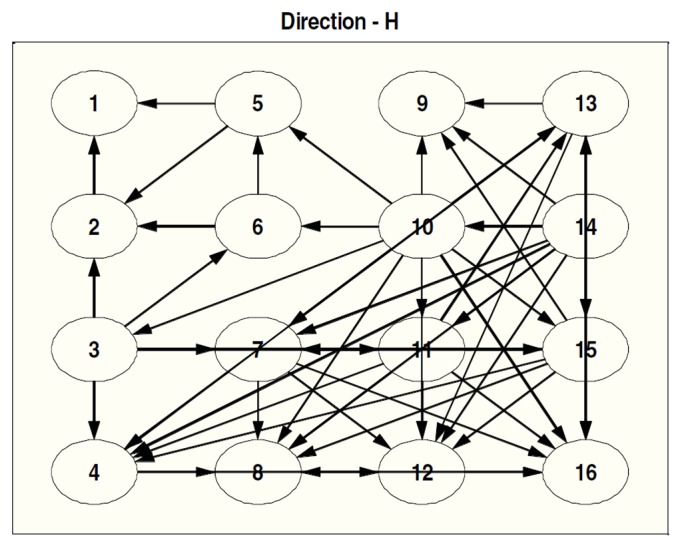
Quantity (top) and direction (bottom) of information flow between the 16 monopolar channels of uterine EMG recorded during a labor contraction using H method.

IV. Discussion

Two synchronization measures (Nonlinear correlation coefficient and the Index of general synchronization) were tested on synthetic signals generated by four-dimensional coupled nonlinear stationary Rössler model.

Both methods were found to be able to detect the synchronization and the direction between the signals with a slight superiority of H over h². The limitation of h² concerning directionality has also been evidenced on [19].

In this paper, we also presented the results obtained by using the measures for estimating the synchronization and mapping the direction of synchronization of uterine EMG bursts recorded during one uterine labor contraction. Results show four more or less active regions in the synchronization matrix and indicate that the signal during labor is propagated and scattered in the entire matrix of electrodes. If this result is obtained on a valid data base of contractions it would confirm the hypothesis that during labor the whole uterus contracts in a short time to give birth, and that directionality of the contractions is toward the cervix to push the baby out. Of course an application on a bigger database is necessary to strengthen our interpretation and conclusion.

In future work, we will compare the results obtained by the results obtained using time varying in complement to the application of these methods.

V. Conclusion

Testing and comparison of two synchronization measures were performed on synthetic signal for the estimation of synchronization and directionality. The methods were then applied on one uterine electrical bursts recorded during labor. The results indicate that the synchronization was spread in the whole matrix and in all directions. We will next apply these methods to a bigger database to draw stronger conclusions that could be useful from clinical point of view.