Characterization of Single-core Magnetite Nanoparticles for Magnetic Imaging by SQUID-relaxometry

Abstract

Optimizing the sensitivity of SQUID (superconducting quantum interference device)-relaxometry for detecting cell-targeted magnetic nanoparticles for in vivo diagnostics requires nanoparticles with a narrow particle size distribution to ensure that the Néel relaxation times fall within the measurement timescale (50 ms - 2 s, in this work). To determine the optimum particle size, single-core magnetite nanoparticles (with nominal average diameters 20, 25, 30, and 35 nm) were characterized by SQUID-relaxometry, transmission electron microscopy (TEM), SQUID-susceptometry, dynamic light scattering, and zeta potential analysis. The SQUID-relaxometry signal (detected magnetic moment/kg) from both the 25 nm and 30 nm particles was an improvement over previously-studied multi-core particles. However, the detected moments were an order of magnitude lower than predicted based on a simple model that takes into account the measured size distributions (but neglects dipolar interactions and polydispersity of the anisotropy energy density), indicating that improved control of several different nanoparticle properties (size, shape, coating thickness) will be required to achieve the highest detection sensitivity. Antibody conjugation and cell incubation experiments show that single-core particles enable a higher detected moment per cell, but also demonstrate the need for improved surface treatments to mitigate aggregation and improve specificity.

1. Introduction

The application of magnetorelaxometry of nanoparticles to biomedical applications is a rapidly growing area of research, with recent work aimed at both in vitro bioassay (Heim et al 2009, Eberbeck et al 2009) and in vivo applications (Jaetao et al 2009, Tietze et al 2009, Adolphi et al 2009, Ge et al 2009). Our goal is to develop magnetorelaxometry using superconducting quantum interference device (SQUID) sensors as a highly-sensitive platform for detecting and localizing superparamagnetic iron oxide nanoparticles specifically targeted to sites of disease in vivo. In this paper, we present results on the binding of antibody-conjugated nanoparticles to T-cells, which are known to infiltrate sites of acute organ transplant rejection (Cornell et al 2008). Our long-term goal is to develop SQUID-relaxometry as a noninvasive method for detecting and imaging transplant rejection to eliminate the need for invasive biopsies, which increase the risk of transplant loss due to infection. Preliminary in vitro experiments suggest that this method will be capable of detecting a few thousand magnetically-labelled cells located several centimetres from the sensors (Flynn and Bryant 2005).

SQUIDs are sensitive detectors of time-varying magnetic fields. In a commercial SQUID magnetometer, the time-varying field is generated by moving the sample relative to the pick-up coil of the sensor, while a constant external field is applied to maintain the sample magnetization. Relaxometry enables the detection of nanoparticles in a stationary sample; the time-varying field is created by briefly magnetizing the nanoparticles using a pulsed DC field and then allowing the nanoparticle magnetization to relax in zero applied field. In our system, the SQUID sensors are turned on after a short delay (50 ms) after the end of the magnetizing pulse, and the decaying field of the magnetized particles is then measured for several seconds. The delay is necessary to allow transient fields, induced in conductive elements of the measurement system by the pulsed field, to decay sufficiently to enable operation of the SQUIDs in their most sensitive range.

In general, magnetic nanoparticles relax by the Brownian and Néel mechanisms. Brownian relaxation involves the physical rotation of the entire nanoparticle relative to the fluid medium, whereas Néel relaxation occurs due to thermal fluctuations of the direction of the magnetic moment relative to the crystal orientation. The magnetization of cell-bound nanoparticles must therefore decay by the Néel mechanism.

In order to detect the decaying magnetization of cell-bound nanoparticles, the Néel relaxation time constant must fall within in the range 50 ms up to several seconds, to match the measurement timescale of the SQUID system. The Néel relaxation time constant is given by

$${\tau }_N={\tau }_0{e}^{KV∕kT}$$ (1)

where τ₀ is customarily taken to be 10⁻⁹ or 10⁻¹⁰ s, K is the effective anisotropy energy density of the magnetic material (including magnetocrystalline, shape and surface contributions), and V is the volume of the magnetic particle (Néel 1955). This sensitive dependence of the relaxation time on nanoparticle properties places stringent demands on the uniformity of the particles. Neglecting interparticle dipolar interactions, and assuming a uniform value of K = 1.35 × 10⁴ J/m³ (the magnetocrystalline anisotropy for bulk magnetite), only a very narrow range of particle diameters (24 +/− 1 nm) yields body-temperature relaxation times detectable within our measurement timescale. The theoretical Néel relaxation times of 20 and 28 nm particles are approximately 10⁻⁶ and 10⁶ seconds, respectively, well outside the measurement timescale. The actual value of K, and hence the optimum particle size, must be determined empirically. In addition to depending sensitively on the distribution of relaxation times of the nanoparticle ensemble, the detectable magnetic moment/kg also depends on the degree to which the particles exhibiting the desired relaxation times are magnetized using the available field strengths. These same considerations are important for the development of related techniques, including hyperthermia (Gazeau et al 2008) and Magnetic Particle Imaging (MPI) (Ferguson et al 2009), which depend on AC excitation and are therefore optimized when the nanoparticles exhibit a particular narrow range of magnetic relaxation times.

The overall relaxation time τ of an unbound nanoparticle is given by

$$\tau ={\left(\frac{1}{{\tau }_N}+\frac{1}{{\tau }_B}\right)}^{-1},$$ (2)

and τ_B , the Brownian time constant, is given by

$${\tau }_B=\frac{3\eta V_h}{k_{B}T}$$ (3)

where η is the viscosity of the medium, V_h is the hydrodynamic volume, k_B is Boltzmann's constant, and T is the absolute temperature (Brown 1963). Note that for particles with hydrodynamic diameters less than a few hundred nanometres, the magnetization of unbound particles in aqueous media decays too quickly to be detected by our method (τ_B << 50 ms). This is an advantage in terms of specificity, because, in principle, only nanoparticles that are bound to cells are detected, allowing the quantification of nanoparticle binding even in a large background of unbound particles (Kötitz et al 1999, Chemla et al 2000).

Achieving the highest sensitivity for in vivo magnetic imaging by SQUID relaxometry requires particles with larger cores, and substantially lower polydispersity, than are typically found in commercial iron oxide particles intended for other applications, such as MRI or magnetic cell separation. Most commercially-available multi-core magnetic beads are reported to have smaller diameter cores (< 10 nm), resulting in relaxation times far too short to be detected by relaxometry. Some multi-core particles (e.g., Chemicell SiMAG or FluidMAG) contain some fraction of cores that are large enough to be detected in our system, although the observable moment/kg[Fe] is at least two orders of magnitude smaller than predicted for a monodisperse ensemble of magnetite particles with ideal properties (Adolphi et al 2009).

The present study was undertaken to determine to what extent single-core magnetite nanoparticles exhibiting relatively low size polydispersity will enable us to improve the sensitivity (detectable moment/kg[Fe]) of our technique. In this work, we have focused on commercially-available single-core magnetite nanoparticles (Ocean Nanotech, SHP series). In addition to SQUID-relaxometry, we performed standard SQUID-susceptometry, transmission electron microscopy (TEM), zeta-potential analysis, and dynamic light scattering (DLS). While the measurement timescale of SQUID-relaxometry (50 ms – 2 s) is sensitive to a narrow distribution of particles, SQUID-susceptometry is sensitive to all particles with relaxation times below ~100 s (i.e., all unblocked particles) enabling a more complete magnetic characterization of the nanoparticle ensemble. Similarly, TEM, DLS, and zeta-potential measurements are sensitive to properties (size and surface charge) of the entire ensemble. Following the methods of Chantrell et al (1983), we analyse the magnetization curves (M vs. B) obtained by relaxometry using a moment superposition model (MSM), which explicitly includes the distribution of nanoparticle sizes, but does not include interparticle dipolar interactions or polydispersity of the anisotropy energy density. The results of conjugating antibodies to the nanoparticles and the incubation of the antibody-conjugated nanoparticles with target cells are also presented.

2. Materials and Methods

2.1 Nanoparticles

SHP nanoparticles (Ocean Nanotech; Springdale, AR, USA) are single-core magnetite particles, coated with a thin (~2-3 nm thick) layer of polymer and functionalized with carboxyl groups to enable conjugation to antibodies. We characterized SHP-20 (lot OCK8), SHP-25 (lot SEP8-0), SHP-30 (lot DE4-P), and SHP-35 (lot SAO7) with nominal core diameters of 20, 25, 30, and 35 nm, respectively. The iron concentration (mg[Fe]/mL) of the stock solution was determined destructively by dissolving in acid, forming the phenanthroline/Fe2+ complex, and then quantifying the concentration of a known dilution spectrophotometrically (ASTM E394-00 2000, Huber et al 2004). For comparison, dynamic lights scattering (DLS) and zeta potential measurements were also performed on three lots of SiMAG nanoparticles (Chemicell; Berlin, Germany), which consist of multiple magnetite cores embedded in a silica matrix with an overall diameter of ~100 nm.

2.2. SQUID-relaxometry

Detection of nanoparticles by relaxometry was performed using a BTi 2004 seven-channel low-temperature SQUID array (4D-Neuroimaging; San Diego, CA, USA) originally designed for magnetoencephalography. Second order gradiometers with a baseline of 4 cm are used to reject background magnetic fields due to distant sources, allowing the measurements to be performed in an unshielded environment. Due to RF interference, the sensitivity of the system is currently limited to ~10⁻¹² $\mathrm{T}∕\surd \mathrm{Hz}$. The seven gradiometer coils are located at the bottom of the liquid He dewar, 1.9 cm from the outer dewar surface, arranged with six in a circle of 2.15 cm radius and one at the centre. For in vitro measurements on small samples, the sample is located at a distance z ≈ 3 cm below the bottom of the centre coil. The samples are uniformly magnetized (parallel to the centre gradiometer axis) using a 60 cm-square Helmholtz array (L = 16 mH, B/I = 0.107 mT/A) powered by a 3 kW current-regulated supply. The decaying magnetization is sampled at a rate of 1 kHz (beginning 50 ms after switching off the magnetizing pulse) and digitized using a National Instruments PXI8336 16-channel digitizer and LabVIEW 8.5.1 acquisition software (National Instruments, Austin, TX, USA). Our standard measurement protocol is to apply a 3.8 mT field for 0.3 s and then acquire data for 2 s, with 10 repetitions, subsequently averaged, to improve signal-to-noise. Magnetization curves (M vs. B) are obtained, using the same apparatus and timing, by varying the applied field between 0 and 4.0 mT.

Data analysis is performed using the Multi-Source Analysis program, written in our lab using MATLAB (The MathWorks Inc.; Natick, MA, USA). After signal averaging and removal of 60Hz line frequency contamination, background data (acquired with no sample) is subtracted from the sample data. The seven relaxation curves are fit by a logarithmic function (Street and Woolley 1949), to determine the DC offset, and an exponential function to the first 200 ms of the decay to determine the magnetic field amplitude at each sensor position 50 ms after the magnetizing pulse is switched off. In order to solve the inverse problem, we fit the spatial dependence of the magnetic field by modelling the sample as a single magnetic dipole, which allows us to determine the location (x, y, z) and magnetic moment (m_z) of the source. It is assumed that the magnetic vector points along the z axis, the direction of the magnetizing field. The least-squares fit is performed using the Levenberg-Marquardt algorithm. For medical imaging, a multiple dipole model may be used to determine the spatial coordinates and moments for multiple discrete sources using n different sample positions – equivalent to a sensor array with 7n elements.

To obtain the desired Néel relaxation of the nanoparticles, the particles must be immobilized. In the case of cell samples, the antibody-conjugated nanoparticles are immobilized by the binding of the antibodies to receptors on the cell surface. In the case of unconjugated nanoparticles, 10-20 μl of stock nanoparticle solution is applied to a Q-tips cotton swab (Unilever, Trumball, CT, USA) and allowed to dry in air.

2.3 SQUID-susceptometry

DC and AC magnetic characterizations were performed using an MPMS-7 SQUID magnetometer system (Quantum Design; San Diego, CA, USA). DC Magnetization curves were acquired by equilibrating the sample at the measurement temperature in zero applied field, then incrementally increasing the field and pausing 100 seconds at each field before measurement. Five sequential measurements were taken at each field, a mean of those measurements calculated, and the three values with the lowest deviation from the mean were averaged and reported as the moment. Zero Field Cooled (ZFC) curves were determined by cooling the sample in the absence of a magnetic field to 5 K, then slowly warming in a 1 mT field. After thermally equilibrating at a target temperature, a series of five measurements was taken and the values processed as described to obtain the magnetization value. AC susceptibility curves were obtained by applying a 0.2 mT (159 A/m) AC magnetic field at various frequencies (f = 0.1 – 1000 Hz) to a thermally equilibrated sample. The in-phase (χ’) and out-of-phase (χ”) AC susceptibilities of the sample were digitized and recorded.

2.4 TEM and Image Analysis

The nanoparticles were imaged by transmission electron microscopy using a Tecnai G² F30 at 300kV (FEI Corporation; Hillsboro, Oregon, USA). Size distributions were determined from the TEM images using ImageJ (public domain software from the National Institutes of Health; Bethesda, MD, USA). Briefly, the Feret diameter (defined as the maximum calliper diameter) was measured from a sample of approximately 2500 particles selected from multiple TEM images. Particles in contact with the edge of an image were automatically excluded, and overlapping particles were manually excluded from size analyses.

2.5 DLS and Zeta Potential

While image analysis of the TEM micrographs gives the diameter of the magnetite cores determined on a statistically small sample, dynamic light scattering (DLS) probes the diffusive motion of the particles to determine the distribution of hydrodynamic diameters of a larger ensemble. The stock nanoparticle suspensions were diluted with de-ionized water to a volume of 2 mL with a concentration of 0.01 mg[Fe₃O₄]/mL to eliminate concentration-dependent effects. A Zeta Nanosizer (Malvern Instruments; Malvern, Worcestershire, UK), with fixed scattering angle at 173°, was used to determine the size distributions. The CONTIN algorithm was employed to analyse the autocorrelation function of the scattered light, and the sizes of the scattering objects were calculated by assuming equivalent spherical particles. Note that the hydrodynamic diameter is defined to be the diameter of a smooth sphere with the same diffusion coefficient in the same viscous environment as the particles being measured and is therefore sensitive to the overall size of the nanoparticles (including the non-magnetic coating). The same apparatus was employed to measure the electrophoretic mobility of the particles diluted to a concentration of 0.01 mg[Fe₃O₄]/mL (volume = 3 mL) in a 0.1 mM NaCl solution. The zeta potentials were then estimated using the Smoluchowski equation (Smoluchowski 1918).

2.6 Nanoparticle-antibody conjugation

Nanoparticles were conjugated by the following method, suggested by the manufacturer (Wang 2007). Ten mg of nanoparticles were aliquotted into 15 ml conical tubes (Greiner Bio-One; San Diego, CA, USA) and brought to a total volume of 10 ml with double distilled water. N-hydroxysulfosuccinimide (Sulfo-NHS) (Pierce; Rockford, IL, USA) and 1-ethyl-3-[3-dimethylaminopropyl] carbodiimide hydrochloride (EDC) (Pierce) were prepared fresh at a concentration of 25 mg/ml each in separate tubes with double distilled water. One hundred microliters of the EDC and Sulfo-NHS were each added to the nanoparticles and incubated at room temperature on a LabQuake shaker (LabIndustries, Inc.; Berkeley, CA, USA) for 20 minutes. Nanoparticles were brought to pH 8.0 with 50 mM NaHCO₃ (Sigma-Aldrich; St. Louis, MO, USA), 50 μg of antibody was added, and the mixture was incubated at room temperature on a LabQuake shaker for 2 hours. Antibodies used were CD3 (Biosource; Camarillo, CA, USA), Her-2/neu (Bender MedSystems; Burlingame, CA, USA) and CD34 (BD Biosciences; San Jose, CA, USA). The antibody-nanoparticle mixture was centrifuged at 12,000 RCF for 45 minutes at 4°C. The supernatant was removed and 10 ml of double distilled water was used to resuspend the pelletted NPs. The centrifugation parameters were repeated once more and the supernatant was removed. The remaining pellet was resuspended in of 800 μl double distilled water to which 200 μl PBS (Gibco-BRL; Rockville, MD, USA) with 0.5% fetal bovine serum (FBS) (HyClone; Logan, UT, USA) was added. Conjugated nanoparticles were stored at 4°C for up to 2 days.

2.7 Incubation of cells with nanoparticles

Jurkat cells were harvested and washed using sterile PBS (Gibco-BRL). Trypsinized Jurkat cells were treated with 3 ml Trypsin/EDTA (Gibco-BRL) at 37°C for 5 minutes. After tyrpsinisation, cells were washed with sterile PBS. Harvested cells were counted using 0.4% Trypan Blue Solution (Sigma; St. Louis, MO, USA) and a hemocytometer (Hausser Scientific; Horsham, PA, USA). Each sample contained 1×10⁷ cells suspended in 200 μl of cold PBS/0.5% FBS solution to which 0.8mg of CD3-coupled Ocean nanoparticles were added. Cells and CD3-nanoparticles were incubated on ice with SQUID measurements taken at 1, 15, 30 and 60 minutes. For light microscopy, glass slide preparations were prepared using a Cyto-centrifuge (Shandon; Pittsburgh, PA, USA) and stained with Prussian blue by TriCore Reference Laboratories (Albuquerque, NM, USA).

3. Results and Discussion

3.1 Characterization by TEM, Relaxometry, and Susceptometry

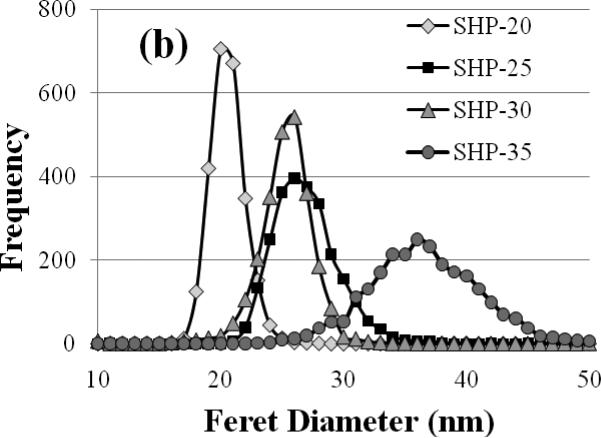
Figure 1(a) shows TEM images of each SHP sample. The SHP-20 particles show the most uniform intensity in TEM, whereas the number of particles exhibiting dark and light banding becomes increasingly prevalent in the SHP-25, -30, and -35 particles. The particle size distributions are shown in Figure 1(b). The average particle diameter determined for each set of particles is in good agreement with the nominal diameters specified by the manufacturer (see Table 1). The narrowest size distribution is obtained for the SHP-20 particles, and the standard deviation in particle diameter is observed to increase with average diameter.

Figure 1.

(a) Transmission electron microscopy of Ocean nanoparticles with nominal diameters of 20, 25, 30, and 35 nm. The SHP-20 particles show a generally uniform intensity in TEM. In the images of the larger particles, an increasing number of particles exhibit intensity variations (light and dark bands), which we attribute to polycrystallinity. (b) Particle size distributions determined by user-guided image analysis of 2500 particles from each sample.

Table 1.

Physical and electrical properties

Sample	Nominal Diameter (nm)	TEM Average Feret Diameter ± Standard Deviation (nm)	DLS Average Diameter (Peak Diameter) (nm)	Electrophoretic Mobility (micron-cm/V-s)	Zeta Potential (mV)
SHP-20	20	20.1 ± 1.5	71 (71)	−3.08	−43.6
SHP-25	25	26.4 ± 2.8	106 (143)	−3.52	−49.7
SHP-30	30	24.7 ± 2.7	73 (84)	−3.78	−53.4
SHP-35	35	36.1 ± 4.9	74 (61)	−3.55	−50.3

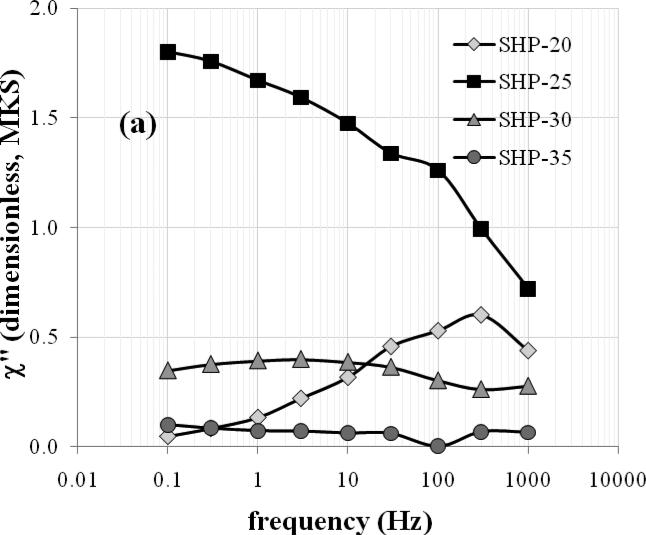
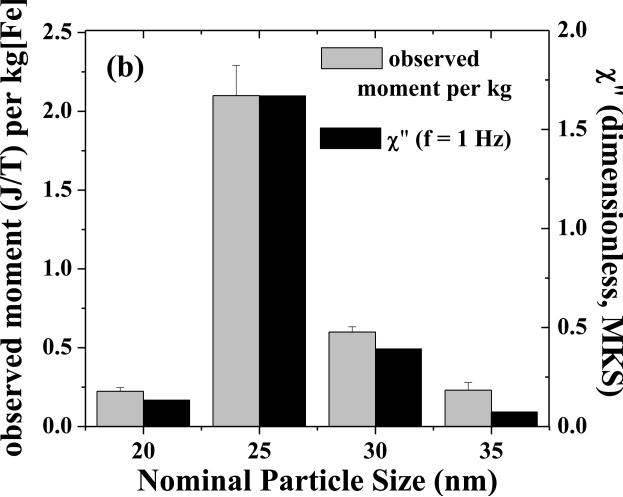
Figure 2(a) shows the imaginary component of the AC susceptibility at room temperature as a function of frequency. While the SHP-20 particles show a clear peak at ~300 Hz and the SHP-25 sample appears to be peaking at or below ~0.1 Hz, there is only a weak maximum in the AC loss for the SHP-30 sample, and no peak is evident for the SHP-35 sample. The measurement timescale of the SQUID-relaxometry technique (50 ms - 2 s) corresponds to frequencies of approximately 0.1-3 Hz. Indeed, the amplitude of χ” at 1.0 Hz correlates well with the magnetic moment/kg detected by SQUID relaxometry at room temperature (using a 0.3 s, 3.8 mT pulse) as shown in Figure 2(b), demonstrating that AC susceptibility measurements may be used to predict the SQUID relaxometry response.

Figure 2.

(a) The amplitude of the out-of-phase component of the AC susceptibility (χ”) vs. frequency for the SHP particles at room temperature. (b) The room-temperature moment/kg observed by SQUID relaxometry (gray bars) correlates well with χ” at 1.0 Hz (black bars).

By assuming that τ = (2πf)⁻¹ at the frequency of maximum loss and τ₀ = 10⁻¹⁰ s, one can use Equation 1 to estimate K for each set of particles, based on the measured particle sizes. By this method, K is found to be 1.5 × 10⁴, 1.0 × 10⁴, and 1.0 × 10⁴ J/m³ for the SHP-20, -25 and -30 particles, respectively. One can similarly estimate K by assuming that τ = 100 s at the blocking temperature of each sample (see Table 2). By this method, K is estimated to be 2.3 × 10⁴, 1.3 × 10⁴, 1.4 × 10⁴ and 0.58 × 10⁴ J/m³ for the SHP-20, -25, -30, and -35 particles, respectively, in reasonable agreement with the estimates based on the AC loss.

Table 2.

Magnetic properties

Sample	Blocking Temperature (K)	Frequency of maximum AC loss (Hz)	Observed Moment/kga (J/T/ kg[Fe3O4])	Saturation Magnetizationb (J/T/kg[Fe3O4])
SHP-20	255	300	0.31	67.3
SHP-25	329	0.1	2.90	85.0
SHP-30	290	3.0	0.83	51.1
SHP-35	374	--	0.32	67.9

^ameasured by SQUID relaxometry using a 3.8 mT, 0.30 s magnetizing pulse

^bmeasured by DC susceptometry

Notably, the SHP-25 particles give rise to the largest detectable moment/kg, roughly 4 times greater than the moment/kg of the SHP-30 particles, and nearly an order of magnitude greater than the moment/kg of multi-core particles we have characterized previously (Adolphi et al 2009). Therefore, we have achieved a significant improvement in detection sensitivity by switching from multi-core particles to single-core particles of relatively uniform diameter.

However, the improvement is not as great as anticipated based on the narrow size distributions of the SHP particles. Given that a relaxometry signal is detected from all four sets of particles, an examination of the size distributions in Figure 1(b) suggests that the optimal particle diameter for room temperature detection is roughly 26 nm, the diameter at which all of the distributions overlap, which implies that K = 1 × 10⁴ J/m³, in good agreement with the values estimated based on the frequency of maximum AC loss. If this is the ideal diameter, then according to Equation 1, particles in the 26 ± 1 nm size range should have the appropriate relaxation time to contribute to the detected moment/kg, assuming uniform K. In that case, we can estimate from the size distributions in Figure 1(b) that the detected moment/kg should be approximately 30 J/T/kg for the SHP-25 particles and 40 J/T/kg for the SHP-30 particles. These estimates further assume that all particles exhibit the bulk value of M_s (4.7 × 10⁵ J/T/m³), are non-interacting, and are magnetized according to the classical Langevin function with B = 3.8 mT and T = 300 K. However, the observed moments/kg (Table 2) are an order of magnitude lower than these estimates, which demonstrates that particle diameter is not the only significant factor determining the detectable moment/kg. In particular, the fact that the observed moment/kg from the SHP-25 particles is ~4 times greater than that of the SHP-30 particles, although the diameters are nearly the same, clearly indicates that other nanoparticle properties must be considered.

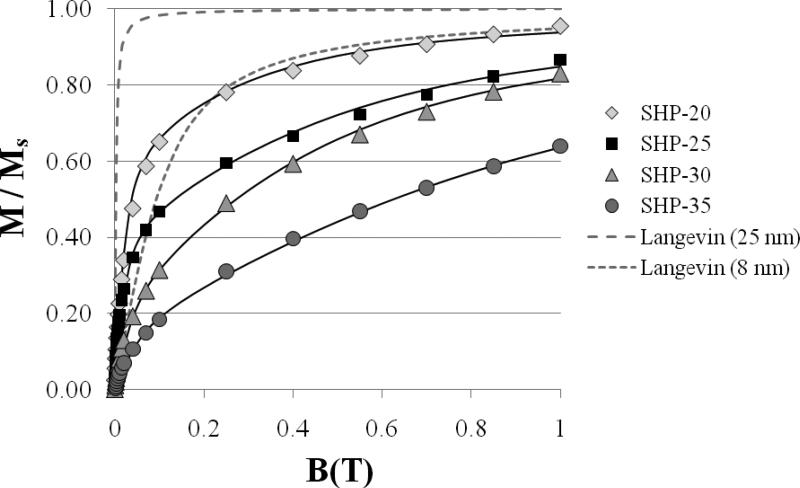
In order to determine why the observed moment/kg is not as large as predicted based on the size distributions, further investigations of the nanoparticle magnetic properties were undertaken. Figure 3 shows magnetization curves measured by DC susceptometry near the blocking temperature (see Table 2) of each sample. The data is plotted as M/M_s (dimensionless) vs. B to compare the shapes of the curves. For all samples, the magnetization does not rise nearly as sharply with field as expected for magnetite particles with diameters in the 20-40 nm range. The theoretical curves for 25 nm and 8 nm diameter particles, calculated using the Langevin function, are plotted in Figure 3 (dashed and dotted lines, respectively) for comparison. For the theoretical curves, we assumed the bulk value of M_s and T = 335 K. The observed slopes of M/M_s vs. B at small B are therefore much smaller than expected, consistent with non-interacting particles in the 7-10 nm diameter range. Before the relaxation of the nanoparticles can be detected by relaxometry, the particles must first be magnetized for a brief period in a ~mT field. The lower than expected magnetization for a given applied field strength in Figure 3 is clearly one reason that the observed SQUID relaxometry signals are smaller than the theoretical prediction. Furthermore, the classical Langevin formalism predicts that the slope of M/M_s vs. B at small B should decrease with decreasing particle diameter; however, this set of samples shows the opposite trend, with the highest slope obtained from the smallest (SHP-20) particles.

Figure 3.

Normalized magnetization vs. field obtained by DC susceptometry (symbols) compared to the Langevin function computed for ideal 25 nm (dashed line) and 8 nm (dotted line) particles. The fits to the data (solid lines) are described in the text.

The magnetization curves in Figure 3 cannot be adequately fit using the Langevin function, if a single value of μ is assumed. Satisfactory fits of the data (solid lines in Figure 3) were obtained using the sum of two Langevin functions corresponding to two distinct μ values. While this simple fitting method is adequate for estimating the saturation magnetization, we ascribe no physical significance to the choice of two distinct μ values. The saturation magnetization values so-obtained (summarized in Table 2) fall between 55 and 92% of the bulk value (92 J/T/kg) for magnetite. We note that the lower saturation magnetization of the SHP-30 sample, relative to the SHP-25 sample, partially explains the lower observed moment/kg.

Dipolar interactions, which have not been considered in our theoretical treatment, are a likely explanation for the lower than expected susceptibilities. Chantrell et al. (2000) and Garcia-Otero et al. (2000) have demonstrated, using Monte Carlo techniques, that the susceptibility is reduced in the case of significant dipolar interactions, due to the formation of flux closure loops (Chantrell 2000), which reduce the magnetization at low field strengths. While the nanoparticles immobilized on cotton swabs are thought to be reasonably well-dispersed (the fibers are roughly the same size as cells), the distribution of interparticle spacings in these samples is not known. The minimum edge-to-edge distance observed by TEM is approximately 3 nm, which implies that the maximum dipolar interaction strength (μ₀//4π)μ²/d³ (where d is the interparticle spacing) for two neighboring particles would be significant compared to other relevant energy scales. For the SHP-25 particles at the minimum d, (μ₀/4π)μ²/d³ is approximately 10⁻¹⁹ J, the same order of magnitude as KV, and more than an order of magnitude greater than k_BT (4 × 10⁻²¹ J). The maximum dipolar interaction strength is also greater than the Zeeman energy during the magnetizing pulse (μB = 2 × 10⁻²⁰ J).

In addition to interparticle dipolar interactions, intraparticle dipolar interactions (coupling of individual crystallites within polycrystalline particles) may also be a factor. Examination of the SHP-30 particles by high resolution TEM shows evidence of polycrystallinity, which would also explain the nonuniform TEM intensities of some particles observed in Figure 1(a). Strong scattering of the electron beam occurs if the beam is incident at a Bragg angle of the crystallite lattice, which only occurs for a subset of crystallites within a polycrystalline particle. A representative image showing a particle with multiple crystallite orientations is shown in Figure 4. It is possible that the observed decrease in the slope of M/M_s vs. B (Figure 3) with increasing particle size is the consequence of increasing polycrystallinity (and therefore increasing intraparticle interactions, resulting in flux closure) with increasing particle diameter.

Fig. 4.

A high-resolution TEM image of the SHP-30 particles shows that some particles are polycrystalline.

Perhaps more important, it has been shown theoretically and experimentally that dipolar interactions alter the Néel relaxation time distribution (Dormann et al 1988, Morup and Tronc 1994, Zhang et al 1996, Jonsson et al 1997, Chamberlin et al 2002). In the high temperature limit, i.e. when (μ₀/4π)μ²/d³ > k_BT, dipolar interactions increase the relaxation times, and the distribution of relaxation times broadens significantly. Essentially, Equation 1 does not hold in the presence of dipolar interactions that are significant compared to KV and k_BT. A shifted and broadened relaxation time distribution would alter the fraction of nanoparticles with relaxation times in the 50 ms - 2 s window. In addition to dipolar broadening of the relaxation times associated with a given particle size, polydispersity of the effective anisotropy energy density K will also broaden the relaxation time distribution and alter the magnitude of the relaxometry signal. The TEM images in Fig. 1 and Fig. 4 show that many particles, while not strongly faceted, are also not spherical, and the variations in shape will lead to polydispersity in K.

3.2 Moment Superposition Model Analysis

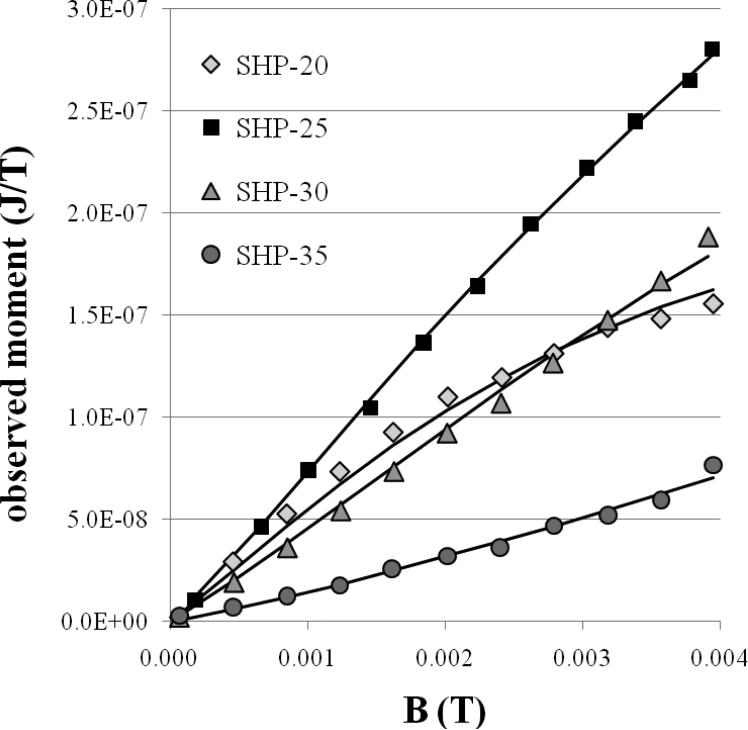
Figure 5 shows M vs. B curves obtained by SQUID relaxometry using a 0.3 s duration pulse at room temperature. Three of the curves are nearly straight lines, indicating that much higher values of the pulsed field (not available using our current hardware) would be required to determine the saturation magnetization of the relaxometry-detected particles. Only the SHP-20 magnetization curve shows the expected shape, consistent with the Langevin function. The SHP-35 magnetization curve exhibits positive curvature, which is inconsistent with the shape of the Langevin function. In general, the Langevin function (computed for a single average value of μ) is not an adequate model for determining the magnetic moment, and therefore the particle size, that gives rise to the relaxometry signal.

Figure 5.

Moment vs. applied field data (symbols) obtained by relaxometry. The solid lines were computed using the Moment Superposition Model, as described in the text.

The moment superposition model (MSM) (Chantrell et al 1983) was developed to treat the case of a distribution of non-interacting, superparamagnetic particles and has been used by other workers to interpret relaxation curves (M vs. t) acquired by magnetorelaxometry (Eberbeck et al 2003,2006; Romanus et al 2004; Enpuku et al 2007; Ludwig et al 2007, 2008). For example, Eberbeck et al (2003) and Ludwig et al (2007) have employed this method to obtain the average K and the distribution of magnetic moments giving rise to the magnetorelaxometry signal. Here we adopt a somewhat different approach by treating the moment distributions as fixed parameters in order to determine how well the non-interacting MSM model describes the magnetization curves (amplitude and shape) obtained by relaxometry.

Similar to Chantrell et al (1983), we model the magnetization observed by relaxometry in terms of a distribution f(μ) of N dipole moments:

$$M=N{\int }_0^{\infty }f\left(\mu \right)L\left(\frac{\mu B}{kT}\right)\left(1-e^{(-tpulse∕\tau (\mu ,B))}\right)e^{(-t∕\tau (\mu ,0))}\mu d\mu ,$$ (4)

where L is the Langevin function, tpulse is the duration of the magnetizing pulse, t is the time after the end of the magnetizing pulse, and the Néel relaxation time τ is taken to be

$$\tau (\mu ,B)={\tau }_{0}exp\left[\left(\frac{\mu B_K}{2kT}\right){\left(1-\frac{B}{B_K}\right)}^a\right],$$ (5)

where B_K is the anisotropy field, with B_K = 2K/M_s.

The measured nanoparticle size distributions (Figure 1(b)) were converted to magnetic moment distributions by multiplying the particle volumes by the volume saturation magnetization, which was calculated using the measured mass saturation magnetization (Table 2) for each sample multiplied by the density of bulk magnetite (5240 kg/m³). We fit each distribution of dipole moments assuming a log-normal form:

$$f\left(\mu \right)={\left(\mu \sigma \sqrt{2\pi }\right)}^{-1}\exp \left[\frac{{(\ln ,\mu -m)}^2}{2{\sigma }^2}\right].$$ (6)

The values of μ and σ so-obtained were then used as fixed parameters in the MSM modelling. The calculated curves in Figure 5 (dashed lines) were obtained from Eqs. 4 and 5 by setting the pre-factor (τ₀) in Equation 5 to 10⁻¹⁰s (Aharoni 2007). The only parameters that were adjusted were N, the total number of nanoparticles, K (the average effective anisotropy energy density) and a (the exponent on the field dependence in Equation 5). The exponent a is customarily taken to be 2. Wenger and Mydosh (1984) have shown that a = 2 is obtained in the limit μB << KV; however, a = 2/3 is obtained for μB > KV. In the case considered here (B = 3.8 mT), μB and KV are similar in magnitude, and a has been allowed to vary.

The calculated curves in Figure 5 (dashed lines) were all obtained with K = 9175 J/m³ and a = 0.9, which reproduced the shape of all four measured curves reasonably well. Using Equation 1, this value of K implies that the ideal particle has a diameter of 27.1 nm (resulting in a relaxation time of 1 s at 300 K), in reasonable agreement with the crude estimate of 26 nm, based on the overlap of the size distributions in Figure 1(b). The value of a resulting in the best overall fit is intermediate between 2 and 2/3, consistent with the limits described by Wenger and Mydosh (1984).

Although the shapes of the magnetization curves in Figure 5 can be explained by taking into account the shape of the distribution of moments from each sample, and a reasonable average value of K is obtained, the non-interacting MSM analysis substantially fails to account for the magnitude of the relaxometry signal. The fitted values of N (the total number of nanoparticles in each sample) obtained using the MSM model disagree significantly with the actual number of nanoparticles in each sample (calculated from the total mass of each sample and the TEM size distribution) as shown in Table 3. Effectively, the SHP-25 and -30 particles give rise to a smaller moment than predicted by the MSM, while the SHP-20 and SHP-35 particles give rise to a larger moment than predicted by the MSM. The discrepancies are consistent with significant broadening of the relaxation time distribution (due to dipolar interactions and/or polydispersity in K) associated with a given particle size. If one calculates the distribution of relaxation times based on size polydispersity alone (assuming uniform K) as we do here, the theoretical number of particles whose relaxation times overlap the measurement timescale may either be larger or smaller than the actual number of particles exhibiting relaxation times in that range. If the measurement time scale overlaps the center of the narrow theoretical distribution (as it does for the SHP-25 and SHP-30 particles), then the actual (broadened) distribution will have fewer particles in the desired relaxation time range, resulting in an observed signal smaller than the theoretical prediction. If the measurement time scale overlaps the tail of the narrower theoretical distribution, the actual, broader distribution will have a greater number of detectable particles, as we observe for the SHP-20 and SHP-35 particles. While the MSM model is certainly useful for characterizing the distribution of relaxation times exhibited by the nanoparticle ensemble (at least for those particles whose relaxation times fall within the measurement window), these results indicate that a one-to-one correspondence between relaxation time and any other individual particle property (e.g., diameter) cannot be assumed.

Table 3.

Number of nanoparticles

Sample	Mass (kg[Fe3O4])	Nexpa	Ntheorb	Ntheor/Nexp
SHP-20	4.2 x 10−7	1.8 x 1013	4.0 x 1014	23
SHP-25	1.3 x 10−7	2.4 x 1012	3.3 x 1011	0.14
SHP-30	3.5 x 10−7	7.5 x 1012	5.3 x 1011	0.07
SHP-35	1.8 x 10−7	1.3 x 1012	4.2 x 1012	3.3

^anumber of nanoparticles based on sample mass and TEM size distribution

^bnumber of nanoparticles determined from non-interacting MSM fit

For the data shown in Figure 5, adding both dipolar interactions and polydispersity in K as unknowns in the MSM model would result in an excessive number of free parameters. However, an analysis of the distribution of effective K values should be possible in the case of an ensemble of nanoparticles engineered to exhibit negligible dipolar interactions. The strength of the dipolar interaction between neighbouring particles may be reduced significantly using a thick, non-magnetic surface coating to ensure a sufficiently large minimum separation, regardless of the method used to immobilize the nanoparticle sample. For example, two neighbouring SHP-25 particles, assuming a non-magnetic coating 2 nm thick, experience a maximum dipolar interaction (μ₀/4π)μ²/d³ of the same order of magnitude as KV (~10⁻¹⁹ J). Increasing the non-magnetic coating thickness to 20 nm would ensure that the dipolar interaction strength is an order of magnitude smaller than KV. Further increasing the coating to 50 nm would reduce the maximum dipolar interaction strength by another order of magnitude, such that (μ₀/4π)μ²/d³ << k_BT also holds. Provided that the total mass, the saturation magnetization, and the particle size distribution are measured and treated as fixed parameters in the model, the center and width of the distribution of effective K values could then be determined, which would shed some light on the importance of polydispersity in K in determining the relaxation time distribution. Such a study will be valuable for guiding the synthetic process, by more firmly establishing the relative importance of the various nanoparticle design parameters (size, shape, coating thickness) in achieving optimum detection sensitivity and what the target values of these parameters should be.

3.3 Antibody Conjugation, Colloidal Stability, and Observable Moment per Cell

Due to their superior observed moment/kg, we attempted to conjugate the SHP-25 particles to Her2/neu antibodies using the protocol recommended by the manufacturer. However, several attempts at conjugation each resulted in the precipitation of very large nanoparticle aggregates, such that the SQUID relaxometry signal from the aggregated particles was indistinguishable from the signal obtained from immobilized particles. We note that the SQUID relaxometry technique is theoretically insensitive to unbound nanoparticles in solution due to their rapid Brownian relaxation; however, if the hydrodynamic diameter of nanoparticle aggregates is sufficiently large, the Brownian relaxation time (Equation 3) of the aggregated particles may fall within the 50 ms – 2 s time scale of the SQUID relaxometry measurement, in which case a signal is detected (although the particles are not bound to cells). For even larger aggregates, the Brownian time constant may exceed 2 s, in which case, the observed relaxation will be dominated by the Néel process (see Equation 2), and the detected signal will be difficult to distinguish from that of cell-bound nanoparticles. Thus aggregation must be avoided in order to retain an important advantage of the SQUID relaxometry technique, namely its specificity for detecting cell-bound particles. Fortunately, conjugation of the SHP-30 particles to a variety of monoclonal antibodies (against Her2/neu, CD34, and CD3) resulted in colloidally-stable nanoparticle solutions, which did not give rise to significant SQUID relaxometry signals. Therefore, the SHP-30 nanoparticles were used in the cell experiments described below.

In order to determine the cause of the stability difference between the SHP-25 and SHP-30 particles upon conjugation, further characterizations of the stock (as-received) SHP nanoparticle solutions were performed. Dynamic light scattering (DLS) was performed to determine the hydrodynamic size distributions of the four samples. Given that the minimum edge-to-edge distance observed between cores (see Figure 1(a)) is consistent with a coating thickness of ~2 nm, the >70 nm hydrodynamic diameters suggest that there was mild aggregation of all of the SHP particles prior to conjugation, although the aggregate size was small enough not to result in a detectable SQUID relaxometry signal from the stock solutions. This mild aggregation is the greatest for the SHP-25 particles, which showed an average hydrodynamic diameter of 106 nm. Because the conjugation chemistry involves pH changes, differences in the zeta potential of the SHP-25 and SHP-30 nanoparticles could explain the different stabilities in the presence of conjugation reagents. However, only small differences in the zeta potential and electrophoretic mobility of the SHP-25 and SHP-30 nanoparticles were observed (see Table 1). For comparison, we also measured the DLS diameter, zeta potential, and electrophoretic mobility of some multi-core nanoparticles (SiMAG particles, nominal 100 nm diameter) which showed varying degrees of stability after conjugation. Nanoparticles from SiMAG lot 0808/07 were reliably conjugated to CD34 antibodies using the same conjugation protocol described here and were then used in a number of leukaemia cell experiments (Jaetao 2009, Adolphi 2009). Although the SiMAG 0808/07 particles (as-received) had a less negative zeta potential (−20.7 mV) compared to any of the Ocean SHP particles, they showed little aggregation by DLS prior to conjugation (129 nm average hydrodynamic diameter), and very minimal aggregation (by SQUID relaxometry) after conjugation. SiMAG lots 1903/08 and 1803/08 showed increasing levels of aggregation by DLS (431 nm and 1760 nm average hydrodynamic diameters, respectively) that correlated with increasingly less negative zeta potentials (−18.8 mV and −8.5 mV, respectively) and an increasing tendency to aggregate further after conjugation. Thus, in the case of the SiMAG particles, differences in aggregation appear to be adequately explained by differences in the zeta potential. However, the zeta potential of the SHP-25 particles, which is quite negative and not very different from that of the SHP-30 particles, does not explain why the SHP-25 particles show severe aggregation upon conjugation.

Instead, we suggest that significant differences in the magnetic properties of the SHP-25 and SHP-30 particles are the underlying cause of the aggregation differences. Previously Martin et al. (2008) have shown that nanoparticles may undergo clustering due to interparticle dipolar interactions, even in the absence of an applied magnetic field. Although the SHP-25 and SHP-30 particles are similar in volume, the saturation magnetization of the SHP-25 particles is ~1.7 times that of the SHP-30 particles, such that the dipolar interactions are roughly ~3 times stronger. We therefore suggest that electrostatic repulsive forces between the SHP-25 particles are great enough to maintain colloidal stability in the as-received solution. However, when the pH is raised just prior to adding antibody, screening of the surface charge on the nanoparticles reduces the electrostatic repulsion and allows the attractive interparticle dipolar interactions to dominate, resulting in spontaneous aggregation. This suggests that increasing the thickness of the non-magnetic coating may be necessary to ensure that particles with large magnetic moments, which are desirable from the magnetic standpoint, can be conjugated to targeting ligands without inducing aggregation.

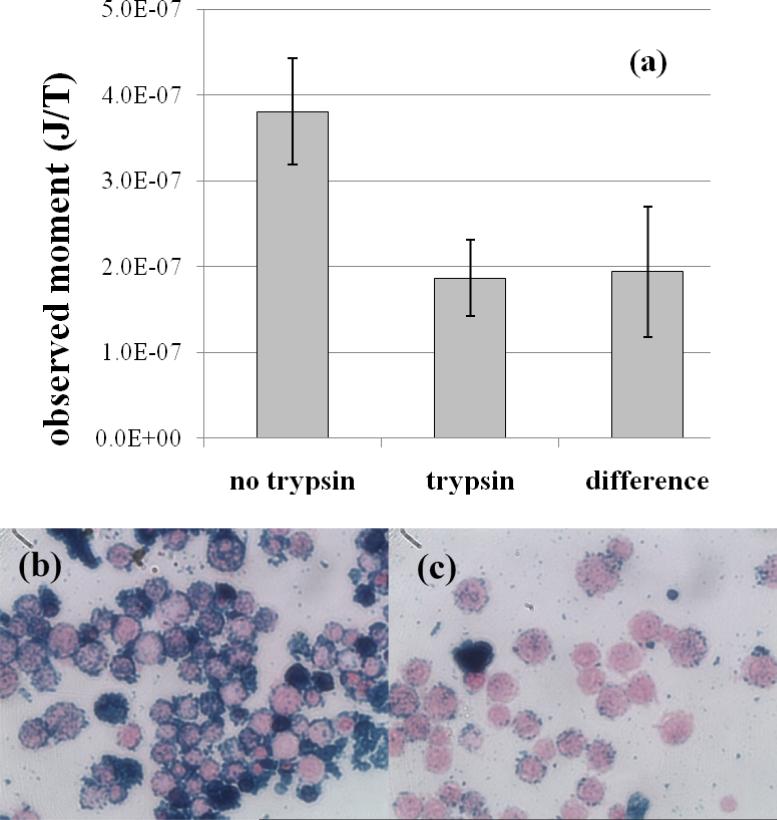
To determine the observable magnetic moment per cell, SHP-30 nanoparticles were conjugated to a monoclonal antibody that targets the CD3 cell-surface antigen, expressed on T-cells, which mediate acute transplant rejection (Cornell et al 2008). The CD3-conjugated nanoparticles were then incubated with 10 million Jurkat cells, which express high levels of the CD3 antigen on the cell surface. To assess the binding specificity, the same CD3-conjugated nanoparticles were also incubated with 10 million Jurkat cells pre-treated with trypsin, an enzyme that hydrolyses proteins, resulting in the digestion of cell surface antigens. Figure 6(a) shows the SQUID relaxometry signal obtained after a 60 minute incubation of the untreated and trypsinized Jurkat cells with the CD3-nanoparticles. The observed moments are the average of three experiments, and the error bars represent the standard error of the mean. The SQUID signal is significantly higher for cells that retain the CD3 antigen, as expected, but there is still a significant relaxometry signal with a Néel (i.e., logarithmic) character observed after incubation with the trypsinized cells. Photomicrographs (Figure 6(b)) suggest that some binding to the surface of the trypsinized cells did occur. However, nanoparticle aggregates, some of which are cell-sized, are visible in both the untreated and trypsinized cell experiments, and these aggregates appear to be responsible for a significant fraction of the signal observed from the trypsinized cells. We note that a cell (~10 micron diameter) is more than 100 times larger than a single antibody-conjugated nanoparticle (~70 nm diameter). Thus single nanoparticles are not visible in the photomicrographs, and visible aggregates can be assumed to be of order 500 nm or larger, large enough to give rise to detectable relaxometry signals (see Equation 2).

Figure 6.

(a) Observed magnetic moment from Ocean-SHP 30 nanoparticles, conjugated to CD3 antibody and incubated for 60 min. with normal Jurkat cells (no trypsin) and Jurkat cells treated with trypsin to remove cell surface antigens. Error bars represent the standard error of the mean (N=3). (b),(c) In photomicrographs of slides prepared after the 60 min. incubation, the Jurkat cells are stained pink, while the nanoparticles are stained blue. Untreated cells (b) express high levels of the CD3 receptor and show greater nanoparticle binding, while the trypsin-treated cells (c) are stripped of cell surface antigens and show significantly reduced binding. The observed SQUID relaxometry signal appears to be attributable to binding of nanoparticles to cells and some nanoparticle aggregation.

The number of nanoparticles that will theoretically bind to a single cell is limited by steric hindrance to roughly 150,000, assuming a single random-close-packed layer of antibody-conjugated particles (modelled as spheres of diameter 70 nm covering a 15 micron diameter cell). The observed signal due to CD3-specific binding (difference signal, Figure 6(a)) is 1.9 × 10⁵ pJ/T for 10⁷ cells. Given that the observable moment/kg is 0.83 J/T/kg[Fe₃O₄], this indicates specific binding of 23 pg of magnetite per cell, which is equivalent to 550,000 nanoparticles per cell. The number of specifically bound nanoparticles therefore exceeds both the steric limit for monolayer coverage and the number of CD3 receptors per cell (~100,000) determined by flow cytometry. The higher than expected number of nanoparticles per cell is certainly beneficial from a detection sensitivity standpoint, but is not yet understood. The additional binding may be the result of internalisation of the nanoparticles by the cells or the tendency of clusters of antigen-bound nanoparticles to attract additional nanoparticles to the cell surface. Another possible explanation is that the observable moment/kg for antibody-conjugated nanoparticles on cells is actually higher (because of reduced dipolar interactions due to the antibody coating) compared to the moment/kg measured on cotton swab samples. Further work will be required to identify the cause of both the apparently enhanced antigen-specific binding and the significant non-specific signal, particularly the development of biocompatible surface coatings that minimize both interparticle dipolar interactions and aggregation.