Interstitial fluid pressure correlates with intra-voxel incoherent motion imaging metrics in a mouse mammary carcinoma model

Abstract

Effective delivery of therapeutic drug to the core of a tumor is often impeded by physiological barriers, such as interstitial fluid pressure (IFP). There are a number of therapies to lower IFP and induce tumor vascular normalization. However, lack of a non-invasive means to measure IFP hinders utilization of such a window of opportunity for maximizing the treatment response. Thus, the purpose of this study was to investigate the feasibility of using intravoxel incoherent motion (IVIM) diffusion parameters as noninvasive imaging biomarkers for IFP. Mice bearing the 4T1 mammary carcinoma model were studied with diffusion weighted magnetic resonance imaging (DWI) immediately followed by wick-in-needle IFP measurement. Voxelwise analysis was conducted with a conventional monoexponential diffusion model as well as a biexponential model taking IVIM into account. There was no significant correlation of IFP with either median apparent diffusion coefficient from the monoexponential model (r = 0.11, p = 0.78) or median tissue diffusivity from the biexponential model (r = 0.30, p = 0.44). On the other hand, IFP was correlated with the median pseudo-diffusivity (D_p) of apparent vascular voxels (r = 0.76, p = 0.02) and with the median product of perfusion-fraction and pseudo-diffusivity (f_p·D_p) of apparent vascular voxels (r = 0.77, p = 0.02). Although the effect of IVIM in tumors has been reported previously, to our knowledge, this study represents the first direct comparison of IVIM metrics with IFP, with the results supporting the feasibility of using IVIM-DWI metrics as noninvasive biomarkers for tumor IFP.

INTRODUCTION

Effective delivery of therapeutic drugs to the core of tumors is often impeded by physiological barriers, such as interstitial fluid pressure (IFP). IFP can be elevated by abnormal (fast growing, leaky, sometimes dysfunctional) tumor blood vessels, high tumor cellularity, and lack of functional lymphatics (1). Boucher and Jain (2) reported that, in tumors, microvascular pressure (MVP) and IFP are in equilibrium due to increased vascular permeability, suggesting that the MVP is the driving force for elevated IFP. In addition, DiResta and colleagues (3) showed that tumor IFP can be lowered by placing artificial lymphatics in tumors, supporting the notion that lack of functional lymphatics contributes to increased IFP. With the IFP raised close to the MVP level, transport from vascular space to interstitial space may be reduced, thereby compromising delivery of therapeutic drugs. IFP, as a hallmark of vascular abnormality, is commonly measured with invasive methods, such as the wick-in-needle (WIN) method (4).

It has been suggested by Jain (5) that abnormal tumor vasculature can be “normalized” with anti-angiogenic therapy that prunes away immature and dysfunctional vessels. However when anti-angiogenic therapy is sustained for too long, it may eventually prune away most vessels and leads to another inadequate vascular condition for drug delivery. Thus, a “normalization” window can be created during anti-angiogenic therapy, during which the delivery of therapeutic drugs and oxygen is optimal (6,7). However, lack of non-invasive ways to detect such normalization windows hinders utilization of this crucial opportunity in clinical practice.

Previous studies have shown that elevated IFP leads to reduced tumor blood flow without physically occluding the vessels (8,9). Milosevic and colleagues found a negative association between IFP and capillary blood flow in a simulation study (10). Here we hypothesize that reduced capillary blood flow can be detected using diffusion weighted imaging (DWI) as a decreased pseudo-diffusion. The pseudo-diffusion effect of orientationally incoherent blood flow is commonly referred to as intravoxel incoherent motion (IVIM) (11). IVIM due to microcirculation can be separated from restricted Brownian self-diffusion using DWI data with multiple diffusion weightings, i.e. b-values (12). The IVIM-DWI technique has been applied in various cancer types, such as hepatic lesions (13), brain tumors (11), breast cancer (14), renal masses (15), pancreas carcinoma (16), general soft tissue tumors (17), and animal models (18,19). However, it has not been shown whether there is any association between IFP and IVIM metrics.

Hence, the purpose of this study was to investigate the feasibility of using IVIM diffusion parameters as noninvasive imaging biomarkers for IFP. The 4T1 mouse mammary carcinoma model was used for DWI experiments immediately followed by WIN IFP measurement, and the correlation between the IVIM diffusion parameters and IFP was evaluated.

MATERIALS AND METHODS

Animal model

Six- to eight-week-old female BALB/c mice were given a subcutaneous injection in the right flank (n = 17) with 1 × 10⁶ 4T1 mouse mammary tumor cells suspended in 0.1 ml of phosphate buffered saline (PBS) (total 20 tumors). The first three mice received additional tumor injection on the left flank as well in case there was no growth on one side; however, the left side tumors were not analyzed because the growth was successful on the right flank. All mice were scanned between post-injection days 10 and 13, inclusive, when the longest diameter of the tumor was approximately 10 mm. Five mice were given an intraperitoneal injection of 0.1 ml of 1mg/ml Avastin (Genentech, CA) approximately 24 hours prior to the scan, in order to ensure that some tumors with low IFP were included (20,21). WIN IFP measurement was performed with IVIM diffusion measurement only once for each animal. All mice were treated in strict accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and this study was approved by the Institutional Animal Care and Use Committee.

MRI data acquisition

MRI experiments were performed on a 7T micro-MRI system, consisting of a Biospec Avance II console (Bruker Biospin MRI, Ettlingen, Germany) interfaced to a 200-mm horizontal bore, superconducting magnet (Magnex Scientific, Yarnton, UK) with an actively shielded gradient coil (Bruker BGA-9S; 20-mm inner diameter, 750 mT/m gradient strength, 100 μs rise time). A quadrature Litz coil (Doty Scientific, Columbia, SC) was used to image the animal mounted on a cradle with respiratory and temperature monitoring probes. General anesthesia was induced by 1.5% isoflurane in air. The animal body temperature was maintained at 32 ± 2 °C during the scan. A T2-weighted rapid acquisition with relaxation enhancement (RARE) sequence was used to image the entire tumor (TR = 2s, TE = 35ms, FA=180°, image matrix = 256 × 256, field of view = 4.56 cm × 4.56 cm, slice thickness = 1.5 mm, 10 slices), and to select two slices near the tumor center. A pulsed gradient spin echo (PGSE) diffusion measurement (pulse duration δ = 7 ms, diffusion time Δ = 14 ms) was performed with a 16-shot echo planar imaging sequence (TR = 1.5 s, TE = 32 ms, image matrix = 128 × 128, field of view = 4.56 cm × 4.56 cm, slice thickness = 1.5 mm, 2 slices). The diffusion weighting gradient was varied from 0 to 22.6 G/cm, giving diffusion weighting factors of b = 0, 30, 60, 100, 150, 200, 300, 500, 750, and 1000 s/mm². MRI scans were followed by WIN IFP measurement.

IFP measurement using the wick-in-needle technique

Following MRI, IFP was measured using the WIN method (4). A 23-gauge needle with a 4 mm notch located 5 mm from the tip was filled with nylon sutures and connected to a fluid-filled pressure transducer and pressure monitoring system (Power Lab 8/30, AD Instruments, Inc, CO). The whole pressure measurement system was calibrated using a sphygmomanometer before starting each experiment. Pressure was recorded continuously, as the needle was inserted and stopped periodically (every 1 mm) for pressure stabilization. Two to three stops were made before the tip of the needle went through the other side of the tumor which was confirmed by a rapid decrease of IFP. The maximum pressure over a series of such tracks (2 – 3 per tumor) was used as a representative IFP value for the tumor.

Data analysis

Diffusion weighted MR signal decay is most commonly analyzed with the monoexponential model:

$$S_b/S_0=exp(-b·\text{ADC})$$ (1)

where S_b is the MRI signal intensity with diffusion weighting b, S₀ is the non-diffusion weighted signal, and ADC is the apparent diffusion coefficient. For this model, two parameters, S₀ and ADC, for each voxel are estimated using weighted multivariate linear regression (22). For a voxel with a large vascular fraction, the MRI data decay can deviate from a monoexponential form, in particular showing a fast decay in the range of low b-values generated by the IVIM effect (11). Thus, in addition to the monoexponential model, a biexponential model was used to estimate the IVIM-related parameters of pseudo-diffusivity (D_p), perfusion fraction (f_p), and tissue diffusivity (D_t). This IVIM biexponential model is defined by

$$S_b/S_0=f_p·exp\left(-b·D_p\right)+\left(1-f_p\right)·exp\left(-b·D_t\right).$$ (2)

Estimation of the four parameters in the biexponential model may often be ill-conditioned because of a limited number of samples, small perfusion fraction, and/or similar compartmental diffusivities, as found in other in vivo IVIM studies (23–27). Thus, we performed a “segmented” analysis procedure as follows. D_p is typically significantly greater than D_t (12); so when the b-value is significantly greater than ~1/D_p (e.g., for D_p ~ 10 μm²/ms, b > 100 s/mm²), the contribution of the pseudo-diffusion term to the signal decay becomes negligible. In this higher b-value regime, Eq.2 can then be simplified into a monoexponential equation whereby D_t and f_p can be estimated:

$$S_{\mathit{high}}/S_0=\left(1-f_p\right)exp\left(-{bD}_t\right).$$ (3)

Operationally, D_t is determined from such a monoexponential fit to data above a chosen threshold (b > 200 s/mm², in this study). With D_t determined by using Eq.3, D_p, f_p, and S₀ values can be estimated by using a nonlinear fit of Eq.2 to the entire dataset that minimizes the residual sum of squares (RSS):

$$\text{RSS}=\sum _{b=1}^N{\left(S_b-P_b\right)}^2.$$ (4)

where N is the number of b-values, S_b is the observed value, and P_b is the predicted value from the model. This analysis was performed for signals from individual voxels. In addition to the basic IVIM metrics, the product f_p·D_p - a quantity including both volume and velocity information - was considered as a parameter roughly analogous to flow as measured in perfusion imaging as suggested earlier by Le Bihan and Turner (28). The same type of RSS minimization was also used for the monoexponential fits with Eqs.1 and 3.

In order to avoid over-fitting the biexponential model (Eq.2) to voxels for which the monoexponential model is more appropriate, the performance of the two models in each voxel were compared with Bayesian Information Criterion (BIC) (29) defined as follows:

$$\text{BIC}=ln\left(\mathit{RSS}/N\right)+\left(\mathit{k}lnN\right)/N$$ (5)

with k degrees of freedom (28). If the BIC for a voxel based on the monoexponential fit (BIC_m) was smaller than that of biexponential fit (BIC_b), the voxel was classified as a apparent avascular voxel (AAV) and was considered to have negligible perfusion fraction. Likewise, voxels with BIC_b < BIC_m were classified as apparent vascular voxels (AVV). These terms are introduced in this report for the sake of clarity. In order to minimize the effect of noise in highly diffusion weighted images (b = 1000 s/mm²), voxelwise analysis was performed with data of b-values ≤ 750 s/mm².

Prior to the model fitting, diffusion weighted raw images were smoothed by convolving with a 2D Gaussian operator with matrix size of 5 × 5 and standard deviation of 0.5. Tumor boundary was identified by hyper-intense areas (i.e., solid tumor) in diffusion weighted images with b = 500 s/mm². Regions of interest (ROI) for tumor were manually drawn to include such hyper-intense voxels. Voxels with ADC less than 2.0 μm²/ms were excluded to avoid necrotic or cystic regions. Median diffusion parameters of tumor ROI were used as representative values for each tumor for the comparison with IFP. The association between diffusion parameters and IFP from WIN measurements was assessed for the tumors larger than 0.2 cm³ (approximately 10 mm in the longest length and 4 mm and 5 mm for width and height) found to be the minimum size for reliable WIN IFP measurement. This data analysis was performed using in-house software written in Matlab (The MathWorks, Inc. Natick, MA).

RESULTS

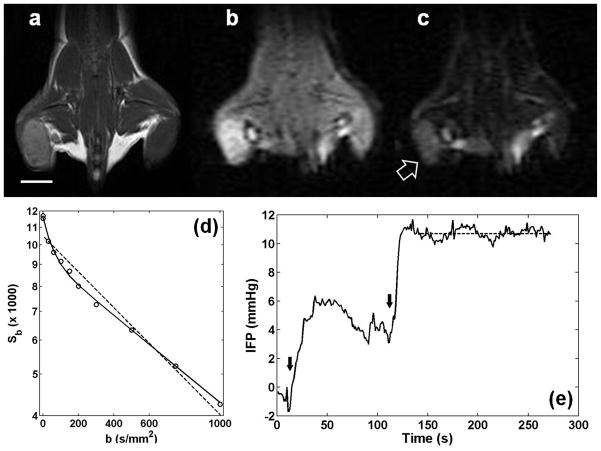
Figure 1a shows an example of a 4T1 tumor in the right flank of a mouse. Signal-to-noise ratios (SNR, defined as mean signal intensity divided by standard deviation of noise) of the tumor (arrow) were 38 and 14 for b = 0 (Fig. 1b) and b = 1000 s/mm² (Fig. 1c), respectively. Figure 1d shows diffusion weighted signals (circles) averaged over the entire tumor, demonstrating that the signal decay pattern substantially deviates from a monoexponential behavior (dashed line). A biexponential model (solid line) appears to be adequate to represent the data for all b-values used in this experiment. The BIC (9.7) of the biexponential fit is smaller than that of the monoexponential fit (13.0). Figure 1e shows an example IFP measurement trace from insertion of the WIN probe to a stable plateau region near the center of the tumor.

Figure 1.

Mouse mammary carcinoma, 4T1, in the flank of a BALB/cJ mouse. (a) T2-weighted image using RARE sequence. The white line is a scale bar for 5 mm. (b) Diffusion weighted image with b=0. (c) Diffusion weighted image with b=1000 s/mm². A block arrow indicates a solid tumor identifiable in a diffusion weighted image. (d) Diffusion weighted signals depending on b-values (S_b). Circles represent the average values from a region of interest covering the entire tumor in (a–c). Dashed and solid lines are the monoexponential and biexponential fits to all data points, respectively. This example shows that a mono-exponential model is not adequate to describe diffusion weighted signal decay in the selected tumor. (e) An example of interstitial fluid pressure measurement using the WIN system. As the needle was inserted into the tumor, the pressure rose slowly. The insertion was stopped at the tumor rim around t = 50 s. Then, it was inserted further to the center of the tumor. The dashed line indicates a plateau region over which the average tumor IFP of 10.7 mmHg was measured. Black arrows show when the needle was moved into the tumor.

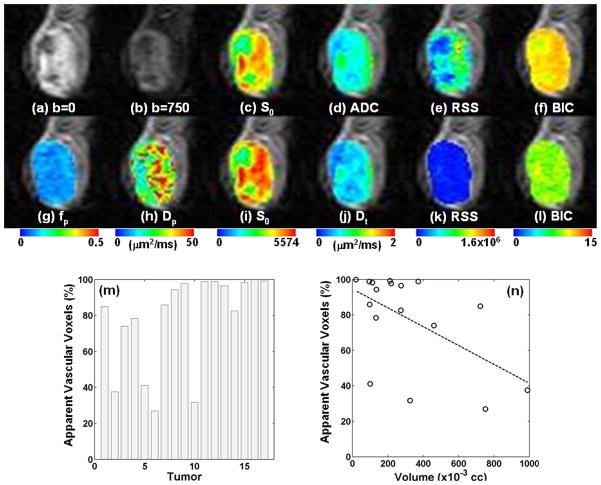
An example of voxelwise analysis is shown in Figure 2. The raw data without diffusion weighting (b = 0) and with diffusion weighting b = 750 s/mm², are shown in Figures 2a and 2b. The results of monoexponential and biexponential fits shown in Figure 2c–f and Figure 2g–i, respectively, demonstrate that the biexponential model provided a better fit to the data in most voxels than the monoexponential model. The median BIC of the monoexponential fit (11.2, IQR: 10.0 – 11.5) was significantly larger (p < 0.001) than that of the biexponential fit (9.3, IQR: 8.8 – 9.7). Similar observations were made with all tumors. Figure 2m shows that a substantial percentage of voxels (78 ± 26 %) had lower BIC’s from the biexponential than from monoexponential models. Figure 2n shows a scatter plot of the percentage of AVV and the tumor volume, which shows a modest association (r = 0.55, p = 0.02). From all tumors, median ADC value in each tumor ranged between 0.72 μm²/ms and 1.23 μm²/ms with its median at 0.96 μm²/ms. Median D_t, D_p, and f_p values from each tumor ROI had their median values of 0.79 μm²/ms (range: 0.62 – 1.12), 22.90 μm²/ms (range: 1.75 – 43.22), and 0.16 (range: 0 – 0.21), respectively.

Figure 2.

Representative diffusion weighted images with voxel-based analysis. The images were cropped to show only the tumor region (51 × 45 voxels, 18.4 mm × 16.2 mm). (a) Diffusion weighted image with b = 0. (b) Diffusion weighted image with b = 750 s/mm². (c–f) Results from mono-exponential analysis. (g–l) Results from bi-exponential analysis. The goodness of fit is shown in terms of RSS (e, k) and BIC (f, l). (m) Percent of AVV which have lower BIC for biexponential model fit than for monoexponential model fit. (n) Scatter plot of tumor volume and percentage of AVV. There was significant correlation between them (r = 0.55, p=0.02).

IFP correlates with D_p and f_p·D_p

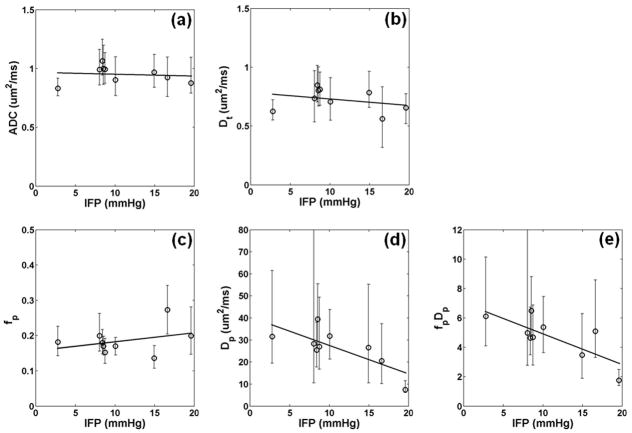
The association between DWI measures and IFP was evaluated for the 9 animals with tumor volumes >0.2 cm³. Figure 3 shows scatter plots of IFP and DWI measurements. Note that the displayed error bars represent 25^th and 75^th percentiles of the spatial distribution of values of all the voxels in the selected tumor, not the uncertainty in parameter estimation. There was only weak association between IFP with either median ADC (r = 0.11), median D_t (r = 0.30), or median f_p (r = 0.34) as shown in Figure 3a, 3b, and 3c, respectively. On the other hand, IFP correlated strongly (r = 0.76) with the median D_p of AVV. A similar strong correlation of r = 0.77 was found between IFP and the median of f_p·D_p of AVV. Table 1 shows correlation coefficients between IFP and DWI metrics measured from all voxels as well as AVV. Strong correlation with IFP were also found with median D_p (r = 0.70) or median f_p·D_p (r = 0.70) measured from all voxels. When the data was analyzed with all data points including b=1000 s/mm², a similarly strong and significant correlation was found between IFP and IVIM metrics: D_p (r = 0.84, p = 0.004) or f_p·D_p (r = 0.70, p = 0.03). Table 2 shows correlation coefficients between IFP and IVIM metrics depending on different ADC threshold values. While using the ADC threshold of 2.0 μm²/ms gave the highest correlation, strong correlations of higher than 0.72 were also found with different ADC threshold values between 1.5 and 3.0 μm²/ms.

Figure 3.

Correlation between diffusion metrics and IFP in tumors larger than 0.2 cc and for voxels with ADC less than 2.0 μm²/ms. (a) Median ADC of the tumor did not correlate with IFP(r = 0.11, p = 0.78). (b) Median D_t of the tumor did not correlate with IFP (r = 0.30, p = 0.44). (c) Median f_p of the AVV did not correlate with IFP (r = 0.34, p = 0.37). (d) Median D_p of the AVV correlated significantly with IFP (r = 0.76, p = 0.02). (e) Median f_p·D_p of the AVV also strongly correlated with IFP (r = 0.77, p = 0.02). The error bars represent 25^th and 75^th percentiles among all the selected voxels in each tumor. The thick solid lines are the linear regression fits to the data.

Table 1.

Pearson correlation coefficients (r) between DWI metrics and IFP.

	All voxels		AVV only
	r	p	r	p
ADC	0.06	0.87	0.11	0.78
Dt	0.18	0.64	0.30	0.44
fp	0.35	0.36	0.34	0.37
Dp	0.70*	0.04	0.76*	0.02
fp·Dp	0.70*	0.03	0.77*	0.02

^*represents significant (p < 0.05) correlation.

Table 2.

ADC threshold and Pearson correlation coefficients (r) between DWI metrics and IFP

ADC threshold (μm2/ms)	Pearson correlation coefficients (r) with IFP
	1.5	2.0	2.5	3.0
Dp (p value)	0.74 (0.023)	0.76 (0.017)	0.76 (0.018)	0.74 (0.021)
fp·Dp (p value)	0.77 (0.016)	0.77 (0.016)	0.76 (0.017)	0.72 (0.027)

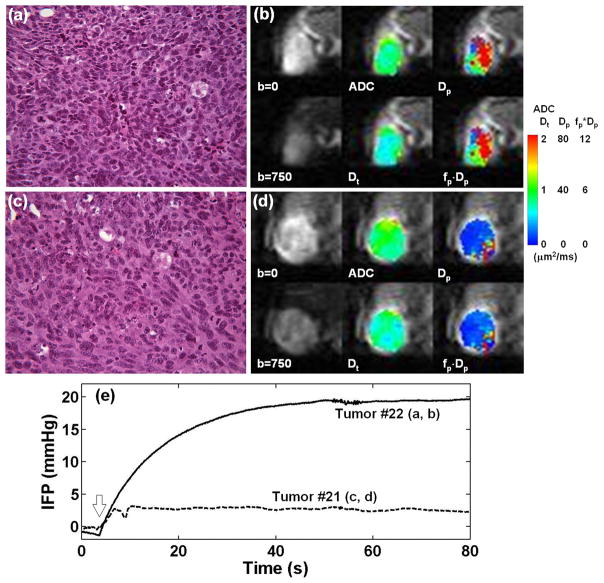
Figure 4 shows two representative cases with low (2.8 mmHg) and high (19.6 mmHg) IFP values. ADC (0.83 μm²/ms, IQR: 0.77 – 0.92) and D_t (0.63 μm²/ms, IQR: 0.55 – 0.73) of the tumor with low IFP (Fig. 4b) were lower (approximately 14% for ADC and 16% for D_t) than those of the tumor with high IFP (ADC = 0.95 μm²/ms, IQR: 0.81 – 1.12 and D_t = 0.73 μm²/ms, IQR: 0.60 – 0.87) (Fig. 4d). This difference in ADC and D_t appears to be in agreement with hematoxylin and eosin (H&E) stained sections from the tumor core, where the tumor with lower ADC and D_t (Fig. 4a) appears to have a higher cell density than the one with high ADC and D_t (Fig. 4c). Both H&E sections show no sign of significant necrosis. D_p (26.55 μm²/ms, IQR: 15.13 – 50.23) and f_p·D_p (5.23 μm²/ms, IQR: 3.46 – 8.65) of the tumor with low IFP (Fig. 4b) were substantially higher (approximately 323% for D_p and 315% for f_p·D_p) than those of the tumor with high IFP (D_p = 6.30 μm²/ms, IQR: 5.33 – 7.93 and f_p·D_p = 1.26 μm²/ms, IQR: 0.73 – 1.77) (Fig. 4d). The recorded IFP traces from these two tumors are shown in Fig. 4e. The two cases are also distinguished by different heterogeneity patterns, particularly illustrated in the D_p and f_p·D_p maps. Histology sections including the ones shown in Fig. 4 did not indicate any directionality that could give rise to diffusion anisotropy.

Figure 4.

Representative examples of tumors with low IFP of 2.8 mmHg (a, b) and high IFP of 19.6 mmHg (c, d). H&E stained sections (×40) from the central parts of these two tumors (a, c) show no sign of significant necrosis. This observation is in agreement with the ADC and D_t maps as well as diffusion weighted images shown in (b) and (d). However, these two tumors differ substantially in terms of D_p and f_p·D_p maps. (e) Interstitial fluid pressure measurement of the two tumors using the wick-in-needle system. The block arrow indicates when the needle was inserted to the tumor. Once the notch on the needle was inserted into the tumor (within a couple of seconds), the needle was hold at the same position until the pressure reading approached a stable value.

DISCUSSION

Correlation between IFP and IVIM metrics

Although the effect of IVIM on DWI experiments in tumors has been reported previously, this study, to our knowledge, represents the first direct comparison of IVIM metrics with IFP. We found IFP negatively correlates with the IVIM metrics, D_p and f_p·D_p, which reflect capillary blood flow and vascularity. Such an inverse relationship between IFP and blood flow is consistent with the simulation study reported by Milosevic et al. (10). Abundant and leaky blood vessels produced by tumor angiogenesis induce excessive extravasation of vascular fluid to the interstitium which can exceed lymphatic draining capacity (1,3). Furthermore, lymphatic drainage can also be constricted by high cell density in an aggressively growing tumor (3,6). Without an adequate, functional lymphatic system, the interstitial pressure rises to the level of microvascular pressure (2), and microvascular flow slows down (8,9). Reduced blood flow in a chaotic vascular network, which appears as reduced pseudo-random motion of water, can be measured as a reduced D_p in a DWI experiment. The prediction of an inverse relationship between IFP and D_p, is now substantiated by the results of this study. In a recent study of IVIM-DWI with breast cancer patients (14), it was found that D_p of breast cancer ranged between 5 and 25 μm²/ms, which is comparable to the range of D_p observed in this study. It was also reported that IFP in breast cancer ranged from 4 to 35 mmHg (30). Thus, strong correlations between IVIM metrics and IFP suggest the potential of using IVIM metrics as noninvasive clinical imaging biomarkers for IFP.

MRI and IFP

One of the advantages of the IVIM-DWI method applied in this study is its use of endogenous image contrast based on blood flow. Previously dynamic contrast-enhanced (DCE)-MRI with exogenous contrast agents, such as gadolinium-diethylenetriaminepentaacetic acid (Gd-DTPA), were compared with direct IFP measurements (31,32). Haider et al. (32) investigated correlation of DCE-MRI measures with IFP in cervical cancer patients and found that there was a significant negative correlation between initial area under the enhancement curve and IFP (r = 0.42, p = 0.016) and between permeability (rK^trans = K^trans of tumor/K^trans of muscle) and IFP (r = 0.47, p = 0.008). In human amelanotic melanoma xenografts, Gulliskrud et al. (31) found that median E·F (E is the initial extraction fraction of contrast agent and F is blood flow), which is also commonly referred to as K^trans, negatively correlated with IFP for the non-necrotic A-07 tumors (r = 0.62, p = 0.04; r = 0.71, p = 0.01 for fraction of voxels with E·F < 0.15 ml/(g·min)) and the non-necrotic R-18 tumors (r = 0.49, p=0.03; r = 0.55, p = 0.05 for fraction of voxels with E·F < 0.15 ml/(g·min)). These two studies demonstrate the possibility of using K^trans from DCE-MRI data as a biomarker for assessing IFP in tumors.

However, the complete biophysical underpinnings of associations between K^trans and IFP are not fully understood (33,34). K^trans is a volume transfer constant between blood plasma and extravascular extracellular space and represents both in-flux and out-flux. The elevated IFP can decrease in-flux (Kⁱⁿ), but can conversely increase out-flux (K^out). Thus, it might be necessary to measure Kⁱⁿ and K^out separately. Hassid et al. (35,36) conducted a DCE-MRI study in orthotopic MCF7 human breast tumors in mice with slow infusion of contrast agent over 80 min and showed that the difference between Kⁱⁿ and K^out correlated with steady state concentration of Gd-DTPA, which was assumed inversely correlated with IFP. Direct comparison with IFP is yet to be shown. In addition, DCE-MRI techniques based on slow infusion are most likely limited to preclinical studies due to the long scan time. In contrast, the IVIM-DWI method demonstrated in our study is straightforward to adapt for clinical applications. This method without exogenous contrast agents can be particularly useful for patients who cannot receive gadolinium-based contrast agent injection due to impaired renal function.

Effect of IVIM in DWI

There are multiple possible contributions to the observed pseudo-diffusivity component in our tumor study; however, microvascular flow is likely the dominant source of such high pseudo-diffusion coefficients (10 – 50 μm²/ms). For a mean vessel branch length (l) of 100 μm and average blood velocity (v) of 1 mm/s, a pseudo-diffusivity of D_p ~ vl/6 = 16.7 μm²/ms would be expected (28), which is in the range observed in this study. This interpretation is also supported by previous studies using intravascular labels (37) and vasodilators (19). However, a full understanding of the fast diffusion signal may require more detailed measurement and analysis. On the measurement side, tools such as flow-compensated gradients, in comparison to conventional diffusion encoding, may provide insight on the velocities involved in the pseudo-diffusion term (38). The dependence of the observed pseudo-diffusivity on diffusion time may also provide opportunity to measure other characteristics of the capillary network, such as segment length and blood velocity dispersion. While analogous in some ways to time-dependent “passive” diffusion in a restricted geometry, the formulation appropriate to active microvascular flow will differ (39). And, as Nevo et. al. (40) pointed out, the conventional “b-value” parameterization may not be optimal for complete characterization; instead, separate regard for wavevector q and diffusion time dependences may be required. Flow heterogeneity effects from vessel branching (41) or intravascular velocity dispersion (40,42) may also be informative. Since the use of higher order models often require more data with higher precision, the balance of biophysical specificity and clinical feasibility must also be considered in determining which IVIM parameters may be collected in the clinic. This will be the subject of future work.

Clinical need for IFP monitoring

IFP has been widely recognized as one of critical obstacles in treating solid tumors (1,43,44). When tumor IFP rises close to microvascular pressures, the pressure gradient becomes negligible and the delivery of drug from vascular space to interstitial space can be reduced. Enhancement of tumor rim, but not in non-necrotic solid tumor core, in contrast enhanced MRI is evidence for such an effect (35). DiResta et al. (45) demonstrated that lowering IFP by an artificial lymphatic system led to increased drug uptake (23.2% increase in Doxorubicin uptake in a rat sarcoma tumor) and 90% faster shrinkage of tumor than in control tumors. In canine spontaneously occurring osteosarcoma, DiResta et al. (46) also showed that blood flow increased by 314% in tumors with an active artificial lymphatic system. In addition, a review by Heldin et al. (43) stresses that at least 5 different types of therapeutic agents that lower IFP have been demonstrated both to lower IFP and to increase subsequent drug uptake in vivo in animal tumor models, such as vascular endothelial growth factor (VEGF) antagonist, platelet-derived growth factor antagonist, tumor necrosis factor-α, Bradykinin antagonist, and prostaglandin E₁.

However, despite a number of different ways available to lower IFP, there is no reliable biomarker to monitor IFP noninvasively, which hinders development of effective therapy based on controlling IFP. Gade et al. (20) monitored the IFP during collagenase treatment in nude mice bearing the HT29 human colon adenocarcinoma using a Mikro-Tip catheter pressure transducer. They found that tumor IFP decreased by about 64% within 120 min after injection. Tumor vascular normalization marked by reduced IFP is transient with continued antiangiogenic therapy. Batchelor and colleagues (47) demonstrated that AZD2171, a pan-VEGF receptor tyrosine kinase inhibitor, temporarily normalizes tumor vasculature in glioblastoma patients. As Jain (6) suggested, there can be a vascular normalization window during antiangiogenic therapy, and it may be crucial to identify this window in order to maximize the treatment response. Thus, a noninvasive imaging method for measuring IFP, such as IVIM-DWI, can play an important role in optimizing antiangiogenic therapy by detecting the onset of tumor vascular normalization.

CONCLUSIONS

In this study, IVIM-DWI was used to study the 4T1 mouse mammary tumor model. It was shown that the IVIM effect is an important factor to be considered in performing DWI experiments in this tumor model, and also that IVIM-DWI data provides useful biomarkers when properly analyzed. We also demonstrated that the pseudo-diffusivity measured by IVIM-DWI correlates with IFP directly measured by the WIN method. The results of this study suggest the potential of using IVIM-DWI metrics as noninvasive biomarkers for tumor IFP, a barrier to drug delivery. The IVIM-DWI metrics may also be of value in assessment of antiangiogenic therapy by helping to identify the tumor vascular normalization window.

ABBREVIATIONS

IFP

interstitial fluid pressure

IVIM

intravoxel incoherent motion

DWI

diffusion weighted imaging

MVP

microvascular pressure

WIN

wick-in-needle

PBS

phosphate buffered saline

RARE

rapid acquisition with relaxation enhancement

PGSE

pulsed gradient spin echo

ADC

apparent diffusion coefficient

RSS

residual sum of squares

BIC

Bayesian information criterion

SNR

signal-to-noise ratio

IQR

inter-quartile range

H&E

haematoxylin and eosin

DCE

dynamic contrast-enhanced

Gd-DTPA

gadolinium-diethylenetriaminepentaacetic acid

EPR

electron paramagnetic resonance

VEGF

vascular endothelial growth factor

ROI

region of interest

AAV

apparent avascular voxel

AVV

apparent vascular voxel