Development of a Predictive Energy Equation for Maintenance Hemodialysis Patients: A Pilot Study

Introduction

End-stage kidney disease (ESKD) and its associated morbidity and mortality risks are recognized as critical public health issues (1, 2). While the causes of the increased death rates in ESKD on maintenance hemodialysis (MHD) are multifaceted, a unique state of deranged nutritional status, aptly termed as protein-energy wasting (PEW), is a well-established factor that predisposes MHD patients to worse outcomes (3–5). PEW is a complex syndrome that develops from the contribution of multiple factors (5). Amongst these, energy balance, i.e. the amount of energy intake relative to the energy consumption, is an important one that has significant clinical implications (3). To provide optimal nutrition care to MHD patients, a clear understanding of their energy requirements is paramount.

In 2000, The National Kidney Foundation-Kidney Disease Outcomes Quality Initiative (KDOQI) Clinical Practice Guidelines for Nutrition (6), which suggested energy requirements of persons with CKD were no different than healthy individuals, recommended 30–35 kcal/kg body weight for CKD patients < 60 years of age and <30 kcal/kg body weight for those ≥ 60 years. However, when more recent studies were reviewed (7), considerable debate ensued over MHD patients’ energy requirements (8–13). In fact, the International Society for Renal Nutrition and Metabolism, in their recent explanation of the etiology of PEW, supports the hypothesis that CKD is hypermetabolic in nature (3). Even though several factors unique to CKD are known to impact energy expenditure (e.g., hyperparathyroidism, glucose intolerance, inflammation) (9, 14, 15), there is a significant gap of knowledge regarding the accurate estimation of energy needs for patients undergoing MHD (13).

Within clinical settings, the gold standard for determination of energy expenditure is indirect calorimetry (IC) (16). Largely due to its cumbersome methods and costly equipment, IC is generally impractical to implement within an ambulatory care setting (17, 18). As such, practitioners often rely on predictive equations for the estimation of energy needs. Currently, there are over 200 predictive energy equations available (19), but none are specific for patients undergoing MHD. Application of commonly used predictive equations in clinical practice (i.e., Harris-Benedict Equation (HBE), Schoenfeld, Mifflin-St Jeor (MJSE), etc.) have been studied on a limited basis in CKD, and have produced conflicting results, e.g., under- or over-estimation of energy requirements when compared to the mREE obtained by IC (8, 11, 20). Consequently, existing predictive energy equations are not reliable for use in CKD, and especially among those patients on MHD (11).

Despite these limitations, nephrologists and dietitians often rely on predictive equations when determining energy requirements for patients on MHD. Hence, the primary aim of this study was to apply a similar methodology as published by Mifflin, et al. (21), and develop a predictive energy equation unique for this patient population. Using a dataset of patients on MHD from several clinical trials where mREE was obtained, we explored the relationships among various anthropometric, demographic, clinical, and laboratory variables to the mREE, and were able to develop a predictive energy equation specific for this population. To establish the overall precision of the newly developed predictive energy equation (MHDE), the level of agreement of the MHDE to mREE was completed, and then the MHDE was compared to the predictive energy needs derived from the MSJE. The MSJE equations were chosen for comparison as research has demonstrated greater predictive accuracy than other common equations (e.g., the Harris-Benedict Equation) (22).

Methods

Study Sample

Between 1998 and 2010, three clinical trials were completed at the General Clinical Research Center (GCRC) at Vanderbilt University Medical Center (VUMC), which measured energy expenditure using indirect calorimetry (23–25). Within a week prior to each study, dual-energy x-ray absorptiometry (DEXA) was performed to estimate lean and fat body masses. For each of these clinical trials, the participants were admitted to the GCRC the day before the study at approximately 7 pm, received a meal from the GCRC bionutrition services upon admission, and remained fasted. The last meal was given at least 10 hours before the initiation of the study for all of the patients and consisted of 18% protein and 30% lipids. Energy intake was kept at maintenance levels on the basis of the Harris-Benedict Equation (HBE) and each patient’s gender, height, weight, and activity levels. The following morning prior to any other study activities, mREE was obtained by indirect calorimetry (TrueOne 2400, ParvoMedics, Inc. Sandy, UT) in accordance to published standards for its measurement. As part of the clinical trial protocol, data were routinely monitored to assure the achievement of such quality standards. Additional specifics regarding study procedures may be consulted elsewhere (23–25). A de-identified merged data set from VUMC clinical trials (23–25) was shared for the purpose of completing the aims of this study according to the methodology for developing a predictive energy equation as published by Mifflin, et al. (21).

Study Variables

The dependent variable was the mREE. The independent variables were categorized into four groups: demographic, anthropometric, clinical, and laboratory characteristics. The demographic variables included age at study date, sex, race and ethnicity. The anthropometric variables included height (HT), weight (WT), body mass index (BMI), fat mass (FM), fat free mass (FFM) and total body fat percentage (%FAT). The clinical variables included diabetes status, dialysis access type, and laboratory data included blood urea nitrogen (BUN), creatinine (CR), glucose (GLU), albumin (ALB), prealbumin (PAB), cholesterol (CHOL), high sensitivity C-reactive protein (CRP) and serum bicarbonate (CO₂). Sample characteristics are reported using descriptive statistics.

Statistical analysis

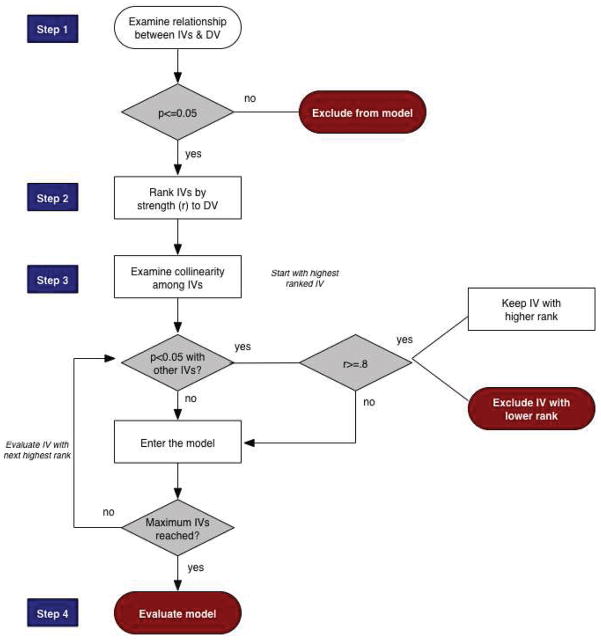
Because the study aims were both to identify the best fitting predictive equation of mREE as well as formulate parsimonious models with practical clinical utility, the exploratory modeling proceeded in two stages. In the first step, to identify the best fitting model without reference to clinical utility, bivariate relationships between the range of potential predictors and mREE were screened using Pearson’s correlation. Even though a range of predictor variables was available for possible inclusion, the limited sample size restricted the maximum number of predictors to six (26). Thus, p≤.05 (rather than more liberal p values of .08 or .10) was used to identify potential predictors. Relationships among potential predictors were then screened using Pearson’s correlation and when highly collinear predictors were identified (r≥0.8), only the variable with the strongest relationship to mREE was included in the model. A diagram of the model building procedure is presented in Figure 1.

Figure 1. Model Building Procedure for Developing Predictive Energy Equation in Maintenance Hemodialysis Patients.

Key: IVs-independent variables; DV-dependent variable

In the second stage, predictors from the best fitting model that were unlikely to be available in many hemodialysis treatment settings were dropped from the model and variables with the next strongest bivariate relation to mREE were substituted. Then, the effects of non-significant predictors on overall model fit were assessed. Predictors that could be dropped without affecting the R² by more than 1% were excluded in order to obtain the most parsimonious model. Non-significant predictors that affected overall model fit by at least 1% and were easily accessible in clinical situations were retained, as their presence could prove statistically significant in larger samples or in the broader hemodialysis population. Diagnostic procedures were carried out on all models to assess for multicollinearity, homoscedasticity, functional form and normality of errors. Assumptions were tenable for all models. Statistical analysis was performed using IBM SPSS version 21 (IBM, Chicago, IL, USA).

Comparison to the Mifflin-St.Jeor Equation (MSJE) was conducted in order to determine the level of bias and precision in the developed formula (MHDE) to a widely accepted one in dietetics practice (27). Two versions of the equations developed by Mifflin, et.al (21) were compared: the model that explained the greatest proportion of variance (MSJE-Best) and the models that the authors suggest for practical use (MSJE-Prac). These equations are as follows:

$$\begin{array}{ll}\text{MSJE}-\text{Best}:\hfill & \text{REE}=19.7(\text{FFM})+413\hfill \\ \text{MSJE}-\text{Prac}:\hfill & \text{REE}=9.99(\text{weight})+6.25(\text{height})-4.92(\text{age})-161(\text{for}\text{females})\hfill \\ \hfill & \text{REE}=9.99(\text{weight})+6.25(\text{height})-4.92(\text{age})-5(\text{for}\text{males})\hfill \end{array}$$

Where weight is in kg, height is in cm, age is in years, and fat free mass (FFM) in kg.

For all models, a band of ±200 kcal was used to determine a band of acceptability (that is, REE within ±200 kcals of the observed REE were considered “accurate”). Using this criteria, Bland-Altman plots were constructed for each model (28). Mean residual difference from zero was tested using one sample t tests. Individual residuals were categorized into one of three categories in accordance to methodologies reported by Ziegler, et al (29) as well as based on the clinical relevance of the mean differences (30): under-predicted (predicted value <200 kcal below measured REE), accurate (predicted value within ±200 kcals of measured REE) and over-predicted (predicted value >200kcal above measured REE). Model results were then compared in terms of the proportion of REE values accurately predicted.

Results

Data from 67 patients were available for analysis (Table 1). The mean (± SD) age was 47.9 ± 13.3 years, 73 % were male (n=49) and 75% were African American (n=50). Hypertension was the most prevalent CKD etiology (n=45, 67 %). Twenty-four percent (n=16) of the subjects were diagnosed with diabetes mellitus, 51% (n=34) of subjects used fistulas as their dialysis access. BMI ranged from 17.2 to 49 kg/m² and total body fat percentage ranged from as low as 5.9 to as high as 54.3%. Obese individuals (BMI ≥30) comprised 38.8% (n=26) of the sample. The mean CRP value was 10.5 ± 9.4 mg/dl (range 0.1 – 43.7), with two extreme values observed (41.5 and 43.7 mg/dl). The mean mREE was 1692.7 ± 366.4 kcal (range = 1112.3 – 2823.6 kcal, median = 1675.0 kcal).

Table 1.

Demographic, Anthropometric, and Clinical Characteristics for a Sample of Maintenance Hemodialysis Patients from Vanderbilt University Medical Center (N=67)

	Available for Analysis (n)	Mean ± SD or percent	Reference Range for CKD (48)
Demographics
Age (yrs), mean ± SD	67	47.85 ± 13.3
Sex
Males, %	49	73.1
Females, %	18	26.9
Race
African American, %	50	74.6
White, %	15	22.4
Asian, %	2	3.0
Ethnicity
Non-Hispanic, %	62	92.5
Hispanic, %	5	7.5
Anthropometrics
HT (cm), mean ± SD	67	171.2 ± 9.6
WT (kg), mean ± SD	67	83.8 ± 21.6
BMI (kg/m2), mean ± SD	67	28.7 ± 7.2
Fat Mass (kg), mean ± SD	67	28.2 ± 15.4
FFM (kg), mean ± SD	67	52.8 ± 9.6
Total Body Fat %, mean ± SD	67	33.1 ± 11.0
BMI Categories
Underweight (<18.5), %	3	4.5
Normal (18.5–24.9), %	22	32.8
Ovrwt (25.0–29.9), %	16	23.9
Obese (>30.0), %	26	38.8
Clinical Characteristics
Diabetes Status
Yes, %	51	76.1
No, %	16	23.9
Dialysis Access Type
Fistula, %	34	50.7
Graft, %	29	43.3
Catheter, %	4	6.0
CKD Etiology
Hypertension, %	45	67.2
Other, %	10	14.9
Diabetes, %	6	9.0
Glomerulonephritis, %	4	6.0
Cystic Kidney Disease, %	2	3.0
Laboratory Values
ALB (g/dl), mean ± SD	67	3.8 ± 0.4	≥4
Blood GLU (mg/dl)			<200
Non – DM, mean ± SD	51	86.2 ± 18.8
DM, mean ± SD	16	121.8 ± 62.0
BUN (mg/dl), mean ± SD	67	39.7 ± 13.5	60–80
CHOL (mg/dl), mean ± SD	61	144.4 ± 37.9	<200
CO2 (mEQ/L), mean ± SD	59	27.2 ± 10.5	≥22
CR (mg/dl), mean ± SD	67	9.4 ± 3.0	2–15
CRP (mg/L), mean ± SD	64	10.5 ± 9.4	<0.8
PAB (mg/dl), mean ± SD	53	33.3 ± 9.7	≥30
TRANS (mcg/dl), mean ± SD	53	167.8 ± 34.3	215–365 (male)
			250–380 (female)

BMI – Body Mass Index, LBM – Lean Body Mass, BUN – Blood Urea Nitrogen, CRP – C- Reactive Protein, CO2 – Carbon Dioxide, DM – Diabetes Mellitus, CKD – Chronic Kidney Disease, ALB-albumin, GLU-glucose, CHOL-cholesterol, CR-Creatinine, PAB-prealbumin, TRANS-transferrin

Independent variables significantly correlated with mREE (in order of descending magnitude) and thus defined the pool of predictor variables (Table 2): FFM, ALB, age at study date, WT, CR, HT, BMI, sex, CRP and FM. All the correlations were positive except age at study date, indicating that as age increased, mREE decreased. Sex was coded as females = 0 and males = 1, so that the positive correlation between sex and mREE indicated that males tended to have higher mREE than females.

Table 2.

Predictor Variables with Significant (p<0.05) Relationships with mREE (in order of strength)

Ranking		Pearson r	P values
1	FFM (kg)	0.60	<0.001
2	ALB (g/dl)	0.48	<0.001
3	Age at Study Date	−0.46	<0.001
4	WT (kg)	0.46	<0.001
5	Creatinine	0.36	0.003
6	HT (cm)	0.31	0.010
7	BMI (kg/m2)	0.28	0.024
8	Sex	0.27	0.026
9	CRP (mg/L)	0.27	0.034
10	FM (kg)	0.26	0.037

BMI – Body Mass Index, FFM – Fat Free Mass, BUN – Blood Urea Nitrogen, CRP – C- Reactive Protein, CO2 – Carbon Dioxide, CKD – Chronic Kidney Disease, ALB-albumin, CR-Creatinine

Multiple inter-variable correlations were observed among predictor variables. While many of the independent variables related to mREE were also significantly (p<0.05) related to each other, only the following posed a priori collinearity problems (r≥0.8) (26): FM and BMI (r=0.93, p<0.001), FM and WT (r=0.91, p<0.001), and WT and BMI (r=0.88, p<0.001). Thus, following the procedure in Figure 1, the following six predictors were entered into the initial model: FFM, WT, ALB, CRP, sex, and age at study date. Initial results indicated substantial multicollinearity problems with both FFM and WT in the model, and so WT was dropped from the model, resulting in the following model (F=11.12, p<0.001, R²=.489):

Base Model (MHDE-Base)

$$\mathit{REE}=\mathit{409.44}+\mathit{15.35}(\mathit{FFM})-\mathit{6.64}(\mathit{Age})+\mathit{4.12}(\mathit{Male})+\mathit{193.82}(\mathit{ALB})+\mathit{4.59}(\mathit{CRP})$$

Where, FFM was measured in kg, age in years, males=1, ALB in g/dl, and CRP in mg/dl

Since the study aims were to identify not only the best predictive, but the most parsimonious model we then assessed whether we could simplify the model without reducing the overall model fit. Two predictors, CRP and sex were not statistically significant (CRP (β=4.589, p=0.230), Sex (β=4.115, p=0.963)). We alternatively dropped each of these predictors from the model and examined the change in model R². Excluding sex did not affect the overall variance explained in the model (R² = 0.489, R² change = 0.00, p=0.963), but removing CRP did (a decrease of just over 1%, R² = 0.477) despite the insignificant statistical change (R² change=0.013, p=0.230). Based on the above trials, four best predictive variables to predict mREE in hemodialysis patients were selected as follows: FFM, age at study date, ALB, and CRP (F=14.14, p<0.001, R²=.489).

Best Predictive Model (MHDE-LBM)

$$\mathit{REE}=\mathit{404.58}+\mathit{15.44}(\mathit{FFM})-\mathit{6.62}(\mathit{age})+\mathit{194.45}(\mathit{ALB})+\mathit{4.58}(\mathit{CRP})$$

Where FFM was measured in kg, age in years, ALB in g/dl, and CRP in mg/dl

Selection of a Model with the Best Clinical Utility

In clinical settings, FFM may not be readily accessible. To develop equations with broader clinical utility, WT (the anthropometric variable with the next highest bivariate relationship to mREE) was substituted for FFM in the model. Then, following the procedure in Figure 1, we again tested whether including additional variables readily available in a clinic setting improved the fit of the model with WT. CR and BMI were not included due to collinearity issues with other variables in the model. Including HT and sex alternatively in the model were therefore the next variables considered for inclusion and they improved the model fit by 2% and 2.7% respectively, although neither change was significant (R²=0.453, R² change=0.020, p=0.156 and R²=0.460, R² change=0.027, p=0.096 respectively). HT and sex were highly collinear and so only sex was included since it produced a model with a higher coefficient of determination (R²=0.460). As a result, the independent variables that were selected into the model with best clinical utility were: WT, age at study date, ALB, CRP, and sex (F=9.88, p<0.001).

Model with the Best Clinical Utility when CRP is Available (MHDE-CRP)

$$\mathit{REE}=\mathit{808.20}+\mathit{4.96}(WT)+-\mathit{8.66}(\mathit{age})+\mathit{192.52}(\mathit{ALB})+\mathit{4.38}(\mathit{CRP})+\mathit{140.14}(\mathit{male})$$

Where WT is measured in kg, age in years, ALB in g/dl, male=1, CRP in mg/dl

CRP testing is not universally included in routine laboratory test panels, and therefore may not be available in all clinical settings. As a result, the proposed model with the best clinical utility above would not be useful in all settings. After excluding CRP, the variance explained by the model was reduced to 44.8% (R²=0.448, R² change=0.012, p=0.271). Three independent variables remained that had significant correlations with mREE: CR, HT, and BMI. Both BMI and HT were not considered due to significant collinear relationships with the independent variables already in the model. CR was left as the best selection. Despite statistically significant collinear relationships with both ALB (r=0.321, p=0.003) and age (r=−0.442, p<0.001), CR was still included in the model because the effect sizes of these relationships were not large enough (r≤0.8) to raise a collinearity concern. The addition of CR improved the predictability of the model to 45.1% (R²=0.451, R² change=0.002, p=0.629). Therefore, when CRP is unavailable, the best predictive variables to estimate mREE are: age at study date, sex, WT, ALB and CR (F=10.00, p<0.001):

Model with the Best Clinical Utility when LBM and CRP are Unavailable (MHDE-Creatinine)

$$\mathit{REE}=\mathit{750.15}+\mathit{5.38}(WT)-\mathit{8.207}(\mathit{age})+\mathit{188.98}(\mathit{albumin})+\mathit{137.94}(\mathit{male})+\mathit{6.68}(CR)$$

Where WT is measured in kg, age in years, ALB in g/dl, male=1, CR in mg/dl

Model diagnostics were then carried out on all three models. Examination of the residuals indicated that the functional form of the model was appropriate, errors were normally distributed and homoscedasticity was tenable.

Comparison of Developed Predictive Energy Equation to Mifflin-St.Jeor Formula

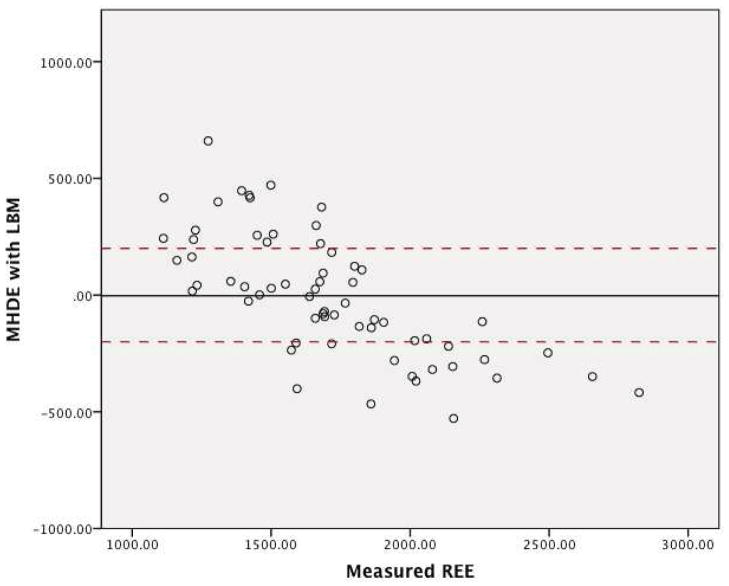
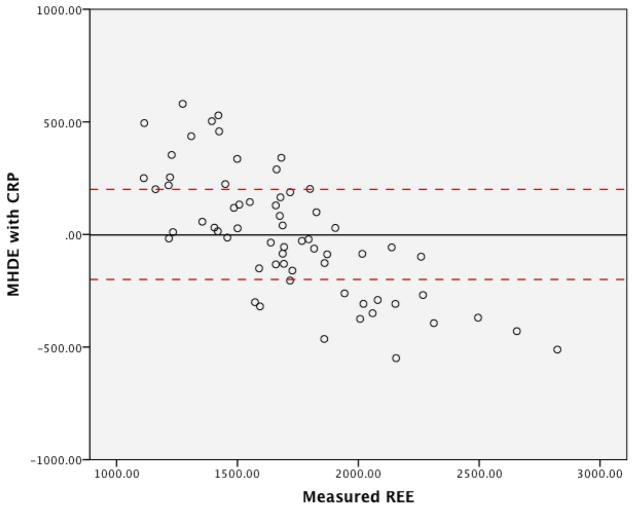
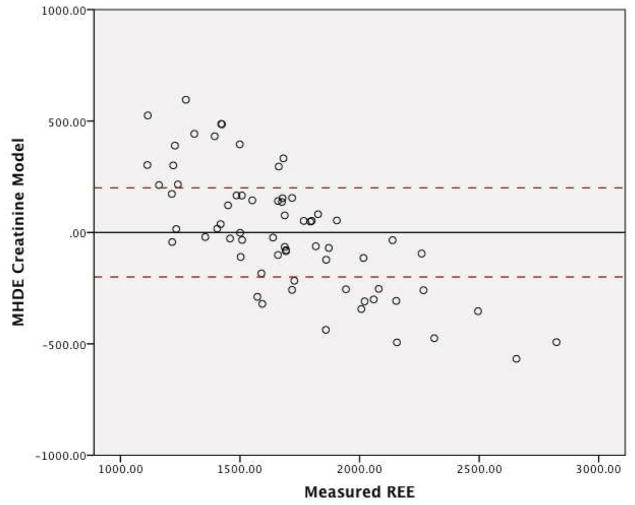
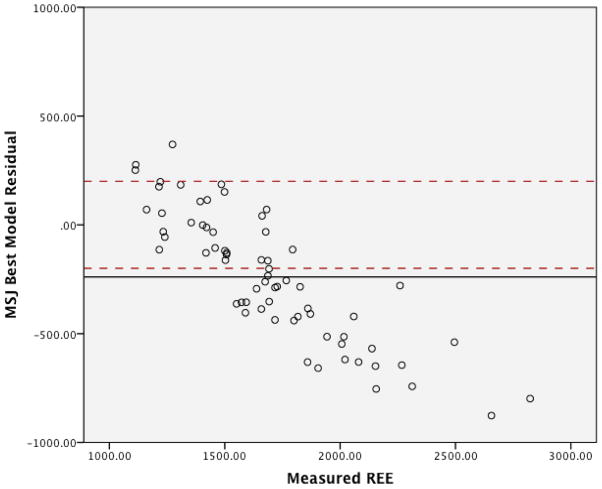
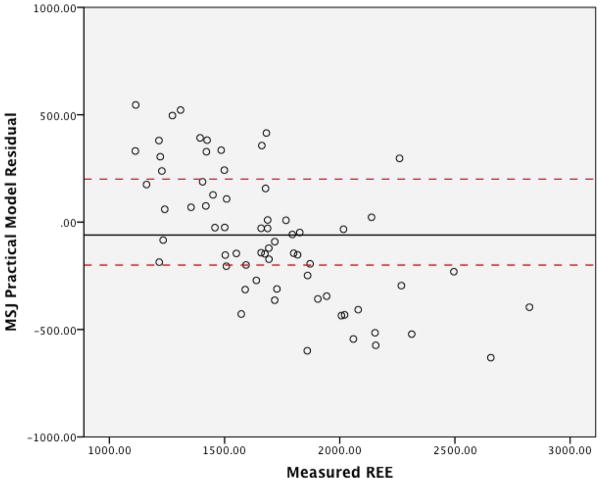
The graphs for the residuals in regards to the three MHDE models (MHDE-LBM, MHDE-CRP and the MHDE-Creatinine) are presented in Figures 2a–2c. In the figures, the solid line indicates the mean difference between predicted and measured REE (thus, a deviation above or below zero indicates consistent bias in the model) and points between the dashed lines indicate the subjects for whom the model predicted within +/−200 kcal of measured REE (and, thus, are considered “accurate”). Points above or below the dashed lines indicate individuals whose predicted REE was substantially over- or under-predicted (respectively) by the model. All models were similar in that they predicted mREE most accurately within the center of the distribution. Models tended to over-predict REE at the lower end of the distribution and under-predict energy needs at the upper end of the distribution. The pattern of over- or under-prediction was similar in the MSJE-Prac model (Figures 3a–3b).

Figure 2.

Figure 2a. MHDE-LBM Model Residuals (inclusive of Fat Free Mass) from a Sample of Maintenance Hemodialysis Patients (N=67) at Vanderbilt University Medical Center

Figure 2b. MHDE-CRP Model Residuals (inclusive of C-Reactive Protein) from a Sample of Maintenance Hemodialysis Patients (N=67) at Vanderbilt University Medical Center

Figure 2c. MHDE-Creatinine Model Residuals (inclusive of Serum Creatinine) from a Sample of Maintenance Hemodialysis Patients (N=67) at Vanderbilt University Medical Center

Note: Solid line indicates the mean difference between predicted and measured REE. Dashed lines indicate the upper and lower boundaries of agreement.

Figure 3.

Figure 3a. MSJE-Best Model Residuals (taken from Mifflin, et al., Am J Clin Nutr, 1990)

Figure 3b. MSJE-Prac Model Residuals (taken from Mifflin, et al., Am J Clin Nutr, 1990)

Note: Solid line indicates the mean difference between predicted and measured REE. Dashed lines indicate the upper and lower boundaries of agreement.

Table 3 presents the results of the tests of accuracy of the residuals. In none of the MHDE models were the residual means significantly different than zero. In contrast, the MSJE-Best model (that included FFM) significantly under-estimated energy needs by −239.39 ± 295.35 kcals (p=0.001). While the mean residual for the MSJE-Prac model (that included WT rather than FFM) tended to underestimate energy needs in this sample of hemodialysis patients by −60.26 ± 303.46 kcals, this was not statistically significant.

Table 3.

Proportion and Direction of Agreement and Residual Bias for Maintenance Hemodialysis (MHDE) and Mifflin-St. Jeor (MSJE) Models

Model	Under-predict (n,%)	Accurate (n,%)	Over-predict (n,%)	Residual Mean ± SD
MHDE-LBM	17 (26.6)	31 (48.4)	16 (25.0)	−3.06 ± 266.24
MHDE-CRP	16 (25.0)	32 (50.0)	16 (25.0)	−1.91 ± 273.82
MHDE- Creatinine	17 (25.4)	36 (53.7)	14 (20.9)	0.00 ± 271.58
MSJE-Best Model	36 (53.7)	28 (41.8)	3 (4.5)	−239.39 ± 295.35*
MSJE- Prac Model	21 (31.3)	31 (46.3)	15 (22.4)	−60.26 ± 303.46

^*Significantly different than zero at p=0.001

Additionally, the error patterns were different for the MHDE versus the MJSE models. Approximately half (48.4%–53.7%) of the subjects had predicted mREE values within ±200 kcal (i.e. operationalized as “accurate”) of the measured values for all MHDE models. The remaining subjects had values that were fairly evenly distributed between under- and over-prediction, with the MHDE-Creatinine model slightly more likely to under-predict (25.4%) than over-predict (20.9%). The MSJE models had a slightly lower proportion of subjects’ mREE accurately predicted (46.3% for the MSJE-Prac model and 41.8% for the MSJE-Best model), and the errors were much less evenly distributed; e.g., 53.7% of subject mREE under-predicted with the MJSE-Best model and approximately one third (31.3%) under-predicted with the MJSE-Prac model.

Discussion

Based on the results of this study, the addition of laboratory data such as ALB, CRP and CR produced a better fitting model of mREE in MHD patients than using demographic and anthropometric characteristics alone (e.g., sex, height, and weight), as commonly done in predictive formulas for healthy populations (21). And, while this research reflects merely a pilot study, it does support the hypothesis that existing predictive energy equations may not be justly applied in patients with CKD on MHD. We have also demonstrated the applicability of employing a methodology, reported in the literature by Mifflin, et al (21) that was conducted for healthy subjects at variable weight categories, to a sample of MHD patients. A smaller variance of the mREE was explained by the MHDE than MSJE, and it may relate to the sheer complexity of CKD and the inability to capture all potential predictors within this finite convenience sample.

As strongly supported by the research literature in non-CKD and CKD samples, demographic (e.g., age (31, 32) and sex (33, 34)) and anthropometric characteristics (e.g., FFM (35–38), weight, height and BMI) are predictors of mREE (35, 39–41). Among them, FFM was found to be the strongest determinant of mREE in this sample. FFM alone explains 50–85% of the inter-individual variability in mREE in healthy adults (36–38, 42, 43). In contrast, simple linear regression in this study demonstrated that FFM alone contributed to 35.7% of the variance in mREE among MHD patients, even when measured by a gold standard for determining FFM; dual-energy x-ray absorptiometry (DEXA). Even though FFM remains the single most predictive factor of mREE in MHD patients, it contributes substantially less to mREE than in healthy subjects. The body composition of CKD patients is very different from healthy counterparts. Patients on MHD have a greater likelihood of experiencing moremore pronounced muscle wasting (5). A smaller sample size in this study may also be a contributing factor fora lower variance explained from the FFM. This in turn implies that there are other possible cofactors of mREE in MHD patients when compared to healthy subjects, and substantiates the need to explore this phenomenon more fully in a broader, more robust sample of patients. While FFM may be a strong predictor of mREE, it is of limited clinical utility to the practitioner, as few have access to valid and reliable instruments for measuring body composition. As seen in the predictive models developed for the MHDEs, WT, which is easily obtained and routinely collected in the dialysis clinic, may be a suitable alternative for FFM.

This investigation substantiated the importance of CKD-specific laboratory parameters necessary in establishing the best predictive models of mREE, which is lacking in other equations commonly used in clinical practice. Similarly, ALB, CR, and CRP were also significantly correlated with mREE in this study as well as reported by others (44–47). ALB is a routine measure collected generally on a monthly basis in dialysis clinics, so would be of particular value to include in the predictive models for MHD patients, if a linear relationship between mREE and ALB continues to exist in future studies. In our study, we found a positive correlation between ALB and mREE, and this seemed counterintuitive among a sample of participants with reported inflammation (e.g., elevated CRP levels). When more closely examined within the dataset, we noted that ALB was also positively correlated to FFM and weight (data not shown). All we can surmise from the positive relationship between ALB and mREE is that individuals that had a greater FFM and/or weight also had higher ALB levels. Thus, in this sample of participants, ALB levels may have reflected overall nutritional status.

Because of the established effects of chronic inflammation present in MHD patients, monitoring CRP levels, an inflammatory marker, seems prudent (46). The inflammatory cytokines contribute to increased protein catabolism, enhanced lipolysis, suppression of appetite, and hypermetabolism. Therefore, CRP is often used as a surrogate marker of inflammation. Both Utaka et al., (46) and Avesani, et al, (44) demonstrated that subjects with higher CRP levels had significantly higher mREE than CKD patients with lower CRP values.

Creatinine is derived from creatine in the muscle at a relatively constant rate. Therefore, creatinine is proportional to muscle creatine content, and hence to the total body muscle mass. Despite being an unreliable muscle mass indicator by itself among patients diagnosed with CKD, changes in serial measurements of serum creatinine (over a three month period) may be an indicator of changes in muscle mass (6). The close relationship of creatinine to muscle mass could explain partially the reason why creatinine was included into the practical model in the absence of CRP.

There is considerable evidence that supports that mREE is positively impacted by secondary hyperparathyroidism, glucose intolerance, as well as insulin resistance (9, 45, 46,(48). In this study, neither self-reported diabetes status nor was blood glucose significantly correlated with mREE. Due to the retrospective nature of the study design, parathyroid levels, HgbA1c and medical history regarding glycemic control and bone disease were not available during chart abstraction methods used. Data included patients on MHD from programs other than VUMC, and this limited the availability of such laboratory data. Thus, the inability to associate the presence of hyperglycemia or a diagnosis of diabetes with mREE may relate to the demographic mix of the sample, as the leading etiology for CKD was hypertension and not diabetes as is reported by the United States Renal Data System (1). Nonetheless, glycemic control and parathyroid levels will need to be explored in future studies for their strong likelihood that they too will serve as potential co-factors in subsequent predictive models.

Despite our findings, there are several limitations of the study which include; possible sampling bias and limited generalizability (e.g., predominantly male, African American, and younger ages); a small sample size precluded the number of predictors in the defined models; and unavailable data of potential (and likely known) predictors (A1c and PTH levels) of mREE. Nonetheless, the strength of this study lies in its originality. The quest for a predictive energy equation for the MHD population will have far-reaching clinical implications. Unlike most commonly used predictive energy equations, the developed models incorporated laboratory parameters such as ALB, CRP and CR to better determine the energy requirements of patients on MHD.

To the investigators’ knowledge, this was the first study to attempt to develop a population-specific predictive energy equation for the MHD patients. However, due to its exploratory nature, findings of our study must be interpreted with caution. Further research with a larger sample size is needed to validate this equation and identify the best combination of predictors of mREE in the MHD population.

Practical Application

Although the predictive energy equation proposed by this pilot study explains less than 50% of the variance in mREE in the convenience sample; it confirms that there are more factors besides demographic and anthropometric characteristics determine energy requirements in MHD patients. This study also accounted for the practicality and clinical utility of the developed predictive energy equations, and therefore afforded alternative formulas for clinicians when certain demographic, clinical, or laboratory parameters are not accessible.