Statistical Methods for Multivariate Meta-analysis of Diagnostic Tests: An Overview and Tutorial

Summary

In this article, we present an overview and tutorial of statistical methods for meta-analysis of diagnostic tests under two scenarios: 1) when the reference test can be considered a gold standard; and 2) when the reference test cannot be considered a gold standard. In the first scenario, we first review the conventional summary receiver operating characteristics (ROC) approach and a bivariate approach using linear mixed models (BLMM). Both approaches require direct calculations of study-specific sensitivities and specificities. We next discuss the hierarchical summary ROC curve approach for jointly modeling positivity criteria and accuracy parameters, and the bivariate generalized linear mixed models (GLMM) for jointly modeling sensitivities and specificities. We further discuss the trivariate GLMM for jointly modeling prevalence, sensitivities and specificities, which allows us to assess the correlations among the three parameters. These approaches are based on the exact binomial distribution and thus do not require an ad hoc continuity correction. Last, we discuss a latent class random effects model for meta-analysis of diagnostic tests when the reference test itself is imperfect for the second scenario. A number of case studies with detailed annotated SAS code in procedures MIXED and NLMIXED are presented to facilitate the implementation of these approaches.

1. Introduction

In the medical literature, a diagnostic test commonly refers to a medical test to classify subjects with respect to a (disease) state of interest. Accurate diagnosis plays an important role in the disease control and prevention. Diagnostic test outcomes could be dichotomous, ordinal or continuous. This article only focuses on the dichotomous outcome. The performance of a binary test is commonly measured by a pair of indices such as sensitivity and specificity. Sensitivity is defined as the probability of testing positive given a person being diseased and specificity is defined as the probability of testing negative given a person being disease-free.^{1, 2} Other frequently used indices include positive and negative predictive values, and positive and negative diagnostic likelihood ratios.^{1, 2}

In meta-analysis of diagnostic tests, there is a great potential for heterogeneity due to differences in such things as disease prevalence, study population characteristics, laboratory methods, and study designs. While some study level covariates such as mean age may explain some variation, random effects models are commonly recommended to account for other unobserved sources of variation. When a reference test can be considered a gold standard, a few methods are available to account for this heterogeneity.^3–12 Specifically, random effects models including the hierarchical summary receiver operating characteristic model³ and bivariate random effects meta-analysis on sensitivities and specificities are recommended.^{5, 11, 12} These approaches are identical in some situations.^{6, 9, 13} Some examples and extensive simulations demonstrated that bivariate random-effects meta-analysis offers numerous advantages over separate univariate meta-analysis.^{14, 15} In general, generalized linear mixed models, which use the exact binomial likelihood, often perform better than the linear mixed models which use a normal approximation.^{12, 16} In addition, a trivariate generalized linear random-effects model were proposed to jointly models the disease prevalence, sensitivities and specificities.¹⁷

In practice, disease status is often measured by a reference test that is subject to nontrivial measurement error. This leads to a setting without a gold standard. When the reference test is subject to measurement error, the evaluation of diagnostic tests in a meta-analysis setting becomes more challenging. To the best of our knowledge, only a few articles have considered meta-analysis methods for diagnostic tests in the absence of a gold standard. Walter et al. discussed a latent class model for a meta-analysis of two diagnostic tests assuming varying prevalence, but constant sensitivity and specificity across studies.¹⁸ A more general latent class random effects model by Chu et al. assumes sensitivity and specificity of both tests as well as prevalence to be random effects.¹⁹ Sadatsafavi et al. presented a model where conditional dependence between tests is allowed, but beyond prevalence, only one of the sensitivity or specificity can be implemented using a random effect.²⁰ Dendukuri et al. presented a Bayesian method for the meta-analysis of a tuberculous pleuritis diagnostic test in the absence of a gold standard.²¹

In this article, we present an overview and tutorial summarizing the pros and cons of these approaches and provide detailed case studies with annotated SAS code. The outline of this article is as follows. In Section 2, we summarize and compare different models when the referent test can be considered a gold standard. In Section 3, we introduce models in the absence of a gold standard. In Section 4, we present case studies to illustrate the approaches described in Sections 2 and 3. The annotated SAS code to implement these approaches is presented in the appendix.

The following notation is used throughout this paper:

π	Disease prevalence
Se (Sp)	Sensitivity (Specificity)
TPR (FPR)	True positive rate (false positive rate)
ROC	Receiver operating characteristic
AIC	Akaike information criterion
BIC	Bayesian information criterion
GLMM	Generalized Linear Mixed Model
BLMM	Bivariate Linear Mixed Model
SE	Standard Error

2. Statistical methods when the reference test is a gold standard

When the reference test can be considered a gold standard, let n_i11, n_i00, n_i01, and n_i10 be the number of true positives, true negatives, false positives and false negatives for the i^th study (i = 1, 2, …, N), respectively. Let n_i1+ = n_i11 + n_i10 and n_i0+ = n_i01 + n_i00 be the study-specific numbers of diseased and disease-free subjects. Then the study-specific sensitivity and specificity can be estimated as ${\widehat{Se}}_i=n_{i11}/n_{i1+}$, and ${\widehat{Sp}}_i=n_{i00}/n_{i0+}$. See Table 1 for a typical 2 by 2 table.

Table 1.

2 by 2 table for i^th study

		Reference test		total
		Positive (+)	Negative (−)
Diagnostic Test	Positive (+)	ni11	ni01
	Negative (−)	ni10	ni00
Total		ni1+	ni0+	ni++

In this section, we will first discuss the conventional summary ROC approach and a bivariate approach using linear mixed models (LMM). Both methods require direct calculations of study-specific sensitivities and specificities, and an ad hoc continuity correction when there are empty cells. Second, we will discuss the hierarchical summary ROC approach for jointly modeling positivity criteria and accuracy parameters, and a bivariate approach using generalized linear mixed models (GLMM) for jointly modeling sensitivities and specificities. At last, we will discuss a trivariate approach using GLMM for jointly modeling prevalence, sensitivities and specificities to account for the correlations among the three parameters. The hierarchical summary ROC approach, and the bivariate and trivariate approaches are based on the exact binomial distribution and thus do not require any ad hoc continuity correction.

2.1 The summary ROC method

The summary ROC curve method was first proposed by Moses et al.²² Reflecting the trade-off between sensitivity and specificity caused by implicit thresholds, this method had been widely used in diagnostic tests studies. As test threshold varies, the observed Se and Sp estimates can form a concave shape for the ROC curve. Such a curve can be fitted by back-transforming the linear relationship between the logit transformations of Se and Sp to the ROC space: First, if some studies have n_i11 =0 or n_i00 =0, an ad hoc continuity correction is applied by adding 0.5 to each of the 4 cells of such studies. After the correction, sensitivity is estimated as ${\widehat{Se}}_i=(n_{i11}+0.5)/(n_{i1+}+1)$ and specificity is estimated as ${\widehat{Sp}}_i=(n_{i00}+0.5)/(n_{i0+}+1)$ for the i^th study. Second, define variables S and D as the sum and the difference of logit transformed sensitivity and specificity, such that $S_i=\text{logit}({\widehat{Se}}_i)+\text{logit}({\widehat{Sp}}_i)$ and $D_i=\text{logit}({\widehat{Se}}_i)-\text{logit}({\widehat{Sp}}_i)$, where logit(p) = log(p / (1– p)). This notation is slightly different than Moses et al.²² because the original transformation is on Se and one minus Sp (1– Sp). One can see that $S_i=log({\widehat{OR}}_i)$, where ${\widehat{OR}}_i=\frac{n_{i11}}{n_{i10}}/\frac{n_{i01}}{n_{i00}}$ is the diagnostic odds ratio for the i^th study. Third, for N studies, fit a linear regression line S = a + bD either by an ordinary least squares or by a weighted least squares method weighing by the inverse of within-study variance $var{(log({\widehat{OR}}_i))}^{-1}$, where $var(log({\widehat{OR}}_i))=1/n_{i11}+1/n_{i10}+1/n_{i01}+1/n_{i00}$.⁵ After fitting the regression line using either un-weighted or weighted method, one can plot the summary ROC curve by the two estimated coefficients (i.e., intercept â and slope b̂),

$$Se={\left[1+{\mathrm{e}}^{-a/(1-\widehat{b})}\times {\left(Sp/(1-Sp)\right)}^{(1+\widehat{b})/(1-\widehat{b})}\right]}^{-1},$$ (1)

with Se on the y-axis and 1– Sp on the x-axis. To adjust for study-level covariates Z (e.g., different anatomical sites from which the diagnostic tests were obtained), one can fit a model with S_i = a +bD_i + cZ_i. We can then have S_i = â + b̂D_i +ĉZ_i = (â + ĉZ_i) + b̂D_i = â′ + b̂′D_i. The summary ROC curve can be plotted according to new estimates â′ and b̂′ given Z.

The summary ROC method is easy to perform but suffers limitations. First, its interpretation is known to be problematic. Walter discussed the interpretation of area under the curve (AUC).²³ A summary ROC curve located closer to the left upper corner of the ROC space will have a larger AUC, indicating better predictive accuracy of a test.²³ However, the conclusion becomes unreliable when comparing tests whose summary ROC curves may cross each other. Alternative statistics, such as the partial AUC²⁴ and the Q point²⁵ also have limited application. Second, the model setting has some drawbacks. First, because $S_i=log({\widehat{OR}}_i)$, the data are reduced to one outcome measure per study: diagnostic odds ratio. Independent summaries of sensitivity and specificity are not available, which could be important in test evaluation. Also, the model is restricted in that the between-study heterogeneity can only be adjusted by study level covariates, such that some components of the variance might not be explained. This is the reason why both Moses et al.²² and Irwig et al.²⁶ recommended the unweighted least squares rather than the weighted, as in a fixed effect model, a few large studies may dominate the result if the between-study variation is present. In addition, in practice, study characteristics besides the cut-point effect contribute to the trade-off between sensitivity and specificity within a study,^{22, 27} which are not incorporated in the summary ROC curves. Finally, an arbitrary continuity correction is needed to handle zero cells. Moses showed that it can push the summary ROC curve far from the ideal upper left corner of the ROC space, giving biased results.²⁴ Moreover, there is a long-standing debate on what arbitrary number should be added to handle zero cells.^{28, 29}

2.2 A Bivariate Approach Based on Linear Mixed Models

To improve upon the summary ROC method, Reitsma et al. proposed a bivariate LMM.¹¹ The model proceeds as follows. First, logit transforms of the sensitivity and specificity are applied to each study. Different from the summary ROC method, they are considered as random by allowing variation according to normal distributions, that is $\text{logit}({Se}_i)~N({\mu }_0,{\sigma }_{\mu }^2)$ and $\text{logit}({Sp}_i)~N({\nu }_0,{\sigma }_{\nu }^2)$. A bivariate normal distribution can include possible correlation between sensitivity and specificity within study: $\left(\begin{array}{c}\text{logit}({Se}_i)\\ \text{logit}({Sp}_i)\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_0\\ {\nu }_0\end{array}\right),\mathrm{\sum }\right)$, where $\mathrm{\sum }=\left(\begin{array}{cc}{\sigma }_{\mu }^2& {\sigma }_{\mu \nu }\\ {\sigma }_{\mu \nu }& {\sigma }_{\nu }^2\end{array}\right)$ and σ_μν denotes the covariance between logit sensitivity and specificity.

Second, to account for the sampling variation, the estimated logit sensitivity and specificity are assumed to be normally distributed as $\left(\begin{array}{c}\text{logit}({\widehat{Se}}_i)\\ \text{logit}({\widehat{Sp}}_i)\end{array}\right)~N\left(\left(\begin{array}{c}\text{logit}({Se}_i)\\ \text{logit}({Sp}_i)\end{array}\right),C_i\right)$ for study i, where C_i is a diagonal matrix with components of $var\left(\text{logit}\left({\widehat{Se}}_i\right)\right)={n_{i11}}^{-1}+{n_{i10}}^{-1}$ and $var\left(log\mathit{it}\left({\widehat{Sp}}_i\right)\right)={n_{i01}}^{-1}+{n_{i00}}^{-1}$. Note that, the general rule that $n_{i1+}\widehat{{Se}_i},n_{i1+}(1-\widehat{{Se}_i}),n_{i0+}\widehat{{Sp}_i}$, and $n_{i0+}(1-\widehat{{Sp}_i})$ are at least five need to hold for normal approximation to be valid. Consequently, $\text{logit}({\widehat{Se}}_i)$ and $\text{logit}({\widehat{Sp}}_i)$ are assumed to have the following bivariate normal distribution:

$$\left(\begin{array}{c}\text{logit}({\widehat{Se}}_i)\\ \text{logit}({\widehat{Sp}}_i)\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_0\\ {\nu }_0\end{array}\right),\mathrm{\sum }+C_i\right).$$ (2)

Because the distributions of sensitivity and specificity are often skewed, one may prefer inference based on the medians rather than means as overall diagnostic test performance summaries. Based on parameter estimates, the median sensitivity and specificity can be back-transformed as ${\widehat{Se}}_M={\text{logit}}^{-1}({\widehat{\mu }}_0)$ and ${\widehat{Sp}}_M={\text{logit}}^{-1}({\widehat{\nu }}_0)$. Similarly, confidence intervals for ${\widehat{Se}}_M$ and ${\widehat{Sp}}_M$ can be transformed from the confidence intervals of μ̂₀ and ν̂₀. The correlation between sensitivity and specificity can be estimated as $\frac{{\widehat{\sigma }}_{\mu \nu }}{{\widehat{\sigma }}_{\mu }\times {\widehat{\sigma }}_{\nu }}$. The standard errors are $SE({\widehat{Se}}_M)=\frac{SE(\widehat{\mu })}{1/{\widehat{Se}}_M+1/(1-{\widehat{Se}}_M)}$ and $SE({\widehat{Sp}}_M)=\frac{SE(\widehat{\nu })}{1/{\widehat{Sp}}_M+1/(1-{\widehat{Sp}}_M)}$ based on the Delta method. A summary ROC curve can be constructed by

$$\text{logit}(Se)={\widehat{\mu }}_0+\frac{{\widehat{\sigma }}_{\mu \nu }}{{{\widehat{\sigma }}_{\nu }}^2}(\text{logit}(Sp)-{\widehat{\nu }}_0).$$ (3)

In general, this approach is superior to the summary ROC model by analyzing sensitivity and specificity jointly in a bivariate linear mixed model. However, the bivariate approach estimates the degree of correlation between sensitivity and specificity, as well as both within- and between-study variation in the two indexes separately. A drawback of this approach is that an ad hoc continuity correction is required in the presence of zero cells, as with the summary ROC approach. In addition, the normal approximation is sometimes violated in practice¹². The bivariate model can adjust for covariates by regression model for the mean vector of the bivariate normal distribution: $\left(\begin{array}{c}\text{logit}({Se}_i)\\ \text{logit}({Sp}_i)\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_0+\gamma Z_i\\ {\nu }_0+\lambda Z_i\end{array}\right),\mathrm{\sum }\right)$, where Z_i is the study-level covariate and γ, λ are the corresponding coefficient parameters.⁵ Adjusting for individual level covariates is also straightforward.

2.3 The Hierarchical summary ROC Approach

Rutter and Gatsonis proposed a hierarchical summary ROC approach,³ which is a simplification of the ordinal regression model by Tosteson and Begg: g(γ_j (x)) =(θ_j –α′x)e^β′x, where g(.) is a link function, γ_j (x) is the probability of a response being in one of the ordered categories given covariates x, θ_j is the cutoff values of each category, α is the location parameters and β is the scale parameter.³⁰ The hierarchical summary ROC approach reduces the ordinal regression model to two categories (j=1,2), with x indicates true disease status (coded as 0.5 for D+ and −0.5 for D−) and γ_j (x) correspond to positive test rates: Se_i and 1– Sp_i (FPR).³

The first stage of this model assumes binomial distributions of the number of positive outcomes in the i^th study, i.e., n_i11 ~ Bin(n_i1+, Se_i) and n_i01 ~ Bin(n_i0+,1 – Sp_i). Choose g(.) to be a logit link, the model is written as,

$$\text{logit}({Se}_i)=({\theta }_i+0.5{\alpha }_i)e^{-0.5\beta },\text{logit}(1-{Sp}_i)=({\theta }_i-0.5{\alpha }_i)e^{0.5\beta },$$ (4)

where the latter is the same as logit(Sp_i) = −(θ_i – 0.5α_i)e^0.5β. The positivity criterion θ_i models the tradeoff between sensitivity and specificity in each study. Direct interpretations of the accuracy parameters α_i are that when β = 0, α_i =logit(Se_i) + logit(Sp_i) = log(DOR_i), which is independent of θ_i. In the second stage, Rutter and Gatsonis allow θ_i and α_i to vary across studies.³ Thus, θ_i and α_i are assumed independently and normally distributed as: $\left(\begin{array}{c}{\theta }_i\\ {\alpha }_i\end{array}\right)~N\left(\left(\begin{array}{c}{\theta }_0\\ {\alpha }_0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\theta }^2& 0\\ 0& {\sigma }_{\alpha }^2\end{array}\right)\right)$.

A summary ROC curve can be derived based on solving functions in (4) as

$$\text{logit}({Se}_i)={\alpha }_i{e}^{-\beta /2}+e^{-\beta }\text{logit}(1-{Sp}_i).$$

Another possible construction of a summary ROC curve pointed out by Chu et al.¹³ is based on the bivariate normal distribution of θ_i and α_i as

$$\text{logit}(Se)=e^{-0.5\widehat{\beta }}\left(0.5{\widehat{\alpha }}_0+{\widehat{\theta }}_0\right)+\frac{0.25{\widehat{\sigma }}_{\alpha }^2-{\widehat{\sigma }}_{\theta }^2}{0.25{\widehat{\sigma }}_{\alpha }^2+{\widehat{\sigma }}_{\theta }^2}\times e^{-\widehat{\beta }}\left[\text{logit}(Sp)-e^{0.5\widehat{\beta }}\left(0.5{\widehat{\alpha }}_0-{\widehat{\theta }}_0\right)\right].$$ (5)

In addition, Arends et al. discussed several choices of SROC curves.¹⁰ Median sensitivity and specificity estimates are ${\widehat{Se}}_M={\left\{1+exp\left[-\left({\widehat{\theta }}_0+0.5{\widehat{\alpha }}_0\right)e^{-0.5\widehat{\beta }}\right]\right\}}^{-1}$ and ${\widehat{Sp}}_M={\left\{1+exp\left[\left({\widehat{\theta }}_0-0.5{\widehat{\alpha }}_0\right)e^{0.5\widehat{\beta }}\right]\right\}}^{-1}$. Also, similar as the previous models, the hierarchical summary ROC approach can incorporate study level covariates by $\left(\begin{array}{c}{\theta }_i\\ {\alpha }_i\end{array}\right)~N\left(\left(\begin{array}{c}{\theta }_0+\gamma Z_i\\ {\alpha }_0+\lambda Z_i\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\theta }^2& 0\\ 0& {\sigma }_{\alpha }^2\end{array}\right)\right)$.

The hierarchical summary ROC approach incorporates both within- and between-study variability and the correlation between the summary statistics by random effects θ_i and α_i. Because sparse data is common in meta-analysis of diagnostic tests, an important advantage over the previous models is that the hierarchical summary ROC approach avoids the continuity correction by assuming the exact binomial distributions.³ A practical limitation of this model is that originally it was fitted using Bayesian Markov Chain Monte Carlo approach implemented in BUGS, which requires some programming expertise. This approach is found to be the same as the following bivariate GLMM with alternative parameterizations in some situations.

2.4 The Bivariate Generalized Linear Mixed Model

Chu and Cole presented a bivariate GLMM to jointly analyze sensitivity and specificity using logit link.¹² Later, the bivariate GLMM was broadened to a general link function.³¹ The model starts with binomial distribution assumptions and applies link functions on the probability parameters:

$$n_{i11}~\text{Bin}\left(n_{i1+},{Se}_i\right),n_{i00}~\text{Bin}\left(n_{i0+},{Sp}_i\right),\mathrm{g}({Se}_i)={\mu }_0+{\mu }_i,g({Sp}_i)={\nu }_0+{\nu }_i,$$ (6)

where μ_i and ν_i are random effects follow bivariate normal distribution $\left(\begin{array}{c}{\mu }_i\\ {\nu }_i\end{array}\right)~N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{\mu }^2& \rho {\sigma }_{\mu }{\sigma }_{\nu }\\ \rho {\sigma }_{\mu }{\sigma }_{\nu }& {\sigma }_{\nu }^2\end{array}\right)\right]$, and g(.) is a link function such as the logit, probit, or complimentary log-log link. Different link functions can be applied to sensitivity and specificity. Though to date the logit link is the most widely used in meta-analysis, Chu et al. argued that, for some meta-analyses, the choice of the link may affect model fit and inference.³¹ The parameters ${\sigma }_{\epsilon }^2,{\sigma }_{\mu }^2,{\sigma }_{\nu }^2$ estimate the between-study variances and ρ_εμ, ρ_εν, ρ_μν explain possible correlations.

The model gives median estimates as ${\widehat{Se}}_M={\text{logit}}^{-1}({\widehat{\mu }}_0)$ and ${\widehat{Sp}}_M={\text{logit}}^{-1}({\widehat{\nu }}_0)$. Similarly, confidence intervals for ${\widehat{Se}}_M$ and ${\widehat{Sp}}_M$ can be transformed from the confidence intervals of μ̂₀ and ν̂₀. Study-level covariate Z can be included as g(Se_i) = μ₀ + μ_i + γZ_i and g(Sp_i) = ν₀ +ν_i + λZ_i, where γ, λ are corresponding coefficient parameters. Different covariates could be used for sensitivity and specificity. A regression line of g(Se) on g(Sp), $g(Se)={\widehat{\mu }}_0+\widehat{\rho }\frac{{\widehat{\sigma }}_{\mu }}{{\widehat{\sigma }}_{\nu }}[g(Sp)-{\widehat{\nu }}_0]$, gives the summary ROC curve by transforming to the ROC space. Also, alternative choices of the regression lines can construct different summary ROC curves with corresponding interpretations.¹⁰

In addition to estimating the heterogeneity and correlation parameters, both hierarchical summary ROC and bivariate GLMM approaches have advantages over the bivariate LMM. First, the bivariate GLMM does not require the normal approximation to estimate $var(\text{logit}(\widehat{{Se}_i}))$ and $var(\text{logit}(\widehat{{Sp}_i}))$. Second, neither of the two approaches requires a continuity correction because direct calculation of study-specific sensitivities and specificities is not involved. In the absence of study-level covariates, the two approaches are equivalent (with alternative parameterizations).⁶

Both hierarchical summary ROC and bivariate GLMM can be fitted using maximum likelihood. Several numerical methods might be used, for instance, the dual quasi-Newton optimization techniques, as implemented in the SAS procedure NLMIXED. The standard errors and confidence intervals for parameters are estimated by the Delta method and are reported automatically if specified in the ESTIMATE statement. To restrict the correlation coefficient ρ in the range [−1, 1] in the bivariate GLMM, one can use the Fisher’s z transformation of ρ. AUC for both hierarchical summary ROC and bivariate GLMM can be computed by numerical integration implemented in a SAS macro, which is available upon request from the first author.

2.5 The Trivariate Generalized Linear Mixed Model

The above approaches involving only sensitivities and specificities work best if all or the majority of the studies use case-control designs. When disease prevalence estimation is allowed, as in cohort study designs, we can derive other clinically interesting indices such as positive and negative predictive values. In this case, the test performance indexes Se and Sp can be correlated with the prevalence, which is commonly termed ‘spectrum bias’.³² Such dependence is particularly of concern when the binary diagnostic outcome is based on a cut-off point on a continuous trait, thus misclassification rates could be higher among subjects with true value near the cut point.³³ To account for this potential dependence, Chu et al. extended the bivariate GLMM to a trivariate GLMM jointly modeling the disease prevalence, sensitivity and specificity.¹⁷ Recently, Li and Fine proposed a Pearson-type correlation coefficient to assess this dependence by an estimating equation-based regression framework.³⁴

Here, we consider a trivariate GLMM based on the parameterization of π_i, Se_i and Sp_i, where π_i is the disease prevalence in the i^th study. The first level of this model assumes binomial distributions:

$$n_{i1+}~\text{Bin}\left(n_{i++},{\pi }_i\right),n_{i11}~\text{Bin}\left(n_{i1+},{Se}_i\right),n_{i00}~\text{Bin}\left(n_{i0+},{Sp}_i\right).$$ (7)

The parameters are modeled via link functions: g(π_i) = ε₀ + ε_i, g (Se_i) = μ₀ + μ_i and g (Sp_i) =ν₀ +ν_i. See Table 2 a two by two table accounting for disease prevalence.

Table 2.

2 by 2 table for ith study accounting for disease prevalence

Diagnostic Test	Reference Test		Total
	Positive (+)	Negative (−)
Positive (+)	ni11	ni01
	πi Sei	(1−πi)(1− Spi)
Negative (−)	ni10	ni00
	πi (1−Sei)	(1−πi)(Spi)
Total	ni1+	ni0+	ni++
	πi	1−πi	1

To consider heterogeneity and potential correlations of the 3 parameters, ε_i, μ_i and ν_i are assumed to be random effects with trivariate normal distribution:

$$\left(\begin{array}{c}{\epsilon }_i\\ {\mu }_i\\ {\nu }_i\end{array}\right)~N\left(\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),\mathrm{\sum }\right),\text{where}\mathrm{\sum }=\left(\begin{array}{ccc}{\sigma }_{\epsilon }^2& {\rho }_{\epsilon \mu }{\sigma }_{\mu }{\sigma }_{\epsilon }& {\rho }_{\epsilon \nu }{\sigma }_{\nu }{\sigma }_{\epsilon }\\ & {\sigma }_{\mu }^2& {\rho }_{\mu \nu }{\sigma }_{\mu }{\sigma }_{\nu }\\ & & {\sigma }_{\nu }^2\end{array}\right).$$

The parameters ${\sigma }_{\epsilon }^2,{\sigma }_{\mu }^2,{\sigma }_{\nu }^2$ capture the between-study variance of the disease prevalence, sensitivity and specificity while ρ_εμ, ρ_εν, ρ_μν represent correlations.

Standard software such as SAS NLMIXED can maximize this likelihood. To avoid including unnecessary parameters, model selection criteria such as AIC can be used. The medians are derived as π̂_M =g⁻¹(ε̂₀), ${\widehat{Se}}_M=g^{-1}({\widehat{\mu }}_0)$ and ${\widehat{Sp}}_M=g^{-1}({\widehat{\nu }}_0)$. In this model, covariates can be incorporated for sensitivities, specificities and disease prevalence as was done for the bivariate GLMM.

3. Statistical methods when the reference test is not a gold standard

Limited meta-analysis tools are available when the reference test is imperfect. Walter et al. discussed the latent class model for a meta-analysis of two diagnostic tests.¹⁸ Sadatsafavi et al. presented a latent class random effects model.²⁰ However, beyond prevalence, only one of the sensitivity and specificity can be implemented as a random effect. Dendukuri et al. presented a Bayesian approach, which is an extension of the hierarchical summary ROC model, to adjust for different reference standards.²¹ We describe the latent class random effects model by Chu et al. using random effects to allow variation and correlation in sensitivity, specificity and prevalence between studies.¹⁹

Let (Se_Bi, Sp_Bi) be the pair of diagnostic accuracy parameters for the reference test while (Se_Ai, Sp_Ai) be the pair for the diagnostic test of interest. To construct the 2 by 2 table (Table 3) for such studies, both the above pairs of statistics and the disease prevalence are needed.

Table 3.

2 by 2 table when the reference test is not a gold standard

		Reference test		Total
		+	−
Diagnostic test	+	ni11	ni01
		pi 11 =πiSeAiSeBi + (1−πi)(1−SpAi)(1−SpBi)	pi 01 = πiSeAi (1−SeBi) + (1−πi)(1−SpAi)SpBi
	−	ni10	ni00
		pi 10 =πi (1− SeAi)SeBi + (1−πi)SpAi (1−SpBi)	pi 00 = πi (1− SeAi)(1 − SeBi) + (1 − πi)SpAi SpBi
Total		ni1+	ni0+	ni++
		pi1+ = πiSeBi + (1 −πi)(1 − SpBi)	pi 0+ = πi (1 − SeBi) + (1−πi)SpBi	1

^*Se_Ai, Sp_Ai are the sensitivity and specificity for the diagnostic test; Se_Bi, Sp_Bi are sensitivity and specificity for the reference test. π_i is the disease prevalence in the i^th study

The four counts in Table 3 follow a multinomial distribution, with the log-likelihood being:

$$logL=\sum _i\{n_{i11}log(p_{i11})+n_{i10}log(p_{i10})+n_{i01}log(p_{i01})+n_{i00}log(p_{i00})\}.$$ (8)

Chu et al. used random effects to model between and within study heterogeneity and potential correlations.¹⁹ We write this model in a form suitable for a general link function:

$$g\left({\pi }_i\right)={\epsilon }_0+{\epsilon }_i;g\left({Se}_{Ai}\right)={\mu }_{A0}+{\mu }_{Ai};g\left({Sp}_{Ai}\right)={\nu }_{A0}+{\nu }_{Ai};g\left({Se}_{Bi}\right)={\mu }_{B0}+{\mu }_{Bi};g\left({Sp}_{Bi}\right)={\nu }_{B0}+v_{Bi},$$

where random effects follow a multivariate normal distribution: (ε_i, μ_Ai, ν_Ai, μ_Bi, ν_Bi)′ ~ N (0, Σ) with variance-covariance matrix $\mathbf{\sum }=\left(\begin{array}{ccccc}{\sigma }_{\epsilon }^2& {\rho }_{\epsilon {\mu }_A}{\sigma }_{\epsilon }{\sigma }_{{\mu }_A}& {\rho }_{\epsilon {\nu }_A}{\sigma }_{\epsilon }{\sigma }_{{\nu }_A}& {\rho }_{\epsilon {\mu }_B}{\sigma }_{\epsilon }{\sigma }_{{\mu }_B}& {\rho }_{\epsilon {\nu }_B}{\sigma }_{\epsilon }{\sigma }_{{\nu }_B}\\ & {\sigma }_{{\mu }_A}^2& {\rho }_{{\mu }_A{\nu }_A}{\sigma }_{{\mu }_A}{\sigma }_{{\nu }_A}& {\rho }_{{\mu }_A{\mu }_B}{\sigma }_{{\mu }_A}{\sigma }_{{\mu }_B}& {\rho }_{{\mu }_A{\nu }_B}{\sigma }_{{\mu }_A}{\sigma }_{{\nu }_B}\\ & & {\sigma }_{{\nu }_A}^2& {\rho }_{{\nu }_A{\mu }_B}{\sigma }_{{\nu }_A}{\sigma }_{{\mu }_B}& {\rho }_{{\nu }_A{\nu }_B}{\sigma }_{{\nu }_A}{\sigma }_{{\nu }_B}\\ & & & {\sigma }_{{\mu }_B}^2& {\rho }_{{\mu }_B{\nu }_B}{\sigma }_{{\mu }_B}{\sigma }_{{\nu }_B}\\ & & & & {\sigma }_{{\nu }_B}^2\end{array}\right)$.

Median estimates of prevalence, sensitivities and specificities can be constructed as π̂_M = g⁻¹(ε̂₀), ${\widehat{Se}}_{AM}=g^{-1}({\widehat{\mu }}_{A0}),{\widehat{Sp}}_{AM}=g^{-1}({\widehat{\nu }}_{A0}),{\widehat{Se}}_{BM}=g^{-1}({\widehat{\mu }}_{B0})$ and ${\widehat{Sp}}_{BM}=g^{-1}({\widehat{\nu }}_{B0})$. Variance and correlation parameter estimates can be derived from Σ̂. Covariates Z_i can be adjusted by linear regressions for the mean vectors, for instance g(π_i) =ε₀ +ε_i +γZ_i.

This latent class random effects model fills a gap in the existing models for meta-analysis with imperfect reference tests. This model can be used to evaluate the performance of both the diagnostic test of interest and the reference test while retaining all the advantages of the GLMMs. A limitation applies when fitting this model by SAS NLMIXED. One may encounter convergence problems because of the limited number of studies and relatively large number of parameters. Possible simplification of model assumptions may include letting disease prevalence be independent of sensitivities and specificities. Also, to avoid including unnecessary random effects whose variance approaches zero, one can apply a forward selection based on AIC. We will illustrate this process in Section 4.2 with an example.

4. Case Study

4.1 A meta-analysis of rotator cuff tears diagnosis using ultra-sound

4.1.1 Study background

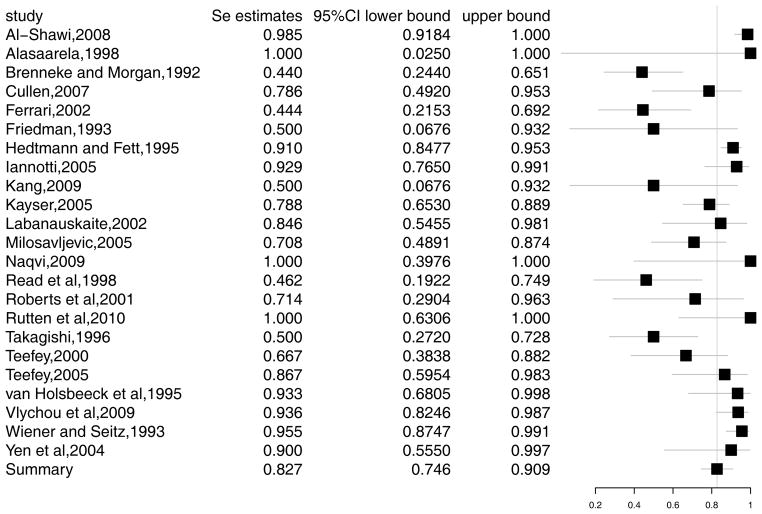
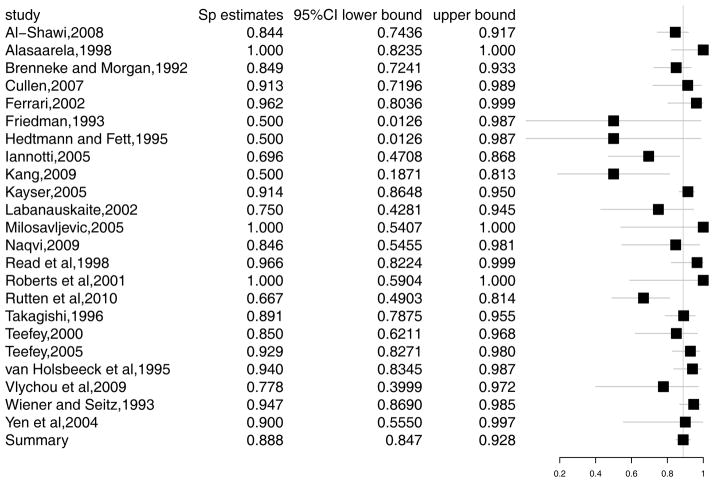
We demonstrate an application of the methods in Section 2 using data on ultra-sound diagnosis of rotator cuff tears. Rotator cuff tears are a common reason for shoulder pain, which is the third most common musculoskeletal complaint. The incidence of partial rotator cuff tears is reported to be 13% to 32% in cadaveric studies, yet much of this incidence goes undiagnosed.³⁵ Among the diagnostic tests for this disease, ultrasound is non-invasive and less expensive. However, it has lower sensitivity and specificity in detecting the disease than MRI or arthroscopic evaluation.³⁶ We will re-analyze the data from a meta-analysis of 30 studies of diagnostic accuracy of ultrasound for rotator cuff tears in adults, performed by Smith et al.³⁷ The studies compared the accuracy of ultrasound with either arthroscopic or open surgical findings as a gold standard test. The data is presented in Appendix A1. Figure 1 and 2 present the forest plots of sensitivity and specificity, respectively. In the rest of this section, we explore this example using the models discussed in Section 2. The corresponding SAS code can be found in Appendix B1-B6.

Figure 1.

Forest plot for sensitivity in rotator cuff tears study

Figure 2.

Forest plot for specificity in rotator cuff tears study

4.1.2 Summary ROC method

Applying the summary ROC method, we analyze the data first by unweighted least squares, then by weighted least squares. The un-weighted method gives estimates â =3.39, b̂ =0.131 and AUC=0.911. The AUC can be interpreted as a likelihood of 91.11% that a randomly selected diseased subject will receive a more suspicious rating than a non-diseased subject. The weighted method give estimates â_w =3.573, b̂_w =0.400 and AUC_w=0.910. To build the summary ROC curve, we plug in â and b̂ (â_w and b̂_w) into equation (1) then plot Se against 1–Sp. The summary ROC curves are presented in Figure 3.

Figure 3.

Summary median estimates and ROC curves from some of the introduced models. Panel A presents summary median Se and Sp estimates with confidence and predictive regions and summary ROC curve from the bivariate GLMM using logit link. Panel B presents summary median Se and Sp estimates with confidence and predictive regions and summary ROC curve from the BLMM and the summary ROC curve from the unweighted summary ROC method.

4.1.3 Bivariate LMM

To fit the bivariate linear mixed model, we use the SAS procedure MIXED. The bivariate LMM method can provide summary estimates of sensitivity and specificity other than the summary ROC curve. Parameter estimates are: μ̂ =1.351, ν̂ = 1.853, ${\widehat{\sigma }}_{\mu }^2=1.040,{\widehat{\sigma }}_{\nu }^2=0.399$, σ̂_μν = −0.116. The sensitivity and specificity are estimated as ${\widehat{Se}}_M=0.794$ and ${\widehat{Sp}}_M=0.865$. Correlation estimate is ρ̂ = −0.18. The standard errors (SE) can be calculated by delta method: $SE(\widehat{Se})=0.043$ and $SE(\widehat{Sp})=0.023$. Plugging in the estimates into the equation (3), one can draw the summary ROC curve as presented in Figure 3. This model gives an AUC of 0.858. With the estimated medians, standard errors and correlation coefficients, one can draw confidence and prediction regions around the median estimates. Compared with the summary ROC method, the Bivariate LMM can provide summary estimates of overall sensitivity and specificity and their confidence regions. It may be more intuitive for investigators to compare different diagnostic tests.

4.1.4 Hierarchical summary ROC model

The hierarchical summary ROC model is fitted using the SAS procedure NLMIXED. Estimates of the parameters are: θ̂₀ = −0.738, σ̂_θ = 0.708, α̂₀ = 3.887, σ̂_α = 1.045 and β̂ = −0.522. The median sensitivity and specificity are ${\widehat{Se}}_M=0.827$ with SE 0.042 and ${\widehat{Sp}}_M=0.888$ with SE 0.021. To draw the summary ROC curve, plug in the estimates into the expected logit sensitivity given specificity as in equation (5), then transform to ROC space, as presented in Figure 3. The AUC is 0.908.

4.1.5 Bivariate GLMM method

The bivariate GLMM models are fitted using the SAS procedure NLMIXED under three link functions: logit, probit and complementary log-log. The ‘estimate’ statements in the NLMIXED procedure can transform the parameter estimates to median sensitivity and specificity and carry out the estimation of standard errors via delta method. Table 4 reports summary indexes with standard errors. When dependence is assumed in the model, the three links give comparable summary estimates. The logit link provides the smallest AIC (214.8), and thus selected as the best fitted model. However, the negative correlation estimate has a large standard error. In fact, if one fit a logit link GLMM assuming independence, the AIC (213.5) is slightly smaller than the correlated model. This example does not strongly support correlation between sensitivity and specificity.

Table 4.

GLMM method estimates and standard errors (SE)

Model	Sensitivity	Specificity	ρ	AUC	σμ(SE)	σν(SE)	AIC	-2logL
logit link	0.827 (0.042)	0.888 (0.021)	−0.298 (0.330)	0.908 (0.049)	1.143 (0.243)	0.679 (0.208)	214.8	204.8
logit link-independence	0.826 (0.042)	0.887 (0.021)	0	0.902 (0.026)	1.138 (0.241)	0.678 (0.206)	213.5	205.5
probit link	0.817 (0.042)	0.885 (0.021)	−0.312 (0.325)	0.915 (0.051)	0.636 (0.132)	0.359 (0.111)	215.2	205.2
c-log-log link	0.801 (0.045)	0.882 (0.021)	−0.329 (0.321)	0.925 (0.041)	0.560 (0.119)	0.284 (0.090)	215.9	205.9

^*AUC denoted the area under the summary ROC curve. The boldfaced cells represent the best chosen model based on AIC. The ‘logit link-independece’ model uses logit link and assumes independence between sensitivity and specificity while the other models assume dependence.

To summarize estimates from bivariate models, we compare the bivariate LMM method, hierarchical summary ROC model and GLMM model using logit link. The summary ROC curves and confidence and prediction ellipses of these models are presented in Figure 3. Hierarchical summary ROC and GLMM models achieve same sensitivity and specificity median estimates and standard errors, which agrees with the argument by Harbord et al. that the two models are the same with different parameterizations.⁶ The bivariate LMM model has lower estimates of sensitivity and specificity. The differences may be due to the continuity correction applied in bivariate LMM and the some degrees of approximation involved in the MIXED procedure when study size is small.⁶ A simulation study from Chu and Cole demonstrated that the GLMM method provides unbiased estimates while the bivariate LMM model has biased estimates of Se_M, Sp_M and ρ.¹²

4.1.6 Trivariate GLMM

When the prevalence of disease is involved as in a trivariate model, case-control studies need to be excluded. All our studies included satisfy the 1st criterion in the QUADAS checklist which requires random selection of the sample.³⁷

To successfully capture possible correlations without including unnecessary correlations, we fit models with all possible correlation combinations. The parameters and desired estimates, AIC and log-likelihoods are summarized in Table 5. The best model with the smallest AIC of 2653.8 is model I with no correlations (boldfaced estimates in Table 5). This suggests no correlations among disease prevalence, sensitivity and specificity in this example. This conclusion agrees with the bivariate GLMM and the estimated median sensitivity and specificity are similar as the estimates from bivariate GLMM method using logit link in Section 4.1.5. This example shows that, when the prevalence is weakly correlated with sensitivity and specificity, the bivariate GLMM gives very similar estimates to that from the trivariate GLMM.

Table 5.

Trivariate model parameter estimates and standard errors

	Se (SE)	Sp (SE)	Disease prevalence (SE)	Test prevalence (SE)	σμ (SE)	σν (SE)	σε (SE)	ρμν (SE)	ρεμ (SE)	ρεμ (SE)	AIC	-2logL
model I	0.826 (0.041)	0.887 (0.021)	0.448 (0.075)	0.433 (0.058)	1.123 (0.236)	0.671 (0.203)	1.387 (0.260)	0	0	0	2653.8	2641.8
model II	0.827 (0.041)	0.888 (0.021)	0.448 (0.075)	0.433 (0.059)	1.130 (0.238)	0.673 (0.205)	1.387 (0.260)	−0.311 (0.328)	0	0	2655.0	2641
model III	0.826 (0.042)	0.877 (0.026)	0.448 (0.076)	0.438 (0.062)	1.138 (0.241)	0.715 (0.235)	1.396 (0.263)	0	0	−0.401 (0.471)	2654.5	2640.5
model IV	0.822 (0.042)	0.887 (0.021)	0.447 (0.075)	0.430 (0.060)	1.109 (0.237)	0.678 (0.206)	1.383 (0.260)	0	0.176 (0.256)	0	2654.5	2640.5
model V	0.823 (0.042)	0.879 (0.026)	0.447 (0.075)	0.435 (0.062)	1.117 (0.240)	0.702 (0.229)	1.381 (0.260)	0	0.122 (0.270)	−0.328 (0.547)	2656.2	2640.2
model VI	0.828 (0.042)	0.880 (0.025)	0.448 (0.076)	0.437 (0.062)	1.146 (0.244)	0.697 (0.223)	1.396 (0.263)	−0.247 (0.340)	0	−0.325 (0.516)	2655.9	2639.9
model VII	0.823 (0.042)	0.888 (0.021)	0.447 (0.075)	0.429 (0.061)	1.114 (0.238)	0.681 (0.208)	1.384 (0.259)	−0.284 (0.329)	0.165 (0.256)	0	2655.9	2639.9
model VIII	0.823 (0.042)	0.881 (0.025)	0.447 (0.075)	0.434 (0.064)	1.117 (0.239)	0.703 (0.226)	1.387 (0.261)	−0.298 (0.323)	0.175 (0.256)	−0.343 (0.502)	2657.5	2639.5

Model I–VIII is trivariate GLMM with all possible combinations of correlation parameters. Model I assumes all correlation coefficient ρ_μν,ρ_εμ and ρ_εν equal to 0. Model II, III, IV assume only one of the correlation coeffecients is not 0: ρ_μν ≠ 0, ρ_εν ≠ 0 and ρ_εμ ≠ 0, respectively. Model V–VII assumes two of the correlation coefficients are not 0: ρ_εμ ≠0 and ρ_εν ≠ 0, ρ_μν ≠0 and ρ_εν ≠ 0, ρ_μν ≠0 and ρ_εμ ≠ 0, respectively. Model VII assumes none of ρ_μν, ρ_εμ and ρ_εν are 0.

4.2 A meta-analysis of cervical cancer diagnosis using Pap smears test

In this section, we re-visit the example used by Walter et al. ¹⁸ and apply the latent class random effects models. The data is collected from a meta-analysis of Papanicolau (Pap) smears test accuracy by Fahey et al. The Pap smear is a quick, noninvasive and relatively inexpensive test for cervical cancer.³⁸ Fahey’s analysis consists of 59 cross-sectional studies using Pap smears as the diagnostic test and histology as the gold standard. However, Walter’s model argued that the histology test has sensitivity of 0.97 and specificity of 0.62, revealing lack of a perfect gold standard.¹⁸ Hence we will treat histology as an imperfect reference test then fit the data by the latent class random effects models in Section 3. The data is listed in Appendix A2 and corresponding SAS code is included in Appendix B7.

When fitting the model using the SAS procedure NLMIXED, convergence problems appeared as more random effects were added. Thus we assume prevalence to be independent of sensitivities and specificities for ease of fitting and apply a forward-selection procedure to select random effects. We begin with a fixed effects model, and add random effects sequentially. The process of selection is outlined in Table 6. The final model obtained is IVe, in which random effects are considered for the disease prevalence, Pap smear test sensitivity and specificity and the specificity of the histology test. The parameter estimates of the best fitted models at each step are provided in Table 7.

Table 6.

Pap test example – model selection procedure

Models	Random effects	-2logL	AIC	BIC
I	NA	45277	45287	45297
IIa	ε	41882	41894	41906
IIb	μA	43329	43341	43353
IIc	μB	43398	43410	43423
IId	νA	43520	43532	43544
IIe	νB	42838	42850	42863
IIIa	ε & μA	40510	40524	40539
IIIb	ε & μB	40888	40902	40917
IIIc	ε & νA	40894	40908	40922
IIId	ε & νB	40520	40534	40548
IVa	ε, μA & μB	39777	39793	39810
IVb	ε, μA & νA	39762	39778	39795
IVc	ε, μA & νB	40506	40522	40539
IVd	ε, μA, μB & ρμAμB	39777	39795	39814
IVe	ε, μA, νA & ρμAμB	39752	39770	39789
IVf	ε, μA, νB & ρμAνB	40503	40521	40540

Models in level I–IV include random effects and possible correlations denoted in the corresponding ‘random effects’ column. The procedure starts from the fixed effects model I. In Level 2, five possible random effects are added one at a time. Model IIa with random effect ε (prevalence) has smallest AIC, thus ε is carried to models in level 3. The same process continued until level IV because model fitting became unstable with more random effects than level IV and AIC was not significantly reduced anymore. The bold faced estimates represents the best model with smallest AIC in each level.

Table 7.

Pap test example—fitted estimates and standard errors

	Model Parameter Estimates (standard error)
	I	IIa	IIIa	IVe
Se_pap test( ${\widehat{Se}}_{AM}$)	0.815(1.420)	0.750(0.006)	0.664(0.043)	0.655(0.042)
Sp_pap testa( ${\widehat{Sp}}_{AM}$)	0.810(1.531)	0.795(0.010)	0.822(0.010)	0.835(0.032)
Se_reference( ${\widehat{Se}}_{BM}$)	0.842(1.418)	0.858(0.010)	0.829(0.009)	0.903(0.013)
Sp_reference( ${\widehat{Sp}}_{BM}$)	0.803(1.629)	0.900(0.009)	0.977(0.012)	0.989(0.014)
Prevalence(π̂M)	0.527(1.708)	0.588(0.061)	0.712(0.050)	0.636(0.048)
σε	NA	1.819(0.195)	1.727(0.194)	1.467(0.164)
σμA	NA	NA	1.367(0.147)	1.292(0.136)
σνA	NA	NA	NA	1.269(0.164)
σμB	NA	NA	NA	NA
σνB	NA	NA	NA	NA
ρμAνA	NA	NA	NA	−0.509(0.136)

Model I, IIa, IIIa and IVe are the same models specified in Table 6.

After adjustment for possible variation and correlations by random effects in our method, the final model IVe shows a low sensitivity for the Pap smears of 0.655 (SE=0.042) and a specificity of 0.835 (SE=0.032). However, the histology test outperforms the Pap smears with sensitivity of 0.903 (SE=0.013) and specificity of 0.989 (SE=0.014). Moreover, our estimates of the histology test differ from the estimates in Walter’s, suggesting a somewhat different interpretation in practice.¹⁸

5. Discussion

In this paper, we discussed methods for evaluating the performance of diagnostic tests for situations when the reference test can be considered a gold standard, as well as situations when it is error-prone. Under the scenario with a gold standard, we reviewed the traditional summary ROC method, bivariate LMM and the hierarchical summary ROC model. Then we focused on the random effect GLMM, because it has several advantages over the simpler methods. We showed how the bivariate GLMM can be fitted using a variety of link functions including logit, probit and complementary log-log, and extended the approach to a trivariate GLMM to jointly model prevalence, sensitivity and specificity. Under the situation with no gold standard, we built upon the latent class model proposed by Walter et al.¹⁸ by adding random effects to quantify possible correlation and variation following the methods by Chu et al..¹⁹ We worked through two empirical examples to illustrate the application of our models. We used the SAS procedures MIXED and NLMIXED to fit all models, and provide SAS code with detailed explanation in the Appendix. The SAS macro METADAS may assist in automating the fitting of bivariate and hierarchical summary ROC models for meta-analysis of diagnostic tests.³⁹

Several extensive simulation studies have been conducted in the literature to compare different methods. Hamza et al.⁴⁰ studied the univariate exact binomial likelihood approach against the univariate approximate normal likelihood approach in different simulation settings. The size of meta-analysis varied from 10 to 100 studies and the true median sensitivity values ranged from 0.6 to 0.93. Overall the simulations showed that the exact likelihood approach performs superior than the approximate approach in terms of bias and coverage probabilities. Riley et al.⁴¹ compared the bivariate random-effects meta-analysis dealing with dependence between two outcomes to the univariate random-effects meta-analysis. Simulation studies showed that the bivariate approach has smaller mean-square error and is recommended over the univariate approach. Chu et al.¹² conducted simulations to study the bivariate GLMM and the BLMM approaches. Size of meta-analysis varied from 25 to 250, and Se/Sp was either relatively low (0.7/0.8) or relatively high (0.9/0.95). The bivariate GLMM was shown to yield unbiased estimates of Se, Sp and their correlation, while the BLMM gave biased results. Another paper of Chu et al.³¹ conducted simulations to compare different links used in bivariate GLMM with 40 meta-studies, 200 subjects in each study and median Se/Sp as 0.8/0.9. It suggested that the AUC and median Se/Sp estimates are relatively robust to the choice of link functions. The trivariate GLMM and bivariate GLMM were compared in Chu et al.¹⁷ under different correlation assumptions. The results suggested that misspecification resulting from AIC-based model selection is reasonably low in studied settings. When the reference test is imperfect, Chu et al.¹⁹ used different selection criteria DIC, AIC and BIC on selecting the appropriate random effects. The simulation results recommended including random effects because omitting important variability can cause inflated variance and decreased coverage.

Among the models presented, the summary ROC approach is simple and widely used. However, it is limited as it does not assess the within- and between-study variations and possible correlations between Se and Sp. The bivariate LMM improves over the summary ROC approach by assuming random effects to explain both within- and between-study variations and possible correlations. The bivariate LMM can provide inferences both in terms of summary ROC curves and summary statistics of overall test performance. However, it has limitations due to the use of a continuity correction and a normal approximation. The GLMMs do not have the limitations of the above models because they assume exact binomial distributions. The bivariate GLMM, which is essentially the same as the hierarchical summary ROC model in certain situations, is recommended when research interests focus on sensitivity and specificity and there’s strong suggestion of independence with disease prevalence. The trivariate GLMM will be most appropriate when there’s interest in estimating PPV or NPV, because estimation of disease prevalence is required and correlation among prevalence and Se, Sp should not be ignored. Besides, the trivariate GLMM is most reliable when most of the studies are cohorts. When the reference test is not a gold standard, the latent class random effects model should be used to avoid biased estimates.

A limitation related to the GLMMs is that the meta-analysis reported often includes a mixture of case-control and cohort studies designs. Thus using either the bivariate or the trivariate GLMM for all the studies can lead to problems. Another issue arises when fitting the trivariate GLMM and the latent class random effects models in the SAS procedure NLMIXED. The more random effects included, the longer it takes to converge. Under such situations, one can first get raw estimates of the desired parameters by fitting the data in models with fewer random effects. The raw estimates can then be used as starting values to improve convergence in a more complex model. For the latent class random effects model, one may need to apply simpler assumptions for ease of fitting. For instance, our example assumes independence between prevalence and the paired indices. However, as discussed, dependence between the indices may be expected.

In the example of rotator cuff tears, we excluded seven studies having the partial verification problem to avoid biased results, though these studies might still be able to contribute to our analysis. To the best of our knowledge, multivariate methods to correct publication bias in a meta-analysis of diagnostic test settings still await for further development. A recent Bayesian approach to correct such bias by de Groot et al. may be applied to diagnostic tests with nominal outcomes.⁴² In summary, sensitivity analysis methods for meta-analysis of diagnostic tests investigating the impact of publication bias through a selection or pattern mixture model framework are yet to be developed.

Appendix A. Data for case studies

Appendix A1.

Partial rotator cuff tears meta-analysis data

study	year	True positive	False positive	False negative	True negative
Al-Shawi	2008	65	12	1	65
Alasaarela	1998	1	0	0	19
Brenneke and Morgan	1992	11	8	14	45
Cullen	2007	11	2	3	21
Ferrari	2002	8	1	10	25
Friedman	1993	2	0	2	0
Hedtmann and Fett	1995	121	0	12	0
Iannotti	2005	26	7	2	16
Kang	2009	2	5	2	5
Kayser	2005	41	16	11	171
Labanauskaite	2002	11	3	2	9
Milosavljevic	2005	17	0	7	6
Naqvi	2009	4	2	0	11
Read et al	1998	6	1	7	28
Roberts et al	2001	5	0	2	7
Rutten et al	2010	8	12	0	24
Takagishi	1996	10	7	10	57
Teefey	2000	10	3	5	17
Teefey	2005	13	4	2	52
van Holsbeeck et al	1995	14	3	1	47
Vlychou et al	2009	44	2	3	7
Wiener and Seitz	1993	64	4	3	71
Yen et al	2004	9	1	1	9

Appendix A2.

Pap smear test meta-analysis data

Study	Type*	ni11	ni10	ni00	ni01
Alloub et al	SC	8	23	84	3
Alons-van Kordelaar and Boon	SC	31	43	14	3
Anderson et al	SC	70	121	25	12
Anderson et al	FU	65	6	6	10
Anderson et al	FU	20	19	4	3
Andrews et al	FU	35	20	156	92
August	FU	39	111	271	7
Bigrigg et al	SC	567	140	157	117
Bolger and Lewis	SC	26	12	18	37
Byme et al	FU	38	17	37	28
Chomet	SC	45	15	48	35
Engineer and Misra	SC	71	10	306	87
Fletcher et al	FU	4	36	5	0
Frisch et al	SC	2	3	21	2
Giles et al	SC	5	3	182	9
Giles et al	FU	38	7	62	21
Gunderson et al	SC	4	16	31	2
Haddad et al	SC	87	12	9	13
Hellberg et al	SC	15	65	15	3
Helmerhorst et al	FU	41	61	29	1
Hirschowitz et al	FU	76	11	12	12
Jones DED et al	FU	10	48	174	4
Jones MH et al	FU	28	28	77	11
Kashimura et al	SC	3	5	1	0
Kealy	FU	79	13	182	26
Koonlng-1 et al	FU	61	27	35	20
Koonlng-2 et al	FU	62	16	49	20
Kwikkel et al	FU	284	68	68	31
Lozowski et al	FU	66	20	44	25
Maggi et al	FU	40	12	47	43
Morrison EAB et al	FU	11	1	2	1
Morrison BW et al	SC	23	10	44	50
Nyirjesy	SC	65	42	13	13
Okagaki and Zelterman	SC	1270	263	1085	927
Oyer and Hanjanl	FU	223	74	83	22
Parker	SC	154	20	237	30
Pearlstone et al	FU	6	12	81	2
Ramlrez et al	SC	7	3	4	4
Reld et al	SC	12	11	60	5
Robertson et al	FU	348	212	103	41
Schauberger et al	SC	8	11	34	4
Shaw	FU	12	6	0	2
Singh et al	FU	95	2	1	9
Skehan et al	FU	40	20	19	18
Smith et al	FU	71	20	18	13
Soost et al	SC	1205	454	241	186
Soutter-1 et al	SC	5	52	27	20
Soutter-2 et al	SC	35	12	12	9
Spitzer et al	FU	10	5	32	31
Stafi	SC	3	3	15	5
Syrjanen et al	FU	118	44	183	40
Szarewski	SC	13	82	17	3
Tait et al	SC	38	13	62	14
Tawa et al	SC	14	67	291	25
Tay et al	FU	12	6	12	14
Upadhyay et al	SC	238	2	16	52
Walker et al	FU	111	20	39	44
Wetrich	FU	491	250	702	164
Wheelock and Kamlnlski	FU	49	39	31	16

^*type of the study denotes the usage of the test clinically, SC as screening and FU as follow up.

Appendix B. SAS codes for fitting models

B1. Unweighted summary ROC

data partial1;                                   | /*‘tp’ stands for true positive, ‘fp’ for
 set partial;                                    | false positive, ‘fn’ for false negative, ‘tn’
 if tp = 0 or fp = 0 or fn = 0 or tn = 0 then do;         | for true negative */
 tp=tp+0.5; fp=fp+0.5; fn=fn+ 0.5; tn=tn+ 0.5;        | /*continuity correction on zero cells*/
 n0=n0+1; n1=n1+1; end;
 se= tp/n1; sp=tn/n0;                             | /*calculate Se and Sp for each study*/
 logitse = log(se/(1-se)); var logitse=1/(se*(1-se)*n1);  | /* logit(Se) and logit(Sp) and their
 logitsp = log(sp/(1-sp)); var logitsp=1/(sp*(1 -sp)*n0); | variances*/
 D=logitse+logitsp; S=logitse-logitsp;                | /* D and S*/
proc reg data=partial1; model D=S; run;             | /*fit linear regression model D=a+bS*/

B2. Weighted summary ROC

data partial2; set partial1;
 w=1/(1/tp+1/fp+1/tn+1/fn);                        | /*calculate the weight for each study*/
proc reg data=partial2; model D=S; weight w; run;     | /*fit weighted regression using the created
                                               | weights*/

B3. SAS MIXED procedure to fit bivariate LMM

data partial3; set partial1; id= n_;          | /* make each study have two observations, one for
 dis=1; non dis=0; logit=logitse;          | sensitivity, the other for specificity.*/
var logit=var logitse; rec+ 1; output;
 dis=0; non dis=1; logit=logitsp;
var logit=var_logitsp; rec+1 ; output; run;
data cov;                             | /* build the data containing variable ‘est’ with 3 starting
 if n eq 1 then do;                     | values for the covariance parameters of the random effects
  est=0; output; est=0; output; est=0 ; output; | and 60 within study arm variances.*/
 end;
 set partial3; est = var_logit; output;
 keep est; run;
proc mixed data=partial3 method=reml cl;   | /*choose the residual (restricted) method(reml), ‘cl’ asks
class id;                               | for confidence limits for covariance parameter estimates.*/
model logit= dis non_dis / noint s cl covb     | /*indicator variables ‘dis’ and ‘non_dis’ are explanatory
df=1000, 1000;                          | variables for logit(Se) and logit(Sp). ‘covb’ asks for
                                      | covariance matrix of fixed effects parameters. Large ‘df”
                                      | approximate a t distribution to a normal distribution.*/
random dis non_dis / subject=id type=un s;    | /* random effects corresponds to disease and non_disease
                                      | status. An unstructured working covariance structure is
                                      | stated to assume possible correlation of ‘dis’ and ‘non_dis’
                                      | within the same study.*/
repeated / group=rec;                     | /* ‘group=rec’ statement specifies the with-in study-arm
                                      | variance in each study.*/
parms / parmsdata=cov hold=4 to 63 ;        | /*‘parmsdata’ option reads in variable ‘est’ from the cov
run;                                   | data. 60 within study-arm variances are kept constant.*/

B4. SAS NLMIXED procedure to fit the hierarchical summary ROC Model

data partial4; set partial; id= n ;                        | /* make each study has two records */
 dis=0.5; ny=tp; n=n1; se=1; output;                     | /*code ‘dis’ as 0.5 and ‘se’=1 for disease
 dis=-0.5; ny=tn; n=n0; se=0 ; output;                    | patients, ‘dis’ as -0.5 and ‘se’=0 for non-
keep id ny n dis se; run;                               | disease subjects*/
proc nlmixed data=partial4;
parms theta=-1 alpha=4 beta=-0.6 sigtheta=0.7 sigalpha=1.7;  | /* assign starting values for parameters.*/
logitp=2*dis*((theta+ut)+(alpha+ua)*dis)*exp(-beta*dis);     | /* code ‘logitp’ as logit(Se) and logit(Sp)
                                                   | */
p=exp(logitp)/(1+exp(logitp));                           | /*logit transform is applied to the
                                                   | probabilities*/
model ny~binomial(n,p);                               | /* number of tp and tn are Bin(n, p)
                                                   | distributed */
random ut ua ~                                       | /* ‘ut’ and ‘ua’ are random effects
normal([0,0],[exp(2*sigtheta),0,exp(2*sigalpha)]) subject=id;  | clustered within study. Independence is
                                                    | assumed between random effects.
                                                    | Exponential formed variance is to ensure
 estimate "se" 1/(1+exp(-((theta+0.5*alpha)*exp(-0.5*beta))));  | positivity.*/
 estimate "sp" 1/(1+exp((theta-0.5*alpha)*exp( 0.5*beta)));     | /*use estimate statement to get
 estimate "sigtheta" exp(sigtheta); estimate "sigalpha"         | estimates of desired indices with standard
exp(sigalpha); run;                                     | errors. */

B5. SAS NLMIXED procedure to fit bivariate GLMM with logit link

proc nlmixed data=partial4 fd cov corr df=1000 gtol=1e-11;  | /* ‘fd’ specifies that all derivatives be
parms mu0=1.5 nu0=-2.2 fz= 0.23 sigse=0.37 sigsp=-0.26;   | computed using finite difference
                                                  | approximations. /
rho= (exp(2*fz)-1)/(1+exp(2*fz));                       | /* use fisher’s z transformation instead of
                                                   | the correlation coefficient ρ directly to
 if Se=1 then beta=mu0+mu; if Se=0 then beta=nu0+nv;      | ensure –1 ≤ ρ 1*/
 pred=exp(beta)/(1+exp(beta));
 model ny~binomial(n, pred);                           | /* ‘tp’ and ‘tn’ are binomially distributed
                                                   | condition on random effects ‘mu’ and
                                                   | ‘nv’.*/
random mu nv ~ normal([0, 0 ],                         | /*random effects ‘mu’ and ‘nv’ are
              [exp(2*sigse), rho*exp(sigse)*exp(sigsp),   | bivariate normally distributed; ‘subject=id’
              exp(2*sigsp)]) subject=id;                | indicates possible correlation of random
estimate "Se" exp(mu0)/(1+exp(mu0));                   | effects within a study*/
estimate "Sp" exp(nu0)/(1+exp(nu0)); run;

B6. SAS NLMIXED procedure to fit trivariate GLMM

proc nlmixed data=partial fd df=1000 gtol=1e-10;           | /* model I is the best fitted model with
parms mu0=0 nv0=3 eta0=-1 sigse=0 sigsp=0 sigpi=-1 ;       | smallest AIC*/
logitsei = mu0 + mu; logitspi = nv0 + nv;
logitpi = eta0 + eta;                                     | /*model prevalence (‘pi’) together with
 Sei= 1 /(1+exp(-logitsei)); Spi=1/(1+exp(-logitspi));          | Se and Sp*/
 pi=1 /( 1+exp(-logitpi));
logL= tp * (log(pi) + log(Sei )) + fp * (log(1-pi) + log( 1-Spi))   | /*log-likelihood for trivariate model*/
+ fn * (log(pi) + log(1-Sei)) + tn * (log(1-pi) + log(Spi ));       | /*specify general log-likelihood
model Y ~ general(logL);                                 | function. Any variable can be used as the
                                                     | dependent variable in this situation.*/
random mu nv eta~normal([0, 0, 0],                         | /*‘mu’, ‘nv’ and ‘eta’ are the random
                    [exp(2*sigse),                      | effects corresponding to Se, Sp and
                    0, exp(2*sigsp),                     | prevalence. Possible correlation could
                    0, 0, exp(2*sigpi)])   subject=id;      | exist within studies. The best model is
estimate "sigse" exp(sigse);                                | achieved when all the correlation
estimate "sigsp" exp(sigsp);                                | coefficients among the random effects
estimate "sigpi" exp(sigpi);                                | ‘mu’, ‘nv’, ‘eta’ are zero.*/
estimate "Se" 1/(1+exp(-mu0));
estimate "Sp" 1/(1+exp(-nv0));   run;

B7. SAS NLMIXED procedure to fit the latent class random effect model IVe for Pap Smears test

proc nlmixed data=walter1999 cov fd;
 parms mua0=0.6 nva0=1.6 mub0=2 nvb0=4.5 eta0=0.6
       sigpi=0.4 sigmua=0.3 signva=0.2 sigmub=0 fz2=-0.5;         | /* five parameters are
                                                          | modeled: ‘SeA’ and ‘SpA’ for
       SeA=exp(mua0+mua)/(1+exp(mua0+mua));                | the Pap smear test, ‘SeB’ and
       SpA =exp(nva0+nva)/(1+exp(nva0+nva));                  | ‘SpB’ for the histology test
       SeB=exp(mub0)/(1+exp(mub0));                         | and ‘pi’ for disease
       SpB =exp(nvb0)/(1+exp(nvb0));                          | prevalence*/
       pi=exp(eta0+eta)/(1+exp(eta0+eta));                       | /*fisher’s z transformation;
                                                           | model V with correlation only
       rho2=(exp(2*fz2)-1)/(exp(2*fz2)+1);                      | between Se and Sp of the Pap
                                                           | smear test*/
       p11=pi*SeA*SeB+(1-pi)*(1-SpA)*(1 -SpB);                | /*expected probabilities in 2*2
       p01=pi*SeA*(1-SeB)+(1-pi)*(1-SpA)*SpB;                 | table*/
       p10=pi*(1-SeA)*SeB+(1-pi)*SpA*(1-SpB);
       p00=pi*(1-SeA)*(1-SeB)+(1-pi)*SpA*SpB;
                                                           | /*log likelihood*/
       logl=n11*log(p11)+n01*log(p01)+n10*log(p10)+n00*log(p00);
model y ~ general(logl);                                        | /*the best model selected
random eta mua nva~normal([0,0,0],[exp(2 *sigpi),                  | evolves four random effects.
             0, exp(2*sigmua),                                | model IVe assumes only
             0, rho2*exp(sigmua)*exp(signva),exp(2*signva)])       | correlation between ‘mua’ and
       subject=id;                                            | ‘nva’, i.e. sensitivity and
estimate       "SeA" exp(mua0)/(1+exp(mua0))                    | specificity of the Pap sme test
estimate       "SpA" exp(nva0)/(1+exp(nva0));                    | are correlated.*/
estimate       "pi" exp(eta0)/(1+exp(eta0));
estimate       "rhomuanva" (exp(2*fz2)-1)/(exp(2*fz2)+1);
estimate       "SeB" exp(mub0)/(1+exp(mub0));
estimate       "SpB" exp(nvb0)/(1+exp(nvb0));  run;