Joint modeling of multivariate longitudinal measurements and survival data with applications to Parkinson’s disease

Abstract

In many clinical trials, studying neurodegenerative diseases including Parkinson’s disease (PD), multiple longitudinal outcomes are collected in order to fully explore the multidimensional impairment caused by these diseases. The follow-up of some patients can be stopped by some outcome-dependent terminal event, e.g. death and dropout. In this article, we develop a joint model that consists of a multilevel item response theory (MLIRT) model for the multiple longitudinal outcomes, and a Cox’s proportional hazard model with piecewise constant baseline hazards for the event time data. Shared random effects are used to link together two models. The model inference is conducted using a Bayesian framework via Markov Chain Monte Carlo simulation implemented in BUGS language. Our proposed model is evaluated by simulation studies and is applied to the DATATOP study, a motivating clinical trial assessing the effect of tocopherol on PD among patients with early PD.

1 Introduction

In many longitudinal studies and clinical trials, researchers often collect some longitudinal outcomes y. The follow-up may be stopped by a dependent terminal event (e.g. death and dropout) whose probability of occurrence is non-ignorable, i.e. dependent on unobserved values of outcomes or latent variables related to outcomes. The scientific focus is often to study changes in outcomes over time and/or to analyze the relationship between y and time to the terminal event. It has been shown that the methods analyzing y alone are biased while a properly specified joint model provide consistent estimates.¹ The approach of joint modeling constructs two sub-models for the longitudinal data and the event time data, linked by a set of subject-specific random effects.² Many joint models involve a mixed effects model for the longitudinal data and a semiparametric Cox proportional hazard model for the event time.³ Many extensions have been proposed in the joint model literature such as using both random effects and a latent stochastic process to link two sub-models ¹; using a spline-based approach to capture the non-linear shapes of subject-specific changes for longitudinal outcomes⁴; relaxation of the normality assumption on the random effects⁵; the incorporation of a cured fraction⁶; and multiple event times.⁷

However, in many clinical trials studying neurodegenerative diseases such as Parkinson’s disease (PD), Huntington disease, and Alzheimer’s disease, multiple longitudinal outcomes are collected to fully explore the multidimensional impairment caused by these diseases. To properly analyze these longitudinal data, one has to account for three sources of correlation, i.e. inter-source (different measures at the same visit time), longitudinal (same measure at different visit times), and cross correlation (different measures at different visits).⁸ Multivariate generalized linear mixed effects models have been applied to analyze the multiple longitudinal outcomes in the joint model.⁴ But the computation associated with the high-dimensional integration is complicated and time-consuming. An alternative approach is the latent variable model.⁹ Specifically, a continuous latent variable is introduced to represent patients’ underlying disease severity and the observed longitudinal data can be viewed as measurements of the latent variable. Because all outcomes share the same latent variable, the dimensionality of the data can be reduced and fewer parameters are needed. To this end, multilevel item response theory (MLIRT) models have been widely used to analyze longitudinal data in social, behavioral, and health sciences.^10–15 Within the MLIRT modeling framework, the observed measurements are viewed as imperfect manifestations of the interaction between subject-specific latent traits and measurement-specific parameters. The latent traits are regressed on covariates of interest (e.g. treatment and disease duration) as well as the confounding variables. All three sources of correlation are accounted for via either random effects or covariance matrix. Advantages of the MLIRT models include better reflection of multilevel data structure, simultaneous estimation of measurement-specific parameters and covariate effects, and accurate inference about high-level measures.^16,17 Marginal maximum-likelihood method¹⁸ and Bayesian method¹⁹ have been used for the MLIRT model inference. Skrondal and Rabe-Hesketh^20,21 have provided detailed description and summary of the IRT models.

In this article, we propose a joint model with a MLIRT sub-model for the multiple longitudinal data and a Cox proportional hazard sub-model for time to the dependent terminal event. Two sub-models are linked by random effects denoting the subject-specific disease characteristics. We develop a Bayesian approach via Markov Chain Monte Carlo (MCMC) method for parameter estimation. To the best of our knowledge, there has been no previous work on the joint analysis based on the MLIRT modeling framework. The rest of the article is organized as follows. In Section 2, we describe the joint model, Bayesian inference, and model selection criterion. In Section 3, we apply the joint model to a motivating study. In Section 4, simulation studies are conducted to assess the performance of the proposed method. Section 5 provides a summary and discussion.

2 Model

2.1 Model Formulation and Likelihood

Let y_ijk be the observed outcome k from patient i at time point j, where i = 1, …, N, j = 1, …, J, and k = 1, …, K. We have coded all outcomes such that larger values are worse clinical conditions. Let y_ij = (y_ij1, …, y_ijk, …, y_ijK)′ be the vector of observation for patient i at visit j and let y_i = (y_i1, …, y_iK)′ be the outcome vector across visits. Let t_i be the observed event time for patient i, and δ_i (1 if the event is observed and 0 otherwise) be the event indicator. We use a MLIRT sub-model for the multiple longitudinal outcomes and a Cox proportional hazard sub-model for the event time. In level 1 measurement model within the MLIRT framework, we model the binary outcome, the cumulative probabilities of ordinal outcome, and the continuous outcome by a two-parameter model,¹⁹ graded response model,¹⁹ and common factor model,²² respectively.

$$\text{logit}\{p(y_{\mathit{ijk}}=1\mid {\theta }_{ij})\}=a_k+b_k{\theta }_{ij},$$ (1)

$$\text{logit}\{p(y_{\mathit{ijk}}\le l\mid {\theta }_{ij})\}=a_{kl}-b_k{\theta }_{ij},\text{with}1=1,2,\dots ,n_k-1,$$ (2)

$$y_{\mathit{ijk}}=a_k+b_k{\theta }_{ij}+{\epsilon }_{\mathit{ijk}},$$ (3)

where random error for continuous outcomes ${\epsilon }_{\mathit{ijk}}~N(0,{\sigma }_k^2)$, a_k and b_k (positive) are the outcome-specific “difficulty” parameter and “discrimination” parameter, respectively. For the ordinal outcome with n_k categories, the order constraint a_k1 < · · · < a_kl < · · · <a_knk−1 must be satisfied, and the probability of being in a particular category is p(Y_ijk = l) = p(Y_ijk ≤ l |θ_ij) − p(Y_ijk ≤ l − 1|θ_ij). The continuous latent variable θ_ij represents disease severity for patient i at time j, with higher value denoting more severe status. In the second level latent trait regression model, we postulate

$${\theta }_{ij}={\mathbf{X}}_{i0}{\mathit{\beta }}_0+u_{i0}+({\mathit{X}}_{i1}{\mathit{\beta }}_1+u_{i1})t_j,$$ (4)

where X_i0 and X_i1 are the covariates of interest associated with the disease severity, X_i0 and X_i1 can share part of or all the covariates. The variable t_j is the visit time with t₁ = 0 for baseline. The random effects u_i0 and u_i1 represent the subject-specific baseline disease severity and disease progression rate, respectively, and they follow normal distribution with mean 0 and variances 1 and ${\sigma }_u^2$, respectively, and correlation coefficient ρ. The regression parameter vectors β₀ and β₁ represent the covariate effects on the baseline disease severity and disease progression rate, respectively. For example, if θ_ij = β₀₁x_i + u_i0 + [β₁₀ + β₁₁x_i + u_i1]t_j, where x_i is an indicator variable of treatment (1 if treatment, 0 otherwise), then β₀₁ is the baseline group difference, and β₁₀ and β₁₀ + β₁₁ are the disease progression rates for the placebo and treatment patients, respectively. The negative significant variable β₁₁ indicates that the treatment is efficacious in slowing down the disease progression. Note that IRT models are over-parameterized because they have more parameters than can be estimated from the data.¹⁹ Additional constraints are usually required to make models identifiable. In the aforementioned models, we set Var[u_i0] = 1 to obtain Var[θ_ij] = 1 at t = 0 (baseline) to make the discrimination parameter b_k identifiable.

One key assumption in the MLIRT model is that all measurements from each patient are independent conditioning on the random effect vector u_i = (u_i0, u_i1)′.¹⁹ The conditional likelihood of the multiple longitudinal outcomes for patient i is

$$L_y({\mathit{y}}_i\mid {\mathit{u}}_i)=\prod _{j=1}^J\prod _{k=1}^{K}p(y_{\mathit{ijk}}\mid {\mathit{u}}_i),$$ (5)

where p(y_ijk|u_i) is the conditional density function of y_ijk obtained from Models (1)–(4). Under the Cox proportional hazard sub-model, the hazard of having a terminal event at time t_i is

$$h(t_i)=h_0(t_i)exp({\mathit{X}}_i\mathit{\gamma }+{\nu }_0{u}_{i0}+{\nu }_1{u}_{i1}),$$ (6)

where ν₀ and ν₁ measure the association between the two sub-models. Two sub-models are linked together via the shared random effects u_i0 and u_i1, which is a popular approach in joint modeling.^1,3 The covariate vector X_i can be the same or different from X_i0 and X_i1. We have selected piecewise constant function to approximate the baseline hazard function h₀(t) because models using a piecewise constant baseline hazard yield good estimators for both fixed effects and frailty,^23,24 although fixed cut points need to specified a priori. Given a set of fixed time points 0 = τ₀ < τ₁ < · · · < τ_m, and the baseline hazard vector g = (g₀, g₁, …, g_m−1), we define the piecewise constant hazard function as $h_0(t)={\sum }_{l=0}^{m-1}{g}_l{I}_l(t)$, with indicator function I_l (t) = 1 if τ_l ≤ t < τ_l+1 and 0 otherwise. The likelihood of event outcome t_i and δ_i for patient i is

$$L_{\mathrm{s}}(t_i,{\delta }_i\mid {\mathit{u}}_i)=h{(t_i)}^{{\delta }_i}S(t_i),$$ (7)

where the survival function $S(t_i)=exp[-{\int }_0^{t_i}h(s)\mathrm{d}s]$. Conditional on the random effect vector u_i, y_i is assumed to be independent of t_i. The full likelihood of the joint model for patient i is

$$p({\mathit{y}}_i,t_i,{\delta }_i,{\mathit{u}}_i)=L_y({\mathit{y}}_i\mid {\mathit{u}}_i)L_s(t_i,{\delta }_i\mid {\mathit{u}}_i)p({\mathit{u}}_i),$$ (8)

where p(u_i) is the density function of u_i. For notation convenience, we let the difficulty parameter vector be $\mathit{a}={({\mathit{a}}_1^{\prime },\dots ,{\mathit{a}}_k^{\prime },\dots ,{\mathit{a}}_K^{\prime })}^{\prime }$, with a_k being numeric for binary and continuous outcomes and a_k = (a_k1, …, a_knk−1)′ for ordinal outcomes. Let the discrimination vector be b = (b₁, …, b_K)′ and $\mathit{\beta }={({\mathit{\beta }}_0^{\prime },{\mathit{\beta }}_1^{\prime })}^{\prime }$. The unknown parameter vector Φ = (a′, b′, β′, γ′, σ_u, ρ, σ_k, ν₀, ν₁, g′)′. We refer to the proposed joint modeling framework (8) as joint model. We refer to as reduced model, the model assuming the occurrence of the terminal event is independent to the longitudinal outcomes (i.e. ν₀ = ν₁ = 0).

2.2 Bayesian Estimation and Model Selection

We develop a fully Bayesian approach via the MCMC method to estimate the unknown parameters. The model fitting is implemented using the BUGS language. Vague prior distributions are imposed on all parameters. Specifically, a normal distribution N(0, 100) is used for all components in a, β, and γ and for ν₀ and ν₁. We let all components in b and g have Uniform[0, 20] as prior distribution to ensure non-negativity. To satisfy the order constraint of a_k for the ordinal outcome with n_k categories, we let a_k1 ~ N(0, 100), and a_kl = a_k,l−1 + ω_l for l = 2, …, n_k − 1, with ω_l ~ N(0, 100)I(0, ), i.e. normal distribution left truncated at 0. We use the prior distributions σ_k ~ Gamma(0.01, 0.01) and ρ ~ Uniform[−1, 1]. Multiple chains with over-dispersed initial values are run to analyze data and the Gelman–Rubin diagnostic²⁵ is used to ensure the scale reduction R̂ of all parameters are smaller than 1.1. Moreover, we use the trace plots and autocorrelation functions²⁵ to ensure the chain convergence.

We have adopted two model selection criteria, i.e. Deviance Information Criterion (DIC)²⁶ and Bayes factor (BF).²⁷ The deviance statistics is defined as D(θ) = −2 log f(y|θ) + 2 log h(y), where f(y|θ) is the likelihood function for the observed data y given the parameter vector θ, and h(y) is some standardizing function of the data alone. The DIC is defined as DIC = D̄ + p_D, where D̄ = E_θ|y[D(θ)] is the posterior expectation of the deviance, D(θ̄) = D(E_θ|y[θ]) is the deviance evaluated at the posterior mean of parameters, and p_D = D̄ − D(θ̂) is the effective number of parameters, which captures model complexity. A smaller DIC indicates a better fit when comparing models.

BFs is a Bayesian alternative to p values for testing hypotheses and for quantifying the degree to which observed data support or conflict with a hypothesis. Let two competing models be M₁ and M₂. The BF in favor of model M₁ over M₂ is defined as:

$$\text{BF}(M_1;M_2)=\frac{p(M_1\mid \mathit{y})/p(M_2\mid \mathit{y})}{p(M_1)/p(M_2)}=\frac{p(\mathit{y}\mid M_1)}{p(\mathit{y}\mid M_2)},$$ (9)

where p(M_i) is the prior probability of model M_i, where i = 1, 2, p(M_i|y) is the posterior probability of model M_i, and p(y|M_i) is the predictive probability of observing y under model M_i, and p(y|M_i) = ∫ f(y|θ_i, M_i) p(θ_i|M_i)dθ_i, where p(θ_i|M_i) is the prior distribution for parameter vector θ_i under model M_i. When the BF is greater than 100, decisive evidence is shown in favor of model M₁. To avoid the integral involved in computation of BF, the Laplace–Metropolis estimator based on the normal distribution²⁸ is adopted to approximate the predictive probability. Specifically, p(y|M_i) ≈ (2π)^d_i/2|Σ_i|^1/2f(y|θ̄_i, M_i) p(θ̄_i|M_i), where d_i is the number of the parameters in θ_i, Σ_i is the posterior covariance matrix of θ_i, θ̄_i is the posterior mean of parameters, p(θ̄_i|M_i) is the prior probability of parameters evaluated at θ̄_i, and f(y|θ̄_i, M_i) is the likelihood when parameters are at the posterior mean values.

3 Application

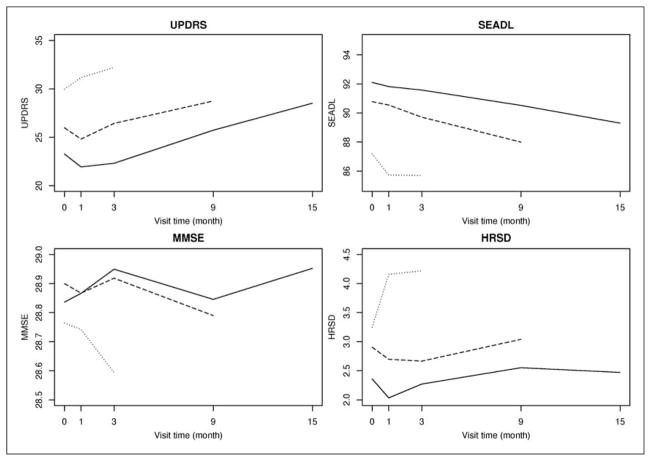
Our work is motivated by the Deprenyl And Tocopherol Antioxidative Therapy of Parkinsonism (DATATOP) study. DATATOP was a double-blind, placebo-controlled multicenter clinical trial to determine whether deprenyl or tocopherol, alone or in combination, administered to patients with early PD will prolong the time until dopaminergic therapy to treat emerging disability.²⁹ Totally 800 patients were randomly assigned in a 2 × 2 factorial design to receive double-placebo, active tocopherol alone, active deprenyl alone, and both active tocopherol and deprenyl. In this article, we investigate the effect of tocopherol and we define the placebo group as patients who did not receive tocopherol (double-placebo and active deprenyl alone groups, 401 patients), and the treatment group as patients who received tocopherol (active tocopherol alone and both active tocopherol and deprenyl groups, 399 patients). The longitudinal outcomes are Unified Parkinson’s Disease Rating Scale (UPDRS) total score, Schwab and England activities of daily living (SEADL), Mini-Mental State Exam (MMSE), and Hamilton rating scale for depression (HRSD) collected at baseline, months 1, 3, 9, and 15. UPDRS total score evaluates patients’ mentation, behavior, activities of daily living, and motor function. It is an approximate continuous variable with integer value from 0 (normal) to 176 (severe).³⁰ SEADL is a measurement of activities of daily living and it is an ordinal variable with integer value from 0 (severe) to 100 (normal) incrementing by 5.³¹ MMSE measures patients’ cognitive impairment and it is an ordinal variable with integer value from 0 (severe) to 30 (normal). HRSD, a depression test measuring the severity of clinical depression symptoms, is an ordinal variable with integer value from 0 (normal) to 52 (severe). During the course of the study, 192 and 184 patients in the placebo and treatment groups, respectively, reached a level of functional disability sufficient to warrant the initiation of dopaminergic therapy, which is a symptomatic therapy to provide temporary relief of PD symptoms. In this case, only the observed outcomes before the initiation of dopaminergic therapy can be used in the assessment of treatment efficacy because dopaminergic therapy can significantly change the values of the outcomes for a short period. Therefore, these individuals would have missing data after the initiation of dopaminergic therapy. Figure 1 displays the mean UPDRS, SEADL, MMSE, and HRSD measurements over time for DATATOP patients with follow-up time less than 6 months (dotted line), 6–12 months (dashed line), and more than 12 months (solid line). Patients with shorter follow-up time tend to have higher UPDRS and HRSD values and lower SEADL and MMSE values, indicating worse clinical outcomes. This phenomenon suggests the existence of association between the longitudinal outcomes and the time to dopaminergic therapy.

Figure 1.

Mean longitudinal measures over time. Follow-up time: less than 6 months (dotted line), 6–12 months (dashed line), and more than 12 months (solid line).

To analyze the DATATOP dataset, we have recoded the outcomes SEADL and MMSE so that higher values in all outcomes are worse clinical conditions. Moreover, we combine some categories in the outcomes SEADL, MMSE, and HRSD with zero or small number of individuals so that they have 7, 7, and 10 categories, respectively. The median follow-up time is 14 months (range: 0–25 months). We first perform the Schoenfeld residual test, the non-significant result (p = 0.43) indicates the validity of the proportionality assumption. To use the MLIRT sub-model, we let X_i0 = 0 and consider the treatment variable x_i (1 treatment, and 0 if placebo) as the only covariate in X_i1. Hence, the level 2 model (4) is θ_ij = u_i0 + (β₁₀ + β₁₁x_i + u_i1)t_ij, with visit time being t_ij = (0, 1, 3, 9, 15) and the random effects u_i0 and u_i1 representing the subject-specific baseline disease severity and disease progression rate, respectively. The survival time is time to the initiation of dopaminergic therapy. The treatment variable is the single covariate in the Cox sub-model so that h(t_i) = h₀(t_i) exp(γx_i + ν₀u_i0 + ν₁u_i1) in Model (6).

For model selection and comparison, we compute the DIC and BF illustrated in Section 2.2. The joint model has smaller DIC (53,168), comparing with 53,502 from the reduced model. The BF in favor of the joint model over the reduced model is much larger than 100, indicating decisive evidence in favor of the joint model according to the interpretation proposed by Kass and Raftery.²⁷ Table 1 compares the posterior mean, standard deviation (SD), and 95% equal-tail credible intervals from the reduced and the best fit joint models. The results from the joint model indicate that the placebo patients have significant disease progression at the rate of 0.392 units per month (β̂₁₀, 95% CI: [0.343, 0.446]). In comparison, the treatment patients have disease progression rate of 0.345 units per month (β̂₁₀ + β̂₁₁, 95% CI: [0.237, 0.461]) with insignificant tocopherol treatment effect of slowing down the disease progression rate by −0.047 per month (β̂₁₁, 95% CI: [−0.106, 0.015]). Moreover, tocopherol decreases the hazard of the initiation of dopaminergic therapy by 5% (γ̂ = −0.054, 1 − exp(−0.054) = 0.05, 95% CI: [−0.27,0.24]). The insignificant tocopherol effect is consistent with Shoulson.²⁹ We observe that ν̂₀ and ν̂₁ are positive and significantly different from zero, (ν̂₀ = 0.348, 95% CI: [0.144, 0.511], and ν̂₂ = 3.854, 95% CI: [2.497, 5.642]), suggesting that the patients with worse baseline disease severity (larger u_i0) and faster disease progression rate (larger u_i1) tend to have higher hazard of need for dopaminergic therapy and vice versa. Both the reduced and joint models give similar estimates to the outcome-specific parameters (a and b

Table 1.

Parameter estimations from joint and reduced modeling and model comparison based on DATATOP trial.

Parameters	Reduced model			Joint model
	Mean	SD	95% CI	Mean	SD	95% CI
For longitudinal outcomes
β10	0.307	0.022	0.264, 0.351	0.392	0.026	0.343, 0.446
β11	−0.051	0.030	−0.108, 0.008	−0.047	0.031	−0.106, 0.015
P	0.297	0.070	0.162, 0.439	0.415	0.062	0.294, 0.535
σu	0.241	0.017	0.209, 0.275	0.287	0.023	0.244, 0.334
For survival
Γ	−0.036	0.100	−0.237, 0.154	−0.054	0.138	−0.321, 0.216
ν0				0.348	0.093	0.144, 0.511
ν1				3.854	0.804	2.497, 5.642

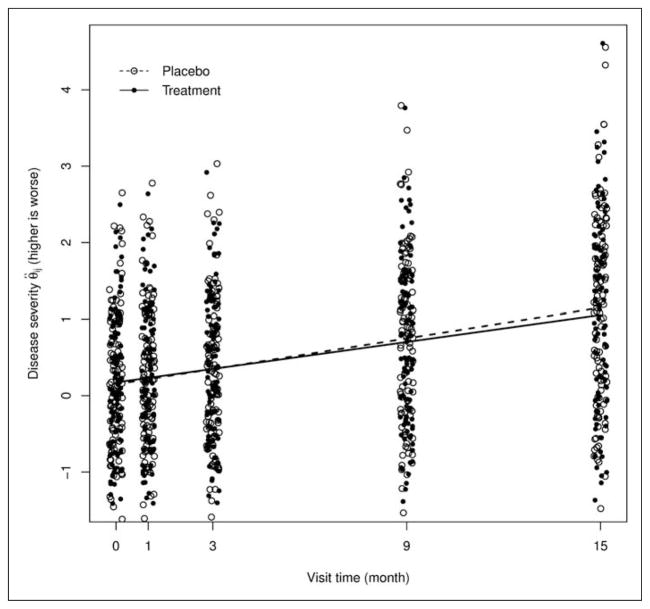
To visualize the difference in the disease progression rates in two groups, Figure 2 displays the estimates of the latent disease severity θ_ij of 100 randomly selected patient at each visit, together with the lowess smooth curves (based on all patients) denoted by the dashed (placebo group) and solid (treatment group) lines, respectively. Figure 2 suggests that two groups have similar disease progression rate before month 9 and the placebo patients deteriorate at a slightly faster rate starting from month 9, as manifested by the departure of two curves.

Figure 2.

Estimates of the subject-specific disease severity 1 θ_ij at each visit and the lowess curve for two groups.

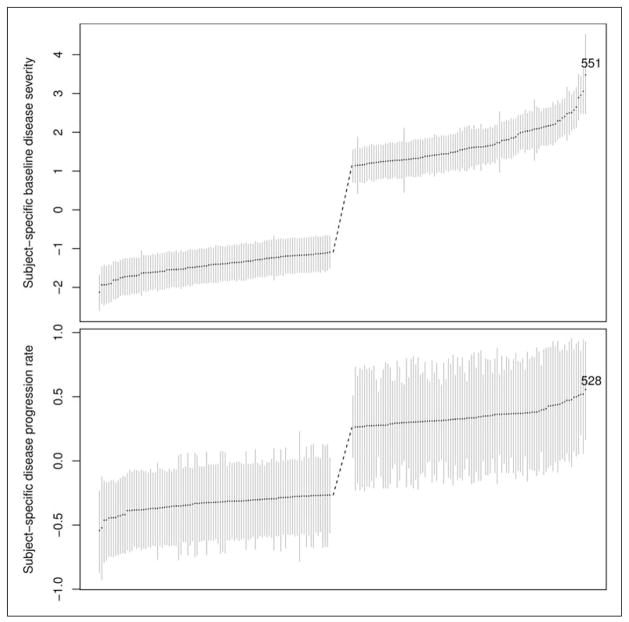
Table 1 also shows positive correlation coefficient ρ between u_i0 and u_i1 (0.415, 95% CI: [0.294,0.535]), suggesting that the patient with worse baseline disease severity tend to have faster disease deterioration and vice versa. To obtain more insight into u_i0, u_i1, and ρ, we plot in Figure 3 u_i0 (upper panel) and u_i1 (lower panel) with their 95% credible intervals. Patients are sorted so that patients at the left have milder disease at baseline and slower disease progression rate (larger ranks), while patients at the right have more severe disease at baseline and faster disease progression rate (smaller ranks). For clarity purpose, only patients with the smallest 100 and the largest 100 ranks are displayed in the figure. We use two patients as an example to illustrate the effect of ρ. Patient 551 has the worst baseline disease severity and he/she ranks No. 8 in the disease progression rate. Patient 528 has the fastest disease progression rate and he/she ranks No. 5 in the baseline disease severity.

Figure 3.

The ranking of subject-specific baseline disease severity (upper panel) and disease progression rate (lower panel) with point estimates and 95% CI. The numbers in the figures are patient numbers.

4 Simulation

In this section, we conduct two simulation studies to compare the performance of the proposed joint model and the reduced model. In the first simulation study, there is a strong correlation between the survival time and the longitudinal outcome (i.e. ν₀ = 0.4, ν₁ = 1), whereas in the second simulation study, there is no correlation (i.e. ν₀ = ν₁ = 0). The simulated datasets have a data structure and parameters similar to the DATATOP study. In each simulation study, we simulate 500 datasets with sample size N = 800 (400 in both treatment and placebo groups).

We simulate one continuous (y_ij1) and three ordinal (denoted by y_ij2, y_ij3, and y_ij4 with 7, 7, and 10 categories, respectively) outcomes at five visits (e.g. baseline, months 1, 3, 9, 15). Treatment variable (x_i = 1 if treatment, and 0 if placebo) is the only covariate under consideration and we assume that the treatment is effective. The level 2 model (4) is θ_ij = u_i0 + (β₁₀ + β₁₁x_i + u_i1)t_ij, with visit time being t_ij = (0, 1, 3, 9, 15), and the Cox sub-model (6) is h(t_i) = h₀(t_i) exp(γx_i + ν₀u_i0 + ν₁u_i1). We set β₁₀ = 0.4, β₁₁ = −0.5, and γ = −0.7. Note that β₁₁ is negative so that we expect the treated patients to have smaller θ_ij and better clinical status. Similarly, γ is negative so that the treated patients are expected to have smaller event hazard at any specific time. We simulate random effects u_i = (u_i0, u_i1)′ ~ N₂(0, Σ), where $\mathit{\sum }=((1,\rho {\sigma }_u),(\rho {\sigma }_u,{\sigma }_u^2))$ and ρ = 0.4, σ_u = 1.3. For continuous outcome y_ij1, we set a₁ = 25, b₁ = 10 and σ₁ = 5, and simulate from $N(a_1+b_1{\theta }_{ij},{\sigma }_1^2)$. For ordinal outcomes, we let a₂ = (−2.7, − 0.6, 2, 2.8, 5, 6), b₂ = 2, a₃ = (−0.1, 1, 1.8, 2.6, 3.3, 4), b₃ = 0.4, a₄ = (−1, − 0.1, 0.5, 1, 1.5, 2, 2.4, 2.8, 3.3), b₄ = 0.7, and use Model (2) to obtain the probability of being in each category for each ordinal outcome at every visit. Then, three ordinal outcomes are simulated from multinomial distributions.

The time to terminal event is simulated from the Cox sub-model with a piecewise constant baseline hazard function. Given a set of fixed time points 0 = τ₀ < τ₁ < · · · < τ_m and the baseline hazard vector g = (g₀, g₁, …, g_m−1), we define the piecewise constant baseline hazard function as $h_0(t)={\sum }_{l=0}^{m-1}{g}_l{I}_l(t)$, with I_l (t) = 1 if τ_l ≤ t ≤ τ_l+1. For a given interval τ_a ≤ t_i< τ_a+1 with a = 0, …, m − 1, the survival function is $S(t_i)=exp\{[-{\sum }_{l=0}^{a-1}{g}_l({\tau }_{l+1}-{\tau }_l)-g_a(t_i-{\tau }_a)]\times exp({\mathit{X}}_i\mathit{\gamma }+{\nu }_0{u}_{i0}+{\nu }_1{u}_{i1})\}$. To solve this equation for t_i, we have

$$t_i={\tau }_a-\frac{log[S(t_i)]}{g_{a}exp({\mathit{X}}_i\mathit{\gamma }+{\nu }_0{u}_{i0}+{\nu }_1{u}_{i1})}=\frac{{\sum }_{l=0}^{a-1}{g}_l({\tau }_{l+1}-{\tau }_l)}{g_a}.$$ (10)

The condition τ_a ≤ t_i< τ_a+1 imposes the following constraint: $-exp({\mathit{X}}_i\gamma +{\nu }_0{u}_{i0}+{\nu }_1{u}_{i1})\times {\sum }_{l=0}^a{g}_l({\tau }_{l+1}-{\tau }_l)<log[S(t_i)]\le -exp({\mathit{X}}_i\gamma +{\nu }_0{u}_{i0}+{\nu }_1{u}_{i1}){\sum }_{l=0}^{a-1}{g}_l({\tau }_{l+1}-{\tau }_l)$. To generate the event time t_i, we set the piecewise baseline hazard vector g = (0.01, 0.05, 0.13) at the fixed time points τ = (0, 8, 13, 30). We generate the censoring time from Uniform[10, 20] and δ_i = 1 if the event time generated from equation (10) is not larger than the censoring time.

In each simulation study, we run two parallel MCMC chains with over-dispersed initial values. Each chain is run for 10,000 iterations. The first 5000 iterations are discarded as burn-in, and the remaining 5000 samples are used to obtain the posterior distribution of the parameters. We have computed the bias (the average of the posterior means minus the true values), standard error (SE, the square root of the average of the posterior variance), SD (the standard deviation of the posterior means), and coverage probabilities (CPs) of 95% equal-tail credible intervals from the reduced and joint models.

Table 2 displays the results from the first simulation study in which the occurrence of the terminal event is strongly correlated with the longitudinal outcomes. The joint model generally provides estimates with negligible bias, SE close to SD, and the CPs reasonably close to 0.95. We notice that the CP of ν₁ is slightly off from 0.95, indicating some difficulty in distinguishing the random effects as reported in Henderson et al.¹ These results suggest that the joint model can generally recover the true values in the presence of dependent terminal event. In contrast, the reduced model gives severely biased estimates and the CPs are far away from the nominal value. Specifically, the treatment effect parameter β₁₁ is biased toward zero and it is thus less likely to detect the treatment effect if the treatment effect is present. Because the parameters ν₀ and ν₁ are set to be positive, the patients with worse baseline disease severity (larger u_i0) and faster disease progression rate (larger u_i1) tend to have a terminal event earlier. By ignoring this phenomenon and treating the missing data after the terminal event as missing at random, the reduced model tends to reduce the difference between two groups and therefore underestimate the treatment effect. This finding is consistent with the literature of the univariate longitudinal data analysis with dependent dropout.³² In addition, both models provide reasonable estimates to the difficulty and discriminating parameter vectors a and b

Table 2.

Simulation results from the reduced and joint models when the terminal event is dependent on the longitudinal outcomes.

Parameters	Reduced model				Joint model
	Bias	SE	SD	CP	Bias	SE	SD	CP
For longitudinal outcomes
β10 = 0.4	−0.193	0.065	0.065	0.178	0.027	0.073	0.079	0.906
β11 = −0.5	0.068	0.089	0.089	0.862	−0.011	0.095	0.096	0.944
ρ = 0.4	−0.033	0.037	0.036	0.860	0.006	0.036	0.038	0.902
σu = 1.3	−0.099	0.047	0.045	0.466	0.022	0.054	0.053	0.930
For survival
γ = −0.7	0.209	0.112	0.115	0.536	−0.072	0.151	0.152	0.910
ν0 = 0.4					−0.001	0.075	0.075	0.934
ν1 = 1.0					0.070	0.090	0.096	0.896

Table 3 displays the results from the second simulation study in which the reduced model is the correct model. The reduced model provides estimates with small bias and CPs reasonably close to the nominal level. The results indicate that the reduced model can successfully recover the true values under independent terminal event. In comparison, under model overparameterization, the results from the joint model still have reasonably small bias, CPs close to nominal level, and it does not inflate the SEs. The estimates of the parameters ν₀ and ν₁ are correctly close to zero, suggesting that the joint model is still a reasonable model even when it is overparameterized. Moreover, both models provide reasonable estimates to the difficulty and discriminating parameter vectors a and b

Table 3.

Simulation results from the reduced and joint models when the terminal event is independent on the longitudinal outcomes.

Parameters	Reduced model				Joint model
	Bias	SE	SD	CP	Bias	SE	SD	CP
For longitudinal outcomes
β10 = 0.4	0.002	0.068	0.070	0.932	0.001	0.068	0.069	0.930
β11 = −0.5	−0.003	0.092	0.095	0.944	−0.001	0.093	0.096	0.946
ρ = 0.4	0.004	0.034	0.035	0.934	0.005	0.034	0.035	0.934
σu = 1.3	0.003	0.048	0.049	0.946	0.001	0.048	0.048	0.954
For survival
γ =−0.7	−0.028	0.129	0.128	0.944	−0.009	0.141	0.138	0.950
ν0 = 0					−0.009	0.075	0.078	0.940
ν1 = 0					0.006	0.061	0.062	0.926

In conclusion, the simulation results suggest that in the presence of dependent terminal event, the joint model provide more accurate estimates for the MLIRT and Cox regression parameters and the random effects parameters. Under independent terminal event, the joint model provides results comparable with the reduced model.

5 Discussion

In clinical trials, it is quite common to have longitudinal outcomes subject to dependent terminal event. Previous work of joint modeling for this type of data has been mainly focused on a single longitudinal outcome accounting for the dependent censoring. In this article, we have proposed a joint modeling framework to jointly analyze the multiple longitudinal data subject to dependent terminal event using the MLIRT sub-model and the Cox proportional hazard sub-model. Two sub-models are linked together via shared random effects representing the subject-specific baseline disease severity and disease progression rate, respectively. The proposed joint model has a better fit than the reduced model in the analysis of the DATATOP dataset. We have found that the treatment tocopherol is insignificant in slowing the PD disease progression. Moreover, we have identified a significant positive correlation between the multiple longitudinal outcomes and the terminal event, in addition to the positive significant correlation between the baseline disease severity and disease progression rate. The simulation studies have shown that in the presence of dependent terminal event, the joint model successfully recovers the true parameters whereas the reduced model underestimates the treatment effect and has large bias in the regression and random effects parameters. Under the scenario of independent terminal event, the joint model provides results comparable with the reduced model.

Our method can be extended to robust inference to handle outlying observations in the longitudinal outcomes. One direction is to relax the normality assumption for the random errors of the continuous outcome to some long-tailed or heavy-tailed distributions, e.g. normal/ independent distributions,³³ skew-normal independent distributions,³⁴ and generalized skew-elliptical distributions.³⁵ Another issue is about the assumption of homogeneous random covariance matrix (the matrix is the same for all subjects). Accounting for heterogeneity in random covariance matrix has been investigated in generalized linear models,³⁶ non-linear mixed models,³⁷ and linear mixed models.³⁸ The use of the heterogenous random covariance matrix in the joint modeling framework of the MLIRT models warrants further investigation.