Binomial regression with a misclassified covariate and outcome

Abstract

Misclassification occurring in either outcome variables or categorical covariates or both is a common issue in medical science. It leads to biased results and distorted disease–exposure relationships. Moreover, it is often of clinical interest to obtain the estimates of sensitivity and specificity of some diagnostic methods even when neither gold standard nor prior knowledge about the parameters exists. We present a novel Bayesian approach in binomial regression when both the outcome variable and one binary covariate are subject to misclassification. Extensive simulation results under various scenarios and a real clinical example are given to illustrate the proposed approach. This approach is motivated and applied to a dataset from the Baylor Alzheimer’s Disease and Memory Disorders Center.

1 Introduction

Many epidemiological studies use binomial regression to quantify the association between a binary outcome variable and some continuous and categorical covariates. Researchers often assume the measurements, either categorical or continuous, are accurate in their analysis. In practice, these observations are often misclassified (for the categorical variables) or inaccurately measured (for the continuous variables). Misclassification involving binary variables is due to many factors, e.g. inaccuracy of data collection methods, limited sensitivity and specificity of the diagnostic tests, inadequacy of information derived from medical or other records, and recall bias in assessing exposure status.¹ It has been shown that misclassification in binomial regression yields biased estimators of the associations of covariates with response.^2,3 Many statistical methods have been developed to account for a misclassified response variable,^4–6 or to correct for a misclassified covariate using matrix method,^7,8 inverse matrix method,^9,10 and maximum likelihood method.^11–14

Most of the available methods require the use of a gold standard, which can estimate the sensitivity and specificity of the imperfect measure and incorporate the external estimates into the likelihood to obtain corrected effect estimates.^7,15–17 Moreover, when an internal validation subsample allowing comparison of an imperfect measure with the gold standard is available, a variety of techniques, e.g. those based on likelihood or on weighted estimating equations, have been proposed.^11,18–20 However, the gold standard may be unavailable, impractical,^21,22 or it may be expensive, time consuming, or unethical to perform on all subjects and is commonly difficult to obtain in clinical studies.²³ When no gold standard, but two imperfect measures are available, one can account for the misclassification using a maximum likelihood approach.²⁴ Because the likelihood function often involves complicated integrations that a closed form is unavailable for most models, the expectation–maximization algorithm¹⁷ and Bayesian inference using Markov chain Monte Carlo (MCMC) methods^5,6,25,26 have been widely used to correct for misclassification. There are several advantages of using Bayesian inference framework: (a) the approximation of the integrals in the likelihood is not required, and the unobserved variables can be sampled along with the model parameters from their full posterior distribution; (b) the available prior information of some parameters can be readily incorporated; and (c) with the development of BUGS projects,²⁷ the implementation in OpenBUGS is made simple by specifying the likelihood function and the prior distribution of all unknown parameters.

In statistical literature of misclassification involving at least two imperfect measures, a common assumption is conditional independence, i.e. multiple measures are independent conditional on the unobserved true status. Hui and Zhou²⁸ have pointed out that this assumption is relatively strong and unrealistic in many practical situations. Some methods have been proposed to relax the conditional independence assumption, e.g. the model with more than two latent classes,^29–31 the random effects model,³² and the model with two additional parameters by Black and Craig.³³ In this article, we adopt the approach by Black and Craig³³ on relaxing the conditional independence assumption. Our article is substantially different in two aspects. First, our model considers covariates in binomial regression setting, while Black and Craig estimated disease prevalence without accounting for covariate effects.³³ Second, a binary outcome and a binary covariate are misclassified in this article, while only the response, i.e. disease status, is subjected to misclassification in Black and Craig.³³

In this article, we consider a cross-sectional study of unmatched subjects with a misclassified binary outcome (referred to as ‘disease’), a misclassified binary covariate (referred to as ‘exposure’), and other perfectly measured continuous and categorical covariates. We use binomial regression to assess the association between the disease and exposure statuses while controlling for some other covariates. We propose a model with two latent variables (i.e. unobserved disease and exposure statuses) using Bayesian inference to correct for misclassification when two imperfect measures are available for each of the two latent variables in the absence of gold standard and validation subsample. The remainder of the article is organized as follows. In Section 2, we describe a modeling framework, a method to relax the conditional independence assumption, and Bayesian inference. Then, proposed method is evaluated via various sets of “Simulations” in Section 3. In Section 4, the method is applied to a motivating example, a dataset of 626 Alzheimer’s Disease (AD) patients who participated in a study conducted by the Alzheimer’s Disease and Memory Disorders Center (ADMDC) at Baylor College of Medicine. Section 5 provides a “Discussion” and future research directions.

2 Model and estimation

2.1 Conditional independence between tests

Consider some outcome disease state D diagnosed by two dichotomous tests that are prone to misclassification. Suppose y (1 if disease, 0 if non-disease) is the unobserved true disease status. Let y₁ and y₂ (1 if disease, 0 if non-disease) be the observed disease outcomes from the two tests that are subject to misclassification. The disease status y is associated with an unobserved binary exposure status x (1 if exposed, 0 if non-exposed) that is also subject to misclassification and some perfectly measured continuous and categorical variables. The exposure status is measured by two imperfect dichotomous tests whose outcomes are denoted by x₁ and x₂ (1 if exposed, 0 if non-exposed), respectively.

Let (p_yj, q_yj), for j=1, 2, be the sensitivity and specificity of the jth test of the disease status given the true status y, i.e. p_yj=P(y_j=1|y=1) and q_yj=P(y_j=0|y=0). Similarly, let (p_xj, q_xj), for j=1, 2, be the sensitivity and specificity of jth test of the exposure status given the true status x, i.e. p_xj=P(x_j=1|x=1) and q_xj=P(x_j=0|x=0). Covariates z_y and z_x are associated with the statuses of disease and exposure, respectively. The observed likelihood function can be written in terms of four submodels,^12,13 i.e. the outcome model P(y|x, z_y), the exposure model P(x|z_x), the measurement model of y, P(y₁, y₂|y), and the measurement model of x, P(x₁, x₂|x). Specifically, the outcome model is

$$g_y[P(y=1\mid x,{\mathit{z}}_y)]={\beta }_0+{\beta }_{1}x+{\mathit{\beta }}_2{\mathit{z}}_y$$ (1)

The exposure model is

$$g_x[P(x=1\mid {\mathit{z}}_x)]={\gamma }_0+{\gamma }_1{\mathit{z}}_x$$ (2)

where g_y[·] and g_x[·] are link functions, e.g. logit, probit, and complementary log-log. Specifically, we use logit function in this article. The measurement model of y is

$$P(y_1,y_2\mid y=1)=p_{y1}^{y_1}·{\overline{p}}_{y1}^{{\overline{y}}_1}·p_{y2}^{y_2}·{\overline{p}}_{y2}^{{\overline{y}}_2}\text{and}P(y_1,y_2\mid y=0)=q_{y1}^{{\overline{y}}_1}·{\overline{q}}_{y1}^{y_1}·q_{y2}^{{\overline{y}}_2}·{\overline{q}}_{y2}^{y_2}$$ (3)

where the overhead bar denotes one minus the variable, e.g. p̄_x1 = 1 − p_x1. The measurement model of x is

$$P(x_1,x_2\mid x=1)=p_{x1}^{x_1}·{\overline{p}}_{x1}^{{\overline{x}}_1}·p_{x2}^{x_2}·{\overline{p}}_{x2}^{{\overline{x}}_2}\text{and}P(x_1,x_2\mid x=0)=q_{x1}^{{\overline{x}}_1}·{\overline{q}}_{x1}^{x_1}·q_{x2}^{{\overline{x}}_2}·{\overline{q}}_{x2}^{x_2}$$ (4)

Note that in the measurement models above, we have assumed conditional independence, i.e. multiple diagnostic tests are independent conditional on the true status. This assumption will be relaxed later. For the ease of notation, let β=(β₀, β₁, β′₂)′, γ=(γ₀, γ′₁)′, p=(p_y1, p_y2, p_x1, p_x2)′, q=(q_y1, q_y2, q_x1, q_x2)′, and π_x=P(x=1|z_x). The parameter vector is θ=(β′, γ′, p′, q′)′. The observed likelihood for one subject is

$$\begin{array}{l}L(\mathit{\theta }\mid {\mathit{z}}_y,{\mathit{z}}_x)=P(y_1,y_2,x_1,x_2\mid {\mathit{z}}_y,{\mathit{z}}_x)\\ =p_{0000}^{{\overline{y}}_1{\overline{y}}_2{\overline{x}}_1{\overline{x}}_2}·p_{0001}^{{\overline{y}}_1{\overline{y}}_2{\overline{x}}_1{x}_2}·p_{0010}^{{\overline{y}}_1{\overline{y}}_2{x}_1{\overline{x}}_2}·p_{0011}^{{\overline{y}}_1{\overline{y}}_2{x}_1{x}_2}·p_{0100}^{{\overline{y}}_1{y}_2{\overline{x}}_1{\overline{x}}_2}·p_{0101}^{{\overline{y}}_1{y}_2{\overline{x}}_1{x}_2}·p_{0110}^{{\overline{y}}_1{y}_2{x}_1{\overline{x}}_2}·p_{0111}^{{\overline{y}}_1{y}_2{x}_1{x}_2}\\ ·p_{1000}^{y_1{\overline{y}}_2{\overline{x}}_1{\overline{x}}_2}·p_{1001}^{y_1{\overline{y}}_2{\overline{x}}_1{x}_2}·p_{1010}^{y_1{\overline{y}}_2{x}_1{\overline{x}}_2}·p_{1011}^{y_1{\overline{y}}_2{x}_1{x}_2}·p_{1100}^{y_1{y}_2{\overline{x}}_1{\overline{x}}_2}·p_{1101}^{y_1{y}_2{\overline{x}}_1{x}_2}·p_{1110}^{y_1{y}_2{x}_1{\overline{x}}_2}·p_{1111}^{y_1{y}_2{x}_1{x}_2}\end{array}$$ (5)

where p_abcd=p(y₁=a, y₂=b, x₁=c, x₂=d|z_y, z_x) for a, b, c, d=1 or 0. The details of likelihood derivation and the expressions of p_abcd are illustrated in Section A of Appendix. We thereafter refer to the model assuming conditional independence in both measurements of y and x as M₁.

2.2 Conditional dependence between tests

In this section, we relax the conditional independence assumption using the approach by Black and Craig.³³ Let $p_{ab\mid k}^y=P(y_1=a,y_2=b\mid y=k)$ and $p_{cd\mid k}^x=P(x_1=c,x_2=d\mid x=k)$, where a, b, c, d, and k are either 1 or 0. To account for the possible dependence between tests, we introduce two additional parameters for y, i.e. $p_{11\mid 1}^y$ and $p_{00\mid 0}^y$; and two for x, i.e. $p_{11\mid 1}^x$ and $p_{00\mid 0}^x$. If conditional independence is assumed, then $p_{11\mid 1}^y=p_{y1}{p}_{y2}$ and $p_{00\mid 0}^y=q_{y1}{q}_{y2}$. If one outcome measurement is completely dependent on another one, then $p_{11\mid 1}^y=min(p_{y1},p_{y2})$ and $p_{00\mid 0}^y=min(q_{y1},q_{y2})$. In general, $p_{11\mid 1}^y$ and $p_{00\mid 0}^y$ vary between complete independence and complete dependence. Hence, the following constraints apply: $p_{y1}{p}_{y2}\le p_{11\mid 1}^y\le min(p_{y1},p_{y2})$ and $q_{y1}{q}_{y2}\le p_{00\mid 0}^y\le min(q_{y1},q_{y2})$. Similar constraints exist for $p_{11\mid 1}^x$ and $p_{00\mid 0}^x$. The other probabilities of $p_{ab\mid k}^y$ are

$$\begin{array}{ll}{p}_{01\mid 1}^y=p_{y2}-p_{11\mid 1}^y\hfill & p_{01\mid 0}^y=q_{y1}-p_{00\mid 0}^y\hfill \\ p_{10\mid 1}^y=p_{y1}-p_{11\mid 1}^y\hfill & p_{10\mid 0}^y=q_{y2}-p_{00\mid 0}^y\hfill \\ p_{00\mid 1}^y=1-p_{y1}-p_{y2}+p_{11\mid 1}^y\hfill & p_{11\mid 0}^y=1-q_{y1}-q_{y2}+p_{00\mid 0}^y\hfill \end{array}$$ (6)

Similarly, the other probabilities of $p_{ab\mid k}^x$ are

$$\begin{array}{ll}{p}_{01\mid 1}^x=p_{x2}-p_{11\mid 1}^x\hfill & p_{01\mid 0}^x=q_{x1}-p_{00\mid 0}^x\hfill \\ p_{10\mid 1}^x=p_{x1}-p_{11\mid 1}^x\hfill & p_{10\mid 0}^x=q_{x2}-p_{00\mid 0}^x\hfill \\ p_{00\mid 1}^x=1-p_{x1}-p_{x2}+p_{11\mid 1}^x\hfill & p_{11\mid 0}^x=1-q_{x1}-q_{x2}+p_{00\mid 0}^x\hfill \end{array}$$ (7)

The parameter vector under conditional dependence has four additional parameters, i.e. $\mathit{\theta }={({\mathit{\beta }}^{\prime },{\mathit{\gamma }}^{\prime },{\mathit{p}}^{\prime },{\mathit{q}}^{\prime },p_{11\mid 1}^y,p_{00\mid 0}^y,p_{11\mid 1}^x,p_{00\mid 0}^x)}^{\prime }$, compared to that in Section 2.1. The likelihood formulation remains identical to equation (5), while each component p_abcd is differently expressed as detailed in Section A of Appendix. We thereafter refer to the model assuming conditional dependence in both measurements of y and x as M₂.

2.3 Bayesian inference

To infer the unknown parameter vector θ, we use Bayesian inference based on MCMC posterior simulations. We use vague priors on all parameters. Specifically, we use normal priors with mean zero and variance four on each component of vectors β and γ in the simulation. We use uniform priors on each component of vectors p, q ~ Unif[0.5, 1], in which we assume the diagnosis tests are more accurate than a coin toss. While this assumption is slightly stronger than the conditions for identifiability (i.e. p+q>1),³⁴ we believe that this assumption is reasonable for tests in practical use. For model M₂, we impose uniform priors for the additional parameters introduced in Section 2.2, i.e. $p_{11\mid 1}^y~\mathit{Unif}[p_{y1}{p}_{y2},min(p_{y1},p_{y2})]$ and $p_{00\mid 0}^y~\mathit{Unif}[q_{y1}{q}_{y2},min(q_{y1},q_{y2})]$. For the ease of sampling in MCMC, we reparameterize $p_{11\mid 1}^y,p_{00\mid 0}^y,p_{11\mid 1}^x$, and $p_{00\mid 0}^x$ as

$$\begin{array}{ll}{d}_p^y=(p_{11\mid 1}^y-p_{y1}{p}_{y2})/[min(p_{y1},p_{y2})-p_{y1}{p}_{y2}];\hfill & d_q^y=(p_{00\mid 0}^y-q_{y1}{q}_{y2})/[min(q_{y1},q_{y2})-q_{y1}{q}_{y2}]\hfill \\ d_p^x=(p_{11\mid 1}^x-p_{x1}{p}_{x2})/[min(p_{x1},p_{x2})-p_{x1}{p}_{x2}];\hfill & d_q^x=(p_{00\mid 0}^x-q_{x1}{q}_{x2})/[min(q_{x1},q_{x2})-q_{x1}{q}_{x2}]\hfill \end{array}$$ (8)

These parameters vary between 0 and 1 and represent the degree of conditional dependency (e.g. 0 for conditional independence and 1 for complete conditional dependence). In each MCMC cycle, we sample $d_p^y,d_q^y,d_p^x,d_q^x~\mathit{Unif}[0,1]$ and then back transform into $p_{11\mid 1}^y,p_{00\mid 0}^y,p_{11\mid 1}^x$, and $p_{00\mid 0}^x$ using equation (8).

The model fitting is performed in OpenBUGS (OpenBUGS version 3.2.1) by specifying the likelihood function and the prior distribution of all unknown parameters. We use the history plots available in OpenBUGS and view the absence of apparent trend in the plot as evidence of convergence. In addition, we use the Gelman–Rubin diagnostic to insure the scale reduction R̂ of all parameters is smaller than 1.1.³⁵

To make selection among models, we adopt a model selection approach using the deviance information criterion (DIC) proposed by Spiegelhalter et al.³⁶ The DIC provides an assessment of model fitting and a penalty for model complexity. The deviance statistic is defined as D(θ)=−2log f(y|θ)+2log h(y), where f(y|θ) is the likelihood function for the observed data matrix y given the parameter vector θ and h(y) denotes a standardizing function of the data alone that has no impact on model selection.³⁷ The DIC is defined as DIC =2D̄ − D(θ̄) = D̄ + p_D, where D̄ = E_θ|y[D] is the posterior mean of the deviance, D(θ̄) = D(E_θ|y[θ]) the deviance evaluated at the posterior mean θ̄ of the parameter vector, and p_D = D̄ − D(θ̄) the effective number of parameters. Smaller values of DIC indicate a better-fitting model. We use OpenBUGS to compute the DIC.

To evaluate evidence against model M₁ within the Bayesian framework, we compute a Bayes factor.³⁸ When equal prior probability is given to each candidate model, the Bayes factor of model M₂, relative to model M₁, is defined as: BF₂₁=f(y|M₂)/f(y|M₁), where f(y|M_k), for k=1, 2, is the predictive probability of the observed data under model M_k and f(y|M_k)=∫ f(y|M_k, θ_k)p(θ_k|M_k)dθ_k, with θ_k being the parameter vector for model M_k and p(θ_k|M_k) being the prior density of the parameter for model M_k. The predictive probability is estimated using the Laplace–Metropolis estimator.³⁹ Model M₂ is supported when BF₂₁>1, and model M₁ is supported otherwise.

3 Simulation study

In this section, we conduct four sets of simulations in which both the binary response variable and a binary covariate are misclassified under various scenarios. We consider a continuous covariate (z) for both the outcome model (1) and the exposure model (2), i.e. z_y=z_x=z. This covariate (i.e. pre-progression rate) is a continuous variable representing disease progression prior to the first visit. Detailed explanation of this variable is provided in Section 4. We generate z from N(0, 2.5²). We simulate 500 datasets with 400 subjects within each. In each simulated dataset, we run two chains with 15,000 iterations per chain. The first 5000 iterations are discarded as burn-in, and the inference is based on the remaining 10,000 iterations. The MCMC convergence and mixing properties are assessed by visual inspection of the history plots of all parameters and Gelman–Rubin diagnostic. In all sets of simulation, the MCMC chains mix well after the burn-in of 5000 iterations. We evaluate the performance of three methods: (a) the ideal analysis which is based on the true unobserved disease (y) and exposure statuses (x); (b) the naive analysis which ignores the misclassification and treats y₁ and x₁ as if they were the actual disease status y and exposure status x; and (c) the proposed models M₁ and M₂. Note that we only have the luxury of doing the ideal analysis in simulations because the true disease and exposure statuses are available.

3.1 Assuming conditional independence

In the first set of simulations, we assume conditional independence for both the disease and exposure measurements. Data are generated by the following algorithm.

1. Simulate the unobserved exposure status x using Bernoulli distribution with probability of exposure π_x following the exposure model (2) with γ=(−0.85, 1.5)′.

2. Simulate the unobserved disease status y using Bernoulli distribution with P(y=1|x, z_y) following the outcome model (1) with β=(−0.70, 1.5, 1.5)′.

3. Conditional on x, simulate the observed exposure statuses x₁ and x₂ with the sensitivity and specificity (p_x1, q_x1, p_x2, q_x2)′ = (0.9, 0.75, 0.7, 0.95)′.

4. Conditional on y, simulate the observed disease statuses y₁ and y₂ with the sensitivity and specificity (p_y1, q_y1, p_y2, q_y2)′ =(0.8, 0.85, 0.85, 0.75)′.

5. Repeat steps 1–4 until all subjects are generated.

Table 1 presents the simulation results of the ideal analysis, the naive analysis, model M₁, and model M₂. The rows labeled ‘EST’ provide the average of the posterior means from 500 replications. The rows labeled ‘BIAS’ is ESTs minus the true values. The rows labeled ‘SE’ provide the square root of the average of the variances. The rows labeled ‘SD’ provide the standard deviation of the posterior means. The 95% credible intervals are obtained from the 2.5% and 97.5% percentiles of the posterior samples of the parameters. The coverage probability (‘CP’) is the proportion of the 95% credible intervals containing true parameters. In Table 1, the ideal analysis has negligible bias on parameter estimates and the CPs fluctuate around 0.95. The naive analysis yields severely biased parameter estimates and the CPs are far away from the nominal levels. Model M₁ is the correct model in this set of simulations and it provides estimates with small bias and CPs reasonably close to the nominal level. These results indicate that model M₁ can successfully recover the true values when conditional independence is present in both measurements of y and x. In comparison, under model overparameterization, the results from model M₂ still have reasonably small bias and CPs close to nominal level, although the bias and CPs are slightly worse than that of the model M₁. Moreover, the parameters of sensitivity and specificity are slightly underestimated by model M₂ when no conditional dependence exists. The estimates and SDs (in parentheses) of $d_p^y,d_q^y,d_p^x$, and $d_q^x$ are 0.121 (0.049), 0.124 (0.053), 0.209 (0.080), and 0.247 (0.107), respectively. The fact that these parameter estimates are reasonably close to zero suggests that model M₂ is still a reasonable model even when it is overparameterized.

Table 1.

Parameter estimates from 500 replications with sample size 400 assuming conditional independence on both measurements y and x.

Truth	β0	β1	β2	γ0	γ1	py1	qy1	py2	qy2	px1	qx1	px2	qx2
	−0.700	1.500	1.500	−0.850	1.500	0.800	0.850	0.850	0.750	0.900	0.750	0.700	0.950
Ideal analysis
EST	−0.712	1.576	1.551	−0.860	1.526
BIAS	−0.012	0.076	0.051	−0.010	0.026
SE	0.227	0.422	0.212	0.182	0.161
SD	0.239	0.439	0.222	0.175	0.159
CP	0.944	0.948	0.948	0.960	0.954
Naive analysis
EST	−0.412	0.427	0.475	0.118	0.473
BIAS	0.288	−1.073	−1.025	0.968	−1.027
SE	0.177	0.253	0.065	0.114	0.057
SD	0.173	0.238	0.077	0.112	0.070
CP	0.616	0.014	0.000	0.000	0.000
Model assuming conditional independence (M1)
EST	−0.737	1.639	1.781	−0.900	1.646	0.797	0.846	0.844	0.746	0.892	0.746	0.695	0.945
BIAS	−0.037	0.139	0.281	−0.050	0.146	−0.003	−0.004	−0.006	−0.004	−0.008	−0.004	−0.005	−0.005
SE	0.435	0.886	0.491	0.305	0.305	0.034	0.030	0.030	0.035	0.029	0.033	0.043	0.019
SD	0.435	0.767	0.450	0.308	0.316	0.032	0.031	0.030	0.033	0.029	0.034	0.042	0.018
CP	0.948	0.968	0.938	0.938	0.928	0.964	0.936	0.958	0.956	0.946	0.964	0.958	0.944
Model assuming conditional dependence (M2)
EST	−0.839	1.881	2.027	−0.952	1.891	0.783	0.838	0.834	0.735	0.875	0.734	0.675	0.936
BIAS	−0.139	0.381	0.527	−0.102	0.391	−0.017	−0.012	−0.016	−0.015	−0.025	−0.016	−0.025	−0.014
SE	0.527	1.077	0.625	0.370	0.421	0.035	0.031	0.032	0.035	0.033	0.033	0.044	0.021
SD	0.480	0.825	0.474	0.357	0.326	0.033	0.031	0.031	0.034	0.030	0.033	0.042	0.019
CP	0.956	0.976	0.922	0.938	0.882	0.924	0.942	0.934	0.932	0.896	0.928	0.924	0.926

CP: coverage probability.

3.2 Assuming conditional dependence

In the second set of simulations, we simulate the conditional dependence relationship illustrated in Section 2.2 and investigate the performance of the proposed modeling framework. Data are generated by the following algorithm.

1. Let $d_p^x=d_q^x=0.5$, obtain $p_{11\mid 1}^x$ and $p_{00\mid 0}^x$ from equation (8) and the other probabilities of $p_{ab\mid k}^x$ from equation (7) with the sensitivity and specificity (p_x1, q_x1, p_x2, q_x2)′=(0.9, 0.75, 0.7, 0.95)′.

2. Let $d_p^y=d_q^y=0.5$, obtain $p_{11\mid 1}^y$ and $p_{00\mid 0}^y$ from equation (8) and the other probabilities of $p_{ab\mid k}^y$ from equation (6) with the sensitivity and specificity (p_y1, q_y1, p_y2, q_y2)′=(0.8, 0.85, 0.85, 0.75)′.

3. Follow steps 1 and 2 in Section 3.1.

4. Simulate the observed exposure statuses x₁ and x₂ from a multinomial distribution with probability vectors ( $p_{11\mid 1}^x,p_{10\mid 1}^x,p_{01\mid 1}^x,p_{00\mid 1}^x$) if x=1, ( $p_{11\mid 0}^x,p_{10\mid 0}^x,p_{01\mid 0}^x,p_{00\mid 0}^x$) if x=0.

5. Simulate the observed disease statuses y₁ and y₂ from a multinomial distribution with probability vectors ( $p_{11\mid 1}^y,p_{10\mid 1}^y,p_{01\mid 1}^y,p_{00\mid 1}^y$) if y=1, ( $p_{11\mid 0}^y,p_{10\mid 0}^y,p_{01\mid 0}^y,p_{00\mid 0}^y$) if y=0.

6. Repeat steps 1–5 until all subjects are generated.

Table 2 displays the simulation results using all four methods. The ideal analysis still performs well because it directly uses the true values of y and x, so that the two conditional dependent measures are not utilized. The naive analysis produces severely biased results and the CPs are far from 0.95. Model M₂ is the correct model in this set of simulation and it provides estimates with small bias and the CPs are reasonably close to 0.95. The estimates for the four additional parameters ( $p_{11\mid 1}^y,p_{00\mid 0}^y,p_{11\mid 1}^x,p_{00\mid 0}^x$) are reasonably good (not shown). These results indicate that model M₂ can successfully recover the true values when conditional dependence exists in both measurements of y and x. The SEs and SDs in model M₂ are larger than those in ideal and naive analysis because that our model accounts for the additional variability from misclassification in response and a covariate. In contrast, under model misspecification, the results from model M₁ have large bias and the CPs for most parameters substantially deviate from 0.95. Moreover, when conditional dependence is present, the parameters of sensitivity and specificity are substantially overestimated by model M₁. This interesting phenomenon was first reported in Vacek,⁴⁰ who also presented the asymptotic bias as a function of sensitivity, specificity, and their covariance. In summary, the results in Tables 1 and 2 suggest that model M₂ is more robust to model overparameterization than model M₁ to model misspecification.

Table 2.

Parameter estimates from 500 replications with sample size 400 assuming conditional dependence on both measurements y and x.

Truth	β0	β1	β2	γ0	γ1	py1	qy1	py2	qy2	px1	qx1	px2	qx2
	−0.700	1.500	1.500	−0.850	1.500	0.800	0.850	0.850	0.750	0.900	0.750	0.700	0.950
Ideal analysis
EST	−0.692	1.498	1.548	−0.860	1.526
BIAS	0.008	−0.002	0.048	−0.010	0.026
SE	0.226	0.419	0.210	0.182	0.161
SD	0.226	0.439	0.215	0.175	0.159
CP	0.952	0.954	0.944	0.960	0.954
Naive analysis
EST	−0.404	0.403	0.480	0.115	0.471
BIAS	0.296	−1.097	−1.020	0.965	−1.029
SE	0.177	0.254	0.065	0.114	0.057
SD	0.185	0.259	0.075	0.111	0.062
CP	0.600	0.006	0.000	0.000	0.000
Model assuming conditional independence (M1)
EST	−0.451	0.919	0.718	−0.756	1.197	0.879	0.925	0.922	0.822	0.934	0.769	0.733	0.966
BIAS	0.249	−0.581	−0.782	0.094	−0.303	0.079	0.075	0.072	0.072	0.034	0.019	0.033	0.016
SE	0.258	0.464	0.167	0.241	0.215	0.034	0.026	0.026	0.034	0.025	0.033	0.044	0.016
SD	0.262	0.472	0.214	0.237	0.251	0.035	0.025	0.026	0.034	0.025	0.033	0.043	0.014
CP	0.816	0.726	0.080	0.924	0.602	0.404	0.258	0.302	0.468	0.742	0.910	0.882	0.846
Model assuming conditional dependence (M2)
EST	−0.656	1.492	1.777	−0.921	1.761	0.799	0.855	0.848	0.752	0.888	0.743	0.687	0.942
BIAS	0.044	−0.008	0.277	−0.071	0.261	−0.001	0.005	−0.002	0.002	−0.012	−0.007	−0.013	−0.008
SE	0.539	1.048	0.701	0.385	0.464	0.041	0.037	0.037	0.040	0.036	0.035	0.047	0.022
SD	0.494	0.832	0.538	0.367	0.389	0.038	0.034	0.034	0.037	0.034	0.032	0.043	0.020
CP	0.950	0.974	0.982	0.952	0.954	0.960	0.986	0.960	0.964	0.958	0.964	0.954	0.960

CP: coverage probability.

Per the suggestions by one of the reviewers, it is of interest to investigate the performance of model M₂ in the scenarios when the degree of conditional dependency parameters vary and when one test is very inaccurate (e.g. p=q=0.6). In the third set of simulation, we let the second test for x be very inaccurate (p_x2=q_x2=0.6) and let the degree of conditional dependency parameters be $d_p^y=d_q^y=0.25$ and $d_p^x=d_q^x=0.75$. The results in Table 3 indicate that bias is small and the CPs are reasonably close to 0.95.

Table 3.

Parameter estimates from 500 replications with sample size 400 assuming conditional dependence on both measurements y and x ( $d_p^y=d_q^y=0.25$ and $d_p^x=d_q^x=0.75$).

Truth	β0	β1	β2	γ0	γ1	py1	qy1	py2	qy2	px1	qx1	px2	qx2
	−0.700	1.500	1.500	−0.850	1.500	0.800	0.850	0.850	0.750	0.900	0.750	0.600	0.600
EST	−0.680	1.485	1.937	−0.939	1.775	0.791	0.845	0.844	0.744	0.890	0.752	0.602	0.606
BIAS	0.020	−0.015	0.437	−0.089	0.275	−0.009	−0.005	−0.006	−0.006	−0.010	0.002	0.002	0.006
SE	0.553	1.179	0.681	0.512	0.584	0.038	0.033	0.034	0.037	0.041	0.042	0.040	0.036
SD	0.495	0.883	0.508	0.471	0.441	0.035	0.030	0.031	0.034	0.037	0.042	0.037	0.035
CP	0.974	0.984	0.958	0.954	0.982	0.944	0.966	0.966	0.966	0.958	0.962	0.956	0.952

CP: coverage probability.

In the fourth set of simulation, we let the second test for y be very inaccurate (p_y2=q_y2=0.6) and let the degree of conditional dependency parameters be $d_p^y=d_q^y=0.75$ and $d_p^x=d_q^x=0.25$. The results in Table 4 indicate that bias is small and the CPs are reasonably close to the nominal level. From Tables 3 and 4, we conclude that our modeling framework performs reasonably well under various degrees of conditional dependency parameters and even when one test is very inaccurate.

Table 4.

Parameter estimates from 500 replications with sample size 400 assuming conditional dependence on both measurements y and x ( $d_p^y=d_q^y=0.75$ and $d_p^x=d_q^x=0.25$).

Truth	β0	β1	β2	γ0	γ1	py1	qy1	py2	qy2	px1	qx1	px2	qx2
	−0.700	1.500	1.500	−0.850	1.500	0.800	0.850	0.600	0.600	0.900	0.750	0.700	0.950
EST	−0.642	1.522	1.821	−0.944	1.802	0.801	0.853	0.606	0.606	0.886	0.738	0.680	0.940
BIAS	0.058	0.022	0.321	−0.094	0.302	0.001	0.003	0.006	0.006	−0.014	−0.012	−0.020	−0.010
SE	0.579	1.121	0.755	0.379	0.442	0.044	0.040	0.039	0.038	0.035	0.034	0.045	0.021
SD	0.494	0.808	0.588	0.327	0.347	0.041	0.033	0.037	0.035	0.029	0.035	0.042	0.019
CP	0.966	0.980	0.968	0.960	0.958	0.962	0.988	0.956	0.966	0.962	0.920	0.936	0.952

CP: coverage probability.

4 Data example

The proposed methodology has been motivated by the dataset including 626 patients who participated in a study conducted by the ADMDC at Baylor College of Medicine. All patients in this study have probable AD as determined by criteria from the National Institute of Neurological and Communicative Disorders and Stroke and Alzheimer’s Disease and Related Disorders Association.⁴¹ Clinical and neuropsychological data are obtained at baseline and at annual follow-up visits. Detailed description of the data, patient recruitment, assessment, and follow-up procedures have been reported in the literature.^42,43 Although the dataset is longitudinal, this article will use only the baseline data for illustration purposes.

To measure these patients’ AD severity, four major neuropsychological test scores have been collected, i.e. Mini-Mental Status Exam (MMSE), Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS), Clinical Dementia Rating Scale-Sum of Boxes (CDR-SB), and Clinical Dementia Rating Scale-Total (CDR-Total). MMSE (ranges from 0 to 30 with higher scores reflecting better clinical outcomes) is a measurement to quantify cognitive function and to screen for cognitive loss.⁴⁴ ADAS (ranges from 0 to 70 with higher scores reflecting more serious cognitive impairment) assesses cognitive domains often impaired in AD including memory, orientation, visuospatial ability, language, and praxis.⁴⁵ CDR-Total (ranges from 0 to 4 with higher score reflecting worse clinical outcome) is based on the ratings in six domains or boxes including memory, orientation, judgment/ problem solving, community affairs, home and hobbies, and personal care. The ratings are derived from patient interview and mental status examination in conjunction with an interview of a collateral source.^46,47 CDR-Total is computed via an algorithm⁴⁷ available online (http://www.biostat.wustl.edu/~adrc/cdrpgm/index.html). CDR-SB score (ranges from 0 to 18 with higher scores reflecting more serious global impairment) is obtained by simply summing ratings of the same six domains.

One question of interest to neurologists is to dichotomize these patients’ cognitive severity and overall disease severity statuses as mild vs moderate-to-severe and investigate how the overall disease severity (i.e. ‘exposure’) impacts the cognitive severity (i.e. ‘disease’). This information has significant implications in therapeutic decision-making and patient management.^48,49 MMSE and ADAS scores mainly quantify cognitive function. MMSE score is dichotomized into ‘mild’ (y₁=1) if MMSE ≥ 20 and ‘moderate-to-severe’ (y₁=0) otherwise. ADAS score is dichotomized into ‘mild’ (y₂=1) if ADAS ≤ 20 and ‘moderate-to-severe’ (y₂=0) otherwise. In contrast, CDR-Total and CDR-SB scores are evaluations of overall functional impairment. CDR-Total score is dichotomized into ‘mild’ (x₁=1) if CDR-Total ≤ 1 and ‘moderate-to-severe’ (x₁=0) otherwise. CDR-SB score is dichotomized into ‘mild’ (x₂=1) if CDR-SB ≤ 9 and ‘moderate-to-severe’ (x₂=0) otherwise. Both CDR-Total and CDR-SB are highly popular tools for staging AD total disease severity. For example, Perneczky et al.⁴⁸ used CDR-Total as a gold standard to evaluate the staging performance of MMSE, while O’Bryant et al.⁴⁹ discussed the advantage of CDR-SB. We thus consider both in our modeling framework. The binary statuses obtained from the above rules are proxies of the unknown ‘true clinical’ cognitive severity (y) and overall disease severity (x) and are subject to misclassification.

Among all the clinical variables collected, the pre-progression rate has been shown to be strongly associated with cognitive severity and progression⁵⁰ and has prognostic value in dichotomizing AD patients’ cognitive severity and overall disease severity while controlling for possible confounding from age at baseline, premorbid IQ, and some other covariates.⁴³ The pre-progression rate is calculated using clinicians’ standardized assessment of symptom duration in years and the baseline MMSE by the formula: (30 – baseline MMSE)/estimated duration of symptoms in years, with higher values reflecting worse clinical outcome. Detailed description of these variables as well as their relationship to the cognitive functions can be found in Rountree et al.⁴³

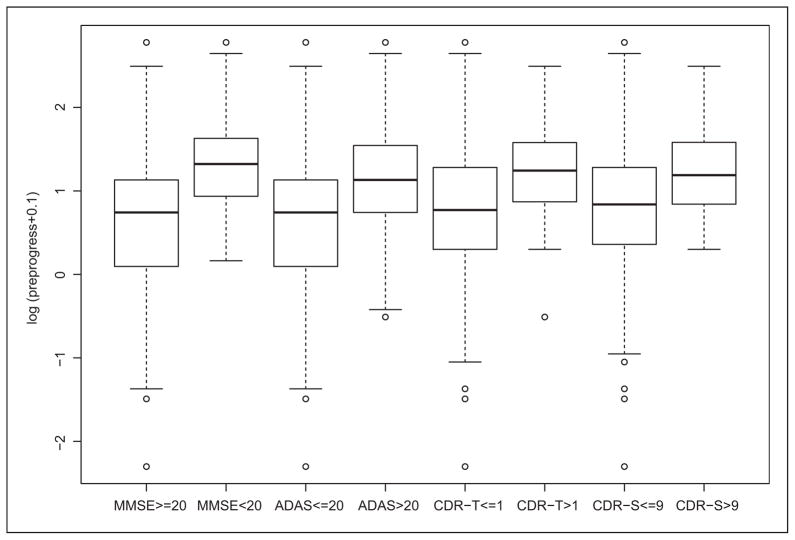
Figure 1 shows the boxplots displaying differences in the logarithm of pre-progression rates (0.1 is added to avoid −∞ when it equals to 0) for patients classified as mild and moderate-to-severe in cognitive severity and in overall disease severity. Specifically, the patients who are mild in cognitive severity have significantly lower log pre-progression rates compared to moderate-to-severe ones (p<0.001 in two-sample t-tests of both MMSE and ADAS scores). Similarly, the patients who are mild in overall disease severity have significantly lower log pre-progression rates compared to moderate-to-severe ones (p<0.001 in two-sample t-tests of both CDR-Total and CDR-SB scores). The information in pre-progression rate will help dichotomize the cognitive severity and overall disease severity in the sense that patients with lower log pre-progression rates are much more likely to be mild than being moderate-to-severe in both cognitive severity and overall disease severity. In the analysis below, the log pre-progression rate, standardized age, and standardized premorbid IQ are included in both the outcome and exposure models with x, y=1 representing mild. Normal priors with mean zero and variance 10 are set on each parameter in the outcome and exposure models. We remove 30 patients with missing values (all occur in ADAS, CDR-SB, and CDR-Total) and our final analysis is based on the sample size of 596.

Figure 1.

Box-plots of log pre-progression rates for patients classified as mild or moderate-to-severe in various scores.

MMSE: Mini-Mental Status Exam; ADAS: Alzheimers Disease Assessment Scale-Cognitive Subscale; CDR-SB: Clinical Dementia Rating Scale-Sum of Boxes; CDR-Total: Clinical Dementia Rating Scale-Total; CDR-T: CDR-Total; and CDR-S: CDR-SB.

In the data analysis, we consider four models, i.e. naive, M₁, M₂, and M₃, the partial dependence model assuming conditional independence in measurements of y and conditional dependence in measurements of x. Table 5 presents estimated DICs and Bayes factors for models M₁, M₂, and M₃. Model M₃ has the lowest DIC value. Moreover, the Bayes factor of model M₃ relative to model M₁ is 10.985, indicating positive evidence against model M₁ according to the interpretation proposed by Kass and Raftery.³⁸ Therefore, model M₃ is selected as the final model. Note that DIC from the naive method are not provided because DICs are comparable only over models with exactly the same observed data³⁶ and the naive model only uses part of the observed data.

Table 5.

Model comparison statistics for Baylor AD dataset.

Model	D̄	pD	DIC	BF
M1	1610.474	14.200	1624.674	Ref
M2	1613.274	11.442	1624.674	0.847
M3a	1609.974	11.398	1621.374	10.985

D̄: the posterior mean of the deviance; p_D: the effective number of parameters; DIC: deviance information criterion; and BF: Bayes factor.

^apreferred model.

Table 6 provides the posterior means, SDs, and 95% credible intervals for some parameters of interest of the final selected model M₃. The results from other models are provided in Section B of Appendix. The outcome model results suggest that the patients who are mild in overall disease severity have statistically significantly higher probability of being mild in cognitive severity. Pre-progression rate is strongly associated with both cognitive severity and overall disease severity, i.e. for 1 unit increase in the natural logarithmic scale of the pre-progression rate, the odds ratios of being mild in cognitive and mild in overall disease severity are 0.183 (i.e. exp(−1.698); 95% credible interval [0.105, 0.303]) and 0.483 (i.e. exp(−0.728); 95% credible interval [0.280, 0.785]), respectively, holding other covariates fixed. Premorbid IQ is also associated with both cognitive severity and overall disease severity, i.e. for 10 units increase from the mean premorbid IQ scores (108.7), the odds ratios of being mild in cognitive severity and mild in overall disease severity are 2.314 (i.e. exp(0.839); 95% credible interval [1.587, 3.294]) and 2.330 (i.e. exp(0.846); 95% credible interval [1.606, 3.854]), respectively, holding other covariates fixed. Note that age is not associated with cognitive severity. This finding is consistent with an article published by our group (Doody et al⁵⁰), in which age is not significantly related to the cognitive score in the adjusted model (Table 3 in Doody et al).

Table 6.

Analysis results of Baylor AD dataset under the final selected model (M₃: the model assuming conditional independence in measurements of y and conditional dependence in measurements of x).

	PMSD	95% CI
Outcome model
Int	−0.518.990	−3.213, 0.854
x	3.3011.029	1.900, 6.014
Pre-prog	−1.698.268	−2.254, −1.195
Age	−0.098.197	−0.450, 0.342
IQ	0.839.185	0.462, 1.192
Exposure model
Int	2.824.397	2.078, 3.648
Pre-prog	−0.728.260	−1.274, −0.242
Age	−0.503.199	−0.943, −0.148
IQ	0.846.222	0.474, 1.349
MMSE
p	0.975.014	0.943, 0.997
q	0.795.046	0.703, 0.883
ADAS
p	0.814.027	0.761, 0.867
q	0.906.030	0.844, 0.907
CDR-Total
p	0.986.010	0.962, 0.999
q	0.796.143	0.568, 0.996
CDR-SB
p	0.989.008	0.970, 0.999
q	0.673.120	0.504, 0.880

MMSE: Mini-Mental Status Exam; ADAS: Alzheimers Disease Assessment Scale-Cognitive Subscale; CDR-Total: Clinical Dementia Rating Scale-Total; CDR-SB: Clinical Dementia Rating Scale-Sum of Boxes; CI: Credible interval; Pre-prog: log pre-progression rate; age: standardized age; and IQ: standardized premorbid IQ.

CDR-Total and CDR-SB exhibit strong conditional dependence. Specifically, the estimates of $d_p^x$ and $d_q^x$ are 0.658 (SD: 0.257) and 0.832 (SD: 0.218), respectively. These results are not unexpected because both CDR-Total and CDR-SB are based on the patients’ ratings in same six domains with the difference being the computing algorithms. If the measurements of ratings incur errors, both CDR-Total and CDR-SB are likely to encounter errors in the same direction (positively correlated). Therefore, it is necessary to assume conditional dependence between CDR-Total and CDR-SB in this example. By comparing the estimates of p and q of CDR-Total and CDR-SB from model M₃ and model M₁ (Table 6 vs Table 7 in Section B of Appendix), we confirm that model M₁ overestimates the parameters of sensitivity and specificity when conditional dependence is present, as reported in Section 3.2. In addition, the estimates of $p_{11\mid 1}^x$ and $p_{00\mid 0}^x$ are 0.982 (SD: 0.010) and 0.663 (SD: 0.120), respectively. Specifically, when the true overall disease severity is mild, the probability that both CDR-Total and CDR-SB are mild is 0.982. In contrast, when true overall disease severity is moderate-to-severe, the probability that both CDR-Total and CDR-SB are moderate-to-severe is 0.663. Clinically speaking, this implies that CDR-Total and CDR-SB are more likely to give consistent and accurate measures for mild patients and less likely to give consistent and accurate measures for moderate-to-severe patients.

5 Discussion

In this article, we present a Bayesian approach to address the issue of misclassification occurring in both the binary response variable and one binary covariate in the absence of a gold standard. We relax the commonly made assumption of conditional independence using the approach by Black and Craig.³³ Extensive simulation results show that the parameters, including the sensitivity and specificity of the imperfect measurements, can be successfully recovered by our proposed models. In addition, the simulation results suggest that the independence model (M₁) substantially overestimates the parameters of sensitivity and specificity when conditional dependence exists, while the dependence model (M₂) only slightly underestimates the parameters of sensitivity and specificity when no conditional dependence exists. In the analysis of the Baylor AD dataset, the cognitive severity and overall disease severity are highly correlated. Both pre-progression rate and premorbid IQ are associated with the cognitive severity and overall disease severity. In general, the proposed method can be broadly applied to binomial regression where misclassification exists in both the response variable and one binary covariate.

Adjustment for potential bias due to misclassification requires information on the misclassification structure to make the model identifiable.²⁶ The covariate, i.e. pre-progression rate, included in the models is an important determinant of both cognitive severity and overall disease severity. This is manifested by the clear dichotomy in log pre-progression rate displayed in Figure 1. As pointed out by Nagelkerke et al.,⁵¹ this variable is an instrumental variable and it makes the model identifiable when its number of different possible realizations is sufficient. Since pre-progression rate is a continuous variable, its number of different possible realizations is potentially unlimited.

Our modeling framework has several limitations that we view as future research direction. One limitation is the non-differential assumption, i.e. the sensitivity and specificity do not depend on the covariates or response. This assumption has been relaxed in some statistical literature.⁵² Another limitation is that our model is fully parametric. It is worth investigating how the model inference changes under various models. In addition, because the information from the covariate (i.e. pre-progression rate) helps in classification, it would be of statistical interest to see how the covariate effect influences the model identifiability. We will address these issues in our future work. Moreover, Bayesian average power criterion has recently been used to evaluate the impact of misclassified variables in logistic regression models.^53,54 As a direction of future research, we can use Bayesian average power to investigate whether misclassification of response or misclassification of a covariate has a larger effect on power and bias.

Appendix

Section A: likelihood derivation

The observed likelihood for one subject is

$$\begin{array}{l}L(\mathit{\theta }\mid {\mathit{z}}_y,{\mathit{z}}_x)=P(y_1,y_2,x_1,x_2\mid {\mathit{z}}_y,{\mathit{z}}_x)\\ =P(y_1,y_2,x_1,x_2\mid x=1,{\mathit{z}}_y,{\mathit{z}}_x){\pi }_x+P(y_1,y_2,x_1,x_2\mid x=0,{\mathit{z}}_y,{\mathit{z}}_x){\overline{\pi }}_x\\ P(y_1,y_2\mid x=1,{\mathit{z}}_y)P(x_1,x_2\mid x=1){\pi }_x+P(y_1,y_2\mid x=0,{\mathit{z}}_y)P(x_1,x_2\mid x=0){\overline{\pi }}_x\end{array}$$

where P(y₁, y₂|x, z_y)=P(y₁, y₂|y=1)p(y=1|x, z_y)+P(y₁, y₂|y=0)p(y=0|x, z_y). Under conditional independence assumption, we have $P(y_1,y_2\mid x,{\mathit{z}}_y)=p_{y1}^{y_1}·{\overline{p}}_{y1}^{{\overline{y}}_1}·p_{y2}^{y_2}·{\overline{p}}_{y2}^{y_2}·p(y=1\mid x,{\mathit{z}}_y)+q_{y1}^{{\overline{y}}_1}·{\overline{q}}_{y1}^{y_1}·q_{y2}^{{\overline{y}}_2}·{\overline{q}}_{y2}^{y_2}·p(y=0\mid x,{\mathit{z}}_y);P(x_1,x_2\mid x=1)=p_{x1}^{x_1}·{\overline{p}}_{x1}^{{\overline{x}}_1}·p_{x2}^{x_2}·{\overline{p}}_{x2}^{{\overline{x}}_2}$, and $P(x_1,x_2\mid x=0)=q_{x1}^{x_1}·{\overline{q}}_{x1}^{{\overline{x}}_1}·q_{x2}^{x_2}·{\overline{q}}_{x2}^{x_2}$; while under conditional dependence assumption, we have $P(y_1,y_2+x,{\mathit{z}}_y)=p_{y_1{y}_2\mid 1}^y·p(y=1\mid x,{\mathit{z}}_y)+p_{y_1{y}_2\mid 0}^y·p(y=0\mid x,{\mathit{z}}_y),P(x_1,x_2\mid x=1)=p_{x_1{x}_2\mid 1}^x$, and $P(x_1,x_2\mid x=0)=P_{x_1{x}_2\mid 0}^x$.

After simplification, the observed likelihood becomes

$$\begin{array}{l}L=p_{0000}^{{\overline{y}}_1{\overline{y}}_2{\overline{x}}_1{\overline{x}}_2}·p_{0001}^{{\overline{y}}_1{\overline{y}}_2{\overline{x}}_1{x}_2}·p_{0010}^{{\overline{y}}_1{\overline{y}}_2{x}_1{\overline{x}}_2}·p_{0011}^{{\overline{y}}_1{\overline{y}}_2{x}_1{x}_2}·p_{0100}^{{\overline{y}}_1{y}_2{\overline{x}}_1{\overline{x}}_2}·p_{0101}^{{\overline{y}}_1{y}_2{\overline{x}}_1{x}_2}·p_{0110}^{{\overline{y}}_1{y}_2{x}_1{\overline{x}}_2}·p_{0111}^{{\overline{y}}_1{y}_2{x}_1{x}_2}\\ ·p_{1000}^{y_1{\overline{y}}_2{\overline{x}}_1{\overline{x}}_2}·p_{1001}^{y_1{\overline{y}}_2{\overline{x}}_1{x}_2}·p_{1010}^{y_1{\overline{y}}_2{x}_1{\overline{x}}_2}·p_{1011}^{y_1{\overline{y}}_2{x}_1{x}_2}·p_{1100}^{y_1{y}_2{\overline{x}}_1{\overline{x}}_2}·p_{1101}^{y_1{y}_2{\overline{x}}_1{x}_2}·p_{1110}^{y_1{y}_2{x}_1{\overline{x}}_2}·p_{1111}^{y_1{y}_2{x}_1{x}_2}\end{array}$$

where p_abcd=p(y₁=a,y₂=b,x₁=c,x₂=d|z_y,z_x)=P(y₁=a,y₂=b|x=1,z_y)P(x₁=c,x₂=d|x=1)π_x+ P(y₁=a,y₂=b|x=0,z_y)P(x₁=c, x₂=d|x=0)π̄_x.

Section B: analysis results of Baylor AD dataset under various models

Table 7.

Analysis results of Baylor AD dataset under various models.

	Naive		M1		M2
	PMSD	95% CI	PMSD	95% CI	PMSD	95% CI
Outcome model
Int	0.683.353	−0.008, 1.374	−0.044.551	−1.200, 0.946	−0.7011.141	−3.831, 0.891
x	1.881.320	1.254, 2.507	2.674.520	1.762, 3.838	3.5391.180	1.887, 6.758
Pre-prog	−1.347.184	−1.707, −0.987	−1.681.241	−2.174, −1.222	−1.796.298	−2.431, −1.258
Age	−0.136.114	−0.360, 0.088	−0.175.148	−0.472, 0.104	−0.113.216	−0.491, 0.387
IQ	0.606.116	0.379, 0.834	0.917.158	0.616, 1.241	0.868.212	0.445, 1.291
Exposure model
Int	2.788.264	2.271, 3.304	2.864.278	2.347, 3.430	2.797.389	2.055, 3.598
Pre-prog	−0.603.200	−0.996, −0.211	−0.623.209	−1.034, −0.224	−0.719.259	−1.267, −0.245
Age	−0.404.141	−0.679, −0.128	−0.412.146	−0.711, −0.130	−0.508.202	−0.943, −0.155
IQ	0.687.135	0.422, 0.953	0.680.140	0.406, 0.955	0.859.225	0.482, 1.370
MMSE
p			0.974.014	0.942, 0.997	0.973.017	0.934, 0.998
q			0.793.046	0.702, 0.881	0.771.052	0.666, 0.870
ADAS
p			0.815.027	0.762, 0.869	0.809.029	0.752, 0.865
q			0.906.029	0.845, 0.960	0.883.038	0.803, 0.951
CDR-Total
p			0.993.005	0.980, 1.000	0.986.010	0.962, 0.999
q			0.982.017	0.936, 1.000	0.786.142	0.566, 0.996
CDR-SB
p			0.997.003	0.990, 1.000	0.989.008	0.969, 0.999
q			0.834.049	0.732, 0.923	0.664.118	0.504, 0.876

Naive: naive analysis which ignores misclassification and treats y₁ and x₁ as y and x, respectively; M₁: the model assuming conditional independence in both measurements of y and x; M₂: the model assuming conditional dependence in both measurements of y and x; pre-prog: log pre-progression rate; age: standardized age; IQ: standardized premorbid IQ; CI: Credible interval; MMSE: Mini-Mental Status Exam; ADAS: Alzheimers Disease Assessment Scale-Cognitive Subscale; CDR-Total: Clinical Dementia Rating Scale-Total; and CDR-SB: Clinical Dementia Rating Scale-Sum of Boxes.