Abstract
In Parkinson’s disease (PD) clinical trials, Parkinson’s disease is studied using multiple outcomes of various types (e.g. binary, ordinal, continuous) collected repeatedly over time. The overall treatment effects across all outcomes can be evaluated based on a global test statistic. However, missing data occur in outcomes for many reasons, e.g. dropout, death, etc., and need to be imputed in order to conduct an intent-to-treat analysis. We propose a Bayesian method based on item response theory to perform multiple imputation while accounting for multiple sources of correlation. Sensitivity analysis is performed under various scenarios. Our simulation results indicate that the proposed method outperforms standard methods such as last observation carried forward and separate random effects model for each outcome. Our method is motivated by and applied to a Parkinson’s disease clinical trial. The proposed method can be broadly applied to longitudinal studies with multiple outcomes subject to missingness.
Keywords: Clinical trial, global statistical test, item-response theory, latent variable, Markov chain Monte Carlo, missing data
1 Introduction
Parkinson’s disease (PD), a degenerative disorder of the central nervous system, is one of the most common movement disorders affecting about 1% of people older than 60 years.1 The symptoms of PD include primary motor symptoms (e.g. resting tremor, slow movement, rigidity, and postural instability, etc.), secondary motor symptoms (e.g. speech problems, cramping, swallowing difficulty, etc.), and non-motor symptoms (e.g. sleep problems, pain, depression, etc.). Because there is no cure for PD, many drugs have been studied over the last 20 years to decrease the progression and disability of the disease.
A major challenge when studying PD is that impairment is multidimensional and progressive. Thus, for efficient development, targeting, and evaluation of treatments, it is necessary to collect longitudinally multiple outcomes (e.g. clinical rating scales or patient completed questionnaires) of various types (e.g. binary, ordinal, continuous). Common approaches for handling multiple outcomes include choosing a single outcome as a primary outcome, the use of a linear combination of several outcomes, multiple tests with adjustment to the overall significance level, omnidirectional tests of any type of treatment difference (e.g. Hotelling’s T2 test, MANOVA, Wald test, and 2 test), and hierarchical models. Detailed review and discussion of these methods can be found in Pocock2 or Tilley et al.3 These methods address a directionless scientific question, i.e. whether there is any difference between two treatments in these outcomes. However, the major scientific question of many PD clinical trials is directional, i.e. whether target treatment is preferred over placebo in slowing PD progression based on all primary outcomes measured. When the treatment slows progression across all outcomes, the aforementioned approaches tend to statistically obscure findings and lose power.2,3 To address this issue, O’Brien4 has introduced a global statistical test (GST) to combine information across outcomes and to examine whether a treatment has a global benefit without the need of multiple tests. The GST is more powerful than a univariate test or other multiple test procedures when there is a common dose effect across outcomes (i.e. treatment effect is of similar magnitude across all outcomes). The GST was further extended and discussed by many authors,5-15 and has found broad application in medical studies on toxicity,16 stroke,17,18 dermatology,19 asthma,20 lower back pain,21 restless legs syndrome,22 neuropsychological impairment,23 multiple sclerosis,24,25 and breast cancer.26
The rank-sum-type GST proposed by O’Brien4 is conducted as follows. First, for each outcome, all individuals are ranked based on their measured outcomes. Then each individual’s ranks are summed to obtain a rank sum. Finally, a two-sample t-test is applied to compare the rank sums between the treatment and placebo groups. This rank-sum-type GST can combine the treatment effect in all outcomes without making any parametric assumption on the outcome distributions and their correlation. However, Huang et al.12 has proved that O’Brien’s rank-sum-type GST cannot control type I error asymptotically when two groups have different joint cumulative distribution functions. To address this issue, Huang et al.12 proposed an adjusted rank-sum-type GST (referred to as adjusted GST) for the case where variances in two groups are different. The adjusted GST is computed similarly to O’Brien’s rank-sum-type GST, but it is divided by an adjustment factor. In addition, Huang et al.13 introduced the concept of global treatment effect (GTE), which measures a treatment’s overall benefit across multiple outcomes. In this article, we have selected the adjusted GST and GTE to assess the efficacy of PD treatment in a clinical trial.
Another challenge in longitudinal PD clinical trials is that missing data are ubiquitous due to missed visits, withdrawals, lost to follow-up, death, etc. However, when missing values are present in the response variables, the adjusted GST and GTE cannot be computed unless all individuals with missing values are excluded. The primary efficacy evaluation in confirmatory clinical trials is often required by agencies to follow the ‘intent-to-treat’ (ITT) principle, i.e. the analysis includes all randomized individuals regardless of the treatment they actually received, drop-out, or withdrawal of consent. By including all patients who are randomized, the ITT analysis preserves the benefits of randomization and is commonly accepted as the most unbiased approach. However, if the individuals drop out of the study, the data after dropout are missing. Therefore, the ITT analysis requires a method of dealing with the missing data. Complete-case (CC) analysis excludingall individuals with any missing values is seriously biased when the missing is not completely at random (MCAR) and less efficient27 and it violates the ITT principle. Other standard methods such as last observation carried forward (LOCF), i.e. imputing with the value at the last available observation or with the worst observation for the group have been used in multiple PD studies.28,29 Although the LOCF and worst observation imputation methods follows the ITT principle, neither are ideal in this context. They are single imputation methods and underestimate the true variability leading to biased tests.30 The LOCF method underestimates disease progression because the last observed visit (when patient is expected to be less affected) is used in lieu of the final time point. Additionally, when there are multiple outcomes, both the LOCF and worst observation methods fail to account for the correlation among outcomes. A good review of the missing data methods for longitudinal studies can be found in Ibrahim et al.31 and Ibrahim and Molenberghs.32
A better approach is to impute the missing outcomes using some imputation model. Imputation uncertainty is handled by multiple imputation (MI), where M > 1 sets of imputed values are created for the missing values in the dataset, as draws from the predictive distribution of the missing values under an assumed imputation model.33 Among the multivariate longitudinal outcomes, there are three-sources of correlation, i.e. inter-source (different measures at the same visit), intra-source (same measure at different visits), and cross correlation (different measures at different visits).34 One may conduct multiple imputation for each outcome using separate random effects models. But this method (referred to as separate models) ignores the inter-source and cross correlation. To the best of our knowledge, there is no available method that readily imputes the missing values in multivariate longitudinal response variables of mixed type while accounting for all sources of correlation. Our objectives in this article are to develop a Bayesian method based on item response theory (IRT) to perform multiple imputation (MI) for the missing multivariate longitudinal outcomes while accounting for all sources of correlation and to assess a treatment’s global effect across multiple outcomes. Because imputation and statistical inference are carried out separately with the MI method, the MI method has the flexibility that the imputation model differs from the model used for assessing treatment effect.35
The remainder of the article is organized as follows. In section 2.1, we introduce a motivating ongoing PD clinical trial where a moderate amount of missing values has been occurring and in section 2.2 we illustrate the primary analysis methods for this trial. In section 3, we describe the imputation model, multiple imputation using MCMC, and the specification of prior distributions. In section 4, sensitivity analysis is performed under various scenarios to evaluate several methods. Section 5 applies the proposed methodology to a PD clinical trial dataset. A discussion is provided in section 6.
2 A motivating ongoing clinical trial and the primary analysis methods
2.1 A motivating ongoing clinical trial
This article is motivated by the ongoing NIH Exploratory Trials in Parkinson’s Disease (NET-PD) Long-term Study-1 (referred to as LS-1 study) funded by the National Institute of Neurological Disorders and Stroke (NINDS). The enrollment ended in 2010 and follow-up will be completed in 2015. The LS-1 study is a randomized, multi-center, double-blind, placebo-controlled Phase III study of creatine (the study drug, 10 g daily) in individuals with early treated PD. A total of 1741 individuals from 45 sites in the US and Canada were equally randomized to either 10 g creatine/day or matching placebo with annual follow-up for a minimum of 5 years. The LS-1 study evaluates the long-term effects of creatine as measured by change from baseline in a variety of clinical domains including modified Rankin score (Rankin), Schwab and England activities of daily living (SEADL), ambulatory capacity (AC), PDQ-39 summary score (PDQ-39), and symbol digit modalities (SDM). Rankin (an ordinal variable with integer value from 0 to 5, with larger value reflecting worse clinical outcomes) is a measurement of overall clinical assessment.36 SEADL (an ordinal variable with integer value from 0 to 100 incrementing by 5, with larger value reflecting better clinical outcomes) is a measurement of activities of daily living.37 AC is an ordinal variable with integer value from 0 to 20, with larger value reflecting worse clinical outcome.38 PDQ-39 (an approximate continuous variable with integer value from 0 to 156, with larger value reflecting worse clinical outcomes) is a measurement of quality of life.39 SDM (an approximate continuous variable with integer value from 0 to 110, with larger value reflecting better clinical outcomes) is a measurement of cognitive function.40 The measurement of these five outcomes are taken at baseline, annual visits from year 1 to 5. The LS-1 study represents the largest number of patients with early treated PD ever enrolled in a clinical trial. Details of the LS-1 study can be found on the study website http://parkinsontrial.ninds.nih.gov/index.htm. It is expected that there will be approximately 20% missing data across the various outcomes. The primary analysis is to compare the creatine versus placebo groups using the adjusted GST and GTE based on these five outcomes’ changes from baseline to the last visit of year 5. Because the computation of the adjusted GST and GTE requires all outcomes to be in the same direction, we recode outcomes SEADL and SDM so that higher values in all outcomes are worse clinical conditions. We will next illustrate how to compute the adjusted GST and GTE in section 2.2.
2.2 The primary analysis methods
Suppose K outcomes are measured for N individuals at a total of J visits. Let yijk (binary, ordinal, and continuous) be the observed outcome k (k = 1, …, K) from individual i (i = 1, …, N) at visit j(j = 1, …, J, where j = 1 is baseline). We assume that the first n1 individuals are in the placebo group and the next n2 individuals are in the treatment group, and then N = n1 + n2. Let zik = yiJk − yi1k be the change from baseline to the last visit (e.g. 5 years) for outcome k (referred to as outcome change). Throughout the article, we code all outcomes so that larger observation values are worse clinical conditions. Because the clinical outcomes of PD patients generally deteriorate over time, we expect zik to be positive. For each outcome change, we rank all N individuals. Define the midrank of an observation as either the regular rank when there is no tie on the observation or the average rank among the tied observations.41 Let Rik = midrank(zik). In general, higher zik values correspond to larger Rik. The rank sum of individual i is . O’Brien’s rank-sum-type test statistic T is defined as the regular univariate two-sample t-test with pooled standard deviation for the two rank sum samples from the placebo and treatment groups.4 Specifically
| (1) |
where , , , and . O’Brien’s test statistic T rejects the null hypothesis of no treatment effect at significant level α when |T|>tdf,α/2, where tdf,α/2 is the (1−α/2)th percentile of the tdf distribution with df degree of freedom, with df=[ζ2/(n1−1)+(1−ζ)2/(n2−1)]−1 and .12
However, Huang et al.12 has proved that O’Brien’s unadjusted rank-sum-type GST cannot control type I error asymptotically when two groups have different joint cumulative distribution functions. Instead, Huang et al.12 proposed an adjusted rank-sum GST test statistic Ta (referred to as adjusted GST statistics)
| (2) |
where (see Huang et al.12 for the details of computation) is the estimate of the asymptotic variance of O’Brien’s test statistic when the variances in the two groups are different. Huang et al.13 has shown that as the N increases, Ta converges to a normal distribution with asymptotic mean and variance 1, where J is a K-dimensional vector with all its elements equal to one, is GTE defined next. Please see Huang et al.13 for the formula to compute Σ and . In this article, we use the adjusted GST statistics to test the efficacy of the treatment. We refer to in Ta as rank sum difference and as estimated variance of the rank sum difference. Note that if the treatment is efficacious in slowing the PD progression, we expect and Ta>0.
To measure a treatment’s overall benefit across multiple outcomes, Huang et al.13 defined GTE as the difference of two probabilities: the probability that a control group individual will do better if the individual is in the treatment group, and the probability that a treatment individual will do better if the individual is in the control group. Let Z1k and Z2k be the change from baseline to the last visit (e.g. 5 years) for outcome k in the placebo and treatment groups, respectively. We expect Z1k and Z2k to be positive and Z1k > Z2k if a treatment is efficacious in slowing the PD progression. Let the treatment effect on outcome k be ψk = p(Z1k > Z2k)−p(Z1k < Z2k). The GTE across all K outcomes is . The GTE takes values between −1 and 1 and it measures the degree of dissimilarity between two groups. When , there is no global preference between groups. When , the treatment group is preferred the most. When , the placebo group is preferred the most. Higher positive corresponds to a higher degree of treatment group preference. We will next illustrate how to impute the missing data so that the ITT principle can be followed when computing the adjusted GST and GTE.
3 Models used in MI inference
3.1 Imputation model
In this section, we propose the imputation model based on the item response theory for the multivariate longitudinal data. Let yij = (yij1, …, yijk, …, yijK)’ be the vector of observation for individual i at visit j, with elements possibly being binary, ordinal, and continuous. Let yi = (yi1, …, yiK)’ be the outcome vector across visits. We model the binary outcomes, the cumulative probabilities of ordinal outcomes, and the continuous outcomes using a two-parameter model,42 graded response model,43 and common factor model,44 respectively.
| (3) |
| (4) |
| (5) |
where random error ,ak is the outcome-specific ‘difficulty’ parameter and bk is the outcome-specific ‘discriminating’ parameter that is always positive and represents the discrimination of outcome k, i.e. the degree to which the outcome discriminates between individuals with different latent disease severity θij. In model (4), the ordinal outcome k has nk categories and nk − 1 thresholds ak1, …, akl, …, aknk−1 that must satisfy the order constraint ak1< …, akl< … <aknk−1. The probability that individual i selects category l on outcome k at visit j is p(Yijk = l|θij) = p(Yijk ≤ l|θij)− p(Yijk ≤l − 1|θij). The latent variable θij is continuous and it indicates individual i’s unobserved disease severity at visit j, with a higher value denoting more severe status. We refer to θij as disease severity. The mean of θij is modeled as a function of covariates and visit time
| (6) |
where Xi is individual i’s covariate vector including some covariates of interest (e.g. treatment assignment) and potential confounding variables (e.g. age, gender), tj is the visit time variable with t1 = 0 for baseline. For example, if Xi only includes the treatment assignment, μij = [β0 + β1Ii(trt)]tj, where I(·) is an indicator function, Ii(trt) = 1 if individual i is in the treatment group. The significant negative coefficient β1 indicates that the treatment significantly improves the disease severity. Model (6) is a latent trait regression model assuming that the disease severity is expected to change linearly over the course of the study, with slope depending on the covariate vector Xi.45
The latent disease severity vector θi = (θi1, …, θiJ)’ is assumed to be independently and identically distributed with normal probability density function h(θi, Σ), i.e. θi|Σ ~ NJ(μi, Σ), where μi = (μi1, …, μiJ)’ is the mean vector of θi, Σ is the J × J covariance matrix of θi with σlm being the (l, m) element. Various assumptions can be made on the covariance matrix, e.g. uniform (equal variance and equal correlation), autoregressive (correlation decreases as time separation increases), heteroscedastic (unequal variance and equal correlation), and more generally, unstructured (unequal variance and unequal correlation).46 We use an unstructured covariance matrix in this article. This IRT model accounts for all three sources of correlations illustrated in section 1. Specifically, the inter-source correlation (different measures at the same visit) is modeled by the disease severity θij. Both the intra-source correlation (same measure at different visits) and cross correlation (different measures at different visits) are modeled by the correlation between θij and θij’ with j ≠ j’ through the off-diagonal elements of covariance matrix Σ.
It is well-known that the item-response models are over-parameterized because they have more parameters than can be estimated from the data.47,48 Hence additional constraints are required to make models identifiable. In the longitudinal setting discussed here, the mean and variance of θij at one visit may be specified to establish the location and scale of the disease severity distribution.49 Specifically, we set σ11 = 1 (the variance of θij at baseline) and additionally we set t1 = 0 at baseline to make μi1 = 0 through model (6) to ensure parameter identifiability.
Under the local independence assumption (i.e. conditioning on the disease severity θij, all components in yij are independent), the full likelihood of individual i across all visits is
| (7) |
For notation convenience, we let the difficulty parameter vector be a = (a1, …, aK)’, the discrimination vector be b = (b1, …, bK)’, and the parameter vector Φ = (a, b, β, Σ)’.
3.2 Bayesian multiple imputation
In this section, we illustrate how to use Markov chain Monte Carlo (MCMC) algorithm to iteratively draw samples for the parameter vector Φ and the missing outcome data from conditional distributions and how to perform multiple imputation to make appropriate statistical inference. Let Ymis and Yobs be the missing and observed responses, respectively. Multiple imputations under models (3), (4), and (5) are M independent draws from the posterior predictive distribution for the missing data, . The observed-data posterior density is , where π(Φ) is the prior distribution, the observed likelihood function . As in most missing data problems with unknown missing patterns, the posterior predictive distribution p(Ymis|Yobs) cannot be simulated directly. We use a Gibbs sampling algorithm to draw the missing values from p(Ymis|Yobs). Specifically, the current versions of the parameter vector Φ(t), the missing data , and the disease severity θ(t) are updated in three steps:
Starting from a reasonable initial values Φ(0) and , these steps define a cycle of Gibbs sampler. Repeating the above Gibbs sampling algorithm with large enough number of iterations, it creates stochastic sequences and whose limiting distributions are p(Φ|Yobs) and p(Ymis|Yobs), respectively. We implement this algorithm in WinBUGS.50 We use the trace plots available in WinBUGS and view the absence of apparent trend in the plots as evidence of convergence. In addition, we run multiple chains with overdispersed initial values and compute the Gelman-Rubin scale reduction statistics to ensure of all parameters are smaller than 1.1.51 The length of burn-in is assessed by trace plots and autocorrelation for each parameter. If diagnostics tools suggest that convergence is achieved after T0 iterations, we would retain simulated missing values every (T − T0)/M iterations starting from t = T0 + 1 and treat them as M imputed datasets.
After M imputed datasets have been created, they can be analyzed using the primary analysis methods illustrated in section 2.2, resulting in M sets of rank sum differences and associated estimated variances computed based on the change of all outcomes from baseline to the last visit. The M sets of rank sum differences and associated estimated variances are combined to create one multiple-imputation inference by Rubin’s MI rules33 as follows. Let Dm and Vm denote the estimated rank sum difference and the associated estimated variance from the mth imputed dataset, respectively. The overall rank sum difference D is estimated by and its variance is estimated by where the between-imputation variance . The test statistic has approximately a central t-distribution under the null hypothesis of no treatment effect with degree of freedom .
Multiple imputation usually provides good MI efficiency and minimizes sampling variability with a moderate M. Specifically, we use M = 100 in this article. After M sets of GTE are computed based on M imputed datasets, the overall GTE is computed as the average of M sets of GTE, but its variance cannot be computed because the variance formula is unavailable.
3.3 Specification of prior distribution
In this section, we illustrate selection of the prior distribution π(Φ). We use vague prior distributions on all elements in the parameter vector Φ. Specifically, the prior distributions of ak, k = 1, …, K, all elements in β are N(0, 100). We use the prior distribution bk ~ Uniform[0, 20], k = 1, … K, to ensure positivity. To obtain the prior distributions for the threshold parameters of ordinal outcome k, we first define unconstrained auxiliary parameters such that for l = 1, …, nk − 1, and set akl equal to the l-th order statistic of the auxiliary parameters. This approach to modeling threshold parameters is recommended by Plummer.52 For the ease of sampling for Σ, we use an approach based on the Cholesky decomposition.53 Let Σ=ΩΩ’, where Ω is a matrix with zero entries above the main diagonal, and let ωlm be the (l, m)th entry for 1 ≤ m ≤ l ≤ J. Consider a latent vector zi = (zi1, …, ziJ)’ with N(0, 1) independent components. Then the linear reparameterization of (with element being , e.g. ) has mean μi and variance Σ. The entries of the matrix Σ are computed as , 1 ≤ l, m ≤ J, where l ∧ m = min(l, m). We impose Uniform(0, 20) prior distribution on ωkk to ensure non-negativity and N(0, 100) prior distribution on ωlm where l ≠ m to allow for possible negative correlation.
To summarize the multiple imputation methods illustrated in section 3, we fit item-response models (3), (4), and (5) with mean model (6) to obtain M full datasets with missing outcome values at all visits imputed, compute the change from baseline to the last visit for each outcome, rank all individuals on each outcome, add up each individual’s ranks to obtain a rank sum, compute the estimated rank sum difference and the estimated variance using equation (2) and compute the GTE, the results are combined using Rubin’s MI rules.
4 Simulation
In this section, we perform a sensitivity analysis under various scenarios. We conduct extensive simulation studies to evaluate the performance of the LOCF, separate models (use linear mixed models and proportional odds models as imputation models for continuous and ordinal outcomes, respectively), and MI method. We simulate the datasets with data structure similar to the LS-1 study, e.g. five outcomes (with the first three ordinal outcomes representing Rankin, SEADL, and AC, respectively and with the last two continuous outcomes representing PDQ-39 and SDM, respectively) and six visits (baseline, annual visits from year 1 to 5). The outcome data are generated from multivariate normal distributions using the following algorithm.
- From the baseline data in the ongoing the LS-1 study, we obtain the baseline mean vector of the five outcomes μ0 = (1.2, 91.1, 1.7, 13.2, 44.5)’ and the baseline inter-source covariance matrix V of the five outcomes
- We select the intra-source correlation coefficient matrix
The covariance matrix Σ of five outcomes across six visits is Σ = V ⨷ W, where ⨷ is a Kronecker product and the dimension of Σ is 30 × 30. From the protocol of the LS-1 study, the expected one year outcome change for the placebo and treatment groups are dP = (0.2, −2, 0.25, 3, −1.1)’ and dT=(0.16, −1.6, 0.184, 2.4, −0.8)’, respectively. The mean vector across six visits for the placebo and treatment groups are and , respectively.
Simulate 400 individuals in the placebo group from a multivariate normal distribution with mean μP and covariance matrix Σ.
Simulate 400 individuals in the treatment group from a multivariate normal distribution with mean μT and covariance matrix Σ.
If the simulated outcomes are out of the reasonable bounds illustrated in section 2.1, they are truncated to the closest bound. Round the outcomes Rankin, AC, PDQ-39, and SDM to the closest integers. Divide the outcome SEADL by 5 and round it to the closest integer because SEADL increments by 5.
Rescale outcomes SEADL and SDM so that larger values in all five outcomes represent worse clinical outcomes. To avoid that some categories have zero observations, we combine some categories in outcomes SEADL and AC so that they have seven and six categories, respectively.
We totally simulate 100 datasets. Let rijk (1 if missing, 0 otherwise) be the missing indicator of individual i’s outcome k at visit j. To simulate the missing data, we specify a model that describes the missing data process as follows.
| (8) |
where φk1 = 0 implies that missingness only depends on the observed data in the last visit and is ignorable dropout mechanism (missing at random, MAR), while φk1 ≠ 0 implies an outcome-dependent non-ignorable dropout mechanism (missing not at random, MNAR).33 We do not simulate any missing data at baseline and hence j = 2, …, 6 in model (8). In the simulation studies, we investigate two missing data mechanisms (MAR and MNAR), and two missing data patterns, i.e. non-monotone (an individual can be missing at one visit and then measured again at later visit) and monotone (sequences of measurements on some individuals terminate prematurely). To generate monotone missing pattern, we exclude yij’k for j’ ≥ j if rijk = 1. We select the appropriate φk,MAR = (φk0, φk2)’ and φk, MNAR = (φk0, φk1, φk2)’ for k = 1, …, 5 so that the overall missing percentages are 20%, 30%, and 40% in all combinations of missing mechanisms and missing patterns.
After the datasets with missing data are simulated, we first compute the adjusted GST statistics Ta and GTE based on the LOCF method, which does not require multiple imputation. Next, we compute Ta and GTE based on the separate models and MI methods. Specifically, we first fit separate models to generate 100 multiply imputed full datasets for each simulated dataset with missing values, then compute the adjusted GST statistics Ta and GTE based on Rubin’s MI rules illustrated in section 3.2. Next, we fit IRT models (4) and (5) and include the binary treatment assignment variable in the mean model (6), i.e. μij = [β0 + β1 Ii(trt)]tj, to each simulated dataset. We run two chains with 10,000 iterations per chain. The first 5000 iterations are discarded as burn-in, and the inference is based on the remaining 5000 iterations. The MCMC convergence and mixing properties are assessed by visual inspection of the history plots of all parameters and the Gelman–Rubin statistics. In all simulation studies, the MCMC chains mix well after a burn-in of 5000 iterations. For each simulated dataset with missing data, we obtain M = 100 full datasets imputed by retaining simulated missing values every 100 iterations starting from the 5001th iteration on each chain. We then compute the Ta and GTE based on Rubin’s MI rules. To evaluate and compare the performance of the LOCF, separate models, and MI methods, we compute the root mean square error (RMSE) of Ta and GTE defined as and respectively, where the subscript n denotes the nth with missing data, and are the estimated adjusted GST and GTE using various methods, the asymptotic mean μTn, (see Huang et al.,13 p.3090) and ψn are computed based on the nth simulated dataset without generating any missing data (i.e. the true dataset).
Table 1 displays the RMSE of Ta and GTE using the LOCF, separate models, and MI methods under various scenarios, i.e. the combinations of three missing percentages (20%, 30%, and 40%), two missing data mechanisms (MAR and MNAR), and two missing data patterns (non-monotone and monotone). Within each combination of missing data mechanism and missing data pattern, RMSE increases as the missing percentage increases. All methods perform better under MAR than under MNAR. While both the LOCF and separate models methods performs better under non-monotone than under monotone pattern, there is no obvious trend observed for the MI method in this comparison. In all simulation settings, the separate models method has the largest RMSE and the MI method always outperforms the LOCF method (except in the first scenario) with a larger advantage as the missing percentage increases.
Table 1.
Root mean square error (RMSE) of the adjusted GST statistics Ta and GTE for change from baseline to 5 years using the LOCF, separate models, and MI methods under various scenarios.
|
Ta
|
GTE |
|||||||
|---|---|---|---|---|---|---|---|---|
| Missing mechanism | Missing pattern | Missing % | LOCF | Separate | MI | LOCF | Separate | MI |
| MAR | Non-monotone | 20 | 1.257 | 2.963 | 1.248 | 0.035 | 0.079 | 0.039 |
| 30 | 2.078 | 3.714 | 1.631 | 0.057 | 0.098 | 0.049 | ||
| 40 | 2.938 | 4.366 | 1.874 | 0.078 | 0.113 | 0.056 | ||
| Monotone | 20 | 1.529 | 3.047 | 1.192 | 0.043 | 0.082 | 0.037 | |
| 30 | 2.370 | 3.884 | 1.632 | 0.064 | 0.101 | 0.049 | ||
| 40 | 3.314 | 4.516 | 1.908 | 0.087 | 0.116 | 0.056 | ||
| MNAR | Non-monotone | 20 | 1.803 | 3.383 | 1.642 | 0.049 | 0.089 | 0.049 |
| 30 | 2.639 | 4.164 | 2.233 | 0.070 | 0.107 | 0.063 | ||
| 40 | 3.469 | 4.709 | 2.805 | 0.091 | 0.120 | 0.076 | ||
| Monotone | 20 | 1.864 | 3.405 | 1.534 | 0.051 | 0.089 | 0.046 | |
| 30 | 2.717 | 4.184 | 1.976 | 0.073 | 0.108 | 0.057 | ||
| 40 | 3.717 | 4.817 | 2.666 | 0.098 | 0.123 | 0.073 | ||
LOCF: last observation carried forward; MI: multiple imputation; GST: global statistical test; GTE: global treatment effect; MAR: missing at random; MNAR: missing not at random.
In the first simulation scenario, the RMSE of GTE based on the MI method is slightly larger than that based on the LOCF method. We have run additional simulation for this scenario. Specifically, we have doubled the expected one year outcome change in both groups to dP = (0.4, −4, 0.5, 6, −2.2)’ and dT = (0.32, −3.2, 0.368, 4.8, −1.6)’. The RMSE of Ta from methods LOCF, separate models, and MI are 4.044, 4.331 and 1.812 and the RMSE of GTE are 0.094, 0.101, and 0.055, respectively. The results suggest that the advantage of the proposed MI method over the LOCF and separate models methods increases as the outcome rates of change get larger. This is because the LOCF method assumes no disease progression after dropout and its performance deteriorates as the disease progression rate increases.
In conclusion, the LOCF method dampens the treatment–response relationships and produces misleading results. The separate models method fails to account for the inter-source and cross correlations. It is not surprising that the LOCF method outperforms the separate models method in the simulation studies because slow disease progression is simulated. In contrast, the proposed MI method based on the IRT model can account for the within-subject correlation across visits and successfully model the treatment effect of the multiple longitudinal outcomes. As a result, the proposed MI method performs better than the LOCF and separate models methods, with larger advantage as the missing percentage and the outcome rates of change increase.
5 Data analysis
In this section, we apply the proposed methodology to analyze a clinical trial dataset. Because the LS-1 study illustrated in section 2.1 is ongoing and the final dataset is not available until 2015, we use the data from a PD clinical trial with the data structure similar to the LS-1 study. DATATOP (Deprenyl And Tocopherol Antioxidative Therapy Of Parkinsonism) was a double-blind, placebo-controlled multicenter clinical trial to determine if deprenyl and/or tocopherol administered to patients with early PD will slow the progression of PD. Totally 800 individuals were randomly assigned in a 2 × 2 factorial design to receive double-placebo, active tocopherol alone, active deprenyl alone, and both active tocopherol and deprenyl. We combine the individuals who did not receive deprenyl (double-placebo and active tocopherol alone groups, 401 individuals) and refer to as placebo group. We combine the individuals who received deprenyl (active deprenyl alone and both active tocopherol and deprenyl groups, 399 individuals) and refer to as treatment group. The details of DATATOP trial can be found in Shoulson et al.54
The outcomes collected include UPDRS (Unified Parkinson’s Disease Rating Scale) total score, Schwab and England activities of daily living (SEADL), Mini-Mental State Exam (MMSE), and Hamilton Depression Scale, measured at five visits, i.e. baseline, 1 month, 3 months, 9 months, and 15 months. UPDRS total score is the sum of 44 questions each measured on a 5-point scale (0–4) and it is approximated by a continuous variable with integer value from 0 (not affected) to 176 (most severely affected). SEADL is illustrated in section 2.1. Mini-Mental State Exam, a measurement of cognitive impairment, is an ordinal variable with integer value from 0 (severe) to 30 (normal). Hamilton Depression Scale, a depression test measuring the severity of clinical depression symptoms, is an ordinal variable with integer value from 0 (normal) to 52 (severe). For ordinal variables, we combine some categories with zero or small number of individuals and have 7, 7, and 10 categories in SEADL, MMSE, and Hamilton depression scale, respectively.
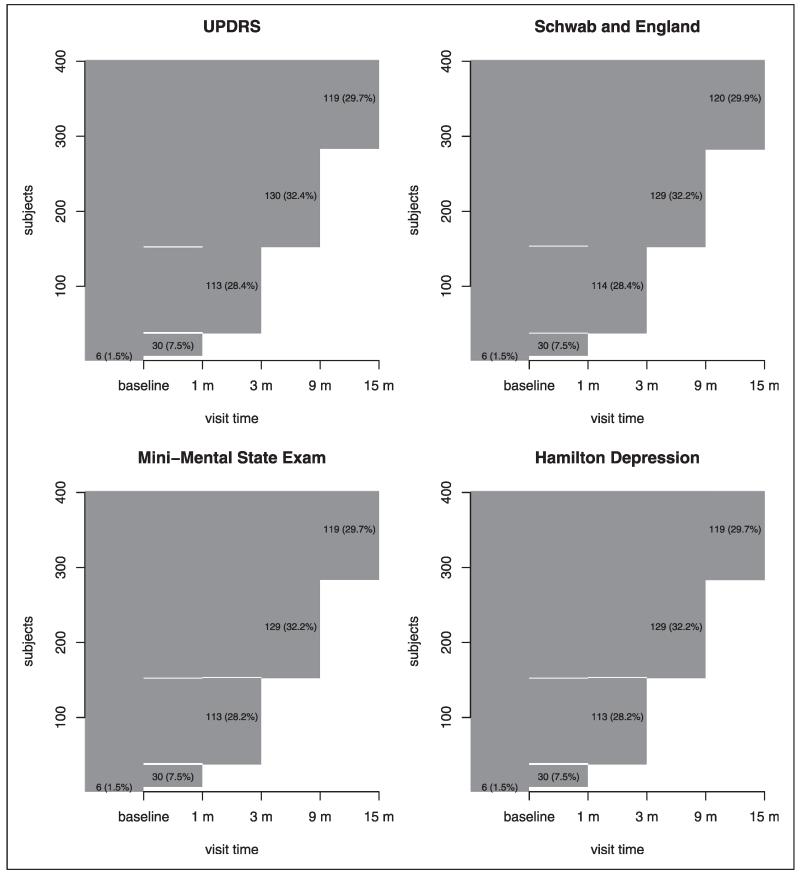
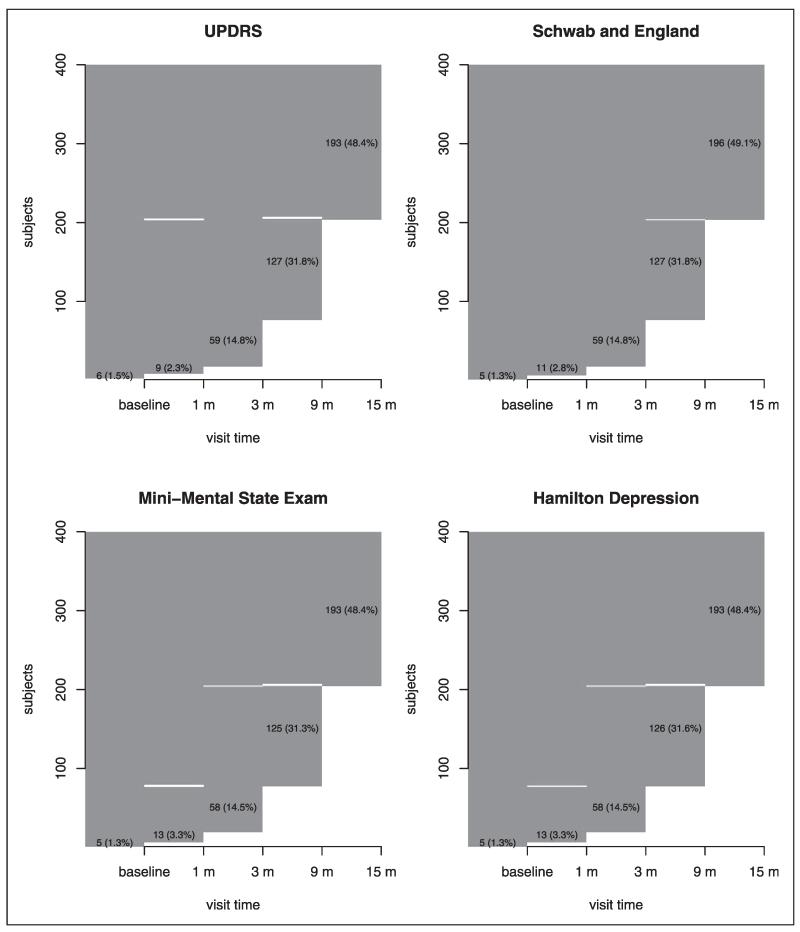
Before the end of the study, some individuals (222 and 154 individuals in the placebo and treatment groups, respectively) reached a level of functional disability sufficient to warrant the initiation of dopaminergic therapy, which is a symptomatic therapy to provide temporary relief of PD symptoms for a short period. In this case, only the observed outcomes before the initiation of dopaminergic therapy can be used in the assessment of treatment efficacy because dopaminergic therapy can significantly change the values of the outcomes collected. Therefore, these individuals would have missing data after the initiation of dopaminergic therapy and this missing mechanism is most likely MAR because the missingness depends only on the observed variables before therapy start. In addition, missing data occurred due to withdrawals, lost to follow-up, missed visits, etc. To visualize and explore the missing patterns in the dataset,55 we plot the missingness map of four outcomes in the placebo and treatment groups in Figures 1 and 2, respectively. The observed values are plotted with dark gray and the missing values are in white. The sporadic white bars indicate non-monotone missing pattern. The numbers in the figures are the number of individuals and the corresponding percentage (in parenthesis). For example, in the placebo group, the numbers and percentages of individuals who have measurements of UPDRS up to 15 months, 9 months, 3 months, 1 month, and baseline only are 119 (29.7%), 130 (32.4%), 113 (28.4%), 30 (7.5%), and 6 (1.5%), respectively. Figures 1 and 2 suggest that most of the missing data are monotone. Although the overall missing percentages are roughly 24% and 16% in the placebo and treatment groups, respectively, the missing percentages at the last visit are around 70% and 50% in the placebo and treatment groups, respectively. In order to compute the adjusted GST and GTE based on the change from baseline to the last visit and follow the ITT principle, we need to impute the missing values.
Figure 1.
The missing patterns for four outcomes in the placebo group. Dark gray area indicates observed data while white area indicates that missing data. The sporadic white bars indicate non-monotone missing pattern. The numbers in the plots are the number of individuals and the percentage (in parenthesis) in the placebo group.
Figure 2.
The missing patterns for four outcomes in the treatment group. Dark gray area indicates observed data while white area indicates that missing data. The sporadic white bars indicate non-monotone missing pattern. The numbers in the plots are the number of individuals and the percentage (in parenthesis) in the treatment group.
In the LOCF analysis, we use the last observed value of the missing outcome to impute the observation at the last visit (15 months) and obtain the sample size of 401 and 398 in the placebo and treatment groups, respectively, after deleting one individual in the treatment group who did not have any data for UPDRS. In separate models analysis, we use linear mixed models and proportional odds models as imputation models for continuous and ordinal outcomes, respectively. In MI analysis, we use item-response models (4) and (5) and include the binary treatment assignment variable in the mean model (6), i.e. μij = [β0 + β1 Ii(trt)]tj. We have run two parallel chains with overdispersed initial values and 10,000 iterations per chain. After discarding a burn-in of 5000 iterations, we obtain 100 multiply-imputed datasets by taking every 100 iterations from the remaining 5000 iterations of each chain. To assess the efficacy of deprenyl, we compute the change from baseline to the last visit for all four outcomes, from which we compute the rank sum difference, the associated variance, and the adjusted GST statistics Ta and GTE using the LOCF, Separate, and MI methods.
Table 2 displays the estimates of the rank sum difference, the associated standard errors, the adjusted GST statistics Ta, p-values, and GTE based on the three methods. The treatment deprenyl shows significant efficacy in all three methods. After consolidating the 100 sets of estimates using Rubin’s rules, the MI method has the most negative rank sum difference, the most negative adjusted GST statistics Ta (with degree-of-freedom being 205), and the smallest p-value. The results of extremely small p-values are consistent with the published DATATOP study results.54 The estimated GTE (i.e. 0.161) from the MI method is the largest among all three methods, indicating that the MI method estimates the largest global treatment effect from deprenyl. The interpretation of GTE is that an individual in the control groups would have a [(100% + 16.1% − P)/2 = (58.1% − P/2)] probability of having a better overall outcome if he/she had been assigned to the treatment group, where P is the probability that the placebo and treatment groups have tied observations. If no ties are observed, then the probability would be equal to 58.1%. Moreover, after fitting the IRT model, we obtain the following estimates of latent variable regression parameters, i.e. (0.179, sd: 0.013, CI: [0.152, 0.207]), and (−0.110, sd: 0.016, CI: [−0.140, −0.079]). The CI of not covering zero indicates the significant benefits of deprenyl in slowing PD progression. This is consistent with the significant adjusted GST statistics Ta in Table 2.
Table 2.
Results by various imputation methods for change of last visit.
| Method | Rank sum difference (SE) |
Ta | p-value | GTE |
|---|---|---|---|---|
| LOCF | −202.6 (37.8) | −5.4 | 8.32 e–8 | 0.127 |
| Separate | −111.5 (40.1) | −2.8 | 5.71 e–3 | 0.070 |
| MI | −257.1 (42.9) | −6.0 | 9.20 e–9 | 0.161 |
LOCF: last observation carried forward; MI: multiple imputation.
6 Discussion
In clinical trials for many complex diseases, a single outcome is often insufficient to determine the efficacy of treatments. In PD clinical trials, researchers have longitudinally measured multiple mixed type outcomes including quality of life, motor fluctuations, depression, and cognition, etc. During the course of follow-up period, missing values have become a common phenomena in clinical trial practice. In this article, we present a Bayesian method based on the item response theory (IRT) to impute the missing data in the multivariate longitudinal data structure, and the inference based on the adjusted GST and GTE is combined using Rubin’s MI rules. In the IRT models, the outcomes are representations of a latent variable which is a function of individual-specific covariates and visit time. All sources of correlation have been accounted for in the IRT modeling framework. We have performed sensitivity analysis under various scenarios. The simulation results suggest that the proposed MI method generally performs better than the standard methods such as last observation carried forward and separate random effects model for each outcome, with larger advantage as the missing percentage and the outcome rates of change increase. Although we did not compare it to other ad hoc methods such as imputation with the mean or imputation with the worst observation, it is likely that such single imputation methods are inferior because they fails to incorporate the missing-data uncertainty and do not account for all sources of correlation.30 The proposed method offers a novel and flexible way to impute the missing multivariate longitudinal data and allows the imputation model to differ from the final analysis model. In the analysis of a PD clinical trial (DATATOP), the treatment of deprenyl has efficacious global effects across all four outcomes indicated by the significant adjusted global statistical test and the significant treatment effect coefficient in the IRT model.
Our modeling framework based on the item response theory has some limitations that we view as future research directions. Note that the discrimination parameter bk controls both within-individual correlation in different outcomes and outcome-specific treatment effect β expressed in equation (6). If there is low within-individual correlation but a large treatment effect, this model may underestimate the treatment effect and overestimate the correlation.56
Acknowledgments
The authors are grateful to our colleague Dr Wenyaw Chan for helpful discussion and to Rong Ye for preparing the analysis dataset. Computations were performed on the high-performance computational capabilities of the Linux cluster system at University of Texas School of Public Health (UTSPH). The authors express their appreciation to UTSPH information technology staff for their technical support of the cluster.
Funding
This work is supported by two NIH/NINDS grants, U01NS043127 and U01NS43128.
References
- 1.Samii A, Nutt J, Ranson B. Parkinson’s disease. Lancet. 2004;363:1783–1793. doi: 10.1016/S0140-6736(04)16305-8. [DOI] [PubMed] [Google Scholar]
- 2.Pocock S. Clinical trials with multiple outcomes: a statistical perspective on their design, analysis, and interpretation. Control Clin Trials. 1997;18(6):530–545. doi: 10.1016/s0197-2456(97)00008-1. [DOI] [PubMed] [Google Scholar]
- 3.Tilley B, Huang P, O’Brien P. Global assessment variables. In: D’Agostino R, Sullivan L, Massaro J, editors. Wiley encyclopedia of clinical trials. John Wiley & Sons; New york, NY: 2008. pp. 1–11. [Google Scholar]
- 4.O’Brien P. Procedures for comparing samples with multiple endpoints. Biometrics. 1984;40(4):1079–1087. [PubMed] [Google Scholar]
- 5.Pocock S, Geller N, Tsiatis A. The analysis of multiple endpoints in clinical trials. Biometrics. 1987;43(3):487–498. [PubMed] [Google Scholar]
- 6.Tang D, Gnecco C, Geller N. An approximate likelihood ratio test for a normal mean vector with nonnegative components with application to clinical trials. Biometrika. 1989;76(3):577–583. [Google Scholar]
- 7.Lehmacher W, Wassmer G, Reitmeir P. Procedures for two-sample comparisons with multiple endpoints controlling the experimentwise error rate. Biometrics. 1991;47:511–521. [PubMed] [Google Scholar]
- 8.Tang D, Geller N, Pocock S. On the design and analysis of randomized clinical trials with multiple endpoints. Biometrics. 1993;49:23–30. [PubMed] [Google Scholar]
- 9.Tang D, Lin S. An approximate likelihood ratio test for comparing several treatments to a control. J Am Stat Assoc. 1997;92(439):1155–1162. [Google Scholar]
- 10.Tang D, Geller N. Closed testing procedures for group sequential clinical trials with multiple endpoints. Biometrics. 1999;55(4):1188–1192. doi: 10.1111/j.0006-341x.1999.01188.x. [DOI] [PubMed] [Google Scholar]
- 11.Karrison T. A rank-sum-type test for paired data with multiple endpoints. J Appl Stat. 2004;31(2):229–238. [Google Scholar]
- 12.Huang P, Tilley B, Woolson R, et al. Adjusting O’Brien’s test to control type I error for the generalized nonparametric Behrens-Fisher problem. Biometrics. 2005;61(2):532–539. doi: 10.1111/j.1541-0420.2005.00322.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang P, Woolson R, O’Brien P. A rank-based sample size method for multiple outcomes in clinical trials. Stat med. 2008;27(16):3084–3104. doi: 10.1002/sim.3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huang P, Woolson R, Granholm A. The use of a global statistical approach for the design and data analysis of clinical trials with multiple primary outcomes. Exp Stroke. 2009;1:100–109. [Google Scholar]
- 15.Liu A, Li Q, Liu C, et al. A rank-based test for comparison of multidimensional outcomes. J Am Stat Assoc. 2010;105(490):578–587. doi: 10.1198/jasa.2010.ap09114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hothorn L. Multiple comparisons in long-term toxicity studies. Environ Health Perspect. 1994;102(Suppl 1):33. doi: 10.1289/ehp.94102s133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tilley B, Marler J, Geller N, et al. Use of a global test for multiple outcomes in stroke trials with application to the National Institute of Nurological Disorders and stroke t-PA stroke Trial. Stroke. 1996;27(11):2136. doi: 10.1161/01.str.27.11.2136. [DOI] [PubMed] [Google Scholar]
- 18.Kwiatkowski T, Libman R, Frankel M, et al. Effects of tissue plasminogen activator for acute ischemic stroke at one year. N Engl J Med. 1999;340(23):1781. doi: 10.1056/NEJM199906103402302. [DOI] [PubMed] [Google Scholar]
- 19.Kaufman K, Olsen E, Whiting D, et al. Finasteride in the treatment of men with androgenetic alopecia. J Am Acad Dermatol. 1998;39(4):578–589. doi: 10.1016/s0190-9622(98)70007-6. [DOI] [PubMed] [Google Scholar]
- 20.Shames R, Heilbron D, Janson S, et al. Clinical differences among women with and without self-reported perimenstrual asthma. Ann Allergy Asthma Immunol. 1998;81(1):65–72. doi: 10.1016/S1081-1206(10)63111-0. [DOI] [PubMed] [Google Scholar]
- 21.van Kleef M, Barendse G, Kessels A, et al. Randomized trial of radiofrequency lumbar facet denervation for chronic low back pain. Spine. 1999;24(18):1937. doi: 10.1097/00007632-199909150-00013. [DOI] [PubMed] [Google Scholar]
- 22.Wetter T, Stiasny K, Winkelmann J, et al. A randomized controlled study of pergolide in patients with restless legs syndrome. Neurology. 1999;52(5):944. doi: 10.1212/wnl.52.5.944. [DOI] [PubMed] [Google Scholar]
- 23.Matser E, Kessels A, Lezak M, et al. Neuropsychological impairment in amateur soccer players. JAMA. 1999;282(10):971. doi: 10.1001/jama.282.10.971. [DOI] [PubMed] [Google Scholar]
- 24.Goodkin D, Rudick R, Medendorp S, et al. Low-dose (7.5 mg) oral methotrexate reduces the rate of progression in chronic progressive multiple sclerosis. Ann Neurol. 1995;37(1):30–40. doi: 10.1002/ana.410370108. [DOI] [PubMed] [Google Scholar]
- 25.Li D, Zhao G, Paty D. Randomized controlled trial of interferon-beta-1a in secondary progressive MS: MRI results. Neurology. 2001;56(11):1505. doi: 10.1212/wnl.56.11.1505. [DOI] [PubMed] [Google Scholar]
- 26.Poole C, Earl H, Hiller L, et al. Epirubicin and cyclophosphamide, methotrexate, and fluorouracil as adjuvant therapy for early breast cancer. N Engl J Med. 2006;355(18):1851. doi: 10.1056/NEJMoa052084. [DOI] [PubMed] [Google Scholar]
- 27.Rubin D, Little R. J Wiley & Sons; Hoboken, NJ: 2002. Statistical analysis with missing data. [Google Scholar]
- 28.NINDS NETPD A randomized, double-blind, futility clinical trial of creatine and minocycline in early Parkinson disease. Neurology. 2006;66(5):664. doi: 10.1212/01.wnl.0000201252.57661.e1. [DOI] [PubMed] [Google Scholar]
- 29.NINDS NETPD A randomized clinical trial of coenzyme Q10 and GPI-1485 in early Parkinson disease. Neurology. 2007;68(1):20. doi: 10.1212/01.wnl.0000250355.28474.8e. [DOI] [PubMed] [Google Scholar]
- 30.Schafer J. Analysis of incomplete multivariate data. Vol. 72. Chapman & Hall/CRC; Boca Raton, FL: 1997. [Google Scholar]
- 31.Ibrahim J, Chen M, Lipsitz S, et al. Missing-data methods for generalized linear models. J Am Stat Assoc. 2005;100(469):332–346. [Google Scholar]
- 32.Ibrahim J, Molenberghs G. Missing data methods in longitudinal studies: a review. Test. 2009;18(1):1–43. doi: 10.1007/s11749-009-0138-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rubin D. Multiple imputation for nonresponse in surveys. Vol. 17. John Wiley & Sons Inc; New York, NY: 1987. [Google Scholar]
- 34.O’Brien L, Fitzmaurice G. Analysis of longitudinal multiple-source binary data using generalized estimating equations. J Roy Statist Soc: Series C. 2004;53(1):177–193. [Google Scholar]
- 35.Little R, Yau L. Intent-to-treat analysis for longitudinal studies with drop-outs. Biometrics. 1996;52(4):1324–1333. [PubMed] [Google Scholar]
- 36.Van Swieten J, Koudstaal P, Visser M, et al. Interobserver agreement for the assessment of handicap in stroke patients. Stroke. 1988;19(5):604. doi: 10.1161/01.str.19.5.604. [DOI] [PubMed] [Google Scholar]
- 37.Schwab R, England A. Projection technique for evaluating surgery in Parkinsons disease. In: Gillingham FJ, Donaldson MC, editors. Third Symposium on Parkinsons Disease. Livingstone; Edinburgh: 1969. pp. 152–157. [Google Scholar]
- 38.Siderowf A, Ravina B, Glick H. Preference-based quality-of-life in patients with Parkinson’s disease. Neurology. 2002;59(1):103. doi: 10.1212/wnl.59.1.103. [DOI] [PubMed] [Google Scholar]
- 39.Bushnell D, Martin M. Quality of life and Parkinson’s disease: translation and validation of the US Parkinson’s disease questionnaire (PDQ-39) Quality Life Res. 1999;8(4):345–350. doi: 10.1023/a:1008979705027. [DOI] [PubMed] [Google Scholar]
- 40.Smith A. Symbol digit modalities test manual. Western Psychological Services; Los Angeles, CA: 1973. [Google Scholar]
- 41.Lehmann E. Nonparametrics: statistical methods based on ranks. Holden Day; New York, NY: 1975. [Google Scholar]
- 42.Lord F. Applications of item response theory to practical testing problems. L. Erlbaum Associates; Hillsdale, NJ: 1980. [Google Scholar]
- 43.Samejima F. Graded response model. In: van der Linden WJ, Hambleton R, editors. Handbook of Modern Item Response Theory. New York, NY: 1997. pp. 85–100. [Google Scholar]
- 44.Lord F, Novick M, Birnbaum A. Statistical theories of mental test scores. Addison-Wesley; 1968. [Google Scholar]
- 45.Douglas J. Item response models for longitudinal quality of life cata in clinical trials. Stat Med. 1999;18:2917–2931. doi: 10.1002/(sici)1097-0258(19991115)18:21<2917::aid-sim204>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 46.Andrade D, Tavares H. Item response theory for longitudinal data: population parameter estimation. J Multivar Anal. 2005;95(1):1–22. [Google Scholar]
- 47.Fox J. Bayesian item response modeling: theory and applications. Springer Verlag; 2010. [Google Scholar]
- 48.Skrondal A, Rabe-Hesketh S. Generalized latent variable modeling: multilevel, longitudinal, and structural equation models. CRC Press; 2004. [Google Scholar]
- 49.Tavares H, Andrade D. Item response theory for longitudinal data: item and population ability parameters estimation. Test. 2006;15(1):97–123. [Google Scholar]
- 50.Lunn D, Thomas A, Best N, et al. WinBUGS-a Bayesian modelling framework: concepts, structure, and extensibility. Stat Comput. 2000;10(4):325–337. [Google Scholar]
- 51.Gelman A, Carlin J, Stern H, et al. Bayesian data analysis. CRC Press; 2004. [Google Scholar]
- 52.Plummer M. JAGS Version 2.1.0 user manual. Lyon, France: 2010. [Google Scholar]
- 53.Anderson T. An introduction to multivariate statistical analysis. 3rd edn John Wiley & Sons; New York, NY: 2003. [Google Scholar]
- 54.Shoulson I. DATATOP: a decade of neuroprotective inquiry. Parkinson Study Group. Deprenyl and tocopherol antioxidative therapy of parkinsonism. Ann neurol. 1998;44(3 Suppl 1):S160. [PubMed] [Google Scholar]
- 55.Honaker J, King G, Blackwell M. Amelia II: A program for missing data. J Stat Software. 2011;45(7):1–47. [Google Scholar]
- 56.Dunson D. Bayesian methods for latent trait modelling of longitudinal data. Stat Meth Med Res. 2007;16(5):399. doi: 10.1177/0962280206075309. [DOI] [PubMed] [Google Scholar]