Simultaneous Imaging of In-vivo Conductivity and Susceptibility

Abstract

Purpose

Approaches for quantitative mapping of electric conductivity and magnetic susceptibility using MRI have been developed independently. The purpose of this study is to present a method to simultaneously acquire information on conductivity and susceptibility and to produce images based on these properties.

Methods

A 3D multi-echo gradient-echo sequence was used. Phase evolution during the multi-echo was used to produce quantitative susceptibility maps, while the phase value at zero echo time (TE) was retrieved, which were used to generate quantitative conductivity maps. Electromagnetic (EM) simulations were performed to evaluate the phase distribution due to conductivity variations. Phantom and in vivo data were also acquired to assess the quality of images produced.

Results

Simulations demonstrated that phase differences across objects increase s with size and conductivity. For an accurate conductivity estimate, the maximum TE was approximately equal to the true T₂* value in order to achieve signal-to-noise ratio maximization. The most accurate susceptibility was obtained when separating phase contribution from conductivity. Phantom and in vivo results showed good quality images representing the EM properties.

Conclusion

A simultaneous quantitative EM property imaging approach is demonstrated here. The approach not only improves the efficiency of mapping EM properties, but can also improve the accuracy of susceptibility mapping by separating image phases introduced by conductivity and susceptibility.

Introduction

MRI is capable of producing in-vivo images containing various forms of information. These include, for example, relaxation properties (T₁, T₂), tissue structure, motional properties (velocity, diffusion), temperature and mechanical properties (stiffness etc). MRI can also provide information regarding the electric and magnetic properties of tissue. Importantly, these properties can be applied to the study of tissue properties and to characterize a number of neurological diseases.

The magnetic property of tissues is typically characterized by magnetic susceptibility (1,2). As one form of susceptibility contrast, susceptibility weighted imaging (SWI) has wide clinical application and is becoming a routine part of diagnostic MRI (3). More recently, it has been shown that the relative susceptibility value can be quantified using quantitative susceptibility mapping (QSM) approaches (4-8). These quantitative approaches require advanced processing methods to invert an ill-posed linear equation. Compared with the rapid progression of SWI and QSM, the advancement of electric property imaging has been relatively slow. Over two decades ago, Haacke et al investigated the feasibility of imaging electric properties using the interaction between transmit radio frequency (RF) and tissue (9). Significant progress was only made recently, in part due to the introduction of high-field MRI scanners. At 7 Tesla and higher, measuring tissue conductivity is important for monitoring the specific absorption rate (SAR) (10-12). In addition, mapping conductivity in vivo also has several potential clinical applications including tumor and stroke imaging (13-15).

While electric and magnetic properties are naturally linked through Maxwell's equations, conductivity and susceptibility are currently measured independently. This practice has several drawbacks. Firstly, it lengthens the imaging time; secondly, it generates images that are not naturally registered and may have different distortions. Most susceptibility acquisition methods rely on a long echo time (TE) or multi echo gradient-echo (GRE) sequence. The phase evolution during the echoes can be related to local susceptibility variations and used to determine quantitative susceptibility values. For conductivity estimates, knowledge of both the magnitude and phase information of the local B₁ field was thought to be necessary. However, recent studies showed that reasonable quantification could be achieved with only the phase distribution of B₁ (16,17). This phase information can be retrieved from a spin-echo sequence or by interpolating the phase at TE = 0 using a multi-echo gradient-echo acquisition.

Here, we demonstrate that conductivity and susceptibility can be simultaneously measured using a multi-echo GRE sequence. Phantom studies were performed to show the feasibility of producing QSM and quantitative conductivity maps (QCM). EM simulations were performed to test the validity and accuracy of the quantification using the proposed method. In-vivo human brain data are also presented as a representative example of simultaneous EM property imaging.

Materials and methods

Theory

The MRI signal including Fourier encoding and T₂^* effects can be modeled as

$$\mathrm{s}(\mathrm{t})={\mathrm{H}}^{-}(\mathrm{r})\iint {\mathrm{M}}^{+}(\mathrm{r},\mathrm{t}){\mathrm{e}}^{-\mathrm{i}2\mathrm{\pi }{\mathrm{k}}_{\mathrm{r}}\cdot \mathrm{r}}{\mathrm{e}}^{-\mathrm{t}/{\mathrm{T}}_2^{\ast }}\mathrm{d}\mathrm{r}$$ [1]

Where M⁺(r,t) ∼ i M_o H⁺ for low flip angle approximation, with M_o representing the ^R2.2equilibrium. The time harmonic H field is divided into a positive and negative rotating term H⁺ and H^-, respectively. The component H^- can be explained from the theory of reciprocity and is related to the receiver coil (18). The spatially varying phase of M⁺(r,t) has two major components, one due to the precession of the magnetization (denoted ∠M_xy⁺(r,t)) and another which is an offset component (∠H⁺(r)) that depends on the initial distribution of phase during RF excitation (6). Noting that the phase evolution due to imaging gradients is removed when forming the image via the inverse Fourier Transform, the phase in s(t) is

$$\angle \mathrm{s}(\mathrm{t})\sim \angle {\mathrm{H}}^{+}(\mathbf{r})+\angle {\mathrm{H}}^{-}(\mathbf{r})+\angle {\mathrm{M}}_{xy}^{+}(\mathbf{r},\mathrm{t})$$ [2]

Phase can be broken down into 1) the ∠H⁺ component that is established at TE=0, 2) the∠H^- component related to the receiver coil, and 3) the ∠M_xy⁺ component related to the susceptibility distributions which includes off-resonance effects. Note that phase due to H⁺ and H^- do not obey the Laplace equation and cannot be removed by harmonic filtering approaches (19).

To summarize, ∠s at t=0 provides information regarding H⁺ and H^-, which is determined by factors including electrical properties, transmit and receive coils, and relative location of the subject to the coils. Phase evolution ∠s at t>0 is determined by the magnetic susceptibility properties, with the phase at t=0 added as an offset. When performing susceptibility mapping or weighting based on measured ∠s, H^- and H⁺ have an additional phase contribution that can deteriorate the susceptibility imaging. Here, simulations are performed to evaluate the amount of phase offset.

To collect the phase evolution information and to extrapolate the t=0 phase value, a multi-echo GRE sequence is used. Accurate extrapolation of the TE=0 phase value is important for conductivity mapping, therefore, we investigated the optimum use of echoes.

Phase due to admittivity

Simulations were performed to investigate the amount of phase that is actually present at TE=0 due to conductivity distributions. Infinite length cylindrical objects of various radii (2, 5, and 10 mm) and conductivity values (0.1 - 2.0 σ/m) were assumed. The phase differences within the objects were noted. The phase distributions were calculated via a fast FDTD algorithm which used Bessel boundary conditions (20).

Optimal number of echoes

To determine the TE=0 phase from the multi-echo GRE data set, a minimum of two echoes should be collected. Generally, the collection of more echoes gives rise to a more accurate phase estimation at TE = 0. However, T₂* decay decreases the SNR of later echoes, which can impair the estimation. Simulations were performed to investigate the optimal number of echoes, and thus the total readout duration needed for accurate TE=0 phase estimation. An exponentially decaying signal model with noise added was used in the complex data set as the multi-echo progressed. The phase was retrieved from these simulated data. Phase unwrapping was performed if necessary and a linear extrapolation based on minimum least squares was performed to determine the TE=0 phase. ^R2.fEchoesin train were assumed to be separated by 5.5 ms. The simulation was repeated to determine the echo time with the minimum standard deviation of the extrapolated phase at TE=0.

Image Reconstruction

Quantitative susceptibility mapping (QSM) was conducted using a regularized l1 norm minimization method similar to (21). Single echo (at approximately 30-40 ms TE) data sets were used for reconstruction, however, since multiple echoes are acquired, a weighted average of the data sets can be used to improve the QSM reconstruction (22,23). A B₀ harmonic filter was used prior to QSM processing (24). While algorithms for susceptibility measurements are commonly use, methods for quantitative conductivity mapping (QCM) are still being active ongoing researched (16,17,25). Here, we rely on an on approach using only the phase of the H⁺ field measurement retrieved from the Helmholtz Eq. which can be derived by assuming local homogeneity. More details can be found regarding this reconstruction equation in Voigt et al. (16). In short, the conductivity maps were generated using the following equation,

$$\mathrm{\sigma }=\frac{{\nabla }^2{\mathrm{e}}^{\mathrm{i}\angle \mathrm{f}\left({\mathrm{H}}^{+}\right)}}{\mathrm{\mu }\mathrm{\omega }{\mathrm{e}}^{\mathrm{i}\angle \mathrm{f}\left({\mathrm{H}}^{+}\right)}}$$ [3]

Here f represents a filter to enhance the SNR of the reconstruction. In this study, we used a Gaussian filter with kernel size of 5 and standard deviation of 1.0 (25). Note that the above phase-based conductivity reconstruction leading to Eq. [3] is valid under several assumptions including: 1) the transceive phase is twice the phase of H⁺, which in turn requires particular symmetry of the sample such as a cylindrical shape and coil arrangement such as a quadrature coil and 2) the spatial variations of the magnitude of H⁺ is small compared with the spatial variations of the phase of H⁺. A detailed description of the requirements for phase-based conductivity can be found in references (16,17,26). In our studies, we used a single channel homogeneous quadrature head coil for both transmit and receive, where the phase of H⁺ can be approximated by taking half the phase value acquired at TE=0 (10).

Imaging

All phantom and in-vivo data were acquired using a 3T scanner (Siemens Tim Trio, Erlangen, Germany) under Institutional Review Board (IRB) approval. A water phantom containing small vials with concentrations of Gadolinium (Gd; Magnevist, Bayer Schering Pharma AG, Berlin, Germany) (0%, 0.5%, and 1%) and NaCl (0%, 0.5%, and 1%) was constructed (length: 55 mm, diameter: 15 mm). Gd concentration was varied to adjust magnetic susceptibility, and NaCl concentration was varied to adjust conductivity. Since QCM provides absolute quantification, a resistance meter was also used to find the true conductivity value, and gave values of 1.2 S/m and 2.4 S/m for the 0.5% and 1% NaCl phantoms, respectively. The expected values of susceptibility were 0.81 ppm and 1.63 ppm for Gd concentrations of 0.5% and 1%, respectively. The imaging parameters were as follows: TR=250ms, first TE = 5.67ms, echo spacing = 5.51ms, flip angle = 30°, number of echoes = 16, voxel size = 1.5 × 1.5 × 2 mm³, number of slices = 22. The brain of a volunteer was scanned using a similar multi-echo GRE sequence. The imaging parameters were as follows: TR = 100 ms, first TE = 3.55ms, echo spacing = 3.55ms, (last TE = 35 ms), flip angle = 25°, number of echoes = 7, FOV = 192 × 192 mm², number of slices = 88, voxel size = 1.5 × 1.5 × 1.5 mm³, scan time = 18 min 50 sec.

Results

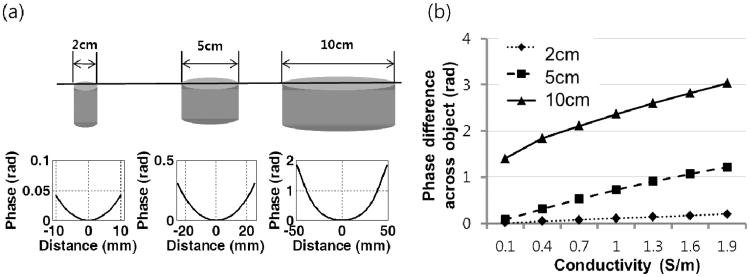
Figure 1 shows the phase distribution at TE=0 across the object with various conductivity values and sizes. In Fig. 1a, the phase profile is shown across the objects with diameters of 2, 5, and 10 cm. The conductivity of these cylindrical shaped objects was assumed to be 0.7 S/m. Objects with larger diameters demonstrated wider phase variations. Figure 1b shows the amount of phase variation across the objects with diameters of 2, 5, and 10 cm for various conductivity values. The large phase variation at TE = 0 reduces the accuracy of susceptibility mapping if it is not removed. On the other hand, a larger phase variation at TE = 0 improves the robustness of conductivity mapping. The range of phase values across an object is affected by its size relative to the wavelength. In turn, wavelength is dependent on the operating frequency and admittivity distribution.

Fig. 1.

Phase distribution at TE = 0 as a function of conductivity and object size. (a) Phase plot (at TE=0) across the object for different sizes (2, 5, and 10 cm diameter). The conductivity was set to 0.7 S/m. All objects in this simulation were assumed to be cylindrical in shape. (b) Phase difference across the objects of various sizes as a function of conductivity. The plot shows that at TE=0, an inhomogeneous phase can exist over the object, regardless of its susceptibility.

Simulations regarding the length of readout duration required for an accurate estimation of phase at TE=0 using the multi-echo GRE sequence are presented in Fig 2. In Fig 2a, the standard deviation of the phase estimate is plotted as a function of readout time used for T₂* values of 30, 50, and 70 ms. A specific readout length is shown to provide the most robust phase estimate. Figure 2b shows the optimal TE required as a function of T₂*. Note that the simulations assumed a spacing of 5.5 ms between multiple echos. From these plots, we can conclude that in order to maximize the accuracy of the phase estimate, the maximum TE used should be roughly equal to the T₂* value. This is critical since conductivity quantification using phase value is very sensitive to noise. Note that these results are in agreement with the results of other studies in which the signal of the phase increased with time, but that the signal amplitude decreases as an exponential function with the time constant T₂* (23,27). Theoretically, the position of the optimum TE does not depend on the noise level, however, as noise is increased, only two data sets might be sufficient to find the TE=0 phase.

Fig. 2.

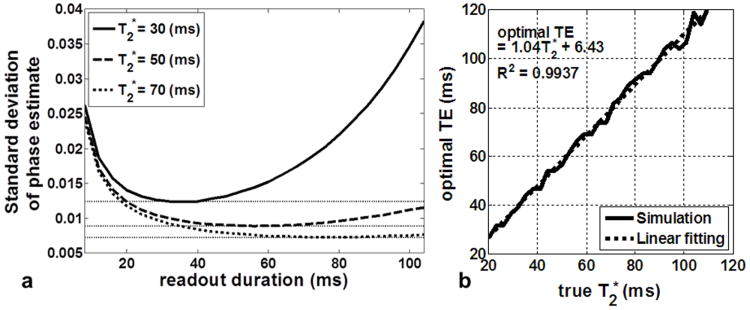
Number of echo sampling for optimal TE=0 estimation. (a) Standard deviation of the estimated initial phase (at TE=0) as a function of readout duration. (b) The optimal TE value collected for minimizing the standard deviation of phase estimate noise as a function of T₂* variations. The plots show that the multiecho GRE sequence should acquire data up to approximately the T₂* value of the object.

The results of from the phantom study are shown in Figure 3. The images demonstrate (a) proton density weighted, (b) SWI, (c) QSM, and (d) QCM results for various combinations of NaCl and Gd concentrations. The resulting contrasts in the QSM and QCM images agree well with the concentration of the individual agents. The quantitative QCM values obtained were (starting from top and moving clockwise): 2.55±0.42, 1.38±0.17, 1.33±0.11, 0.20±0.01, 2.27±0.25, and 2.49±0.26 S/m, which are in good agreement with the predicted values. The central vial, which contained no solvents, had a conductivity value of 0.38±0.07 S/m. Similarly, the quantitative QSM values obtained were: 0.17±0.02, 1.73±0.42, 0.87±0.25, 1.87±0.30, 1.04±0.32, and 1.41±0.25 ppm. The central vial was used as the reference for QSM with value of 0±0.02 ppm.

Fig. 3.

Phantom study with varying amounts of conductivity and susceptibility. (a) phantom proton density (PD) image, (b) susceptibility weighted image (SWI), (c) QSM, (d) Quantitative conductivity map (QCM) (note: NaCl conductivity of 0.5% gives 1.2 S/m). The images show contrast which is in good agreement depending on the amount of materials added.

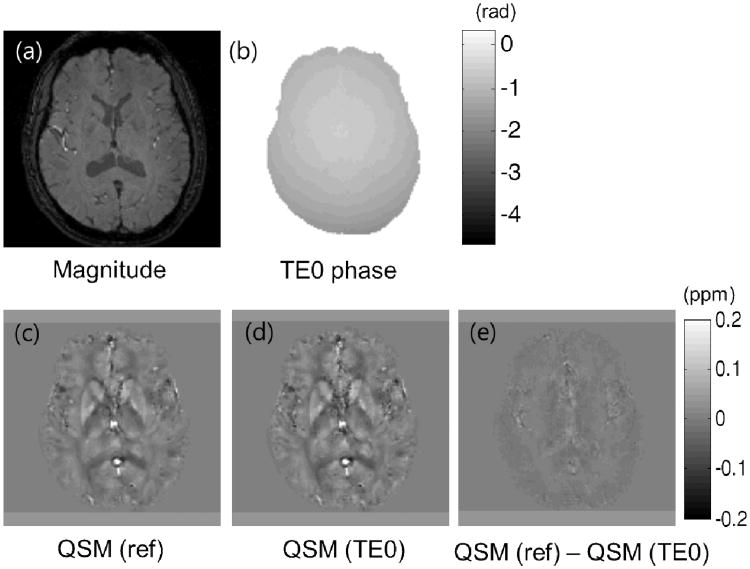
Figure 4 shows an illustration from the in vivo data of the effects of removing the TE=0 phase components prior to QSM processing. In Fig. 4b, the retrieved phase at TE=0 which is used for the QCM processing is shown. Figs. 4c and 4d show the QSM results prior to and after TE=0 phase removal respectively. The removal appeared to enhance the QSM contrast (Fig. 4d). The difference image between Figs. 4c and 4d is provided in Fig 4e which shows structural features. These results show that removal of the TE=0 phase components prior to QSM processing provides a more accurate account of the QSM values.

Fig. 4.

In vivo result.(a) Magnitude image, (b) The phase value at TE=0 retrieved using the multi echo GRE. (c) QSM reconstruction without removing the TE=0 phase component. (d) QSM reconstruction after removing the TE=0 phase component. (e) Difference image between the results of (c) and (d).

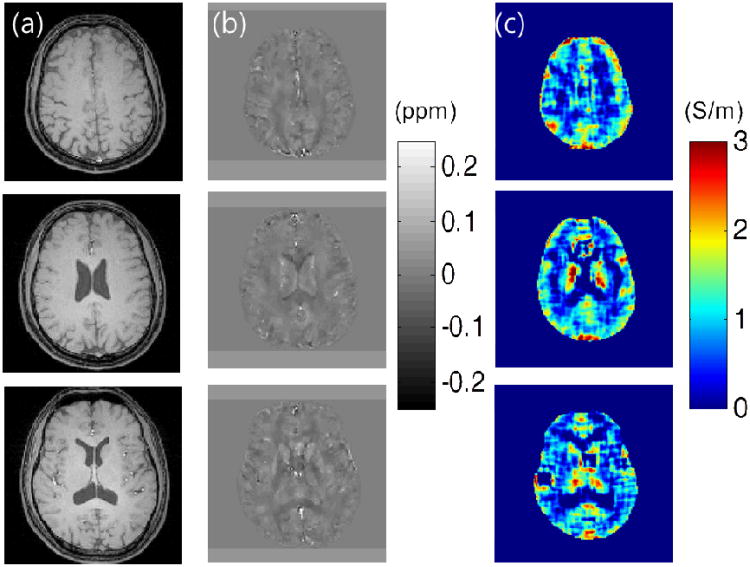
Reconstructed QSM and QCM in-vivo maps for several slices are provided in Fig. 5. As shown, QSM provides high resolution images compared to QCM. Both methods provide quantitative values that are in good agreement with values reported by previous studies (21,28). However, QCM still has artificial features due to the limited SNR and dispersion of the phase signal (29). More sophisticated reconstruction approaches can enhance the quality of the reconstruction, however, there seemed to be a limit to the maximum quality QCM map that could be acquired.

Fig. 5.

In-vivo results for three slices. (a) Magnitude image. (b) Reconstructed QSM image with corresponding range bar in ppm. (c) Reconstructed QCM image with corresponding range bar in S/m.

Discussion

A method for simultaneous EM (electro-magnetic) property imaging has been demonstrated in this study. Using this technique, characterization of both the electric conductivity and magnetic susceptibility of tissues can be performed simultaneously. The technique will be useful for applications where conductivity and susceptibility provide complementary information. Further investigations are necessary to identify these areas. The capability to simultaneously acquire both properties is advantageous since it eliminates the need for image registration. While contrast due to susceptibility has been linked with the distribution of iron, myelin, oxygenation, calcification, vasculature changes, and other factors, the origin and usage of conductivity in neuroimaging has yet to be determined. Clinically, conductivity has shown the potential to be useful in tumor or stroke imaging (13,15,30,31). A recent study suggested that changes in regional brain conductivity measured at low frequencies are associated with brain neuronal activity (32). Vasculature flow has also been reported to change conductivity (33,34). In general, contrast in conductivity imaging is related to molecular composition, cellular structure, the presence of intra- and extra-cellular fluid, concentration and mobility of ions in fluids, and temperature. Similar to the existence of susceptibility anisotropy (35), white matter conductivity anisotropy is known to be existent (36).

While the relationships between susceptibility and conductivity and their potential usages are still under investigation, it is worth noting the frequency characteristics of the measurement values. The susceptibility measured is the value at DC, i.e., at zero frequency. The conductivity, on the other hand, is the value at the Larmor frequency (in this case, approximately 128 MHz) (28). The frequency dependence of conductivity in biophysical models is determined by different mechanisms which are dominant at different frequencies (37). In the Larmor frequency range, the tissue exhibits both ‘beta’ and ‘gamma’ dispersion. In this range, the cell membranes have negligible impedance and the current passes through both the extracellular and intracellular media (38). Current MR-based non-invasive conductivity mapping is limited to AC conductivity. Methods to measure DC or low frequency conductivity using MR are available but the compatibility of these methods with susceptibility is questionable (39,40). In addition, measurement of AC susceptibility has yet to be demonstrated. We showed quantitative methods for susceptibility and conductivity mapping. Though non-quantitative, susceptibility weighted imaging (SWI) is a commonly used technique for contrast generation (1). Our results can readily be used to generate SWI images. This may have a more immediate clinical impact since the reconstruction procedures for SWI are straightforward and quick. Similarly, conductivity weighted imaging (CWI) could be feasible by combining, for example, image intensity with a weighted conductivity. Although conductivity mapping is advantageous in terms of tissue property quantification, the use of the full Laplacian term in Eq. [3] is inherently sensitive to noise. To reduce the noise sensitivity, rather than using the full Laplacian term, a simple phase-based approach to generate tissue contrast, i.e., a conductivity weighted imaging approach may be attractive for certain applications.

Our study is limited to the quantification of the conductivity property. Permittivity was not included in the study. For permittivity imaging, it is known that the magnitude of H⁺ plays an important role (16). The use of H⁺ phase alone cannot reliably determine the permittivity. Hence, multi-echo GRE sequence alone might not be apt for measurement of the magnitude of H⁺. For simultaneous measurement of the magnetic properties while acquiring the magnitude of H⁺, approaches similar to (41,42) can be utilized.

The existing phase at TE=0 is theoretically non-Laplacian and cannot be removed by spherical harmonic filters. In our simulations, the effects of not removing these components were not significant. However, other studies have shown that these phase components can affect in-vivo QSM (19). Normal QSM techniques do not take into account these non-Laplacian phases, as most filters account for the removal of Laplacian components alone (5,8,24). Further investigation is required to understand the effects of not removing the non-Laplacian components.

Conclusions

In conclusion, we have demonstrated a simultaneous quantitative EM property imaging approach. A multi-echo GRE sequence was used to measure the phase at TE=0 and multiple echo times. We showed that conductivity can be quantified using the phase at TE=0 while susceptibility can be quantified using the phase at later echo times. This approach not only improves the efficiency of conductivity and susceptibility mapping, it can also improve the accuracy of susceptibility mapping by separating image phases introduced by conductivity and susceptibility.