Magnetic Susceptibility as a B₀ Field Strength Independent MRI Biomarker of Liver Iron Overload

Abstract

Purpose

MR-based quantification of liver magnetic susceptibility may enable field strength-independent measurement of liver iron concentration (LIC). However, susceptibility quantification is challenging, due to non-local effects of susceptibility on the B₀ field. The purpose of this work is to demonstrate feasibility of susceptibility-based LIC quantification using a fat-referenced approach.

Methods

Phantoms consisting of vials with increasing iron concentrations immersed between oil/water layers, and twenty-seven subjects (9 controls/18 subjects with liver iron overload) were scanned. Ferriscan (1.5T) provided R2-based reference LIC. Multi-echo 3D-SPGR (1.5T/3T) enabled fat-water, B₀- and R2*-mapping. Phantom iron concentration (mg Fe/l) was estimated from B₀ differences (ΔB₀) between vials and neighboring oil. Liver susceptibility and LIC (mg Fe/g dry tissue) was estimated from ΔB₀ between the lateral right lobe of the liver and adjacent subcutaneous adipose tissue (SAT).

Results

Estimated phantom iron concentrations had good correlation with true iron concentrations (1.5T:slope=0.86, intercept=0.72, r²=0.98; 3T:slope=0.85, intercept=1.73, r²=0.98). In liver, ΔB₀ correlated strongly with R2* (1.5T:r²=0.86; 3T:r²=0.93) and B₀-LIC had good agreement with Ferriscan-LIC (slopes/intercepts nearly 1.0/0.0, 1.5T:r²=0.67, slope=0.93±0.13, p≈0.50, intercept=1.93±0.78, p≈0.02; 3T:r²=0.84, slope=1.01±0.09, p≈0.90, intercept=0.23±0.52, p≈0.68).

Discussion

Fat-referenced, susceptibility-based LIC estimation is feasible at both field strengths. This approach may enable improved susceptibility mapping in the abdomen.

Introduction

Excessive accumulation of iron in the body can result from abnormal intestinal absorption in hereditary hemochromatosis or repeated intravenous blood transfusions (ie: transfusional hemosiderosis) (1–3). Excess body iron is toxic, and requires treatment aimed at reducing body iron stores (4). Measurement of body iron stores is critical for detection of iron overload, staging its severity and monitoring of iron-reducing therapies that are often extremely expensive and carry their own toxicities (5–8).

The simplest method available to assess body iron is the use of serum markers of iron overload: measuring serum ferritin or serum transferrin receptor concentration from a blood sample. Unfortunately, it is well known that serum biochemical tests are often confounded by a number of factors such as inflammatory states and do not accurately reflect body iron levels (9).

Liver iron content (LIC) is widely considered the best reference for assessing total body iron stores, because the amount of iron in the liver is closely correlated to total body iron (8). Currently, chemical analysis of liver biopsy samples is the best available reference standard to measure LIC. However, biopsy is limited because it is invasive, expensive, and has poor sampling variability (8,10). In addition, biopsy is contraindicated in patients who have thrombocytopenia or coagulopathies, which commonly occur in patients with anemia receiving blood transfusions, due to the risk of uncontrolled bleeding.

Iron is the only non-trace element in the body that impacts tissue magnetic susceptibility, which is proportional to iron concentration (8,11). Liver iron susceptometry using superconducting quantum interference devices (SQUID) provides an alternative non-invasive method for measuring LIC (12–15). Although SQUID has been calibrated, validated and used for clinical studies, its complexity, high cost and limited availability have precluded its widespread use (8).

MRI is widely available and accessible, has been shown to be very sensitive to the presence of iron, and is capable of measuring magnetic susceptibility in some regions of the body, such as the brain (16,17). However, MR-based susceptibility mapping in the abdomen is a challenging problem, due to the lack of focal sources of susceptibility, the presence of fat and air, as well as motion related artifacts (18). Instead, current methods to measure iron using MRI are indirect and include signal intensity ratio (19), R2 relaxometry (20,21), and R2* relaxometry (22–27). R2- or R2*-based liver iron quantification is performed using empirically-derived calibration curves relating the relaxation parameter (R2 or R2*) to LIC (20–28). Although these methods have been shown to work well in practice, there is significant interest in the quantification of iron concentration based on measurement of magnetic susceptibility, a fundamental parameter of tissue.

The purpose of this work is to demonstrate the feasibility of susceptibility as a biomarker for liver iron concentration measurements. In previous work by other groups, it has been shown that MRI-based liver susceptometry is feasible using “boundary” B₀ field measurements (29–31), by measuring B₀ in the liver and adjacent muscle, resulting in “muscle-referenced” liver iron measurements that correlate well with R2*-derived LIC at 1.5T (18). This important work demonstrated the feasibility of liver susceptometry using a boundary approach, however it has several limitations: 1) the use of muscle as a reference for boundary measurements may not easily lead to automated methods for liver susceptometry (ie: without the need for manually tracing regions of interest), and 2) validation at only 1.5T. In this work, we expand on previous studies by performing fat-referenced liver susceptibility quantification with subcutaneous adipose tissue (SAT) as reference for B₀ measurements (32). Further, we test this approach at both 1.5T and 3T, and validate our technique with an FDA-approved R2-based measure of liver iron (Ferriscan) (20,33). The inherent ability of chemical shift-encoded imaging to perform fat-water separation in addition to B₀ mapping provides automated and co-registered mapping of adipose tissue locations (34,35). Thus, the locations and magnetic susceptibility of adipose tissue may provide a useful constraint to enable the development of automated quantitative susceptibility mapping techniques in the abdomen. The main purpose of this manuscript is to demonstrate that the fundamental information contained in B₀ field maps allows susceptibility measurement in the liver at both 1.5T and 3T. Based on these results, we aim to provide a foundation for future development of comprehensive quantitative susceptibility mapping techniques in the liver as a fundamental biomarker of liver iron overload.

Theory

The susceptibility difference between two adjacent tissues (Δχ, in ppm) is related to the difference in magnetic field (ΔB₀, in ppm) at both sides of the boundary, based on the boundary conditions for Maxwell’s equations. Including the sphere of Lorentz effects and hyperfine shift the susceptibility difference and magnetic field difference can be written (29,30,32):

$$\mathrm{\Delta }\chi =\frac{3\mathrm{\Delta }{B}_0}{1-3{\text{cos}}^2\theta +S_{hf}}$$ [1]

where ΔB₀=B_0,liver − B_0,SAT is the magnetic field difference (in ppm) between the liver and the adjacent SAT, θ is the angle between the vector perpendicular to the boundary and the main B₀ field, and S_hf is the hyperfine shift assumed to be −0.133 from previous works (18). In this work, boundaries parallel to the main magnetic field were selected such that θ ≈ 90° (and thus cos θ ≈ 0), by measuring B₀ fields in the lateral aspect of the right lobe of the liver (figure 1). With this constraint, Eq. 1 can be simplified as:

$$\mathrm{\Delta }\chi =3.46\mathrm{\Delta }{B}_0$$ [2]

Figure 1.

Geometry of proposed boundary B₀ measurements. The boundary between liver and subcutaneous adipose tissue (SAT) is nearly parallel to the main B₀ field (thus θ≈90° and cos(θ)≈0 in Eq. 1), simplifying the analysis and estimation of liver susceptibility. Note that the measurements are obtained from axial slices, but a coronal schematic view is shown here for clarity.

In this work, we focus on susceptibility differences between liver tissue and nearby subcutaneous adipose tissue (SAT). Note that even if SAT and liver are not in direct contact, SAT can be used as a reference for susceptibility measurements due to the fact that the distance to the liver is usually small. In addition, we assume that SAT is homogeneous with no significant iron accumulation since it is not part of the reticuloendothelial system (RES) that accumulates iron tissue in Kupffer cells and other phagocytic white blood cells.

In this setting, we can decompose the susceptibility difference between liver and SAT into two components, as follows:

$$\mathrm{\Delta }\chi =\mathrm{\Delta }{\chi }_{\mathit{\text{base}}}+{\chi }_{Fe}$$ [3]

where Δχ_base is the baseline susceptibility difference between both tissues (in the absence of liver iron), and Δχ_Fe is the additional paramagnetic contribution of iron to the susceptibility of liver (11,36). Equation 3 is an approximation, by assuming that iron is the only factor affecting the magnetic susceptibility of liver tissue (eg: it ignores the potential presence of liver fat).

Based on the paramagnetic properties of storage iron, the paramagnetic contribution of iron to susceptibility can be described as (36):

$$\mathrm{\Delta }{\chi }_{Fe}=\frac{N{\mu }_0{\mu }_{eff}^2{\mu }_B^2}{3kT}$$ [4]

where N is the number of iron particles per m³, μ₀=4π×10⁻⁷ V·s/(A·m) is the vacuum permeability, μ_eff is the effective number of Bohr magnetons per atom, approximately =3.78 as in (36), μ_B=9.274×10⁻²⁴ is the Bohr magneton, k=1.38×10⁻²³ J·K⁻¹ is the Boltzmann constant, and T≈310 K is body temperature. Based on Eq. 4, and using the approximated density 1.05 g/cm³ for liver tissue (11), the iron concentration (in mg Fe/g wet tissue) can be related to the paramagnetic contribution of iron to the susceptibility, as follows (11,36):

$${[Fe]}_{\mathit{\text{wet}}}=0.74\mathrm{\Delta }{\chi }_{Fe}=0.74(\mathrm{\Delta }\chi -\mathrm{\Delta }{\chi }_{\mathit{\text{base}}})$$ [5]

Finally, combining Eqs [2] and [4], we can express the iron concentration in terms of the measured magnetic field difference ΔB₀ as follows:

$${[Fe]}_{\mathit{\text{wet}}}=2.56\mathrm{\Delta }{B}_0-0.74\mathrm{\Delta }{\chi }_{\mathit{\text{base}}}$$ [6]

Note that liver iron concentration is typically expressed in mg Fe/g dry tissue, ie: [Fe]_dry instead of [Fe]_wet (in this manuscript LIC is equivalent to [Fe]_dry unless explicitly stated otherwise). The relationship between these two measures of iron concentration is not completely understood. Recent works have suggested a conversion factor of 5.5+/−1.0 (37). Using the conversion factor [Fe]_dry = 5.5[Fe]_wet, we arrive at the final expression for iron concentration in mg Fe/g dry tissue:

$${[Fe]}_{\mathit{\text{dry}}}=14.08\mathrm{\Delta }{B}_0-4.07\mathrm{\Delta }{\chi }_{\mathit{\text{base}}}$$ [7]

where [Fe]_dry (mg Fe/g dry tissue) is related directly to ΔB₀ (ppm) and Δχ_base (ppm). In this work, the baseline susceptibility difference Δχ_base is calibrated from a set of control subjects, by assigning them an average [Fe]_dry = 0.99 mg Fe/g dry tissue, which is the mean of LIC measured in control subjects in this study (33,38). Aside from this baseline, this approach requires no calibration, in contrast with R2- or R2*-based iron quantification techniques.

Methods

Phantoms

Iron concentration phantoms were constructed using super-paramagnetic iron oxides (SPIOs, Feridex, Bayer Inc, Wayne, NJ). Five cylindrical 20ml vials were constructed with iron concentrations of 0, 25, 50, 75 and 100 mg/l suspended in agar gel, following the technique described by Hines et al (39).

Subjects

All subjects were scanned in accordance to the local Institutional Review Board, and in compliance with HIPAA. 9 healthy volunteers were recruited as controls (5 men aged 24–44 years, and 4 women aged 33–62 years), and 18 patients with known or suspected iron overload (11 men aged 11–79 years, and 7 women aged 12–70 years) were scanned. Patients had a variety of transfusion-dependent anemias, leukemia, myelodysplastic syndrome. One of the patients was heterozygotic with the HFE gene for hemochromatosis.

Imaging Protocol

Data were acquired at 1.5T (Signa HDxt, GE Healthcare, Waukesha, WI) and 3T (MR750, v22.0, GE Healthcare, Waukesha, WI), using investigational versions of a 3D multiecho SPGR sequence with monopolar readouts and flyback gradients (40).

Phantoms were scanned one at a time at both 1.5T and 3T using a single-channel head coil, by placing them in a holder within a plastic container with a layer of water and a layer of peanut oil. This setup enabled a fat-referenced assessment of iron concentration in the vials, similarly to the in vivo case. Phantoms were placed in the magnet with the long axis of the cylindrical vials parallel to the main magnetic field. Acquisition parameters at 1.5T included: axial plane, readout direction R/L, 28 × 22cm field of view, 160×160 matrix, 4mm slice thickness, 32 slices, 10° flip angle, ±125 kHz receiver bandwidth, TR = 20.4 ms, and 12 echoes (2 interleaved echo trains) with TE_init=1.1 ms and ΔTE=0.9 ms. Acquisition parameters at 3T included: axial plane, readout direction R/L, 28 × 20cm field of view, 160×160 matrix, 4mm slice thickness, 32 slices, 10° flip angle, ±125 kHz receiver bandwidth, TR = 9.7 ms, and 8 echoes (two interleaved echo trains) with TE_init=1.1 ms and ΔTE=0.9 ms.

In vivo liver acquisitions included a spin-echo sequence for R2-based liver iron quantification (Ferriscan) at 1.5T. This was performed using a 2D multi-slice spin-echo sequence. Acquisition parameters included: 18 minutes free-breathing, axial plane, readout direction R/L, 44cm field of view, 256×256 matrix, 6mm slice thickness, 11 slices, ±62.5 kHz receiver bandwidth, TR = 1000 ms, five separate echo times (6, 9, 12, 15, 18 ms).

Chemical shift encoded acquisitions for R2* quantification and Bo field mapping were performed at both 1.5T and 3T, using similar acquisitions at both field strengths:

• Acquisition parameters at 1.5T included: 19s breath-hold, axial plane, readout direction R/L, 40×36cm field of view, 256×160 matrix, 8mm slice thickness, 32 slices, 5° flip angle, ±125 kHz readout bandwidth, self-calibrated parallel imaging with acceleration factor 2×2 (effective acceleration = 3.8 accounting for auto-calibration lines and k-space corner-cutting) (41), TR = 14.1 ms. An echo train was collected for each TR, consisting of 6 TEs with TE_init=1.2 ms, ΔTE=2.0 ms.

• Acquisition parameters at 3T included: 22s breath-hold, axial plane, readout direction R/L, 40×32cm field of view, 256×144 matrix, 8mm slice thickness, 32 slices, 3° flip angle, ±125 kHz readout bandwidth, self-calibrated parallel imaging with acceleration factor 2×2 (effective acceleration = 3.6 accounting for auto-calibration lines and k-space corner-cutting) (41), TR = 8.6 ms. Two interleaved echo trains (3 echoes/TR) were collected to achieve shorter echo spacing, resulting in 6 TEs with TE_init=1.2 ms, ΔTE=1.0 ms. Additionally, the 3T SPGR sequence included baseline phase correction, obtained by acquiring additional low-resolution phase encodes with opposite polarity, in order to remove residual phase errors between the interleaved echo trains (42).

Image Reconstruction

Multi-coil chemical shift encoded data were combined before fat-water separation using the eigenvector filter method described by Walsh et al. (43). The chemical shift-encoded complex signal for echo time t_n at a voxel containing water and fat in the presence of R2* decay and B₀ field offset can be described as (44,45):

$$S_n({\mathrm{\rho }}_W,{\mathrm{\rho }}_F,R_2^{*},f_B)=({\mathrm{\rho }}_W+{\mathrm{\rho }}_F\sum _{p=1}^P{\alpha }_p{e}^{i2\mathrm{\pi }{f}_{F,p}{t}_n})e^{-R_2^{*}{t}_n}{e}^{i2\mathrm{\pi }{f}_B{t}_n}$$ [8]

where ρ_W and ρ_F are the amplitudes of water and fat signals, respectively, R2* = 1/T2*, f_B is the frequency shift due to local magnetic B₀ field inhomogeneities, f_F,p are the known frequencies for the multiple spectral peaks of the fat signal relative to the water peak, and α_P are the relative amplitudes of the fat signal (44,46). The unknown parameters (ρ_W, ρ_F, R2*, f_B) are estimated in this work by nonlinear least-squares fitting at each voxel using a Levenberg-Marquardt algorithm from the GNU Scientific Library (GSL) in MEX under Matlab (The Mathworks, Natwick, MA). In order to provide a good initialization for the fitting procedure (particularly to avoid fat-water swaps in regions of large field inhomogeneity), an initial guess for the unknown parameters is obtained by regularized estimation from the complex data using a graph-cut algorithm (47). Using the estimated water and fat images, and proton-density fat-fraction (PDFF) maps are generated, including correction for noise bias (48).

Data Analysis (Phantoms)

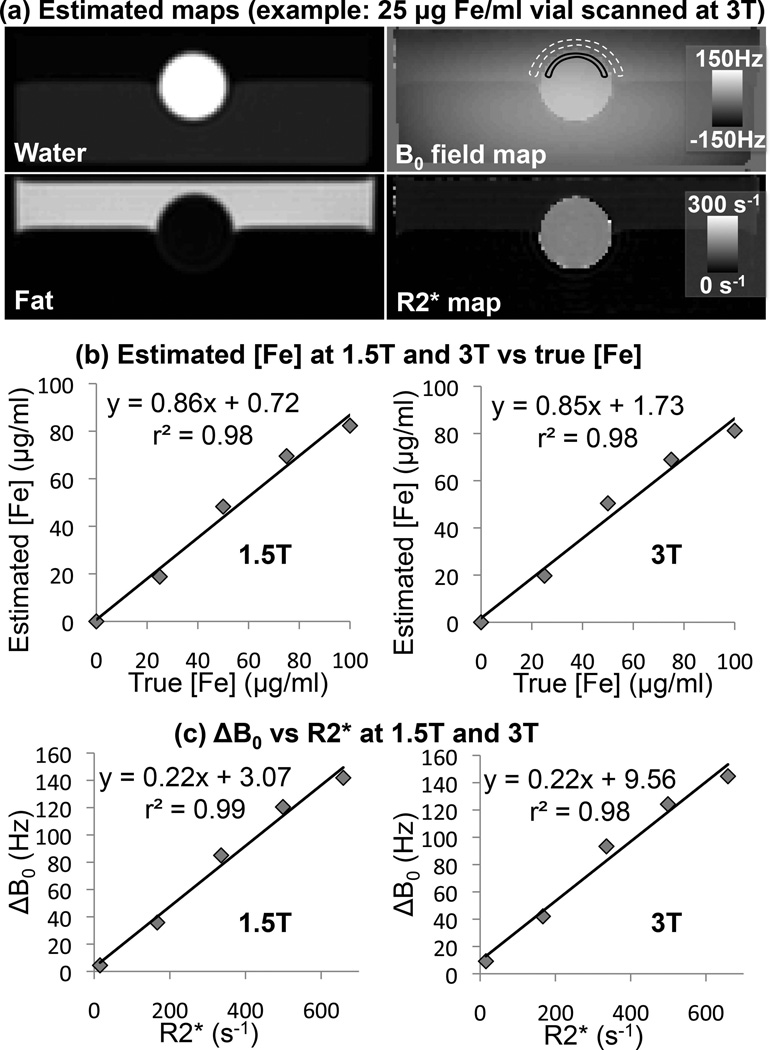
In each of the phantom datasets, ΔB₀ measurements were obtained from a single slice (chosen to have minimum slice-to-slice variation in B0 within the vial, to minimize susceptibility artifacts from the top and bottom of the cylindrical vial) by placing regions of interest (ROIs) inside the vial and in the adjacent oil (figure 2), and subtracting the B₀ measurement in the oil from that in the vial to obtain ΔB₀. Note that the analysis of B₀ field measurements in SPIO phantoms is conveniently performed in units of Hz rather than ppm due to the magnetization saturation of SPIOs. The measured ΔB₀ (in Hz) was converted to iron concentration based on the saturation magnetization (M_s) of ferumoxides, assuming M_s=93.6 Am²/kg (49) (including sphere of Lorentz effects as in Eq. 1, but assuming hyperfine shift S_hf=0). The conversion was expressed as [Fe] = aΔB₀+b, where a ≈ 0.6 µg Fe/ml/Hz and b (in µg Fe/ml) is a “baseline” constant (analogously to the in vivo case) to account for the ΔB₀ between agar and peanut oil, chosen to impose that the vial with no iron has [Fe]=0. Additionally, R2* measurements were obtained in each vial by placing an ROI over the vial in one slice. For each field strength, estimated [Fe] (in µg Fe/ml) was compared to true [Fe] using linear regression, and measured ΔB₀ (in Hz) was compared to measured R2* (in s⁻¹) using linear regression.

Figure 2.

Phantom results at both 1.5T and 3T (example images in (a)) show that boundary B₀ (ΔB₀)-based iron concentration estimates correlate well with true iron concentration (b), and ΔB₀ measurements correlate well with measured R2* (c). ΔB₀ field measurements were obtained by measuring B₀ at both sides of the boundary of cylindrical vials containing iron in increasing concentrations. R2* was measured by placing one ROI inside the vial for each iron concentration.

Data Analysis (In Vivo)

Ferriscan is an FDA-approved R2-based method for measurement of LIC, based on previously published calibration data described by St. Pierre et al (21). Ferriscan spin-echo acquisitions were uploaded to Resonance Health (Claremont, Australia), where they were processed to generate R2 maps (50). An R2 measurement was made by Resonance Health (Claremont, Australia) in an ROI over a slice free of severe motion artifacts, while avoiding large vessels and bile ducts. The R2 measurement was converted to an LIC measurement (“Ferriscan-LIC”, with units of mg Fe/g dry tissue), based on a previously validated calibration (21).

In all 27 subjects, an ROI was chosen in segments 5 or 6, in the inferior aspect of the right lobe of the liver, at a level where there were no obvious background B₀ field gradients visualized on the field map (mid-liver, away from the liver/lung boundary). An oval region of interest, measuring approximately 3 cm² in area was chosen near the lateral aspect of the liver, avoiding large vessels and bile ducts. The average value and standard deviation of the B₀ field at this location were recorded. In addition, a similar size ROI was placed in the SAT on the PDFF map and copied into the B₀ field map, where the average value and standard deviation of the B₀ field were recorded. These ROIs were placed avoiding regions of rapid background B₀ field variation. Using Eq. 7, the estimated iron concentration was calculated.

Additionally, muscle-referenced liver iron estimates were calculated for comparison. This was performed by using analogous measurements of B₀ in liver (inferior aspect of the right lobe of the liver) and adjacent muscle, similarly to the approach described in Ref. (18). From these measurements, LIC was estimated using Eq. 7 as in the fat-referenced case.

Further, a larger circular ROI (approximate area 11 cm²) was chosen in the same or adjacent slice on the R2* map, in either Couinaud segment 5 or 6, avoiding large blood vessels and bile ducts. This ROI was copied to the PDFF map, and the averages and standard deviations of R2* and PDFF were recorded.

Statistical Analysis

Linear regression analysis was performed in phantoms to compare the measured ΔB₀ to R2* for each vial, and the estimated iron concentration to the true iron concentration. Linear regression was performed with the in vivo measurements to compare ΔB₀ to R2*, and B₀-LIC to Ferriscan-LIC. Additionally, Bland-Altman analysis was performed to compare in vivo B₀-LIC (fat- and muscle-referenced at each field strength) to Ferriscan-LIC, as well as to compare B₀-LIC across field strengths.

Results

Figure 2 shows phantom results, comparing the measured ΔB₀ with the true iron concentration, as well as with the measured R2* inside each vial. Phantom iron estimation resulted in a constant offset b=−2.66 µg Fe/ml (1.5T), and b=−5.50 µg Fe/ml (3T). A strong correlation was observed between the true and estimated iron concentration (figure 2b, 1.5T: r²=0.98, 3T: r²=0.98), as well as between ΔB₀ and R2* (figure 2c, 1.5T: r²=0.99, 3T: r²=0.98). Regression between estimated and true iron concentration in the phantom resulted in a slope smaller (although not significantly different) than 1.0 (1.5T: 0.86 ± 0.06, p≈0.11, 3T: 0.85 ± 0.07, p≈0.12), and intercept close to 0 (1.5T: 0.72 ± 3.76, p≈0.86, 3T: 1.73 ± 4.34, p≈0.72).

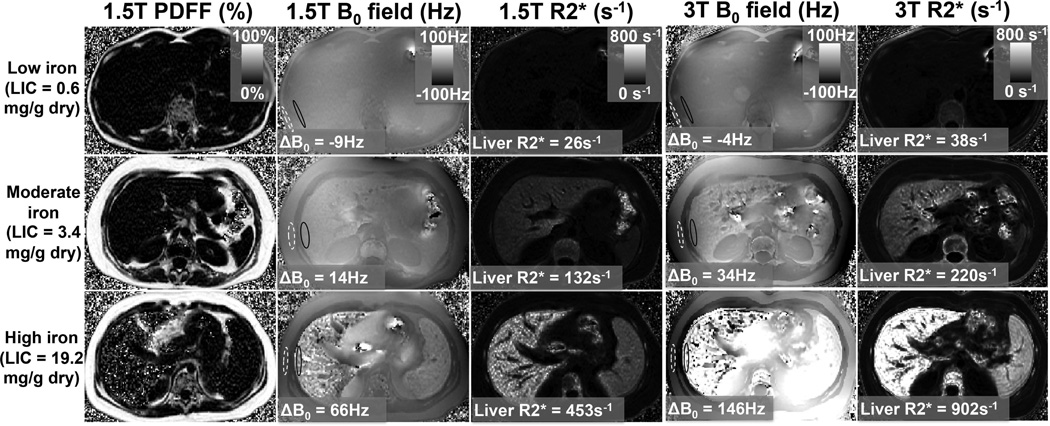
Figure 3 shows examples of the B₀ field maps and R2* maps in three subjects with no iron overload, moderate iron overload and more severe iron overload at both 1.5T and 3.0T. The R2* maps show a definite increase with increasing levels of iron overload. Further, the B₀ field maps show an apparent increase in the “step-off” difference in the B₀ field between the liver and the SAT as iron overload in the liver increases. Note that there are potential complications for B₀ field mapping in the presence of very high iron concentrations (figure 3, bottom row). In these cases, the R2* decay of the measured multi-echo signal is very rapid, thus complicating the measurement of B₀ fields. This problem may be addressed by acquiring shorter and more closely spaced echoes.

Figure 3.

Example results at 1.5T and 3T: Proton Density Fat-Fraction (PDFF), B₀ field maps, and R2* maps from subjects with no iron overload, moderate iron overload and high iron overload. Note the increase in ΔB₀ (as well as R2*) with increasing liver iron (Ferriscan-LIC).

In control subjects, the measured ΔB₀ between liver and SAT was 3.9 ± 7.3 Hz (1.5T), and 9.0 ± 10.1 Hz (3T). Figure 4 compares the calculated iron concentration B₀-LIC (mg Fe/g dry) against Ferriscan-LIC (determined by Resonance Health from 1.5T R2 mapping) at 1.5T (4a) and 3.0T (4b). In addition to good correlation (r²=0.67 at 1.5T, r²=0.84 at 3T), good agreement between the predicted iron concentration and measured iron concentration is also observed evidenced by a slope close to 1.0 (1.5T: slope =0.93 ± 0.13, 95% confidence interval=[0.67,1.18], p≈0.5; 3T: slope =1.01 ± 0.09, 95% confidence interval=[0.84,1.18], p≈0.9) and an intercept close to 0.0 (1.5T: intercept = 1.93 ± 0.78, 95% confidence interval=[0.40,3.47], p≈0.02 (significantly different from 0); 3T: intercept = 0.23 ± 0.52, 95% confidence interval=[−0.80,1.24], p≈0.6). Note that estimation of LIC using the boundary B₀ measurement approach leads to relatively large variability (particularly at 1.5T), including some negative LIC values. This is likely due in part to the presence of uncorrected background B0 field variations, and possibly also to imperfect alignment of the boundary with the B₀ field (ie: θ≠90° in Eq. 1). Comparison of B₀-LIC at 1.5 and 3T (figure 4c) results in a correlation r² = 0.84 with slope = 0.89 ± 0.08 (95% confidence interval=[0.70,1.04], p=0.16), and intercept = −0.77 ± 0.59 (95% confidence interval=[−1.92,0.38], p=0.20).

Figure 4.

Good correlation and agreement was observed between LIC estimated from susceptibility measurements (at a) 1.5T and b) 3.0T), and LIC estimated from R2 measurements (Ferriscan, measured at 1.5T). Good correlation and agreement was observed between LIC estimated from susceptibility measurements at 1.5T vs 3T (c).

Muscle-referenced ΔB₀-based LIC estimation produced results similar to fat-referenced estimation, including correlation (r²=0.61 at 1.5T, r²=0.83 at 3T), slope (1.5T: slope =0.74 ± 0.12, 95% confidence interval=[0.51,0.97], p≈0.04 (significantly different from 1); 3T: slope =0.89 ± 0.08, 95% confidence interval=[0.75,1.05], p≈0.20) and intercept (1.5T: intercept = 1.35 ± 0.71, 95% confidence interval=[−0.80,1.24], p≈0.07; 3T: intercept = −0.02 ± 0.49, 95% confidence interval=[−0.98,0.94], p≈0.96). Bland-Altman analysis results for fat- and muscle-referenced B₀-LIC at both field strengths are summarized in Table 1.

Table 1.

Bland-Altman analysis results comparing different LIC estimation techniques.

	1.5T B0-LIC vs Ferriscan-LIC	3T B0-LIC vs Ferriscan-LIC	1.5T B0-LIC vs 3T B0-LIC
Fat-referenced	1.66 ± 3.07 mg Fe/g dry	0.26 ± 2.02 mg Fe/g dry	−1.40 ± 2.13 mg Fe/g dry
	95% CI = [−4.35,7.67]	95% CI = [−3.70,4.22]	95% CI = [−5.58,2.78]
Muscle-referenced	0.34 ± 3.01 mg Fe/g dry	0.44 ± 1.96 mg Fe/g dry	−0.77 ± 2.38 mg Fe/g dry
	95% CI = [−5.57,6.25]	95% CI = [−4.29,3.41]	95% CI = [−5.43,3.89]

In addition, scatter plots comparing ΔB₀ and R2* values measured at 1.5T and 3.0T are shown in figure 5, demonstrating good correlation (r²=0.86 at 1.5T and r²=0.93 at 3.0T). Finally, it should be noted that the ratio of the slope of the R2* measured at 3.0T compared to 1.5T is 1.91 ± 0.04 (with very strong correlation r²=0.99), demonstrating a strong field strength dependence of R2* measurements for iron overload. This slope is close to the expected value of 2.00 (51).

Figure 5.

Good correlation was observed between magnetic field offset measurements ΔB₀ and R2* measurements at a) 1.5T and b) 3.0T.

Discussion

In this work, we have demonstrated the feasibility of a fat-referenced approach for measuring magnetic susceptibility in the liver as a biomarker of liver iron overload, using an R2-based measure of liver iron concentration (LIC) as reference standard. Although full dipole inversion of the B₀ field map was not performed, the results of this work demonstrate that the fundamental information of susceptibility measurements can be ascertained from B₀ field maps derived from multi-echo chemical shift based fat-water separation methods.

This work builds on previous studies (18,30,31) suggesting that susceptibility, which is a fundamental property of tissue with a well-understood relationship to iron concentration, may serve as a useful biomarker for tissue iron concentration. Further, this work illustrates the potential of susceptibility measurement techniques based on 3D chemical shift-encoded acquisitions, in combination with complex reconstructions. These techniques allow simultaneous measurement of PDFF (with 0–100% dynamic range), R2* maps and B₀ field maps. In this way, PDFF (and potentially R2*) can be used to enable or improve susceptibility measurements based on the B₀ field map.

The main technical drawback of MRI susceptibility-based iron quantification methods (compared to relaxivity-based methods) is the inability to directly estimate susceptibility at every voxel in the liver by considering only the measured signal at that particular voxel. Magnetic susceptibility affects the observed B₀ field map in a non-local manner. In this work, susceptibility was obtained from nearby values in the B₀ field using boundary conditions (30). This approach is based on techniques recently demonstrated in phantoms (29), heart (31), and liver (18,29).

Another technical difficulty is the fact that B₀ field measurements are noisy at very high iron concentrations (where the signal decays very rapidly with increasing echo time). This rapid signal decay may limit the range of LIC values that can be reliably measured, particularly at 3T. Note that in this work we use SPGR acquisitions with small flip angles in order to provide T1-independent measurements of liver fat-fraction (PDFF) jointly with measurements of liver iron. These small flip angles result in reduced SNR, and alternatively data could be obtained with higher flip angles at the cost of potential T1 bias in fat-fraction quantification.

A previous technique used the adjacent muscle as a reference for Bo field measurements (18). In this work, we have chosen to use subcutaneous adipose tissue (SAT) as a reference. This may enable constrained quantitative susceptibility mapping (QSM) by imposing the known locations and susceptibility of fat tissues. Note that fat regions (eg: subcutaneous and visceral adipose tissue) can be easily segmented automatically from fat-water separated images, obtained in the same acquisitions. This work is a feasibility study towards the overall goal of liver QSM using fat as a constraint to regularize the ill-posed QSM inversion problem.

If uncorrected for fat, phase variations due to the presence of fat in tissue (particularly in subcutaneous and visceral adipose tissue) will confound the B₀ measurements. A possible alternative approach to avoid this confounder is to use “in-phase” echoes, where the relative phase of water and the main methylene fat peak is constant for all echoes (32). However, the long echo spacing imposed by “in-phase” acquisitions will likely complicate B₀ field map estimation (and thus susceptibility measurements) in cases of high liver iron where the signal decays very rapidly (eg: T2*=1–2ms with an echo spacing of 4.6ms). In contrast, chemical shift encoded fat-water separation techniques are well suited for mapping of B₀ using closely spaced echo times. The B₀ field maps measured in this work are corrected for the presence of liver fat, similarly to the R2* measurements (note that liver R2* has been shown to be unaffected by liver fat, as long as the spectral complexity of the fat signal is included in the estimation (52)). This fat-corrected B₀ mapping also enables fat-corrected susceptibility measurements. The presence of liver fat may have an effect on the conversion between susceptibility and LIC (given that the susceptibility of fat is different from that of water). However, this effect was not included in this manuscript as it resulted in a small correction of LIC values upon preliminary evaluation, and required further assumptions about the fraction of MR-visible material in liver.

This study included susceptibility and liver iron quantification at both 1.5T and 3T. In this work, the correlation between B₀-LIC and Ferriscan-LIC were superior at 3T compared to 1.5T. The reason for this difference is currently under investigation. A possible reason may be the larger B₀ field offsets (in Hz) observed at 3T, which may be relatively less affected by low-level artifacts and noise.

There is some uncertainty in the conversion of iron concentration units from [Fe]_wet to [Fe]_dry. A factor of 3.3 has been employed in the past, although this value had not been validated (53) and more recent results have suggested that a factor of 5.5 +/− 1.0 may be more appropriate (37). The uncertainty present in this conversion results in uncertainty in the accuracy validation performed in this work. However, the strong correlation between measured ΔB₀ and Ferriscan-LIC suggests that the measured B₀ field map contains the necessary information to assess LIC.

The main theory and results of this work were originally presented as a conference abstract in Ref. (54). Subsequently, in an erratum published by Taylor et al (18), B₀-LIC ([Fe]_wet, mg Fe/mL wet) measurements were compared to R2*-LIC based on Hankins’ calibration (27) ([Fe]_dry, mg Fe/g dry), resulting in a slope of 5.17 and intercept of −3.31. In this work, this calculation results in a slope of 3.44 and an intercept of −0.29. The remaining discrepancy with the results reported by Taylor et al and our work may be due to differences in the techniques used to calculate R2* or B₀ maps, as well as slight differences in the value of μ_eff (4 vs 3.78), and possibly due to differences in the patient groups.

Phantom results seemed to underestimate the true iron concentration (although the slope was not statistically different from 1.0). This may be due to residual background B₀ variations from the top and bottom of the vials, as well as uncertainty in the saturation magnetization of Feridex: we have used a value of 93.6 Am²/kg (49), although recent reports have measured lower values, eg: 80–82 Am²/kg (55). Using Ms=80 Am²/kg would lead to a slope nearly 1.0 in phantom iron concentration estimation (1.5T: 1.00 ± 0.07, 3T: 0.99 ± 0.08).

In the proposed technique (as in previous susceptibility-based techniques) we have made several assumptions in converting measured susceptibility values to iron concentration. Specifically, the relation between susceptibility and iron concentration may depend on the type of iron deposition (eg: ferritin vs hemosiderin), which may in turn be dependent on the type of iron overload and give rise to inter-organ, inter-patient or inter-disease variability (56). Further, we have assumed that liver iron is the only factor affecting magnetic susceptibility. In principle, the presence of liver fat may also affect liver susceptibility. It may be possible to include this in the formulation, as fat quantification (measurement of PDFF) can be performed using the proposed chemical shift-encoded technique. However, this approach may in turn require further approximations, as the measured PDFF includes only MR-visible proton signals. A thorough characterization of the effects of liver fat on liver susceptibility is beyond the scope of this work.

Another limitation of this study is the lack of exact co-localization between B₀, R2* and Ferriscan measurements. B₀ measurements need to be performed near the interface liver-muscle on the right side of the liver. R2 and R2* measurements could be co-localized, but the R2 maps contain substantial motion artifacts. This work assumed that iron concentration does not vary substantially throughout the liver in the scanned subjects.

The major limitation of this study is that a complete dipole inversion of the B₀ field map (ie: QSM) was not performed to determine values of susceptibility over the entire liver. Dipole inversion is a mathematically challenging, ill-posed problem (16,29). The majority of QSM techniques have been applied in the brain (17), where a number of filtering and regularization techniques have been developed to estimate the susceptibility distribution from the measured B₀ field map. However, it is unclear whether these techniques are appropriate for abdominal susceptibility mapping. Adipose tissue, however, is unaffected by iron overload and, as we have demonstrated, can serve as an excellent reference to regularize the inversion problem and help determine the absolute susceptibility (and hence iron concentration) within the tissue of interest (eg. liver). The main purpose of this manuscript was to demonstrate that the fundamental information contained in the B₀ field maps will in principle facilitate QSM in the liver as an alternative to R2* and R2 mapping.

In conclusion, we have demonstrated the feasibility of using B₀ field maps derived from multi-echo chemical shift encoded imaging at 1.5T or 3T to quantity iron in the liver. In addition, this work demonstrates the use of adipose tissue as a possible baseline reference that is required for all QSM related methods. Although further work is needed for dipole inversion of the B₀ field map to measure iron concentration over the entire abdomen, these results are promising and demonstrate the feasibility of this approach. Finally, these results could be extended into quantification of iron in other abdominal tissues, such as the pancreas and spleen.