Calibrated Predictions for Multivariate Competing Risks Models

Abstract

Prediction models for time-to-event data play a prominent role in assessing the individual risk of a disease, such as cancer. Accurate disease prediction models provide an efficient tool for identifying individuals at high risk, and provide the groundwork for estimating the population burden and cost of disease and for developing patient care guidelines. We focus on risk prediction of a disease in which family history is an important risk factor that reflects inherited genetic susceptibility, shared environment, and common behavior patterns. In this work family history is accommodated using frailty models, with the main novel feature being allowing for competing risks, such as other diseases or mortality. We show through a simulation study that naively treating competing risks as independent right censoring events results in non-calibrated predictions, with the expected number of events overestimated. Discrimination performance is not affected by ignoring competing risks. Our proposed prediction methodologies correctly account for competing events, are very well calibrated, and easy to implement.

1 Introduction

Often, in survival data, the probability of experiencing the event of interest is altered by the occurrence of other events, known as competing risk events. Caution is needed in analyzing such data. For example, suppose a breast cancer patient undergoes a prophylactic oophorectomy after surgery for breast cancer. This prophylactic treatment substantially reduces the probability of developing ovarian cancer, and undergoing this treatment should be treated as a competing event when calculating ovarian cancer incidence. The naive Kaplan-Meier estimator with competing risk events treated as independent right censoring is biased, because subjects who experienced a competing risk event are mistakenly treated as being censored in a non-informative manner. A naive analysis based on the standard Cox proportional hazards model can be conducted with competing risks data, but the interpretation of the results is not the same as in the setting without competing risks. Specifically, there is no simple direct relationship between the cause-specific hazard function and the cause-specific cumulative incidence function; as seen in equation (2) below, the cause-specific cumulative incidence function of the event of interest depends on the sum of all the cause-specific hazard functions. Hence, if some covariates are included in the model for two or more competing events, there is no simple formula to relate between the cause-specific cumulative incidence functions of two values of the covariate vector. Both the effect of the covariates on the competing risks and the baseline hazards of the competing risks influence the effect of the covariate on the cumulative incidence of the event of interest. On the other hand, in the absence of competing events, the survival functions of two values of the covariate vector are related by a simple formula based on the relationship between the baseline survival function and the baseline cumulative hazard function. A comprehensive discussion of competing risks for univariate survival data is provided by Kalbfleisch and Prentice (2008, Chapter 8) and the references therein. For clustered survival data with competing risks and covariates, it has been shown that treating competing risks as independent censoring often leads to substantial bias in the regression coefficient estimator and some bias in the baseline hazard function estimator, if the event of interest is often censored by competing risk events (Gorfine and Hsu, 2011).

Bandeen-Roche and Liang (2002) and Bandeen-Roche and Ning (2008) presented models and methods for analyzing bivariate failure times in the presence of competing risks with no covariates, under a multiplicative frailty effect. Chatterjee et al. (2003) considered competing risks with kin-cohort data where the covariate of the relatives is unobserved. Their estimation technique is based on the assumption that the relatives are independent given the proband’s covariate value. Thus, the problem is simplified to a competing risks problem with no clustered data, which can be easily handled using the approach of Prentice et al. (1978). Although the cause-specific hazards are consistently estimated, the dependence of various competing risks among cluster members, which is itself of interest, is not estimated. Chen et al. (2008) developed a nonparametric estimator of the cumulative incidence functions under the cause-specific hazard model of Prentice et al. (1978) with no covariates. Gorfine and Hsu (2011) proposed a class of flexible frailty models for competing risks analysis of clustered survival data with covariates, assuming a proportional hazards frailty model for each failure type. Flexibility is provided in the correlation structure allowed among failure types within a cluster. This class of models includes the model of Bandeen-Roche and Liang (2002) as a special case. Zhou et al. (2012) estimated the average regression model parameters to assess the marginal effect of covariates on the cumulative incidence function for clustered data in the competing risks setting. As in Chatterjee et al. (2003), their estimators are based on an independence working assumption, and again the dependence among cluster members is not estimated.

Aside from the effect of competing risks on estimation of the model parameters, it is also practically important to investigate the effect of competing risks on risk prediction, i.e., predicting the risk of experiencing the event of interest over time. Wolbers et al. (2009) studied risk prediction of coronary heart disease (CHD) in women aged 55–90, based on a univariate survival model with non-CHD death as a competing risk. They compared a competing risk model to a naive model with the competing risk treated as independent right censoring. The values of the concordance index c (Harrell, 2001, p. 493) with these two models are virtually identical. However, although the competing risk models are well calibrated, the naive model overestimates the expected number of events. Wolbers et al. (2009) concluded that it is important to account for non-CHD death as a competing risk in frail populations such as the elderly. Pencina et al. (2009) showed that estimation of the 30-year risk of hard cardiovascular disease ignoring the competing risk of death inflates the estimates by 10%, leading to inferior calibration performance. The current work concerns clustered survival data with competing risks, and is aimed at assessing the effect of the competing risks on predicting the probability of occurrence of a given event of interest in this multivariate survival setting.

Individuals with multiple affected family members are often sent for counseling to assess their probability of developing the disease over time. The prediction is performed based on known risk factors and family history of the disease and other relevant outcomes. Our motivating example is disease risk prediction in which the counselee’s family history plays a central role in prediction. Breast cancer, for example, tends to cluster in families; the disease is approximately twice as common among first-degree relatives of patients as among women in the general population (Pharoah et al., 1997; Collaborative Group on Hormonal Factors in Breast Cancer, 2001). Management strategies have already been in place for families with known breast cancer mutations, such as BRCA1/2. For example, various disease prophylactic measures such as prophylactic mastectomy or chemoprevention and an intensified screening program are options in breast cancer mutation carriers. However, a given mutation may affect multiple types of cancers. For example, the BRCA1 mutation is known to markedly increase the risk of breast, ovarian, and testicular cancer (Risch et al., 2006). Hence, in predicting breast cancer risk, the possible dependent censoring due to ovarian cancer, or death from other causes should be correctly accounted for in the prediction procedure.

Katki et al. (2008) studied the effect of competing risks on predicting a person’s carrier status with respect to the high-risk allele for a disease of interest. They considered the positive-stable copula model for modeling the dependence among the possible outcomes within a subject. However, this specific choice of copula function induces identical dependence parameters for any pair of outcomes, an assumption that is likely to be violated. In addition, their method is based on the strong assumption that, given the observed risk factors, each family member’s phenotype is conditionally independent of all other family members’ phenotypes. To the best of our knowledge, no work has been published on Mendelian-based survival risk prediction (Parmigiani et al. 1998) with competing risks based on correlated survival data.

Using the frailty-based competing risks model and estimation techniques of Gorfine and Hsu (2011), we extend the risk prediction methods of Gorfine et al. (2013) to handle competing risks. The current work focuses on competing risk analysis based on the first event to occur, and thus is restricted to the setting where either the probability of multiple events is negligible (e.g., when all the events are rare) or interest is focused on the first event. It will be shown, through a simulation study, that methods that wrongly treat competing risks as independent right censoring are poorly calibrated due to overestimation of the expected number of events of interest. By contrast, our proposed methods are very well calibrated. It is interesting to note, however, that ignoring competing risks has no effect on discrimination performance in terms of the area under the curve of the receiver operating characteristic (ROC-AUC).

2 Some formal notation and definitions

Consider N independent families where family i, i = 1,…, N, is of size n_i. Denote by $T_{ij}^o$ and C_ij the first failure time and the censoring time, respectively, i = 1,…, N, j = 1,…, n_i. The observed follow-up time of subject j of family i is defined by $T_{ij}=\text{min}(T_{ij}^o,C_{ij})$, and R_ij ∈ {1,…,L} is the type of the first observed failure with R_ij = 0 for a censored observation. The cause-specific event indicator equals ${\delta }_{ij}^{(r)}=I(T_{ij}^o\le C_{ij})I(R_{ij}=r)r=1,\dots ,L$. Also, let G_ij be the subject’s carrier status with respect to the high-risk allele for the disease of interest, with G_ij defined as 1 if the subject is a carrier and 0 otherwise, and let Z_ij be a vector of additional risk factors (e.g., body mass index, obstetric history).

In addition, we introduce the unobservable frailty vectors W_i = (W_i1,…, W_iL)^T, i = 1,…, N, taken to be independent and multivariate normally distributed with zero mean and unknown covariance matrix Σ. The frailty W_i induces dependence among the outcomes of the members of the ith family. Given W_i, G_i = (G_i1,…, G_ini)^T, and ${\mathbf{Z}}_i={({\mathbf{Z}}_{i1}^T,\dots ,{\mathbf{Z}}_{i{n}_i}^T)}^T$, the family members’ failure times are assumed independent. The diagonal entry Σ_rr, reflects the dependence between two family members with respect to the risk of failure type r, while the off-diagonal entry Σ_rs reflects the dependence between one family member’s risk of a failure type r and another family member’s risk of a failure of type s. For example, consider a study in which breast cancer is the event of interest (the event time being age at diagnosis), with G_ij being the subject’s carrier status with respect to BRCA1/2 mutations, and ovarian cancer and death of other causes as competing risks. Thus, W_i = (W_i1,W_i2,W_i3)^T, with Σ₁₁,Σ₂₂ and Σ₃₃ reflecting the within-family dependence with respect to the risk of breast cancer, ovarian cancer, and death from other causes, respectively, while Σ₁₂ represents the dependence between one family member’s risk of breast cancer and another family member’s risk of ovarian cancer.

The overall hazard function of subject ij given W_i, G_ij and Z_ij, is defined by

$${\lambda }_{ij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)=\underset{h\downarrow 0}{\text{lim}}\frac{1}{h}{P}_r(t\le T_{ij}^o<t+h|T_{ij}^o\ge t,G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i).$$

The cause-specific hazard functions are defined by

$${\lambda }_{rij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)=\underset{h\downarrow 0}{\text{lim}}\frac{1}{h}{P}_r(t\le T_{ij}^o<t+h,R_{ij}=r|T_{ij}^o\ge t,G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i),$$

r = 1,…, L. We assume that λ_rij(t | G_ij, Z_ij, W_i) follows the model

$${\lambda }_{rij}(t|G_{ij}=g,{\mathbf{Z}}_{ij},{\mathbf{W}}_i)={\lambda }_{0gr}(t)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_{ij}+W_{ir})$$ (1)

for g = 0,1 and r = 1,…, L, where β₁,…, β_L and λ₀₀₁(·), …, λ_00L(·), λ₀₁₁(·), …, λ_01L(·) are, respectively, the cause-specific regression coefficients, the cause-specific baseline hazard functions among non-carriers (G_ij = 0), and the cause-specific baseline hazard functions among carriers (G_ij = 1). If the carrier status has a proportional effect on the hazards, G_ij can be included as one of the components of Z_ij, and a common baseline hazard function for carriers and non-carriers can be used.

It is assumed, in addition, that at each time point only one failure type can occur, so that by the law of total probability we get

$${\lambda }_{ij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)=\sum _{r=1}^L{\lambda }_{rij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i),$$

and the rth cause-specific density, r = 1,…, L, equals

$${\lambda }_{rij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)=S_{ij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)$$

where

$$S_{ij}(t|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)=\text{exp}\{-{\int }_0^t\sum _{r=1}^L{\lambda }_{rij}(u|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i)du\}.$$ (2)

We also make the following standard assumptions:

1. Conditional on (G_i1,…, G_ini, Z_i1, …, Z_ini, W_i), the censoring times are independent of the failure times and non-informative for the frailty process and the model parameters {β_r, λ_0gr,g = 0,1,r=1,…,L}.

2. The frailty variate W_i is independent of (G_i1,…, G_ini, Z_i1, …, Z_ini).

3. The covariates effect is subject specific: for i = 1,…, N, j = 1,…, n_i,

   $$\text{Pr}(T_{ij},R_{ij}|G_{i1},\dots ,G_{i{n}_i},{\mathbf{Z}}_{i1},\dots ,{\mathbf{Z}}_{i{n}_i},{\mathbf{W}}_i)=\text{Pr}(T_{ij},R_{ij}|G_{ij},{\mathbf{Z}}_{ij},{\mathbf{W}}_i).$$

The likelihood function can then be expressed in terms of the cause-specific hazard functions as

$$\prod _{i=1}^N\int \prod _{j=1}^{n_i}\prod _{r=1}^L{\{{\lambda }_{0G_{ij}r}(T_{ij})\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_{ij}+W_{ir})\}}^{{\delta }_{ij}^{(r)}}\text{exp}\{-{\mathrm{\Lambda }}_{0G_{ij}r}(T_{ij})\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_{ij}+W_{ir})\}{\varphi }_L({\mathbf{W}}_i|\mathbf{\Sigma })d{\mathbf{W}}_i$$

where ${\mathrm{\Lambda }}_{0gr}(t)={\int }_0^t{\lambda }_{0gr}(u)du$, g = 0, 1, r = 1,…, L, and φ_L(·|Σ) denotes the L–dimensional zero-mean multivariate normal density with covariance matrix Σ. Gorfine and Hsu (2011, Section 4) pointed out that if the W_ir’s (r = 1,…, L) are independent, the likelihood function factors into a product of separate components for each cause-specific hazard function. The r-th factor is precisely the likelihood that would be obtained if failures of types other than r were regarded as instance of independent censoring and the frailty W_ir accounts for the unobservable family-level effect related specifically to failure type r. In the case where such independence holds, a naive frailty-based estimation procedure (e.g., Zeng and Lin, 2007) can be applied, although caution is needed in interpreting the results. In particular, the cause-specific cumulative incidence function of the event of interest depends on the sum of all the cause-specific hazard functions. In the general case, for estimating β_r, λ_0gr g = 0,1, r = 1,…,L, and Σ, the EM-algorithms of Gorfine and Hsu (2011) can be applied, for either parametric or non-parametric specification of the baseline hazard functions. For non-parametric baseline hazard functions that depend on carrier status, the required minor modification in the estimators is presented in Appendix A.

The rest of this paper presents two new survival prediction methods based on the above multivariate competing risks model (1), and contrasts these methods with those that ignore the competing risks and treat them as independent censoring. In order to focus on prediction issues as opposed to estimation issues, the parameters β_r, λ_0gr(·) g = 0,1, r = 1,…, L and Σ are assumed to be known.

3 Survival prediction methodology

3.1 Introduction

In this section, we concentrate on survival prediction for a counselee given his/her family history. For example, consider a woman of age T₀ who is seeking a breast cancer risk prediction given her BRCA1/2 mutation carrier status, additional risk factors, and her family history of breast and ovarian cancers, death from other causes, mutation carrier status and other risk factors. If one of the family members experienced both breast and ovarian cancer, only the first event will be included in the prediction model. In many cases, experiencing both types of events is rare (albeit possible), as with breast and ovarian cancer.

Since prediction is performed for each counselee separately, we omit the subscript i, and modify the notation as follows. Assume a counselee of age T₀ with n relatives. Define T_j, j = 1,…,n, as the age of relative j’s first observed failure as of the time of the consultation, or relative j’s age at the time of the consultation if the relative is alive and did not undergo any failure as of that time, or relative j’s age at death if the relative is not alive at the time of consultation and did not undergo any failure. Note that there are two time scales operating here, calendar time and the time scale on which the survival time is measured (e.g., age, as in our examples). Let T = (T₁,…,T_n). Also let R₀ = 0 and R = (R₁,…, R_n) denote the type of the first observed failure (0 denotes censoring), and let G₀, Z₀, G = (G₁,…,G_n), $\mathbf{Z}={({\mathbf{Z}}_1^T,\dots ,{\mathbf{Z}}_n^T)}^T$ denote the corresponding carrier status and vectors of covariates. Our main concern is estimating the probability of a counselee developing a disease of type r by age t, t > T₀, given the observed information ℱ = {T₀, R₀ = 0, G₀, Z₀, T, R, Z, G}. The risk prediction methods presented below are in the spirit of Gorfine et al. (2013), with the required modifications to accommodate competing risks. In addition, each method is contrasted with its counterpart in the case where competing risks are wrongly considered as independent right censoring.

3.2 Marginalized approach

3.2.1 Marginalized approach accounting for competing risks

Under the competing risks marginalized approach, the predicted risk of developing a disease of type r by age t (> T₀) is computed as $\text{Pr}(T_0^o\le t,R_0=r|ℱ)$ where $T_0^o$ denotes the counselee’s first failure time. Specifically, we have

$$\text{Pr}(T_0^o\le t,R_0=r|ℱ)=\int \text{Pr}(T_0^o\le t,R_0=r|ℱ,\mathbf{W})f(\mathbf{W}|ℱ)d\mathbf{W}=\frac{\int \text{Pr}(T_0<T_0^o\le t,R_0=r|G_0,Z_0,\mathbf{W})\text{Pr}(\mathbf{T},\mathbf{R}|\mathbf{G},\mathbf{Z},\mathbf{W}){\varphi }_L(\mathbf{W}|\mathbf{\Sigma })d\mathbf{W}}{\int \text{Pr}(T_0^o>T_0|G_0,Z_0,\mathbf{W})\text{Pr}(\mathbf{T},\mathbf{R}|\mathbf{G},\mathbf{Z},\mathbf{W}){\varphi }_L(\mathbf{W}|\mathbf{\Sigma })d\mathbf{W}}$$ (3)

where

$$\text{Pr}(T_0<T_0^o\le t,R_0=r|G_0,{\mathbf{Z}}_0,\mathbf{W})={\int }_{T_0}^t{\lambda }_{0G_{0}r}(u)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_0+W_r)\times \text{exp}\{-\sum _{k=1}^L{\mathrm{\Lambda }}_{0G_{0}k}(u)\text{exp}({\mathit{\beta }}_k^T{\mathbf{Z}}_0+W_k)\}du,\text{Pr}(T_0^o>T_0|G_0,{\mathbf{Z}}_0,\mathbf{W})=\text{exp}\{-\sum _{r=1}^L{\mathrm{\Lambda }}_{0G_{0}r}(T_0)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_0+W_r)\},$$

and Pr(T, R|G, Z, W) in (3) is replaced by

$$\prod _{j=1}^n\prod _{r=1}^L{\{{\lambda }_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)\}}^{{\delta }_j^{(r)}}\text{exp}\{-{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)\}.$$

The probabilistic terms above are all conditional on T₀. All the unknown parameters are replaced by their estimates, and the integration with respect to the frailty vector W can be done by numerical approximations, such as Gauss-Hermite quadrature, as long as the dimension of W is not too high (e.g. ≤ 6).

3.2.2 Misspecified marginalized approach ignoring competing risks

Let ${\tilde{T}}_j^o=T_j^{o}I(R_j=r)+\infty I(R_j\ne r)$ and ${\tilde{C}}_j=C_j\{I(R_j=0)+I(R_j=r)\}+T_j^{o}I(R_j>0)I(R_j\ne r)$, j = 0, 1, …, n, be the respective failure and censoring times if the competing risks are wrongly treated as independent right censoring events. Clearly, the observed time of the _jth family member equals $T_j=\text{min}({\tilde{T}}_j^o,{\tilde{C}}_j)$. Let ${\mathit{\delta }}^{(r)}=({\delta }_1^{(r)},\dots ,{\delta }_n^{(r)})$.

Under the marginalized approach with competing risks as independent censoring and hazard function in the spirit of model (1), the estimated risk of developing the disease of type r by age t (> T₀) is based on the conditional probability that ${\tilde{T}}_0^o\le t$ given $\widetilde{ℱ}=\{T_0,{\delta }_0^{(r)}=0,G_0,{\mathbf{Z}}_0,\mathbf{T},{\mathit{\delta }}^{(r)},\mathbf{G},\mathbf{Z}\}$. Specifically, the risk is expressed in terms of the probability

$$1-\frac{\int \text{Pr}({\tilde{T}}_0^o>t|G_0,{\mathbf{Z}}_0,W_r)\text{Pr}(\mathbf{T},{\mathit{\delta }}^{(r)}|\mathbf{G},\mathbf{Z},W_r){\varphi }_1(W_r|{\mathrm{\Sigma }}_{rr})d{W}_r}{\int \text{Pr}({\tilde{T}}_0^o>T_0|G_0,{\mathbf{Z}}_0,W_r)\text{Pr}(\mathbf{T},{\mathit{\delta }}^{(r)}|\mathbf{G},\mathbf{Z},W_r){\varphi }_1(W_r|{\mathrm{\Sigma }}_{rr})d{W}_r}$$ (4)

where

$$\text{Pr}({\tilde{T}}_0^o>t|G_0,{\mathbf{Z}}_0,W_r)=\text{exp}\{-{\mathrm{\Lambda }}_{0G_{0}r}(t)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_0+W_r)\}$$

and Pr(T, δ^(r)|G, Z, W_r) is replaced by

$$\prod _{j=1}^n{\{{\lambda }_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)\}}^{{\delta }_j^{(r)}}\text{exp}\{-{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)\}.$$

In Section 4 we study by simulation the above risk predictor (3) in the case where the parameters β_r, Λ_0gr, g = 0,1, and Σ_rr are correctly specified and also in the case where the competing risks were ignored in the estimation stage as well as the prediction stage.

3.3 Conditional approach

3.3.1 Conditional approach accounting for competing risks

The main idea of the conditional approach is to avoid integrating with respect to the frailty variate, as required in the marginalized approach. Hence, we predict the frailty vector W. The competing risks conditional approach is thus based on temporarily treating the L-dimensional frailty vector W as an unknown vector of parameters, and estimating this vector as if the joint distribution of the survival data and the frailty vector is a likelihood function for W.

For the “likelihood” construction, write

$$\text{Pr}(T_0,R_0=0,\mathbf{T},\mathbf{R},\mathbf{W}|G_0,{\mathbf{Z}}_0,\mathbf{G},\mathbf{Z})=\text{Pr}(T_0,R_0=0,\mathbf{T},\mathbf{R}|\mathbf{W},G_0,{\mathbf{Z}}_0,\mathbf{G},\mathbf{Z}){\varphi }_L(\mathbf{W}|\mathbf{\Sigma })$$

where Pr(T₀, R₀ = 0, T, R|W, G₀, Z₀, G, Z) is proportional to

$$\text{exp}\{-\sum _{j=0}^n\sum _{r=1}^L{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_r+W_r)\}\prod _{j=1}^n\prod _{r=1}^L{\{{\lambda }_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_r+W_r)\}}^{{\delta }_j^{(r)}}.$$

Then, the “log-likelihood” for W is equal to a constant plus the quantity

$$\sum _{j=1}^n\sum _{r=1}^L{\delta }_j^{(r)}{W}_r-\sum _{j=0}^n\sum _{r=1}^L{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)+\text{log}{\varphi }_L(\mathbf{W}|\mathbf{\Sigma }).$$

Taking the derivatives with respect to W_r, r = 1,…, L, the estimating equations for W become

$$\sum _{j=1}^n{\delta }_j^{(r)}-\sum _{j=0}^n{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)-{[{\mathbf{W}}^T{\mathbf{\Sigma }}^{-1}]}_r=0$$ (5)

for r = 1, …,L, where [X]_r denotes the rth component of the vector X. For example, if L = 2,

$${\left[{\mathbf{W}}^T{\mathbf{\Sigma }}^{-1}\right]}_r=\frac{W_r}{(1-{\rho }^2){\mathrm{\Sigma }}_{rr}}-\frac{\rho W_{r^{\prime }}}{(1-{\rho }^2)\sqrt{{\mathrm{\Sigma }}_{11}{\mathrm{\Sigma }}_{22}}}$$

where r, r′ = 1,2, r′ ≠ r and $\rho ={\mathrm{\Sigma }}_{12}/\sqrt{{\mathrm{\Sigma }}_{11}{\mathrm{\Sigma }}_{22}}$. The above expression will help us in contrasting the current approach to one that naively ignores the competing risks.

The resulting predicted risk of having the disease of type r by age t (> T₀) is based on $\text{Pr}(T_0^o\le t,R_0=r|ℱ,\mathbf{W})$ with W replaced by its estimator Ŵ:

$$\frac{{\int }_{T_0}^t{\lambda }_{0G_{0}r}(u)\text{exp}\{{\mathit{\beta }}_r^T{\mathbf{Z}}_0+{\widehat{W}}_r\}\text{exp}\{-{\sum }_{k=1}^L{\mathrm{\Lambda }}_{0G_{0}k}(u)\text{exp}({\mathit{\beta }}_k^T{\mathbf{Z}}_0+{\widehat{W}}_k)\}du}{\text{exp}\{-{\sum }_{k=1}^L{\mathrm{\Lambda }}_{0G_{0}k}(T_0)\text{exp}({\mathit{\beta }}_k^T{\mathbf{Z}}_0+{\widehat{W}}_k)\}}$$ (6)

3.3.2 Misspecified conditional approach ignoring competing risks

In the conditional risk prediction approach for event of type r with the competing risks treated as independent censoring, we predict W_r while treating

$$\text{Pr}(T_0,{\delta }_0^{(r)}=0,\mathbf{T},{\mathit{\delta }}^{(r)},W_r|G_0,{\mathbf{Z}}_0,\mathbf{G},\mathbf{Z})=\text{Pr}(T_0,{\delta }_0^{(r)}=0,\mathbf{T},{\mathbf{\delta }}^{(r)}|W_r,G_0,{\mathbf{Z}}_0,\mathbf{G},\mathbf{Z}){\varphi }_1(W_r|{\mathrm{\Sigma }}_{rr})$$

as the “likelihood” for W_r. Since $\text{Pr}(T_0,{\delta }_0^{(r)}=0,\mathbf{T},{\mathit{\delta }}^{(r)}|W_r,G_0,{\mathbf{Z}}_0\mathbf{G},\mathbf{Z})$ is proportional to

$$\text{exp}\{-\sum _{j=0}^n{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_r+W_r)\}\prod _{j=1}^n{\left\{{\lambda }_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_r+W_r)\right\}}^{{\delta }_j^{(r)}},$$

the “log-likelihood” for W_r is equal to a constant plus the quantity

$$\sum _{j=1}^n{\delta }_j^{(r)}{W}_r-\sum _{j=0}^n{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)+\text{log}{\varphi }_1(W_r|{\mathrm{\Sigma }}_{rr}).$$

The estimator W̃_r of W_r is thus the solution of the following equation

$$\sum _{j=1}^n{\delta }_j^{(r)}-\sum _{j=0}^n{\mathrm{\Lambda }}_{0G_{j}r}(T_j)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_j+W_r)-\frac{W_r}{{\mathrm{\Sigma }}_{rr}}=0.$$

Then, the predicted risk of having the disease of type r by age t (> T₀) is based on

$$1-\frac{\text{exp}\{-{\mathrm{\Lambda }}_{0G_{0}r}(t)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_0+{\tilde{W}}_r)\}}{\text{exp}\{-{\mathrm{\Lambda }}_{0G_{0}r}(T_0)\text{exp}({\mathit{\beta }}_r^T{\mathbf{Z}}_0+{\tilde{W}}_r)\}}$$

after replacing the unknown parameters by their estimators. In Section 4, the above misspecified conditional approach will be studied in two versions, one using the true parameter values and the other using biased parameter estimators under a frailty model that naively regards the competing risks as independent censoring.

3.4 Confidence Intervals

In practice, when a counselee is attending the clinic for risk prediction, he/she will be given a risk estimate based on population parameter estimates, β̂_r, λ̂_ogr, g = 0,1, r = 1,…, L, and Σ̂, calculated using an external dataset. It is assumed that the counselee and the dataset used for parameter estimation belong to the same population. In the following confidence interval construction, the uncertainty due to the population parameter estimation is accounted for.

Assume that the external dataset consists of N families. Under parametric modeling of λ_0gr, g = 0,1, r = 1,…,L, let ψ̂_P denote the maximum likelihood estimators of β_r, the parameters associated with λ_0gr, g = 0,1, r = 1,…,L, and with Σ. Clearly, $N^{1/2}({\widehat{\psi }}_P-{\psi }_P^o)$ converges weakly to a zero-mean multivariate normal distribution, where ${\psi }_P^o$ denotes the true values of the population parameters under the parametric setting. The covariance matrix can be estimated by the inverse of the observed information matrix and is denoted by Ξ̂_P. Similarly, under nonparametric modeling of λ_0gr, g = 0,1, r = 1,…, L, denote by ψ̂_NP and ${\psi }_{NP}^o$ the nonparametric maximum likelihood estimators and the true values of the population parameters. Then, $N^{1/2}({\widehat{\psi }}_{NP}-{\psi }_{NP}^o)$ converges weakly to a zero-mean Gaussian process, and the estimated covariance matrix Ξ̂_NP can be calculated by the inversion of the observed information matrix or the bootstrap approach in case of a high dimensional matrix (Gorfine and Hsu, 2011).

Since the variance of the proposed estimators of the survival probability, cannot be derived analytically in a closed form, the simple resampling-based procedure of Gorfine et al. (2013) is adopted. The confidence intervals construction under the parametric or non-parametric hazard functions are similar, so the subscript P or NP are omitted in the following. Assume that either the competing risks marginalized approach or the competing risks conditional approach is used; henceforth “the adopted procedure”.

Resampling-based confidence interval procedure:

1. Generate B ψ̃’s from the multivariate normal distribution N(ψ̂, Ξ̂).

2. For each ψ̃^(b), b = 1,…,B, calculate the counselee risk prediction based on the adopted procedure, denoted by p̂^(b), b = 1,…, B.

3. Estimate the risk prediction variance by the empirical variance of p̂⁽¹⁾, …, p̂^(B) and construct a Wald-type confidence interval.

In Gorfine et al. (2013), a similar procedure in the a setting of no competing risks was studied by simulation. Results indicate that under a well-specified frailty distribution, the procedure performs very well, with empirical coverage rates very close to the nominal rates. Hence we do not provide simulation results here.

4 An empirical study

In the following simulation study we investigate the performance of the proposed marginalized and conditional competing risks prediction procedures and contrast each method with its counterpart in the case where the competing risks are naively ignored.

We considered two competing diseases and 50,000 designated counselees. For each counselee, one parent and two siblings were defined as his/her family members. The carrier status indicators G of the family members were generated based on Mendel’s law with a high-risk allele frequency of 0.1. No additional covariates were considered. The frailty variates were randomly sampled from a bivariate normal distribution with mean zero and 2×2 covariance matrix Σ based on the parameters (Σ₁₁,Σ₂₂, ρ) = (1.5,2,0.5). The cumulative baseline hazard functions were taken to be Λ_0gr(t) = t exp(β_rg)/55 r = 1,2, g = 0,1, with (β₁,β₂) = (0.5,2.5). Under these regression coefficient values, the disease r = 1 is frequently censored by the other disease, but the disease r = 2 is rarely censored by the disease r = 1. Given (β₁, β₂), the carrier status, and the frailty vector W, the age of occurrence of the first disease was generated for each family member from an exponential distribution with parameter α = Σ_r=1,2 exp(β_rG + W_r)/55. The failure type of each family member was generated based on a Bernoulli distribution, with the disease being of type r = 1 with probability α₁/α, where α₁ = exp(β₁G + W₁)/55. In addition, independent consultation times c_0i, i = 1,…, 50,000, were sampled from an exponential distribution with parameter 1/20. Out of the 50,000 designated counselees, we are left with 23,204 after excluding counselees affected by one of the two diseases. Namely, an individual with failure time $t_{0i}^o$ less than the consultation time c_0i, was excluded; otherwise, t_0i = c_0i is considered as the current age of counselee i, and survival prediction was performed for the risk of having the designated event by time t_0i + 10 or t_0i + 15. We then contrasted predictions with the true event occurrence status of each counselee at the end of the x-year interval, x = 10 or 15. The one- or two-dimensional integrals were approximated by one-or two-dimensional Gauss-Hermite quadrature with 20 or 20×20 function evaluations, respectively.

As is customary (Steyerberg et al., 2010, among others), three performance measures are considered, as follows.

Discrimination is studied by the area under the curve of the receiver operating characteristic (ROC-AUC). Assume prediction is performed for m independent counselees for predicting at the x-year interval, resulting in p̂₁, …, p̂_m; let ${\delta }_1^{(r)},\dots ,{\delta }_m^{(r)}$ denote each counselee’s respective event status at the end of the x-year interval; $m_1^{(r)}={\sum }_{i=1}^m{\delta }_i^{(r)}$; and $m_0^{(r)}=m-m_1^{(r)}$. A nonparametric estimator of the ROC-AUC (also known as the c statistic; Harrell, 2001, p. 493), for prediction of an event of type r, is defined by ${\sum }_{i=1}^m{\sum }_{j=1}^{m}U({\widehat{p}}_i,{\widehat{p}}_j){\delta }_i^{(r)}(1-{\delta }_j^{(r)})/m_0^{(r)}{m}_1^{(r)}$, where U(a,b) = I (a > b) + 0.5I (a = b). It varies between 0.5 and 1.0 with higher values indicating a better discriminative model.

Calibration is investigated by the ratio of the observed and expected number of events. Let $t_{0i}^o$, and t_0i be the respective values of the first failure time and age at consultation of counselee $i(t_{0i}^o>t_{0i})$; and r_0i indicates the event type of counselee i, i = 1,…, m. Then, for an x-year interval and r as the event type of main interest, the total number of observed events is defined as $O={\sum }_{i=1}^{m}I(t_{0i}^o\le t_{0i}+x,r_{0i}=r)$ and the estimator of the expected number of events is $\widehat{E}={\sum }_{i=1}^m{\widehat{F}}_{ri}(t_{0i}+x)$, where F̂_ri is the estimated risk of counselee i for event type r. If the model is well calibrated we expect O/Ê to be close to 1.

Accuracy of prediction (also called the overall performance) is expressed in terms of the mean squared error of prediction (MSEP). Let S be the true survival probability of a random counselee. The MSEP is defined by E(S – Ŝ)², where Ŝ is the estimated probability and the expectation is with respect to the joint distribution of (S,Ŝ). The natural empirical estimator of the MSEP is ${\sum }_{i=1}^m{(S_i-{\widehat{S}}_i)}^2/m$.

Tables 1–3 present simulation results for the two possible situations with each outcome in turn designated as the event of interest. We present the results of the marginalized and conditional methods. We also present, as a gold standard benchmark, the ideal prediction based on the true value of the frailty variate. Each prediction approach was studied under three scenarios: (i) Competing Risks (CR) - the competing risk is correctly handled with respect to the population parameters β_r,λ_0gr and Σ and at the prediction stage with the proposed prediction procedure; (ii) Partially Non-Competing Risks (PNCR) -the competing risk is correctly handled with respect to the population parameters, but naively ignored at the prediction stage, so that the competing event was considered as independent right censoring at the prediction stage; (iii) Non-Competing Risks (NCR) - the competing risk is naively considered as independent right censoring in both the estimation and prediction stages. For CR and PNCR, the true values of the population parameters were used. However, under the NCR setting, since the bias of the population parameter estimators has no analytical closed form, the population parameters were estimated based on external simulated datasets of 50,000 families and the EM-algorithm of Zeng and Lin (2007). The resulting estimate of (β₁, Σ₁₁) was (0.2601,1.4725), and that of (β₂, Σ₂₂) was (2.4658,1.9256). It is evident that the estimate of β₁ is dramatically biased, in contrast to all the other estimates. This is because the event of type r = 1 is frequently censored by the event of type r = 2, while event of type r = 2 is rarely censored by the other event. The estimates of the cumulative baseline hazard functions also slightly underestimate the true functions, mainly at later time points (results not shown).

Table 1.

Simulation results of ROC-AUC

			Marginalized			Conditional			Known frailty
	m	m1	CR	PNCR	NCR	CR	PNCR	NCR	CR	PNCR	NCR
event type r = 1 is singled out
Prediction at 10-year interval
Whole	23204	3312	0.674	0.666	0.667	0.673	0.664	0.665	0.772	0.765	0.766
Non-carriers	21164	3059	0.675	0.672	0.671	0.674	0.670	0.669	0.771	0.768	0.767
Carriers	2040	253	0.664	0.664	0.663	0.658	0.663	0.662	0.778	0.753	0.752
Prediction at 15-year interval
Whole	23204	4325	0.678	0.667	0.669	0.677	0.665	0.668	0.775	0.764	0.765
Non-carriers	21164	4024	0.677	0.675	0.674	0.676	0.674	0.673	0.774	0.768	0.768
Carriers	2040	301	0.670	0.666	0.666	0.666	0.667	0.666	0.781	0.740	0.739
event type r = 2 is singled out
Prediction at 10-year interval
Whole	23204	4147	0.745	0.745	0.745	0.744	0.745	0.745	0.825	0.823	0.822
Non-carriers	21164	3172	0.706	0.706	0.706	0.705	0.706	0.705	0.804	0.802	0.801
Carriers	2040	975	0.728	0.729	0.728	0.744	0.728	0.728	0.808	0.800	0.800
Prediction at 15-year interval
Whole	23204	5244	0.734	0.734	0.734	0.733	0.734	0.735	0.816	0.812	0.812
Non-carriers	21164	4128	0.697	0.698	0.698	0.697	0.698	0.698	0.796	0.791	0.791
Carriers	2040	1116	0.726	0.724	0.725	0.721	0.723	0.723	0.814	0.800	0.800

m - total number of counselees; m₁ - number of events;

CR - the competing risks based method; PNCR - ignoring competing risks only at prediction; NCR - ignoring competing risks at estimation and prediction.

Table 3.

Simulation results of MSEP (× 100)

Marginalized			Conditional
CR	PNCR	NCR	CR	PNCR	NCR
event type r = 1 is singled out
Prediction at 10-year interval
1.0717	1.3819	1.2321	1.0913	1.4032	1.2548
Prediction at 15-year interval
1.5535	2.1843	1.8860	1.5854	2.2828	1.9495
event type r = 2 is singled out
Prediction at 10-year interval
1.3594	1.4922	1.4291	1.4999	1.6388	1.5394
Prediction at 15-year interval
1.8146	2.1035	1.9557	1.9557	2.3866	2.1566

CR - the competing risks based method;

PNCR - ignoring competing risks only at prediction;

NCR - ignoring competing risks at estimation and prediction.

Tables 1–3 provide, respectively, the ROC-AUC values, the ratios of the observed and expected number of events O/Ê, and the empirical MSEPs. The ROC-AUC results are negligibly affected by treating the competing risks as independent censoring at the prediction stage, regardless of whether the population parameter values used are correct or biased due to naively ignoring the competing risk at the estimation stage. This finding is understandable because, under our sampling design, naively ignoring competing risks is expected to influence all predictions in the same direction. Hence it does not substantially influence the concordance of the estimated risks for events and non-events. The calibration performance of the prediction, on the other hand, is substantially degraded by neglecting to correctly accommodate the competing risk, mainly when the event of interest is frequently censored by the other event and within the carriers population. Under the proposed competing risks prediction methods (CR), the calibration performance measures are reasonably close to 1. By contrast, the expected number of events under PNCR or NCR is an overestimate, because some of the predicted disease events are due to occur only after the competing risk event. Interestingly, this overestimation issue is more of a concern when the competing risk is being partially ignored (PNCR) than when it is being completely ignored (NCR). This result is most probably due to the inconsistency of the PNCR approach, which combines competing and non-competing risks methods. The MSEP is the smallest under the proposed competing risks approaches, and again the worst performance is seen with PNCR. Failing to account for competing risks has a more severe impact when the event of interest is frequently censored by the competing event.

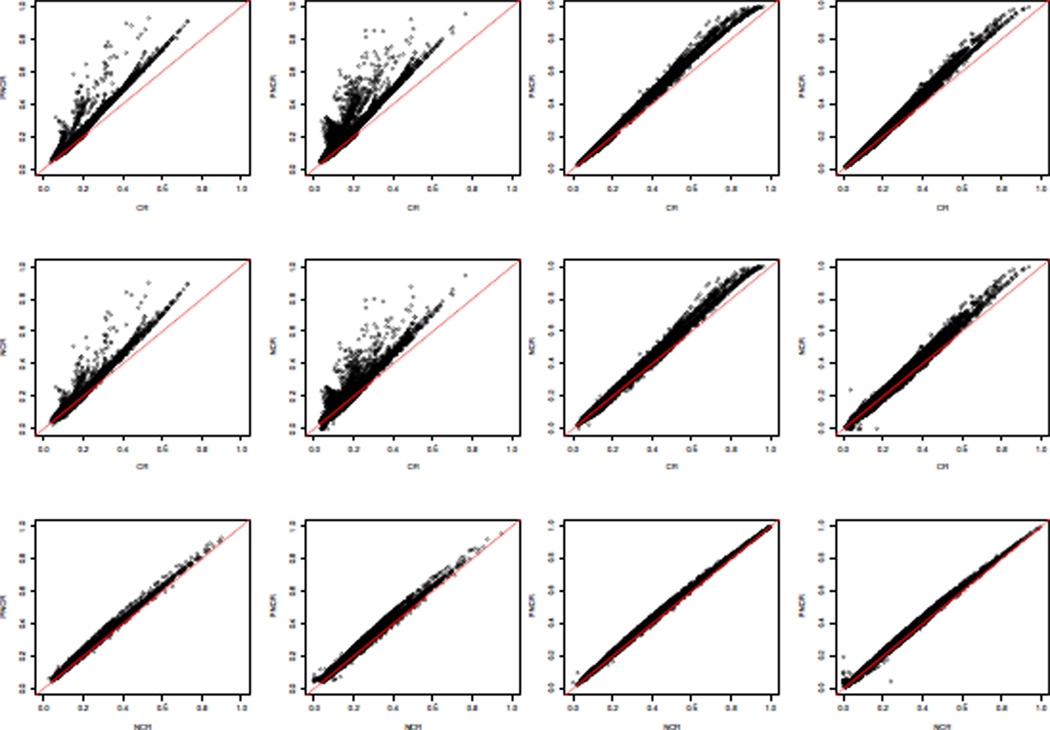
In Figure 1, the various predicted failure probabilities of the marginalized approach for a ten-year interval are plotted, separately, for event and non-event counselees. The fact that the events and non-events plots are similar explains the similarity in the ROC-AUC values among CR, PNCR and NCR. The inferior calibration performance of PNCR and NCR is illustrated by the tendency of these methods to produce predictions above the unit-slope line relative to CR, particularly when r = 1 is the designated event of interest (left two columns). Similar results are seen at other follow-up times and with the conditional approach.

Figure 1.

Simulation results of the marginalized approach, predicting at ten-year interval: two left columns - r = 1 is singled out, two right columns - r = 2 is singled out.

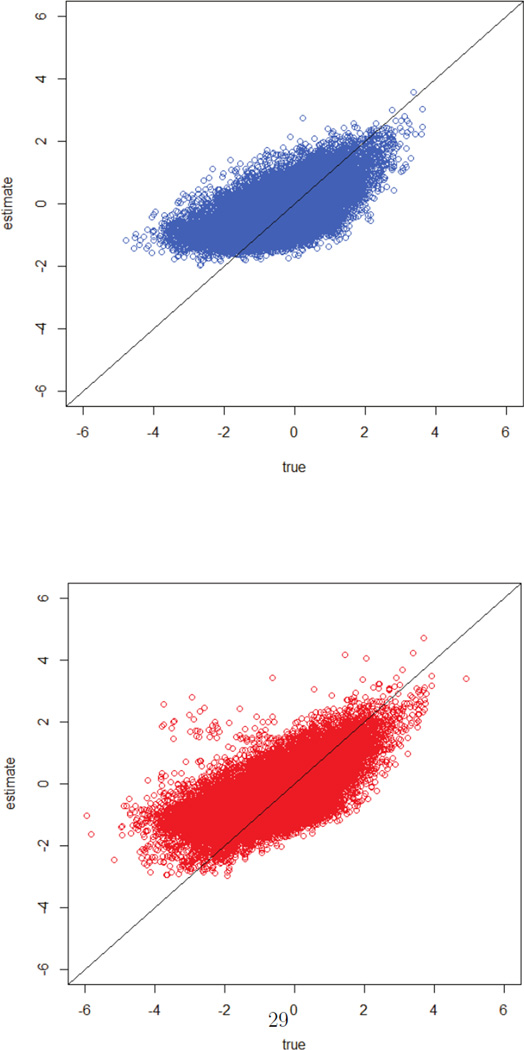
Figure 2 displays W₁ versus Ŵ₁ (top) and W₂ versus Ŵ₂ (bottom), corresponding to the first setting of Table 1 (r = 1 is singled out, and prediction at a 10-year interval). In spite of the fact that the association between the true random variable and its predicted value is not perfect (Pearson correlations of 0.67 and 0.63, respectively), we see in Table 2 that the conditional approach performs well in terms of bias under this setting.

Figure 2.

Simulation results of the conditional approach, predicting at ten-year interval: W₁ versus Ŵ₁ (top) and W₂ versus Ŵ₂ (bottom).

Table 2.

Simulation results of calibration: the ratio of the observed and expected number of events

			Marginalized			Conditional			Known frailty
	m	m1	CR	PNCR	NCR	CR	PNCR	NCR	CR	PNCR	NCR
event type r = 1 is singled out
Prediction at 10-year interval
Whole	23204	3312	0.988	0.798	0.876	0.990	0.852	0.949	0.968	0.834	0.966
Non-carriers	21164	3059	1.023	0.838	0.909	1.021	0.898	0.986	1.053	0.865	0.966
Carriers	2040	253	0.989	0.506	0.611	0.989	0.527	0.658	0.989	0.584	0.781
Prediction at 15-year interval
Whole	23204	4325	0.992	0.769	0.848	1.007	0.799	0.894	0.992	0.801	0.929
Non-carriers	21164	4024	0.994	0.810	0.884	1.004	0.845	0.934	0.993	0.834	0.953
Carriers	2040	301	0.968	0.457	0.549	1.056	0.461	0.573	0.986	0.521	0.689
event type r = 2 is singled out
Prediction at 10-year interval
Whole	23204	4147	1.002	0.873	0.932	1.006	0.882	0.945	0.988	0.884	0.973
Non-carriers	21164	3172	0.977	0.868	0.932	1.005	0.901	0.976	0.897	0.883	0.980
Carriers	2040	975	0.996	0.893	0.933	1.001	0.823	0.857	0.980	0.886	0.949
Prediction at 15-year interval
Whole	23204	5244	1.005	0.846	0.910	0.967	0.841	0.910	0.999	0.867	0.949
Non-carriers	21164	4128	1.012	0.839	0.911	0.992	0.853	0.933	1.007	0.792	0.956
Carriers	2040	1116	0.981	0.856	0.907	0.886	0.854	0.826	0.973	0.861	0.922

m - total number of counselees; m₁ - number of events;

CR - the competing risks based method; PNCR - ignoring competing risks only at prediction; NCR - ignoring competing risks at estimation and prediction.

5 Remarks

Disease prediction models are used to guide public health policy and patient care. A natural requirement for a prediction method in these application areas is that the predictions are well calibrated. We have shown that naive prediction procedures ignoring competing risks yield poorly-calibrated predictions, whereas our proposed methods yield well-calibrated predictions.

The classification and calibration performances of the competing risks marginalized and conditional methods are usually comparable. The MSEP of the marginalized approach is always smaller. The Pearson correlation between the risk predicted by the marginalized and the conditional methods is above 0.98. However, the conditional approach does not require any integration, which is a major advantage in handling a large number of competing risks or, more importantly, in extending the proposed methods to accommodate a flexible dependence structure among family members.

We presented a simple resampling-based confidence interval construction procedure. In the case of parametric baseline hazards λ_0gr, g = 0,1, r = 1,…,L, the proposed approach can be replaced by the delta method with numerical derivatives.

In some situations, for example, when the high-risk allele frequency is very low (e.g. 0.01), the predicted value of the frailty variate, W, tends to be substantially attenuated toward zero. Hence, in these cases, the competing risks conditional method based on (6) may underestimate the total number of events in the population. When this is a concern, Gorfine et al.’s (2013) technique of calibrating the risk prediction by considering Ŵ as a risk index can be easily adopted to correct the underestimation.

Appendix

Define the counting processes $\{N_{ij}^{(r)}(t),t\ge 0\}$ as $N_{ij}^{(r)}(t)={\delta }_{ij}I(T_{ij}\le t)I(J_{ij}=r)$, r = 1,…,L, and let Y_ij(t) = I(T_ij ≥ t) be the at-risk process of subject ij. In the setting with non-parametric baseline hazard functions depending on the carrier status g, the cumulative hazard for event type r under carrier status g is estimated by

$${\widehat{\mathrm{\Lambda }}}_{0gr}(t)={\int }_0^t\frac{{\sum }_{i=1}^N{\sum }_{i=1}^{n_i}I(G_{ij}=g)d{N}_{ij}^{(r)}(u)}{{\sum }_{i=1}^N{\sum }_{j=1}^{n_i}I(G_{ij}=g)Y_{ij}(u)\text{exp}\{{\widehat{\mathit{\beta }}}_r^T{\mathbf{Z}}_{ij}\}{\widehat{\mu }}_{ir}},$$

where μ̂_ir equals the posterior expectation of exp{W_ir} given the observed data and the current parameter values.