Deformable Image Registration of CT and Truncated Cone-beam CT for Adaptive Radiation Therapy

Abstract

Truncation of a cone-beam computed tomography (CBCT) image, mainly caused by the limited field of view (FOV) of CBCT imaging, poses challenges to the problem of deformable image registration (DIR) between CT and CBCT images in adaptive radiation therapy (ART). The missing information outside the CBCT FOV usually causes incorrect deformations when a conventional DIR algorithm is utilized, which may introduce significant errors in subsequent operations such as dose calculation. In this paper, based on the observation that the missing information in the CBCT image domain does exist in the projection image domain, we propose to solve this problem by developing a hybrid deformation/reconstruction algorithm. As opposed to deforming the CT image to match the truncated CBCT image, the CT image is deformed such that its projections match all the corresponding projection images for the CBCT image. An iterative forward-backward projection algorithm is developed. Six head-and-neck cancer patient cases are used to evaluate our algorithm, five with simulated truncation and one with real truncation. It is found that our method can accurately register the CT image to the truncated CBCT image and is robust against image truncation when the portion of the truncated image is less than 40% of the total image.

1. Introduction

Adaptive radiation therapy (ART) is a novel radiotherapy technology that adjusts a treatment plan to account for patient anatomical variations over a treatment course. In this process, deformable image registration (DIR) is a crucial step to establish the voxel correspondence between the current patient anatomy and a reference one (Gao et al., 2006; Paquin et al., 2009; Yang et al., 2009; Godley et al., 2009). The deformation vector fields (DVFs) generated by DIR algorithm can be used for many purposes, for instance, to deform the contours of the target and organs at risk from the planning computed tomography (CT) images to the daily cone-beam computed tomography (CBCT) images. Hence, the effectiveness and robustness of DIR algorithms has a great impact on the accuracy of treatment re-planning and the consequent treatments in ART.

One challenge for DIR between CT and CBCT images is the CBCT truncation problem, which is common in ART due to the following several reasons. Firstly, limited size of the detector of a CBCT yields a field of view (FOV) roughly 27cm (full fan) or 48cm (half fan) in diameter (Oelfke et al., 2006), which is much smaller than the FOV of a conventional helical CT scanner. Secondly, the patient is usually positioned such that the tumor centroid is near the isocenter of the linac. If the tumor is located far from the body center, part of the patient body may be outside the FOV. Thirdly, in order to reduce the imaging dose to a patient, it is sometimes preferable to further restrict the CBCT FOV to the volume of interest (VOI) that is sufficient for the positioning purpose, as recommended by AAPM Task Group 75 (Murphy et al., 2007). This can be achieved by collimating down the CBCT fan angle (Sheng et al., 2005; Oldham et al., 2005; Cho et al., 2009), leading to a truncation in the CBCT image.

One fundamental assumption of most DIR algorithms is that there should be one-toone correspondence for every voxel in the moving image and the static image. Some feature-based DIR methods (Lian et al., 2004; Schreibmann and Xing, 2006; Xie et al., 2008; Xie et al., 2009) might rely slightly on this assumption, however, it is a prerequisite for most of the intensity-based DIR algorithms. If this assumption is violated when truncation in CBCT exists, the intensity-based DIR algorithm cannot deliver correct results in the truncated region. This will also cause inaccuracy in the nearby area (Yang et al., 2010; Crum, 2004). Moreover, truncation also results in ‘bowl’ artifacts and Hounsfield Unit (HU) inaccuracy in the reconstructed CBCT image (Ruchala et al., 2002a; Seet et al., 2009). This further poses challenges to those DIR algorithms that are based on the assumption that corresponding voxels at the two images attain the same intensity, e.g. Demons (Thirion, 1998), leading to severely distortions in the deformed image after DIR (Nithiananthan et al., 2011; Hou et al., 2011; Zhen et al., 2012).

Some researchers have studied the DIR problem in the presence of truncation. Periaswamy et al (2006) incorporated an expectation maximization algorithm into the registration model to simultaneously segment and register image with partial or missing data. However, this algorithm is based on an affine transformation model, which might not be sufficient to describe complicated deformations between the two images. Yang et al (2010) proposed to assign those missing voxels outside of the FOV with NaN (not-a-number) value. Nonetheless, since the resulting DVFs on the NaN voxels are essentially obtained through a diffusion process from neighboring voxels containing valid intensity values, the result might not be sufficiently accurate. On the reconstruction side, efforts have also been made to retrieve the missing information outside of the FOV as much as possible (Ohnesorge et al., 2000; Ruchala et al., 2002b; Hsieh et al., 2004; Wiegert et al., 2005; Zamyatin and Nakanishi, 2007; Bruder et al., 2008; Kolditz et al., 2011). The validity of using images as such in the subsequent registration problem has not been investigated comprehensively.

In this paper, we propose to solve this problem from a different angle. As opposed to finding the DVFs that deforms a CT to match a truncated CBCT directly, we deform the CT image, such that the x-ray projections of the deformed image match the projection measurements of the CBCT. This idea is inspired by the works (Prümmer et al., 2006; Zikic et al., 2008; Bodensteiner et al., 2009; Groher et al., 2009; Marami et al., 2011) in the field of 2D/3D image registration for image guided surgical interventions, whose goal is to find the appropriate deformation field to register the 3D image (e.g. CT) and the 2D projection image (e.g. fluoroscopy image) by optimizing an objective function consisting of an image matching term and a regularization term of the DVFs. Similar objective function is also pursued for other applications such as 3D and 4D CBCT estimation. Ren et al (2012) proposed to deform the patient’s previous CBCT data to estimate a new CBCT volume by minimizing the deformation energy and maintaining new projection data fidelity using a nonlinear conjugate gradient method. Wang and Gu (2013) also estimated the DVFs by minimize the sum of the squared difference between the forward projection of the deformed planning CT and the measured 4D-CBCT projection to deform the planning CT as the high-quality 4D-CBCT image in lung cancer patients. Similarly, in this paper, we also formulate the estimation of DVFs to deform the CT image to match the measured CBCT projection with truncation as an unconstrained optimization problem. Instead of solving it directly using the gradient-type optimization method, in which optimal result may not be obtained for low-contrast or small-size object if zero initials are used (Wang and Gu, 2013), we rewrite the objective function and introduce auxiliary terms which make it easy to solve with a hybrid deformation/reconstruction scheme. It is found that our method is robust against image truncation and can effectively and accurately register CT image to the truncated CBCT image.

2. Methods and Materials

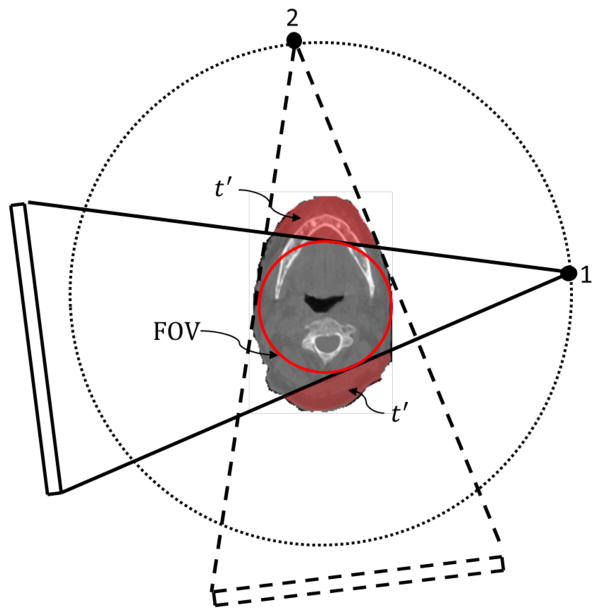
An illustration of CBCT truncation geometry is shown in Fig. 1. Although the patient volume is truncated in the CBCT image, the information outside the FOV may still exist in some projections. For instance, the volume t′ is not included in the projection 1 but is in the projection 2. Hence, we prefer to utilize all the information in the CBCT projection domain for DIR instead of merely the truncated CBCT image in the image domain. Specifically, we would like to compute the DVFs, such that when being applied to the CT image, the projections of the deformed CT image match the measured ones for the CBCT.

Figure 1.

Illustration of CBCT geometry with truncation. While part of the patient volume, t′, is truncated in projection 1, but as the gantry rotates, it is still included in other projections such as projection 2.

2.1 The truncation DIR model

Let us consider a patient volumetric image (CT image) represented by a function f(x), where x = (x, y, z) ∈ R³ is a vector in three-dimensional Euclidean space. In this paper, the CT image (termed as the moving image) is the one to be registered to a reference CBCT image (termed as the static image). A displacement mapping ν(x) is used to deform the CT image f₀(x) to the CBCT image: f(x) = f₀(x + ν(x)). We also define P as an x-ray projection matrix in cone beam geometry that maps f into the projection domain. As opposed to registering the CT image and the reconstructed CBCT image in the image domain directly, we attempt to estimate the displacement ν based on the CT image function f₀ and the measured CBCT projection g by minimizing the following energy function:

$$v=arg{min}_{v}E[v]=\frac{1}{2}{\Vert P{f}_0(x+v)-g\Vert }_2^2+\frac{\lambda }{2}{\Vert \nabla v\Vert }_2^2,$$ (1)

where ||·||₂ denotes l₂ norm of functions and ∇ is the gradient operator. In equation (1), the first term is a fidelity term, which ensures the consistency between the deformed CT image and the CBCT image in the projection domain. The second term is a regularization term with λ being a constant weight, and it is used to enforce the smoothness of the displacement field.

Let us consider the optimality condition of the problem:

$$\nabla f_0{P}^T[P{f}_0(x+v)-g]-\lambda \mathrm{\Delta }v=0,$$ (2)

where P^T denotes the transposition matrix of P, and Δ is the Laplacian operator. By introducing an auxiliary function s(x) and a term ∇f₀[f₀ − s], we can split equation (2) into

$$\nabla f_0{P}^T[P{f}_0(x+v)-g]-\nabla f_0[f_0(x+v)-s]=0,$$ (3)

$$\nabla f_0[f_0(x+v)-s]-\lambda \mathrm{\Delta }v=0.$$ (4)

We notice that equation (4) is essentially the Euler-Lagrange equation of a function $\epsilon (v)={\Vert f_0(x+v)-s\Vert }_2^2+\lambda {\Vert \nabla v\Vert }_2^2$, which is an energy function of the DIR problem between the moving image f₀(x) and the static image s (Lu et al., 2004). Assuming ∇f₀ ≠ 0, s can be obtained from equation (3) as

$$s=f_0(x+v)-P^T[P{f}_0(x+v)-g],$$ (5)

which is a typical gradient descent update step for a CBCT reconstruction problem.

This inspires us that the optimization problem of equation (1) can be solved by alternatively performing DIR and CBCT reconstruction update as in Eq. (5). The underlying interpretation of this approach is that s is an intermediate variable representing a CBCT volumetric image. It is updated during the iteration process based on the current deformed image f₀(x + ν). The moving image f₀ is then deformed via a DIR step to match this image, yielding the solution DVFs as well as an updated f₀(x + ν) to be used in the next iteration step.

In practice, these two steps are modified for the considerations of both resulting quality and convergence rate. Specifically, for the registration part, because of unavoidable contaminations in the projection measurement g, the updated intermediate image s contains reconstruction artifacts and its HU value is not consistent with that of f₀. Hence, the DISC (Zhen et al., 2012) algorithm is adopted as the DIR algorithm as opposed to conventional DIR algorithms based on intensity consistency, e.g. Demons (Thirion, 1998). DISC itself is an iterative algorithm with two steps alternatively performed. First, a linear transformation of voxel intensity is estimated at each voxel to unify the intensities of s and f₀. This is achieved by matching the first and the second moment of intensity distributions at a cubic area around a voxel. After that, a registration step is applied to estimate the DVFs based on the images with unified intensities. By iterating these two steps, the intensity of the CBCT is gradually corrected and the displacement field can be hence accurately calculated.

As for the step to compute s, we note that it corresponds to an typical gradient descent update step for a CBCT reconstruction problem based on an initial solution of f₀(x + ν). In practice, we substitute the backprojection operator P^T by a filtered backprojection operator F for CBCT reconstruction, e.g.

$$s=f_0(x+v)-F(P{f}_0(x+v)-g).$$ (6)

It has been demonstrated by Zeng et al. (2000) that the convergence speed of Eq. (6) is faster than that of Eq. (5) in terms of CBCT reconstruction.

2.2 Implementation

Our algorithm is implemented under the Compute Unified Device Architecture (CUDA) programming environment and GPU hardware platform. This platform enables parallel processing of the same operations on different CUDA threads simultaneously, which speeds up the performance of the entire algorithm. In the rest of this subsection, we will present a few practical issues pertaining to the algorithm implementation.

Algorithm A1.

Rigidly register the CT image to the reconstructed CBCT image with truncation

Initialize the moving vector ν to zero

Down-sample the CT image f0 and the CBCT projection g to the coarsest resolution

Repeat for each resolution level

while l(k−10) − l(k) ≤ ε, do

1. Compute the static image s based on Eq. (6)

2. Use the DISC algorithm to register f0(k) and s to obtain ν, and update f0(k+1) = f0(k)(x + ν).

Up-sample the moving vector ν to a finer resolution level

Until the finest resolution is reached

Before starting the algorithm, the CBCT image is first reconstructed using the conventional FDK algorithm (Feldkamp et al., 1984), and then a mutual information based rigid registration is performed between the CT image and the truncated CBCT image to align them to a satisfactory degree. The mutual information based rigid registration algorithm has been demonstrated to be effective in matching CT and truncated CBCT image (Ruchala et al., 2002a).

During each iteration of our algorithm, operations corresponding to the operators P and F are calculated repeatedly, as seen in the equation (6). For the operation P, it actually corresponds to the calculation of forward x-ray projection. This can be easily performed in parallel on GPU by making each thread responsible for one ray line using, e.g. Siddon’s ray tracing algorithm (Siddon, 1985). As for the latter one F, namely FDK CBCT reconstruction, we implemented it on GPU in the way as described previously (Sharp et al., 2007).

A multi-scale strategy is also adopted. This strategy helps to reduce the magnitude of the displacement vectors with respect to the voxel size and hence avoid the local minima problem in registration to a certain extent (Gu et al., 2010). It also improves efficiency by enhancing convergence speed and reducing number of variables. As such, the CT image is down-sampled in the image domain, while the CBCT projection images are down-sampled in the projection domain, both to a set of different resolution levels. The iteration starts with the lowest resolution images, and at the end of each level, the moving vectors are up-sampled to serve as the initial solution at the finer level. In this work, we consider two different resolution levels. Further down-sampling was found to be unnecessary to improve registration accuracy or efficiency.

For the stopping criteria regarding whether the moving image has been correctly deformed, we use a convergence criterion based on the difference between successive deformation fields. We define a relative norm l^(k) = Σ|dr^(k+1)|/Σ|r^(k)|, and use l^(k−10) − l^(k) ≤ ε, where ε = 1.0×10⁻⁴ as our stopping criterion. This measure is found to have a close correspondence with accuracy, as DIR is stopped when there is no ‘force’ to push voxels any more (Gu et al., 2010).

In summary, our algorithm is implemented as follows:

2.3 Clinical data and truncation simulation

The performance of our algorithm has been evaluated using clinical CT and CBCT data of six head-and-neck cancer patients. The truncations in the Cases 1~5 are simulated, while that in the Case 6 is a real. The benefit of simulating truncation with real clinical data is that the complete CBCT image can be used as the ground truth, as well as the impacts of different truncation levels on the performance of our algorithm can be evaluated.

For all the cases, each patient has a planning CT image acquired before treatment and a set of CBCT projection images acquired 2–8 weeks after the first fraction of treatment on a Varian On-board-Imaging (OBI) system (Varian Medical Systems, Inc., Palo Alto, CA) using a full-fan mode. For the planning CT images, the image resolution in the transverse plane is 512×512 and the pixel size in the transverse plane varies from 0.68 to 1.07 mm. The slice thickness is either 1.25 or 2.5 mm. For the CBCT projection images, the source to axes distance is 100 cm, while the source to detector distance is 150 cm. The detector size is 40×30 cm² with a resolution of 1024×768 pixels. The number of projections is 364 for Case 4 (with scan angle of about 198°), and is down-sampled from 656 to 328 for Case 1, 2, 3, 5, 6 (with scan angle of about 358°) for the consideration of computational efficiency. We also down-sample all projections to a resolution of 512×384 while maintain the area of the projection image. The CT images are resampled to yield voxel size and dimension of 1.02×1.02×1.99 mm³ and 256×256×88 for Cases 1–5, respectively, and 1.54×1.54× 2.98 mm³ and 256×256×62 for Case 6. The range of the planning CT in superior-inferior (SI) direction is generally larger than that of the CBCT. The planning CT image is therefore cropped and re-sampled to match the dimension and the resolution of the CBCT image after rigid registration. Hence, the image resolution for both the CT and the CBCT images after rigid registration are the same.

Truncation in CBCT image can be easily simulated by adjusting the sizes of the projection images. In this study, we simulate the truncation by cutting the projection images at the two sides symmetrically and keeping the middle portion. To evaluate the influence of different truncation levels on the DIR result, CBCT images with different percentage of truncation are reconstructed. We perform DIR between the CT image and the non-truncated CBCT image and the results are regarded as the ground truth in the simulation studies.

The percentage of truncation is quantified differently for two scenarios. At the truncation simulation stage, the percentage of truncation is defined as t₁ = 1 − r′/r, where r′ is the radius of the FOV corresponding to the truncated imager, while r is that corresponding to the original imager, as illustrated in Figure 2 left. We truncated the projection images so that t₁ increases from 10% to 80% with an increment step of 10%. However, the purpose of simulating truncation with different t₁ values is to find out how the truncation level to the patient volume would affect the DIR. Since for a given t₁ level, some part of the patient body could be well contained inside the FOV (see e.g. Figure 2 right), which is not affected by the truncation, it is necessary to have another metric to quantify the actual degree of truncation to the patient volume in the image domain. Therefore, we define the truncation percentage for each transverse CT slice, termed as t₂, as the ratio between the number of patient body voxels that are outside the FOV and the total number of patient body voxels in this slice. Note that t₂ could vary among slices even for the same t₁ value.

Figure 2.

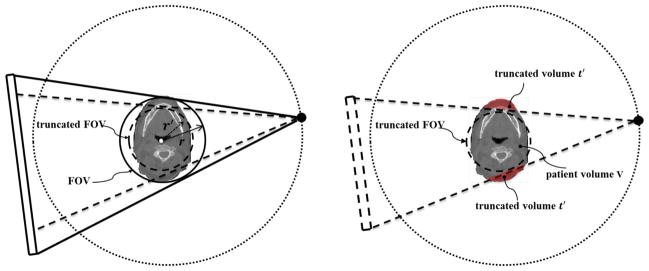
Definitions of the truncation percentages. Left: in the truncation simulation stage, the percentage of truncation is calculated by the ratio between the radius of the truncated FOV r′ and the radius of the non-truncated FOV r; Right: in the evaluation stage, for a given truncation level, the degree of truncation to the patient volume is calculated by the ratio between the truncated volume t′ and the entire patient volume V.

2.4 Quantification of registration performance

Since ultimately it is of clinical interest to deform the CT image to the CBCT, we therefore evaluate the registration accuracy by comparing the deformed CT image and the CBCT. Specifically, we use three similarity metrics to quantitatively evaluate the DIR results in this work. The first metric is the normalized mutual information (NMI), scoring from 0 to 1 with 1 representing the highest image similarity. The second metric is the feature similarity index (FSIM) (Zhang et al., 2011; Yan et al., 2012), which tries to simulate the mechanism of the human visual system by capturing the main image features such as the phase congruency of the local structure and the image gradient magnitude. The score of FSIM varies between 0 and 1 with 1 representing the most image similarity. The third metric is the root mean squared error (RMSE) between two edge images:

$${\text{RMSE}}_{\text{edge}}=\sqrt{{\sum }_i^N{({\mathit{I}}_1^{\mathit{edge}}(i)-{\mathit{I}}_2^{\mathit{edge}}(i))}^2/N},$$ (7)

where ${\mathit{I}}_1^{\mathit{edge}}(i)$ and ${\mathit{I}}_2^{\mathit{edge}}(i)$ are the binary Canny edge images of image I₁ and I₂, respectively (Canny, 1986), N is the number of voxel of image I₁ or I₂. When two images are perfectly registered, RMSE_edge should be zero. These three similarity metrics serve as quantitative evaluation tools in addition to the visual inspection of the registration results, namely comparing the deformed CT and the CBCT.

3. Results

For clarity, here we use the following symbols to represent different images used in the algorithm evaluation. CT_original is the CT image before DIR; proj_complete and proj_truncated are the CBCT projection images without and with truncations, respectively; ${\text{CBCT}}_{\text{original}}^{\text{complete}}$ and ${\text{CBCT}}_{\text{original}}^{\text{truncated}}$ are the non-truncated and the truncated CBCT images before DIR, respectively; ${\text{CT}}_{\text{deformed}}^{\text{demons}},{\text{CT}}_{\text{deformed}}^{\text{NaN}}$ and ${\text{CT}}_{\text{deformed}}^{\text{New}}$ are the deformed CT images using the original demons, the NaN method (Yang et al., 2010), and our new algorithm, respectively; ${\text{CT}}_{\text{deformed}}^{\text{groundtruth}}$ is the deformed CT image to the ${\text{CBCT}}_{\text{original}}^{\text{complete}}$ using the DISC algorithm.

3.1 Simulated truncation cases

Figure 3 shows an example (Case 5) of the simulation and the registration results. Figure 3(a) and 3(b) are the complete CBCT projections and the corresponding reconstructed CBCT image, respectively. Figure 3(c) and 3(d) are the truncated CBCT projection (t1=30%) and the corresponding reconstructed CBCT image with truncation. Note that the CBCT projection image is truncated symmetrically and the pixels in the truncated regions are set to zero. In order to alleviate artifacts in the reconstructed CBCT images, such as ‘bowl’ artifacts, smooth boundary condition at the boundary of truncation is imposed in our CBCT reconstruction algorithm. Therefore, the ‘bowl’ artifacts in ${\text{CBCT}}_{\text{original}}^{\text{truncated}}$ are not as severe as those reported in other literatures (Ruchala et al., 2002a; Ruchala et al., 2002b). Figure 3(e) is the CT image before DIR. Figure 3(f) is the deformed CT image using the original demons algorithm between the original CT and the truncated CBCT. As shown in Figure 3(f), tissues in the truncated region in the deformed CT image are distorted (as indicated by the arrow in Figure 3(f)) mainly caused by the loss of information and inaccurate HU value in this region (as indicated by the arrow in Figure 3(d)). The NaN method can mitigate this effect visually, as can be seen in Figure 3(g). However, since only those DVFs from the vicinity of the outside of the FOV can be propagated by smoothing, this method yields incorrect images outside the FOV and unrealistic artifacts near the edge of the FOV, as indicated by the arrow in Figure 3(g). On the contrary, our method can generate a much more accurate result, as shown in Figure 3(h).

Figure 3.

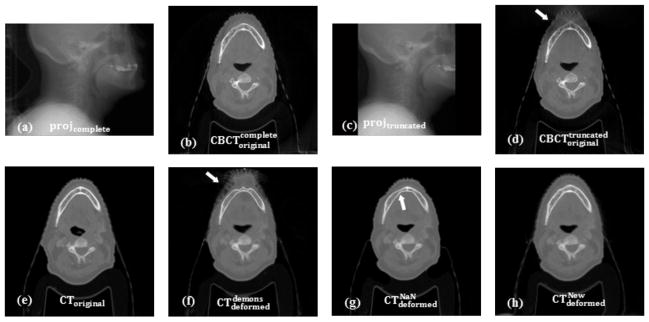
Truncation simulation and registration results (Case 5). (a)proj_complete: complete CBCT projection; (b) ${\text{CBCT}}_{\text{original}}^{\text{complete}}$: reconstructed CBCT image using complete projection; (c) proj_truncated: truncated CBCT projection; (d) ${\text{CBCT}}_{\text{original}}^{\text{truncated}}$: reconstructed CBCT image using truncated projection; (e)CT_original: CT image before DIR; (f) ${\text{CT}}_{\text{deformed}}^{\text{demons}}$: deformed CT image using demons; (g) ${\text{CT}}_{\text{deformed}}^{\text{NaN}}$: deformed CT image using NaN method; (h) ${\text{CT}}_{\text{deformed}}^{\text{New}}$: deformed CT image using our method. The arrows indicate regions that affected by truncation.

Figure 4 shows the results of checkerboard comparisons before and after DIR. The misalignment is evident between the CT image and the non-truncated CBCT image before DIR, as shown in Figure 4(a). The original demons algorithm and the NaN method perform quite well while registering those structures inside of the FOV, but both fail in regions near, and especially outside the FOV (Figure 4(b) and Figure 4(c)). Our method, on the contrary, can produce a more accurate registration result even outside of the FOV, which can be clearly seen in the zoomed-in views of the transverse and sagittal images in Figure 4(d)-2 and Figure 4(d)-4. In the other four simulated cases, we observed similar results.

Figure 4.

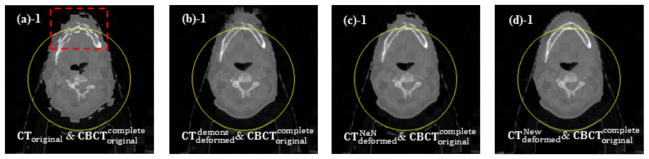
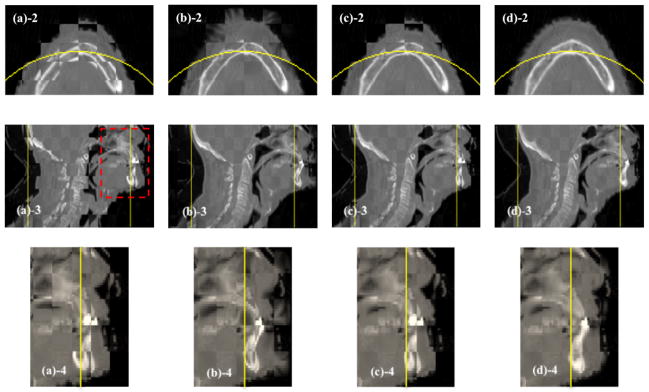
Checkerboard comparisons of the DIR results (Case 5). Columns: (a) ${\text{CT}}_{\text{original}}\&\mathit{CBC}{T}_{\text{original}}^{\text{complete}}$; (b) ${\text{CT}}_{\text{deformed}}^{\text{demons}}\&\mathit{CBC}{T}_{\text{original}}^{\text{complete}}$; (c) ${\text{CT}}_{\text{deformed}}^{\text{NaN}}\&\mathit{CBC}{T}_{\text{original}}^{\text{complete}}$; (d) ${\text{CT}}_{\text{deformed}}^{\text{New}}\&\mathit{CBC}{T}_{\text{original}}^{\text{complete}}$. Rows: (a)-1 ~ (d)-1: transverse images; (a)-2 ~ (d)-2: zoomed-in views of the transverse images; (a)-3 ~ (d)-3: sagittal images; (a)-4 ~ (d)-4: zoomed-in views of the sagittal images. Circles in (a)-1 ~ (d)-1 and lines in (a)-3 ~ (d)-3 indicate the FOV after truncation, and the dashed rectangles indicate the regions to be zoomed in.

3.2 Effect of truncation percentage on DIR

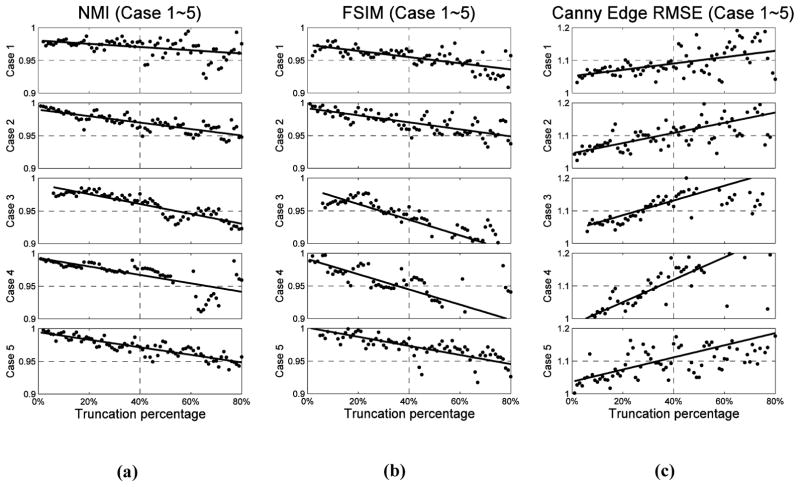
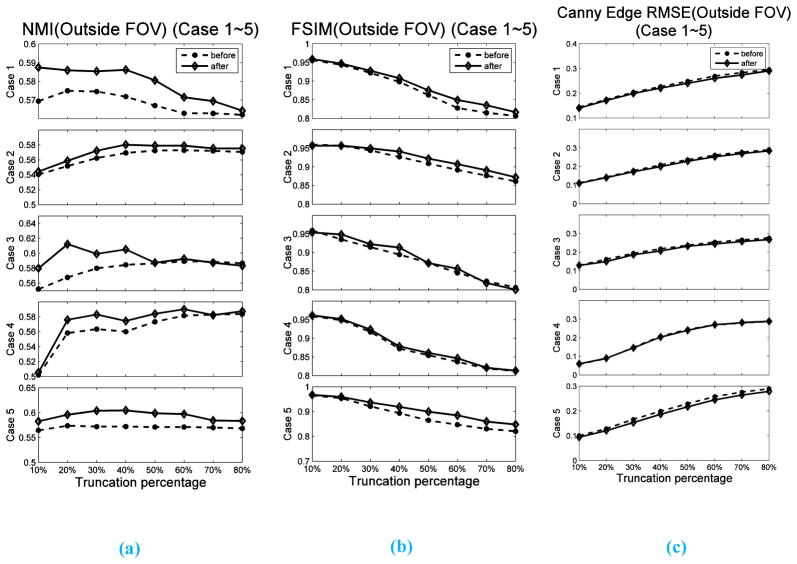
It is also of interest to find out how the truncation percentage t₂ would affect the DIR results. Hence, we calculate the similarities between ${\text{CT}}_{\text{deformed}}^{\text{New}}$ and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$ slice by slice for all the five cases using metrics NMI, FSIM and RMSE of Canny edge image, as described in Section 2.4, and normalize them by the corresponding similarity quantities for the case between ${\text{CT}}_{\text{deformed}}^{\text{groundtruth}}$ and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$ (the ground truth similarity). The dependence of these quantities on the truncation levels t₂ for different simulation cases are depicted in Figure 5. Note that all the similarity values plotted in Figure 5 are the normalized ones, with 1 representing the closest to the ground truth similarity. We can see that for all three similarity metrics and for all the five cases, the relative similarity changes monotonically as the percentage of truncation is increased, indicating decreased registration quality. The solid lines are the linear fitting results to show the trend of the points. This reduction of relative similarity is less than 10% for NMI and FSIM and the increasing is less than 20% for RMSE of Canny edge image, when the truncation level increases up to 80%. Visual inspection informs us that a good DIR result, in general, corresponds to those cases when reduction of relative similarity of NMI and FSIM is less that 5%, or the increase of RMSE of Canny edge image is less than 10%. We observe that when the truncation is less than 40%, the relative similarity is above 0.95 for NMI and FSIM, and below 1.1 for RMSE of Canny edge image. These numbers reveal that our method is very robust against truncation, especially when the truncation percentage is lower than 40%. In order to evaluate the effects of the truncation percentage t₂ on the estimation accuracy of DVFs out of FOV, we also calculated the above-mentioned three similarity metrics only in the region outside FOV before DIR (between CT_original and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$) and after DIR (between ${\text{CT}}_{\text{deformed}}^{\text{New}}$ and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$). The corresponding results for the five cases are shown in Figure 6. We can see that both NMI and FSIM have increased, and RMSE of Canny Edge has decreased after DIR for all five cases. This reveals that our algorithm is also effective in estimating the DVFs out of FOV.

Figure 5.

Similarity scores of each transverse slice at different levels of truncation. The similarity score is calculated between ${\text{CT}}_{\text{deformed}}^{\text{New}}$ and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$, and normalized to the similarity score between ${\text{CT}}_{\text{deformed}}^{\text{groundtruth}}$ and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$. (a), (b) and (c) are results of NMI, FSIM and RMSE of Canny edge image, respectively. The solid lines are the linear fitting curves of the points, and five rows correspond to Case 1 to Case 5, respectively.

Figure 6.

Similarity scores calculated in the region out of FOV at different levels of truncation. The similarity scores are calculated between CT_original and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$ before DIR and between ${\text{CT}}_{\text{deformed}}^{\text{New}}$ and ${\text{CBCT}}_{\text{original}}^{\text{complete}}$ after DIR. (a), (b) and (c) are results of NMI, FSIM and RMSE of Canny edge image, respectively.

3.3 A real truncation case

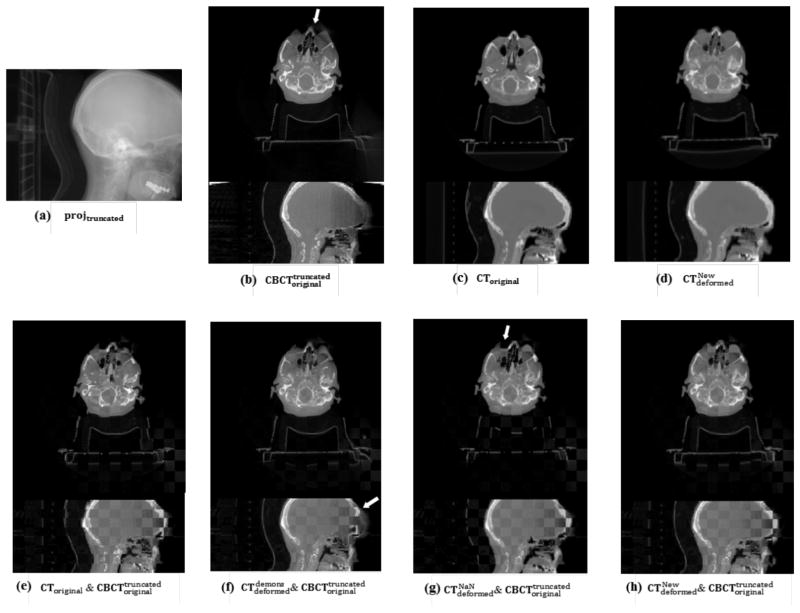
The DIR result of a real truncation case of the head-and-neck cancer patient is shown in Figure 7. As we can see in Figure 7(a), some volume of the patient’s head is truncated in the CBCT projection image. Reconstruction of the truncated projection leads to artifacts and inaccurate HU values near and outside the FOV in the CBCT image, as indicated by the arrow in Figure 7(b). However, these artifacts do not affect the DIR in the registered CT image using our method, as shown in Figure 7(d). Checkerboard comparisons in Figure 7(e) show the evident misalignment between the CT and the CBCT images before DIR. Demons algorithm can align those structures inside the FOV, however, the skull (as indicated by the arrow in Figure 7(f)) near the FOV has been distorted severely due to the artifacts caused by truncation. The NaN method also fails in matching those regions outside the FOV, as shown in Figure 7(g). On contrast, our algorithm can successfully register the two images (Figure 7(h)). Here, we want to point out that, because of the absence of a non-truncated CBCT image as the ground truth in this case, it is difficult to quantitatively evaluate the performance of our DIR algorithm on those regions near and outside of the FOV.

Figure 7.

DIR results for a real truncated head-and-neck cancer patient case. (a) CBCT projection with truncation; (b)~(d) transverse and sagittal view of ${\text{CBCT}}_{\text{original}}^{\text{truncated}}$, CT_original and ${\text{CT}}_{\text{deformed}}^{\text{New}}$; (e)~(h) checkerboard image of the transverse and sagittal view of CT_original and ${\text{CBCT}}_{\text{original}}^{\text{truncated}},{\text{CT}}_{\text{deformed}}^{\text{demons}}$ and ${\text{CBCT}}_{\text{original}}^{\text{truncated}},{\text{CT}}_{\text{deformed}}^{\text{NaN}}$ and ${\text{CBCT}}_{\text{original}}^{\text{truncated}},{\text{CT}}_{\text{deformed}}^{\text{New}}$ and ${\text{CBCT}}_{\text{original}}^{\text{truncated}}$. The arrow indicates the region affected by truncation.

4. Discussion and Conclusions

In summary, we have successfully developed an algorithm and implemented it on a GPU architecture under NVIDIA CUDA platform for the DIR between a CT image and a CBCT image with truncation. As opposed to finding the DVFs that deforms a CT to match a truncated CBCT directly, we deform the CT image, such that the x-ray projections of the deformed image match the projection measurements of the CBCT. Specifically, we try to solve this DIR problem by minimizing an energy function, as shown is equation (1). A two-step algorithm is invented to solve the problem. In this process, the image information is borrowed from the CBCT projections at each iteration to compensate those missing image contents outside the CBCT FOV, and form an intermediate image as the static image. A DISC algorithm is then employed to register CT and this intermediate image. As the DIR proceeds, the CT image can gradually deform to match the non-truncated CBCT image. Results of five simulated truncation cases and one real clinical truncation case show that our algorithm can robustly and accurately register the CT image and the truncated CBCT image.

In fact, equation (1) can be solved directly by using some optimization strategies, e.g. gradient-type optimization. However, because of the highly non-convex nature of this problem, the solution quality may be impacted by local minima. It is hence necessary to employ some techniques to avoid this issue. As pointed out in the work (Wang and Gu, 2013), estimation of the DVFs is very sensitive to the initial values, and therefore DVFs obtained from demons registration of the CT image and a CBCT image reconstructed by total variation minimization is utilized as initials instead of the zero initials in the optimization process. However, in our application, such initial DVFs are usually difficult to obtain, because if CT is registered to the truncated CBCT image directly, DVFs that calculated in the region near and out of FOV is far from the true ones. Using such DVFs as initials may deteriorate instead of facilitating the optimization process. It is mainly for this reason that we designed a two-step algorithm. As for substituting the backprojection operator P^T by a filtered backprojection operator for CBCT reconstruction, it is motivated by the so-called iterative-FBP algorithm. In CBCT reconstruction problem, it was observed that such a scheme can increase the rate of convergence (Xu et al., 1993; Lalush and Tsui, 1994; Zeng and Gullberg, 2000; Sunnegardh and Danielsson, 2008), which is also observed in our studies.

The key reason for the success of this algorithm is the introduction of the intermediate variable s, which is also the feature that distinguishes our algorithm from other DIR algorithms that work on image domains directly. Specifically, at any iteration step, the intermediate variable s is computed according to equation (6), which can be interpreted as a temporary target CBCT image for registration. Such an image is obtained via a typical iterative CBCT reconstruction step using the current deformed CT image as an initial guess. Because there is no truncation in the CT image, the term Pf₀(x + ν) − g in (6) is relatively small, and hence the resulting variable s does not have much truncation-caused artifacts. The relatively good quality of s facilitates the registration process to a satisfactory extent. Note that the variable s is actually updated at each iteration. It serves as a guide that gradually leads the deformation of the CT image towards the CBCT image. When the CT image is fully deformed to the CBCT image, the term Pf₀(x + ν) − g vanishes and further iteration will not change s any more, namely, the DIR process converges.

However, the intermediate image s not only has intensity inconsistency with the CT image, but also contains lots of reconstruction artifacts. Therefore, we adopt the DISC algorithm as opposed to conventional DIR algorithm based on intensity consistency for the calculation of the displacement field at each iteration step. Here, we would like to point out that other CT-CBCT DIR algorithms, such as the works by Hou et al. (2011) and Nithiananthan et al. (2011) which are capable of handling intensity inconsistency, may potentially be used here as well. Further investigations of the overall gains of using other DIR models other than DISC are needed.