An efficient algorithm coupled with synthetic minority over-sampling technique to classify imbalanced PubChem BioAssay data

Abstract

It is common that imbalanced datasets are often generated from high-throughput screening (HTS). For a given dataset without taking into account the imbalanced nature, most classification methods tend to produce high predictive accuracy for the majority class, but significantly poor performance for the minority class. In this work, an efficient algorithm, GLMBoost, coupled with Synthetic Minority Over-sampling TEchnique (SMOTE) is developed and utilized to overcome the problem for several imbalanced datasets from PubChem BioAssay. By applying the proposed combinatorial method, those data of rare samples (active compounds), for which usually poor results are generated, can be detected apparently with high balanced accuracy (Gmean). As a comparison with GLMBoost, Random Forest (RF) combined with SMOTE is also adopted to classify the same datasets. Our results show that the former (GLMBoost + SMOTE) not only exhibits higher performance as measured by percentage correct classification for the rare samples (Sensitivity) and Gmean, but also demonstrates greater computational efficiency than the latter (RF + SMOTE). Therefore, we hope that the proposed combinatorial algorithm based on GLMBoost and SMOTE could be extensively used to tackle the imbalanced classification problem.

1. Introduction

PubChem [1], consisted of three related databases of Compound, Substance and BioAssay, is a public repository of chemical structures and their activity. It is developed and maintained by the National Center for Biotechnology Information (NCBI). The purpose of PubChem is to collect and disseminate information on the biological activity of small molecules and make them easily accessible to biomedical community. Currently, the PubChem BioAssay database contains an increasing amount of experimental data often generated by high-throughput screening (HTS), making it an invaluable resource for researchers capturing knowledge by using data mining related techniques [2–6]. Xie et al. developed a chemoinformatics approach using the HTS bioassay data in PubChem for constructing the representative and structure-diverse library [7]; Guha et al. [8] utilized HTS data to build predictive toxicology models with the purpose of distinguishing the false-positives among HTS hits; Chen and Wild [9] built naïve Bayesian predictive models based on the HTS data and successfully applied these models for virtual screening.

However, mining PubChem BioAssay resources is often hampered by the imbalanced nature of HTS data, which usually contains from a handful to a few hundreds of hits (active compounds) but many folds of inactive compounds. Existing classification models such as decision tree (DT), neural network (NN), support vector machine (SVM) and k-nearest neighbor (KNN) are constructed on an adequate, representative and relatively balanced set of training data to draw an estimated decision boundary amongst different classes. These learning algorithms have been developed and applied to many fields including financial forecasting [10], text classification [11] and many others [12, 13]. Despite recent progress in machine learning, constructing efficient algorithms that learn from imbalanced datasets remains a challenging task.

To cope with imbalanced datasets, many studies have been conducted to improve traditional learning algorithms, which basically involve approaches both at the algorithmic level, such as cost-sensitive learning and ensemble learning approaches, and at the data processing level, such as re-sampling methods [14]. The former approach mainly focuses on improving the algorithms themselves, which may, to some extent, hinder the extensive applications by researchers not specialized in statistics or related areas. On the contrary, the latter is more amenable for non-statistician to approach, which basically involves two straightforward steps: (1) balancing the original imbalanced dataset and (2) performing the traditional statistical approaches on the balanced dataset. In fact, the previous report from Breiman has shown that prediction accuracy of an algorithm can be improved using the pseudo-data on a variety of data sets [15]. In this work, we aim at enhancing the data processing procedure for the classification task on imbalanced datasets.

The key idea of re-sampling is to preprocess the training data to minimize discrepancy between class samples. In other words, the re-sampling method is employed to modify the prior distributions of the majority and minority class samples in the training set to obtain a more balanced number of samples in each class. The conventional re-sampling technique includes two basic methods, namely under-sampling and over-sampling [16].

Under-sampling extracts a smaller set of majority samples while preserving all the minority samples. The prevalent class samples are randomly removed until a balanced ratio between all classes is reached. Under-sampling is suitable for such applications where the number of majority samples is immense and decreasing the training samples will reduce the model training time. However, a drawback with under-sampling that discards samples leads to the loss of information for the majority class [17].

Over-sampling is another approach to deal with the imbalanced data. It increases the number of minority class samples by replicating them [18]. The advantage is that no information is lost since all samples are employed. However, over-sampling also has its own limitation. By creating additional training samples, over-sampling leads to a higher computational cost. Thus, more efficient algorithms are required to compensate this limitation.

Although re-sampling methods are widely used for tackling class imbalance problems, there is little established strategy to determine the suitable class distribution for a given dataset [19]. As a result, the optimal class distribution varies from one dataset to another. Recent variants of re-sampling methods derived from over-sampling and under-sampling overcome some of the weaknesses of the existing technologies, among which, one popular over-sampling approach is SMOTE (Synthetic Minority Over-sampling TEchniques), which adds information to the training set by introducing new, no-replicated minority class samples [20]. Unlike the traditional over-sampling method, SMOTE over-samples the minority class by creating synthetic examples rather than by over-sampling with replacement. The SMOTE algorithm introduces synthetic examples along the line segments joining the k minority class nearest neighbors, which can be set by user. An important feature for SMOTE is that the synthetic samples lead to the classifier to build larger decision regions that contain nearby minority class points, which is desired effect to most classifiers, while with replication, the decision region that results in a classification decision for the minority class becomes smaller and more specific, making this approach prone to overfitting. More details on SMOTE are described in the work by Chawla et al. [20]. It has shown that SMOTE potentially performs better than simple over-sampling and has been successfully applied in many fields. For example, SMOTE was used for human miRNA gene prediction [21] and for identifying the binding specificity of regulatory proteins from chromatin immunoprecipitation data [22]. SMOTE was also utilized for sentence boundary detection in speech [23] and so forth. In the light of this, we also determine to adopt SMOTE as the final re-sampling method for the currently studied imbalanced datasets.

Classification for imbalanced data in PubChem represents a difficult problem, while selection of statistical methods and re-sampling techniques may be dependent on the studied system. For the PubChem BioAssay data, several methods have been illustrated in the recent publications. For example, the report from our previous study [24] suggested that the granular support vector machines repetitive under sampling method (GSVM-RU) was a novel method for mining highly imbalanced HTS data in PubChem, where the best model recognized the active and inactive compounds at the accuracy of 86.60% and 88.89% respectively, with a total accuracy of 87.74% by cross-validation test and blind test. Guha et al. [8] constructed Random Forest (RF) ensemble models to classify the cell proliferation datasets in PubChem, producing classification rate on the prediction sets in a range between 70% to 85% depending on the nature of datasets and descriptors employed. Chang et al. [17] applied the over-sampling technique to explore the relationship between dataset composition, molecular descriptor and predictive modeling method, concluding that SVM models constructed from over-sampled dataset exhibited better predictive ability for the training and external test sets compared to previous results in the literature. Though several proposed methods have successfully countered the imbalanced datasets in PubChem, however, many of the previous works were time consuming in calculation and little work explored the problem of enhancement in the computational efficiency in addition to the statistical performance, which in turn should be largely addressed in the era of big data. Especially, with the advent of ‘omics’ technologies, both researcher and government funding agencies are increasingly paying attention to the large-scale data analysis which is highly demanding in computational power.

Recent studies [25, 26] have reported that the functional gradient descent algorithm utilizing component-wise least squares to fit generalized linear model (referred to GLMBoost in this work) was computationally attractive for high dimensional problems. The work from Hothorn and Bühlmann [25] showed that fitting the GLMBoost model including 7129 gene expression levels in 49 breast cancer tumor samples just took ~3s on a simple desktop. Besides the high computational efficiency, GLMBoost also exhibits other advantages [27, 28]: (1) it is easy to implement, works well without fine tuning for the hyper parameter (m_stop) and no sophisticated nonlinear optimization is necessary; (2) it can be used for ‘large p, small n’ paradigm, since variable selection is carried out during the fitting process; (3) it enjoys a computational simplicity and analytical tractability; and (4) it is an ensemble algorithm with high competitive prediction accuracy.

Although GLMBoost possesses these advantages, it has just been applied to a limited research field [25] and there is still no record of developing computational models for small molecular compounds, especially for the situation that the studied datasets are imbalanced. Therefore, to extend the range of application, a SMOTE coupled with GLMBoost method is proposed in this work to classify several imbalanced datasets from PubChem BioAssay with the aims to: (1) validate whether SMOTE has an impact on the performance of developed models; (2) explore whether the GLMBoost algorithm is suitable and efficient to identify the interesting samples from large-size datasets. Additionally, for comparing with GLMBoost, the state-of-the-art statistical method, Random Forest, is also employed to classify the same datasets.

2. Material and experimental methods

2.1. Computational data

AID 540252 (Data source: Burnham Center for Chemical Genomics (SBCCG-A664-pfG6PDH-OE-DR-Assay)): The aim of the project is to find chemical probes that inhibit Plasmodium G6PD activity that might lead to novel anti-malarial therapies (accession date: 5/28/2013). The original bioassay dataset included 586 unique compounds. After removing 40 mixtures, a set of 546 compounds including 111 active compounds and 435 inactive ones was left in this work to construct classification models.

AID 652128 (Data source: Broad Institute (7018-02_Inhibitor_Dose_CherryPick_Activity)): The goal of this project is to develop specific small-molecule inhibitors of human RAD52, one of the key homologous recombination proteins (accession date: 5/28/2013). This bioassay dataset consisted of 998 unique compounds classifying three categories: 85 active compounds, 887 inactive compounds and 36 inconclusive compounds. Since we mainly considered the current work as a binary classification problem, 36 inconclusive ones were first removed. In the next step, 366 mixtures were removed. Finally, 596 compounds were left in this work to construct classification models, where active and inactive molecules were 40 and 556, respectively.

AID 687000 (Data source: Broad Institute (2162-01_Inhibitor_Dose_CherryPick_Activity)): This assay is to detect molecules that directly kill Cryptococcus yeast cells through the detection of adenylate kinase released into the growth medium by cells that have undergone lysis (accession date: 5/28/2013). Originally, this bioassay tested 1024 compounds. Among them, there were 72 active molecules, 938 inactive compounds and 20 inconclusive ones. Likewise, due to the two-class classification, 20 inconclusive compounds were first removed from this work. Then, 19 mixtures were removed. As a result, 986 unique compounds, including 70 active compounds and 916 inactive compounds, were considered as the final dataset in this work to construct classification models. For each of the three imbalanced datasets, the diversity was calculated according to Perez’s report [29] based on the 881 PubChem fingerprints (PCFP) discussed in the following section, resulting in 0.553, 0.502 and 0.457, for AID 540252, AID 652128 and AID 687000, respectively, which suggests that all the three original datasets possess moderate diversity. Table 1 lists all three datasets, along with some pertinent statistics: the number of active (positive) and inactive (negative) compounds as well as their ratios. The detailed information for them can be found in the supplementary files.

Table 1.

Summary of the datasets used in the work.

Data set	Active	Inactive	Ratio
AID 540252	111	435	~1:4
AID 652128	40	556	~1:14
AID 687000	70	916	~1:13

2.2. Descriptor calculation

PaDEL [30], an open source molecular descriptor calculation software with the high speed characteristic and simple operation, was chosen for the current work, where 729 PaDEL molecular descriptors were calculated from two-dimensional structures of molecules, which requires no specific orientation or through-space distances and thus alleviates the need for geometry optimization of the structures [31]. Herein, in the process of descriptor calculation, all parameters were adopted by default in PaDEL unless otherwise indicated. In addition to PaDEL descriptors, 881 extensively exploited PubChem fingerprints [32–34] were also calculated for the comparison of model performance derived from PaDEL descriptors. The definitions and explanations about these descriptors and fingerprints can be referred to numerous publications [30, 35].

2.3. Computational details

The SMOTE algorithm [20, 36] was used to balance the original imbalanced datasets, guaranteeing that the number of the minority class samples was as close to that of the majority class samples as possible. The DMwR package (access date: 5/28/2013) in R 3.0.1 [37] was used to implement the SMOTE computation.

After obtaining the balanced datasets, we first adopted the GLMBoost algorithm [28, 38], embedded in the caret package (access date: 5/28/2013) [39] as a classification method, to distinguish the current datasets. For comparison, the state-of-the art RF algorithm [40] was also employed to differentiate the same datasets. Here, the RF models were constructed and validated using the same caret package.

All statistical calculations were performed using R 3.0.1 [37] on 64-bit Windows 7 Enterprise (Intel 3.16 GHz E8500 Duo Core processor and 4.00 GB RAM).

2.4. Statistical metrics

To assess the predictive ability of constructed models, three statistical evaluation methods were employed and they are defined as follows:

1. Sensitivity: the percentage of positive samples which are correctly classified;

   $$\text{Sensitivity}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$$ (1)

Where true positives (TP) denote the correct classifications of positive samples (i.e., active compounds in this work); true negatives (TN) denote the correct classifications of negative samples (i.e., inactive compounds); false positives (FP) denote the incorrect classifications of negative samples into the positive samples; and false negatives (FN) denote the positive samples incorrectly classified into the negative samples.

• (2)
  Specificity: the percentage of negative samples which are correctly classified;

  $$\text{Specificity}=\frac{\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}}$$ (2)
• (3)
  Gmean: It provides a simple way to evaluate the model’s ability to correctly classify the active and inactive compounds by the combination of Sensitivity and Specificity into a single metric. Gmean is considered as a measure of the balanced accuracy and is defined as:

  $$\text{Gmean}=\sqrt{\text{Sensitivity}*\text{Specificity}}$$ (3)

3. Results and discussion

3.1. Descriptor preprocessing

It has been reported that those uninformed descriptors, which may cause the model to fail [39], should be removed before training a model [12, 41]. In this work, both PaDEL descriptors and PubChem fingerprints were preprocessed in the same procedure as follows: (1) zero- and near zero-variance predictors were deleted; (2) descriptors containing larger than 85% zero values were removed; and (3) If two descriptors had absolute correlations above 0.95, one of them was omitted. After these procedures, there were 231, 213, and 213 PaDEL descriptors to be retained for AID 540252, AID 652128 and AID 687000, respectively; while 162, 148 and 117 PubChem fingerprints descriptors were retained for the respective AID.

3.2. Split of training and test sets

For the current datasets, the leave-some-out (LSO) method was used to create a random partition for holdout validation on observations. This partition divides the observations into a training set and a test set (also called a holdout set). Specifically, for all three PubChem BioAssay datasets, both one-fourth active and inactive compounds were randomly selected from the whole dataset as the test set, respectively, and the remaining ones as the training set. The training set was used to construct models under the situations without SMOTE (denoted as noSMOTE) and SMOTE, and the test set was used to validate the real performance of developed models. To achieve a statistically unbiased estimation of the predictive performance, the LSO process was repeated 200 times. Then, the mean values ± standard deviations of Sensitivity, Specificity and Gmean for the developed models were calculated and reported for the test set.

3.3. Results of SMOTE setup

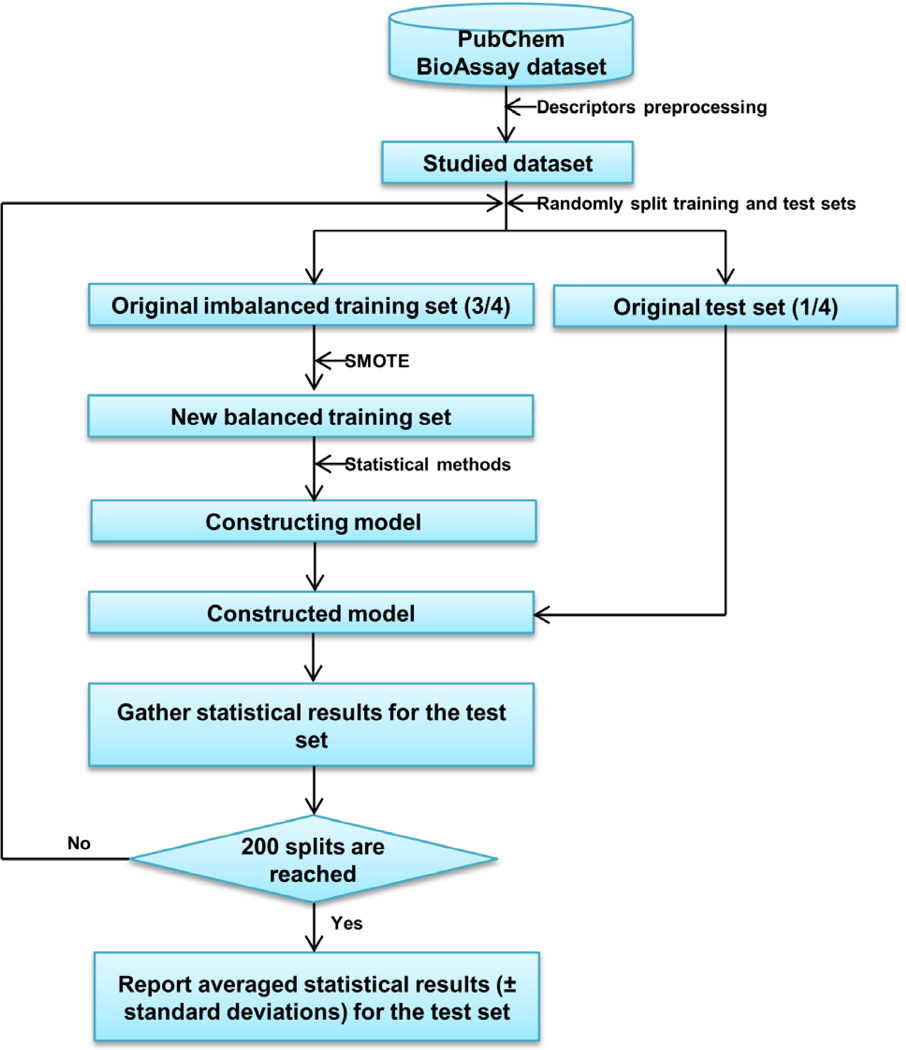
The R package DMwR was used to perform the SMOTE operation and detail of the algorithm was described in previous work [20, 36]. Briefly, SMOTE over-samples the minority class by taking each minority class sample and introducing synthetic examples along the line segments joining any or all of the k minority class nearest neighbors [20]. Depending upon the amount of over-sampling required, synthetic examples from the k-nearest neighbors are randomly chosen. Herein, three parameters, k nearest neighbor, percentage of over-sampling (perc.over), and percentage of under-sampling (perc.under) implemented in the DMwR package generally need to be set. In the present work, perc.over and perc.under were set to guarantee that, after being processed by SMOTE, the number of minority samples (active compounds) should be as close to the number of majority samples (inactive compounds) as possible. It should be pointed out that all SMOTE operations were based on the training sets only. As a result, the final ratio of perc.over:perc.under for AID 54025 was set to 300:130, leading to the new ratio between active and inactive compounds of 336:327 compared to the original ratio, 84:327. Likewise, for AID 652128 and AID 687000, the final ratios of perc.over:perc.under were set to 1300:107 (new ratio between active and inactive: 420:417 versus 30:417 in the original set), and 1200:108 (new ratio between active and inactive: 689:686 versus 53:687 in the original set), respectively. In all SMOTE calculations, k value was set to 5. Table 2 summarizes the results of the SMOTE set. Figure 1 describes the proposed combinatorial approach between SMOTE and GLMBoost (or RF), where one can notice that it is very flexible to combine SMOTE with the corresponding statistical methods. It should also be pointed out that for both GLMBoost and RF, a 10-fold cross-validation method, in the process of constructing models, was used to determine the optimal parameter. For GLMBoost, a list of default m_stop values including 50, 100 and 150 given in the caret package were used; while for the RF algorithm, only the default m_try value, the square root of the number of used descriptors, was used to construct the classification models, since previous work has illustrated that RF can perform well even when used “off-the-shelf” [42]. As shown in Figure 1, due to its simplicity and generality, the proposed combinatorial method may be useful for those non-statistical experts to employ for classifying imbalanced data.

Table 2.

Results of datasets processed by SMOTE.

Data set	Original training set		Training set after SMOTE
	Active	Inactive	Active	Inactive
AID 540252	84	327	336	327
AID 652128	30	417	420	417
AID 687000	53	687	689	686

Figure 1.

Flow chart for the proposed combinatorial algorithm with SMOTE and statistical methods for imbalanced data.

3.4. Statistical performance of GLMBoost combined with SMOTE

For validating the influence of SMOTE on the GLMBoost algorithm, it is interesting to compare the performance for GLMBoost with and without SMOTE. However, selecting objective statistical metrics to estimate the performance for different classifiers is not always straightforward, and how to tackle the evaluation problem is still a current topic for investigation [43, 44]. Indeed, for the imbalanced classification problem, the overall classification accuracy is often not an appropriate measure of performance given that a trivial classifier that predicts every sample as the majority class could achieve very high accuracy in extremely skewed domains. In the present work, instead of the complicated metrics, three intuitive and practical measures (Sensitivity, Specificity and Gmean) were adopted to estimate the current classifiers based on the following reasons: first, both Sensitivity and Specificity provide a class-by-class performance estimate, making one easily investigate the predictive ability of a classification method for each sample class, especially the predictive ability for the interesting but minority class (i.e. active compounds in this work); second, Gmean is a combination of both Sensitivity and Specificity, which indicates the balance between classification performance on the majority and minority class. A poor performance in prediction of the positive (interesting) samples still leads to a low Gmean value, even if the negative samples are classified with high accuracy, which is a common case for imbalanced dataset.

It is highly recommended that the external prediction be used to establish a reliable prediction model [45]. Therefore, the reported results in this work are all based on the test sets only. Mean results (± standard deviations) of 200 replications for the test sets, which were never used to construct the models, are reported in Tables 3 and 4.

Table 3.

Comparison of mean statistical results ± standard deviations for the test set based on 200 predictions for GLMBoost with (SMOTE) and without SMOTE (noSMOTE) preprocessing using PaDEL descriptors.

Dataset	noSMOTE/SMOTE	Sensitivity	Specificity	Gmean	Computational time (minutes)
AID 540252	noSMOTE	0.442 ±0.099	0.948 ± 0.023	0.643 ± 0.074	8.538
	SMOTE	0.772 ± 0.081	0.807 ± 0.042	0.788 ± 0.043	10.745
AID 652128	noSMOTE	0.004 ± 0.022	0.997 ± 0.004	0.012 ± 0.062	7.859
	SMOTE	0.766 ± 0.138	0.872 ± 0.033	0.813 ± 0.074	11.873
AID 687000	noSMOTE	0.412 ± 0.119	0.981 ± 0.012	0.629 ± 0.092	10.189
	SMOTE	0.812 ± 0.082	0.909 ± 0.029	0.858 ± 0.047	16.585

Table 4.

Comparison of mean statistical results ± standard deviations for the test set based on 200 predictions for GLMBoost with (SMOTE) and without SMOTE (noSMOTE) preprocessing using PubChem fingerprints (PCFP).

Dataset	noSMOTE/SMOTE	Sensitivity	Specificity	Gmean	Computational time (minutes)
AID 540252	noSMOTE	0.404 ± 0.105	0.957 ± 0.024	0.616 ± 0.082	7.308
	SMOTE	0.794 ± 0.079	0.777 ± 0.046	0.784 ± 0.041	9.502
AID 652128	noSMOTE	0 ± 0	1 ± 0	0 ± 0	6.754
	SMOTE	0.658 ± 0.148	0.843 ± 0.038	0.739 ± 0.085	9.923
AID 687000	noSMOTE	0.455 ± 0.123	0.978 ± 0.013	0.660 ± 0.092	8.101
	SMOTE	0.836 ± 0.080	0.877 ± 0.045	0.855 ± 0.047	12.233

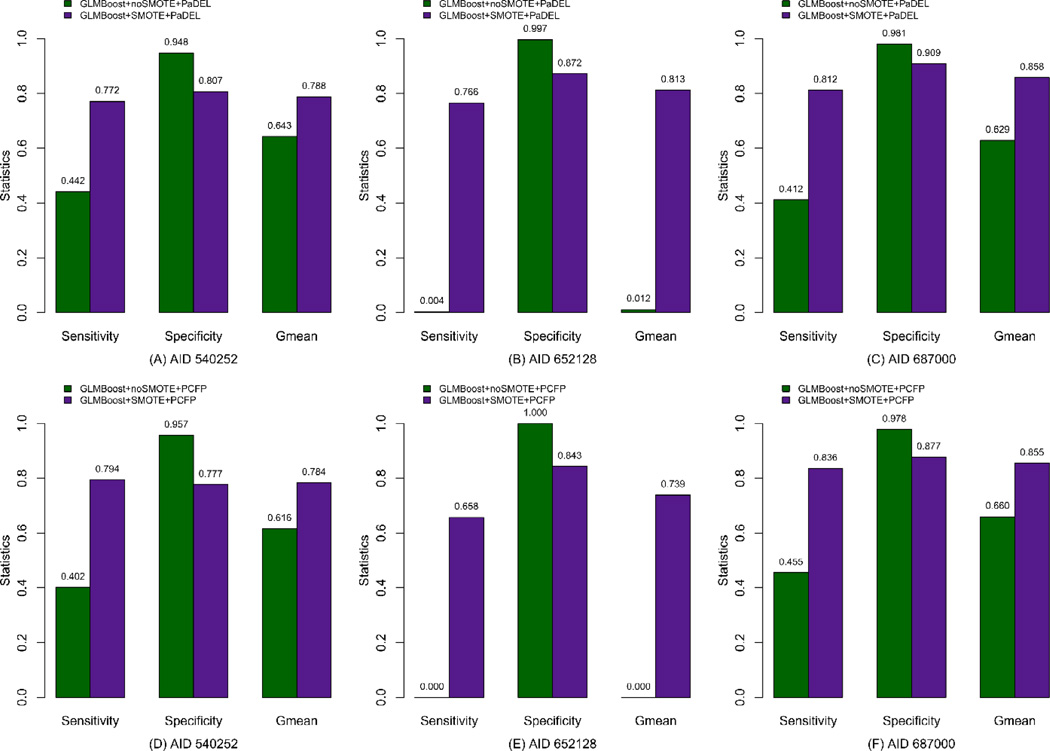
It is well known that the classes of descriptors play an important role in the classification performance. Two kinds of descriptors, PaDEL and PubChem fingerprints, are used to construct the GLMBoost models to validate their effect on the model performance. Table 3 reports the mean statistical results (± standard deviations) for the test set based on 200 predictions using GLMBoost with and without SMOTE preprocessing using PaDEL descriptors. As seen from this Table, for data set AID 540252, the GLMBoost model from original dataset (i.e. without SMOTE re-sampling) gives a poor Sensitivity value of 44.2% for the minority class (i.e. active compounds), while a Specificity value of 94.8% is obtained for the majority class (i.e. inactive compounds), leading to a combined accuracy, Gmean of 64.3% in this case. In an attempt to improve the predictive power for the interesting class which represents the active compounds, the SMOTE algorithm was used to over-sample this minority class. A noticeable increase on Sensitivity is achieved following the application of SMOTE, jumping from 44.2% to 77.2%. Despite the relatively large decrease in Specificity from 94.8% to 80.7%, the balanced accuracy, Gmean increases from 64.3% to 78.8%. A more dramatic enhancement is noted for AID 652128, where the original model hardly identifies the rare class (active compounds), illustrated by an extremely poor Sensitivity of 0.4%, and a Gmean value of as low as 1.2%, despite a Specificity value of 99.7% for the majority class (inactive compounds), indicating that the original GLMBoost classifier is not capable at all for this skewed dataset. However, with the incorporation of SMOTE, the Sensitivity value significantly increases from 0.4% to 76.6%, while the Specificity value just decreases by 12% but with the Gmean value sharply improved from 1.2% to 81.3%. A similar improvement in the model classification is observed for AID 687000, where Sensitivity and Gmean increase by 40% and 22.9%, respectively, at a small cost of decrease by 7.2% in Specificity. In summary, for the models using PaDEL descriptors as independent variables, while the minority class is hardly recognized by GLMBoost alone for certain datasets, the performance is improved significantly with the employment of SMOTE as illustrated by increases not only in the Sensitivity for picking up the minority class but also in the balanced accuracy measure.

Besides PaDEL descriptors, PubChem fingerprints, which have been successfully applied to the related domains [32, 46], were also used to construct the classification models to assess their influence on the predictive ability. In this work, results obtained by using PCFP for all three data sets are shown in Table 4. It is noticed that the performance is comparable to those from the models using PaDEL descriptors. Similar to the application using PaDEL descriptors, the GLMBoost algorithm is still not suitable on its own to classify the original dataset of AID 652128 using PCFP, where for the samples in the minority class the classifier cannot identify them at all, leading to the Gmean value of zero. Therefore, based on the statistical results (noSMOTE/SMOTE) from the models using both PaDEL and PCFP descriptors, it can be concluded that SMOTE undoubtedly plays a central role in enhancing the ability of identification for the rare class samples. Figure 2 gives barplots of the results for an intuitive comparison to those obtained from both noSMOTE and SMOTE procedures, respectively, where Figure 2A – 2C indicate the statistical results from the GLMBoost models using PaDEL descriptors as the independent variables, while Figure 2D – 2F illustrate the performance of the GLMBoost models using PCFP as the independent variables. These plots clearly suggest that the SMOTE approach significantly improves the performance of classifiers, especially for the AID 652128 dataset which has a larger inactive versus active ratio among the compounds. A comparison of the constructed models yielded by using PaDEL descriptors and PubChem fingerprints (e.g. Figure 2B versus Figure 2E; Figure 2D versus Figure 2F) shows all these models exhibit comparable performance, but the models developed by using PaDEL descriptors present slightly better performance in terms of balanced accuracy (Gmean) after SMOTE preprocessing.

Figure 2.

Comparison of statistics for GLMBoost with (SMOTE) and without SMOTE (noSMOTE) for the test set, where A – C are for models from PaDEL descriptors, and D – F are for models from PubChem fingerprints (PCFP).

3.5. Statistical performance of Random Forest combined with SMOTE

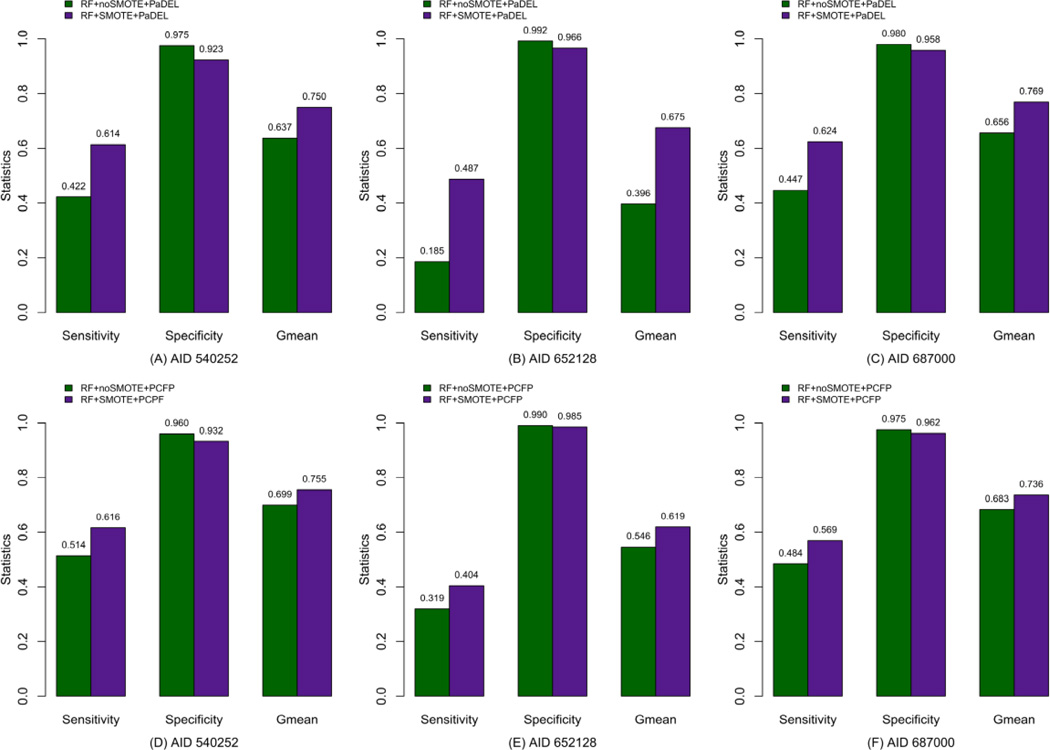
Random Forest recently has gained greater popularity in various fields [47, 48] due to its high prediction accuracy and several advanced features including: (1) RF is against overfitting; (2) it can be used “off-the-shelf” [42]. Therefore, RF was also employed in this work to identify the rare class samples and estimate the impact of SMOTE on RF. Tables 5 and 6 illustrate the statistical results of Random Forest for PaDEL descriptors and PubChem fingerprints, respectively. A careful inspection of these results as shown in Figure 3 suggests that the SMOTE algorithm indubitably increases the performance for the external prediction for both RF models produced by using PaDEL descriptors and PCFP respectively. In summary, the statistical performance of Random Forest combined with SMOTE shows a similar tendency with those from GLMBoost with SMOTE, indicating that the SMOTE approach plays a critical role in improving the prediction accuracy of conventional classifiers, especially for the minority class samples, by creating synthetic minority class examples.

Table 5.

Comparison of mean statistical results ± standard deviations for the test set based on 200 predictions for Random Forest with (SMOTE) and without SMOTE (noSMOTE) preprocessing using PaDEL descriptors.

Dataset	noSMOTE/SMOTE	Sensitivity	Specificity	Gmean	Computational time (minutes)
AID 540252	noSMOTE	0.422 ± 0.092	0.975 ± 0.016	0.637 ± 0.070	77.915
	SMOTE	0.614 ± 0.093	0.923 ± 0.028	0.750 ± 0.057	128.901
AID 652128	noSMOTE	0.185 ± 0.113	0.992 ± 0.007	0.396 ± 0.165	58.331
	SMOTE	0.487 ± 0.165	0.966 ± 0.017	0.675 ± 0.118	134.319
AID 687000	noSMOTE	0.447 ± 0.120	0.980 ± 0.009	0.656 ± 0.089	106.596
	SMOTE	0.624 ± 0.121	0.958 ± 0.014	0.769 ± 0.076	241.332

Table 6.

Comparison of mean statistical results ± standard deviations for the test set based on 200 predictions for Random Forest with (SMOTE) and without SMOTE (noSMOTE) preprocessing using PubChem fingerprints (PCFP).

Dataset	noSMOTE/SMOTE	Sensitivity	Specificity	Gmean	Computational time (minutes)
AID 540252	noSMOTE	0.514 ± 0.091	0.960 ± 0.019	0.699 ± 0.063	52.539
	SMOTE	0.616 ± 0.088	0.932 ± 0.028	0.755 ± 0.054	89.215
AID 652128	noSMOTE	0.319 ± 0.129	0.990 ± 0.008	0.546 ± 0.134	42.951
	SMOTE	0.404 ± 0.148	0.985 ± 0.011	0.619 ± 0.119	88.154
AID 687000	noSMOTE	0.484 ± 0.106	0.975 ± 0.011	0.683 ± 0.078	64.570
	SMOTE	0.569 ± 0.121	0.962 ± 0.015	0.736 ± 0.081	134.499

Figure 3.

Comparison of statistics for Random Forest with (SMOTE) and without SMOTE (noSMOTE) for the test set, where A – C are for models are from PaDEL descriptors, and D – F are for models from PubChem fingerprints (PCFP).

3.6. Comparison between GLMBoost and Random Forest

It has been reported that the Random Forest algorithm is a great modeling tool, which has been successfully applied to the bioinformatics and chemoinformatics domains and many other fields [42, 47, 49–51]. Therefore, it is interesting to compare RF and GLMBoost in the context of imbalanced data. In this work, two aspects of these algorithms are compared as follows: (1) statistical performance and (2) computational efficiency.

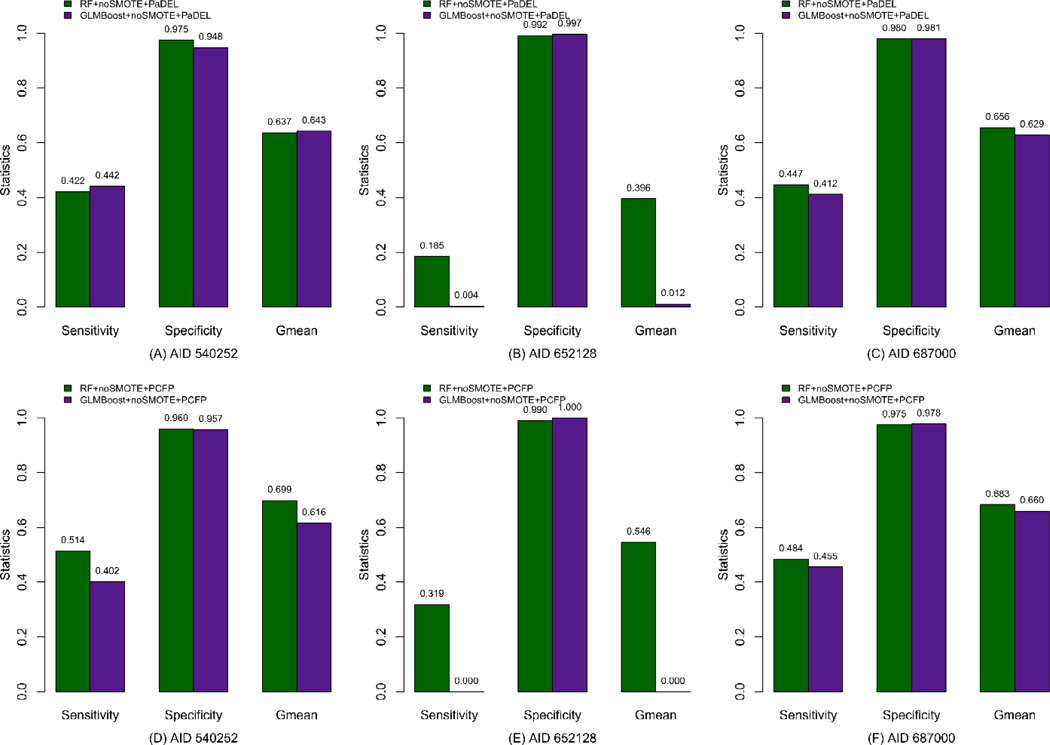
As shown in Figure 4, in the case when SMOTE was not applied, the Specificity values of both GLMBoost and RF (Figure 4A – 4F) are comparable but both of them do not exhibit the satisfied results for the current classification task. However, an apparent advance of RF in comparing to GLMBoost can be noticed when performing the classification for dataset AID 652128, where RF gives the Sensitivity values of 18.5% and 31.9% for PaDEL descriptor and PCFP, respectively, while GLMBoost almost cannot identify this minority class at all, indicating that RF possesses a better predictive ability for the original imbalanced dataset. In general, under the situation of noSMOTE, RF presents slightly better performance than GLMBoost for all three datasets. However, none of these results is satisfactory, since the classifiers exhibit highly correct prediction only for the majority but uninteresting class, which represents inactive compounds, but basically fails for the interesting class (i.e. active compounds). It is at this point that SMOTE demonstrates its significance for improving both prediction accuracy for the interesting class (Sensitivity) and balanced accuracy for the whole dataset (Gmean).

Figure 4.

Comparison of statistics between GLMBoost and RF without SMOTE (noSMOTE) for the test set, where A – C are for models from PaDEL descriptors, and D – F are for models from PubChem fingerprints (PCFP).

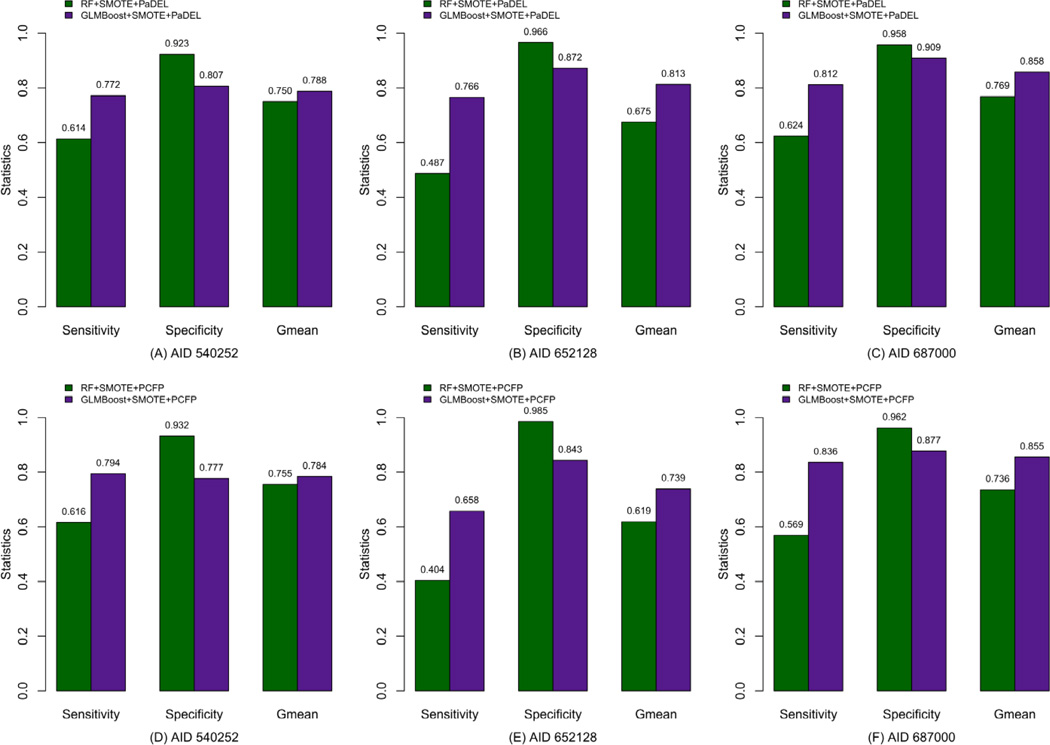
Results obtained by applying SMOTE are shown by Figure 5. It can be seen that the performance from both GLMBoost and Random Forest is significantly increased measured by Sensitivity and Gmean and with more significant improvement in Sensitivity especially when comparing to the results without SMOTE (shown in Figure 4). By carefully investigating those statistical metrics deriving from SMOTE (Figure 5), we notice that the performance of GLMBoost dominates that from RF in terms of Gmean. Especially for the dataset with a larger ratio of active to inactive compounds (AID 652128, AID 687000), the Gmean values from GLMBoost significantly outperform those from RF. The Specificity values of GLMBoost decrease to some extent, but they are still acceptable. It indicates that, by combining the GLMBoost and SMOTE algorithms, the classifier succeeds in identifying the rare class with high prediction accuracy, especially for the largely imbalanced datasets.

Figure 5.

Comparison of statistics between GLMBoost and Random Forest with SMOTE for the test set, where A – C are for models from PaDEL descriptors, and D – F are for models from PubChem fingerprints (PCFP).

Though Sensitivity, Specificity and Gmean are general to be used by researchers for classifier assessment over imbalanced data set [52, 53], it is still arguable that Matthews correlation coefficient (MCC) [54] may be more favored for evaluating imbalanced classification problems. Thus, we also calculated MCC values (mean statistical results ± standard deviations) for the test set based on 200 predictions for AID 540252, AID 652128 and AID 687000 as shown in the supplementary file, which exhibit the same tendency of performance enhancement as measured using Gmean with the help of SMOTE. It is worth noting that for AID 652128, with the incorporation of SMOTE, MCC values are sharply improved, again indicating that SMOTE has an important impact on the performance of the constructed models.

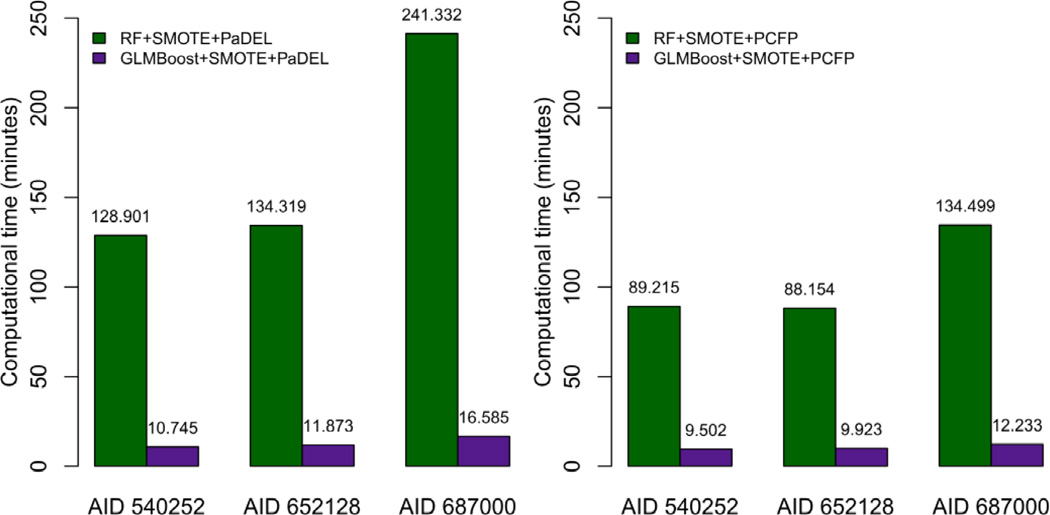
In addition to the prediction performance, the computational efficiency is also considered as a very important index to assess a classifier. Herein, since the models without SMOTE cannot achieve satisfactory performance, especially for the minority class samples, we only compare the computational time of GLMBoost and RF with the employment of SMOTE, which have demonstrated to be successful by the Sensitivity and Gmean values for all three PubChem BioAssay datasets (Figure 5). The computational time reported in Table 3 – 6 is compared and shown in Figure 6. It is very interesting to note that using PaDEL descriptors, RF costs 10-fold or more time to achieve the comparable performance from 200 holdout predictions as the GLMBoost algorithm does, while using PubChem fingerprints produces a similar difference in computational efficiency among the two methods.

Figure 6.

Comparison of computational time (minutes) of 200 holdout predictions for methods of GLMBoost and Random Forest respectively, both combined with SMOTE.

Recent advances in technology allow high-throughput screening facilities, large-scale sequencing centers, and individual laboratories producing vast amounts of data in an unprecedented speed, which are increasingly drawing attentions from researchers and government funding agencies to the research area for large-scale information management and analysis. Thus, computational approaches for efficiently processing and mining big data are highly in demand. It is encouraging that a comparison between GLMBoost and Random Forest demonstrates that the former proves to have not only better performance, but also higher computational efficiency, making it a promising tool that may be extensively utilized in data mining to investigate biological problems, especially with large imbalanced datasets.

3.7. Y-randomization test

Y-randomization test is often used to check the chance correlation for the constructed model [55]. In this work, since GLMBoost with SMOTE based on PaDEL descriptors not only exhibits satisfied performance, but also is more computationally efficient, we just focus on Y-randomization test to this model. We randomly shuffled the dependent variable and re-built the models. 200 times of Y-randomization test were repeated and the final results, reported by mean values (± standard deviations), were compared with the prediction statistics without this test (denoted as noY-randomization) for the test set. The final results show that for AID 540252, the Sensitivity, Specificity and Gmean values from Y-randomization test decrease to 53.9%, 46.5% and 49.7%, from original 77.2%, 80.7% and 78.8%, respectively; similarly, for AID 652128 and AID 687000, the individual statistical results also decrease largely as shown in Table 7. All these results indicate that the constructed models are not due to a chance correlation.

Table 7.

Comparison of mean statistical results ± standard deviations for the test set based on 200 predictions for GLMBoost with (Y-randomization) and without Y-randomization (noY-randomization) test combined with SMOTE using PaDEL descriptors.

Dataset	noY-randomization/Y-randomization	Sensitivity	Specificity	Gmean
AID 540252	noY-randomization	0.772 ± 0.081	0.807 ± 0.042	0.788 ± 0.043
	Y-randomization	0.539 ± 0.126	0.465 ± 0.080	0.497 ± 0.083
AID 652128	noY-randomization	0.766 ± 0.138	0.872 ± 0.033	0.813 ± 0.074
	Y-randomization	0.531 ± 0.172	0.482 ± 0.075	0.498 ± 0.101
AID 687000	noY-randomization	0.812 ± 0.082	0.909 ± 0.029	0.858 ± 0.047
	Y-randomization	0.511 ± 0.160	0.494 ± 0.072	0.496 ± 0.099

3.8. Effect of varying k in SMOTE on model prediction

Although models based on the default k in SMOTE produced satisfied results, it might still be interesting to explore the effect of k on the final model prediction. In this work, the best GLMBoost models based on PaDEL descriptors were used to perform this test for all three datasets. Nine models were constructed as described in the previous section by varying k value from one to nine with an increasing step of one for each individual dataset. The final results show that, for AID 540252, the model using the default k value (k = 5) exhibits the best performance in terms of Gmean (78.8%); for AID 652128, the maximum Gmean value gives 82% with k = 4, showing a marginal increase only by 0.7% comparing to the one obtained from the default k value (shown in Table 3); for AID 687000, the maximum Gmean value of 86.6% is obtained with k = 9, again only showing an increase by 0.8% than the value of 85.8% obtained with the default k value. The results in this test indicate that it is sufficient to obtain satisfied results by employing the default k value (k = 5).

4. Conclusion

In this work, a SMOTE coupled with GLMBoost method was proposed to perform the classification of imbalanced datasets from PubChem BioAssay. To test the generalized application of SMOTE, both PaDEL descriptors and PubChem fingerprints were used to construct the classification models. Our analysis indicated that both Sensitivity and Gmean exhibited a significant improvement following the employment of SMOTE. In particular, samples from the minority class (active compounds) were recognized successfully and the satisfactory prediction accuracy was achieved. In addition, models constructed by using PaDEL descriptors produced better performance. By comparing with Random Forest, a well-recognized classification algorithm, GLMBoost not only demonstrated stronger predictive power, but also exhibited higher computational efficiency. We anticipate that the proposed combinatorial method with SMOTE and GLMBoost can be extended to other classification problems with imbalanced data from PubChem BioAssay and other public information resources.

Highlights.

1. A GLMBoost coupled with SMOTE algorithm is proposed to classify imbalanced data.

2. It is easy for non-statistical experts to employ for classifying imbalanced data.

3. GLMBoost proves to have stronger predictive power and higher computational efficiency.