Nanotextured Superhydrophobic Electrodes enable Detection of attomolar-scale DNA concentration within a Droplet by non-Faradaic Impedance Spectroscopy

Abstract

Label-free, rapid detection of biomolecules in microliter volumes of highly diluted solutions (sub-femtomolar) is of essential importance for numerous applications in medical diagnostics, food safety, and chem-bio sensing for homeland security. At ultra-low concentrations, regardless of the sensitivity of the detection approach, the sensor response time is limited by physical diffusion of molecules towards the sensor surface. We have developed a fast, low cost, non-faradaic impedance sensing method for detection of synthetic DNA molecules in DI water at attomolar levels by beating the diffusion limit through evaporation of a micro-liter droplet of DNA on a nanotextured superhydrophobic electrode array. Continuous monitoring of the impedance of individual droplets as a function of evaporation time is exploited to dramatically improve the sensitivity and robustness of detection. Formation of the nanostructures on the electrode surface not only increases the surface hydrophobicity, but also allows robust pinning of the droplet contact area to the sensor surface. These two features are critical for performing highly stable impedance measurements as the droplet evaporates. Using this scheme, the detection limit of conventional non-faradaic methods is improved by five orders of magnitude. The proposed platform represents a step-forward towards realization of ultra-sensitive lab-on-chip biomolecule detectors for real time point-of-care application. Further works are however needed to ultimately realize the full potential of the proposed approach to appraise biological samples in complex buffer solutions rather than DI water.

Introduction

Detection of ultra-low concentrations of DNA molecules has recently attracted the attention of numerous research groups in various fields for its potential applications in clinical diagnostics, food safety, and homeland security. ^1–3 To approach this ultimate goal, different approaches have been proposed, such as Raman spectroscopic detection ^2,4, detection based on surface plasmons ^2,5, bio-barcode assays ⁶, nanowire-based field effect biosensors ^7,8, detection using carbon nanotube-based devices ^9,10, and electrochemical sensors with surface circular strand-replacement polymerization (CSRP) to amplify the signal. ¹ Among these approaches, most optical and barcode-based techniques need labelling which increases pre-processing time and cost, and requires a complicated apparatus for subsequent highly sensitive detection. In contrast, label-free electrical detection platforms simplify design and detection, and can be implemented in a portable format for in-situ diagnostics, and/or combined with integrated circuit technology for massive, parallel detection. ^7–9,11 Unfortunately, while transistor-based label-free sensors offer high sensitivities in the transconductance (~femtomolar, fM) or the impedance mode (~0.1 fM), the need for a reference electrode and the fluid stability of the gate oxide introduces additional challenges. ^7–9 In contrast, label-free sensing by passive (transistor-less) impedance spectroscopy, which can be categorized into faradaic and non-faradaic modes, is inexpensive and can offer robust performance in a fluidic environment and can detect the analyte in a bulk solution. In the faradaic mode, however, the need for a reference electrode, sophisticated surface functionalization steps, and the presence of a redox couple complicates the sensing platform. ^12–14 These issues can be addressed using non-faradaic impedance spectroscopy; however, the sensitivity of this approach has so far been limited to ~picomolar (pM) concentration. ^15,16

Detection of analytes at ultra-low concentrations (fM to aM) poses a fundamental challenge, especially for surface-based label-free sensors such as cantilever ¹⁷ or field-effect biosensors. ^7,8 In highly diluted solutions, the sensor response time is limited by physical diffusion of the biomolecules to the sensor surface. ^3,18,19 It has been demonstrated that the diffusion limit prevents a planar biosensor from being able to detect – within an acceptable time duration – statistically unambiguous signals associated with a few copies of the biomolecules dispersed within an electrolyte. ^17,18,20 The diffusion limitation can be overcome by a number of approaches. For example, in the magnetic biobarcode scheme, the sensing is achieved by release and detection of barcode molecules unique to each target species. ^6,21 Although an ultra-low concentration of 500 aM can be detected using this approach ⁷, the cost and pre-processing time associated with magnetic labeling remains a concern.

In another approach, De Angelis et al. overcame the diffusion limit through evaporation of a droplet on a superhydrophobic surface to deliver a few copies of λ–DNA in DI water to an integrated Surface-Enhanced Raman Scattering (SERS) sensor. ² Although detection at attomolar concentration was achieved (albeit of a very large DNA molecule containing ~50k base pairs, bp), the intricate design and nanofabrication of the Raman probe, localization of the sessile droplet, complex instrumentation, and scaling to smaller sizes for portable applications remain challenging. Moreover, both these approaches rely on single end-point detection of ultra-low concentrations; therefore, the statistical robustness of the result at highly diluted solutions is unknown.

Here, we report the use of multifunctional textured superhydrophobic electrodes for label-free impedance sensing of an evaporating droplet containing a few copies of synthetic DNA molecules in DI water. In contrast to the previously reported passive (super)hydrophobic surfaces (in the sense that the surface cannot be electrically or thermally activated ^2,3,22,23), the proposed nanotextured surface acts simultaneously as (i) a sensing electrode array, eliminating the need for integrating a separate sensing unit, and (ii) a superhydrophobic fluid delivery scheme that beats the diffusion limit and eliminates the need for packaging techniques. The nanotextured superhydrophobic electrodes are optimized so that the surface-energy distribution results in localization (pinning) of the target droplet immediately after deposition on the electrode surface, thereby creating a platform to continuously monitor the impedance (Z(t)) of a single droplet as a function of time, t. The proposed technique is an attractive candidate for highly sensitive, low-cost detection of biomolecules as it offers fast response (unencumbered by diffusion limits), a simple fabrication process, the elimination of a reference electrode, and the ability to conduct time-multiplexed impedance spectroscopy of the analyte within the solution. In addition, the detection time can be further reduced by using the hydrophobic electrodes as an integrated heater to expedite the droplet evaporation. The multifaceted role of the same electrodes as a ‘virtual container’, sensor, and heater is a distinctive feature of the sensing scheme developed in this paper.

Concept and Device Structure

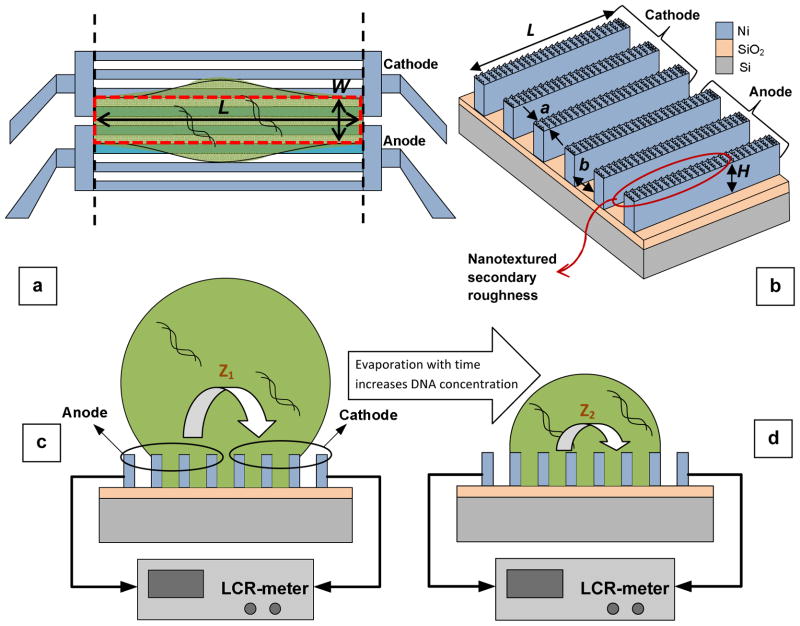
Classical (bulk) impedance spectroscopy involves two planar (or cylindrical) electrodes immersed in a milliliter-sized (mL) sample fluid volume. ²⁴ Instead, we have designed and fabricated a spatially asymmetric superhydrophobic, yet electrically conductive, array grouped into anode and cathode electrodes, as schematically illustrated in Fig. 1(a). A microliter-sized (μL) droplet containing the DNA molecules is placed onto the surface of the nickel electrodes, a three-dimensional diagram and optical microscope image of which are shown in Fig. 1(b) and Fig. 2(a)-(left), respectively.

Fig. 1.

Schematic diagram of: (a) top view of a pinned elongated droplet containing DNA molecules on the asymmetric hydrophobic fin array that forms the anode and cathode electrodes. The black dashed lines indicate the sensor edges to which the droplet parallel spread is limited, and the red dotted rectangle shows the droplet contact line which does not change with time. (b) Multifunctional electrode array with the design parameters denoted. Also, the nanotextured surface of the Ni-electrodes is pointed out by the red oval. (c) Impedance measurement system for the droplet at time t₁, and (d) impedance measurement of the same droplet at a later time t₂ (t₂ > t₁). Over time, droplet evaporation results in an increase in concentration of the DNA molecules in solution, which consequently leads to an increase in the solution conductance (equivalently, a decrease in the impedance magnitude).

Fig. 2.

(a) Left: Optical microscope image of the asymmetric electrode array. Center: an SEM image of a selected region of part (a)-left, showing the electroplated nickel stripes of height 8–9 μm. The two figures on the right show a SEM image and an AFM profile illustrating magnified views of the nanometer-sized features on the Ni electrodes created after the electrodeposition step. (b) An optical image of a droplet on the electrode array 4 min after deposition, along with two cross-sectional images (A–A′ and B–B′) captured using a high-speed camera. (c) The same set of images of the same droplet in part (c) captured 10 min later. The droplet volume and its parallel/perpendicular contact angles (θ_||/θ_⊥) decrease as it evaporates, while the contact line remains pinned by design.

After deposition, the droplet immediately reaches an equilibrium shape defined by a rectangular contact line, as shown graphically with a red dotted line in Fig. 1(a). Parallel to the electrodes, the elongated droplet is pinned by the sensor edges (dashed black lines) while in the perpendicular direction it is pinned by the nanotextured surface of the electrodes, specifically optimized for this specific design goal. The Scanning Electron Microscope (SEM) and Atomic Force Microscope (AFM) images in Fig. 2(a) illustrate the nanoscale roughness of the nickel electrode surface. These nanoscale features are formed as a result of the nickel electroplating process and, as will be discussed later, are essential for reliable impedance measurements. (See Supplementary Section S1 for the design details, S2 for details of the fabrication process, and S3 for additional information regarding the time evolution of an evaporating droplet.)

As the droplet evaporates, its impedance is continuously measured and stored (see Fig. 1(c) and (d)), so that a complete map of Z (ρ, f, t) is available. Here, ρ is the initial analyte density, f is the frequency of measurement, and t is the time elapsed since the impedance measurement is started. Differential analysis of the data with respect to the reference droplet with deionized (DI) water allows determination of the concentration of the DNA solutions.

As shown graphically in Fig. 1(b), the anode and cathode each consists of 30 electrically-connected, rectangular fins with width (a) of 10 μm, height (H) of 8–9 μm, and length (L) of 4 mm. The spacing between adjacent fins (b) is 20 μm resulting in a period of a+b = 30 μm, so that the total area of each electrode (anode and cathode) is 0.9×4 mm². An electric signal consisting of a 50 mV DC bias and an AC voltage of 10 mV is applied between anode and cathode electrodes.

The impedance of a droplet depends on the frequency of measurement. As will be discussed later, the measurement frequency must exceed 100 Hz so that the electrokinetic diffusion is negligible ²⁵ and the low-frequency noise does not contaminate the accuracy of impedance measurement. On the other hand, based on the impedance data obtained for the frequency range of 120 Hz – 50 kHz, we found empirically (and validated theoretically) that the measurement sensitivity is maximized at lower frequencies. A working frequency of 120 Hz provides a good compromise and has been used for all the measurements reported in this paper.

In all the experiments, 3 μL droplets containing 850 bp synthetic DNA in DI water are investigated with impedance measurements as the droplets evaporate (see Supplementary Section S4 for details regarding sample preparation). The measured DNA concentration covers a dynamic range of almost nine orders of magnitude, i.e., from 1.6 nM to 6 aM solution concentrations. Measurements obtained with several droplets suggest that the mean evaporation time is ~20 min (see Supplementary Section S5-A). The cross-sectional and top-view images of a typical droplet after 4 and 14 min of its deposition are depicted in Fig. 2(b) and (c), respectively. Comprehensive information on the dynamics of droplet evaporation and its shape evolution are provided in Supplementary Section S3.

The volume of the elongated droplet decreases as it evaporates, but very importantly, its contact line (and equivalently its contact area) does not recede, as the line is pinned both by surface tension and the secondary roughness of the Ni-plated electrode surface. The geometric invariance of the contact area with respect to the electrodes has significant implications for the robustness/reliability of impedance measurements. ²⁴ If the droplet contact line was changing with time, the loss of the area-coverage would have increased the electrode impedance in an uncontrolled manner, confounding the measured effect of evaporation on decreasing the impedance. With a fixed contact area, the increase in the DNA concentration with electrolyte evaporation (DI water) is accurately reflected in a decrease of the droplet impedance as a function of time.

To experimentally justify the importance of the secondary roughness on the Ni electrodes, we created a set of test structures in which the nanostructures are intentionally eliminated by exposing them to plasma etching. The droplets deposited on such smooth electrodes are no longer self-aligned and pinned to the electrodes. This leads to very large variability in the impedance of droplets with the same initial volume and analyte concentration. For a more detailed discussion of this topic, see the Supplementary Section S5-A′.

Results and Discussion

Experimental Results

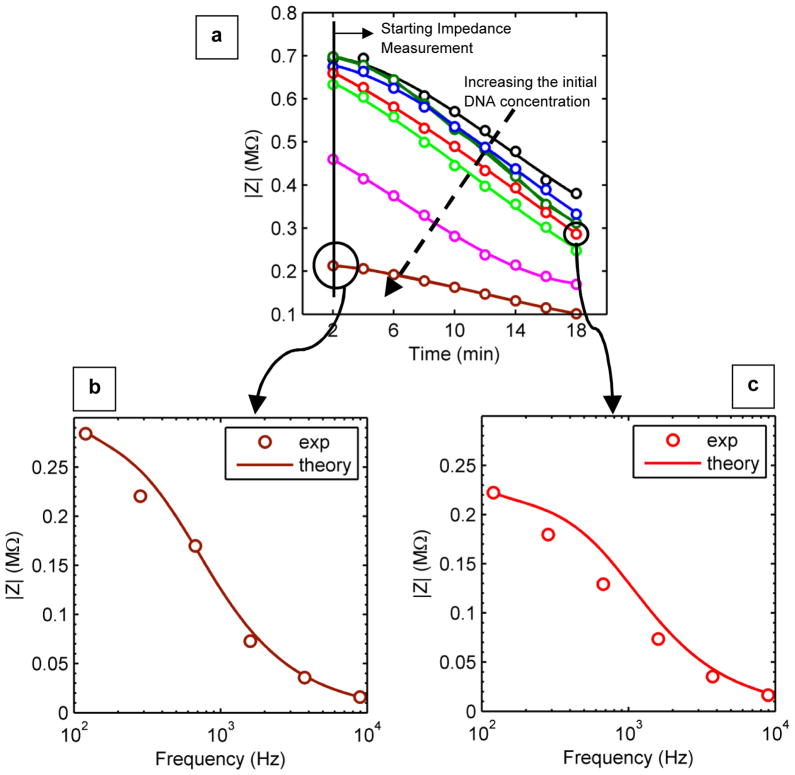
Fig. 3(a) shows the average of three sets of impedance measurements on DNA-containing droplets as a function of time for various initial DNA concentrations, all measured at 120 Hz. As indicated with a dashed vertical line in Fig. 3(a), the impedance measurements start 2 min after deposition of the droplet. As the fluid volume decreases with evaporation, the net DNA concentration increases. Therefore, the impedance magnitude (|Z|) of the same droplet (with specific initial DNA concentration) decreases over time, providing the opportunity for repeated impedance measurements during the course of evaporation. The repeated sampling of the same amount of analyte contained within a single droplet enhances the statistical robustness of the results.

Fig. 3.

(a) Average impedance magnitude (|Z|) as a function of time for different initial DNA concentrations. At each time, the higher the solution concentration, the lower its impedance magnitude. In addition, over time, the impedance magnitude decreases as the droplet evaporates. The applied frequency is 120 Hz. The dashed arrow indicates the increase of the initial concentration: DI water (black), 6 aM (dark green), 60 aM (blue), 1 fM (red), 50 fM (light green), 33 pM (magenta), and 160 pM (brown). From this figure it is clear that the sensor does not distinguish the 6 aM DNA concentration from the 60 aM concentration, and therefore the detection limit is ~60 aM. (b) Experimental data for impedance magnitude versus frequency at 2 min after deposition of a 160 pM droplet on to the electrode surface. (c) Measured data for impedance magnitude versus frequency 18 min after deposition of a 1 fM droplet. In part (b) and (c), the solid lines indicate the simulation results which are in reasonable agreement with the experimental results.

The top black curve in Fig. 3(a) is obtained from impedance-spectroscopy for analyte-free DI water. Even at an extremely low concentration of 60 aM, the impedance signal is clearly distinguishable from this reference curve (although the differentiation is lost at an even lower concentration of 6 aM). Higher concentrations of analyte exhibit lower initial impedance, as expected, but follow the same overall time-trajectory as the droplet evaporates.

Fig. 3(b) and (c) provide additional details of the impedance results as a function of frequency at two different times (t = 2 min and t = 18 min) for initial concentrations of 160 pM and 1 fM, respectively. As mentioned previously and as is expected from theoretical considerations, the sensitivity is maximized at lower frequency because the impedance magnitude decreases with increasing frequency.^16,26 Moreover, the similarity in magnitude of the impedances implies that while the initial concentrations differed by five orders of magnitude, the enhancement of concentration during evaporation ensures that the effective concentration at t = 18 min for a 1 fM analyte (Fig. 3(c)) approaches that of the 160 pM sample at time t = 2 min (Fig. 3(b)).

In Fig. 4(a), we have plotted the magnitude of average differential admittance ( $\left|\mathrm{\Delta }Y(t)\right|=\left|Y_{\rho }^{\mathit{avg}}(t)-Y_{DI}^{\mathit{avg}}(t)\right|$, where Y = 1/Z) with respect to DI water, as a function of the initial DNA concentration (ρ) at three different times (t = 2, 10, and 18 min) after droplet deposition. The solution concentration of the droplet at t = 2 min is essentially identical (within 10%) to that of the bulk solution from which it was drawn. This figure allows us to conclude that the admittance increases due to the increase in DNA concentration as a result of evaporation. Furthermore, the change in the differential admittance of various concentrations increases with time leading to a continually improving detection resolution.

Fig. 4.

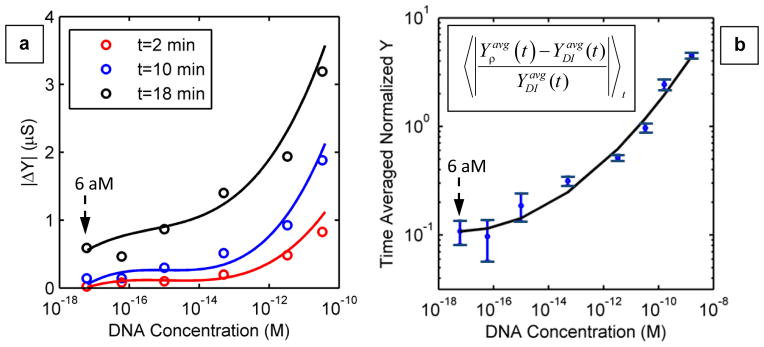
(a) The relative change in admittance (Y) magnitude with respect to DI water ( $\mid \mathrm{\Delta }Y(t)\mid =\mid Y_{\rho }^{\mathit{avg}}(t)-Y_{DI}^{\mathit{avg}}(t)\mid$, where Y = 1/Z) as a function of the initial DNA concentration (ρ), after 2 min (open red circles), 10 min (open blue circles), and 18 min (open black circles) of droplet deposition on device surface. The average from three different impedance measurements is plotted in each case. (b) Time-averaged magnitude of the normalized relative admittance with respect to DI water (defined by the given relationship in the plot) as a function of DNA concentration. From this plot, it is concluded that the detection limit would be ~60 aM. The solid lines in both figures are merely trendlines. This plot is derived from three independent measurements. The error bars correspond to the standard deviation of the experimental values.

In addition, the approach provides an opportunity to continually measure the impedance of the same droplet as it evaporates and collect a large number of data points in a single impedance measurement cycle. To demonstrate the important role of repeated sampling of data points over time, the time-average of the relative change in admittance with respect to DI water (defined as ${\langle \left|\frac{Y_{\rho }^{\mathit{avg}}(t)-Y_{DI}^{\mathit{avg}}(t)}{Y_{DI}^{\mathit{avg}}(t)}\right|\rangle }_t$) is plotted in Fig. 4(b). The time-averaged signal is fully resolved to the 60 aM level, which reflects a gain of almost five orders of magnitude in sensor sensitivity compared to conventional non-faradaic impedance sensing approaches. ^15,16 As mentioned previously, the resolution is eventually lost between 6 aM and 60 aM concentrations, and therefore, we conclude that the detection limit of the proposed method is approximately 60 attomolar for a typical DNA size of 850 bp. This limit is defined by several factors such as the statistical fluctuation of the number of molecules in micro-liter droplets and the stability of the reference conductance of DI water. The solid lines in both figures (Fig. 4(a) and (b)) are merely trendlines. Phase plots provide additional complementary information for theoretical interpretation of the experiments, and are presented in Supplementary Section S5-B.

As a final note, the experimental results demonstrating the capability of the evaporation-enhanced non-Faradaic impedance sensing in selectively identifying different DNA length and state, i.e. single stranded DNA (ssDNA) versus double stranded DNA (dsDNA), are provided in Supplementary Section S5-C.

Beating the Diffusion Limit: Evaporation on Nanotextured Superhydrophobic Electrodes

In the present work, we have designed an asymmetric electrode array with hierarchical roughness to trap a biomolecule-containing droplet for impedance spectroscopy. The electrodes, as graphically depicted in Fig. 1(b), are parallel fins comprising grooves and ridges with geometrical dimensions a, b, and H as defined previously.

It is well established that when a droplet is deposited on a symmetric surface, it forms an equilibrium spherical-cap shape defined by minimization of the surface energy of the total system. ^2,3,27–29 On the other hand, the shape of a droplet on an asymmetric surface consisting of parallel fins is no longer spherical but elongated, exhibiting different contact angles parallel (θ_||) and perpendicular (θ_⊥) to the orientation of the fins. The fluid faces no energy barrier parallel to the fins, and therefore the droplet spreads longitudinally until it is pinned by the sensor edge (dashed black lines in Fig. 1(a)) to form an elongated shape. ^30–32 This pinning of the contact line by surface tension and the secondary roughness of the electrodes prevents the droplet from retracting from the sensor-edge as it evaporates. Similarly, in the direction perpendicular to the electrodes, the droplet contact line is pinned by energy barriers associated with the fin-like geometry of the superhydrophobic surface.³³

As the droplet evaporates, its parallel contact angle remains constant, while the perpendicular contact angle decreases to reflect the decrease in the droplet volume. Using images of an evaporating droplet captured using a high-speed camera, we found that the volume of a droplet (V(t)) evolves with time as: $V(t)=V_0{(1-t/T)}^{\frac{3}{2}}$, where V₀ is the initial volume of the droplet and T is the total time needed for complete evaporation (for our case, V₀ = 3 μL and T = 20 min). ³⁴ The experimental and simulation data are provided in the Supplementary Section S3.

Referring to Kusumaatmaja et al. ³³, the perpendicular contact angle on an asymmetric surface of parallel fins can be related to the parallel contact angle as:

$$tan\frac{{\theta }_{\perp }}{2}=etan\frac{{\theta }_{\Vert }}{2}$$ (1)

where e is the elongation factor, defined as the ratio of the maximum base lengths of the droplet contact line in the parallel and perpendicular directions, L and W, respectively (See Fig. 1(a)). The elongation factor is ~5 in these experiments and remains unchanged during the evaporation period.

Right after deposition of the droplet on the surface of the textured array, the measured parallel contact angle is ~45°. Using Eq. (1), the perpendicular contact angle is calculated to be ~130°, which is in reasonable agreement with the measured value of θ_⊥~(146 ± 6)°. The enhanced hydrophobicity of our nanostructured electrodes is attributed to the secondary roughness created on the surface of the nickel electrodes, which is not accounted for in Eq. (1). While a smooth nickel layer is hydrophilic, an electroplated nickel film exhibits superhydrophobic properties due to the creation of secondary structures on the surface. AFM measurements (Fig. 2(a)-far right) show that the electroplated Ni surface has a very large rms roughness of ~70 nm, which explains the amplified hydrophobic response of the electrode surface. ³⁵ Superhydrophobicity of electroplated nickel films, with measured contact angle of ~155°, has been previously reported. ³⁶ Therefore, the secondary roughness nanostructures add to the micron-scale hydrophobicity of the asymmetric design ²³ and increase the contact angle. The hierarchical roughness is also essential for robust pinning of the droplet contact line. As discussed previously, the contact line pinning and the superhydrophobicity are both critical for the droplet to self-align on the electrodes, and this self-alignment allows highly stable impedance spectroscopy. For a detailed discussion, see Supplementary Sections S1, S2, and S5-A′.

Impedance Simulation

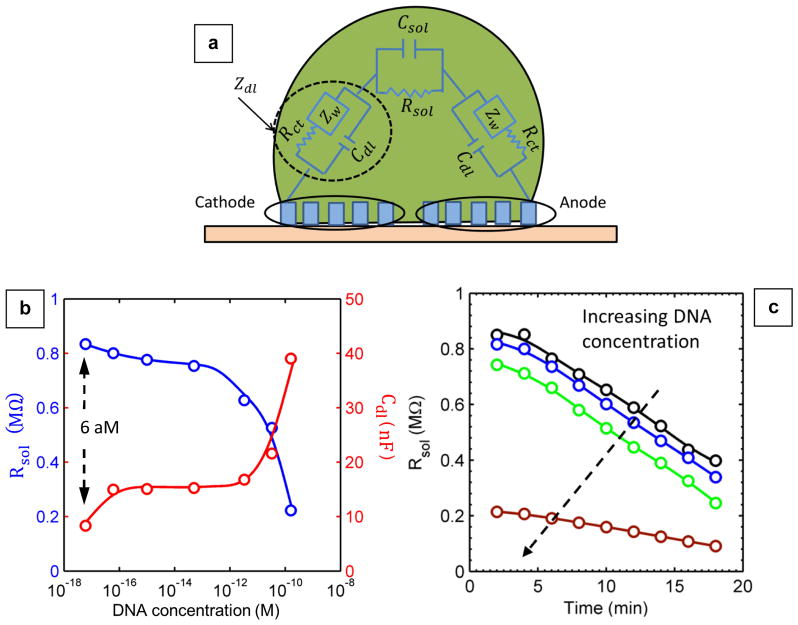
In order to interpret the experimental results in Fig. 4(a) and to explain how the impedance spectroscopy is affected by DNA concentration, we adapted a classical equivalent circuit model for the specific goal of droplet spectroscopy. ³⁷ Details of the model are discussed in Supplementary Section S5-B. Briefly, the net impedance of the circuit is given by Z =R_electrode + (Z_sub || Z_droplet), where we define $Z_{\mathit{droplet}}=2Z_{dl}+\frac{R_{\mathit{sol}}}{1+j\omega C_{\mathit{sol}}{R}_{\mathit{sol}}}$ to be the effective impedance of the droplet (Fig. 5(a)), Z_sub the parasitic impedance due to the substrate, and R_electrode the resistance of the electrodes. The parasitic components of the impedance (i.e., Z_sub and R_electrode) are obtained from a droplet-free impedance measurement of the sensor surface. Subsequently, Z_droplet is obtained by subtracting the parasitic impedance from the total impedance (Z) measured during the evaporation of the droplet.

Fig. 5.

(a) Equivalent circuit diagram for droplet impedance. (b) Extracted R_sol (blue circles) and C_dl (red circles) as a function of DNA concentration for t = 2 min. With the increase in DNA concentration, R_sol and C_dl show a steep decrease and increase, respectively. (c) Plot of R_sol with time at different DNA concentrations for DI water (black), 60 aM (blue), 50 fM (light green), and 160 pM (brown). Solid lines in the figures are merely trendlines.

The droplet impedance is composed of five components: the Warburg impedance (Z_W), the double-layer capacitance (C_dl) and charge-transfer resistance (R_ct), the dielectric capacitance of the solution (C_sol), and the solution resistance (R_sol). All these impedances, in principle, depend on the shape of the droplet and the DNA concentration.

The working frequency of our measurements (120 Hz) is high enough that the electrokinetic diffusion (and the corresponding Warburg impedance) can be neglected.²⁵ On the other hand, this frequency is sufficiently low so that the parasitic substrate impedance (Z_sub) is maximized and its effect on overall impedance is minimized (Supplementary Fig. S5.5). Finally, I–V measurement of DNA-free DI droplet (Supplementary Fig. S5.6) confirms that the charge transfer resistance (R_ct) approaches Giga-Ohm (G) levels for non-faradaic impedance spectroscopy, allowing the element to be treated effectively as an open circuit. The net change in the intrinsic droplet impedance, therefore, can be attributed to three physically meaningful parameters, i.e., R_sol, C_dl, and C_sol.

Although the permittivity of the solution may change with the DNA concentration due to an induced dipole moment in the presence of applied bias ¹⁶, we assume that the change is negligible for very low DNA concentrations (< 1 nM). Therefore, C_sol which is determined exclusively by the permittivity of the solution and the geometry of the droplet, is presumed independent of DNA concentration.

Once the parasitic components are measured and excluded, the remaining two parameters (R_sol and C_dl) are determined by matching the theoretically predicted impedance at a given frequency (Supplementary Table S5.2 summarizes the equations) to the corresponding impedance observed in the experiment. This procedure allows determination of R_sol and C_dl as a function of time for different DNA concentrations. In Fig. 5(b) R_sol and C_dl are plotted as a function of DNA concentration at time t = 2 min. While the extracted R_sol decreases with an increase in DNA concentration, C_dl shows an opposite trend. The results may be interpreted as follows.

R_sol is inversely proportional to the conductivity of the solution which in turn is proportional to the density of ions in the solution (n₀). As the concentration of DNA increases, the number of counter-ions (or effectively n₀) surrounding them increases, and hence, we expect the solution resistance to decrease. For the same reason, R_sol is expected to decrease with time because evaporation increases the DNA concentration (See Fig. 5(c)).

The Guoy-Chapman theory ³⁸ suggests that C_dl is proportional to √n₀ for a system that allows ion diffusion in a semi-infinite medium. Even though the droplet is finite, we expect C_dl to increase with the counter-ion concentration, and hence to increase with increase in DNA concentration. To summarize, the explicit dependence of R_sol and C_dl on DNA concentration provides the theoretical foundation of the impedance measurement results summarized in Fig. 3(a).

Finally, it should be emphasized that the resultant values of the different circuit components depend on geometry of the droplet and electrode geometry (including the secondary roughness), and this dependence is implicitly accounted for in our back-extraction procedure.

Conclusion

Highly sensitive detection of attomolar concentrations of synthetic DNA molecules suspended in microliter-sized droplets of DI water is achieved by using evaporation-improved impedance sensing on an electrically-active superhydrophobic surface. Our approach offers implementation of multiple arrays of nanotextured superhydrophobic electrodes which would allow simultaneous measurement of multiple samples or droplets. The specific design of the superhydrophobic electrodes and their nanotextured surface play a critical role in performing sturdy impedance measurements. In addition, the time-multiplexing capability further enhances the device sensitivity and detection robustness by increasing the number of data points obtained in one measurement cycle. It should be mentioned that our ability to detect ~60 aM DNA concentrations does not define the ultimate limit of the approach; the sensitivity can be further improved by using inter-digitated multifunctional electrode configurations that would allow higher-resolution measurement of impedance changes associated with even lower DNA concentrations. And finally, we should emphasize that additional steps are needed for the evaporation-enhanced impedance sensing approach to be applicable to target molecules suspended in complex electrolytes (rather than DI water). For example, our sensor can be integrated with a pre-filtration step to achieve the specificity necessary for analyte detection. The target molecules could first be dielectrophoretically separated from other molecules that are present in a fluid stream. Subsequently, a droplet containing the target molecules can be separated and guided through the integrated microfluidic chip to the impedance sensor region ^39–42. Another approach would be to perform Polymerase Chain Reaction (PCR) or isothermal amplifications in the droplets which would increase the concentration in real time for detection by embedded electrodes for impedance spectroscopy ⁴³. Such integration will be necessary for analyzing real samples relevant for medical diagnostics, food safety, and chem-bio sensing, and will be the focus of our future work.