Neural cell alignment by patterning gradients of the extracellular matrix protein laminin

Abstract

Anisotropic orientation and accurate positioning of neural cells is achieved by patterning stripes of the extracellular matrix protein laminin on the surface of polystyrene tissue culture dishes by micromoulding in capillaries (MIMICs). Laminin concentration decreases from the entrance of the channels in contact with the reservoir towards the end. Immunofluorescence analysis of laminin shows a decreasing gradient of concentration along the longitudinal direction of the stripes. The explanation is the superposition of diffusion and convection of the solute, the former dominating at length scales near the entrance (characteristic length around 50 μm), the latter further away (length scale in excess of 900 μm). These length scales are independent of the channel width explored from about 15 to 45 μm. Neural cells are randomly seeded and selectively adhere to the pattern, leaving the unpatterned areas depleted even upon 6 days of incubation. Cell alignment was assessed by the orientation of the long axis of the 4′,6-diamidino-2-phenylindole-stained nuclei. Samples on patterned the laminin area exhibit a large orientational order parameter. As control, cells on the unpatterned laminin film exhibit no preferential orientation. This implies that the anisotropy of laminin stripes is an effective chemical stimulus for cell recruiting and alignment.

1. Introduction

The ability to spatially control and guide cell proliferation, recruitment and tissue organization onto technological surfaces are relevant issues for several biomedical applications, including tissue engineering, stem-cell-based therapies, biosensing and drug screening [1–4]. A technology for controlling cell behaviour on hybrid surfaces implies the control of an artificial environment across multiple length scales, which aims to recreate the dynamic three-dimensional native cellular microenvironment [5,6].

It is well known that cells respond to a variety of stimuli: topographical, physical, electrical, mechanical and chemical cues, both short- and long-ranged, cooperating at multi-length scales [5,7–11]. Gradients of chemoattractants or cell-adhesive molecules enable the guidance and the alignment of cells into a hierarchical organization. Smooth gradients of proteins or peptides from the extracellular matrix (ECM), such as fibronectin, laminin, arginin–glycin–aspartic acid (RGD), as well as soluble factors such as growth factors and chemokines, are known to affect adhesion, migration, proliferation and differentiation of different cell types [12–18]. For neural cells, chemical gradients have paramount importance in guiding the constitution of the neuronal network: directing the axonal growth, through the formation of synapses [12,19–22]; and in the chemotaxis of neural stem cells towards injured sites aimed at repairing nervous tissue following a trauma or a pathology, as in stroke, spinal cord injury, multiple sclerosis [23–26]. Laminin is the most investigated ECM protein for nerve regeneration [27,28] and specific domains of laminin, such as IKVAV, YIGSR, RGD have been identified to promote neuronal survival and differentiation, to induce axonal growth cone, and to display cell adhesive and/or neurite outgrowth-promoting capabilities [21,23,29–31].

Different technological approaches have been devised for generating on the substrate surface gradients containing a single soluble guidance cue: microfluidics systems [12,19,32,33] controlled molecule diffusion from reservoirs [34], covalent protein immobilization by photo-linking [35–37], inkjet printing [13], specific protein binding to a primer [12] or by using hydrogels [17,38]. Soft lithography offers a toolbox of simple methods suitable for the fabrication of chemically modulated surfaces, with feature sizes down to a few tens of nanometres across large areas [39,40]. These techniques exploit chemical and physical interactions for the deposition/adsorption/self-assembly of the biochemical cues at precise positions on the surface. Linear gradients exhibiting a slope in excess of 0.06 μg(μl μm)⁻¹ of laminin [12] have been developed as a route to fabricate protein-bound surfaces, which, in turn, may induce cell patterning [41–44]. These methods can be used to create gradients through the interplay between capillary forces and self-organization phenomena occurring in the confined region between the stamp protrusions and the surface [41,45]. Micro- and nano-fabrication techniques have been applied for creating patterned substrates of laminin, or its peptides, in order to guide neural cell growth and promote neurite extension [12,22,35,46,47], as well as to induce the alignment of other cellular phenotypes [13,33]. Quantification of the response of neural cells to gradients of guidance cues is an issue.

In this study, we report a quantitative analysis of how laminin gradients, generated through patterning by micromoulding in capillaries (MIMICs) onto commercial plastic tissue culture (TC) dishes, yields selective confinement and guidance of neural cell proliferation onto the surface, and how it affects the spatial organization of the cells. We designed and fabricated a multi-length scale gradient of laminin by patterning laminin stripes of variable width ranging from about 15 to 70 μm. Laminin concentration decreases from the MIMIC channel inlet along the stripe length with a double exponential decay, whose length scales were identified along the stripes and shown to be largely independent of the channel width. By means of finite-element method (FEM) modelling, we ascribe the smaller length scale (less than 100 μm) to diffusion of laminin, which yields the steeper gradient characterized by an exponential decay constant k₂ = 0.037 (±0.0143) μm⁻¹, whereas the larger length scale (greater than 900 μm) is determined by convective transport yielding a milder gradient with k₁ = −0.0013 (±0.0003) μm⁻¹ [12].

An astrocytoma cell line was chosen in the frame of neural cells because they display very good adhesion and migration thus are suitable for assessing the effect of a surface modification such as the laminin gradients on their adhesion and orientation.

In this work, neural cells show preferential adhesion on the laminin-patterned areas of the surface and they follow laminin concentration gradients along the patterned stripes at prolonged times of incubation (6 days) in serum-containing medium. They tend to pack as two or more cells side-by-side depending on the stripe width. We analysed their orientation within and outside the patterned areas, by estimating an orientational order parameter measuring the anisotropy of the cell nuclei orientation. We found that there is a significant non-zero-order parameter, which implies that the pattern effectively aligns the cells. In the absence of the pattern, the order parameter vanishes. These results provide a modular approach to engineer anisotropic cell architectures using patterned biochemical cues.

2. Material and methods

2.1. Fabrication of laminin patterns

Human laminin (Sigma-Aldrich) was patterned on the surface of commercial polystyrene TC dishes (Corning, Sigma-Aldrich) by the MIMICs technique essentially as previously described [48]. Poly-(dimethylsiloxane) (PDMS) stamps were prepared by replica moulding of a master fabricated by photolithography as reported in [42]. The PDMS stamp has 22 parallel channels, whose length is 8 mm, and whose width ranges from about 15 to 70 μm, height is 1.5 μm and are spaced apart 160 and 230 μm. The PDMS stamp was placed on the substrate surface and adhered by soft pressure on the top. A droplet (5 μl volume) of laminin solution (20 μg ml⁻¹ in cell culture medium without serum) poured in an open end of the channels fills the channels upon the action of Laplace pressure. After the medium is completely evaporated (2 h, RT), the stamp is gently peeled-off, leaving a pattern of laminin deposited on the polystyrene surface.

2.2. Laminin pattern characterization

The laminin patterns were analysed by bright field, fluorescence optical microscopy and scanning probe microscopy. Optical images were collected with an Olympus IX70 in transmission mode with 10× objective. Scanning probe microscope (SPM) images were acquired with a Smena microscope (NT-MDT, Moscow, Russia) operated in semi-contact mode in ambient conditions. NSG cantilevers (NT-MDT) with a nominal tip radius of curvature of 10 nm and a resonance frequency between 90 and 230 KHz were used. SPM images were analysed by using the software Image Analysis (NT-MDT); the dimensions of the pattern features was measured by the Section Analysis tool.

Immunofluorescence assays were performed to visualize the local distribution of laminin onto the substrate and evaluate the occurrence of specific functional binding. Non-specific staining was blocked by incubating laminin-patterned substrates with 1% bovine serum albumin in phosphate-buffered saline (PBS 1×; blocking buffer) for at least 30 min at RT, then the samples were incubated for 1 h at RT with a rabbit anti-laminin antibody (Sigma-Aldrich) diluted 1 : 25 in blocking solution, washed three times with PBS 1×, and incubated with the fluorescent Alexa Fluor 594 anti-rabbit antibody (Invitrogen; diluted 1 : 200 in PBS 1×) for 90 min at RT. Control samples were incubated in blocking solution with no primary antibody. To verify the stability of the protein pattern, some samples were incubated in the presence of the cell culture medium only under standard cell culture conditions (37°C, 5% CO₂, humidified atmosphere) for at least 24 h before performing immunofluorescence assays. Images were acquired with an Olympus IX70 microscope, equipped with appropriate fluorescence filters and a Nis-elements F300 CCD camera.

2.3. Laminin concentration gradient analysis

In order to quantify the concentration gradient of laminin on polystyrene TC dishes along the patterned stripes, densitometry analysis from fluorescence images was performed. Fluorescence pixel intensity values were estimated for all captured images (n = 6) with the software gimp v. 2.6.7 (GNU image manipulation program; copyright 1995–2008 Spencer Kimball, Peter Mattis) by using the function histogram luminosity that exploits K-means clustering. Analysis was performed by subdividing each stripe length into longitudinal regions 10 μm long (comparable with the average dimension of a neural cell) and variable widths corresponding to the lateral channel dimension. The pixel intensity unit was normalized, where 100% represents the highest intensity on the substrate, and 0% corresponds to no fluorescence signal. Gradient analysis was performed for each stripe as follows: the normalized fluorescence intensity was plotted against the relative position along each stripe, and the gradient was quantified by estimating the best fit of a double exponential decay.

2.4. Cell culture conditions and growth on patterned surfaces

Human astrocytoma 1321N1 cells (purchased from ECACC no. 86030402) were cultured in Dulbecco's modified Eagle medium: nutrient mixture F12 (DMEM/F12), supplemented with 10% fetal bovine serum, 2 mM l-glutamine, penicillin (100 U ml⁻¹) and streptomycin (100 μg ml⁻¹; complete medium). The cell line was maintained in standard culture conditions (37°C in a humidified atmosphere with 5% CO₂) and was fed every 2–3 days.

Subconfluent cells were seeded (3000 cells cm⁻²) on laminin-patterned TC dishes in the presence of 1 ml of the complete medium, and the cells were allowed to proliferate under standard culture conditions up to 6 days.

2.5. Analysis of cell nuclei anisotropy and orientation

After 6 days of incubation, the cells were fixed with paraformaldehyde 4% in PBS 1× for 20 min, washed with PBS 1×, permeabilized with 0.1% Triton X-100 and incubated with the nuclear dye 4′,6-diamidino-2-phenylindole (DAPI; dil. 1.500 in PBS 1×) for 5 min at RT in order to visualize the cell nuclei. Cell images were acquired with the fluorescence microscope Olympus IX70 as described above. Experiments were repeated at least three times.

The alignment of the cells was statistically analysed from fluorescence images by measuring the orientation angle of DAPI-stained nuclei using Gwyddion image software (v. 2.0). The analysis was performed both on laminin-patterned and -unpatterned regions on the surface. Each analysis was performed on fluorescence images at the same magnification (4×), with the grain analysis function used to identify the stained nuclei. The contour of each cell nucleus is fitted with an ellipse whose major and a minor axes are identified. For the kth cell, the Θ_k,x angle is measured as the angle between the major axis and an arbitrary direction of the image, which we chose as the horizontal (x-axis; figure 5a). The {Θ_x} values in degrees (°) were reported in polar plots whose azimuth ranges from −90° to 90°, and the 0° corresponds to the elongation direction of the patterned stripes, stretching parallel to the y-axis. The distribution of {Θ_x} values was analysed along the length of the stripes up to a distance of 700 μm from the channel entrance (taken as L = 0), and up to 200 μm for the unpatterned region. Both distances were extracted from the fluorescence micrographs.

Analysis of the alignment of cell nuclei was also performed by estimating the order parameter that quantifies the average orientation of the nuclei [49]. In the azimuthal plane (two-dimensional), the order parameter is estimated using the procedure described in [50]. First, we construct the 2 × 2 order matrix S whose entry S_xy = [2 < cos Θ_x·cos Θ_y >− δ_xy], where δ_xy is Kronecker's delta, brackets indicate the arithmetic mean of the product of direction cosines, and Θ_y = 90° − Θ_x. Then, we diagonalize the S matrix, to yield the main alignment axis (director) as the one corresponding to the largest eigenvalue S_XX = < cos 2Θ>. The order parameter S_XX is equal to 1 when the nuclei are perfectly aligned along the director, whereas S is 0 when the orientation of the cell nuclei is random or the nucleus has an isotropic contour.

2.6. Data analysis

Graphic presentation and statistical analyses were performed using the OriginPro v. 8 SR2 software. Curve fitting was carried out on data weighted by their respective standard error (s.e.) using IgorPro Carbon (Wavemetrics, Lake Oswego, OR). FEM simulation was carried out with the Comsol Multiphysics software (Comsol, Inc.; see the electronic supplementary material). Pearson (one- and two-tailed) tests and regression analysis were performed by using GraphPad software Inc. (GraphPad Prism v. 5, San Diego, CA). A p-value ≤ 0.05 was considered statistically significant. All data are presented as mean ± s.e.m.

3. Results

3.1. Laminin patterns by micromoulding in capillaries

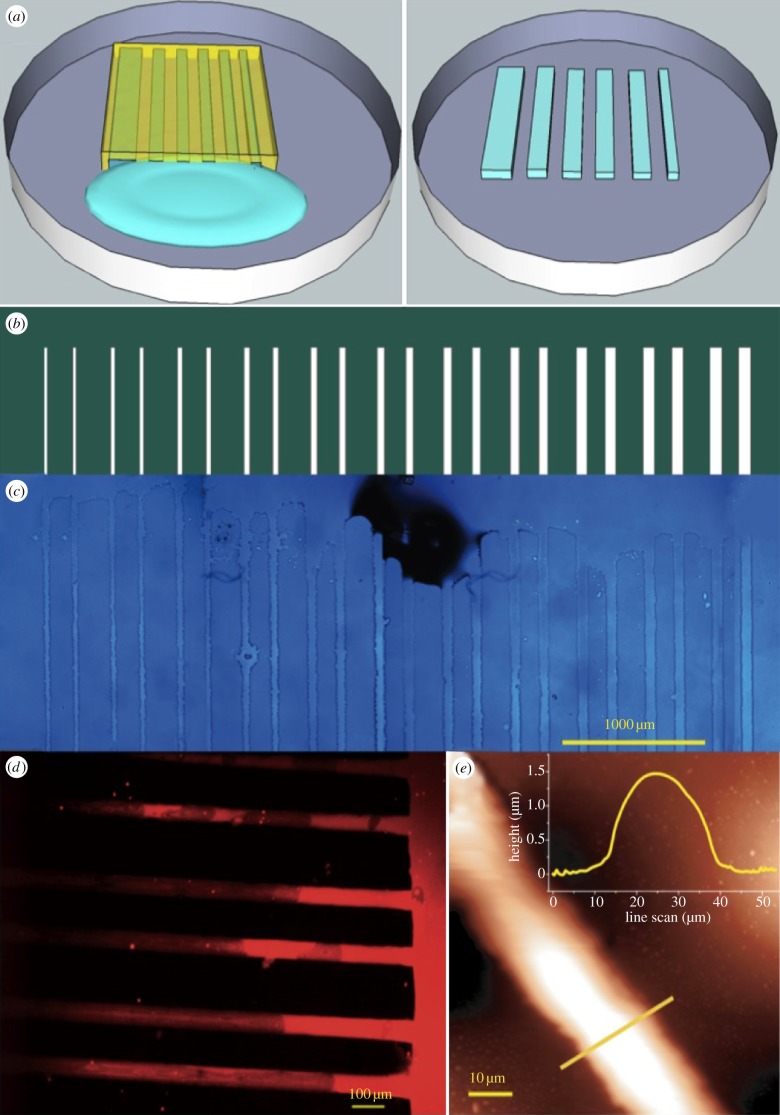
In figure 1, a description of the surface patterning using MIMICs is reported. The principle of this soft lithography approach is schematized in figure 1a, and the mask layout used for stamp replica moulding is shown in figure 1b. The length scales of the pattern were chosen because they match the typical average size of a neural cell such as the glial cell line used here (ca 10 µm). The laminin patterns were imaged by combining optical, fluorescence and scanning probe microscopies (figure 1c, d and e, respectively). The laminin stripes conformably reproduce the motif and the lateral sizes of the stamp channels (figure 1c,d). The maximum height of the protein stripes, upon fabrication, was approximately 1.5 μm as evidenced by the SPM topography image profile analysis (figure 1e), and stripe widths vary consistently with the lateral sizes of the stamp channels. The immunofluorescence assays performed after 24 h of incubation in cell culture medium show that the laminin pattern remains stable under cell culture conditions (figure 1d), indicating a good absorption of the protein onto the surface. The specificity of fluorescence labelling is demonstrated by the absence of fluorescence signals between the stripes and in control samples incubated in the absence of the primary anti-laminin antibody. The recognition of epitopes of laminin molecules by anti-laminin antibody indicates that it locally retains its conformational structure upon absorption onto the plastic surface.

Figure 1.

Laminin patterning on polystyrene TC dishes. (a) A schematic of the MIMIC patterning technique; (b) layout of the mask used for lithography: white lanes represent the channels at increasing widths (c) optical- (d) immunofluorescence- and (e) scanning probe micrographs with line profile (inset) of the patterned laminin stripes.

These results demonstrated that MIMICs are suitable method to fabricate a stable and geometrically controlled laminin deposition onto TC dishes, with no need of grafting or chemically modifying the substrate.

3.2. Analysis of laminin gradients

The formation of laminin surface concentration gradients along the patterned stripes was assessed by the quantitative analysis of immunofluorescence signals. For each stripe width, the fluorescence intensity was estimated on 70 adjacent areas along the stripe length of 700 μm calculated from the entrance of the channels. Each fluorescence intensity point comes from the integration on an area whose side is 10 μm long and whose width corresponds to the lateral size of the channel. The monotonic decrease of the fluorescence intensity versus the distance from the channel entrance, as depicted in the representative result in figure 2 (black dots), evidences the laminin gradient formation. The fluorescence intensity carries information about the local amount of the protein adsorbed onto the surface [20].

Figure 2.

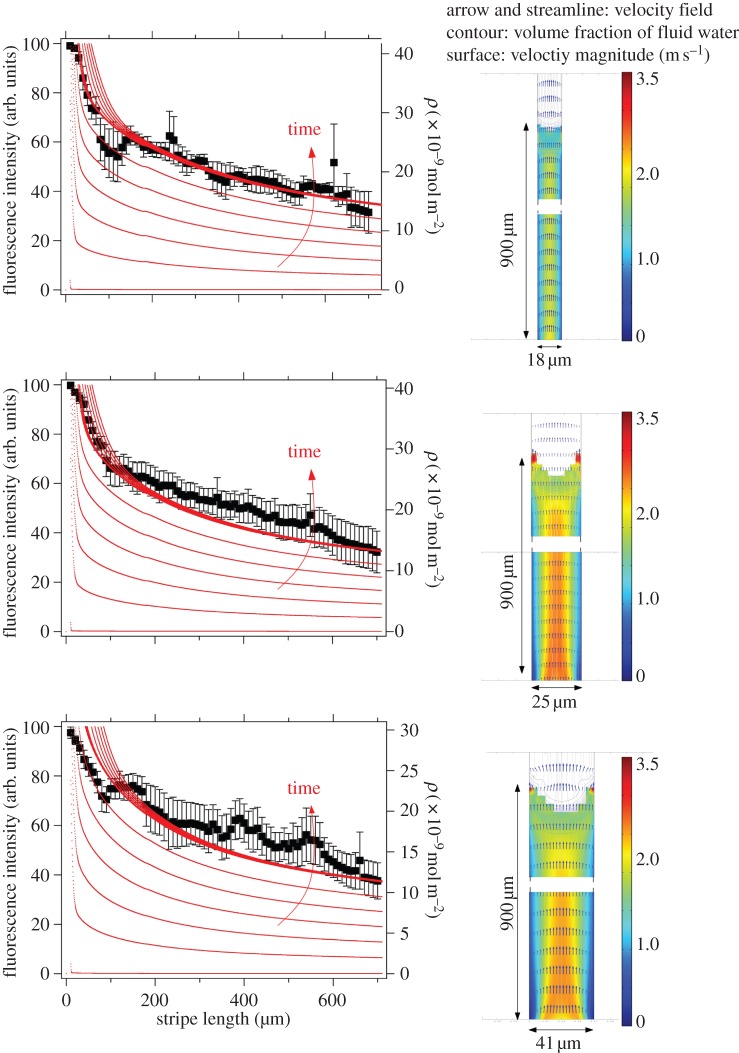
Laminin gradient analysis. (right panel) Velocity fields calculated on the horizontal plane of microchannels with width equal to 18, 25 and 41 μm; (left panel) representative data of laminin fluorescence intensities (y-axis, left) versus stripe length are shown for the same stripes. The black dots outline the decrease in fluorescence intensity. Concentration of adsorbed laminin (y-axis, right), obtained from finite-element calculation (see the electronic supplementary material), is plotted versus stripe length (continuous lines). The concentration gradient is increasing with time during MIMICs deposition.

We observed that the decrease of the fluorescence intensity along each stripe exhibits a double exponential decay: the first one accounting for the steeper slope (k₂) at distances approximately up to 100 μm, the latter (k₁) for the milder decreases at distances larger than 100 μm. We extracted the two parameters characterizing the decays for each stripe width and we plotted them in the graph of figure 3. The mean values for the inverse of decay length accounting for large distances and corresponding to k₁ = −0.0013 (±0.0003) μm⁻¹ do not significantly change as a function of the stripe width while a marked instability versus width is observed in the region less than 100 μm (closer to the reservoir), because k₂ = 0.037 (±0.0143) μm⁻¹.

Figure 3.

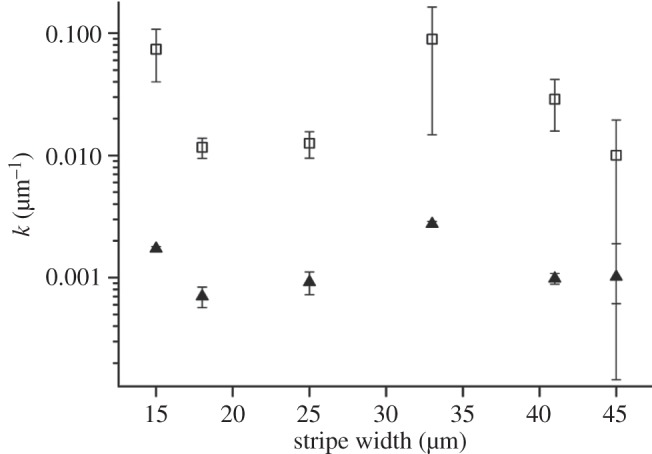
Inverse decay lengths of the double exponential fit extracted from the analysis of laminin fluorescence intensity. k₁ describes the slope of gradient at large distances from the reservoir (filled symbol), whereas k₂ regulates the second slope close to the reservoir (open symbol). Values are expressed as mean±s.e.m.

Assuming that the fluorescence intensity depends on the local density of laminin deposited on the surface, we can explain this result by a simple model where the laminin solution infills the capillaries upon the action of Laplace pressure, then the solute diffuses to the substrate. The density of deposited laminin reflects the concentration profile of the solution in the capillary.

FEM was carried out on the characteristic section of the microchannel involved in the MIMICs process (see the electronic supplementary material). The model domain has been simplified to a two-dimensional section of single PDMS microchannel, including the elastomeric wall and the TC dish for the cell culture as lower boundary. The velocity field was calculated by the Navier–Stokes equation, adapted to take into account the effect of surface tension acting along the channel boundaries. The transport of protein is governed predominantly by convection during the infilling (figure 2) and by diffusion at later stages when the microchannel is filled up, and there is no replenishment by fresh protein solution. The density of laminin adsorbed onto the TC dish surface (expressed as ρ; continuous thin lines in figure 2 at different times) was determined assuming surface diffusivity and kinetic equilibrium at the solid–liquid interface. The diffusion coefficient for laminin in cell culture medium was calculated using the Einstein–Stokes equation and equals 1.14×10⁻⁷ cm² s⁻¹ in the FEM model. This value is in the same range of that previously reported in the literature [12]. The velocity profile induced by surface tension differs from the standard Poiseuille parabolic distribution: it is not constant in time, and is locally modified by the change of the wetting properties upon adsorption. The flow of the medium may experience a deceleration caused by pinning effects, which occurs mainly at the TC surface boundary owing to the surface tension of PDMS lower than polystyrene.

FEM analysis yields an amount of adsorbed laminin that increases with time. Concentration is always higher at the entrance of the microchannels and decreases along the longitudinal axis of the channel. A comparison between the local density estimated from the simulation (figure 2, continuous thin lines) and the fluorescence intensity of laminin revealed by immunofluorescence staining (figure 2, black marker) supports the evidence that MIMICs generate a gradient of laminin along the main axis of the microfluidics channels.

MIMICs are responsible for the formation of the initial gradient of concentration inside the microchannel. After this, adsorption is mainly ruled by diffusion from the solution to the surface.

As the width of the microfluidics channel is larger than the steric hindrance of the protein, the channel does not filter laminin. This might not be the case when the MIMICs are performed with mesoscopic or nanochannels.

In figure 3, we report the two parameters k₁ and k₂ describing the double exponential decay of the gradient as a function of the channel width. These data show the behaviour of the two constants does not depend on the channel width.

3.3. Neural cell grown on laminin pattern

The ability of the laminin pattern to guide neural cell adhesion and proliferation was investigated through the analysis of nuclei orientation and cellular density. The 1321N1 astrocytoma cells were randomly seeded onto laminin-patterned substrates and they were let to proliferate under standard cell culture conditions in the presence of serum-containing medium. To visualize their shape, optical micrographs were collected, and sample images are reported in figure 4c,e. To visualize the nuclei, the cells were fixed and subsequently stained with the specific nuclei dye DAPI. Representative results after 6 days of incubation are also reported in figure 4.

Figure 4.

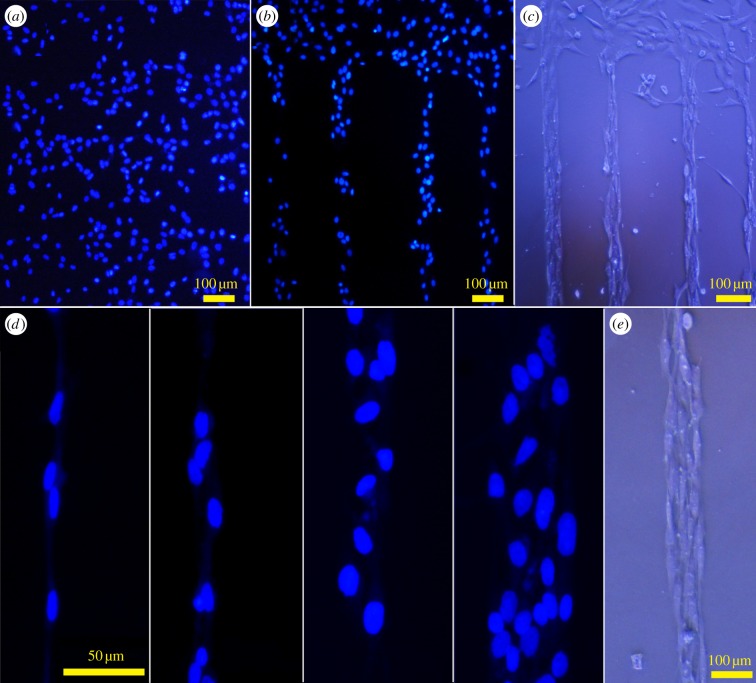
Optical and fluorescence micrographs of 1321N1 astrocytoma cells after 6 days of incubation under standard cell culture conditions (37°C, 5% CO₂, 90% RH). Nuclei of 1321N1 astrocytoma cells stained with DAPI on laminin-unpatterned (a) and -patterned (b) regions of polystyrene TC dishes; (d) higher magnification images showing details of nuclei organization in parallel lanes onto laminin stripes with increasing widths. In (c,e), optical images of the patterned culture where the whole cell shape can be appreciated.

On laminin-patterned TC dishes, selective adhesion of the neural cells along patterned stripes was observed (figure 4b), whereas on unpatterned regions, cells proliferated without any preferential orientation and position on the surface (figure 4a). This cell behaviour was observed despite the presence of serum in the culture medium and in the absence of passivation of the TC dish surface with any anti-fouling agent even at prolonged cell incubation times. Figure 4b clearly shows that the proliferation of cells follows the geometrical distribution of the laminin pattern onto the surface. Cell nuclei are visible over the laminin-patterned areas. They are accommodated in almost parallel lanes within a stripe (figure 4d). The number of cells across the stripe scales proportionally to the stripe width, ranging from a single cell lane in the case of the smaller stripes (15 µm; figure 4d, left panel) up to four parallel lanes for the larger ones (45 µm; figure 4d, right panel). Interestingly, no cells are found between the laminin stripes, independently of the spacing between the stripes. This indicates that during the culture, all adhered cells migrate preferentially towards the protein stripes and proliferate onto them [18]. This happens without any previous anti-fouling passivation processes of the surface between the stripes, but by exploiting the hydrophobicity contrast of polystyrene surface with respect to the laminin pattern that creates adjacent cell-adhesive/cell-repulsive regions on the substrate.

We also infer that the lateral diffusion of laminin from the patterned stripe creates spontaneously a concentration gradient that cells follow to migrate and anchor to the stripe. This is confirmed by the observation that the number of attached neural cells per area unit decreases by increasing the distance from the reservoir proportionally to the stripe width (data not shown). Moreover, the statistical analysis performed by Pearson tests (n = 7) between the cell density and the immunofluorescence signal values shows a significant positive correlation (r = 0.7546, p < 0.05, for 25.8 μm stripe width) and linear regression.

3.4. Correlation between laminin gradient and orientation order parameter

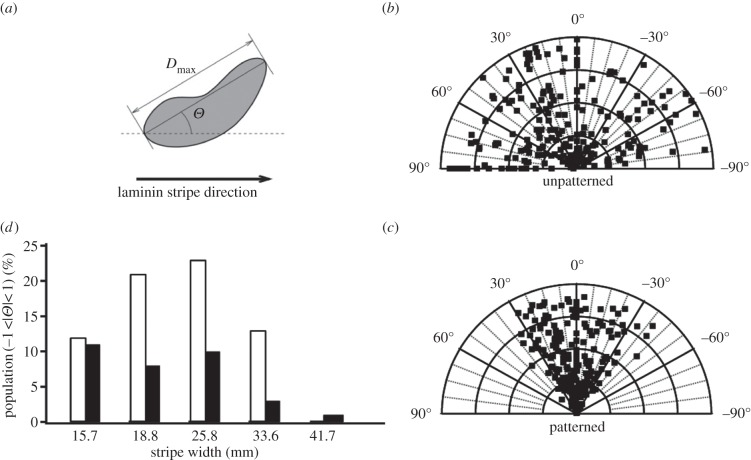
We assessed the influence of laminin gradient on neural cell alignment. The orientation of the neural cell nuclei was quantitatively analysed in both laminin-unpatterned and -patterned areas by measuring the orientation of the nucleus as described in the experimental section. For the laminin-patterned surface, the angle Θ is defined as the angle between the direction of the laminin stripe and the major axis of the cell nucleus, as shown in figure 5a. The distribution of Θ angles was analysed along the stripes for each width. Representative polar plots for laminin-unpatterned and -patterned regions are shown in figure 5b and c, respectively. The data revealed a random distribution for cells grown on unpatterned areas with an angle mean value = 44.2°±2.3°. On laminin-patterned surfaces, the values of Θ angles were mainly distributed in the –20°/+20° range. More specifically, in figure 5d, we plot the percentile population of cell nuclei aligned within −1° < Θ < 1° versus stripe width for various distances from the reservoir. The population showing Θ angles in this range was always higher in the region closer to the reservoir (white column), which is characterized by the higher laminin immunofluorescence intensity and a steeper gradient slope. This trend was observed for each stripe width. The narrower channels yield a higher percentage of aligned cells with a maximum of 25% corresponding to the stripe with 25.8 μm nominal width. The population of aligned cells tends to decrease with increasing stripe width down to only 2% for 41.5 μm nominal width. This indicates that the aligning effect of the gradient is more relevant when the stripe can host only one cell inducing also a lateral confinement.

Figure 5.

Analysis of the orientation angles of 1321N1 cell nuclei. (a) Definition of the orientation angle Θ of nucleus along the laminin stripe direction. Polar plots of angle values for cells on laminin-unpatterned (b) and -patterned (c) regions of TC dishes (representative example for stripe with 25.8 μm nominal width is shown). (d) Percentage population of nuclei with angle values −1° < Θ < 1° (indicating high grade of alignment) versus stripe width, estimated in region closer (white bars) and further from the reservoir (black bars).

To quantify and correlate the effect of the laminin gradient on cell nuclei orientation, we plot (figure 6) the order parameter S (expressed as <cos 2Θ>) versus gradient slope, for short (k₂, squares) and long (k₁, triangles) distances from the reservoir. First of all, it is crucial that the S-values on patterned stripes are much higher than the ones on the laminin-unpatterned regions (S = 0.128 ± 0.057). The order parameter tends to decrease from 0.8 to 0.65 as the stripe width increases close to the reservoir, whereas it is almost constant in the other region with values ranging from 0.65 to 0.7. Owing to the weak correlation found between the mean gradient at both length scales and the stripe width in the range explored (figure 3), we cannot establish without uncertainty a correlation between the orientational order parameter and the laminin gradient. The existence of such a correlation is instead suggested by the data in figure 6, at least for the steeper regions of the gradient where the local laminin concentration vary over distances comparable with the cell size (≈15 µm). The same effect does not take place for long distances where the gradient is probably too smooth for the cells to appreciate the differences.

Figure 6.

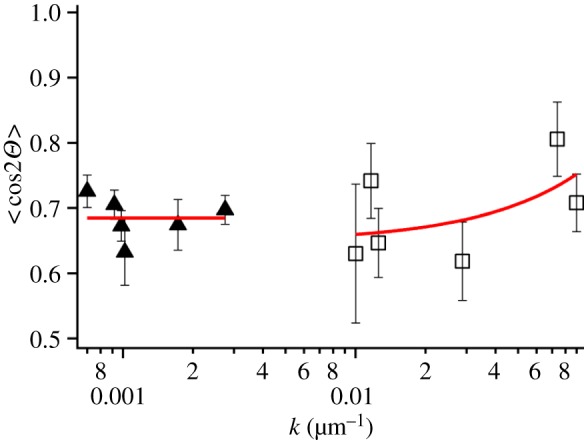
Correlation between order parameter S = < cos2Θ > versus exponential decay length (k₁ and k₂) of the gradients. Values corresponding to the region close to (squares) and far from (triangles) the reservoir. (Online version in colour.)

These results support the hypothesis that the laminin concentration gradient along the stripe promotes cellular recruitment and adhesion at the patterned regions, as well as their anisotropic alignment along the patterned stripes. The large laminin gradient observed in the initial 100 μm appears correlated to the enhanced alignment. The dependence of the degree of alignment on stripe width suggests that neighbouring cells interact side by side, and the signals exchanged by the neighbour cells can overcome the ones induced by the patterned cues.

4. Discussion

In this work, we generated a gradient of the ECM protein laminin onto a commercial TC dish surface by MIMICs for selectively favouring the neural cell adhesion and proliferation. We have recently demonstrated that cell guidance may be achieved even on anti-fouling surfaces, such as Teflon, by patterning laminin stripes [42]. In such substrates, the adhesion propensity gradient of the cells between the pattern and the substrate was even sharper. Here, we have shown that stringent control can be achieved even on a plastic, non-anti-fouling surface through a simple technological method to pattern laterally confined laminin gradients as the chemical cell guidance cue.

Our approach does not require any background passivation step, whereas many other methods use surface pre-treatment with an anti-cell-adhesion layer such as poly(ethylene glycol) to enhance compositional contrast [51,52] or by creating double-cue opposing gradients [19]. Here, we have exploited the surface tension feature of the polystyrene substrate (contact angle = 67.3°±1.5°) to maintain the cell culture confinement for a prolonged time in the presence of serum-containing medium.

In fact, the uncharged and mildly hydrophobic surface of untreated polystyrene TC dishes used in this work is reported to partially prevent the adsorption of proteins and other biomolecules contained in the cell culture medium; cells and biomolecules bind this surface only through passive hydrophobic interactions [53]. Hydrophilic (wettable) surfaces such as those of polylysine-coated glass slides [54] as well as positive surface charges have a beneficial effect on cell adhesion [55,56]. The effectiveness of laminin in adhesion-promoting properties may also depend on the addition of serum in the medium and on the nature of the substrate [57]. In our experiments, we have combined all the above-mentioned effects; the specific immunofluorescence staining of the patterned laminin indicates that the protein epitope is functionally maintained upon protein adsorption onto the polystyrene surface, suggesting a functional assembling of the laminin that allows to mediate the specific cell adhesion via integrins. The molecular structure of laminin, a cruciform heterodimer, through its cell-surface receptor binding domain may interact with the neural cell anchorage to the pattern and guide cell proliferation.

In summary, this study shows that is possible to achieve directional and spatial control of neural cell growth over long periods of time by means of patterned protein gradients. Similar results were obtained by using two different neural cell phenotypes such as the human astrocytoma 1321N1 and neuroblastoma SH-SY5Y cell lines. Both cell types proliferate according to directional cues in the patterned signal. Larger laminin gradients were found to favour the adhesion and alignment of neural cells along the direction of the patterned stripes. This result is in agreement with previous studies reporting a gradual decrease in cell density in relation to a laminin concentration decrease [13,19] and of well-oriented axons in the direction of increasing surface density of laminin [12].

5. Conclusion

We have demonstrated an easy method for fabricating ECM protein gradients with a controlled and reproducible geometry. The resulting patterns guide neural cell growth and orient cells along the pattern direction. The MIMICs technique described is a general route to fabricate surface gradients of soluble biomolecules. Compared with techniques that use diffusion of protein in gels [17,38], controlled doping of porous membrane with protein solutions [58] or electric-field-induced formation of gradients in supported lipid bilayers [59], this approach allows an easy formation and the immobilization of gradients over multiple length scales in one step and without any surface passivation. By this process, a stable and localized topographical functionalization of the polystyrene surface has been achieved. The applied method has the advantage of being simple, quick, low-cost, versatile and reproducible. It is worth noting that, being based on the balance of the protein diffusion and protein surface adsorption, this procedure may allow fabrication of a tunable gradient by varying the length of the stamp channels as well as the concentration of the molecules of interest [13,60]. The detailed analysis of the spatial organization of neural cells on diffusive protein gradients generated through this method evidenced a preferential adhesion of cells onto laminin stripes and their proliferation in confined stripes for several days with lateral control and orientation of nuclei.

Patterning is an effective tool to govern the chemical stimuli-induced organization of different cell phenotypes, also in co-culture studies. It could open up a new way for fabricating arrays or multi-layer architectures of multiple cell types to investigate cell–cell interactions, signalling cross-talk and cell response to toxic and/or pharmacological agents with potential applications in pharmaceuticals, diagnostics and toxicology as well as in implant technology, including tissue engineering. To the best of our knowledge, this is the first study to exploit MIMICs and the fluid dynamics underlying this method to fabricate in one-step a laminin gradient onto polystyrene TC surfaces, allowing control of neural cell growth.

Funding statement

This work was supported by the EU projects ESF-EUROCORES (10-EuroBioSAS-FP-009) ‘Intelligent Cell Surfaces (ICS)’; FP7-NMP-2011280772-2 ‘Implantable Organic Nano-Electronics’ (I-ONE) and the Italian projects PRIN 2008 (2008JJTFCW_003) ‘Multiscale Patterning for Tridimensional Tubular Scaffold’; Consorzio Spinner 2013 (Call 2010) ‘Biological Innovative Analysis by Software (BIAS)’.