Honeybee navigation: critically examining the role of the polarization compass

Abstract

Although it is widely accepted that honeybees use the polarized-light pattern of the sky as a compass for navigation, there is little direct evidence that this information is actually sensed during flight. Here, we ask whether flying bees can obtain compass cues derived purely from polarized light, and communicate this information to their nest-mates through the ‘waggle dance’. Bees, from an observation hive with vertically oriented honeycombs, were trained to fly to a food source at the end of a tunnel, which provided overhead illumination that was polarized either parallel to the axis of the tunnel, or perpendicular to it. When the illumination was transversely polarized, bees danced in a predominantly vertical direction with waggles occurring equally frequently in the upward or the downward direction. They were thus using the polarized-light information to signal the two possible directions in which they could have flown in natural outdoor flight: either directly towards the sun, or directly away from it. When the illumination was axially polarized, the bees danced in a predominantly horizontal direction with waggles directed either to the left or the right, indicating that they could have flown in an azimuthal direction that was 90° to the right or to the left of the sun, respectively. When the first half of the tunnel provided axial illumination and the second half transverse illumination, bees danced along all of the four principal diagonal directions, which represent four equally likely locations of the food source based on the polarized-light information that they had acquired during their journey. We conclude that flying bees are capable of obtaining and signalling compass information that is derived purely from polarized light. Furthermore, they deal with the directional ambiguity that is inherent in polarized light by signalling all of the possible locations of the food source in their dances, thus maximizing the chances of recruitment to it.

1. Introduction

Over the past five decades, considerable effort has been devoted to understanding the strategies and visual cues that honeybees use to navigate to food sources, and to uncovering the underlying mechanisms. We now know that bees are not only capable of estimating the distance and the direction of an attractive food source, but also of communicating this information to their nest-mates, through the famous ‘waggle dance’ [1]. In the waggle dance, which is performed on the vertical surface of a honeycomb, bees indicate the azimuthal direction of the food source relative to the azimuth of the sun as the angle between the vertical and the direction of the axis of the waggle. The sun is used as a reference in the bee's internal compass. Thus, a dance with a waggle axis oriented 30° clockwise with respect to the vertical implies that the food source is positioned along a direction that is oriented 30° clockwise with respect to the sun's azimuth. As the day advances, the sun changes its azimuthal position in the sky. Consequently, when a bee flies regularly to and from a given food source through the day, the direction of the waggle axis changes systematically as the sun marches across the sky. When the sun is obscured by a cloud, it is believed that bees are still able to obtain a compass reference from the unoccluded part of the sky, by making use of the pattern of polarization that the sun creates in the sky [2,3].

Rayleigh scattering of sunlight by the Earth's atmosphere causes the sun to produce a characteristic pattern of polarization in the sky [3], as shown in figures 2 and 3. If the sun is imagined to be at the pole of the celestial sphere, the e-vectors of the polarized-light pattern in the sky are oriented parallel to the lines of latitude of the sphere, and the degree of polarization of the light is strongest at the equator. Thus, when the sun is near the horizon but obscured by a patch of cloud, the degree of polarization in the sky will be strongest at the zenith, and, if that part of the sky is visible, then a bee can make use of the direction of the e-vector in that region to infer its direction of flight. Flight in a direction perpendicular to the e-vector must mean that the bee is heading directly towards the sun, or directly away from it. On the other hand, flight in a direction parallel to the e-vector must mean that the sun is directly to the left or to the right of the bee, i.e. that the bee is flying at an azimuthal direction that is oriented 90° away, either clockwise or counterclockwise, from the direction of the sun.

Figure 2.

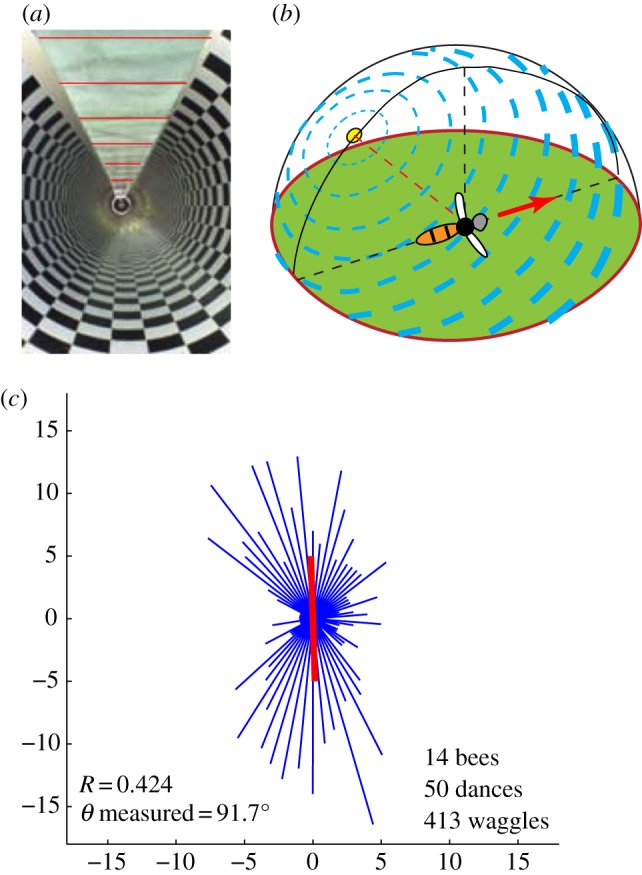
Results of Experiment 2, in which bees flew in a tunnel with transversely polarized illumination, as depicted by the lines on the ceiling in (a). This illumination mimics the pattern of polarized illumination that a bee would experience if it were to fly directly away from the sun, as shown in (b), or directly towards it. In (c), the thin lines (blue in the online version) depict the dance orientation histogram. The thick line (red in the online version) depicts the mean direction of the waggle axis, taking into account the up–down symmetry in the dance directions, as described in §2. This mean direction is oriented 91.7° counterclockwise relative to the horizontal rightward direction. (Online version in colour.)

Figure 3.

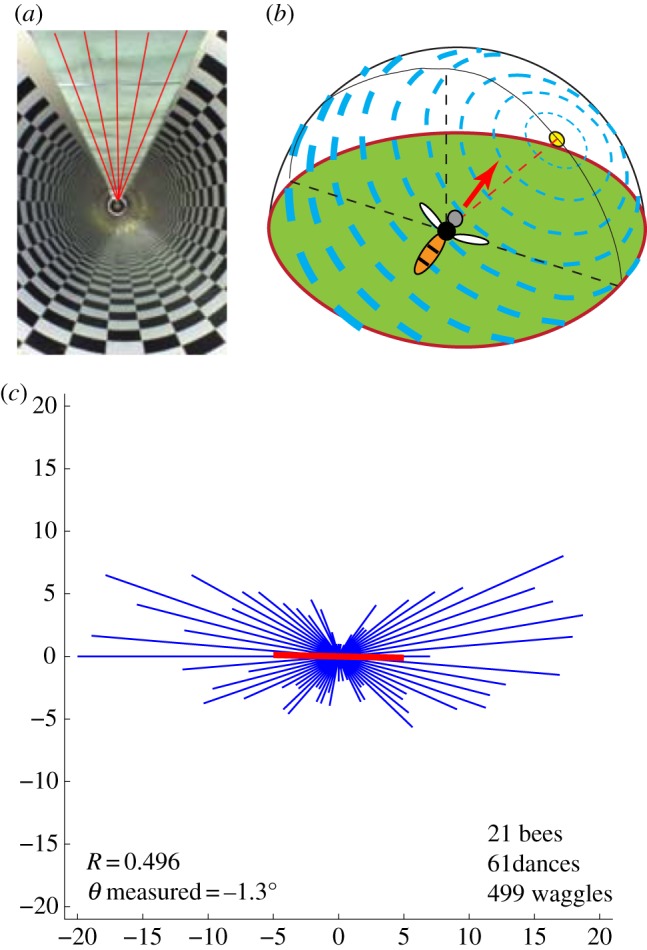
Results of Experiment 3, in which bees flew in a tunnel with axially polarized illumination, as depicted by the lines on the ceiling in (a). This illumination mimics the pattern of polarized illumination that a bee would experience if it were to fly in a direction such that the sun is 90° to the right, as shown in (b), or 90° to the left. In (c), the thin lines (blue in the online version) depict the dance orientation histogram. The thick line (red in the online version) depicts the mean direction of the waggle axis, taking into account the left–right symmetry in the dance directions, as described in §2. This mean direction is oriented 1.3° clockwise relative to the horizontal rightward direction. (Online version in colour.)

There is considerable evidence that bees have the capacity to sense the direction of the e-vectors in the celestial polarization pattern [1,4–9]. The photoreceptors in the dorsal rim area of the honeybee's compound eyes exhibit a strong sensitivity to polarized light [10,11]. Moreover, polarization-sensitive interneurons have been found in the medulla [12], suggesting that the polarization pattern in the sky may indeed be analysed by the brain. However, these observations do not, on their own, demonstrate that bees perceive the polarization pattern of the sky and use it to measure or set their flight course. The requisite proof must come from a behavioural experiment.

To our knowledge, there is so far only one study that has examined whether flying bees can use information based purely on the e-vector pattern of the overhead illumination, to navigate to food sources. Kraft et al. [13] showed that bees can be trained to navigate a four-armed maze by learning routes in which the direction of polarization of the overhead illumination remained constant. However, that study did not explore whether or how this navigational information is transmitted to other bees.

The lack of direct evidence that bees use information on the polarization of light to gauge and signal the position of a food source to their nest-mates is not surprising, given the technical difficulties of creating and presenting artificially polarized celestial patterns to freely flying, foraging bees. The question is an important one that needs to be tackled.

Here, we address this question by training bees to fly along a short, narrow tunnel to a food reward, and recording their dances when they return to the hive. Earlier studies have shown that flight in such tunnels can simulate considerably longer flights outdoors, because of the relatively large magnitude of optic flow that they induce in the bees’ eyes, when compared with outdoor flight in a normal environment [14–16]. It is well established that distances and directions to food sources are determined only on the outbound journey, and not during the homeward flight [1,17–19]. By recording changes in the dances of the returning bees when the polarized-light pattern in the ceiling of the tunnel is artificially manipulated, we are able to show, clearly and conclusively, that bees are indeed capable of using the e-vector pattern in the sky to measure the direction of their flight to the food source and report it in their dances.

We also find that the bees indicate more than one direction for the food source in their dances, demonstrating that they take into account all of the ambiguities that are associated with inferring flight directions on the basis of the e-vector pattern alone. Depending upon the experimental situation, a bee can signal up to four possible directions of the food source in a single dance.

2. Material and methods

The experiments were conducted at a location in the Southern Hemisphere (Brisbane, Australia). Individually marked bees (Apis mellifera, L.) were trained to fly from an observation hive into a tunnel of a circular cross section, 12 m long and 23 cm in inside diameter, to forage from a sugar water feeder placed at the far end. The inside of the tunnel was lined with a black-white checkerboard texture, of check size 2.5 cm. The tunnel was positioned directly in front of the hive entrance, pointing approximately towards the north (in exact terms, 7° east of magnetic north and 18° east of true north). Thus, bees flew approximately northward towards the food inside the tunnel, as shown in figure 1. The distance from the hive entrance to the tunnel entrance was 175 cm. Therefore, the dominant portion of the flight to and from the food occurred within the tunnel.

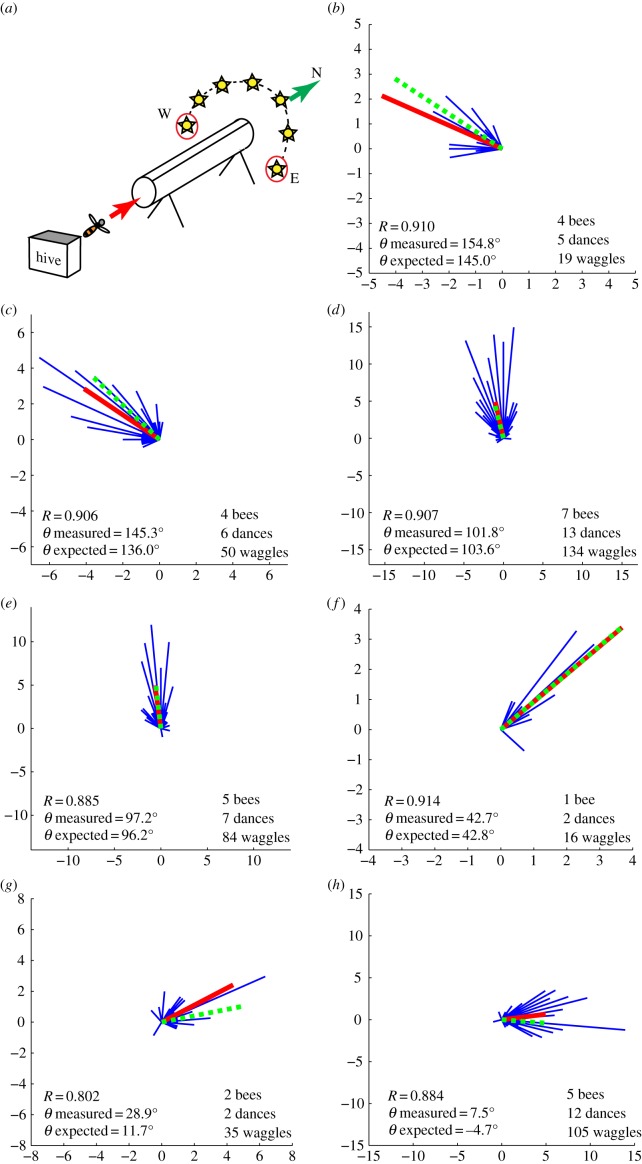
Figure 1.

Results of Experiment 1, in which bees flew in a tunnel with a view of the natural sky over a period of 1 day (13 March 2008) with the sun at various positions as shown in (a). The tunnel pointed in a direction 18° east of true North. The panels show orientation histograms of the waggle axes obtained on this day at various times of the day: (b) 7.56–9.09, (c) 9.15–9.30, (d) 10.47–11.10, (e) 11.10–11.20, (f) 12.41–12.46, (g) 14.13–14.25 and (h) 15.20–16.15. In each panel, the thin lines (blue in the online version) depict the dance orientation histogram. The thick continuous line (red in the online version) shows the mean dance vector. For clarity, the mean dance vector is shown as 6× the actual length. Thus, the maximum possible length of the mean vector as shown here would be 6.0, rather than 1.0. The thick broken line (green in the online version) denotes the dance direction expected at that particular time of day, calculated as described in §2. These values are 145.0°, 136.0°, 103.6°, 96.2°, 42.8°, 11.7° and –4.7°, respectively in (b) through (h), the angles being defined as positive counterclockwise with respect to the rightward horizontal direction. The length of this line has no significance, but it is shown equal to the length of the thick line to facilitate comparison of their directions. In this and subsequent figures each panel shows the magnitude (R) and direction (θ) of the mean vector calculated as described in §2, and the number of bees, number of dances and number of waggles analysed. (Online version in colour.)

An 11 cm wide dorsal section of the tunnel was open to the sky, throughout its length. Depending upon the experiment, this open section was covered either with an insect-screen mesh to retain the bees in the tunnel on their way to the feeder, or with UV-transmitting polarization filters (HN22 linearly polarizing filter, Polaroid) placed under a sheet of diffusing paper. When flying under the mesh, bees were able to see the open sky. For a bee flying along the axis of the tunnel, the overhead opening would have subtended a vertical angle of ca 53°. When flying under the filters, the bees were exposed only to an artificially polarized light stimulus. The diffusing paper above the polarizers removed any polarization in the light incident on the tunnel before it reached the polarization filters. It also eliminated any view of the sun or other overhead landmarks. The polarization filters could be oriented so as to make the e-vector of the overhead illumination either parallel to the long axis of the tunnel (hereafter referred to as axial polarization) or perpendicular to the long axis (hereafter referred to as transverse polarization).

Four experiments were carried out, each with a fresh group of individually marked bees. In Experiment 1, bees were trained to fly through the tunnel with a view of the sky—the top of the tunnel was covered with the insect screen mesh. Based on the geometry of the tunnel, the width of the dorsal opening, and the trajectory of the sun on the dates that the experiments were conducted we estimate that, on a clear day, the sun would have been directly visible to a bee flying along the axis of the tunnel, for about 3.5 h (ca 9.20–12.45). In Experiment 2, the entire length of the tunnel provided transverse polarization. In Experiment 3, the entire length of the tunnel provided axial polarization. In Experiment 4, the first half of the tunnel (the first 6 m) provided transverse polarization, whereas the second half provided axial polarization.

Dances of marked bees returning from the feeder were video-filmed on both sides of the observation hive at 25 frames per second using two Canon MV920 video cameras. For each of the four experiments, the video was played back, frame by frame, to measure the direction of the waggle axis, using an electronic protractor (Trilithon Software Inc.). Since flight through the narrow tunnel simulated a much longer flight outdoors [14–16], the waggle durations were long enough (typically of the order of 230 ms) to enable the direction of the waggle axis to be measured with a precision of 5°.

In the case of Experiment 1 (flight with view of the sky), the expected direction of the waggle axis for each dance was obtained from knowledge of the orientation of the tunnel (18° east of true north), and of the sun's azimuth at the time of recording of the dance. The sun's azimuth was obtained from tables available on the Internet (US Naval Observatory, Washington, DC, USA, http://aa.usno.navy.mil/data/docs/AltAz.php) for the time of the day, the day of the year and the latitude and longitude of the experimental site in Brisbane. The expected direction of the waggle axis was thus the azimuthal angle between the sun and the tunnel direction, measured eastward from the sun to the tunnel direction. This angle was plotted counterclockwise from the vertically upward direction in the plane of the honeycomb and is shown as the thick broken line in the plots of figure 1 (green in the online version). Dances were recorded throughout the day, and dance data were analysed separately for a series of short time windows (each typically 10–30 min in duration) by pooling data within each window. For each time window, the solar azimuth was taken to be that prevailing at the mid-point of that window.

Waggle durations were also measured for each of the four experiments by stepping though the dances frame by frame, counting the number of frames during which the waggle occurred, and multiplying this number by the inter-frame interval (40 ms).

(a). Data analysis

Polar histograms of the distribution of waggle axis orientations, accumulated over several dances and several bees, were plotted using 5° bins. The value in each bin represents the number of waggle phases whose orientation was within ±2.5° of the mean orientation represented by that bin. For simplicity, we refer to the number of waggle phases analysed in each experiment as the number of waggles. These numbers, as well as the number of dances analysed and the number of bees involved are specified in the panels of figures 1–3 and 6 and electronic supplementary material, figure S2. In the cases where the number of dances is greater than the number of bees, some bees contributed more than one dance to the analysis.

Figure 6.

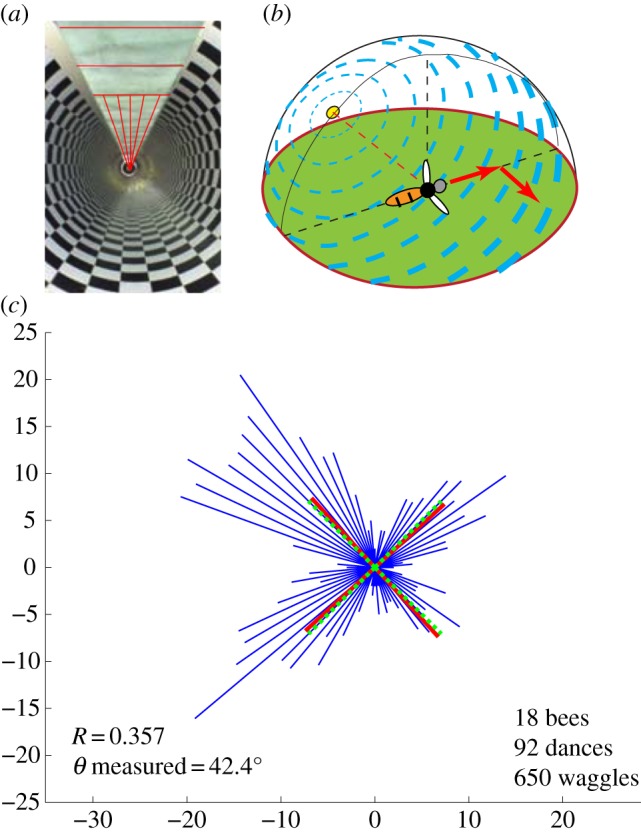
Results of Experiment 4, in which bees flew in a tunnel with transversely polarized illumination in the first half and axially polarized illumination in the second half, as depicted by the lines in the ceiling in (a). This arrangement mimics the overhead illumination that a bee would experience if it were to fly initially in a direction directly away from the sun, as shown in (b), or directly towards it, and subsequently in a direction such that the sun is 90° to the right, as shown in (b), or 90° to the left. In (c), the thin lines (blue in the online version) depict the dance orientation histogram. The thick continuous lines (red in the online version) show the four modal dance directions, computed as described in §2. The thick broken lines (green in the online version) show, for comparison, the four principal diagonal directions: 45°, 135°, 225° and 315°. (Online version in colour.)

In Experiment 1, the mean dance vector for each histogram was calculated as the vector sum of the waggle counts in the individual directional bins, divided by the sum of all of the counts, as described by Batschelet [20]. The result was a vector whose direction represented the mean direction of the waggle axis, and whose length was an inverse measure of the scatter of the data about this mean direction. A mean dance vector of length 1.0 implied that all of the individually measured waggle axis directions were in exactly the same direction, i.e. that there was no scatter. On the other hand, a mean dance vector of length 0.0 implied that the waggle axes were distributed uniformly in all directions, i.e. that there was no tendency for the bees to dance in any particular direction. The Rayleigh test [20, pp. 54–58] was used to test whether the mean dance vector was significantly different from zero, i.e. to examine whether there was a significant tendency for the bees to dance in a particular direction, rather than in a randomly oriented fashion. The V test [20, pp. 58–60] was used to test the hypothesis that the dance directions were significantly different from random and were clustered around the dance direction expected on the basis of the sun's azimuth.

In Experiments 2 and 3, the direction of the waggle axis was calculated by taking into account the observed mirror symmetry in the dance directions (up versus down in figure 2, and left versus right in figure 3). This was accomplished by computing the mean dance vector after doubling the measured waggle axis angles, then halving the angle of the resulting vector and plotting the result as an axis oriented along this direction and the diametrically opposite direction. This procedure is described by Batschelet [20, pp. 21–29].

In Experiment 4, the modal directions of the waggle axes were calculated by taking into account the observed fourfold mirror symmetry in the dance directions (45°, 135°, 225° and 315° in figure 4). This was accomplished by computing the mean dance vector after quadrupling the measured waggle axis angles, and then taking one-quarter of the angle of the resulting mean vector and plotting the mean preferred directions as axes oriented along this direction, as well as three other directions oriented at 90°, 180° and 270° to the direction. This procedure for analysing periodically arranged, multimodal peaks in orientation distributions is described by Batschelet [20, pp. 21–30].

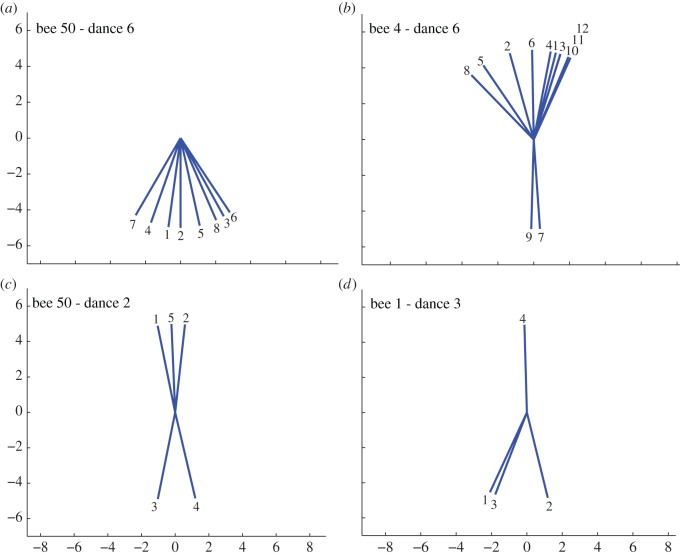
Figure 4.

(a–d) Four examples of dances of individual bees returning from a tunnel that provided transversely polarized illumination (Experiment 2). Each panel shows the waggle axis orientations recorded sequentially in a single dance. (Online version in colour.)

In Experiments 2–4, the statistical significance of the preferred dance directions was evaluated by applying the Rayleigh test to the doubled angles (Experiments 2 and 3) or to the quadrupled angles (Experiment 4), as described by Batschelet [20, pp. 20–30].

In analysing the distances indicated by the dancing bees in Experiments 2–4, the waggle durations were measured for at least 90 waggles under each experimental condition. The Student's t-test and single factor ANOVA were used to test for statistically significant differences.

3. Results

(a). Experiment 1

Here, bees were flown in the tunnel with a view of the sky, and their dances were recorded at various times of the day (13 March 2008), as described in §2. The tunnel pointed approximately in the northern direction (or, more precisely, 18° east of true north) so that the sun was to the right of the flight direction in the morning and to the left in the afternoon (figure 1). The bees display a mean dance direction that is shifted counterclockwise with respect to the vertical in the morning, and clockwise in the afternoon. As the sun's azimuth shifts progressively from east to west through the day, the mean dance vector rotates progressively in the clockwise direction, commencing with an early-morning direction that is oriented nearly 90° counterclockwise from vertical, and finishing with a late-afternoon direction that is oriented nearly 90° clockwise from vertical (figure 1). At each of the time windows (figure 1b–h), the mean dance vector is significantly different from zero in magnitude (p < 0.001 in each case, Rayleigh test), implying that the dances are not randomly oriented. Furthermore, the mean dance direction is not significantly different in direction from the direction that is expected at that time (p < 0.0001 in each case, V test). Similar results were obtained when the experiment was repeated on another day (21 April 2008; data not shown). These results indicate that the bees flying in the open tunnel of Experiment 1 were clearly able to use celestial cues to determine the direction of their flight in the tunnel. However, this experiment does not reveal what celestial cues the bees were using to determine their flight direction. Potential cues could have been the position of the sun, the pattern of polarization in the sky, as well as gradients of intensity or colour that migrated with the sun as it moved across the sky.

(b). Experiment 2

To examine whether bees use the pattern of polarization in the sky as a cue to establish their flight direction, in Experiment 2 the open section of the tunnel was covered with polarization filters oriented so as to provide illumination with the e-vector oriented transversely to the tunnel's long axis, as shown in figure 2a. Bees foraging in this tunnel displayed a striking and statistically significant tendency to dance in a preferred direction—the dances were not randomly oriented (R = 0.42, p < 0.001, Rayleigh test). The dances were directed predominantly upwards or downwards. Horizontally oriented dances (oriented either to the left or the right) were very infrequent. The mean direction of the dance axis was oriented 91.7° counterclockwise with respect to the rightward horizontal direction (thick line, figure 2c). This was very close to the vertical direction and was not significantly different from it (p < 0.0001, V test).

How do individual bees signal the direction of the food source under these conditions? Detailed analysis of individual dances revealed that some bees tended to orient their waggles consistently in the downward direction (figure 4a), and others predominantly in the upward direction (figure 4b). A third group of bees signalled both directions within a single dance: the waggle was directed upward in some loops and downward in others (figure 4c,d).

(c). Experiment 3

In Experiment 3, the open section of the tunnel was covered with polarization filters oriented so as to provide illumination with the e-vector oriented parallel to the tunnel's long axis, as shown in figure 3a. Bees foraging in this tunnel again did not orient their dances randomly, but displayed a strong and statistically significant tendency (R = 0.50, p < 0.001, Rayleigh test) to direct their dances predominantly leftwards or rightwards. Vertically oriented dances (oriented either upwards or downwards) were very infrequent. The mean direction of the dance axis was oriented 1.3° clockwise with respect to the rightward horizontal direction (thick line, figure 3c) and was not significantly different from it (p < 0.0001, V test).

Detailed analysis of individual dances in this experimental condition revealed a pattern that was analogous to that observed in Experiment 2. Some bees tended to orient their waggle consistently in the rightward direction (see electronic supplementary material, figure S1a), others in the leftward direction (see electronic supplementary material, figure S1b), and a third group of bees signalled both directions within a single dance (see electronic supplementary material, figure S1c,d).

(d). Influence of time of day when foraging under constant, artificially polarized illumination

When the view of the sky was eliminated and the bees were shown artificially polarized illumination, as in Experiments 2 and 3, the dance directions were not at all affected by the time of day. With the transverse e-vector illumination, the waggle dances were always oriented vertically (upwards or downwards), regardless of the time of day. An example is shown in figure 5, which compares orientation histograms for dances measured between 12.55 and 13.14 (figure 5a), and between 14.40 and 15.16 (figure 5b). In each case, the mean dance orientation was very close to the vertical axis (upwards or downwards), even though the mid-points of the time windows during which the two sets of dances were recorded (13.04 and 14.58, respectively) were separated by nearly 2 h. If the bees were using the azimuthal position of the sun to direct their dances at these times, their dance directions would be expected to be unimodal and oriented at 37° and 4° counterclockwise, respectively, relative to the rightward horizontal direction.

Figure 5.

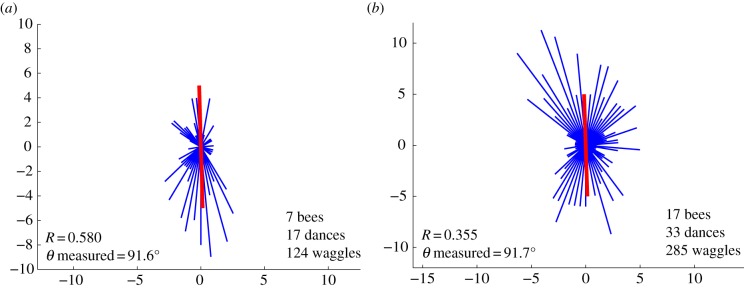
Dance orientation histograms for bees flying in a tunnel with transversely polarized illumination (Experiment 2) between 12.55 and 13.14 on 1 May 2008 (a), and between 14.40 and 15.16 on 30 April 2008 (b). In each case, the mean orientation of the dance axis is shown (in the lower left corner) as the angle measured counterclockwise from the horizontal rightward direction. Other details are as in figures 2 and 3. (Online version in colour.)

With the axial e-vector illumination, the mean dance orientation was very close to the horizontal axis (leftwards or rightwards), regardless of the time of day. An example is shown in the electronic supplementary material, figure S2, which compares orientation histograms for dances measured between 13.26 and 14.00 (see electronic supplementary material, figure S2a) and between 13.59 and 14.51 (see electronic supplementary material, figure S2b). In each case, the mean dance orientation was very close to the horizontal axis, even though the mid-points of the time windows during which the two sets of dances were recorded (13.43 and 14.26, respectively) were separated by nearly three-quarters of an hour. If the bees were using the azimuthal position of the sun to direct their dances at these times, their dance directions would be expected to be unimodal and oriented at 22° and 10° counterclockwise, respectively, relative to the rightward horizontal direction.

These experiments also indicate that the bees’ dances were not influenced by any artefactual ‘hot spot’ created by the sun when viewed through the diffuser paper, or by any brief glimpse of the sun before entering the tunnel: the dances were influenced only by the direction of the polarized illumination in the tunnel.

(e). Experiment 4

In Experiment 4, the e-vector illumination was transverse in the first half of the tunnel and axial in the second half, as shown in figure 6a. Bees foraging in this tunnel displayed four preferred dance directions, as shown in figure 6c: (i) leftward and upward, (ii) rightward and upward, (iii) leftward and downward and (iv) rightward and downward. Relatively few dances were oriented in the horizontal or the vertical directions. Statistical analysis of the data (as described in §2) indicates that the orientations are not randomly distributed (p < 0.001). Analysis of the dance directions, carried out as described in §2, reveals four modal directions, shown as the thick continuous lines (red in online version). These are oriented at angles of 42.4°, 132.4°, 222.4° and 312.4°, measured counterclockwise with respect to the rightward horizontal axis. These directions are very close to the four principal diagonal directions of 45°, 135°, 225° and 315°, shown as the thick broken lines (green in online version). Statistical analysis (see §2) reveals that the observed modal dance orientations are not significantly different from the four principal diagonal directions (p < 0.0001, V test).

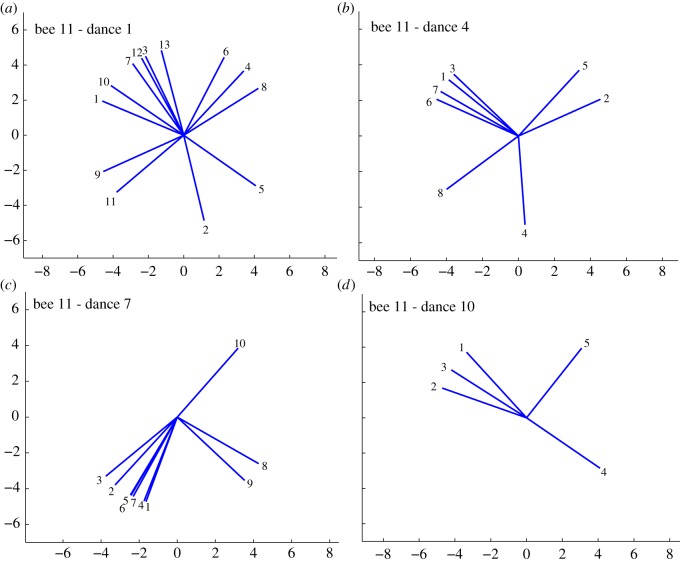
Detailed analysis of the dances of individual bees reveals that, at the level of the individual bee, the fourfold ambiguity in direction is addressed in a manner similar to the twofold ambiguity in Experiments 2 and 3. Some individuals tend to signal a single direction (i.e. one of the four possible directions), while others indicate several of the possible directions within a single dance. Figure 7 shows data obtained from analysing four different dances of an individual bee (bee no. 11) participating in this experiment. Each panel shows the distribution of waggle orientations recorded in a single dance. We see that the number of distinct directions indicated in a single dance can vary from three (figure 7c,d) to four (figure 7a,b). Electronic supplementary material, figure S3 shows four examples of single dances from another individual (bee no. 55). Here again, we see that an individual bee can signal anything from two (see electronic supplementary material, figure S3a) up to four (see electronic supplementary material, figure S3b–d) distinct directions in a single dance.

Figure 7.

(a–d) Four examples of dances of an individual bee (bee no. 11) recorded in Experiment 4. Each panel shows waggle axis orientations recorded sequentially in a single dance. (Online version in colour.)

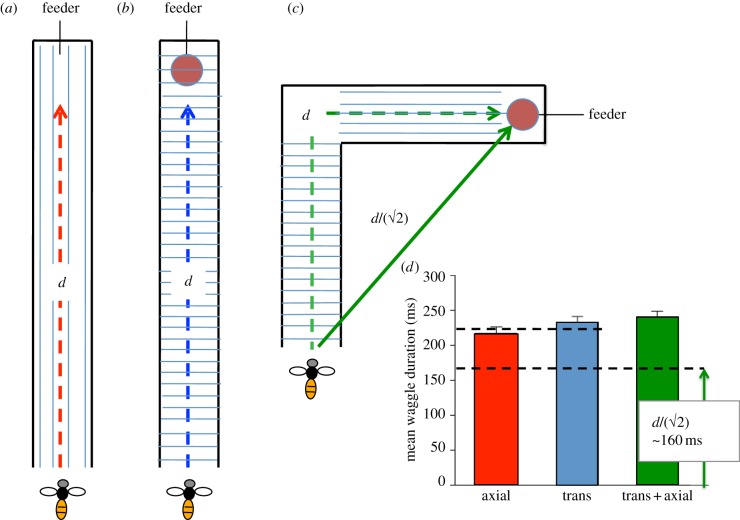
The waggle dance of the honeybee signals not only the apparent direction of the food source, but also the apparent distance; the distance is proportional to the duration of the waggle. What distances do the bees signal under the various experimental conditions that we have explored? Figure 8 shows the results of three experiments in which we compared the durations of waggle dances of bees that had returned from a 12 m long tunnel illuminated with polarized light that was oriented either axially (figure 8a), or transversely (figure 8b), or transversely for the first 6 m and axially for the final 6 m (figure 8c).

Figure 8.

Measurements of mean waggle durations in the dances of bees returning from a 12 m tunnel that was illuminated with axially polarized light (a), transversely polarized light (b), or transversely polarized light for the first 6 m and axially polarized light for the next 6 m, simulating flight through an L-shaped tunnel (c). The waggle durations measured under these three conditions are shown in (d) (mean ± s.e.). The upper dashed line represents the average of the mean waggle durations recorded in conditions (a,b), and the lower dashed line indicates (1/√2) times this value. (Online version in colour.)

The mean waggle duration recorded with axial polarization (216.4 ± 1.9 (s.e.) ms; 11 bees, 11 dances, 100 waggles) is not significantly different from that recorded with transverse polarization (234.4 ± 8.3 (s.e.) ms; 17 bees, 17 dances, 102 waggles) (t-test, p = 0.07). The average of these two durations is 227.3 ± 6.4 ms. The waggle durations recorded in each of these conditions are very similar to those recorded for flights under the open sky in Experiment 1. Those durations, recorded on 13 March 2008, are: 191.9 ± 20 (s.e.) ms (9.15–9.30), 229.5 ± 7.1 (s.e.) ms (10.47–11.10) and 236.9 ± 17.3 (s.e.) ms (11.10–11.20).

From the results of figure 6, it is clear that a bee having flown through the tunnel with the e-vector illumination transverse in the first half of the tunnel and axial in the second half signals a direction of approximately 45°, which is in between these two directions. This suggests that by illuminating a straight tunnel with two successive, mutually perpendicular e-vector directions we can simulate a flight through an L-shaped tunnel consisting of two perpendicularly oriented legs, each leg being half the total length. When bees fly in a simulated L-shaped tunnel, do they indicate a measure of the total distance flown (d), or the ‘shortcut’ (vector) distance (d/√2) to the food source as illustrated in figure 8c? If they indicated the total distance, we would expect the waggle duration to be approximately 227 ms; if they indicated the vector distance, we would expect the waggle duration to be in the vicinity of (227/√2) = 160 ms. The measured mean waggle duration in the simulated L-shaped tunnel is 240.3 ± 7.9 (s.e.) ms (12 bees, 12 dances, 94 waggles; figure 8d), which is significantly greater than 160 ms (t-test, p < 0.01), but close to the durations measured in the ‘straight’ tunnels (one factor ANOVA, p = 0.18). Thus, in the simulated L-shaped tunnel the bees signal the total distance flown, rather than the vector distance corresponding to the imaginary shortcut.

The flight distances that these waggle durations would represent in outdoor flight are approximately 300 m for the distance to the food source in the straight tunnel and approximately 210 m for the vector distance to the food source in the L-shaped tunnel. These estimates of equivalent outdoor flight distances are obtained from calibrations of the honeybee's odometer as described in [16].

4. Discussion

The ability to use polarized light for navigation or orientation has been demonstrated clearly and unequivocally in walking animals such as the desert ant [21], the desert wood louse [22] and the dung beetle [23,24]. This has been achieved by showing that the direction of locomotion of a homing desert ant, or of a dung beetle departing with its treasure, can be systematically altered by changing the direction of the e-vector of the overhead illumination. However, this ability has so far not been demonstrated in honeybees—or, indeed, in any other airborne animal—because of the obvious technical difficulties associated with varying the overhead illumination during flight over large distances. This study has overcome this hurdle, at least for honeybees, by using a tunnel to simulate a long journey, and manipulating the illumination in the tunnel.

Earlier studies have shown that the waggle dances of bees returning from a food source can be systematically altered by illuminating the hive with artificially polarized light and varying the direction of polarization of this illumination [1,7]. These experiments are telling, in that they demonstrate that bees can perceive and react to polarization patterns, but such experiments are restricted to modifying behaviour within the hive. They do not reveal whether bees flying outdoors to a food source are able to gauge their flight direction purely from the pattern of polarization that is present in the sky.

Observations of the ability of animals to orient spontaneously to e-vector patterns have been documented in a number of invertebrate species (e.g. locusts, shrimps, bees, etc. [25]). In one series of experiments, Jacobs-Jessen [26] showed that when foraging bees were captured and released from a hole in the centre of a circular table, which was illuminated from above with polarized light, the walking bees oriented their body axes in four different preferred directions relative to the e-vector of the illumination. While this experiment suggests that bees have the capacity to sense the direction of the e-vector, they do not indicate whether they use this information to measure or set their direction of flight when they fly towards a known food source. In another series of experiments, Jacobs-Jessen [26] arranged for bees to emerge from their hive through an aperture at the centre of a circular table (as above), with a horizontal sheet of glass positioned just above the table. This encouraged the bees to walk, rather than fly, to the periphery of the table before flying out through a specific exit. There were exit holes all around the periphery, but only one was open. He found that, when the experiment was carried out under the open sky, the bees learned to walk in the correct direction to find the exit hole. This was true regardless of whether the sun was visible, or screened off by a mask, allowing only a part of the remaining blue sky to be visible. While this elegant experiment demonstrates that the bees were using celestial cues to gauge and set their walking direction, it does not reveal the nature of the relevant cue—which could be the position of the sun, the polarization pattern of the sky, the intensity or spectral gradients in the sky, or a combination of all of these cues.

Our experiments demonstrate that foraging bees can sense and signal the direction of their flight by using information that is based purely on the polarized-light pattern of the sky. It should be noted, however, that the polarization filters in our experiments provided a degree of polarization of around 95%, whereas the degree of polarization of natural skylight is somewhat lower, rarely exceeding 60% [2,27].

Experiment 1 has shown that bees can read a compass direction and report it in their dances when they fly in a tunnel under the open sky. However, this experiment on its own does not tell us whether the compass information is obtained from the sun, from the polarization pattern or from the other cues listed above.

Experiments 2 and 3 address this question, by providing overhead illumination that contains only polarized-light cues. Here, bees can estimate their flight direction only from the direction of the e-vector of the illumination. These experiments show clearly that the direction of the waggle axis in the honeybees’ dances can be manipulated by varying the direction of the e-vector illumination in the tunnels. The transverse e-vector illumination causes the bees to signal a flight direction that is directly towards, or directly away, from the sun, corresponding to the pattern of polarization that they would experience when flying in either of these directions under an open sky. The axial e-vector simulation, on the other hand, causes the bees to signal a flight direction that is 90° to the left or the right of the sun's azimuth, which again corresponds to the pattern of polarization that they would experience when flying in either of these directions under an open sky. These findings imply that the bees are capable of gauging and signalling their heading direction purely on the basis of the direction of the e-vector illumination in the ceilings of the tunnels. How do bees deal with the 180° directional ambiguity that is inherent in the polarized-light stimulus? Analysis of the dances of individual bees under these conditions reveals that some bees tend to prefer one direction, others the opposite direction, and a third group of bees signals both directions within a single dance (figure 4; electronic supplementary material, figure S1). Thus, the colony, as a whole, is provided with unbiased information about both of the possible locations of the food source. If this were to occur in reality, then one half of the bees recruited by the dances would end up at the food source, while the other half would not; but, in the absence of any additional information, ‘unbiased reporting’ seems to be the best way to deal with the ambiguity.

We have seen that when the view of the sky was eliminated and the bees were shown artificially polarized illumination, as in Experiments 2 and 3, the dance directions were not at all affected by the time of day (figure 5; electronic supplementary material, figure S2). On the other hand, changing the orientation of the polarized illumination from axial (13.26–14.00, 30 April 2008; electronic supplementary material, figure S2) to transverse soon thereafter (14.40–15.16 on the same day, figure 5) caused the dance directions to change by approximately 90°. Similarly, changing the orientation of the polarized illumination from transverse (12.55–13.14, 1 May 2008; figure 5) to axial soon thereafter (13.59–14.51 on the same day, electronic supplementary material, figure S2) caused the dance directions to change by approximately 90°. Thus, in these experiments, the dances depended only upon the direction of the e-vector of the overhead illumination—they were not influenced by any internal, clock-driven representation that the bees may have possessed about the expected direction of the sun, or the change in this direction with the time of day. That is, they were not influenced by a learned ephemeris function (an internal representation of how the azimuth of the sun should vary with the time of day; cf. [28–30]). They were also not affected by any brief glimpses of the sun that they might have received prior to entering the tunnel.

In Experiment 4, the e-vector illumination was transverse in the first half of the tunnel and axial in the second half. Clearly, the bees interpreted the abrupt shift of the e-vector direction in the middle of the tunnel as a 90° change in their heading direction, even though they did not physically execute a turn. Since flight in the first half could be interpreted as movement in a direction towards or away from the sun, and flight in the second half as movement in a perpendicular direction (with the sun 90° to the left or the right of the heading direction), the two sets of ambiguities lead to four possible locations of the food source. They correspond to (i) a flight towards the sun, followed by a turn to the right; (ii) a flight towards the sun, followed by a turn to the left; (iii) a flight away from the sun, followed by a turn to the right and, finally, (iv) a flight away from the sun, followed by a turn to the left. All of these four possible locations are signalled by the bees (figure 6), and our findings reveal that some bees signal all four locations in a single dance (figure 7; electronic supplementary material, figure S3). This is again a case of ‘unbiased reporting’ in response to the fourfold ambiguity that the stimulus presents. However, the four peaks in the distribution of dance orientations (figure 6) do not have the same magnitude. The largest peaks are in the vicinity of 135° and 225°, followed by 45° and then 315°. The reason for this non-uniformity is not clear. It is possible that small non-uniformities in the ambient illumination of the observation hive could have influenced the dance directions when the extent of ambiguity about the location of the food source became very large. It is well known that illumination of the honeycomb by a punctate light source, simulating the sun, can affect dance direction (see, for example, [7]). Another possibility is that, in this condition of extreme ambiguity, the bees were additionally influenced by a mechanism that used the current position of the sun, as estimated by an internal clock, or a brief glimpse of the sun before entering the tunnel, to bias the dance orientations in favour of outdoor food sources that they had previously visited, thus changing the frequencies with which the four cardinal orientations are chosen. The use of a learned ephemeris function by bees has been demonstrated in many studies [29–31]. While our results with the purely transverse and purely axial polarization argue against this possibility (see figure 5 and the discussion thereof), one cannot exclude it in the case of the dual polarization experiment which generates an extreme, fourfold ambiguity that could promote the use of other cues to attempt to resolve the ambiguity.

Direction information conveyed by bees that have flown a path involving differently oriented segments has previously been studied under more natural conditions. von Frisch [1] trained foragers to fly around a mountain ridge, or a large building or a forest edge separating the food source from the hive. In their dances, the bees indicated a direction pointing straight towards the food source, a direction the bee had actually never flown. A similar result was also obtained in a more recent experiment where bees were trained to fly a route that involved an outdoor leg followed by a leg through a tunnel oriented at right angles [32]. In these experiments, bees flew under a stationary celestial polarization pattern and were forced to physically change their flight direction when they entered the tunnel. In our experiments, on the other hand, the bees flew in a straight line, under a polarization pattern whose orientation was changed by 90° half way down the tunnel. Despite maintaining a constant flight direction on their way to the food source, our bees interpreted their journey as a flight through an L-shaped tunnel, as revealed by the ‘shortcut’ direction that they indicated in their dances. Thus, it appears that changes in flight direction are sensed primarily in terms of changes in the orientation of the overhead polarized light, when such cues are available.

While the bees signal the direction of the vector that specifies the apparent location of the food source in Experiment 4, they do not signal the length of this vector in their dances. Rather, they signal the total distance travelled along the two (seemingly perpendicular) legs. This finding is in good agreement with earlier studies of distance estimates conveyed by the waggle dance in other conditions where bees flew around a hill [1], along an outdoor route and then through a tunnel oriented at right angles [32] or along tunnels that comprised a horizontal leg followed by a vertical leg [33].

In a foraging experience that is riddled with ambiguity, as in Experiment 4, do different bees signal different locations (with each individual displaying a preference for a particular location), or does a given bee signal more than one location in a single dance? The data in figure 7 and electronic supplementary material, figure S3 suggest that both outcomes are likely. While certain bees appear to display individual preferences, others behave as though they carry up to four different representations of the location of the food source, and can signal all of these locations simultaneously in a single dance. It is not inconceivable that ambiguous, ‘multiple’ solutions arise even when bees forage in natural outdoor conditions. For example, ambiguities of 180° in flight direction could arise when the sun is low on the horizon and obscured by a hill or a cloud, so that the unoccluded part of the sky provides only e-vector information, but no cues on spectral or intensity gradients. It would then be beneficial for a bee, returning from an attractive food source, to signal all of the (equally) likely positions of the targets in its dance, so that at least some of the recruits arrive at the correct location. Signalling just one of the possible locations (by arbitrary choice) would waste colony resources, if this happened to be the wrong location. Multimodal dance directions have previously been observed in the presence of contradicting information, for example, when the landscape is set in conflict with a learned ephemeris function for the sun [31].

Results analogous to ours have recently been obtained by Lebhardt et al. [34], who studied polarized-light-based navigation of the desert ant Cataglyphis by training them to walk to a food source in a tunnel that provided polarized overhead illumination, and observed their trajectories when they were allowed to return to their home in an open environment under the natural sky. When the entire length of the tunnel provided a single direction of polarized light, the ants’ homing directions displayed the same 180° ambiguity that we have observed in the dances of our bees, although the ants showed a considerable preference for one direction over the other (e.g. when homing they preferred to walk towards the sun, rather than away from it, when the tunnel presented transversely oriented polarized light). When the tunnel offered two different directions of polarized light—one direction in the first half and another direction in the second half—the ants displayed a fourfold ambiguity in their home runs, analogous to the fourfold ambiguity on the dance directions displayed by our bees. Like the bees, the ants showed a preference for some of the homing directions, but with a stronger bias, the reasons for which are not yet clear. Interestingly, the lengths of the ants’ homing runs were shorter in the case of the dual-polarizer experiments, compared with those in which the orientation of the polarized light was constant over the entire length of the tunnel, indicating that the ants were computing the apparent vector distance (the ‘shortcut’ distance) of the food source from their outbound journeys. By contrast, our bees appear to compute the total distance travelled, rather than the apparent vector distance. However, both animals seem to compute the apparent vector direction of the food source.

Our results beg the question as to how ‘multiple’ solutions as to the location of the food source are computed and represented in the neural machinery of the brain. It has been suggested that the so-called mushroom bodies in the insect brain are structures that are analogous in function to the hippocampus of the vertebrate brain [35]. Indeed, there is some evidence for the existence of neurons in the mushroom bodies that display responses similar to the ‘place’ neurons in the vertebrate hippocampus [36,37]. If this is the case, then one possibility is that locations of food sources are represented by target ‘place cells’. In the case of the tunnel with the transverse e-vector illumination, for example, the two possible locations of the food source would be represented by the firing of two place cells, one corresponding to a location at the appropriate distance from the hive in the direction of the sun, and the other to a location at the same distance but in the opposite direction. The tunnel with the axial e-vector illumination would lead to activity in two other place cells, again representing two locations equidistant from the hive, but which would be reached by flying in directions that are 90° to the left or the right of the sun. Extending this logic one step further, the tunnel with transverse e-vector illumination in the first half and axial e-vector illumination in the second half would lead to activity in four different place cells, each positioned at the vertex of a square and representing a location of the food source along one of the diagonal directions. Whether this is indeed how the brain represents ambiguous locations remains to be explored.

Funding statement

This research was supported partly by the ARC Centre of Excellence in Vision Science (CE0561903), by a Queensland Smart State Premier's Fellowship and by U.S. AOARD Award no. FA4869-07-1-0010.