Contrast sensitivity and the detection of moving patterns and features

Abstract

Theories based on optimal sampling by the retina have been widely applied to visual ecology at the level of the optics of the eye, supported by visual behaviour. This leads to speculation about the additional processing that must lie in between—in the brain itself. But fewer studies have adopted a quantitative approach to evaluating the detectability of specific features in these neural pathways. We briefly review this approach with a focus on contrast sensitivity of two parallel pathways for motion processing in insects, one used for analysis of wide-field optic flow, the other for detection of small features. We further use a combination of optical modelling of image blur and physiological recording from both photoreceptors and higher-order small target motion detector neurons sensitive to small targets to show that such neurons operate right at the limits imposed by the optics of the eye and the noise level of single photoreceptors. Despite this, and the limitation of only being able to use information from adjacent receptors to detect target motion, they achieve a contrast sensitivity that rivals that of wide-field motion sensitive pathways in either insects or vertebrates—among the highest in absolute terms seen in any animal.

1. Background

(a). Introduction

As the contrast in brightness between an object and its background decreases, it becomes more difficult to see. This is because the random nature of photon emission or reflection by features of the environment leads to variability in the photon numbers sampled by photoreceptors within a given neural integration time, even if they are viewing parts of the scene with identical average brightness [1]. At the absolute limits of vision in dim light, the ability to distinguish even a black object from a bright background (or vice versa) fails owing to the unreliability of the photon catch [1,2]. At higher light levels, as the signal-to-noise ratio improves, photoreceptors still need to capture a large sample of photons if the visual system is to reliably distinguish the boundaries of low-contrast features [1,3]. Indeed, Land [1] estimates that to achieve 95% reliable discrimination of a contrast boundary at the threshold for contrast detection reported in human vision (minimum contrast around 0.5%) would require the photoreceptors viewing the two sides of that feature to each capture more than 10⁵ photons. As a consequence, the ability to distinguish the finest detail at low contrasts remains limited by photon catch for many animals under typical illumination conditions [1,3].

Early studies of visual acuity were concerned primarily with tests of minimum separation between high-contrast white and black lines [4]. In humans, Schade [5] first proposed the approach of determining the detectability of striped grating patterns of a particular spatial frequency by varying the luminance modulation (contrast) of the grating. Extensive application of such techniques in the late 1960s and early 1970s using psychophysical methods led to an appreciation of the bandwidth and performance of vision in humans and other primates (see [6]) and also revealed much about the receptive field organization of neurons in early visual processing by mammals [7].

(b). Contrast sensitivity for large patterns in vertebrates

Contrast sensitivity can be defined as the ability to discriminate patterns as contrast decreases, in either a visual pathway (determined physiologically) or via the sum of such pathways, as evidenced by whole animal behaviour. It is typically expressed as the inverse of the threshold contrast for detection of a given pattern. Because contrast sensitivity is limited by the ability of the eye to capture light, it provides a means to examine the trade-offs between optical sensitivity and visual acuity that have evolved in a given eye, and the habitat in which it is used. This makes it a useful tool for exploring the actual performance of the visual system under different conditions and comparing it with theory based on optical sampling.

The basic human contrast sensitivity function is easily demonstrated by a variable contrast and spatial frequency grating such as that in figure 1. Because each element of this pattern decreases in contrast along its length (i.e. towards the top in the image), the apparent length of each segment is proportional to our contrast sensitivity. Depending on the viewing distance and brightness of a pattern such as this, the longest stripes are typically perceived in the middle of the pattern. At the low spatial frequency end of the pattern, contrast sensitivity is attenuated by lateral inhibition (spatial antagonism) in early visual pathways [6]. At higher spatial frequencies, contrast sensitivity is attenuated by optical blur, which leads to demodulation of the pattern in the image formed on the retina. Hence, contrast sensitivity gradually declines as the spatial frequency approaches the limits imposed by the resolving power of the optics and sampling by the retina, with no useful sensitivity by around 40 cycles per degree for humans and other primates in even the brightest light [6].

Figure 1.

Variable spatial frequency and variable contrast pattern to demonstrate contrast sensitivity. The pattern contrast of the sinusoidally modulated stripes decreases from lower to upper, whereas spatial frequency increases from right to left. At a typical viewing distance (45–50 cm), the bars of the pattern should appear longest around one-third of the way between the left- and right-hand edges, revealing maximum contrast sensitivity around approximately three cycles per degree.

Under optimal viewing conditions (i.e. bright light and optimal spatial frequency of around 3–5 cycles per degree), the human contrast sensitivity function peaks close to 200, i.e. the threshold contrast is around 0.5% [6,8]. Psychophysical analysis of other vertebrate species reveals slightly less impressive contrast sensitivity: peaks are around 116 in cats [9]; less than 30 in typical rodents [10,11]; in the 7–30 range in various bird species (for review, see [12]); and around 50 in goldfish [13].

A number of factors influence the maximal contrast sensitivity revealed in studies such as those cited above. For example, as luminance decreases (and photon catch with it), peak contrast sensitivity declines, and this peak is seen at progressively lower spatial frequencies [4], revealing both the limits imposed on contrast detection owing to declining photon catch, and increasing degrees of spatial pooling from multiple local photoreceptors in the retina and brain to compensate. Some of the variability in reported contrast sensitivity values may thus reflect the limited brightness available from typical visual stimulus displays (e.g. CRT monitors), which has typically exposed the eye to luminance well below the typical range seen in outdoor scenes (and for which the eyes of many diurnal species evolved). Furthermore, in many of the above studies, the animals were freely behaving and thus unrestrained during detection and analysis of the patterns, so the degree to which retinal motion influenced detectability of the patterns is difficult to determine. Once a grating pattern is in motion (either imposed by the pattern, or owing to the movement of the retina), contrast sensitivity is limited not only by the resolving power and spatial filtering properties of early visual pathways, but also by the neural filters intrinsic to the motion detectors of underlying neural pathways. Indeed, by controlling for retinal movement, contrast sensitivity analysis has been useful for studying the trade-offs between parameters such as the luminance and spatial frequency of the pattern, and the speed it is moving at [8].

(c). Contrast sensitivity for grating patterns in insects

By comparison with the wealth of studies applying variable contrast grating stimuli to vertebrate species, less is known about contrast sensitivity in insects. A landmark study [14] based on electrophysiological recording from the wide-field motion detecting neuron H1 in the blowfly lobula plate revealed a maximal sensitivity to gratings comparable with that of typical vertebrates, peaking between 25 and 40 (if the stimulus screen area was large enough). This was, however, observed at a relatively low spatial frequency (approx. 0.05 cycles per degree), as might be expected given the limited resolving power of the insect compound eye [14]. Similar values have since been observed (also using electrophysiological analysis of responses to moving gratings) in both day-active and nocturnal sphingid moths [15,16] and in both honeybees [17] and bumble-bees [15]. More impressive performance has been found in day-active butterflies, with similar peak contrast sensitivity (approx. 30) but at a much higher spatial frequency of 0.12 cycles per degree [18]. In large male hoverflies such as Eristalis tenax and Volucella pellucens, contrast sensitivity peaks at between 40 and 100 in the frontal/dorsal acute zone [15,16,19], also at 0.12 cycles per degree. To put this visual performance into perspective, both the absolute maximal contrast sensitivity and the spatial frequency at which it is observed are not dissimilar to those of the domestic cat [9]. Indeed, the peak sensitivity is around 10 times that seen in the rat, and at a similar spatial frequency [11]. This is particularly impressive considering the much poorer light gathering power of these apposition compound eyes compared with their vertebrate counterparts [1], and the famously high temporal resolving power of fly photoreceptors—around five times faster than in mammals [20]. It remains to be seen whether this reflects a fundamental advantage of the r-opsins and transduction cascades in the rhabdomeric photoreceptors of insects over mammalian ciliary opsins [21,22], where signal-to-noise ratio is limiting.

2. Contrast sensitivity for small-target features

(a). Image contrast for small targets

While grating patterns as described above have been tremendously useful in examining the trade-offs between optical sensitivity and visual acuity that have evolved in a given eye given the habitat in which it is used, less is known about the influence of contrast sensitivity on detection of other features. Neurons such as those in the wide-field motion pathways used for tasks such as optical flow analysis are believed to integrate the outputs of many local ‘elementary motion detectors’, each of which can view the local motion generated by different parts of the a grating pattern. The influence of spatial integration on contrast sensitivity was demonstrated in blowfly tangential neurons by Dvorak et al. [14], who showed that peak contrast sensitivity increased substantially (from approx. 25 to 40) when they increased the visual area of the screen on which grating patterns were presented from 45° to around 90° in angular subtense. By contrast, the neural pathways processing motion of targets as small (or smaller) than the resolution of the underlying photoreceptor mosaic do not have the luxury of integrating motion at many points in the retinal image simultaneously. The image of such a tiny feature will only ever be at a single location as it moves across the retina and thus must be processed by comparison of neighbouring photoreceptors.

Given the limited spatial acuity of the compound eye [1] and because detection of small targets (either conspecifics or prey) is a task of fundamental importance to many insects, they have evolved impressive optical specializations and neural machinery to subserve it (for a recent review, see [23]). Insects are thus an ideal group to examine the limitations imposed by contrast sensitivity for feature detection.

However, defining contrast sensitivity for small target detection is less straightforward than for the analysis of grating patterns, for several reasons. First, it is more difficult to define the effective contrast of a point object seen against the background than of a striped grating pattern. The most commonly used definition of pattern contrast (Michelson) works well to predict the discriminability of grating patterns but is less useful for small objects because it predicts that a black feature would have the same contrast against different backgrounds, regardless of their brightness (i.e. 1.0), whereas a bright object against the same backgrounds would always have contrast less than 1.0, irrespective of its brightness. Given the earlier discussion of limits of detection imposed by photon catch (see review by Land [1]), this would clearly not be the case: a tiny black object may be completely unresolved by a given eye against the twilight sky, yet a distant star or planet (a true point source) might be easily visible, if sufficiently bright. For this reason, it is common to define the contrast for a small feature by the Weber contrast:

where I is intensity. In this case, C_w can vary between 0 and −1.0 for a black object against a bright background, and between 0 and values to above +1.0 for bright objects.

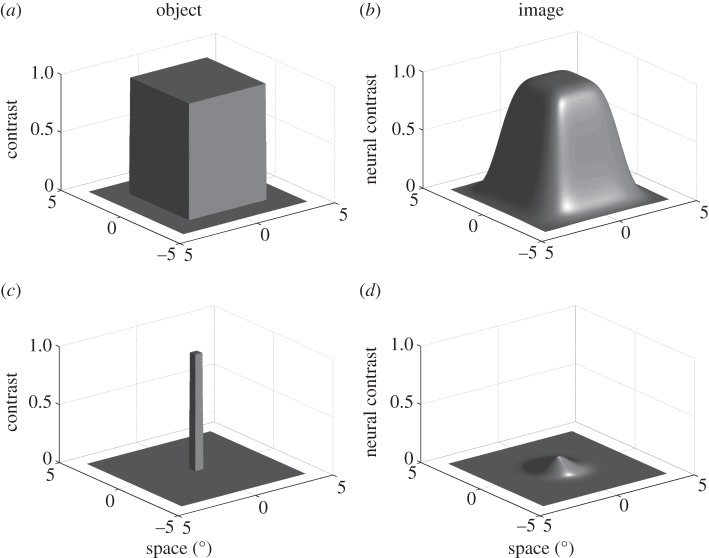
The second problem follows from considering the influence of optical blur on the task solved by neurons such as the small target motion detector (STMD) neurons in insects [23], i.e. detection of a dark target against a bright background, such as the image of prey or a conspecific seen silhouetted against the sky. Optical blur degrades the actual contrast in the image and leads to crosstalk between the signal detected for an object by the central photoreceptor and that of its near neighbours, just as this attenuates the image contrast of gratings at the highest spatial frequencies resolvable by the retina. As illustrated by a simple optical model in figure 2, this means that the actual contrast in the retinal image for small objects will be lower than that of the object against its background. Indeed, as target size gets smaller, below the nominal limits of resolution supported by the photoreceptor mosaic (0.5° square in figure 2c,d for an acceptance angle, Δρ, of 1.4°), the target no longer fills the receptive field of a single receptor. This leads to a neural image that resembles the angular acceptance function of the photoreceptors themselves, i.e. the Gaussian blur that results from the optical sampling. Smaller targets thus all produce a similar image on the retina, except for their effective contrast. As a consequence, ‘hyperacuity’ for targets or point sources—the detection of features smaller than the nominal resolution of the eye, should be limited only by the contrast sensitivity of the individual photoreceptors.

Figure 2.

Optical modelling of large and small features in the retinal image. (a) Luminance distribution of a 5 × 5° object. The z-axis shows relative luminance (contrast). (b) Luminance distribution in the retinal image of the same feature for an eye with an acceptance angle (Δρ) of 1.4°. The peak contrast for the image is similar to that of the object. (c,d) Similar analysis for a 0.5 × 0.5° feature shows reduced contrast in the retinal image (peak = contrast 0.106). Note the resemblance of the retinal image to the 1.4° Gaussian function used to blur the object.

(b). Maximum neural contrast

The best case in terms of luminance difference for the neural pathways detecting small features is to compare the signal generated by a photoreceptor that views the centre of the target with the signal generated for the background by more distant photoreceptors (i.e. outside the blurred boundary between the two). This allows us to define a concept for contrast of the image of an object that we subsequently refer to as maximum neural contrast. For example, if an object is large enough relative to the optical blur, then photoreceptors viewing the centre will still be seeing an image that reflects the actual luminance of the object (i.e. maximal neural contrast will be 1.0 for a black object; figure 2a). This is illustrated in figure 3, which shows the luminance image predicted for small objects (5°, 2° and 1° square, respectively), superimposed onto a mosaic of neighbouring photoreceptors, for a model eye with optics similar to the hoverfly male acute zone. The maximum neural contrast for a 5 × 5° target is the same as that of the object (in this case, 1.0), but if we decrease target size to 2 × 2°, then this value has already declined to 60% and by 1 × 1°, to just 36% of the original contrast of the feature. For the 0.5° square object in figure 2d, this maximal neural contrast is just 10%. Note that because some of the luminance signal of the feature is smeared across its six neighbours, regardless of how small the feature is, a nearest-neighbour measure of neural contrast will actually be even lower than the maximum neural contrast predicted by our measure. Detection of moving features at the limits of resolution would require just such a nearest-neighbour comparison, so small target detection is probably even more challenging than suggested by our simple analysis. Nevertheless, we can use the predicted image blur to correct the Weber contrast to effective (neural) image contrast for different-sized objects and thus examine the limits of target resolution defined by the effective contrast sensitivity of neurons at various stages of visual processing.

Figure 3.

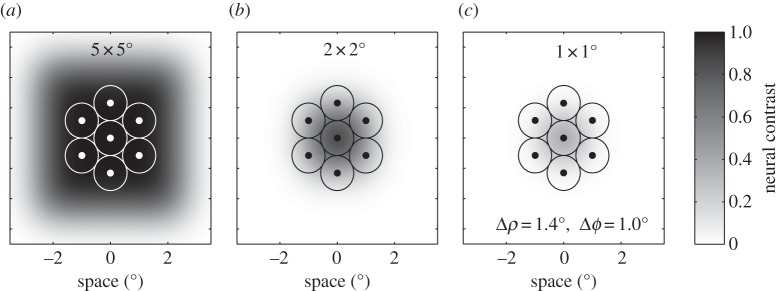
Results from the same optical model (acceptance angle, Δρ = 1.4°) to that used in figure 2, illustrating the scale and magnitude of the retinal image for three different size square features (a–c, 5 × 5°, 2 × 2° and 1 × 1°, respectively). In each case, the retinal image is superimposed onto the retinal mosaic in the fly dorsal eye (inter-receptor angle, Δϕ = 1.0°) to illustrate the spread of the luminance image from the central photoreceptor to neighbouring photoreceptors.

3. Physiologically measured contrast sensitivity for small objects

(a). Contrast sensitivity of blowfly photoreceptors for small targets

To explore the effect of target size in comparison with the predictions of optical modelling of maximum neural contrast, we recorded responses to different-sized targets from both photoreceptors and higher-order STMD neurons in blowflies and dragonflies, respectively. Figure 4 shows the response to different-sized black targets that were drifted across an LCD screen along a trajectory that passed through the centre of the receptive field of a single photoreceptor from the fronto-dorsal acute zone in the eye of a male blowfly, Calliphora stygia. The drift velocity was 45° s⁻¹ and thus well below the ‘characteristic velocity’, V_c, (approx. 170° s⁻¹) predicted for photoreceptors in blowflies [24]. Because V_c is a measure of the image velocity required to move across a typical receptive field in a typical integration time for the photoreceptor [25], we would expect that at target velocities below V_c (as in figure 4), the peak response observed would be associated with the time when the target crosses the receptive field centre and would be primarily limited by its neural contrast. In other words, for such stimuli, the attenuation of responses as target size gets smaller is dominated by the spatial blur in the eye, rather than by temporal blur due to the kinetics of phototransduction. Responses to target sizes below 1° decline rapidly, falling below 2 mV by 0.75° and barely discernable from the noise in the recording at a target size of 0.33°, despite the data in this case being averaged across 40 trials. As predicted by the neural contrast measure, by 5 × 5°, targets are fully resolved and elicit maximal peak hyperpolarization, saturating at around 15 mV amplitude (figure 4 lower).

Figure 4.

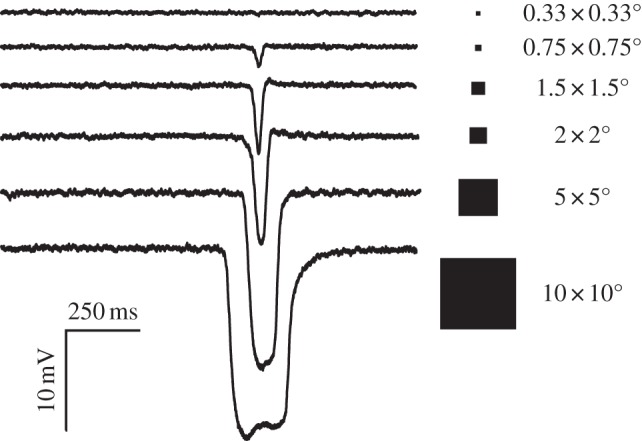
Membrane potential recorded in response to different-sized black targets (Weber contrast 1.0) drifted across against a bright background on an LCD screen along a trajectory that passed through the centre of the receptive field of a single photoreceptor from the fronto-dorsal acute zone in the eye of a male blowfly, Calliphora stygia. The drift velocity was 45° s⁻¹. As predicted by the optical model, response peaks saturate for target sizes above 5°, and decline rapidly for targets below 1°. Data shown are the average of 40 trials (targets up to 1.5°) or 10 trials (target sizes >1.5°).

Given that optical blur is the prime influence on the effective contrast attenuation for the smallest targets in this series (i.e. if they are effectively point objects relative to the acceptance angle, Δρ, of the photoreceptors), we ought to see a linear relationship between target area (i.e. the square of target width in these experiments) and peak response. Data averaged from nine different photoreceptors (figure 5) confirm that this is the case, although responses to targets above 1 deg² saturate rapidly. The latter reflects both the inherent nonlinearity in the photoreceptor's response once the membrane potential departs from the adapting level by more than 1–2 mV, and the fact once resolved, large targets are equally black for a receptor that views its centre, regardless of their width. However, an enlargement of the response to the smallest targets tested, eliciting responses below 1 mV (figure 5b), shows a perfectly linear response, with a gain of approximately 3.4 mV deg⁻².

Figure 5.

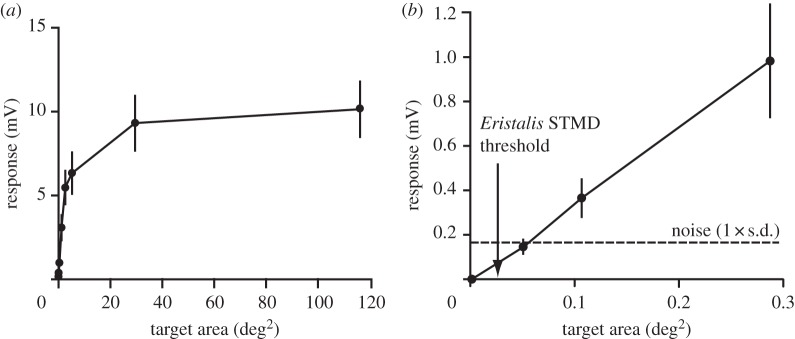
Sensitivity functions averaged from nine photoreceptors in response to different-sized black targets, as in figure 4, in this case plotted against the area of the target (which should be approximately proportional to neural contrast for targets below the resolution limit of the eye). All targets had the same Weber contrast (1.0). (a) As predicted by the optical model, response peaks saturate at target sizes above 3° (i.e. 9 deg²); (b) detail for small targets shows the linear relationship. The noise level shown (1 s.d.) was determined by recording the membrane potential to the background stimulus, i.e. a bright stimulus screen (see appendix). The arrow indicates the smallest target size for which responses were previously observed in higher-order STMD neurons of the hoverfly, Eristalis tenax [26].

The horizontal dashed line in figure 5b shows the average noise level (at 1 s.d.) recorded from these same cells when viewing the bright background of the screen. The measured noise level reported here is corrected for the intrinsic noise in our recording set-up, determined by recording with the same electrodes from the extracellular space immediately adjacent to the recorded photoreceptors. This reveals that the useful threshold for resolving single targets would be around 0.05 deg², corresponding to a square black target of around 0.22° across. If we now apply our optical model to this ‘limiting’ target, we get a maximal neural contrast threshold of 0.022. In other words, the contrast sensitivity of single photoreceptors for small targets (the inverse of this predicted threshold value) is around 45.

(b). Contrast sensitivity of small target motion detector neurons for small targets

How does the contrast sensitivity of single photoreceptors for drifting targets compare with that measured in downstream STMD neurons? In our earlier recordings from the optic lobes of the hoverfly E. tenax, we encountered some remarkable STMD neurons that responded vigorously to the smallest targets that we could animate on our computer monitor at that time, a single pixel (angular subtense approx. 0.16°) with a target area of just 0.026 deg² [26]. For comparison, the size of this single pixel target is indicated by an arrow in figure 5b. Based on our data, such tiny targets would only be producing modulations of individual photoreceptors on the order of 0.1 mV. This is well below (at around 0.5 s.d.) the photoreceptor noise level and thus indicative of a contrast sensitivity (approx. 90) around double that for single photoreceptors. Although these recordings were from a different species, males of both E. tenax and C. stygia have similar optics in the fronto-dorsal acute zone, with ommatidial facet diameters around 40–50 µm and inter-receptor angles close to 1° [19,27]. The discrepancy between the observed contrast threshold in the STMD neuron and the noise in individual photoreceptor responses thus most likely reflects the fact that the dipteran eye uses a neural superposition mechanism: downstream second-order lamina monopolar cells (LMCs) sum responses of six photoreceptors in adjacent ommatidia that all view the same target (see [28]). Assuming that the noise is Gaussian and independent, responses summed across photoreceptors could give an improvement in the signal-to-noise ratio as high as √N, where N is the number of photoreceptors [1], i.e. a factor of a little over 2 in this case. While this accounts for the discrepancy, it still underscores the fact that the STMD neurons are capable of responding reliably right at the absolute limits imposed by the noise in single photoreceptors.

Perhaps the most remarkable feature of this observation is that initial modulations on the order of just 0.1 mV in the photoreceptors (around 1/500th of the useful operating range of membrane potential) are amplified by subsequent neural processing to generate reliable STMD responses on the order of tens or hundreds of spikes per second. Yet, STMDs are typically silent when viewing the same blank screen used to measure the photoreceptor noise levels here! Indeed, Nordström et al. [26] observed 50% maximal responses for targets with an area just four times this limit. The remarkable absolute sensitivity of STMD neurons to tiny features underscores both the enormous contrast gain (amplification) and the sophistication of the nonlinear processing in the downstream STMD pathway that extracts feature motion [29–31].

(c). Contrast sensitivity of dragonfly small target motion detector neurons

Dragonfly STMD neurons are an excellent model system for analysing spatial and temporal coding of small targets, in part because the large size of some neurons and the stability of the dragonfly optic lobe preparation allows more robust and repeatable measurements than in dipteran STMDs. Because dragonflies lack the benefit of neural superposition seen in the dipteran flies, it is also intrinsically interesting to compare contrast sensitivity in these species. We therefore studied responses to drifting targets of different size and different contrast in several different classes of dragonfly STMD neurons. Figure 6 shows the effect of varying target contrast on the response to different-sized targets, averaged across five recordings in different animals from an unidentified STMD neuron class with a receptive field centre that corresponds to the frontal–dorsal acute zone in the dragonfly Hemicordulia tau. In each case, the (horizontally drifted) targets have a constant width (1°) and vary only in their length (i.e. orthogonal to the direction of travel). Above 2–3°, responses are attenuated by the spatial inhibition mechanisms that define these neurons as STMDs (see [31] and review [23]). Below this size, however, as the targets fall below the receptive field size of single photoreceptors, the roll-off thus reveals contrast attenuation by the optics.

Figure 6.

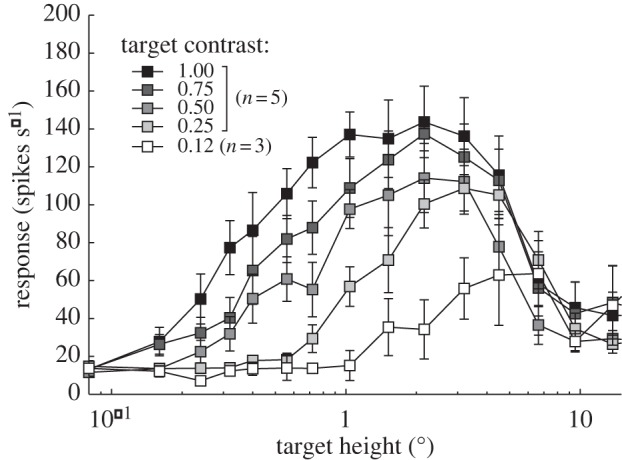
Spatial response tuning averaged from five STMD neurons in the dragonfly H. tau, to targets with different Weber contrast. All targets had an angular width of 1.0° and were drifted through the receptive field at 45° s⁻¹. Although roll-off for large targets reflects neural inhibitory mechanisms, the dependency of roll-off at smaller sizes on target contrast is predicted by optical blur in the photoreceptors (see text).

Using a similar experimental approach, but this time with recordings from the well characterized dragonfly STMD neuron, CSTMD1 [32], we examined this trade-off as a means to infer the neural contrast sensitivity function (i.e. the relationship between neural contrast and response). Plotting raw contrast of different targets against STMD response yields a confusing mess (figure 7a). However, we can correct for the differential effects of optical blur on the different-sized targets using our optical model to determine the maximum neural contrast, with an assumed acceptance half-width (Δρ) of 1.5° as recorded previously in this same dragonfly [33]. This yields contrast sensitivity functions that overlie closely at low contrasts for smaller target sizes (figure 7b). These contrast sensitivity functions reveal a common threshold for response at around 2–3% contrast and then display an unusually steep rise in response to saturate at higher contrast (figure 7b). Once targets exceed the size of single ommatidia (approx. 1.5°), responses are similarly sensitive at low contrast, but inhibition attenuates responses at higher contrasts (open symbols in figure 7b). Interestingly, the threshold for recruiting such inhibition decreases as target size increases, suggesting that the underlying detectors of target motion have lower contrast thresholds than the mechanisms of inhibition that shape small target selectivity [31]. An equivalent analysis of the data from the five neurons averaged in figure 6 yields similar results, with a threshold response for maximal neural contrasts of around 2–3%. This indicates an underlying contrast sensitivity of a similar order to that which we determined for individual blowfly photoreceptors, but, in this case, without the benefit of neural superposition that yields the even higher sensitivity in the hoverfly STMD neurons.

Figure 7.

Contrast sensitivity functions averaged from seven recordings of the STMD neuron CSTMD1 in the dragonfly H. tau, to targets with different angular size, for Weber contrasts of 1.0, 0.75, 0.5, 0.25 and 0.125. All targets had an angular width of 1.0°. (a) The response as a function of the raw (Weber) contrast of the targets. Open symbols illustrate target lengths above 1.5°. (b) The response after correction for the Weber contrast to take account of optical blur by the photoreceptors (angular sensitivity of 1.5°), revealing a threshold for the effective image contrast on the order of 2–3%.

There are very few prior studies that have attempted to quantify contrast sensitivity for small target detection in insects. Vallet & Coles [34] used a behavioural approach to study honeybee drone (male) visual responses to objects near to a lure that had been doped with queen pheromone. Drones responded to objects subtending small visual angles—as small as 0.41°, but still two to three times larger than we have observed here as the limiting size for targets to stimulate STMD neurons in flies and dragonflies. Using a similar approach to the one we have used here for determining the contrast modulation that such targets would induce at the retina, they estimated this to correspond to a neural contrast of approximately 8%, i.e. a contrast sensitivity on the order of 12.5. In a more recent study, Burton & Laughlin [35] examined performance of the photoreceptors in the dorsal acute zone of the male housefly, Musca domestica—the famous ‘lovespot’ region specialized for detection and pursuit of conspecifics [36]). They observed similar noise thresholds to those we report here for a similar eye region in males of C. stygia (see figure 5), which they estimate to correspond to target sizes of 0.3° (i.e. around double the value we observe). Using stimuli designed to mimic the optical luminance signals that would be experienced by fly photoreceptors observing the transit of a moving target, they further observed an interesting nonlinearity in the response to moving targets: when the stimulus duration is greater than 7 ms male photoreceptors amplify high-contrast targets more than low-contrast targets. Females show a similar nonlinearity, but only for slow moving features (stimulus duration greater than 100 ms) [35]. Placing their results in a more ecological context, Burton & Laughlin [35] estimated that these adaptations to boost sensitivity in the lovespot were sufficient for the male photoreceptors to generate a detectable response to a cruising fly at a distance of at least 76 cm. Given (i) our observations that sensitivity of higher-order neurons operates well beyond the noise limits of single photoreceptors, at least in the neural superposition eyes of dipteran flies, and (ii) the even higher contrast sensitivity of the larger insect species that we report on here, it seems likely that the limits for detection in these higher-order neurons of the dragonfly or hoverfly extend to targets at a distance of several metres, at least when viewed against the bright sky. An additional benefit for such high contrast sensitivity is that it would also enable reliable discrimination against more cluttered backgrounds typical of natural scenes—a task that STMD neurons of both species are capable of [26,37]. Indeed, we can conclude by noting that the contrast sensitivity of moving target detection in both flies and dragonflies is remarkable compared with the contrast sensitivity for grating patterns observed in either insects or vertebrates (see §1b,c): without the benefit of the spatial averaging across multiple local motion detectors that can contribute to the psychophysically measured contrast thresholds or those of wide-field motion neurons, the insect STMD pathway, nevertheless, achieves a contrast sensitivity that rivals the highest seen in any animal.

Appendix A. Methods

Data are stored within the DataConnect repository at the University of Adelaide with descriptions shared on Research Data Australia.

(a). Physiological recording

Experiments were carried out on either wild-caught dragonflies (H. tau) of either sex or males of laboratory-reared blowflies (C. stygia). Insects were immobilized with a wax–rosin mixture (1 : 1). For optic lobe recording (dragonflies), the head was tilted forward to gain access to the posterior head surface, and a small hole was cut in the cuticle above the left lobula and lateral midbrain, leaving the perineural sheath intact. For photoreceptor recording (blowflies), a small triangular hole was cut through the cornea near the frontal midline and just above the frontal–dorsal acute zone (easily identified by the large ommatidial facets) which was then filled with silicone vacuum grease to prevent desiccation. Neurons were recorded intracellularly using aluminium silicate micropipettes pulled on a Sutter Instruments P-97 puller and filled with 2 M KCl (typical tip resistance between 80 and 130 MΩ).

(b). Stimuli

Visual stimuli (drifting targets) were presented to the animals on a high-resolution LCD computer monitor at 120 Hz frame rate using custom software implemented using the Psychophysics Toolbox for MATLAB. Nominal Weber contrasts were calculated from RGB values (linearized monitor, white background 315 cd m⁻²), C = (target – background)/background. Data were digitized at 5 kHz using a 16-bit A/D converter (National Instruments, Austin, TX, USA) and analysed off-line with MATLAB. STMD neurons were identified based on their strong response to small targets and lack of response to elongated features or grating patterns. Receptive fields were first mapped for optic lobe neurons using 37 horizontal and 21 vertical scans of a 1.25° dark target across the monitor (approx. 100° × 80° viewing extent) at 45° s⁻¹. Subsequent test stimuli were drifted through the receptive field centre as determined by the initial characterization. For full details of these methods, see [31].

For photoreceptors, receptive field location was first determined approximately by moving a dark bar across the screen horizontally and vertically and then mapped in detail using 50 or 100 successive scans of a 1.25° dark target across a 10 × 10° region of interest centred on the receptive field location, at 45° s⁻¹. The receptive field centre was then determined by fitting a Gaussian function to the resultant receptive field map. All subsequent test stimuli were presented, so that the targets drifted through the centre of the receptive field. Average noise level of photoreceptors was determined from the standard deviation of the membrane potential recorded in response to a blank screen of maximum luminance (i.e. 315 cd m⁻²), i.e. equivalent to the background against which the targets were viewed. This value was then corrected for noise in the instrument amplifiers and recording circuitry by digitizing the extracellular potential adjacent to the recorded photoreceptors immediately following each recording, using the same electrode.

(c). Optical modelling

An optical model was developed in MATLAB to account for the influence on image contrast of optical blur due to the point-spread function of the optics and the acceptance area of photoreceptors at the focal plane. The object was first rendered at the desired luminance contrast into a two-dimensional matrix defined on a spatial baseline with 0.01° resolution. A second matrix was constructed as a convolution kernel, assumed to be Gaussian with a full-width at half-maximum that accounts for the desired acceptance function, Δρ. Both matrices were dimensioned appropriate to the size of the rendered feature and the width of the Gaussian. The neural image was then determined by two-dimensional convolution of these two matrices. A mosaic of photoreceptors with the desired inter-receptor angular separation (Δϕ) was then projected onto this neural image. Maximum neural contrast was determined from the Weber contrast of the maximum and minimum luminance in this neural image. This is functionally equivalent to the difference in the integrated luminance signal detected by a central photoreceptor of the mosaic (i.e. centred precisely on the imaged feature) and that detected by distant photoreceptors that view the background of the image.

Funding statement

Research was supported by the Australian Research Council's Discovery Projects funding scheme (project no. DP130104572) and the US Air Force Office of Scientific Research (FA2386-10-1-4114).