Abstract
Resistance parameters are essential for the prediction of pressure drop in bag filters. The reported values for limestone dust differ in magnitude and also depend on operating parameters. In this work, experimental data is provided from a pilot scale pulse-jet regenerated bag filter test facility for three types of needle felts using air and limestone dust at ambient conditions. Results reveal that specific resistance of filter media is independent of velocity while the specific resistance of filter cake increases linearly with filtration velocity. Residual pressure drop is almost constant, independent of upper pressure drop limit. The cake resistance at constant velocity fits to a second degree polynomial whereas it increases linearly with the velocity. A linear relation is reported here for all the cases. The resistance of filter cake decreases at higher upper pressure drop limit.
Keywords: Off-gas purification, Pulse-jet bag filter, Operating parameters, Cake properties, Needle felt
Graphical abstract

Highlights
► Residual pressure drop is independent of upper pressure drop. ► Specific resistance of filter media is independent of velocity. ► Specific cake resistance versus cake area load fit to 2nd degree polynomial. ► Specific cake resistance is proportional to velocity and decreases with ΔPmax limit.
1. Introduction
In surface filters, dust laden gas pervades through a permeable filter media leaving the dust on filter surface. The separated dust forms a layer called filter cake, which is a source of increasing pressure drop. The pressure drop depends on operation parameters (e.g. filtration velocity and dust concentration), filter media (e.g. permeability and surface properties), dust (e.g. composition, shape, and size distribution of particles), gas properties (e.g. composition and temperature), and parameters of bag cleaning system (e.g. pulse-jet over pressure and duration). There are two basic approaches to correlate filter pressure drop to the operating parameters. In the first approach, pressure drop is related to operating parameters through regression analysis [1]
| (1) |
and [1,2].
| (2) |
where c is the dust concentration (g/m3), Pjet is the compressed air pressure in the reservoir (bar), N is the number of cleaning pulses (–), u is the filtration velocity (mm/s), w is the cake area load (g/m2), and ai and bi are the regeneration coefficients.
In the second and more common approach, overall pressure drop () is usually taken as a sum of pressure drop across regenerated filter media () and pressure drop across the cake (). The two resistances are assumed in series.
| (3) |
Since filtration velocity is generally low at low Reynolds number (Re < 1), Darcy's law can be applied to describe gas flow through the fibrous filter and dust cake to compute individual pressure drops;
| (4) |
and
| (5) |
where μ is the gas viscosity (Pa·s), u is the face velocity or superficial velocity, Lm and Lc are the thicknesses (mm) of filter media and the dust cake, respectively, Bm and Bc are the permeabilities (m2) of filter media after regeneration and the dust cake, respectively. Overall pressure drop can be written as:
| (6) |
However, Bc depends on the thickness (Lc) and mass of filter cake (w), which can be calculated using mass balance at any time t:
| (7) |
where c is the dust concentration, t is the filtration time (s), ρs is the density of particles(kg/m3), Se is the total separation efficiency (–), ϵc is the porosity of cake (–), and w is the cake area load. Combining Eqs. (6) and (7):
| (8) |
or
| (9) |
where is the specific resistance of filter media (m− 1) and is the specific resistance of dust cake (m/kg).
Eq. (9) is one the most commonly used for describing the filter pressure drop [1]. It is obvious that will rise with filtration velocity only due to a proportional increase of filter cake thickness or cake area load at all other conditions being fixed. Mathematically, w is related to c, u and t in Eq. (10)
| (10) |
and to cake height (X) and density (ρc) in Eq. (11).
| (11) |
Resistance parameters km and kc are not constant as is often assumed but complicated functions of many other variables. Various correlations are reported in literature [1,3] for their estimation. Filter media resistance (Km = km ⋅ μ) is related to pulse pressure [4], reservoir pressure [5], decay of pressure pulse in the bag, and velocity [1]. Specific resistance of filter cake (kc) also depends on, for example, dust properties, particle size and its distribution, cake structure and porosity, gas properties, temperature and composition, and operating parameters like velocity, , and dust concentration. Cake resistance parameter (kc) is determined from the pressure drop curve provided information on cake area load is available as a fit parameter. It can also be determined from Carmon–Kozney equation if cake porosity is known from independent measurements [1].
Specific resistance (Kc = kc ⋅ μ) of limestone dust (dp = 2.53MMAD) at ambient conditions is reported as 3.65e5–8.44e5 [6] at μ = 10 − 90 mm/s and c = 2.83 − 3.40 g/m3. The Kc is exponentially related to u as Kc ∝ u0.38. It is also reported that Kc of limestone dust (X50, 3 = 5 μm) at ambient conditions is 0.69e5–1.45e5 at μ = 42 − 83 mm/s and c = 1 − 10 g/m3 [7]. Others [8] determined the Kc of limestone dust (X50, 3 = 3.5 μm) at ambient conditions as and at μ = 28 − 45.8 mm/s, respectively.
Variability of resistance parameters is not surprising because of the types and surface treatment of filter media, types and properties of dusts, operating conditions, gas properties, and equipment design. To be able to develop simulations that can truly replicate the pressure drop curves, it is necessary to have the realistic estimates of these parameters. In this work, experiments are performed with three types of needle felts over a range of operating conditions in a pilot scale test facility to estimate resistance parameters using air and limestone dust at ambient conditions.
2. Experimental
The experimental set-up consists of three rows of bags (two bags per row at maximum) enclosed in one chamber, which closely resembles a large scale bag filter equipped with necessary instrumentation for acquiring important data simultaneously. Operating conditions are selected in the range of commercial bag filter [1]. Sequence of bag cleaning, mode of cleaning, fraction of area to be cleaned and other parameters remain the choice of the experimenter.
2.1. The test facility
A schematic diagram of the test facility is shown in Fig. 1. A two screw single component feeder (1) delivers a controlled constant mass (gravimetric control, variation 1% at steady state) of powder into the dispersion nozzle (3) through a vibrating chute (2). Compressed, filtered and dried air meets the dust tangentially in the dispersion nozzle at controllable pressure up to 6 bar. Ambient air is sucked in and mixed with dispersed dust to make the dust laden gas stream. The raw gas flows through a 100 mm diameter pipe into the bag filter (4) near the bottom. The raw gas pipe is gradually expanded near the filter to reduce gas velocity before entering the filter. The separated dust settles into a dust collector at the bottom of the housing. The dust collector rests freely on a plate supported on a load cell. Both (the load cell and the dust collector (5)) are enclosed in the housing (4). The arrangement allows transient measurement of dust reaching the collector. The load cell is calibrated from 0 to 4000 ± 2 g. The range can be extended at the loss of accuracy of measurement. The gas pervades through the filter bags (6) into the clean gas header and then to the discharge fan (8).
Fig. 1.
A schematic diagram of the pulse-jet bag filter test facility.
The differential pressure regulator (3 ms time constant) monitors pressure drop across the filter. Cake detachment is accomplished on line using reverse pulse-jet. A pulse of compressed air (9) enters the bag through an 8 mm diameter hole in the gas supply pipe (27 mm diameter) tapping secondary gas from the clean gas side. One pulse is issued to each row at the upper pressure drop limit. To which row of bags the 1st jet pulse will be issued depends on the last row cleaned, however, the cyclic order is always followed unless manual cleaning is adopted. Provisions are made for three jet pulse control mechanisms. The reservoir pressure of the cleaning air can be set up to 4 bar, the time of cleaning pulse can be set between 10 and 100 ms, and the interval between cleaning pulses can be set between 2 and 450 s.
The gas flow is measured using an orifice plate. The pressure drop across the orifice plate, absolute upstream pressure and temperature are recorded at 1 s resolution. The gas flow is calculated by the Labview ® software according to DIN EN-ISO5167-1: 1995 (large fan) and ISO 5167:2003 (small fan) depending on the fan in use and recorded. The gas flow measured was calibrated using Pitot tube measurements. A frequency converter is provided to regulate the gas flow.
Filter pressure drop (), gas temperature (T), absolute pressure (Pa), pressure in the compressed air tank (Pjet) and temperature (Tjet), dust feed rate (), and collected dust (m) are recorded along with date and time at 1 s interval. Relative humidity (H), impulse time (τImpulse), interval between consecutive pulses (τint), and dispersion air pressure (Pdis) are recorded manually. Also the mass of dust in the feeder hopper is recorded at the start and at the end of the experiment along with the dust collector reading. Dust concentration measurements on clean gas side revealed concentrations in the range of 2–4 mg/m3 using gravimetric methods. The overall material balance was closed at less than 1%.
Dust fraction settling in the filter and dust concentration relevant for filtration can be calculated because transient dust feed and dust collected in the filter are known. Besides an optical system is used to measure cake heights in-situ and intermittently [9,10].
2.1.1. Filter media
Three types of needle felts are tested (Table 1). TAN5448 is made of two polymers; polyimide (PI) and polyphenylensulfide (PPS) and TAN5446 is made of a single polymer polyimide (PI). These two needle felts are heat treated on dust side and are provided by Inspec Fibers, Lenzing, Austria. The third one is PTFE laminated polyester needle felt which is provided by GORETEX.
Table 1.
Mechanical properties of the tested needle felts [Source: Company data sheets].
| Fiber content |
Polyimide + polyphenylenesulfide |
Polyimide + polyimide |
PTFE laminated polyester |
Unit |
|---|---|---|---|---|
| ID | TAN5448 | TAN5446 | GORETEX | |
| Breaking strength, machine direction | 841 | 743.2 | 601 | |
| Breaking strength, cross-machine direction | 1464 | 2013.4 | 890 | |
| Strain, machine direction | 27.7 | 29.8 | – | % |
| Strain, cross-machine direction | 35.4 | 48,4 | – | % |
| Air permeability at 200 Pa | 79.5 | 73.5 | – | l/dm2/min |
| Weight | 575 | 624 | 407 | g/m2 |
| Felt construction | Supported needle felt | Supported needle felt | Supported needle felt | – |
| Service temperature | – | – | 135 | °C |
| Max. surge temperature | – | – | 149 | °C |
| Thickness | – | – | 1.4 | mm |
2.1.2. The dust
Commercial grade non-precipitated limestone (, ρs = 2700 kg/m3) with weight median diameter (d50, 3) of 5 μm and bulk density (ρb) of 1200 kg/m3 is used as dust. A sample cumulative size distribution is presented in Fig. 2.
Fig. 2.
Cumulative mass distribution of Non-precipitated Commercial grade Limestone dust from OMYACARB, Austria using Laser diffraction particle analyzer SediGraph 5100 V3.07A. The commercial name as used is OMYACARB 5GU.
3. Results and discussion
The microscopic images of the filter surface are shown in Fig. 3 while the experimental conditions are listed in Table 2.
Fig. 3.
Surface roughness of (a) TAN5448 needle felt, (b) TAN5446 needle felt and (c) GORETEX needle felt.
Table 2.
Test conditions for the study of the influence of u and w on and ks on uniformly loaded filter media at ambient conditions with limestone dust (d50, 3 = 5 μm) in a jet pulsed bag filter.
| No. |
A |
u |
c |
Pjet |
|
H |
T |
|---|---|---|---|---|---|---|---|
| m2 | mm/s | g/m3 | bar | Pa | % | °C | |
| TAN5448 needle felt | |||||||
| 1 | 2.03 | 20.5 | 4.2 | 4 | 2300 | 34 | 25.5 |
| 1 | 2.03 | 27.3 | 4.55 | 4 | 2300 | 34 | 25.5 |
| 2 | 2.03 | 34.1 | 4.55 | 4 | 2300 | 34 | 25.5 |
| 3 | 2.03 | 40.96 | 4.49 | 4 | 2400 | 34 | 25.5 |
| 4 | 2.03 | 47.78 | 4.7 | 4 | 2400 | 34 | 25.5 |
| TAN5446 needle felt | |||||||
| 1 | 2.03 | 27.3 | 5 | 4 | 2200 | 44 | 27 |
| 2 | 2.03 | 34.1 | 5 | 4 | 2200 | 44 | 27 |
| 3 | 2.03 | 40.96 | 4.97 | 4 | 2200 | 44 | 27 |
| 4 | 2.03 | 47.78 | 4.63 | 4 | 2200 | 44 | 27 |
| 4 | 2.03 | 54.61 | 4.86 | 4 | 2200 | 44 | 27 |
| GORETEX needle felt | |||||||
| 1 | 2.03 | 27.3 | 4.97 | 4 | 2300 | 36 | 28 |
| 2 | 2.03 | 34.1 | 4.8 | 4 | 2300 | 36 | 28 |
| 3 | 2.03 | 40.96 | 4.90 | 4 | 2300 | 36 | 28 |
| 4 | 2.03 | 47.78 | 4.68 | 4 | 2400 | 36 | 28 |
| 4 | 2.03 | 54.61 | 5.2 | 4 | 2434 | 36 | 28 |
3.1. Effect of cake area load
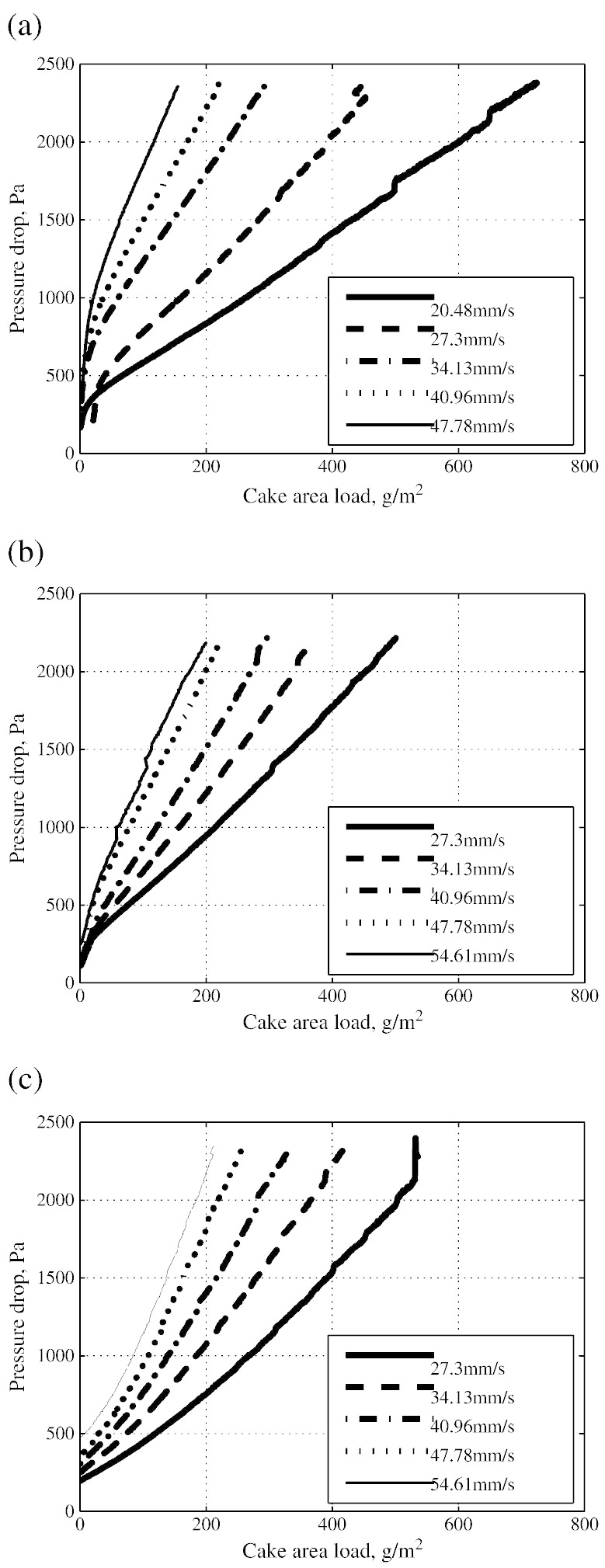
Transient pressure drop versus average cake area load is depicted in Fig. 4a at five filtration velocities for three types of needle felts. The GORETEX bags are installed with membrane on the clean side. The TAN5448 bags are thoroughly regenerated except at 27.3 mm/s. It is evident that the pressure drop is higher at higher filtration velocity at the same cake area load. The pressure drop curves corresponding to 20.48 mm/s and 27.3 mm/s show sudden jumps. These jumps are probably due to irreversible cake compression. At 20.48 mm/s these jumps are observed at 1300 Pa, 1700 Pa, and 2100 Pa, respectively. At 27.3 mm/s the jumps are observed at 1600 Pa and 2000 Pa. No such jumps in the curves are observed at higher velocities. Perhaps the cake formed at lower filtration velocity possesses low mechanical stability. It is clear that the pressure drop increases with the filter cake thickness. This pressure difference across the cake is a source of compressive stress on the cake. In the course of filtration a point is reached at which the mechanical strength of the cake is not sufficient to withstand the compressive stress exerted by the increasing pressure drop. Possibly at this point a mechanical failure occurs and cake compression takes place. The cake formed at higher velocity is compact [8] and possesses higher mechanical stability. Therefore, the cake is capable of withstanding pressure drop and no jumps in the curves are recorded. The data reveal that only two jumps are observed at 27.3 mm/s as compared to three at 20.48 mm/s. Further the first jump appears at 1300 Pa and 1650 Pa at 20.48 mm/s and 27.3 mm/s, respectively. The pressure drop is related to operating parameters through characteristics Eq. (12):
| (12) |
Fig. 4.
Effect of cake area load (w) on pressure drop at constant velocity (u); (a) TAN5448 needle felt; (b) TAN5446 needle felt; and (c) GORETEX needle felt. PTFE membrane on clean side.
If the starting pressure drop is subtracted from the L.H.S., one gets a pressure drop solely due to the cake on the filter media.
| (13) |
or
| (14) |
Thus is proportional to u and w at constant temperature and composition. At a constant u one expects a linear versus w. However, all curves in Fig. 4a are concave. Since the dust feed and gas flow rates are constant, a constant dust concentration is expected too. At constant dust concentration a concave rise can only be expected due to non-uniform gas flow distribution arising from permeability distribution of filter media. A locally higher filtration velocity results in faster cake growth at some areas probably with higher cake resistance and a slower cake growth at other areas at lower filtration velocity. The non-uniform cake formation is quickly leveled off and a uniform cake formation at uniformly distributed gas flow is realized. The duration over which the concave rise is observed depends on surface characteristics of filter media and operating conditions. It is interesting to see that there is a certain cake area load (20 − 25 g/m2) after which the pressure drop curves become linear for TAN5448 filter media irrespective of filtration velocity. One observes that a significant increase in is obtained without any significant dust deposition at higher velocity leading to drastic reduction of filtration time. A higher cake area load (730 g/m2) is observed at the end of the cycle at lower velocity (20.48 mm/s) at the same upper pressure drop limit compared to 160 g/m2 at 47.78 mm/s. A 2.35 times increase in filtration velocity reduces the cake area load by 4.56 times.
Transient pressure drop versus cake area load of TAN5446 filter medium is also shown in Fig. 4b at five filtration velocities. In all cases the pressure drop evolves from a thoroughly regenerated filter bags. The dust supply is turned off for cake height measurements at 54.61 mm/s, therefore, the curve shows two discontinuities which are not due to cake compaction. The curve at 27.3 mm/s shows four jumps at 1350 Pa, 1700 Pa, 1850 Pa, and 2100 Pa, respectively. The 1st jump is higher in magnitude than the other three. The curve corresponding to 34.13 mm/s and 40.96 mm/s show jumps at 2000 Pa and 2050 Pa, respectively. There are no jumps at higher velocities. One can observe that the pressure drop curves tend to be linear after (20 − 25 g/m2) cake area load. The filtration cycles are longer at low filtration velocity due to low cake resistance. Thus a higher cake area load (500 g/m2) is observed corresponding to 27.3 mm/s at the end of cycle at the same pressure drop in comparison to 200 g/m2 at 54.61 mm/s. A 2 times increase of velocity decreases the cake area load by 2.5 times.
The transient pressure drop curves versus cake area load of GORETEX filter medium at five filtration velocities are included in Fig. 4 too. The upper limit is set at 2200 Pa on . The pressure drop evolves from completely regenerated filter bags. Contrary to TAN5448 and TAN5446, the pressure drop curves are convex and show a continuous compaction of initial cake layers at all velocities. Additionally sudden jumps in the curves can be seen at all velocities similar to those observed with the other two filter media. Therefore, the formed cake possesses low mechanical stability at all filtration velocities in this case. The jump at 27.3 mm/s is bigger in magnitude as compared to the others. The residual pressure drop is significantly higher at higher velocities. (The cake area load is 540 g/m2 at 27.3 mm/s in comparison to 210 g/m2 at 54.61 mm/s.) A 2 times increase of filtration velocity decreases the cake area load by 2.57 times.
Despite pressure drop curves showing different cake formations at different filtration velocities and different filter media, it is evident that the filtration should be carried out at relatively lower filtration velocity. The concave ΔP rise is small and formed cake provides low resistance consequently thicker cakes for the same upper limit of ΔP can be obtained at lower filtration velocity. It is also experienced that thicker cake is relatively easily detached resulting in cleaner regenerated bags. A similar behavior is also reported in literature [11]. Pressure drop at zero cake area load ΔP0 is plotted in Fig. 5. The pressure drop increases with filtration velocity, which is the highest for GORETEX bags at respective filtration velocity. However, ΔP0 of TAN5448 filter medium is higher than that of the TAN5446.
Fig. 5.
Effect of filtration velocity on pressure drop of filter media at zero cake area load for the three needle felts.
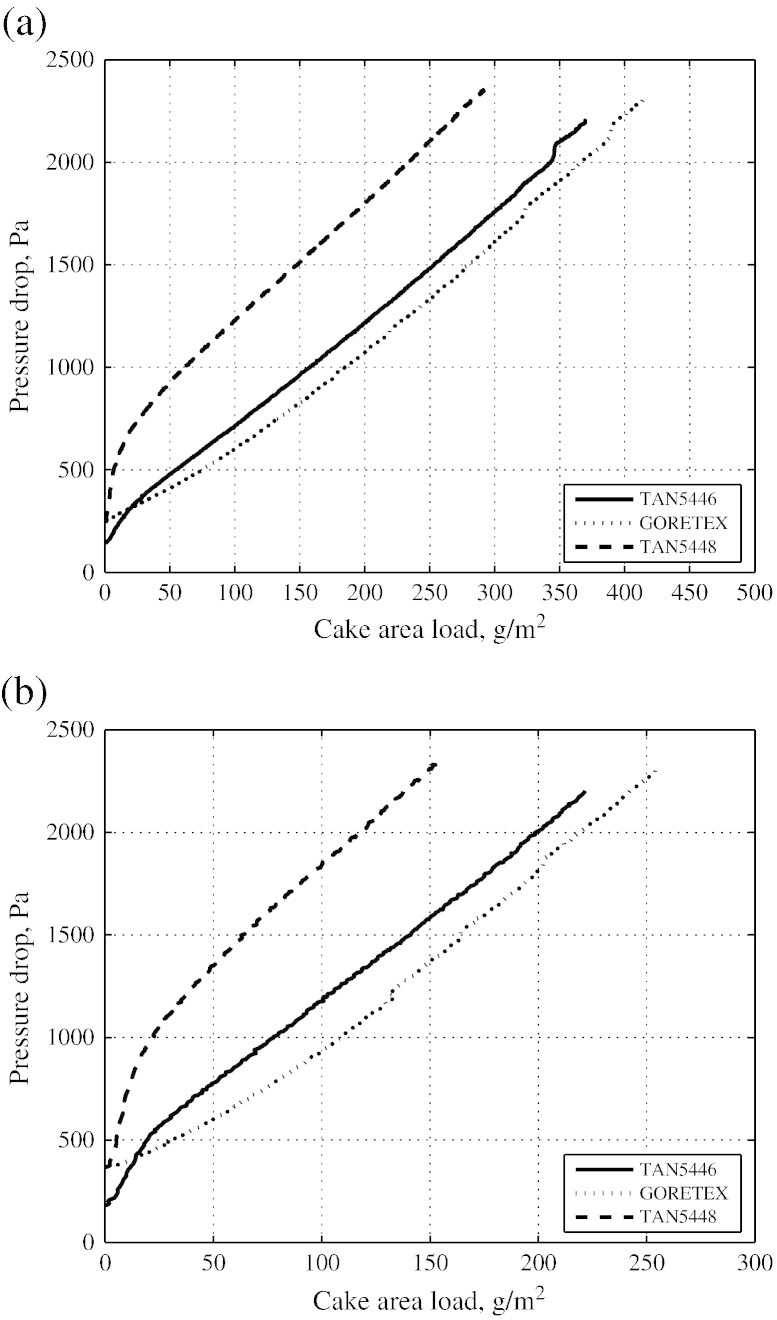
Transient pressure drop of three filter media at 34.13 mm/s and 47.78 mm/s is depicted in Fig. 6a and b, respectively. It can be noticed that the residual pressure drop is higher for TAN5448 and GORETEX needle felts [Fig. 6a]. The trend of pressure drop curves is similar for two needle felts namely TAN5446 and TAN5448. However, the pressure drop of TAN5448 is higher at the same cake area load. The pressure drop curves are concave initially which become linear afterwards. The cake formed on TAN5446 needle felt undergoes a sudden compaction at 2000 Pa. The cake area load on TAN5448 and TAN5446 needle felts at 2000 Pa is 230 g/m2 and 345 g/m2, respectively which is significantly different. The pressure drop of TAN5446 is initially lower which becomes higher at w = 25 g/m2 than that of the GORETEX needle felt. The cake area load is 365 g/m2 on GORETEX bags at 2000 Pa, which reflects that GORETEX bags carry higher cake area load at the same upper limit of pressure drop and yield longer filtration cycle at the same filtration velocity. Similar trend is observed at higher velocity (Fig. 6b) as well.
Fig. 6.
Comparison of transient pressure drop of three types of filter media at constant filtration velocity (a) 34.13 mm/s and (b) 47.78 mm/s .
3.2. Effect of filtration velocity
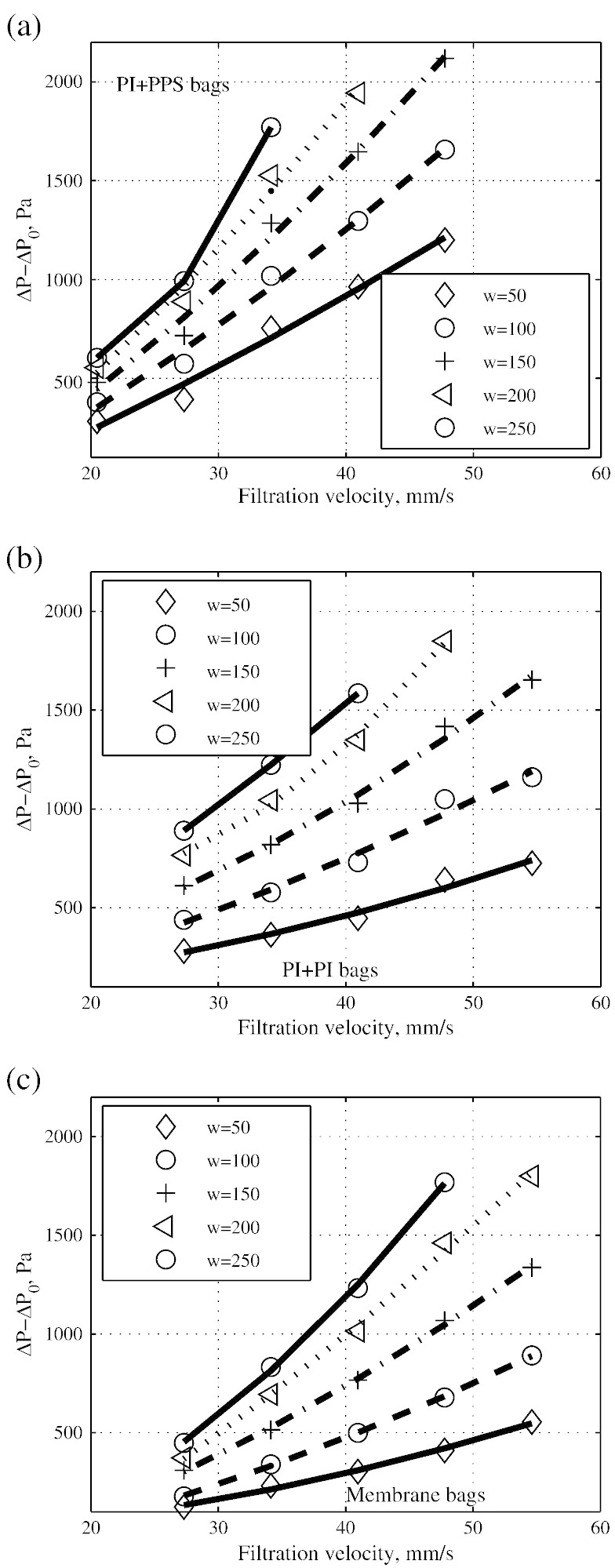
The residual pressure drop is subtracted from the transient pressure drop at the same cake area load but different filtration velocity and the difference is plotted versus filtration velocity (u) at constant cake area load (w) for three filter media in Fig. 7. Pressure drop is increasing non-linearly with u at constant w for all three types of filter media. The data are fitted to a 2nd degree polynomial using least squares method. The parameters of the fit are given in Tables 3, 4, and 5.
Fig. 7.
Pressure drop due to dust cake versus filtration velocity at constant cake area load; (a) TAN5448 needle felt; (b) TAN5446 needle felt; and (c) GORETEX needle felt.
Table 3.
Parameters of a 2nd degree polynomial () fit to the data of Fig. 7 (a).
| w (g/m2) | a | b | c |
|---|---|---|---|
| 50 | 0.14897 | 25.033 | − 323.22 |
| 100 | 0.25546 | 30.582 | − 380.26 |
| 150 | 0.40452 | 34.04 | − 421.77 |
| 200 | 0.44269 | 43.193 | − 542.09 |
| 250 | 4.1652 | − 141.99 | 1764.4 |
Table 4.
Parameters of a 2nd degree polynomial () fit to the data of Fig. 7b.
| w (g/m2) | a | b | c |
|---|---|---|---|
| 50 | 0.17046 | 3.1262 | 61.648 |
| 100 | 0.1706 | 14.1 | − 87.931 |
| 150 | 0.36229 | 9.5877 | 71.678 |
| 200 | 1.1948 | − 37.629 | 911.08 |
| 250 | 0.29773 | 30.515 | − 164.56 |
Table 5.
Parameters of a 2nd degree polynomial () fit to the data of Fig. 7(c).
| w (g/m2) | a | b | c |
|---|---|---|---|
| 50 | 0.1657 | 1.6029 | − 34.283 |
| 100 | 0.18732 | 10.525 | − 245.37 |
| 150 | 0.27176 | 15.926 | − 334.61 |
| 200 | 0.24744 | 32.771 | − 712.18 |
| 250 | 0.81341 | 2.836 | − 229.81 |
The specific resistance of filter media at different filtration velocities is displayed in Fig. 8. Despite some scatter in the data, the resistance appears independent of filtration velocity. Two outliers are identified. The specific resistance of TAN5448 needle felt is comparable to that of the GORETEX needle felt at 40 mm/s. The TAN5446 possesses the least resistance. The resistance of GORETEX filter bags is two orders of magnitude higher than that of TAN5446 filter bags at all filtration velocities.
Fig. 8.
Effect of filtration velocity on filter media resistance.
The filter cake resistance at different filtration velocities is displayed in Fig. 9. The specific cake resistance is increasing in general for all filter media. The cake on TAN5446 filter bags possesses less resistance than that on GORETEX or TAN5448 filter bags. It should be pointed out that the specific resistance is calculated from the slope of the linear part of the pressure drop curves and the corrected dust concentration. The resistance of the cake on TAN5448 filter bags is higher as compared to the cake on TAN5446 filter bags.
Fig. 9.
Effect of filtration velocity on lime stone dust cake resistance.
Resistance parameters and influence of operating parameters have been investigated by others [1,3]. The results of this study are compared with the literature values for limestone dust (Table 6).
Table 6.
Comparison of Kc values.
| Author | Filter medium |
dp |
u |
c |
T |
Kc |
Function |
|---|---|---|---|---|---|---|---|
| μm | mm/s | g/m3 | °C | 1/s | |||
| [6] | – | 2.53 | 10–90 | 2.83–3.4 | – | 3.65e5–8.44e5 | Kc ∝ u0.38 |
| [7] | – | 5 | 42–83 | 1–10 | – | 0.69e5–1.45e5 | – |
| [8] | – | 3.5 | 28–45.8 | – | – | 0.9–0.98() | – |
| [8] | – | 3.5 | 28–45.8 | – | – | 1.05–1.2() | – |
| This work | TAN5448 | 5 | 20–47 | 4–5 | – | 1.4e5–1.9e5 | Kc ∝ u |
| This work | TAN5446 | 5 | 20–47 | 4–5 | – | 1.33e5–1.78e5 | Kc ∝ u |
| This work | GORETEX | 5 | 20–47 | 4–5 | – | 1.36e5–1.89e5 | Kc ∝ u |
The values in this work are in close agreement to those reported in [7] but lower than those reported in [6]. As far as the relation of cake resistance parameter to velocity is concerned, a linear relation is observed for all filter media in this work whereas literature [6] reports an exponential function.
3.3. Effect of
Effect of on resistance parameters at two filtration velocities is investigated. The results are presented in Fig. 10 for TAN5448 filter bags. Only one value of the filter media resistance at 55 mm/s is included. At 27 mm/s four data points are displayed. Residual resistance of filter media is almost constant. This shows that the residual resistance of the filter bags is independent of the upper limit of pressure drop provided that the bags are properly cleaned. Specific resistance of filter cake is decreasing with increasing pressure drop limit. However, it appears approaching a limiting value. The effect of at low filtration velocity as compared to high filtration velocity is less. Specific resistance decreases by two orders of magnitude from 1200 Pa to 2400 Pa at 55 mm/s. It decreases only by 25% from 800 Pa to 2400 Pa at 27 mm/s.
Fig. 10.
Effect of upper pressure drop limit on filter media and dust cake resistance parameters.
The decrease of specific resistance at higher on aging can be explained by the better/uniform distribution of gas flow either due to accumulated dust in the interior of the filter medium or the thick cake layer at higher upper limit. A uniform local velocity results in the formation of a relatively porous cake and hence low specific resistance to gas flow. Specific resistance of filter cake decreases sharply versus upper pressure drop limit at higher velocity as compared to that at lower velocity. At higher velocity the non-uniform distributions is stronger at lower cake area load at lower upper pressure drop limit. At the higher limit, a higher cake area load and relatively less steep pressure drop resulting in lower specific resistance. Beyond 2400 Pa the effect appears insignificant. At low velocity, the effect of upper pressure drop limit is negligible after 1200 Pa.
Perhaps here again the high value at the first measurement at 55 mm/s is because of a shorter cycle which results in small cake area load and higher % error. As the cycle time increases the average error reduces and relatively constant Kc values are computed.
4. Conclusions
Experiments with three types of needle felts using air and limestone dust are performed over a range of operating conditions in a pilot scale test facility to estimate resistance parameters of the needle felts and the filter cake under uniformly loaded conditions.
The pressure drop is higher at higher velocity at constant filter cake area load. It increases non-linearly with cake area load at constant filtration velocity. Residual pressure drop is almost constant, independent of upper pressure drop limit and velocity. The specific resistance of filter media is independent of velocity.
The specific cake resistance of limestone dust versus cake area load, at constant velocity, fit to a second degree polynomial, is proportional to the velocity, and decreases with increasing upper pressure drop limit. The specific resistance decreases by two orders of magnitude from 1200 Pa to 2400 Pa at 55 mm/s. It decreases only by 25% from 800 Pa to 2400 Pa at 27 mm/s. At low velocity, the effect of upper pressure drop limit is negligible after 1200 Pa.
Acknowledgments
Authors acknowledge financial support of Higher Education Commission, Islamabad, Pakistan, the project funding by Austrian Science Foundation (FWF) under project P 16313-No.7, supply of needle felts by M/S Inspec Fibers (Lenzing, Austria), GORETEX, and M/SAlicona Imaging (Graz, Austria) for microscopic analysis of needle felts.
References
- 1.Löffler F., Dietrich H., Flatt W. Fried Vieweg and Sons; Braunschweig, Germany: 1988. Dust Collection with Bag and Envelop Filters. [Google Scholar]
- 2.Leith D., Ellenbecker M.J. Theory for pressure drop in a pulse-jet cleaned fabric filter. Atmospheric Environment. 1980;14(7):845–852. [Google Scholar]
- 3.H. Risnes, High temperature filtration in biomass combustion and gasification processes, Ph.D. thesis, NTNU Trondheim (2002).
- 4.Strangert S. Predicting performance of bag filters. Filtration and Separation. January–February 1978:42–48. [Google Scholar]
- 5.Dennis R., Klemm H.A. Modeling concepts for pulse jet filtration. Journal of the Air Pollution Control Association. 1980;30:38–48. [Google Scholar]
- 6.Cheng Y.H., Tsai C.J. Factors influencing pressure drop through a dust cake during filtration. Aerosol Science and Technology. 1998;29:315–328. [Google Scholar]
- 7.Klingel R. Vol. 76. Verein Deutscher Ingenieure(VDI)-Verlag GmbH; Düsseldorf: 1983. (Untersuchung der Partikelabscheidung aus Gasen an einem Schlauchfilter mit Druckstossabreinigung). [Google Scholar]
- 8.Schmidt E. Experimental investigations into the compression of dust cakes deposited on filter media. Filtration and Separation. 1995;32(8):789–793. [Google Scholar]
- 9.Saleem M., Krammer G. Optical in-situ measurement of filter cake height during bag filter plant operation. Powder Technology. 2007;173:93–106. [Google Scholar]
- 10.Saleem M., Khan R.U., Tahir M.S., Krammer G. Experimental study of cake formation on heat treated and membrane coated needle felts in a pilot scale pulse jet bag filter using optical in-situ cake height measurement. Powder Technology. 2011;214(3):388–399. doi: 10.1016/j.powtec.2011.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sievert J., Löffler F. Dust cake release from non-woven fabrics. Filtration and Separation. 1987:424–427. [Google Scholar]