Quantifying the Temperature Dependence of Glycine Betaine RNA Duplex Destabilization

Abstract

Glycine betaine stabilizes folded protein structure due to its unfavorable thermodynamic interactions with amide oxygen and aliphatic carbon surface area exposed during protein unfolding. However, glycine betaine can attenuate nucleic acid secondary structure stability, although its mechanism of destabilization is not currently understood. In this work we quantify glycine betaine interactions with the surface area exposed during thermal denaturation of nine RNA dodecamer duplexes with guanine-cytosine (GC) contents of 17–100%. Hyperchromicity values indicate increasing glycine betaine molality attenuates stacking. Glycine betaine destabilizes higher GC content RNA duplexes to a greater extent than low GC content duplexes due to greater accumulation at the surface area exposed during unfolding. The accumulation is very sensitive to temperature and displays characteristic entropy-enthalpy compensation. Since the entropic contribution to the m-value (used to quantify GB interaction with the RNA solvent accessible surface area exposed during denaturation) is more dependent on temperature than the enthalpic contribution, higher GC content duplexes with their larger transition temperatures are destabilized to a greater extent than low GC content duplexes. The concentration of glycine betaine at the RNA surface area exposed during unfolding relative to bulk was quantified using the solute partitioning model. Temperature correction predicts a glycine betaine concentration at 25 °C to be nearly independent of GC content, indicating that glycine betaine destabilizes all sequences equally at this temperature.

In order to gain full comprehension of nucleic acid structure stabilization or destabilization with cosolutes, it is essential to understand how cosolutes interact with nucleic acid secondary structures. In general, interactions of cosolutes and water with the chemical functional groups in the newly accessible surface area exposed during an unfolding transition drive biopolymer stabilization or destabilization (1–3). Cosolutes that have more thermodynamically favorable interactions with the chemical functional groups on the unfolded state relative to the native state destabilize the native state. The opposite is true for cosolutes that stabilize the native state.

Glycine betaine (GB), also referred to as an osmoprotectant (4–8), is a protein stabilizer because of its exclusion from anionic surfaces and the amide backbone exposed upon protein unfolding (9). However, the generality of proposed GB interactions have not been extensively tested with nucleic acids. Analysis of DNA duplex transition temperatures indicate GB eliminates the base pair composition dependence of duplex DNA and RNA by destabilizing GC (guanine-cytosine) base pairs more so than AT (adenine-thymine) or AU (adenine-uracil) base pairs (10–14). GB has also been shown to stabilize RNA tertiary structure, although the degree of stabilization is dependent on base sequence (15) and ionic strength (14).

Hong et al. used vapor pressure osmometry to demonstrate that GB is excluded from the surface of calf-thymus duplex DNA (42% GC content), independent of monovalent salt concentration (1). GB exclusion was attributed to strong exclusion from the hydration layer of anionic phosphate oxygens with random GB distribution elsewhere. In general, the transition from nucleic acid duplex to single-strands is accompanied by a minor burial of anionic oxygen (1, 16) which should lessen GB exclusion from the nucleic acid surface. Additionally, the exposure of aromatic and amine surface areas should facilitate favorable GB interactions and accumulation at the solvent accessible surface area exposed in the unfolding transition (ΔASA) (17, 18). However, the strongest correlation between GB accumulation at RNA secondary structure ΔASA was a decreasing, linear function of the fraction of ΔASA dedicated to nonpolar functional groups.

To date there has been no comprehensive analysis of the temperature dependence of GB interactions with nucleic acid secondary structure ΔASA. Felitsky et al. demonstrated that GB interaction with the lac1 HTH DNA binding domain was strongly temperature dependent and almost exclusively entropically driven (9). Since GC-rich duplexes are more stable than AT- or AU-rich duplexes (19–23), the larger transition temperatures for GC-rich duplexes could strongly affect GB interactions at nucleic acid secondary structure ΔASA if GB interaction with the nucleic acid surface area is temperature dependent.

As mentioned previously, the driving force for nucleic acid stability in cosolute solutions is tied directly to favorable or unfavorable interactions of cosolutes with chemical functional groups in the ΔASA. The magnitude of nucleic acid secondary structure destabilization with cosolutes is quantified directly by the m-value defined as (3, 16)

$$m-\text{value}={\left(\frac{\partial \mathrm{\Delta }{G}_{\text{obs}}^{\mathrm{o}}}{\partial m_3}\right)}_{T,m_4}=-RT{\left(\frac{\partial ln{K}_{\text{obs}}}{\partial m_3}\right)}_{T,m_4}=\mathrm{\Delta }{\mu }_{23,4}$$ (1)

where $\mathrm{\Delta }{G}_{\text{obs}}^{\mathrm{o}}$ is the difference in Gibbs energy between the two single-strands and the duplux, K_obs is the observed unfolding equilibrium constant, m₃ is the cosolute molality, and m₄ is the salt molality. The interaction potential, Δμ_23,4, is the difference in μ_23,4 (μ_23,4 = (∂μ₂/∂m₃)_T,P,m2,m4 where μ₂ is the chemical potential of nucleic acid) between the single-strands and duplex (Δμ_23,4 = μ_23,4,S1 + μ_23,4,S2 − μ_23,4,S1S2 where S₁ is strand 1 and S₂ is strand 2) and represents the interaction of cosolute with the surface area exposed during unfolding. Negative Δμ_23,4 and m-values indicate favorable thermodynamic interactions of the cosolute with ΔASA and concomitant destabilization of the folded nucleic acid structure. The magnitudes of the m-value and Δμ_23,4 are in direct proportion to the strength of cosolute interactions with ΔASA and the magnitude of ΔASA. The degree of nucleic acid secondary structure stability modulation with cosolutes is therefore dependent on the chemical composition of the water accessible surface area that would be exposed to solvent in a conformational change.

In this work, we have used nine RNA duplex dodecamers with GC contents ranging from 17–100% to quantify GB Δμ_23,4 and m-values at the surface area exposed during thermal denaturation in aqueous GB solutions. GB Δμ_23,4 and m-values have been determined within the transition region for all duplexes to ascertain the temperature dependence of these quantities. We find the m-values are strongly temperature dependent with characteristic entropy-enthalpy compensation. The observed m-value temperature dependence is used to elucidate the observed greater destabilization of GC-rich duplexes at their transition temperatures.

EXPERIMENTAL PROCEDURES

Materials

Lyophilized dodecamer single-stranded RNA was purchased from Integrated DNA Technologies (IDT). Reagent grade GB (N,N,N-trimethyl glycine inner salt) was purchased from Sigma and phosphate buffer components NaH₂PO₄·H₂O, Na₂HPO₄, and NaCl were purchased from Fisher Scientific. All reagents were used without further purification.

RNA Dodecamer Thermal Denaturation

Lyophilized dodecamer RNA single-strands were suspended as 50–100 μM solutions in a 133 mM sodium chloride, 10 mM sodium phosphate pH 6.9 buffer (149 mM Na⁺ overall). Single-strand dodecamer concentrations were determined by uv-absorbance at 260 nm using extinction coefficients determined from the nearest-neighbor method from Gray et al. (24). Dodecamer RNA duplexes were annealed by mixing complementary single-strands at a 1:1 mole ratio, heating to approximately 60 °C, and slowly cooling to room temperature before being stored at 4 °C. The RNA sequences (only one complementary strand shown) are given in Table 1.

Table 1.

Glycine Betaine Δμ_23,4/RT and m-Values with RNA Duplex Dodecamers During Thermal Denaturation

sequence	%GC	T/°Ca	Δμ23,4/RT/m−1b	m-value/kcal mol−1 m−1b	d(m-value)/dT/kcal mol−1 m−1 K−1	dΔHobso/dm3/kcal mol−1 m−1
5′-r(GAAAUUAUAAAG)-3′	17	27.3	−0.315 ± 0.029	−0.188 ± 0.017	−0.0044 ± 0.0003	1.12 ± 0.09
5′-r(GAAAGUAUAAAG)-3′	25	34.8	−0.398 ± 0.044	−0.244 ± 0.027	−0.0065 ± 0.0002	1.76 ± 0.05
5′-r(GAUAGUAGAUAG)-3′	33	45.5	−0.598 ± 0.027	−0.378 ± 0.017	−0.0191 ± 0.0012	4.03 ± 0.18
5′-r(GAAAGUAGAAAC)-3′	33	40.4	−0.418 ± 0.036	−0.260 ± 0.022	−0.0139 ± 0.0006	5.71 ± 0.39
5′-r(GCAAAGUAAACG)-3′	42	44.6	−0.670 ± 0.069	−0.423 ± 0.044	−0.0142 ± 0.0009	4.22 ± 0.28
5′-r(GCAAAGCAAACG)-3′	50	49.0	−1.02 ± 0.07	−0.655 ± 0.045	−0.0195 ± 0.0004	5.61 ± 0.12
5′-r(GCAUAGCAUACG)-3′	50	52.0	−0.811 ± 0.032	−0.524 ± 0.020	−0.0188 ± 0.0004	5.63 ± 0.15
5′-r(GCGAAGCCAACG)-3′	67	59.6	−0.948 ± 0.037	−0.627 ± 0.024	−0.0266 ± 0.0021	8.41 ± 0.69
5′-r(GCGCCGCCGGCG)-3′	100	80.9	−1.44 ± 0.03	−1.010 ± 0.023	−0.0405 ± 0.0031	12.9 ± 1.1

^aReference temperatures for RNA duplex unfolding during thermal denaturation determined at the temperature where the fraction of unfolded duplex total strand was 0.2 in 0 m glycine betaine.

^bDetermined at reference temperature.

RNA dodecamer duplex-GB solutions were prepared gravimetrically by massing stock dodecamer solution, solid GB, and phosphate buffer solution to ensure constant RNA duplex and salt molality with desired GB molality. Final GB concentrations ranged between 0 and 2 molal (m) with 134 mmolal sodium chloride (150 mmolal Na⁺ overall) and RNA dodecamer concentrations of 2–3 μM. Solutions were degassed under vacuum using a ThermoVac (MicroCal) prior to thermal denaturation. Dodecamer duplex thermal transitions were monitored at 260 nm using a Cary 100 uv-visible spectrophotometer (Varian) equipped with a Peltier temperature controller. Dodecamer duplex samples were heated at a rate of 0.3 °C/min and absorbance readings were collected every 0.2 °C. Dodecamer duplex and single-stranded plateau regions in the absorbance melting profiles were fit by linear regression. The fraction of unfolded dodecamer total strand at a given temperature was determined from the ratio of the difference in absorbance between the experimentally measured absorbance and the duplex extrapolated fit relative to the difference in absorbance between the unfolded and duplex fits (25, 26).

The observed unfolding equilibrium constant K_obs was determined from

$$K_{\mathit{obs}}=\frac{[{\mathrm{S}}_1][{\mathrm{S}}_2]}{[\text{duplex}]}=\frac{{\theta }^2{C}_T}{2(1-\theta )}$$ (2)

Where θ is the fraction of unfolded dodecamer total strand and C_T represents the total concentration of strands (16). Values of K_obs were determined over the range of GB concentrations where 0.2 < θ < 0.8 (27). RNA duplex unfolding enthalpy values, $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$, at specific GB concentrations were determined from the slopes of van’t Hoff plots (ln K_obs as a function of 1/T) (25, 28).

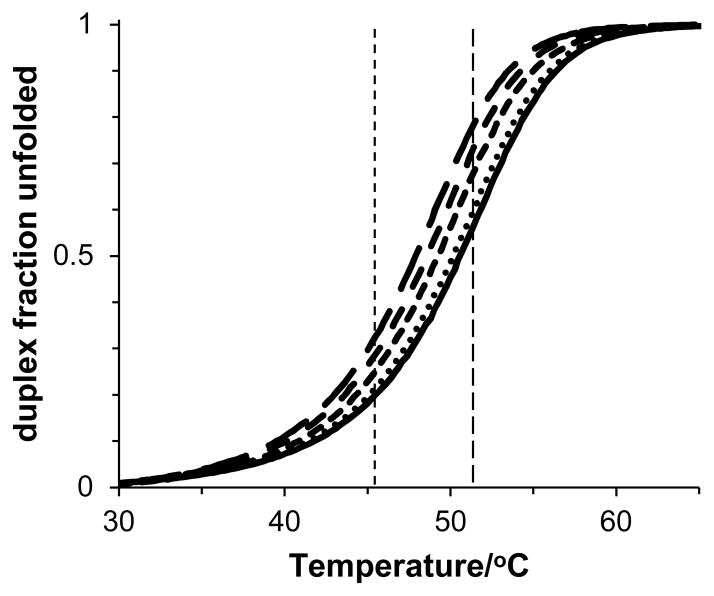
To calculate Δμ_23,4/RT and m-values as functions of temperature, K_obs values were determined at five evenly spaced temperatures in the transition region starting with θ = 0.2 (the reference temperature and lowest temperature used in the transition region) with no added GB and θ = 0.8 (the highest temperature used in the transition region) in 2 m GB. For clarification, Figure 1 contains representative plots of the fraction of unfolded 5′-r(GAUAGUAGAUAG)-3′ total strand as a function of temperature indicating the reference temperature at 0 m GB and the temperature at 2 m. Values of ln K_obs at a given temperature were averaged from duplicate or triplicate trials with standard errors propagated. Linear regression of ln K_obs with GB molality was used to calculate Δμ_23,4/RT and m-values (with errors from linear regression) at each of the five temperatures in the transition region using equation 1. Errors in all subsequent thermodynamic quantities were propagated from errors in the Δμ_23,4/RT and m-values calculated in the RNA duplex transition region.

Figure 1.

Fraction of the 5′-r(GAUAGUAGAUAG)-3′ duplex total strand unfolded as a function of temperature during thermal denaturation in 0 (solid curve), 0.5 (dotted curve), 1.0 (small dash), 1.5 (medium dash), and 2.0 m glycine betaine (long dash). Vertical lines correspond to an unfolded duplex total strand fraction of 0.2 in the absence of glycine betaine (short dash) at 45.5 °C and 0.8 in 2.0 m glycine betaine (long dash) at 51.7 °C.

ASA Calculations

The surface area exposed during unfolding, ΔASA, for each RNA dodecamer duplex in Table 1 was based on nucleobase stacked and half-stacked models for the single-strands (1). The xleap module in AMBER 10 (29) was used to construct the A-form of the RNA dodecamer duplexes. The ASAs of the duplex and two single-strands in the A-form conformation were calculated using naccess (30) with a probe radius of 1.4 Å and the set of van der Waals radii from Richards (31). Single-strands in the A-form were considered to have stacked nucleobases. Starting at the 5′ end of the single-strands, the torsion angles about the O3′ – P bonds were rotated 120 degrees in UCSF chimera (32) to break up base stacking. Single-strands with the nucleobases in this conformation were considered unstacked. The ASA for nucleotides in the single-strands in the half-stacked model was calculated by averaging the ASA for stacked and unstacked single-strands. The ΔASA for duplex unfolding was calculated by summing the ASA of the two single-strands and then subtracting the ASA of the duplex.

RESULTS AND DISCUSSION

RNA hyperchromicities and unfolding enthalpies from thermal denaturation

Tables S1 and S2 (Supporting Information) tabulate RNA dodecamer duplex unfolding enthalpies $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ and duplex concentration-normalized transition hyperchromicities, respectively, as functions of GB molality. The unfolding enthalpies in Table S1 increase with GB molality with the greatest increases in $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ occurring for the higher GC content dodecamers. A similar trend for $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ was found by Spink and coworkers with poly(dAdT) and poly(dGdC) (13). As a test of two-state transitions in the RNA dodecamer duplexes, absorbance unfolding profiles were fit to the nonlinear two-state transition equation (23, 33). Quality of the two-state equation fits were excellent and unfolding enthalpies determined from this method were identical (within error) to those in Table S1 (data not shown). We therefore found no evidence of end-fraying for the higher GC content dodecamers despite the larger transition temperatures of these duplexes.

The slopes from linear fits to the folded and unfolded regions in the absorbance versus temperature plots were used to correct hyperchromicity values determined in the unfolding transition temperature region to remove any GB effects to the absorbance of the duplex and single strands. Therefore, any hyperchromicity dependence on GB concentration was interpreted as potential unstacking of the single strands. RNA duplex concentration-normalized hyperchromicities in Table S2 are nearly independent of GC content and GB molality for duplexes with GC content under 33%. Above 33% GC content, the hyperchromicities depend more strongly on GC content. At 0 molal GB, the 100% GC content duplex has a hyperchromicity approximately half that of the lowest GC content duplexes studied. This observation is in good agreement with that predicted for the change in molar absorptivity for unfolding a 100% GC RNA dodecamer duplex relative to the 17% GC duplex at 25 °C, even though our duplexes unfold at different temperatures (34). Additionally, the hyperchromicities exhibit some dependence on GB molality, with the largest increases in absorbance with GB molality occurring in duplexes with GC contents greater than 50%. The RNA hyperchromicity values exhibit a small increase in magnitude at 0.5 molal GB for 33% and larger GC content duplexes and then attain nearly constant values at GB molalities above 0.5 m. Only the 100% GC content RNA hyperchromicity values monotonically increase with GB molality. Above 33% GC content GB appears to facilitate unstacking of the nucleobases in the single-strands with a small to moderate increase in ΔASA. The observation that GB reduces residual stacking in the single-strands should not be surprising since GB facilitates exposure of buried surface area in the RNA duplexes through thermodynamically favorable interactions with nucleobase accessible surface area. Additionally, the attenuation of nucleobase stacking with GB molality in the higher GC content duplexes must contribute to the greater dependence of $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ on GB molality. The dependence of $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ on GB molality is quantified in the next section.

RNA glycine betaine m-values from thermal denaturation

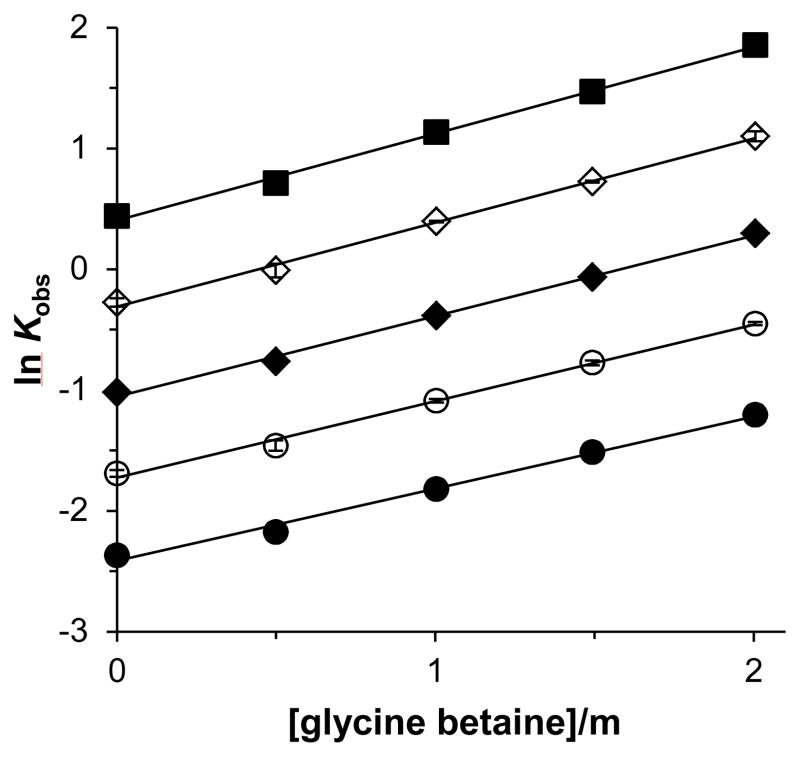
GB Δμ_23,4/RT values were determined from linear regression of the natural logarithm of the observed unfolding equilibrium constant, ln K_obs, as a function of GB molality (Experimental Procedures, equation 1). Representative plots of ln K_obs versus GB molality are shown in Figure 2 for the 5′-r(GAUAGUAGAUAG)-3′ duplex at temperatures determined in the range corresponding to a fraction of unfolded duplex total strand of 0.2 at 0 molal GB (the reference temperature) to 0.8 at 2 molal GB. General scatter in plots such as Figure 2 precluded any identification of nonlinearity due to nucleobase unstacking in the single-strands and an increasing ΔASA with GB molality for most duplexes with GC contents above 33% (Table S2). However, the 5′-r(GCGCCGCCGGCG)-3′ duplex (100% GC) did exhibit a small degree of nonlinearity as the slope of the plot increased with GB molality. In this case, only the first three data points were used in the determination of Δμ_23,4/RT and such values should be considered limiting values at low GB molality. Plots of ln K_obs versus GB molality for all RNA duplexes used in this study are shown in Figure S1 (Supporting Information).

Figure 2.

Natural logarithm of the observed unfolding equilibrium constant K_obs for thermal denaturation of the 5′-r(GAUAGUAGAUAG)-3′ duplex as a function of glycine betaine molality at 45.5 (filled circles), 47.1 (open circles), 48.6 (filled diamonds), 50.2 (open diamonds), and 51.7 °C (filled squares). Linear regression slopes are equal to − Δμ_23,4/RT. Error bars on ln K_obs are smaller than symbols.

Table 1 compiles Δμ_23,4/RT values at reference temperatures for GB interaction with the surface area exposed during dodecamer RNA duplex unfolding using thermal denaturation. Corresponding m-values were calculated at the reference temperatures using equation 1 and are also tabulated in Table 1. As anticipated, the reference temperature increased as the GC content of the dodecamer duplex increased due to increased thermal stability of higher GC content duplexes (12, 35). Negative Δμ_23,4/RT and m-values in Table 1 indicate GB destabilized all of the RNA secondary structure in this study due to thermodynamically favorable GB interactions with the surface area exposed upon unfolding. The m-values in Table 1 for GB interaction with the RNA duplex ΔASA agree favorably with those found for RNA secondary structures in more complex RNA folded molecules (15). The RNA m-values in Table 1 are larger than those measured in the work of Lambert and Draper (15); the dodecamers used in this study have larger ΔASA values and more potential for GB interaction than the five or six base pair RNA secondary structures studied by Lambert and Draper (15).

The m-values in Table 1 are more dependent on GC content than m-values for urea interaction with the ΔASA of RNA and DNA secondary structures (15, 16). Urea m-values were predicted to be independent of GC content when unfolded DNA and RNA single-strands were modeled with nucleobases in either a stacked or half-stacked conformation (16). However, experimentally determined urea m-values for duplex unfolding increased with GC content. This m-value GC dependence was attributed to lower GC content unfolded duplexes having single-strands with nucleobases in the half-stacked conformation (larger ΔASA) while higher GC content single-strands possessed nucleobases in a stacked conformation (lower ΔASA) (16). In contrast, GB m-values (Table 1) are more negative for higher GC content duplexes, indicating GB interactions with the surface area exposed during unfolding are more thermodynamically favorable at the reference temperatures for higher GC content duplexes. This observation is surprising, considering the smaller ΔASA for stacked (higher GC content) relative to half-stacked (lower GC content) single-strands (16).

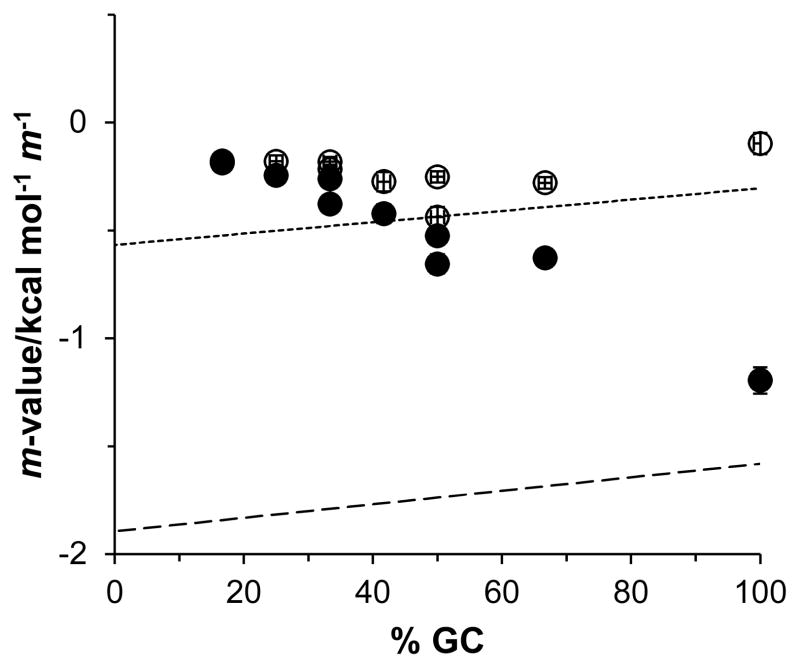
In an effort to identify the origin of GB mediated stability of RNA duplexes, Figure 3 plots the m-values from Table 1 as a function of GC content. Also plotted in Figure 3 are predicted m-values at 25 °C for stacked and half-stacked single-strand ΔASA models (Tables S3 and S4). Predicted GB Δμ_23,4/RT interaction potentials with the surface area exposed upon RNA unfolding were estimated using

Figure 3.

Glycine betaine m-values at the reference temperatures in Table 1 (filled circles) and at 25 °C (open circles) as a function of GC content. Predicted m-values also included for single-strands in a stacked conformation (short dash line) and half-stacked conformation (large dash line).

$$\frac{\mathrm{\Delta }{\mu }_{23,4}}{RT}\approx \sum _i{\left(\frac{{\mu }_{23}}{RT\text{ASA}}\right)}_i{(\mathrm{\Delta }\text{ASA})}_i$$ (3)

where (μ₂₃/RTASA)_i represents the GB interaction potential with 1 Ų of surface area type i in salt-free solutions (17, 18) and (ΔASA)_i is the surface area of type i exposed during unfolding. The GB interaction potential with sodium ions was set to zero (18). In utilizing equation 3 and the GB interaction potentials with model compounds (17, 18), O5′ and O4′ sugar atoms were treated as hydroxyl oxygens, amide and amide-like oxygen as amide oxygen, amine groups as cationic amines, and nitrogen atoms in aromatic rings as aromatic carbon atoms. Predicted m-values were then calculated from equation 1 at 25 °C.

Since higher GC content duplexes have a smaller ΔASA due to single-strand nucleobases adopting a nearly stacked conformation (16), we would anticipate experimental m-values to increase with GC content as single-strands transition from the half-stacked conformation at low to moderate GC content to the stacked conformation at high GC content. We find this order reversed; lower GC content RNA experimental m-values agree more favorably with those predicted using a fully-stacked model for single-strand nucleobases while the higher GC content duplex m-values are more similar in value to those predicted assuming a half-stacked model. In general, buffers with salt concentrations approaching physiological ionic strengths can dramatically lower polar solute interactions with nucleic acids (11). This may explain the discrepancy between experimentally-measured and predicted m-values at low to moderate GC contents, but it cannot explain the increasingly favorable interaction of GB with RNA ΔASA as GC content increases.

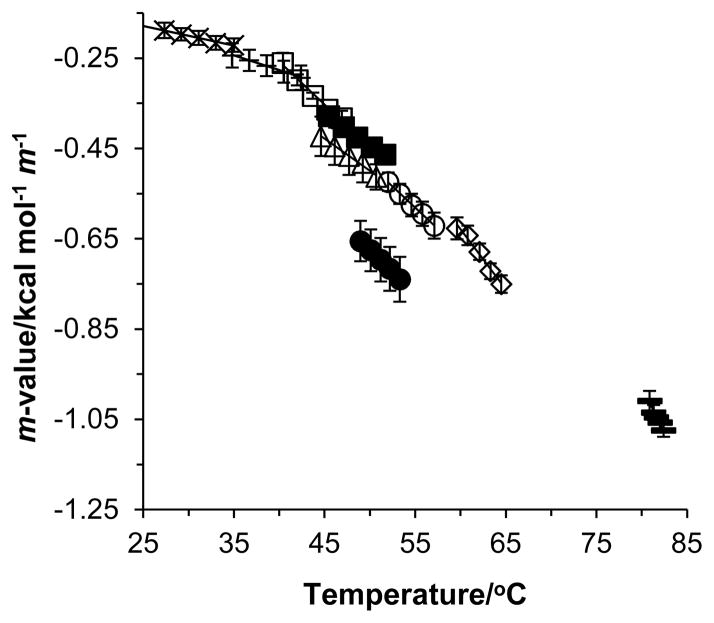
Since GB does not dramatically destabilize RNA duplexes, m-values for a given duplex can be calculated over several degrees within the unfolding transition region. Figure 4 plots RNA m-values calculated in the RNA unfolding transition regions using the slopes in Figures 2 and S1 as a function of temperature for all the duplexes used in this study. The RNA m-values show significant temperature dependence as the temperature increases. Values of dm-value/dT are included in Table 1. Since the predicted m-values in Figure 3 are nearly independent of GC content for a given single-strand conformation, we anticipate the m-value behavior in Figure 4 is due mainly to temperature dependence and not GC content. However, since the temperatures where the m-values were calculated do depend on GC content, we cannot decouple any m-value dependence on temperature and GC content. That is, the dm-value/dT values decrease (become more negative) as GC content increases due to an increase in the duplex transition temperature. Additionally, for the duplexes with similar GC content (33% and 50% GC content), dm-value/dT values are very similar despite different sequences.

Figure 4.

RNA duplex m-values as a function of temperature. 5′-r(GAAAUUAUAAAG)-3′ (crosses), 5′-r(GAAAGUAUAAAG)-3′ (plus symbols), 5′-r(GAUAGUAGAUAG)-3′ (filled squares), 5′-r(GAAAGUAGAAAC)-3′ (open squares), 5′-r(GCAAAGUAAACG)-3′ (open triangles), 5′-r(GCAAAGCAAACG)-3′ (filled circles), 5′-r(GCAUAGCAUACG)-3′ (open circles), 5′-r(GCGAAGCCAACG)-3′ (open diamonds), 5′-r(GCGCCGCCGGCG)-3′ (dash).

Felitsky et al. demonstrated that the GB m-value for interaction with the lacI HTH DNA binding domain protein was independent of GB concentration but strongly dependent on temperature (9). GB stabilized the protein since it was strongly excluded from the surface area exposed on unfolding lacI HTH due to unfavorable thermodynamic interactions with the buried protein surface area. GB exclusion from the buried protein surface was shown to be entropically driven with little, if any, enthalpy dependence (9). Except for 100% GC content RNA, we also find GB m-values to be independent of GB concentration at a fixed temperature where linear regression works well to capture trends in ln K_obs versus GB molality (Figures 2 and S1).

To investigate the m-value temperature dependence in Figure 4, we determined the enthalpic and entropic components of the m-values using

$$m-\text{value}=\frac{d\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}}{{dm}_3}-T\frac{d\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}}{{dm}_3}$$ (4)

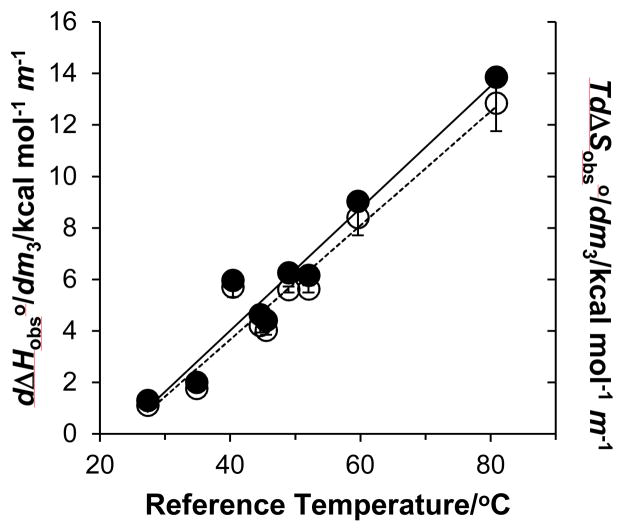
where m₃ is the molality of GB. Values of $d\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}/{dm}_3$ can be determined from − R d² ln K_obs/dm₃d(1/T). Figure S2 plots d ln K_obs/dm₃ as a function of inverse temperature for all RNA duplexes used in this study. The slopes are equal to d² ln K_obs/dm₃d (1/T) and used to determine $d\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}/{dm}_3$ values (Table 1). Values of $d\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}/{dm}_3$ increase with GC content and mirror the larger increases in $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ with GB molality for the higher GC content RNA duplexes relative to lower GC content duplexes (Table S1). Values of $T\left(d\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}/{dm}_3\right)$ were determined from equation 4 at the reference temperatures and are shown in Figure 5 along with $d\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}/{dm}_3$ values. Figure 5 indicates there is strong entropy-enthalpy compensation for duplex unfolding in GB solutions which also provides a rationale for the “isostabilizing” effect of GB (12). Higher GC content duplexes unfold at higher temperatures relative to low GC content duplexes which results in a larger endothermic enthalpic contribution to the m-value. However, entropy increases dominate to decrease duplex stability with GB molality. That is, the greater entropy gain for GB interactions with the ΔASA at higher temperatures drives the greater destabilization (more negative m-values) of higher GC content duplexes at or near their transition temperatures.

Figure 5.

Enthalpic (open circles) and entropic (filled circles) contributions to the RNA dodecamer m-values at the reference temperatures in Table 1. Regression lines to the data are also shown.

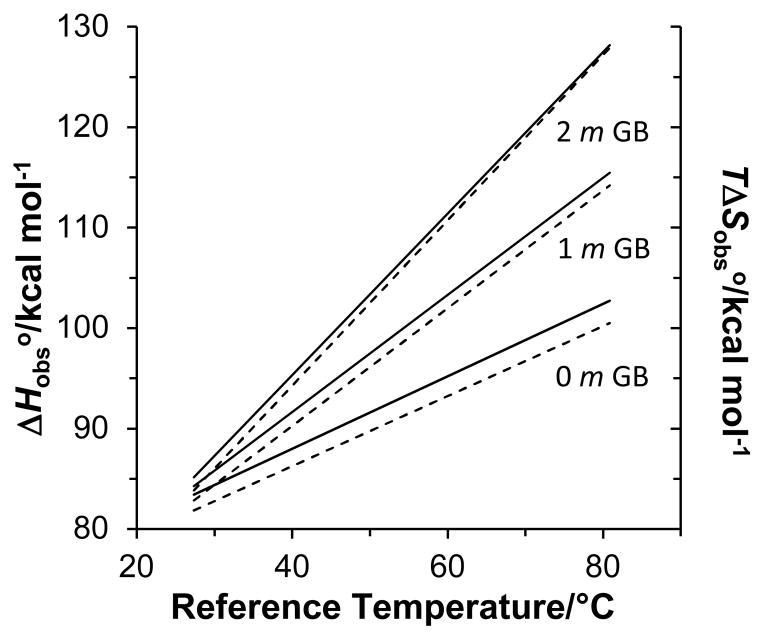
Figure 6 plots the predicted $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ and $T\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}$ contributions to the RNA duplex unfolding free energy as a function of reference temperature and GB molality. The predicted $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ and $T\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}$ values for the duplexes were calculated by adding the experimentally determined $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ and $T\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}$ values in 0 molal GB and the $d\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}/{dm}_3$ and $T\left(d\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}/{dm}_3\right)$ values in Figure 5 multiplied by GB molality. At a given GB molality and temperature, the difference between the $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ and $T\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}$ plots represents the RNA unfolding free energy. The unfolding free energy is positive at the reference temperature since the fraction of unfolded duplex total strand is 0.2. The difference between the $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$ and $T\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}$ plots decreases as GB molality increases reflecting increasing RNA destabilization. With GB, $T\mathrm{\Delta }{S}_{\text{obs}}^{\mathrm{o}}$ increases at a faster rate with reference temperature than $\mathrm{\Delta }{H}_{\text{obs}}^{\mathrm{o}}$, indicating higher GC content duplexes (with larger reference or transition temperatures) are destabilized to a greater extent than lower GC content duplexes. This effect becomes more pronounced as GB molality increases.

Figure 6.

Predicted DNA dodecamer duplex unfolding enthalpy (solid lines) and entropy (dotted lines) contributions to unfolding free energy at 0, 1, and 2 molal GB as a function of the reference temperatures in Table 1.

GB is well known for significantly increasing the osmolality of aqueous solutions because of its large amount of hydration (1, 9). In addition, exposure of aromatic carbon and nitrogen atoms and amine groups, along with sequestration of anionic oxygens, drives duplex destabilization with GB (17, 18). It is quite possible that water release from GB is a major contributor to the large entropy gains at higher temperatures when GB interacts with the duplex ΔASA.

Figure 3 plots m-values temperature-corrected to 25 °C as a function of GC content. The m-values were temperature corrected by parsing the dm-value/dT values in Table 1 into temperature ranges of 25–35, 35–40, 40–50, 50–60, and 60–80 °C based on Figure 4 and averaging any multiple dm-value/dT values in these temperature regions, assuming no GC content dependence. Temperature correction for the r(GCGAAGCCAACG)-3′ and 5′-r(GCGCCGCCGGCG)-3′ duplexes assumed 70% and 50% ΔASA, respectively, of the lower GC content duplexes (16). The temperature corrected m-values in Table 1 are nearly independent of GC content and no longer decrease with reference temperature. However, we do not observe an increase in the m-value with GC content after temperature correction. There are several possible reasons for this. 1) Hong et al. demonstrated that GB is excluded from the duplex surface of a 42% GC DNA duplex (1). If duplex hydration is GC dependent and some of this hydration is lost upon thermal denaturation (36–38), our analysis would underestimate the ΔASA for calculation of predicted m-values. 2) The m-value temperature correction we employed may have some dependence on RNA GC content (and therefore ΔASA chemical functional group composition) and hence different GB interaction with chemically different surface areas with temperature. 3) Our calculation of predicted m-values assumed cationic amine GB interaction potentials were the same as those for nucleobase amine. Since the amine functional group ΔASA increases with GC content (Tables S3 and S4), the predicted error in m-value would be largest for the higher GC content duplexes.

GB Interactions with ΔASA in Context of the Solute Partitioning Model

The destabilization of the RNA duplex dodecamers used in this study must be driven by thermodynamically favorable GB interactions with the RNA surface area exposed upon unfolding. To quantify the interactions of GB with the ΔASA, we have used the solute partitioning model (SPM) (1, 17, 18). Briefly, GB Δμ_23,4/RT interaction potentials were interpreted as GB partitioning between a ΔASA local hydration layer and bulk solution. The link between GB Δμ_23,4/RT interaction potentials and the GB partition coefficient K_p is described through (1, 17, 18)

$$\frac{\mathrm{\Delta }{\mu }_{23,4}}{RT}-\frac{(K_p-1)b_1\mathrm{\Delta }\mathit{ASA}}{55.5}\left(1+\epsilon \right)$$ (5)

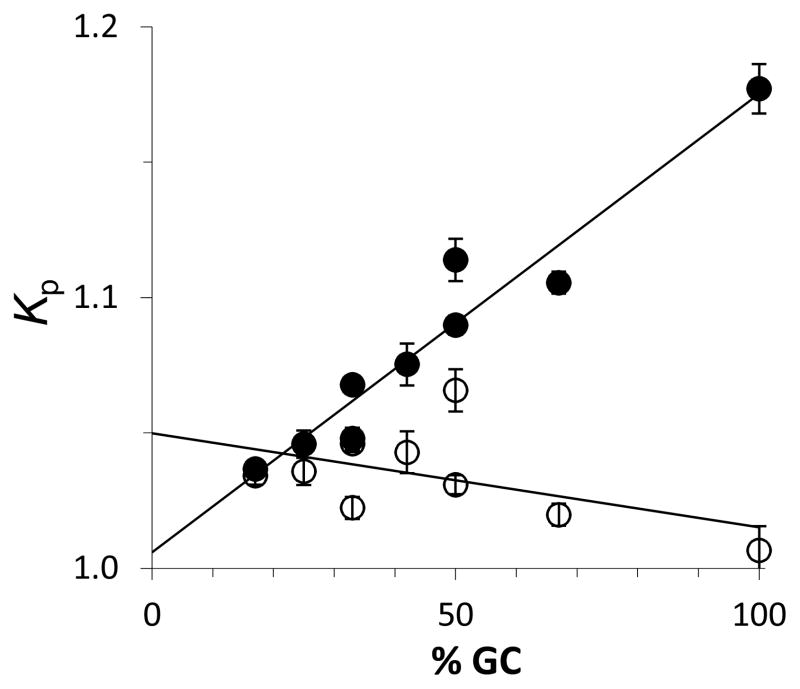
where b₁ = 0.18 H₂O/Ų (approximately two hydration layers) and ε = 0.14 is the self-nonideality correction factor for GB. SPM K_p values calculated from the GB Δμ_23,4/RT interaction potentials at the reference temperatures in Table 1 are plotted in Figure 7 as a function of GC content. As anticipated, values of K_p are greater than one, indicating a higher concentration of GB at the RNA ΔASA relative to bulk. For the lowest GC content duplex, K_p is only slightly greater than one, indicating only a slight preference of GB for the ΔASA relative to bulk. However, the 100% GC content duplex has a K_p of almost 1.2; GB concentration at the 100% GC duplex ΔASA is almost 20% larger than that of bulk. This number is significantly less than the K_p = 1.7 predicted for a GC base pair (1). However, the analysis of Hong et al. used b₁ = 0.11 H₂O/Ų and DNA ΔASA exposed in solutions with an ionic strength less than 10 mM (12). The larger ionic strength used in this study would be expected to screen a significant amount of GB interactions with the RNA ΔASA and result in lower K_p values.

Figure 7.

Glycine betaine partition coefficient K_p for glycine betaine distribution between local hydration surrounding the surface area exposed during RNA dodecamer duplex unfolding and bulk solution as a function of GC content at the dodecamer reference temperatures in Table 1 (filled circles) and at 25 °C (open circles).

Using the m-values temperature corrected to 25 °C in Figure 3 along with the GB Δμ_23,4/RT interaction potentials in Table 1 at the reference temperatures, we temperature corrected K_p values to 25 °C (Figure 7). Values of K_p are nearly independent of GC content, varying between 1.0 and 1.05, indicating that GB destabilizes all sequences equally at this temperature. Thus, the strong temperature dependence of GB interaction with nucleic acid surface area leads to the greater destabilization (uptake of GB) of high GC content duplexes at larger transition temperatures. The uptake of GB must be accompanied by changes in hydration of both GB and nucleic acid and can contribute to the entropic dependence of the m-values in Figure 5.

CONCLUSIONS

The greater destabilization of GC-rich RNA dodecamer duplexes in aqueous GB solutions relative to low GC content duplexes is due to the greater entropic contribution of GB interaction with the surface area exposed during denaturation. Since the entropic contribution to the m-value (used to quantify GB interaction with the RNA solvent accessible surface area exposed during denaturation) is more dependent on temperature than the enthalpic contribution, higher GC content duplexes with their larger transition temperatures are destabilized to a greater extent than low GC content duplexes. When temperature corrected to 25 °C, m-values depend only minimally on GC content. Thus, the “isostailizing” ability (12) of GB to destabilize GC base pairs more so than AT or AU base pairs is dependent more so on transition temperatures than the chemical makeup of the surface area exposed during denaturation. It is not clear if all zwitterions similar to GB will have such a strong temperature dependence. For instance, the osmoprotectant proline is a stronger destabilizer of nucleic acid secondary structure than glycine betaine (39–41) and shares some structural features with glycine betaine (nonpolar functional groups attached to the amine). However, in the tar-tar* kissing loop complex, the lower GC content five base pair duplex was destabilized to a greater extent than the GC rich duplex (15). Elucidation of the destabilization mechanism of proline on nucleic acid secondary structures would be helpful in identifying any commonality with GB attenuation of duplex stability. Additionally, additional knowledge of the physical chemistry of nucleic acids would aid in our understanding of the interactions of nucleic acids and interactions with biological molecules or potential therapeutics.

ABBREVIATIONS

ASA

solvent accessible surface area

AT

adenine-thymine

AU

adenine-uracil

GB

glycine betaine

GC

guanine-cytosine