Abstract
Background
Scoliosis of the vertebral column can be assessed with the Cobb angle (Cobb 1948). This examination is performed manually by measuring the angle on radiographs and is considered the gold standard. However, studies evaluating the reproducibility of this procedure have shown high variability in intra- and inter-observer agreement. Because of technical advancements, interests in new procedures to determine the Cobb angle has been renewed. This review aims to systematically investigate the reproducibility of various new techniques to determine the Cobb angle in idiopathic scoliosis and to assess whether new technical procedures are reasonable alternatives when compared to manual measurement of the Cobb angle.
Method
Systematic review. Studies examining procedures used to determine the Cobb angle were selected. Two review authors independently selected studies for inclusion, extracted data and assessed risk of bias. Statistical results of reliability and agreement were summarised and described.
Results
Eleven studies of new measuring procedures were included, all reporting the reproducibility. The new procedures can be divided into computer-assisted procedures, automatic procedures and smartphone apps.
Conclusions
All investigated measuring procedures showed high degrees of reliability. In general, digital procedures tend to be slightly better than manual ones. For all other measurement procedures (automatic or smartphone), results varied. Studies implementing vertebral pre-selection and observer training achieved better agreement.
Keywords: Cobb angle, Idiopathic scoliosis, Systematic review, Reproducibility, Measuring methods, Computer-assisted measuring
Introduction
The measuring method according to Cobb [1] is the standard method to quantify spinal curvature. Although the Cobb angle measures only the amount of the most tilted vertebrae on an anterior–posterior (AP) or posterior–anterior (PA) radiographs in the coronal plane, and is not an objective measurement of all three-dimensional aspects of the spinal deformity, this determination is used to guide decisions regarding progression, physiotherapeutic and orthotic options, as well as surgical interventions [2, 3]. Thus, an accurate and reproducible measuring procedure is crucial. Reproducibility concerns the degree to which repeated measurements yield similar results. Differences in repeated measurement may result from the subjects under investigation (e.g. biological variance), the equipment (e.g. lack of calibration), or the observers (e.g. lack in technical competence). To interpret the measurement results correctly, the orthopaedic examiner should be cognizant of the reproducibility parameters of the used measurement procedure.
Generally, in the technique developed by Cobb, lines are superimposed manually onto a hardcopy radiographic film of the vertebrae, and the angles are determined using a protractor [1]. Morrissy et al. [4] reported decreased measurement error when a standardised pencil and protractor were used to measure pre-selected (previously marked) end-vertebrae.
Even when the same end-vertebrae are selected, measurements may vary by up to 5° [4, 5]. Thus, a change of 5° or more is considered progression of the scoliotic curvature [5]. To improve reproducibility, and in response to technical advancements, new measurement procedures to determine the Cobb angle have emerged.
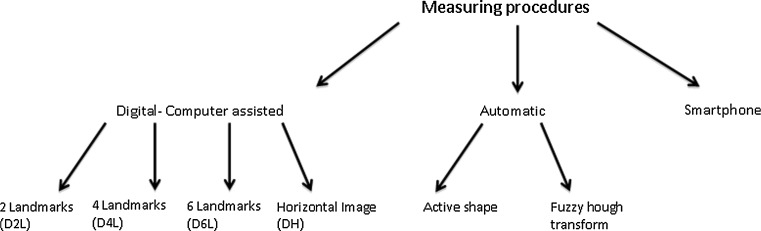
Aside from the manual procedure, there are so-called digital computer-assisted (semi-automatic) [6–12], automatic [13, 14] and smartphone app procedures [15, 16].
Included in the digital computer-assisted measurement group were all studies in which the Cobb angle was calculated independently by a software program.
The landmarks used to calculate the angle must be manually entered using a computer mouse. The angle is then calculated automatically.
Depending on the software program, the numbers of landmarks to be placed, and/or the positioning of the radiograph (e.g. horizontal rotation) varies (see Fig. 1).
Fig. 1.
Different measuring procedures
Automatic procedures still require definition of the regions of interest, i.e. “fuzzy hough transform procedure [14]”, or initial points, i.e. the “active shape procedure [13]”, to be imputed on a radiograph by the observer. The computer itself recognises the exact profile of the vertebrae or the landmarks, and will calculate the angle automatically.
As a result of the new technical capabilities of smartphones (S), there are applications available to calculate the Cobb angle. To use the app described by Qiao et al. [16], the smartphone must be aligned to the upper vertebrae and the lower vertebral endplate, and the software automatically displays the angle. The smartphone app described by Shaw et al. [15] uses an accelerometer.
The present review aims to systematically investigate the reliability and agreement of various techniques used to determine the Cobb angle in idiopathic scoliosis, and to assess whether new technical procedures are reasonable alternatives when compared to manual measurement of the Cobb angle.
Methods
Search strategy
A search strategy was developed in collaboration with a spine specialist and a radiological specialist. Relevant computerised databases were searched and analysed from the earliest date to 30 June 2012 consisting of PubMed (including MEDLINE), Medpilot, and Cochrane Library (including Cochrane Reviews).
Languages were restricted to English, Dutch, and German.
The search was performed using the following keywords and their combinations. Idiopathic scoliosis, Cobb angle, measurement, automatic, digital, computer-assisted, validity, accuracy, reliability, variability, reproducibility, agreement, X ray, radiography.
Titles were independently assessed for eligibility by two investigators. The articles were divided into two groups: “definitely exclude”, or “possibly include”. The articles to “possibly include” were assessed using the abstracts. Studies with abstracts not fulfilling the inclusion criteria were excluded. In the remaining articles, the entire text was assessed. Duplicates were deleted.
At each step, disagreements among the reviewers were resolved by discussion. In addition, the references of all included articles were checked, and potentially relevant articles were obtained as a full-text publication, rated, and included when fulfilling the inclusion criteria.
Selection criteria
Studies were included if the patients had an idiopathic scoliosis and if the Cobb angle was measured using computer-assisted, automatic, or a smartphone application procedures on an AP/PA radiograph.
Studies were excluded if: (a) measurements were performed on non-human subjects (e.g. spine models), (b) only manual procedures were reported (c) the study subjects measured had undergone instrumented fusions, (d) three-dimensional measuring methods were used (e) rasterstereography and or topographical methods were used, or (f) radiographs were compared to digital printouts.
Data extraction and management
One aim of this review is to investigate the reproducibility of various new measuring procedures. The term “reproducibility” has been deliberately chosen, as it encompasses both terms of agreement and reliability [17, 18] (see Fig. 2). Reliability relates measurement error to the variability between study objects: in this case, radiographs of patients and varying degrees of the spinal deformity. If the measurement error is small compared to the variability in the degrees of spinal deformity, the reliability parameter approaches 1.
Fig. 2.
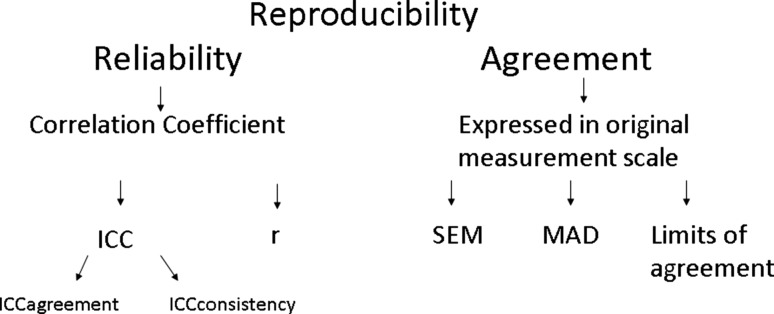
Example for reproducibility parameters
In most of the included studies, the Intraclass Correlation Coefficient (ICC) was used as a measure of reliability [19]. Two variants of the ICC can be distinguished as ICCagreement and ICCconsistency [17]; ICCagreement incorporates the systematic difference between the observers and ICCconsistency ignores the systematic difference.
Various guidelines exist for the interpretation of ICC, but one reasonable interpretation is that an ICC value of less than 0.40 indicates poor reliability, 0.40–0.75 indicates fair to good reliability, and values greater than 0.75 reflect excellent reliability [20].
Additional correlations (r) are presented as shown in the studies.
For the presentation of agreement, different terms are given according to those used in the original studies.
From studies attempting to evaluate the validity through inter-methodological comparison, the statistical values were recorded.
The details of the selected studies are shown in Table 1.
Table 1.
Characteristics of included studies
| Author | Aim of the study | Procedures | Radio-graphs | Scoliotic curvature | Observer | Times | Training | Predefinition of to used vertebrae |
|---|---|---|---|---|---|---|---|---|
| Srinivasalu et al. [6] | Reliability, Agreement | Digital 2 landmarks | 318 AP | 10°–>40° | 3 observers; (varying level of experience, 1 spine fellow, 2 spine surgeons) |
Digital 2 landmarks: 3 observers 3× |
Digital 2 landmarks: Not described |
Yes |
| Corona et al. [7] | Reliability | Digital 2 landmarks | 45 PA/AP | 0°–82° | 4 observers; (3 paediatric spine surgeons, 1 paediatric orthopaedic surgeon) |
Digital 2 landmarks: 4 observers 2× |
Digital 2 landmarks: Not described |
No |
| Jones et al. [8] | Reliability, Agreement, comparison between procedures | Digital 2 landmarks | 26 PA | Not described | 6 observers | Digital 2 landmarks: 6 observers 2× |
Digital 2 landmarks: Not described |
Yes |
| Manual | Manual: 4 observers, times not described |
Manual: Not described |
||||||
| Tanure et al. [9] | Reliability, Agreement, comparison between procedures | Digital 2 landmarks | 49 PA | 12°–80° | 3 observers; (spine surgeons) |
Digital 2 landmarks: 3 observers 3× |
Digital 2 landmarks: Training set |
No |
| Manual | Manual: 3 observers 3× |
Manual: No training, observers were familiar with manual procedure |
||||||
| Shea et al. [10] | Reliability, Agreement, comparison between procedures | Digital 2 landmarks | 24 PA | 20°–40° | 6 observers; (3 paediatric orthopaedic surgeons, 2 paediatric orthopaedic fellows, 1 senior orthopaedic resident) |
Digital 2 landmarks: 6 observers 2× |
Digital 2 landmarks: Training set |
Yes |
| Manual | Manual: 6 observers 2× |
Manual: No training, observers were familiar with manual procedure |
||||||
| Cheung et al. [11] | Agreement, comparison between procedures | Digital 6 landmarks | 30 PA | 10°–60° | 5 observers; (1 orthopaedic surgeon, 3 orthopaedic residents, 1 radiologist) |
Digital 6 landmarks: 5 observers 3× |
Digital 6 landmarks: Training set |
Not described |
| Digital 2 landmarks | Digital 2 landmarks: Not described |
Digital 2 landmarks: Not described |
||||||
| Chockalingam et al. [12] | Reliability, Agreement, comparison between procedures | Digital horizontal image | 9 PA | Not described | 10 observers; (including experienced clinicians, radiographers and novice volunteers) |
Digital horizontal image: 10 observers 3× |
Digital horizontal image: Not described |
Not described |
| Manual | Manual: 3 observers (times and which 3 of the 10 is not specified) |
Manual: Not described |
||||||
| Allen et al. [13] | Reliability, Agreement, comparison between procedures | Automatic (active shape model) | 22 PA | 20°–50° | 2 observers; (trained novice & intermediate skill levels) |
Automatic: 2 observers 3× |
Automatic: Training set with 47 images |
No |
| Digital 2 landmarks | Digital 2 landmarks: 2 observers 3× |
Digital 2 landmarks: Not described |
||||||
| Manual | Manual: 2 observers 3× |
Manual: Not described |
||||||
| Zhang et al. [14] | Reliability, Agreement | Automatic (fuzzy hough transform) | 70 PA | <90° | 3 observers; (observer 1 experienced, observer 2 software developer without clinical experience, observer 3 no technical & clinical experience) |
Automatic: 3 observers 2× |
Automatic: Not described |
Yes |
| Digital 4 Landmarks | Digital 4 landmarks: observer 2 & 3: 2× |
Digital 4 landmarks: Not described |
||||||
| Shaw et al. [15] | Agreement, comparison between procedures | Smartphone | 20 PA | 15°–72° | 7 observers; (2 experienced spinal orthopaedic specialist, 2 spinal fellows, 1 specialist physiotherapist, 1 experienced spinal orthotist, 1 training grade registrar) |
Smartphone: 5 observers 2×; 2 observers 1× |
Smartphone: No training |
No |
| Manual | Manual: 5 observers 2×; 2 observers 1× |
Manual: No training |
||||||
| Qiao et al. [16] | Reliability, Agreement | Smartphone & | 53 PA | 17°–58° | 5 observers; (spinal surgeons) | Smartphone: 7 observers 2× |
Smartphone: Training period for smartphone |
Yes |
| Manual | Manual: 7 observers 2× |
Manual: No training, familiar with manual procedure |
The data presented are taken directly from the Result sections of the included articles. The authors were not able to perform independent analysis of the source data.
Risk of bias assessment
The “Quality Assessment of Diagnostic Accuracy Studies” (QUADAS) checklist was used to assess internal validity of the included studies [21]. Generally, this checklist is used to evaluate a new test (index test) against a reference test (golden standard) and not for evaluating the reproducibility of studies. For reproducibility, the “Quality Appraisal of Reliability Studies” (QAREL) checklist is used [22]. For this review, items from both checklists appeared relevant. To assess studies examining the reproducibility of two different measuring procedures, we elected to modify the QUADAS checklist. The new procedure under investigation was considered the index test, and the comparative procedure the reference test. Items that appeared relevant in the context of reproducibility were added.
These items evaluates whether
observers were representative,
observers were blinded to their own prior findings,
observers were blinded to the findings of other observers,
the order of examination was randomized,
all assessments described in the Method section of the article were presented in the Result section.
Items without contextual relevance were deleted.
The items were scored as “yes”, “no” or “unclear” as described by Whiting et al. [21].
Not applicable (NA) was used when studies had no comparative design. Because the study by Allen et al. [13] examined three different measuring procedures, we divided the reference column into two parts. The manual and digital procedures were then used as the reference test.
Two reviewers assessed the risk of bias of the included studies independently, and disagreements regarding study quality were resolved by a third reviewer.
Individual checklist items were not weighted, and no summary score was used to exclude studies not attaining a certain level of quality.
Results
Search results
The electronic searches generated a total of 2,915 records, with 47 remaining after exclusion by title. Twenty-two abstracts did not fulfil the inclusion criteria as mentioned in the Method section and therefore 25 full-text articles were obtained. Included articles, and reasons for the exclusion of 14 of these 25, are listed in Fig. 3.
Fig. 3.
Flow chart of selected articles
Three papers appeared to report the same cohort but with different numbers of patients and observers [14, 23, 24]. To avoid duplication of data, we chose to include only the study with the most complete information [14]. In total, 11 studies were included in our review.
Risk of bias assessment
The risk of bias regarding the included studies is presented in Table 2. The initial agreement of the reviewers was 90 % (130 of 145 items). Disagreements were resolved by consensus. All studies presented a representative spectrum and had relevant clinical information’s (modified QUADAS item numbers 1 and 11). In most of the studies, poor description of the selection criteria, lack of details regarding the reference test and uninterpretable data, lack of blinding to the others’ and own prior findings, lack of randomization, and incompleteness of results were evident (modified QUADAS item numbers 3, 5, 6, 7, 8, 9, 10, 13). This may lead to selection, reviewer and information bias and bias the assessment of test characteristics. Three studies [11, 12, 14] with a high risk of bias were included.
Table 2.
Risk of bias of included studies
| Study | Representative participants? | Representative observers? | Selection criteria clearly? | Detailed description of index test? | Detailed description of reference test? | Index test: blinding to the findings of other observers? | Reference test: blinding to the findings of other observers? | Index test: blinding to their own prior findings? | Reference standard: blinding to their own prior findings? | Order of examination randomized? | Relevant clinical information? | Uninterpretable data reported? | Completeness of results? | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Srinivasalu et al. [6] | + | + | + | ? | NA | + | NA | + | NA | ? | + | + | + | |||
| Corona et al. [7] | + | + | + | + | NA | ? | NA | ? | NA | ? | + | + | + | |||
| Jones et al. [8] | + | ? | ? | + | ? | + | + | + | + | + | + | + | ? | |||
| Tanure et al. [9] | + | + | ? | + | + | + | + | + | + | + | + | ? | + | |||
| Shea et al. [10] | + | + | ? | + | + | + | + | + | + | + | + | + | + | |||
| Cheung et al. [11] | + | + | ? | + | ? | ? | ? | ? | ? | ? | + | ? | + | |||
| Chockalingam et al. [12] | + | + | ? | + | ? | ? | ? | ? | ? | + | + | + | ? | |||
| Allen et al. [13]a | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + |
| Zhang et al. [14] | + | ? | + | + | ? | ? | ? | ? | ? | ? | + | + | + | |||
| Shaw et al. [15] | + | + | + | ? | + | + | + | + | + | ? | + | + | + | |||
| Qiao et al. [16] | + | + | ? | + | + | + | + | + | + | + | + | + | + | |||
+ done, − not done, ? unclear, NA not assessed, study without reference test
astudy examining three procedures
Measuring methods
We found several new procedures to determine the Cobb angle. They can be divided methodologically into three categories. These are digital computer-assisted (D2, 4, 6L or DH), automatic (A), and smartphone app (S) techniques (see Fig. 1).
Under automatic measurement procedures are assigned all methods that the authors of the primary article have expressly designated as such. The difference between the digital computer-assisted procedures and the automatic procedure is that no manual entering of landmarks is needed but the regions of interest [14] or initial points [13] have to be marked manually by the observers.
In recent years, the manual procedure described and used by Cobb has been seen in the literature as reference test. Thus, most of the included studies used the manual procedure as the reference test. In cases where the technical description of the reference test was lacking within the Method section of the paper, we assumed that the authors used the best known reference standard, and included and denote such reference test as a manual test.
The different technical procedures and their use in the studies are displayed in Fig. 1 and Table 1.
Study description
Of the 11 studies, 8 reported in their Methods section that they evaluated both agreement and reliability. One study assessed reliability only and two examined agreement only.
Inter-methodological comparison between individual measuring procedures (e.g. smartphone vs. manual procedure) was carried out in five of the studies [8, 9, 11, 13, 15].
The individual selection of statistical methods used to calculate observer agreement, reliability, or inter-methodological comparison was made and presented in various ways.
Findings agreement
The results of the different procedures are divided into intra- and inter-observer agreement and are presented in Table 3. The original publications presented varied statistics. When appropriate, statistical terms have been unified for clarity (e.g. absolute average difference (AAD) = mean absolute difference (MAD), technical error of measurement (TEM) = standard error of measurement (SEM)). Nevertheless, a summary estimate was not possible.
Table 3.
Results agreement: data presented as taken from the Result section of the article
| Study | Intra-observer | Inter-observer |
|---|---|---|
| Srinivasalu et al. [6] | ||
| D2L | Average variability 95 % CI: ±1.3° | Average variability 95 % CI: ±1.26° |
| Corona et al. [7] | ||
| D2L | No analysis of agreement | No analysis of agreement |
| Jones et al. [8] | ||
| D2L | Range MD: −0.38°–0.73° | Not presented |
| Range SD: 1.97°–3.35° | ||
| M | Not presented | Not presented |
| Tanure et al. [9] | ||
| D2L | Range MAD: 2.06°–3.46° | MAD: 3.61° |
| Range SD: 1.69°–2.73° | SD: 3.18° | |
| M | Range MAD: 2.69°–3.25° | MAD: 3.85° |
| Range SD: 2.14°–2.60° | SD: 3.45° | |
| Shea et al. [10] | ||
| D2L | Overall SEM: 1.35°; (range: 1.17°–1.69°) | No analysis of inter-observer agreement |
| Limits of agreementa: ±2.6°; (range: 2.3°–3.3°) | ||
| M | Overall SEM: 1.66°; (range: 1.25°–2.29°) | |
| Limits of agreementa: ±3.25°; (range: 2.46°–4.48°) | ||
| Cheung et al. [11] | ||
| D6L | Limits of agreementb: ±3.05° | No analysis of inter-observer agreement |
| D2L | Limits of agreementb: ±2.22° | |
| Chockalingam et al. [12] | ||
| DH | Mean SEMc: 0.739° | SEMc: 1.22° |
| M | Not presented | SEMc: 1.855° |
| Allen et al. [13] | ||
| A | Range SEM: 1.71°–2.3° | Range SEM: 1.63°–3.37° |
| D2L | Range SEM: 2.97°–3.39° | Range SEM: 3.10°–4.09° |
| M | Range SEM: 2.09°–2.28° | Range SEM: 2.31°–4.09° |
| Zhang et al. [14] | ||
| A | MADd: 1.4° | MADd: 2.2° |
| D4L | MADd: 3.4° | MADd: 5.1° |
| Shaw et al. [15] | ||
| S | MAD: 2.3° | SD of differences: 4.0° |
| Limits of agreement: ±3.9° | Limits of agreement: ±8.3° | |
| M | MAD: 2.1° | SD of differences: 3.4° |
| Limits of agreement: ±3.3° | Limits of agreement: ±7.1° | |
| Qiao et al. [16] | ||
| S | Overall SD of diff.: 1.1° | |
| Limits of agreementa: ±2.2°; (range: 1.8°–2.4°) | Limits of agreementa: ±3.6° | |
| M | Overall SD of diff.: 1.8° | |
| Limits of agreementa: ±3.5°; (range: 3.1°–3.7°) | Limits of agreementa: ±5.4° | |
CI confidence interval, CR coefficient of repeatability, MD mean difference, MAD mean absolute difference, SD standard deviation, SEM standard error of the measurement, A automatic, D2,4,6L digital 2,4,6 landmarks, DH digital horizontal, M manual, S smartphone
aOriginal term: 95 % CI for measurement error/variability
bOriginal term: coefficient of repeatability (CR)
cOriginal term: technical error of measurement (TEM)
dOriginal term: average absolute difference (AAD)
Findings reliability
Reliability was also analysed using various procedures. All studies presenting the ICC showed excellent intra- and inter-observer reliability with ICCs >0.75. Further differentiation between ICCagreement and ICC consistency was not possible due to lack of information.
Studies calculating a correlation coefficient showed values above r = 0.96. Only the study by Chockalingam et al. [12] showed a lower correlation r = 0.781 among the observers using the manual procedure (see Table 4).
Table 4.
Results reliability: data presented as taken from the Result section of the article
| Study | Intra-observer | Inter-observer |
|---|---|---|
| Srinivasalu et al. [6] | ||
| D2L | ICC: ≥0.970 | ICC: 0.986 |
| Corona et al. [7] | ||
| D2L | ICC: 0.99 | ICC: 0.99 |
| Jones et al. [8] | ||
| D2L | Not presented | r = 0.975 |
| M | Not presented | Not presented |
| Tanure et al. [9] | ||
| D2L | ICC: ≥0.95 | ICC: ≥0.96 |
| Range 95 % CI: 0.91–0.99 | Range 95 % CI: 0.92–0.97 | |
| M | ICC: ≥0.94 | ICC: ≥0.95 |
| Range 95 % CI: 0.89–0.98 | Range 95 % CI: 0.91–0.97 | |
| Shea et al. [10] | ||
| D2L | Overall SC: 0.97; (range 0.96–0.98) | No analysis of inter-observer reliability |
| M | Overall SC: 0.96; (range 0.93–0.98) | |
| Cheung et al. [11] | ||
| D6L | No analysis of reliability | No analysis of reliability |
| D2L | ||
| Chockalingam et al. [12] | ||
| DH | r = 0.985 | r = 0.988 |
| M | Not presented | r = 0.781 |
| Allen et al. [13] | ||
| A | Range ICC: ≥0.91 | Range ICC: ≥0.89 |
| Range 95 % CI: 0.84–0.98 | Range 95 % CI: 0.76–0.97 | |
| D2L | Range ICC: ≥0.92 | Range ICC: ≥0.83 |
| Range 95 % CI: 0.85–0.97 | Range 95 % CI: 0.63–0.98 | |
| M | Range ICC: ≥0.95 | Range ICC: ≥0.93 |
| Range 95 % CI: 0.90–0.98 | Range 95 % CI: 0.83–0.98 | |
| Zhang et al. [14] | ||
| A | Range ICC: 0.944 | ICC: 0.985 |
| Range 95 % CI: 0.990–0.966 | Range 95 % CI: 0.983–0.987 | |
| D4L | ICC: 0.962 | ICC: 0.929 |
| Shaw et al. [15] | ||
| S | No analysis of reliability | No analysis of reliability |
| M | ||
| Qiao et al. [16] | ||
| S | Overall ICC: 0.985; (range 0.981–0.988) | ICC: 0.956; (range 0.949–0.982) |
| M | Overall ICC: 0.955; (range 0.942–0.965) | ICC: 0.955; (range 0.942–0.965) |
CI confidence interval, ICC intraclass correlation coefficient, r correlation coefficient, SC stability coefficient, A automatic, D2,4,6L digital 2,4,6 landmarks, DH digital horizontal, M manual, S smartphone
Inter-methodological comparison between procedures
Comparing the manual and digital two landmarks procedure, Jones et al. [8] reported a mean difference range of 0.15°–1.69° with a range of standard deviations (SD) of 2.81°–3.32°. Tanure et al. [9] identified no statistically significant difference in variability of the manual versus the digital two landmarks method (t: 0.51 > 0.05). Comparing the two and six landmarks procedure, Cheung et al. [11] demonstrated that, using the two landmarks procedure, the Cobb angle is 0.3° greater than using the six landmarks digital procedure (p < 0.05).
Allen et al. [13] reported poor inter-methodological reliability (range ICC 0.25–0.35) with a standard error of measurement (SEM) of 8.64°–9.54°. After eliminating four outliers, the reliability and SEM showed improvements (range ICC 0.68–0.74; SEM 4.13°–5.08°). Examining measurements obtained with smartphone app and manual measurements, Shaw et al. [15] identified a MAD of 2.1°, with limits of agreement of ±3.3°.
Discussion
In the past, the Cobb angle was measured manually, mostly on AP X-rays. Various studies confirmed higher intra-observer agreement than inter-observer agreement. A positive effect was evident if the end-vertebrae to be measured were previously marked, and if the observers used the same measuring instruments [4, 5, 25–27].
New technical advancements to determine the Cobb angle must establish themselves as at least equivalent to the manual procedure. It might be of more use to ascertain in a study the reliability and agreement of the new procedure alone and then compare these results to those of the reference test. This was not done or the data were not presented in a few of the available studies [6–8, 12].
Even more reasonable would be to application of the “Bland–Altman” method [28]. To further assess these studies, agreement should be prioritized over reliability, because this is expressed on the original measurement scale and does not depend on patient sample heterogeneity.
Agreement
Studies evaluating the agreement of digital and manual procedures have shown only minor differences in the extent of agreement on direct comparison. Detailed analysis indicates lower inter-observer agreement versus intra-observer agreement.
Allen et al. [13] yielded the lowest SEM for intra-and inter-observer agreement using the automatic procedure when compared to digital and manual procedures.
Zhang et al. [14] also reported a lower MAD for the automatic procedure than the digital one. All automatic procedures showed smaller intra-observer measurement error in comparison to inter-observer error. Even the so-called “automatic” procedures require some observer input prior to calculations. This might explain the inter-observer difference.
Results of the smartphone studies have shown contradictory results. Qiao et al. [16] yielded higher intra- and inter-observer agreement of the smartphone app, while Shaw et al. [15] found an advantage for the manual procedure.
The main difference in study design was the use of observer training and the pre-selection of vertebrae. Thus, it appears that these variables increase intra- and inter-observer agreement for the manual and smartphone procedure. The app described by Qiao et al. [16] calculates the angle automatically, and that described by Shaw et al. [15] must be calculated by the observer. This might also be a potential source of error.
Furthermore, for a more appropriate comparison, agreement should be presented using the SEM.
Reliability
The reliability was remarkably high in all analysed studies (range ICC 0.83–0.99). There was no clear trend for any of the procedures or between intra- and inter-observer reliability. Evaluation was limited by the variety of statistical methods applied. It would have been beneficial had the type of ICC used, i.e. agreement or consistency, been reported.
Inter-methodological comparison between procedures
A number of the evaluated studies tried to compare the validity of the procedures with inter-methodological comparison.
To achieve this, a number of statistical techniques were used. Tanure et al. [9] and Cheung et al. [11] assessed the statistical significance and observed no difference between procedures. This result is not remarkable due to the fact that both procedures are designed to measure the same quantity. The test of significance is irrelevant to the question of agreement. Shaw et al. [15] used the Bland–Altman method [28] and presented the MAD and limits of agreement.
The Bland–Altman method is the only one that determines the actual agreement between the two measurement methodologies. With the graphical presentation of the Bland–Altman plot, differences between the methods are shown against the mean differences. Thus, an impression is made regarding the agreement as well as systematic differences between the investigated methods.
Factors affecting interpretation
Due to the extensive broad search strategy, it can be assumed that no relevant articles in English, French or Dutch, were overlooked.
One of the limitations of this review is based on the high variability of the statistical tests implemented in the observed studies. This makes generalisation of results impossible. Only half of the studies presented sufficient data allowing conclusions regarding reproducibility. The risk of bias assessment, as judged by the modified QUADAS, revealed only one study that clearly fulfilled all parameters.
Another issue affecting interpretation of the data was that terminology such as reproducibility, reliability, agreement, variability, variance, and validity are not used in a consistent way. Even in different studies, same statistics were calculated but given different names (e.g. average absolute difference = mean absolute difference, limits of agreement = coefficient of repeatability). In some cases, the SD was pure measurement deviation, in other cases it includes variability between radiographs. Therefore, no overall assessment was possible.
Conclusion
All of the measurement procedures investigated here showed high degrees of reliability.
The agreement of digital procedures tends to be slightly better than that of manual ones. For all other measurement procedures (automatic or smartphone), results were variable. It is notable that studies implementing vertebral pre-selection and observer training achieved better agreement. Therefore, we cannot currently favour a measuring procedure to determine the Cobb angle, but it is to be noted that emphasis should be placed on observer training. Another point would be to consider the cost–benefit ratio of the measurement procedure used.
For the future, we recommend the establishment of a widely recognised standard for study and reporting of the Cobb angle to enable an entire statement.
Conflict of interest
None.
Abbreviations
- D2L, D4L, D6L
Digital two, four or six landmarks
- DH
Digital horizontal
- A
Automatic
- S
Smartphone
- ICC
Intraclass Correlation
- R
Correlation Coefficient
- QUADAS
Quality Assessment of Diagnostic Accuracy Studies
- QAREL
Quality Appraisal of Reliability Studies
- NA
Not assessed
- SD
Standard Deviation
- SEM
Standard Error of Measurement
- MAD
Mean Absolute Difference
- CI
Confidence Interval
References
- 1.Cobb JR. Outline for the study of scoliosis. Am Acad Orthop Surg Instr Course Lect. 1948;5:261–275. [Google Scholar]
- 2.Romano M, Minozzi S, Bettany-Saltikov J, Zaina F, Chockalingam N, Kotwicki T, Maier-Hennes A, Negrini S. Exercises for adolescent idiopathic scoliosis. Cochrane Database Syst Rev. 2012;8:CD007837. doi: 10.1002/14651858.CD007837.pub2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Negrini S, Minozzi S, Bettany-Saltikov J, Zaina F, Chockalingam N, Grivas TB, Kotwicki T, Maruyama T, Romano M, Vasiliadis ES. Braces for idiopathic scoliosis in adolescents. Spine (Phila Pa 1976) 2010;35(13):1285–1293. doi: 10.1097/BRS.0b013e3181dc48f4. [DOI] [PubMed] [Google Scholar]
- 4.Morrissy RT, Goldsmith GS, Hall EC, Kehl D, Cowie GH. Measurement of the Cobb angle on radiographs of patients who have scoliosis. Evaluation of intrinsic error. J Bone Joint Surg Am. 1990;72(3):320–327. [PubMed] [Google Scholar]
- 5.Carman DL, Browne RH, Birch JG. Measurement of scoliosis and kyphosis radiographs. Intraobserver and interobserver variation. J Bone Joint Surg Am. 1990;72(3):328–333. [PubMed] [Google Scholar]
- 6.Srinivasalu S, Modi HN, Smehta S, Suh SW, Chen T, Murun T. Cobb angle measurement of scoliosis using computer measurement of digitally acquired radiographs-intraobserver and interobserver variability. Asian Spine J. 2008;2(2):90–93. doi: 10.4184/asj.2008.2.2.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Corona J, Sanders JO, Luhmann SJ, Diab M, Vitale MG. Reliability of radiographic measures for infantile idiopathic scoliosis. J Bone Joint Surg Am. 2012;94(12):e861–e868. doi: 10.2106/JBJS.K.00311. [DOI] [PubMed] [Google Scholar]
- 8.Jones JK, Krow A, Hariharan S, Weekes L. Measuring angles on digitalized radiographic images using Microsoft PowerPoint. West Indian Med J. 2008;57(1):14–19. [PubMed] [Google Scholar]
- 9.Tanure MC, Pinheiro AP, Oliveira AS. Reliability assessment of Cobb angle measurements using manual and digital methods. Spine J. 2010;10(9):769–774. doi: 10.1016/j.spinee.2010.02.020. [DOI] [PubMed] [Google Scholar]
- 10.Shea KG, Stevens PM, Nelson M, Smith JT, Masters KS, Yandow S. A comparison of manual versus computer-assisted radiographic measurement. Intraobserver measurement variability for Cobb angles. Spine (Phila Pa 1976) 1998;23(5):551–555. doi: 10.1097/00007632-199803010-00007. [DOI] [PubMed] [Google Scholar]
- 11.Cheung J, Wever DJ, Veldhuizen AG, Klein JP, Verdonck B, Nijlunsing R, Cool JC, Van Horn JR. The reliability of quantitative analysis on digital images of the scoliotic spine. Eur Spine J. 2002;11(6):535–542. doi: 10.1007/s00586-001-0381-7. [DOI] [PubMed] [Google Scholar]
- 12.Chockalingam N, Dangerfield PH, Giakas G, Cochrane T, Dorgan JC. Computer-assisted Cobb measurement of scoliosis. Eur Spine J. 2002;11(4):353–357. doi: 10.1007/s00586-002-0386-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Allen S, Parent E, Khorasani M, Hill DL, Lou E, Raso JV. Validity and reliability of active shape models for the estimation of cobb angle in patients with adolescent idiopathic scoliosis. J Digit Imaging. 2008;21(2):208–218. doi: 10.1007/s10278-007-9026-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang J, Lou E, Hill DL, Raso JV, Wang Y, Le LH, Shi X. Computer-aided assessment of scoliosis on posteroanterior radiographs. Med Biol Eng Comput. 2010;48(2):185–195. doi: 10.1007/s11517-009-0556-7. [DOI] [PubMed] [Google Scholar]
- 15.Shaw M, Adam CJ, Izatt MT, Licina P, Askin GN. Use of the iPhone for Cobb angle measurement in scoliosis. Eur Spine J. 2012;21(6):1062–1068. doi: 10.1007/s00586-011-2059-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Qiao J, Liu Z, Xu L, Wu T, Zheng X, Zhu Z, Zhu F, Qian B, Qiu Y. Reliability analysis of a smartphone-aided measurement method for the Cobb angle of scoliosis. J Spinal Disord Tech. 2012;25(4):E88–E92. doi: 10.1097/BSD.0b013e3182463964. [DOI] [PubMed] [Google Scholar]
- 17.de Vet HC, Terwee CB, Knol DL, Bouter LM. When to use agreement versus reliability measures. J Clin Epidemiol. 2006;59(10):1033–1039. doi: 10.1016/j.jclinepi.2005.10.015. [DOI] [PubMed] [Google Scholar]
- 18.Bartlett JW, Frost C. Reliability, repeatability and reproducibility: analysis of measurement errors in continuous variables. Ultrasound Obstet Gynecol. 2008;31(4):466–475. doi: 10.1002/uog.5256. [DOI] [PubMed] [Google Scholar]
- 19.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86(2):420–428. doi: 10.1037/0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- 20.Streiner DL, Norman GR. Health measurement scales a practical guide to their development and use. Oxford: Oxford University Press; 2008. [Google Scholar]
- 21.Whiting P, Rutjes AW, Dinnes J, Reitsma J, Bossuyt PM, Kleijnen J. Development and validation of methods for assessing the quality of diagnostic accuracy studies. Health Technol Assess. 2004;8(25):1–234. doi: 10.3310/hta8250. [DOI] [PubMed] [Google Scholar]
- 22.Lucas NP, Macaskill P, Irwig L, Bogduk N. The development of a quality appraisal tool for studies of diagnostic reliability (QAREL) J Clin Epidemiol. 2010;63(8):854–861. doi: 10.1016/j.jclinepi.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 23.Zhang J, Lou E, Le LH, Hill DL, Raso JV, Wang Y. Automatic Cobb measurement of scoliosis based on fuzzy Hough transform with vertebral shape prior. J Digit Imaging. 2009;22(5):463–472. doi: 10.1007/s10278-008-9127-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhang J, Lou E, Shi X, Wang Y, Hill DL, Raso JV, Le LH, Lv L. A computer-aided Cobb angle measurement method and its reliability. J Spinal Disord Tech. 2010;23(6):383–387. doi: 10.1097/BSD.0b013e3181bb9a3c. [DOI] [PubMed] [Google Scholar]
- 25.Goldberg MS, Poitras B, Mayo NE, Labelle H, Bourassa R, Cloutier R. Observer variation in assessing spinal curvature and skeletal development in adolescent idiopathic scoliosis. Spine (Phila Pa 1976) 1988;13(12):1371–1377. doi: 10.1097/00007632-198812000-00008. [DOI] [PubMed] [Google Scholar]
- 26.Lonstein JE, Carlson JM. The prediction of curve progression in untreated idiopathic scoliosis during growth. J Bone Joint Surg Am. 1984;66(7):1061–1071. [PubMed] [Google Scholar]
- 27.Pruijs JE, Hageman MA, Keessen W, van der Meer R, van Wieringen JC. Variation in Cobb angle measurements in scoliosis. Skeletal Radiol. 1994;23(7):517–520. doi: 10.1007/BF00223081. [DOI] [PubMed] [Google Scholar]
- 28.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–310. doi: 10.1016/S0140-6736(86)90837-8. [DOI] [PubMed] [Google Scholar]