Abstract
Maternal mortality is widely regarded as a key indicator of population health and of social and economic development. Its levels and trends are monitored closely by the United Nations and others, inspired in part by the UN’s Millennium Development Goals (MDGs), which call for a three-fourths reduction in the maternal mortality ratio between 1990 and 2015. Unfortunately, the empirical basis for such monitoring remains quite weak, requiring the use of statistical models to obtain estimates for most countries.
In this paper we describe a new method for estimating global levels and trends in maternal mortality. For countries lacking adequate data for direct calculation of estimates, we employed a parametric model that separates maternal deaths related to HIV/AIDS from all others. For maternal deaths unrelated to HIV/AIDS, the model consists of a hierarchical linear regression with three predictors and variable intercepts for both countries and regions. The uncertainty of estimates was assessed by simulating the estimation process, accounting for variability both in the data and in other model inputs.
The method was used to obtain the most recent set of UN estimates, published in September 2010. Here, we provide a concise description and explanation of the approach, including a new analysis of the components of variability reflected in the uncertainty intervals.
Final estimates provide evidence of a more rapid decline in the global maternal mortality ratio than suggested by previous work, including another study published in April 2010. We compare findings from the two recent studies and discuss topics for further research to help resolve differences.
Keywords: maternal mortality, multilevel regression model, AIDS mortality, Millennium Development Goals
1 INTRODUCTION
A maternal death is widely regarded as one of life’s most tragic outcomes. There is a cruel irony in the death of a woman who is engaged in the act of creating life, and her death is an incomparable loss for any children who are left behind. Such deaths are almost entirely preventable given proper medical surveillance and intervention, and as such maternal mortality is often viewed as a sentinel indicator of the quality of a health care delivery system.
1.1 Millennium Development Goals
The United Nations recognized the unique significance of maternal mortality as part of the Millennium Declaration issued by the UN General Assembly in September 2000. As part of a broader set of Millennium Development Goals (MDGs), the UN Member States called for the reduction by three quarters, between 1990 and 2015, of the maternal mortality ratio (the number of maternal deaths per live birth) in all countries and regions where the risk of maternal death remained unacceptably high in 1990. Such a target implies that the maternal mortality ratio (MMR) should decline at an average rate of at least 5.5% per year over the 25-year interval.
1.2 Global Estimates of Maternal Mortality
In order to track progress (or lack thereof) toward the MDG target, various agencies of the broader UN system have joined in an effort to estimate both levels and trends of the MMR and associated measures of maternal mortality over this time period. Previously, a series of estimates referring to years 1990, 1995, 2000, and 2005 had been published by a combination of four agencies: the World Health Organization (WHO) and UNICEF, initially the sole partners in this enterprise, were joined in later rounds by UNFPA and The World Bank.
Earlier rounds focused on estimating the level of maternal mortality for just one or at most two years in the 5-yearly series. Estimates from different rounds were not comparable and thus inappropriate for the evaluation of trends. The immediately preceding round (World Health Organization et al., 2007, Hill et al., 2007) included estimates for both 2005 and 1990, which were derived by similar but separate procedures, each involving a regression model for imputing estimates for countries without data in a given time period.
The most recent round of UN estimates (World Health Organization et al., 2010) was conceived to be different in this regard. Rather than deriving estimates for one or two time points only, the new method provides an integrated evaluation of maternal mortality over the full interval from 1990 to 2008, utilizing all available data over this period. A key goal of this analysis was to create comparable estimates of the MMR and related indicators for 172 countries (or territories), with reference to 5-year time intervals centered on 1990, 1995, 2000, 2005, and 2008.
A similar, independent re-evaluation of maternal mortality levels and trends was carried out by Hogan et al. (2010) covering the period from 1980 to 2008. A brief discussion (and comparison) of their methods and results will be presented as part of this analysis. The main purpose of the current study, however, is to present and evaluate the methods used for deriving the new UN estimates.
We are writing this article on behalf of the group of agencies and persons who collaborated in the production of the new UN estimates of maternal mortality. Our purpose is to provide additional explanation of the methods utilized and to offer some suggestions for possible improvements in future rounds of such work. Additional documentation beyond that contained in the present article or earlier documents is being provided through a supplemental report (Wilmoth et al., 2012).
1.3 Main Findings about Levels and Trends since 1990
We begin with a brief overview of the study’s main findings about global levels and trends in maternal mortality since 1990. At the global level, the estimated total number of maternal deaths declined from approximately 546,000 to 358,000 between 1990 and 2008. Similarly, the global maternal mortality ratio (MMR) declined from 397 maternal deaths per 100,000 live births in 1990 to 263 in 2008, for an average annual decline of 2.3%. Given the sparseness of data available on maternal mortality in some countries, the uncertainty intervals around these global estimates are quite large. While the point estimates for the global MMR in 1990 and 2008 are 397 and 263 respectively, the 95% uncertainty intervals around these estimates are 290–585 in 1990 and 201–373 in 2008. Similarly, for the global estimate of total maternal deaths, the 95% uncertainty intervals are 388,000–800,000 in 1990 and 265,000–503,000 in 2008.
Global and regional estimates of the MMR in 1990 and 2008 are presented in Table 1 along with average annual rates of decline. The table also shows a 95% uncertainty interval (95% UI) for all estimates (see later explanation). Regional groupings follow those used by the United Nations for evaluating progress toward the MDGs and are thus known as the “MDG regions.”
Table 1.
Levels and average annual rates of decline from 1990 to 2008 in the maternal mortality ratio (MMR) with 95% uncertainty intervals, for the world and major regions
| Region | MMR
|
Average annual decline (%)1990–2008 | |
|---|---|---|---|
| 1990 | 2008 | ||
| World | 400 (290, 580) | 260 (200, 370) | 2.3 (1.8, 2.8) |
| Developed regions | 16 (15, 20) | 14 (13, 16) | 0.8 (0.1, 1.7) |
| CIS | 68 (60, 81) | 40 (34, 48) | 3.0 (2.2, 3.8) |
| Developing regions | 450 (330, 660) | 290 (220, 410) | 2.3 (1.8, 2.9) |
| Africa | 780 (550, 1200) | 590 (430, 850) | 1.6 (1.0, 2.0) |
| Northern Africa | 230 (150, 360) | 92 (60, 140) | 5.0 (4.1, 5.9) |
| Sub-Saharan Africa | 870 (610, 1300) | 640 (470, 930) | 1.7 (1.1, 2.1) |
| Asia | 390 (270, 580) | 190 (130, 270) | 4.0 (3.5, 4.6) |
| Eastern Asia | 110 (66, 190) | 41 (27, 66) | 5.5 (4.5, 6.5) |
| Southern Asia | 590 (390, 920) | 280 (190, 420) | 4.2 (3.6, 4.8) |
| South-Eastern Asia | 380 (260, 600) | 160 (110, 240) | 4.7 (3.8, 5.6) |
| Western Asia | 140 (88, 240) | 68 (45, 110) | 4.0 (3.1, 5.0) |
| Latin America and the Caribbean | 140 (120, 190) | 85 (72, 100) | 2.9 (2.4, 3.5) |
| Oceania | 290 (130, 660) | 230 (100, 500) | 1.4 (−4.5, 7.2) |
- CIS = Commonwealth of Independent States (includes most countries of the former USSR).
- See the Appendix, section 5.2, regarding calculation of the average annual rate of decline.
- Following the practice used in the official report (World Health Organization et al., 2010), MMR values shown here have been rounded according to the following scheme: < 100, no rounding; 100–999, rounded to nearest 10; and > 1000, rounded to nearest 100. Rates of change were computed before rounding.
The estimates presented in Table 1 suggest differential rates of progress in reducing maternal mortality across regions. In all of the MDG sub-regions of Asia, we have estimated that the MMR declined by 4% or more per year over the period 1990 to 2008. For the region as a whole, the MMR declined at an estimated rate of 4% per annum (95% UI, 3.5–4.6%). In contrast, for Sub-Saharan Africa the estimated annual rate of decline is only 1.7% (95% UI, 1.1–2.2%).
From 1990 to 2008, the annual number of births in Asia decreased by 0.5% per year (falling from 82 to 74 million), whereas in Sub-Saharan Africa the total number of births increased by 1.5% per year (rising from 23 to 32 million). The slower progress in reducing the MMR for Sub-Saharan Africa relative to Asia, coupled with differential trends in the number of births, has resulted in a major regional shift in the burden of maternal mortality over the period of this study. Thus, in 1990 roughly 58% of global maternal deaths occurred in Asia and 36% in Sub-Saharan Africa; in 2008 this composition had largely reversed, with an estimated 39% of global maternal deaths occurring in Asia and 57% in Sub-Saharan Africa. In a companion paper, we discuss and interpret the results of this analysis in greater depth (Zureick-Brown et al., 2012). Country-specific estimates of the MMR can be found in the official report (World Health Organization et al., 2010) and online via MME Info (http://www.maternalmortalitydata.org).
2 DATA AND METHODS
In this section we describe the data and methods used to derive the estimates of maternal mortality summarized above. A brief overview of data and methods (Wilmoth et al., 2010) was published with the official report (World Health Organization et al., 2010).
2.1 Definitions and Measures
We begin by reviewing the technical definition of a maternal death and the different measures used to quantify the level of maternal mortality within a population.
2.1.1 Maternal vs. Pregnancy-Related Deaths
In the 10th revision of the International Classification of Diseases (ICD-10), the WHO defines a maternal death as:
The death of a woman while pregnant or within 42 days of termination of pregnancy, irrespective of the duration and site of the pregnancy, from any cause related to or aggravated by the pregnancy or its management but not from accidental or incidental causes (World Health Organization, 2004).
Maternal deaths can be further subdivided into direct and indirect maternal deaths: direct maternal deaths are those due to obstetric complications of pregnancy (including delivery and 42 days postpartum), while indirect maternal deaths are those linked to other diseases or conditions when aggravated by the physiological effects of pregnancy. A pregnancy-related death is defined in the ICD-10 as:
The death of a woman while pregnant or within 42 days of termination of pregnancy, irrespective of the cause of death (World Health Organization, 2004).
Thus, maternal deaths are a subset of pregnancy-related deaths, specifically, those with a putative causal relation to the pregnancy itself.
2.1.2 Measures of Maternal Mortality
There are two main factors influencing a woman’s lifetime risk of maternal death: (a) the risk of dying during a single pregnancy and (b) how many times a woman faces this risk (i.e., her fertility level). The maternal mortality ratio (MMR) reflects (a) only; it is calculated as the number of maternal deaths in a given time period divided by the number of live births during the same period:
| (1) |
The maternal mortality rate (MMRate) reflects both (a) and (b). It is defined as the number of maternal deaths divided by person-years lived by women of reproductive age in a population:
| (2) |
The MMR is generally regarded as the preferred measure of maternal mortality because it describes the frequency of maternal death relative to its risk pool, as measured (imperfectly, but not badly) by the number of live births. In practice, however, the MMR is prone to measurement bias because data for the numerator and denominator are often collected through different means. As a result, for estimation purposes it is often better to start with data on the proportion of maternal deaths (PM) among women of reproductive age:
| (3) |
Even if a given data source yields an underestimate of the number of maternal deaths (as occurs quite frequently due to under-reporting of events), it is plausible that the reported proportion of maternal deaths is more reliable (Hill et al., 2007).
Given the appropriate data, the MMR and MMRate can be derived from the PM by reference to the following relationships:
| (4) |
| (5) |
This general estimation strategy – i.e., combining observed values of the proportion of maternal deaths with separate estimates of overall levels of mortality and fertility in a population – was employed in deriving both sets of maternal mortality estimates published in 2010 (Hogan et al., 2010, World Health Organization et al., 2010).
The following relationship linking the MMR and MMRate can be derived easily using equations (1) and (2):
| (6) |
where the general fertility rate (GFR) equals the number of live births per woman-year lived at ages 15–49. Equation (6) illustrates clearly that the MMRate reflects both the risk of maternal death per live birth (MMR) and the level of fertility (GFR). In building regression models of these or other indicators of maternal mortality, the above relationship implies that models of the MMR and the MMRate are closely related. Specifically, when log(GFR) is included as an explanatory variable, regression models of log(MMR) and log(MMRate) differ only in the coefficient for log(GFR), which changes by exactly one. The same is true, approximately, when using another measure of fertility that is highly correlated with the GFR, such as the total fertility rate (TFR).
2.2 Data Sources for Maternal Mortality
National-level data on maternal mortality come from a number of sources. Depending on the data available, we used different methods to estimate country-specific levels and trends of maternal mortality for the period 1990–2008. The 172 countries (or territories) included in this analysis were divided into three categories based on the underlying data used to generate the country-specific estimates: (A) countries with relatively complete civil registration systems and good attribution of causes of death, (B) countries that lack complete registration systems but for which other nationally representative data are available for measuring maternal mortality, and (C) countries with no available national-level data on maternal mortality. Table 2 describes the global distribution of countries and live births across these three different categories. Nearly half of all countries belong to group B; moreover, this group accounts for over four-fifths of global births.
Table 2.
Country groupings by data source used for estimating maternal mortality
| Country Group | Source of maternal mortality data | Number of countries/territories | Percent of countries/territories in each category | Percent of births in 172 countries/territories |
|---|---|---|---|---|
| A | Civil registration characterized as complete, with good attribution of causes of death | 63 | 37 | 15 |
| B | Countries lacking complete registration data, but where other types of data are available | 85 | 49 | 82 |
| C | No national data available for estimating maternal mortality | 24 | 14 | 4 |
|
| ||||
| Total | – | 172 | 100 | 100 |
Note: Percentages may not sum to 100 due to rounding.
Other than civil registration, methods of collecting data on maternal mortality include: sample surveys, censuses, periodic inquiries (often called “reproductive-age mortality studies” or RAMOS), and various ongoing surveillance systems (including “sample registration” in India). Censuses and some surveys have been used to collect data on the number of recent deaths occurring in a household, along with some information about cause of death (sometimes a complete verbal autopsy). A more common survey technique is the (direct) sisterhood method, which gathers detailed information about all past deaths among sisters of respondents, including whether they occurred during the maternal risk period (but typically without additional information about the underlying cause of death). More information about the different data sources is available in the supplemental report (Wilmoth et al., 2012).
After applying various selection criteria (see section 2.3.1), we obtained a final data set consisting of 484 observations of the level of maternal or pregnancy-related mortality at various time points for 153 countries or territories. Most of these observations cover time intervals of 5–7 years. For comparison to other studies, it is helpful to describe the data in terms of country-years of observations. Thus, our dataset with 484 observations provides a total of 2,842 country-years of data, including 1,891 country-years from civil registration data, 819 from survey-based sisterhood data, and the remainder from other sources.
Table 3a describes the distribution of the 484 observations across the data types described above; Table 3b shows the same information for Sub-Saharan Africa alone. Thus, globally most data come from vital registration systems; however, for Sub-Saharan Africa, which accounts for more than half of all maternal deaths in recent years, most of the available information comes from sample surveys. More information about data sources for individual countries is available online (http://www.who.int/gho/maternalhealth/countries/en/index.html).
Table 3.
Distribution of maternal mortality observations by data type
| (a) World
| ||
|---|---|---|
| Data type | Number of observations | Percent of observations |
| Vital registration | 296 | 61 |
| Survey - sisterhood direct | 103 | 21 |
| Survey - recent household deaths | 15 | 3 |
| Census | 14 | 3 |
| Sample registration system | 4 | 1 |
| Surveillance | 41 | 8 |
| Inquiry (RAMOS, etc.) | 11 | 2 |
|
| ||
| All data types | 484 | 100 |
| (b) Sub-Saharan Africa
| ||
|---|---|---|
| Data type | Number of observations | Percent of observations |
| Vital registration | 4 | 5 |
| Survey - sisterhood direct | 61 | 81 |
| Survey - recent household deaths | 3 | 4 |
| Census | 6 | 8 |
| Sample registration system | 0 | 0 |
| Surveillance | 1 | 1 |
| Inquiry (RAMOS, etc.) | 0 | 0 |
|
| ||
| All data types | 75 | 100 |
Note: Percentages may not sum to 100 due to rounding.
For countries with complete and reliable information from civil registration systems (group A), we computed estimates of maternal mortality directly using procedures described here in Section 2.4. For the remaining countries (groups B and C), estimates were derived using a two-part parametric model (Section 2.5); the main component of that model was a hierarchical, or multilevel, regression model (Section 2.6).
2.3 Data Preparations
Initial preparations of available data on levels of maternal mortality involved two steps: (1) selection of data for inclusion, and (2) adjustments to account for inconsistency of definitions and under-reporting of events.
2.3.1 Selection Criteria
To be included in the analysis, an observation of the maternal mortality level for a population had to meet certain criteria. To begin, we considered only data that were considered to be representative of the national population and to refer to a well-specified time interval within the period from the late 1980s until today.
Data from civil registration systems were used only if such data were available for several years between 1990 and 2008, and if the available evidence indicated that data from the system achieved minimally-acceptable levels of completeness in reporting and accuracy in the attribution of cause of death. The following specific criteria were applied:
Earliest year of available data in 1995 or before; latest year of available data in 2003 or later; and data available for more than half of the full range of years (from first available to last available for each country);
Estimated completeness of death registration of at least 85% for almost all years (no more than 2 exceptional years per country);
Deaths coded to ill-defined causes (i.e., R codes in ICD-10) not above 20% for almost all years (no more than 2 exceptional years per country).
For sibling survival information from the Demographic and Health Surveys or similar studies, all data were obtained from published reports. When those reports presented data for multiple time intervals, we pooled the information to derive a single observation from each survey. The observed proportion of maternal deaths (PM) was standardized according to the age distribution of the female population of respondent households at the time of survey (Wilmoth et al., 2012).
In all cases available data on the number of maternal deaths were not acceptable on their own; in other words we required that counts of maternal deaths be accompanied by an appropriate denominator, or else those observations were excluded from the study. The preferred denominator was the total number of deaths to women of reproductive age (yielding the PM); the other acceptable denominator for an input observation was the number of live births (the MMR). For observations where only the MMR was available but not the PM, we converted the former to the latter by multiplying the MMR by the estimated number of live births (United Nations Population Division, 2009) and dividing by the estimated number of deaths among women aged 15–49 in the population. The latter were approximated by multiplying WHO estimates of age-specific death rates (World Health Organization, 2010) times UN estimates of population by age (United Nations Population Division, 2009).
If estimates of both maternal and pregnancy-related deaths were available from a single study, we only used data based on a true “maternal” definition as inputs for this analysis. We excluded all estimates of maternal mortality calculated using the indirect sisterhood method for reasons that have been articulated elsewhere (Stanton et al., 2000).
2.3.2 Adjustment for Underreporting of Events
In order to account for the frequent under-enumeration of maternal deaths, different adjustments were made depending on the data type. For vital registration data, maternal and all-cause deaths of unknown age were distributed over the age range in proportion to the number of reported deaths where age was known. In addition, to account for under-identification of maternal deaths in data pertaining to cause of death, estimates from vital registration were adjusted upwards by a factor of 1.5, or by a country-specific factor when appropriate data were available. The default adjustment factor of 1.5 was chosen because it was the median of values derived from country-specific studies from group A countries. Full details of this analysis are available in the supplemental report. Estimates of maternal mortality derived using methods other than vital registration were adjusted upward by a factor of 1.1 to correct for the likely under-identification of deaths from maternal causes that is thought to occur almost universally (for example, due to secrecy around abortion-related deaths).
2.3.3 Adjustment for Inconsistent Definitions
Some observations used as inputs to our model of maternal mortality refer to pregnancy-related rather than maternal deaths. In order to improve the comparability of data inputs, pregnancy-related observations were adjusted by removing a fraction of deaths, π, that were assumed to be pregnancy-related but not maternal (i.e., accidental or incidental deaths). The true value of π is typically unknown and may vary by country and over time. To choose a specific value of this parameter, we examined the difference in estimates of maternal and pregnancy-related mortality in studies where both sorts of data were collected. Table C of the supplemental report provides the ratio of maternal to pregnancy-related deaths from such studies. We also examined WHO data on injury-related deaths. Together, these analyses suggested values of π around 10–15 percent. For countries of Sub-Saharan Africa we assumed π=0.10, and for all others we assumed π=0.15. For countries with negligible levels of HIV/AIDS, observed values of PM based on a pregnancy-related definition were multiplied by 1−π before serving as an input to the model. For populations affected by HIV/AIDS, we first removed all AIDS-related deaths from the PM before making this same adjustment. The procedure used to remove AIDS-related deaths is explained later (Section 2.7).
Although we have made these adjustments based on the best information available to us, the evidentiary basis is quite weak for most of the underlying assumptions, and the resulting model is clearly an enormous simplification of reality. We have attempted to take these issues into account in our evaluation of estimation uncertainty (see Section 2.8). Future work in this area could benefit from additional research on such topics.
2.4 Estimating MMR Trends from Death Registration Data
For countries whose death registration data met the criteria outlined above, such data were used to derive estimates of the MMR by direct calculation. For all other countries, estimates were obtained using the model discussed in the next sections.
For these direct calculations, death registration data for maternal mortality were adjusted for both completeness and misclassification, where completeness refers to the fraction of deaths registered by the system as a whole, and misclassification refers to inaccuracy or missing information in the formal attribution of the decedent’s cause of death. Completeness of death registration was assessed using methods described in Mathers et al. (2005). Methods of adjusting for misclassification of cause of death were identical to those used for constructing the PM: multiply by 1.5 (the default), or by a country-specific adjustment factor if an appropriate study exists.
For target year t, where t=1990, 1995, 2000, or 2005, maternal mortality death counts adjusted for completeness and misclassification and the corresponding live births from the UN Population Division were pooled for 5-year periods from t − 2 to t + 2. The pooled maternal deaths were divided by the pooled live births to obtain final estimates. If data were available for 2008 or 2009, the average of 2004–2008 or 2004–2009 was taken as the point estimate for 2008. When data were not yet available for 2008 or 2009, the point estimate for 2005 (based on the 2003–2007 average) was assumed to remain constant through 2008.
In some cases a country had only one year of observation in an interval centered on year t; for such cases estimates for year t from the multilevel model were used instead. Also, for four countries with complete registration systems but very small numbers of maternal deaths (Bahamas, Belgium, Iceland, and Malta), estimates were derived from the parametric model for all time periods.
2.5 Overview of the Parametric Model
To estimate maternal mortality levels for countries with limited or no data, we developed a model of maternal mortality that uses more readily available information as predictors. After adjusting observed proportions of maternal deaths for inconsistent definitions and underreporting of events, such observations were used to estimate a multilevel linear regression model, which lies embedded within a larger model.
The full model includes two components, separating indirect maternal deaths related to HIV/AIDS from all others, and has the following form:
| (7) |
where
| (8) |
| (9) |
| (10) |
Estimated values of a for all countries over time were derived by combining information from three sources. Numerators were taken from published estimates of AIDS deaths from UNAIDS (UNAIDS, 2008). For the denominators total deaths were obtained by multiplying WHO estimates of age-specific death rates (World Health Organization, 2010) times female population estimates from the United Nations Population Division (2009). It is worth noting that the WHO death rates include a component of AIDS mortality that is derived from, and thus fully consistent with, the UNAIDS estimates.
The two-part model was motivated by a need to consider the interaction of AIDS and maternal causes of death among HIV-positive women who die during pregnancy, and to highlight the impact of assumptions made in this regard on estimated levels and trends of maternal mortality. The separate treatment of AIDS-related deaths will be discussed further in section 2.7, after first describing the multilevel model applied to maternal deaths unrelated to HIV/AIDS in section 2.6.
2.6 Multilevel Linear Regression Model
A multilevel, or hierarchical, linear regression model was used to depict variation in log(PMna) as a function of three predictor variables, with variable intercepts (or random effects) included for both countries and regions. The model was estimated using available data from all A and B countries. The fitted model was then used to derive estimates of non-AIDS maternal deaths for countries in both the B and C groups of Table 2. In its final version, the model has the following form:
| (11) |
where GDP is the gross domestic product per capita, GFR is the general fertility rate, and SAB (for “skilled attendant at birth”) is the proportion of live births where the delivery was attended by a skilled health worker. We use j[i] and k[i] to indicate that observation i is associated with country j and region k, for i = 1, …, n, j = 1, …, J, and k = 1, …, K. In our example, n = 484, J = 153, and K = 12. The model was estimated using the lmer4 package in R (Bates et al., 2011, R Development Core Team, 2011).
2.6.1 Dependent Variable
The dependent variable, , was constructed from observed proportions of maternal or pregnancy-related deaths (among deaths to women aged 15–49) after adjusting for under- or misreporting of events (section 2.3.2). This step involved simple calculations to remove (approximately) all accidental or incidental deaths (section 2.3.3), and all AIDS-related deaths (section 2.7) from the adjusted proportions. The exact procedure depended on the categories of deaths included in an observed datum (see supplemental report for details).
As shown in Table 3, a majority of the dependent observations were derived from vital registration data, referring mostly to 5-year time intervals depending on data availability. Survey data on the survival of sisters formed the second largest category of observations; following the presentation in the summary tables of individual survey reports, these refer mostly to 7-year time intervals. Since the age distribution of sisterhood data differs noticeably from that of the general population, the observed proportion of pregnancy-related deaths at ages 15–49 was standardized according to the age distribution of all females residing in survey households (see supplemental report).
2.6.2 Predictor Variables
The potential predictor variables that we considered fall into three categories: indicators of socioeconomic development, measures of fertility, and process variables. In the final model, the gross domestic product per capita (GDP) represents socioeconomic development, fertility is measured by the general fertility rate (GFR), and the proportion of live births with a skilled attendant at time of delivery (SAB) serves as a direct measure of the conditions under which births occur in a given population.
The GDP was measured in constant 2005 international dollars, or units of purchasing power parity (PPP). Data for this covariate come mostly from the World Bank, but for some countries we used information from the Penn World Tables or from WHO’s unpublished National Health Accounts Series. Values of the GFR, which equals the ratio of live births to the number of person-years lived by reproductive-age women, were derived using data from the United Nations Population Division (2009). Data on SAB were taken from a database maintained by UNICEF (UNICEF, 2010). In order to produce estimates corresponding to 5-year intervals centered on 1990, 1995, 2000, 2005, and 2008, we collected or created annual estimates of predictor variables during 1988–2010 and then averaged the annual values over time intervals corresponding to each observation. Details of this work are documented in the supplemental report (Wilmoth et al., 2012).
Estimated coefficients for the three predictor variables are shown here in Table 4. As expected, the level of maternal mortality tends to decline with an increase in per capita income or in the proportion of births attended by a skilled health worker, and it tends to increase in tandem with fertility. Although used for predictive purposes only, it is reassuring that the model has a plausible causal interpretation. To give an idea of the model’s explanatory power, we estimated equivalent OLS regression models with and without country/region effects, yielding R-squared values of 0.82 and 0.96.
Table 4.
Estimated β coefficients of multilevel regression model
| Variable | Estimate | Standard Error | T-value |
|---|---|---|---|
| Intercept | 2.253 | 0.414 | 5.4 |
| log(GDP) | −0.217 | 0.054 | −4.0 |
| log(GFR) | 1.272 | 0.119 | 10.6 |
| SAB | −0.652 | 0.248 | −2.6 |
Note: Estimated coefficients for countries and regions are provided in Table A of the supplemental report (Wilmoth et al., 2012).
2.6.3 Variable Intercepts
For estimating the multilevel regression model, countries were grouped into regions according to the global categories used by the UN Statistics Division in reporting on progress toward achievement of the MDGs, with some minor modifications (for example, Romania and Bulgaria were grouped with “Transition countries of Southeastern Europe” rather than with “Eastern Europe”). Table A of the supplemental report specifies the regional category associated with each country while fitting the model.
The variance components of the multilevel model are summarized here in Table 5, which presents variance estimates for εi, , and of equation (11). These values were used for the formal assessment of estimation uncertainty (see later explanation). It is notable that the degree of variability observed across regions exceeds that of countries within their respective regions, confirming the utility of grouping countries into regions within a hierarchical model.
Table 5.
Estimated variance components of the multilevel model
| Level | Variance σ2 | Standard deviation σ |
|---|---|---|
| Observation | 0.119 | 0.345 |
| Country | 0.134 | 0.367 |
| Region | 0.205 | 0.453 |
2.6.4 Observation Weights
We made very limited use of weights in estimating the multilevel regression model. In fact, weights were used in only one situation: multiple observations taken from the same data source were downweighted proportionally, but this occurred rarely.
We did not use weights to adjust for the differential uncertainty of observations, because we did not have plausible measures of their total uncertainty. Although we could have assigned weights based on standard assessments of stochastic variability, we believe that the total uncertainty in most cases includes a substantial (perhaps dominant) portion of systematic error, which is difficult (perhaps impossible) to quantify.
We made an implicit choice about the relative weight given to vital registration data by grouping them into 5-year intervals rather than using single-year data as observations. In this way we reduced the total number of vital registration data points, and thus their total weight in the analysis, by roughly a factor of five. This approach was adopted to avoid giving excessive weight to vital registration data, which tend to come from countries where levels of maternal mortality are relatively low. Furthermore, other types of published information typically refer to multi-year intervals (for example, the 7-year intervals often used with survey data on survival of sisters).
2.6.5 Alternative Models: Dependent Variable
As discussed earlier, for the dependent variable of the regression model, we chose log(PMna), the logarithm of the proportion of maternal deaths among women of reproductive age after deleting some fraction associated with HIV/AIDS. An alternative dependent variable that we examined closely was log(MMRna), the logarithm of the maternal mortality ratio after an identical adjustment for AIDS-related maternal deaths. A third possibility, log(MMRatena), was not considered, because models based on the MMR and the MMRate (with the same treatment of AIDS-related deaths) are exactly equivalent so long as log(GFR) is included among the independent variables, since MMRate = MMR * GFR.
Thus, we estimated and analyzed two versions of the multilevel model. As an alternative to our preferred model, we substituted log(MMRna) in place of log(PMna) in equation (11), keeping the same predictor variables and hierarchical structure of random effects. In order to facilitate a comparison of these two models, it is convenient to define the following quantity:
| (12) |
Noting that PM* = (1 − a)PMna, it is possible to estimate the multilevel model (equation 11) by choosing log(PM*) as the dependent variable and inserting an offset of log(1 − a) on the right-hand side of the regression equation. Similarly, the alternative model with log(MMRna) as the dependent variable can be specified by using log(PM*) as the dependent variable with an offset of , where B is the number of live births and D is the number of deaths to women aged 15–49. Formulating the two models in this manner enables us to compare them directly.
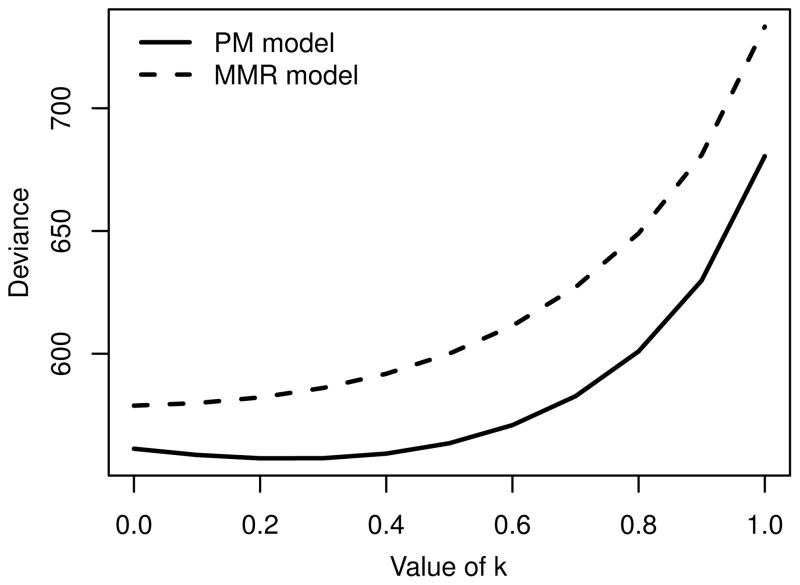
It was not clear a priori which of the two models would provide a closer fit to the data. Prior rounds of UN estimates had employed a variant of the PM model, whereas Hakkert (2001) had argued in favor of the MMR model. In the end we chose to use the PM model because it appears to fit the data better given our current choices of predictor variables and treatment of AIDS-related deaths.
Figure 1 shows deviance scores for the two models as a function of the k parameter, which affects the dependent variable, PM*, via PMa (see equation 12, and section 2.7 on AIDS-related maternal deaths). Based on its consistently lower deviance scores, we chose the PM model over the MMR model. As explained later, we also used Figure 1 to guide our assumption about the value of k.
Figure 1.
Deviance scores as a function of parameter k for two variants of the multilevel regression model
2.6.6 Alternative Models: Predictor Variables
We considered other indicators of socioeconomic development, such as life expectancy at birth for females, the probability of dying between birth and age 5 for both males and females, and the Human Development Index (HDI). Unfortunately, the HDI was not available for all countries over the full time period, especially during the 1990s. Lacking a usable synthetic measure of development, we chose GDP per capita over the mortality measures in order to have a model based on plausible causal mechanisms rather than merely predictive correlations.
The general fertility rate (GFR) was chosen over other fertility measures, such as the total fertility rate (TFR), because the GFR links two fundamental measures of maternal mortality: MMRate = MMR * GFR. In any case this choice matters for little, as the correlation between the two fertility measures is very high.
Other than the proportion of births with a skilled attendant at delivery (SAB), process variables that we considered include the proportion of live births where the mother received antenatal care (ANC) or where the delivery occurred in an institutional setting (IDLV). SAB was chosen in part because it was considered to be more informative and comparable across countries, and also because it was more widely available than the other two measures.
Thus, the predictor variables for this study were chosen based primarily on theoretical concerns and data availability. As the available dataset is expanded, further study of alternative specifications could help in fine-tuning the model. For example, if HDI data were extended backward in time, this variable might provide a more stable measure of development that is less sensitive to short-term economic fluctuations (whether or not greater stability is advantageous depends on whether maternal mortality follows economic trends closely or at a distance).
2.7 AIDS-Related Maternal Deaths
For countries with a high prevalence of HIV infection, AIDS has become a leading cause of death during pregnancy and the postpartum period. There is evidence from community studies that infection with HIV is associated with a higher risk of dying from direct obstetric causes, though this effect may be attenuated at the population level by a tendency toward lower fertility among infected women, especially in later stages of the disease (Chen and Walker, 2010).
When HIV is widespread in a population, reproductive-age women experience much higher risks of mortality. It is reasonable to assume in such settings that some or many AIDS deaths among pregnant women would have happened even if the woman had not been pregnant. In such cases the death is incidental to the pregnancy and does not qualify as a maternal death by definition.
On the other hand, some or many deaths generally regarded as due to HIV/AIDS may have been complicated by physiological changes associated with pregnancy, or they may have been accelerated by the difficulty of aggressive treatment while pregnant. Although HIV/AIDS may often be seen as the primary cause of death in such cases, according to ICD-10 protocols the death is due to indirect maternal causes and should be included within an estimate of maternal mortality. Since AIDS deaths have become much more common than maternal deaths among women of reproductive age (both worldwide and in most of the countries at greatest risk), it is important to separate these AIDS-related maternal deaths from all others to avoid presenting a distorted picture of the risks posed by pregnancy itself.
Our choice to include a separate AIDS component in the estimation model was motivated by the innovative estimates of maternal mortality published by Hogan et al. (2010). Our approach is fundamentally different, however, in that we use UNAIDS estimates of total AIDS deaths as the starting point for estimating the number of such deaths that occur during pregnancy or within 42 days postpartum, rather than estimating this number from a regression model that includes the level of HIV prevalence as an additional predictor variable. Moreover, whereas Hogan and colleagues chose to count as maternal all pregnancy-related deaths associated with HIV, we have made a crucial distinction between AIDS deaths that are incidental to the pregnancy and those with some causal connection to the pregnancy. The implications of these differences for the overall evaluation of global levels and trends in maternal mortality will be addressed later in this article. Table D of the supplemental report provides regional estimates of the MMR with and without AIDS-related deaths.
2.7.1 Simple Model
Our two-part estimation model includes a component, PMa, representing the proportion of AIDS deaths that qualify as indirect maternal deaths out of the total number of AIDS deaths among women aged 15–49. We adopted a very simple approach for estimating this proportion as the product of two quantities:
| (13) |
where v is the proportion of AIDS deaths occurring within the maternal risk period, and u is the fraction of such deaths that qualify as maternal because of some causal relationship with the pregnancy.
Although u must be chosen merely by assumption, it is possible to estimate the value of v for a given population by use of the following identity (see Appendix, section 5.1, for derivation):
| (14) |
where c is the average woman-years lived within the maternal risk period per live birth, and k is the relative risk of dying from AIDS for a pregnant versus a non-pregnant woman (where “pregnant” in this usage includes 42 days postpartum). Thus, the AIDS component of our estimation model includes three unknown parameters: c, k, and u.
2.7.2 Parameter Estimates and Assumptions
Since there was very little empirical information to guide the choice of these parameters, we were forced to choose values based on weak evidence in some cases and on no evidence at all in others. The values used for deriving final estimates are as follows: c = 1, k = 0.4, and u = 0.5.
The c parameter is the least challenging of the three, as it is determined mostly by the 9-month duration of gestation (approximately) for a human pregnancy plus the 42-day postpartum interval specified in the definition of a maternal death. Thus, if all pregnancies ended in live births, the value of c would be roughly 10.5 months. An additional 1.5 months were included to account for pregnancies ending in miscarriage, stillbirth, or abortion, or where the mother dies before delivery, yielding a total exposure-to-risk of one woman-year per live birth.
Since k is a relative risk, a value of one would imply that pregnant and non-pregnant women face equal risks of dying from AIDS. We have assumed, however, that k = 0.4 suggesting that pregnant women are, in fact, much less likely to die from AIDS than their non-pregnant counterparts. For a woman who is HIV-positive and symptomatic, the conditions of pregnancy may increase the risk of mortality due to AIDS, suggesting that perhaps k should be greater than one. However, since HIV-positive women, especially those with full-blown AIDS, are much less likely to become pregnant (Chen and Walker, 2010), the relative risk of an AIDS death for all pregnant versus all non-pregnant women seems likely to be less than one.
Our assumed value of k = 0.4 was chosen based in part on the analysis of deviance scores as a function of this parameter, as presented already in Figure 1. That analysis indicated that the model provides a somewhat better representation of the data when using values of k below 0.6. By this standard, a value of 0.3 would have been slightly closer to optimal than 0.4. Given a lack of direct evidence, however, we were doubtful about such an extreme assumption and thus chose 0.4 instead of 0.3.
Clearly, this goodness-of-fit criterion is rather imprecise (all values between 0 and 0.6 are close to optimal) and in general provides a weak basis for choosing this parameter. Nevertheless, in the absence of data permitting us to measure k directly, it was the only method available to us. We have learned more recently that some data from epidemiologic follow-up studies appear to be broadly consistent with our assumption for k (Garenne, 2011).
Furthermore, as shown in Table 6, the final global estimate of the number of maternal deaths from all causes (i.e., AIDS-related or not) is somewhat insensitive to the chosen value of k. As the assumed value of k increases from 0 to 1, the estimated number of AIDS-related maternal deaths goes up, while the number of maternal deaths unrelated to HIV/AIDS goes down. This tradeoff occurs because of the procedure for removing AIDS-related maternal deaths that was used in constructing the dependent variable of the multilevel model. With higher values of k, there are more AIDS-related deaths that occur during pregnancy (of which half are assumed to be true maternal deaths); however, higher values of k also mean that a larger fraction of deaths to pregnant women is removed from an observed value of PM before using that observation to fit the multilevel model, resulting in lower estimates of maternal mortality unrelated to HIV/AIDS.
Table 6.
Global estimates in 2008 of maternal deaths and pregnancy-related AIDS deaths as a function of parameter k
| k | Maternal deaths
|
Pregnancy-related AIDS deaths | ||
|---|---|---|---|---|
| Total | Non-AIDS | AIDS-related | ||
| 0.0 | 375,800 | 375,800 | 0 | 0 |
| 0.1 | 372,000 | 366,600 | 5,500 | 10,900 |
| 0.2 | 367,400 | 356,700 | 10,700 | 21,400 |
| 0.3 | 363,100 | 347,300 | 15,800 | 31,600 |
| 0.4 | 357,700 | 337,000 | 20,700 | 41,500 |
| 0.5 | 351,700 | 326,200 | 25,500 | 50,900 |
| 0.6 | 351,400 | 321,300 | 30,100 | 60,100 |
| 0.7 | 348,900 | 314,300 | 34,500 | 69,000 |
| 0.8 | 344,100 | 305,200 | 38,800 | 77,700 |
| 0.9 | 350,300 | 307,200 | 43,000 | 86,100 |
| 1.0 | 347,800 | 300,700 | 47,100 | 94,200 |
Note: For these calculations, all data inputs and parameter assumptions were held constant except for the value of k.
Lastly, it is worth emphasizing that the assumed value for u was chosen based on no evidence at all. As stated already, u represents the proportion of AIDS deaths occurring during pregnancy, delivery, or the puerperium that are linked to maternal causes and thus qualify as indirect maternal deaths. A simple representation of our framework for classifying pregnancy-related deaths into four categories is as follows:
| A) Maternal death, not AIDS-related | B) Maternal death, AIDS-related |
| C) Accidental/incidental death, not AIDS-related | D) Death due to AIDS, not aggravated by pregnancy |
At least in theory, the estimates described here include deaths in categories A and B only, but not in C and D. Categories B and D together comprise all pregnancy-related AIDS deaths, and the parameter u is the fraction of those deaths that we counted as maternal. Thus, u = B/(B +D).
Lacking hard evidence about the correct value, we chose to set u equal to one half. Within the possible range of zero to one, there are only two values of u that can be dismissed a priori as incorrect: zero and one. That is, we should assume that at least some AIDS deaths that occur among pregnant women have been complicated by the pregnancy, suggesting u > 0; conversely, it is implausible to suggest at all pregnancy-related AIDS deaths were more likely to occur, or occurred earlier, because the woman was pregnant, implying u < 1. In short, the correct value must lie somewhere between these two extremes. By setting u = 0.5, we minimize the size of the potential error associated with this parameter.
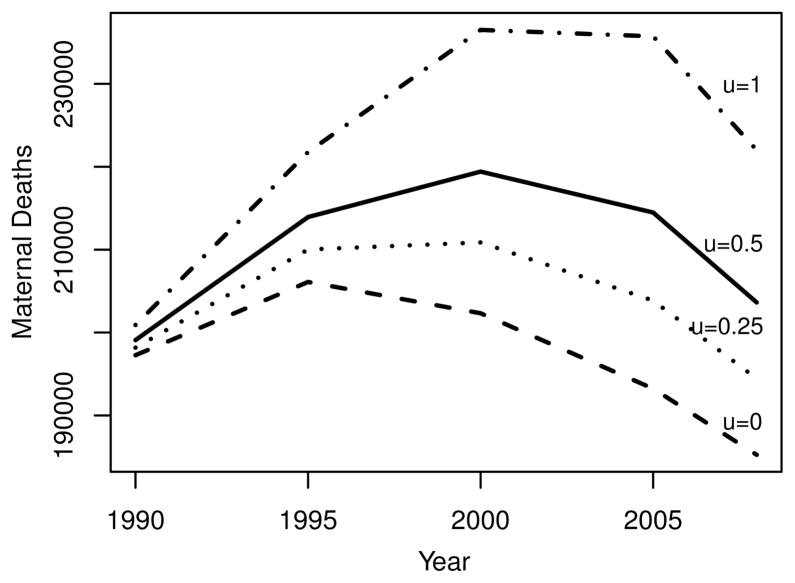
Final results for some countries or regions are quite sensitive to this choice, as illustrated in Figure 2, which shows estimated numbers of maternal deaths in Sub-Saharan Africa given four choices for u. In 2008, for example, the estimated total number of maternal deaths in this region varies from 185,000 to 222,000 depending on the value of u. Our preferred estimate (with u = 0.5) lies in the middle of this range at around 204,000. Thus, the maximum absolute error in this case is roughly 18,000 deaths, or around 9% of the central estimate.
Figure 2.
Total numbers of maternal deaths in Sub-Saharan Africa implied by different values of parameter u
Although it seems likely that the c, k, and u parameters may vary over time and across populations, given the weak empirical basis for making such decisions, we chose a single value for each and treated them as universal constants when deriving our best estimates. In addition to analyzing the sensitivity of the resulting estimates given alternative parameter assumptions, we have also studied the contribution of such choices to the overall uncertainty of estimation, as described in the next section.
2.8 Uncertainty of Estimates
The uncertainty of estimates was assessed by simulating the estimation process, accounting for variability both in the data on maternal mortality and in other model inputs. Uncertainty intervals for 1990 and 2008 estimates are given for regions in Table 1 of this article, and for individual countries in Table B of the supplemental report (Wilmoth et al., 2012).
In Table 7 we compare the (relative) widths of uncertainty intervals by country group. For all available intervals in a group (across countries and time), we computed the average ratio of upper and lower endpoints to the best estimate. The resulting values provide a sense of the relative size of the uncertainty intervals for various groups of countries. For example, the C countries – those with no data on maternal mortality – have typical uncertainty intervals that extend from around 40% of the best estimate to around 2.3 times the best estimate.
Table 7.
Mean ratio of uncertainty interval boundaries to best estimate by country group according to final evaluation of uncertainty
| Country Group | Mean Ratio
|
|
|---|---|---|
| Lower | Upper | |
| A | 0.81 | 1.27 |
| B | 0.58 | 1.72 |
| C | 0.43 | 2.34 |
| World | 0.64 | 1.64 |
Details of our uncertainty assessment are given in Wilmoth et al. (2012). Here, we provide an overview of the method and discuss key decisions that guided the analysis.
2.8.1 Overview of Calculations
We considered the following components of estimation uncertainty:
Uncertainty about factors used to adjust observed data;
Imprecise knowledge of key model parameters (c, k, u, and π);
Variability of data relative to the multilevel regression model (for B and C countries), or stochastic variability of vital registration data (for A countries);
Uncertainty about data inputs used for calculations that occur outside the regression model (estimated births, deaths, and fraction of AIDS deaths); and
Uncertainty related to alternative model choices (functional form, dependent variable, predictors).
In this analysis we quantify the uncertainty implied by (a) through (d) but not (e). Since (e) is not included in the evaluation, the resulting intervals represent a lower bound of the uncertainty inherent in our final estimates.
For (a), (b), and (d), we chose a set of a priori distributions to represent our uncertainty about the assumed values. These choices were based mostly on our own intuition, as appropriate empirical evidence is lacking. Sensitivity testing based on plausible alternative assumptions did not qualitatively change the main outcomes summarized here; this result is not surprising given that the bulk of the uncertainty resides within (c). For more information about the assumed distributions, see the supplemental report (Wilmoth et al., 2012).
Assumed distributions for items within (a), (b), and (d) were used to generate a number (N1 = 100) of model replicates. For each replicate the model was re-estimated using the slightly altered set of data and input parameters. Within each replicate, an additional number (N2 = 10) of simulations were performed to assess the impact of (c), using standard output from the multilevel regression analysis. Thus, the full simulation yielded a total of 1000 distinct outcomes (N1 * N2 = 100 * 10 = 1000).
Proceeding in this manner, simulated data were used to compute full sets of model estimates (for each time period in every country, region, and the world), reflecting the uncertainty of (a), (b), (c), and (d). From the distributions of simulated estimates, we derived 95% uncertainty intervals using the 2.5 and 97.5 percentiles.
In describing the simulations we performed to assess the uncertainty of our estimates, it is helpful to distinguish between sources of variability within the multilevel regression model (internal) and all other sources (external). This distinction helps to structure our analysis of the components of uncertainty, as presented here in Table 8. External uncertainty includes all elements listed above under points (a), (b), and (d), while internal uncertainty refers to (c).
Table 8.
Mean standard deviations of simulated log(MMR) estimates by country group according to various evaluations of uncertainty
| Scenario | Components of Uncertainty Included in Scenario
|
Standard Deviation of log(MMR) across 1000 Simulations
|
||||
|---|---|---|---|---|---|---|
| A countries | B & C countries | Country Group | ||||
| A | B | C | World | |||
| (1) | E | E | 0.068 | 0.092 | 0.073 | 0.081 |
| (2) | I | I | 0.219 | 0.248 | 0.410 | 0.260 |
| (3) | P | P | 0.335 | 0.324 | 0.342 | 0.330 |
| (4) | I, P | I, P | 0.399 | 0.409 | 0.534 | 0.423 |
| (5) | E, I | E, I | 0.235 | 0.280 | 0.432 | 0.285 |
| (6) | E, I, P | E, I, P | 0.417 | 0.439 | 0.557 | 0.448 |
| (7) | E, S | E, I | 0.117 | 0.280 | 0.432 | 0.241 |
- For each scenario (i.e., combination of components of uncertainty), the table presents the mean (across all countries in a set and across time) of the standard deviation of the estimated log(MMR) across 1000 simulations of the complete estimation procedure. The components of uncertainty are abbreviated as follows: E = External, I = Inferential, P = Prediction, S = Stochastic (S pertains to vital registration data only). See text for more explanation.
- For scenarios 2 thru 6, values for all countries were derived using the multilevel regression model (I and P components). Scenario 7 is equivalent to scenario 5, except that vital registration data and an estimate of their stochastic uncertainty are substituted for A countries only.
- The bottom row corresponds to the final evaluation of uncertainty proposed here. Thus, for a typical country with VR data, the uncertainty range for the MMR extends from around 0.79 (=exp(−2 * 0.117)) to around 1.26 (=exp(2 * 0.117)) multiplied times its estimated value; for a country with other forms of data, from around 0.57 to around 1.75; for a country without data, from around 0.42 to around 2.3 (note similarity to mean ratios of Table 7).
2.8.2 Uncertainty of Estimates from the Multilevel Regression Model
For the analysis of internal uncertainty via simulation, we followed closely the framework of Gelman and Hill (2007). We distinguished between inferential and predictive uncertainty of the multilevel model in a manner that seems appropriate for our particular problem. Inferential uncertainty was defined to include variability in all elements of the model used for deriving best estimates for individual countries. Thus, for B countries (those with some available data and whose estimates are derived from the model), the sources of inferential uncertainty are variability in estimates of the β, αC, and αR parameters; for C countries (those with no available data and whose estimates are derived from the model), an additional source of inferential uncertainty is the variability associated with a single draw from the normal distribution assumed to have generated the observed country effects (whose variance is given in the second row of Table 5). In other contexts this last component might be associated with predictive uncertainty; here, because it adds to the uncertainty of estimates for the C countries, it is included as a component of inferential uncertainty for those countries only.
For both B and C countries, the predictive uncertainty of the model was simulated by a single draw from a normal distribution with variance as given in the first row of Table 5. Because we wish to assess the uncertainty of estimation, not the uncertainty associated with one additional data point, we did not include this component of uncertainty in our final evaluation.
2.8.3 Uncertainty of Estimates from Vital Registration Data
Our assessment of estimation uncertainty for the A countries also included two components: random variation in maternal death counts from vital registration data (stochastic) and variability due to other inputs and assumptions (external). The stochastic component of uncertainty was simulated using an approximation for the variance of log(PM) (see supplemental report for details).
2.8.4 Relative Importance of Uncertainty Components
Table 8 documents the magnitude of uncertainty by country group that is attributable to the various components of variability. In this case we express uncertainty in terms of the mean standard deviation of the simulated estimates of log(MMR) across countries and time periods. Note 3 of Table 8 explains the simple relationship that links this quantity to the typical uncertainty intervals presented in Table 7.
The first three rows of Table 8 show the uncertainty due to the external, inferential, and predictive components alone. The remaining rows show various combinations of these three elements. Our final evaluation of uncertainty (scenario 7) includes the external and inferential components for B and C countries, while substituting a direct calculation of stochastic variability for the A countries.
Four main conclusion emerge from this analysis. First, the external component is relatively small compared to either the inferential or predictive components. Thus, the uncertainty due to choices of adjustment factors and unknown parameters appears rather small compared to the variability of observed data points around predictions of the regression model.
Second, there appears to be a slight positive correlation between errors in the external and inferential components. If the two components were independent, we would expect the standard deviations for scenario 5 to be roughly the square root of the sum of squared values for scenarios 1 and 2. Calculations show, however, that the simulated variability is somewhat greater than predicted under a model of independence, suggesting a slight positive correlation of errors in these two components: simulated values for the fifth scenario (0.235, 0, .280, 0.432, and 0.285) slightly exceed those expected under an assumption of independence (0.229, 0.265, 0.416, and 0.272). This result seems inconsistent with our earlier observation of the countervailing effects of changes in the k parameter on estimates of non-AIDS and AIDS-related maternal deaths. For unknown reasons, there is overall a slight compounding rather than cancellation of errors. In contrast (and as expected), the inferential and predictive components appear to be fully independent.
Third, the gain in precision when using vital registration data for A countries versus the multilevel model (scenario 7 versus 5) is perhaps smaller than one might expect. Uncertainty intervals for A countries based on the multilevel model would be roughly from 0.6 to 1.6 times the best estimate, whereas those based on vital registration data are from 0.8 to 1.3 (see Note 3 of Table 8, and compare Table 7).
Fourth, when considering the plausibility of future observations of the MMR for B and C countries, it is important to bear in mind that the uncertainty intervals presented here do not include the predictive uncertainty in relation to future observations. From scenario 6 of Table 8, we can infer that typical predictive intervals (for individual observations) would extend from 0.4 to 2.4 times the best estimate for B countries, and from 0.3 to 3.0 for C countries. In contrast, our final uncertainty intervals (as reported in Table 7, or as implied by scenario 7 of Table 8) extend from 0.6 to 1.7, and from 0.4 to 2.3, respectively.
3 DISCUSSION
The estimates described here were derived using the best available data, and with methods chosen to exploit those data as fully as possible. Nonetheless, the numbers that emerge from this exercise are subject to important limitations and differ – substantially in some cases – from other evaluations of essentially the same information.
3.1 Limitations Due to Sparse Data
It is important to note that the underlying data are sparse. In the dataset we used for this analysis, there were an average of 2.8 observations per country from the late 1980s until 2008. However, most of the available data pertain to countries with low levels of maternal mortality. Among those with an estimated maternal mortality ratio of 100 or more in 2008, the average number of input data points was only 1.9.
In short, the reality of sparse and imperfect data has shaped the production and now the interpretation of global estimates of maternal mortality. Existing data limitations led us to create a complex model with several unknown parameters. The model was used to derive estimates for most countries, but those estimates depend also on several weakly justified assumptions regarding certain input parameters that must be specified a priori. As we have shown earlier, in some cases the sensitivity of final results to specific choices is not great, but in others it is quite important. Furthermore, estimates generated in this manner have other inherent limitations, including distortions due to trends in predictor variables for some countries.
3.2 Influence of Trends in Predictor Variables
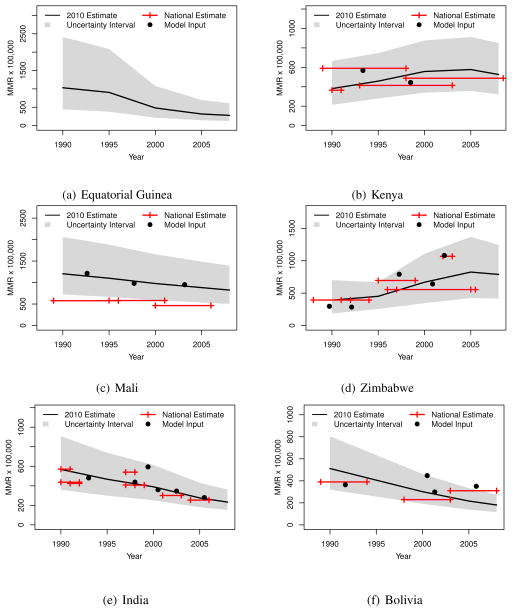
Figure 3 presents trends in the estimated maternal mortality ratio for six countries. The shaded area around each trend depicts a 95% uncertainty interval. Input data points used in this study are shown as black dots plotted at interval midpoints (these observations include any relevant adjustments, including for AIDS-related maternal deaths, making them comparable to final estimates). For comparison, official national estimates drawn from a separate database maintained by UNICEF are shown as horizontal bars (the horizontal extension of each bar depicts the associated time interval).
Figure 3.
Six country examples of the estimated maternal mortality ratio, with 95% uncertainty intervals and national estimates, 1990–2008 (Note: National estimates, from a separate database maintained by UNICEF, are shown here with reference time intervals. Model inputs, from original sources but with various adjustments, refer to similar intervals, but each is plotted here as a dot at the interval midpoint. In addition to differences of level as discussed in the text, the two collections disagree slightly in certain cases regarding the exact time reference for a given estimate.)
For countries where we use the regression model to derive estimates of the MMR, trends in those estimates are driven entirely by trends in the three predictor variables: GDP, GFR, and SAB. In many cases, such trends seem plausible: for example, Mali (Figure 3c), India (3e), and Bolivia (3f). In some cases, however, rapid changes in predictor variables have yielded trend estimates that seem less plausible. In Equatorial Guinea (3a), for example, the petroleum boom of the late 1990s produced a rapid increase in GDP per capita; the sudden upturn in GDP, combined with an unusually rapid rise in the estimated level of SAB, has resulted in a sharp drop in the estimated MMR. In contrast, for Kenya (3b) the economic crisis of the 1990s produced what seems to be an implausibly large rise in the MMR.
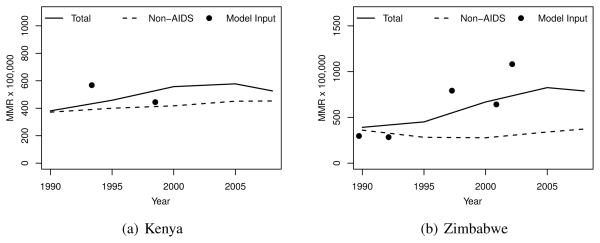
For countries heavily affected by the HIV/AIDS epidemic, the contribution of AIDS-related maternal deaths is often quite significant. The increasing MMR trend for Zimbabwe is quite noticeable but also entirely consistent with available data (Figures 3d); for this country the HIV epidemic is the major cause of the increase of the MMR over this period (Figure 4b). For Kenya, on the other hand, the HIV epidemic was a contributing factor to the increase in the MMR, but it cannot explain the adverse trend on its own (4a).
Figure 4.
Two country examples of the estimated maternal mortality ratio with and without AIDS-related maternal deaths, 1990–2008
3.3 Comparison to National Estimates
As noted above, Figure 3 shows the MMR values corresponding to the adjusted PM data points that served as inputs to the estimation model described above. For countries affected by HIV, these MMR values include the AIDS component of the MMR. It is reassuring that there is a good correspondence in most cases between these input data point and the trends estimated by the model.
However, in some cases there is a notable disagreement between the new estimates described here and previously published national estimates (UNICEF, 2010). Among the examples shown in Figure 3, disagreement is most severe for Mali, which is typical in this regard of many countries for which the underlying data consisted primarily of survey data collected using the (direct) sisterhood method. The disparity in these cases is due to a tendency toward under-estimation of all-cause mortality when using such data (Stanton et al., 2000, Gakidou and King, 2006). The “national estimates” are typically derived from published DHS reports (e.g., CPS/MS et al., 2002, 2007), which do not correct for this known problem.
The estimates presented here are derived from the same data source but include an implicit correction for the under-estimation of all-cause mortality. Thus, many differences in comparison to existing national estimates are due to our method of modeling the proportion of maternal deaths (PM), which is then converted into an estimate of the maternal mortality ratio (MMR) using external estimates of numbers of live births and of deaths from all causes for women aged 15–49.
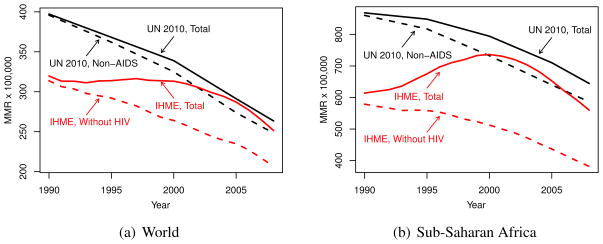
3.4 Comparison to IHME Estimates
Lastly, we present a brief comparison of the two sets of maternal mortality estimates that were published in 2010 (Hogan et al., 2010, World Health Organization et al., 2010). The first set is called the IHME estimates as they were produced at the Institute for Health Metrics and Evaluation of the University of Washington in Seattle. Figure 5 illustrates that there was both a level difference in 1990 and a trend difference over the period from 1990 to 2008 between 2010 IHME and UN estimates. At a global level, it is clear that most of the trend difference resulted from distinctive choices about how to describe the interaction between maternal causes of death and HIV/AIDS: the trends were much more similar when comparing the “non-AIDS estimates” of the UN group to the “no-HIV scenario” of Hogan and colleagues. In short the IHME estimate of total maternal deaths in 2008 included many more AIDS or AIDS-related deaths than did the UN estimate.
Figure 5.
Estimated maternal mortality ratio with and without AIDS-related maternal deaths, and IHME estimates with and without HIV, 1990–2008
If the trend difference was caused mostly by the treatment of HIV/AIDS, the level difference between the two sets of estimates (in 1990, though diminishing thereafter) appears to have been caused mostly by the use of different input values of all-cause mortality among women aged 15–49. Figure A of the supplemental report compares the two sets of adult female mortality estimates by region and over time. The most dramatic difference was for South Asia, where the 2010 IHME estimates were from 20 to 30% lower than the 2010 WHO estimates used for the UN analysis of maternal mortality described here. There were smaller but still notable differences in the same direction for Southeast Asia and Sub-Saharan Africa.
The IHME released a new set of maternal mortality estimates in 2011 (Lozano et al., 2011). A full review of the methodological or substantive changes between the 2010 and 2011 IHME estimates is beyond the scope of this article. Nevertheless, it is worth noting that the 2011 IHME estimates (unlike their 2010 counterparts) were derived using the method described both here and previously (Wilmoth et al., 2010) for estimating AIDS-related maternal deaths, but with k = 1 rather than 0.4 and with u = 1 instead of 0.5.
A more detailed comparison of the various sets of estimates has been impossible because the IHME data and programs have not been made available for public scrutiny. Questions of how to move forward in a world with competing sets of global maternal mortality estimates has been a topic of discussion on several recent occasions, including a collection of essays in the November 2010 issue of PLOS Medicine. Abouzahr (2011) offers a more detailed looked at differences between the UN and IHME estimates. Like our own analysis, however, hers was handicapped by lack of access to the data used in creating the IHME estimates. By contrast, the data and programs used for creating the UN estimates have been publicly available since the day those estimates were released in September 2010.
4 CONCLUSION
The estimation procedure described here was developed in response to a call by UN Member States to prioritize the monitoring of maternal mortality levels and trends. It is important to derive such estimates using the best available data and methods. However, it is also important to be modest and honest about the limitations of our knowledge in this area. More and better data are needed but will become available only slowly in the coming years, especially for the most affected countries. Improved methods are surely possible as well but cannot overcome the inherent limitations imposed by the underlying data.
For better or worse, all existing estimates of levels and trends in maternal mortality provide no more than an image of a reality that may have been. The image presented here is consistent with the available data and is plausible based on widely observed correlations between various measures of health and socioeconomic development. This kind of analysis serves an important purpose but is no substitute for a well-functioning civil registration system, which offers the most reliable method available for measuring levels and tracking trends in maternal mortality over time.
The major substantive result of this work is that the risk of maternal mortality per live birth appears to have been declining more rapidly in recent decades than had been found previously, including another study conducted in the same year (Hogan et al., 2010). In this paper we have quantified the uncertainty of the estimated rate of decline. Thus, for the world as a whole from 1990 to 2008, we estimate that the average annual rate of decline in the MMR was 2.3% (95% UI, 1.8–2.8%). For major world regions, the estimated rate of decline varies considerably, from over 4% in most parts of Asia, to less than 2% in Sub-Saharan Africa and under 1% in developed countries.
We have also analyzed the components of estimation uncertainty in this paper, concluding that the largest part of that uncertainty results from variability of the observed data around predictions of the multilevel regression model. In comparison, the uncertainty due to assumed values of those model parameters that must be specified a priori appears to be much less important.
Finally, we compared our estimates to those published in 2010 by the IHME (Hogan et al., 2010). Although a precise comparison was not possible since the full data from that exercise are not publicly available, we were able to pinpoint two major sources of the discrepancy between the two sets of estimates at a global level: a different treatment of AIDS-related maternal deaths and different estimates of all-cause female mortality during reproductive ages.
Future work in this area could include further refinements of the current model, especially with regard to alternative or additional predictor variables, and perhaps also the choices of regional groupings. Alternative modeling strategies should be explored as well, including the methods of spatial statistics, which may offer improvements in goodness-of-fit and/or greater flexibility in the use of data for both national and sub-national populations. Estimation uncertainty could be explored by other means, including cross-validation exercises. An analysis of differential trends by age groups might be desirable as well, though perhaps inconclusive given data limitations.
Acknowledgments
Funding for the project was provided by the World Health Organization, The World Bank Netherlands Partnership Program, the MacArthur Foundation, and the U.S. National Institute on Aging (R01 AG11552 and R01 AG033713).
5 APPENDIX
5.1 AIDS Deaths among Pregnant Women
Equation (14) states that the proportion of AIDS deaths occurring during the maternal risk period, v, can be expressed in terms of the general fertility rate (GFR) and two unknown parameters, c and k, where c is the average woman-years lived within the maternal risk period per live birth, and k is the relative risk of dying from AIDS for a pregnant versus a non-pregnant woman (where “pregnant” and “pregnancy” in this usage includes delivery and the puerperium).
For a given time period, let W represent the number of woman-years lived at ages 15–49, which can be divided between time spent in or out of pregnancy: W =W p +W p′. Similarly, let Da represent the number of deaths from AIDS among women aged 15–49 during the same time period, which also can be divided into those occurring among pregnant and non-pregnant women: .
Let and be the death rates due to AIDS for pregnant and non-pregnant women, respectively. Also, let B represent the number of live births occurring during the period in question. Then, noting that W p = cB and , it follows that and that .
Finally, noting that GFR = B/W, it follows that:
| (15) |
5.2 Computing Rates of Decline
The “average annual decline” of Table 1 was computed using the following formula:
| (16) |
where t1 and t2 are denoted in years (in this case t1 = 1990 and t2 = 2008). Since , this quantity gives the “average annualized rate of decline” or the “average annual rate of decline.”
In Table 1 it may appear inaccurate that the average rate of decline for Africa as a whole (1.6%) does not lie between the comparable values for Sub-Saharan Africa (1.7%) and Northern Africa (5.0%). Nevertheless, the results are correct as presented. The apparent anomaly can be understood by noting that
| (17) |
where MMR1(t) and MMR2(t) are the MMR at time t for Sub-Saharan Africa and Northern Africa, respectively, and where f (t) = B1(t)/B(t) is the fraction of African births occurring in the former sub-region. Therefore,
| (18) |
Thus, at any moment the change in MMR(t) equals the weighted average of changes in the MMR for the two sub-populations, plus a third component that depends on the change in f (t) and the size of the gap between the two MMR values. In relatively extreme cases (like this one) with a rapid change in f (t) and a large gap between the MMR for the two sub-regions, the third term of equation (18) may cause the rate of change for the population to lie outside the range for the two sub-populations. Within Asia the shift in the distribution of births from the Eastern to the Southern sub-region, combined with a large MMR gap, results in a similar phenomenon: the average rate of decline for the entire region, 4.0% per annum, lies at the lower extremity of the range of sub-regional values.
Footnotes
The views expressed in this article are the responsibility of the authors and do not necessarily represent those of the World Health Organization or its member countries.
Contributor Information
John R. Wilmoth, Department of Demography, University of California, Berkeley
Nobuko Mizoguchi, Institute of Behavioral Science, University of Colorado, Boulder.
Mikkel Z. Oestergaard, World Health Organization
Lale Say, World Health Organization.
Colin D. Mathers, World Health Organization
Sarah Zureick-Brown, Department of Global Health, Emory University.
Mie Inoue, World Health Organization.
Doris Chou, World Health Organization.
References
- Abouzahr C. New estimates of maternal mortality and how to interpret them: choice or confusion? Reprod Health Matters. 2011;19(37):117–128. doi: 10.1016/S0968-8080(11)37550-7. [DOI] [PubMed] [Google Scholar]
- Bates D, Maechler M, Bolker B. R package version 0.999375-42. 2011. lme4: Linear mixed-effects models using S4 classes. [Google Scholar]
- Cellule de Planification et de Statistique du Ministère de la Santé (CPS/MS), Direction Nationale de la Statistique et de l’Informatique (DNSI), and ORC Macro. Enquête Démographique et de Santé au Mali 2001. CPS/DNSI and ORC Macro; Calverton, Maryland, USA: 2002. [Google Scholar]
- Cellule de Planification et de Statistique du Ministère de la Santé (CPS/MS), Direction Nationale de la Statistique et de l’Informatique du Ministére de l’Économie, de l’Industrie et du Commerce (DNSI/MEIC), and Macro International Inc. Enquête Démographique et de Santé au Mali 2006. CPS/DNSI and Macro International Inc; Calverton, Maryland, USA: 2007. [Google Scholar]
- Chen W, Walker N. Fertility of HIV-infected women: insights from demographic and health surveys. Sexually Transmitted Infections. 2010;86(Suppl 2):ii22–ii27. doi: 10.1136/sti.2010.043620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gakidou E, King G. Death by survey: estimating adult mortality without selection bias from sibling survival data. Demography. 2006;43(3):569–585. doi: 10.1353/dem.2006.0024. [DOI] [PubMed] [Google Scholar]
- Garenne M. Estimating obstetric mortality from pregnancy-related deaths recorded in demographic censuses and surveys. Stud Fam Plann. 2011;42(4):237–246. doi: 10.1111/j.1728-4465.2011.00287.x. [DOI] [PubMed] [Google Scholar]
- Gelman A, Hill J. Data analysis using regression and multilevel/hierarchical models. Cambridge University Press; New York: 2007. [Google Scholar]
- Hakkert R. Country estimates of maternal mortality: an alternative model. Statistics in Medicine. 2001;20(23):3505–3524. doi: 10.1002/sim.1075. [DOI] [PubMed] [Google Scholar]
- Hill K, Thomas K, AbouZahr C, Walker N, Say L, Inoue M, Suzuki E Maternal Mortality Working Group. Estimates of maternal mortality worldwide between 1990 and 2005: an assessment of available data. Lancet. 2007;370(9595):1311–1319. doi: 10.1016/S0140-6736(07)61572-4. [DOI] [PubMed] [Google Scholar]
- Hogan MC, Foreman KJ, Naghavi M, Ahn SY, Wang M, Makela SM, Lopez AD, Lozano R, Murray CJ. Maternal mortality for 181 countries, 1980–2008: a systematic analysis of progress towards Millennium Development Goal 5. Lancet. 2010;375(9726):1609–1623. doi: 10.1016/S0140-6736(10)60518-1. [DOI] [PubMed] [Google Scholar]
- Lozano R, Wang H, Foreman KJ, Rajaratnam JK, Naghavi M, Marcus JR, Dwyer-Lindgren L, Lofgren KT, Phillips D, Atkinson C, Lopez AD, Murray CJL. Progress towards millennium development goals 4 and 5 on maternal and child mortality: an updated systematic analysis. Lancet. 2011;378(9797):1139–1165. doi: 10.1016/S0140-6736(11)61337-8. [DOI] [PubMed] [Google Scholar]
- Mathers CD, Fat DM, Inoue M, Rao C, Lopez AD. Counting the dead and what they died from: an assessment of the global status of cause of death data. Bulletin of the World Health Organization. 2005;83(3):171–177. [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2011. [Google Scholar]
- Stanton C, Abderrahim N, Hill K. An assessment of DHS maternal mortality indicators. Stud Fam Plann. 2000;31(2):111–123. doi: 10.1111/j.1728-4465.2000.00111.x. [DOI] [PubMed] [Google Scholar]
- UNAIDS. Report on the global HIV/AIDS epidemic 2008. UNAIDS; Geneva: 2008. [Google Scholar]
- UNICEF. [Accessed 5 March 2010];UNICEF global databases 2010. 2010 http://www.childinfo.org/deliverycarecountrydata.php.
- United Nations Population Division. World population prospects, 2008 revision. United Nations; New York: 2009. [Google Scholar]
- Wilmoth J, Mizoguchi N, Oestergaard M, Say L, Mathers C, Zureick-Brown S, Inoue M, Chou D. A new method for deriving global estimates of maternal mortality: Supplemental report. 2012 doi: 10.1515/2151-7509.1038. Available online from Statistics, Politics and Policy, http://www.degruyter.com/view/j/spp. [DOI] [PMC free article] [PubMed]
- Wilmoth J, Zureick S, Mizoguchi N, Inoue M, Oestergaard M. Technical report. 2010. Levels and trends of maternal mortality in the world: The development of new estimates by the United Nations. submitted to WHO, UNICEF, UNFPA, and The World Bank. [Google Scholar]
- World Health Organization. International statistical classification of diseases and related health problems: Instruction manual. World Health Organization; Geneva: 2004. [Google Scholar]
- World Health Organization. [Accessed 10 July 2010];Life tables for WHO member states. 2010 http://www.who.int/healthinfo/statistics/mortalitylifetables/en/
- World Health Organization, UNICEF, UNFPA, and The World Bank. Maternal mortality in 2005. Estimates developed by WHO, UNICEF, UNFPA and The World Bank. World Health Organization; Geneva: 2007. [Google Scholar]
- World Health Organization, UNICEF, UNFPA, and The World Bank. Trends in maternal mortality: 1990 to 2008. Estimates developed by WHO, UNICEF, UNFPA and The World Bank. World Health Organization; Geneva: 2010. http://www.who.int/reproductivehealth/publications/monitoring/9789241500265/en/ [Google Scholar]
- Zureick-Brown S, Newby H, Chou D, Mizoguchi N, Say L, Suzuki E, Wilmoth J. Understanding global trends in maternal mortality. International Perspectives on Sexual and Reproductive Health. 2012 doi: 10.1363/3903213. forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]