Vector Diffusion Maps and the Connection Laplacian

Abstract

We introduce vector diffusion maps (VDM), a new mathematical framework for organizing and analyzing massive high-dimensional data sets, images, and shapes. VDM is a mathematical and algorithmic generalization of diffusion maps and other nonlinear dimensionality reduction methods, such as LLE, ISOMAP, and Laplacian eigenmaps. While existing methods are either directly or indirectly related to the heat kernel for functions over the data, VDM is based on the heat kernel for vector fields. VDM provides tools for organizing complex data sets, embedding them in a low-dimensional space, and interpolating and regressing vector fields over the data. In particular, it equips the data with a metric, which we refer to as the vector diffusion distance. In the manifold learning setup, where the data set is distributed on a low-dimensional manifold ℳ^d embedded in ℝ^p, we prove the relation between VDM and the connection Laplacian operator for vector fields over the manifold.

1 Introduction

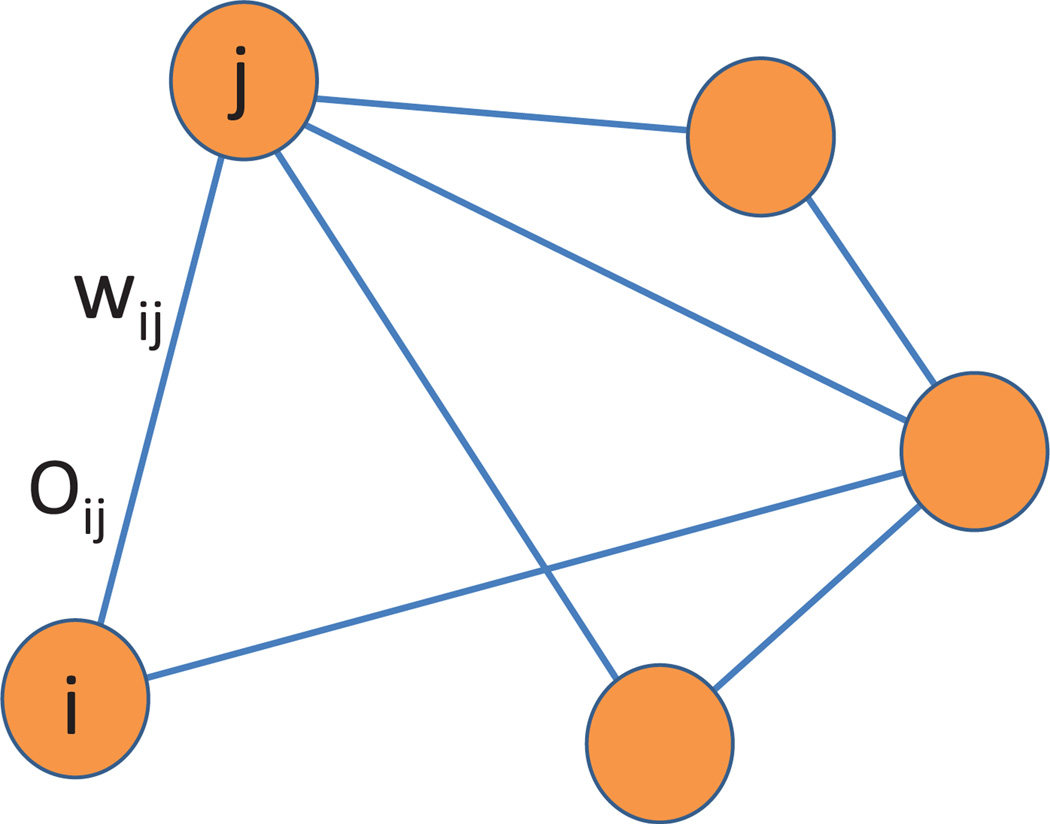
A popular way to describe the affinities between data points is using a weighted graph, whose vertices correspond to the data points, edges that connect data points with large enough affinities, and weights that quantify the affinities. In the past decade we have witnessed the emergence of nonlinear dimensionality reduction methods, such as locally linear embedding (LLE) [33], ISOMAP [39], Hessian LLE [12], local tangent space alignment (LTSA) [42], Laplacian eigenmaps [2], and diffusion maps [9]. These methods use the local affinities in the weighted graph to learn its global features. They provide invaluable tools for organizing complex networks and data sets, embedding them in a low-dimensional space, and studying and regressing functions over graphs. Inspired by recent developments in the mathematical theory of cryo-electron microscopy [18, 37] and synchronization [10, 35], in this paper we demonstrate that in many applications, the representation of the data set can be vastly improved by attaching to every edge of the graph not only a weight but also a linear orthogonal transformation (see Figure 1.1).

Figure 1.1.

In VDM, the relationships between data points are represented as a weighted graph, where the weights w_ij are accompanied by linear orthogonal transformations O_ij.

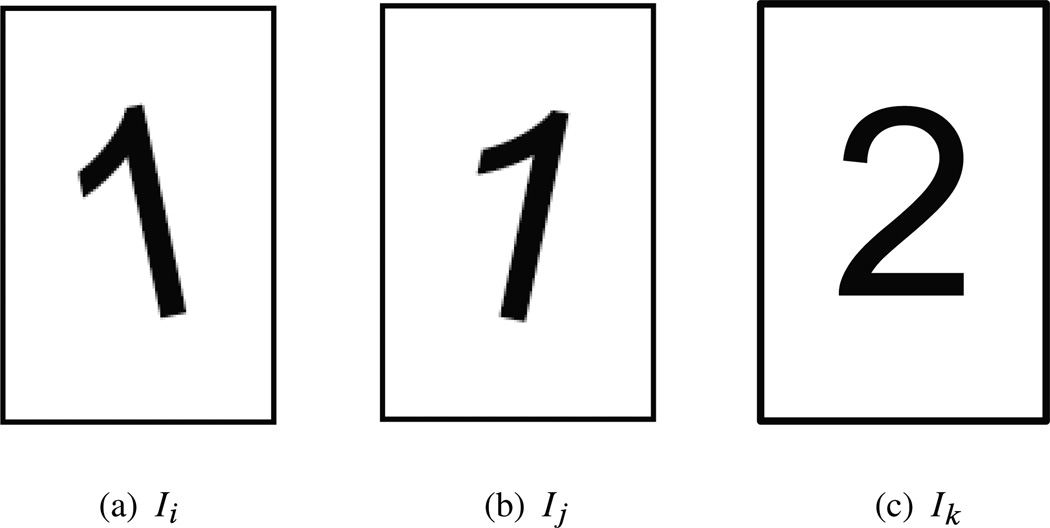
Consider, for example, a data set of images, or small patches extracted from images (see, e.g., [8, 27]). While weights are usually derived from the pairwise comparison of the images in their original representation, we instead associate the weight w_ij to the similarity between image i and image j when they are optimally rotationally aligned. The dissimilarity between images when they are optimally rotationally aligned is sometimes called the rotationally invariant distance [31]. We further define the linear transformation O_ij as the 2 × 2 orthogonal transformation that registers the two images (see Figure 1.2). Similarly, for data sets consisting of three-dimensional shapes, O_ij encodes the optimal 3 × 3 orthogonal registration transformation. In the case of manifold learning, the linear transformations can be constructed using local principal component analysis (PCA) and alignment, as discussed in Section 2.

Figure 1.2.

An example of a weighted graph with orthogonal transformations: I_i and I_j are two different images of the digit 1, corresponding to nodes i and j in the graph. O_ij is the 2 × 2 rotation matrix that rotationally aligns I_j with I_i and w_ij is some measure for the affinity between the two images when they are optimally aligned. The affinity w_ij is large, because the images I_i and O_ijI_j are actually the same. On the other hand, I_k is an image of the digit 2, and the discrepancy between I_k and I_i is large even when these images are optimally aligned. As a result, the affinity w_ik would be small, perhaps so small that there is no edge in the graph connecting nodes i and k. The matrix O_ik is clearly not as meaningful as O_ij. If there is no edge between i and k, then O_ik is not represented in the weighted graph.

In this paper, the linear transformations relating data points are restricted to orthogonal transformations in O(d). Transformations belonging to other matrix groups, such as translations and dilations, are not treated here.

While diffusion maps and other nonlinear dimensionality reduction methods are either directly or indirectly related to the heat kernel for functions over the data, our VDM framework is based on the heat kernel for vector fields. We construct this kernel from the weighted graph and the orthogonal transformations. Through the spectral decomposition of this kernel, VDM defines an embedding of the data in a Hilbert space. In particular, it defines a metric for the data, that is, distances between data points that we call vector diffusion distances. For some applications, the vector diffusion metric is more meaningful than currently used metrics, since it takes into account the linear transformations, and as a result, it provides a better organization of the data. In the manifold learning setup, we prove a convergence theorem illuminating the relation between VDM and the connection Laplacian operator for vector fields over the manifold.

The paper is organized in the following way: First, Table 1.1 summarizes the notation used throughout this paper. In Section 2 we describe the manifold learning setup and a procedure to extract the orthogonal transformations from a point cloud scattered in a high-dimensional euclidean space using local PCA and alignment. In Section 3 we specify the vector diffusion mapping of the data set into a finite-dimensional Hilbert space. At the heart of the vector diffusion mapping construction lies a certain symmetric matrix that can be normalized in slightly different ways. Different normalizations lead to different embeddings, as discussed in Section 4. These normalizations resemble the normalizations of the graph Laplacian in spectral graph theory and spectral clustering algorithms. In the manifold learning setup, it is known that when the point cloud is uniformly sampled from a low-dimensional Riemannian manifold, then the normalized graph Laplacian approximates the Laplace-Beltrami operator for scalar functions. In Section 5 we formulate a similar result, stated as Theorem 5.3, for the convergence of the appropriately normalized vector diffusion mapping matrix to the connection Laplacian operator for vector fields.¹

TABLE 1.1.

Summary of symbols used throughout the paper.

Symbol	Meaning
p	Dimension of the ambient euclidean space
d	Dimension of the low-dimensional Riemannian manifold
ℳd	d-dimensional Riemannian manifold embedded in ℝp
ι	Embedding of ℳd into ℝp
g	Metric of ℳ induced from ℝp
dV	Volume form associated with the metric g
n	Number of data points sampled from ℳd
x1 …,xn	Points sampled from ℳd
expx	Exponential map at x
Δ	Laplace-Beltrami operator
Tℳ	Tangent bundle of ℳ
Txℳ	Tangent space to ℳ at x
X	Vector field
Ck(Tℳ)	Space of kth continuously differentiable vector fields, k = 1,2,…
L2(Tℳ)	Space of squared-integrable vector fields
Px,y	Parallel transport from y to x along the geodesic linking them
∇	Connection of the tangent bundle
∇2	Connection (rough) Laplacian
et∇2	Heat kernel associated with the connection Laplacian
ℛ	Riemannain curvature tensor
Ric	Ricci curvature
s	Scalar curvature
Π	Second fundamental form of the embedding ι
K, KPCA	Kernel functions
∊,∊PCA	Bandwidth parameters of the kernel functions

The proof of Theorem 5.3 appears in Appendix B. We verify Theorem 5.3 numerically for spheres of different dimensions, as reported in Section 6 and Appendix C. We also use other surfaces to perform numerical comparisons between the vector diffusion distance, the diffusion distance, and the geodesic distance. In Section 7 we briefly discuss out-of-sample extrapolation of vector fields via the Nyström extension scheme. The role played by the heat kernel of the connection Laplacian is discussed in Section 8. We use the well-known short-time asymptotic expansion of the heat kernel to show the relationship between vector diffusion distances and geodesic distances for nearby points. In Section 9 we briefly discuss the application of VDM to cryo-electron microscopy, as a prototypical multireference rotational alignment problem. We conclude in Section 10 with a summary followed by a discussion of some other possible applications and extensions of the mathematical framework.

2 Data Sampled from a Riemannian Manifold

One of the main objectives in the analysis of a high-dimensional large data set is to learn its geometric and topological structure. Even though the data itself is parametrized as a point cloud in a high-dimensional ambient space ℝ^pthe correlation between parameters often suggests the popular “manifold assumption” that the data points are distributed on (or near) a single low-dimensional Riemannian manifold ℳ^d embedded in ℝ^p, where d is the dimension of the manifold and d ≪ p. Suppose that the point cloud consists of n data points x₁; x₂, …, x_n that are viewed as points in ℝ^p but are restricted to the manifold.

We now describe how the orthogonal transformations O_ij can be constructed from the point cloud using local PCA and alignment.

Local PCA. For every data point x_i we suggest estimating a basis to the tangent plane T_xiℳ to the manifold at x_i using the following procedure, which we refer to as local PCA. We fix a scale parameter ∊_PCA > 0 and define 𝒩_{xi, ∊PCA} as the neighbors of x_i inside a ball of radius $\sqrt{{\epsilon }_{\text{PCA}}}$ centered at x_i:

$${𝒩}_{x_i,{\epsilon }_{\text{PCA}}}=\{x_j:0<{\Vert x_j-x_i\Vert }_{{ℝ}^p}<\sqrt{{\epsilon }_{\text{PCA}}}\}.$$

Denote the number of neighboring points of x_i by N_i,² that is, N_i |𝒩x_i, ∊_PCA|, and denote the neighbors of x_i by x_i1, x_i2, …, x_iNi. We assume that ∊_PCA is large enough so that N_i ≥ d, but at the same time ∊_PCA is small enough such that N_i ≪ n. At this point we assume d is known; methods to estimate it will be discussed later in this section. In Theorem B.1 we show that a satisfactory choice for ∊_PCA is given by ∊_PCA = O(n^−2/(d+1)), so that N_i = O(n^1/(d+1)). In fact, it is even possible to choose ∊_PCA = O (n^−2/(d+2)) if the manifold does not have a boundary.

Observe that the neighboring points are located near T_xiℳ, where deviations are possible due to curvature. Define X_i to be a p × N_i matrix whose j_th column is the vector x_ij – x_i that is,

$$X_i=[x_{i_1}-x_i{x}_{i_2}-x_i\cdots x_{i_{N_i}}-x_i].$$

In other words, X_i is the data matrix of the neighbors shifted to be centered at the point x_i. Notice that while it is more common to shift the data for PCA by the mean ${\mu }_i=\frac{1}{N_i}{\mathrm{\Sigma }}_{j=1}^{N_i}{x}_{i_j}$, here we shift the data by x_i. Shifting the data by µ_i is also possible for all practical purposes, but has the slight disadvantage of complicating the proof for the convergence of the local PCA step (see Appendix B.1).

The local covariance matrix corresponding to the neighbors of x_i is $X_i{X}_i^{\mathrm{{\rm T}}}$. Among the neighbors, those that are further away from x_i contribute the most to the covariance matrix. However, if the manifold is not flat at x_i then we would like to give more emphasis to the nearby points, so that the tangent space estimation is more accurate. In order to give more emphasis to nearby points, we weigh the contribution of each point by a monotonically decreasing function of its distance from x_i. Let K_PCA be a C² positive monotonic decreasing function with support on the interval [0, 1], for example, the Epanechnikov kernel K_PCA(u) = (1–u₂)χ_[0,1], where χ is the indicator function. Let D_i be an N_i × N_i diagonal matrix with

$$D_i(j,j)=\sqrt{K_{\text{PCA}}\left(\frac{{\Vert x_i-x_{i_j}\Vert }_{{ℝ}^p}}{\sqrt{{\epsilon }_{\text{PCA}}}}\right)},j=1,2,\dots ,N_i,$$

and define the p × N_i matrix B_i as

$$B_i=X_i{D}_i.$$ (2.1)

The local weighted covariance matrix at x_i, which we denote by Ξ_i is

$${\mathrm{\Xi }}_i=B_i{B}_i^{\mathrm{{\rm T}}}=\sum _{j=1}^{N_i}{K}_{\text{PCA}}\left(\frac{{\Vert x_i-x_{i_j}\Vert }_{{ℝ}^p}}{\sqrt{{\epsilon }_{\text{PCA}}}}\right)(x_{i_j}-x_i){(x_{i_j}-x_i)}^{\mathrm{{\rm T}}}.$$ (2.2)

Since K_PCA is supported on the interval [0, 1] the covariance matrix Ξ_i can also be represented as

$${\mathrm{\Xi }}_i=\sum _{j=1}^n{K}_{\text{PCA}}\left(\frac{{\Vert x_i-x_j\Vert }_{{ℝ}^p}}{\sqrt{{\epsilon }_{\text{PCA}}}}\right)(x_j-x_i){(x_j-x_i)}^{\mathrm{{\rm T}}}.$$ (2.3)

The definition of D_i(j, j) above is via the square root of the kernel, so it appears linearly in the covariance matrix. We denote the singular values of B_i by σ_i;1 ≥ σ_i;2≥⋯ ≥σ_i,Ni. The eigenvalues of the p × p local covariance matrix Ξ_i equal the squared singular values. Since the ambient space dimension p is typically large, it is usually more efficient to compute the singular values and singular vectors of B_i rather than the eigendecomposition of Ξ_i.

Suppose that the singular value decomposition (SVD) of B_i is given by

$$B_i=U_i{\mathrm{\Sigma }}_i{V}_i^{\mathrm{{\rm T}}}.$$

The columns of the p × N_i matrix U_i are orthonormal and are known as the left singular vectors

$$U_i=[u_{i_1}{u}_{i_2}\cdots u_{i_{N_i}}].$$

We define the p × d matrix O_i by the first d left singular vectors (corresponding to the largest singular values):

$$O_i=[u_{i_1}{u}_{i_2}\cdots u_{i_d}].$$ (2.4)

The d columns of O_i are orthonormal, i.e., $O_i^{\mathrm{{\rm T}}}{O}_i=I_{d\times d}$. The columns of O_i represent an orthonormal basis to a d-dimensional subspace of ℝ^p. This basis is a numerical approximation to an orthonormal basis of the tangent plane T_xiℳ. The order of the approximation (as a function of ∊_PCA and n, where n is the number of the data points) is established later in Appendix B, using the fact that the columns of O_i are also the eigenvectors (corresponding to the d largest eigenvalues) of the p × p; weighted covariance matrix. Ξ_i. We emphasize that the covariance matrix is never actually formed due to its excessive storage requirements, and all computations are performed with the matrix B_i.

In cases where the intrinsic dimension d is not known in advance, the following procedure can be used to estimate d. The underlying assumption is that data points lie exactly on the manifold, without any noise contamination. We remark that in the presence of noise, other procedures (e.g., [28]) could give a more accurate estimation.

Because our previous definition for the neighborhood size parameter ∊_PCA involves d, we are not allowed to use it when trying to estimate d. Instead, we can take the neighborhood size ∊_PCA to be any monotonically decreasing function of n that satisfies $n{\epsilon }_{\text{PCA}}^{d/2}\to \mathrm{\infty }\text{as}n\to \mathrm{\infty }$. This condition ensures that the number of neighboring points increases indefinitely in the limit of an infinite number of sampling points. One can choose, for example, ∊_PCA = 1/log(n), though other choices are also possible.

Notice that if the manifold is flat, then the neighboring points in 𝒩_{xi, ∊PCA} are located exactly on T_xiℳ and as a result rank (X_i) = rank (B_i) = d and B_i has exactly d nonvanishing singular values (i.e., σ_i;d+1 = σ_i,d+2 = ⋯ = σ_i,Ni = 0). In such a case, the dimension can be estimated as the number of nonzero singular values. For nonflat manifolds, due to curvature, there may be more than d nonzero singular values. Clearly, as n goes to infinity, these singular values approach 0, since the curvature effect disappears. A common practice is to estimate the dimension as the number of singular values that account for a high enough percentage of the variability of the data. That is, one sets a threshold γ between 0 and 1 (usually closer to 1 than to 0), and estimates the dimension as the smallest integer d_i for which

$$\frac{{\sum }_{j=1}^{d_i}{\sigma }_{i,j}^2}{{\sum }_{j=1}^{N_i}{\sigma }_{i,j}^2}>\gamma .$$

For example, setting γ = 0:9 means that d_i singular values account for at least 90% variability of the data, while d_i − 1 singular values account for less than 90%. We refer to the smallest integer d_i as the estimated local dimension of ℳ at x_i. From the previous discussion it follows that this procedure produces an accurate estimation of the dimension at each point as n goes to infinity. One possible way to estimate the dimension of the manifold would be to use the mean of the estimated local dimensions d₁; d₂; …, d_n, that is, $\widehat{d}=\frac{1}{n}{\mathrm{\Sigma }}_{i=1}^n{d}_i$ (and then round it to the closest integer). The mean estimator minimizes the sum of squared errors ${\mathrm{\Sigma }}_{i=1}^n{(d_i-\widehat{d})}^2$. We estimate the intrinsic dimension of the manifold by the median value of all the d_i’s; that is, we define the estimator d̂ for the intrinsic dimension d as

$$\widehat{d}=\text{median}\{d_1,d_2,\dots ,d_n\}.$$

In all proceeding steps of the algorithm we use the median estimator d̂, but in order to facilitate the notation we write d instead of y d̂.

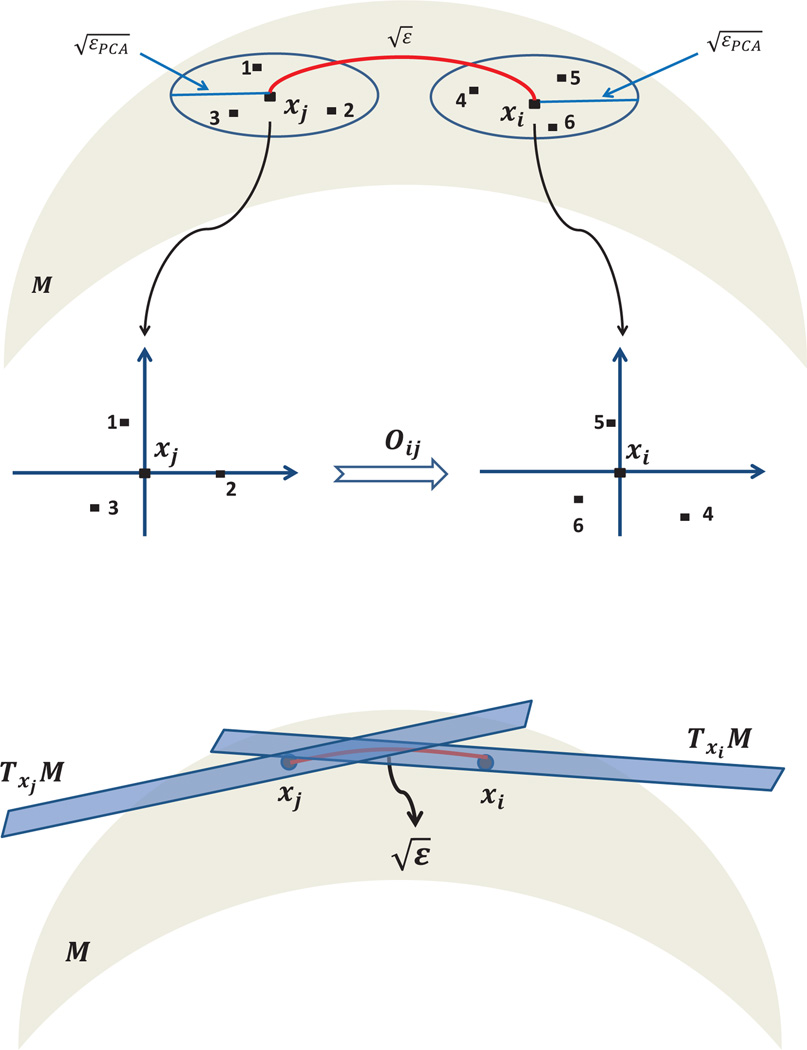
Alignment Suppose x_i and x_j are two nearby points whose euclidean distance satisfies $\Vert x_i-x_j\Vert {ℝ}^p<\sqrt{\epsilon }$, where ∊ > 0 is a scale parameter different from the scale parameter ∊_PCA. In fact, ∊ is much larger than ∊_PCA as we later choose ∊ = O(n^−2/(d+4)), while, as mentioned earlier, ∊_PCA = O(n^−2/(d+1)) (manifolds with boundary) or ∊_PCA = O(n^−2/(d+2)) (manifolds with no boundary). In any case, ∊ is small enough so that the tangent spaces T_xiℳ and T_xjℳ are also close (in the sense that their Grassmannian distance given approximately by the operator norm $\Vert O_i{O}_i^{\mathrm{{\rm T}}}-O_j{O}_j^{\mathrm{{\rm T}}}\Vert$ is small). Therefore, the column spaces of O_i and O_j are almost the same. If the subspaces were to be exactly the same, then the matrices O_i and O_j would differ by a d × d orthogonal transformation O_ij satisfying O_iO_ij = O_j, or equivalently $O_{ij}=O_i^{\mathrm{{\rm T}}}{O}_j$. In that case, $O_i^{\mathrm{{\rm T}}}{O}_j$ would be the matrix representation of the operator that transport vectors from T_xjℳ to T_xjℳ, viewed as copies of ℝ_d. The subspaces, however, are usually not exactly the same, due to curvature. As a result, the matrix $O_i^{\mathrm{{\rm T}}}{O}_j$ is not necessarily orthogonal, and we define O_ij as its closest orthogonal matrix, i.e.,

$$O_{ij}=\underset{O\in O(d)}{\text{argmin}}{\Vert O-O_i^{\mathrm{{\rm T}}}{O}_j\Vert }_{\text{HS},}$$ (2.5)

where ∥·∥_HS is the Hilbert-Schmidt (HS) norm (given by ${\Vert A\Vert }_{\text{HS}}^2=\text{Tr}(A{A}^{\mathrm{{\rm T}}})$ for any real matrix A) and O(d) is the set of orthogonal d × d matrices. This minimization problem has a simple solution³ [1, 13, 21, 25] via the SVD of $O_i^{\mathrm{{\rm T}}}{O}_j$. Specifically, if

$$O_i^{\mathrm{{\rm T}}}{O}_j=U\mathrm{\Sigma }{V}^{\mathrm{{\rm T}}}$$

is the SVD of $O_i^{\mathrm{{\rm T}}}{O}_j$, then O_ij is given by

$$O_{ij}=U{V}^{\mathrm{{\rm T}}}.$$

We refer to the process of finding the optimal orthogonal transformation between bases as alignment. Later in Appendix B we show that the matrix O_ij is an approximation to the parallel transport operator⁴ from T_xjℳ to T_xiℳ whenever x_i and x_j are nearby.

Note that not all bases are aligned; only the bases of nearby points are aligned. We set E to be the edge set of the undirected graph over n vertices that correspond to the data points, where an edge between i and j exists if and only if their corresponding bases are aligned by the algorithm₅ (or equivalently, if and only if $0<\Vert x_i-x_j\Vert {ℝ}^p<\sqrt{\epsilon }$. The weights w_ij are defined⁶ using a kernel function K as

$$w_{ij}=K\left(\frac{{\Vert x_i-x_j\Vert }_{{ℝ}^p}}{\sqrt{\epsilon }}\right),$$ (2.6)

where we assume that K is supported on the interval [0, 1]. For example, the Gaussian kernel K(u) = exp {−u²}χ_[0,1] leads to weights of the form $w_{ij}=\text{exp}\{-{\Vert x_i-x_j\Vert }^2/\epsilon \}\text{for}0<\Vert x_i-x_j\Vert <\sqrt{\epsilon }$ and 0 otherwise. Notice that the kernel K used for the definition of the weights w_ij could be different from the kernel K_PCA used for the previous step of local PCA.

3 Vector Diffusion Mapping

We construct the following matrix S:

$$S(i,j)=\{\begin{array}{cc}{w}_{ij}{O}_{ij}\hfill & (i,j)\in E,\hfill \\ 0_{d\times d}\hfill & (i,j)\notin E.\hfill \end{array}$$ (3.1)

That is, S is a block matrix, with n × n blocks, each of which is of size d × d. Each block is either a d × d orthogonal transformation O_ij multiplied by the scalar weight w_ij or a zero d × d matrix. (As mentioned in a previous footnote, the edge set does not contain self-loops, so w_ii = 0 and S(i, i) = 0_{d × d}.) The matrix S is symmetric since $O_{ij}^{\mathrm{{\rm T}}}=O_{ji}$ and w_ij = w_ji, and its overall size is nd × nd. We define a diagonal matrix D of the same size, where the diagonal blocks are scalar matrices given by

$$D(i,i)=\text{deg}(i)I_{d\times d},$$ (3.2)

and

$$\text{deg}(i)=\sum _{j:(i,j)\in E}{w}_{ij}$$ (3.3)

is the weighted degree of node i. The matrix D⁻¹S can be applied to vectors v of length nd, which we regard as n vectors of length d, such that v(i) is a vector in ℝ^d viewed as a vector in T_xiℳ. The matrix D⁻¹S is an averaging operator for vector fields, since

$$(D^{-1}Sv)(i)=\frac{1}{\text{deg}(i)}\sum _{j:(i,j)\in E}{w}_{ij}{O}_{ij}v(j).$$ (3.4)

This implies that the operator D⁻¹S : (ℝ^d)ⁿ → (ℝ^d)ⁿ transports vectors from the tangent spaces T_xjℳ (that are nearby to T_xiℳ) to T_xiℳ and then averages the transported vectors in T_xiℳ.

Notice that diffusion maps and other nonlinear dimensionality reduction methods make use of the weight matrix $W={(w_{ij})}_{i,j=1}^n$ but not of the transformations O_ij. In diffusion maps, the weights are used to define a discrete random walk over the graph, where the transition probability a_ij in a single time step from node i to node j is given by

$$a_{ij}=\frac{w_{ij}}{\text{deg}(i)}.$$ (3.5)

The Markov transition matrix $A={(a_{ij})}_{i,j=1}^n$ can be written as

$$A={𝒟}^{-1}W,$$ (3.6)

where 𝒟 is an n × n diagonal matrix with

$$𝒟(i,i)=\text{deg}(i).$$ (3.7)

While A is the Markov transition probability matrix in a single time step, A_t is the transition matrix for t steps. In particular, A_t (i, j) sums the probabilities of all paths of length t that start at i and end at j. Coifman and Lafon [9, 26] showed that A_t can be used to define an inner product in a Hilbert space. Specifically, the matrix A is similar to the symmetric matrix 𝒟_−1/2W 𝒟_−1/2 through A = 𝒟_−1/2(𝒟_−1/2W𝒟_−1/2)𝒟_1/2. It follows that A has a complete set of real eigenvalues and eigenvectors ${\{{\mu }_l\}}_{l=1}^n\text{and}{\{{\varphi }_l\}}_{l=1}^n$, respectively, satisfying Aφ_l = µ_lφ_l. Their diffusion mapping Φ_t is given by

$${\mathrm{\Phi }}_t(i)=({\mu }_1^t{\varphi }_1(i),{\mu }_2^t{\varphi }_2(i),\dots ,{\mu }_n^t{\varphi }_n(i)),$$ (3.8)

where φ_l(i) is the i^th entry of the eigenvector φ_l. The mapping Φ_t satisfies

$$\sum _{k=1}^n\frac{A^t(i,k)}{\sqrt{\text{deg}(k)}}\frac{A^t(j,k)}{\sqrt{\text{deg}(k)}}=\langle {\mathrm{\Phi }}_t(i),{\mathrm{\Phi }}_t(j)\rangle ,$$ (3.9)

where 〈·,·〉 is the usual dot product over euclidean space. The metric associated to this inner product is known as the diffusion distance. The diffusion distance d_DM,t (i, j) between i and j is given by

$$d_{\text{DM},t}^2(i,j)=\sum _{k=1}^n\frac{{(A^t(i,k)-A^t(j,k))}^2}{\text{deg}(k)}=\langle {\mathrm{\Phi }}_t(i),{\mathrm{\Phi }}_t(i)\rangle +\langle {\mathrm{\Phi }}_t(j),{\mathrm{\Phi }}_t(j)\rangle -2\langle {\mathrm{\Phi }}_t(i),{\mathrm{\Phi }}_t(j)\rangle .$$ (3.10)

Thus, the diffusion distance between i and j is the weighted-ℓ₂ proximity between the probability clouds of random walkers starting at i and j after t steps.

In the VDM framework, we define the affinity between i and j by considering all paths of length t connecting them, but instead of just summing the weights of all paths, we sum the transformations. A path of length t from j to i is some sequence of vertices j₀, j₁, …, j_t with j₀ = j and j_t = i, and its corresponding orthogonal transformation is obtained by multiplying the orthogonal transformations along the path in the following order:

$$O_{j_t,j_{t-1}}{O}_{j_{t-1},j_{t-2}}\cdots O_{j_2,j_1}{O}_{j_1,j_0}.$$ (3.11)

Every path from j to i may therefore result in a different transformation. This is analogous to the parallel transport operator from differential geometry that depends on the path connecting two points whenever the manifold has curvature (e.g., the sphere). Thus, when adding transformations of different paths, cancellations may happen.

We would like to define the affinity between i and j as the consistency between these transformations, with higher affinity expressing more agreement among the transformations that are being averaged. To quantify this affinity, we consider again the matrix D⁻¹S, which is similar to the symmetric matrix

$$\tilde{S}=D^{-1/2}S{D}^{-1/2}$$ (3.12)

through D⁻¹S = D^−1/2S̃D^1/2, and define the affinity between i and j as

$${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2,$$

that is, as the squared HS norm of the d × d matrix S̃^2t (i, j), which takes into account all paths of length 2t, where t is a positive integer. In a sense, ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$ measures not only the number of paths of length 2t connecting i and j but also the amount of agreement between their transformations. That is, for a fixed number of paths, ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$ is larger when the path transformations are in agreement and is smaller when they differ.

Since S̃ is symmetric, it has a complete set of eigenvectors v₁; v₂; …, v_nd and eigenvalues λ₁, λ₂; …, λ_nd. We order the eigenvalues in decreasing order of magnitude |λ₁|≥ |λ₂|≥…≥|λ_nd|. The spectral decompositions of S̃ and S̃_2t are given by

$$\tilde{S}(i,j)=\sum _{l=1}^{nd}{\lambda }_l{v}_l(i)v_l{(j)}^{\mathrm{{\rm T}}}\text{and}{\tilde{S}}^{2t}(i,j)=\sum _{l=1}^{nd}{\lambda }_l^{2t}{v}_l(i)v_l{(j)}^{\mathrm{{\rm T}}},$$ (3.13)

where v_l(i) ∈ ℝ^d for i = 1, 2, …, n and l = 1, 2, …, nd. The HS norm of S̃_2t (i, j) is calculated using the trace:

$${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2=\text{Tr}[{\tilde{S}}^{2t}(i,j){\tilde{S}}^{2t}{(i,j)}^{\mathrm{{\rm T}}}]=\sum _{l,r=1}^{nd}{({\lambda }_l{\lambda }_r)}^{2t}\langle v_l(i),v_r(i)\rangle \langle v_l(j),v_r(j)\rangle .$$ (3.14)

It follows that the affinity ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$ is an inner product for the finite-dimensional Hilbert space ℝ_(nd)2 via the mapping V_t:

$$V_t:i\mapsto {({({\lambda }_l{\lambda }_r)}^t\langle v_l(i),v_r(i)\rangle )}_{l,r=1}^{nd}.$$ (3.15)

That is,

$${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2=\langle V_t(i),V_t(j)\rangle .$$ (3.16)

Note that in the manifold learning setup, the embedding i ↦ V_t(i) is invariant to the choice of basis for T_xiℳ because the dot products 〈v_l(i), v_r(i)〉 are invariant to orthogonal transformations. We refer to V_t as the vector diffusion mapping.

From the symmetry of the dot products 〈v_l (i), v_r (i)〉, it is clear that ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$ is also an inner product for the finite-dimensional Hilbert space ℝ_nd(nd+1)/2 corresponding to the mapping

$$i\mapsto {(c_{lr}{({\lambda }_l{\lambda }_r)}^t\langle v_l(i),v_r(i)\rangle )}_{1\le l\le r\le nd}\text{where}{c}_{lr}=\{\begin{array}{cc}\sqrt{2}\hfill & l<r,\hfill \\ 1\hfill & l=r.\hfill \end{array}$$

We define the symmetric vector diffusion distance d_VDM,t (i, j) between nodes i and j as

$$d_{\text{VDM},t}^2(i,j)=\langle V_t(i),V_t(i)\rangle +\langle V_t(j),V_t(j)\rangle -2\langle V_t(i),V_t(j)\rangle .$$ (3.17)

The matrices I − S̃ and I + S̃ are positive semidefinite due to the following identity:

$$v^{\mathrm{{\rm T}}}(I\pm D^{-1/2}S{D}^{-1/2})v=\sum _{(i,j)\in E}{\Vert \frac{v(i)}{\sqrt{\text{deg}(i)}}\pm \frac{w_{ij}{O}_{ij}v(j)}{\text{deg}(j)}\Vert }^2\ge 0$$ (3.18)

for any v ∈ ℝ^nd. As a consequence, all eigenvalues λ_l of S̃ reside in the interval [−1; 1]. In particular, for large enough t, most terms of the form (λ_lλ_r)^2t in (3.14) are close to 0, and ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$ can be well approximated by using only the few largest eigenvalues and their corresponding eigenvectors. This lends itself to an efficient approximation of the vector diffusion distances d_VDM;t(i, j) of (3.17), and it is not necessary to raise the matrix S̃ to its 2t power (which usually results in dense matrices). Thus, for any δ > 0, we define the truncated vector diffusion mapping $V_t^{\delta }$ that embeds the data set in ℝ^m2 (or equivalently, but more efficiently, in ℝ_m(m+1)/2) using the eigenvectors v₁, v₂; …, v_m as

$$V_t^{\delta }:i\mapsto {({({\lambda }_l{\lambda }_r)}^t\langle v_l(i),v_r(i)\rangle )}_{l,r=1}^m$$ (3.19)

where m = m(t, δ) is the largest integer for which

$${\left(\frac{{\lambda }_m}{{\lambda }_1}\right)}^{2t}>\delta \text{and}{\left(\frac{{\lambda }_{m+1}}{{\lambda }_1}\right)}^{2t}\le \delta .$$

We remark that V_t is defined through ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$ rather than ${\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2$, because we cannot guarantee that in general all eigenvalues of S̃ are nonnegative. In Section 8, we show that in the continuous setup of the manifold learning problem all eigenvalues are nonnegative. We anticipate that for most practical applications that correspond to the manifold assumption, all negative eigenvalues (if any) would be small in magnitude (say, smaller than δ). In such cases, one can use any real t > 0 for the truncated vector diffusion map $V_t^{\delta }$.

4 Normalized Vector Diffusion Mappings

It is also possible to obtain slightly different vector diffusion mappings using different normalizations of the matrix S. These normalizations are similar to the ones used in the diffusion map framework [9]. For example, notice that

$$w_l=D^{-1/2}{v}_l$$ (4.1)

are the right eigenvectors of D₋₁S, that is, D₋₁Sw_l = λ_lw_l. We can thus define another vector diffusion mapping, denoted $V_t^{\prime }$, as

$$V_t^{\prime }:i\mapsto {({({\lambda }_l{\lambda }_r)}^t\langle w_l(i),w_r(i)\rangle )}_{l,r=1}^{nd}.$$ (4.2)

From (4.1) it follows that $V_t^{\prime }$ and V_t satisfy the relations

$$V_t^{\prime }(i)=\frac{1}{\text{deg}(i)}{V}_t(i)$$ (4.3)

and

$$\langle V_t^{\prime }(i),V_t^{\prime }(j)\rangle =\frac{\langle V_t(i),V_t(j)\rangle }{\text{deg}(i)\text{deg}(j)}.$$ (4.4)

As a result,

$$\langle V_t^{\prime }(i),V_t^{\prime }(j)\rangle =\frac{{\Vert {\tilde{S}}^{2t}(i,j)\Vert }_{\text{HS}}^2}{\mathrm{deg}(i)\mathrm{deg}(j)}=\frac{{\Vert {(D^{-1}S)}^{2t}(i,j)\Vert }_{\text{HS}}^2}{\mathrm{deg}{(j)}^2}.$$ (4.5)

In other words, the Hilbert-Schmidt norm of the matrix D⁻¹S leads to an embedding of the data set in a Hilbert space only upon proper normalization by the vertex degrees (similar to the normalization by the vertex degrees in (3.9) and (3.10) for the diffusion map). We define the associated vector diffusion distances as

$$d_{\text{VDM}\prime ,t}^2(i,j)=\langle V_t^{\prime }(i),V_t^{\prime }(i)\rangle +\langle V_t^{\prime }(j),V_t^{\prime }(j)\rangle -2\langle V_t^{\prime }(i),V_t^{\prime }(j)\rangle .$$ (4.6)

We comment that the normalized mappings $i\mapsto \frac{V_t(i)}{\Vert V_t(i)\Vert }\text{and}i\mapsto \frac{V_t^{\prime }(i)}{\Vert V_t^{\prime }(i)\Vert }$ that map the data points to the unit sphere are equivalent, that is,

$$\frac{V_t^{\prime }(i)}{\Vert V_t^{\prime }(i)\Vert }=\frac{V_t(i)}{\Vert V_t(i)\Vert }.$$ (4.7)

This means that the angles between pairs of embedded points are the same for both mappings. For a diffusion map, it has been observed that in some cases the distances

$$\Vert \frac{{\mathrm{\Phi }}_t(i)}{\Vert {\mathrm{\Phi }}_t(i)\Vert }-\frac{{\mathrm{\Phi }}_t(j)}{\Vert {\mathrm{\Phi }}_t(j)\Vert }\Vert$$

are more meaningful than ∥Φ_t(i)–Φ_t(j)∥ (see, for example, [17]). This may also suggest the usage of the distances

$$\Vert \frac{V_t(i)}{\Vert V_t(i)\Vert }-\frac{V_t(j)}{\Vert V_t(j)\Vert }\Vert$$

in the VDM framework.

Another important family of normalized diffusion mappings is obtained by the following procedure. Suppose 0 ≤ α ≤ 1, and define the symmetric matrices W_α and S_α as

$$W_{\alpha }={𝒟}^{-\alpha }W{𝒟}^{-\alpha }$$ (4.8)

and

$$S_{\alpha }=D^{-\alpha }S{D}^{-\alpha }.$$ (4.9)

We define the weighted degrees deg_α(1), deg_α(2), …, deg_α(n) corresponding to W_α by

$${\text{deg}}_{\alpha }(i)=\sum _{j=1}^n{W}_{\alpha }(i,j),$$

the n × n diagonal matrix D_α as

$${𝒟}_{\alpha }(i,i)={\text{deg}}_{\alpha }(i),$$ (4.10)

and the n × n block diagonal matrix D_α (with blocks of size d × d) as

$$D_{\alpha }(i,i)={\text{deg}}_{\alpha }(i)I_{d\times d}.$$ (4.11)

We can then use the matrices S_α and D_α (instead of S and D) to define the vector diffusion mappings $V_{\alpha ,t}\text{and}{V}_{\alpha ,t}^{\prime }$. Notice that for α = 0 we have S₀ = S and D₀ = D, so that V_0,t = V_t and $V_{0,t}^{\prime }=V_t^{\prime }$. The case α = 1 turns out to be especially important as discussed in the next section.

5 Convergence to the Connection Laplacian

For diffusion maps, the discrete random walk over the data points converges to a continuous diffusion process over that manifold in the limit n → ∞ and ∊ → 0. This convergence can be stated in terms of the normalized graph Laplacian L given by

$$L={𝒟}^{-1}W-I.$$

In the case where the data points ${\{x_i\}}_{i=1}^n$ are sampled independently from the uniform distribution over ℳ^d the graph Laplacian converges pointwise to the Laplace-Beltrami operator, as we have the following proposition [3, 20, 26, 34]: If f: ℳ^d → ℝ is a smooth function (e.g., f ∈ C₃(ℳ)), then with high probability

$$\frac{1}{\epsilon }\sum _{j=1}^n{L}_{ij}f(x_j)=\frac{1}{2}{\Delta }_{ℳ}f(x_i)+O(\epsilon +\frac{1}{n^{1/2}{\epsilon }^{1/2+d/4}}),$$ (5.1)

where Δ_ℳ is the Laplace-Beltrami operator on ℳ^d. The error consists of two terms: a bias term O(∊) and a variance term that decreases as $1/\sqrt{n}$ but also depends on ∊. Balancing the two terms may lead to an optimal choice of the parameter ∊ as a function of the number of points n. In the case of uniform sampling, Belkin and Niyogi [4] have shown that the eigenvectors of the graph Laplacian converge to the eigenfunctions of the Laplace-Beltrami operator on the manifold, which is stronger than the pointwise convergence given in (5.1).

In the case where the data points ${\{x_i\}}_{i=1}^n$ are independently sampled from a probability density function p(x) whose support is a d-dimensional manifold ℳ^d and satisfies some mild conditions, the graph Laplacian converges pointwise to the Fokker-Planck operator as stated in following proposition [3, 20, 26, 34]: If f ∈ C₃(ℳ), then with high probability

$$\frac{1}{\epsilon }\sum _{j=1}^n{L}_{ij}f(x_j)=\frac{1}{2}{\Delta }_{ℳ}f(x_i)+\nabla U(x_i)·\nabla f(x_i)+O(\epsilon +\frac{1}{n^{1/2}{\epsilon }^{1/2+d/4}}),$$ (5.2)

where the potential term U is given by U(x) = −2 log p(x). The error is interpreted in the same way as in the uniform sampling case. In [9] it is shown that it is also possible to recover the Laplace-Beltrami operator for nonuniform sampling processes using W₁ and 𝒟₁ (that correspond to α = 1 in (4.8) and (4.11)). The matrix $D_1^{-1}{W}_1-I$ converges to the Laplace-Beltrami operator independently of the sampling density function p(x).

For VDM, we prove in Appendix B the following theorem, Theorem 5.3, that states that the matrix $D_{\alpha }^{-1}{S}_{\alpha }-I$, where 0 ≤ α ≤ 1, converges to the connection Laplacian operator (defined via the covariant derivative; see Appendix A and [32]) plus some potential terms depending on p(x). In particular, $D_1^{-1}{S}_1-I$ converges to the connection Laplacian operator, without any additional potential terms. Using the terminology of spectral graph theory, it may thus be appropriate to call $D_1^{-1}{S}_1-I$ the connection Laplacian of the graph.

The main content of Theorem 5.3 specifies the way in which VDM generalizes diffusion maps: while diffusion mapping is based on the heat kernel and the Laplace-Beltrami operator over scalar functions, VDM is based on the heat kernel and the connection Laplacian over vector fields. While for diffusion maps the computed eigenvectors are discrete approximations of the Laplacian eigenfunctions, for VDM the l^th eigenvector v_l of $D_1^{-1}{S}_1-I$ is a discrete approximation of the l^th eigenvector field X_l of the connection Laplacian ▽² over ℳ, which satisfies ▽²X_l= −λ_lX_l for some λ₁ ≥ 0.

In the formulation of Theorem 5.3, as well as in the remainder of the paper, we slightly change the notation used so far in the paper, as we denote the sampled data points in ℳ^d by x₁; x₂; …, x_n, and the observed data points in ℝ_p by ι(x₁), ι(x₂), …, ι(x_n), where ι : ℳ ↪ ℝ^p is the embedding of the Riemannian manifold ℳ in ℝ^p. Furthermore, we denote by ι_*T_xiℳ the d-dimensional subspace of ℝ^p that is the embedding of T_xiℝ in ℝ^p. It is important to note that in the manifold learning setup, the manifold ℳ, the embedding ι, and the points x₁, x₂; …, x_n ∈ ℳ are assumed to exist but cannot be directly observed.

Theorems 5.3, 5.5, and 5.6, stated later in this section, and their proofs in Appendix B all share the following assumption:

ASSUMPTION 5.1.

1. ι : ℳ ↪ ℳ^p is a smooth d-dimensional compact Riemannian manifold embedded in ℳ^p, with metric g induced from the canonical metric on ℳ^p.

2. When ∂ ℳ ≠, we denote ℳ_t = {x ∈ ℳ : min_y∈∂ℳd(x, y) ≤ t}, where t > 0 and d(x; y) is the geodesic distance between x and y.

3. The data points x₁, x₂; …, x_n are independent samples from ℳ according to the probability density function p ∈ C³ (ℳ) supported on ℳ ⊂ ℝ_p, where p is uniformly bounded from below and above, that is, 0 < p_m ≤ p(x) ≤ p_M < ∞.

4. K ∈ C₂([0, 1)) is a positive function. Also, m_l := ∫ℝ^d ∥x∥^lK(∥x∥)dx and $m_l^{\prime }:={\displaystyle \int R^d{\Vert x\Vert }^{l}K\prime }(\Vert x\Vert )dx,l=0,1,2,\dots$. We assume m₀ = 1.

5. The vector field X is in C₃(Tℳ).

6. Denote τ to be the largest number having the following property: the open normal bundle about ℳ of radius r is embedded in ℝ_p for every r < τ [30]. This condition holds automatically since ℳ is compact. In all theorems, we assume that $\sqrt{\epsilon }<\tau$. In [30], 1/τ is referred to as the “condition number” of ℳ.

7. To ease notation, in what follows we use the same notation ▽ to denote different connections on different bundles whenever there is no confusion and the meaning is clear from the context.

DEFINITION 5.2. For ∊ > 0, define

$$K_{\epsilon }(x_i,x_j)=\{\begin{array}{cc}K\left(\frac{{\Vert \mathit{\iota }(x_i)-\mathit{\iota }(x_j)\Vert }_{{ℝ}^p}}{\sqrt{\epsilon }}\right)\hfill & \text{for}0<\Vert \mathit{\iota }(x_i)-\mathit{\iota }(x_j)\Vert <\sqrt{\epsilon },\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

We define the empirical probability density function by

$$p_{\epsilon }(x_i)=\sum _{j=1}^n{K}_{\epsilon }(x_i,x_j)$$

and for 0 ≤ α ≤ 1 define the α-normalized kernel K_{∊, α} by

$$K_{\epsilon ,\alpha }(x_i,x_j)=\frac{K_{\epsilon }(x_i,x_j)}{p_{\epsilon }^{\alpha }(x_i)p_{\epsilon }^{\alpha }(x_j)}.$$

For 0 ≤ α ≤ 1, we define

$$T_{\epsilon ,\alpha }X(x)=\frac{{\int }_{ℳ}{K}_{\epsilon ,\alpha }(x,y)P_{x,y}X(y)p(y)\mathrm{d}V(y)}{{\int }_{ℳ}{K}_{\epsilon ,\alpha }(x,y)p(y)\mathrm{d}V(y)}.$$

THEOREM 5.3. In addition to Assumption 5.1, suppose ℳ is closed and ∊_PCA = O(n^−2/(d+2)). For all x_i with high probability (w.h.p.)

$$\frac{1}{\epsilon }[\frac{{\sum }_{j=1}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}-{\overline{X}}_i]=\frac{m_2}{2d}{(\langle {\mathit{\iota }}_{*}\{{\nabla }^{2}X(x_i)+\frac{2\nabla X(x_i)·\nabla (p^{1-\alpha })(x_i)}{p^{1-\alpha }(x_i)}\},u_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }^{\frac{1}{2}}+{\epsilon }^{-1}{n}^{-\frac{3}{d+2}}+n^{-\frac{1}{2}}{\epsilon }^{-\frac{d+2}{4}})=\frac{m_2}{2d}{(\langle {\mathit{\iota }}_{*}\{{\nabla }^{2}X(x_i)+\frac{2\nabla X(x_i)·\nabla (p^{1-\alpha })(x_i)}{p^{1-\alpha }(x_i)}\},e_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }^{\frac{1}{2}}+{\epsilon }^{-1}{n}^{-\frac{3}{d+2}}+n^{-\frac{1}{2}}{\epsilon }^{-\frac{d+2}{4}})$$ (5.3)

where ${\overline{X}}_i\equiv {(\langle {\iota }_{*}X(x_i),u_l(x_i)\rangle )}_{l=1}^d\in {ℝ}^{d}foralli,{\{u_l(x_i)\}}_{l=1}^d$ is an orthonormal basis for a d-dimensional subspace of ℝ_p determined by local PCA (i.e., the columns of O_i), ${\{e_l(x_i)\}}_{l=1}^d$ is an orthonormal basis for ι_*T_xiℳ, O_ij is the optimal orthogonal transformation determined by the alignment procedure, and $\nabla X(x_i)\cdot \nabla (p^{1-\alpha })(x_i):={\mathrm{\Sigma }}_{l=1}^d{\nabla }_{E_l}X{\nabla }_{E_l}(p^{1-\alpha })$, where E_l is an orthonormal basis for T_xiℳ.

When ∊_PCA = O(n^−2/(d+1)), then the same almost surely convergence results above hold but with a slower convergence rate.

COROLLARY 5.4. For ∊ = O(n^−2/(d+4)) almost surely,

$$\underset{n\to \infty }{\text{lim}}\frac{1}{\epsilon }[\frac{{\sum }_{j=1}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}-{\overline{X}}_i]=\frac{m_2}{2d}{(\langle {\mathit{\iota }}_{*}\{{\nabla }^{2}X(x_i)+\frac{2\nabla X(x_i)·\nabla (p^{1-\alpha })(x_i)}{p^{1-\alpha }(x_i)}\},e_l(x_i)\rangle )}_{l=1}^d,$$ (5.4)

and in particular

$$\underset{n\to \infty }{\text{lim}}\frac{1}{\epsilon }[\frac{{\sum }_{j=1}^n{K}_{\epsilon ,1}(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1}^n{K}_{\epsilon ,1}(x_i,x_j)}-{\overline{X}}_i]=\frac{m_2}{2d}{(\langle {\mathit{\iota }}_{*}{\nabla }^{2}X(x_i),e_l(x_i)\rangle )}_{l=1}^d.$$ (5.5)

When the manifold is compact with boundary, (5.3) does not hold at the boundary. However, we have the following result for the convergence behavior near the boundary:

THEOREM 5.5. Suppose the boundary ∂ℳ is smooth and that Assumption 5.1 applies. Choose ∊_PCA = O(n^−2/d+1)). When $x_i\in ℳ\sqrt{\epsilon },$ we have

$$\frac{{\sum }_{j=1}^n{K}_{\epsilon ,1}(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1}^n{K}_{\epsilon ,1}(x_i,x_j)}={(\langle {\mathit{\iota }}_{*}{P}_{x_i,x_0}(X(x_0)+\frac{m_1^{\epsilon }}{m_0^{\epsilon }}{\nabla }_{{\partial }_d}X(x_0)),e_l(x_i)\rangle )}_{l=1}^d+O(\epsilon +n^{-\frac{3}{2(d+1)}}+n^{-\frac{1}{2}}{\epsilon }^{-\frac{d-2}{4}}),$$ (5.6)

where x₀ = argmin_y∈∂ℳ d(x_i, y), $m_1^{\epsilon }and{m}_0^{\epsilon }$ are constants defined in (B.93) and (B.94)and ∂^d is the normal direction to the boundary at x₀.

For the choice ∊ = O(n^−2/(d+4)) (as in Corollary 5.4), the error appearing in (5.6) is O(∊^3/4), which is asymptotically smaller than $O(\sqrt{\epsilon })$, which is the order of $m_1^{\epsilon }/m_0^{\epsilon }$. A consequence of Theorem 5.3, Theorem 5.5, and the above discussion about the error terms is that the eigenvectors of $D_1^{-1}{S}_1-I$ are discrete approximations of the eigenvector fields of the connection Laplacian operator with homogeneous Neumann boundary condition that satisfy

$$\{\begin{array}{cc}{\nabla }^{2}X(x)=-\lambda X(x)\hfill & \text{for}x\in ℳ,\hfill \\ {\nabla }_{{\partial }_d}X(x)=0\hfill & \text{for}x\in \partial ℳ.\hfill \end{array}$$ (5.7)

We remark that the Neumann boundary condition also emerges for the choice ∊_PCA = O(n^−2/(d+2)). This is due to the fact that the error in the local PCA term is $O({\epsilon }_{\text{PCA}}^{1/2})=0(n^{-1/(d+2)})$, which is asymptotically smaller than O(∊^1/2 = O(n^−1/(d+4)) error term.

Finally, Theorem 5.6 details the way in which the algorithm approximates the continuous heat kernel of the connection Laplacian:

THEOREM 5.6. Under Assumption 5.1, for any t > 0, the heat kernel e^t▽2 can be approximated on L²(Tℳ) by $T_{\epsilon ,1}^{t/\epsilon }$, that is,

$$\underset{\epsilon \to 0}{\text{lim}}{T}_{\epsilon ,1}^{t/\epsilon }=e^{t{\nabla }^2}.$$

6 Numerical Simulations

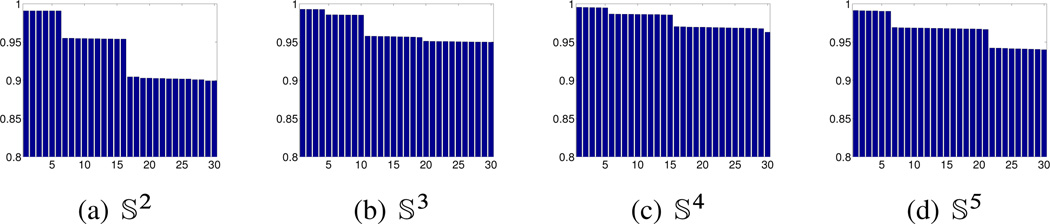
In all numerical experiments reported in this section, we use the normalized vector diffusion mapping $V_{1,t}^{\prime }$ corresponding to α = 1 in (4.9) and (4.10); that is, we use the eigenvectors of $D_1^{-1}{S}_1$ to define the VDM. In all experiments we used the kernel function K (u) = e^−5u2χ_[0,1] for the local PCA step as well as for the definition of the weights w_ij. The specific choices for ∊ and ∊_PCA are detailed below. We remark that the results are not very sensitive to these choices; that is, similar results are obtained for a wide regime of parameters. The purpose of the first experiment is to numerically verify Theorem 5.3 using spheres of different dimensions. Specifically, we sampled n = 8000 points uniformly from 𝕊^d embedded in ℝ^d+1 for d = 2, 3, 4, 5. Figure 6.1 shows bar plots of the largest 30 eigenvalues of the matrix $D_1^{-1}{S}_1$ for ∊_PCA = 0:1 when d = 2, 3, 4 and ∊_PCA = 0:2 when d = 5, and $\epsilon ={\epsilon }_{\text{PCA}}^{(d+1)/(d+4)}$. It is noticeable that the eigenvalues have numerical multiplicities greater than 1. Since the connection Laplacian commutes with rotations, the dimensions of its eigenspaces can be calculated using representation theory (see Appendix C). In particular, our calculation predicted the following dimensions for the eigenspaces of the largest eigenvalues:

$$\begin{array}{cc}{𝕊}^2:6,10,14,\dots ,\hfill & {𝕊}^3:4,6,9,16,16,\dots ,\hfill \\ {𝕊}^4:5,10,14,\dots ,\hfill & {𝕊}^5:6,15,20,\dots .\hfill \end{array}$$

Figure 6.1.

Bar plots of the largest 30 eigenvalues of $D_1^{-1}{S}_1$ for n = 8000 points uniformly distributed over spheres of different dimensions.

These dimensions are in full agreement with the bar plots shown in Figure 6.1.

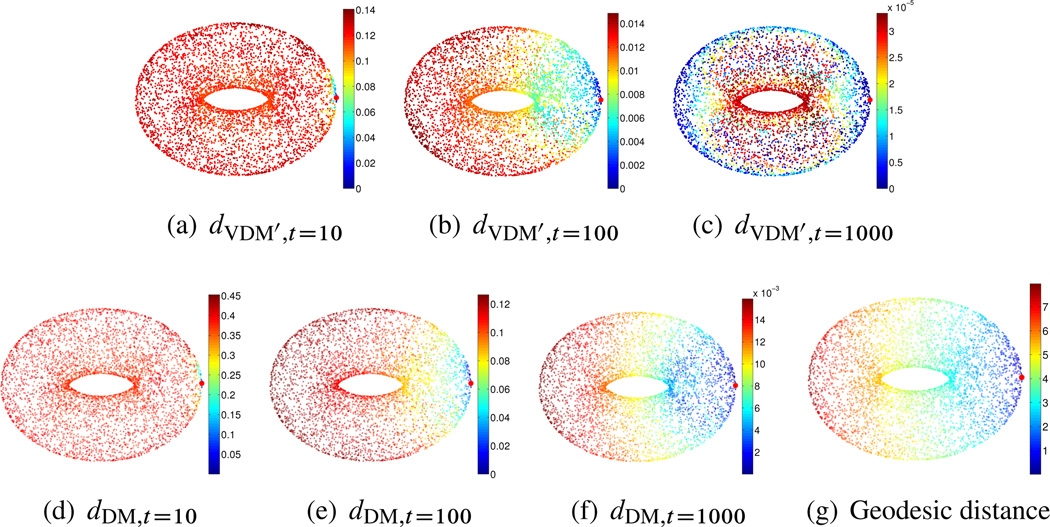
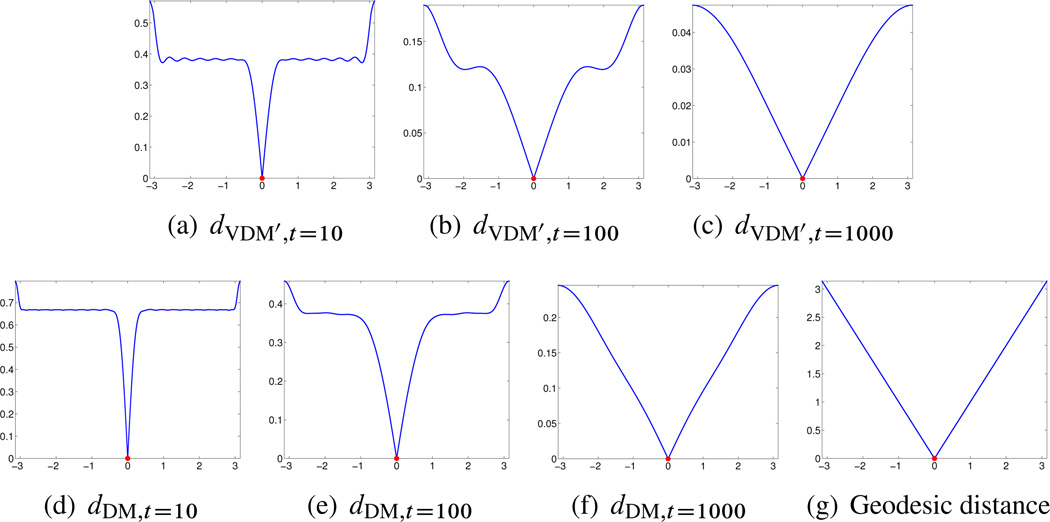
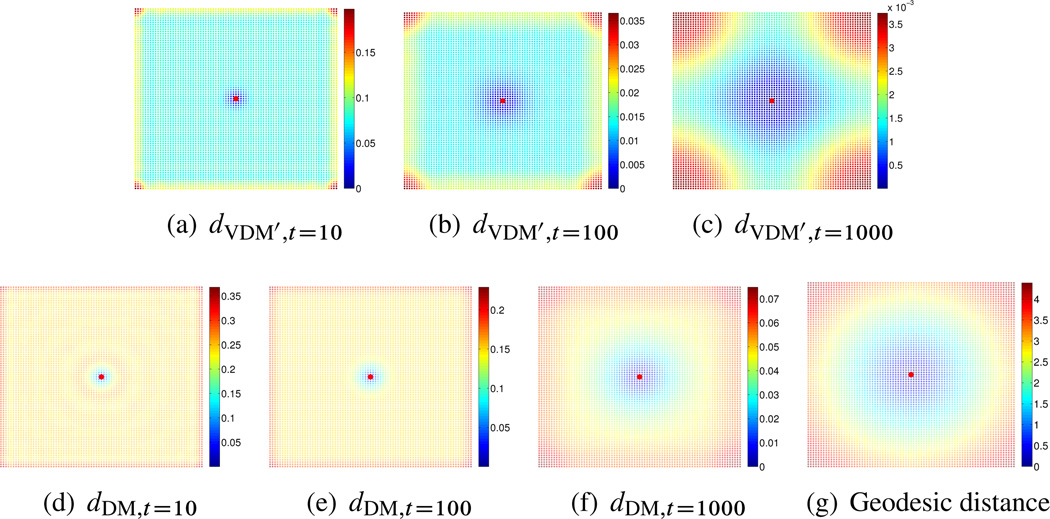
In the second set of experiments, we numerically compare the vector diffusion distance, the diffusion distance, and the geodesic distance for different compact manifolds with and without boundaries. The comparison is performed for the following four manifolds: (1) the sphere 𝕊² embedded in ℝ³; (2) the torus 𝕋² embedded in ℝ³; (3) the interval [−π, π] in ℝ and (4) the square [0, 2π] × [0, 2π] in ℝ². For both VDM and DM we truncate the mappings using δ = 0.2; see (3.19). The geodesic distance is computed by the algorithm of Dijkstra on a weighted graph, whose vertices correspond to the data points, the edges link data points whose euclidean distance is less than $\sqrt{\epsilon }$, and the weights w_G(i, j) are the euclidean distances, that is,

$$w_G(i,j)=\{\begin{array}{cc}{\Vert x_i-x_j\Vert }_{{ℝ}^p},\hfill & \Vert x_i-x_j\Vert <\sqrt{\epsilon },\hfill \\ +\infty \hfill & \text{otherwise}.\hfill \end{array}$$

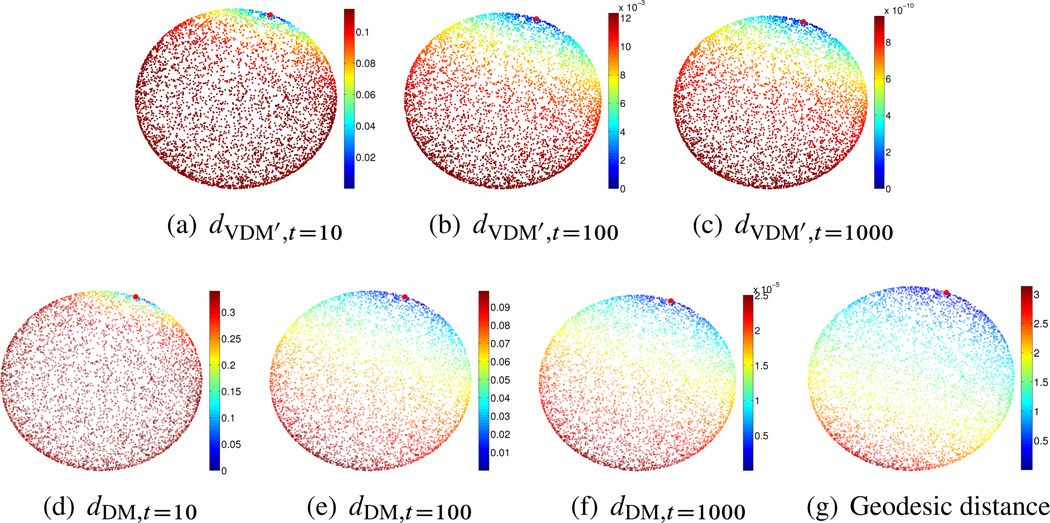
𝕊² case: We sampled n = 5000 points uniformly from 𝕊² = {x ∈ ℝ₃ : ∥x∥ = 1} ⊂ ℝ³ and set ∊_PCA = 0.1 and $\epsilon =\sqrt{{\epsilon }_{\text{PCA}}}\approx 0.316$. For the truncated vector diffusion distance, when t = 10, we find that the number of eigenvectors whose eigenvalue is larger (in magnitude) than ${\lambda }_1^t\delta$ is m_VDM = m_VDM(t = 10, δ = 0.2) = 16 (recall the definition of m(t, δ) that appears after (3.19)). The corresponding embedded dimension is m_VDM(m_VDM + 1)/2, which in this case is 16 · 17/2 = 136. Similarly, for t = 100, m_VDM = 6 (embedded dimension is 6 · 7/2 = 21), and when t = 1000, m_VDM = 6 (embedded dimension is again 21). Although the first eigenspace (corresponding to the largest eigenvalue) of the connection Laplacian over 𝕊² is of dimension 6, there are small discrepancies between the top 6 numerically computed eigenvalues, due to the finite sampling. This numerical discrepancy is amplified upon raising the eigenvalues to the t^th power, when t is large, e.g., t = 1000. For demonstration purposes, we remedy this numerical effect by artificially setting λ_l = λ_l for l = 2, 3, …, 6. For the truncated diffusion distance, when t = 10, m_DM = 36 (embedded dimension is 36 − 1 = 35), when t = 100, m_DM = 4 (embedded dimension is 3), and when t = 1000, m_DM = 4 (embedded dimension is 3). Similarly, we have the same numerical effect when t = 1000, that is, µ₂, µ₃, and µ₄ are close but not exactly the same, so we again set µ_l = µ₂ for l = 3, 4. The results are shown in Figure 6.2.

Figure 6.2.

𝕊² case. Top: truncated vector diffusion distances for t = 10, t = 100, and t = 1000. Bottom: truncated diffusion distances for t = 10, t = 100, and t = 1000, and the geodesic distance. The reference point from which distances are computed is marked in red.

𝕋² case: We sampled n = 5000 points (u, v) uniformly over the [0, 2π) × [0, 2π) square and then mapped them to ℝ₃ using the following transformation, which defines the surface 𝕋² as

$${\mathrm{{\rm T}}}^2=\{((2+\text{cos}(v))\text{cos}(u),(2+\text{cos}(v))\text{sin}(u),\text{sin}(v)):(u,v)\in [0,2\pi )\times [0,2\pi )\}\subset {ℝ}^3.$$

Notice that the resulting sample points are not uniformly distributed over 𝕋². Therefore, the usage of S₁ and D₁ instead of S and D is important if we want the eigenvectors to approximate the eigenvector fields of the connection Laplacian over 𝕋². We used ∊_PCA = 0:2 and $\epsilon =\sqrt{{\epsilon }_{\text{PCA}}}\approx 0.447$, and find that for the truncated vector diffusion distance, when t = 10, the embedded dimension is 2628, when t = 100, the embedded dimension is 36, and when t = 1000, the embedded dimension is 3. For the truncated diffusion distance, when t = 10, the embedded dimension is 130; when t = 100, the embedded dimension is 14; and when t = 1000, the embedded dimension is 2. The results are shown in Figure 6.3.

Figure 6.3.

𝕋² case. Top: truncated vector diffusion distances for t = 10, t = 100, and t = 1000. Bottom: truncated diffusion distances for t = 10, t = 100, and t = 1000, and the geodesic distance. The reference point from which distances are computed is marked in red.

One-dimensional interval case: We sampled n = 5000 equally spaced grid points from the interval [−π, π] ⊂ ℝ¹ and set ∊_PCA = 0.01 and $\epsilon ={\epsilon }_{\text{PCA}}^{2/5}\approx 0.158$. For the truncated vector diffusion distance, when t = 10, the embedded dimension is 120, when t = 100, the embedded dimension is 15, and when t = 1000, the embedded dimension is 3. For the truncated diffusion distance, when t = 10, the embedded dimension is 36, when t = 100, the embedded dimension is 11, and when t = 1000, the embedded dimension is 3. The results are shown in Figure 6.4.

Figure 6.4.

One-dimensional interval case. Top: truncated vector diffusion distances for t = 10, t = 100, and t = 1000. Bottom: truncated diffusion distances for t = 10, t = 100, and t = 1000, and the geodesic distance. The reference point from which distances are computed is marked in red.

Square case: We sampled n = 6561 = 81₂ equally spaced grid points from the square [0, 2π] × [0, 2π] and fixed ∊_PCA = 0:01 and $\epsilon =\sqrt{{\epsilon }_{\text{PCA}}}=0.1$. For the truncated vector diffusion distance, when t = 10, the embedded dimension is 20;100 (we only calculate the first 200 eigenvalues); when t = 100, the embedded dimension is 1596; and when t = 1000, the embedded dimension is 36. For the truncated diffusion distance, when t = 10, the embedded dimension is 200 (we only calculate the first 200 eigenvalues); when t = 100, the embedded dimension is 200; and when t = 1000, the embedded dimension is 28. The results are shown in Figure 6.5.

Figure 6.5.

Square case. Top: truncated vector diffusion distances for t = 10, t = 100, and t = 1000. Bottom: truncated diffusion distances for t = 10, t = 100, and t = 1000, and the geodesic distance. The reference point from which distances are computed is marked in red.

7 Out-of-Sample Extension of Vector Fields

Let $𝒳={\{x_i\}}_{i=1}^n\text{and}𝒴={\{y_i\}}_{i=1}^m$ so that 𝒳, 𝒴 ⊂ ℳ^d where ℳ is embedded in ℝ^p by ι. Suppose X is a smooth vector field that we observe only on 𝒳 and want to extend to 𝒴. That is, we observe the vectors ι_*X(x₁), ι_*X(x₂), …, ι_*X(x_n) ∈ ℝ^p and want to estimate ι_*X(y₁), ι_*X(y₂), …, ι_*X(y_m). The set 𝒳 is assumed to be fixed, while the points in 𝒴 may arrive on the fly and need to be processed in real time. We propose the following Nyström scheme for extending X from 𝒳 to 𝒴.

In the preprocessing step we use the points x₁, x₂; …, x_n for local PCA, alignment, and vector diffusion mapping as described in Sections 2 and 3. That is, using local PCA, we find the p × d matrices O_i (i = 1, 2, …, n) such that the columns of O_i are an orthonormal basis for a subspace that approximates the embedded tangent plane ι_*T_xiℳ; using alignment, we find the orthonormal d × d matrices O_ij that approximate the parallel transport operator from T_xjℳ to T_xiℳ; and using w_ij and O_ij we construct the matrices S and D and compute (a subset of) the eigenvectors v₁, v₂, …, v_nd and eigenvalues λ₁, λ₂, …, λ_nd of D⁻¹S.

We project the embedded vector field ι_*X(x_i) ∈ ℝ^p into the d-dimensional subspace spanned by the columns of O_i and define X_i ∈ ℝ^d as

$$X_i=O_i^{\mathrm{{\rm T}}}{\mathit{\iota }}_{*}X(x_i).$$ (7.1)

We represent the vector field X on 1D4B3 by the vector x of length nd, organized as n vectors of length d, with

$$\mathit{x}(i)=X_i\text{for}i=1,2,\dots ,n.$$

We use the orthonormal basis of eigenvector fields v₁; v₂, …, v_nd to decompose x as

$$\mathit{x}=\sum _{l=1}^{nd}{a}_l{v}_l,$$ (7.2)

where a_l = x^Τv_l. This concludes the preprocessing computations.

Suppose y ∈ 𝒴 is a “new” out-of-sample point. First, we perform the local PCA step to find a p × d matrix, denoted O_y whose columns form an orthonormal basis to a d-dimensional subspace of ℝ^p that approximates the embedded tangent plane ι_*T_yℳ. The local PCA step uses only the neighbors of y among the points in 𝒳 (but not in 𝒴) inside a ball of radius $\sqrt{{\epsilon }_{\text{PCA}}}$ centered at y.

Next, we use the alignment process to compute the d × d orthonormal matrix O_y,i between x_i and y by setting

$$O_{y,i}=\underset{O\in O(d)}{\text{argmin}}{\Vert O_y^{\mathrm{{\rm T}}}{O}_i-O\Vert }_{\text{HS}}.$$

Notice that the eigenvector fields satisfy

$$v_l(i)=\frac{1}{{\lambda }_l}\frac{{\sum }_{j=1}^n{K}_{\epsilon }(\Vert x_i-x_j\Vert )O_{ij}{v}_l(j)}{{\sum }_{j=1}^n{K}_{\epsilon }(\Vert x_i-x_j\Vert )}.$$

We denote the extension of v_l to the point y by ṽ_l(y) and define it as

$${\tilde{v}}_l(y)=\frac{1}{{\lambda }_l}\frac{{\sum }_{j=1}^n{K}_{\epsilon }(\Vert y-x_j\Vert )O_{y,j}{v}_l(j)}{{\sum }_{j=1}^n{K}_{\epsilon }(\Vert y-x_j\Vert )}.$$ (7.3)

To finish the extrapolation problem, we denote the extension of x to y by x̃(y) and define it as

$$\tilde{\mathit{x}}(y)=\sum _{l=1}^{m(\delta )}{a}_l{\tilde{v}}_l(y),$$ (7.4)

where m(δ) = max_l|λ_l| > and > 0 is some fixed parameter to ensure the numerical stability of the extension procedure (due to the division by λ_l in (7.3); 1/δ can be regarded as the condition number of the extension procedure).

8 The Continuous Case: Heat Kernels

As discussed earlier, in the limit n → ∞ and ∊ ∞ 0 considered in (5.2), the normalized graph Laplacian converges to the Laplace-Beltrami operator, which is the generator of the heat kernel for functions (0-forms). Similarly, in the limit n → ∞ considered in (5.3), we get the connection Laplacian operator, which is the generator of a heat kernel for vector fields (or 1-forms). The connection Laplacian ▽₂ is a self-adjoint, second-order elliptic operator defined over the tangent bundle Tℳ. It is well-known [16] that the spectrum of ▽₂ is discrete inside ℝ⁻, and the only possible accumulation point is −∞. We will denote the spectrum as ${\{-{\lambda }_k\}}_{k=0}^{\mathrm{\infty }}$, where 0 ≤ λ₀ ≤ λ₁ ≤ …. From classical elliptic theory (see, for example, [16]), we know that e^t▽2 has the kernel

$$k_t(x,y)=\sum _{n=0}^{\infty }{e}^{-{\lambda }_{n}t}{X}_n(x)\otimes \overline{X_n(y)}.$$

where ▽²X_n = −λ_nX_n. Also, the eigenvector fields X_n of ▽² form an orthonormal basis of L²(Tℳ). In the continuous setup, we define the vector diffusion distance between x; y ∈ ℳ using ${\Vert k_t(x,y)\Vert }_{\text{HS}}^2$. An explicit calculation gives

$${\Vert k_t(x,y)\Vert }_{\text{HS}}^2=\text{Tr}[k_t(x,y)k_t{(x,y)}^{*}]=\sum _{n,m=0}^{\infty }{e}^{-({\lambda }_n+{\lambda }_m)t}\langle X_n(x),X_m(x)\rangle \overline{\langle X_n(y),X_m(y)\rangle }.$$ (8.1)

It is well-known that the heat kernel k_t(x, y) is smooth in x and y and analytic in t [16], so for t > 0 we can define a family of vector diffusion mappings V_t that map any x ∈ ℳ into the Hilbert space ℓ₂ by

$$V_t:x\mapsto {(e^{-({\lambda }_n+{\lambda }_m)t/2}\langle X_n(x),X_m(x)\rangle )}_{n,m=0}^{\infty },$$ (8.2)

which satisfies

$${\Vert k_t(x,y)\Vert }_{\text{HS}}^2={\langle V_t(x),V_t(y)\rangle }_{{\ell }^2}.$$ (8.3)

The vector diffusion distance d_VDM,t (x, y) between x ∈ M and y ∈ M is defined as

$$d_{\text{VDM},t}(x,y)≔{\Vert V_t(x)-V_t(y)\Vert }_{{\ell }^2},$$ (8.4)

which is clearly a distance function over ℳ. In practice, due to the decay of e^{−(λ_n+λ_m)t} only pairs (n, m) for which λ_n + λ_m is not too large are needed to get a good approximation of this vector diffusion distance. As in the discrete case, the dot products 〈X_n (x), X_m(x)〉 are invariant to the choice of basis for the tangent space at x.

We now study some properties of the vector diffusion map V_t (8.2). First, we claim that for all t > 0, the vector diffusion mapping V_t is an embedding of the compact Riemannian manifold ℳ into ℓ².

THEOREM 8.1. Given a d-dimensional closed Riemannian manifold (ℳ, g) and an orthonormal basis ${\{X_n\}}_{n=0}^{\mathrm{\infty }}of{L}^2(TM)$ composed of the eigenvector fields of the connection Laplacian ▽², then for any t > 0, the vector diffusion map V_t is a diffeomorphic embedding of ℳ in ℓ².

PROOF. We show that V_t: ℳ → ℓ₂ is continuous in x by noting that

$${\Vert V_t(x)-V_t(y)\Vert }_{{\ell }^2}^2=\sum _{n,m=0}^{\infty }{e}^{-({\lambda }_n+{\lambda }_m)t}{(\langle X_n(x),X_m(x)\rangle -\langle X_n(y),X_m(y)\rangle )}^2=\text{Tr}(k_t(x,x)k_t{(x,x)}^{*})+\text{Tr}(k_t(y,y)k_t{(y,y)}^{*})-2\text{Tr}(k_t(x,y)k_t{(x,y)}^{*})$$ (8.5)

From the continuity of the kernel k_t(x, y) it is clear that ${\Vert V_t(x)-V_t(y)\Vert }_{{\ell }^2}^2\to 0$ as y → x. Since ℳ is compact, it follows that V_t(ℳ) is compact in ℓ₂. Finally, we show that V_t is one-to-one. Fix x ≠ y and a smooth vector field X that satisfies 〈X(x),X(x)〉 ≠ 〈X(y), X(y)〉. Since the eigenvector fields ${[X_n]}_{n=0}^{\mathrm{\infty }}$ form a basis for L₂ (Tℳ), we have

$$X(z)=\sum _{n=0}^{\infty }{c}_n{X}_n(z)\text{for all}z\in ℳ,$$

where c_n = ∫ℳ〈X,X_n〉dV. As a result,

$$\langle X(z),X(z)\rangle =\sum _{n,m=0}^{\infty }{c}_n{c}_m\langle X_n(z),X_m(z)\rangle .$$

Since 〈X(x), X(x)〉 ≠ 〈X(y), X(y)〉, there exist n, m ∈ ℕ such that

$$\langle X_n(x),X_m(x)\rangle \ne \langle X_n(y),X_m(y)\rangle ,$$

which shows that V_t (x) ≠ V_t (y); i.e., V_t is one-to-one. From the fact that the map V_t is continuous and one-to-one from ℳ, which is compact, onto V_t (ℳ), we conclude that V_t is an embedding.

Next, we demonstrate the asymptotic behavior of the vector diffusion distance d_VDM,t(x, y) and the diffusion distance d_DM,t (x, y) when t is small and x is close to y. The following theorem shows that in this asymptotic limit both the vector diffusion distance and the diffusion distance behave like the geodesic distance.

THEOREM 8.2. Let (ℳ, g) be a smooth d-dimensional closed Riemannian manifold. Suppose x, y ∈ ℳ so that x = exp_y(v), where v ∈ T_y ℳ. For any t > 0, when ∥v∥² ≪ t ≪ 1 we have the following asymptotic expansion of the vector diffusion distance:

$$d_{\mathit{\text{VDM}},t}^2(x,y)=d{(4\pi )}^{-d}\frac{{\Vert v\Vert }^2}{t^{d+1}}+O\left(\frac{{\Vert v\Vert }^2}{t^d}\right)$$

Similarly, when ∥v∥² ≪ t ≪ 1, we have the following asymptotic expansion of the diffusion distance:

$$d_{\mathit{\text{DM}},t}^2(x,y)={(4\pi )}^{-d/2}\frac{{\Vert v\Vert }^2}{2t^{d/2+1}}+O\left(\frac{{\Vert v\Vert }^2}{t^d}\right).$$

PROOF. Fixing y and a normal coordinate around y, we define j(x, y) = |det(d_v exp_y)|, where x = exp_y(v), v ∈ T_xℳ. Suppose ∥v∥ is small enough so that x = exp_y(v) is away from the cut locus of y. It is well-known that the heat kernel k_t(x, y) for the connection Laplacian ▽² over the vector bundle ℰ possesses the following asymptotic expansion when x and y are close [5, p. 84] or [11]:

$${\Vert {\partial }_t^k(k_t(x,y)-k_t^N(x,y))\Vert }_l=O(t^{N-d/2-l/2-k}),$$ (8.6)

, where ∥·∥_l is the C_l norm,

$$k_t^N(x,y)≔{(4\pi t)}^{-\frac{d}{2}}{e}^{-\frac{{\Vert v\Vert }^2}{4t}}j{(x,y)}^{-\frac{1}{2}}\sum _{i=0}^N{t}^i{\mathrm{\Phi }}_i(x,y),$$ (8.7)

N > d/2, and Φ_i is a smooth section of the vector bundle ℰ ⊗ ℰ over ℳ × ℳ. Moreover, Φ₀(x, y) = P_{x, y} is the parallel transport from ℰ_y to ℰ_x. In the VDM setup, we take ℰ = Tℳ, the tangent bundle of ℳ. Also, by [5, prop. 1.28], we have the following expansion:

$$j(x,y)=1+\frac{\text{Ric}(v,v)}{6}+O({\Vert v\Vert }^3).$$ (8.8)

Equations (8.7) and (8.8) lead to the following expansion under the assumption ∥v∥² ≪ t:

$$\text{Tr}(k_t(x,y)k_t{(x,y)}^{*})={(4\pi t)}^{-d}{e}^{-\frac{{\Vert v\Vert }^2}{2t}}{(1+\frac{\text{Ric}(v,v)}{6}+O({\Vert v\Vert }^3))}^{-1}\times \text{Tr}((P_{x,y}+O(t))({(P_{x,y}+O(t))}^{*})={(4\pi t)}^{-d}{e}^{-\frac{{\Vert v\Vert }^2}{2t}}(1-\frac{\text{Ric}(v,v)}{6}+O({\Vert v\Vert }^3))(d+O(t))=(d+O(t)){(4\pi t)}^{-d}(1-\frac{{\Vert v\Vert }^2}{2t}+O\left(\frac{{\Vert v\Vert }^4}{t^2}\right)).$$

In particular, for ∥v∥ = 0 we have

$$\text{Tr}(k_t(x,x)k_t{(x,x)}^{*})=(d+O(t)){(4\pi t)}^{-d}.$$

Thus, for ∥v∥² ≪ t ≪ 1, we have

$$d_{\text{VDM},t}^2(x,y)=\text{Tr}(k_t(x,x)k_t{(x,x)}^{*})+\text{Tr}(k_t(y,y)k_t{(y,y)}^{*})-2\text{Tr}(k_t(x,y)k_t{(x,y)}^{*})=d{(4\pi )}^{-d}\frac{{\Vert v\Vert }^2}{t^{d+1}}+O\left(\frac{{\Vert v\Vert }^2}{t^d}\right).$$ (8.9)

By the same argument we can carry out the asymptotic expansion of the diffusion distance d_DM,t (x, y). Denote the eigenfunctions and eigenvalues of the Laplace-Beltrami operator Δ by φ_n and µ_n. We can rewrite the diffusion distance as follows:

$$d_{\text{DM},t}^2(x,y)=\sum _{n=1}^{\infty }{e}^{-{\mu }_{n}t}{({\varphi }_n(x)-{\varphi }_n(y))}^2={\tilde{k}}_t(x,x)+{\tilde{k}}_t(y,y)-2{\tilde{k}}_t(x,y),$$ (8.10)

where k̃_t is the heat kernel of the Laplace-Beltrami operator. Note that the Laplace- Beltrami operator is equal to the connection Laplacian operator defined over the trivial line bundle over ℳ. As a result, equation (8.7) also describes the asymptotic expansion of the heat kernel for the Laplace-Beltrami operator as

$${\tilde{k}}_t(x,y)={(4\pi t)}^{-\frac{d}{2}}{e}^{-\frac{{\Vert v\Vert }^2}{4t}}{(1+\frac{\text{Ric}(v,v)}{6}+O({\Vert v\Vert }^3))}^{-\frac{1}{2}}(1+O(t)).$$

Putting these facts together, we obtain

$$d_{\text{DM},t}^2(x,y)={(4\pi )}^{-d/2}\frac{{\Vert v\Vert }^2}{2t^{d/2+1}}+O\left(\frac{{\Vert v\Vert }^2}{t^d}\right),$$ (8.11)

, when ∥v∥² ≪ t ≪ 1.

9 Application of VDM to Cryo-Electron Microscopy

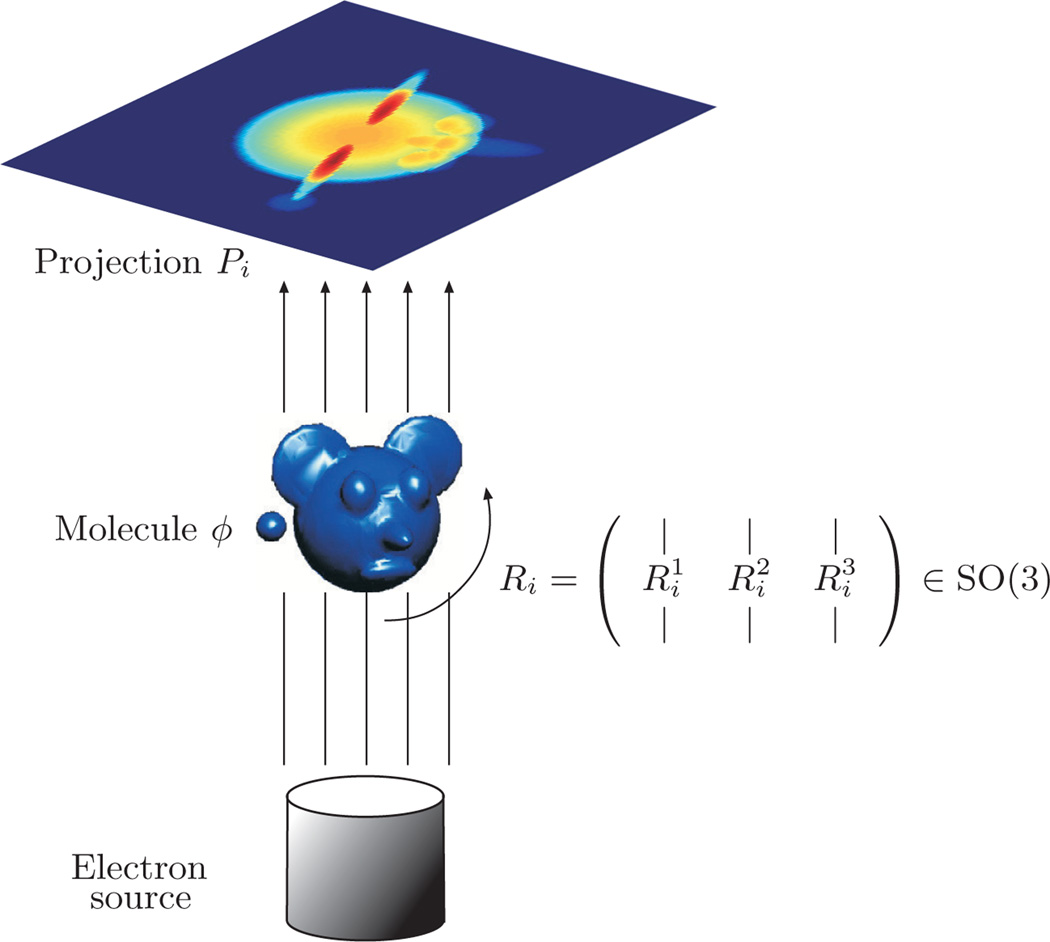
In addition to being a general framework for data analysis and manifold learning, VDM is useful for performing robust multireference rotational alignment of objects, such as one-dimensional periodic signals, two-dimensional images, and three-dimensional shapes. In this section, we briefly describe the application of VDM to a particular multireference rotational alignment problem of two-dimensional images that arise in the field of cryo-electron microscopy (cryo-EM). A more comprehensive study of this problem can be found in [19, 37]. It can be regarded as a prototypical multireference alignment problem, and we expect many other multireference alignment problems that arise in areas such as computer vision and computer graphics to benefit from the proposed approach.

The goal in cryo-EM [14] is to determine three-dimensional macromolecular structures from noisy projection images taken at unknown random orientations by an electron microscope, i.e., a random computational tomography (CT). Determining three-dimensional macromolecular structures for large biological molecules remains vitally important, as witnessed, for example, by the 2003 Chemistry Nobel Prize, co-awarded to R. MacKinnon for resolving the three-dimensional structure of the Shaker K⁺ channel protein, and by the 2009 Chemistry Nobel Prize, awarded to V. Ramakrishnan, T. Steitz, and A. Yonath for studies of the structure and function of the ribosome. The standard procedure for structure determination of large molecules is X-ray crystallography. The challenge in this method is often more in the crystallization itself than in the interpretation of the X-ray results, since many large proteins have so far withstood all attempts to crystallize them.

In cryo-EM, an alternative to X-ray crystallography, the sample of macromolecules is rapidly frozen in an ice layer so thin that their tomographic projections are typically disjoint; this seems the most promising alternative for large molecules that defy crystallization. The cryo-EM imaging process produces a large collection of tomographic projections of the same molecule, corresponding to different and unknown projection orientations. The goal is to reconstruct the three-dimensional structure of the molecule from such unlabeled projection images, where data sets typically range from 10⁴ to 10⁵ projection images whose size is roughly 100 × 100 pixels. The intensity of the pixels in a given projection image is proportional to the line integrals of the electric potential induced by the molecule along the path of the imaging electrons (see Figure 9.1). The highly intense electron beam destroys the frozen molecule, and it is therefore impractical to take projection images of the same molecule at known different directions as in the case of classical CT. In other words, a single molecule can be imaged only once, rendering an extremely low signal-to-noise ratio (SNR) for the images (see Figure 9.2 for a sample of real microscope images), mostly due to shot noise induced by the maximal allowed electron dose (other sources of noise include the varying width of the ice layer and partial knowledge of the contrast function of the microscope). In the basic homogeneity setting considered hereafter, all imaged molecules are assumed to have the exact same structure; they differ only by their spatial rotation. Every image is a projection of the same molecule but at an unknown random three-dimensional rotation, and the cryo-EM problem is to find the three-dimensional structure of the molecule from a collection of noisy projection images.

Figure 9.1.

Schematic drawing of the imaging process: every projection image corresponds to some unknown three-dimensional rotation of the unknown molecule.

Figure 9.2.

A collection of four real electron microscope images of the E. coli 50S ribosomal subunit; courtesy of Dr. Fred Sigworth (Yale Medical School).

The rotation group SO(3) is the group of all orientation-preserving orthogonal transformations about the origin of the three-dimensional euclidean space ℝ³ under the operation of composition. Any three-dimensional rotation can be expressed using a 3 × 3 orthogonal matrix

$$R=\left(\begin{array}{ccc}\hfill |\hfill & \hfill |\hfill & \hfill |\hfill \\ R^1& \hfill R^2\hfill & \hfill R^3\hfill \\ \hfill |\hfill & \hfill |\hfill & \hfill |\hfill \end{array}\right)$$

satisfying RR^Τ = R^ΤR = I_3×3 and det R = 1. The column vectors R₁, R₂, R₃ of R form an orthonormal basis to ℝ³. To each projection image P there corresponds a 3 × 3 unknown rotation matrix R describing its orientation (see Figure 9.1). Excluding the contribution of noise, the intensity P(x, y) of the pixel located at (x, y) in the image plane corresponds to the line integral of the electric potential induced by the molecule along the path of the imaging electrons, that is,

$$P(x,y)={\int }_{-\infty }^{\infty }\varphi (x{R}^1+y{R}^2+z{R}^3)dz$$ (9.1)

where φ : ℝ³ ↦ ℝ is the electric potential of the molecule in some fixed “laboratory” coordinate system. The projection operator (9.1) is also known as the X-ray transform [29].

We therefore identify the third column R³ of R as the imaging direction, also known as the viewing angle of the molecule. The first two columns R¹ and R² form an orthonormal basis for the plane in ℝ³ perpendicular to the viewing angle R³. All clean projection images of the molecule that share the same viewing angle look the same up to some in-plane rotation. That is, if R_i and R_j are two rotations with the same viewing angle $R_i^3=R_j^3,\text{then}{R}_i^1,R_i^2\text{and}{R}_j^1,R_j^2$ are two orthonormal bases for the same plane. On the other hand, two rotations with opposite viewing angles $R_i^3=-R_j^3$ give rise to two projection images that are the same after reflection (mirroring) and some in-plane rotation.

As projection images in cryo-EM have extremely low SNR, a crucial initial step in all reconstruction methods is “class averaging” [14, 41]. Class averaging is the grouping of a large data set of n noisy raw projection images P₁, P₂; …, P_n into clusters such that images within a single cluster have similar viewing angles (it is possible to artificially double the number of projection images by including all mirrored images). Averaging rotationally aligned noisy images within each cluster results in “class averages”; these are images that enjoy a higher SNR and are used in later cryo-EM procedures such as the angular reconstitution procedure [40] that requires better-quality images. Finding consistent class averages is challenging due to the high level of noise in the raw images as well as the large size of the image data set. A sketch of the class-averaging procedure is shown in Figure 9.3.

Figure 9.3.

(a) A clean simulated projection image of the ribosomal subunit generated from its known volume. (b) Noisy instance of (a), denoted P_i, obtained by the addition of white Gaussian noise. For the simulated images we chose the SNR to be higher than that of experimental images in order for image features to be clearly visible. (c) Noisy projection, denoted P_j, taken at the same viewing angle but with a different in-plane rotation. (d) Averaging the noisy images (b) and (c) after in-plane rotational alignment. The class average of the two images has a higher SNR than that of the noisy images (b) and (c), and it has better similarity with the clean image (a).

Penczek, Zhu, and Frank [31] introduced the rotationally invariant K-means clustering procedure to identify images that have similar viewing angles. Their rotationally invariant distance d_RID(i, j) between image P_i and image P_j is defined as the euclidean distance between the images when they are optimally aligned with respect to in-plane rotations (assuming the images are centered)

$$d_{\text{RID}}(i,j)=\underset{\theta \in [0,2\pi )}{\text{min}}\Vert P_i-R(\theta )P_j\Vert ,$$ (9.2)

, where R(θ) is the rotation operator of an image by an angle θ in the counterclockwise direction. Prior to computing the invariant distances of (9.2), a common practice is to center all images by correlating them with their total average $\frac{1}{n}{\mathrm{\Sigma }}_{i=1}^n{P}_i$, which is approximately radial (i.e., has little angular variation) due to the randomness in the rotation. The resulting centers usually miss the true centers by only a few pixels (as can be validated in simulations during the refinement procedure). Therefore, like [31], we also choose to focus on the more challenging problem of rotational alignment by assuming that the images are properly centered, while the problem of translational alignment can be solved later by solving an overdetermined linear system.

It is worth noting that the specific choice of metric to measure proximity between images can make a big difference in class averaging. The cross-correlation and euclidean distance (9.2) are by no means optimal measures of proximity. In practice, it is common to denoise the images prior to computing their pairwise distances. Although the discussion that follows is independent of the particular choice of filter or distance metric, we emphasize that filtering can have a dramatic effect on finding meaningful class averages.

The invariant distance between noisy images that share the same viewing angle (with perhaps a different in-plane rotation) is expected to be small. Ideally, all neighboring images of some reference image P_i in a small invariant distance ball centered at P_i should have similar viewing angles, and averaging such neighboring images (after proper rotational alignment) would amplify the signal and diminish the noise.

Unfortunately, due to the low SNR, it often happens that two images of completely different viewing angles have a small invariant distance. This can happen when the realizations of the noise in the two images match well for some random in-plane rotational angle, leading to spurious neighbor identification. Therefore, averaging the nearest-neighbor images can sometimes yield a poor estimate of the true signal in the reference image.

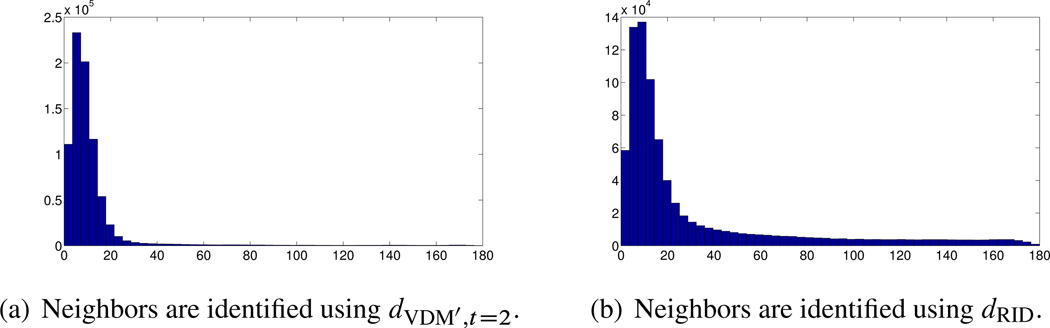
The histograms of Figure 9.5 demonstrate the ability of small rotationally invariant distances to identify images with similar viewing directions. For each image we use the rotationally invariant distances to find its 40 nearest neighbors among the entire set of n = 40;000 images. In our simulation we know the original viewing directions, so for each image we compute the angles (in degrees) between the viewing direction of the image and the viewing directions of its 40 neighbors. Small angles indicate successful identification of “true” neighbors that belong to a small spherical cap, while large angles correspond to outliers. We see that for $\text{SNR=}\frac{1}{2}$ there are no outliers, and all the viewing directions of the neighbors belong to a spherical cap whose opening angle is about 8°. However, for lower values of the SNR, there are outliers, indicated by arbitrarily large angles (all the way to 180°).

Figure 9.5.

Histograms of the angle (in degrees, x-axis) between the viewing directions of 40,000 images and the viewing directions of their 40 nearest neighboring images as found by computing the rotationally invariant distances. (Courtesy of Zhizhen Zhao, Princeton University)

Clustering algorithms, such as the K-means algorithm, perform much better than naive nearest-neighbors averaging, because they take into account all pairwise distances, not just distances to the reference image. Such clustering procedures are based on the philosophy that images that share a similar viewing angle with the reference image are expected to have a small invariant distance not only to the reference image but also to all other images with similar viewing angles. This observation was utilized in the rotationally invariant K-means clustering algorithm [31]. Still, due to noise, the rotationally invariant K-means clustering algorithm may suffer from misidentifications at the low SNR values present in experimental data.

VDM is a natural algorithmic framework for the class-averaging problem, as it can further improve the detection of neighboring images even at lower SNR values. The rotationally invariant distance neglects an important piece of information, namely, the optimal angle that realizes the best rotational alignment in (9.2):

$${\theta }_{ij}=\underset{\theta \in [0,2\pi )}{\text{argmin}}\Vert P_i-R(\theta )P_j\Vert ,i,j=1,2,\dots ,n.$$ (9.3)

In VDM, we use the optimal in-plane rotation angles θ_ij to define the orthogonal transformations O_ij and to construct the matrix S in (3.1). The eigenvectors and eigenvalues of D⁻¹S (other normalizations of S are also possible) are then used to define the vector diffusion distances between images.

This VDM based classification method has proven to be quite powerful in practice. We applied it to a set of n = 40;000 noisy images with $\text{SNR=}\frac{1}{64}$. For every image we found the 40 nearest neighbors using the vector diffusion metric. In the simulation we knew the viewing directions of the images, and we computed for each pair of neighbors the angle (in degrees) between their viewing directions. The histogram of these angles is shown in Figure 9.6 (left panel). About 92% of the identified images belong to a small spherical cap of opening angle 20° whereas this percentage is only about 65% when neighbors are identified by the rotationally invariant distances (right panel). We remark that for $\text{SNR=}\frac{1}{50}$, the percentage of correctly identified images by the VDM method goes up to about 98%.

Figure 9.6.

$\text{SNR =}\frac{1}{64}$: Histogram of the angles (x-axis, in degrees) between the viewing directions of each image (out of 40;000) and its 40 neighboring images. Left: neighbors are post-identified using vector diffusion distances. Right: neighbors are identified using the original rotationally invariant distances d_RID.

The main advantage of the algorithm presented here is that it successfully identifies images with similar viewing angles even in the presence of a large number of spurious neighbors, that is, even when many pairs of images with viewing angles that are far apart have relatively small rotationally invariant distances. In other words, the VDM-based algorithm is shown to be robust to outliers.

10 Summary and Discussion

This paper introduced vector diffusion maps, an algorithmic and mathematical framework for analyzing data sets where scalar affinities between data points are accompanied by orthogonal transformations. The consistency among the orthogonal transformations along different paths that connect any fixed pair of data points is used to define an affinity between them. We showed that this affinity is equivalent to an inner product, giving rise to the embedding of the data points in a Hilbert space and to the definition of distances between data points, to which we referred as vector diffusion distances.

For data sets of images, the orthogonal transformations and the scalar affinities are naturally obtained via the procedure of optimal registration. The registration process seeks to find the optimal alignment of two images over some class of transformations (also known as deformations), such as rotations, reflections, translations, and dilations. For the purpose of vector diffusion mapping, we extract from the optimal deformation only the corresponding orthogonal transformation (rotation and reflection). We demonstrated the usefulness of the vector diffusion map framework in the organization of noisy cryo-electron microscopy images, an important step towards resolving three-dimensional structures of macromolecules. Optimal registration is often used in various mainstream problems in computer vision and computer graphics, for example, in optimal matching of three-dimensional shapes. We therefore expect the vector diffusion map framework to become a useful tool in such applications.

In the case of manifold learning, where the data set is a collection of points in a high-dimensional euclidean space, but with a low-dimensional Riemannian manifold structure, we detailed the construction of the orthogonal transformations via the optimal alignment of the orthonormal bases of the tangent spaces. These bases are found using the classical procedure of PCA. Under certain mild conditions about the sampling process of the manifold, we proved that the orthogonal transformation obtained by the alignment procedure approximates the parallel transport operator between the tangent spaces. The proof required careful analysis of the local PCA step, which we believe is interesting in its own right. Furthermore, we proved that if the manifold is sampled uniformly, then the matrix that lies at the heart of the vector diffusion map framework approximates the connection Laplacian operator. Following spectral graph theory terminology, we call that matrix the connection Laplacian of the graph. Using different normalizations of the matrix we proved convergence to the connection Laplacian operator also for the case of nonuniform sampling. We showed that the vector diffusion mapping is an embedding and proved its relation with the geodesic distance using the asymptotic expansion of the heat kernel for vector fields. These results provide the mathematical foundation for the algorithmic framework that underlies the vector diffusion mapping.

We expect many possible extensions and generalizations of the vector diffusion mapping framework. We conclude by mentioning a few of them.

• Topology of the data. In [36] we showed how the vector diffusion mapping can determine if a manifold is orientable or nonorientable, and in the latter case to embed its double covering in a euclidean space. To that end we used the information in the determinant of the optimal orthogonal transformation between bases of nearby tangent spaces. In other words, we used just the optimal reflection between two orthonormal bases. This simple example shows that vector diffusion mapping can be used to extract topological information from the point cloud. We expect more topological information can be extracted using appropriate modifications of the vector diffusion mapping.

• Hodge and higher-order Laplacians. Using tensor products of the optimal orthogonal transformations it is possible to construct higher-order connection Laplacians that act on p-forms (p ≥ 1). The index theorem [16] relates topological structure with geometrical structure. For example, the so-called Betti numbers are related to the multiplicities of the harmonic p-forms of the Hodge Laplacian. For the extraction of topological information it would therefore be useful to modify our construction in order to approximate the Hodge Laplacian instead of the connection Laplacian.

• Multiscale, sparse, and robust PCA. In the manifold learning case, an important step of our algorithm is local PCA for estimating the bases for tangent spaces at different data points. In the description of the algorithm, a single-scale parameter ∊_PCA is used for all data points. It is conceivable that a better estimation can be obtained by choosing a different, location-dependent scale parameter. A better estimation of the tangent space T_xiℳ may be obtained by using a location-dependent scale parameter ∊_PCA,i due to several reasons: nonuniform sampling of the manifold, varying curvature of the manifold, and global effects such as different pieces of the manifold that are almost touching at some points (i.e., varying the “condition number” of the manifold). Choosing the correct scale was recently considered in [28], where a multiscale approach was taken to resolve the optimal scale. We recommend the incorporation of such multiscale PCA approaches into the vector diffusion mapping framework. Another difficulty that we may face when dealing with real-life data sets is that the underlying assumption about the data points being located exactly on a low-dimensional manifold does not necessarily hold. In practice, the data points are expected to reside off the manifold, either due to measurement noise or due to the imperfection of the low-dimensional manifold model assumption. It is therefore necessary to estimate the tangent spaces in the presence of noise. Noise is a limiting factor for successful estimation of the tangent space, especially when the data set is embedded in a high-dimensional space and noise affects all coordinates [23]. We expect recent methods for robust PCA [7] and sparse PCA [6, 24] to improve the estimation of the tangent spaces and as a result to become useful in the vector diffusion map framework.

• Random matrix theory and noise sensitivity. The matrix S that lies at the heart of the vector diffusion map is a block matrix whose blocks are either d × d orthogonal matrices O_ij or the zero blocks. We anticipate that for some applications the measurement of O_ij would be imprecise and noisy. In such cases, the matrix S can be viewed as a random matrix, and we expect tools from random matrix theory to be useful in analyzing the noise sensitivity of its eigenvectors and eigenvalues. The noise model may also allow for outliers, for example, orthogonal matrices that are uniformly distributed over the orthogonal group O(d) (according to the Haar measure). Notice that the expected value of such random orthogonal matrices is 0, which leads to robustness of the eigenvectors and eigenvalues even in the presence of a large number of outliers (see, for example, the random matrix theory analysis in [35]).

• Compact and noncompact groups and their matrix representation. As mentioned earlier, the vector diffusion mapping is a natural framework to organize data sets for which the affinities and transformations are obtained from an optimal alignment process over some class of transformations (deformations). In this paper we focused on utilizing orthogonal transformations. At this point the reader has probably asked herself the following question: Is the method limited to orthogonal transformations, or is it possible to utilize other groups of transformations such as translations, dilations, and more? We note that the orthogonal group O(d) is a compact group that has a matrix representation and remark that the vector diffusion mapping framework can be extended to such groups of transformations without much difficulty. However, the extension to noncompact groups, such as the euclidean group of rigid transformation, the general linear group of invertible matrices, and the special linear group is less obvious. Such groups arise naturally in various applications, rendering the importance of extending the vector diffusion mapping to the case of noncompact groups.

Figure 2.1.

The orthonormal basis of the tangent plane T_xiℳ is determined by local PCA using data points inside a euclidean ball of radius $\sqrt{{\epsilon }_{\text{PCA}}}$ centered at x_i. The bases for T_xiℳ and T_xjℳ are optimally aligned by an orthogonal transformation O_ij that can be viewed as a mapping from T_xjℳ to T_xiℳ.

Figure 9.4.

Simulated projection with various levels of additive Gaussian white noise.

Appendix A

Some Differential Geometry Background

The purpose of this appendix is to provide the required mathematical background for readers who are not familiar with concepts such as the parallel transport operator, connection, and the connection Laplacian. We illustrate these concepts by considering a surface ℳ embedded in ℝ³.

Given a function f (x) : ℝ³ → ℝ, its gradient vector field is given by

$$\nabla f≔(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}).$$

Through the gradient, we can find the rate of change of f at x ∈ ℝ³ in a given unit vector v ∈ ℝ³, using the directional derivative:

$$\nabla f(x)(v)≔\underset{t\to 0}{\text{lim}}\frac{f(x+tv)-f(x)}{t}.$$

Define ▽_vf(x) := ▽f(x)(v).

Let X be a vector field on ℝ³,

$$X(x,y,z)=(f_1(x,y,z),f_2(x,y,z),f_3(x,y,z)).$$

It is natural to extend the derivative notion to a given vector field X at x ∈ ℝ³ by mimicking the derivative definition for functions in the following way:

$$\underset{t\to 0}{\text{lim}}\frac{X(x+tv)-X(x)}{t}$$ (A.1)

where v ∈ ℝ³. Following the same notation for the directional derivative of a function, we denote this limit by ▽_vX(x). This quantity tells us that at x, following the direction v, we compare the vector field at two points x and x + tv, and see how the vector field changes. While this definition looks good at first sight, we now explain that it has certain shortcomings that need to be fixed in order to generalize it to the case of a surface embedded in ℝ³.

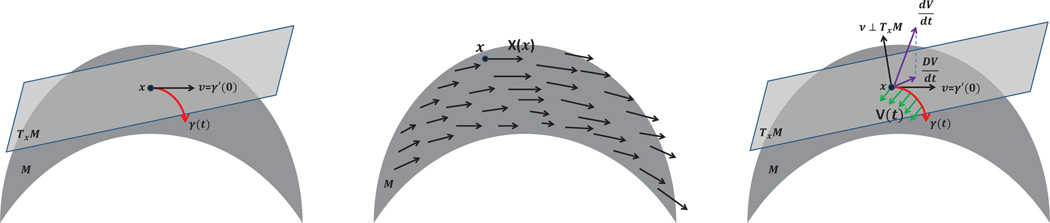
Consider a two-dimensional smooth surface ℳ embedded in ℝ³ by ι. Fix a point x ∈ ℳ and a smooth curve γ(t) : (−∊, ∊); → ℳ ⊂ ℝ³ where ∊ ≪ 1 and γ(0) = x. We call γʹ(₀) ∈ ℝ³ a tangent vector to ℳ at x. The two-dimensional subspace in ℝ³ spanned by the collection of all tangent vectors to ℳ at x is defined to be the tangent plane at x and denoted by T_xℳ;⁷ see Figure A.1 (left panel). Having defined the tangent plane at each point x ∈ ℳ, we define a vector field X over ℳ to be a differentiable map that maps x to a tangent vector in T_xℳ.⁸

Figure A.1.

Left: a tangent plane and a curve γ. Middle: a vector field. Right: the covariant derivative.

We now generalize the definition of the derivative of a vector field over ℝ³ (A.1) to define the derivative of a vector field over ℳ. The first difficulty we face is how to make sense of “X(x +tv),” since x + tv does not belong to ℳ. This difficulty can be tackled easily by changing the definition (A.1) a bit by considering the curve γ: (−∊, ∊) → ℳ ⊂ ℝ³ so that γ(0) = x and γʹ(₀) = v. Thus, (A.1) becomes

$$\underset{t\to 0}{\text{lim}}\frac{X(\gamma (t))-X(\gamma (0))}{t}$$ (A.2)

where v ∈ ℝ³. In ℳ, the existence of the curve γ: (−∊, ∊) → ℝ³ and γ(0) = x and γʹ(0) = v is guaranteed by the classical ordinary differential equation theory. However, (A.2) still cannot be generalized to ℳ directly even though X(γ(t)) is well-defined. The difficulty we face here is how to compare X(γ(t)) and X(x), that is, how to make sense of the subtraction X(γ(t)) − X(γ(0)). It is not obvious since a priori we do not know how T_γ(t)ℳ and T_γ(0)ℳ are related. The way we proceed is by defining an important notion in differential geometry called “parallel transport,” which plays an essential role in our VDM framework.

Fix a point x ∈ ℳ and a vector field X on ℳ, and consider a parametrized curve γ: (−∊, ∊) → ℳ so that γ(0) = x. Define a vector-valued function V : (−∊, ∊) → ℝ³ by restricting X to γ, that is, V(t) = X(γ(t)). The derivative of V is well-defined as usual:

$$\frac{\mathrm{d}V}{\mathrm{d}t}(h)≔\underset{t\to 0}{\text{lim}}\frac{V(h+t)-V(h)}{t},$$

where h ∈ (−∊; ∊). The covariant derivative $\frac{DV}{dt}(h)$ is defined as the projection of $\frac{dV}{dt}(h)$ onto T_γ(h)ℳ. Then, using the definition of $\frac{DV}{dt}(h)$, we consider the following equation:

$$\{\begin{array}{c}\frac{DW}{\mathrm{d}t}(t)=0,\hfill \\ W(0)=w,\hfill \end{array}$$

where w ∈ T_γ(0)ℳ. The solution W(t) exists by the classical ordinary differential equation theory. The solution W(t) along γ(t) is called the parallel vector field along the curve γ(t), and we also call W(t) the parallel transport of w along the curve γ(t) and denote W(t) = P_{γ(t),γ (0)}w.

We come back to address the initial problem: how to define the “derivative” of a given vector field over a surface ℳ. We define the covariant derivative of a given vector field X over ℳ as follows:

$${\nabla }_{v}X(x)=\underset{t\to 0}{\text{lim}}\frac{P_{\gamma (0),\gamma (t)}X(\gamma (t))-X(\gamma (0))}{t},$$ (A.3)

where γ: (−∊, ∊) → ℳ with γ(0) = x ∈ ℳ, γʹ (0) = v ∈ T_γ(0)ℳ. This definition says that if we want to analyze how a given vector field at x ∈ ℳ changes along the direction v, we choose a curve γ so that γ(0) = x and γʹ(₀) = v, and then “transport” the vector field value at point γ(t) to γ(0) = x so that the comparison of the two tangent planes makes sense. The key point of the whole story is that without applying parallel transport to transport the vector at point γ(t) to T_γ(0)ℳ, then the subtraction X(γ(t)) – X(γ(0)) ∈ ℝ³ in general does not live on T_xℳ, which distorts the notion of derivative. For comparison, let us reconsider definition (A.1). Since at each point x ∈ ℝ³, the tangent plane at x is T_xℝ³ = ℝ³, the subtraction X(x + tv) – X(x) always makes sense. To be more precise, the true meaning of X(x+tv) is P_γ(0),γ(t)X(γ(t)), where P_γ(0),γ(t) = id, and γ(t) = x + tv.

With the above definition, when X and Y are two vector fields on ℳ, we define ▽_XY to be a new vector field on ℳ so that

$${\nabla }_{X}Y(x)≔{\nabla }_{X(x)}Y.$$

Note that X(x) ∈ T_xℳ. We call ▽ a connection on ℳ. (The notion of connection can be quite general. For our purposes, this definition is sufficient.)

Once we know how to differentiate a vector field over ℳ, it is natural to consider the second-order differentiation of a vector field. The second-order differentiation of a vector field is a natural notion in ℝ³. For example, we can define a second-order differentiation of a vector field X over ℝ³ as follows:

$${\nabla }^{2}X≔{\nabla }_x{\nabla }_{x}X+{\nabla }_y{\nabla }_{y}X+{\nabla }_z{\nabla }_{z}X,$$ (A.4)

where x, y, z are standard unit vectors corresponding to the three axes. This definition can be generalized to a vector field over ℳ as follows:

$${\nabla }^{2}X(x)≔{\nabla }_{E_1}{\nabla }_{E_1}X(x)+{\nabla }_{E_2}{\nabla }_{E_2}X(x),$$ (A.5)

where X is a vector field over ℳ, x ∈ ℳ, and E₁, E₂ are two vector fields on ℳ that satisfy ▽_EiE_j = 0 for i, j = 1, 2. The condition ▽_EiE_j = 0 (for i, j = 1, 2) is needed for technical reasons. (Please see [32] for details.) Note that in the ℝ³ case (A.4), if we set E₁ = x, E₂ = y, and E₃ = z, then ▽_EiE_j = 0 for i, j = 1, 2, 3. The operator ▽₂ is called the connection Laplacian operator, which lies at the heart of the VDM framework. The notion of an eigenvector field over ℳ is defined to be the solution of the following equation:

$${\nabla }^{2}X(x)=\lambda X(x)$$

for some λ ∈ ℝ. The existence and other properties of the eigenvector fields can be found in [16]. Finally, we comment that all the above definitions can be extended to the general manifold setup without much difficulty, where, roughly speaking, a “manifold” is the higher-dimensional generalization of a surface. (We will not provide details in the manifold setting, and refer readers to standard differential geometry textbooks, such as [32].)

Appendix B

Proofs of Theorems 5.3, 5.5, and 5.6

Throughout this appendix, we adapt Assumption 5.1 and Definition 5.2 (see also Table 1.1). We divide the proof of Theorem 5.3 into four theorems, each of which has its own interest. The first theorem, Theorem B.1, states that the columns of the matrix O_i that are found by local PCA (see (2.4)) form an orthonormal basis to a d-dimensional subspace of ℝ^p that approximates the embedded tangent plane ι_*T_xiℳ. The proven order of approximation is crucial for proving Theorem 5.3. The proof of Theorem B.1 involves geometry and probability theory.

THEOREM B.1. In addition to Assumption 5.1, suppose K_PCA ∈ C₂([0, 1]). If ∊_PCA = O(n^−2/(d+2)) and $x_i\notin ℳ\sqrt{{\epsilon }_{\text{PCA}}}$ then, with high probability (w.h.p.), the columns ${\{u_l(x_i)\}}_{l=1}^d$ of the p × d matrix O_i, which is determined by local PCA, form an orthonormal basis to a d-dimensional subspace of ℝ^p that deviates from ${\iota }_{*}{T}_{x_i}ℳ\text{by}O({\epsilon }_{\text{PCA}}^{3/2})$ in the following sense:

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{3/2})=O(n^{-\frac{3}{d+2}}),$$ (B.1)

where Θ_i is a p × d matrix whose columns form an orthonormal basis to ι_*T_xiℳ. Let the minimizer in (B.1) be

$${\widehat{O}}_i=\underset{O\in O(d)}{\text{argmin}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}},$$ (B.2)

and denote by Q_i the p × d matrix

$$Q_i≔{\mathrm{\Theta }}_i{\widehat{O}}_i^{\mathrm{{\rm T}}},$$ (B.3)

and e_l(x_i) the l^th column of Q_i. The columns of Q_i form an orthonormal basis to ι_*T_xiℳ, and

$${\Vert O_i-Q_i\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}).$$ (B.4)

If $x_i\in ℳ\sqrt{{\epsilon }_{\text{PCA}}}$ then, w.h.p.

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{1/2})=O(n^{-\frac{1}{d+2}}).$$

Better convergence near the boundary is obtained for ∊_PCA = O(n^−2/(d+1)), which gives

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{3/4})=O(n^{-\frac{3}{2(d+1)}})$$

for $x_i\in ℳ\sqrt{{\epsilon }_{\text{PCA}}}$, and

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{5/4})=O(n^{-\frac{5}{2(d+1)}})$$

for $x_i\notin ℳ\sqrt{{\epsilon }_{\text{PCA}}}$.

Theorem B.1 may seem a bit counterintuitive at first glance. When considering data points in a ball of radius $\sqrt{{\epsilon }_{\text{PCA}}}$, it is expected that the order of approximation would be O(∊_PCA), while equation (B.1) indicates that the order of approximation is higher $(\frac{3}{2}\text{in stead of}1)$. The true order of approximation for the tangent space, as observed in (B.4), is still O(∊_PCA). The improvement observed in (B.1) is of relevance to Theorem B.2, and we relate it to the probabilistic nature of the PCA procedure, more specifically, to a large-deviation result for the error in the law of large numbers for the covariance matrix that underlies PCA. Since the convergence of PCA is slower near the boundary, then for manifolds with boundary we need a smaller ∊_PCA. Specifically, for manifolds without boundary we choose ∊_PCA = O(n_−2/(d+2)), and for manifolds with boundary we choose ∊_PCA = O(n^−2/(d+1)). We remark that the first choice also works for manifolds with boundary at the expense of a slower convergence rate.

The second theorem, Theorem B.2, states that the d × d orthonormal matrix O_ij which is the output of the alignment procedure (2.5), approximates the parallel transport operator P_xi,_xj from x_j to x_i along the geodesic connecting them. Assuming that $\Vert x_i-x_j\Vert =0(\sqrt{\epsilon })$ (here, ∊ is different than ∊_PCA), the order of this approximation is $O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})$ whenever x_i, x_j are away from the boundary. This result is crucial for proving Theorem 5.3. The proof of Theorem B.2 uses Theorem B.1 and is purely geometric.

THEOREM B.2. Consider $x_i,x_j\notin ℳ\sqrt{{\epsilon }_{PCA}}$ satisfying that the geodesic distance between x_i and x_j is $O(\sqrt{\epsilon })$. For ∊_PCA = O(n^−2/(d+2)) w.h.p., O_ij approximates P_{xi, xj} in the following sense:

$$O_{ij}{\overline{X}}_j={(\langle {\iota }_{*}{P}_{x_i,x_j}X(x_j),u_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})\text{for all}X\in C^3(Tℳ),$$ (B.6)

where ${\overline{X}}_i\equiv {(\langle {\iota }_{*}X(x_i),u_l(x_i)\rangle )}_{l=1}^d\in {ℝ}^{d}and{\{u_l(x_i)\}}_{l=1}^d$ is an orthonormal set determined by local PCA. For $x_i,x_j\in ℳ\sqrt{{\epsilon }_{PCA}}$

$$O_{ij}{\overline{X}}_j={(\langle {\iota }_{*}{P}_{x_i,x_j}X(x_j),u_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{1/2}+{\epsilon }^{3/2})\text{for all}X\in C^3(Tℳ).$$ (B.7)

For∊_PCA = O(n^−2/(d+1)), the orders of ∊_PCA in the error terms change according to Theorem B.1.

The third theorem, Theorem B.3, states that the n × n block matrix $D_{\alpha }^{-1}{S}_{\alpha }$ is a discrete approximation of an integral operator over smooth sections of the tangent bundle. The integral operator involves the parallel transport operator. The proof of Theorem B.3 mainly uses probability theory.

THEOREM B.3. In addition to Assumption 5.1 suppose ∊_PCA = O(n^−2/(d+2)). For $x_i\notin ℳ\sqrt{{\epsilon }_{\text{PCA}}}$ we have w.h.p.

$$\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}={(\langle {\iota }_{*}{T}_{\epsilon ,\alpha }X(x_i),u_l(x_i)\rangle )}_{l=1}^d+O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}}+{\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}),$$ (B.8)

where T_{∊, α} is defined in (5.2), ${\overline{X}}_i\equiv {(\langle {\iota }_{*}X(x_i),u_l(x_i)\rangle )}_{l=1}^d\in {ℝ}^d,{\{u_l(x_i)\}}_{l=1}^d$ is the orthonormal set determined by local PCA, and O_ij is the optimal orthogonal transformation determined by the alignment procedure.

For $x_i\in ℳ\sqrt{{\epsilon }_{\text{PCA}}}$ we have w.h.p.

$$\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}={(\langle {\iota }_{*}{T}_{\epsilon ,\alpha }X(x_i),u_l(x_i)\rangle )}_{l=1}^d+O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}}+{\epsilon }_{\text{PCA}}^{1/2}+{\epsilon }^{3/2}).$$ (B.9)

For ∊_PCA = O(n^−2/(d+1)) the orders of ∊_PCA in the error terms change according to Theorem B.1.

The fourth theorem, Theorem B.4, states that the operator T_{∊, α} can be expanded in powers of $\sqrt{\epsilon }$, where the leading-order term is the identity operator, the second-order term is the connection Laplacian operator plus some possible potential terms, and the first- and third-order terms vanish for vector fields that are sufficiently smooth. For α = 1, the potential terms vanish, and as a result, the second-order term is the connection Laplacian. The proof is based on geometry.

THEOREM B.4. For $x\notin ℳ\sqrt{\epsilon }$ we have

$$T_{\epsilon ,\alpha }X(x)=X(x)+\epsilon \frac{m_2}{2d}\{{\nabla }^{2}X(x)+\frac{2\nabla X(x)·\nabla (p^{1-\alpha })(x)}{p^{1-\alpha }(x)}\}+O({\epsilon }^2),$$ (B.10)

where T_{∊, α} is defined in (5.2).

COROLLARY B.5. Under the same conditions and notation as in Theorem B.4 if X ∈ C³(Tℳ), then for all $x\notin ℳ\sqrt{\epsilon }$ we have

$$T_{\epsilon ,1}X(x)=X(x)+\epsilon \frac{m_2}{2d}{\nabla }^{2}X(x)+O({\epsilon }^2).$$ (B.11)

Putting Theorems B.1, B.3, and B.4 together, we now prove Theorem 5.3.

PROOF OF THEOREM 5.3. Suppose $x_i\notin ℳ\sqrt{\epsilon }$. By Theorem B.3, w.h.p.

$$\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}={(\langle {\iota }_{*}{T}_{\epsilon ,\alpha }X(x_i),u_l(x_i)\rangle )}_{l=1}^d+O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}}+{\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})={(\langle {\iota }_{*}{T}_{\epsilon ,\alpha }X(x_i),e_l(x_i)\rangle )}_{l=1}^d+O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}}+{\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}),$$

where ∊_PCA = O(n^−2/(d+2)), and Theorem B.1 was used to replace u_l(x_i) by e_l(x_i). Using Theorem B.4 for the right-hand side of (B), we get

$$\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}={(\langle {\iota }_{*}X(x_i)+\epsilon \frac{m_2}{2d}{\iota }_{*}\{{\nabla }^{2}X(x_i)+\frac{2\nabla X(x_i)·\nabla (p^{1-\alpha })(x_i)}{p^{1-\alpha }(x_i)}\},e_l(x_i)\rangle )}_{l=1}^d+O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}}+{\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}).$$

For ∊ = O(n^−2/(d+4)), upon dividing by ∊, the three error terms are

$$\frac{1}{n^{1/2}{\epsilon }^{d/4+1/2}}=O(n^{-\frac{1}{d+4}}),\frac{1}{\epsilon }{\epsilon }_{\text{PCA}}^{3/2}=O(n^{-\frac{d+8}{(d+1)(d+2)}}),{\epsilon }^{\frac{1}{2}}=O(n^{-\frac{1}{d+4}}).$$

Clearly the three error terms vanish as n → ∞. Specifically, the dominant error is O(n^−1/(d+4)), which is the same as $O(\sqrt{\epsilon })$. As a result, in the limit n → ∞, almost surely,

$$\underset{n\to \infty }{\text{lim}}\frac{1}{\epsilon }[\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}-{\overline{X}}_i]=\frac{m_2}{2d}{(\langle {\iota }_{*}\{{\nabla }^{2}X(x_i)+\frac{2\nabla X(x_i)·\nabla (p^{1-\alpha })(x_i)}{p^{1-\alpha }(x_i)}\},e_l(x_i)\rangle )}_{l=1}^d,$$

as required.

B.1 Preliminary Lemmas

For the proofs of Theorems B.1 through B.4, we need the following lemmas: LEMMA B.6. In polar coordinates around x ∈ ℳ, the Riemannian measure is given by

$$\mathrm{d}V({\text{exp}}_{x}t\theta )=J(t,\theta )\mathrm{d}t\mathrm{d}\theta ,$$

, where θ ∈ T_xℳ, ∥θ∥ = 1, t > 0 and

$$J(t,\theta )=t^{d-1}+t^{d+1}\text{Ric}(\theta ,\theta )+O(t^{d+2}).$$

PROOF. Please see [32].

The following lemma is needed in Theorems B.1 and B.2.

LEMMA B.7. Fix x ∈ ℳ and denote by exp_x the exponential map at x and by ${\exp }_{\iota (x)}^{{ℝ}^p}$ the exponential map of ℝ^p at ι(x). With the identification of T_ι(x) ℝ^p with ℝ^p, for v ∈ T_xℳ with ∥v∥ ≪ 1 we have

$$\iota \circ {\text{exp}}_x(v)=\iota (x)+d\iota (v)+\frac{1}{2}\mathrm{\Pi }(v,v)+\frac{1}{6}{\nabla }_v\mathrm{\Pi }(v,v)+O({\Vert v\Vert }^4).$$ (B.12)

Furthermore, for w ∈ T_xℳ ≅ ℝ^d, we have

$$d{[\iota \circ {\text{exp}}_x]}_v(w)=d{[\iota \circ {\text{exp}}_x]}_{v=0}(w)+\mathrm{\Pi }(v,w)+\frac{1}{6}{\nabla }_v\mathrm{\Pi }(v,w)+\frac{1}{3}{\nabla }_w\mathrm{\Pi }(v,v)+O({\Vert v\Vert }^3).$$ (B.13)

PROOF. Define $\varphi :={({\text{exp}}_{\iota (x)}^{{ℝ}^p})}^{-1}\circ \iota \circ {\text{exp}}_x$, that is,

$$\iota \circ {\text{exp}}_x={\text{exp}}_{\iota (x)}^{{ℝ}^p}\circ \varphi .$$ (B.14)

Since φ can be viewed as a function from T_xℳ ≅ ℝ^d to T_ι,(x)ℝ^p≅ ℝ^p we can Taylor-expand it to get

$$\iota \circ {\text{exp}}_x(v)=\iota (x)+d\varphi {|}_0(v)+\frac{1}{2}\nabla d\varphi {|}_0(v,v)+\frac{1}{6}{\nabla }^{2}d\varphi {|}_0(v,v,v)+O({\Vert v\Vert }^4),$$

where the equality holds since φ(0) = 0 and ${\text{exp}}_{\iota (x)}^{{ℝ}^p}(w)=\iota (x)+w$ for all w ∈ T_ι(x)ℝ^p if we identify T_ι(x)ℝ^p with ℝ^p. To conclude (B.12), we claim that

$${\nabla }^{k}d\varphi {|}_0(v,\dots ,v)={\nabla }^{k}d\iota {|}_x(v,\dots ,v)\text{for all}k\ge 0,$$

which comes from the chain rule and the fact that

$${\nabla }^{k}d{\text{exp}}_x{|}_0(v,\dots ,v)=0\text{for all}k\ge 1.$$ (B.15)

Indeed, we have that d ${\text{exp}}_x\in \mathrm{\Gamma }(T^{*}{T}_xℳ\otimes {\text{exp}}_x^{*}Tℳ)$ from the definition of the exponential map, where ${\text{exp}}_x^{*}Tℳ$ is the pullback tangent bundle, and

$$\nabla d{\text{exp}}_x(v\prime (t),v\prime (t))={\nabla }_{d{\text{exp}}_x(v\prime (t))}d{\text{exp}}_x(v\prime (t))-d{\text{exp}}_x({\nabla }_{v\prime (t)}v\prime (t))=0,$$

where v ∈ T_xℳ, v(t) = tv ∈ T_xℳ, and vʹ(t) = v ∈ T_tvT_xℳ. The claim (B.15) for k = 1 follows when t = 0. The result for k ≥ 2 follows from a similar argument. Hence

$$\iota \circ {\text{exp}}_x(v)=\iota (x)+d\iota (v)+\frac{1}{2}\nabla d\iota (v,v)+\frac{1}{6}{\nabla }^{2}d\iota (v,v,v)+O({\Vert v\Vert }^4),$$

which gives us (B.12) since ▽dι =Π and ▽₂dι = ▽Π.

Next we show (B.13). When w ∈ T_vT_xℳ, we view d[ι○exp_x].(w) as a function from T_xℳ≅ ℝ^d to ℝ^p so that when ∥v∥ ≪ 1, Taylor expansion gives us

$$d{[\iota \circ {\text{exp}}_x]}_v(w)=d{[\iota \circ {\text{exp}}_x]}_0(w)+\nabla (d[\iota \circ {\text{exp}}_x].(w)){|}_0(v)+\frac{1}{2}{\nabla }^2(d[\iota \circ {\text{exp}}_x].(w)){|}_0(v,v)+O({\Vert v\Vert }^3);$$ (B.16)

here d and ▽ are understood as the ordinary differentiation over ℝ^d. To simplify the calculation of ▽(d[ι ○ exp_x].(w))|₀ (v) and ▽²(d[ι ○ exp_x].(w))|₀ (v,v), we denote

$$H_w(v)=\frac{1}{6}{\nabla }_w\mathrm{\Pi }(v,v)+\frac{1}{6}{\nabla }_v\mathrm{\Pi }(w,v)+\frac{1}{6}{\nabla }_v\mathrm{\Pi }(v,w)$$

and

$$G_w(u,v)=\frac{1}{3}({\nabla }_w\mathrm{\Pi }(u,v)+{\nabla }_u\mathrm{\Pi }(w,u)+{\nabla }_u\mathrm{\Pi }(u,w)),$$

where u, v, w ∈ ℝ^d. By (B.12), when ∥v∥ is small enough, we have

$$d{[\iota \circ {\text{exp}}_x]}_v(w)=\underset{\delta \to 0}{\text{lim}}\frac{\iota \circ {\text{exp}}_x(v+\delta w)-\iota \circ {\text{exp}}_x(v)}{\delta }=\underset{\delta \to 0}{\text{lim}}\frac{d\iota (\delta w)+\mathrm{\Pi }(v,\delta w)+\delta H_w(v)+R(v+\delta w)-R(v)}{\delta },$$

where R(v) is the remainder term in the Taylor expansion:

$$R(v)=\sum _{|\alpha |=4}\frac{1}{\alpha !}({\int }_0^1{(1-t)}^3{\nabla }^4(\iota \circ {\text{exp}}_x)(tv)\mathrm{d}t)v^{\alpha }.$$

Thus

$$d{[\iota \circ {\text{exp}}_x]}_v(w)=d\iota (w)+\mathrm{\Pi }(v,w)+H_w(v)+O(\Vert v\Vert \Vert w\Vert )$$ (B.17)

since

$$\frac{R(v+\delta w)-R(v)}{\delta }=O(\Vert v\Vert \Vert w\Vert ).$$

Similarly, from (B.17), when ∥u∥ is small enough we have

$$\nabla (d[\iota \circ {\text{exp}}_x].(w)){|}_u(v)=\underset{\delta \to 0}{\text{lim}}\frac{d{[\iota \circ {\text{exp}}_x]}_{u+\delta v}(w)-d{[\iota \circ {\text{exp}}_x]}_u(w)}{\delta }=\mathrm{\Pi }(v,w)+G_w(u,v)+O(\Vert u\Vert \Vert v\Vert \Vert w\Vert )$$ (B.18)

and

$${\nabla }^{2}d([\iota \circ {\text{exp}}_x].(w)){|}_0(v,v)=G(v,v).$$ (B.19)

As a result, from (B.17), (B.18), and (B.19) we have that

$$d{[\iota \circ {\text{exp}}_x]}_0(w)=d\iota (w),\nabla (d[\iota \circ {\text{exp}}_x].(w)){|}_0(v)=\mathrm{\Pi }(v,w),G(v,v)=\frac{1}{3}{\nabla }_v\mathrm{\Pi }(v,w)+\frac{2}{3}{\nabla }_w\mathrm{\Pi }(v,v).$$

Plugging them into (B.16) we get (B.13) as required.

LEMMA B.8. Suppose x, y ∈ ℳ such that y = exp_x(tθ)where θ ∈ T_xℳ and ∥θ∥ = 1. If t ≪ 1, then h = ∥ι(x) – ι(y)∥ ≪ 1 satisfies

$$t=h+\frac{1}{24}\Vert \mathrm{\Pi }(\theta ,\theta )\Vert h^3+O(h^4).$$ (B.20)

PROOF. Please see [9] or apply (B.12) directly.

LEMMA B.9. Fixx ∈ ℳ and y = exp_x(tθ)where θ ∈ T_xℳ and ∥θ∥ = 1. Let ${\{{\partial }_l(x)\}}_{l=1}^d$ be the normal coordinate on a neighborhood U of x; then for a sufficiently small t we have

$${\iota }_{*}{P}_{y,x}{\partial }_l(x)={\iota }_{*}{\partial }_l(x)+t\mathrm{\Pi }(\theta ,{\partial }_l(x))+\frac{t^2}{6}{\nabla }_{\theta }\mathrm{\Pi }(\theta ,{\partial }_l(x))+\frac{t^2}{3}{\nabla }_{{\partial }_l(x)}\mathrm{\Pi }(\theta ,\theta )-\frac{t^2}{6}{\iota }_{*}{P}_{y,x}(ℛ(\theta ,{\partial }_l(x))\theta )+O(t^3)$$ (B.21)

for all l = 1, 2, …, d.

PROOF. Choose an open subset U ⊂ ℳ small enough and find an open neighborhood B of 0 ∈ T_xℳ so that exp_x : B → U is diffeomorphic. It is well-known that

$${\partial }_l({\text{exp}}_x(t\theta ))=\frac{J_l(t)}{t},$$

where J_l(t) is the Jacobi field with J_l(0) = 0 and ▽_tJ_l (0) = ∂_l(x). By applying Taylor’s expansion in a neighborhood of t = 0, we have

$$J_l(t)=P_{y,x}(J_l(0)+t{\nabla }_t{J}_l(0)+\frac{t^2}{2}{\nabla }_t^2{J}_l(0)+\frac{t^3}{6}{\nabla }_t^3{J}_l(0))+O(t^4).$$

Since $J_l(0)={\nabla }_t^2{J}_l(0)=0$, the following relationship holds:

$${\partial }_l({\text{exp}}_x(t\theta ))=P_{y,x}({\nabla }_t{J}_l(0)+\frac{t^2}{6}{\nabla }_t^3{J}_l(0))+O(t^3)=P_{y,x}{\partial }_l(x)+\frac{t^2}{6}{P}_{y,x}(ℛ(\theta ,{\partial }_l(x))\theta )+O(t^3).$$ (B.22)

Thus we obtain

$$P_{y,x}{\partial }_l(x)={\partial }_l({\text{exp}}_x(t\theta ))-\frac{t^2}{6}{P}_{y,x}(ℛ(\theta ,{\partial }_l(x))\theta )+O(t^3).$$ (B.23)

On the other hand, from (B.13) in Lemma B.7 we have

$${\iota }_{*}{\partial }_l({\text{exp}}_x(t\theta ))={\iota }_{*}{\partial }_l(x)+t\mathrm{\Pi }(\theta ,{\partial }_l(x))+\frac{t^2}{6}{\nabla }_{\theta }\mathrm{\Pi }(\theta ,{\partial }_l(x))+\frac{t^2}{3}{\nabla }_{{\partial }_l(x)}\mathrm{\Pi }(\theta ,\theta )+O(t^3).$$ (B.24)

Putting (B.23) and (B.24) together, it follows that, for l = 1, 2, … d,

$${\iota }_{*}{P}_{y,x}{\partial }_l(x)=l_{*}{\partial }_l({\text{exp}}_x(t\theta ))-\frac{t^2}{6}{\iota }_{*}{P}_{y,x}(ℛ(\theta ,{\partial }_l(x))\theta )+O(t^3)=l_{*}{\partial }_l(x)+t\mathrm{\Pi }(\theta ,{\partial }_l(x))+\frac{t^2}{6}{\nabla }_{\theta }\mathrm{\Pi }(\theta ,{\partial }_l(x))+\frac{t^2}{3}{\nabla }_{{\partial }_l(x)}\mathrm{\Pi }(\theta ,\theta )-\frac{t^2}{6}{\iota }_{*}{P}_{y,x}(ℛ(\theta ,{\partial }_l(x))\theta )+O(t^3).$$ (B.25)

B.2 Proof of Theorem B.1

Fix $x_i\notin ℳ\sqrt{{\epsilon }_{\text{PCA}}}$. Denote by ${\{v_k\}}_{k=1}^p$ the standard orthonormal basis of ℝ^pthat is, v_k has 1 in the k_th entry and 0 elsewhere. We can properly translate and rotate the embedding ι so that ι(x_i) = 0 and the first d components {v₁, v₂; …, v^d} ⊂ ℝ^p form the orthonormal basis of ι_*T_xiℳ, and we find a normal coordinate ${\{{\partial }_k\}}_{k=1}^d$ around x_i so that ι_*∂_k(x_i) = v_k. Instead of directly analyzing the matrix B_i that appears in the local PCA procedure given in (2.3), we analyze the covariance matrix ${\mathrm{\Xi }}_i:=B_i{B}_i^{\mathrm{{\rm T}}}$, whose eigenvectors coincide with the left singular vectors of B_i. Throughout this proof, we let K = K_PCA to simply the notation. We rewrite Ξ_i as

$${\mathrm{\Xi }}_i=\sum _{j\ne i}^n{F}_j,$$ (B.26)

where

$$F_j=K\left(\frac{{\Vert \iota (x_i)-\iota (x_j)\Vert }_{{ℝ}^p}}{\sqrt{{\epsilon }_{\text{PCA}}}}\right)(\iota (x_j)-\iota (x_i)){(\iota (x_j)-\iota (x_i))}^{\mathrm{{\rm T}}}$$ (B.27)

and

$$F_j(k,l)=K\left(\frac{{\Vert \iota (x_i)-\iota (x_j)\Vert }_{{ℝ}^p}}{\sqrt{{\epsilon }_{\text{PCA}}}}\right)\langle \iota (x_j)-\iota (x_i),v_k\rangle \langle \iota (x_j)-\iota (x_i),v_l\rangle .$$ (B.28)

Let $B\sqrt{{\epsilon }_{\text{PCA}}}(x_i)$ denote the geodesic ball of radius $\sqrt{{\epsilon }_{\text{PCA}}}$ around x_i. We apply the same variance error analysis as in [34, sec. 3] to approximate Ξ_i. Since the points x_i are independent identically distributed (i.i.d.), F_j, j ≠ i , are also i.i.d.; by the law of large numbers one expects

$$\frac{1}{n-1}\sum _{j\ne i}^n{F}_j\approx 𝔼F,$$ (B.29)

where F = F₁,

$$𝔼F=\underset{B_{\sqrt{{\epsilon }_{\text{PCA}}}}(x_i)}{\int }{K}_{{\epsilon }_{\text{PCA}}}(x_i,y)(\iota (y)-\iota (x_i)){(\iota (y)-\iota (x_i))}^{\mathrm{{\rm T}}}p(y)\mathrm{d}V(y)$$ (B.30)

and

$$𝔼F(k,l)=\underset{B_{\sqrt{{\epsilon }_{\text{PCA}}}}(x_i)}{\int }{K}_{{\epsilon }_{\text{PCA}}}(x_i,y)\langle \iota (y)-\iota (x_i),v_k\rangle \langle \iota (y)-\iota (x_i),v_l\rangle p(y)\mathrm{d}V(y).$$ (B.31)

In order to evaluate the first moment 𝔼F (k, l) of (B.31), we note that for y = exp_xi v, where v ∈ T_xiℳ, by (B.12) in Lemma B.7 we have

$$\langle \iota ({\text{exp}}_{x_i}v)-\iota (x_i),v_k\rangle =\langle {\iota }_{*}v,v_k\rangle +\frac{1}{2}\langle \mathrm{\Pi }(v,v),v_k\rangle +\frac{1}{6}\langle {\nabla }_v\mathrm{\Pi }(v,v),v_k\rangle +O({\Vert v\Vert }^4).$$ (B.32)

By substituting (B.32) into (B.31), applying Taylor’s expansion, and combining Lemma B.8 and Lemma B.6, we have

$$\underset{B_{\sqrt{{\epsilon }_{\text{PCA}}}}(x_i)}{\int }{K}_{{\epsilon }_{\text{PCA}}}(x_i,y)\langle \iota (y)-\iota (x_i),v_k\rangle \langle \iota (y)-\iota (x_i),v_l\rangle p(y)\mathrm{d}V(y)=\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{{\epsilon }_{\text{PCA}}}}\left[K\right(\frac{t}{\sqrt{{\epsilon }_{\text{PCA}}}})+O(\frac{t^3}{\sqrt{{\epsilon }_{\text{PCA}}}}\left)\right]\times \{t^2\langle {\iota }_{*}\theta ,v_k\rangle \langle {\iota }_{*}\theta ,v_l\rangle +\frac{t^3}{2}(\langle \mathrm{\Pi }(\theta ,\theta ),v_k\rangle \langle {\iota }_{*}\theta ,v_l\rangle +\langle \mathrm{\Pi }(\theta ,\theta ),v_l\rangle \langle {\iota }_{*}\theta ,v_k\rangle )+O(t^4)\}\times (p(x_i)+t{\nabla }_{\theta }p(x_i)+O(t^2))(t^{d-1}+O(t^{d+1}))\mathrm{d}t\mathrm{d}\theta =\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{{\epsilon }_{\text{PCA}}}}\left[K\right(\frac{t}{\sqrt{{\epsilon }_{\text{PCA}}}})\langle {\iota }_{*}\theta ,v_k\rangle \langle {\iota }_{*}\theta ,v_l\rangle p(x_i)t^{d+1}+O(t^{d+3})]\mathrm{d}t\mathrm{d}\theta ,$$

where the last equality holds since integrals involving odd powers of θ must vanish due to the symmetry of the sphere 𝕊 _d−1. Note that 〈ι_*θ, v_k〉 = 0 when k = d + 1, d + 2, … p. Therefore,

$$𝔼F(k,l)=\{\begin{array}{cc}{D{\epsilon }_{\text{PCA}}}^{d/2+1}+O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{for}1\le k=l\le d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{otherwise}.\hfill \end{array}$$ (B.33)

where $D=p(x_i){\int }_{{𝕊}^{d-1}}{\left|\langle {\iota }_{*}\theta ,v_1\rangle \right|}^{2}d\theta {\int }_0^{1}K(u)u^{d+1}\mathrm{d}u$ is a positive constant. Similar considerations give the second moment of F(k, l) as

$$𝔼[F{(k,l)}^2]=\{\begin{array}{cc}O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{for}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+4})\hfill & \text{for}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+3})\hfill & \text{otherwise}.\hfill \end{array}$$ (B.34)

Hence, the variance of F(k, l) becomes

$$\text{Var}F(k,l)=\{\begin{array}{cc}O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{for}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+4})\hfill & \text{for}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+3})\hfill & \text{otherwise}.\hfill \end{array}$$ (B.35)

We now move on to establish a large-deviation bound on the estimation of $\frac{1}{n-1}{\mathrm{\Sigma }}_{j\ne i}{F}_j(k,l)$ by its mean 𝔼F_j(k, l). For that purpose, we measure the deviation from the mean value by α and define its probability by

$$p_{k,l}(n,\alpha )≔\text{Pr}\left\{\right|\frac{1}{n-1}\sum _{j\ne i}^n{F}_j(k,l)-𝔼F(k,l)|>\alpha \}.$$ (B.36)

To establish an upper bound for the probability p_k,l(n, α), we use Bernstein’s inequality; see, e.g., [22]. Define

$$Y_j(k,l)≔F_j(k,l)-𝔼F(k,l).$$

Clearly Y_j (k, l) are zero mean i.i.d. random variables. From the definition of F_j (k, l) (see (B.27) and (B.28)) and from the calculation of its first moment (B.33), it follows that Y_j (k, l) are bounded random variables. More specifically,

$$Y_j(k,l)=\{\begin{array}{cc}O({\epsilon }_{\text{PCA}})\hfill & \text{for}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^2)\hfill & \text{for}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{3/2})\hfill & \text{otherwise}.\hfill \end{array}$$ (B.37)

.

Consider first the case k, l = 1, 2, …, d, for which Bernstein’s inequality gives

$$p_{k,l}(n,\alpha )\le \text{exp}\{-\frac{(n-1){\alpha }^2}{2𝔼(Y_1{(k,l)}^2)+O({\epsilon }_{\text{PCA}})\alpha }\}\le \text{exp}\{-\frac{(n-1){\alpha }^2}{O({{\epsilon }_{\text{PCA}}}^{d/2+2})+O({\epsilon }_{\text{PCA}})\alpha }\}.$$ (B.38)

From (B.38) it follows that for

$$\alpha =O\left(\frac{{{\epsilon }_{\text{PCA}}}^{d/4+1}}{n^{1/2}}\right)$$

and

$$\frac{1}{n^{1/2}{{\epsilon }_{\text{PCA}}}^{d/4}}\ll 1,$$ (B.39)

the probability p_{k, l}(n, α) is exponentially small.

Similarly, for k, l = d + 1, d + 2, …, p, we have

$$p_{k,l}(n,\alpha )\le \text{exp}\{-\frac{(n-1){\alpha }^2}{O({{\epsilon }_{\text{PCA}}}^{d/2+4})+O({{\epsilon }_{\text{PCA}}}^2)\alpha }\},$$

, which means that for

$$\alpha =O\left(\frac{{{\epsilon }_{\text{PCA}}}^{d/4+2}}{n^{1/2}}\right)$$

and (B.39), the probability p_{k, l}(n, α) is exponentially small.

Finally, for k = d+1, d+2, …, p, l = 1, 2, …, d or l = d+1, d+2; …, p, and k = 1, 2, …, d, we have

$$p_{k,l}(n,\alpha )\le \text{exp}\{-\frac{(n-1){\alpha }^2}{O({{\epsilon }_{\text{PCA}}}^{d/2+3})+O({{\epsilon }_{\text{PCA}}}^{3/2})\alpha }\},$$

, which means that for

$$\alpha =O\left(\frac{{{\epsilon }_{\text{PCA}}}^{d/4+3/2}}{n^{1/2}}\right)$$

and (B.39), the probability p_k,l(n, α) is exponentially small. The condition (B.39) is quite intuitive as it is equivalent to n∊_PCA^d/2 ≫ 1, which says that the expected number of points inside $B\sqrt{{\epsilon }_{\text{PCA}}}(x_i)$ should be large.

As a result, when (B.39) holds, w.h.p., the covariance matrix Ξ_i is given by

$${\mathrm{\Xi }}_i={{\epsilon }_{\text{PCA}}}^{d/2+1}D\left[\begin{array}{cc}\hfill I_{d\times d}\hfill & \hfill 0_{d\times p-d}\hfill \\ \hfill 0_{p-d\times d}\hfill & \hfill 0_{p-d\times p-d}\hfill \end{array}\right]$$ (B.40)

$$+{{\epsilon }_{\text{PCA}}}^{d/2+2}\left[\begin{array}{cc}O(1)\hfill & O(1)\hfill \\ O(1)\hfill & O(1)\hfill \end{array}\right]$$ (B.41)

$$+\frac{{{\epsilon }_{\text{PCA}}}^{d/4+1}}{\sqrt{n}}\left[\begin{array}{cc}\hfill O(1)\hfill & \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill \\ \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill & \hfill O({\epsilon }_{\text{PCA}})\hfill \end{array}\right],$$ (B.42)

where I_d×d is the identity matrix of size d×d, and 0_m×mʹ is the zero matrix of size m × mʹ. The error term in (B.41) is the bias term due to the curvature of the manifold, while the error term in (B.42) is the variance term due to finite sampling (i.e., finite n). In particular, under the condition in the statement of the theorem for the sampling rate, namely, ∊_PCA = O(n^−2/(d+2)), we have w.h.p.

$${\mathrm{\Xi }}_i={\epsilon }_{\text{PCA}}^{d/2+1}D\left[\begin{array}{cc}\hfill I_{d\times d}\hfill & \hfill 0_{d\times p-d}\hfill \\ \hfill 0_{p-d\times d}\hfill & \hfill 0_{p-d\times p-d}\hfill \end{array}\right]+{\epsilon }_{\text{PCA}}^{d/2+2}\left[\begin{array}{cc}\hfill O(1)\hfill & \hfill O(1)\hfill \\ \hfill O(1)\hfill & \hfill O(1)\hfill \end{array}\right]+{\epsilon }_{\text{PCA}}^{d/2+3/2}\left[\begin{array}{cc}\hfill O(1)\hfill & \hfill O({\epsilon }_{\text{PCA}}^{1/2})\hfill \\ \hfill O({\epsilon }_{\text{PCA}}^{1/2})\hfill & \hfill O({\epsilon }_{\text{PCA}})\hfill \end{array}\right]={\epsilon }_{\text{PCA}}^{d/2+1}\left\{D\right[\begin{array}{cc}\hfill I_{d\times d}\hfill & \hfill 0_{d\times p-d}\hfill \\ \hfill 0_{p-d\times d}\hfill & \hfill 0_{p-d\times p-d}\hfill \end{array}]+[\begin{array}{cc}\hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill & \hfill O({\epsilon }_{\text{PCA}})\hfill \\ \hfill O({\epsilon }_{\text{PCA}})\hfill & \hfill O({\epsilon }_{\text{PCA}})\hfill \end{array}\left]\right\}.$$ (B.43)

Note that by definition Ξ_i is symmetric, so we rewrite (B.43) as

$${\mathrm{\Xi }}_i={\epsilon }_{\text{PCA}}^{d/2+1}D\left[\begin{array}{cc}\hfill I+{\epsilon }_{\text{PCA}}^{1/2}A\hfill & \hfill {\epsilon }_{\text{PCA}}C\hfill \\ \hfill {\epsilon }_{\text{PCA}}{C}^{\mathrm{{\rm T}}}\hfill & \hfill {\epsilon }_{\text{PCA}}B\hfill \end{array}\right],$$ (B.44)

where I is the d × d identity matrix, A is a d × d symmetric matrix, C is a d × (p – d) matrix, and B is a (p – d) × (p – d) symmetric matrix. All entries of A, B, and C are O(1).

Denote by u_k and λ_k, k = 1, 2, …, p, the eigenvectors and eigenvalues of Ξ_i, where the eigenvectors are orthonormal and the eigenvalues are listed in decreasing order. Using regular perturbation theory, we find that λ_k = D∊_PCA^d/2+1 (1 + O (∊_PCA^1/2)) (for k = 1, 2, …, d), and that the expansion of the first d eigenvectors ${\{u_k\}}_{k=1}^d$ is given by

$$u_k=\left[\begin{array}{c}\hfill {[w_k+O({{\epsilon }_{\text{PCA}}}^{3/2})]}_{d\times 1}\hfill \\ \hfill {[O({\epsilon }_{\text{PCA}})]}_{p-d\times 1}\hfill \end{array}\right]\in {ℝ}^p,$$ (B.45)

where ${\{w_k\}}_{k=1}^d$ are orthonormal eigenvectors of A satisfying $A{w}_k={\lambda }_k^A{w}_k$. Indeed, a direct calculation gives us

$$\left[\begin{array}{cc}\hfill I+{\epsilon }_{\text{PCA}}^{1/2}A\hfill & \hfill {\epsilon }_{\text{PCA}}C\hfill \\ \hfill {\epsilon }_{\text{PCA}}{C}^{\mathrm{{\rm T}}}\hfill & \hfill {\epsilon }_{\text{PCA}}B\hfill \end{array}\right]\left[\begin{array}{c}\hfill w_k+{\epsilon }_{\text{PCA}}^{3/2}{v}_{3/2}+{\epsilon }_{\text{PCA}}^2{v}_2+O({{\epsilon }_{\text{PCA}}}^{5/2})\hfill \\ \hfill {\epsilon }_{\text{PCA}}{z}_1+{\epsilon }_{\text{PCA}}^{3/2}{z}_{3/2}+O({{\epsilon }_{\text{PCA}}}^2)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill w_k+{\epsilon }_{\text{PCA}}^{1/2}A{w}_k+{\epsilon }_{\text{PCA}}^{3/2}{v}_{3/2}+{\epsilon }_{\text{PCA}}^2(A{v}_{3/2}+v_2+C{z}_1)+O({\epsilon }_{\text{PCA}}^{5/2})\hfill \\ \hfill {\epsilon }_{\text{PCA}}{C}^{\mathrm{{\rm T}}}{w}_k+{\epsilon }_{\text{PCA}}^{2}B{z}_1+O({\epsilon }_{\text{PCA}}^{5/2})\hfill \end{array}\right],$$ (B.46)

where v_3/2, v₂ ∈ ℝ^d and z₁, z_3/2 ∈ ℝ_p–d. On the other hand,

$$(1+{\epsilon }_{\text{PCA}}^{1/2}{\lambda }_k^A+{\epsilon }_{\text{PCA}}^2{\lambda }_2+O({\epsilon }_{\text{PCA}}^{5/2}))\left[\begin{array}{c}\hfill w_k+{\epsilon }_{\text{PCA}}^{3/2}{v}_{3/2}+{\epsilon }_{\text{PCA}}^2{v}_2+O({\epsilon }_{\text{PCA}}^{5/2})\hfill \\ \hfill {\epsilon }_{\text{PCA}}{z}_1+{\epsilon }_{\text{PCA}}^{3/2}{z}_{3/2}+O({\epsilon }_{\text{PCA}}^2)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill w_k+{\epsilon }_{\text{PCA}}^{1/2}{\lambda }_k^A{w}_k+{\epsilon }_{\text{PCA}}^{3/2}{v}_{3/2}+{\epsilon }_{\text{PCA}}^2({\lambda }_k^A{v}_2+v_{3/2}+{\lambda }_2{w}_k)+O({\epsilon }_{\text{PCA}}^{5/2})\hfill \\ \hfill {\epsilon }_{\text{PCA}}{z}_1+{\epsilon }_{\text{PCA}}^{3/2}({\lambda }_k^A{z}_1+z_{3/2})+O({\epsilon }_{\text{PCA}}^2)\hfill \end{array}\right],$$ (B.47)

where γ₂ ∈ R. Matching orders of ∊_PCA between (B.46) and (B.47), we conclude that

$$O({\epsilon }_{\text{PCA}}):z_1=C^{\mathrm{{\rm T}}}{w}_k,O({{\epsilon }_{\text{PCA}}}^{3/2}):z_{3/2}=-{\lambda }_k^A{z}_1,O({{\epsilon }_{\text{PCA}}}^2):(A-{\lambda }_k^{A}I)v_{3/2}={\lambda }_2{w}_k-C{C}^{\mathrm{{\rm T}}}{w}_k.$$ (B.48)

Note that the matrix $(A-{\lambda }_k^{A}I)$ appearing in (B.48) is singular and its null space is spanned by the vector w_k so the solvability condition is ${\lambda }_2={\Vert C^{\mathrm{{\rm T}}}{w}_k\Vert }^2/{\Vert w_k\Vert }^2$. We mention that A is a generic symmetric matrix generated due to random finite sampling, so almost surely the eigenvalue ${\lambda }_k^A$ is simple.

Denote by O_i the p × d matrix whose k^th column is the vector u_k. We measure the deviation of the d-dimensional subspace of ℝ^p spanned by u_k, k = 1, 2, …, d, from ιT_xiM by

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}},$$ (B.49)

where Θ_i is a p×d matrix whose k_th column is v_k (recall that v_k is the k_th standard unit vector in ℝ^p). Let Ô be the d × d orthonormal matrix

$$\widehat{O}={\left[\begin{array}{c}\hfill w_1^{\mathrm{{\rm T}}}\hfill \\ ⋮\\ w_d^{\mathrm{{\rm T}}}\end{array}\right]}_{d\times d}.$$

Then,

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}\le {\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-\widehat{O}\Vert }_{\text{HS}}=O({{\epsilon }_{\text{PCA}}}^{3/2}),$$ (B.50)

which completes the proof for points away from the boundary.

Next, we consider $x_i\in ℳ\sqrt{{\epsilon }_{\text{PCA}}}$. The proof is almost the same as the above, so we just point out the main differences without giving the full details. The notations Ξ_i, F_j (k, l), p_k,l(n, α), and Y_j (k, l) refer to the same quantities. Here the expectation of F_j (k, l) is

$$𝔼F(k,l)=\underset{B_{\sqrt{{\epsilon }_{\text{PCA}}}}(x_i)\cap ℳ}{\int }{K}_{{\epsilon }_{\text{PCA}}}(x_i,y)\langle \iota (y)-\iota (x_i),v_k\rangle \times \langle \iota (y)-\iota (x_i),v_l\rangle p(y)\mathrm{d}V(y).$$ (B.51)

Due to the asymmetry of the integration domain ${\text{exp}}_{x_i}^{-1}(B\sqrt{{\epsilon }_{\text{PCA}}}(x_i)\cap ℳ)$ when x_i is near the boundary, we do not expect 𝔼F_j (k, l) to be the same as (B.33) and (B.34), since integrals involving odd powers of θ do not vanish. In particular, when l = d + 1, …, p, k = 1, 2, …, d or k = d + 1, d + 2, …, p, l = 1, 2, …, d, 𝔼F(k, l) becomes

$$\underset{{\text{exp}}_{x_i}^{-1}(B_{\sqrt{{\epsilon }_{\text{PCA}}}}(x_i)\cap ℳ)}{\int }K\left(\frac{t}{\sqrt{{\epsilon }_{\text{PCA}}}}\right)\langle {\iota }_{*}\theta ,v_k\rangle \langle \mathrm{\Pi }(\theta ,\theta ),v_l\rangle p(x_i)t^{d+2}\mathrm{d}t\mathrm{d}\theta +O({{\epsilon }_{\text{PCA}}}^{d/2+2}),$$

which is O(∊_PCA^d/2+3/2). Note that for $x_i\in ℳ\sqrt{{\epsilon }_{\text{PCA}}}$ the bias term in the expansion of the covariance matrix differs from (B.41) when l = d + 1, d = 2, …, p, k = 1, 2, …, d or k = d +1, d +2, …, p, l = 1, 2, …, d. Similar calculations show that

$$𝔼F(k,l)=\{\begin{array}{cc}O({{\epsilon }_{\text{PCA}}}^{d/2+1})\hfill & \text{when}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{when}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+3/2})\hfill & \text{otherwise},\hfill \end{array}$$ (B.52)

$$𝔼[F{(k,l)}^2]=\{\begin{array}{cc}O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{when}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+4})\hfill & \text{when}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+3})\hfill & \text{otherwise},\hfill \end{array}$$ (B.53)

$$\text{Var}F(k,l)=\{\begin{array}{cc}O({{\epsilon }_{\text{PCA}}}^{d/2+2})\hfill & \text{when}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+4})\hfill & \text{when}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{d/2+3})\hfill & \text{otherwise}.\hfill \end{array}$$ (B.54)

Similarly, Y_j (k, l) are also bounded random variables satisfying

$$Y_j(k,l)=\{\begin{array}{cc}O({\epsilon }_{\text{PCA}})\hfill & \text{for}k,l=1,2,\dots ,d,\hfill \\ O({{\epsilon }_{\text{PCA}}}^2)\hfill & \text{for}k,l=d+1,d+2,\dots ,p,\hfill \\ O({{\epsilon }_{\text{PCA}}}^{3/2})\hfill & \text{otherwise}.\hfill \end{array}$$ (B.55)

Consider first the case k, l = 1, 2, …, d, for which Bernstein’s inequality gives

$$p_{k,l}(n,\alpha )\le \text{exp}\{-\frac{(n-1){\alpha }^2}{O({{\epsilon }_{\text{PCA}}}^{d/2+2})+O({\epsilon }_{\text{PCA}})\alpha }\}.$$ (B.56)

From (B.56) it follows that w.h.p.

$$\alpha =O\left(\frac{{{\epsilon }_{\text{PCA}}}^{d/4+1}}{n^{1/2}}\right)$$

provided (B.39). Similarly, for k, l = d + 1, d + 2, …, p, we have

$$p_{k,l}(n,\alpha )\le \text{exp}\{-\frac{(n-1){\alpha }^2}{O({{\epsilon }_{\text{PCA}}}^{d/2+4})+O({{\epsilon }_{\text{PCA}}}^2)\alpha }\},$$

which means that w.h.p.

$$\alpha =O\left(\frac{{{\epsilon }_{\text{PCA}}}^{d/4+2}}{n^{1/2}}\right)$$

provided (B.39). Finally, for k = d + 1, d + 2, …, p, l = 1, 2, …, d, or l = d + 1, d + 2, …, p, k = 1, 2, …, d, we have

$$p_{k,l}(n,\alpha )\le \text{exp}\{-\frac{(n-1){\alpha }^2}{O({{\epsilon }_{\text{PCA}}}^{d/2+3})+O({{\epsilon }_{\text{PCA}}}^{3/2})\alpha }\},$$

which means that w.h.p.

$$\alpha =O\left(\frac{{{\epsilon }_{\text{PCA}}}^{d/4+3/2}}{n^{1/2}}\right)$$

provided (B.39). As a result, under the condition in the statement of the theorem for the sampling rate, namely, ∊_PCA = O(n^−2/(d+2)), we have w.h.p.

$${\mathrm{\Xi }}_i={{\epsilon }_{\text{PCA}}}^{d/2+1}\left[\begin{array}{cc}\hfill O(1)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]+{{\epsilon }_{\text{PCA}}}^{d/2+3/2}\left[\begin{array}{cc}\hfill O(1)\hfill & \hfill O(1)\hfill \\ \hfill O(1)\hfill & \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill \end{array}\right]+\frac{{{\epsilon }_{\text{PCA}}}^{d/4+1}}{\sqrt{n}}\left[\begin{array}{cc}\hfill O(1)\hfill & \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill \\ \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill & \hfill O({\epsilon }_{\text{PCA}})\hfill \end{array}\right]={{\epsilon }_{\text{PCA}}}^{d/2+1}\left\{\right[\begin{array}{cc}\hfill O(1)\hfill & \hfill 0_{d\times p-d}\hfill \\ \hfill 0_{p-d\times d}\hfill & \hfill 0_{p-d\times p-d}\hfill \end{array}]+[\begin{array}{cc}\hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill & \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill \\ \hfill O({{\epsilon }_{\text{PCA}}}^{1/2})\hfill & \hfill O({\epsilon }_{\text{PCA}})\hfill \end{array}\left]\right\}.$$

Then, by the same argument as in the case when $x_i\notin ℳ\sqrt{{\epsilon }_{\text{PCA}}}$, we conclude that

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({{\epsilon }_{\text{PCA}}}^{1/2}).$$

Similar calculations show that for ∊_PCA = O(n^−2/(d+1)) we get

$$\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({{\epsilon }_{\text{PCA}}}^{5/4})\text{for}{x}_i\notin {ℳ}_{\sqrt{{\epsilon }_{\text{PCA}}}},\underset{O\in O(d)}{\text{min}}{\Vert O_i^{\mathrm{{\rm T}}}{\mathrm{\Theta }}_i-O\Vert }_{\text{HS}}=O({{\epsilon }_{\text{PCA}}}^{3/4})\text{for}{x}_i\in {ℳ}_{\sqrt{{\epsilon }_{\text{PCA}}}}.$$

B.3 Proof of Theorem B.2

Denote by O_i the p × d matrix whose columns u_l(x_i), l = 1, 2, …, d, are orthonormal inside ℝ^p as determined by local PCA around x_i. As in (B.3), we denote by e_l(x_i) the l^th column of Q_i where Q_i is a p × d matrix whose columns form an orthonormal basis of ι_*T_xiℳ so by Theorem B.1 ${\Vert O_i^{\mathrm{{\rm T}}}{Q}_i-\text{Id}\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{3/2})for{\epsilon }_{\text{PCA}}=O(n^{-2/(d+2)})$, which is the case of focus here (if ∊_PCA = O(n_−2/(d+1)), then ${\Vert O_i^{\mathrm{{\rm T}}}{Q}_i-\text{Id}\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{5/4})$).

Fix x_i and the normal coordinate ${\{{\partial }_l\}}_{l=1}^d$ around x_i so that ι_*∂_l(x_i) = e_l(x_i). Let x_j = exp_xi tθ, where θ ∈ T_xiℳ, $\Vert \theta \Vert =1,\text{and}t=O(\sqrt{\epsilon })$. Then, by the definition of the parallel transport, we have

$$P_{x_i,x_j}X(x_j)=\sum _{l=1}^{d}g(X(x_j),P_{x_j,x_i}{\partial }_l(x_i)){\partial }_l(x_i),$$ (B.57)

and since the parallel transport and the embedding ι are isometric, we have

$$g(P_{x_i,x_j}X(x_j),{\partial }_l(x_i))=g(X(x_j),P_{x_j,x_i}{\partial }_l(x_i))=\langle {\iota }_{*}X(x_j),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle .$$ (B.58)

Local PCA provides an estimation of an orthonormal basis spanning ι_*T_xiℳ, which is free up to O(d). Thus, there exists R ∈ O(p) so that ι_*T_xjℳ is invariant under R and e_l(x_j) = Rι_*P_xj,xi ∂_l (x_i) for all l = 1, 2, …, d. Hence we have the following relationship:

$$\langle {\iota }_{*}X(x_j),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle =\langle \sum _{k=1}^d\langle {\iota }_{*}X(x_j),e_k(x_j)\rangle e_k(x_j),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle =\sum _{k=1}^d\langle {\iota }_{*}X(x_j),e_k(x_j)\rangle \langle e_k(x_j),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle =\sum _{k=1}^d\langle R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_j),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle \langle {\iota }_{*}X(x_j),e_k(x_j)\rangle ≔\sum _{k=1}^d{\overline{R}}_{l,k}\langle {\iota }_{*}X(x_j),e_k(x_j)\rangle ≔\overline{R}{X}_j,$$ (B.59)

where ${\overline{R}}_{l,k}:=\langle R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle ,\overline{R}:={[{\overline{R}}_{l,k}]}_{l,k=1}^d,\text{and}{X}_j={(\langle {\iota }_{*}X(x_j),e_k(x_j)\rangle )}_{k=1}^d$

On the other hand, since $Q_i^{\mathrm{{\rm T}}}{Q}_j={[{\iota }_{*}{\partial }_l{(x_i)}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)]}_{l,k=1}^d$, Lemma B.9 gives us

$$Q_i^{\mathrm{{\rm T}}}{Q}_j={[{\iota }_{*}{P}_{x_j,x_i}{\partial }_l{(x_i)}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)]}_{l,k=1}^d-t{[\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)]}_{l,k=1}^d-\frac{t^2}{6}{[2{\nabla }_{{\partial }_l(x_i)}\mathrm{\Pi }{(\theta ,\theta )}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)+{\nabla }_{\theta }\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)-{({\iota }_{*}{P}_{x_j,x_i}ℛ(\theta ,{\partial }_l(x_i))\theta )}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)]}_{l,k=1}^d+O({\mathrm{{\rm T}}}^3).$$

We now analyze the right-hand side term by term. Note that since ι_*T_xjℳ is invariant under R, we have $R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)={\mathrm{\Sigma }}_{r=1}^d{\overline{R}}_{r,k}{\iota }_{*}{P}_{x_j,x_i}{\partial }_r(x_i)$. For the O(t) term, we have

$$\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)=\sum _{r=1}^d{\overline{R}}_{r,k}\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}{\iota }_{*}{P}_{x_j,x_i}{\partial }_r(x_i)=\sum _{r=1}^d{\overline{R}}_{r,k}\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}[{\iota }_{*}{\partial }_r(x_i)+t\mathrm{\Pi }(\theta ,{\partial }_r(x_i))+O(t^2)]=t\sum _{r=1}^d{\overline{R}}_{r,k}\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}\mathrm{\Pi }(\theta ,{\partial }_r(x_i))+O(t^2)$$ (B.60)

where the second equality is due to Lemma B.9 and the third equality holds since Π(θ, ∂_l(x_i)) is perpendicular to ι_*∂_r(x_i) for all l, r = 1, 2, …, d. Moreover, the Gauss equation gives us

$$0=\langle ℛ(\theta ,\theta ){\partial }_r(x_i),{\partial }_l(x_i)\rangle =\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}\mathrm{\Pi }(\theta ,{\partial }_r(x_i))-\mathrm{\Pi }{(\theta ,{\partial }_r(x_i))}^{\mathrm{{\rm T}}}\mathrm{\Pi }(\theta ,{\partial }_l(x_i)),$$

which means the matrix

$$S_1≔{[[\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}\mathrm{\Pi }(\theta ,{\partial }_r(x_i))]}_{l,r=1}^d$$

is symmetric.

Fix a vector field X on a neighborhood around x_i so that X(x_i) = θ. By definition we have

$${\nabla }_{{\partial }_l}\mathrm{\Pi }(X,X)={\nabla }_{{\partial }_l}(\mathrm{\Pi }(X,X))-2\mathrm{\Pi }(X,{\nabla }_{{\partial }_l}X).$$ (B.61)

Viewing Tℳ as a subbundle of Tℝ^pwe have the equation of Weingarten:

$${\nabla }_{{\partial }_l}(\mathrm{\Pi }(X,X))=-A_{\mathrm{\Pi }(X,X)}{\partial }_l+{\nabla }_{{\partial }_l}^{\perp }(\mathrm{\Pi }(X,X)),$$ (B.62)

where AΠ(X, X)^∂_l and ${\nabla }_{{\partial }_l}^{\perp }(\mathrm{\Pi }(X,X))$ are the tangential and normal components of ▽_∂l, respectively. Moreover, the following equation holds:

$$\langle A_{\mathrm{\Pi }(X,X)}{\partial }_l,{\iota }_{*}{\partial }_k\rangle =\langle \mathrm{\Pi }({\partial }_l,{\partial }_k),\mathrm{\Pi }(X,X)\rangle .$$ (B.63)

By evaluating (B.61) and (B.62) at x_i we have

$${\nabla }_{{\partial }_l(x_i)}\mathrm{\Pi }{(\theta ,\theta )}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)=\sum _{r=1}^d{\overline{R}}_{r,k}{\nabla }_{{\partial }_l(x_i)}\mathrm{\Pi }{(\theta ,\theta )}^{\mathrm{{\rm T}}}{\iota }_{*}{P}_{x_j,x_i}{\partial }_r(x_i)=\sum _{r=1}^d{\overline{R}}_{r,k}{(-A_{\mathrm{\Pi }(\theta ,\theta )}{\partial }_l(x_i)+{\nabla }_{{\partial }_l(x_i)}^{\perp }(\mathrm{\Pi }(X,X))-2\mathrm{\Pi }(\theta ,{\nabla }_{{\partial }_l(x_i)}X))}^{\mathrm{{\rm T}}}\times [{\iota }_{*}{\partial }_r(x_i)+t\mathrm{\Pi }(\theta ,{\partial }_r(x_i))+O(t^2)]=-\sum _{r=1}^d{\overline{R}}_{r,k}{(A_{\mathrm{\Pi }(\theta ,\theta )}{\partial }_l(x_i))}^{\mathrm{{\rm T}}}{\iota }_{*}{\partial }_r(x_i)+O(t)=-\sum _{r=1}^d{\overline{R}}_{r,k}\langle \mathrm{\Pi }(\theta ,\theta ),\mathrm{\Pi }({\partial }_l(x_i),{\partial }_r(x_i))\rangle +O(t).$$ (B.64)

where the third equality holds since $\mathrm{\Pi }(\theta ,{\nabla }_{{\partial }_l}(x_i)X)\text{and}{\nabla }_{{\partial }_l(x_i)}^{\perp }(\mathrm{\Pi }(X,X))$ are perpendicular to ι_*∂_l(x_i) and the last equality holds by (B.63). Due to the symmetry of the second fundamental form, we know that the matrix

$$S_2={[\langle \mathrm{\Pi }(\theta ,\theta ),\mathrm{\Pi }({\partial }_l(x_i),{\partial }_r(x_i))\rangle ]}_{l,r=1}^d$$

is symmetric.

Similarly we have

$${\nabla }_{\theta }\mathrm{\Pi }{({\partial }_l(x_i),\theta )}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)=\sum _{r=1}^d{\overline{R}}_{r,k}{(A_{\mathrm{\Pi }({\partial }_l(x_i),\theta )}\theta )}^{\mathrm{{\rm T}}}{\iota }_{*}{\partial }_r(x_i)+O(t).$$ (B.65)

Since ${(A_{\mathrm{\Pi }({\partial }_l(x_i),\theta )}\theta )}^{\mathrm{{\rm T}}}{\iota }_{*}{\partial }_r(x_i)=\mathrm{\Pi }{(\theta ,{\partial }_l(x_i))}^{\mathrm{{\rm T}}}\mathrm{\Pi }(\theta ,{\partial }_r(x_i))$ by (B.63), which we denoted earlier by S₁ and used the Gauss equation to conclude that it is symmetric.

To estimate the last term, we work out the following calculation by using the isometry of the parallel transport:

$${({\iota }_{*}{P}_{x_j,x_i}ℛ(\theta ,{\partial }_l(x_i))\theta )}^{\mathrm{{\rm T}}}R{\iota }_{*}{P}_{x_j,x_i}{\partial }_k(x_i)=\sum _{r=1}^d{\overline{R}}_{r,k}\langle {\iota }_{*}{P}_{x_j,x_i}(ℛ(\theta ,{\partial }_l(x_i))\theta ),{\iota }_{*}{P}_{x_j,x_i}{\partial }_r(x_i)\rangle =\sum _{r=1}^d{\overline{R}}_{r,k}g(P_{x_j,x_i}(ℛ(\theta ,{\partial }_l(x_i))\theta ),P_{x_j,x_i}{\partial }_r(x_i))=\sum _{r=1}^d{\overline{R}}_{r,k}g(ℛ(\theta ,{\partial }_l(x_i))\theta ,{\partial }_r(x_i)).$$ (B.66)

Denote $S_3={[g(ℛ(\theta ,{\partial }_l(x_i))\theta ,{\partial }_r(x_i))]}_{l,r=1}^d$, which is symmetric by the definition of ℛ.

By (B.60), (B.64), (B.65), and (B.66) we have

$$Q_i^{\mathrm{{\rm T}}}{Q}_j=\overline{R}+t^2(-S_1-\frac{S_2}{3}+\frac{S_1}{6}-\frac{S_3}{6})\overline{R}+O(t^3)=\overline{R}+t^{2}S\overline{R}+O(t^3),$$ (B.67)

where S:= −S₁ − S₂/3 + S₁/6 − S₃/6 is a symmetric matrix.

Suppose that both x_i and x_j are not in $ℳ\sqrt{\epsilon }$. To finish the proof, we have to understand the relationship between $O_i^{\mathrm{{\rm T}}}{O}_j\text{and}{Q}_i^{\mathrm{{\rm T}}}{Q}_j$ which is rewritten as

$$O_i^{\mathrm{{\rm T}}}{O}_j=Q_i^{\mathrm{{\rm T}}}{Q}_j+{(O_i-Q_i)}^{\mathrm{{\rm T}}}{Q}_j+O_i^{\mathrm{{\rm T}}}(O_j-Q_j).$$ (B.68)

From (B.1) in Theorem B.1, we know

$${\Vert {(O_i-Q_i)}^{\mathrm{{\rm T}}}{Q}_i\Vert }_{\text{HS}}={\Vert O_i^{\mathrm{{\rm T}}}{Q}_i-\text{Id}\Vert }_{\text{HS}}=O({\epsilon }_{\text{PCA}}^{3/2}),$$

which is equivalent to

$${(O_i-Q_i)}^{\mathrm{{\rm T}}}{Q}_i=O({\epsilon }_{\text{PCA}}^{3/2}).$$ (B.69)

Due to (B.67) we have Q_j = Q_i R̄+t²Q_iSR̄+O(t³), which together with (B.69) gives

$${(O_i-Q_i)}^{\mathrm{{\rm T}}}{Q}_j={(O_i-Q_i)}^{\mathrm{{\rm T}}}(Q_i\overline{R}+t^2{Q}_{i}S\overline{R}+O(t^3))=O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}).$$ (B.70)

Together with the fact that $Q_i^{\mathrm{{\rm T}}}=\overline{R}{Q}_j^{\mathrm{{\rm T}}}+t^{2}S\overline{R}{Q}_j^{\mathrm{{\rm T}}}+O(t^3)$ derived from (B.67), we have

$$O_i^{\mathrm{{\rm T}}}(O_j-Q_j)=Q_i^{\mathrm{{\rm T}}}(O_j-Q_j)+{(O_i-Q_i)}^{\mathrm{{\rm T}}}(O_j-Q_j)=(\overline{R}{Q}_j^{\mathrm{{\rm T}}}+t^{2}S\overline{R}{Q}_j^{\mathrm{{\rm T}}}+O(t^3))(O_j-Q_j)+{(O_i-Q_i)}^{\mathrm{{\rm T}}}(O_j-Q_j)=O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})+{(O_i-Q_i)}^{\mathrm{{\rm T}}}(O_j-Q_j).$$ (B.71)

Recall that the following relationship between O_i and Q_i holds (B.45)

$$O_i=Q_i+\left[\begin{array}{c}O({\epsilon }_{\text{PCA}}^{3/2})\hfill \\ O({\epsilon }_{\text{PCA}})\hfill \end{array}\right]$$ (B.72)

when the embedding ι is translated and rotated so that it satisfies ι(x_i) = 0, the first d standard unit vectors {v₁, v₂, … v_d} ⊂ ℝ^p form the orthonormal basis of ι_*T_xiℳ, and the normal coordinates ${\{{\partial }_k\}}_{k=1}^d\text{around}{x}_i\text{satisfy}{\iota }_{*}{\partial }_k(x_i)=v_k$. Similarly, the following relationship between O_j and Q_j holds (B.45):

$$O_j=Q_j+\left[\begin{array}{c}O({\epsilon }_{\text{PCA}}^{3/2})\hfill \\ O({\epsilon }_{\text{PCA}})\hfill \end{array}\right]$$ (B.73)

when the embedding ι is translated and rotated so that it satisfies ι(x_j) = 0, the first d standard unit vectors {v₁, v₂, … v_d} ⊂ ℝ^p form the orthonormal basis of ι_*T_xjℳ, and the normal coordinates ${\{{\partial }_k\}}_{k=1}^d$ around x_j satisfy ι_*∂_k(x_j) = R̄ι_*P_xj,xi∂_k(x_i)=v_k. Also, recall that ι_*T_xjℳis invariant under the rotation R and from Lemma B.9, e_k(x_i) and e_k(x_j) are related by $e_k(x_j)=e_k(x_i)+O(\sqrt{\epsilon })$. Therefore,

$$O_j-Q_j=(R+O(\sqrt{\epsilon }))\left[\begin{array}{c}O({\epsilon }_{\text{PCA}}^{3/2})\hfill \\ O({\epsilon }_{\text{PCA}})\hfill \end{array}\right]=\left[\begin{array}{c}O({\epsilon }_{\text{PCA}}^{3/2})\hfill \\ O({\epsilon }_{\text{PCA}})\hfill \end{array}\right]$$ (B.74)

when expressed in the standard basis of ℝ^p so that the first d standard unit vectors {v₁, v₂, … v_d} ⊂ ℝ^p form the orthonormal basis of ι_*T_xiℳ. Hence, plugging (B.74) into (B.71) gives

$$O_i^{\mathrm{{\rm T}}}(O_j-Q_j)=O({\epsilon }_{\text{PCA}}^{3/2})+{(O_i-Q_i)}^{\mathrm{{\rm T}}}(O_j-Q_j)=O({\epsilon }_{\text{PCA}}^{3/2}).$$ (B.75)

Inserting (B.71) and (B.75) into (B.68), we conclude

$$O_i^{\mathrm{{\rm T}}}{O}_j=Q_i^{\mathrm{{\rm T}}}{Q}_j+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}).$$ (B.76)

Recall that O_ij is defined as O_ij = UV^Τ, where U and V come from the singular value decomposition of $O_i^{\mathrm{{\rm T}}}{O}_{j,}\text{that is},O_i^{\mathrm{{\rm T}}}{O}_j=U\mathrm{\Sigma }{V}^{\mathrm{{\rm T}}}$. As a result,

$$O_{ij}=\underset{O\in O(d)}{\text{argmin}}{\Vert O_i^{\mathrm{{\rm T}}}{O}_j-O\Vert }_{\text{HS}}=\underset{O\in O(d)}{\text{argmin}}{\Vert Q_i^{\mathrm{{\rm T}}}{Q}_j+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-O\Vert }_{\text{HS}}=\underset{O\in O(d)}{\text{argmin}}{\Vert {\overline{R}}^{\mathrm{{\rm T}}}{Q}_i^{\mathrm{{\rm T}}}{Q}_j+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-{\overline{R}}^{\mathrm{{\rm T}}}O\Vert }_{\text{HS}}=\underset{O\in O(d)}{\text{argmin}}{\Vert \text{Id}+t^2{\overline{R}}^{\mathrm{{\rm T}}}S\overline{R}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-{\overline{R}}^{\mathrm{{\rm T}}}O\Vert }_{\text{HS}}.$$

Since R̄^ΤSR̄ is symmetric, we rewrite R̄^ΤSR̄ = UΣU^Τ, where U is an orthonormal matrix and Σ is a diagonal matrix with the eigenvalues of R̄^ΤSR̄ on its diagonal. Thus,

$$\text{Id}+t^2{\overline{R}}^{\mathrm{{\rm T}}}S\overline{R}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-{\overline{R}}^{\mathrm{{\rm T}}}O=U(\text{Id}+t^2\mathrm{\Sigma })U^{\mathrm{{\rm T}}}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-{\overline{R}}^{\mathrm{{\rm T}}}O.$$

Since the Hilbert-Schmidt norm is invariant to orthogonal transformations, we have

$${\Vert \text{Id}+t^2{\overline{R}}^{\mathrm{{\rm T}}}S\overline{R}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-{\overline{R}}^{\mathrm{{\rm T}}}O\Vert }_{\text{HS}}={\Vert U(\text{Id}+t^2\mathrm{\Sigma })U^{\mathrm{{\rm T}}}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-{\overline{R}}^{\mathrm{{\rm T}}}O\Vert }_{\text{HS}}={\Vert \text{Id}+t^2\mathrm{\Sigma }+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})-U^{\mathrm{{\rm T}}}{\overline{R}}^{\mathrm{{\rm T}}}OU\Vert }_{\text{HS}}.$$

Since U^ΤR̄^ΤOU is orthogonal, the minimizer must satisfy $U^{\mathrm{{\rm T}}}{\overline{R}}^{\mathrm{{\rm T}}}OU=\text{Id}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})$, as otherwise the sum of squares of the matrix entries would be larger. Hence we conclude $O_{ij}=\overline{R}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})$

Applying (B.59) and (B.45), we conclude

$$O_{ij}{\overline{X}}_j=\overline{R}{\overline{X}}_j+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})=\overline{R}{(\langle {\iota }_{*}X(x_j),u_l(x_j)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})=\overline{R}{(\langle {\iota }_{*}X(x_j),e_l(x_j)+O({\epsilon }_{\text{PCA}}^{3/2})\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})={(\langle {\iota }_{*}X(x_j),{\iota }_{*}{P}_{x_j,x_i}{\partial }_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})={(\langle {\iota }_{*}{P}_{x_i,x_j}X(x_j),e_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})={(\langle {\iota }_{*}{P}_{x_i,x_j}X(x_j),u_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}).$$

This concludes the proof for points away from the boundary.

When x_i and x_j are in $ℳ\sqrt{{\epsilon }_{\text{PCA}}}$, by the same reasoning as above we get

$$O_{ij}{\overline{X}}_j={(\langle {\iota }_{*}{P}_{x_i,x_j}X(x_j),u_l(x_i)\rangle )}_{l=1}^d+O({\epsilon }_{\text{PCA}}^{1/2}+{\epsilon }^{3/2}).$$

This concludes the proof. Similar results hold for ∊_PCA = O(n_−2/(d+1)) by using the results in Theorem B.1.

B.4 Proof of Theorem B.3

We demonstrate the proof for the case when the data is uniformly distributed over the manifold. The proof for the nonuniform sampling case is the same but more tedious. Note that when the data is uniformly distributed, T_∊,α = T_∊,0 for all 0 < α ≤ 1, so in the proof we focus on analyzing T_∊ := T_{∊, 0}. Denote K_∊ := K_{∊, 0}. Fix $x_i\notin ℳ\sqrt{{\epsilon }_{\text{PCA}}}$. We rewrite the left-hand side of (B.8) as

$$\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon }(x_i,x_j)}=\frac{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{F}_j}{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{G}_j}$$ (B.77)

where

$$F_j=K_{\epsilon }(x_i,x_j)O_{ij}{\overline{X}}_j,G_j=K_{\epsilon }(x_i,x_j).$$

Since x₁, x₂; …, x_n are i.i.d. random variables, then G_j for j ≠ i are also i.i.d. random variables. However, the random vectors F_j for j ≠ i are not independent, because the computation of O_ij involves several data points, which leads to possible dependency between O_ij1 and O_ij2. Nonetheless, Theorem B.2 implies that the random vectors F_j are well approximated by the i.i.d. random vectors $F_j^{\prime }$ that are defined as

$$F_j^{\prime }≔K_{\epsilon }(x_i,x_j){(\langle {\iota }_{*}{P}_{x_i,x_j}X(x_j),u_l(x_i)\rangle )}_{l=1}^d,$$ (B.78)

and the approximation is given by

$$F_j=F_j^{\prime }+K_{\epsilon }(x_i,x_j)O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}),$$ (B.79)

where we use ∊_PCA = O(n_−2/(d+2)) (the following analysis can be easily modified to apply to the case ∊_PCA = O(n_−2/(d+1)).

Since G_j when j ≠ i are identical and independent random variables and $F_j^{\prime }$ when j ≠ i are identical and independent random vectors, we hereafter replace $F_j^{\prime }$ and G_j by Fʹ and G in order to ease notation. By the law of large numbers we should expect the following approximation to hold:

$$\frac{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{F}_j}{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{G}_j}=\frac{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n[F_j^{\prime }+G_{j}O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2})]}{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{G}_j}\approx \frac{𝔼F\prime }{𝔼G}+O({\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}),$$ (B.80)

where

$$𝔼F\prime ={(\langle {\iota }_{*}\underset{ℳ}{\int }{K}_{\epsilon }(x_i,y)P_{x_i,y}X(y)\mathrm{d}V(y),u_l(x_i))\rangle )}_{l=1}^d$$ (B.81)

and

$$𝔼G=\underset{ℳ}{\int }{K}_{\epsilon }(x_i,y)\mathrm{d}V(y).$$ (B.82)

In order to analyze the error of this approximation, we make use of the result in [34, eq. (3.14), p. 132] to conclude a large-deviation bound on each of the d coordinates of the error. Together with a simple union bound, we obtain the following large-deviation bound:

$$\text{Pr}\{\Vert \frac{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{F}_j^{\prime }}{\frac{1}{n-1}{\sum }_{j=1,j\ne i}^n{G}_j}-\frac{𝔼F\prime }{𝔼G}\Vert >\alpha \}\le C_1\text{exp}\left\{\frac{-C_2(n-1){\alpha }^2{\epsilon }^{d/2}\text{vol}(ℳ)}{2\epsilon [{\Vert \nabla {|}_{y=x_i}\langle {\iota }_{*}{P}_{x_i,y}X(y),u_l(x_i)\rangle \Vert }^2+O(\epsilon )]}\right\},$$ (B.83)

where C₁ and C₂ are some constants (related to d). This large-deviation bound implies that w.h.p. the variance term is $O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}})$. As a result,

$$\frac{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)O_{ij}{\overline{X}}_j}{{\sum }_{j=1,j\ne i}^n{K}_{\epsilon ,\alpha }(x_i,x_j)}={(\langle {\iota }_{*}{T}_{\epsilon ,\alpha }X(x_i),u_l(x_i)\rangle )}_{l=1}^d+O(\frac{1}{n^{1/2}{\epsilon }^{d/4-1/2}}+{\epsilon }_{\text{PCA}}^{3/2}+{\epsilon }^{3/2}),$$

which completes the proof for points away from the boundary. The proof for points inside the boundary is similar.

B.5 Proof of Theorem B.4

We begin the proof by citing the following lemma from [9, lemma 8]: LEMMA B.10. Suppose f ∈ 𝒞³(ℳ) and $x\notin {ℳ}_{\sqrt{\epsilon }}$ then

$$\underset{B_{\sqrt{\epsilon }}(x)}{\int }{\epsilon }^{-d/2}{K}_{\epsilon }(x,y)f(y)\mathrm{d}V(y)=f(x)+\epsilon \frac{m_2}{d}[\frac{\mathrm{\Delta }f(x)}{2}+w(x)f(x)]+O({\epsilon }^2)$$

where $w(x)=s(x)+\frac{m_3^{\prime }z(x)}{24\left|{𝕊}^{d-1}\right|}\mathit{\text{and}}z(x)={\int }_{{𝕊}^{d-1}}\Vert \mathrm{\Pi }(\theta ,\theta )\Vert d\theta$.

By Lemma B.10, we get

$$p_{\epsilon }(y)=p(y)+\epsilon \frac{m_2}{d}(\frac{\mathrm{\Delta }p(y)}{2}+w(y)p(y))+O({\epsilon }^2),$$ (B.84)

which leads to

$$\frac{p(y)}{p_{\epsilon }^{\alpha }(y)}=p^{1-\alpha }(y)[1-\alpha \epsilon \frac{m_2}{d}(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)}\left)\right]+O({\epsilon }^2).$$ (B.85)

Plug (B.85) into the numerator of T_∊,αX(x):

$$\underset{B_{\sqrt{\epsilon }}(x)}{\int }{K}_{\epsilon ,\alpha }(x,y)P_{x,y}X(y)p(y)\mathrm{d}V(y)=p_{\epsilon }^{-\alpha }(x)\underset{B_{\sqrt{\epsilon }}(x)}{\int }{K}_{\epsilon }(x,y)P_{x,y}X(y)p_{\epsilon }^{-\alpha }(y)p(y)\mathrm{d}V(y)=p_{\epsilon }^{-\alpha }(x)\underset{B_{\sqrt{\epsilon }}(x)}{\int }{K}_{\epsilon }(x,y)P_{x,y}X(y)p^{1-\alpha }(y)\times [1-\alpha \epsilon \frac{m_2}{d}(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)}\left)\right]\mathrm{d}V(y)+O({\epsilon }^{d/2+2})≔p_{\epsilon }^{-\alpha }(x)A-\frac{m_2\epsilon }{d}\alpha p_{\epsilon }^{-\alpha }(x)B+O({\epsilon }^{d/2+2})$$

where

$$\{\begin{array}{c}A≔{\int }_{B_{\sqrt{\epsilon }}(x)}{K}_{\epsilon }(x,y)P_{x,y}X(y)p^{1-\alpha }(y)\mathrm{d}V(y),\hfill \\ B≔{\int }_{B_{\sqrt{\epsilon }}(x)}{K}_{\epsilon }(x,y)P_{x,y}X(y)p^{1-\alpha }(y)(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)})\mathrm{d}V(y).\hfill \end{array}$$

We evaluate A and B by changing the integration variables to polar coordinates, and the odd monomials in the integral vanish because the kernel is symmetric. Thus, applying Taylor’s expansion to A leads to

$$A=\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{\epsilon }}\left[K\right(\frac{t}{\sqrt{\epsilon }})+K\prime (\frac{t}{\sqrt{\epsilon }})\frac{\Vert \mathrm{\Pi }(\theta ,\theta )\Vert t^3}{24\sqrt{\epsilon }}+O(\frac{t^6}{\epsilon }\left)\right]\times [X(x)+{\nabla }_{\theta }X(x)t+{\nabla }_{\theta ,\theta }^{2}X(x)\frac{t^2}{2}+O(t^3)]\times [p^{1-\alpha }(x)+{\nabla }_{\theta }(p^{1-\alpha })(x)t+{\nabla }_{\theta ,\theta }^2(p^{1-\alpha })(x)\frac{t^2}{2}+O(t^3)]\times [t^{d-1}+\text{Ric}(\theta ,\theta )t^{d+1}+O(t^{d+2})]\mathrm{d}t\mathrm{d}\theta ,$$

which after rearrangement becomes

$$A=p^{1-\alpha }(x)X(x)\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{\epsilon }}\left\{K\right(\frac{t}{\sqrt{\epsilon }})[1+\text{Ric}(\theta ,\theta )t^2]t^{d-1}\times K\prime (\frac{t}{\sqrt{\epsilon }}\left)\frac{\Vert \mathrm{\Pi }(\theta ,\theta )\Vert t^{d+2}}{24\sqrt{\epsilon }}\right\}\mathrm{d}t\mathrm{d}\theta +p^{1-\alpha }(x)\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{\epsilon }}K\left(\frac{t}{\sqrt{\epsilon }}\right){\nabla }_{\theta ,\theta }^{2}X(x)\frac{t^{d+1}}{2}\mathrm{d}t\mathrm{d}\theta +X(x)\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{\epsilon }}K\left(\frac{t}{\sqrt{\epsilon }}\right){\nabla }_{\theta ,\theta }^2(p^{1-\alpha })(x)\frac{t^{d+1}}{2}\mathrm{d}t\mathrm{d}\theta +\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{\epsilon }}K\left(\frac{t}{\sqrt{\epsilon }}\right){\nabla }_{\theta }X(x){\nabla }_{\theta }(p^{1-\alpha })(x)t^{d+1}\mathrm{d}t\mathrm{d}\theta +O({\epsilon }^{d/2+2}).$$

From the definition of z(x) it follows that

$$\underset{B_{\sqrt{\epsilon }}(0)}{\int }\frac{1}{{\epsilon }^{d/2}}K\prime \left(\frac{t}{\sqrt{\epsilon }}\right)\frac{\Vert \mathrm{\Pi }(\theta ,\theta )\Vert t^{d+2}}{24\sqrt{\epsilon }}\mathrm{d}t\mathrm{d}\theta =\frac{{\epsilon }^{d/2+1}{m}_3^{\prime }z(x)}{24|{𝕊}^{d-1}|}.$$

Suppose ${\{E_l\}}_{l=1}^d$ is an orthonormal basis of T_xℳ and express $\theta ={\mathrm{\Sigma }}_{l=1}^d{\theta }_l{E}_l$. A direct calculation shows that

$$\underset{{𝕊}^{d-1}}{\int }{\nabla }_{\theta ,\theta }^{2}X(x)\mathrm{d}\theta =\sum _{k,l=1}^d\underset{{𝕊}^{d-1}}{\int }{\theta }_l{\theta }_k{\nabla }_{E_l,E_k}^{2}X(x)\mathrm{d}\theta =\frac{|{𝕊}^{d-1}|}{d}{\nabla }^{2}X(x),$$

and similarly

$$\underset{{𝕊}^{d-1}}{\int }\text{Ric}(\theta ,\theta )d\theta =\frac{|{𝕊}^{d-1}|}{d}s(x).$$

Therefore, the first three terms of A become

$${\epsilon }^{d/2}{p}^{1-\alpha }(x)\left\{\right(1+\frac{\epsilon m_2}{d}\frac{\mathrm{\Delta }(p^{1-\alpha })(x)}{2p^{1-\alpha }(x)}+\frac{\epsilon m_2}{d}w(x))X(x)+\frac{\epsilon m_2}{2d}{\nabla }^{2}X(x)\},$$

and the last term is simplified to

$${\epsilon }^{\frac{d}{2}+1}\frac{m_2}{d}\nabla X(x)·\nabla (p^{1-\alpha })(x).$$

Next, we consider B. Note that since there is an ∊ in front of B, we only need to consider the leading-order term. Let $Q(y)=p^{1-\alpha }(y)(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)})$ to simplify notation. Thus, applying Taylor’s expansion to each of the terms in the integrand of B leads to

$$B=\underset{B_{\sqrt{\epsilon }}(x)}{\int }{K}_{\epsilon }(x,y)P_{x,y}X(y)Q(y)\mathrm{d}V(y)=\underset{{𝕊}^{d-1}}{\int }{\int }_0^{\sqrt{\epsilon }}\left[K\right(\frac{t}{\sqrt{\epsilon }})+O(\frac{t^3}{\sqrt{\epsilon }}\left)\right][X(x)+{\nabla }_{\theta }X(x)t+O(t^2)]\times [Q(x)+{\nabla }_{\theta }Q(x)t+O(t^2)][t^{d-1}+\text{Ric}(\theta ,\theta )t^{d+1}+O(t^{d+2})]\mathrm{d}t\mathrm{d}\theta ={\epsilon }^{\frac{d}{2}}X(x)Q(x)+O({\epsilon }^{d/2+1}).$$

In conclusion, the numerator of T_∊,αX(x) becomes

$${\epsilon }^{d/2}\frac{p^{1-\alpha }(x)}{p_{\epsilon }^{\alpha }(x)}\{1+\frac{\epsilon m_2}{d}[\frac{\mathrm{\Delta }(p^{1-\alpha })(x)}{2p^{1-\alpha }(x)}-\alpha \frac{\mathrm{\Delta }p(x)}{2p(x)}\left]\right\}X(x)+{\epsilon }^{\frac{d}{2}+1}\frac{m_2}{d{p}_{\epsilon }^{\alpha }(x)}\{\frac{p^{1-\alpha }(x)}{2}{\nabla }^{2}X(x)+\nabla X(x)·\nabla (p^{1-\alpha })(x)\}+O({\epsilon }^{\frac{d}{2}+2}).$$

Similar calculation of the denominator of the T_∊,αX(x) gives

$$\underset{B_{\sqrt{\epsilon }}(x)}{\int }{K}_{\epsilon ,\alpha }(x,y)p(y)\mathrm{d}V(y)=p_{\epsilon }^{-\alpha }(x)\underset{B_{\sqrt{\epsilon }}(x)}{\int }{K}_{\epsilon }(x,y)p^{1-\alpha }(y)[1-\alpha \epsilon \frac{m_2}{d}(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)}\left)\right]\mathrm{d}V(y)+O({\epsilon }^{\frac{d}{2}+2})=p_{\epsilon }^{-\alpha }(x)C-\frac{\epsilon m_2}{d}\alpha p_{\epsilon }^{-\alpha }(x)D+O({\epsilon }^{\frac{d}{2}+2})$$

where

$$\{\begin{array}{c}C≔{\int }_{B_{\sqrt{\epsilon }}(x)}{K}_{\epsilon }(x,y)p^{1-\alpha }(y)\mathrm{d}V(y),\hfill \\ D≔{\int }_{B_{\sqrt{\epsilon }}(x)}{K}_{\epsilon }(x,y)p^{1-\alpha }(y)(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)})\mathrm{d}V(y).\hfill \end{array}$$

We apply Lemma B.10 to C and D and get

$$C={\epsilon }^{\frac{d}{2}}{p}^{1-\alpha }(x)[1+\frac{\epsilon m_2}{d}(w(x)+\frac{\mathrm{\Delta }(p^{1-\alpha })(x)}{2p^{1-\alpha }(x)}\left)\right]+O({\epsilon }^{\frac{d}{2}+2})$$

$$D={\epsilon }^{\frac{d}{2}}{p}_{\epsilon }^{1-\alpha }(x)(s(x)+\frac{\mathrm{\Delta }p(x)}{2p(x)})+O({\epsilon }^{\frac{d}{2}+1}).$$

In conclusion, the denominator of T_∊,αX(x) is

$${\epsilon }^{\frac{d}{2}}{p}_{\epsilon }^{-\alpha }(x)p^{1-\alpha }(x)\{1+\epsilon \frac{m_2}{d}(\frac{\mathrm{\Delta }(p^{1-\alpha })(x)}{2p^{1-\alpha }(x)}-\alpha \frac{\mathrm{\Delta }p(x)}{2p(x)}\left)\right\}+O({\epsilon }^{\frac{d}{2}+2}).$$

Putting all the above together, we have

$$T_{\epsilon ,\alpha }X(x)=X(x)+\epsilon \frac{m_2}{2d}({\nabla }^{2}X(x)+\frac{2\nabla X(x)·\nabla (p^{1-\alpha })(x)}{p^{1-\alpha }(x)})+O({\epsilon }^2).$$

In particular, when α = 1, we have

$$T_{\epsilon ,1}X(x)=X(x)+\epsilon \frac{m_2}{2d}{\nabla }^{2}X(x)+O({\epsilon }^2).$$

B.6 Proof of Theorem 5.5

Suppose min_y∈∂ℳd(x, y) =∊̃. Choose a normal coordinate {∂₁, ∂₂; …, ∂^d} on the geodesic ball B_∊^1/2(x) around x so that x₀ = exp_x(∊̃∂_d(x)). Due to the Gauss lemma, we know span {∂₁(x₀), ∂₁(x₁), …, ∂_d–1(x₀)}=T_x0∂ℳ and ∂_d(x₀) is outer normal at x₀.

We focus first on the integral appearing in the numerator of T_{∊, 1}X(x):

$$\underset{B_{\sqrt{\epsilon }}(x)\cap ℳ}{\int }\frac{1}{{\epsilon }^{d/2}}{K}_{\epsilon ,1}(x,y)P_{x,y}X(y)p(y)\mathrm{d}V(y).$$

We divide the integral domain ${\text{exp}}_x^{-1}(B_{\sqrt{\epsilon }}(x)\cap ℳ)$ into slices S_η defined by

$$S_{\eta }=\{(\mathit{u},\eta )\in {ℝ}^d:\Vert (u_1,u_2,\dots ,u_{d-1},\eta )\Vert <\sqrt{\epsilon }\},$$

where η ∈ [−∊^1/2,∊^1/2] and u = (u₁, u₂, …, u_d–1) ∈ ℝ^d–1. By Taylor’s expansion and (B.85), the numerator of T_∊,1X becomes

$$\begin{gathered} \underset{B_{\sqrt{\epsilon }}(x)\cap ℳ}{\int }{K}_{\epsilon ,1}(x,y)P_{x,y}X(y)p(y)\mathrm{d}V(y)=p_{\epsilon }^{-1}(x)\underset{S_{\eta }}{\int }{\int }_{-\sqrt{\epsilon }}^{\sqrt{\epsilon }}K\left(\frac{\sqrt{{\Vert \mathit{u}\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right) \\ \times (X(x)+\sum _{i=1}^{d-1}{u}_i{\nabla }_{{\partial }_i}X(x)+\eta {\nabla }_{{\partial }_d}X(x)+O(\epsilon ))\times [1-\epsilon \frac{m_2}{d}(w(y)+\frac{\mathrm{\Delta }p(y)}{2p(y)})+O({\epsilon }^2)]\mathrm{d}\eta d\mathit{u} \\ =p^{-1}(x)\underset{S_{\eta }}{\int }{\int }_{-\sqrt{\epsilon }}^{\sqrt{\epsilon }}K\left(\frac{\sqrt{{\Vert \mathit{u}\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right)\times (X(x)+\sum _{i=1}^{d-1}{u}_i{\nabla }_{{\partial }_i}X(x)+\eta {\nabla }_{{\partial }_d}X(x)+O(\epsilon ))\mathrm{d}\eta \mathrm{d}\mathit{u}. \end{gathered}$$ (B.86)

Note that in general the integral domain S_η is not symmetric with relation to (0, …, 0, η), so we will try to symmetrize S_η by defining the symmetrized slices:

$${\tilde{S}}_{\eta }=\underset{i=1}{\overset{d-1}{\cap }}(R_i{S}_{\eta }\cap S_{\eta }),$$

where R_i(u₁; …, u_i, …, η) = (u₁, …, −u_i, …, η). Note that from (B.22) in Lemma B.9, the orthonormal basis {P_x0,x∂₁(x), P_x0,x∂₂(x), …, P_x0,x∂_d–1(x)} of T_x0∂ℳ differs from (∂₁(x₀),∂₂(x₀), … ∂_d–1(x₀)} by O(∊). Also note that up to error of order ∊^3/2, we can express ∂ℳ ∩ B_∊^1/2(x) by a homogeneous degree 2 polynomial with variables {P_x0,x∂₁(x), P_x0,x∂₂(x), …, P_x0,x∂_d–1(x)}. Thus the difference between S̃_η and S_η is of order ∊ and (B.86) can be reduced to

$$p^{-1}(x)\underset{{\tilde{S}}_{\eta }}{\int }{\int }_{-\sqrt{\epsilon }}^{\sqrt{\epsilon }}K\left(\frac{\sqrt{{\Vert \mathit{u}\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right)\times (X(x)+\sum _{i=1}^{d-1}{u}_i{\nabla }_{{\partial }_i}X(x)+\eta {\nabla }_{{\partial }_d}X(x)+O(\epsilon ))\mathrm{d}\eta \mathrm{d}\mathit{u}.$$ (B.87)

Next, we apply Taylor’s expansion to X(x):

$$P_{x,x_0}X(x_0)=X(x)+\tilde{\epsilon }{\nabla }_{{\partial }_d}X(x)+O(\epsilon ).$$

Since

$${\nabla }_{{\partial }_d}X(x)=P_{x,x_0}({\nabla }_{{\partial }_d}X(x_0))+O({\epsilon }^{\frac{1}{2}}),$$

the Taylor expansion of X(x) becomes

$$X(x)=P_{x,x_0}(X(x_0)-\tilde{\epsilon }{\nabla }_{{\partial }_d}X(x_0)+O(\epsilon )).$$ (B.88)

Similarly for all i = 1, 2, …, d we have

$$P_{x,x_0}({\nabla }_{{\partial }_i}X(x_0))={\nabla }_{{\partial }_i}X(x)+O({\epsilon }^{\frac{1}{2}}).$$ (B.89)

Plugging (B.88) and (B.89) into (B.87) further reduces (B.86) into

$$p^{-1}(x)\underset{{\tilde{S}}_{\eta }}{\int }{\int }_{-\sqrt{\epsilon }}^{\sqrt{\epsilon }}K\left(\frac{\sqrt{{\Vert \mathit{u}\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right)\times P_{x,x_0}(X(x_0)+\sum _{i=1}^{d-1}{u}_i{\nabla }_{{\partial }_i}X(x_0)+(\eta -\tilde{\epsilon }){\nabla }_{{\partial }_d}X(x_0)+O(\epsilon ))\mathrm{d}\eta \mathrm{d}\mathit{u}.$$ (B.90)

The symmetry of the kernel implies that for i = 1, 2, …, d – 1,

$$\underset{{\tilde{S}}_{\eta }}{\int }K\left(\frac{\sqrt{{\Vert \mathit{u}\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right)u^i\mathrm{d}\mathit{u}=0,$$ (B.91)

and hence the numerator of T_1,∊X(x) becomes

$$p^{-1}(x)P_{x,x_0}(m_0^{\epsilon }X(x_0)+m_1^{\epsilon }{\nabla }_{{\partial }_d}X(x_0))+O({\epsilon }^{\frac{d}{2}+1})$$ (B.92)

where

$$m_0^{\epsilon }=\underset{{\tilde{S}}_{\eta }}{\int }{\int }_{-\sqrt{\epsilon }}^{\sqrt{\epsilon }}K\left(\frac{\sqrt{{\Vert u\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right)\mathrm{d}\eta \mathrm{d}x=O({\epsilon }^{\frac{d}{2}})$$ (B.93)

and

$$m_1^{\epsilon }=\underset{{\tilde{S}}_{\eta }}{\int }{\int }_{-\sqrt{\epsilon }}^{\sqrt{\epsilon }}K\left(\frac{\sqrt{{\Vert u\Vert }^2+{\eta }^2}}{\sqrt{\epsilon }}\right)(\eta -\tilde{\epsilon })\mathrm{d}\eta \mathrm{d}x=O({\epsilon }^{\frac{d}{2}+\frac{1}{2}}).$$ (B.94)

Similarly, the denominator of T_∊,1X can be expanded as

$$\underset{B_{\sqrt{\epsilon }}(x)\cap ℳ}{\int }{K}_{\epsilon ,1}(x,y)p(y)\mathrm{d}V(y)=p^{-1}(x)m_0^{\epsilon }+O({\epsilon }^{\frac{d}{2}+\frac{1}{2}}),$$ (B.95)

which together with (B.92) gives us the following asymptotic expansion:

$$T_{\epsilon ,1}X(x)=P_{x,x_0}(X(x_0)+\frac{m_1^{\epsilon }}{m_0^{\epsilon }}{\nabla }_{{\partial }_d}X(x_0))+O(\epsilon ).$$ (B.96)

Combining (B.96) with (B.9) in Theorem B.3, we conclude the theorem.

B.7 Proof of Theorem 5.6

We denote the spectrum of ▽² by ${\{{\lambda }_l\}}_{l=0}^{\mathrm{\infty }},\text{where 0}\le {\lambda }_0\le {\lambda }_1\le \dots$ and the corresponding eigenspaces by E_l := {X ∈ L²(Tℳ) : ▽²X = −λ_lX}, l = 0, 1, …. The eigenvector fields are smooth and form a basis for L₂(Tℳ), that is,

$$L^2(Tℳ)=\overline{\underset{l\in \mathbb{N}\cup \left\{0\right\}}{\oplus }{E}_l.}$$

Thus we proceed by considering the approximation through eigenvector field subspaces. To simplify notation, we rescale the kernel K so that $\frac{m_2}{2d}=1$.

Fix X_l ∈ E_l. When $x\notin {ℳ}_{\sqrt{\epsilon }}$ from Corollary B.5 we have uniformly

$$\frac{T_{\epsilon ,1}{X}_l(x)-X_l(x)}{\epsilon }={\nabla }^2{X}_l(x)+O(\epsilon ).$$

When $x\in {ℳ}_{\sqrt{\epsilon }}$, from Theorem 5.5 and the Neumann condition, we have uniformly

$$T_{\epsilon ,1}{X}_l(x)=P_{x,x_0}{X}_l(x_0)+O(\epsilon ).$$ (B.97)

Note that we have

$$P_{x,x_0}{X}_l(x_0)=X_l(x)+P_{x,x_0}\sqrt{\epsilon }{\nabla }_{{\partial }_d}{X}_l(x_0)+O(\epsilon );$$

thus again by the Neumann condition at x₀, (B.97) becomes

$$T_{\epsilon ,1}{X}_l(x)=X_l(x)+O(\epsilon ).$$

In conclusion, when $x\in {ℳ}_{\sqrt{\epsilon }}$ uniformly we have

$$\frac{T_{\epsilon ,1}{X}_l(x)-X_l(x)}{\epsilon }=O(1).$$

Note that when the boundary of the manifold is smooth, the measure of ${ℳ}_{\sqrt{\epsilon }}\text{is}O({\epsilon }^{1/2})$. We conclude that in the L² sense,

$${\Vert \frac{T_{\epsilon ,1}{X}_l-X_l}{\epsilon }-{\mathrm{\nabla }}^2{X}_l\Vert }_{L^2}=O({\epsilon }^{1/4}).$$ (B.98)

Next we show how $T_{\epsilon ,1}^{t/\epsilon }$ converges to e^−t▽2. We know I + ∊▽² is invertible on E_l with norm $\frac{1}{2}\le \Vert I+\epsilon {\nabla }^2\Vert <1\text{when}\epsilon <\frac{1}{2{\lambda }_l}$. Next, note that if B is a bounded operator with norm ∥B∥ < 1, we have the following bound for any s > 0 by the binomial expansion:

$$\Vert {(I+B)}^s-I\Vert =\Vert sB+\frac{s(s-1)}{2!}{B}^2+\frac{s(s-1)(s-2)}{3!}{B}^3+\cdots \Vert \le s\Vert B\Vert +\frac{s(s-1)}{2!}{\Vert B\Vert }^2+\frac{s(s-1)(s-2)}{3!}{\Vert B\Vert }^3+\cdots =s\Vert B\Vert \{1+\frac{s-1}{2!}\Vert B\Vert +\frac{(s-1)(s-2)}{3!}{\Vert B\Vert }^2+\cdots \}\le s\Vert B\Vert \{1+\frac{s-1}{1!}\Vert B\Vert +\frac{(s-1)(s-2)}{2!}{\Vert B\Vert }^2+\cdots \}=s\Vert B\Vert {(1+\Vert B\Vert )}^{s-1}.$$ (B.99)

On the other hand, note that on E_l

$$e^{t{\nabla }^2}={(I+\epsilon {\nabla }^2)}^{\frac{t}{\epsilon }}+O(\epsilon ).$$ (B.100)

Indeed, for X ∈ E_l we have $e^{t{\nabla }^2}X=(1-t{\lambda }_l+t^2{\lambda }_l^2/2+\dots )X$ and

$${(I+\epsilon {\nabla }^2)}^{\frac{t}{\epsilon }}X=(1-t{\lambda }_l+\frac{t^2{\lambda }_l^2}{2}-\frac{t\epsilon {\lambda }_l^2}{2}+\cdots )X$$

by the binomial expansion. Thus we have the claim.

Putting all the above together, over E_l for all l ≥ 0, when $\epsilon <1/{\lambda }_l^{16+2d}$ we have

$$\Vert T_{\epsilon ,1}^{t/\epsilon }-e^{t{\nabla }^2}\Vert =\Vert {(I+\epsilon {\nabla }^2+O({\epsilon }^{\frac{5}{4}}))}^{\frac{t}{\epsilon }}-{{(I+\epsilon {\nabla }^2)}^{}}^{\frac{t}{\epsilon }}+O(\epsilon )\Vert \le \Vert {{(I+\epsilon {\nabla }^2)}^{}}^{\frac{t}{\epsilon }}\Vert \Vert {[I+{(I+\epsilon {\nabla }^2)}^{-1}O({\epsilon }^{5/4})]}^{\frac{t}{\epsilon }}-I+O(\epsilon )\Vert =(1+t+O(\epsilon ))({\epsilon }^{1/4}t+O(\epsilon )=O({\epsilon }^{\frac{1}{4}}),$$

where the first equality comes from (B.98) and (B.100), and the third inequality comes from (B.99). Thus on $\overline{\oplus l:{\lambda }_{l<{\epsilon }^{-1/(16+2d)}}El}\text{we have}\Vert T_{\epsilon ,1}^{t/\epsilon }-e^{t{\nabla }^2}\Vert \le O({\epsilon }^{1/8})$. By taking ∊ → 0, the proof is completed.

Appendix C

Multiplicities of Eigen 1-Forms of Connection Laplacian over 𝕊ⁿ

All results and proofs in this section can be found in [15, 38]. Consider the following setting:

$$G=\text{SO}(n+1),K=\text{SO}(n),ℳ=G/K={𝕊}^n,𝔤=\text{so}(n+1),𝔨=\text{so}(n).$$

Denote by Ω¹(𝕊ⁿ) the complexified smooth 1-forms, which is a G-module by (g · s)(x) = g · s(g⁻¹x) for g ∈ G, s ∈ Ω¹(𝕊ⁿ), and x ∈ 𝕊_n. Over ℳ we have the Haar measure dµ defined by the bi-invariant Hermitian metric 〈·, ·〉, which comes from the Killing form of G and the Hodge Laplacian operator Δ = dδ+ δd defined by 〈·, ·〉. Since Δ is a self-adjoint and uniform second-order elliptic operator on Ω¹(𝕊_n), the eigenvalues λ_i are discrete and nonnegative real numbers, with an accumulation point only at ∞, and their related eigenspaces E_i are of finite dimension. We also know ${\oplus }_{i=1}^{\mathrm{\infty }}{E}_i$ is dense in Ω¹(𝕊ⁿ) in the topology defined by the inner product (f, g)_𝕊ⁿ := ∫_𝕊ⁿ 〈f, g〉dµ. Note that ℊ/ 𝓉⊗_ℝ ℂ ≅ ℂ_n when G = SO(n + 1) and K = SO(n). Denote by V = ℂⁿ the standard representation of SO(n). We split the calculation of the multiplicity of eigenforms of Δ over 𝕊ⁿ into four steps. Step 1. Clearly Ω¹(𝕊ⁿ) is a reducible G-module. Fix an irreducible representation λ of G acting on Γ_λ and construct a G-homomorphism

$${\text{Hom}}_G({\mathrm{\Gamma }}_{\lambda },{\mathrm{\Omega }}^1({𝕊}^n)){\otimes }_{ℂ}{\mathrm{\Gamma }}_{\lambda }\to {\mathrm{\Omega }}^1({𝕊}^n)$$

by φ ⊗ v ↦ φ (v). We call the image the Γ_λ-isotypical summand in Ω¹(𝕊ⁿ) with multiplicity dim_ℂHom_G(Γ_λ, Ω¹(𝕊ⁿ)). Then we apply the Frobenius reciprocity law:

$${\text{Hom}}_G({\mathrm{\Gamma }}_{\lambda },{\mathrm{\Omega }}^1({𝕊}^n))\cong {\text{Hom}}_K({\text{res}}_K^G{\mathrm{\Gamma }}_{\lambda },V).$$

Thus if we can calculate dim_ℂ Hom_K$({\text{res}}_K^G{\mathrm{\Gamma }}_{\lambda },V)$, we know how many copies of the irreducible representation Γ_λ are inside Ω¹(𝕊_n).

Denote by L₁, L₂, …, L_n the basis for the dual space of Cartan subalgebra of so(2n) or so(2n+1). Then L₁, L₂; …, L_n together with $\frac{1}{2}{\mathrm{\Sigma }}_{i=1}^n{L}^i$ generate the weight lattice. The Weyl chamber of SO(2n + 1) is

$$𝒲=\{\sum a_i{L}_i:a_1\ge {\alpha }_2\ge \cdots \ge a_n\ge 0\},$$

and the edges of the W are thus the rays generated by the vectors L₁, L₁ + L₂; …, L₁ + L₂ + … + L_n; for SO(2n), the Weyl chamber is

$$𝒲=\{\sum a_i{L}_i:a_1\ge {\alpha }_2\ge \cdots \ge |a_n|\},$$

and the edges are thus the rays generated by the vectors L₁, L₁ + L₂, …, L₁ + L₂ + …, + L_n–3 + L_n–2, L₁ + L₂ + … + L_n–3 + L_n–2 + L_n–1 + L_n, and L₁ + L₂ + … + L_n–3 + L_n–2 + L_n–1 – L_n.

To keep the notation unified, we denote the fundamental weights ω_i separately. When G = SO(2n), denote

$$\{\begin{array}{cc}{\omega }_0=0\hfill & \text{when}p=0,\hfill \\ {\omega }_p={\sum }_{i=1}^p{\lambda }_i\hfill & \text{when}1\le p\le n-1,\hfill \\ {\omega }_n=\frac{1}{2}{\sum }_{i=1}^n{\lambda }_i\hfill & \text{when}p=n;\hfill \end{array}$$ (C.1)

when G = SO(2n + 1), denote

$$\{\begin{array}{cc}{\omega }_0=0\hfill & \text{when}p=0,\hfill \\ {\omega }_p={\sum }_{i=1}^p{\lambda }_i\hfill & \text{when}1\le p\le n-2,\hfill \\ {\omega }_{n-1}=\frac{1}{2}({\sum }_{i=1}^{n-1}{\lambda }_i-{\lambda }_n)\hfill & \text{when}p=n,\hfill \\ {\omega }_n=\frac{1}{2}({\sum }_{i=1}^{n-1}{\lambda }_i-{\lambda }_n)\hfill & \text{when}p=n.\hfill \end{array}$$ (C.2)

THEOREM C.1.

1. When m = 2n + 1, the exterior powers Λ^pV of the standard representation V of so(2n + 1) are the irreducible representations with the highest weight ω_p when p < n and 2ω_n when p = n.

2. When m = 2n, the exterior powers Λ^pV of the standard representation V of so(2n) are the irreducible representations with the highest weight ω_p when p ≤ n–1; when p = n, ΛⁿV splits into two irreducible representations with the highest weights 2ω_m–1 and 2ω_m.

PROOF. Please see [15] for details.

THEOREM C.2 (Branching Theorem). When G = SO(m) and K = SO(m – 1) the restriction of the irreducible representations of G to K will be decomposed as the direct sum of the irreducible representations of K in the following way: Let Γ_λ be an irreducible G-module over ℂ with the highest weight $\lambda ={\mathrm{\Sigma }}_{i=1}^n{\lambda }_i{L}_i\in 𝒲$.

1. If m = 2n

   $${\mathrm{\Gamma }}_{\lambda }=\oplus {\mathrm{\Gamma }}_{{\sum }_{i=1}^n{\lambda }_i^{\prime }{L}_i}$$

   where ⊕ runs over all ${\lambda }_i^{\prime }$ such that

   $${\lambda }_1\ge {\lambda }_1^{\prime }\ge {\lambda }_2\ge {\lambda }_2^{\prime }\ge \cdots \ge {\lambda }_{n-1}^{\prime }\ge |{\lambda }_n|$$

   with ${\lambda }_i^{\prime }$ and λ_i simultaneously all integers or all half-integers. Here ${\mathrm{\Gamma }}_{{\mathrm{\Sigma }}_{i=1}^n{\lambda }_i^{\prime }{L}_i}$ is the irreducible K-module with the highest weight ${\mathrm{\Sigma }}_{i=1}^n{\lambda }_i^{\prime }{L}_i$.
2. If m = 2n+1

   $${\mathrm{\Gamma }}_{\lambda }=\oplus {\mathrm{\Gamma }}_{{\sum }_{i=1}^n{\lambda }_i^{\prime }{L}_i}$$

   where ⊕ runs over all ${\lambda }_i^{\prime }$ such that

   $${\lambda }_1\ge {\lambda }_1^{\prime }\ge {\lambda }_2\ge {\lambda }_2^{\prime }\ge \cdots \ge {\lambda }_{n-1}^{\prime }\ge {\lambda }_n\ge |{\lambda }_n^{\prime }|$$

   with ${\lambda }_i^{\prime }$ and λ_i simultaneously all integers or all half-integers. Here ${\mathrm{\Gamma }}_{{\mathrm{\Sigma }}_{i=1}^n{\lambda }_i^{\prime }{L}_i}$ is the irreducible K-module with the highest weight ${\mathrm{\Sigma }}_{i=1}^n{\lambda }_i^{\prime }{L}_i$.

PROOF. Please see [15] for details.

From the above theorems, we know how to calculate dim_ℂ Hom_G(Γ_λ,Ω₁(ℳ)). To be more precise, since the right-hand side of Hom_K$({\text{res}}_K^G{\mathrm{\Gamma }}_{\lambda },V)$ is the irreducible representation of K with the highest weight ω₁ (or splits in the low-dimension case), we know the dim_ℂ Hom_K$({\text{res}}_K^G{\mathrm{\Gamma }}_{\lambda },V)$ can be 1 only if ${\text{res}}_K^G{\mathrm{\Gamma }}_{\lambda }$ has the same highest weight by Schur’s lemma and the classification theorem.

Step 2. In this step we relate the irreducible representation Γ_λ ⊂ Ω¹(𝕊ⁿ) to the eigenvalue of the Hodge-Laplace operator Δ.

THEOREM C.3. Suppose Γ_µ ⊂ Ω¹(𝕊ⁿ) is an irreducible G-module with the highest weight µ; then we have

$$\mathrm{\Delta }f=\langle \mu +2\rho ,\mu \rangle f$$

where f ∈ Γ_µ, ρ is the half sum of all positive roots, and 〈·, ·〉 is induced inner product on the dual Cartan subalgebra of ℊ from the Killing form B.

PROOF. Please see [38] for details.

Note that for $\text{SO}(\text{2}n\text{+1}),\rho ={\mathrm{\Sigma }}_{i=1}^n(n+\frac{1}{2}-i)L_i$ since R⁺={L_i–L_j, L_i+L_j,L_i:i < j} for $\text{SO}(\text{2}n),\rho ={\mathrm{\Sigma }}_{i=1}^n(n-i)L_i$ since R⁺={L_i–L_j, L_i+L_j : i < j}.

Combining these theorems, we know if Γ_µ is an irreducible representation of G, then it is an eigenspace of Δ with eigenvalue λ = 〈µ +2ρ, µ〉. In particular, if we can decompose the eigen 1-form space E_λ ⊂ Ω¹(𝕊ⁿ) into an irreducible G-module and calculate the dimension of the irreducible G-module, we can determine the multiplicity of E_λ.

Step 3. Now we apply the Weyl character formula to calculate the dimension of Γ_λ for G.

THEOREM C.4.

1. When m = 2n + 1, consider $\lambda ={\mathrm{\Sigma }}_{i=1}^n{\lambda }_i{L}_i$ where λ₁ ≥ λ₂ ≥ … ≥ λ_n ≥ 0, the highest weight of an irreducible representation Γ_λ. Then

   $$\text{dim}{\mathrm{\Gamma }}_{\lambda }={\mathrm{\Pi }}_{i<j}\frac{l_i-l_j}{j-i}{\mathrm{\Pi }}_{i\le j}\frac{l_i+l_j}{2n+1-i-j}\text{where}{l}_i={\lambda }_i+n+i+\frac{1}{2}.$$
2. When m = 2n, consider $\lambda ={\mathrm{\Sigma }}_{i=1}^n{\lambda }_i{L}_i$ where λ₁ ≥ λ₂ ≥ … ≥|λ_n|, the highest weight of an irreducible representation Γ_λ. Then

   $$\text{dim}{\mathrm{\Gamma }}_{\lambda }={\mathrm{\Pi }}_{i<j}\frac{l_i-l_j}{j-i}\frac{l_i+l_j}{2n-i-j}\text{where}{l}_i={\lambda }_i+n-1.$$

PROOF. Please see [15] for details.

Step 4. We need the following theorem about real representations of G to solve the original problem.

TABLE C.1.

Eigenvalues and their multiplicity of 𝕊^m, where m ≥ 2. l_0,i = λ_i + n – i, m_0,i = n – i, l_1/2,_i = ${\lambda }_i+n-i+\frac{1}{2}$ , and $m_{1/2,i}=n-i+\frac{1}{2}$ .

	λ	eigenvalues	multiplicity
𝕊2n, n ≥ 2	kL1, k ≥ 1 kL1 + L2, k ≥ 1	k(k + 2n − 1) (k + 1)(k + 2n − 2)	${\mathrm{\Pi }}_{i<j}\frac{l_{0,i}^2-l_{0,j}^2}{m_{0,i}^2-m_{0,j}^2}{\mathrm{\Pi }}_{i<j}\frac{l_{0,i}^2-l_{0,j}^2}{m_{0,i}^2-m_{0,j}^2}$
𝕊2n+1, n ≥ 2	kL1, k ≥ 1 kL1 + L2, k ≥ 1	k(k + 2n) (k + 1)(k + 2n − 1)	${\mathrm{\Pi }}_{i<j}\frac{l_{1/2,i}^2-l_{1/2,j}^2}{m_{1/2,i}^2-m_{1/2,j}^2}{\mathrm{\Pi }}_i\frac{l_{1/2,i}}{m_{1/2,i}}{\mathrm{\Pi }}_{i<j}\frac{l_{1/2,i}^2-l_{1/2,j}^2}{m_{1/2,i}^2-m_{1/2,j}^2}{\mathrm{\Pi }}_i\frac{l_{1/2,i}}{m_{1/2,i}}$
𝕊3	kL1, k ≥ 1 kL1 + L2, k ≥ 1 kL1 − L2, k ≥ 1	k(k + 2) (k + 1)2 (k + 1)2	(k + 1)2 k(k + 2) k(k + 2)
𝕊2	kL1 k ≥ 1	k(k + 1)	2(2k + 1)

THEOREM C.5.

1. When n is odd, for any weight λ = a₁ω₁ + a₂ω₂ +… + a_n–1ω_n–1 + a_nω_n/2 of so_2n+1ℝ, the irreducible representation Γ_λ with the highest weight λ is real if a_n is even or if n ≅ 0 or 3 mod 4, if a_n is odd and n ≡ 1 or 2 mod 4 then Γ_λ is quaternionic.

2. When n is even, the representation Γ_λ of so_2n ℝ with highest weight λ = a₁ω₁ + a₂ω₂ + … + a_n–2ω_n–2 + a_n–1ω_n–1 + a_nω_n will be complex if n is odd and a_n–1 ≠ a_n; it will be quaternionic if n ≡ 2 mod 4 and a_n–1 +a_n is odd; and it will be real otherwise.

PROOF. Please see [15] for details.

Combining Table C.1 and this theorem, we know all the eigen 1-form spaces are real form.

Step 5. Now we put all the above together. All the eigen 1-form spaces of 핊^m as an irreducible representation of SO(m+1), m ≥ 2, are listed in Table C.1. The highest weight is denoted by λ.

Consider SO(3) for example. In this case, n = 1 and ℳ = 𝕊². From the analysis in cryo-EM [18], we know that the multiplicities of eigenvectors are 6, 10, …, which echoes the above analysis. Moreover, the first few multiplicities of 𝕊₃, 𝕊₄, and 𝕊₅ are 4, 6, 9, 16, 16, …; 5, 10, 14, …; and 6, 15, 20, …, respectively.