Abstract
Nonlinear microscopy techniques developed over the past two decades have provided dramatic new capabilities for biological imaging. The initial demonstrations of nonlinear microscopies coincided with the development of solid-state femtosecond lasers, which continue to dominate applications of nonlinear microscopy. Fiber lasers offer attractive features for biological and biomedical imaging, and recent advances are leading to high-performance sources with the potential for robust, inexpensive, integrated instruments. This article discusses recent advances, and identifies challenges and opportunities for fiber lasers in nonlinear bioimaging.
Introduction
Optical microscopy offers well-established techniques for imaging with sub-micron spatial resolution. In the last two decades, researchers have found that ultrashort light pulses can be exploited in a variety of new biomedical imaging modalities. Several techniques exploit the high peak power that is possible with ultrashort pulses, which can be focused to high intensity to drive nonlinear-optical processes such as multiphoton absorption in molecules used as fluorescent labels.
Since the initial demonstration in 1990 [1], two-photon microscopy (2PM) has been increasingly applied to cell biology and the neurosciences [2,3,4,5]. A number of variations, including three-photon microscopy (3PM) [6,7,8], second- and third-harmonic generation imaging [9,10,11,12], near-field enhanced multiphoton excitation [13], multiphoton endoscopic imaging [14], and super-resolution imaging using stimulated-emission-depletion [15] have significantly broadened the field. The development of various fluorescent indicators, and in particular, geneticallyengineered probes based on fluorescent proteins [16], further enhances the capabilities of multiphoton microscopy (MPM). Current microscope technology is summarized in [17]. Efficient multiphoton excitation requires peak intensities of 0.1 to 1 TW (1 TW = 1012 W). In addition to tight spatial focusing, MPM typically requires pulsed excitation sources so that efficient excitation can be obtained at a practical average power. For example, a femtosecond laser with 100-fs pulse duration (τ) at 100 MHz pulse repetition rate (f) will enhance the 2-photon excitation probability by the inverse of the duty cycle (fτ), which is a factor near 105.
Multiphoton and harmonic-generation microscopies are based on electronic transitions. A number of biologically-important substances (lipids, nucleic acids, sugars, e.g.) have characteristic vibrational spectra, which allows them to be distinguished easily. The combination of microscopy with vibrational spectroscopy thus allows the generation of images with chemical contrast, and this is the basis of coherent Raman scattering (CRS) microscopies. Coherent anti-Stokes Raman scattering (CARS) microscopy is a sensitive nonlinear technique that offers chemical selectivity [18,19] without the use of exogenous dyes. The CARS signal is complicated by the presence of an electronic contribution, and stimulated Raman scattering (SRS) microscopy [20,21] was developed largely to isolate the vibrational response.
A dye laser supplied the femtosecond pulses for the first multiphoton fluorescence images [1], but the power was low and dye lasers required expert operators. The discovery of Kerr-lens modelocking in titanium-doped sapphire lasers [22, 23] was critical to the proliferation of nonlinear microscopy. Commercial Ti:sapphire lasers became available in the early 1990’s. Other solid-state laser media, such as Nd:glass [24], Yb:glass [25], Yb:tungstate [26], and Cr:forsterite [27] have also been developed. These sources have enabled the dramatic growth of multiphoton and harmonic-generation imaging. Standard Ti:sapphire lasers are tunable between 700 and 1000 nm, with pulse energies of 20–30 nJ, pulse durations under 100 fs, repetition rates around 100 MHz, and average powers of 2 W. Existing solid-state lasers are outstanding laboratory tools. At least one commercial instrument covers the range of 680–1300 nm, which is remarkable [28]. The infrastructure to support 2PM within this spectral window is wellestablished. However, stable, user-friendly instruments that are less expensive and more compact should allow multiphoton fluorescence microscopy to find application in a range of new settings. The development of appropriate short-pulse sources will also facilitate the expansion of CRS microscopies. The continued demonstration of new microscopy techniques further motivates the development of appropriate short-pulse sources.
Advances in high-energy femtosecond fiber oscillators
Fiber lasers have attractive properties for imaging applications:
The waveguide medium largely eliminates the need for precise optical alignment, enables long cavity length (i.e., low repetition rate), and ensures good beam quality.
Fiber gain media are efficient and can easily supply the power needed for bioimaging.
Fiber lasers are naturally suitable for integration with endoscopic instruments.
Short-pulse fiber lasers have attracted substantial research attention, and progress has been reviewed in a number of papers [29,30,31,32]. However, fiber lasers have historically lagged behind the performance of solid-state lasers. Amplifier systems have been required, with attendant complexity and cost. In addition, fiber lasers are not broadly wavelength-tunable. As a result, solid-state lasers still dominate the field of nonlinear microscopy.
Recently-demonstrated femtosecond fiber lasers can match, and even exceed, the performance of solid-state lasers, albeit at one wavelength. Work will be needed to extend the wavelength range, but the power levels will allow efficient frequency-conversion to new wavelengths. Thus, short-pulse fiber sources will continue to improve, and offer new alternatives to existing solid-state lasers in many nonlinear bioimaging applications. Although this will have substantial impact, we believe that fiber lasers should be capable of much more than simply matching existing capabilities. Fiber lasers offer design flexibility that will allow creation of new combinations of performance parameters, which can be customized to specific bioimaging applications.
Since the first demonstrations of reliable instruments in the 1980’s [33], femtosecond lasers have been based on cavities with anomalous-dispersion segments. Soliton pulses form by the balance of nonlinear refraction and anomalous dispersion. The soliton energy in a fiber laser is 10–100 times lower than in a solid-state laser, which highlights the challenge that arises in the design of fiber lasers for photophysical applications. The first step in increasing the peak power of fiber lasers was the demonstration of lasers with segments of normal and anomalous dispersion with nearly-equal magnitudes. The resulting “breathing” of the pulse temporal profile reduces the intracavity peak power, and disrupts the resonant production of dispersive waves that occurs with ordinary solitons and ultimately limits their energy. Femtosecond fiber lasers based on this “stretched-pulse” technique [34,35] have reached nanojoule energy and 10-kW power levels.
The demonstration of femtosecond fiber lasers without any anomalous-dispersion components [36] countered two decades of accumulated understanding of short-pulse generation. Pulses in these lasers form by balancing nonlinear gain and loss as well as nonlinear refraction and dispersion. They are called dissipative solitons because dissipative processes such as nonlinear gain and loss play a key role in their formation [37,38,39]. The important point for applications is that dissipative solitons can be stable at energies at least an order of magnitude larger than ordinary or dispersion-managed solitons. This is partly because dissipative solitons are chirped to 10–100 times the transform-limited duration throughout the laser cavity; the pulse does not breathe much. Intuitively, pulse-shaping is the result of filtering of the chirped pulse: cutting the edges of the spectrum corresponds to cutting the leading and trailing wings of the pulse in time.
A dissipative-soliton laser was the first fiber laser to reach the power of a standard Ti:sapphire laser [40]. This laser (Fig. 1) consists mostly of Yb-doped gain fiber. The filter dominates the steady-state pulse-shaping. The wave plates and polarizing beam splitter implement a saturable-absorber function through nonlinear polarization rotation, which is needed to start the mode-locking from noise. The laser generates 20-nJ and 80-fs pulses (Fig. 1) after dechirping. Chichkov et al. reported further scaling of dissipative-soliton lasers, to 80-nJ and 30-fs pulses [41]. The cat-ear spectrum is characteristic of the dissipative-soliton lasers, and the steep sides imply some secondary structure in the time-domain pulse (Fig. 1). For the nonresonant processes that are exploited in nonlinear microscopy, the pedestals have little consequence beyond reducing the peak power by ~10% compared to a gaussian pulse, e.g. For applications that place a premium on temporal pulse contrast, it is possible to take the output of a dissipative-soliton laser after the filter [42]. This produces a smoother spectrum and cleaner pulse, with some sacrifice in pulse energy. A normal-dispersion laser based on self-similar pulse evolution in the gain segment would be an alternative approach to high-energy pulses with clean profiles [43].
Figure 1. Dissipative soliton laser and pulses.
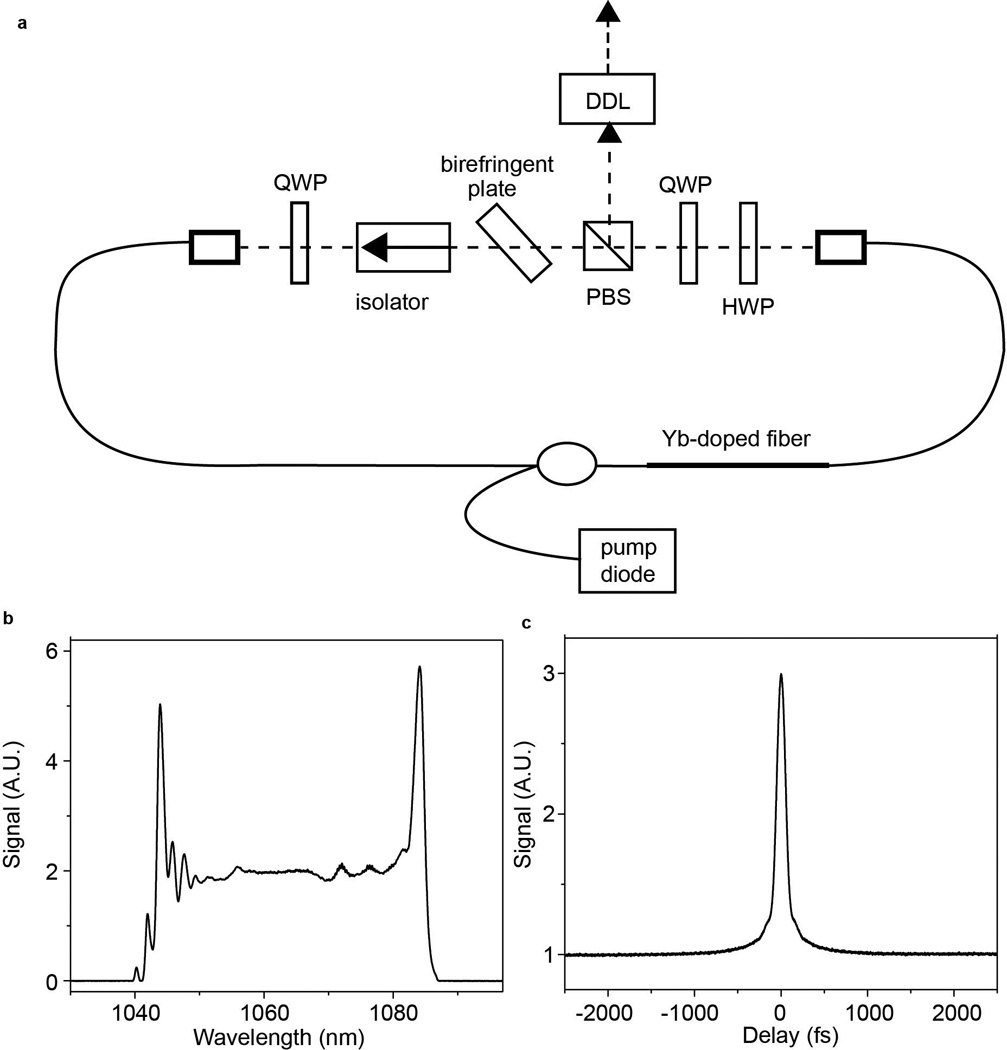
(a) Schematic of dissipative-soliton laser cavity. QWP: quarter wave plate, HWP: half wave plate, PBS: polarizing beam splitter, DDL: dispersive delay line. Spectrum (b) and autocorrelation (c) of 80-fs pulse from dissipative-soliton laser. From [40].
The high peak power and 1050-nm wavelength of Yb-based dissipative soliton lasers are attractive for nonlinear microscopy. As an early example, images of the neurons and vasculature at depths of nearly 1 mm in living mouse cortex (Fig. 2) have been produced [44]. A similar laser was integrated with a delivery fiber and hand-held probe to produce a compact, portable system capable of 2PM and second-harmonic images [45].
Figure 2. Two-photon fluorescence images excited by dissipative–soliton fiber laser.
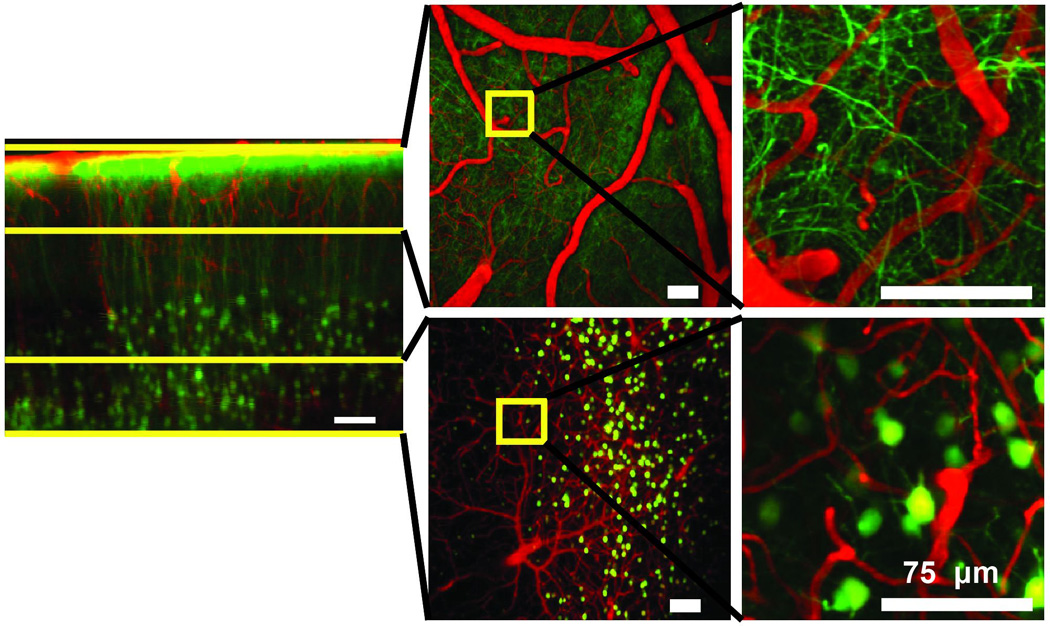
Images of the cortex of a live, anesthetized mouse with a glass-covered craniotomy, recorded in the laboratory of Prof. C. Schaffer at Cornell University. Pyramidal neurons are labeled by yellow fluorescent protein (green) and blood vessels are labeled by intravenously-injected Texas Red dextran (red). The top row shows surface vessels and dendritic processes in the top 150 µm; the bottom row shows arterioles, venules and capillaries as well as neuron cell bodies at depths of 450–650 µm. Yellow boxes (left) delineate areas of higher magnification (right). From Ref. 44.
The stable pulse energy in a laser is determined primarily by the nonlinear phase accumulated by the pulse, so it scales with mode-field area. Fibers with larger mode area [46,30] can be used to enhance lasers based on any pulse evolution. Lefrancois et al. reported a dissipative-soliton laser with Yb-doped photonic-crystal fiber (PCF) with a 40-µm core diameter replacing the ordinary gain fiber [47]. The laser generated 100-nJ and 100-fs pulses, for a peak power of 1 MW, while the average power was 8 W. By use of a photonic crystal (PC) rod with even larger mode area, Baumgartl et al. achieved 850-nJ pulses, 6 MW peak power, and over 60 W average power from a dissipative-soliton laser [48]. These remarkable performance levels currently require sacrificing some of the benefits of standard fiber, but they highlight the potential of mode-locked fiber lasers. Another possible approach for increasing the mode-field area is based on higherorder mode (HOM) fiber [49], which retains the mechanical flexibility of a large-mode-area fiber, but requires two mode conversions in order to propagate in the HOM and then return to the fundamental mode. HOM fibers with mode-field area similar to that of PC rod have been demonstrated [50].
Emerging trends in multiphoton microscopy
Tissue generally scatters light effectively, and this creates a challenge to imaging structures deep in tissue. Optical imaging has been limited to thin (typically ~0.5 mm) samples or superficial tissue. Non-invasive imaging techniques that deliver sub-micron spatial resolution and millimeter tissue penetration depth will have major impact in bioimaging. Applications that require imaging deep in scattering tissues [5], particularly in vivo, showcase the unique advantages of MPM. 2PM has been successfully applied to a variety of deep tissue imaging applications, such as direct visualization of neuronal activity [51] and anatomy [52], developing embryos [53], and tissue morphology and pathology [54,55]. 2PM offers 2 to 3 times greater penetration depth than linear confocal microscopy [56].
The imaging depth for high-resolution 2PM is limited by the signal-to-background ratio (SBR) of the fluorescence distribution in scattering tissue [57]. This depth limit for 2PM is approximately 5 to 6 effective attenuation lengths (le) [58,59] (e.g., ~700 µm in the mouse neocortex with 775-nm excitation). The use of longer excitation wavelengths is effective in reducing the impact of tissue scattering [60, 61, 62]; however, there is a trade-off between tissue scattering and absorption. This trade-off defines the optimum excitation wavelength for tissue penetration. Figure 3 shows the water absorption length (la) and the calculated scattering length (ls) of mouse brain tissue. The combined effect of absorption and scattering is represented by le=(1/la+1/ls)−1 [63]. The validity of Fig. 3 for brain imaging is confirmed by previous measurements of the effective attenuation coefficient (indicated by red stars). Fig. 3 clearly indicates that the optimum wavelength windows for deep tissue imaging are near 1300 nm and 1700 nm.
Figure 3. Attenuation length in brain tissue as a function of wavelength.
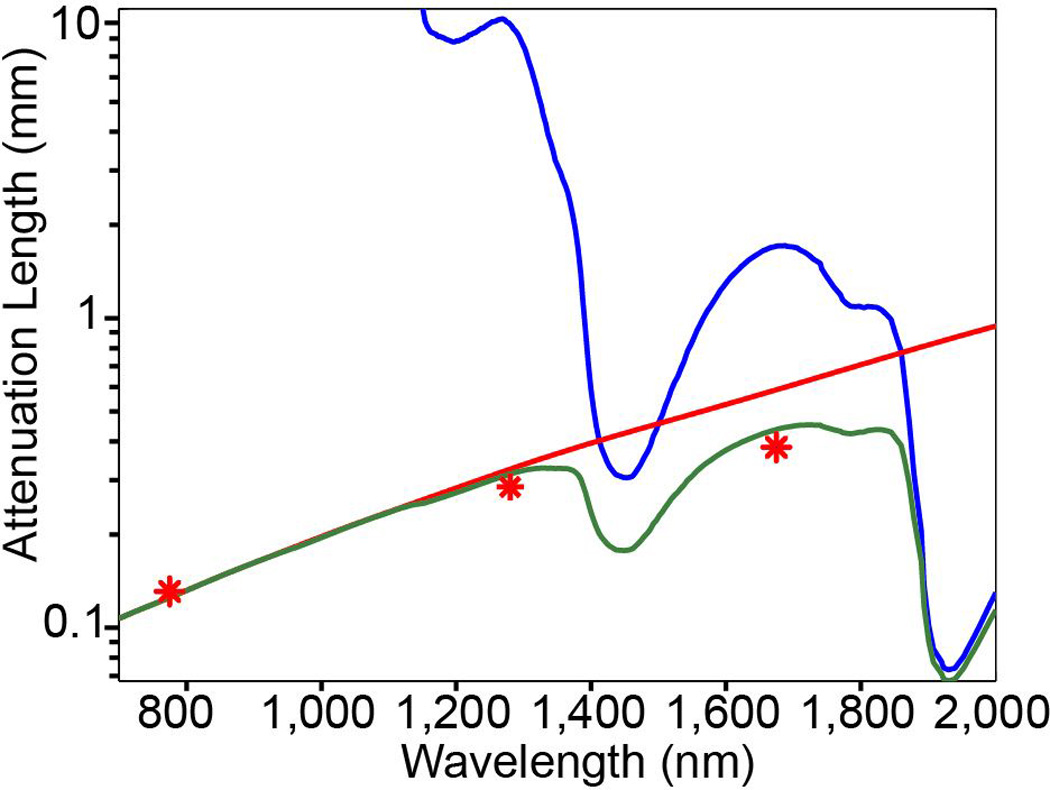
The water absorption length (blue line), the scattering length of mouse brain cortex (red line), and the effective attenuation length (green line). Note the logarithmic scale of the vertical axis. The scattering length is obtained by numerical simulation using Mie theory for a tissue-like phantom that resembles the scattering property of the cortex. The phantom contains 1 mm diameter polystyrene beads at a concentration of 5.4×109/ml. The red stars indicate the reported attenuation lengths for mouse cortex in vivo from previous work. From Refs. 58 and 61.
With longer-wavelength excitation, particularly ~1700 nm, many endogenous fluorophores (e.g., NADH) become inaccessible, even by three-photon excitation (3PE). While this may limit clinical applications involving human subjects, the longer excitation wavelengths are beneficial for imaging extrinsic indicators by eliminating the intrinsic fluorescence background, and therefore improving the image contrast.
The depth limit imposed by the SBR of 2PM can be overcome by 3PM. In the 1990s, several groups demonstrated the feasibility of 3PM [6,7,8], which was mainly used to expand the spectral coverage of the excitation source [64]. Although it was realized in the early demonstrations that 3PE provides significant improvement in excitation confinement [6], such an advantage is largely inconsequential in imaging non-scattering samples or superficial layers of tissue. The SBR is mainly determined by the long range behavior of the fluorescence generation (i.e., fluorescence generation far away from the focal plane), which varies as 1/z4 and 1/z2 (z is the distance away from the focal plane) for 3PE and two-photon excitation (2PE), respectively. Orders of magnitude improvement in SBR can be achieved by 3PE when imaging deep into scattering tissue. Furthermore, 3PE makes a number of existing fluorophores accessible in the 1700-nm spectral window (e.g., fluorophores with one-photon absorption ~560 nm). This is particularly important since currently there is no biologically-relevant fluorescent indicator for 2PE in the 1700-nm spectral window. To make 3PE a practical contrast mechanism for biological imaging, however, a source with high pulse energy and low duty cycle is needed, so that adequate signal (inversely proportional to the square of the duty cycle) can be obtained at average powers that do not cause tissue heating.
The ideal sources for deep-tissue MPM will deliver energetic (>> 10 nJ) femtosecond pulses in the 1300- or 1700-nm windows, with repetition rates matched to the imaging speed without causing excessive sample heating. However, wavelength tunability of fiber lasers is limited by the gain bandwidth of the dopants to tens of nanometers, and this significantly limits their application to biological and medical imaging.
A soliton can continuously transfer energy from shorter to longer wavelength via intrapulse stimulated Raman scattering; this is the soliton self-frequency shift (SSFS) [65]. Continuous tuning to longer wavelengths is achieved by simply increasing the input power [66]. In addition, soliton pulses generated through SSFS typically have superb pulse quality and femtosecond pulse duration. The combination of fiber lasers and SSFS is ideal for MPM applications. A variety of nonlinear media have been used to demonstrate SSFS in the past, ranging from highly-nonlinear PCF [67,68,69] to air-core photonic bandgap fibers (PBF) [70]. The soliton energy is proportional to the effective mode area Aeff. Increasing the soliton energy by increasing the mode area is particularly effective for soliton wavelengths beyond 1300 nm, where silica glass has anomalous dispersion. SSFS at wavelengths beyond 1300 nm can be achieved in a variety of large-core fibers where the waveguide contribution to the dispersion is insignificant. Such design freedom allows the generation of wavelength-tunable, energetic solitons over the range 1600 to 2200 nm [71]. The soliton energy in large mode area fiber or PC rod is 10 to 100 times higher than that of single-mode fiber. When combined with an energetic fiber based source at 1550 nm, SSFS in these structures provides a convenient mechanism for generating energetic femtosecond pulses in the 1700-nm spectral window for deep-tissue imaging. Indeed, megawatt peak power solitons near 1700 nm were demonstrated using SSFS in a PC rod. This source was used to image neurons labelled with red fluorescent protein in a mouse brain using 3PE (Fig. 4) [63]. In vivo imaging of sub-cortical structures in an intact mouse brain was achieved for the first time with this approach. Although a fiber CPA system at 1550 nm was used as the pump source, the required pulse energy is within the range of a dissipative-soliton fiber laser. Deep-tissue MPM in the long-wavelength spectral windows presents significant motivation for new development of fiber-based sources.
Figure 4. SSFS in a PC rod and in vivo 3PM of subcortical structures in a mouse brain.
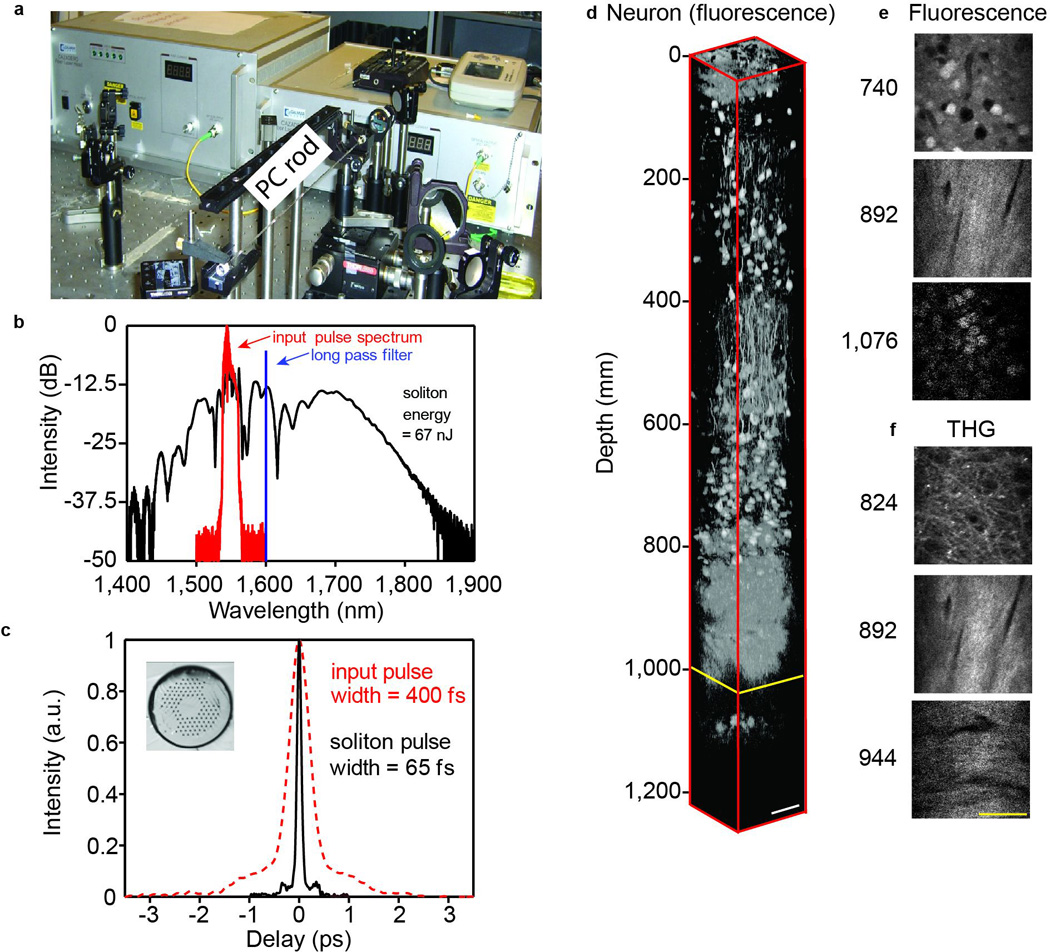
(a) Experimental setup of SSFS in a PC rod pumped by a fiber CPA system. The measured spectrum (b) and the corresponding second-order autocorrelation trace (c) of the input pulse (red) and the 1,675-nm soliton generated in the PC rod (black). The soliton energy, integrated from 1,617 nm, is 67 nJ. Inset in (c) shows the cross section of the PC rod. (d) 3D reconstruction of in vivo 3PM images in the brain of a mouse, which contains RFP-labelled pyramidal neurons. The external capsule extends from approximately 840 to 976 µm below the surface of the brain, and the stratum pyramidale extends from approximately 1,060 to 1,120 µm below the surface. Normalized x-y frames of the fluorescence (e) and THG (f) signal at various depths. The scale bar is 50 µm.
Fiber sources for coherent Raman microscopy
The requirement of two synchronized trains of ultrashort pulses for Raman microscopies presents a serious technical challenge. A practical light source for CRS imaging needs to meet these performance requirements: (1) The source must deliver two excitation wavelengths, with at least one wavelength tunable in order to selectively excite the specific molecular vibration. (2) The two pulse trains must be synchronized and temporally overlapped. The relative timing jitter should be a small fraction of the pulse width. (3) The spectral width of the excitation pulse should be narrower than that of the vibrational resonances. A transform-limited pulse with pulse duration of several picoseconds is typically ideal. (4) The output power must be sufficient for both wavelengths. Because of the losses of microscope optics and overfilling of the objective lens, pulse energies of a few nanojoules are required. Therefore, an average power of at least 100 mW at a repetition rate of 10 – 100 MHz is desired.
The source most commonly used in CRS microscopy is a picosecond Nd-doped vanadate laser that is frequency-doubled to synchronously pump an optical parametric oscillator (OPO) based on a quadratic nonlinear crystal [72]. Commercial versions exist [73] and offer excellent performance, but the cost, complexity, and limited potential for integration of the bulk solid state lasers have impeded the widespread applications of Raman imaging in biomedical research. The need for a robust, fiber-based, and cost-effective source is even more urgent for clinical environments.
Several fiber-based sources for CRS imaging have been reported in the past few years. An early optical parametric amplifier (OPA) generated picosecond and femtosecond pulses with an allfiber design [74]. One recent approach is based on frequency-shifting the output from a picosecond Er-doped fiber laser in nonlinear fiber and then using second harmonic generation to reach the desired wavelengths [75]. Another uses the output from an Er-doped fiber laser to generate the higher-frequency light through second harmonic generation and the lower frequency light by filtering a supercontinuum [76]. These sources are integrated, but higher output powers will be desirable for many biological imaging applications.
Four-wave mixing (FWM) in fiber, typically dispersion-engineered PCF, is the basis of several OPAs designed for CRS imaging. FWM in the normal-dispersion regime can produce the spectrally-narrow but widely-spaced frequency bands desired for CRS microscopy [77]. An allfiber OPA was successfully used to perform CARS imaging, but it generates long (~140 ps) pulses, which yield much lower peak powers than are available from solid-state sources [78]. Spontaneous FWM naturally produces a highly-fluctuating output. Lefrancois et al. showed that seeding the FWM process not only reduces the fluctuations, which was well-known, but also allows the generation of high-energy, transform-limited picosecond pulses by suppressing continuum generation and Raman scattering [79]. This led to the first fiber source to match the pulse parameters of the solid-state OPO [72,73]. A Yb-doped fiber laser drives the FWM process, which produces 3-nJ and 2-ps pulses tunable around 800 nm (Fig. 5). These pulses are combined with 1050-nm pulses from the fiber laser to excite vibrational modes between 2650 and 3200 cm−1. High-quality CARS images (Fig. 5) of mouse ear and brain, as well as fibroblast cells, were produced with this source.
Figure 5. Fiber source for CARS microscopy and imaging of mouse tissue.
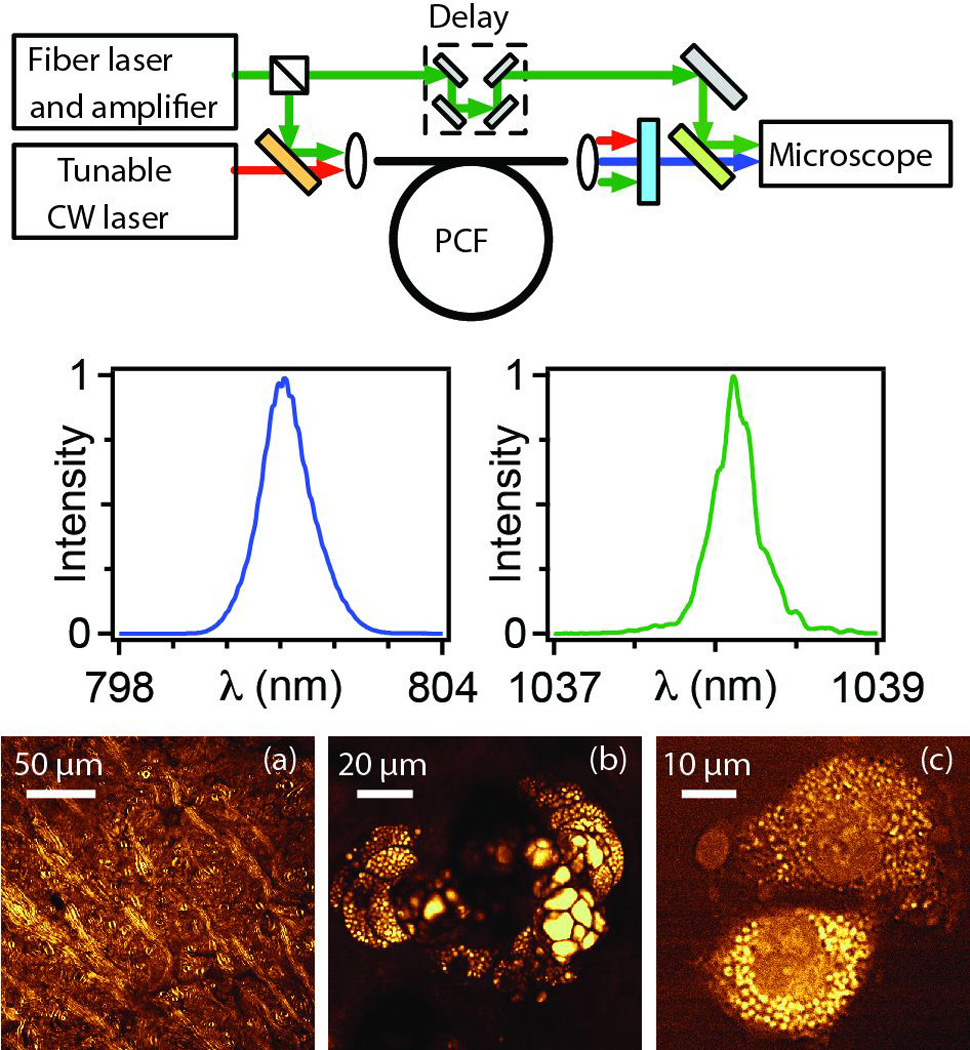
Top: schematic of fiber source based on FWM in PCF. Middle: spectra of generated pulses. Bottom: CARS images at the 2850 cm−1 mode of CH2: (a) mouse brain, (b) sebaceous gland 40 µm deep in mouse ear and (c) isolated rat fibroblast cells. From Ref. 79.
Attention has recently turned to the development of OPOs based on FWM. A fiber OPO with a femtosecond seed laser has been demonstrated [80]. Multimodal CARS imaging was performed with this instrument, but the pulse energy is fairly low (0.1–0.5 nJ). Very recently, an OPO based on FWM at normal dispersion reached the performance levels of the corresponding OPA [79] – at least twice the peak power and three times the average power of other fiber sources -- with major reduction in the intensity fluctuations [81]. This enables faster imaging with better signal-to-background ratio. As practical advantages, the OPO is more efficient than an OPA and eliminates the need for a tunable, narrowband (i.e., expensive) seed laser.
A fiber laser can be used to provide one of the two wavelengths for CRS imaging, which requires it to be synchronized to a wavelength-tunable source. In free-space lasers or OPOs, phase-locked loops and mechanical cavity adjustments are used to dynamically match the cavity lengths for synchronization. In an all-fiber laser, adjustment of the cavity over a macroscopic length is more difficult. Thus, mode-locked fiber lasers typically are used as master clocks to which other pulsed sources are synchronized, making a fiber-based synchronized source difficult to realize.
The time-lens approach [82, 83] explores a new route to generation of energetic picosecond pulses in an all-fiber configuration, where, in contrast to mode-locking, ultrafast pulses are directly "synthesized" from CW light. By electro-optic phase modulation (i.e., the time-lens), a broad spectral bandwidth is generated, and this is subsequently compressed into a short pulse by dispersive elements (e.g., chirped fiber Bragg grating). Picosecond time-lens sources have been realized with telecom components [84]. Video-rate CRS imaging of mouse tissues [85] and close to shot-noise limited SRS imaging sensitivity [86] have been demonstrated using time-lens sources synchronized to Ti:sapphire lasers. Since the repetition rate of a time-lens source is entirely determined by an electrical drive signal, an all-fiber time-lens source can synchronize to a mode-locked laser (solid-state or fiber-based) at any repetition rate. In addition, electronic delay is used to adjust the relative time delay for temporal overlap of the excitation pulses, eliminating the mechanical optical delay line and its effect on spatial alignment. Compared to pulses from lasers, pulses from time-lens sources have some secondary structure in the time domain.
Summary and perspective
In summary, recent advances in short-pulse fiber sources will impact several aspects of bioimaging. Femtosecond oscillators that can match the performance of solid-state lasers will find applications, and higher-power versions will offer some wavelength versatility through nonlinear optics. Sources in the long-wavelength excitation windows, combined with 3-photon excitation, will enhance deep-tissue imaging capabilities. Coherent Raman microscopies should benefit substantially from recent developments in fiber sources of synchronized picosecond pulses with high energy.
Priorities for future development include the following:
Femtosecond sources at new wavelengths
Although 3PM at 1700-nm has yielded record imaging depth in mouse brain, some of the most commonly-used fluorophores, such as GFPs, cannot be excited in this window. Excitation on the short-wavelength side of the water absorption, near 1300 nm, will allow much higher excitation power at the focus due to lower tissue absorption. Development of a high-energy femtosecond source in the 1300-nm window is thus desirable. Shifting of the output of Yb-doped sources at 1050 nm via the SSFS faces major challenges. Both PCF and air-core PBF can provide anomalous dispersion in the range 1050 – 1300 nm. However, the soliton energy in PCF (a fraction of 1 nJ) is nearly two orders of magnitude smaller than the desired pulse energy, while the bandgap of air-core PBFs is not broad enough to support the entire tuning range. HOM fibers may be an alternative for SSFS below 1300 nm. Experiments have demonstrated that launching 1064-nm pulses into an HOM fiber with Aeff = 70 µm2 produces 1-nJ solitons at wavelengths to 1300 nm. However, it is difficult to design and fabricate HOM fibers with anomalous dispersion below 1300 nm and large mode area [87].
Custom pulse energies and repetition rates
The pulse energy and repetition rate of the excitation source are ultimately constrained by the fluorophore cross section and tissue photodamage. Theory and experiment show that 2PE cross-sections and 3PE cross-sections of standard dyes are on the order of 10−49 cm4․(s/photon) and 10−82 cm6․(s/photon)2, respectively [6]. Under short-pulse excitation, fluorescence saturates at the limit of one transition per pulse per fluorophore. The pulse energies for saturation of fluorescence excitation under 2PE and 3PE are then approximately 1 nJ and 5 nJ, respectively, assuming 1700-nm excitation with 100-fs pulses and a numerical aperture NA = 1.0. These pulse energies are significantly below the breakdown threshold for biological tissues [88] for wavelengths greater than 1000 nm. Thus, linear absorption (i.e., the average power) is likely the leading concern when imaging deep into tissue using the 1300-nm or 1700-nm windows. The optimum excitation source should provide pulses with approximately the saturation pulse energy at the focus at various depths in the tissue, and at average power (i.e., repetition rate) levels that are tailored to avoid significant sample heating. The required pulse energy (hundreds of nJ) and repetition rate (on the order of 1 MHz) are challenging for bulk solid-state systems [89]. The use of fiber will greatly simplify the long cavity lengths required for low repetition rates, and new pulse evolutions allow stable high-energy pulses to be generated.
Fiber sources for Raman microscopy
To date, there is still not an all-fiber source with low enough intensity fluctuations to record SRS images without balanced detection. Sources with the pulse parameters stated above and fluctuations near the fundamental limits are needed.
All-fiber, environmentally-stable sources with high performance
The best-performing devices generally include some bulk optical components, which detract from the benefits of fiber to some degree. The ideal solutions would be completely fiber-integrated instruments made with polarization-maintaining fiber. The goal is to construct integrated instruments that do not sacrifice too much of the performance attained by lasers with bulk components. This will be particularly challenging with new large-mode area fibers such as PCF and chirally-coupled-core fibers [90].
The development of these fiber-based lasers has the potential to transform nonlinear microscopy. By providing compact, robust and cost-effective excitation sources, fiber lasers will deepen the penetration of nonlinear imaging techniques into the biological and biomedical communities, and accelerate their clinical translation. Furthermore, fiber-based excitation sources have the potential to provide new performance parameters that are challenging for bulk solid state systems. The needs of nonlinear microscopy provide ample motivation for continued development of short-pulse fiber sources, and in turn, new fiber sources will undoubtedly expand the boundaries of bioimaging.
Acknowledgements
Portions of this work were supported by the National Institutes of Health (EB002019, R01CA133148, R01EB014873, and R21RR032392) and the National Science Foundation (ECCS-0901323, BIS-0967949).
Footnotes
Author contributions
C.X. and F.W.W. co-wrote the paper.
Competing Financial Interests
The authors declare no competing financial interests.
References
- 1.Denk W, Strickler JH, Webb WW. Two-photon laser scanning fluorescence microscopy. Science. 1990;248:73–76. doi: 10.1126/science.2321027. [DOI] [PubMed] [Google Scholar]
- 2.Yuste R, Denk W. Dendritic spines as basic function units of neuronal integration. Nature. 1995;375:682–684. doi: 10.1038/375682a0. [DOI] [PubMed] [Google Scholar]
- 3.Williams RM, Piston DW, Webb WW. Two-photon molecular excitation provides intrinsic 3-dimensional resolution for laser-based microscopy and microphotochemistry. FASEB J. 1994;8:804–813. doi: 10.1096/fasebj.8.11.8070629. [DOI] [PubMed] [Google Scholar]
- 4.Denk W, Piston DW, Webb WW. Two-photon molecular excitation in laser scanning microscopy. In: Pawley J, editor. The Handbook of Confocal Microscopy. New York: Plenum; 1995. pp. 445–458. [Google Scholar]
- 5.Helmchen F, Denk W. Deep tissue two-photon microscopy. Nat. Methods. 2005;2:932–940. doi: 10.1038/nmeth818. [DOI] [PubMed] [Google Scholar]
- 6.Xu C, Zipfel W, Shear JB, Williams RM, Webb WW. Multiphoton fluorescence excitation: new spectral windows for biological nonlinear microscopy. Proc. Nat. Acad. Sci. USA. 1996;93:10763–10768. doi: 10.1073/pnas.93.20.10763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wokosin DL, Centonze VE, Crittenden S, White JG. Three-photon excitation fluorescence imaging of biological specimens using an all-solid-state laser. Bioimaging. 1996;4:208–214. [Google Scholar]
- 8.Hell SW, Bahlmann K, Schrader M, Soini A, Malak H, Gryczynski I, Lakowicz JR. Three-photon excitation in fluorescence microscopy. J. Biomed. Opt. 1996;1:71–74. doi: 10.1117/12.229062. [DOI] [PubMed] [Google Scholar]
- 9.Campagnola PJ, Wei MD, Lewis A, Loew LM. High-resolution nonlinear optical imaging of live cells by second harmonic generation. Biophys. J. 1999;77:3341–3349. doi: 10.1016/S0006-3495(99)77165-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Moreaux L, Sandra O, Mertz J. Membrane imaging by second harmonic generation microscopy. J. Opt. Soc. Am. B. 2000;17:1685–1694. [Google Scholar]
- 11.Barad Y, Eisenberg H, Horowitz M, Silberberg Y. Nonlinear laser scanning microscopy by third harmonic generation. Appl. Phys. Lett. 1997;70:922–924. [Google Scholar]
- 12.Muller M, Squier J, Wilson KR, Brakenoff GJ. 3D microscopy of transparent objects using third-harmonic generation. J. Microsc. 1998;191:266–274. doi: 10.1046/j.1365-2818.1998.00399.x. [DOI] [PubMed] [Google Scholar]
- 13.Sánchez EJ, Novotny L, Xie XS. Near-field fluorescence microscopy based on two-photon excitation with metal tips. Phys. Rev. Lett. 1999;82:4014–4017. [Google Scholar]
- 14.Jung JC, Schnitzer MJ. Multiphoton endoscopy. Opt. Lett. 2003;28:902–904. doi: 10.1364/ol.28.000902. [DOI] [PubMed] [Google Scholar]
- 15.Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated emission depletion microscopy. Opt. Lett. 1994;19:780–782. doi: 10.1364/ol.19.000780. [DOI] [PubMed] [Google Scholar]
- 16.Shaner NC, Steinbach PA, Tsien RY. A guide to choosing fluorescent proteins. Nat. Methods. 2005;2:905–909. doi: 10.1038/nmeth819. [DOI] [PubMed] [Google Scholar]
- 17.Hoover EE, Squier JA. Advances in multiphoton microscopy technology. Nature Photon. 2013;7:93–101. doi: 10.1038/nphoton.2012.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Duncan MD, Reintjes J, Manuccia TJ. Scanning coherent anti-stokes Raman microscope. Opt. Lett. 1982;7:350–352. doi: 10.1364/ol.7.000350. [DOI] [PubMed] [Google Scholar]
- 19.Zumbusch A, Holtom GR, Xie XS. Three-dimensional vibrational imaging by coherent anti-Stokes Raman scattering. Phys. Rev. Lett. 1999;82:4142–4145. [Google Scholar]
- 20.Ploetz E, Laimgruber S, Berner S, Zinth W, Gilch P. Femtosecond stimulated Raman microscopy. Appl. Phys. B. 2007;87:389–393. [Google Scholar]
- 21.Freudiger CW, Min W, Saar BG, Lu S, Holtom GR, He C, Tsai JC, Kang JX, Xie XS. Label-free biomedical imaging with high sensitivity by stimulated Raman scattering microscopy. Science. 2008;322:1857–1861. doi: 10.1126/science.1165758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Spence D, Kean P, Sibbett W. 60-femtosecond pulse generation from a self mode-locked Ti:Sapphire laser. Opt. Lett. 1991;16:42–44. doi: 10.1364/ol.16.000042. [DOI] [PubMed] [Google Scholar]
- 23.Negus DK, Spinelli L, Goldblatt N, Feuget G. Digest of the OSA Topical Meeting on Advanced Solid State Lasers. Memphis, TN: 1991. Sub-100 fs Pulse Generation by Kerr Lens Modelocking in Ti: Al203. [Google Scholar]
- 24.Aus der Au J, Kopf D, Morier-Genoud F, Moser M, Keller U. 60-fs pulses from a diode-pumped Nd:glass laser. Opt. Lett. 1997;22:307–309. doi: 10.1364/ol.22.000307. [DOI] [PubMed] [Google Scholar]
- 25.Honninger C, Morier-Genoud F, Moser M, Keller U, Brovelli LR, Harder C. Efficient and tunable diode-pumped femtosecond Yb: glass lasers. Opt. Lett. 1998;23:126–128. doi: 10.1364/ol.23.000126. [DOI] [PubMed] [Google Scholar]
- 26.Druon F, Balembois F, Georges P. Laser crystals for the production of ultrashort laser pulses. Ann. Chim. Sci. Mat. 2003;28:47–72. [Google Scholar]
- 27.Seas A, Petričević V, Alfano RR. Generation of sub-100-fs pulses from a cw mode-locked chromium-doped forsterite laser. Opt. Lett. 1992;17:937–939. doi: 10.1364/ol.17.000937. [DOI] [PubMed] [Google Scholar]
- 28.Model Insight™ Deep See™ from Newport Spectra-Physics.
- 29.Fermann ME, Galvanauskas A, Sucha G, Harter D. Fiber-lasers for ultrafast optics. Appl. Phys. B. 1997;65:259–275. [Google Scholar]
- 30.Limpert J, Roser F, Schreiber T, Tunnerman A. High-power ultrafast fiber laser systems. IEEE J. Select Topics Quantum Electron. 2006;12:233–244. [Google Scholar]
- 31.Ruehl A, Wandt D, Morgner U, Kracht D. Normal Dispersive Ultrafast fiber Oscillators. IEEE J. Select Topics Quantum Electron. 2009;15:170–181. [Google Scholar]
- 32.Fermann M, Hartl I. Ultrafast fiber laser technology. IEEE J. Select Topics Quantum Electron. 2009;15:191–206. [Google Scholar]
- 33.Valdmanis JA, Fork RL, Gordon JP. Generation of optical pulses as short as 27 fs directly from a laser balancing self-phase modulation, group-velocity dispersion, sautrable absorption, and saturable gain. Opt. Lett. 1985;10:131–133. doi: 10.1364/ol.10.000131. [DOI] [PubMed] [Google Scholar]
- 34.Tamura K, Ippen EP, Haus HA, Nelson LE. 77-fs pulse generation from a stretched-pulse mode-locked all-fiber ring laser. Opt. Lett. 1993;18:1080–1082. doi: 10.1364/ol.18.001080. [DOI] [PubMed] [Google Scholar]
- 35.Ober MH, Hofer M, Fermann ME. 42-fs pulse generation from a mode-locked fiber laser started with a moving mirror. Opt. Lett. 1993;18:367–369. doi: 10.1364/ol.18.000367. [DOI] [PubMed] [Google Scholar]
- 36.Chong A, Buckley J, Renninger W, Wise F. All-normal-dispersion femtosecond fiber laser. Opt. Express. 2006;14:10095–10100. doi: 10.1364/oe.14.010095. [DOI] [PubMed] [Google Scholar]
- 37.Renninger W, Chong A, Wise FW. Dissipative solitons in normal-dispersion fiber lasers. Phys. Rev. A. 2008;77:023814-1–023814-4. [Google Scholar]
- 38.Zhao LM, Tang DY, Wu J. Opt. Lett. 2006;31:1788–1790. doi: 10.1364/ol.31.001788. [DOI] [PubMed] [Google Scholar]
- 39.Grelu P, Akhmediev N. Dissipative solitons for mode-locked lasers. Nat. Photon. 2012;6:84–92. [Google Scholar]
- 40.Kieu K, Renninger W, Chong A, Wise FW. Sub-100-fs pulses at watt-level powers from a dissipative-soliton fiber laser. Opt. Lett. 2009;34:593–595. doi: 10.1364/ol.34.000593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chichkov NB, Hapke C, Neumann J, Kracht D, Wandt D, Morgner U. Pulse duration and energy scaling of femtosecond all-normal dispersion fiber oscillators. Opt. Express. 2012;20:3844–3852. doi: 10.1364/OE.20.003844. [DOI] [PubMed] [Google Scholar]
- 42.Chong A, Renninger W, Wise FW. Properties of normal-dispersion femtosecond fiber lasers. J. Opt. Soc. Am. B. 2008;25:140–148. [Google Scholar]
- 43.Renninger W, Chong A, Wise FW. Self-similar pulse evolution in an all-normal-dispersion laser. Phys. Rev. A. 2010;82:021805(R). doi: 10.1103/PhysRevA.82.021805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wise FW. Femtosecond fiber lasers based on dissipative processes for nonlinear microscopy. IEEE J. Select Topics Quantum Electron. 2012;18:1412–1421. doi: 10.1109/JSTQE.2011.2179919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liu G, Kieu K, Wise FW, Chen Z. Multiphoton microscopy system with a compact fiber-based femtosecond-pulse laser and handheld probe. J. Biophotonics. 2011;4:34–39. doi: 10.1002/jbio.201000049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Galvanauskas A. Mode-scalable, fiber-based, chirped-pulse amplification systems. IEEE J. Select Topics Quantum Electron. 2001;7:504–517. [Google Scholar]
- 47.Lefrancois S, Kieu K, Deng Y, Kafka JD, Wise FW. Scaling of dissipative-soliton fiber lasers to megawatt peak powers by use of large-area photonic-crystal fiber. Opt. Lett. 2010;35:1569–1571. doi: 10.1364/OL.35.001569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Baumgartl M, Lecaplain C, Hideur A, Limpert J, Tunnerman A. 66 W average power from a microjoule-class sub-100 fs fiber oscillator. Opt. Lett. 2012;37:1640–1642. doi: 10.1364/OL.37.001640. [DOI] [PubMed] [Google Scholar]
- 49.Ramachandran S, Nicholson JW, Ghalmi S, Yan MF, Wisk P, Monberg E, Dimarcello FV. Light propagation with ultralarge modal areas in optical fibers. Opt. Lett. 2006;31:1797–1799. doi: 10.1364/ol.31.001797. [DOI] [PubMed] [Google Scholar]
- 50.Nicholson JW, Fini JM, Phillips J, DeSantolo A, Liu X, Feder K, Supradeepa VR, Westbrook P, Monberg E, DiMarcello F, Headley C, DiGiovanni DJ. Nanosecond pulse amplification in a 6000 µm2 effective area higher-order mode erbium-doped fiber amplifier. Proc. Conf. Lasers Electro Optics. 2012 2012, paper JTh1I.2. [Google Scholar]
- 51.Svoboda K, Tank DW, Denk W. Direct measurement of coupling between dendritic spines and shafts. Science. 1996;272:716–719. doi: 10.1126/science.272.5262.716. [DOI] [PubMed] [Google Scholar]
- 52.Mostany R, Portera-Cailliau C. Absence of large-scale dendritic plasticity of layer 5 pyramidal neurons in peri-infarct cortex. J. Neuroscience. 2011;31:1734–1738. doi: 10.1523/JNEUROSCI.4386-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Squirrell JM, Wokosin DL, White JG, Bavister BD. Long-term two-photon fluorescence imaging of mammalian embryo without compromising viability. Nature Biotechnol. 1999;17:763–767. doi: 10.1038/11698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zipfel WR, Williams RM, Christie R, Nikitin AY, Hyman BT, Webb WW. Live tissue intrinsic emission microscopy using multiphoton-excited native fluorescence and second harmonic generation. Proc. Natl. Acad. Sci. USA. 2003;100:7075–7080. doi: 10.1073/pnas.0832308100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.So PTC, Dong CY, Masters BR, Berland KM. Two-photon excitation fluorescence microscopy. Annu. Rev. Biomed. Eng. 2000;2:399–429. doi: 10.1146/annurev.bioeng.2.1.399. [DOI] [PubMed] [Google Scholar]
- 56.Centonze VE, White JG. Multiphoton excitation provides optical sections from deeper within scattering specimens than confocal imaging. Biophys. J. 1998;75:2015–2024. doi: 10.1016/S0006-3495(98)77643-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Theer P, Hasan MT, Denk W. Two-photon imaging to a depth of 1000 µm in living brains by use of a Ti:Al2O3 regenerative amplifier. Opt. Lett. 2003;28:1022–1024. doi: 10.1364/ol.28.001022. [DOI] [PubMed] [Google Scholar]
- 58.Leray A, Odin C, Huguet E, Amblard F, Le Grand Y. Spatially distributed two-photon excitation fluorescence in scattering media: Experiments and time-resolved Monte Carlo simulations. Opt. Commun. 2007;272:269–278. [Google Scholar]
- 59.Kobat D, Horton NG, Xu C. In vivo two-photon microscopy to 1.6-mm depth in mouse cortex. J. Biomed. Opt. 2011;16:106014-1–106014-4. doi: 10.1117/1.3646209. [DOI] [PubMed] [Google Scholar]
- 60.Kobat D, Durst ME, Nishimura N, Wong AW, Schaffer CB, Xu C. Deep tissue multiphoton microscopy using longer wavelength excitation. Opt. Express. 2009;17:13354–13364. doi: 10.1364/oe.17.013354. [DOI] [PubMed] [Google Scholar]
- 61.Balu M, Baldacchini T, Carter J, Krasieva TB, Zadoyan R, Tromberg BJ. Effect of excitation wavelength on penetration depth in nonlinear optical microscopy of turbid media. J. Biomed. Opt. 2009;14:010508. doi: 10.1117/1.3081544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Andresen V, Alexander S, Heupel W-M, Hirschberg M, Hoffman RM, Friedl P. Infrared multiphoton microscopy: Subcellular resolved deep tissue imaging. Curr. Opin. Biotechnol. 2009;20:54–62. doi: 10.1016/j.copbio.2009.02.008. [DOI] [PubMed] [Google Scholar]
- 63.Horton NG, Wang K, Kobat D, Clark C, Wise F, Schaffer C, Xu C. In vivo three-photon microscopy of subcortical structures of an intact mouse brain. Nature Photon. 2009;7:205–209. doi: 10.1038/nphoton.2012.336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Maiti S, Shear JB, Williams RM, Zipfel WR, Webb WW. Measuring serotonin distribution in live cells with three-photon excitation. Science. 1997;275:530–532. doi: 10.1126/science.275.5299.530. [DOI] [PubMed] [Google Scholar]
- 65.Gordon J. Theory of the soliton self-frequency shift. Opt. Lett. 1986;11:662–664. doi: 10.1364/ol.11.000662. [DOI] [PubMed] [Google Scholar]
- 66.Zysset B, Beaud P, Hodel W. Generation of optical solitons in the wavelength region 1.37–1.49 mm. Appl. Phys. Lett. 1987;50:1027–1029. [Google Scholar]
- 67.Liu X, Xu C, Knox WH, Chandalia JK, Eggleton BJ, Windler RS, Kosinski SG. Soliton self-frequency shift in a short tapered air-silica microstructure fiber. Opt. Lett. 2001;26:358–360. doi: 10.1364/ol.26.000358. [DOI] [PubMed] [Google Scholar]
- 68.Knight JC, Broeng J, Birks TA, Russell PSJ. Photonic band gap guidance in optical fibers. Science. 1998;282:1476–1478. doi: 10.1126/science.282.5393.1476. [DOI] [PubMed] [Google Scholar]
- 69.Unruh JR, Price ES, Molla RG, Stehno-Bittel L, Johnson CK, Hui R. Two-photon microscopy with wavelength switchable fiber laser excitation. Opt. Express. 2006;14:9825–9831. doi: 10.1364/oe.14.009825. [DOI] [PubMed] [Google Scholar]
- 70.Ouzounov DG, Ahmad FR, Muller D, Venkataraman N, Gallagher MT, Thomas MG, Silcox J, Koch KW, Gaeta AL. Generation of megawatt optical solitons in hollow-core photonic band-Gap fibers. Science. 2003;301:1702–1704. doi: 10.1126/science.1088387. [DOI] [PubMed] [Google Scholar]
- 71.Wang K, Xu C. Tunable high-energy soliton pulse generation from a large-mode-area fiber and its application to third harmonic generation microscopy. Appl.Phys. Lett. 2011;99:071112-1–071112-3. doi: 10.1364/OL.36.000942. [DOI] [PubMed] [Google Scholar]
- 72.Ganikhanov F, Carrasco S, Xie XS, Katz M, Seitz W, Kopf D. Broadly tunable dual-wavelength light source for coherent anti-Stokes Raman scattering microscopy. Opt. Lett. 2006;31:1292–1294. doi: 10.1364/ol.31.001292. [DOI] [PubMed] [Google Scholar]
- 73.Model Levante Emerald™ from APE GmbH (Berlin).
- 74.Andresen ER, Nielsen CK, Thogersen J, Keiding SR. Fiber laser-based light source for coherent anti-Stokes Raman scattering microspectroscopy. Opt. Express. 2007;15:4848–4856. doi: 10.1364/oe.15.004848. [DOI] [PubMed] [Google Scholar]
- 75.Krauss G, Hanke T, Sell A, Trautlein D, Leitenstorfer A, Selm R, Winterhalder M, Zumbusch A. Compact coherent anti-Stokes Raman scattering microscope based on a picosecond two-color Er:fiber laser system. Opt. Lett. 2009;34:2847–2849. doi: 10.1364/OL.34.002847. [DOI] [PubMed] [Google Scholar]
- 76.Kieu K, Peyghambarian N. Synchronized picosecond pulses at two different wavelengths from a compact fiber laser source for Raman microscopy. Proc. SPIE. 2011:790310-1–790310-7. [Google Scholar]
- 77.Mosley PJ, Bateman SA, Lavoute L, Wadsworth WJ. Low-noise, high-brightness, tunable source of picosecond pulsed light in the near-infrared and visible. Opt. Express. 2011;19:25337–25345. doi: 10.1364/OE.19.025337. [DOI] [PubMed] [Google Scholar]
- 78.Baumgartl M, Gottschall T, Abreu-Afonso J, Diez A, Meyer T, Dietzek B, Rothhardt M, Popp J, Limpert J, Tunnermann A. Alignment-free, all-spliced fiber laser source for CARS microscopy based on four-wave-mixing. Opt. Express. 2012;20:21010–21018. doi: 10.1364/OE.20.021010. [DOI] [PubMed] [Google Scholar]
- 79.Lefrancois S, Fu D, Holtom GR, Kong L, Wadsworth WJ, Schneider P, Herda S, Zach A, Xie XS, Wise FW. Fiber four-wave mixing source for coherent anti-Stokes Raman scattering microscopy. Opt. Lett. 2012;37:1652–1654. doi: 10.1364/OL.37.001652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Zhai Y-H, Goulart C, Sharping JE, Wei H, Chen S, Tong W, Slipchenko MN, Zhang D, Cheng J-X. Multimodal coherent anti-Stokes Raman spectroscopic imaging with a fiber optical parametric oscillator. Appl. Phys. Lett. 2011;98:191106-1–191106-3. doi: 10.1063/1.3589356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Lamb E, Lefrancois S, Ji M, Wadsworth WJ, Xie XS, Wise FW. Fiber optical parametric oscillator for coherent anti-Stokes Raman scattering microscopy. Opt. Lett. doi: 10.1364/OL.38.004154. doc. ID 193646 (posted 18 September 2013, in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Godil AA, Auld BA, Bloom DM. Picosecond time-lenses. IEEE J. Quantum Electron. 1994;30:827–837. [Google Scholar]
- 83.Kolner BH. Space–time duality and the theory of temporal imaging. IEEE J. Quantum Electron. 1994;30:1951–1963. [Google Scholar]
- 84.van Howe J, Hansryd J, Xu C. Multiwavelength pulse generator using time-lens compression. Opt. Lett. 2004;29:1470–1472. doi: 10.1364/ol.29.001470. [DOI] [PubMed] [Google Scholar]
- 85.Wang K, Freudiger CW, Lee JH, Saar BG, Xie XS, Xu C. Synchronized time-lens source for coherent Raman scattering microscopy. Opt. Exp. 2010;18:14262–14269. doi: 10.1364/OE.18.024019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Wang K, Zhang D, Charan K, Slipchenko MN, Wang P, Xu C, Cheng J. Time-lens based hyperspectral stimulated Raman scattering imaging and quantitative spectral analysis. J. Biophotonics. 2013 doi: 10.1002/jbio.201300005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Pedersen MEV, Cheng J, Charan K, Wang K, Xu C, Grüner-Nielsen L, Jakobsen D. Higher-order-mode fiber optimized for energetic soliton propagation. Opt. Lett. 2012;37:3459–3461. doi: 10.1364/OL.37.003459. [DOI] [PubMed] [Google Scholar]
- 88.Olivié G, Giguère D, Vidal F, Ozaki1 T, Kieffer J-C, Nada O, Brunette I. Wavelength dependence of femtosecond laser ablation threshold of corneal stroma. Opt. Express. 2008;16:4121–4129. doi: 10.1364/oe.16.004121. [DOI] [PubMed] [Google Scholar]
- 89.The Femtosource™ XL from Femtolasers GmbH (Vienna) generates femtosecond pulses with hundreds of nanojoules at 5 MHz repetition rate.
- 90.Liu C-H, Chang G, Litchinitser N, Galvanauskas A, Guertin D, Jacobson N, Tankala K. In Advanced Solid-State Photonics, paper ME2. Washington: Optical Society of America; 2007. [Google Scholar]


