Summary
Recurrent event data frequently arise in longitudinal studies when study subjects possibly experience more than one event during the observation period. Often, such recurrent events can be categorized. However, part of the categorization may be missing due to technical difficulties. If the event types are missing completely at random, then a complete case analysis may provide consistent estimates of regression parameters in certain regression models, but estimates of the baseline event rates are generally biased. Previous work on nonparametric estimation of these rates has utilized parametric missingness models. In this paper, we develop fully nonparametric methods in which the missingness mechanism is completely unspecified. Consistency and asymptotic normality of the nonparametric estimators of the mean event functions accommodate nonparametric estimators of the event category probabilities, which converge more slowly than the parametric rate. Plug-in variance estimators are provided and perform well in simulation studies, where complete case estimators may exhibit large biases and parametric estimators generally have a larger mean squared error when the model is misspecified. The proposed methods are applied to data from a cystic fibrosis registry.
Some key words: Cystic fibrosis, Local polynomial regression, Nelson–Aalen estimation, Pseudomonas aeruginosa infection, Rate proportion
1. Introduction
Recurrent event data frequently occur in biomedical studies where subjects may suffer from repeated symptoms, infections or hospitalizations. Such data also arise in industrial manufacturing when tested units or equipment may experience multiple failures and repairs. Often, such recurrent events can be categorized. Taking cystic fibrosis for example, patients may experience repeated Pseudomonas aeruginosa infections in early childhood and later acquire other mutated types of infection, which also occur recurrently even after aggressive antibiotic use (Li et al., 2005). However, the identification of the event category may not be complete due to technical difficulties. As demonstrated in § 5, such missingness poses challenges for the analysis of the rates of particular event types.
A common approach for the analysis of recurrent events is based on a rate function. In contrast to an intensity function approach, which conditions on all previous information, a rate function approach conditions only on the current value of covariates (Pepe & Cai, 1993; Lin et al., 2000; Cook & Lawless, 2007; Cook et al., 2009). Complete case analyses that censor missing event types lead to underestimation of either the intensity or the rate function (Schaubel & Cai, 2006). Cai & Schaubel (2004) studied a proportional rate model for multiple recurrent event processes, with unbiased estimation of the regression parameters but not the baseline rate function obtained with missingness completely at random. Schaubel & Cai (2006) later proposed an estimation procedure that is valid under weaker missingness assumptions and yields unbiased estimates of the baseline rate function. Parametric models were used to estimate the missingness probabilities, which were then used as weights in the usual rate model estimating equation. Chen & Cook (2009) specified a parametric frailty model to characterize dependence amongst the events and employed maximum likelihood analysis, which requires correct specification of rate models for all event types, as well as of the frailty distribution. In this paper, we consider nonparametric estimation of the rate function without specifying parametric models for the missingness or imposing restrictions on the models for other event types.
To formalize the data set-up, suppose that there are n independent subjects with K recurrent event categories. Let denote the total number of category k events occurring before time t for subject i, such that and for k ≠ ℓ. The mean function is continuous with a smooth derivative rk(t) = dμk(t)/dt. Let Ci denote the censoring time for subject i. The observed number of events is given by , where a ∧ b denotes the minimum of a and b. Assuming Ci is independent of for each i and k, we have E{Nik(t) | Yi (t)} = Yi (t)μk(t) with Yi (t) = I (Ci ≥ t) indicating whether subject i is at risk for any event type.
With event categories always being observed, a Nelson–Aalen-type estimator (Nelson, 1988), defined by
| (1) |
is consistent for μk(t) for each k, where denotes the total number of subjects who are at risk at time t. The variance of can be consistently estimated by
In the previous literature, this estimator was studied only for events of a single type (Andersen et al., 1993; Lawless & Nadeau, 1995; Cook et al., 1996; Chiang et al., 2005). With multiple event types, one may choose to explicitly model the dependence amongst the events, e.g., using a mixed Poisson process (Abu-Libdeh et al., 1990) or to construct marginal models that may be fitted separately (Cai & Schaubel, 2004). Intuitively, should behave like estimators with a single type, since the estimator is calculated separately for each k.
The estimator (1) cannot be computed when event category information is missing. Naively censoring such events in a complete case analysis leads to underestimation. On the other hand, even with such missingness, the overall event process is observable. Using this information and information on events with known event types, one may estimate the probabilities of different event types conditionally on the observed data. These probabilities may be incorporated as weights in (1), yielding valid inferences. Schaubel & Cai (2006) employed a fully parametric logit model for the event category probabilities. When the model is misspecified, the resulting estimate for μk(t) could be biased. In this paper, we develop a fully nonparametric method for estimating μk(t) that is able to estimate the probability of an event being type k without any model assumption. The event category probabilities cannot be estimated at the usual parametric rate, which greatly complicates the analysis of the weighted version of (1). We show that the resulting estimator is root-n consistent and asymptotically normal, with variance which may be estimated using a simple plug-in formula.
2. Estimation methods
Let δi (t) ∈ {1,…, K } denote the type of the event that occurs to subject i at time t, and let δik(t) = I{δi (t) = k} be an indicator function that indicates the category. Let Ri (t) = 1 when the event category is observed and Ri (t) = 0 otherwise. When some of the event categories are missing, a complete case analysis based on events with known event types, which is defined by
will underestimate μk(t) even when the event category is missing completely at random.
Note that dNik(t) = δik(t) dNi·(t), since dNik(t) dNiℓ(t) = 0 for k ≠ ℓ. Thus, dNik(t) = Ri (t) dNik(t) + {1 − Ri (t)} δik(t) dNi·(t), and in (1) can be written as
| (2) |
Since δik(t) is unobservable when Ri (t) = 0, the complete case estimator underestimates the truth due to ignorance of the second part in (2). A prediction of δik(t), based on observable data, could be inserted to estimate the unknown part and correct the underestimation of .
Assume that πi (t) = E{Ri (t) | dNik(t) = 1} is the same for each k. One can show that
for k = 1,…, K, which equals . Thus, if one can estimate pk(t) based on the rate functions rk(t), a consistent estimator may be derived by inserting in the estimated probabilities for the missing δik(t) in (2). However, it is not clear how to estimate the rate function rk(t) when events with missing type are present in the data. Interestingly, without estimating rk(t) for each k, one may estimate pk(t), a rate proportion, by utilizing the events with known type, i.e., from a complete case analysis.
One can show that the limiting processes of and its derivatives, respectively, are
where and . One may utilize to estimate the rate proportion pk(t), using the fact that
That is, although the complete case estimator itself underestimates the true underlying rate function, it can otherwise consistently estimate the probability of an observed event being type k. We hereafter refer to this approach as the rate proportion method, since the probability is simply a proportion of the overall rate.
To estimate pk(t), we propose a nonparametric estimator for θk(t) = log{pk(t)/ pK (t)} via a local likelihood method and estimate pk(t) through . For any time t0 ∈ [0, τ], define the νth derivative of θk(t) as . One may expand θk(t) as
if t is in the neighbourhood of t0, say, t ∈ [t0 − h, t0 + h] with bandwidth h. Let , βk = (β0k, …, βqk)T, and . The local log-likelihood for is defined by
with
where
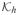 (·) =
(·) =
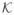 (·/ h)/ h with
(·/ h)/ h with
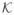 (·) being a kernel function; τ is a constant that satisfies pr(Ci ≥ τ) > 0 for each i. By theory of local polynomial modelling (Fan & Gijbels, 1996), we can approximate θk(t) by
, where β̂k = (β̂0k,…, β ^qk)T maximizes the local likelihood ℓ(β). Consequently, an estimator for θk(t0) is simply the local intercept β̂0k, and by moving t0 within [0, τ], we can obtain functional estimates for θk(t).
(·) being a kernel function; τ is a constant that satisfies pr(Ci ≥ τ) > 0 for each i. By theory of local polynomial modelling (Fan & Gijbels, 1996), we can approximate θk(t) by
, where β̂k = (β̂0k,…, β ^qk)T maximizes the local likelihood ℓ(β). Consequently, an estimator for θk(t0) is simply the local intercept β̂0k, and by moving t0 within [0, τ], we can obtain functional estimates for θk(t).
Our goal, however, is to replace δik(t) in (2) with an estimate of pk(t) by
where θ̂ = (β̂01,…, β̂0(K−1))T with β ^0k (k = 1,…, K − 1) being local likelihood estimates at t, and β ^0K ≡ 0. Our estimator of the mean function by the rate proportion method is
| (3) |
with consistent variance estimator
| (4) |
where φ̂ik(t; θ) is defined in Theorem 1 in § 3 and pk(t) is estimated only when an event with unknown category occurred at t.
3. Asymptotic properties
Let A(υ) be a column vector that satisfies and A(υ)⊗2 = A(υ) A(υ)T. Take for k = 1,…, K … 1. In addition, let {(K − 1) × (q + 1)}-square matrix ℍ denote blockdiag{H,…, H} with H = diag{1, h, …, hq}, and take β̂* = ℍβ ^ and , where β0 is the true value of β. Let and .
We first provide the following lemma showing the consistency and large sample normality of the local likelihood estimator, which can be derived from a local polynomial method (Fan & Gijbels, 1996).
Lemma 1
Assume that the regularity conditions in the Appendix hold. Given t0 ∈ [0, τ], we have
in distribution, where , with
, Ωk(t0) is a (K − 1)-column vector with ρk(t0) = pk(t0){1 − pk(t0)} in the kth element and ρkℓ(t0) = − pk(t0) pℓ(t0) in the ℓth element, for ℓ ≠ k;
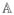 (t0) consists of diagonal block elements
(t0) consists of diagonal block elements
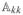 (k = 1,…, K … 1), and off-diagonal block elements
(k = 1,…, K … 1), and off-diagonal block elements
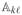 =
=
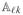 , k ≠ ℓ, where
, k ≠ ℓ, where
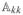 = ρk(t0) f (t0) ∫ A(υ)⊗2
= ρk(t0) f (t0) ∫ A(υ)⊗2
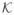 (υ) dυ and
(υ) dυ and
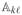 = ρkℓ(t0) f (t0) ∫ A(υ)⊗2
= ρkℓ(t0) f (t0) ∫ A(υ)⊗2
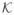 (υ) dυ;
(υ) dυ;
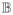 (t0), the limiting variance matrix of the score function, consists of block elements
(t0), the limiting variance matrix of the score function, consists of block elements
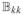 = ρk(t0) f (t0) ∫A(υ)⊗2
= ρk(t0) f (t0) ∫A(υ)⊗2
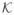 (υ)2 dυ, and
(υ)2 dυ, and
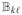 =
=
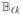 = ρkℓ(t0) f (t0) ∫ A(υ)⊗2
= ρkℓ(t0) f (t0) ∫ A(υ)⊗2
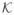 (υ)2 dυ, for k ≠ ℓ.
(υ)2 dυ, for k ≠ ℓ.
In the special case with q = 1 and K = 2, Lemma 1 can be simplified to the following corollary.
Corollary 1
Under the conditions of Lemma 1, we have
in distribution, where the bias
and the variance
with μ2 = ∫ υ2
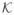 (υ) dυ, ν0 = ∫
(υ) dυ, ν0 = ∫
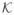 (υ)2 dυ, and ν2 = ∫ υ2
(υ)2 dυ, and ν2 = ∫ υ2
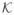 (υ)2 dυ. Furthermore,
(υ)2 dυ. Furthermore,
in distribution, where σ2(t0) = ν0ρ1(t0)−1 f(t0)−1.
When q = 1 and K = 2, the theoretical optimal bandwidth for estimating θ1(·) can be derived by minimizing the asymptotic integrated mean squared error ∫ {b(s)2 + σ2(s)/(nh)}ω(s) ds with some weighting function ω. One can show that
For arbitrary K ≥2, one can show that the optimal choice of the bandwidth for θk(·) is of order n−1/(2q+3) for q ≥0. This is a critical result for the proof of the root-n weak convergence rate for , due to the slower convergence rate of the local polynomial estimator θ̂
Large sample properties of are summarized in the following theorem, whose proof is given in the Appendix.
Theorem 1
Under the conditions of Lemma 1, the rate proportion estimator is uniformly consistent for μk(t) in t ∈ [0, τ], and converges weakly to a Gaussian process with mean zero and covariance function Vk(s, t), s, t ∈ [0, τ], which can be consistently estimated by
| (5) |
where
with Ω̂ k(s) being a consistent estimate of Ωk(s) obtained by replacing pk(s) with p̂k(s; θ) for k =1,…, K − 1, with (q + 1)-column vectors e1 = (1, 0,…, 0)T, b̂ (s) being an estimate of the bias term b(s), and
The summation of the first term in φ̂ik(t; θ) will be dominated by the summation of the second term. Hence the naive variance estimator for , defined by
is applicable when the sample size is large, without considering the variation contributed by the local likelihood estimates. That is, the limiting variance equals that from an estimator in which the event category probabilities are known. This differs from the case where parametric missingness models are fitted (Schaubel & Cai, 2006), where the resulting variance estimators depend on the variability in the parametric model estimates.
Observe, however, that the weak convergence rate of the two summation terms can be very close, e.g., O(n−3/5) versus O(n−1/2), when applying the local linear model. The naive variance estimator will likely underestimate the true variance when the sample size is relatively small, while the proposed variance estimator in (5) incorporates the variability of the local polynomial estimate. Specifically, one can estimate the bias term b(s) by using a higher order polynomial. For example, in the special case with q = 1 and K = 2, the bias term depends on the second derivative of θ1(t), which can be estimated by 2β̂21 in a local cubic regression for θ1(t). In short, we denote , as in (4).
4. Simulation studies
In this section, simulation experiments are presented to demonstrate finite sample properties of our proposed estimation procedures. Three methods were evaluated. In the analysis of event category always being observed, we include every event in the estimation to serve as a reference for comparison. This kind of analysis is not feasible in practice with missing category data. Another method is the weighted estimating equations method (Schaubel & Cai, 2006) with a parametric logit model for the probability of a target category. A biased estimate may be anticipated when the true model is misspecified by the parametric model. Our proposed method, however, aims to provide consistent and robust estimates.
We consider three scenarios. In the first and second scenarios, we considered two types of recurrent events in 200 subjects. Let λ1(t) = 1, λ2(t) = t, and λ3(t) = t2/3. We first generated event processes with intensity functions Gr01λ1(t) and Gr02λ2(t), where the shared random variable G was sampled from a Gamma(1/α, α) with E(G) = 1 and var(G) = α. The mean functions we aim to estimate, therefore, are μ1(t) = r01t and μ2(t) = r02t2/2. In this setting the parametric logistic model in the weighted estimating equations method may correctly specify the model for pk(t) if one uses log(t) as a covariate since log{p1(t)/ p2(t)} = log(r01/r02) − log(t). However, in a second scenario, if the second process is generated by an intensity function Gr02{λ1(t) + λ2(t) + λ3(t)} with a mean function μ2(t) = r02(t + t2/2 + t3/9), the parametric model may be off the truth if one uses t as a covariate, especially when t is large. In the third scenario, we consider three types of recurrent events when n = 50 or 200 with intensity functions Gr01λ1(t), Gr02{λ1(t) + λ2(t)}, and Gr02λ3(t), where G = log(W)/ exp(0·5) with W generated from a standard normal distribution.
The probability of having a missing category when an event occurred is
| (6) |
where zi (t) = {1, t, Ni·(t·), Zi }T with Ni·(t·) counting the total number of events before t; Zi = 1 if i is odd, and 0 otherwise. In the simulation we set κ= (κ0, κt, κn, κz)T, with κt = −0·1, κn = 0·05, and κz = 0 or log(8), in which κz ≠ 0 indicated missing due to covariates or missing at random in Little & Rubin (2002). Various values of κ0 were set to create different amount of events with missing category in order to systematically explore the effects of missingness, for which estimators would have more variation when events with missing category occurred more often. The simulation results shown in Tables 1 and 2 support this.
Table 1.
Simulation results for μ1(t) = r01t at t = 3; all entries except and are shown after multiplication by 102
| α | Biasn |
|
κz |
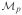
|
Biasr |
|
|
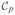
|
Biasω |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ2(t) = r02t2/2 | ||||||||||||||||||
| 0·5 | −0·45 | 17·9 | 0 | 10% | −0·13 | 18·0 | 18·2 | 94·5 | −0·38 | 17·9 | 0·99 | 0·99 | ||||||
| 20% | 0·09 | 18·3 | 18·1 | 94·6 | −0·38 | 18·1 | 0·96 | 0·98 | ||||||||||
| 30% | 0·25 | 18·7 | 18·0 | 94·0 | −0·48 | 18·4 | 0·91 | 0·97 | ||||||||||
| 2·08 | 10% | −0·18 | 18·3 | 18·1 | 93·8 | −0·45 | 18·2 | 0·96 | 0·99 | |||||||||
| 20% | 0·00 | 18·6 | 18·1 | 93·7 | −0·46 | 18·3 | 0·93 | 0·98 | ||||||||||
| 30% | 0·49 | 18·9 | 18·1 | 92·9 | −0·34 | 18·6 | 0·90 | 0·97 | ||||||||||
| 1·0 | 0·93 | 22·8 | 0 | 10% | 1·05 | 22·9 | 22·2 | 93·8 | 0·86 | 22·9 | 0·99 | 0·99 | ||||||
| 20% | 1·30 | 23·3 | 22·2 | 93·8 | 0·85 | 23·1 | 0·96 | 0·99 | ||||||||||
| 30% | 1·79 | 23·4 | 22·3 | 94·2 | 1·10 | 23·2 | 0·94 | 0·98 | ||||||||||
| 2·08 | 10% | 1·12 | 23·1 | 22·3 | 93·6 | 0·95 | 23·0 | 0·98 | 0·99 | |||||||||
| 20% | 1·42 | 23·1 | 22·3 | 94·2 | 0·99 | 23·0 | 0·97 | 0·99 | ||||||||||
| 30% | 1·84 | 23·6 | 22·3 | 94·0 | 1·10 | 23·3 | 0·93 | 0·97 | ||||||||||
| μ2(t) = r02(t + t2/2 + t3/9) | ||||||||||||||||||
| 0·5 | 0·52 | 18·3 | 0 | 10% | 0·17 | 18·6 | 18·1 | 93·8 | 2·04 | 18·7 | 0·97 | 1·03 | ||||||
| 20% | 0·03 | 19·0 | 17·9 | 92·6 | 3·21 | 19·2 | 0·92 | 1·05 | ||||||||||
| 30% | −0·06 | 19·7 | 17·8 | 91·5 | 4·56 | 19·8 | 0·86 | 1·07 | ||||||||||
| 2·08 | 10% | 0·29 | 18·5 | 18·1 | 93·7 | 1·81 | 18·7 | 0·98 | 1·03 | |||||||||
| 20% | 0·11 | 19·0 | 17·9 | 92·9 | 2·92 | 19·3 | 0·93 | 1·05 | ||||||||||
| 30% | 0·52 | 19·7 | 17·8 | 91·9 | 4·72 | 20·4 | 0·86 | 1·13 | ||||||||||
| 1·0 | 2·07 | 21·8 | 0 | 10% | 1·63 | 22·0 | 22·1 | 94·6 | 4·90 | 22·5 | 0·98 | 1·09 | ||||||
| 20% | 1·35 | 22·3 | 21·9 | 94·4 | 6·62 | 23·1 | 0·96 | 1·16 | ||||||||||
| 30% | 1·20 | 22·8 | 21·8 | 93·7 | 8·55 | 23·8 | 0·91 | 1·22 | ||||||||||
| 2·08 | 10% | 1·59 | 21·9 | 22·2 | 94·9 | 4·32 | 22·4 | 0·99 | 1·08 | |||||||||
| 20% | 1·32 | 22·3 | 22·0 | 94·4 | 6·21 | 23·1 | 0·95 | 1·14 | ||||||||||
| 30% | 1·35 | 22·7 | 21·9 | 94·1 | 8·13 | 23·8 | 0·92 | 1·23 | ||||||||||
Table 2.
Simulation results for μ1(t) = r01t when K = 3 and the frailty follows a log-normal distribution; all entries except and are shown after multiplication by 102
| t | n | Biasn | Ṽn1/2 | κz |
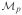
|
Biasr | Ṽr1/2 | V̄r1/2 |
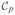
|
Biasω | Ṽω1/2 |
|
|
||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 0·83 | 14·5 | 0 | 15% | 0·76 | 14·7 | 16·1 | 92·4 | 0·46 | 14·6 | 0·99 | 0·98 | ||
| 25% | 0·63 | 14·9 | 18·1 | 93·8 | 0·09 | 14·7 | 0·96 | 0·98 | |||||||
| 35% | 0·65 | 15·2 | 20·7 | 94·3 | −0·16 | 14·9 | 0·92 | 0·96 | |||||||
| 2·08 | 15% | 0·80 | 14·7 | 16·3 | 92·0 | 0·47 | 14·6 | 0·97 | 0·98 | ||||||
| 25% | 0·76 | 15·0 | 18·1 | 93·9 | 0·19 | 14·8 | 0·95 | 0·97 | |||||||
| 35% | 0·68 | 15·2 | 20·9 | 94·5 | −0·20 | 14·9 | 0·92 | 0·96 | |||||||
| 200 | 0·24 | 7·11 | 0 | 15% | 0·35 | 7·24 | 7·78 | 95·7 | −0·13 | 7·19 | 0·96 | 0·98 | |||
| 25% | 0·36 | 7·31 | 8·39 | 96·3 | −0·51 | 7·20 | 0·94 | 0·97 | |||||||
| 35% | 0·52 | 7·39 | 9·14 | 96·8 | −0·81 | 7·24 | 0·92 | 0·97 | |||||||
| 2·08 | 15% | 0·32 | 7·20 | 7·84 | 95·3 | −0·21 | 7·15 | 0·97 | 0·98 | ||||||
| 25% | 0·40 | 7·27 | 8·46 | 96·4 | −0·51 | 7·18 | 0·95 | 0·98 | |||||||
| 35% | 0·48 | 7·46 | 9·36 | 97·1 | −0·95 | 7·30 | 0·90 | 0·97 | |||||||
| 3 | 50 | 3·66 | 38·6 | 0 | 15% | 4·45 | 38·2 | 38·9 | 92·1 | 5·47 | 39·4 | 1·02 | 1·07 | ||
| 25% | 5·10 | 38·3 | 40·3 | 92·9 | 6·33 | 40·0 | 1·01 | 1·10 | |||||||
| 35% | 5·54 | 38·3 | 42·1 | 92·5 | 6·86 | 40·2 | 1·01 | 1·11 | |||||||
| 2·08 | 15% | 4·49 | 38·4 | 39·0 | 91·6 | 5·16 | 39·4 | 1·01 | 1·06 | ||||||
| 25% | 5·03 | 38·4 | 40·4 | 92·0 | 5·92 | 39·9 | 1·00 | 1·08 | |||||||
| 35% | 6·58 | 39·5 | 42·7 | 93·1 | 7·55 | 41·6 | 0·94 | 1·11 | |||||||
| 200 | 0·48 | 19·0 | 0 | 15% | 1·17 | 19·0 | 18·8 | 93·1 | 2·28 | 19·6 | 1·00 | 1·07 | |||
| 25% | 1·76 | 19·3 | 19·2 | 94·0 | 3·13 | 20·0 | 0·96 | 1·09 | |||||||
| 35% | 2·33 | 19·3 | 19·7 | 94·0 | 3·81 | 20·1 | 0·96 | 1·10 | |||||||
| 2·08 | 15% | 1·28 | 19·3 | 18·9 | 93·9 | 2·17 | 19·8 | 0·97 | 1·06 | ||||||
| 25% | 1·83 | 19·3 | 19·3 | 94·5 | 2·88 | 19·9 | 0·97 | 1·08 | |||||||
| 35% | 2·88 | 19·3 | 20·0 | 95·1 | 4·00 | 20·3 | 0·95 | 1·12 |
We assumed r01 = 0·75 or 1·25, r02 = 0·625, and the Gamma parameter α = 0·5 or 1 in the first two scenarios, where a larger α represents higher dependence between event processes. On average, we observed about 4 events per subject when μ2(t) = r02t2/2 and about 7 events when μ2(t) = r02(t + t2/2 + t3/9). In the third scenario, we assumed r01 = 0·5 and r02 = 0·625, which also results in about 7 events per subject. Censoring times were independently generated by a uniform distribution between 0 and 5. All of our local likelihood estimation was implemented using the Epanechnikov kernel
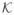 (x) = 0·75(1 − x2), |x| < 1, and a local linear model, i.e., q = 1. When K = 2, a nearest-neighbour method was used to calculate the varying bandwidth and AIC (Akaike, 1974) was used as a bandwidth selection criteria. These procedures can be implemented using an R (R Development Core Team, 2013) package locfit (Loader, 2010). When K = 3, a fixed bandwidth proportional to n−1/5 was applied. While log(t) was used in the first scenario for the correct model specification in the weighted estimating equations method, covariates zi (t) in (6) were used in the other two scenarios for the purpose of model misspecification.
(x) = 0·75(1 − x2), |x| < 1, and a local linear model, i.e., q = 1. When K = 2, a nearest-neighbour method was used to calculate the varying bandwidth and AIC (Akaike, 1974) was used as a bandwidth selection criteria. These procedures can be implemented using an R (R Development Core Team, 2013) package locfit (Loader, 2010). When K = 3, a fixed bandwidth proportional to n−1/5 was applied. While log(t) was used in the first scenario for the correct model specification in the weighted estimating equations method, covariates zi (t) in (6) were used in the other two scenarios for the purpose of model misspecification.
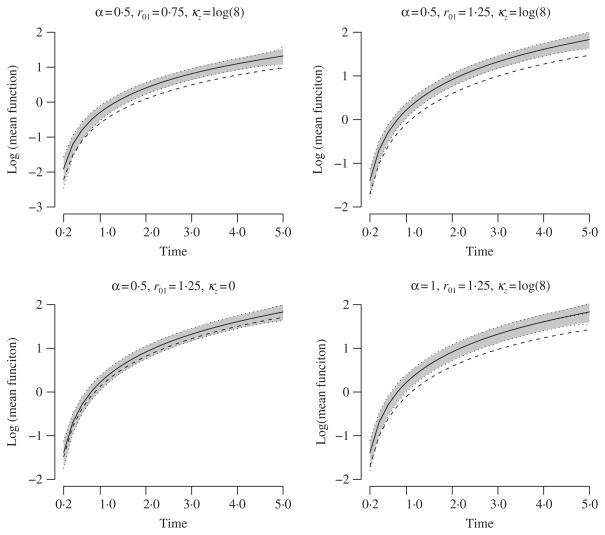
We first show graphic results for μ1(t) over the observation period with different combinations of α and κz in Fig. 1 when μ2(t) = r02t2/2. In these figures, the solid lines correspond to the true μ1(t) and grey areas represent , where is the empirical variance of the replicated estimates ; dotted lines show the average of the replicated and its pointwise confidence limits, where is the average of the replicated variance estimates ; dashed lines show the average of the replicated based on the complete case analysis. Overall, the estimation by the complete case analysis performs worse as the follow-up time t increases, due to more events with missing category at the later part of the observation period. On the contrary, our proposed estimator based on the rate proportion method is approximately unbiased. Also, the upper and lower dotted lines cover the grey area. This means that the point estimator is approximately unbiased and that the variance estimator approximates the asymptotic variance well.
Fig. 1.
Mean function estimation of the truth (solid) by the rate proportion method with 95% confidence interval (dot) and complete case analysis (dash) under different simulation scenarios, with grey areas showing the truth ±1·96×(empirical standard errors).
Table 1 shows the simulation results for μ1(t) = r01t at t = 3 when r01 = 0·75 in the first two scenarios using
in (1), the rate proportion method
in (3), and the weighted estimating equations method
. We report the bias of the estimation, defined by the average of the replicated estimates minus the true value, the empirical standard deviation
, defined by the sample standard deviation of the replicated estimates, the average of the replicated standard deviation estimates
, empirical coverage probability at a 0·95 nominal level, denoted by
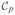 , and the relative mean squared error to the rate proportion method, denoted by
, where
and mr is defined similarly. The empirical percentage of recurrent events with missing category is denoted by
, and the relative mean squared error to the rate proportion method, denoted by
, where
and mr is defined similarly. The empirical percentage of recurrent events with missing category is denoted by
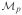 . When μ2(t) = r02t2/2 and the weighted estimating equations method correctly specifies the model, all of the three estimators have bias close to 0 but
has slightly larger empirical variance that results in a larger mean squared error. However, the relative error is rather moderate to
and minimal to
. Hence our nonparametric estimator is very competitive with the current existing parametric method even when the parametric method correctly specifies the model. When μ2(t) = r02(t + t2/2 + t3/9) and the model was misspecified by the parametric method, only
and
are consistent. The estimator
is generally biased and has larger empirical variance than
, resulting in a high ratio of mean squared errors. Overall, the rate proportion method has comparable variation to the analysis when the event category is always observed, has variance estimation close to the empirical variance that results in good empirical coverage, and has substantially better mean squared error when the true model is misspecified by the weighted estimating equations method. Similar results can be seen in Table 2, where the relative mean squared error is much greater in a later time when events with missing types occur more often. Interestingly, the empirical variance Ṽ1 changes only slightly in both the rate proportion method and the weighted estimating equations method when the missingness depends on the covariate, so both estimators seem to be robust to the mechanics of missingness. However, when the data have more events with missing category, both estimators have larger variation but the rate proportion method performs better than the misspecified weighted estimating equations method.
. When μ2(t) = r02t2/2 and the weighted estimating equations method correctly specifies the model, all of the three estimators have bias close to 0 but
has slightly larger empirical variance that results in a larger mean squared error. However, the relative error is rather moderate to
and minimal to
. Hence our nonparametric estimator is very competitive with the current existing parametric method even when the parametric method correctly specifies the model. When μ2(t) = r02(t + t2/2 + t3/9) and the model was misspecified by the parametric method, only
and
are consistent. The estimator
is generally biased and has larger empirical variance than
, resulting in a high ratio of mean squared errors. Overall, the rate proportion method has comparable variation to the analysis when the event category is always observed, has variance estimation close to the empirical variance that results in good empirical coverage, and has substantially better mean squared error when the true model is misspecified by the weighted estimating equations method. Similar results can be seen in Table 2, where the relative mean squared error is much greater in a later time when events with missing types occur more often. Interestingly, the empirical variance Ṽ1 changes only slightly in both the rate proportion method and the weighted estimating equations method when the missingness depends on the covariate, so both estimators seem to be robust to the mechanics of missingness. However, when the data have more events with missing category, both estimators have larger variation but the rate proportion method performs better than the misspecified weighted estimating equations method.
5. Cystic fibrosis registry data
Cystic fibrosis is the most common life-shortening genetic disorder in Caucasians, with an incidence of approximately 1 in 3000 white live births (Kosorok et al., 1996). Chronic lung disease in children can be characterized by recurrent infections of P. aeruginosa, the most important pathogen that leads to the airway obstruction and lung function decay. Pseudomonas aeruginosa infection was found to be a major predictor of morbidity and mortality (Kosorok et al., 2001). Young cystic fibrosis patients aged 1–5 years in 1990 with positive respiratory cultures for P. aeruginosa have significantly higher death rates and worse lung function during the following 8 years (Emerson et al., 2002). According to Li et al. (2005), about 30% of newborn infants acquired nonmucoid type of infection in the first 6 months of life, with a mucoid type of infection prevailing after age 4 years. It is of interest to characterize these patterns of infection in young cystic fibrosis patients.
The United States Cystic Fibrosis Foundation Patient Registry has documented the diagnosis and follow-up of all known cystic fibrosis patients from 114 accredited centres since the 1970s. The quality of this database improved greatly in 1986 because of more consistent reporting and quality control (FitzSimmons, 1993). In the 2007 registry data, there are 6585 subjects who were born after 1997 and have at least two follow-ups before the end of year 2007. The total length of follow-up is 27 412·7 person-years, averaging 4·2 years per subject. In these follow-up years, there were 10 353 nonmucoid and 3190 mucoid P. aeruginosa infections, along with 1339 events missing their category. Roughly, the occurrence rates are 3·8 for nonmucoid type and 1·2 for mucoid type per 10 years, not counting events with missing type. However, a patient may test positive for both nonmucoid and mucoid types at the same visit. To simplify the analysis, we treat the event with both types positive in the same visit as a third type of recurrent event process. Accordingly, there are 1582 such events during the follow-ups.
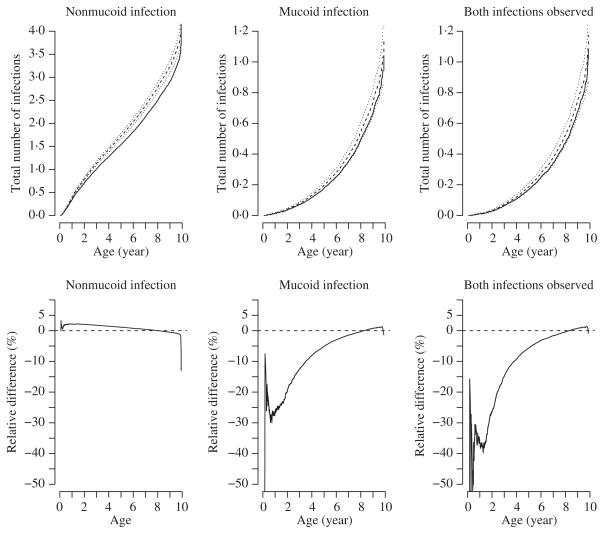
A large percentage of infections have missing category, so our estimation methods are preferable, as the complete case analysis that censors those events would have dramatic underestimation. Figure 2, derived by the rate proportion method and complete case analysis, reveals this. Particularly in nonmucoid type infections, there is substantial discrepancy between our estimates and the complete case analysis after the first year of age. In general, the two estimates diverge as age increases, partly due to more events with missing type being recorded over time. Based on the rate proportion method, the average number of nonmucoid type infections per patient is 2·4 by age 7, while that for mucoid type infections is 0·4. The rate for having both types of infections is similar to the rate for the mucoid type. Both increase more rapidly after age 7.
Fig. 2.
The upper panels show the mean function estimation of P. aeruginosa infections by the rate proportion method (dash) with 95% pointwise confidence interval (dot) and complete case analysis (solid); the lower panels present the relative difference between the rate proportion method and the weighted estimating equations method (solid) with the dashed line representing a reference line of zero difference.
In Fig. 2, we also compare the estimation results between the rate proportion method and the weighted estimating equations method. We define the relative difference as the percent change of the weighted estimating equation estimates from the rate proportion estimates. In the weighted estimating equations approach, we used patient’s gender and mode of diagnosis as covariates.
The two methods produced similar results in estimating the nonmucoid P. aeruginosa infection rate with the relative difference being less than 5% over the range of the 10-year period. However, the infection rates of the mucoid type and of having both types in the same visit were significantly underestimated by the weighted estimating equation approach. The relative difference may reach as much as 50% in the first year of age.
6. Remarks
We assume that the observation probability πik(t) is the same for each event type, which may not be realistic in practice when some types of events are more likely to have a missing category. However, the observation probability may not be estimable due to lack of information in those events with missing types. One possible generalization of our approach is to assume that the observation probability is known a priori for each category. One can show that, if πik(t) is different for each k, our current approach leads to the estimation of , which differs from pik(t) = E{δik | dNi·(t) = 1, Ri(t) = 0, Yi(t)}, the unknown quantity in our mean function estimator. However, with and , one may estimate pik(t) with the estimation of and known πik(t).
In the rate proportion method, the local likelihood procedure yields a nonparametric estimator via a regression model that uses time as a covariate. One may prefer to apply different non-parametric regression methods for categorized outcomes, such as the generalized additive model (Hastie & Tibshirani, 1990) or smoothing splines (Gu, 2002). It will be of interest to develop asymptotic theory for estimates based on such approaches and compare the performance across different nonparametric regression methods.
Acknowledgments
The authors thank Dr Preston Campbell from the United States Cystic Fibrosis Foundation for providing the registry data, and the editor and two referees for their helpful comments. This work is partially supported by the U.S. National Institutes of Health.
Appendix
We first provide the following regularity conditions.
Condition A1. Variables {Ni1(·), …, NiK(·)} (i = 1, …, n) are independent and identically distributed.
Condition A2. The expected number of subjects at risk for every t ∈ [0, τ].
Condition A3. The total number of events Ni·(τ) < η < ∞.
Condition A4. For t ∈ [0, τ], observation probability πi(t) = E{Ri(t)|dNik(t) = 1} is the same for every k.
Condition A5. The likelihood function ℓ(β*) is bounded and twice differentiable. The Hessian matrix ℓ̈(β*) = ∂2ℓ(β*)/∂β*∂β*T is negative definite and invertible.
Condition A6. The function θk(·) for each k ∈ {1, …, K} has a continuous (q + 1)th derivative for q > 0.
Condition A7. The kernel function
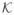 (·) has a bounded and symmetric density with a compact support, and satisfies ∫ υ
(·) has a bounded and symmetric density with a compact support, and satisfies ∫ υ
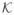 (υ) dυ = ∫ υ3
(υ) dυ = ∫ υ3
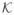 (υ) dυ = 0.
(υ) dυ = 0.Condition A8. Assume nh → ∞ as h → 0 and n → ∞.
Conditions A1–A3 are regularity conditions for recurrent event processes. We require data from the subjects to be independent and identically distributed in Condition A1. Our estimation, however, accommodates multiple dependent recurrent event processes. Condition A4 assumes that each type of event has the same probability for the category being missing. Conditions A5–A8 are otherwise regularity conditions for the large sample properties of the local likelihood estimates.
Proof of Theorem 1
To show the consistency of , we decompose as with
Let . First, we write
Then, expanding around θ = (θ1, …, θK − 1)T, we have
It can be shown that converges in probability to
Since the bias term b(t) converges uniformly in probability to 0 when h → 0, we can conclude that converges in probability to 0, uniformly in t. With uniformly in t, we can prove the uniform consistency of by the fact that uniformly converge to μk(t).
To prove the large sample normality we need to obtain the rate of the weak convergence when inserting in the local polynomial estimate. One can show that has the same weak convergence rate as
| (A1) |
Recall that the local polynomial estimate θ̂(s) is O(n−1/(2q+3)) when using the optimal bandwidth. Under the smoothness assumption of θ, one can show that (A1) is O(n−(q+2)/(2q+3)), which is faster than O(n−1/2). That means the sequence of will be dominated by the sequence of , which has a O(n−1/2) weak convergence rate.
Combined with the asymptotic equivalency of and , where , one can show that n1/2ωk(t; θ̂) is asymptotically equivalent to , where
Notice that φik(t; θ0) (i = 1, …, n) are independent and identically distributed zero-mean variables, so converges to a multivariate normal distribution with mean zero and covariance Vk(s, t) = E{φ1k(s; θ0)φ1k(t; θ0)} for s, t ∈ [0, τ]. Hence n1/2ωk(t; θ̂) converges weakly to a Gaussian process by the functional central limit theorem (Pollard, 1990), as the φik(t; θ0) is composed of functions that are monotone in t, i.e., φik(t; θ0) is manageable and n1/2ωk(t; θ0) is tight.
Contributor Information
FENG-CHANG LIN, Email: flin@bios.unc.edu, Department of Biostatistics, University of North Carolina, Chapel Hill, North Carolina 27599, U.S.A.
JIANWEN CAI, Email: cai@bios.unc.edu, Department of Biostatistics, University of North Carolina, Chapel Hill, North Carolina 27599, U.S.A.
JASON P. FINE, Email: jfine@bios.unc.edu, Department of Biostatistics, University of North Carolina, Chapel Hill, North Carolina 27599, U.S.A
HUICHUAN J. LAI, Email: hlai@wisc.edu, Department of Nutritional Sciences, University of Wisconsin, Madison, Wisconsin 53706, U.S.A
References
- Abu-Libdeh H, Turnbull BW, Clark LC. Analysis of multi-type recurrent events in longitudinal studies: Application to a skin cancer prevention trial. Biometrics. 1990;46:1017–34. [PubMed] [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE Trans Auto Contr. 1974;19:716–23. [Google Scholar]
- Andersen P, Borgan Ø, Gill R, Keiding N. Statistical Models Based on Counting Processes. New York: Springer; 1993. [Google Scholar]
- Cai J, Schaubel D. Marginal means/rates models for multiple type recurrent event data. Lifetime Data Anal. 2004;10:121–38. doi: 10.1023/b:lida.0000030199.23383.45. [DOI] [PubMed] [Google Scholar]
- Chen BE, Cook RJ. The analysis of multivariate recurrent events with partially missing event types. Lifetime Data Anal. 2009;15:41–58. doi: 10.1007/s10985-008-9091-3. [DOI] [PubMed] [Google Scholar]
- Chiang CT, Wang MC, Huang CY. Kernel estimation of rate function for recurrent event data. Scand J Statist. 2005;32:77–91. doi: 10.1111/j.1467-9469.2005.00416.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook RJ, Lawless JF. The Statistical Analysis of Recurrent Events. New York: Springer; 2007. [Google Scholar]
- Cook RJ, Lawless JF, Lakhal-Chaieb L, Lee KA. Robust estimation of mean functions and treatment effects for recurrent events under event-dependent censoring and termination: Application to skeletal complications in cancer metastatic to bone. J Am Statist Assoc. 2009;104:60–75. [Google Scholar]
- Cook RJ, Lawless JF, Nadeau C. Robust tests for treatment comparisons based on recurrent event responses. Biometrics. 1996;52:557–71. [PubMed] [Google Scholar]
- Emerson J, Rosenfeld M, McNamaral S, Ramsey B, Gibson RL. Pseudomonas aeruginosa and other predictors of mortality and morbidity in young children with cystic fibrosis. Pediatric Pulmonol. 2002;34:91–100. doi: 10.1002/ppul.10127. [DOI] [PubMed] [Google Scholar]
- Fan J, Gijbels I. Local Polynomial Modelling and Its Applications. London: Chapman & Hall; 1996. [Google Scholar]
- FitzSimmons SC. The changing epidemiology of cystic fibrosis. J Pediatrics. 1993;122:1–9. doi: 10.1016/s0022-3476(05)83478-x. [DOI] [PubMed] [Google Scholar]
- Gu C. Smoothing Spline ANOVA models. New York: Springer; 2002. [Google Scholar]
- Hastie T, Tibshirani R. Generalized Additive Models. London: Chapman & Hall; 1990. [DOI] [PubMed] [Google Scholar]
- Kosorok MR, Wei WH, Farrell PM. The incidence of cystic fibrosis. Statist Med. 1996;15:449–62. doi: 10.1002/(SICI)1097-0258(19960315)15:5<449::AID-SIM173>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- Kosorok MR, Zeng L, West SE, Rock MJ, Splaingard ML, Laxova A, Green CG, Collins J, Farrell PM. Acceleration of lung disease in children with cystic fibrosis after Pseudomonas aeruginosa acquisition. Pediatric Pulmonol. 2001;32:277–87. doi: 10.1002/ppul.2009.abs. [DOI] [PubMed] [Google Scholar]
- Lawless J, Nadeau C. Some simple robust methods for the analysis of recurrent events. Technometrics. 1995;37:158–68. [Google Scholar]
- Li Z, Kosorok MR, Farrell PM, Laxova A, West SEH, Green CG, Collins J, Rock MJ, Splaingard ML. Longitudinal development of mucoid Pseudomonas aeruginosa infection and lung disease progression in children with cystic fibrosis. J Am Med Assoc. 2005;293:581–8. doi: 10.1001/jama.293.5.581. [DOI] [PubMed] [Google Scholar]
- Lin DY, Wei LJ, Yang I, Ying Z. Semiparametric regression for the mean and rate functions of recurrent events. J R Statist Soc B. 2000;62:711–30. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. New York: Wiley; 2002. [Google Scholar]
- Loader C. R package version 1.5-6. 2010. locfit: Local Regression, Likelihood and Density Estimation. [Google Scholar]
- Nelson WB. Graphical analysis of system repair data. J Qual Technol. 1988;20:24–35. [Google Scholar]
- Pepe MS, Cai J. Some graphical displays and marginal regression analyses for recurrent failure times and time dependent covariates. J Am Statist Assoc. 1993;88:811–20. [Google Scholar]
- Pollard D. Empirical Processes: Theory and Applications. Hayward: Institute of Mathematical Statistics; 1990. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2013. http://www.R-project.org. [Google Scholar]
- Schaubel D, Cai J. Rate/mean regression for multiple-sequence recurrent event data with missing event category. Scand J Statist. 2006;33:191–207. [Google Scholar]