A Unified Framework for Cross-modality Multi-atlas Segmentation of Brain MRI

Abstract

Multi-atlas label fusion is a powerful image segmentation strategy that is becoming increasingly popular in medical imaging. A standard label fusion algorithm relies on independently computed pairwise registrations between individual atlases and the (target) image to be segmented. These registrations are then used to propagate the atlas labels to the target space and fuse them into a single final segmentation. Such label fusion schemes commonly rely on the similarity between intensity values of the atlases and target scan, which is often problematic in medical imaging - in particular, when the atlases and target images are obtained via different sensor types or imaging protocols.

In this paper, we present a generative probabilistic model that yields an algorithm for solving the atlas-to-target registrations and label fusion steps simultaneously. The proposed model does not directly rely on the similarity of image intensities. Instead, it exploits the consistency of voxel intensities within the target scan to drive the registration and label fusion, hence the atlases and target image can be of different modalities. Furthermore, the framework models the joint warp of all the atlases, introducing interdependence between the registrations.

We use variational expectation maximization and the Demons registration framework in order to efficiently identify the most probable segmentation and registrations. We use two sets of experiments to illustrate the approach, where proton density (PD) MRI atlases are used to segment T1-weighted brain scans and vice versa. Our results clearly demonstrate the accuracy gain due to exploiting within-target intensity consistency and integrating registration into label fusion.

1. Introduction

Registration-based segmentation (Rohlfing et al., 2005) is the main inspiration behind many modern segmentation algorithms. The principle behind this technique is simple: if an image with delineated labels (henceforth an “atlas”¹) is available, then one can deform (“register”) it to a previously unseen scan (henceforth “target”), and use the resulting spatial transformation to propagate the labels to target space in order to obtain a segmentation. Registration-based segmentation is a general framework, but it has a particularly strong impact in neuroimaging, partly thanks to the maturity of inter-subject registration methods in this domain.

The main disadvantage of registration-based segmentation is that a single atlas endowed with a deformation model is seldom a sufficiently rich representation of the whole population. If a target volume’s anatomy differs significantly from that of the atlas, for example if there are topological differences not modeled by the registration algorithm, the segmentation will be poor. A possible solution to this problem is to use multiple atlases that constitute a richer representation of anatomical variation. The question is then how to combine the propagated labels into a final segmentation; this problem is known as label fusion.

Such multi-atlas approaches are becoming increasingly popular mainly for three reasons. First, the maturity and availability of registration methods (Klein et al., 2009; Avants et al., 2008) help boost the performance of multi-atlas label fusion algorithms. Second, label fusion methods, registration aside, are relatively easy to implement. And third, the rapid development of computer hardware is making the heavy computational cost of label fusion, which is mostly due to the many registration instances, manageable.

1.1. Related work

The simplest forms of label fusion are the so-called “best atlas” approach and majority voting (Rohlfing et al., 2004, 2005). In best atlas selection, the labels from the atlas most similar to the target volume after registration are propagated to yield the final segmentation. In majority voting, first applied to human brain MRI segmentation in Heckemann et al. (2006), the most frequently propagated label is assigned to each voxel in the target volume.

Label fusion performance can be improved via weighting, i.e., by increasing the contribution of the atlases that are more similar to the target scan, either globally or locally (Artaechevarria et al., 2009). Langerak et al. (2010) use an iterative method, in which the performance of the individual atlases and the joint segmentation are alternately estimated, using global weights in label fusion. Local weights are used by Isgum et al. (2009), who propose to compute the contribution of each atlas at each voxel by the inverse of the absolute intensity difference after registration. A more principled version of the method, based on a statistical generative model of labels and intensities, was proposed by Sabuncu et al. (2010). In fact, Isgum et al.’s method can be seen as a special case of Sabuncu et al.’s model, where a Laplace distribution is used to model image intensities. Coupé et al. (2010) compare the local appearance of the target volume around each voxel not only with patches of the atlases centered at that voxel, but also patches which are slightly shifted from it. The final label is a mixture of contributions from all such patches, each weighed by the similarities. This is analogous to the non-local means denoising algorithm (Buades et al., 2005).

Research in multi-atlas segmentation is also focused on improving computational efficiency, usually by reducing the burden of multiple registrations. For example, Aljabar et al. (2009) propose using only the most similar atlases (measured with image similarity before detailed nonlinear registration, or based on meta-data such as subject age) in the segmentation. This idea is taken one step further by van Rikxoort et al. (2010), who propose selecting the most appropriate atlases “on the fly,” and stop registering atlases when no further improvement is expected. An alternative approach to reduce the computational burden was suggested by Depa et al. (2011), where the atlases are pre-registered.

To enhance the performance of multi-atlas segmentation, van der Lijn et al. (2012) use the propagated labels to create a spatial prior, which is combined with label likelihoods given by a voxel classifier, and then use graph-cuts to generate an enhanced segmentation. Asman and Landman (2012) propose adding a smoothness constraint to the estimated map of spatially varying performance of each registered atlas. Wang et al. (2011) use machine learning techniques to correct systematic errors produced by multi-atlas segmentation in a given dataset. Other recent contributions to the framework can be found in Landman and Warfield (2011, 2012).

1.2. Limitations of current label fusion methods

A limitation of current weighted label fusion methods is that they typically require the intensities of the atlases to be consistent with those of the target scan. While this is not a problem in calibrated modalities such as CT (e.g., Isgum et al. 2009), it often prevents the application of these methods in MRI, unless the scans have a similar type of contrast (e.g., T1-weighted) and are preprocessed with an intensity standardization algorithm (Nyul et al., 2000; Sabuncu et al., 2010). Even in this case, a drop in performance is observed compared to using training and test data acquired with exactly the same hardware and pulse sequence; see for instance Han and Fischl (2007), who use MPRAGE data from a Siemens scanner to segment SPGR data from a GE scanner.

There are many scenarios that could benefit from a cross-modality label fusion algorithm. Assuming that the atlases are T1-weighted, such a framework would be useful to analyze data acquired with other T1 MRI sequences. This is for example the case of legacy and clinical data. In the latter case, the MRI acquisition protocols are often very different from those used in Neuroscience research. Moreover, clinical data is often multispectral, so a cross-modality method makes it possible to take advantage of channels other than T1. Inter-modality label fusion algorithm could also be used to analyze data acquired with MRI contrasts different from T1. For instance, T2-weighted MRI is frequently used to image the hippocampus, as in Mueller et al. (2007), or the new hippocampal data in the ADNI study². Another potential application is the analysis of infant MRI, in which the ongoing myelination changes the T1 and T2 of the tissue rapidly. This renders relying on intensity correspondences impractical.

The inter-modality registration literature has coped with the issue of intensity variation mainly through statistical metrics, such as those based on mutual information (Maes et al., 1997; Wells III et al., 1996; Pluim et al., 2003). Similarly, one can envision a label fusion strategy that uses mutual information (MI) for identifying the contribution of each atlas. This approach will have to deal with two challenges. First, in the case of local weights, it would be necessary to define a window around each voxel to compute the metric. The size of the window would represent a trade-off between spatial precision and the reliability of the metric. The second challenge is finding a principled way of defining a MI-based weight. For example, using MI directly as the weights does not sufficiently differentiate the contributions of the atlases. This can be alleviated by defining the weights as a power of the metric (see for instance Artaechevarria et al. 2009; Iglesias and Karssemeijer 2009). Whether this heuristic strategy is optimal is an open question.

Another aspect that is often overlooked in multi-atlas segmentation is the actual registration of the atlases. Typically, registration is seen as a preprocessing step, and the resulting deformation fields are kept constant during segmentation. However, if the registration is allowed to be updated during the fusion process, it is in principle possible to obtain more accurate segmentations by updating the deformations with information from the current estimate of the segmentation. This strategy has been successfully adopted in the single probabilistic atlas segmentation literature (Ashburner and Friston, 2005; Pohl et al., 2006a; Yeo et al., 2008; Van Leemput et al., 2009). Furthermore, in label fusion such an approach will allow the registrations to interact between themselves. For instance, if the image intensities indicate that one atlas is well registered in a given region while a second one is poorly registered, it should be possible to improve the latter by using information from the former. In a related approach, Depa et al. (2011) propose pre-registering the atlases, building a summary image by averaging the deformed intensities, and finally deforming this average to the target scan. The spatial correspondences between the atlases and the target are then computed by concatenating the appropriate transforms. While this framework ties the deformations of the atlases together, it does not allow them to influence one another during registration.

1.3. Contribution

This article builds on our previous conference papers (Iglesias et al., 2012a,b), which presented a generative model for label fusion across modalities, taking advantage of the potential multimodal character of the data to segment. The method is based on exploiting the consistency of voxel intensities within the segmentation regions, as well as their relation with the propagated labels. Here, we extend our contributions along several novel directions. First, we integrate registration into the multi-atlas label fusion framework across modalities. Rather than considering registration a preprocessing step, we regard the deformation fields as model parameters that must be optimized during the fusion. Second, we propose a true joint registration framework, in which the registrations of the different atlases are explicitly linked by the prior in a generative model. This ensures that the contributions of the atlases are consistent, considerably reducing the presence of outliers in the deformation fields. Finally, we present a computationally efficient strategy to “invert” the model and obtain the most probable voxel labels in the target volume using Bayesian inference. The algorithm does not depend on the modality of the target data, which can be monomodal or multimodal.

The rest of this paper is organized as follows. Section 2 describes the generative model, and a segmentation algorithm derived from it is presented in Section 3. Section 4 describes the data and experiments used to demonstrate the proposed approach, and presents the empirical results. Finally, Section 5 discusses the results and concludes the article.

2. Generative Model

The proposed approach is based on a generative model of MRI images that can be “inverted” using Bayes’ rule to obtain the most likely segmentation given a target scan and a set of atlases. The generative model is described here, whereas an algorithm to infer the labels of a test scan is presented in Section 3.

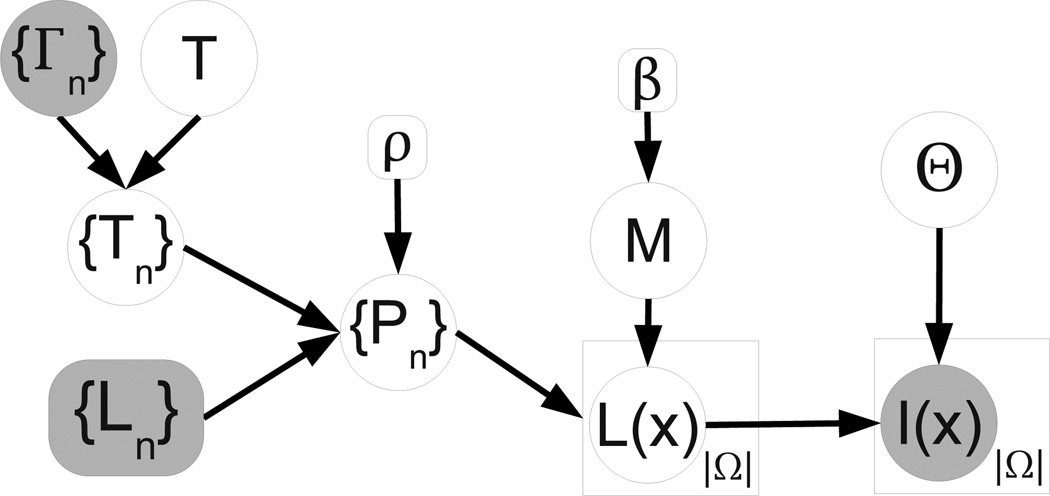
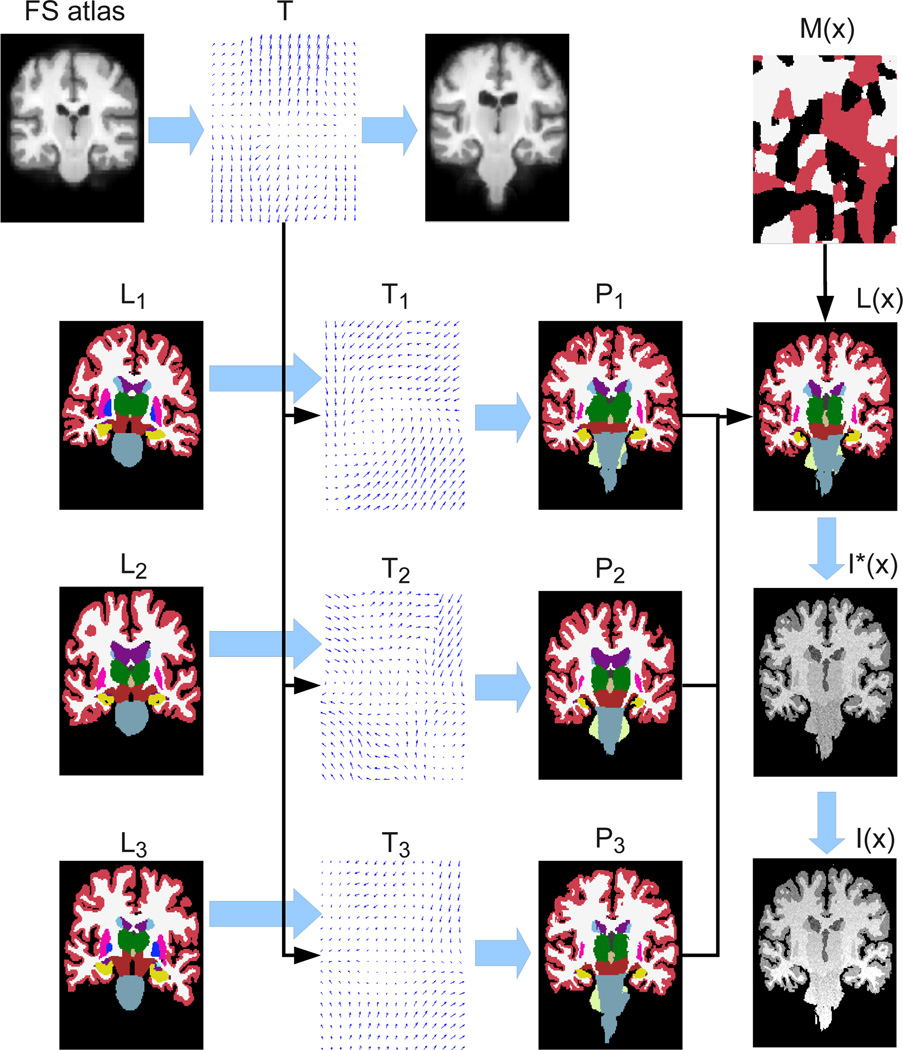
The different elements of the model detailed below are represented in the graphical model in Figure 1, and the corresponding equations listed in Table 1. Moreover, the variables in the model are summarized in Table 2, and the process through which the model generates a sample image is illustrated in Figure 2. We will now describe this process step by step.

Figure 1.

Graphical model. Random variables are in circles, while deterministic parameters are in boxes. Observed variables are shaded. Plates indicate replication.

Table 1.

Equations corresponding to the model in Figure 1.

$T~\frac{1}{Z_{k_1}}\text{exp}[-k_1{\Vert \mathbf{\nabla }T\Vert }^2]$ $T_n~\frac{1}{Z_{k_1,k_2}}\text{exp}[-k_1{\Vert \mathbf{\nabla }{T}_n\Vert }^2-k_2{\Vert T_n-{\mathrm{\Gamma }}_n^{-1}T\Vert }^2]$ $P_n^l(x)\propto \text{exp}[\rho D_n^l(T_n(x))]$ $M~\frac{1}{Z_{\beta }}{\prod }_{x\in \mathrm{\Omega }}\text{exp}(\beta {\sum }_{y\in {𝒩}_x}\delta (M(x)=M(y)))$ $L(x)~{\mathbf{P}}_{M(x)}(x)$ $Ĩ(x)~\frac{1}{\sqrt{2\pi {\sigma }_{L(x)}^2}}\text{exp}[-\frac{{(Ĩ(x)-{\mu }_{L(x)})}^2}{2{\sigma }_{L(x)}^2}]$ $I(x)=Ĩ(x)\text{exp}[-{\sum }_p{b}_k{\psi }_k(x)]$

Table 2.

List of variables in the model.

·x: a location in space. ·𝒩x: neighborhood of x on image grid. ·Ω: the target image domain. ·N: number of atlases. ·ℒ: number of discrete labels, including one for background/unknown. ·Ln(x): (discrete) label of atlas n at location x. ·T: transformation from target image coordinates to fsaverage. ·Tn: transformation from target image coordinates to atlas n. ·Γn: transformation from fsaverage coordinates to atlas n. ·$D_n^l(x)$ : signed distance transform (+ = in, − = out) for label l, atlas n. ·$P_n^l(x)$ : prior probability of label l at location x based on atlas n. ·${\mathbf{P}}_n(x)=[P_n^1(x),\dots ,P_n^{ℒ}(x)].$ ·k1, k2 > 0: parameters of the deformation priors. ·Zk1, Zk1,k2, Zβ: normalizing coefficients for probability densities. ·ρ> 0: slope parameter of the logOdds based label prior. ·L(x) ∈ {1, …, ℒ}: labels of the subject that is being segmented. ·M(x) ∈ {1, …, N}: field of discrete memberships in subject space. ·β: parameter of the Markov Random Field ensuring smooth M(x). ·Ĩ(x): underlying, latent image intensities before bias field corruption. ·I(x): observed image intensities. ·Θ: intensity model parameters {{μl}, $\{{\sigma }_l^2\}$, {bk}}. ·μl, ${\sigma }_l^2$: parameters of Gaussian distribution of intensities for label l. ·{ψk}: basis functions for bias field modeling. ·{bk}: coefficients corresponding to {ψk}.

Figure 2.

Illustration of the generative process: from atlases {L_n} to intensities I(x). Rather than sampling from a uniform Θ, we borrowed values from a sample MRI scan to make I(x) and Ĩ(x) resemble a T1-weighted MRI volume. For simplicity, we also assumed ρ = ∞ i.e., P_n(x) is one for a certain label and zero for all other classes at each voxel. Note that spatial transformations follow the opposite direction of the arrows representing the deformations. For example, T₁ deforms L₁ into P₁ by computing P₁(x) = L₁[T₁(x)].

If we were to draw a sample from the generative model, the first step would be to randomly sample T, which is a transformation that maps the target image coordinate space to that of a universal template. This template represents the population average (in this study we used FreeSurfer’s “fsaverage”, Fischl et al. 2002). We impose a prior on T that favors smooth transformations (see Equation 1 in Table 1).

The next step would be sampling {T_n}, the transforms from the target image coordinates to the n^th atlas. We adopt a prior on T_n which encourages both smoothness and consistency across the deformations of the different atlases. To achieve the latter, we pre-compute the deformation fields {Г_n} that establish the correspondence between the n^th atlas and fsaverage, and then we penalize the deviation of T_n from ${\mathrm{\Gamma }}_n^{-1}T$ (Equation 2 in Table 1). This way, T_n is modeled as a “noisy” version of the combination of T and Г_n.

Next, the transforms {T_n} are used to map to target space the label probability maps $P_n^l$ corresponding to each atlas. These probability maps are computed from the discrete manual labels using a log Odds model (Pohl et al. 2006b, see Equation 3 in Table 1). In this model, {L_n}, n = 1, …, N represents the gold standard labels, with discrete values between 1 and ℒ at each voxel. $D_n^l$ are the signed distance maps for each label and atlas, and the slope of the model ρ is fixed. Again, because the transforms are linked through T, the deformed probability maps are expected to be similar.

Now, for each voxel location x, we assume that the underlying (unknown) label of the target volume is sampled from one of the (deformed) atlases, indexed by a hidden variable M(x). The indices M(x), which take discrete values between 1 and N, are not spatially independent, but follow a Markov Random Field (MRF) model instead (Equation 4 in Table 1). Then, the prior probability for underlying segmentation of a voxel given the atlas index p(L(x) = l|M(x)) is given by $P_{M(x)}^l(x)$ (Equation 5 in the table), which is a categorical distribution over labels.

Once the label L(x) is drawn from P_M(x)(x), the underlying “true” intensity Ĩ(x) (meaning, before bias field corruption) is sampled from a Gaussian distribution with mean μ_L(x) and variance ${\sigma }_{L(x)}^2$ (Equation 6 in Table 1). Finally, the intensity Ĩ(x) is modulated by a bias field to yield the observed intensities I(x). Also known as B1-inhomogeneity, this bias field is the product of non-uniform coil sensitivity profiles, and it manifests itself as a slow-varying multiplicative gain. We model it with a set of low-spatial-frequency basis functions (Equation 7 in the table, where {b_k} are the coefficients, {ψ_k} are the basis functions and the exponential ensures non-negativity). We use the variable Θ to group all the image intensity parameters i.e., $\mathrm{\Theta }=\{\{{\mu }_l\},\{{\sigma }_l^2\},\{b_k\}\}$, and we assume a flat, uninformative prior distribution over them, i.e., p(Θ) ∝ 1.

Relation with other models: some popular segmentation methods can be seen as solutions to particular instantiations of the proposed framework. If β = k₂ = 0, the model becomes similar to that in classical statistical-atlas-based segmentation, e.g., Ashburner and Friston (2005), with two differences. First, there are N individual warps in the generative process, rather than a single deformation of the statistical atlas. Second, in the proposed model the label priors are built in subject space, as opposed to pre-merging them into a single probabilistic atlas in a common coordinate frame. Also, if we assume that the deformation fields are fixed (e.g., obtained by a registration method), and we set β = 0, ${\sigma }_l^2\to \infty$, ∀l, and ρ → ∞, we eliminate the membership dependence between neighboring voxels and also the dependence between labels and intensities. Therefore, the solution to the model becomes majority voting. Finally, when β → ∞ (still assuming fixed deformation fields), we are forcing all the voxels to be originated by the same atlas. Then, the solution to the model simplifies to the “best atlas” method of Rohlfing et al. (2004), where the labels are propagated from the single atlas estimated to be closest to the target volume.

Moreover, the proposed model can be viewed as bridging the gap between single probabilistic atlas based segmentation, e.g., Ashburner and Friston (2005), and multi-atlas label fusion. In the former approach, there is a single spatial transformation mapping target image coordinates to the common atlas coordinate frame. In classical label fusion, there are N independent registrations between the atlases and target image. In our model, when k₂ = 0, the registrations are independent a priori, which is similar to classical multi-atlas label fusion. When k₂ → ∞, all the atlases deform together, making the algorithm equivalent to the use of a single probabilistic atlas. Any finite, positive value for k₂ represents a case between the two extremes.

3. Segmentation of a target subject

Given the generative model, segmentation is cast as an inference problem in a Bayesian framework. The idea is to find the most probable label map L (given the image intensities I and the atlas labels {L_n}) according to the model:

$$\mathrm{L̂}=\underset{L}{\text{argmax}}p(L|I,\{L_n\})=\underset{L}{\text{argmax}}{\int }_{\mathrm{\Theta },\{T_n\},T}p(L,\mathrm{\Theta },\{T_n\},T|I,\{L_n\})d\mathrm{\Theta }d\{T_n\}dT=\underset{L}{\text{argmax}}{\int }_{\mathrm{\Theta },\{T_n\},T}p(L|\mathrm{\Theta },\{T_n\},I,\{L_n\})\times \times p(\mathrm{\Theta },\{T_n\},T|I,\{L_n\})d\mathrm{\Theta }d\{T_n\}dT.$$

This expression is intractable because of the integral over all registrations {T_n} and the integral over all imaging parameters Θ. Instead, if we make the standard assumption that the distribution of these parameters in light of the observed data is sharp, we can compute point estimates:

$$\{\mathrm{\Theta ̂},\{{\mathrm{T̂}}_n\},\mathrm{T̂}\}=\underset{\mathrm{\Theta },\{T_n\},T}{\text{argmax}}p(\mathrm{\Theta },\{T_n\},T|I,\{L_n\}),$$

and approximate:

$$p(\mathrm{\Theta },\{T_n\},T|I,\{L_n\})\approx \delta (\mathrm{\Theta }-\mathrm{\Theta ̂},\{T_n-{\mathrm{T̂}}_n\},T-\mathrm{T̂}).$$

Then, the most likely labels can finally be computed as:

$$\mathrm{L̂}\approx \underset{L}{\text{argmax}}p(L|\mathrm{\Theta ̂},\{{\mathrm{T̂}}_n\},I,\{L_n\}).$$ (1)

We will first discuss in Section 3.1 an algorithm to obtain point estimates of the model parameters. In short, these are computed with a variational expectation algorithm in which the posterior probability function of the memberships M(x) is approximated by a distribution q that factorizes over voxels. The E step of the algorithm updates q, whereas the M step updates the Gaussian and bias field parameters, as well as the registrations. Once the algorithm has converged, the final segmentation can be easily computed using the point estimates of the model parameters and the final value of the distribution q, as we will explain in Section 3.2.

3.1. Finding the most probable registration and image intensity parameters

The core of the proposed algorithm is presented in this section. The problem is to find the most likely values of Θ, {T_n} and T given the observed data. Bearing in mind that we have assumed a flat prior for Θ we have:

$$\{\mathrm{\Theta ̂},\{{\mathrm{T̂}}_n\},\mathrm{T̂}\}=\underset{\mathrm{\Theta },\{T_n\},T}{\text{argmax}}p(\mathrm{\Theta },\{T_n\},T|I,\{L_n\})=\underset{\mathrm{\Theta },\{T_n\},T}{\text{argmax}}p(I|\mathrm{\Theta },\{T_n\},\{L_n\})p(\{T_n\}|T)p(T),$$ (2)

where p(I|Θ, {T_n}, {L_n}) involves summing over all membership fields M, which makes Equation 2 intractable. To overcome this problem, we use variational expectation maximization (VEM) and optimize a lower bound instead. Taking logarithms, we define the negated free energy −J as:

$$-J(q,\mathrm{\Theta },\{T_n\})=\text{log}p(\{T_n\},T)+\text{log}p(I|\mathrm{\Theta },\{T_n\},\{L_n\})--KL(q(M)\Vert p(M|I,\mathrm{\Theta },\{L_n\},\{T_n\})),$$ (3)

where KL(·‖·) is the Kullback-Leibler divergence and q is a distribution that approximates the posterior probability of M. The negated free energy −J is a lower bound of the logarithm of the objective function in Equation 2, because the KL divergence is always non-negative.

VEM can be seen as a coordinate descent algorithm that alternately maximizes −J in Equation 3 with respect to q(M) (expectation or E step) and the model parameters Θ, T, {T_n} (maximization or M step). In the E step of VEM, q is optimized over a class of restricted functions. The standard computational approximation is that q factorizes (mean field approximation) such that

$$q(M)=\prod _{x\in \mathrm{\Omega }}{q}_x(M(x)),$$

where q_x(m) is a categorical distribution over the atlas indices m = 1, …, N. In the particular case that β = 0, we recover a standard Expectation Maximization (EM) algorithm: the expression p(M|I,Θ, {L_n}, {T_n}) factorizes over voxels and therefore it can be exactly matched by q(M). In that case, the KL divergence becomes zero and −J is a lower bound of the objective function that touches it at the current parameter values. Consequently, optimizing it in the M step guarantees an increase in the objective function. In the general case of β > 0, the KL divergence is greater than zero, the lower bound does not touch the objective function and the M step is not guaranteed to increase the objective function; this is the reason why VEM is an approximate solver. We now describe the E and M steps of the algorithm.

3.1.1. E step - optimizing q

The only term in Equation 3 depending on q is the KL divergence. Using the definition KL(A‖B) = ∑ _z A(z) log[A(z)/B(z)], we have:

$$\mathrm{q̂}=\underset{q}{\text{argmin}}\sum _{M}q(M)\text{log}\frac{q(M)}{p(M|I,\mathrm{\Theta },\{T_n\},\{L_n\})}=\underset{q}{\text{argmin}}\sum _{M}q(M)\text{log}\frac{q(M)}{p(I|M,\mathrm{\Theta },\{T_n\},\{L_n\})p(M)}=\underset{q}{\text{argmin}}\sum _{M}q(M)\text{log}\frac{q(M)}{p(M){\sum }_{L}p(I|L,\mathrm{\Theta })p(L|\{T_n\},\{L_n\},M)}=\underset{q}{\text{argmin}}\sum _{x\in \mathrm{\Omega }}\sum _{m=1}^N{q}_x(M)[\text{log}{q}_x(m)-\beta \sum _{x\prime \in {𝒩}_x}{q}_{x\prime }(m)]--\sum _{x\in \mathrm{\Omega }}\sum _{m=1}^N{q}_x(m)\text{log}[\sum _{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l)p(L_m(x)=l|T_m)],$$

where p(L_m(x) = l|T_m) is the prior for label l at location x according to atlas m (deformed by T_m), given by Equation 3 in Table 1; and p(I(x)|Θ_l) is the probability of observing the intensity I(x) according to the Gaussian distribution corresponding to label l and the current estimate of the bias field (Equations 6 and 7 in Table 1).

If we write down the Lagrangian (with Lagrange multipliers λ_x that ensure ${\sum }_{m=1}^N{q}_x(m)=1$), take derivatives and set them to zero, we obtain:

$$q_x(m)\propto \text{exp}[\beta \sum _{x\prime \in {𝒩}_x}{q}_{x\prime }(m)]\sum _{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l)p(L_m(x)=l|T_m),$$ (4)

which we iterate to update q until convergence. After each iteration, q_x(M(x)) is normalized so that the constraint ∑_m q_x(m) = 1 is satisfied. Note that we do not need to handle the non-negativity constraint because the probabilities and exponentials ensure that q_x ≥ 0.

3.1.2. M step – optimizing Θ

Equation 3 can be rewritten:

$$-J(q,\mathrm{\Theta },\{T_n\})=\text{log}p(\{T_n\},T)+H(q)++\sum _{M}q(M)\text{log}p(M,I|\mathrm{\Theta },\{L_n\},\{T_n\}),$$ (5)

where H(q) is the entropy of the distribution q(M). The first two terms of this expression do not depend on Θ, and can therefore be ignored in the optimization. Moreover, the structure of q allows to rewrite the third term as a sum over voxels. The problem of maximizing −J with respect to Θ becomes:

$$\mathrm{\Theta ̂}=\underset{\mathrm{\Theta }}{\text{argmax}}\sum _{x\in \mathrm{\Omega }}\sum _{m=1}^N{q}_x(m)\text{log}\sum _{l=1}^{ℒ}[p(I(x)|{\mathrm{\Theta }}_l)p(L_m(x)=l|T_m)],$$

where ${\mathrm{\Theta }}_l=\{{\mu }_l,{\sigma }_l^2,\{b_k\}\}$. We optimize this expression³ by updating {μ_l}, $\{{\sigma }_l^2\}$ and {b_k} one at a time (i.e., coordinate descent). The means and variances can be updated using a standard EM algorithm (Dempster et al., 1977). In the expectation (E) step, the conditional distribution for the hidden variables (the label at each voxel) given the current estimate of the means and variances is computed as:

$$w_x(l)=\sum _{m=1}^N{q}_x(m)\frac{p(I(x)|{\mathrm{\Theta }}_l)p(L_m(x)=l|T_m)}{{\sum }_{l\prime =1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_{l\prime })p(L_m(x)=l\prime |T_m)}.$$

In the maximization (M) step, the means and variances are updated as:

$${\mu }_l\leftarrow \frac{{\sum }_{x\in \mathrm{\Omega }}{w}_x(l)Ĩ(x)}{{\sum }_{x\in \mathrm{\Omega }}{w}_x(l)},$$ (6)

$${\sigma }_l^2\leftarrow \frac{{\sum }_{x\in \mathrm{\Omega }}{w}_x(l){(Ĩ(x)-{\mu }_l)}^2}{{\sum }_{x\in \mathrm{\Omega }}{w}_x(l)}.$$ (7)

Equations 6 and 7 update the means and variances of the model assuming constant {b_k} (and therefore constant corrected intensities Ĩ). Then, we update the bias field coefficients with constant {μ_l}, $\{{\sigma }_l^2\}$. Since there is no closed-form expression for this update, we use the BFGS method with backtracking (Nocedal and Wright, 1999) to optimize it numerically instead. The expression for the gradient is:

$$\frac{\partial (-J)}{\partial b_k}=\sum _{x\in \mathrm{\Omega }}{\psi }_k(x)\sum _{l=1}^{ℒ}{q}_x^L(l)(\frac{Ĩ(x)(Ĩ(x)-{\mu }_l)}{{\sigma }_l^2}-1).$$ (8)

$$\begin{gathered} {\mathbf{u}}_n(x)={(\frac{2\kappa }{q_x(n)}I+\frac{{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l){\mathbf{H}}_n^l(T_n(x))}{{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l)P_n^l(T_n(x))}-\frac{[{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l){\mathbf{G}}_n^l(T_n(x))]{[{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l){\mathbf{G}}_m^l(T_n(x))]}^t}{{[{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l)P_n^l(T_n(x))]}^2})}^{-1} \\ (q_x(n)\frac{{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l){\mathbf{G}}_n^l(T_n(x))}{{\sum }_{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l)P_n^l(T_n(x))}) \end{gathered}$$ (9)

Since there is no dependency on k in the sum over labels, Equation 8 can be seen as the dot product of basis function ψ k with an image that needs to be computed just once, making the gradient relatively fast to evaluate.

3.1.3. M step - optimizing T and {T_n}

The goal is now to maximize −J with respect to the spatial transformations. As for Θ, it is more convenient to work with Equation 5 rather than Equation 3, as we can ignore the term H(q). To carry out this optimization, we use the so-called “Demons algorithm” trick (Thirion, 1998; Vercauteren et al., 2007), which provides a computationally efficient strategy to perform nonlinear registration. The basic idea of the Demons trick is to decouple the optimization of the image likelihood term and the prior on the deformations; we briefly describe the algorithm in Appendix A for completeness.

Expanding Equation 5, we need to solve:

$$\underset{\{T_n\},T}{\text{argmax}}\sum _n\sum _{M}q(M)\text{log}p(M,I|\mathrm{\Theta },\{L_n\},\{T_n\})+\text{log}p(\{T_n\}|T)+\text{log}p(T).$$ (10)

This equation is analogous to the original Demons algorithm. The data likelihood term

$$\sum _{M}q(M)\text{log}p(M,I|\mathrm{\Theta },\{L_n\},\{T_n\})$$

replaces the sum of squared differences that appears in the original method (Equation A.1). The prior on the deformations has the same shape as in the original Demons method as well. The difference is that now we have N terms that encourage the individual T_n’s to be close to ${\mathrm{\Gamma }}_n^{-1}◦T$, leading to the joint solution of N + 1 registration problems (including T)

Following Vercauteren et al. (2007), we decouple the optimization of the image likelihood term and the priors by performing a two-step optimization. In the first step, the algorithm minimizes

$$\underset{{\mathbf{u}}_n}{\text{argmin}}\kappa {\Vert {\mathbf{u}}_n\Vert }^2-\sum _{x\in \mathrm{\Omega }}{q}_x(n)\text{log}[\sum _{l=1}^{ℒ}p(I(x)|{\mathrm{\Theta }}_l)p_n^l(T_n(x)+{\mathbf{u}}_n(x))],$$ (11)

which is analogous to Equation A.2 in Appendix A. Here, κ > 0 is a free parameter of the algorithm that influences optimization efficiency, and u_n is an additive deformation update field i.e., u_n(x) is a three-dimensional vector that updates T_n(x), the estimate of the mapping of point x in target image space to its corresponding point x + T_n(x) + u_n(x) in atlas n.

The optimization of u_n is fast because it can be carried out voxel by voxel. Furthermore, the gradient and Hessian at u_n = 0 have closed-form expressions; see Equation 9, where I is the 3 × 3 identity matrix, ${\mathbf{H}}_n^l(x)$ and ${\mathbf{G}}_n^l(x)$ are the Hessian and gradient of $P_m^l(x)$ respectively, and we have computed a Gauss-Newton update. Since our model is based on the small deformation assumption, in practice we limit the norm of the update field to 3 mm.

Given an update field u_n, the second step of the optimization effectively performs a regularization by considering the priors. Working in the Fourier domain, it can be shown that an efficient solution is equivalent to the following convolution (Vercauteren et al., 2007):

$$T_n\leftarrow (\frac{\kappa }{\kappa +k_2}(T_n+{\mathbf{u}}_n)+\frac{k_2}{\kappa +k_2}{\mathrm{\Gamma }}_m^{-1}T)★K,$$ (12)

where ★ denotes convolution and K is a smoothing kernel (Cachier et al., 2003). As suggested in Vercauteren et al. (2007), we use a Gaussian kernel. This update is analogous to Equation A.3 in Appendix A.

Finally, the update of T can also be easily be derived in the Fourier domain, yielding:

$$T\leftarrow [(1/N)\sum _{m=1}^N{\mathrm{\Gamma }}_n{T}_n]★K.$$ (13)

We only take one registration step at each iteration of the VEM algorithm, since the cost function changes when we update {T_n}, i.e., we go back to quickly recompute q and Θ (for which EM converges quickly, except for the first few iterations) and then we update the registrations again. Therefore, we are not really optimizing Equation 3, but improving it instead. Dempster et al. (1977) refer to this type of EM algorithms (which improve rather than optimize at each step) as “generalized EM”.

3.2. Obtaining the most probable labels

By substituting the point estimates Θ̂, {T̂_n} from Section 3.1 into Equation 1 and utilizing the approximation for the posterior of M, we obtain:

$$\mathrm{L̂}\approx \underset{L}{\text{argmax}}p(L|I,\mathrm{\Theta ̂},\{L_n\},\{{\mathrm{T̂}}_n\})=\underset{L}{\text{argmax}}\sum _{M}p(L|M,I,\mathrm{\Theta ̂},\{L_n\},\{{\mathrm{T̂}}_n\})p(M|I,\mathrm{\Theta ̂},\{L_n\},\{{\mathrm{T̂}}_n\})\approx \underset{L}{\text{argmax}}\sum _{M}p(L|M,I,\mathrm{\Theta ̂},\{L_n\},\{{\mathrm{T̂}}_n\})q(M)=\underset{L}{\text{argmax}}\prod _{x\in \mathrm{\Omega }}\sum _{m=1}^N{q}_x(m)\frac{p(I(x)|{\mathrm{\Theta ̂}}_{L(x)})p(L(x)|L_m,\widehat{T_m})}{{\sum }_{l\prime =1}^{ℒ}p(I(x)|{\mathrm{\Theta ̂}}_{l\prime })p(L(x)=l\prime |L_m,\widehat{T_m})}.$$

Computing the most likely segmentation then simplifies to taking the maximum across labels of this expression at each voxel:

$$\mathrm{L̂}(x)\approx \underset{l}{\text{argmax}}\sum _{m=1}^N{q}_x(m)\frac{p(I(x)|{\mathrm{\Theta ̂}}_l)p(L(x)=l|L_m,\widehat{T_m})}{{\sum }_{l\prime =1}^{ℒ}p(I(x)|\widehat{{\mathrm{\Theta }}_{l\prime }})p(L(x)=l\prime |L_m,\widehat{T_m})}.$$ (14)

3.3. Overview of the algorithm

The whole segmentation algorithm is summarized in Table 3. First, the registrations are initialized with affine transforms, the bias field estimate with a constant field equal to one at every spatial location, the Gaussian parameters with sample means and variances (based on the labels propagated with the affine registrations), and the distribution q to a constant value equal to the inverse of the number of atlases (independently of the spatial location). Then, the algorithm iterates between the E and M steps of the VEM algorithm to estimate the model parameters. The E step updates q(M), whereas the M step sequentially reestimates the Gaussian parameters, bias field parameters and registrations. For these VEM iterations, we use a multi-resolution scheme for computational efficiency and to avoid getting stuck in local maxima of the objective function. Once the VEM algorithm has converged, the estimated model parameters and the final value of q(M) can be used to estimate the most probable segmentation using Equation 14.

Table 3.

Summary of the proposed unified registration / label fusion framework.

Initialize registrations with affine transforms. Initialize Gaussian parameters with sample means and variances. Set bias field coefficients bk = 0, ∀k. Set qx(m) = 1/N, ∀x, m. For each resolution level, from coarse to fine: a) update q with Equation 4 until convergence. b) update means and variances with Equations 6 and 7. c) update the bias field parameters with the BFGS algorithm, using the expression in Equation 8 for the gradient. d) Update the registration by: computing un(x) with Equation 9. adding the result to the current estimate of the deformation, i.e., Tn ← Tn + un. update Tn’s with Equation 12 update T with Equation 13 d) If parameter estimates not converged, go to (b) Use the latest estimate of q to obtain the final segmentation with Equation 14.

4. Experiments and results

Here we describe a set of experiments that validate the proposed model. In Section 4.1, the MRI data used in the study are described. The experimental setup and a number of competing methods are presented in Section 4.2. The results are presented in Section 4.3.

4.1. Materials

In this study, we used two datasets: one of proton density (PD) weighted MRI scans and another of T1-weighted MRI scans.

The PD dataset consists of PD-weighted brain scans from eight healthy subjects. The original purpose of this dataset was to infer the underlying MRI properties of the tissue (Fischl et al., 2004), for which a multiecho FLASH sequence was used (1.5T, TR=20ms, TE=min, α = {3°, 5°, 20°, 30°}, 1 mm. isotropic voxels). The PD-weighted images correspond to the smallest flip angle α = 3°. A total of 36 structures were manually labeled using the protocol described in Caviness Jr. et al. (1989). In the annotation process, the human raters took advantage of the higher contrast, T1-weighted images corresponding to the largest flip angle α = 30°. The PD and T1 images are intrinsically aligned due to the nature of the pulse sequence. As in Iglesias et al. (2012a); Sabuncu et al. (2010), we only used a representative subset of the structures for evaluation in this study: white matter (WM), cerebral cortex (CT), lateral ventricle (VE, including the inferior lateral ventricle and the choroid plexus), cerebellum white matter (CWM), cerebellum cortex (CCT), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA), hippocampus (HP) and amygdala (AM).

The T1 dataset, which is the training dataset described in Han and Fischl (2007), consists of 39 T1-weighted brain MRI scans⁴ (MP-RAGE, 1.5T, TR=9.7ms, TE=4.ms, TI=20ms, α= 10°, 1 mm. isotropic resolution) and corresponding manual delineations of the same brain structures (same labeling protocol). We note that these are the same subjects that were used to construct the probabilistic atlas in FreeSurfer⁵.

The choice of these two datasets for the experiments is motivated by the fact that the same labeling protocol was used to make the manual annotations on both of them. Therefore, we can directly compare the gold standard segmentations of a dataset with the automated segmentations based on knowledge from the other without introducing a bias in the evaluation. All the scans from both datasets were skull-stripped using FreeSurfer and tightly cropped around the whole-brain mask in order to reduce the computational burden of the algorithms.

4.2. Experimental setup

To evaluate the proposed method, we used two different setups. In the first one, the PD scans are segmented using the T1 volumes as atlases. The second setup is symmetric: the T1 scans are segmented with the PD scans playing the role of atlases. For each of the two setups, the performance of four competing methods was measured with the Dice overlap score, defined as: Dice(A, M) = 2|A ∩ M|/(|A| + |M|), where A is the automatic segmentation, M is the manual segmentation, and |·| denotes the corresponding volume. These four methods are described next.

The first method we assess is majority voting, where the atlases were registered to the target volume using Elastix (Klein et al., 2010). A grid of control points and b-splines were used to model the nonlinear deformations of the atlases (Rueckert et al., 1999), which were initialized with affine transforms. Mutual information was used as cost function. A multi-resolution scheme with three levels – 4 mm, 2 mm and 1 mm – was used to optimize the deformations, with separation between control points equal to 32 mm, 16 mm and 8 mm, respectively. The choice for the control point separation at the finest level was based on pilot experiments which revealed that, below 8 mm, the quality of the registration began to degrade. The performance degraded even more when replacing b-splines by a demons-like registration algorithm, specifically the publicly available diffeomorphic method SyN (Avants et al., 2008). It seemed the case that, in our dataset, mutual information simply cannot steer very flexible models towards the right registration. We must, however, note that much smaller spacings between control points have been successfully used in the literature in other scenarios (e.g., 2.5 mm for intra-modality T1 MRI registration in Klein et al. 2009).

The second method is label fusion without integrating registration into the framework, which we will refer to as “label fusion with precomputed registrations.” We used the same Elastix registration as in majority voting, and never updated it during the fusion. In other words, we skipped step 2d in Table 3. This method is essentially very similar to the one presented in a previous workshop paper by the authors (Iglesias et al. 2012b; notice the improvement in the inference algorithm with respect to Iglesias et al. 2012a, marginalizing over the segmentations when solving for the intensity likelihood parameters in the M-step).

The third approach integrates registration into the framework. The deformations were initialized with affine registrations computed via Elastix, and all subsequent nonlinear warps were estimated within the proposed framework. Therefore, the intensities of the atlases were not used during the label fusion phase. We assume that k₂ = 0, i.e., the prior probability for the registrations treats them as independent. Henceforth, we refer to this method, which constitutes our third benchmark, as “unified label fusion with independent registrations.” The fourth and final method we implemented in our experiments represents a full instantiation of the proposed model, with k₂ > 0. We refer to this method as “unified label fusion with linked registrations.”

The parameter settings for the experiments were the following. We set β = 0.75 and ρ = 1.0. The free parameter κ of the Demons algorithm was set to κ = 0.05/N, and then we set k₂ to a value such that k₂/(κ + k₂) = 15%. The constant k₁ is directly related to the width of Gaussian kernel used to approximate Equation A.3; we set the standard deviation of this Gaussian to 2.5 mm. The bias field basis {ψ_k} corresponds to a third-order polynomial (which has 20 coefficients). The values for ρ and β were borrowed from Sabuncu et al. (2010); Iglesias et al. (2012a). The values for k₁, k₂, κ were tuned by visual inspection in pilot experiments with a T1 dataset from the first author’s brain.

To precompute the deformations {Г_n} in the method with linked registrations, we used two different algorithms. For the T1 dataset, we reused the registrations from Sabuncu et al. (2009), which rely on a log-domain diffeomorphic registration method. The registrations are based on the sum of squared differences between intensity-normalized versions of the scans. The intensity normalization was carried out with FreeSurfer, which is T1 specific. For the PD dataset, rather than preprocessing the data to normalize the intensities (which is relatively unexplored for brain MRI acquired with weighting other than T1), we used SyN with local cross-correlation, which is known to work well in intra-modality scenarios without normalizing the intensities (Klein et al., 2009).

We ran two sets of experiments. In the first set, we explored the performance of the algorithms as a function of N, the number of training atlases. To summarize the performance across the brain structures of interest, we computed for each target scan a single score, which we denominate “brainwide Dice overlap”. This score is simply the mean of the Dice scores across these structures. In the second set of experiments, the number of atlases was set to a high value, which is the scenario we would ideally operate in practice: N = 20 for the PD data and N = 8 (the maximum) for the T1 data. The Dice overlap was assessed for each brain structure independently. Nonparametric Mann-Whitney U-tests were used for statistical hypothesis testing of whether one method outperforms another. In all cases, we repeated the experiments 10 times (or as many times as possible combinations of atlases, if less than 10) with different randomly selected subsets of atlases in order to reduce the bias introduced by the (random) atlas selection.

4.3. Results

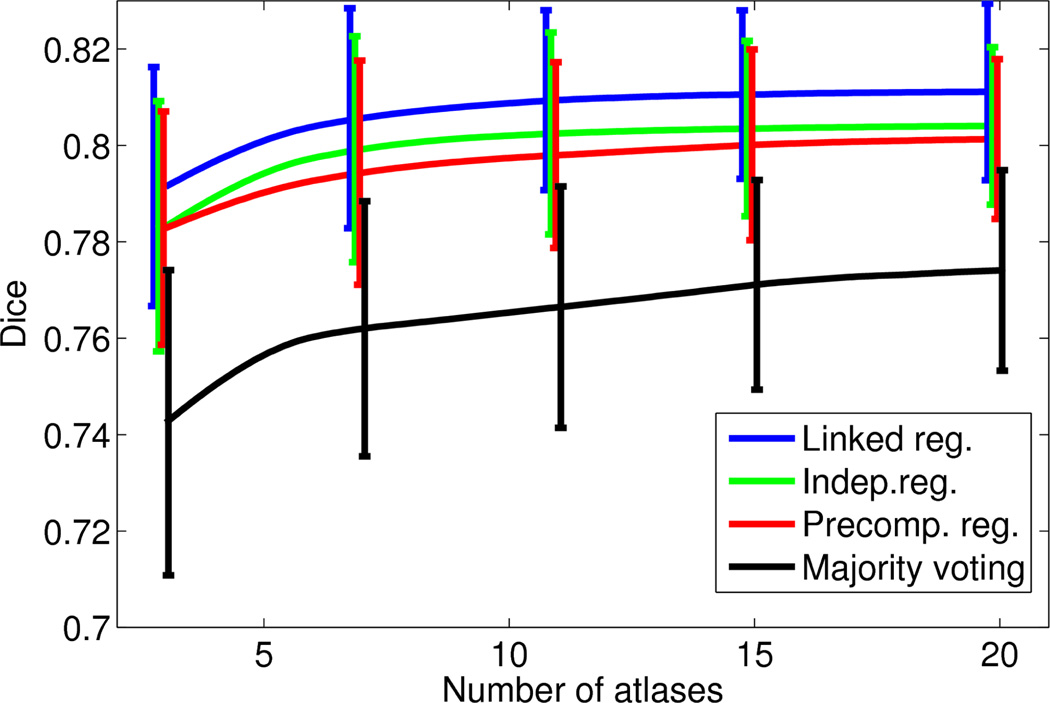
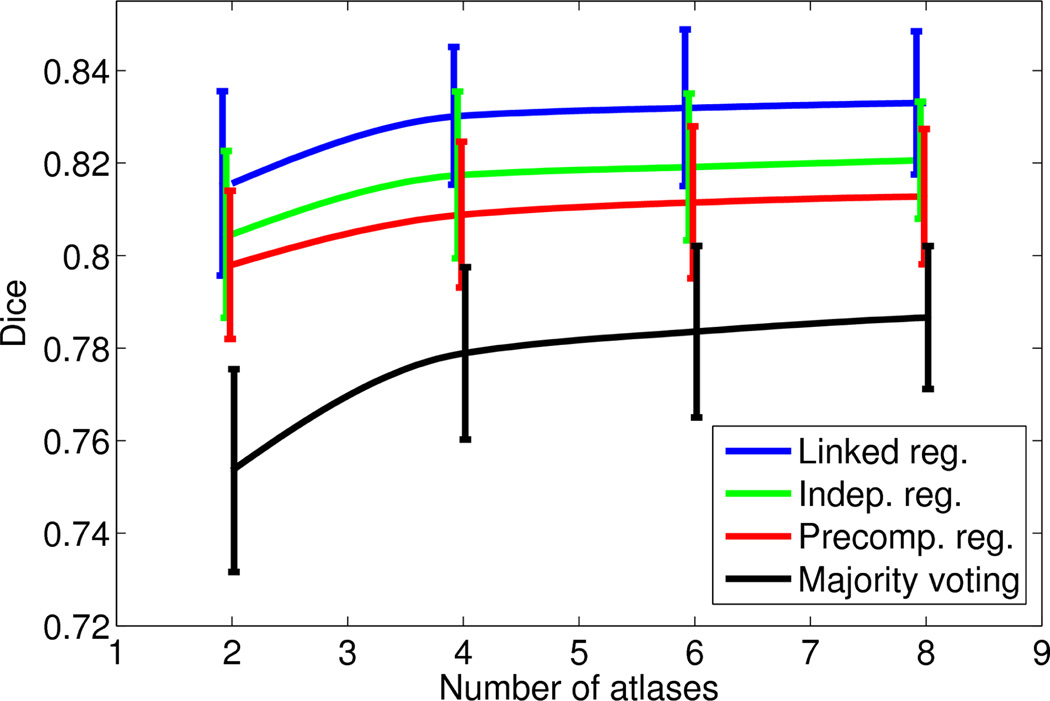
Figures 3 and 4 show, for each of the two datasets, the mean and the standard deviation of the the brainwide Dice overlap as a function of the number of training atlases. For the PD dataset, we consider values of N up to 20, since the performances of the algorithms seem to have flattened by then, as seen in Figure 3. For the T1 dataset, we consider values of N up to eight, which is the maximum number of available atlases.

Figure 3.

Average brainwide Dice overlap of the four different algorithms as a function of the number of training atlases: PD dataset. The error bars span one standard deviation of the data.

Figure 4.

Average brainwide Dice overlap of the four different algorithms as a function of the number of training atlases: T1 dataset. As in Figure 3, the error bars span one standard deviation of the data.

Similar conclusions can be drawn from both figures. The full version of the framework with integrated and linked registrations produces a consistent improvement over the version with independent registrations, which in turn outperforms label fusion with precomputed registrations. By taking advantage of the consistency of the intensities in the target volume, all the fusion-based methods (both with and without integrated registration) clearly outperform majority voting. Moreover, for the same reason, they are also able to produce decent results even with N = 2, 3 atlases. Of course, their performance also flattens earlier, so the gap with respect to majority voting narrows as N increases.

In the second experiment, N is set to 8 for the T1 dataset and 20 for the PD dataset. The boxplots for the structure-wise Dice overlap scores for the two datasets are shown in Figures 5 and 6, which also display whether there are statistically significant differences (at p < 0.01) between the performances of the different methods.

Figure 5.

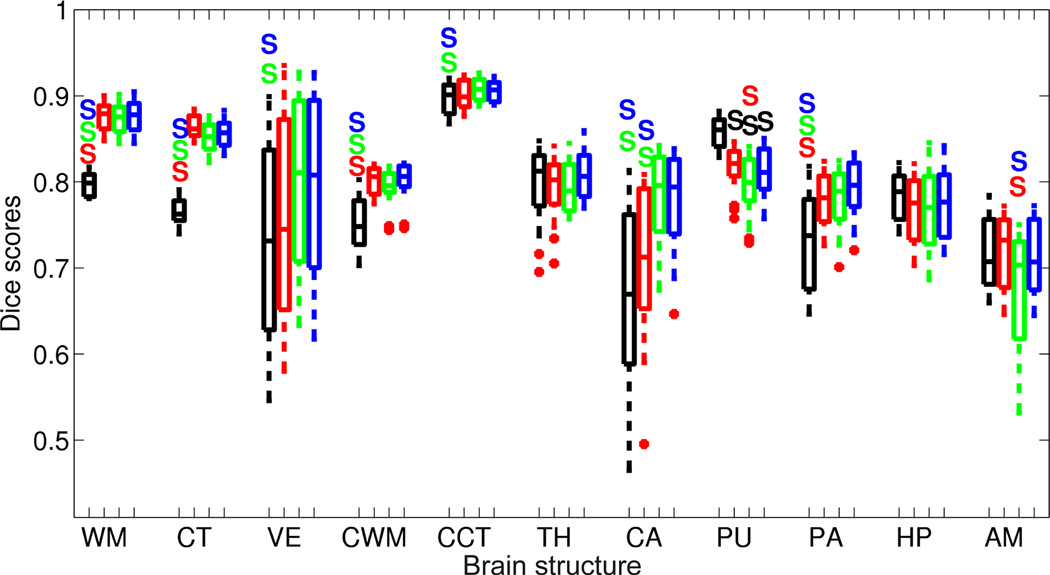
Boxplot of Dice overlap scores corresponding to the 11 structures of interest when automatically segmenting the PD-weighted data with N = 20 atlases; see Section 4.1 for the abbreviations. The segmentation methods are majority voting (black), label fusion with precomputed registrations (red), unified label fusion with independent registrations (green), and unified label fusion with linked registrations (blue). A colored S above a box means that the method corresponding to the color of the S is significantly better than the method at hand with p < 0.01. Horizontal box lines indicate the three quartile values. Whiskers extend to the most extreme values within 1.5 times the interquartile range from the ends of the box. Samples beyond those points (outliers) are marked with crosses.

Figure 6.

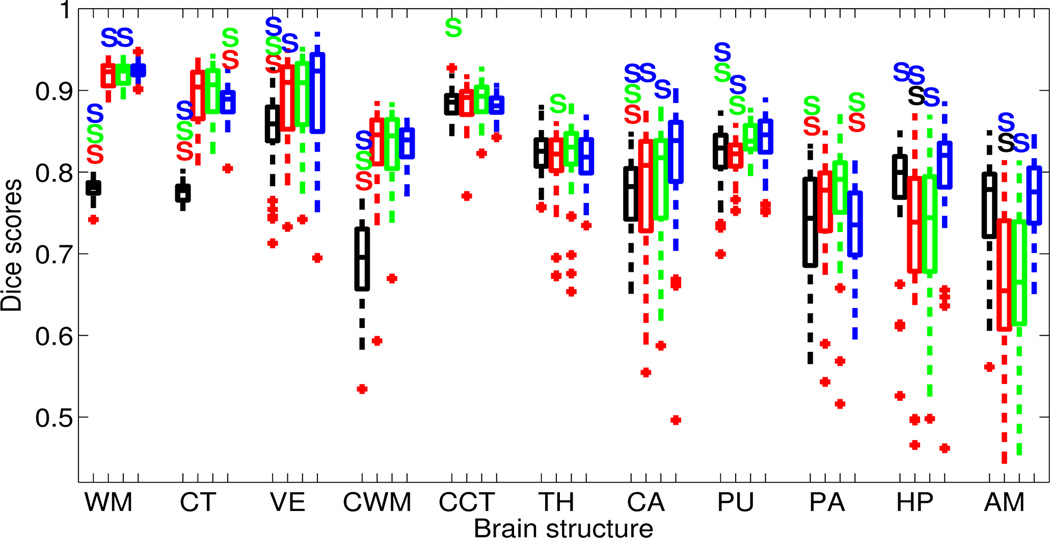
Boxplot of Dice overlap scores corresponding to the 11 structures of interest when automatically segmenting the T1-weighted data with N = 8 atlases. See caption of Figure 5 for an explanation of the figure.

Compared with majority voting, the label fusion approaches produce significantly higher Dice scores for almost every structure. As expected, the difference is especially large for structures with convoluted surfaces (which are more difficult to register), such as the cortex and the white matter of the cerebrum and the cerebellum. There is only one structure out of 22 (in both datasets), for which the proposed framework is significantly worse than majority voting: the putamen in the PD dataset. This is due to the inability of the Gaussian intensity assumption to model the claustrum, a thin layer of gray matter in the white matter located between the putamen and the cortex. Because the claustrum is not manually annotated in the gold standard, it is often labeled as putamen and/or cortex by the label fusion algorithms.

Within the label fusion strategies, we observe significant improvement with respect to majority voting in more structures as we increase the complexity of the model. The fusion scheme with precomputed registrations significantly outperforms majority voting in 10 structures, whereas the models with integrated registrations display significant improvement in 15. Unified label fusion with independent registrations outperforms label fusion with precomputed registrations for three structures (caudate in PD, thalamus in putamen in T1). However, it is also significantly worse for other two: putamen and amygdala in PD. On the other hand, when we link the registrations in the prior, the resulting method improves upon the algorithm with precomputed registrations in seven structures, while being outperformed only in two (cortex and pallidum in T1). Finally, a small improvement (though not always significant) can be observed from the version with independent registrations to the version with linked registrations: the amygdala improves significantly in PD, whereas the white matter, caudate and amygdala do so in T1. On the other hand, the cerebral cortex and the pallidum get worse in T1.

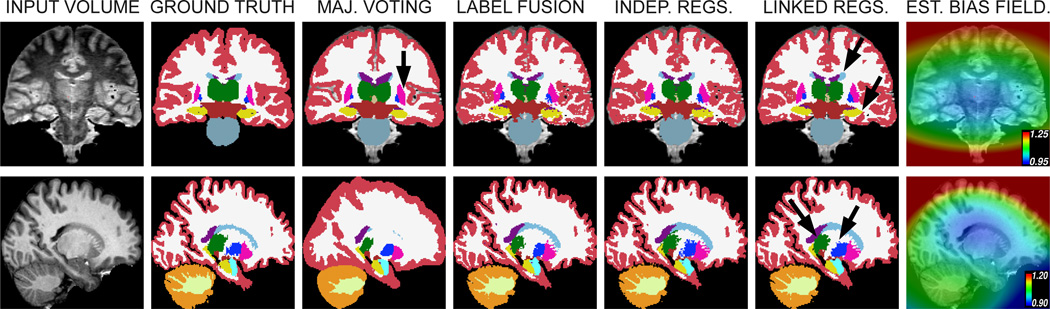
Finally, Figure 7 displays a typical segmentation from each dataset. Majority voting produces overly smooth boundaries which often do not agree with the manual labels, especially for the white matter and cortex. Its independence from the image intensities in the fusion only represents and advantage when segmenting the putamen, which the proposed framework undersegments due to its inability to model the intensities of the claustrum; this region is highlighted by an arrow in the segmentation of the sample PD scan generated by majority voting. Label fusion with precomputed registrations produces much sharper boundaries, and unified label fusion with integrated registration (especially with the linked prior) produces slightly better segmentations; see for example the left caudate and hippocampus in the PD volume, or the thalamus and pallidum in the T1 volume (highlighted by arrows in the figure).

Figure 7.

Sample slices of two representative scans, one from the PD dataset (top row, coronal view, segmented with N = 20 atlases) and one from the T1 dataset (bottom row, sagittal view, segmented with N = 8 atlases). The first column displays the original MRI data. The second column shows gold standard labels. The next four columns display the outputs from the different segmentation methods. Finally, the rightmost column overlays the estimate of the bias field on the original MRI data. The color map is the following: WM = white, CT = red, VE = purple, CWM = light yellow, CCT = orange, TH = green, CA = pale weak cyan, PU = pink, PA = blue, HP = yellow, AM = cyan. The arrows point at regions in which one a method outperforms the others.

5. Discussion and Future Work

Multi-atlas label fusion is a flexible approach that yields robust and accurate automatic segmentation tools. Most prior label fusion methods treat registration as a separate problem, which is typically solved in a pre-processing step, where each atlas is registered to the target scan independently. However, probabilistic atlas-based segmentation methods have demonstrated that unifying registration and segmentation can produce significant improvements in the final result, since both problems are interdependent. Furthermore, in the label fusion approach, coupling the multiple atlas registrations might have the potential to further improve the accuracy in the individual registration results, which in turn might benefit segmentation accuracy. On the other hand, many of the successful label fusion algorithms make use of the appearance similarities between the atlases and target scan in order to determine the relative contribution of each atlas. To date, however, there has been little effort to devise a principled weighted label fusion method that can handle intensity variations in a setting where the atlases and target scan are obtained using different imaging modalities. In this work, we presented a probabilistic label fusion model that (i) unifies the registration and label fusion steps, (ii) couples the multiple atlas registrations, and (iii) can handle intensity variations due to modality differences between atlases and the target scan.

The proposed algorithm is designed to handle situations where the atlas images and target scan were acquired via different pulse sequences with different tissue contrasts. The method does not rely on the similarity of intensities across the atlases and the target volume per se, but on the consistency of intensities within regions in the target volume. In fact, the proposed method does not require the image intensities of the atlases to be available, which might be a useful feature when the images themselves cannot be released due to restrictions, but the labels can.

The presented approach can be viewed as a generalization of existing supervised segmentation methods. For example, we can set some model parameters such that the atlas registrations are decoupled and not updated during label fusion, which effectively is equivalent to more traditional label fusion methods. In this set-up, many flavors of label fusion (such as majority voting, or weighted averaging) can be easily derived. Alternatively, we can force all atlas registrations to be equal (by setting k₂ → ∞), which will in turn make the model equivalent to a classical probabilistic segmentation atlas, where there is a single atlas coordinate frame. Hence, we can regard the proposed model as a bridge that connects classical segmentation methods that rely on a single probabilistic atlas and more recent label fusion methods.

Our results clearly demonstrate that the presented framework produces segmentations that are significantly more accurate than those obtained with majority voting, a classical label fusion approach that is also suitable for cross-modality scenarios. We only observed a significant decrease a performance for one structure in our experiments: the putamen in the PD dataset. We are confident that such difference would disappear if the claustrum was labeled in the training dataset. The global improvement in Dice score, which is around 4–5%, has a direct, positive impact on subsequent analyses. For instance, in volumetric studies, it can be found in practice that the increases in Dice score and in the precision of volume estimates are often on the same order.

Furthermore, we quantify the accuracy gain offered by the different components of the proposed model. Firstly, unifying registration and label fusion, as opposed to pre-computing the multiple atlas registrations, clearly provides an improvement, as revealed by the comparison with a version of the proposed model where the registrations were computed in a preprocessing step (by maximizing the mutual information between atlas and target scan intensities) and not allowed to be updated in label fusion. We note that the latter method in fact makes use of atlas intensities during pre-processing, which is not the case for the full version of the proposed method that relies solely on the target scan intensities. Secondly, coupling atlas registrations also provides a significant performance boost. We believe the prior we adopt on the deformations that links the atlases through a pre-computed co-registration, provides a more realistic model for the geometric relationship between the atlases and the target scan, yielding more accurate segmentations as observed in our results.

The proposed framework offers another advantage that was not explored in this manuscript: the model can easily exploit multi-channel target subject data to improve segmentation quality. This can be achieved by simply modifying the image likelihood term, p(I|Θ), which could take the form of a multi-variate Gaussian, similar to the model adopted in Iglesias et al. (2012b).

The presented algorithm was implemented in Matlab without optimizing for speed of execution or memory usage. The run time of the algorithm on a single CPU core was roughly one hour per training atlas, and the memory footprint approximately 8 GB. In addition to optimizing the code (possibly implementing it in a low-level language such as C++), the efficiency of the algorithm could be improved by first identifying a small subset of atlases that are similar to the target volume (e.g., through an affine transform), and then using only the subset in the segmentation (e.g., as in Depa et al. 2011).

We instantiated our model in the context of brain MRI scans. This application motivates the choice of intensity corruption model (i.e., bias field / B1 inhomogeneity), which is specific to MRI. However, other corruption models could in principle be used to apply the proposed framework to segmentation of images from organs acquired with other modalities; testing the performance is such alternative scenarios remains as future work.

There are other obvious directions to explore. For example, we can investigate the use of other registration algorithms. In particular, a diffeomorphic implementation of the employed Demons-style algorithm would be straightforward (Vercauteren et al., 2007). Even though the registration is inherently asymmetric (labels to intensities), the diffeomorphic constraint usually produces more realistic deformation fields. Furthermore, we plan to conduct a detailed analysis of how the degree of coupling between atlas registrations effects segmentation accuracy. This will allow us to further characterize the relationship between classical probabilistic atlas-based segmentation methods and multi-atlas label fusion.

• -A label fusion framework based on a generative model that works across modalities.
• -The registrations are not precomputed, but estimated during the fusion.
• -The registrations are explicitly linked in the generative model.

Appendix A. Summary of the Demons algorithms

In the classical Demons framework, registration is cast as a minimization problem:

$$ŝ=\underset{s}{\text{argmin}}\sum _x[{\Vert F(x)-M(x+s(x))\Vert }^2+k_1{\Vert \nabla s(x)\Vert }^2],$$ (A.1)

where F(x), M(x) and s(x) are the fixed image, the moving image and the spatial transform, respectively. Rather than optimizing for s directly, the Demons trick introduces an auxiliary field c(x) such that c defines point correspondences between image voxels and s now includes an error term we allow in the field. The problem becomes:

$$\{ŝ,ĉ\}=\underset{s,c}{\text{argmin}}\sum _x{\Vert F(x)-M(x+c(x))\Vert }^2++\kappa \sum _x{\Vert s(x)-c(x)\Vert }^2+k_1\sum _x{\Vert \nabla s(x)\Vert }^2,$$

where κ is a free parameter that influences the efficiency of the optimization. This problem can be solved using coordinate descent, i.e., iteratively solving for c assuming s fixed and vice versa.

To optimize for c, we do not need to consider the term k₁‖∇s(x)‖². Therefore, the field can be updated at each voxel location independently. Using the change of variables u(x) = c(x) − s(x), the problem becomes:

$$û(x)=\underset{u(x)}{\text{argmin}}{[F(x)-M(x)+s(x)+u(x))]}^2+\kappa {\Vert u(x)\Vert }^2,$$ (A.2)

which has a closed-form solution (Vercauteren et al., 2007). Once u(x) has been computed, c is updated as follows: c(x) ← s(x) + u(x).

To optimize for s, we need to solve:

$$ŝ=\underset{s}{\text{argmin}}\sum _x[{\Vert s(x)-c(x)\Vert }^2+\frac{k_1}{\kappa }{\Vert \nabla s(x)\Vert }^2].$$

Working in the Fourier domain, it is easy to show that:

$$Ŝ(w)=\underset{S(w)}{\text{argmin}}{\Vert S(x)-C(x)\Vert }^2+\frac{k_1}{\kappa }{\Vert w\Vert }^2{\Vert S(w)\Vert }^2,$$

where w is the complex spatial frequency and C(w) and S (w) are the Fourier transforms of c(x) and s(x) respectively. Taking derivatives, it is straightforward to show that the optimal field S is:

$$Ŝ(w)=\frac{1}{1+\frac{k_1}{\kappa }{\Vert w\Vert }^2}C(w).$$ (A.3)

In practice, convolution with a Gaussian kernel is used to approximate the low-pass filtering effect of the term ${[1+\frac{k_1}{\kappa }{\Vert w\Vert }^2]}^{-1}$.

In equation 10, there are two data terms next to the penalty term ‖∇s‖². Again, it is easy to show in the Fourier domain that the solution is a smoothed version of the weighted sum of the penalty terms (Equation 12). A similar reasoning is behind Equation 13, in this case with uniform weights.