A Framework for Estimating Causal Effects in Latent Class Analysis: Is There a Causal Link Between Early Sex and Subsequent Profiles of Delinquency?

Abstract

Prevention scientists use latent class analysis (LCA) with increasing frequency to characterize complex behavior patterns and profiles of risk. Often, the most important research questions in these studies involve establishing characteristics that predict membership in the latent classes, thus describing the composition of the subgroups and suggesting possible points of intervention. More recently, prevention scientists have begun to adopt modern methods for drawing causal inference from observational data because of the bias that can be introduced by confounders. This same issue of confounding exists in any analysis of observational data, including prediction of latent class membership. This study demonstrates a straightforward approach to causal inference in LCA that builds on propensity score methods. We demonstrate this approach by examining the causal effect of early sex on subsequent delinquency latent classes using data from 1,890 adolescents in 11th and 12th grade from wave I of the National Longitudinal Study of Adolescent Health. Prior to the statistical adjustment for potential confounders, early sex was significantly associated with delinquency latent class membership for both genders (p=0.02). However, the propensity score adjusted analysis indicated no evidence for a causal effect of early sex on delinquency class membership (p=0.76) for either gender. Sample R and SAS code is included in an Appendix in the ESM so that prevention scientists may adopt this approach to causal inference in LCA in their own work.

Introduction

Despite all that is known about predictors of subsequent problem behaviors, until the actual causal determinants are identified, preventive interventions cannot be maximally effective. This study sets the stage for prevention scientists to identify underlying causes of complex behavior patterns using existing data from observational studies. We will describe the benefit of using latent class analysis (LCA) to measure behavior patterns, how covariates can be incorporated in LCA to identify predictors of membership in latent classes, and how a modern causal inference technique—inverse propensity score weighting—can be incorporated into this analytic framework in a straightforward way. We provide sample SAS and R code so that prevention scientists may adopt these techniques in their own research. This is presented in the context of the causal effect of early sex on later delinquency latent class membership.

A Motivating Example: the Relationship Between Early Sex and Later Delinquency

Many studies have documented the co-occurrence of multiple problem behaviors, such as substance use, risky sexual behavior, and delinquent behavior, during adolescence (e.g., Donovan and Jessor 1985; Donovan et al. 1988; Willoughby et al. 2004). One theory for this co-occurrence is that a common factor may explain all associations among these problem behaviors, suggesting a “problem behavior syndrome” (Donovan and Jessor 1985; Donovan et al. 1988). Related to our motivating example of a possible causal link between early sex and later delinquency, observational studies have consistently shown a significant association between early sexual activity and delinquent behavior in adolescence (Armour and Haynie 2007; McCarthy and Casey 2008). Further, few studies have specifically investigated gender's role in the association between early sex and delinquency, although associations between various constructs related to early sex (e.g., romantic relationship involvement, a delinquent romantic partner) and delinquency have been shown to be stronger for females than for males, suggesting the importance of considering differential causal effects of early sexual activity on adolescent delinquency by gender (Eklund et al. 2010; Haynie et al. 2005). Since it is impossible to randomize individuals to early sex or not, it is difficult to know whether there is a causal chain of events from early sex to later delinquency or if the different behaviors are two manifestations of an underlying problem behavior syndrome.

Latent Class Analysis to Measure Complex Behavior Patterns

Operationalizing patterns of behavior is complex due to their multidimensional nature. In many previous studies, delinquency has been operationalized with a scale that sums the frequency of various behaviors (e.g., shoplifting, fighting; Beaver 2008; Demuth and Brown 2004). However, such an approach is inadequate to capture the multidimensionality of delinquent behavior. In some studies, subscales have been created to assess multiple dimensions of delinquency (e.g., theft, vandalism; Demuth and Brown 2004; Haynie et al. 2005). Factor analysis, which identifies a few continuous latent “factors” that explain the variability among correlated observed indicators, is another approach that could be used to identify different dimensions of delinquency (McDonald 1985). However, delinquency data often are not compatible with factor analysis, which assumes that the latent factors are continuous and normally distributed. Delinquency is often highly skewed due to low endorsement of delinquent behaviors; therefore this assumption may not be plausible. In addition, factor analysis is only appropriate for research questions assessing differences in amount or frequency of delinquency rather than differences in patterns of co-occurring delinquent behaviors.

In contrast, LCA enables identification of underlying population subgroups (i.e., latent classes), characterized by different patterns of delinquency involvement, using data from multiple observed categorical indicators. The latent classes are mutually exclusive and exhaustive, but the class membership of any particular individual is unknown. LCA is useful for measuring multidimensional patterns of delinquent behavior, as shown by Collins and Lanza (2010). Although we rely on a somewhat different sample, the current study builds directly on a measurement model of delinquency presented in Collins and Lanza, which suggested the following four latent classes of adolescents: non-delinquents (49 %), verbal antagonists (26 %), shoplifters (18 %), and general delinquents (6 %). As implied by the class labels, the classes represented different types of individuals based on their respective patterns of engaging in the multiple behaviors.

In LCA with covariates, covariates (i.e., predictors) are included in a latent class model to determine whether they are associated with latent class membership. As with any prediction model based on observational data, however, such associations cannot be interpreted as causal. See Collins and Lanza (2010) for a thorough introduction to LCA and LCA with covariates.

Propensity Score Analysis

If the relationship between problem behaviors, such as early sex and later delinquency, is in fact causal, then preventing the early trigger (i.e., early sex) may prevent this series of behavioral outcome (i.e., delinquency) and associated consequences. However, although problem behaviors tend to co-occur, observational studies cannot determine whether correlated problem behaviors are causally related, even when examined longitudinally, due to the presence of confounders (i.e., pre-exposure variables associated with both the exposure and outcome) that could explain an association.

The randomized controlled trial (RCT) is the gold standard for testing causality (West 2009), yet it is often impossible or unethical to randomize subjects to treatments (i.e., exposures), such as early sex, in order to estimate the causal effect on a later outcome, such as delinquency. Propensity score methods offer a solution to this methodological problem by simulating the randomization in an RCT through balancing exposure groups (i.e., early sex vs. no early sex) on the confounders. This makes causal inference possible with observational data assuming that all confounders are measured and included in the propensity model (Harder et al. 2010; Stuart 2010).

The propensity score π_i is the probability that an individual received the exposure (in this case, experienced early sex) given the measured confounders (Rosenbaum and Rubin 1983). These are typically estimated using logistic regression, although data-mining procedures such as generalized boosted modeling (GBM) perform better under some circumstances (Ghosh 2011; Lee et al. 2010; Stuart 2010). GBM iteratively fits many regression tree models and then adds these models together to produce a smooth function of the confounders, which can be used to estimate the propensity score (McCaffrey et al. 2004). This approach reduces the risk of model misspecification and incorporates nonlinear and interaction terms (McCaffrey et al. 2004). GBM can be implemented using the twang package in R (Ridgeway et al. 2012). Propensity scores can then be used to adjust the data through weighting (Hirano and Imbens 2001), matching (Rosenbaum and Rubin 1985), or subclassification (Rosenbaum and Rubin 1984). Here, we focus on weighting (see Lanza et al. 2013, for a discussion of the different approaches in LCA).

Several assumptions must be made when estimating a causal effect using propensity score methods. First, use of these methods assumes unconfoundedness, meaning that all confounders of the exposure-outcome relationship are included in the propensity score model that predicts exposure (Rosenbaum and Rubin 1983). Second, it is assumed that every individual in the population has a non-zero probability of being exposed (Rosenbaum and Rubin 1983). Third, the stable unit treatment value assumption has two parts (Rubin 1980). One part is that the exposure status of any one individual does not affect the potential outcome of any other individual in the population (no-interference assumption), and the other part is that an individual's outcome had he been exposed would be identical regardless of the way in which he was exposed (no-versions-of-treatment assumption; Rubin 1980).

Provided that these assumptions hold, propensity score methods have advantages over standard analyses, such as linear regression adjustment. The propensity score is a scalar summarizing a high-dimensional vector of confounders; it facilitates removal of bias due to confounding by controlling for a large number of measured confounders at once. In other words, propensity score adjustment allows the comparison of individuals with a similar distribution on the measured confounders (i.e., a similar propensity score), and therefore isolates the effect of interest (Rosenbaum and Rubin 1983; Stuart 2010). In addition, use of standard linear regression adjustment can be biased if the association between the confounders and the outcome is nonlinear (Stuart 2010). Propensity score methods separate the “design” (controlling for confounders) and “analysis” (assessing the relationship between the exposure and the outcome) stages of a study, so controlling for the confounders is completed before a model is fit for the outcome (Austin 2011; Stuart 2010). Propensity score methods also have straightforward diagnostics to assess whether there is sufficient overlap of the distribution of the confounders between exposure groups to justify comparison, and whether differences between exposure groups (i.e., imbalances) remain on any measured confounders after propensity score adjustment (Austin 2011; Stuart 2010).

The process for causal inference in LCA with covariates is quite similar to any other propensity score analysis; this approach was first described by Lanza et al. (2013). Below, we provide a step-by-step demonstration of this method, using the motivating example of estimating the causal effect of early sex on adolescent delinquency latent class membership.

The Current Study

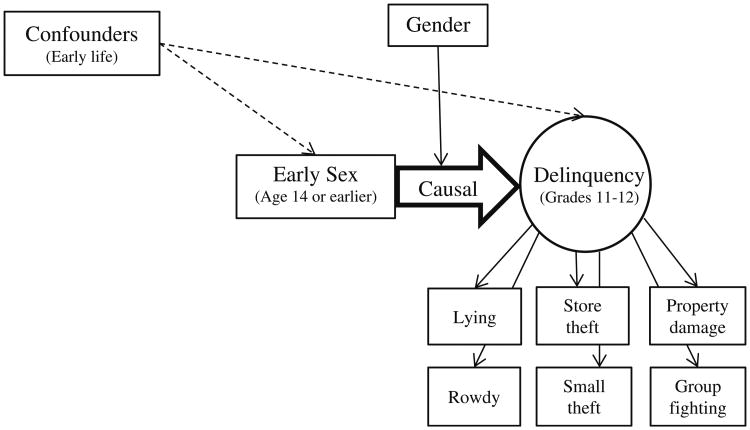
The primary goal of this study is to illustrate a new framework for estimating the causal effect of an observed variable on latent class membership. We demonstrate this framework by estimating the average causal effect (ACE) of early sex on complex patterns of delinquent behavior in adolescence, and assessing whether the estimated causal effect differs for males and females (see Fig. 1). The findings from this empirical demonstration answer the prevention-relevant question, “If we are able to reduce early sexual initiation, will we see a resultant drop in later delinquency?” We include SAS and R syntax in the Appendix in the Electronic Supplementary Material (ESM) to facilitate the adoption of these techniques by prevention scientists.

Fig. 1. Graphical depiction of hypothesized model for causal effect of early sex on latent classes of adolescent delinquency, moderated by gender.

An Empirical Demonstration: Investigating the Causal Link Between Early Sex and Delinquency Latent Class Membership

Sample

This study used data from the National Longitudinal Study of Adolescent Health (Add Health), a nationally representative, longitudinal study that collected data on factors contributing to adolescents' health and risk behaviors (Harris 2009). We used data from wave I of the Add Health public-use dataset, which was measured in 1994–1995 using in-school questionnaires, in-home interviews, and parent questionnaires. The primary research question could be addressed using data from this single wave because the exposure was a retrospective account of early behavior, thus it occurred prior to the outcome. Add Health selected a school-based sample using systematic sampling methods and implicit stratification to ensure that the schools were nationally representative on various demographic characteristics (Harris et al. 2009). All analyses incorporated Add Health school cluster codes to account for the sampling design. Participants included in this study were in 11th or 12th grade; those missing on all delinquency items or on early sex were deleted from the analysis (4.9 %). This resulted in a sample of 1,890 adolescents (mean age 17.3 years, SD=0.79; 52.3 % female; 70.2 % White, 17.6 % African American, 1.1 % American Indian or Native American, 4.8 % Asian or Pacific Islander, 6.3 % other; nine participants did not give information on their race).

Measures

Six items were used to assess delinquency behaviors. The original questionnaire items asked how often the participant engaged in the behavior during the past 12months (never, one or two times, three or four times, four or more times). However, among those that engaged in the behaviors there was little variation in frequency of behaviors, and the focus of this study was on the patterns of types of adolescent delinquent behavior rather than the frequency of delinquent behavior. Therefore, items were recoded to reflect yes (participated in the behavior at least once) and no (did not participate in the behavior). The frequency of a yes response for each of the indicators are as follows: lying to parents or guardians (57 %); behaving loud, rowdy, or unruly in a public place (46 %); stealing from a store (20 %); stealing items worth less than $50 (17 %); damaging property (15 %); and participating in a group fight (15 %). For both males and females, lying to parents or guardians was most common (56 and 58 % respectively). Stealing items worth less than $50 was least common for males (22 %), whereas damaging property was least common for females (8 %).

Early sex was defined as first sexual intercourse at age 14 or younger (17.9 %). Participants that indicated first sexual intercourse after age 14 or that they never engaged in sexual intercourse were classified as no early sex (82.1 %). Early sex was reported by 21.3 % of males and 14.8 % of females.

A variety of family, demographic, risk behavior, and biological variables that could potentially confound an observed association between early sex and adolescent delinquency latent classes were measured. Table 1 summarizes the potential confounders examined herein.

Table 1. Balance table: standardized effect sizes before (unadjusted) and after (adjusted) applying inverse propensity weights.

Confounders	Unadjusted	Adjusted	Confounders	Unadjusted	Adjusted
Family			Demographics
Birth order among children of biological parents	0.05	−0.02	Race
Missinga	0.08	0.01	White	−0.27b	−0.00
Number of people in household	−0.22b	−0.07	Black	0.38b	0.05
Missing	0.25b	−0.02	Native American	0.15	0.05
Maternal age at birth	−0.15	−0.04	Asian	−0.14	−0.02
Missing	0.24b	0.07	Other	−0.02	−0.08
Maternal education			Missing	−0.03	−0.04
Never finished high school	0.05	−0.05	Hispanic origin	0.05	−0.01
High school graduate	0.05	0.05	Missing	−0.03	−0.03
School beyond high school	−0.29b	−0.05	English spoken in home	0.09	0.08
Missing	0.35b	0.07	Missing	−0.03	−0.03
Mother works more than 30 h/week for pay	0.04	0.09	Born in USA	0.05	0.00
Missing	0.18	0.02
Religious parent	−0.12	−0.05	Risk behaviors
Missing	0.19	0.06	Early cigarette use (by age 12)	0.38b	0.10
Household income	−0.07	−0.05	Missing	0.03	0.02
Missing	0.19	0.07	Early alcohol use (by age 12, not with family)	0.42b	0.09
Family structure at age 10			Missing	0.13	−0.01
Two biological parents	−0.48b	−0.04
One biological parent and opposite-sex partner	0.09	−0.00	Biological
Single parent	0.38b	0.03	Early menarche (by age 11)	0.32b	0.03
Other	0.24b	0.02	Missing	0.23b	0.23b
Neighborhood
Rural	0.12	0.12
Suburban	−0.14	−0.11
Residential-only urban	−0.00	0.01
Non-residential/other	0.08	−0.00
Missing	−0.02	−0.04
Residential parent received public assistance	0.06	−0.00
Missing	0.17	0.06

Note. A positive standardized effect size indicates a higher mean value of the confounder in the early sex group

^aMissing variables were treated as indicator variables during propensity score estimation

^bAbsolute standardized effect size≥0.2

Analytic Approach

Estimating the Propensity Scores

Potential confounders were selected for inclusion in the propensity score model based on predictors of early sex and delinquency identified in the literature (e.g., Jordahl and Lohman 2009; Longmore et al. 2009). It is important to include as many known confounders of the exposure–outcome association in the propensity score model as possible to satisfy the assumption of unconfoundedness and to minimize bias due to unmeasured confounding (Rosenbaum and Rubin 1983; Stuart 2010). However, by definition, confounders must occur before the exposure variable; therefore, confounders were selected that took on their values early in life so that they could not be influenced by the exposure (i.e., timing of sexual initiation). The propensity scores were estimated using GBM to regress early sex on 17 measured confounders and the moderator (i.e., gender); the propensity scores, then, were the predicted probabilities from the GBM regression model (McCaffrey et al. 2004). Next, overlap of the distribution of the propensity scores between the exposure groups was assessed to determine whether there were similar individuals between the early sex group and the no early sex group on the measured confounders. Overlap was assessed by comparing the range of the estimated propensity scores by exposure group. This could also be done visually by comparing side-by-side boxplots or stacked histograms of the estimated propensity scores by exposure group. Sufficient overlap is necessary to justify the use of propensity scores for causal inference (Harder et al. 2010).

Calculating the Inverse Propensity Weights

The estimated propensity scores were then used to compute inverse propensity weights (IPWs). Applying IPWs adjusts the data to mimic random assignment into exposure groups by down-weighting the over-represented participants (people with a high probability of being in their respective exposure group) and upweighting the under-represented participants (people with a low probability of being in their respective exposure group). Thus, the IPW is the inverse of the probability that the participant would be in his or her respective exposure group given the measured confounders (Hirano and Imbens 2001). However, when incorporating a baseline moderator Z, such as gender, in the analysis, the numerator of the weights should be modified to incorporate the probability that the individual was exposed (i.e., had early sex) conditional on the moderator: for the early sex group(T=1) $\mathrm{I}\mathrm{P}\mathrm{W}=\frac{P(T_i=1|Z_i)}{{\widehat{\pi }}_i}$ and for the no early sex group (T=0) $\mathrm{I}\mathrm{P}\mathrm{W}=\frac{1-P(T_i=1|Z_i)}{1-{\widehat{\pi }}_i}$ (Cole and Hernán2008). These weights were then used like survey weights in analyses.

Assessing Balance

Next, balance was assessed to confirm that the two exposure groups did not differ on the measured confounders after propensity score weighting. Balance was assessed before and after weighting by computing standardized effect sizes (i.e., mean differences) for the confounders between the exposure groups using the unadjusted and adjusted (i.e., weighted by the IPWs) samples. An absolute standardized effect size less than 0.2 is considered small and indicates balance has been achieved (Cohen 1988; Harder et al. 2010).

Conducting LCA with Covariates Using IPWs

The ACE of early sex on delinquency latent class membership was estimated using LCA with covariates, incorporating the IPWs as survey weights. Six items measuring different delinquent behaviors were included as indicators of adolescent delinquency latent classes, and gender was included as a grouping variable. Weighted LCA models of delinquency with one through six classes were compared. The size of the model was chosen based on the Akaike's information criterion (AIC; Akaike 1987), Bayesian information criterion (BIC; Schwartz 1978), consistent AIC (CAIC; Bozdogan 1987), adjusted BIC (a-BIC; Sclove 1987), and interpretability of the classes. Information criteria can be used to compare relative model fit for LCA models with different numbers of classes, and smaller values of these statistics indicate better balance between model fit and parsimony (Collins and Lanza 2010).

We then tested our assumption of measurement invariance in the selected model. In LCA, measurement invariance holds if the item-response probabilities (i.e., the conditional probabilities of reporting a particular delinquent behavior given class membership) are identical for all groups, providing the latent classes with identical interpretations across groups (Collins and Lanza 2010). In this study, after selecting the number of classes, a model with item-response probabilities constrained to be equal across gender (measurement-invariant model) was compared to a model with all parameters freely estimated (unrestricted model) based on the G² difference statistic, AIC, BIC, CAIC, a-BIC, and manual inspection of the differences in the item-response probabilities between groups. If these criteria favored the model with item-response probabilities constrained equal across gender, then measurement invari-ance could reasonably be assumed (Collins and Lanza 2010). The G² difference statistic is a sensitive test, especially when a large number of parameters (in this case, item-response probabilities) are included in equivalence sets, and the distribution of the G² test statistic is unknown when the degrees of freedom is large; therefore it is often useful to rely more on information criteria when testing for measurement invariance (Collins and Lanza 2010).

Early sex was then incorporated into the weighted model as a covariate to estimate its association with delinquency latent class membership (see Lanza et al. 2007 for details on LCA with a grouping variable and a covariate). The exponentiated logistic regression coefficient (odds ratio) from the weighted LCA with covariates model represented the estimate of the ACE of early sex on delinquency latent class membership.

To facilitate a comparison of the conclusions that may be drawn from each set of results, we also employed LCA with covariates without propensity score weighting, the standard approach to test for an association between early sex and delinquency latent class membership. Using the unweighted model, we tested whether the latent class prevalences differed by gender.¹ The G² difference statistic was used to compare the selected model with freely estimated latent class prevalences (unrestricted model) to the same model with latent class prevalences constrained to be equal across gender (restricted model). A significant value of the G² statistic indicates better fit for the unrestricted model (Collins and Lanza 2010).

Syntax for the propensity score analysis described herein appears in Appendix A in the ESM. Syntax used to estimate the outcome model, the causal effect of early sex on delinquency latent class membership, appears in Appendix B in the ESM. All LCA models were fit in SAS using PROC LCA version 1.2.7 (2011; Lanza et al. 2011).

Results

Propensity Score Analysis

There was sufficient overlap in the distribution of the propensity scores between the exposure groups (early sex group: mean=0.33, SD=0.18, minimum= 0.04, maximum=0.86; no early sex group: mean=0.15, SD=0.11, minimum=0.02, maximum=0.69), justifying the use of propensity score methods in this study. The estimated propensity scores were then used to calculate the IPWs (mean=0.95; SD=0.32; minimum=0.18; maximum=4.44). Table 1 shows the standardized effect sizes for the confounders based on the unadjusted and adjusted (weighted by the IPWs) data. Prior to propensity score adjustment, eight confounders had nontrivial (greater than 0.2) absolute standardized effect sizes, denoted by an asterisk. However, after propensity score adjustment the absolute standardized effect sizes were less than 0.2 for all potential confounders except for being missing on early menarche (0.23), indicating that balance was successfully achieved for most confounders.

The LCA Model

Next, the LCA model selection process was conducted incorporating the IPWs as survey weights. Table 2 shows the values of the information criteria, along with the entropy and percentage of 100 sets of random starting values that converged to the maximum-likelihood (ML) solution (solution %), for each model. This percentage was used to assess whether the LCA solution was adequately identified. The four-class model was the largest model that was adequately identified (35 %) and was selected based on (1) minimum CAIC; (2) relatively small AIC, BIC, and a-BIC; and (3) distinct, interpretable latent classes. We note that a four-class model was also selected using the unadjusted data.

Table 2. Fit statistics for different size latent class models of delinquency using inverse propensity weights.

Number of classes	df	G2	AIC	BIC	CAIC	a-BIC	Entropy	Solution %a
1	121	1,946.2	1,958.2	1,991.5	1,997.5	1,972.4	1.00	100
2	113	558.7	586.7	664.3	678.3	619.8	0.78	100
3	105	294.6	338.6	460.6	482.6	390.7	0.70	100
4	97	216.5	276.5	442.9	472.9	347.6	0.72	35
5	89	152.3	228.3	439.0	477.0	318.3	0.72	1
6	81	119.3	211.3	466.3	512.3	320.2	0.72	11

Note. The bold solution indicates the selected model

^aSolution % is the percentage of times the solution was selected out of 100 random sets of starting values

The interpretation of the four latent classes was similar for the unadjusted (standard approach) and adjusted models. The item-response probabilities are reported in Table 3. The non-delinquents class was characterized by low probabilities of reporting any delinquent behaviors. Members of the verbal antagonists class were likely to report lying to parents or guardians and behaving loud, rowdy, or unruly in a public place, but were unlikely to report the other behaviors. Members of the shoplifters class were likely to report stealing from a store and stealing items worth less than $50, in addition to the behaviors that characterized the verbal antagonists class. The general delinquents class was characterized by a moderate probability of reporting participating in a group fight and high probabilities of reporting all of the other delinquent behaviors.

Table 3. Item-response probabilities for four-class model of delinquency using inverse propensity weights.

	Non-delinquents	Verbal antagonists	Shoplifters	General delinquents
Lied to parents	0.37	0.76	0.84	0.84
Behaved rowdy	0.15	0.81	0.60	0.82
Stolen from a store	0.02	0.08	0.89	0.83
Stolen item worth<$50	0.01	0.00	0.75	0.83
Damaged property	0.00	0.25	0.13	0.61
Participated in group fight	0.04	0.24	0.05	0.43

Note. Item-response probabilities>0.50 appear in bold to facilitate interpretation

Although the G² difference statistic favored the unrestricted model (G²=132.6, df=24, p<0.0001) when testing for measurement invariance across gender, the BIC (442.9 measurement-invariant vs. 491.4 unrestricted) and CAIC (472.9 measurement-invariant vs. 545.4 unrestricted) favored the measurement-invariant model. Conducting model selection separately by gender, a four-class model fit best among males, consisting of all of the same classes as the measurement-invariant model for the full sample (non-delinquents, verbal antagonists, shoplifters, and general delinquents); among females the best fit model consisted of three classes (non-delinquents, verbal antagonists, and shoplifters), all of which were also present among males. This indicated that the main difference in latent class measurement across genders was the existence of a fourth class (general delinquents) among males that was not present among females. Therefore, the model with item-response probabilities constrained to be equal across gender was selected.

Using the unadjusted model, latent class prevalences differed across gender (G²=83.02, df=3, p<0.0001), with 44 % of males and 63 % of females in the non-delinquents class (G²=36.96, df=1, p<0.0001), 30 % of males and 20 % of females in the verbal antagonists class (G²=8.09, df=1, p=0.005), and 12 % of males and 1 % of females in the general delinquents class (G²=51.32, df=1, p<0.0001). With 15 % of males and 16 % of females, the prevalence of the Shoplifters class was not significantly different across gender (G²=0.03, df=1, p=0.86).

The Effect of Early Sex on Delinquency

Using unadjusted LCA with covariates (the standard approach), early sex was a significant predictor of delinquency class membership overall (p=0.02, twice log-likelihood difference=14.9, df=6; see Table 4). The nature of the association, however, differed across genders. Specifying non-delinquents as the reference class, we found that among females, early sex was significantly associated with 2.11 times greater odds of membership in the shoplifters class. Specifying general delinquents as the reference class, we found that among males, early sex was significantly associated with being less than half as likely (OR=0.43) to belong to the verbal antagonists class. However, after propensity score adjustment, the effect of early sex on later delinquency class membership was not significant (p=0.76, twice log-likelihood difference=3.3, df =6; see Table 4). Therefore, this study found no evidence of a causal effect of early sex on adolescent delinquency, suggesting an alternative explanation for the observed association between early sex and later delinquency.

Table 4. Odds ratios (ORs) and confidence intervals (CIs) for effect of early sex on delinquency before (unadjusted) and after (adjusted) applying inverse propensity weights.

Class	Standard analysis OR [CI] (p=0.02)		Causal analysis OR [CI] (p=0.76)
	Male	Female	Male	Female
Reference class: non-delinquents
Non-delinquents	REF	REF	REF	REF
Verbal antagonists	0.75 [0.37, 1.53]	1.49 [0.80, 2.79]	0.90 [0.47, 1.75]	1.40 [0.77, 2.53]
Shoplifters	0.85 [0.46, 1.54]	2.11 [1.25, 3.54]*	0.38 [0.00, 86.51]	1.38 [0.63, 3.01]
General delinquents	1.75 [0.78, 3.95]	–	1.40 [0.80, 2.47]	1.11 [0.08, 15.54]
Reference class: general delinquents
Non-delinquents	0.57 [0.25, 1.29]	–	0.71 [0.41, 1.26]	0.90 [0.06, 12.68]
Verbal antagonists	0.43 [0.19, 0.96]*	–	0.65 [0.33, 1.25]	1.26 [0.09, 17.12]
Shoplifters	0.48 [0.19, 1.24]	–	0.27 [0.00, 78.79]	1.25 [0.06, 27.88]
General delinquents	REF	REF	REF	REF

Note. REF indicates reference latent class, dashes indicate nearly empty comparison class, and therefore odds ratios cannot be reliably estimated

^*p<0.05 significant OR

Discussion

Causal Inference in Latent Class Analysis

This study demonstrates the integration of modern causal inference methods in LCA with covariates. Even when predictors temporally precede the outcome, coefficients in LCA with covariates can be interpreted only as associations. Propensity score weighting allows us to infer cause, assuming no unmeasured confounders. With recent popularity of LCA in behavioral research (e.g., Coffman et al. 2007; Henry and Muthén 2010), this approach sets the stage for examination of multivariate consequences of early risk exposure.

This approach is new in LCA, but the benefits of propensity score adjustment are well-documented. Incorporating the propensity score into LCA with covariates allows the researcher to easily control for many confounders at once (Stuart 2010). By removing selection bias due to the measured confounders, propensity score methods isolate the causal effect of the exposure on the outcome, and reduce the possibility that an observed association is due to the presence of measured confounders rather than a cause–effect relationship between the variables of interest (Rosenbaum and Rubin 1983). Propensity score methods involve checking that the exposure groups are balanced on measured confounders (i.e., no systematic differences remain) after the propensity scores are applied to the data, allowing the researcher to assess whether measured confounding is sufficiently eliminated (Austin 2011; Stuart 2010). In addition, this method facilitates checking the overlap of the distribution of the confounders by exposure group (via the propensity score distribution by exposure group) to avoid extrapolation (Austin 2011; Stuart 2010). Also, this method requires controlling for confounders (i.e., estimating the propensity score model) prior to including the outcome variable in the analysis, which prevents the outcome analysis from influencing the propensity score model (Austin 2011; Stuart 2010).

This approach requires that all confounders temporally precede the exposure, which in turn occurs prior to the latent class outcome. We were able to meet this requirement with a single wave of Add Health by carefully defining the variables. The confounders were primarily measures of constructs that would have occurred, and therefore been exerting their effects, early in life (e.g., maternal education), before sexual initiation would have occurred. In addition, the exposure was carefully constructed so that early sex (defined as sex prior to or at age 14) would have necessarily occurred before adolescent delinquency (measured in 11th or 12th grade for the previous 12-month period).

In addition to inverse propensity weighting, other methods for causal inference can be incorporated into LCA with covariates. In propensity score matching, each individual from the exposed group is “matched” with one or more individuals from the unexposed group with a similar propensity score; any individuals that do not receive a match are discarded from the sample, resulting in a new sample that is balanced on the measured confounders (Rosenbaum and Rubin 1985). Propensity score matching has recently been incorporated into LCA with covariates to estimate the causal effect of college enrollment on adult substance use patterns (for details, see Lanza et al. 2013). Another propensity score method, subclassification, involves creating subgroups of individuals with similar propensity score values, conducting an outcome analysis separately within each subgroup, and calculating a weighted average of the results across subgroups (Rosenbaum and Rubin 1984). Using this method with LCA can be impractical, however, because combining the results across subgroups requires assuming measurement invariance across subgroups, which may not be plausible if the subgroups differ considerably on the latent class outcome variable (see Lanza et al. 2013). Another way to estimate causal effects is using an instrumental variable, which is a randomly assigned variable that is associated with the exposure, but is only associated with the outcome via its association with the exposure (Angrist et al. 1996). The local ACE of the exposure on the outcome can be estimated by the ratio of the ACE of the instrumental variable on the outcome to the ACE of the instrumental variable on the exposure (for details, see Angrist et al. 1996). Instrumental variable methods for causal inference have not been used with LCA; this is an area for further research.

Implications for the Prevention of Adolescent Delinquency

This study presents an investigation of whether early sex, a risk factor for later adolescent delinquency, represents a plausible point of early intervention to reduce future delinquent behavior. We addressed the specific causal question, “What difference in adolescent delinquent behavior prevalence would we expect if every early adolescent in the U.S. population were to engage in early sex, compared to if every early adolescent were not to engage in early sex?” This study provides empirical evidence that, while early sex is significantly associated with later delinquent behavior patterns, if prevention scientists were able to prevent early sexual initiation, a subsequent reduction in the incidence of later delinquency may not result. In other words, early sexual behavior may not be an effective intervention target for reducing rates of adolescent delinquency. These results suggest that early sex and adolescent delinquency may have a common cause; the lack of balance on potential confounders prior to propensity score adjustment (see Table 1) suggests that early factors such as family structure, maternal education, and early risk behaviors may be common to both early sexual initiation and delinquency, and therefore may help to explain the association between these two constructs. This would indicate the need for multifaceted prevention programs that target multiple behaviors across time. Further research is needed to identify early predictors that are causally related to adolescent delinquency, so that programs can target the predictors that, if altered, will ultimately reduce adolescent delinquency.

Limitations

Reliable inference about the causal effect of a predictor assumes that all confounders are measured and included in the propensity score model (Rosenbaum and Rubin 1983). Fortunately, due to extensive literature on the topic, many predictors of early sex have been identified, including demographics (e.g., Jordahl and Lohman 2009; Longmore et al. 2009), economic factors (e.g., Jordahl and Lohman 2009; Paul et al. 2000), neighborhood factors (e.g., Longmore et al. 2009), family characteristics (e.g., Jordahl and Lohman 2009; Longmore et al. 2009), parental background (e.g., Jordahl and Lohman 2009; Paul et al. 2000), substance use (e.g., Longmore et al. 2009; Paul et al. 2000), and timing of puberty (e.g., Cavanagh 2004; Paul et al. 2000). Most known predictors of early sex were measured in the Add Health study, and therefore were included in the propensity score model. However, since the exposure was defined as sexual initiation prior to or at age 14 and the confounders must occur before the exposure, we could only include confounders that occurred at a young age, before sexual initiation could occur; unfortunately, there were no early life measures available for some predictors of early sex (e.g., peer factors), and so these confounders could not be included in analyses. Nevertheless, propensity score methods can reduce bias due to any unmeasured confounders that are correlated with the measured confounders, to the extent that they are correlated (Stuart 2010).

Use of propensity score methods also assumes no individual's potential outcome is affected by any other individual's exposure status (Rubin 1980). This assumption means that an individual's delinquency latent class given that he engaged in early sex is unaffected by whether anyone else engaged in early sex. A related assumption states that an individual's outcome if he had been exposed would be equal regardless of how he had been exposed (Rubin 1980). Here, this would mean that the effect of delaying sexual activity would be identical regardless of how it was delayed.

There are several limitations with the empirical study. First, participants of Add Health were only asked to report on vaginal, heterosexual behavior. Although early sex is a documented risk factor for later problem behavior (Armour and Haynie 2007; McCarthy and Casey 2008), it will be important to examine the causal effect of specific sexual behaviors in future work. Also, participants with missing data on either the exposure or all indicators of the outcome were deleted. The use of multiple imputation with LCA is not straightforward (Enders and Gottschall 2011), and further research in this area is needed. Fortunately, GBM does not require complete data on confounders. In behavioral research confounders often have the highest rates of missing data despite being first in temporal order; this is because sensitive items such as income are often included as confounders.

Conclusions

This study provides the first empirical demonstration of using a propensity score approach to identify potential causes of latent class membership. In the empirical demonstration, propensity score analysis was used to estimate the ACE of early sex on delinquency class membership, moderated by gender. Although early sex was associated with delinquency latent class membership based on a standard analysis (LCA with covariates), a causal analysis that fully accounted for observed confounders provides no evidence that early sex causes delinquency. The approach presented here is broadly applicable to research on the prevention of complex behavior patterns, and can be implemented with existing software.