Truth and Memory: Linking Instantaneous and Retrospective Self-Reported Cigarette Consumption

Abstract

Studies of smoking behavior commonly use the time-line follow-back (TLFB) method, or periodic retrospective recall, to gather data on daily cigarette consumption. TLFB is considered adequate for identifying periods of abstinence and lapse but not for measurement of daily cigarette consumption, thanks to substantial recall and digit preference biases. With the development of the hand-held electronic diary (ED), it has become possible to collect cigarette consumption data using ecological momentary assessment (EMA), or the instantaneous recording of each cigarette as it is smoked. EMA data, because they do not rely on retrospective recall, are thought to more accurately measure cigarette consumption. In this article we present an analysis of consumption data collected simultaneously by both methods from 236 active smokers in the pre-quit phase of a smoking cessation study. We define a statistical model that describes the genesis of the TLFB records as a two-stage process of mis-remembering and rounding, including fixed and random effects at each stage. We use Bayesian methods to estimate the model, and we evaluate its adequacy by studying histograms of imputed values of the latent remembered cigarette count. Our analysis suggests that both mis-remembering and heaping contribute substantially to the distortion of self-reported cigarette counts. Higher nicotine dependence, white ethnicity and male sex are associated with greater remembered smoking given the EMA count. The model is potentially useful in other applications where it is desirable to understand the process by which subjects remember and report true observations.

1. Introduction

A common technique for eliciting consumption in studies of substance abuse is the time-line follow-back (TLFB) method, in which one asks subjects to report daily consumption retrospectively over the preceding week, month or other designated period. In smoking cessation research, for example, TLFB is one important method for measuring cigarette consumption and defining periods of quit and lapse.

Although TLFB is a practical approach to quantifying average smoking behavior (Brown et al. 1998), TLFB data can harbor substantial errors as measures of daily consumption (Klesges et al. 1995). TLFB questionnaires request exact daily cigarette counts, which smokers are unlikely to remember, particularly after several days have passed. Moreover some smokers may understate consumption to avoid the social stigma attached to excessive smoking or an inability to quit (Boyd et al. 1998). Thus smoking cessation studies typically require validation of TLFB reports of zero consumption by biochemical measurement of exhaled carbon monoxide or nicotine metabolites from saliva or blood.

A second concern is that histograms of TLFB-derived daily cigarette counts commonly exhibit spikes at multiples of 20, 10 or even 5 cigarettes. This phenomenon, known as “digit preference” or “heaping”, is thought to reflect a tendency to report consumption in terms of packs (each pack in the US contains 20 cigarettes) or half or quarter packs. The heaps presumably arise because many smokers do not remember precisely how many cigarettes they smoked and therefore report their count rounded off to a nearby convenient number. It has also been hypothesized that some smokers consume exactly an integral number of packs per day as a self-rationing strategy (Farrell, Fry and Harris 2003), but evidence so far suggests that such behavior, if it exists, causes only a small fraction of the observed heaping (Wang and Heitjan 2008). Indeed, Klesges et al. (1995) observed that the distribution of biochemical residues of smoking is smooth, suggesting that heaping is a phenomenon of reporting rather than consumption.

Recall bias and heaping bias in self-reported longitudinal cigarette counts potentially affect estimates of both means and treatment effects. Moreover, heaping may lead to underestimation of within-subject variability, thanks to smokers who regularly report one pack rather than a precise count that varies around some mean in the vicinity of 20. If a large enough fraction of subjects in a study are of this kind, estimates of both within-subject and between-subject variability can be distorted.

Although there has been substantial research on statistical modeling of heaping and digit preference in a range of disciplines (Heitjan and Rubin 1990; Heitjan and Rubin 1991; Ridout and Morgan 1991; Pickering 1992; Klerman 1993; Torelli and Trivellato 1993; Dellaportas et al. 1996; Roberts and Brewer 2001; Wright and Bray 2003; Wolff and Augustin 2003), the only such application in smoking cessation research is that of Wang and Heitjan (2008), who described a latent-variable rounding model for heaped univariate TLFB cigarette count data. They postulated that the reported cigarette count is a function of the unobserved true count and a latent heaping behavior variable. The latter can take one of four values, representing exact reporting, rounding to the nearest 5, rounding to the nearest 10, and rounding to the nearest 20. Except for “exact” reporters (i.e., those who report counts not divisible by 5), one obtains at best partial information on the true count and the heaping behavior. They analyzed univariate count data from a smoking cessation clinical trial, assuming a zero-inflated negative binomial distribution for the true underlying counts together with an ordered categorical logistic selection model for heaping behavior given true count.

The analysis of Wang and Heitjan (2008) has three important limitations: First, they included only data from the last day of eight weeks of treatment, ignoring the 55 preceding days. Second, they assumed — without empirical verification — that reported counts not divisible by 5 were accurate. And third, they assumed that the preference for counts ending in 0 or 5 actually represented rounding rather than some other form of reporting error. That is, a declared count of 20 cigarettes was taken to mean that the true count was somewhere between 10 and 30 cigarettes, and was merely misreported as 20. In the absence of more accurate data on the true, underlying count, attempts to model heaping must rely on some such assumptions.

Precise assessment of smoking behavior has taken on increasing importance as researchers explore the value of reducing consumption as a way to lessen the harms of smoking (Shiffman et al. 2002, Hatsukami et al. 2002) and to improve the chance of ultimately quitting (Shiffman et al. 2009, Cheong et al. 2007). The advent of the inexpensive hand-held electronic diary (ED) that allows the instantaneous recording of ad libitum smoking has created the possibility of making much more accurate measurements. Such evaluation is an instance of ecological momentary assessment (EMA; Stone and Shiffman 1994), in that it generates records of events logged as they occur in real-life settings. In Shiffman (2009), researchers asked 236 participants in a smoking cessation study to use a specially programmed ED to record each cigarette as it was smoked over a 16-day pre-quit period; moreover the ED periodically prompted the smokers to record any cigarettes they had missed. At days 3, 8 and 15, subjects visited the clinic to complete a TLFB assessment of daily smoking since the preceding visit (2, 5 or 7 days previously), stating how many cigarettes they had smoked each day. The study found that while the TLFB data contained the expected heaps at multiples of 10 and 20, the EMA data had practically none. Average smoking rates from the two methods were moderately correlated (r = 0.77), but the within-subject correlation of daily consumption between TLFB and EMA was modest (r = 0.29). Self-report TLFB consumption was on average higher than EMA (by 2.5 cigarettes), but on 32% of days, subjects recorded more cigarettes by EMA than they later recalled by TLFB.

These data provide us with an opportunity — unprecedented, so far as we know — to study the relationship between self-reports of daily cigarette consumption by TLFB and EMA. To describe this relationship, we develop a statistical model with two components: The first is a regression that predicts the patient's notional “remembered” cigarette count (a latent factor) from the EMA count. The second is a regression that predicts the rounding behavior — described as in Wang and Heitjan (2008) with an ordinal logistic regression — from the remembered count and fully observed predictors. The models include random subject effects that describe the propensities of the subjects to mis-remember their actual consumption (in the first component) and to report the remembered consumption with a characteristic degree of accuracy (in the second). Assuming that EMA represents the true count, the first component of the model allows us to examine the recall bias resulting from mis-remembering, while the second component describes the heaped reporting errors.

2. Notation and model

Let Y_it denote the observed heaped TLFB consumption for subject i on day t, i = 1,…, n, t = 1,…, m_i, and let Y_i = (Y_i1,…, Y_imi)^T denote the vector of TLFB data for subject i. Let X_it be the EMA consumption on subject i, day t, and let X_i = (X_i1,…, X_imi)^T be the vector of EMA data for subject i. We furthermore let $Z_i=(Z_i^R,Z_i^H)$ be a vector of baseline predictors for subject i, with $Z_i^R$ representing predictors of recall and $Z_i^H$ predictors of heaping. These predictor sets may overlap.

2.1. A model for remembered cigarette count

The first part of our model assumes that for each day and subject there is a notional remembered cigarette count, denoted W_it(W_i = (W_i1, …, W_imi)^T). We assume W_it is distributed as Poisson conditionally on a random effect b_i, the EMA smoking pattern X_it and the covariate vector Z_i, with mean

$$\text{E}(W_{\mathit{\text{it}}}|X_{\mathit{\text{it}}},Z_i,b_i)=\text{exp}({\beta }_0+\text{ln}(X_{\mathit{\text{it}}}){\beta }_1+Z_i^R{\beta }_2+b_i).$$ (2.1)

The parameters β₁ and β₂ represent the effects of EMA consumption and baseline predictors, respectively, on the latent remembered count. The random effect b_i, which we assume normally distributed with mean 0 and variance ${\sigma }_b^2$, represents heterogeneity among subjects. We note that there are no 0 values of X_it in the Shiffman data, which are from a pre-quit study in which subjects were encouraged to smoke as normal. Thus we can include ln(X_it) as a predictor. In more general contexts where 0 EMA counts are possible, one can adjust the model in simple ways to avoid this problem. Moreover when excessive 0 counts occur in the TLFB data, one can fit a zero-inflated count model, as in Wang and Heitjan (2008), for the remembered count.

2.2. A model for the latent heaping process

Following Wang and Heitjan (2008), we assume that a latent rounding indicator G_it(G_i = (G_i1, …, G_imi)^T) dictates the degree of rounding to be applied to the notional remembered count W_it. Specifically, we let G_it take one of four possible values: G_it = 1 implies reporting the exact count, G_it = 2 implies rounding to the nearest multiple of 5, G_it = 3 implies rounding to the nearest multiple of 10, and G_it = 4 implies rounding to the nearest multiple of 20. We assume that the probability distribution of the heaping indicator depends on W_it, a subject-level random effect $u_i\sim N(0,{\sigma }_u^2)$ that is independent of b_i, and a baseline predictor vector $Z_i^H$. Specifically, we propose the following proportional odds model for the conditional distribution of G_it:

$$f(G_{\mathit{\text{it}}}|W_{\mathit{\text{it}}},Z_i,u_i)=\{\begin{array}{c}\begin{array}{l}1-q({\gamma }_1+{\eta }_{\mathit{\text{it}}}+u_i),\text{if}g=1;\hfill \\ q({\gamma }_1+{\eta }_{\mathit{\text{it}}}+u_i)-q({\gamma }_2+{\eta }_{\mathit{\text{it}}}+u_i),\text{if}g=2;\hfill \\ q({\gamma }_2+{\eta }_{\mathit{\text{it}}}+u_i)-q({\gamma }_3+{\eta }_{\mathit{\text{it}}}+u_i),\text{if}g=3;\hfill \\ q({\gamma }_3+{\eta }_{\mathit{\text{it}}}+u_i),\text{if}g=4.\hfill \end{array}\end{array}$$ (2.2)

Here ${\eta }_{\mathit{\text{it}}}=W_{\mathit{\text{it}}\gamma 0}+Z_i^H{\beta }_3$, and q(·) is the inverse logit function q(x) = exp(x)/(1 + exp(x)). The parameters γ₁ > γ₂ > γ₃ refer to the successive intercepts of the logistic regressions, γ₀ refers to its slope with respect to the remembered count, and β₃ refers to its slopes with respect to the vector of heaping predictors $Z_i^H$. The random effect u_i describes between-subject differences in heaping propensity not otherwise accounted for in the model.

2.3. The coarsening function

As in Wang and Heitjan (2008), the model links the observed Y_it to the latent W_it and G_it via the coarsening function h(·, ·):

$$Y_{\mathit{\text{it}}}=h(W_{\mathit{\text{it}}},G_{\mathit{\text{it}}}),i=1,\dots ,n,t=1,\dots ,m_i.$$

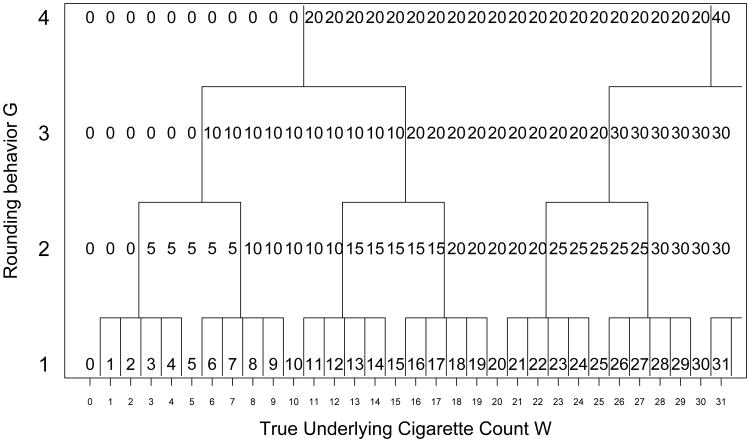
For example, at time t, subject i with W_it = 14 and G_it = 1 reports h(14, 1) = 14, whereas h(14, 2) = 15, h(14, 3) = 10, and h(14, 4) = 20. Figure 1 illustrates this heaping mechanism.

Fig 1.

Reported cigarette count Y as a function of the underlying count W and the rounding behavior G.

A coarsened outcome y_it may arise from possibly several (w_it, g_it) pairs. We denote the set of such pairs as WG(y_it) = {(w_it, g_it): y_it = h(w_it, g_it)}. For example, a reported consumption of y_it = 5 may represent a precise unrounded value ((w_it, g_it) = (5, 1)) or rounding across a range of nearby values ((w_it, g_it) ∈ {(3, 2), (4, 2), (5, 2), (6, 2), (7, 2)}). For subject i, the probability of the observed y_it at time t is the sum of the probabilities of the (w_it, g_it) pairs that would give rise to it. The density of reported consumption y_it given the random effects can therefore be expressed as

$$f(y_{\mathit{\text{it}}}|b_i,u_i)=\sum _{(w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}})}f(w_{\mathit{\text{it}}}|b_i)f(g_{\mathit{\text{it}}}|w_{\mathit{\text{it}}},u_i).$$

2.4. Estimation

We estimate the model by a Bayesian approach that employs importance sampling (Gelman et al. 2004; Tanner 1993) to avoid iterative simulation of parameters. The steps are as follows: We first compute the posterior mode and information using a quasi-Newton method with finite-difference derivatives (Dennis et al. 1983). We then approximate the posterior with a multivariate t₅ density with mean equal to the posterior mode and dispersion equal to the inverse of the posterior information matrix at the mode. Next, we draw a large number (4,000) of samples from this proposal distribution, at each draw computing the importance ratio r of the true posterior density to the proposal density. We then use sampling-importance resampling (SIR) to improve the approximation of the posterior (Gelman et al. 2004). We evaluate posterior moments by averaging functions of the simulated parameter draws with the importance ratios r as weights. The choice of a t with a small number of degrees of freedom as the importance density is intended to balance the convergence of the MC integrals and the efficiency of the simulation.

Letting θ = (β₀, β₁, β₂, β₃, σ_b, γ₁, γ₂, γ₃, γ₀, σ_u), the likelihood contribution from subject i is

$$L(\theta ;y_i)=\int \int \prod _{t=1}^{m_i}\sum _{(w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}})}f(w_{\mathit{\text{it}}}|b_i)f(g_{\mathit{\text{it}}}|w_{\mathit{\text{it}}},u_i)f(b_i)f(u_i)d{b}_{i}d{u}_i;$$ (2.3)

we approximate the integral in (2.3) by Gaussian quadrature. We choose proper but vague priors for the parameters, which we assume are a priori independent (except for γ_j, j = 1, 2, 3, as noted below). The parameter β₁ in the Poisson mixed model (2.1), representing the slope of the latent recall on the EMA recorded consumption, is given a normal prior β₁ ∼ N(1, 10²), whereas the priors of the other regression parameters in both model parts are set to N(0, 10²) subject to the constraint γ₁ > γ₂ > γ₃. We assign the random-effect variances inverse-gamma priors with mean and SD both equal to 1, a reasonably vague specification (Carlin and Louis, 2000). We obtain the posterior mode and information using SAS PROC NLMIXED, and implement Bayesian importance sampling in R.

3. Model checking

With heaped data, the unavailability of simple graphical diagnostics such as residual plots complicates model evaluation. We therefore resort to examination of repeated draws of latent quantities from their posterior distributions, in the spirit of Bayesian posterior predictive checks (Rubin 1984; Gelman et al. 1996; Gelman et al. 2005). Specifically, we evaluate the adequacy of model assumptions using imputed values of the latent recall W, which we compare to its implied marginal distribution under the model.

Imputations of latent W_i and G_i are ultimately based on the posterior density f(θ|y_i) of the model parameter θ given the observed data y_i. Heitjan and Rubin (1990), sampling univariate y values, used an acceptance-rejection procedure to draw quantities analogous to our W and G from a confined bivariate normal distribution. In our model, the correlation within W_i and G_i vectors poses a challenge to simulation. Note however that given the subject-specific effects b_i and u_i, the components of W_i and G_i are independent. Thus, we can readily simulate (W_i, G_i) from the joint posterior of (W_i, G_i, b_i, u_i). For each simulated θ and the observed data y_i, the posterior distribution of (W_i, G_i, b_i, u_i) is

$$f(w_i,g_i,b_i,u_i|y_i,\theta )=f(w_i,g_i,b_i,u_i|\theta )\frac{f(y_i|w_i,g_i,b_i,u_i,\theta )}{f(y_i|\theta )}$$

Because the values of w_it and g_it together determine y_it, we have that

$$f(y_i|w_i,g_i,b_i,u_i,\theta )=\prod _{t=1}^{m_i}I((w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}})),$$

where I is an indicator function. Accordingly,

$$f(w_i,g_i,b_i,u_i|y_i,\theta )\propto f(w_i,g_i,b_i,u_i|\theta )\prod _{t=1}^{m_i}I((w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}}))=f(w_i,g_i|b_i,u_i,\theta )f(b_i,u_i|\theta )\prod _{t=1}^{m_i}I((w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}}))=f(w_i|b_i,\theta )f(g_i|w_i,u_i,\theta )f(b_i,u_i|\theta )\prod _{t=1}^{m_i}I((w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}}))=(\prod _{t=1}^{m_i}f(w_{\mathit{\text{it}}}|b_i,\theta )f(g_{\mathit{\text{it}}}|w_{\mathit{\text{it}}},u_i,\theta )I((w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}})))\cdot f(b_i|{\sigma }_b)f(u_i|{\sigma }_u).$$

Thus given random effects b_i and u_i, the imputation of (w_i, g_i) is obtained by independent draws of (w_it, g_it), t = 1,…,m_i, which can be implemented as an acceptance-rejection procedure. We therefore impute the data as follows:

1. Make independent draws, θ^(k), k = 1,…,K from f(θ|y_i) by SIR.

2. Given θ^(k), for i = 1,…, n, independently draw $b_i^{(k)}\sim N(0,{\sigma }_b^{(k)2})$ and $u_i^{(k)}\sim N(0,{\sigma }_u^{(k)2}).$.

3. For i = 1,…, n, given θ^(k) and $b_i^{(k)}$, for t = 1,…, m_i, draw $w_{\mathit{\text{it}}}^{(k)}$ as Poisson with mean (2.1). Then given θ^(k), $u_i^{(k)}$ and $w_{\mathit{\text{it}}}^{(k)}$, draw misreporting type $g_{\mathit{\text{it}}}^{(k)}$ from (2.2). If $I((w_{\mathit{\text{it}}}^{(k)},g_{\mathit{\text{it}}}^{(k)})\in \text{WG}(y_{\mathit{\text{it}}}))=0$, discard $(w_{\mathit{\text{it}}}^{(k)},g_{\mathit{\text{it}}}^{(k)})$ and repeat this step until $I((w_{\mathit{\text{it}}}^{(k)},g_{\mathit{\text{it}}}^{(k)})\in \text{WG}(y_{\mathit{\text{it}}}))=1$.

To assess model fit, we plot K histograms of the imputed latent count ω. Implausible patterns in these histograms, such as peaks or troughs at multiples of 5, suggest incorrect modeling of the heaping. We can also base discrepancy diagnostics specifically on the fractions of reported consumptions that are divisible by 5.

4. Simulations

To examine the performance of our approach, we conducted simulations replicating the structure of the Shiffman data with m = 12 non-visit-day observations per subject. Each data set consisted of n = 100 subjects, and for simplicity we do not consider baseline covariates. For each subject we first set x_i as an observed EMA count vector from the data and generated a random effect $b_i\sim N(0,{\sigma }_b^2=0.09)$. We then generated W_it values as independent Poisson deviates with conditional mean (2.1). With β₀ = 2.358, β₁ = 0.2628, when b_i = 0 and EMA count x_it = 20, the mean latent recall is 23.2, and when x_it = 30 it is 25.8. With the random effect distributed as designated above, the marginal mean recalls for x_it = 20 and x_it = 30 are 24.3 and 27.0, respectively.

Next we generated the latent heaping behavior indicator G_it from (2.2). We set the parameters to their estimates from the Shiffman data: The intercepts γ₁, γ₂, γ₃ were −1.485, −5.280 and −10.141, respectively, and the slope γ₀ was 0.1098. We simulated the random effect $u_i\sim N(0,{\sigma }_u^2=7.1)$. Under this setting, when u_i = 0 and w_it = 22, the probability of exact reporting is 28.3%, and the probabilities of rounding to the nearest multiples of 5, 10 and 20 are 66.3%, 5.4% and 0.04%, respectively. When the latent count w_it = 36, these probabilities are 7.8%, 71.2%, 20.8% and 0.2%, respectively. The simulated latent w_it and g_it determined y_it as illustrated in Figure 1.

These parameter values allow for considerable discrepancy between remembered and recorded consumption. To examine our methods when the latent recall and EMA match more closely, we conducted a second simulation under parameter values that gave better agreement. In this scenario, we assumed β₀ = 0 and β₁ = 1 with b_i ∼ N(0, 0.05). Thus when b_i = 0, the expected precise recall E(w_it) = x_it, and the marginal mean recalls are 20.5 and 30.8 for EMA counts of 20 and 30, respectively. We set the parameters in the heaping behavior models at −1.07, −4.37, −6.52 and 0.088 for γ₁, γ₂, γ₃ and γ₀, respectively, and ${\sigma }_u^2=5.9$. In this case,when u_it = 0, the probabilities of reporting exactly and to the nearest multiples of 5, 10 and 20 for a true count of 22 are 29.6%, 62.3%, 7.1% and 1%, respectively.

Table 1 presents summaries of 100 simulations of estimates of the parameter θ = (β₀, β₁, σ_b, γ₁, γ₂, γ₃, γ₀, σ_u). Under both scenarios, the MLEs of the fixed-effect coefficients fell near the true values on average, with no more than 0.5% bias for the parameters in the recall model and no more than 2.7% bias for those in the heaping model. The random effects variance estimates are also well estimated, with bias less than 1%. The coverage probabilities of nominal 95% confidence intervals range from 93% to 98%, except for γ₃ in Case 1, where coverage is only 80%. The poor coverage rate for this parameter is a consequence of instability in the inverse Hessian matrix; it can be improved by creating parametric bootstrap confidence intervals (Table 2). The simulation shows good performance of the MLEs, and as the sample size is large we expect the Bayesian estimates to behave similarly. Moreover, the maximization part of the MLE calculation can help identify multimodality of the likelihood, should it occur, and singularity of the Hessian that we use in the Bayesian sampling.

Table 1.

Results of 100 simulations of the mis-remembering/heaping model.

Parameter	True value	Mean of estimate	SD of estimate	Bias	$\sqrt{\text{MSE}}$	Coverage of 95% CI(%)
Case 1: Estimated mis-remembering
Latent recall
β0	2.36	2.36	0.07	0.002	0.07	95
β1	0.26	0.26	0.02	0.001	0.02	93
σb	0.30	0.30	0.02	0.001	0.02	95
Heaping behavior
γ1	−1.49	−1.53	0.56	−0.04	0.56	94
γ2	−5.28	−5.31	0.66	−0.03	0.66	98
γ3	−10.14	−9.99	2.55	0.15	2.54	80
γ0	0.11	0.11	0.02	0.002	0.02	96
σu	2.67	2.61	0.29	−0.06	0.29	98
Case 2: Minimal mis-remembering
Latent recall
β0	0.0	−0.01	0.09	−0.01	0.09	94
β1	1.0	1.00	0.03	0.005	0.03	94
σb	0.22	0.22	0.02	−0.001	0.02	97
Heaping behavior
γ1	−1.07	−1.08	0.43	−0.007	0.43	98
γ2	−4.37	−4.36	0.60	0.007	0.59	94
γ3	−6.52	−6.43	0.66	0.09	0.67	94
γ0	0.088	0.090	0.02	0.002	0.02	95
σu	2.44	2.41	0.27	−0.02	0.27	95

Table 2.

Results of 100 simulations of the mis-remembering/heaping model with parameters estimated from the data (Case 1) and SEs computed by the parametric bootstrap.

Parameter	True value	Mean of estimate	SD of estimate	Bias	$\sqrt{\text{MSE}}$	Coverage of 95% CI(%)
Latent recall
β0	2.36	2.36	0.08	−0.003	0.08	90
β1	0.26	0.26	0.02	0.001	0.02	90
σb	0.30	0.30	0.02	−0.001	0.02	95
Heaping behavior
γ1	−1.49	−1.61	0.55	−0.12	0.56	94
γ2	−5.28	−5.42	0.69	−0.14	0.70	96
γ3	−10.14	−10.61	3.56	−0.47	3.58	87
γ0	0.11	0.11	0.02	0.005	0.02	95
σu	2.67	2.64	0.32	−0.03	0.32	92

5. Data analysis

We applied the method of §2 to the Shiffman data, with the aim of evaluating our posited two-stage process as an explanation for the discrepancy between actual and reported consumption. To focus on the link between the self-report and true count, our first analysis included only log EMA count in (2.1) and a visit day indicator in (2.2). The latter is important because it seems reasonable that distance in time from the event would be a strong predictor of heaping coarseness. Our second analysis expanded the recall model to include a range of baseline characteristics: demographics (age, sex, race and education); addiction; measures of nicotine dependence (the Fagerströom Test for Nicotine Dependence [FTND] and the Nicotine Dependence Syndrome Scale [NDSS]); and EMA compliance measured as the daily percentage of missed prompts. Age, education, FTND, and EMA compliance are considered as quantitative variables, sex and race are binary indicators, and addiction is a categorical variable taking three levels (possible, probable, and definite). They are the first variables that a smoking researcher would think to investigate, and could potentially affect remembered count or heaping probability. The two measures of nicotine dependence FTND and NDSS showed only a modest correlation, with Spearman r = 0.56 in our data. So we considered both in the model. The dataset and programming code are included in the supplementary materials (Wang et al. 2012).

5.1. Evaluating goodness of fit

We evaluated model fit by creating multiple draws from the posterior predictive distribution of latent quantities as discussed in §3. Lack of smoothness in the histogram of the imputed latent count would suggest an inadequate heaping model.

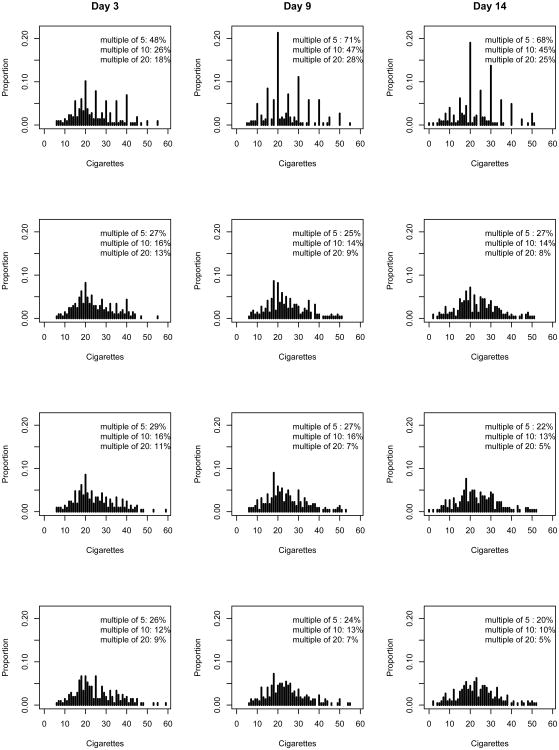
We evaluated goodness of fit for the model that includes log EMA count in (2.1) and a visit day indicator in (2.2).The top row in Figure 2 displays the histograms of TLFB cigarette consumption at Days 3 (a visit day), 9 and 14. The spikes at 10, 15, 20, 25, 30, etc. are characteristic of self-reported cigarette counts (Wang and Heitjan 2008). As many as 70% of subjects reported cigarette smoking in multiples of 5 for non-visit-day consumption, whereas for the visit day (Day 3) that number is only 48%. Only 1/4 of the counts on the visit day ended in 0.

Fig 2.

Top row: Histogram of self-reported cigarette consumption. Lower three rows: Histograms of draws from the posterior distribution of the latent exact consumption recall.

The next three rows represent independent draws of the latent count W_it. The spikes at multiples of 20, 10 or 5 have disappeared. Compared to the selfreported count, the percentage of subjects whose exact counts are divisible by 5 (or 10 or 20) is smaller and consistent across time. Averaged over three imputations, the fraction of counts ending in multiples of 5 is 27%, 25%, 23% on Days 3, 9 and 14, respectively, and 15%, 14% and 12% end in multiples of 10. These checks indicate that our model offers a plausible explanation for the heaping.

5.2. The fitted model

In order to assess the impact of the assumed correlation structure, we fit the model as proposed in (2.1) and (2.2) and also a model that exclude random effects. Posterior modes and 95% credible intervals (CIs) appear in Tables 3 and 4. The estimates in both the remembered count model that characterizes the latent recall process and the heaping behavior model are sensitive to the assumption of random effects. The Bayesian information criterion (BIC) of the model with two random effects is 14,705 when including EMA as the only predictor and 14,059 when including EMA and the baseline patient characteristic predictors. The BICs for the corresponding models excluding random effects are 18,340 and 16,641, respectively. Thus the evidence is overwhelming that the mixed model is preferable. Furthermore, we included the patient characteristic predictors as covariates in both the remembered count model and heaping process model, but this model (BIC = 14,079) is less favorable compared to the model with the covariates in just the latent remembered count model. None of these predictors is significant in the heaping process model (results not shown).

Table 3.

Estimated parameters from the Shiffman data under simple models for recall (EMA only) and heaping (remembered count and visit day indicator).

	Random Effects Model		Independence Model
Parameter	Posterior mode	95% CI	Posterior mode	95% CI
Latent recall: Poisson model
Intercept: β0	2.32	[2.24, 2.40]	1.14	[1.09, 1.20]
ln(EMA): β1	0.27	[0.25, 0.30]	0.68	[0.66, 0.69]
${\sigma }_b^2$	0.09	[0.08, 0.11]
Heaping behavior: Proportional odds model
Intercept 1: γ1	−1.50	[−2.17, −0.85]	−1.06	[−1.30, −0.84]
Intercept 2: γ2	−5.21	[−6.14, −4.43]	−2.94	[−3.26, −2.65]
Intercept 3: γ3	−10.15	[−12.49, −8.48]	−4.17	[−4.59, −3.82]
Exact count (latent): w	0.11	[0.09, 0.13]	0.07	[0.06, 0.08]
Visit day	−2.96	[−3.50, −2.50]	−1.29	[−1.54, −1.06]
${\sigma }_u^2$	6.65	[5.12, 9.08]

Table 4.

Estimated parameters from the Shiffman data under an expanded model for recall.

	Random Effects Model		Independence Model
Parameter	Posterior mode	95% CI	Posterior mode	95% CI
Latent recall: Poisson model
Intercept: β0	2.34	[2.21, 2.49]	1.51	[1.44, 1.58]
ln(EMA): β1	0.25	[0.23, 0.28]	0.53	[0.51, 0.55]
Addicted
Possible vs. Definite	0.07	[−0.10, 0.24]	0.05	[0.01, 0.09]
Probable vs. Definite	−0.01	[−0.11, 0.08]	−0.02	[−0.04, 0.006]
FTND	0.06	[0.04, 0.08]	0.04	[0.03, 0.05]
NDSS	0.08	[0.05, 0.12]	0.05	[0.04, 0.06]
EMA compliance	0.13	[−0.28, 0.51]	0.39	[0.29, 0.49]
Age	0.002	[−0.001, 0.006]	0.003	[0.002, 0.004]
Race (Black vs. White)	−0.14	[−0.27, −0.01]	−0.06	[−0.10, −0.03]
Sex (Male vs. Female)	0.16	[0.10, 0.23]	0.12	[0.09, 0.23]
Education	−0.001	[−0.03, 0.02]	0.003	[−0.004, 0.009]
${\sigma }_b^2$	0.06	[0.05, 0.07]
Heaping behavior: Proportional odds model
Intercept 1: γ1	−1.62	[−2.35, −0.90]	−1.14	[−1.37, −0.91]
Intercept 2: γ2	−5.52	[−6.42, −4.61]	−3.15	[−3.47, −2.82]
Intercept 3: γ3	−10.31	[−12.65, −8.37]	−4.54	[−4.99, −4.08]
Exact count: w	0.11	[0.09, 0.14]	0.07	[0.06, 0.08]
Visit day	−2.99	[−3.51, −2.47]	−1.26	[−1.50, −1.02]
${\sigma }_u^2$	6.79	[4.73, 8.68]

The 95% CI of β₁ is [0.23,0.28], indicating that remembered consumption is positively associated with recorded EMA consumption. In addition, baseline patient characteristics FTND, NDSS, race and gender have significant effects on the recall process. For fixed EMA count, the following characteristics are associated with greater remembered smoking: higher nicotine dependence (measured by both FTND and NDSS), white ethnicity (compared to black), and male sex.

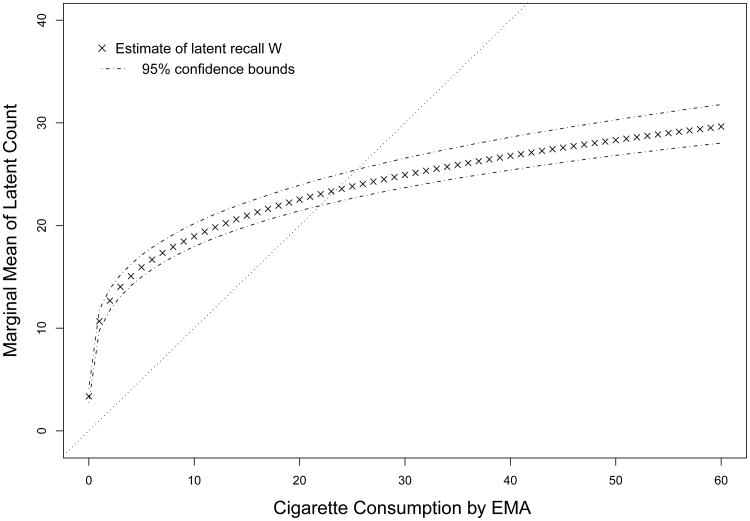
Figure 3 displays the estimated curve of the mean of W_it against the EMA count. A natural hypothesis is that the estimated latent mean agrees with EMA, which would be reflected in the Poisson model by an estimated intercept of 0 and slope of 1; one might call this a model of unbiased memory. To the contrary, Figure 3 shows that the fitted mean curve diverges substantially from the 45° line, with the lighter smokers on average overestimating their consumption and the heavier smokers underestimating consumption. The mean remembered consumption agrees with the true count roughly in the range 22–26 cigarettes, or slightly more than a pack per day.

Fig 3.

Estimate of the conditional mean of recalled count given EMA count in the Poisson mis-remembering model. Covariates are fixed at education=high school, addicted=definitely, race=white, sex=female, and mean values of the quantitative predictors: FTND=5.97, NDSS=−0.023, age=43.5, and EMA non-compliance=10.1%.

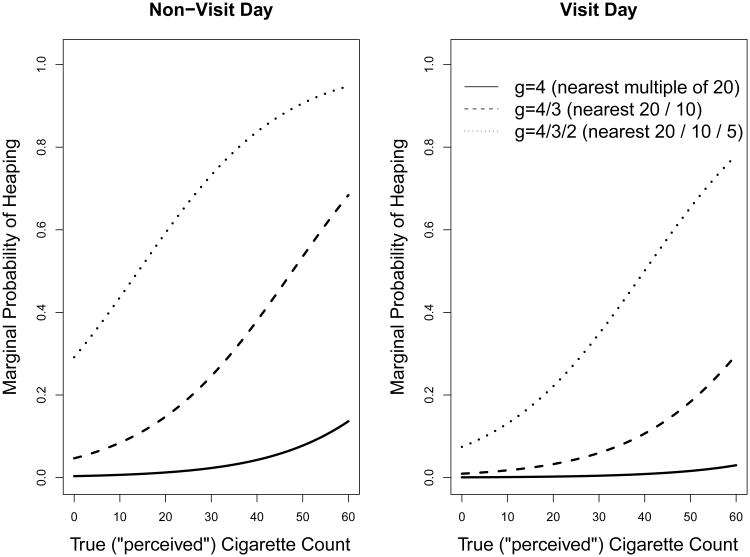
Figure 4 shows the estimated heaping probability as a function of remembered cigarette consumption for visit and non-visit days. The possibility of rounded-off reporting increases rapidly as the remembered count increases, although surprisingly the probability of rounding to the nearest 20 is not large for either type of day. When the perception of smoking is more than two packs, say 41 cigarettes, the chance of heaped reporting rises to more than 84%, of which 37% is attributed to half-pack rounding. The results confirm that the degree of heaping is much smaller on visit days. For example, only 51% of subjects round off the visit-day count when reporting 41 cigarettes, and among those 39% round off to the nearest multiple of 5.

Fig 4.

Estimated rounding behavior given EMA count in the proportional odds heaping model.

6. Discussion

We have developed a model to describe the process whereby exact longitudinal measurements become distorted by retrospective recall. Our approach uses latent processes to explain the data as a result of mis-remembering and rounding: A model of the latent exact value describes subject-level recall and allows for association over time and with baseline predictors, while a misreporting model describes the dependence of heaping coarseness on the latent value and other predictors. Random effects represent individual propensities in recall and heaping; in our data, inferences depend strongly on the inclusion of these random effects.

The data suggest that both mis-remembering and heaping contribute substantially to the distortion of cigarette counts. The curve of mean remembered count as a function of EMA count departs markedly from the 45° line, with lighter smokers overstating consumption and heavier smokers understating consumption. The remembered smoking coincides with the accurate EMA count at around 24 cigarettes, suggesting that the popularity of reporting one pack per day is partially a result of the general heaping behavior rather than a particular affinity for remembering a pack a day. The curves of heaping probabilities suggest that exact reporting is uncommon and practically disappears beyond about 40 cigarettes/day. Nevertheless it is interesting just how much of the misreporting is due to mis-remembering. The remembered cigarette consumption depends not only on true consumption, but also on the subject's sex, race and degree of nicotine dependence.

The interpretation of our model components as representing memory and rounding depends on the assumption that EMA data are exact. Of course, even EMA data are subject to errors, as smokers may neglect to record cigarettes both at the time of smoking and later. Yet good correspondence with smoking biomarkers strongly supports the use of EMA over TLFB as a proxy for the truth (Shiffman 2009).

We have implemented our model with a combination of standard numerical methods including Gaussian quadrature, quasi–Newton optimization, and sampling-importance resampling. Our experience suggests that with the model as specified, and incorporating a modest numbers of predictors, the method is robust and efficient. Increasing the number of random effects would increase the time demands (from the numerical integration) and raise the possibility of numerical instability (from possible errors in integration). For more extensive models, sophisticated approaches based on MCMC sampling would be necessary.

Our model allows for the inclusion of covariates to better explain the discrepancy between smokers' self-perceived behaviors and reality. It also provides a basis for predicting true counts (effectively the EMA data) from reported TLFB counts. This would be a valuable activity in the large number of studies that do not collect EMA data. To predict true counts from the recalled counts, we first need to estimate the parameters θ in the model using a subset of the primary study or an external independent study that collects both TLFB count Y and accurate EMA count X. Then we can impute the true count together with the latent remembered count and heaped reporting behavior. Specifically, the posterior distribution of (W_i, G_i, x_i, b_i, u_i) is

$$f(w_i,g_i,x_i,b_i,u_i|y_i,\theta )=f(w_i,g_i,x_i,b_i,u_i|\theta )\frac{f(y_i|w_i,g_i,x_i,b_i,u_i,\theta )}{f(y_i|\theta )}\propto (\prod _{t=1}^{m_i}f(w_{\mathit{\text{it}}}|x_{\mathit{\text{it}}},b_i,\theta )f(g_{\mathit{\text{it}}}|w_{\mathit{\text{it}}},u_i,\theta )I((w_{\mathit{\text{it}}},g_{\mathit{\text{it}}})\in \text{WG}(y_{\mathit{\text{it}}})))\cdot f(x_i)f(b_i|{\sigma }_b)f(u_i|{\sigma }_u).$$

where f(x_i) is the density function of the true count. Imputation follows similar steps as described in §3 with θ set equal to the maximum likelihood estimates.

The methods developed here also can have application in a wide variety of settings in social and medical science involving self-reported data — for example, assessing sexual risk behavior, trial drug consumption, eating episodes and financial expenditures.