Eigenvector synchronization, graph rigidity and the molecule problem

Abstract

The graph realization problem has received a great deal of attention in recent years, due to its importance in applications such as wireless sensor networks and structural biology. In this paper, we extend the previous work and propose the 3D-As-Synchronized-As-Possible (3D-ASAP) algorithm, for the graph realization problem in ℝ³, given a sparse and noisy set of distance measurements. 3D-ASAP is a divide and conquer, non-incremental and non-iterative algorithm, which integrates local distance information into a global structure determination. Our approach starts with identifying, for every node, a subgraph of its 1-hop neighborhood graph, which can be accurately embedded in its own coordinate system. In the noise-free case, the computed coordinates of the sensors in each patch must agree with their global positioning up to some unknown rigid motion, that is, up to translation, rotation and possibly reflection. In other words, to every patch, there corresponds an element of the Euclidean group, Euc(3), of rigid transformations in ℝ³, and the goal was to estimate the group elements that will properly align all the patches in a globally consistent way. Furthermore, 3D-ASAP successfully incorporates information specific to the molecule problem in structural biology, in particular information on known substructures and their orientation. In addition, we also propose 3D-spectral-partitioning (SP)-ASAP, a faster version of 3D-ASAP, which uses a spectral partitioning algorithm as a pre-processing step for dividing the initial graph into smaller subgraphs. Our extensive numerical simulations show that 3D-ASAP and 3D-SP-ASAP are very robust to high levels of noise in the measured distances and to sparse connectivity in the measurement graph, and compare favorably with similar state-of-the-art localization algorithms.

1. Introduction

In the graph realization problem, one is given a graph G =(V, E) consisting of a set of |V| = n nodes and |E| = m edges, together with a non-negative distance measurement d_ij associated with each edge, and is asked to compute a realization of G in the Euclidean space ℝ^d for a given dimension d. In other words, for any pair of adjacent nodes i and j, (i, j) ∈ E, the distance d_ij =d_ji is available, and the goal is to find a d-dimensional embedding p₁, p₂,…, p_n ∈ ℝ^d such that ∥p_i − p_j∥=d_ij, for all (i, j) ∈ E.

Owing to its practical significance, the graph realization problem has attracted a lot of attention in recent years, across many communities. The problem and its variants come up naturally in a variety of settings such as wireless sensor networks [10, 54], structural biology [32], dimensionality reduction, Euclidean ball packing and multidimensional scaling (MDS) [20]. In such real-world applications, the given distances d_ij between adjacent nodes are not accurate, d_ij =∥p_i − p_j∥ + ε_ij, where ε_ij represents the added noise, and the goal was to find an embedding that realizes all known distances d_ij as best as possible.

The classical MDS yields an easy solution to the graph realization problem provided that all n(n − 1)/2 pairwise distances are known. Unfortunately, whenever most of distance constraints are missing, as it is typically the case in real applications, the problem becomes significantly more challenging because the rank-d constraint on the solution is not convex. Note that for a fixed embedding, all pairwise distances are invariant to rigid transformations, i.e., compositions of rotations, translations and possibly reflections. Whenever an embedding exists, we say that it is unique (up to rigid transformations) only if there are enough distance constraints, in which case the graph is said to be globally rigid (see, e.g., [31]). The graph realization problem is strongly NP-complete in one dimension, and strongly NP-hard for higher dimensions [45, 60]. Despite its difficulty, there exist many approximation algorithms for the graph realization problem, many of which come from the sensor networks community [2, 4, 5, 37], and rely on methods such as global optimization [15], semidefinite programming (SDP) [10, 11, 14, 51, 52, 62] and local to global approaches [41, 43, 46, 48, 61].

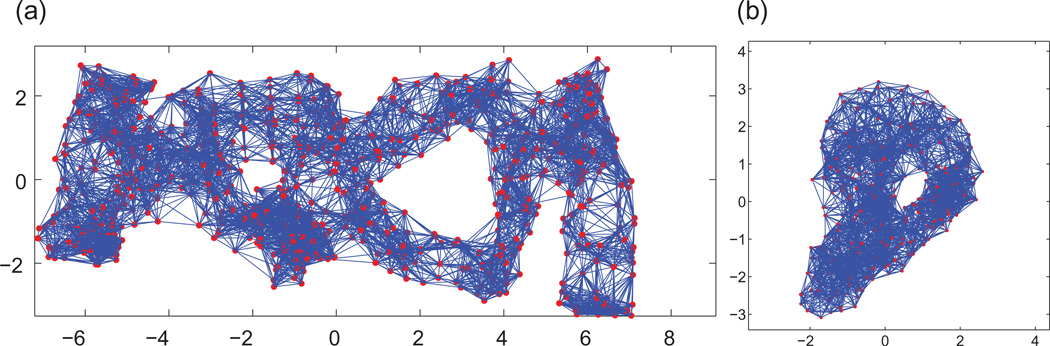
In typical real applications, the available measurements follow a geometric graph model where distances between pairs of nodes are available if and only if they are within sensing radius ρ of each other, i.e., (i, j) ∈ E ⇔ d_ij ≤ ρ. In Fig. 1, we illustrate with an example the measurement graph associated to a dataset of 500 nodes, with a sensing radius of (ρ) 0.092 and an average degree (deg) of 18, i.e., each node knows, on average, the distance to its 18 closest neighbors. It was shown in [4] that the graph realization problem remains NP-hard even under the geometric graph model.

Fig. 1.

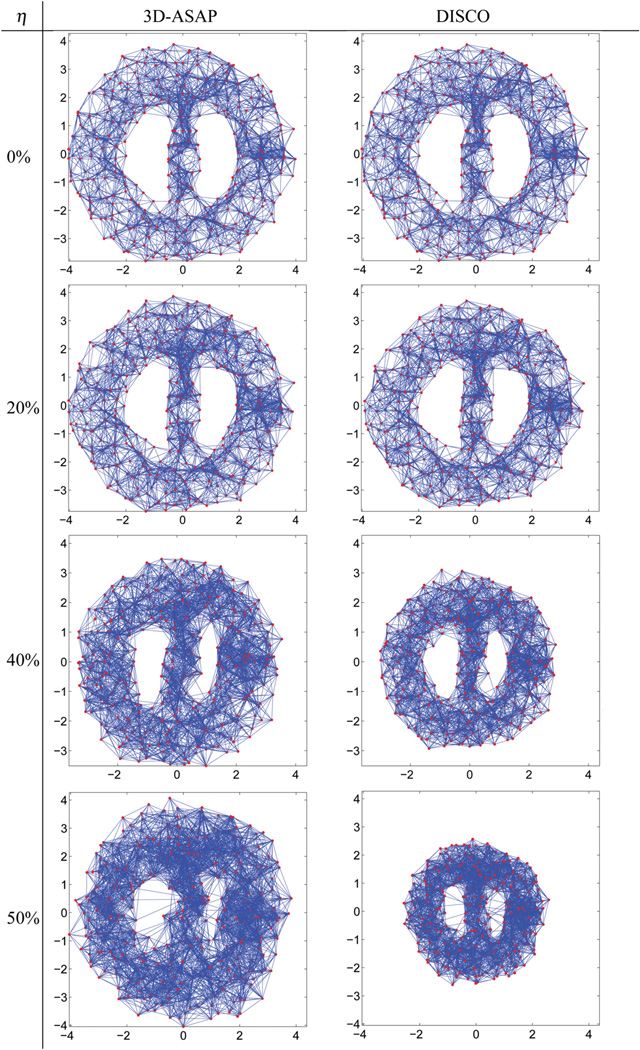
2D view of the BRIDGE-DONUT dataset, a cloud of n=500 points in ℝ³ in the shape of a donut (left), and the associated measurement geometric graph of radius (ρ) =0.92 and average degree (deg)=18 (right).

The graph realization problem in ℝ³ is of particular importance because it arises naturally in the application of nuclear magnetic resonance (NMR) to structural biology. NMR spectroscopy is a well-established modality for atomic structure determination, especially for relatively small proteins (i.e., with atomic mass <40 kDa) [59], and contributes to progress in structural genomics [1]. General properties of proteins such as bond lengths and angles can be translated into accurate distance constraints. In addition, peaks in the NOESY experiments are used to infer spatial proximity information between pairs of nearby hydrogen atoms, typically in the range of 1.8–6 Å. The intensity of such NOESY peaks is approximately proportional to the distance to the minus sixth power, and it is thus used to infer the distance information between pairs of hydrogen atoms nuclear overhauser effects (NOEs). Unfortunately, NOEs provide only a rough estimate of the true distance, and hence the need for robust algorithms that are able to provide accurate reconstructions even at high levels of noise in the NOE data. In addition, the experimental data often contains potential constraints that are ambiguous, because of signal overlap resulting in incomplete assignment [44]. The structure calculation based on the entire set of distance constraints, both accurate measurements and NOE measurements, can be thought of as an instance of the graph realization problem in ℝ³ with noisy data.

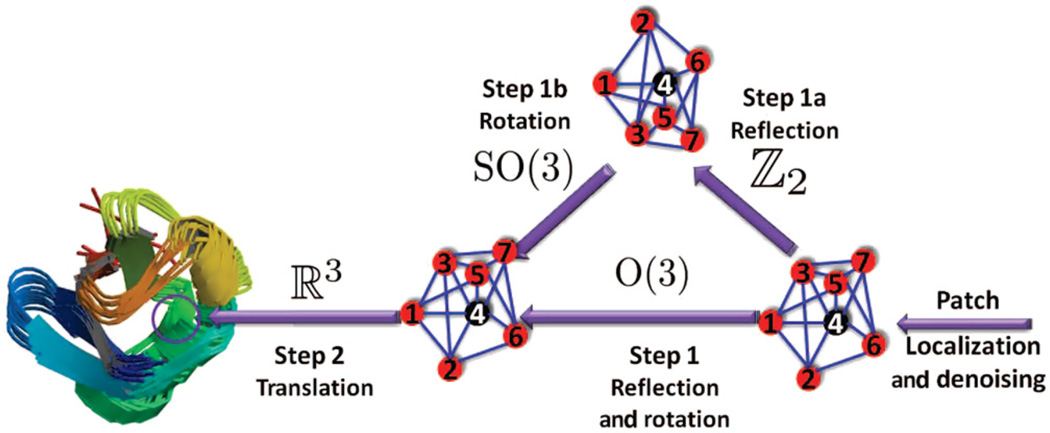
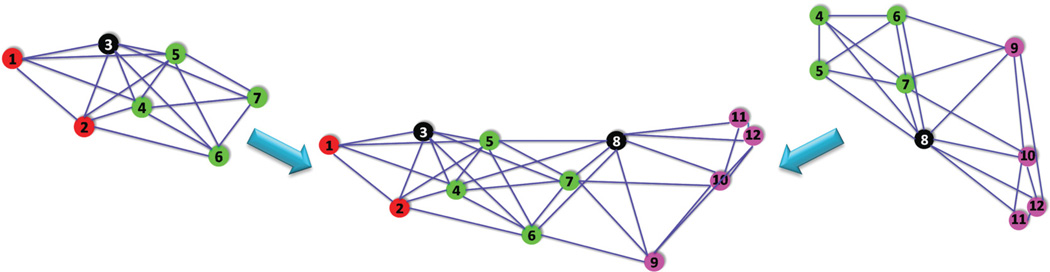
In this paper, we focus on the molecular distance geometry problem (to which we will refer from now on as the molecule problem) in ℝ³, although the approach is applicable to other dimensions as well. In [21], we introduced 2D-ASAP, an eigenvector-based synchronization algorithm that solves the sensor network localization problem in ℝ². We summarize below the approach used in 2D-ASAP and further explain the differences and improvements that its generalization to three dimensions brings. Figure 2 shows a schematic overview of our algorithm, which we call 3D-As-Synchronized-As-Possible (3D-ASAP).

Fig. 2.

The 3D-ASAP recovery process for a patch in the 1d3z molecule graph. The localization of the rightmost subgraph in its own local frame is obtained from the available accurate bond lengths and noisy NOE measurements by using one of the SDP algorithms. To every patch, like the one shown here, there corresponds an element of Euc(3) that we try to estimate. Using the pairwise alignments, in Step 1 we estimate both the reflection and rotation matrix from an eigenvector synchronization computation over O(3), while in Step 2 we find the estimated coordinates by solving an overdetermined system of linear equations. If there is available information on the reflection or rotations of some patches, one may choose to further divide Step 1 into two consecutive steps. Step 1a is synchronization over ℤ₂, while Step 1b is synchronization over SO(3), in which the missing reflections and rotations are estimated.

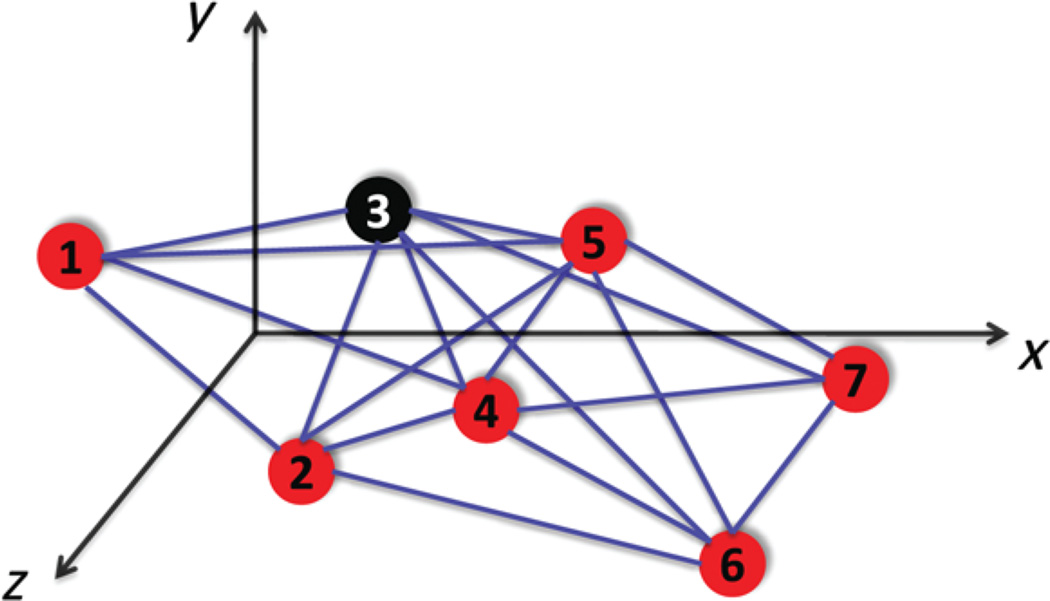
The 2D-ASAP algorithm proposed in [21] belongs to the group of algorithms that integrate local distance information into a global structure determination. For every sensor, we first identify uniquely localizable (UL) subgraphs of its 1-hop neighborhood that we call patches. For each patch, we compute an approximate localization in a coordinate system of its own using either the stress minimization approach of [28], or by using SDP. In the noise-free case, the computed coordinates of the sensors in each patch must agree with their global positioning up to some unknown rigid motion, that is, up to translation, rotation and possibly reflection (Fig. 3). To every patch there corresponds an element of the Euclidean group, Euc(2), of rigid transformations in the plane, and the goal is to estimate the group elements that will properly align all the patches in a globally consistent way. By finding the optimal alignment of all pairs of patches whose intersection is large enough, we obtain measurements for the ratios of the unknown group elements. Finding group elements from noisy measurements of their ratios is also known as the synchronization problem [26, 38]. For example, the synchronization of clocks in a distributed network from noisy measurements of their time offsets is a particular example of synchronization over ℝ. Singer [49] introduced an eigenvector method for solving the synchronization problem over the group SO(2) of planar rotations. This algorithm serves as the basic building block for our 2D-ASAP and 3D-ASAP algorithms. Namely, we reduce the graph realization problem to three consecutive synchronization problems that overall solve the synchronization problem over Euc(2). In the first two steps, we solve synchronization problems over the compact groups ℤ₂, respectively, SO(2), for the possible reflections, respectively rotations, of the patches using the eigenvector method. In the third step, we solve another synchronization problem over the non-compact group ℝ² for the translations by solving an overdetermined linear system of equations using the method of least squares. This solution yields the estimated coordinates of all the sensors up to a global rigid transformation.

Fig. 3.

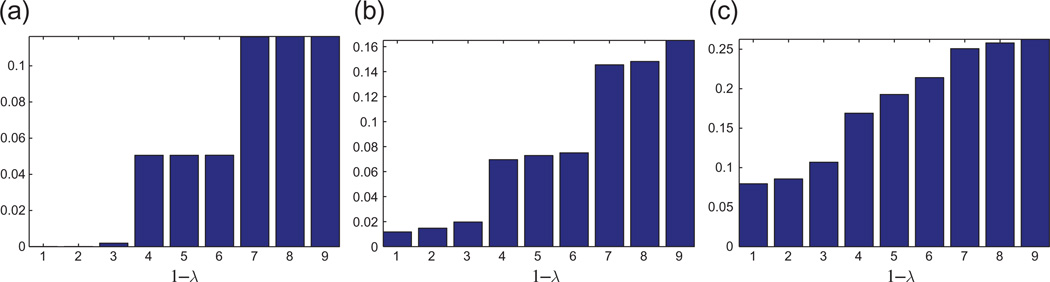
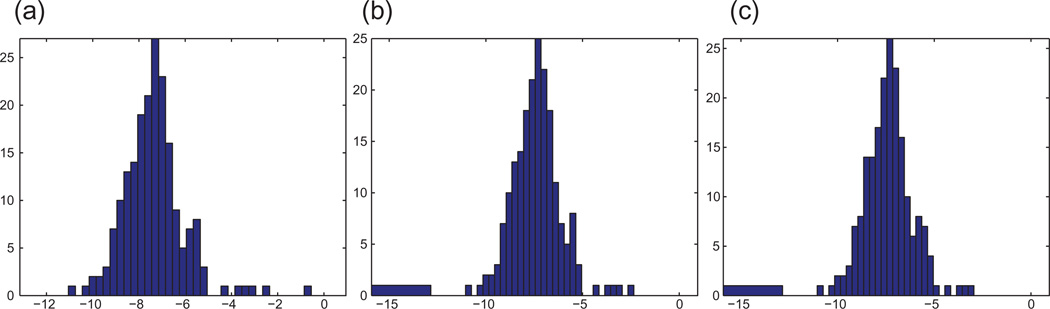
Bar plot of the top nine eigenvalues of ℋ for the UNITCUBE graph and various noise levels η. The resulting error rate τ is the percentage of patches whose reflection was incorrectly estimated. To ease the visualization of the eigenvalues of ℋ, we choose to plot 1 − λ^ℋ because the top eigenvalues of ℋ tend to pile up near 1, so it is difficult to differentiate between them by looking at the bar plot of λ ^ℋ. (a) η =0%, τ =0%, and MSE=6e − 4. (b) η =20%, τ =0%, and MSE=0.05. (c) η =40%, τ =4%, and MSE=0.36.

In the present paper, we extend the approach used in 2D-ASAP to accommodate for the additional challenges posed by rigidity theory in ℝ³ and other constraints that are specific to the molecule problem. In addition, we also increase the robustness to noise and speed of the algorithm. The following paragraphs are a brief summary of the improvements that 3D-ASAP bring, in the order in which they appear in the algorithm.

First, we address the issue of using a divide-and-conquer approach from the perspective of three-dimensional global rigidity, i.e., of decomposing the initial measurement graph into many small over-lapping patches that can be uniquely localized. Sufficient and necessary conditions for two-dimensional combinatorial global rigidity have been established only recently, and motivated our approach for building patches in 2D-ASAP [31, 35]. Owing to the recent coning result in rigidity theory [18], it is also possible to extract globally rigid patches in dimension three. However, such globally rigid patches cannot always be localized accurately by SDP algorithms, even in the case of noise-free data. To that end, we rely on the notion of unique localizability [52] to localize noise graphs and introduce the notion of a weakly uniquely localizable (WUL) graph, in the case of noisy data.

Secondly, we use a median-based denoising algorithm in the preprocessing step, that overall produces more accurate patch localizations. Our approach is based on the observation that a given edge may belong to several different patches, the localization of each of which may result in a different estimation for the distance. The median of these different estimators from the different patches is a more accurate estimator of the underlying distance.

Thirdly, we incorporated in 3D-ASAP the possibility to integrate prior available information. As it is often the case in real applications (such as NMR), one has readily available structural information on various parts of the network that we are trying to localize. For example, in the NMR application, there are often subsets of atoms (referred to as ‘molecular fragments’, by analogy with the fragment molecular orbital approach, e.g., [25]) whose relative coordinates are known a priori, and thus it is desirable to be able to incorporate such information in the reconstruction process. Of course, one may always input into the problem all pairwise distances within the molecular fragments. However, this requires increased computational efforts while still not taking full advantage of the available information, i.e., the orientation of the molecular fragment. Nodes that are aware of their location are often referred to as anchors, and anchor-based algorithms make use of their existence when computing the coordinates of the remaining sensors. Since in some applications the presence of anchors is not a realistic assumption, it is important to have efficient and noise-robust anchor-free algorithms, which can also incorporate the location of anchors if provided. However, note that having molecular fragments is not the same as having anchors; given a set of (possibly overlapping) molecular fragments, no two of which can be joined in a globally rigid body, only one molecular fragment can be treated as anchor information (the nodes of that molecular fragment will be the anchors), as we do not know a priori how the individual molecular fragments relate to each other in the same global coordinate system.

Fourthly, we allow for the possibility of combining the first two steps (computing the reflections and rotations) into one single step, thus doing synchronization over the group of orthogonal transformations O(3) =ℤ₂ × SO(3) rather than individually over ℤ₂ followed by SO(3). However, depending on the problem being considered and the type of available information, one may choose not to combine the above two steps. For example, when molecular fragments are present, we first do synchronization over ℤ₂ with anchors, as detailed in Section 7, followed by synchronization over SO(3).

Fifthly, we incorporate another median-based heuristic in the final step, where we compute the translations of each patch by solving, using least squares, three overdetermined linear systems, one for each of the x-, y- and z-axis. For a given axis, the displacement between a pair of nodes appears in multiple patches, each resulting in a different estimation of the displacement along that axis. The median of all these different estimators from different patches provides a more accurate estimator for the displacement. In addition, after the least squares step, we introduce a simple heuristic that corrects the scaling of the noisy distance measurements. Owing to the geometric graph model assumption and the uniform noise model, the distance measurements taken as input by 3D-ASAP are significantly scaled down, and the least-squares step further shrinks the distances between nodes in the initial reconstruction.

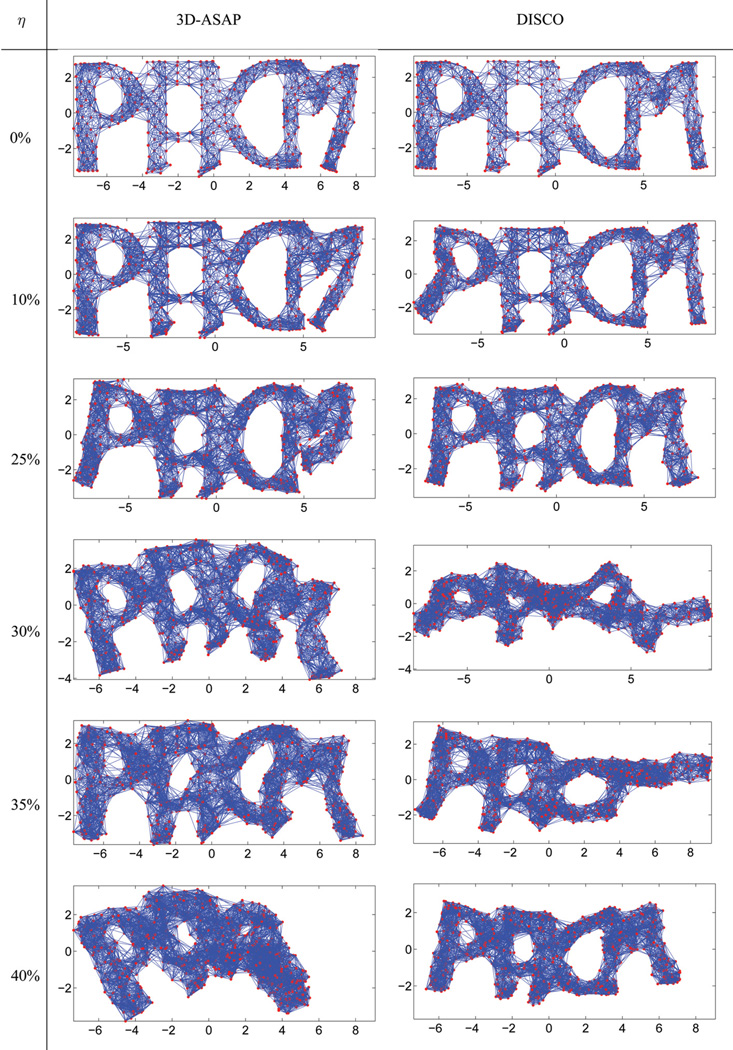
Finally, we introduce 3D-SP-ASAP, a variant of 3D-ASAP that uses a spectral partitioning algorithm in the pre-processing step of building the patches. This approach is somewhat similar to the recently proposed DIStributed COnformation (DISCO) algorithm of [42]. The philosophy behind DISCO is to recursively divide large problems into two smaller problems, thus building a binary tree of subproblems, which can ultimately be solved by the traditional SDP-based localization methods. The 3D-ASAP has the disadvantage of generating a number of smaller subproblems (patches) that is linear in the size of the network, and localizing all resulting patches is a computationally expensive task, which is exactly the issue addressed by 3D-SP-ASAP.

From a computational point of view, all steps of the algorithm can be implemented in a distributed fashion and scale linearly in the size of the network, except for the eigenvector computation, which is nearly linear.¹ We show the results of numerous numerical experiments that demonstrate the robustness of our algorithm to noise and various topologies of the measurement graph. In all our experiments we used multiplicative and uniform noise, as detailed in equation (8.1). Throughout the paper, ANE denotes the average normalized error (ANE) that we introduce in (8.2) to measure the accuracy of our reconstructions.

This paper is organized as follows: Section 2 is a brief survey of related approaches for solving the graph realization problem in ℝ³. Section 3 gives an overview of the 3D-ASAP algorithm that we propose. Section 4 introduces the notion of WUL graphs used for breaking up the initial large network into patches and explains the process of embedding and aligning the patches. Section 5 proposes a variant of the 3D-ASAP algorithm by using a spectral clustering algorithm as a preprocessing step in breaking up the measurement graph into patches. In Section 6, we introduce a novel median-based denoising technique that improves the localization of individual patches, as well as a heuristic that corrects the shrinkage of the distance measurements. Section 7 gives an analysis of different approaches to the synchronization problem over ℤ₂ with anchor information, which is useful for incorporating molecular fragment information when estimating the reflections of the remaining patches. In Section 8, we detail the results of numerical simulations in which we tested the performance of our algorithms in comparison to existing state-of-the-art algorithms. Finally, Section 9 is a summary and a discussion of possible extensions of the algorithm and its usefulness in other applications.

2. Related work

Owing to the importance of the graph realization problem, many heuristic strategies and numerical algorithms have been proposed in the last decade. A popular approach to solving the graph realization problem is based on SDP and has attracted considerable attention in recent years [9–11, 14, 62]. We defer to Section 4.3 a description of existing SDP relaxations of the graph realization problem. Such SDP techniques are usually able to localize accurately small-to-medium-sized problems (up to a couple thousands atoms). However, many protein molecules have more than 10,000 atoms and the SDP approach by itself is no longer computationally feasible due to its increased running time. In addition, the performance of the SDP methods is significantly affected by the number and location of the anchors, and the amount of noise in the data. To overcome the computational challenges posed by the limitations of the SDP solvers, several divide and conquer approaches have been proposed recently for the graph realization problem. One of the earlier methods appears in [13], and more recent methods include the Distributed Anchor Free Graph Localization (DAFGL) algorithm of [12], and the DISCO algorithm of [42].

One of the critical assumptions required by the distributed SDP algorithm in [13] is that there exist anchor nodes distributed uniformly throughout the physical space. The algorithm relies on the anchor nodes to divide the sensors into clusters, and solves each cluster separately via an SDP relaxation. Combining smaller subproblems together can be a challenging task; however, this is not an issue if there exist anchors within each smaller subproblem (as it happens in the sensor network localization problem) because the solution to the clusters induces a global positioning; in other words, the alignment process is trivially solved by the existence of anchors within the smaller subproblems. Unfortunately, for the molecule problem, anchor information is scarce, almost inexistent, hence it becomes crucial to develop algorithms that are amenable to a distributed implementation (to allow for solving large scale problems) despite there being no anchor information available. The DAFGL algorithm of [12] attempted to overcome this difficulty and was successfully applied to molecular conformations, where anchors are inexistent. However, the performance of DAFGL was significantly affected by the sparsity of the measurement graph and the algorithm could tolerate only up to 5% multiplicative noise in the distance measurements.

The recent DISCO algorithm of [42] addressed some of the shortcomings of DAFGL and used a similar divide-and-conquer approach to successfully reconstruct conformations of very large molecules. At each step, DISCO checks whether the current subproblem is small enough to be solved by itself, and if so, solves it via SDP and further improves the reconstruction by gradient descent. Otherwise, the current subproblem (subgraph) is further divided into two subgraphs, each of which is then solved recursively. To combine two subgraphs into one larger subgraph, DISCO aligns the two overlapping smaller subgraphs and refines the coordinates by applying gradient descent. In general, a divide-and-conquer algorithm consists of two ingredients: dividing a bigger problem into smaller subproblems and combining the solutions of the smaller subproblems into a solution for a larger subproblem. With respect to the former aspect, DISCO minimizes the number of edges between the two subgroups (since such edges are not taken into account when localizing the two smaller subgroups), while maximizing the number of edges within subgroups, since denser graphs are easier to localize both in terms of speed and robustness to noise. As for the latter aspect, DISCO divides a group of atoms in such a way that the two resulting subgroups have many overlapping atoms. Whenever the common subgroup of atoms is accurately localized, the two subgroups can be further joined together in a robust manner. DISCO employs several heuristics that determine when the overlapping atoms are accurately localized, and whether there are atoms that cannot be localized in a given instance (they do not attach to a given subgraph in a globally rigid way). Furthermore, in terms of robustness to noise, DISCO compared favorably with the above-mentioned divide-and-conquer algorithms.

Finally, another graph realization algorithm amenable to large-scale problems is maximum variance unfolding (MVU), a non-linear dimensionality reduction technique proposed by [58]. MVU produces a low-dimensional representation of the data by maximizing the variance of its embedding while preserving the original local distance constraints. MVU builds on the SDP approach and addresses the issue of the possibly high-dimensional solution to the SDP problem. While rank constraints are non-convex and cannot be directly imposed, it has been observed that low-dimensional solutions emerge naturally when maximizing the variance of the embedding (also known as the maximum trace heuristic). Their main observation is that the coordinate vectors of the sensors are often well approximated by just the first few (e.g., 10) low-oscillatory eigenvectors of the graph Laplacian. This observation allows one to replace the original and possibly large-scale SDP by a much smaller SDP that leads to a significant reduction in running time.

While there exist many other localization algorithms, we provide here two other such references. One of the more recent iterative algorithms that was observed to perform well in practice compared with other traditional optimization methods is a variant of the gradient descent approach called the stress majorization algorithm, also known as SMACOF [15], originally introduced by [22]. The main draw-back of this approach is that its objective function (commonly referred to as the stress) is not convex and the search for the global minimum is prone to getting stuck at local minima, which often makes the initial guess for gradient descent-based algorithms important for obtaining satisfactory results. DILAND, recently introduced in [40], is a distributed algorithm for localization with noisy distance measurements. Under appropriate conditions on the connectivity and triangulation of the network, DILAND was shown to converge almost surely to the true solution.

3. The 3D-ASAP algorithm

3D-ASAP is a divide-and-conquer algorithm that breaks up the large graph into many smaller overlapping subgraphs, which we call patches, and ‘stitches’ them together consistently in a global coordinate system with the purpose of localizing the entire measurement graph. Unlike previous graph localization algorithms, we build patches that are WUL (a notion that is defined later in Section 4.1 and is stronger than global rigidity²) which is required to avoid foldovers in the final solution.³ We also assume that the given measurement graph is UL to begin with; otherwise, the algorithm will discard the parts of the graph that do not attach uniquely to the rest of the graph. Alternatively, one may run the algorithm on the UL subcomponents, and later piece them together using application specific information.

We build the patches in the following way. For every node i we denote by V(i) = {j : (i, j) ∈ E} ∪ {i} the set of its neighbors together with the node itself, and by G(i)=(V(i), E(i)) its subgraph of 1-hop neighbors. If G(i) is globally rigid, which can be checked efficiently using the randomized algorithm of [27], then it has a unique embedding in ℝ³. However, embedding a globally rigid graph is NP-hard as shown in [4, 5]. As a result, using one of the existing embedding algorithms, such as SDP, for globally rigid (sub)graphs can produce inaccurate localizations, even for noise-free data. In order to ensure that SDP would give the correct localization, a stronger notion of rigidity is needed, that of unique localizability [52]. However, in practical applications the distance measurements are noisy, so we introduce the notion of weakly localizable subgraphs and use it to build patches that can be accurately localized. The exact way we break up the 1-hop neighborhood subgraphs into smaller WUL subgraphs is detailed in Section 4.1. In Section 5, we describe an alternative method for decomposing the measurement graph into patches, using a spectral-partitioning algorithm. We denote by N the number of patches obtained in the above decomposition of the measurement graph, and note that it may be different from n, the number of nodes in G, since the neighborhood graph of a node may contribute several patches or none. Also, note that the embedding of every patch in ℝ³ is given in its own local frame. To compute such an embedding, we use the following SDP-based algorithms: FULL-SDP for noise-free data [14] and SNL-SDP for noisy data [53]. Once each patch is embedded in its own coordinate system, one must find the reflections, rotations and translations that will stitch all patches together in a consistent manner, a process to which we refer as synchronization.

We denote the resulting patches by P₁, P₂,…, P_N. To every patch P_i there corresponds an element e_i ∈ Euc(3), where Euc(3) is the Euclidean group of rigid motions in ℝ³. The rigid motion e_i moves patch P_i to its correct position with respect to the global coordinate system. Our goal is to estimate the rigid motions e₁,…, e_N (up to a global rigid motion) that will properly align all the patches in a globally consistent way. To achieve this goal, we first estimate the alignment between any pair of patches P_i and P_j that have enough nodes in common, a procedure we detail later in Section 4.5. The alignment of patches P_i and P_j provides a (perhaps noisy) measurement for the ratio $e_i{e}_j^{-1}$ in Euc(3). We solve the resulting synchronization problem in a globally consistent manner, such that information from local alignments propagates to pairs of non-overlapping patches. This is done by replacing the synchronization problem over Euc(3) by two different consecutive synchronization problems.

In the first synchronization problem, we simultaneously find the reflections and rotations of all the patches using the eigenvector synchronization algorithm over the group O(3) of orthogonal matrices. When prior information on the reflections of some patches is available, one may choose to replace this first step by two consecutive synchronization problems, i.e., first estimate the missing rotations by doing synchronization over ℤ₂ with molecular fragment information, as described in Section 7, followed by another synchronization problem over SO(3) to estimate the rotations of all patches. Once both reflections and rotations are estimated, we estimate the translations by solving an overdetermined linear system. Taken as a whole, the algorithm integrates all the available local information into a global coordinate system over several steps by using the eigenvector synchronization algorithm and least squares over the isometries of the Euclidean space. The main advantage of the eigenvector method is that it can recover the reflections and rotations even if many of the pairwise alignments are incorrect. The algorithm is summarized in Table 1.

Table 1.

Overview of the 3D-ASAP algorithm

Input	G =(V, E), |V| = n, |E| = m, dij for (i, j) ∈ E
Pre-processing Step	1. Break the measurement graph G into N WUL patches P1,…, PN.
Patch Localization	2. Embed each patch Pi separately using either FULL-SDP (for noise-free data), or SNL-SDP (for noisy data), or cMDS (for complete patches).
Step 1	1. Align all pairs of patches (Pi, Pj) that have enough nodes in common.
	2. Estimate their relative rotation and possibly reflection hij ∈ O(3).
	3. Build a sparse 3N × 3N symmetric matrix H = (hij) as defined in (3.1).
Estimating Reflections and Rotations	4. Define ℋ=D−1H, where D is a diagonal matrix with D3i−2,3i−2 =D3i−1,3i−1 =D3i,3i =deg(i), for i=1,…,N.
	5. Compute the top 3 eigenvectors ${\nu }_i^{\mathscr{H}}$ of ℋ satisfying $\mathscr{H}{\nu }_i^{\mathscr{H}}={\lambda }_i^{\mathscr{H}}{\nu }_i^{\mathscr{H}},i=1,2,3$
	6. Estimate the global reflection and rotation of patch Pi by the orthogonal matrix ĥi that is closest to h̃i in Frobenius norm, where ĥi is the submatrix corresponding to the ith patch in the 3N × 3 matrix formed by the top three eigenvectors [${\nu }_1^{\mathscr{H}}{\nu }_2^{\mathscr{H}}{\nu }_3^{\mathscr{H}}$].
	7. Update the current embedding of patch Pi by applying the orthogonal transformation ĥi obtained above (rotation and possibly reflection)
Step 2	1. Build the m × n overdetermined system of linear equations given in (3.20), after applying the median-based denoising heuristic.
Estimating	2. Include the anchors information (if available) into the linear system.
Translations	3. Compute the least squares solution for the x-axis, y-axis and z-axis coordinates.
OUTPUT	Estimated coordinates p̂1,…, p̂n

3.1 Step 1: Synchronization over O(3) to estimate reflections and rotations

As mentioned earlier, for every patch P_i that was already embedded in its local frame, we need to estimate whether or not it needs to be reflected with respect to the global coordinate system, and what is the rotation that aligns it in the same coordinate system. In 2D-ASAP, we first estimated the reflections, and based on that, we further estimated the rotations. However, it makes sense to ask whether one can combine the two steps, and perhaps further increase the robustness to noise of the algorithm. By doing this, information contained in the pairwise rotation matrices helps in better estimating the reflections, and vice versa, information on the pairwise reflection between patches helps in improving the estimated rotations. Combining these two steps also reduces the computational effort by half, since we need to run the eigenvector synchronization algorithm only once.

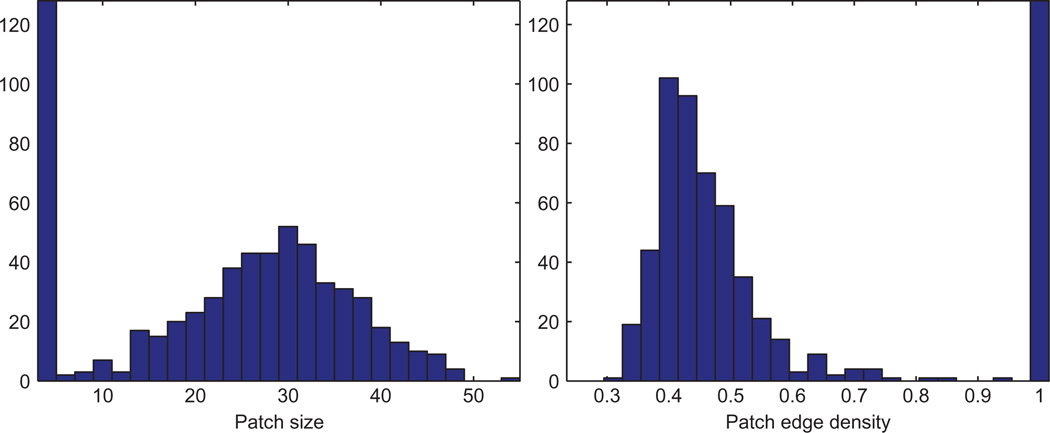
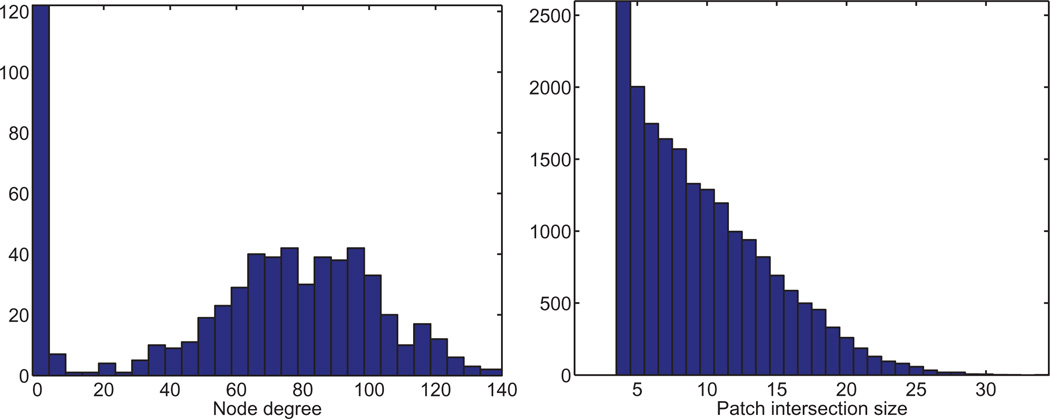
We denote the orthogonal transformation of patch P_i by h_i ∈ O(3), which is defined up to a global orthogonal rotation and reflection. The alignment of every pair of patches P_i and P_j whose intersection is sufficiently large provides a measurement h_ij (a 3 × 3 orthogonal matrix) for the ratio $h_i{h}_j^{-1}$. However, some ratio measurements can be corrupted because of errors in the embedding of the patches due to noise in the measured distances. We denote by G^P =(V^P, E^P) the patch graph whose vertices V^P are the patches P₁,…, P_N, and two patches P_i and P_j are adjacent, (P_i, P_j) ∈ E^P, iff they have enough vertices in common to be aligned such that the ratio $h_i{h}_j^{-1}$ can be estimated. We let A^P denote the adjacency matrix of the patch graph, i.e., $A_{ij}^p=1$ if (P_i, P_j) ∈ E^P, and $A_{ij}^p=0$ otherwise. Obviously, two patches that are far apart and have no common nodes cannot be aligned, and there must be enough⁴ overlapping nodes to make the alignment possible. Figures 4 and 5 show a typical example of the sizes of the patches we consider, as well as their intersection sizes.

Fig. 4.

Histogram of patch sizes (left) and edge density (right) in the BRIDGE-DONUT graph, n=500 and deg=18. Note that a large number of the resulting patches are of size 4, thus complete graphs on four nodes (K₄), which explains the same large number of patches with edge density 1.

Fig. 5.

Histogram of the node degrees of patches in the patch graph G^P (left) and the intersection size of patches (right), in the BRIDGE-DONUT graph with n=500 and deg=18. G^P has N =615 nodes (i.e., patches) and average degree 24, meaning that, on average, a patch overlaps (in at least four nodes) with 24 other patches.

The first step of 3D-ASAP is to estimate the appropriate rotation and reflection of each patch. To that end, we use the eigenvector synchronization method as it was shown to perform well even in the presence of a large number of errors. The eigenvector method starts off by building the following 3N × 3N sparse symmetric matrix H =(h_ij), where h_ij is the a 3 × 3 orthogonal matrix that aligns patches P_i and P_j

$$H_{ij}=\{\begin{array}{cc}{h}_{ij}\hfill & (i,j)\in E^P(P_i\text{and}{P}_j\text{have enough points in common}),\hfill \\ 0_{3\times 3}\hfill & (i,j)\notin E^P(P_i\text{and}{P}_j\text{cannot be aligned}).\hfill \end{array}$$ (3.1)

We explain in more detail in Section 4.5 the procedure by which we align pairs of patches, if such an alignment is at all possible.

Prior to computing the top eigenvectors of the matrix H, as introduced originally in [49], we choose to use the following normalization (similar to 2D-ASAP in [21]). Let D be a 3N × 3N diagonal matrix,⁵ whose entries are given by D_{3i−2,3i−2}=D_{3i−1,3i−1}=D_3i,3i =deg(i), for i=1,…,N. We define the matrix

$$\mathscr{H}=D^{-1}H,$$ (3.2)

which is similar to the symmetric matrix D^−1/2HD^−1/2 through

$$\mathscr{H}=D^{-1/2}(D^{-1/2}{\mathit{\text{HD}}}^{-1/2})D^{-1/2}.$$

Therefore, ℋ has 3N real eigenvalues ${\lambda }_1^{\mathscr{H}}\ge {\lambda }_2^{\mathscr{H}}\ge {\lambda }_3^{\mathscr{H}}\ge {\lambda }_4^{\mathscr{H}}\ge \dots \ge {\lambda }_{3N}^{\mathscr{H}}$ with corresponding 3N orthogonal eigenvectors ${\nu }_1^{\mathscr{H}},\dots ,{\nu }_{3N}^{\mathscr{H}}$, satisfying $\mathscr{H}{\nu }_i^{\mathscr{H}}={\lambda }_i^H{\nu }_i^{\mathscr{H}}$. As shown in the next paragraphs, in the noise-free case, ${\lambda }_1^{\mathscr{H}}={\lambda }_2^{\mathscr{H}}={\lambda }_3^{\mathscr{H}}$, and furthermore, if the patch graph is connected, then ${\lambda }_3^{\mathscr{H}}>{\lambda }_4^{\mathscr{H}}$. We define the estimated orthogonal transformations ĥ₁,…,ĥ_N ∈ O(3) using the top three eigenvectors ${\nu }_1^{\mathscr{H}},{\nu }_2^{\mathscr{H}},{\nu }_3^{\mathscr{H}}$, following the approach used in [50].

Let us now show that, in the noise-free case, the top three eigenvectors of ℋ perfectly recover the unknown group elements. We denote by h_i the 3 × 3 matrix corresponding to the ith submatrix in the 3N × 3 matrix [${\nu }_1^{\mathscr{H}},{\nu }_2^{\mathscr{H}},{\nu }_3^{\mathscr{H}}$]. In the noise-free case, h_i is an orthogonal matrix and represents the solution which aligns patch P_i in the global coordinate system, up to a global orthogonal transformation. To see this, we first let h denote the 3N × 3 matrix formed by concatenating the true orthogonal transformation matrices h₁,…, h_N. Note that when the patch graph G^P is complete, H is a rank 3 matrix since H =hh^⊤, and its top three eigenvectors are given by the columns of h

$$Hh=h{h}^{\top }h=hN{I}_3=Nh.$$ (3.3)

In the general case when G^P is a sparse connected graph, note that

$$Hh=Dh,\text{hence}{D}^{-1}Hh=\mathscr{H}h=h,$$ (3.4)

and thus the three columns of h are each eigenvectors of matrix ℋ, associated to the same eigenvalue λ = 1 of multiplicity 3. It remains to show that this is the largest eigenvalue of ℋ. We recall that the adjacency matrix of G^P is A^P, and denote by 𝒜^P the 3N × 3N matrix built by replacing each entry of value 1 in A^P by the identity matrix I₃, i.e., 𝒜^P =A^P ⊗ I₃, where ⊗ denotes the tensor product of two matrices. As a consequence, the eigenvalues of 𝒜^P are just the direct products of the eigenvalues of I₃ and A^P, and the corresponding eigenvectors of 𝒜^P are the tensor products of the eigenvectors of I and A^P. Furthermore, if we let Δ denote the N × N diagonal matrix with Δ_ii =deg(i), for i=1,…,N, it holds true that

$$D^{-1}{𝒜}^P=({\Delta }^{-1}{A}^P)\otimes I_3,$$ (3.5)

and thus the eigenvalues of D⁻¹ 𝒜^P are the same as the eigenvalues of Δ⁻¹ A^P, each with multiplicity 3. In addition, if Υ denotes the 3N × 3N matrix with diagonal blocks h_i, i = 1,…,N, then the normalized alignment matrix ℋ can be written as

$$\mathscr{H}={\rm Y}{D}^{-1}{𝒜}^P{{\rm Y}}^{-1},$$ (3.6)

and thus ℋ and D⁻¹ A^P have the same eigenvalues, which are also the eigenvalues of Δ⁻¹ A^P, each with multiplicity 3. Whenever it is understood from the context, we will omit from now on the remark about the multiplicity 3. Since the normalized discrete graph Laplacian ℒ is defined as

$$ℒ=I-{\Delta }^{-1}{A}^P,$$ (3.7)

it follows that in the noise-free case, the eigenvalues of I − ℋ are the same as the eigenvalues of ℒ. These eigenvalues are all non-negative, since ℒ is similar to the positive semidefinite matrix I − Δ^−1/2A^P Δ^−1/2, whose non-negativity follows from the identity

$$x^{\top }(I-{\Delta }^{-1/2}{A}^P{\Delta }^{-1/2})x=\sum _{(i,j)\in E^P}{(\frac{x_i}{\sqrt{\text{deg}(i)}}-\frac{x_i}{\sqrt{\text{deg}(j)}})}^2\ge 0.$$

In other words,

$$1-{\lambda }_{3i-2}^{\mathscr{H}}=1-{\lambda }_{3i-1}^{\mathscr{H}}=1-{\lambda }_{3i}^{\mathscr{H}}={\lambda }_i^{ℒ}\ge 0,i=1,2,\dots ,N,$$ (3.8)

where the eigenvalues of ℒ are ordered in increasing order, i.e., ${\lambda }_1^{ℒ}\le {\lambda }_2^{ℒ}\le \dots \le {\lambda }_N^{ℒ}$. If the patch graph G^P is connected, then the eigenvalue ${\lambda }_1^{ℒ}=0$ is simple (thus ${\lambda }_2^{ℒ}>{\lambda }_1^{ℒ}$) and its corresponding eigenvector ${\nu }_1^{ℒ}$ is the all-ones vector 1=(1, 1,…, 1) ^⊤. Therefore, the largest eigenvalue of ℋ equals 1 and has multiplicity 3, i.e., ${\lambda }_1^{\mathscr{H}}={\lambda }_2^{\mathscr{H}}={\lambda }_3^{\mathscr{H}}=1$, and ${\lambda }_4^{\mathscr{H}}>{\lambda }_3^{\mathscr{H}}$. This concludes our proof that, in the noise-free case, the top three eigenvectors of ℋ perfectly recover the true solution h₁,…, h_N ∈ O(3), up to a global orthogonal transformation.

However, when the distance measurements are noisy and the pairwise alignments between patches are inaccurate, an estimated transformation h̃_i may not coincide with h_i, and in fact may not even be an orthogonal transformation. For that reason, we estimate h_i by the closest orthogonal matrix to h̃_i in the Frobenius matrix norm⁶

$${\widehat{h}}_i=\underset{X\in O(3)}{\text{argmin}}\Vert {\tilde{h}}_i-X{\Vert }_F.$$ (3.9)

We do this by using the well-known procedure (e.g., [3]), ĥ_i =U_iV_i^⊤, where h̃_i =U_iΣ_iV_i^⊤ is the singular value decomposition of h̃_i, see also [24, 39]. Note that the estimation of the orthogonal transformations of the patches are up to a global orthogonal transformation (i.e., a global rotation and reflection with respect to the original embedding). Also, the only difference between this step and the angular synchronization algorithm in [49] is the normalization of the matrix prior to the computation of the top eigen-vector. The usefulness of this normalization was first demonstrated in 2D-ASAP, in the synchronization process over ℤ₂ and SO(2). In very recent work, the authors of [7] prove performance guarantees for the above synchronization algorithm in terms of the eigenvalues of I − ℋ (the normalized graph connection Laplacian) and the second eigenvalue of L (the normalized (classical) graph Laplacian).

We use the mean-squared error (MSE) to measure the accuracy of this step of the algorithm in estimating the orthogonal transformations. To that end, we look for an optimal orthogonal transformation Ô ∈ O(3) that minimizes the sum of squared distances between the estimated orthogonal transformations and the true ones:

$$\widehat{O}=\underset{O\in O(3)}{\text{argmin}}\sum _{i=1}^N\Vert h_i-O{\widehat{h}}_i{\Vert }_F^2.$$ (3.10)

In other words, Ô is the optimal solution to the registration problem between two sets of orthogonal transformations in the least squares sense. Following the analysis of [50], we make use of properties of the trace such as Tr(AB) =Tr(BA), Tr(A)=Tr(A^⊤) and notice that

$$\sum _{i=1}^N{\Vert h_i-O{\widehat{h}}_i\Vert }_F^2=\sum _{i=1}^N\mathrm{T}\mathrm{r}[(h_i-O{\widehat{h}}_i){(h_i-O{\widehat{h}}_i)}^{\top }]=\sum _{i=1}^N\mathrm{T}\mathrm{r}[2I-2O{\widehat{h}}_i{h_i}^{\top }]=6N-2\mathrm{T}\mathrm{r}[O\sum _{i=1}^N{\widehat{h}}_i{h_i}^{\top }].$$ (3.11)

If we let Q denote the 3 × 3 matrix

$$Q=\frac{1}{N}\sum _{i=1}^N{\widehat{h}}_i{h_i}^{\top }$$ (3.12)

it follows from (3.11) that the MSE is given by minimizing

$$\frac{1}{N}\sum _{i=1}^N{\Vert h_i-O{\widehat{h}}_i\Vert }_F^2=6-2\mathrm{T}\mathrm{r}(OQ).$$ (3.13)

In [3] it is proved that Tr(OQ)≤Tr(VU^⊤Q), for all O ∈ O(3), where Q=UΣV^⊤ is the singular value decomposition of Q. Therefore, the MSE is minimized by the orthogonal matrix Ô =VU^⊤ and is given by

$$\frac{1}{N}\sum _{i=1}^N{\Vert h_i-\widehat{O}{\widehat{h}}_i\Vert }_F^2=6-2\mathrm{T}\mathrm{r}(V{U}^{\top }U\Sigma V^{\top })=6-2\sum _{k=1}^3{\sigma }_k,$$ (3.14)

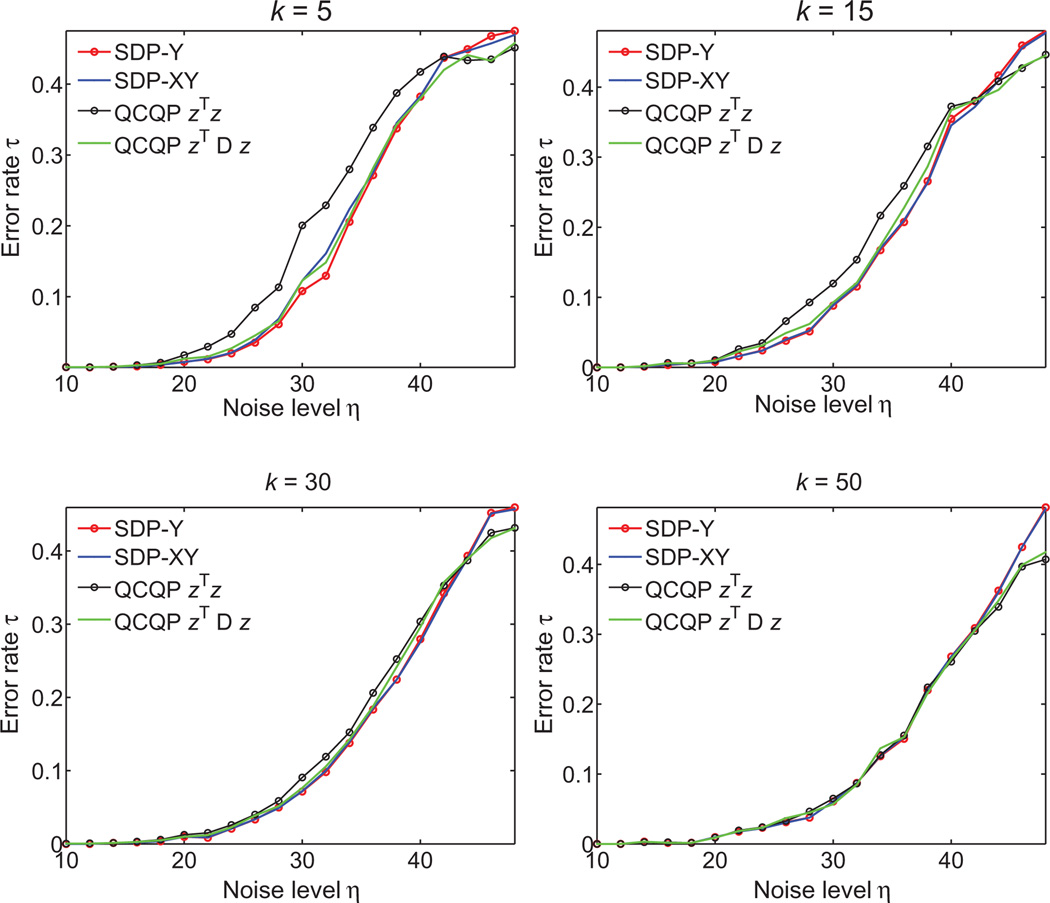
where σ₁, σ₂, σ₃ are the singular values of Q. Therefore, whenever Q is an orthogonal matrix for which σ₁ = σ₂ = σ₃ = 1, the MSE vanishes. Indeed, the numerical experiments in Table 2 confirm that for noise-free data, the MSE is very close to zero. To illustrate the success of the eigenvector method in estimating the reflections, we also compute τ, the percentage of patches whose reflection was incorrectly estimated. Finally, the last two columns in Table 2 show the recovery errors when, instead of doing synchronization over O(3), we first synchronize over ℤ₂ followed by SO(3).

Table 2.

The errors in estimating the reflections and rotations when aligning the N =200 patches resulting from for the UNITCUBE graph on n =212 vertices, at various levels of noise. We used τ to denote the percentage of patches whose reflection was incorrectly estimated

	O(3)		ℤ2 and SO(3)
η (%)	τ (%)	MSE	τ (%)	MSE
0	0	6e−4	0	7e−4
10	0	0.01	0	0.01
20	0	0.05	0	0.05
30	5.8	0.35	5.3	0.32
40	4	0.36	5	0.40
50	7.4	0.65	9	0.68

3.2 Step 2: Synchronization over ℝ³ to estimate translations

The final step of the 3D-ASAP algorithm is computing the global translations of all patches and recovering the true coordinates. For each patch P_k, we denote by G_k = (V_k, E_k)⁷ the graph associated to patch P_k, where V_k is the set of nodes in P_k, and E_k is the set of edges induced by V_k in the measurement graph G =(V, E).

We denote by $p_i^{(k)}={(x_i^{(k)},y_i^{(k)},z_i^{(k)})}^{\top }$ the known local frame coordinates of node i ∈ V_k in the embedding of patch P_k (see Fig. 6).

Fig. 6.

An embedding of a patch P_k in its local coordinate system (frame) after it was appropriately reflected and rotated. In the noise-free case, the coordinates $p_i^{(k)}={(x_i^{(k)},y_i^{(k)},z_i^{(k)})}^{\top }$ agree with the global positioning p_i =(x_i, y_i, z_i) ^⊤ up to some translation t^(k) (unique to all i in V_k).

At this stage of the algorithm, each patch P_k has been properly reflected and rotated so that the local frame coordinates are consistent with the global coordinates, up to a translation t^(k) ∈ ℝ³. In the noise-free case, we should therefore have

$$p_i=p_i^{(k)}+t^{(k)},i\in V_k,k=1,\dots ,N.$$ (3.15)

We can estimate the global coordinates p₁,…, p_n as the least-squares solution to the overdetermined system of linear equations (3.15), while ignoring the by-product translations t⁽¹⁾,…, t^(N). In practice, we write a linear system for the displacement vectors p_i − p_j for which the translations have been eliminated. Indeed, from (3.15) it follows that each edge (i, j) ∈ E_k contributes a linear equation of the form⁸

$$p_i-p_j=p_i^{(k)}-p_j^{(k)},(i,j)\in E_k,k=1,\dots ,N.$$ (3.16)

In terms of the x, y and z global coordinates of nodes i and j, (3.16) is equivalent to

$$x_i-x_j=x_i^{(k)}-x_j^{(k)},(i,j)\in E_k,k=1,\dots ,N,$$ (3.17)

and similarly for the y and z equations. We solve these three linear systems separately, and recover the coordinates x₁,…, x_n, y₁,…, y_n and z₁,…, z_n. Let T be the least-squares matrix associated with the overdetermined linear system in (3.17), x be the n × 1 vector representing the x-coordinates of all nodes, and b^x be the vector with entries given by the right-hand side of (3.17). Using this notation, the system of equations given by (3.17) can be written as

$$Tx=b^x,$$ (3.18)

and similarly for the y and z coordinates. Note that the matrix T is sparse with only two non-zero entries per row and that the all-ones vector 1=(1, 1,…, 1) ^⊤ is in the null space of T, i.e., T1=0, so we can find the coordinates only up to a global translation.

To avoid building a very large least-squares matrix, we combine the information provided by the same edges across different patches in only one equation, as opposed to having one equation per patch. In 2D-ASAP [21], this was achieved by adding up all equations of the form (3.17) corresponding to the same edge (i, j) from different patches, into a single equation, i.e.,

$$\sum _{k\in \{1,\dots ,N\}\mathrm{s}.\mathrm{t}.(i,j)\in E_k}{x}_i-x_j=\sum _{k\in \{1,\dots ,N\}\mathrm{s}.\mathrm{t}.(i,j)\in E_k}{x}_i^{(k)}-x_i^{(k)},(i,j)\in E,$$ (3.19)

and similarly for the y- and z-coordinates. For very noisy distance measurements, the displacements $x_i^{(k)}-x_j^{(k)}$ will also be corrupted by noise and the motivation for (3.19) was that adding up such noisy values will average out the noise. However, as the noise-level increases, some of the embedded patches will be highly inaccurate and will thus generate outliers in the list of displacements above. To make this step of the algorithm more robust to outliers, instead of averaging over all displacements, we select the median value of the displacements and use it to build the least-squares matrix

$$x_i-x_j=\underset{k\in \{1,\dots ,N\}\mathrm{s}.\mathrm{t}.(i,j)\in E_k}{\text{median}}\{x_i^{(k)}-x_j^{(k)}\},(i,j)\in E,$$ (3.20)

We denote the resulting m × n matrix by T̃, and its m × 1 right-hand-side vector by b̃^x. Note that T̃ has only two non-zero entries per row,⁹ T̃_e,i =1, T̃_e,j =−1, where e is the row index corresponding to the edge (i, j). The least squares solution p̂= p̂₁,…, p̂_n to

$$\tilde{T}x={\tilde{b}}^x,\tilde{T}y={\tilde{b}}^y\text{and}\tilde{T}z={\tilde{b}}^z,$$ (3.21)

is our estimate for the coordinates p=p₁,…, p_n, up to a global rigid transformation.

Whenever the ground truth solution p is available, we can compare our estimate p̂ with p. To that end, we remove the global reflection, rotation and translation from p̂, by computing the best procrustes alignment between p and p̂, i.e., p̃=Op̂ + t, where O is an orthogonal rotation and reflection matrix, and t a translation vector, such that we minimize the distance between the original configuration p and p̃, as measured by the least-squares criterion ${\sum }_{i=1}^n{\Vert p_i-{\tilde{p}}_i\Vert }^2$. Figure 7 shows the histogram of errors in the coordinates, where the error associated with node i is given by ∥p_i − p̂_i∥.

Fig. 7.

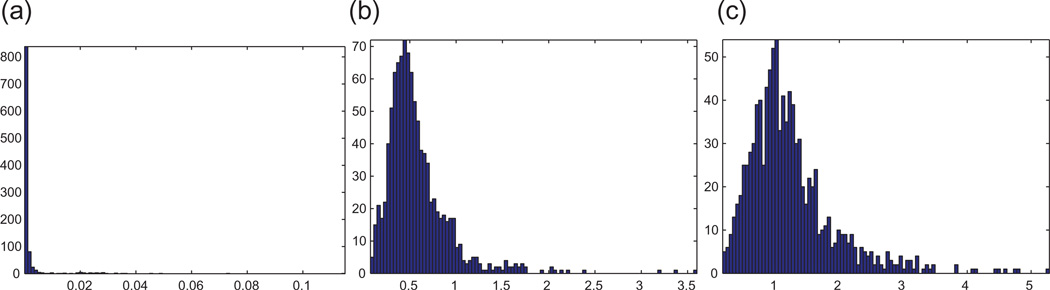
Histograms of coordinate errors ∥p_i − p̂_i∥ for all atoms in the 1d3z molecule, for different levels of noise. In all figures, the x-axis is measured in angstroms. Note the change of scale for (a), and the fact that the largest error showed that there is 0.12. We used ERR_c to denote the average coordinate error of all atoms. (a) η =0%, ERR_c =2e − 3. (b) η =30%, ERR_c =0.57. (c) η =50%, ERR_c =1.23.

We remark that in 3D-ASAP anchor information can be incorporated similarly to the 2D-ASAP algorithm [21]; however we do not elaborate on this here since there are no anchors in the molecule problem.

4. Extracting, embedding and aligning patches

This section describes how to break up the measurement graph into patches, and how to embed and pairwise align the resulting patches. In Section 4.1, we recall a recent result of [52] on uniquely d-localizable graphs, which can be accurately localized by SDP-based methods. We thus lay the ground for the notion of WUL graphs, which we introduce with the purpose of being able to localize the resulting patches even when the distance measurements are noisy. Section 4.2 discusses the issue of finding ‘pseudo-anchor’ nodes, which are needed when extracting WUL subgraphs. In Section 4.3, we discuss several SDP relaxations to the graph localization problem, which we use to embed the WUL patches. In Section 4.4, we remark on several additional constraints specific to the molecule problem, which are currently not incorporated in 3D-ASAP. Finally, Section 4.5 explains the procedure for aligning a pair of overlapping patches.

4.1 Extracting WUL subgraphs

We first recall some of the notation introduced earlier, that is needed throughout this section and Section 7 on synchronization over ℤ₂ with anchors. We consider a cloud of points in ℝ³ with k anchors denoted by 𝒜, and n atoms denoted by 𝒮. An anchor is a node whose location a_i ∈ ℝ³ is readily available, i=1,…, k, and an atom is a node whose location p_j is to be determined, j =1,…, n. We denote by d_ij the Euclidean distance between a pair of nodes, (i, j) ∈ 𝒜 ∪ 𝒮. In most applications, not all pair-wise distance measurements are available, therefore we denote by E(𝒮, 𝒮) and E(𝒮, 𝒜) the set of edges denoting the measured atom–atom and atom–anchor distances. We represent the available distance measurements in an undirected graph G =(V, E) with vertex set V =𝒜 ∪ 𝒮 of size |V| = n + k, and edge set of size |E| = m. An edge of the graph corresponds to a distance constraint, that is, (i, j) ∈ E iff the distance between nodes i and j is available and equals d_ij =d_ji, where i, j ∈ 𝒜 ∪ 𝒮. We denote the partial distance measurements matrix by D = {d_ij : (i, j) ∈ E(𝒮, 𝒮) ∪ E(𝒮, 𝒜)}. A solution p together with the anchor coordinates a comprise a localization or realization q=(p, a) of G. A framework in ℝ^d is the ensemble (G, q), i.e., the graph G together with the realization q which assigns a point q_i in ℝ^d to each vertex i of the graph.

Given a partial set of noise-free distances and the anchor set a, the graph realization problem can be formulated as the following system

$${\Vert p_i-p_j\Vert }_2^2=d_{ij}^2\text{for}(i,j)\in E(𝒮,𝒮),{\Vert a_i-p_j\Vert }_2^2=d_{ij}^2\text{for}(i,j)\in E(𝒮,𝒜),p_i\in {ℝ}^d\text{for}i=1,\dots ,n.$$ (4.1)

Unless the above system has enough constraints (i.e., the graph G has sufficiently many edges), G is not globally rigid and there could be multiple solutions. However, if the graph G is known to be (generically) globally rigid in ℝ³, and there are at least four anchors (i.e., k ≥ 4), and G admits a generic realization,¹⁰ then (4.1) admits a unique solution. Owing to recent results on the characterization of generic global rigidity, there now exists a randomized efficient algorithm that verifies if a given graph is generically globally rigid in ℝ^d [27]. However, this efficient algorithm does not translate into an efficient method for actually computing a realization of G. Knowing that a graph is generically globally rigid in ℝ^d still leaves the graph realization problem intractable, as shown in [5]. Motivated by this gap between deciding if a graph is generically globally rigid and computing its realization (if it exists), So and Ye [52] introduced the following notion of unique d-localizability. An instance (G, q) of the graph localization problem is said to be uniquely d-localizable if

1. the system (4.1) has a unique solution p̃=(p̃₁;…; p̃_n) ∈ ℝ^nd and

2. for any l > d, p̃ = ((p̃₁; 0),…, (p̃_n; 0)) ∈ ℝ^nl is the unique solution to the following system:

   $${\Vert p_i-p_j\Vert }_2^2=d_{ij}^2\text{for}(i,j)\in E(𝒮,𝒮),{\Vert (a_i;\mathbf{0})-p_j\Vert }_2^2=d_{ij}^2\text{for}(i,j)\in E(𝒮,𝒜),p_i\in {ℝ}^l\text{for}i=1,\dots ,n,$$ (4.2)

where (v; 0) denotes the concatenation of a vector v of size d with the all-zeros vector 0 of size l − d. The second condition states that the problem cannot have a non-trivial localization in some higher dimensional space ℝ^l (i.e., a localization different from the one obtained by setting p_j =(p̃_j; 0) for j = 1,…, n), where anchor points are trivially augmented to (a_i; 0), for i=1,…, k. A crucial observation should now be made: unlike global rigidity, which is a generic property of the graph G, the notion of unique localizability depends not only on the underlying graph G but also on the particular realization q, i.e., it depends on the framework (G, q).

We now introduce the notion of a WUL graph, essential for the preprocessing step of the 3D-ASAP algorithm, where we break the original graph into overlapping patches. A graph is weakly uniquely d-localizable if there exists at least one realization q ∈ ℝ^(n+k)d (we call this a certificate realization) such that the framework (G, q) is UL. If a framework (G, q) is UL, then G is a WUL graph; however, the reverse is not necessarily true since unique localizability is not a generic property. Furthermore, note that while a WUL graph may not be UL, it is guaranteed to be globally rigid, since global rigidity is a generic property.

Let us make clear the distinction between the related notions of rigidity, unique localizability and strong localizability introduced in [52]. Loosely speaking, a graph is strongly localizable if it is UL and remains so even under small perturbations. Formally stated, the problem (4.1) is strongly localizable if the dual of its SDP relaxation has an optimal dual slack matrix of rank n. As shown in [52] strong localizability implies unique localizability, but the reverse if not true. By the above observation, strong localizability also implies weak unique localizability.

The advantage of working with UL graphs becomes clear in light of the following result by [52], which states that the problem of deciding whether a given graph realization problem is UL, as well as the problem of determining the node positions of such a UL instance, can be solved efficiently by considering the following SDP

$$\text{maximize}0\text{subject to}(\mathbf{0};e_j-e_j){(\mathbf{0};e_j-e_j)}^{\top }\cdot Z=d_{ij}^2,\text{for}(i,j)\in E(𝒮,𝒮)(a_i;-e_j){(a_i;-e_j)}^{\top }\cdot Z=d_{ij}^2,\text{for}(i,j)\in E(𝒮,𝒜)Z_{1:d,1:d}=I_{d}Z\in {𝒦}^{n+d},$$ (4.3)

where e_i denotes the all-zeros vector with a 1 in the ith entry and ${𝒦}^{n+d}=\{Z_{(n+d)\times (n+d)}|Z=[\begin{array}{cc}{I}_d\hfill & X\hfill \\ X^{\top }\hfill & Y\hfill \end{array}]\ge 0\}$ where Z ≥ 0 means that Z is a positive semidefinite matrix. The SDP method relaxes the constraint Y =XX^⊤ to Y ≥ XX^⊤, i.e., Y − XX^⊤ ≥ 0, which is equivalent to the last condition in (4.3). The following predictor for UL graphs introduced in [52], established for the first time that the graph realization problem is UL if and only if the relaxation solution computed by an interior point algorithm (which generates feasible solutions of max-rank) has rank d and Y =XX^⊤.

Theorem 4.1 ([52, Theorem 2]) Suppose G is a connected graph. Then the following statements are equivalent:

1. Problem (4.1) is UL.

2. The max-rank solution matrix Z of (4.3) has rank d.

3. The solution matrix Z represented by (b) satisfies Y =XX^⊤.

Algorithm 1 summarizes our approach for extracting a WUL subgraph of a given graph. The algorithm has to cope with two main difficulties. The first difficulty is that only noisy distance measurements are available, yet the SDP (4.3) requires noise-free distances. This difficulty is bypassed by choosing a random realization for which noise-free distances are computed. This realization serves the purpose of the sought after certificate for WUL, and is not related to the actual locations of the atoms. The second difficulty is that the number of anchor points could be smaller than four. A necessary (but not sufficient) condition for the statements in Theorem 4.1 to hold true is the existence of at least four anchor nodes. While this may seem a very restrictive condition (since in many real life applications anchor information is rarely available), there is an easy way to get around this, provided the graph contains a clique (complete subgraph) of size at least 4. As discussed in Section 4.2, a patch of size at least 10 is very likely to contain such a clique, as confirmed by our numerical simulations. However, note that in our simulations for detecting pseudo-anchors, we placed the nodes at random within a disc of radius ρ, while in many real applications the position of the nodes is not necessarily random, as is often the case of certain three-dimensional biological data sets where the atoms lie along a one-dimensional curve. Once such a clique has been found, one may use cMDS to embed it and use the coordinates as anchors. We call such nodes pseudo-anchors.

Algorithm 1.

Finding a WUL subgraph of a graph with four anchors or pseudo-anchors

Require: Simple graph G =(V, E) with n atoms, k anchors, and ε a small positive constant (e.g., 10−4).

1: Randomize a realization q1,…, qn in ℝ3 and compute the distances dij =∥qi − qj∥ for (i, j) ∈ E.

2: If k < 4, find a complete subgraph of G on 4 vertices (i.e., K4) and compute an embedding of it (using classical MDS) with distances dij computed in step 1. Denote the set of pseudo-anchors by 𝒜.

3: Solve the SDP relaxation problem formulated in (4.3) using the anchor set 𝒜 and the distances dij computed in step 1 above.

4: Denote by the vector w the diagonal elements of the matrix Y − XX⊤.

5: Find the subset of nodes V0 ∈ V\𝒜 such that wi < ε.

6: Denote G0 =(V0, E0) the weakly uniquely localizable subgraph of G.

Note that Step 1 of the algorithm should be used only in the case of noisy distances. For noise-free data, this step may be skipped as the diagonal elements of the matrix Y − XX^⊤ can be readily used to extract the UL subgraph.

Our approach is to extract a WUL subgraph from the 4-connected components of each patch, since 4-connectivity is a necessary condition for global rigidity [17, 31], and as mentioned earlier, WUL implies global rigidity. Then, we apply Algorithm 1 on these components to extract the WUL subgraphs. Ultimately, we would like to extract subgraphs that are UL since they can be embedded accurately using SDP. However, UL is a property that depends on the specific realization, not just the underlying graph. Since the realization is unknown (after all, our goal is in fact to find it), we have to resort to WUL, which is a slightly weaker notion of UL but stronger than global rigidity. We have observed in our simulations that this approach significantly improves the accuracy of the localization compared with embedding patches that are globally rigid but not necessarily WUL. The explanation for this improved performance might be the following: if the randomized realization in Algorithm 1 (or what remains of it after removing some of the nodes) is ‘faithful’, meaning close enough to the true realization, then the WUL subgraph is perhaps generically UL, and hence its localization using the SDP in (4.3) under the original distance constraints can be computed accurately, as predicted by Theorem 4.1.

We also consider a slight variation of Algorithm 1, where we replace Step 3 with the SDP relaxation introduced in the FULL-SDP algorithm of [14]. We refer to this different approach as Algorithm 2. Algorithm 2 is mainly motivated by computational considerations, as the running time of the FULLSDP algorithm is significantly smaller compared with our CVX-based SDP implementation [29, 30] of problem (4.3).

Figure 8 and Table 3 show the reconstruction errors of the patches (in terms of ANE, an error measure introduced in Section 8) in the following scenarios. In the first scenario, we directly embed each 4-connected component (using either FULL-SDP or SNL-SDP, as detailed below), without any prior preprocessing. In the second, respectively third, scenario we first extract a WUL subgraph from each 4-connected component using Algorithm 1, respectively Algorithm 2, and then embed the resulting subgraphs. Note that the subgraph embeddings are computed using FULL-SDP, respectively SNL-SDP, for noise-free, respectively noisy data. Figure 8 contains numerical results from the UNITCUBE graph with noise-free data, in the three scenarios presented above. As expected, the FULL-SDP embedding in scenario 1 gives the highest reconstruction error,¹¹ at least one order of magnitude larger when compared with Algorithms 1 and 2. Surprisingly, Algorithm 2 produced more accurate reconstructions than Algorithm 1, despite its lower running time. These numerical computations suggest¹² that Theorem 4.1 remains valid when the formulation in problem (4.3) is replaced by the one considered in the FULL-SDP algorithm [14].

Fig. 8.

Histogram of reconstruction errors (measured in ANE) for the noise-free UNITCUBE graph with n=212 vertices, sensing radius ρ =0.3 and average degree deg=17. $\overline{\text{ANE}}$ denotes the average errors over all N =197 patches. Note that the x-axis shows the ANE in logarithmic scale. Scenario 1: directly embedding the 4-connected components. Scenario 2: embedding the WUL subgraphs extracted using Algorithm 1. Scenario 3: embedding the WUL subgraphs extracted using Algorithm 2. Note that for the subgraph embeddings we use FULL-SDP. (a) Scenario 1: $\overline{\text{ANE}}$ =8.4e − 4. (b) Scenario 2: $\overline{\text{ANE}}$ =2.3e − 5. (c) Scenario 3: $\overline{\text{ANE}}$ =7.2e − 6.

Table 3.

Average reconstruction errors (measured in ANE) for the UNITCUBE graph with n=212 vertices, sensing radius (ρ) 0.26 and average degree (deg) 12. Note that we consider only patches of size greater than or equal to 7, and there are 192 such patches. Scenario 1: directly embedding the 4-connected components. Scenario 2: embedding the WUL subgraphs extracted using Algorithm 1. Scenario 3: embedding the WUL subgraphs extracted using Algorithm 2. Note that for the subgraph embeddings we use FULL-SDP for noise-free data, and SNL-SDP for noisy data

η (%)	Scenario 1	Scenario 2	Scenario 3
0	5.3e−02	4.9e−03	1.3e−03
10	8.8e−02	5.2e−02	5.3e−02
20	1.5e−01	1.1e−01	1.1e−01
30	2.3e−01	2.0e−01	2.0e−01

The results detailed in Fig. 8, while showing improvements of the second and third scenarios over the first one, may not entirely convince the reader of the usefulness of our proposed randomized algorithm, since in the first scenario a direct embedding of the patches using FULL-SDP already gives a very good reconstruction, i.e., 8.4e−4 on average. We regard 4-connectivity a significant constraint that very likely renders a random geometric star graph to become globally rigid, thus diminishing the marginal improvements of the WUL extraction algorithm. To that end, we run experiments similar to those reported in Fig. 8, but this time on the 1-hop neighborhood of each node in the UNITCUBE graph, without further extracting the 4-connected components. In addition, we sparsify the graph by reducing the sensing radius from ρ =0.3 to 0.26. Table 3 shows the reconstruction errors, at various levels of noise. Note that in the noise-free case, Scenarios 2 and 3 yield results which are an order of magnitude better than that of Scenario 1, which returns a rather poor average ANE of 5.3e−02. However, for the noisy case, these marginal improvements are considerably smaller.

Table 4 shows the total number of nodes removed from the patches by Algorithms 1 and 2, the number of 1-hop neighborhoods which are readily WUL, and the running times. Indeed, for the sparser UNITCUBE graph with ρ =0.26, the number of patches which are already WUL is almost half, compared with the case of the denser graph with ρ =0.30.

Table 4.

Comparison of the two algorithms for extracting WUL subgraphs, for the UNICUBE graphs with sensing radius (ρ) 0.30 and 0.26, and noise level (η) 0%. The WUL patches are those patches for which the subgraph extraction algorithms did not remove any nodes

	ρ =0.30, n=197		ρ =0.26, n=192
	Algorithm 1	Algorithm 2	Algorithm 1	Algorithm 2
Total number of nodes removed	31	26	258	285
Nr of WUL patches	188	191	104	101
Running time (s)	887	48	632	26

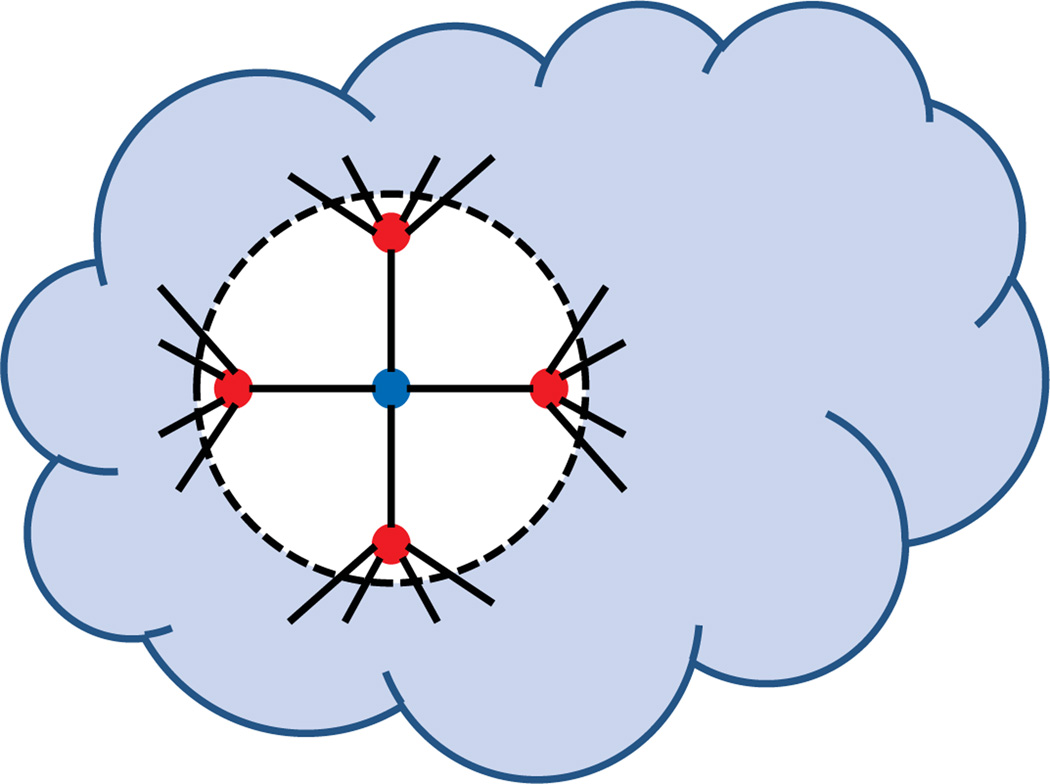
Finally, we remark on one of the consequences of our approach for breaking up the measurement graph. It is possible for a node not to be contained in any of the patches, even if it attaches in a globally rigid way to the rest of the measurement graph. An easy example is a star graph with four neighbors, no two of which are connected by an edge, as illustrated by the graph in Fig. 9. However, we expect such pathological examples to be very unlikely in the case of random geometric graphs.

Fig. 9.

An example of a graph with a node that attaches globally rigidly to the rest of the graph, but is not contained in any patch, and thus it will be discarded by 3D-ASAP.

4.2 Finding pseudo-anchors

To satisfy the conditions of Theorem 4.1, at least d + 1 anchors are necessary for embedding a patch, hence for the molecule problem we need k ≥ 4 such anchors in each patch. Since anchors are not usually available, one may ask whether it is still possible to find such a set of nodes that can be treated as anchors. If one were able to locate a clique of size at least d + 1 inside a patch graph, then using cMDS it is possible to obtain accurate coordinates for the d + 1 nodes and treat them as anchors. Whenever this is possible, we call such a set of nodes pseudo-anchors. Intuitively, the geometric graph assumption should lead one into thinking that if the patch graph is dense enough, it is very likely to find a complete subgraph on d + 1 nodes. While a probabilistic analysis of random geometric graphs with forbidden K_d+1 subgraphs is beyond of scope of this paper, we provide an intuitive connection with the problem of packing spheres inside a larger sphere, as well as numerical simulations that support the idea that a patch of size at least ≈10 is very likely to contain four such pseudo-anchors.

To find pseudo-anchors for a given patch graph G_i, one needs to locate a complete subgraph (clique) containing at least d + 1 vertices. Since any patch G_i contains a center node that is connected to every other node in the patch, it suffices to find a clique of size at least three- in the 1-hop neighborhood of the center node, i.e., to find a triangle in G_i\i. Of course, if a graph is very dense (i.e., has high average degree) then it will be forced to contain such a triangle. To this end, we remind one of the first results in extremal graph theory (Mantel 1907), which states that any given graph on s vertices and more than $\frac{1}{4}{s}^2$ edges contains a triangle, the bipartite graph with V₁ =V₂ =s/2 being the unique extremal graph without a triangle and containing $\frac{1}{4}{s}^2$ edges. However, this quadratic bound which holds for general graphs is very unsatisfactory for the case of random geometric graphs.

Recall that we are using the geometric graph model, where two vertices are adjacent if and only if they are less than distance ρ apart. At a local level, one can think of the geometric graph model as placing an imaginary ball of radius ρ centered at node i, and connecting i to all nodes within this ball; and also connecting two neighbors j, k of i if and only if j and k are less than ρ units apart. Ignoring the center node i, the question to ask becomes how many nodes can one fit into a ball of radius ρ such that there exist at least d nodes whose pairwise distances are all less than ρ. In other words, given a geometric graph H inscribed in a sphere of radius ρ, what is the smallest number of nodes of H that forces the existence of a K_d.

The astute reader might immediately be led into thinking that the problem above can be formulated as a sphere packing problem. Denote by x₁, x₂,…, x_m the set of m nodes (ignoring the center node) contained in a sphere of radius ρ. We would like to know what is the smallest m such that at least d =3 nodes are pairwise adjacent, i.e., their pairwise distances are all less than ρ.

To any node x_i associate a smaller sphere S_i of radius ρ/2. Two nodes x_i, x_j are adjacent, meaning less than distance ρ apart, if and only if their corresponding spheres S_i and S_j overlap. This line of thought leads one into thinking how many non-overlapping small spheres can one pack into a larger sphere. One detail not to be overlooked is that the radius of the larger sphere should be $\frac{3}{2}\rho$, and not ρ, since a node x_i at distance ρ from the center of the sphere has its corresponding sphere S_i contained in a sphere of radius $\frac{3}{2}\rho$. We have thus reduced the problem of asking what is the minimum size of a patch that would guarantee the existence of four anchors, to the problem of determining the smallest number of spheres of radius $\frac{1}{2}\rho$ that can be ‘packed’ in a sphere of radius $\frac{3}{2}\rho$ such that at least three of the smaller spheres pairwise overlap. Rescaling the radii such that $\frac{3}{2}\rho =1$ (hence $\frac{3}{2}\rho =\frac{1}{3}$), we ask the equivalent problem: How many spheres of radius $\frac{1}{3}$ can be packed inside a sphere of radius 1, such that at least three spheres pairwise overlap.

A related and slightly simpler problem is that of finding the densest packing on m equal spheres of radius r in a sphere of radius 1, such that no two of the small spheres overlap. This problem has been recently considered in more depth, and analytical solutions have been obtained for several values of m. If $r=\frac{1}{3}$ (as in our case), then the answer is m=13 and this constitutes a lower bound for our problem.

However, the arrangements of spheres that prevent the existence of three pairwise overlapping spheres are far from random, and motivated us to conduct the following experiment. For a given m, we generate m randomly located spheres of radius $\frac{1}{3}$ inside the unit sphere, and count the number of times at least three spheres pairwise overlap. We ran this experiment 15, 000 times for different values of m=5, 6, 7, respectively 8, and obtained the following success rates 69, 87, 96%, respectively 99%, i.e., the percentage of realizations for which three spheres of radius $\frac{1}{3}$ pairwise overlap. The simulation results show that for m=9, the existence of three pairwise overlapping spheres is very highly likely. In other words, for a patch of size 10 including the center node, there are very likely to exist at least four nodes that are pairwise adjacent, i.e., the four pseudo-anchors we are looking for.

4.3 Embedding patches

After extracting patches, i.e., WUL subgraphs of the 1-hop neighborhoods, it still remains to localize each patch in its own frame. Under the assumptions of the geometric graph model, it is likely that 1-hop neighbors of the central node will also be interconnected, rendering a relatively high density of edges for the patches. Indeed, as indicated by Fig. 4 (right panel), most patches have at least half of the edges present. For noise-free distances, we embed the patches using the FULL-SDP algorithm [14], while for noisy distances we use the SNL-SDP algorithm of [53]. To improve the overall localization result, the SDP solution is used as a starting point for a gradient-descent method.

The remaining part of this subsection is a brief survey of recent SDP relaxations for the graph localization problem [9–11, 14, 62]. A solution p₁,…, p_n ∈ ℝ³ can be computed by minimizing the following error function

$$\underset{p_1,\dots ,p_n\in {ℝ}^3}{\text{min}}\sum _{(i,j)\in E}{({\Vert p_i-p_j\Vert }^2-d_{ij}^2)}^2.$$ (4.4)

While the above objective function is not convex over the constraint set, it can be relaxed into an SDP [10]. Although SDP can be generally solved (up to a given accuracy) in polynomial time, it was pointed out in [11] that the objective function (4.4) leads to a rather expensive SDP, because it involves fourth-order polynomials of the coordinates. Additionally, this approach is rather sensitive to noise, because large errors are amplified by the objective function in (4.4), compared with the objective function in (4.5) discussed below.

Instead of using the objective function in (4.4), [11] considers the SDP relaxation of the following penalty function

$$\underset{p_1,\dots ,p_n\in {ℝ}^3}{\text{min}}\sum _{(i,j)\in E}|{\Vert p_i-p_j\Vert }^2-d_{ij}^2{|}^2.$$ (4.5)

In fact, [11] also allows for possible non-equal weighting of the summands in (4.5) and for possible anchor points. The SDP relaxation of (4.5) is faster to solve than the relaxation of (4.4) and it is usually more robust to noise. Constraining the solution to be in ℝ³ is non-convex, and its relaxation by the SDP often leads to solutions that belong to a higher dimensional Euclidean space, and thus need to be further projected to ℝ³. This projection often results in large errors for the estimation of the coordinates. A regularization term for the objective function of the SDP was suggested in [11] to assist it in finding solutions of lower dimensionality and preventing nodes from crowding together towards the center of the configuration.

4.4 Additional information specific to the molecule problem

In this section, we discuss several additional constraints specific to the molecule problem, which are currently not being exploited by 3D-ASAP. While our algorithm can benefit from any existing molecular fragments and their known reflection, there is still information that it does not take advantage of, and which can further improve its performance. Note that many of the remarks below can be incorporated in the pre-processing step of embedding the patches, described in the previous section.

The most important piece of information missing from our 3D-ASAP formulation is the distinction between the ‘good’ edges (bond lengths) and the ‘bad’ edges (noisy NOEs). The current implementations of the FULL-SDP and SNL-SDP algorithms do not incorporate such hard distance constraints.

One other important information which we are ignoring is given by the residual dipolar coupling (RDC) measurements that give noisy angle information (cos²(θ)) with respect to a global orientation [8].

Another approach is to consider an energy-based formulation that captures the interaction between atoms in a readily computable fashion, such as the Lennard–Jones potential. One may then use this information to better localize the patches, and prefer patches that have lower energy.

The minimum distance constraint, also referred to as the ‘hard sphere’ constraint, comes from the fact that any two atoms cannot get closer than a certain distance κ ≈ 1 Å. Note that such lower bounds on distances can be easily incorporated into the SDP formulation.

It is also possible to use the information carried by the non-edges of the measurement graph. Specifically, the distances corresponding to the missing edges cannot be smaller than the sensing radius ρ. Two remarks are in place however; under the current noise model, it is possible for true distances smaller than the sensing radius not to be part of the set of available measurements, and vice versa, it is possible for true distances larger than the sensing radius to become part of the distance set. However, since this constraint is not as certain as the hard sphere constraint, we recommend using the latter one.

Finally, one can envisage that significant other information can be reduced to distance constraints and incorporated into the approach described here for the calculation of structures and complexes. Such development could significantly speed such calculations if it incorporates larger molecular fragments based on modeling, similarly to chemical shift data etc., as done with computationally intensive experimental energy methods, e.g., HADDOCK [56].

4.5 Aligning patches

Given two patches P_k and P_l that have at least four nodes in common, the registration process finds the optimal 3D rigid motion of P_l that aligns the common points (as shown in Fig. 10). A closed form solution to the registration problem in any dimension was given in [34], where the best rigid transformation between two sets of points is obtained by various matrix manipulations and eigenvalue/eigenvector decomposition.

Fig. 10.

Optimal alignment of two patches that overlap in four nodes. The alignment provides a measurement for the ratio of the two group elements in Euc(3). In this example we see that a reflection was required to properly align the patches.

Since alignment requires at least four overlapping nodes, the K4 patches that are fully contained in larger patches are initially discarded. Other patches may also be discarded if they do not intersect any other patch in at least four nodes. The nodes belonging to such patches but not to any other patch would not be localized by ASAP.

As expected, in the case of the geometric graph model, the overlap is often small, especially for small values of ρ. It is therefore crucial to have robust alignment methods even when the overlap size is small. We refer the reader to Section 6 of [21] for other methods of aligning patches with fewer common nodes in ℝ², i.e., the combinatorial method and the link method which can be adjusted for the three-dimensional case. The combinatorial score method makes use of the underlying assumption of the geometric graph model. Specifically, we exploit the information in the non-edges that correspond to distances larger than the sensing radius ρ and use this information for estimating both the relative reflection and rotation for a pair of patches that overlap in just three nodes (or more). The link method is useful whenever two patches have a small overlap, but there exist many cross edges in the measurement graph that connect the two patches. Suppose that the two patches P_k and P_l overlap in at least one vertex, and call a link edge an edge (u, v) ∈ E that connects a vertex u in patch P_k (but not in P_l) with a vertex v in patch P_l (but not in P_k ). Such link edges can be incorporated as additional information (besides the common nodes) into the registration problem that finds the best alignment between a pair of patches. The right plot in Fig. 5 shows a histogram of the intersection sizes between patches in the BRIDGE-DONUT graph that overlap in at least four nodes.

5. Spectral-Partitioning-ASAP (3D-SP-ASAP)

In this section, we introduce 3D-Spectral-Partitioning-ASAP (3D-SP-ASAP), a variation of the 3D-ASAP algorithm, which uses spectral partitioning as a preprocessing step for the localization process.

3D-SP-ASAP combines ideas from both DISCO [42] and ASAP. The philosophy behind DISCO is to recursively divide large problems into smaller problems, which can ultimately be solved by the traditional SDP-based localization methods. If the number of atoms in the current group is not too large, DISCO solves the atom positions via SDP and refines the coordinates by using gradient descent; otherwise, it breaks the current group of atoms into smaller subgroups, solves each subgroup recursively, aligns and combines them together, and finally it improves the coordinates by applying gradient descent. The main question that arises is how to divide a given problem into smaller subproblems. DISCO chooses to divide a large group of nodes into exactly two subproblems, solves each problem recursively and combines the two solutions. In other words, it builds a binary tree of problems, where the leaves are problems small enough to be embedded by SDP. However, not all available information is being used when considering only a single spanning tree of the graph of patches. The 3D-ASAP approach fuses information from different spanning trees via the eigenvector computation. However, compared with the number of patches used in DISCO, 3D-ASAP generates many more patches, since the number of patches in 3D-ASAP is linear in the size of the network. This can be considered as a disadvantage, since localizing all the patches is often the most time-consuming step of the algorithm. 3D-SP-ASAP tries to reduce the number of patches to be localized while using the patch graph connectivity in its full.

When dividing a graph into two smaller subgraphs, one wishes to minimize the number of edges between the two subgraphs, since in the localization of the two subgraphs the edges across are being left out. Simultaneously, one wishes to maximize the number of edges within the subgraphs, because this makes the subgraphs more likely to be globally rigid and easier to localize. In general, the graph partitioning problem seeks to decompose a graph into K disjoint subgraphs (clusters), while minimizing the number of cut edges, i.e., edges with endpoints in different clusters. We refer the reader to the literature on normalized cuts and spectral relaxations that can be computed efficiently [47, 57]. We use the spectral clustering method in [47] to partition the measurement graph in the molecule problem. The gist of the approach is to use the classical K-means clustering algorithm on the Laplacian eigenmap embedding of the set of nodes. If A is the adjacency matrix of the graph G, and D is a diagonal matrix with D_i,i =deg(i), i=1,…, n, then the Laplacian eigenmap embedding of node i in ℝ^k is given by (ϕ₁(i), ϕ₂(i),…, ϕ_K(i)), where ϕ_j is the jth eigenvector of the matrix D⁻¹ A. For an extensive literature survey on spectral clustering algorithms, we refer the reader to [55]. We remark that other clustering algorithms (e.g., [33]) may also be used to partition the graph.

The approach we used for localization in conjunction with the above-normalized spectral clustering algorithm is as follows (3D-SP-ASAP):

1. We first decompose the measurement graph into K partitions 𝒫₁,…,𝒫_K, using the normalized spectral clustering algorithm.

2. We extend each partition 𝒫_i, i=1,…,K to include its 1-hop neighborhood, and denote the new patches by P_i, i=1,…,K.

3. For every pair of patches P_i and P_j which have nodes in common or are connected by link edges,¹³ we build a new (link) patch that contains all the common points and link edges. The vertex set of the new patch consists of the nodes that are common to both P_i and P_j, together with the endpoints of the link edges that span across the two patches. Note that the new list of patches contains the extended patches built in Step (2) P₁,…, P_K, as well as the newly built patches P_K+1,…, P_L.

4. We extract from each patch P_i, i=1,…, L the WUL subgraph, and embed it using the FULL-SDP algorithm for noise-free data, and the SNL-SDP algorithm for noisy data.

5. Synchronize all available patches using the eigenvector synchronization algorithm used in ASAP.

Note that when the extended patches from Step (2) are highly overlapping, Step (3) of the algorithm should be omitted, for reasons detailed below related to the robustness of the embedding. The reason for having Steps (2), and possibly (3), is to be able to align nearby patches. Without Step (2) patches will have disjoint sets of nodes, and the alignment will be based only on the link edges, which is not robust for high levels of noise. Without Step (3) the existing patches may have little overlap, in which case we expect the alignment involving link edges not to be robust at high levels of noise. By building the link patches, we provide 3D-SP-ASAP more accurate pairwise alignments. Note that embedding link patches is less robust to noise, due to their bipartite-like structure, especially when the bipartitions are very loosely connected to each other (also confirmed by our computations involving link patches). In addition, having to localize a larger number of patches may significantly increase the running time of the algorithm. However, for our numerical experiments with 3D-SP-ASAP conducted on the BRIDGE-DONUT graph, the extended partitions built in Step (2) were highly overlapping, and allowed us to localize the entire network without the need to build the link patches in Step (3).

The advantage of combining a spectral partitioning algorithm with 3D-ASAP is a decrease in running time as shown in Tables 5 and 6, due to a significantly smaller number of patches that need to be localized. Note that the graph partitioning algorithm is extremely fast, and partitions the BRIDGE-DONUT measurement graph in less than half a second. Table 7 shows the ANE reconstruction errors for the BRIDGE-DONUT graph, when we partition the measurement graph into K =8 and K =25 clusters. For K =8, some of the extended partitions become very large, containing as many as 150 nodes, and SNL-SDP does a very poor job at embedding such large patches when the distance measurements are noisy. By increasing the number of partitions to K = 25, the extended partitions contain less nodes, and are small enough for SNL-SDP to localize accurately even for high levels of noise. Note that the ANE errors for 3D-SP-ASAP with K = 25 are comparable with those of ASAP, while the running time is dramatically reduced (by an order of magnitude, for the BRIDGE-DONUT example with η =35%). Figures 11 and 12 show various K-partitions of the PACM and the BRIDGE-DONUT graphs.

Table 5.

Running times (in seconds) of the 3D-SP-ASAP algorithm for the BRIDGE-DONUT graph with n=500 nodes, η =0%, 35%, deg=18, 21, and k =8, 25 partitions. For η =0% we embed the patches using FULL-SDP, while for η =35% we use SNL-SDP since the regularization term improves the localization

Number of partitions k	k = 8		k = 25
Noise level η	0%	35%	35%
Spectral partitioning	0.3	0.3	0.7
Finding WUL subgraphs	48	81	89
Embedding FULL-SDP	53	(82)	(89)
Embedding SNL-SDP	(26)	50	86
Step 1 (ℤ2 × SO(3))	1	1	1
Step 2 (least squares)	6	8	9
Total	108	140	186

Table 6.

Running times (in seconds) of the 3D-ASAP algorithm for the BRIDGE-DONUT graph with n=500 nodes, η =0%, 35%, deg =18, 21, n=533, 541 patches, and average patch sizes 17.8, 20.3. For η =0% we embed the patches using FULL-SDP, while for η =35% we use SNL-SDP since the regularization term improves the localization. For η =35%, during the least-squares step we also use the scaling heuristic, and run the gradient descent algorithm several times, hence the increase in the running time from 6 to 21 s

	η =0%	η =35%
Break G into patches	59	90
Finding WUL subgraphs	210	233
Embedding FULL-SDP	154	(252)
Embedding SNL-SDP	(966)	1368
Denoising patches	30	39
Step 1 (ℤ2 × SO(3))	15	19
Step 2 (least squares)	6	21
3D-ASAP	474	1770
DISCO	196	197
3D-SP-ASAP	108	186

Table 7.

Reconstruction errors (measured in ANE) for the BRIDGE-DONUT graph with n= 500 vertices, sensing radius (ρ) =0.92 and average degrees (deg)=18 − 25. We used k to denote the number of partitions of the vertex set. For η =0 we embed each of the k patches (extended partitions) using FULL-SDP, while for η > 0 we used the SNL-SDP algorithm. At η = 50%, 3D-SP-ASAP_k=8localizes only 435 out of the 500 nodes

η (%)	3D-ASAP	3D-SP-ASAPk=8	3D-SP-ASAPk=25	DISCO
0	6e–4	4e–4	2e–4	4e–3
10	0.04	0.59	0.03	0.03
20	0.05	0.48	0.04	0.07
30	0.11	0.52	0.14	0.30
35	0.12	0.33	0.15	0.21
40	0.24	0.42	0.19	0.27
45	0.28	0.71	0.32	0.35
50	0.23	0.35	0.35	0.40

Fig. 11.

Partitions of the PACM graph (K is the number of partitions).

Fig. 12.

Partitions of the BRIDGE-DONUT graph (K is the number of partitions).

6. The MDA and a rescaling heuristic

In this section, we describe a method to improve the localization of the individual patches prior to the patch alignment and global synchronization steps. The main observation here is the following: suppose a pair of nodes appear in several different patches, then each patch provides a different estimation for their distance, and all these estimators can be averaged together to provide a perhaps more accurate estimator. The improved re-estimated distances are then used to localize the individual patches again, this time using the cMDS algorithm since patches no longer contain any missing distances. The second part of this section introduces a simple rescaling procedure, which increases the accuracy of the final reconstruction.

Denote by C_k (k = 1,…,N) the set of all pairwise edges within patch P_k (so if P_k has t nodes then C_k contains all $(\begin{array}{c}t\\ 2\end{array})$ edges). Let 𝒞 denote the set of all edges that appear in at least one patch, i.e., $𝒞={\cup }_{k=1}^N{C}_k$. Note that 𝒞 contains edges (i, j) that were initially missing from the measurement set (i.e., (i, j) ∉ E) but for which we now have an estimate due to the initial localization of the patches (using, say, SDP). After the initial embedding, we have at least one estimated distance for each edge (i, j) ∈ 𝒞, but because patches overlap, most of the edges appear in more than one patch. Denote by $d_{ij}^1,d_{ij}^2$, … the set of estimates for the (possibly missing) distance (i, j), where $d_{ij}^k,$ is the distance between nodes i and j in the SDP embedding of patch P_k. To obtain a more accurate estimate of d_ij, we take the median of all the above estimates and denote the updated value by

$${\tilde{d}}_{ij}=\text{median}(d_{ij}^1,d_{ij}^2,\dots ).$$ (6.1)

If the noise level in the originally measured distances is small, then we expect the estimates $d_{ij}^1,d_{ij}^2$, … to have small variance and take values close to the true distance. However, for higher levels of noise, many of the estimates can be very inaccurate (either highly overestimating or underestimating the true distances), and we choose the median value to approximate the true distance. Tables 8 and 9 show that MDA is indeed effective and reduces the noise level in the distances, usually by at least a few percentages. Note that the SDP improves by itself on the initial distance measurements (those that are available) and the MDA decreases their noise even further.

Table 8.

Denoising distances at various levels of noise, for the UNITCUBE data set. ${\overline{\text{ANE}}}_{\text{old}}$ and ${\overline{\text{ANE}}}_{\text{new}}$ denote the average ANE of all patches after the SDP embedding, respectively, after the cMDS embedding with the distances denoised by MDA. η̄ is the empirical noise level (averaged over all noisy distances), η̄_SDP is the noise level after the SDP embedding, η̄_MDA is the noise level after running MDA. We show the noise levels individually for both the existing and missing distances. Note that η̄ ≠ η since the former denotes the average absolute value deviation from the true distance as a percentage of the true distance, while the latter is the parameter in the uniform distribution in (8.1) that is used to define the noise model (in fact, 𝔼[η̄]=η/2)

			Existing distances			Missing distances
η (%)	${\overline{\text{ANE}}}_{\text{old}}$	${\overline{\text{ANE}}}_{\text{new}}$	η̄	η̄SDP	η̄MDA	η̄SDP	η̄MDA
10	0.04	0.03	5.06	3.75	3.42	3.37	3.13
20	0.10	0.078	10.28	8.22	7.5	8.91	8.12
30	0.18	0.14	15.95	14.09	13.03	17.99	16.83
40	0.27	0.22	21.74	20.66	19.31	29.09	27.72
50	0.37	0.32	29.11	28.76	27.5	42.14	40.92

Table 9.

Denoising distances at various levels of noise for the ubiqutin (PDG 1d3z, [19]). η̄_SDP,GOOD denotes the average noise of the hard constraint (‘good’) distances after the SDP embeddings. Note that the current implementation of the SNL-SDP algorithm used for the patch embeddings does not allow for hard distance constraints

				Existing distances				Missing distances
η (%)	${\overline{\text{ANE}}}_{\text{old}}$	${\overline{\text{ANE}}}_{\text{new}}$	η̄	η̄SDP	η̄SDP,GOOD	η̄MDA	η̄SDP	η̄MDA
0	0.00048	0.00039	0	0.02	0.14	0	0.38	0.32
10	0.00316	0.00266	4.91	3.42	1.79	3.13	3.2	2.99
20	0.00590	0.00506	9.81	7.01	3.68	6.44	6.18	5.81
30	0.00957	0.00803	14.74	10.75	5.59	9.88	9.51	8.95
40	0.01292	0.01120	19.65	14.5	7.62	13.42	13.55	12.8
50	0.01639	0.01462	24.57	18.1	9.82	16.93	18.24	17.35

To take advantage of the more accurate updated distance values, we recompute the embeddings of all N patches using the cMDS algorithm, since there exists an estimate for all pairwise distances within a patch. Whenever a hard constrained distance (a ‘good’ edge) is present, such as a bond length, we use its true distance in the cMDS embeddings and ignore the noisy value returned by the SDP since hard constrained distances are not enforced in the SDP.

Tables 8 and 9 show the average ANE of the patches after the SDP embeddings (${\overline{\text{ANE}}}_{\text{old}}$), and after the cMDS embeddings ran on the updated distances (${\overline{\text{ANE}}}_{\text{new}}$). Note that the new patch embeddings are significantly more accurate, in some cases the ANE decreasing by as much as 25%. We also experimented with an iterative version of this denoising algorithm, where at each round we run the cMDS and recompute the median of the updated distances. However, subsequent iterations of this procedure did not improve the accuracy furthermore.

In the remaining part of this section, we discuss the issue of scaling of the distances after different steps of the algorithm, and propose a simple rescaling heuristic that improves the overall reconstruction.

We denote the true distance measurements by l_ij = ∥p_i − p_j∥, (i, j) ∈ E, and the empirical measurements by d_ij = l_ij + ε_ij, (i, j) ∈ E, where ε_ij is random independent noise, as introduced in (8.1). We generically refer to d̃_ij as the distance between nodes i and j, after different steps of the algorithm, as indicated by the columns of Tables 10 and 11. We denote by δ the average scaling of the distances with respect to their ground truth values, and similarly by κ the average empirical noise of the distance measurements

$$\delta =\text{mean}(\frac{l_{ij}}{{\tilde{d}}_{ij}},(i,j)\in E),\kappa =\text{mean}\left(\right|\frac{{\tilde{d}}_{ij}-l_{ij}}{l_{ij}}|,(i,j)\in E).$$

Table 10.

Average scaling and noise of the existing edges (and where appropriate the ANE of the reconstruction) for the UNITCUBE graph, at various steps of the algorithm: after the original measurements, after the SDP-MDA-cMDS denoising step, after the least squares in Step 3, after rescaling of the available distances by the empirical scaling factor δ*, and after running gradient descent on the rescaled (originally available) distances

	Original		MDA-cMDS		Least squares			Rescaled		Gradient descent
η (%)	δ	κ(%)	δ	κ(%)	δ	κ(%)	ANE	δ*	ANE	δ	κ(%)	ANE
10	1.01	5.1	1.01	3.4	1.02	3.6	0.05	1.01	0.05	1.00	3.0	0.04
20	1.05	10.3	1.04	7.5	1.08	8.8	0.12	1.04	0.10	1.02	6.1	0.07
30	1.12	16.0	1.11	13.0	1.21	17.0	0.25	1.09	0.20	1.04	9.9	0.16
40	1.22	21.8	1.21	19.3	1.43	27.8	0.36	1.21	0.26	1.04	13.9	0.19
45	1.29	26.0	1.28	23.8	1.65	35.6	0.45	1.32	0.30	1.02	17.8	0.26
50	1.38	29.2	1.36	27.5	1.92	43.8	0.53	1.47	0.35	0.99	22.4	0.32

Table 11.

Average scaling and noise of all edges (good+NOE) of the ubiqutin (PDG 1d3z) (and where appropriate the ANE of the reconstruction) at various steps of the algorithm: after the original measurements, after the SDP-MDA-cMDS denoising step, after the least squares in Step 3, after rescaling of the available distances by the empirical scaling factor δ*, and after running gradient descent on the rescaled NOE distances

	Original		MDA-cMDS		Least squares			Rescaled		Gradient descent
η (%)	δ	κ(%)	δ	κ(%)	δ	κ(%)	ANE	δ*	ANE	δ	κ(%)	ANE
10	1.00	0.03	1.00	0.02	1.02	0.04	0.01	1.02	4e–3	0.99	0.01	3e–3
20	1.01	0.06	1.00	0.04	1.04	0.07	0.01	1.03	0.01	0.99	0.02	0.01
30	1.02	0.08	1.01	0.06	1.06	0.10	0.02	1.05	0.01	0.99	0.03	0.01
40	1.03	0.11	1.01	0.08	1.10	0.14	0.02	1.09	0.02	0.99	0.05	0.01
50	1.06	0.14	1.02	0.10	1.18	0.19	0.04	1.16	0.03	0.98	0.08	0.01

The first column of the tables contains the scaling and noise values of the initial distance measurements, taken as input by ASAP. The fact that κ is approximately half the value of the noise level η stems from the fact that the measurements are uniformly distributed in [(1 − η)l_ij, (1 + η)l_ij]. Note that the initial scaling is quite significant, and this is a consequence of the same noise model and the geometric graph assumption. Distances that are scaled down by the noise will still be available to 3D-ASAP, while distances that are scaled up and become larger than the sensing radius will be ignored. Therefore, on average, the empirical distances are scaled down and δ is > 1.

The second column gives the scaling and noise values after the MDA algorithm followed by cMDS to recompute the patches. Note that after this denoising heuristic, while the scaling δ remains very similar to the original values, the noise κ decreases considerably especially for the lower levels of noise.

The third column computes the scaling, noise and ANE values after the least-squares step for estimating the translations, where by ANE we mean the ANE introduced in (8.2). Note that both the scaling and the noise levels significantly increase after integrating all patches in a globally consistent frame-work. To correct the scaling issue, we scale up all the available distances (thus taking into account only the edges of the initial measurement graph) by δ*, computed as

$${\delta }^{*}=\text{mean}(\frac{d_{ij}}{{\tilde{d}}_{ij}^{LS}},(i,j)\in E),$$

where d_ij denotes the initial distances, and ${\tilde{d}}_{ij}^{LS}$ the distances after the least-square step. Note that, as a consequence, the ANE error of the reconstruction decreases significantly.

Finally, we refine the solution by running gradient descent, on the initial distances d_ij scaled up by δ*, which further improves the scaling, noise and ANE values.

7. Synchronization with molecular fragments

In the molecule problem, as mentioned earlier, there are molecular fragments whose local configuration is known in advance up to an element of the special Euclidean group SE(3) rather than the Euclidean group E(3). In other words, these are small structures that need to be translated and rotated with respect to the global coordinate system, but no reflection is required. As a result, for their corresponding patches we know the corresponding group element in ℤ₂. This motivates us to consider the problem of synchronization over ℤ₂ when ‘molecular fragment’ information is available, and refer to it from now on as SYNC(ℤ₂). We propose and compare four methods for solving SYNC(ℤ₂): two relaxations to a quadratically constrained quadratic program (QCQP) and two SDP formulations.

Mathematically, the synchronization problem over the group ℤ₂ = {±1} can be stated as follows: given k group elements (anchors) 𝒜 = {a₁,…, a_k} and a set of (possibly) incomplete (noisy) pairwise group measurements $Z_{ij}=a_i{x}_j^{-1}$ and $Z_{ij}=x_i{x}_j^{-1}$, (i, j) ∈ E(G), find the unknown group elements (atoms) 𝒮 = {x₁,…, x_l}. We may sometimes abuse notation and denote all nodes by x = {x₁,…, x_l, x_l+1,…, x_N}, where N =l + k, with the understanding that the last k elements denote the anchors. Whenever we say that indices i ∈ 𝒮 and j ∈ 𝒜, it should be understood that we refer to atoms x_i ∈ 𝒮, respectively anchor a_j ∈ 𝒜. In the molecule problem, k denotes the number of patches whose reflection is known a priori, and the goal is to estimate the reflection of the remaining l = N − k patches.

7.1 Synchronization by relaxing a QCQP

When anchor information is available, meaning that we know a priori some of the group elements which we refer to as anchors, we follow a similar approach to the objective function that motivated the eigen-vector synchronization method. Similarly, we are interested in finding the set of unknown elements that maximize the number of satisfied pairwise measurements, but this time, under the additional constraints imposed by the anchors, i.e., x_i =a_i, i ∈ 𝒜. Unfortunately, maximizing the quadratic form x^⊤ Zx under the anchor constraints is no longer an eigenvector problem. Our approach is to combine under the same objective function both the contribution of the atom–atom pairwise measurements (as a quadratic term) and the contribution of the anchors–atom pairwise measurements (as a linear term). To that end, we start by formulating the synchronization problem as a least-squares problem, by minimizing the following quadratic form

$$\underset{x}{\text{min}}\sum _{(i,j)\in E}{(x_i-z_{ij}{x}_j)}^2=\underset{x}{\text{min}}\sum _{(i,j)\in E}{z}_i^2+Z_{ij}^2{x}_j^2-2Z_{ij}{x}_i{x}_j=\underset{x}{\text{min}}\sum _{(i,j)\in E}{x}_i^2+x_j^2-2Z_{ij}{x}_i{x}_j=\underset{x}{\text{min}}\sum _{i=1}^n{d}_i{x}_i^2-\sum _{(i,j)\in E}2Z_{ij}{x}_i{x}_j=\underset{x}{\text{min}}{x}^{\top }Dx-x^{\top }Zx=\underset{x}{\text{min}}{x}^{\top }(D-Z)x.$$ (7.1)

To account for the existence of anchors, we first write the matrices Z and D in the following block format

$$Z=[\begin{array}{cc}\hfill S\hfill & \hfill U\hfill \\ \hfill U^{\top }\hfill & \hfill V\hfill \end{array}],D=[\begin{array}{cc}\hfill D_S\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill D_V\hfill \end{array}],$$

where S_l×l, U_l×k and V_k×k denote the atom–atom, atom–anchor, respectively, anchor–anchor measurements, respectively, and D is a diagonal matrix with $D_{ii}={\sum }_{j=1}^N|Z_{ij}|$. Note that V is a matrix with all nonzero entries, since the measurement between any two anchors is readily available. Similarly, we write (with a slight abuse of notation) the solution vector in the form x=[s a]^⊤, where s denotes the signs of the atom nodes and a the signs of the anchor nodes. The quadratic function minimized in (7.1) can now be written in the following form

$$[s^{\top }{a}^{\top }]\left[\begin{array}{cc}{D}_s-S\hfill & \hfill -U\hfill \\ \hfill -U^{\top }\hfill & \hfill D_V-V\hfill \end{array}\right]\left[\begin{array}{c}s\hfill \\ a\hfill \end{array}\right]=s^{\top }(D_S-S)s-2s^{\top }Ua+a^{\top }(D_V-V)a.$$ (7.2)

The vector (Ua)_l×1 can be interpreted as the anchor contribution in the estimation of the atoms. Note that in the case when the atom–anchor measurements should be trusted more than the atom– atom measurements, the anchor contribution can be weighted accordingly, and equation (7.2) becomes z^⊤ (D_S − S)z − 2γ z^⊤ Ua + a^⊤ (D_V − V)a, for a given weight γ Since a^⊤ (D_V − V)a is a (nonnegative) constant, we are interested in minimizing the integer quadratic form minimize

$$\underset{z\in {\mathbb{Z}}_2^l}{\text{minimize}}{z}^{\top }(D_S-S)z-2z^{\top }Ua.$$

Unfortunately, solving such a problem is NP-hard, and thus we introduce the following relaxation to a QCQP

$$\underset{z=(z_1,\dots ,z_l)}{\text{minimize}}{z}^{\top }(D_S-S)z-2z^{\top }Ua,\text{subject to}{z}^{\top }z=l.$$ (7.3)

We proceed by considering the Lagrangian function

$$\varphi (z,\lambda )=z^{\top }(D_S-S)z-2z^{\top }Ua+\lambda (z^{\top }z-l),$$ (7.4)

where λ is the Lagrange multiplier. Differentiating (7.4) with respect to z, we are led to the following equation

$$2(D_S-S)z-2Ua+2\lambda z=0,$$

which can be written as

$$(D_S-S+\lambda I)z=Ua.$$ (7.5)

Using the fact that z^⊤z =l, (7.5) becomes

$${(Ua)}^{\top }{(D_S-S+\lambda I)}^{-2}(Ua)=l,$$ (7.6)

which we solve for λ. We refer the reader to [6] for a more detailed analysis of eigenvalue solutions to such quadratically constrained optimization problems. Finally, the solution to the minimization problem formulated in (7.3) is given by

$$z^{*}={(D_S-S+\lambda I)}^{-1}(Ua),$$ (7.7)

For simplicity, we choose to solve the nonlinear matrix equality (7.6) in MATLAB using the lsqnonlin command, whose success in finding λ is contingent upon a good initialization. To that end, we consider the eigen decomposition of the symmetric positive definite matrix

$$D_S-S=\sum _{i=1}^l{\lambda }_i{\varphi }_i{{\varphi }_i}^{\top },$$

where (D − S)ϕ_i =λ_iϕ_i, for i=1,…, l, and expand the vectors Ua and z in the form $Ua={\sum }_{i=1}^l{\beta }_i{\varphi }_i$ and $z={\sum }_{i=1}^l{\alpha }_i{\varphi }_i$. Rewriting equation (7.5), (D_S − S)z + λz = Ua, in terms of the above expansion yields

$$\sum _{i=1}^l{\lambda }_i{\alpha }_i{\varphi }_i+\lambda \sum _{i=1}^l{\alpha }_i{\varphi }_i=\sum _{i=1}^l{\beta }_i{\varphi }_i.$$ (7.8)

Thus, for every i=1,…, l, it must hold true that

$${\lambda }_i{\alpha }_i+\lambda {\alpha }_i={\beta }_i,$$ (7.9)

i.e., α_i =β_i/(λ + λ_i). Since z^⊤z = l and ${\sum }_{i=1}^l{\alpha }_i^2=l$, the Lagrange multiplier λ must satisfy

$$\sum _{i=1}^l\frac{{\beta }_i^2}{{(\lambda +{\lambda }_i)}^2}=l.$$ (7.10)

The condition that λ + λ_i > 0 ensures that the solution search for λ lies outside the set of singularities of (7.10). Thus λ > − λ₀, where λ₀ is the smallest eigenvalue of the matrix D_S − S. Note that the row sums of D_S − S are non-negative since the diagonal entries in D_S are the degree of the atom nodes in the entire graph, taking into account the atom–anchor edges as well, not just the atom–atom edges. Furthermore, D_S − S is a positive semidefinite matrix (thus λ₀ ≥ 0), as it can be seen from the following identity:

$$X^{\top }(D_S-S)x=\sum _{i=1}^l{x}_i^2{d}_i-\sum _{(i,j)\in E_{SS}}2x_i{x}_j{S}_{ij}\ge \sum _{(i,j)\in E_{SS},S_{ij}=\pm 1}{(x_i-S_{ij}{x}_j)}^2\ge 0,$$

where E_SS denotes the set of atom–atom edges.

We also consider the following formulation similar to (7.3), but we replace the constraint z^⊤z =l with z^⊤D_Sz =Δ, where $\Delta ={\sum }_{i=1}^l$ d_i is the sum of the degrees of all atom nodes. Note that the following change of variable $\overline{z}=D_S^{1/2}z$ brings the new optimization problem to a form similar to (7.3)

$$\underset{\overline{z}}{\text{minimize}}{\overline{z}}^{\top }{D}_S^{-1/2}(D_S-S)D_S^{-1/2}\overline{z}-2{\overline{z}}^{\top }{D}_S^{-1/2}Ua,\text{Subject to}{\overline{z}}^{\top }\overline{z}=\Delta$$ (7.11)

with the corresponding Lagrangian λ̄ satisfying λ̄ > − λ̄₀, where λ̄₀ is the smallest eigenvalue of the matrix $D_S^{-1/2}(D_S-S)D_S^{-1/2}$.

7.2 Synchronization by SDP

An alternative approach to solving SYNC(ℤ₂) is by using SDP. The connection between the Lagrangian relaxation of the QCCP shown in the previous section and the SDP relaxation we are about the introduce was investigated in [23] and the references therein. The minimization of the least squares objective function in (7.1) is equivalent to the maximization of the following objective function:

$$\sum _{i,j=1}^N{x}_j{Z}_{ij}{x}_j-\text{Trace}(Z{\rm Y}),$$ (7.12)

where Υ is the N × N symmetric rank-one matrix with ±1 entries

$${{\rm Y}}_{ij}=\{\begin{array}{cc}{x}_i{x}_j^{-1}\hfill & \text{if}i,j,\in 𝒮,\hfill \\ x_i{a}_j^{-1}\hfill & \text{if}i,\in 𝒮,j,\in 𝒜,\hfill \\ a_i{a}_j^{-1}\hfill & \text{if}i,j,\in 𝒜.\hfill \end{array}$$ (7.13)

Note that Υ has ones on its diagonal Υ_ii =1, ∀i =1,…,N, and the anchor information gives another layer of hard constraints. The SDP relaxation in the presence of anchors becomes

$$\underset{{\rm Y}\in {ℝ}^{N\times N}}{\text{maximize}}\text{Trace}(Z{\rm Y})\text{subject to}{{\rm Y}}_{ij}=1,i=1,\dots ,N{{\rm Y}}_{ij}=a_i{a}_j^{-1},\text{if}i,j,\in 𝒜{\rm Y}\ge 0,$$ (7.14)

where the maximization is taken over all semidefinite positive real-valued matrices Υ ≥ 0. While Υ as defined in (7.14) has rank 1, the solution of the SDP is not necessarily of rank 1. We therefore compute the top eigenvector of that matrix and estimate x₁,…, x_s based on the sign of its first s entries.

Alternatively, to reduce the number of unknowns in (7.14) from N = l + k to l, one may consider the following relaxation:

$$\underset{{\rm Y}\in {ℝ}^{l\times l};x\in {ℝ}^l}{\text{maximize}}\text{Trace}(S{\rm Y})+2x^{\top }Ua\text{subject to}{{\rm Y}}_{ii}=1,\forall i=1,\dots ,l\left[\begin{array}{cc}\hfill {\rm Y}\hfill & \hfill x\hfill \\ \hfill x^{\top }\hfill & \hfill 1\hfill \end{array}\right]\ge 0.$$ (7.15)

Ideally, we would like to enforce the constraint Υ =xx^⊤, which guarantees that Υ is indeed a rank-1 solution. However, since rank constrains do not lead to convex optimization problems, we relax this constraint via Schur’s lemma to Υ ≥ zz^⊤. This last matrix inequality is equivalent [16] to the last constraint in the SDP formulation in (7.15). Finally, we obtain estimators ẑ₁,…, ẑ_l for the atoms by setting ẑ_i = sign(x_i), ∀_i =1,…, l.

7.3 Comparison of algorithms for SYNC(ℤ₂)

Figure 13 compares the performance of the algorithms that we proposed for synchronization in the presence of molecular fragment information. The adjacency graph of available pairwise measurements is an Erdős–Rényi graph G(N, p) with N =75 and p=0.2 (i.e., a graph with N nodes, where each edge is present with probability p, independent of the other edges). We show numerical experiments for four scenarios, where we vary the number of anchors k = {5, 15, 30, 50} chosen uniformly at random from the N nodes. As the number of anchors increases, compared with the number of atoms s=N − k, the performance of the four algorithms is essentially similar. Only when the number of anchor nodes is small (k =5), the SDP-Y formulation shows superior results, together with SDP-XY and QCQP with constraint z^⊤Dz =Δ, while the QCQP with constraint z^⊤z =s performs less well. In practice, one would choose the QCQP formulation with constraint z^⊤Dz =Δ, since the SDP-based methods are computationally expensive as the size of the problem increases. This was also our method of choice for computing the reflection of the patches in the localization of the ubiqutin (PDG 1d3z), when molecular fragment information was available and the reflection of many of the patches was known a priori.

Fig. 13.

Comparison, in terms of robustness to noise, of the four algorithms we proposed for SYNC(ℤ₂): the two QCQP formulations using the two different constraints: z^⊤z =s and z^⊤Dz =Δ as they appear in equations (7.3) and (7.11), the two SDP-based formulations SDP-Y and SDP-XY as formulated in (7.14) and (7.15). The adjacency graph of available pairwise measurements is an Erdős–Rényi graph G(N, p) with N =75 and p=0.2. Also, k denotes the number of anchors, chosen uniformly at random from the N nodes. Results are averaged over 50 runs.

8. Experimental results

We have implemented our 3D-ASAP algorithm and compared its performance with other methods across a variety of measurement graphs, varying parameters such as the number of nodes, average degree (sensing radius) and level of noise.

In our experiments, the noise is multiplicative and uniform, meaning that to each true distance measurement l_ij = ∥ p_i − p_j ∥, we add random independent noise ε_ij in the range [−ηl_ij, ηl_ij], i.e.,

$$d_{ij}=l_{ij}+{\epsilon }_{ij}{\epsilon }_{ij}~\text{Uniform}([-\eta l_{ij},\eta l_{ij}]).$$ (8.1)

The percentage noise added is 100η (e.g., η =0.1 corresponds to 10% noise).

The sizes of the graphs we experimented with range from 200 to 1000 nodes taking different shapes, with average degrees in the range 14–26 and noise levels up to 50%. Across all our simulations, we consider the geometric graph model, meaning that all pairs of nodes within range ρ are connected. Note that all the graphs considered throughout the paper are three dimensional, even if they visually look two dimensional in the attached figures.

We denote the true coordinates of all nodes by the 2 × n matrix P =(p₁ ⋯ p_n), and the estimated coordinates by the matrix P̂ =(p̂₁ ⋯ p̂_n). To measure the localization error of our algorithm, we first factor out the optimal rigid transformation between the true embedding P and our reconstruction P̂, and then compute the following ANE

$$\text{ANE}=\frac{\sqrt{{\sum }_{i=1}^n{\Vert p_i-{\widehat{p}}_i\Vert }^2}}{\sqrt{{\sum }_{i=1}^n{\Vert p_i-p_0\Vert }^2}}=\frac{{\Vert P-\widehat{P}\Vert }_F}{{\Vert P-p_0{\mathbf{1}}^{\top }\Vert }_F},$$ (8.2)

where $p_0=(1/n){\sum }_{i=1}^n{p}_i$ is the center of mass of the true coordinates. The normalization factor in the denominator of (8.2) ensures that the ANE is not only rigid invariant, but it is also scale free, i.e., it is invariant to scaling the underlying configuration by a constant factor.

The experimental results in the case of noise-free data (i.e., incomplete set of exact distances) should already give the reader an appreciation of the difficulty of the problem. As mentioned before, the graph realization problem is NP-hard, and the most we can aim for is an approximate solution. The main advantage of introducing the notion of a WUL graph and using it for breaking the original problem into smaller subproblems can be seen in the experimental results for noise-free data. Note that across all experiments, except for the PACM graph reconstructions, we are able to compute localizations which are at least one order of magnitude more accurate than what those computed by DISCO or SNL-SDP. Note that all algorithms are followed by a refinement procedure, in particular steepest descent with backtracking line search.

As expected, FAST-MVU performs at its best when the data are a set of random points uniformly distributed in the unit cube. In this case, the top three eigenvectors of the Laplacian matrix used by FAST-MVU provide an excellent approximation of the original coordinates. Indeed, as the experimental results in Table 12 show, the FAST-MVU algorithm gives the best precision across all algorithms, returning an ANE of 2e–6. However, in the case of noisy data, the performance of FAST-MVU degrades significantly, making FAST-MVU the least robust to noise algorithm tested on the UNITCUBE graph. Furthermore, FAST-MVU performs extremely poor on more complicated topologies, even in the absence of noise, as it can be seen in the reconstructions of the PACM and BRIDGE-DONUT graphs shown in Fig. 14. For comparison, the original underlying graphs are shown in Figs 15 and 16.

Table 12.

Reconstruction errors (measured in ANE) for the UNITCUBE graphs with n=212 vertices, sensing radius (ρ)=0.3 and average degrees (deg)=17 – 25

η (%)	3D-ASAP	DISCO	SNL-SDP	MVU
0	5e–4	8e–3	2e–3	2e–6
10	0.04	0.06	0.04	0.07
20	0.07	0.10	0.09	0.12
30	0.16	0.17	0.17	0.26
40	0.19	0.29	0.29	0.50
45	0.26	0.34	0.35	0.48
50	0.32	0.42	0.43	0.61

Fig. 14.

Reconstructions of the PACM and BRIDGE-DONUT graphs using the FAST-MVU algorithm, in the case of noise-free data (compare with the original measurement graphs shown in Figs 15 and 16). (a) PACM graph with noise η =0%. (b) DONUT graph with noise η =0%.

Fig. 15.

Reconstructions of the PACM graph with n=800 nodes, sensing radius ρ =1.2 and η =0, 10, 25, 30, 35 and 40%.

Fig. 16.

Reconstructions of the BRIDGE-DONUT graph with n=500 nodes, sensing radius ρ =0.92 and η =0, 10, 20, 30, 40 and 50%.

The second dataset used in our experiments is a synthetic example of the molecule problem and represents the ubiqutin protein represented by PDB entry 1d3z [19], with 1288 atoms, 686 of which are hydrogen atoms. However, after removing the nodes of degree <4, n=1009 atoms remain. For this dataset, the available distances can be divided into groups: the first group contains distances inferred from known bond length and torsion angles (‘good’ edges) which are kept accurate across different levels of noise and the second group contains distances (NOE edges) which are perturbed with noise η at each stage of the experiment. On average, each node is incident with six good edges and eight NOE edges, thus the average degree (deg) of the entire measurement graph is 14. In addition, besides knowledge of good and NOE edges, we also use information from molecular fragments in the form of subgroups of atoms (molecular fragments) whose coordinates are readily available. We incorporate 280 such molecular fragments, whose average size is close to 5 atoms. To exploit such information, we slightly modify the approach to break up the measurement graph and synchronize the patches. We build patches from molecular fragments by selecting a WUL subgraph from each extended molecular fragment, where by an extended molecular fragment we mean the graph resulting from a molecular fragment and all its 1-hop neighbors. Once we extract patches from all extended molecular fragments, we consider all remaining nodes (singletons) that are not contained in any of the patches obtained so far. Depending on the noise level, the number of such singleton nodes is between 10 and 15. Finally, we extract WUL patches from the 1-hop neighborhoods of the singleton nodes, following the approach of Section 4. Since we know a priori the localization, and in particular the reflection of each molecular fragment, and the reflection of a molecular fragment induces a reflection on the patch that contains it, we have readily available information on the reflection of all patches that contain molecular fragments. In other words, we are solving a synchronization problem over ℤ₂ when molecular fragment information is available. Using the synchronization method introduced in Section 7.1, we compute the reflection of the remaining patches. In terms of the reconstruction error, 3D-ASAP and DISCO return comparable results, slightly in favor of our algorithm. For noise-free NOE distances, we compute a localization that is one order of magnitude more accurate than the solution returned by DISCO.

Another graph that we tested is the BRIDGE-DONUT graph shown in Fig. 16. It has n=500 nodes, sensing radius ρ =0.92 and average degree in the range 18 − 25, depending on the noise level. Table 7 contains the reconstruction errors for various levels of noise showing that 3D-ASAP consistently returns more accurate solutions than DISCO. For the BRIDGE-DONUT graph, we included in our numerical simulations the spectral partitioning 3D-SP-ASAP algorithm, which performed just as well as the 3D-ASAP algorithm (while significantly reducing the running time as shown in Tables 5 and 6), and consistently outperformed the DISCO algorithm at all levels of noise. Note that 3D-SP-ASAP returns very poor localizations when using only k =8 partitions; in this case, the extended partitions have large size (up to 150 nodes) and SNL-SDP fails to embed them accurately, even at small levels of noise, as shown in Table 7. By increasing the number of partitions from k = 8 to k = 25 and thus decreasing the size of each partition (and also of the extended partitions), the running time of 3D-SP-ASAP increases slightly from 140 to 186 s (at 35% noise), but we are now able to match the accuracy of 3D-ASAP which requires almost ten times more running time (1770 s).

Finally, for the PACM graphs in Fig. 15, the network takes the shape of the letters P, A, C, M that form a connected graph on n=800 vertices. The sensing radius is ρ =1.2 and the average degree in the range deg ≈ 21 – 26. This graph was particularly useful in testing the sensitivity of the algorithm to the topology of the network. In Table 13, we show the reconstruction errors for various levels of noise DISCO returns better results for η =0, 10, 40%, but less accurate for η =20, 30, 35%. We believe that DISCO returns results comparable with 3D-ASAP (unlike the previous three graphs) because the topology of the PACM graph favors the graph decomposition used by DISCO. Note that at η = 0% noise, the 3D-ASAP reconstruction differs from the original embedding mainly in the right-hand side of the letter M, which is loosely connected to the rest of the letters, and also parts of its underlying graph are very sparse, thus rendering the SDP localization algorithms less accurate. This can also be seen in the spectral partitioning of the PACM graph shown in Fig. 11, where for k (number of clusters) as low as 3 or 4, the right-hand side of letter M is picked up as an individual cluster. At higher levels of noise, 3D-SP-ASAP proves to be more accurate than DISCO, and it returns results comparable with ASAP.

Table 13.

Reconstruction errors (measured in ANE) for the PACM graph with n =800 vertices, sensing radius (ρ) =1.2 and average degrees (deg)=21 – 26. For 3D-SP-ASAP we used k =40 partitions. Note that even for the noise-free case the error is not negligible due to incorrect embeddings of subgraphs that are contained in the right leg of the letter M

η (%)	3D-ASAP	3D-SP-ASAPk=40	DISCO
0	0.05	0.05	0.02
10	0.08	0.12	0.07
20	0.07	0.16	0.18
30	0.27	0.15	0.45
35	0.18	0.32	0.28
40	0.48	0.20	0.26

Table 6 shows the running time of the various steps of the 3D-ASAP algorithm corresponding to our not particularly optimized MATLAB implementation. Our experimental platform was a PC machine equipped with an Intel(R) Core(TM)2 Duo CPU E8500 at 3.16 GHz 4GB RAM. Note that all steps are amenable to a distributed implementation, thus a parallelized implementation would significantly reduce the running times. Note the running time of 3D-ASAP is significantly larger than that of 3D-SP-ASAP and DISCO, due to the large number of patches (linear in the size of the network) that need to be localized. 3D-SP-ASAP addresses this issue, and reduces the running time from 474 to 108 s (for η =0%), and from 1770 to 186 s (for η =35%). Note that all steps of the algorithm scale linearly in the size of the network, except for the eigenvector computation, which is nearly linear. We refer the reader to Section 7 of [21] for a complexity analysis of each step of 2D-ASAP, and remark that it is very similar to the complexity of 3D-ASAP (Table 14).

Table 14.

Reconstruction errors (measured in ANE) for the 1d3z molecule graph with n=1009 vertices, sensing radius (ρ) =5 angstrom and average degree (deg)=14

η (%)	3D-ASAP	DISCO
0	0.0001	0.0024
10	0.0031	0.0029
20	0.0052	0.0058
30	0.0069	0.0078
35	0.0130	0.0104
40	0.0094	0.0107
45	0.0168	0.0207
50	0.0146	0.0151

9. Summary and discussion

In this paper, we introduced 3D-ASAP, a novel divide-and-conquer, non-incremental, non-iterative, anchor-free algorithm for solving (ab-initio) the molecule problem. In addition, we also proposed 3D-SP-ASAP, a faster version of 3D-ASAP, which uses a spectral partitioning algorithm as a preprocessing step for dividing the initial graph into smaller subgraphs. Our extensive numerical simulations show that 3D-ASAP and 3D-SP-ASAP are very robust to high levels of noise in the measured distances and to sparse connectivity of the measurement graph.

We build on the approach used in 2D-ASAP to accommodate for the additional challenges posed by rigidity theory in ℝ³ as opposed to ℝ². In particular, we extract patches that are not only globally rigid, but also WUL, a notion that is based on the recent unique localizability of So and Ye [52]. In addition, we also increase the robustness to noise of the algorithm by using a median-based denoising algorithm in the preprocessing step, by combining into one step the methods for computing the reflections and rotations, thus doing synchronization over O(3) =ℤ₂ × SO(3) rather than individually over ℤ₂ followed by SO(3), and finally by incorporating a scaling correction in the final step where we compute the translations of each patch by solving an overdetermined linear system by least squares. Another feature of 3D-ASAP is being able to incorporate readily available structural information on various parts of the network.

Furthermore, in terms of robustness to noise, 3D-ASAP compares favorably with some of the current state-of-the-art graph localization algorithms. The 3D-ASAP algorithm follows the same ‘divide and conquer’ philosophy that is behind our previous 2D-ASAP algorithm, and starts with local coordinate computations based only on the 1-hop neighborhood information (of a single node, or set of nodes whose coordinates are known a priori), but unlike previous incremental methods, it synchronizes all such local information in a noise robust global optimization process using an efficient eigenvector computation. In the preprocessing step of doing the local computations, a median-based denoising algorithm improves the accuracy of the patch reconstructions, previously computed by the SDP localization algorithm.

Across almost all graphs that we have tested, 3D-ASAP constantly gives better results in terms of the averaged normalized error of the reconstruction. Except for the PACM graph, whose topology greatly favors the divide-and-conquer approach used by DISCO, 3D-ASAP returns reconstructions that are often significantly more accurate in the presence of large noise. Furthermore, for the case of noise-free distance measurements, the notion of WUL graphs that we introduced leads to reconstructions that are an order of magnitude more accurate than DISCO and SNL-SDP.

The geometric graph assumption, which comes up naturally in many problems of practical interest, is essential to the performance of the 3D-ASAP algorithm as it favors the existence of globally rigid or WUL patches of relatively large size. When the geometric graph assumption does not hold, the 1-hop neighborhood of a node may be extremely sparse, and thus breaking up such a sparse star graph leads to many small patches (i.e., most of them may contain only a few nodes), with only a few of them having a large enough pairwise intersection. Since small patches lead to small patch intersections, it would therefore be difficult for 3D-ASAP to align patches correctly and compute a robust final solution. Note that in the case of random Erdős–Rényi graphs we expect the SDP methods, or even the low-rank matrix completion approaches, to work well. In other words, while these methods rely on randomness, our 3D-ASAP algorithm benefits from structure the most.

For the molecule problem, while 3D-ASAP can benefit from any existing molecular fragments, there is still information that it does not take advantage of, and which can further improve the performance of the algorithm. The most important information missing from our 3D-ASAP formulation are the RDC measurements that give angle information (cos²(θ)) with respect to a global orientation. Another possible approach is to consider an energy-based formulation that captures the interaction between pairs of atoms (e.g., Lennard–Jones potential) and use this information to better localize the patches.

Another information one may use to further increase the robustness to noise is the distinction between the ‘good’ and ‘noisy’ edges. There are two parts of the algorithm that can benefit from such information. First, in the preprocessing step for localizing the patches one may enforce the ‘good’ distances as hard constraints in the SDP formulation. Secondly, in the step that synchronizes the translations using least squares, one may choose to give more weight to equations involving the ‘good’ edges, keeping in mind however that such equations are not noise free since the direction of an edge may be noisy as a result of steps 1 and 2, even if the distances are accurate. However, note that 3D-ASAP does use the ‘good’ edges as hard constraints in the gradient descent refinement at the end of step 3.

One other possible future direction is combining the reflection, rotation and translation steps into a single step, thus doing synchronization over the Euclidean group. Our current approach in 3D-ASAP takes one step in this direction and combines the reflection and rotations steps by doing synchronization over the Orthogonal group O(3). However, incorporating the translations step imposes additional challenges due to the non-compactness of the group Euc(3), rendering the eigenvector method no longer applicable directly.

In general, there exist very few theoretical guarantees for graph localization algorithms, especially in the presence of noise. A natural extension of this paper is a theoretical analysis of ASAP, including performance guarantees in terms of robustness to noise for a variety of graph models and noise models. However, a complete analysis of the noise propagation through the pipeline of Fig. 2 is out of our reach at the moment, and first calls for theoretical guarantees for the SDP formulations used for localizing the patches in the preprocessing step. Recent work in this direction is due to [36], whose main result provides a theoretical characterization of the robustness properties of an SDP-based algorithm, for random geometric graphs and uniformly bounded adversarial noise.

While the experimental results returned by 3D-ASAP are encouraging when compared with other graph realization algorithms, we still believe that there is room for improvement, and expect that further combining the approaches of 3D-ASAP and DISCO would increase the robustness to noise even more. The disadvantage of 3D-ASAP is that it sometimes uses patches of very small size, which in the noisy scenario can be poorly aligned with neighboring patches because of small, possibly inaccurate set of overlapping nodes. One of the advantages of DISCO is that it uses larger patches, which leads to larger overlappings and more robust alignments. At the same time, the number of patches that need to be localized by an SDP algorithm is small in the case of DISCO (2^h, where h is the height of the tree in the graph decomposition), thus reducing the computational cost of the algorithm. However, DISCO does not take advantage, at a global level, of pairwise alignment information that may involve more than two patches, while the eigenvector synchronization algorithm of 3D-ASAP incorporates such local information in a globally consistent framework. Straddling the boundary between SDP computational feasibility and robustness to noise, as well as finding the ‘right’ method of dividing the initial problem are future research directions. For a given patch of size k, is it better to run an SDP localization algorithm on the whole graph, or to first split the graph into two or more subgraphs, localize each one and then merge the solutions to recover the initial whole patch? An analysis of this question, both from a computational point of view and with respect to robustness to noise, would reveal more insight into creating a hybrid algorithm that combines the best aspects of 3D-ASAP and DISCO. The 3D-SP-ASAP algorithm is one step in this direction, and was able to address some of these challenges.