Statistical Contributions to Proteomic Research

Abstract

Proteomic profiling has the potential to impact the diagnosis, prognosis, and treatment of various diseases. A number of different proteomic technologies are available that allow us to look at many proteins at once, and all of them yield complex data that raise significant quantitative challenges. Inadequate attention to these quantitative issues can prevent these studies from achieving their desired goals, and can even lead to invalid results. In this chapter, we describe various ways the involvement of statisticians or other quantitative scientists in the study team can contribute to the success of proteomic research, and we outline some of the key statistical principles that should guide the experimental design and analysis of such studies.

Introduction

The field of proteomics has been rapidly advancing in recent years, and shows tremendous promise for research in various diseases, including cancer. Proteomic studies have been conducted to search for proteins and combinations of proteins that can be used as biomarkers to diagnose cancer, to provide more detailed prognostic information for individual patients, and even to identify which patients will respond to which treatments, with the ultimate hope of developing molecular-based personalized therapies that are more effective than the treatment strategies currently employed. Some arguments for the use of protein-based methods over mRNA or DNA-based methods to accomplish these goals are that proteins are more relevant to the biological functioning of the cell, being typically downstream from the DNA and mRNA, and are subject to post-translational modifications, plus proteomic assays can be applied to readily available biological samples like serum and urine, while mRNA-based methods in general cannot be applied in these settings, because these fluids are acellular and thus should not contain nucleic acids.

Various proteomic instruments have been developed that are able to survey a biological sample and reveal a slice of their proteomic profile. One of the oldest technologies in this field is 2d gel electrophoresis (2DE), which was developed in the 1970’s and has been extensively used since. While this technology has been around for a while, computational limitations and other factors have prevented it from reaching its potential impact in biomedical research. The advanced computing tools now available and the significantly improved preprocessing algorithms being developed for this technology may make it possible for 2DE to overcome some of its perceived shortcomings and make a much stronger contribution to biomedical research in the near future. In recent years, mass spectrometry-based techniques have gained popularity in proteomic profiling studies as an alternative to 2DE. Methods used include matrix-assisted laser desorption and ionization mass spectrometry (MALDI-MS) and the closely related surface-enhanced laser desorption and ionization mass spectrometry (SELDI-MS) commercially developed by Ciphergen, Inc. (Fremont, CA). The interest in these technologies was fueled by some early studies reporting incredible results, for example 100% sensitivity and 94% specificity for diagnosing ovarian cancer based on serum samples (Petricoin, et al. 2002). Unfortunately, many of these results have not held up to scrutiny, with experimental design flaws in these studies drawing their results into question (Sorace and Zhan 2004, Baggerly, et al. 2004, Diamandis 2004a, Diamandis 2004b, Baggerly, et al. 2005a, Baggerly, et al. 2005c). Subsequent well-designed studies have been performed that, while falling short of the incredible results of the initial studies, have identified potential biomarkers that may be useful for improving the early diagnosis of certain cancers (e.g. Zhang, et al. 2005). In recent years, liquid chromatography coupled to mass spectrometry (LC-MS) has been increasingly used for proteomic profiling. This technology has some advantages over MALDI-MS, with its 2 dimensional nature allowing one to resolve more proteins and simultaneously discern their identities, but at the price of reduced throughput capabilities.

While quite different in many ways, all of these technologies share some common characteristics. First, all of these instruments are very sensitive. This sensitivity is good when it comes to detecting subtle proteomic changes in a sample, but unfortunately this sensitivity also extends to small changes in sample handling or processing. Because of this, experimental design considerations are crucial in order to obtain valid results from proteomic studies. Second, all of these technologies yield complex, high dimensional data, either noisy spectra (MALDI-MS, SELDI-MS) or images (2DE, LC-MS), which must be preprocessed. This preprocessing is a challenge, and if not done properly, can prevent one from identifying the significant proteomic patterns in a given study. Third, these technologies all produce simultaneous measurements of hundreds or thousands of peptides or proteins in a sample. Given these large numbers, multiple testing and validation need to be done properly in order to ensure that reported results are likely to be from real changes in the proteome, and not false positive results due to random chance alone.

All of these characteristics raise quantitative issues that must be adequately addressed in order to perform successful proteomic studies. The goal of this chapter is to demonstrate the benefit of involving statisticians or other quantitative scientists in all areas of proteomic research, and to elucidate some of the statistical principles and methods we have found to be essential for this field. We will illustrate these principles using a series of case studies, some from studies performed at The University of Texas M. D. Anderson Cancer Center, and some performed at other institutions.

There are four key areas in which a statistician can make a major impact on proteomic research: experimental design, data visualization, preprocessing, and biomarker identification. We will organize this chapter according to these four areas, and finish with some general conclusions.

Experimental Design

In this section, we will describe 3 case studies, point out important experimental design principles highlighted by them, and then provide some general experimental design guidelines for proteomic studies.

Case Study 1: Brain cancer MALDI study

A group of researchers conducted an experiment at M. D. Anderson Cancer Center on tissue samples from 50 patients with brain cancer, which were believed to include two subtypes of the disease (Hu, et al. 2005). The disease subtype information was ”stripped out” and the resultant blinded dataset consisting of MALDI spectra from these samples was brought to our group for analysis. The aim of the analysis was to perform unsupervised clustering of the data to see if the two subtypes could be identified correctly and blindly. After preprocessing the data using in-house routines of simultaneous peak detection and baseline correction (SPDBC, Coombes, et al. 2003), we performed hierarchical clustering on the set of peaks consistently detected across spectra. This clustering produced two distinct groups, which excited us (See Figure 1).

Figure 1.

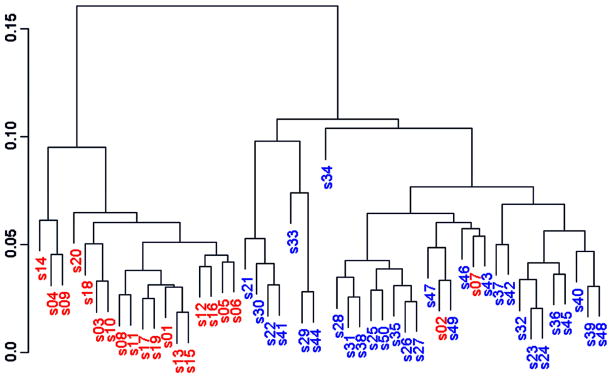
Discovery of clusters in data from bsa70 fraction of brain tumor samples.

Upon being unblinded, however, we found that these groups did not cluster according to disease subtypes, but according to sample number, with samples 1–20 roughly clustering in one group and 21–50 clustering into the other. We found out that the sample collection protocol had been changed after the first 20 patients had been collected. This change in protocol resulted in systematic and reproducible changes in the serum proteome that were stronger than the changes between the subtypes of brain cancer present in the study. While mass spectrometry can be exquisitely sensitive to changes in the part of the proteome it can measure accurately, it can be even more sensitive to changes in sample collections and handling protocols. Thus, it is crucial with these sensitive technologies to ensure consistent protocols throughout a given study, and especially take care not to differentially handle cases and controls – since this can induce large scale differences between them that is not driven by the biology of interest, but rather the nuisance factor of handling. Sample handling and processing is not the only nuisance factor that can impact a study in this way.

Case Study 2: Leukemia SELDI study

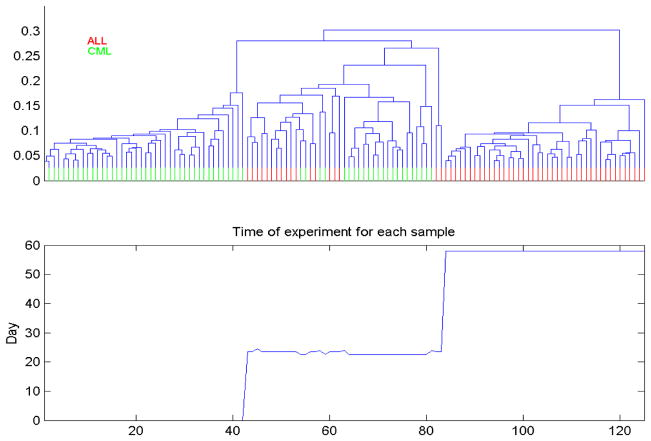
In another study performed at MD Anderson Cancer Center, SELDI spectra were obtained from blood serum of 122 Leukemia patients, some with chronic myelogenous leukemia (CML), and others with acute lymphoblastic leukemia (ALL). Since with leukemia, the “tumors” are in the blood, we expected that it should not be difficult to distinguish these two subtypes using these blood serum spectra. Again, in a blinded fashion as the previous example, we preprocessed the data and performed hierarchical clustering. Rather than 2 clusters, we found 3 very strong clusters (see Figure 2, top panel).

Figure 2.

Unsupervised clustering of Leukemia spectra reveals clustering driven by run date, not type of leukemia.

Upon unblinding, we were encouraged that cluster 1 was 100% CML, cluster 3 was 100% AML, showing good discrimination, and cluster 2 was split between the two. Did cluster 2 represent a subtype of CML and ALL that were proteomically similar, or was something else going on here? We plotted the sample number versus run date (Figure 2, bottom panel), and found that the spectra were obtained in 3 distinct blocks over a period of 2 months. Block 1 contained only CML samples, block 3 contained only ALL samples, and block 2 contained a mix of CML and AML samples. These 3 processing blocks corresponded to the three clusters our unsupervised analysis discovered. This demonstrates that the SELDI instrument can vary systematically over time, especially over the scope of weeks and months. This systematic difference was stronger than the proteomic difference between ALL and CML in blood serum. Time effects are not just limited to SELDI-MS instruments, nor are they limited to long term effects over weeks and months – sometimes these instruments can give very different results from day-to-day.

Case Study 3: Ovarian cancer high resolution MALDI study

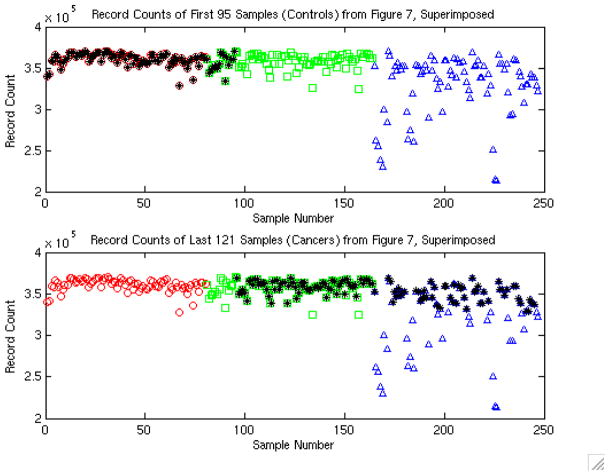
A study was performed by the NCI-FDA group (Conrads, et al. 2004) using high resolution Qstar profiling of serum for ovarian cancer detection, with 100% sensitivity and 100% specificity reported. In Figure 6A of their paper, they plotted a QA/QC measure for each spectrum against sample number, with different symbols indicating the 3 days on which the samples were run. As the authors noted, this figure clearly showed that something was going wrong on the third day. Figure 7 of their paper showed the record numbers of the spectra deemed of high enough quality for data analysis, with controls on the left and cancers on the right. Superimposing these figures (see Figure 3, adapted from Baggerly, et al. 2004, Endocrine Related Cancers), we see that they coincide perfectly.

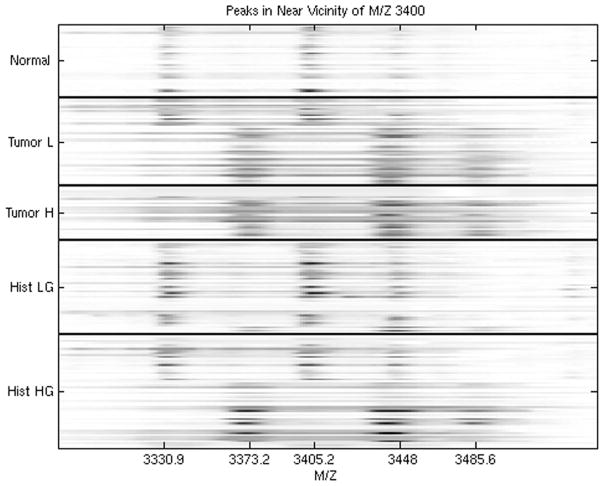
Figure 6.

Comparisons of urine spectra in the vicinity of M/Z 3400, revealing calibration issues between the spectra in different groups.

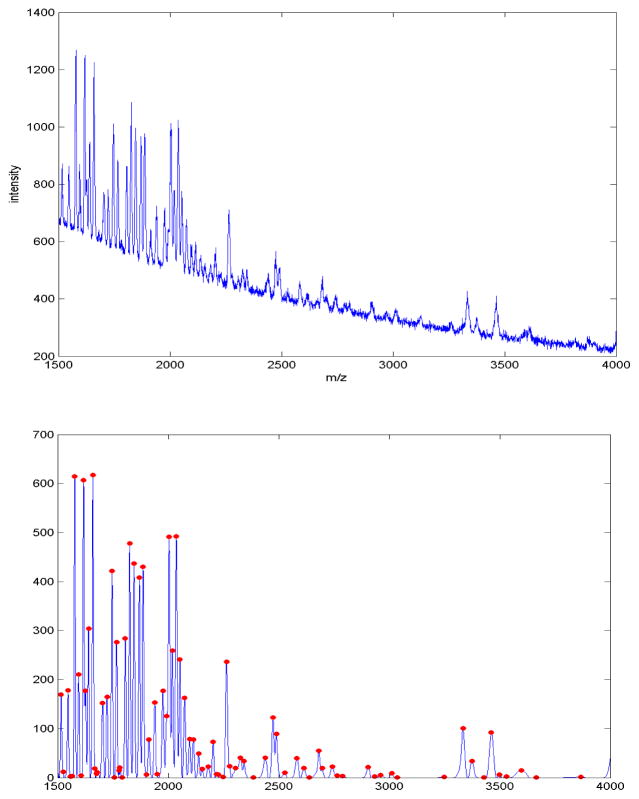
Figure 7.

Portion of a raw MALDI spectrum (top), along with the preprocessed version after denoising, baseline correction and normalization (bottom) using the method described in Morris, et al. (2005), with detected peaks indicated by the dots.

Figure 3.

Plot reveals confounding between cancer status and run date in the study design, which is especially problematic given the quality control problems evident on day 3.

This indicates that almost all of the controls were run on day 1, with a small number on day 2, and that cancers were run on days 2 and 3. This is a serious problem, since any systematic changes in the machine from day to day can systematically bias the results by distorting one group more than the other. The authors noted this type of trend, since the reduced quality signals on the third day they mentioned would affect only cancer spectra. Thus, it is possible that the observed 100% sensitivity and specificity was driven by the machine effect, and not the case/control status.

The previous two case studies highlight the danger of confounding in experimental design – in which by design (usually inadvertently) a nuisance factor is inseparably intermingled with a factor of interest in the study. In case study 2, block was confounded with CML/ALL type and in case study 3; run day was confounded with case/control status. This confounding can also occur at the sample collection and handling level as well – if all cases come from one center, and all controls from another, then there is no way to tell whether differences between the groups are due to case/control status or to factors specific to the centers. This is an especially sinister problem because it can make a study appear to have strikingly strong effects for the factor of interest, when in fact these effects may be driven by the confounding nuisance factor, not the factor of interest. This can be ultimately revealed when later studies are not able to replicate the earlier findings. For example, in case study 3, it is impossible to tell whether the observed remarkable separation was due to the day effect or the case versus control effect. When the two effects are completely confounded, no statistical modeling can fix this problem – the data set is essentially worthless unless one is willing to arbitrarily assume that the confounded nuisance factor is not significant, which would clearly be a wrong assumption in case studies 2 and 3.

How can one prevent confounding from ruining their proteomics studies? Confounding can be prevented by following certain experimental design principles during the planning phase of the study. There has been extensive statistical work in the area of experimental design – some principles can be found in standard textbooks in the area (e.g. Box, et al. 2005). Two key principles are blocking and randomization. Blocking is necessary when for whatever reason it is not possible to perform the entire experiment at one time. Each block is then a portion of the experiment, for example a certain point in time where a batch of gels or spectra are run, a given set of samples collected from a given site at a given time, or a given SELDI chip is used. In practice, the blocks are typically constructed merely by convenience, not based on any sense of balance between study groups nor using any statistical principles. As seen in the case studies above, this practice can lead to confounding of study factor with the blocking factor. Instead of convenience, blocks should be thoughtfully constructed trying to balance the samples within each block with respect to the study factors of interest. For example, one design is to have balanced numbers of cases and controls within each block. In this case, strong block effects, if they exist, will only add random noise to the data, not systematic bias, since the block effect will impact both cases and controls equally. For a given proteomic technology, one should identify which factors and steps of the process introduce the most variability, and then block on these factors. At the point where further blocking is not possible, then randomization should be used to determine run order, sample position, etc. This randomization protects against bias caused by some unknown or unexpected source. The randomization can be done using a random number generator, which is an easy exercise for any quantitative scientist. Note that picking what seems to be a “random-like” sequence is not the same as randomization. Studies have clearly shown that individuals do a poor job acting as random number generators; so true randomization should be done. If the studies in case 2 and case 3 had randomized the run order of their experiments, or used block designs, they would have prevented the confounding that for all practical purposes invalidated these data sets.

In summary, the key design issues to remember include:

• Sample collection and handling must be carefully controlled.

• Block on factors that are likely to impact on the data, including sample collection and handling.

• At whatever level you stop blocking, randomize.

In many areas of science, these principles are routinely incorporated into study conduct. In our experience, we have found this not to be the case in biological laboratory science, including proteomics. Even in the best-run laboratory, given the extreme sensitivity of proteomic instruments, it is crucial to take these factors into consideration. This point cannot be made too strongly: to ignore them is to risk obtaining data that are completely worthless for detecting group differences, i.e. achieving the goals of the study.

Data Visualization

One of the most important statistical principles in analyzing proteomic data is also the simplest – look at the data! Frequently, simple plots of the data can reveal experimental design problems like those discussed in the previous section or other issues that need to be addressed before the data can be properly analyzed. In this section, we will look at three case studies that illustrate the benefit of data visualization techniques, and then we will discuss some tools we have found useful for this purpose.

Case Study 4: Duke University Lung Cancer MALDI Data

These data are from the First Annual Proteomics Data Mining Competition at Duke University, and consist of 41 MALDI spectra obtained from blood serum from 24 lung cancer patients and 17 normal controls (Baggerly, et al. 2003). The goal is to identify proteomic peaks from serum that can distinguish individuals with and without lung cancer.

We plotted a heat map of the entire set of 41 spectra. A heat map is an image plot of the data, with rows corresponding to individual spectra and columns corresponding to individual clock ticks within the spectra. Upon looking at the heat map, an anomaly jumped out at us – we noticed a distinguishing pattern in the low mass region of the first 8 spectra from normal controls. Specifically, we saw that these samples contained recurring peaks at precise integer multiples of 180.6 Da, suggesting the presence of some unknown substance with identical subunits (see Figure 4). This is unlikely to be a protein, since no combination of amino acids sums to this mass, so what we are seeing here may be a matrix or detergent effect that affected a single batch (or block) of samples. Thus, we removed this region of the spectra (1200 Da to 2500 Da) from consideration in our search for differentially expressed peaks. Had we not looked at the heat map, we likely would have missed this pattern, and would have mistakenly reported these peaks as potential lung cancer biomarkers, as done by many other groups analyzing this data set as part of the competition.

Figure 4.

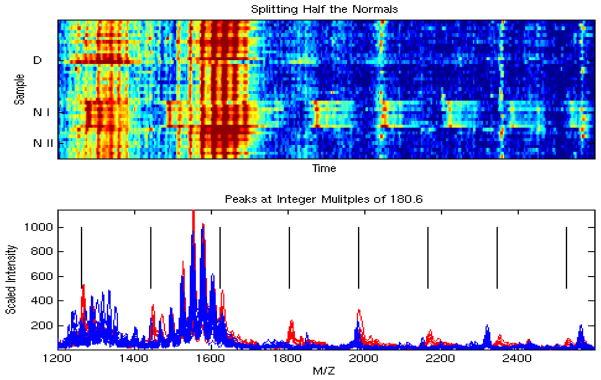
A simple heat map revealed peaks at integer multiples of 180.6, which is unlikely to be driven by biology, so we removed these peaks from consideration when discriminating between cancers and normals.

Case Study 5: NCI-FDA Ovarian Cancer SELDI Study

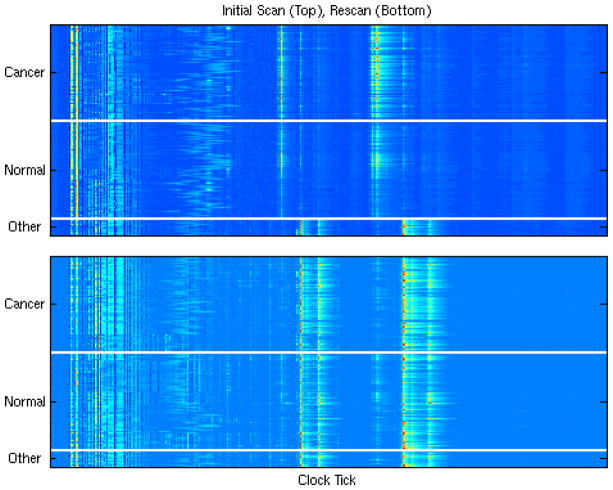
These data are from a seminal paper appearing in February, 2002, in The Lancet (Petricoin, et al. 2002) that reported finding patterns in SELDI proteomic spectra that can distinguish between serum samples from healthy women and those from women with ovarian cancer. The data consisted of 100 cancer spectra, 100 normal spectra, and 16 “benign disease” spectra. The cancer and normal spectra were randomly split, with 50 cancer and normal spectra used to train a classification algorithm. The resulting algorithm was used to classify the remaining spectra. It correctly classified 50/50 of the cancers, 47/50 of the normals, and called 16/16 of the benign disease spectra “other” than normal or cancer. There have been a large number of criticisms and issues raised with this study (Sorace and Zhan 2004, Baggerly, Morris, and Coombes, 2004, Baggerly, et al. 2005, Baggerly, Coombes, and Morris, 2005, Diamandis 2004a, 2004b, 2004c), but here we will focus on the remarkable result that they were able to recognize all 16 of the benign disease spectra as being something other than cancer or normal.

After publication, the authors made their data publicly available on their website. We downloaded these data, and one of our first steps was to plot a heat map of the data, given by the top panel of Figure 5 (adapted from Baggerly, Morris, and Coombes, 2004, Bioinformatics), with the samples in order from the cancers to the normals to the benign disease spectra (other).

Figure 5.

Heat map of all 216 samples run on the H4 chip (top), and on the WCX2 chip (bottom). The extreme difference in the ‘benign disease’ group in the spectra on the top, along with the similarity of these profiles to the WCX2 spectra, suggest a change in protocol occurred in the middle of the first experiment.

From this heat map, it is not surprising that their classification algorithm was able to distinguish the benign disease spectra from cancer and normal. What is surprising is that the cancer and normal spectra look quite alike to the naked eye, while the benign disease spectra looked completely different from the others. Why would spectra from normals be more similar to those from cancers than those from individuals with benign disease? These spectra, the ones reported in the Lancet paper, were obtained using Ciphergen’s H4 SELDI chip. The authors also reran the same 216 biological samples on the WCX2 SELDI chip, and posted these data on their website. The bottom figure contains a heatmap of these 216 spectra. Plotting these figures adjacent to one another, we see that the benign spectra reportedly run on the H4 chip are very similar to all of the spectra from the WCX2 chip, suggesting a change in protocol occurred in the middle of the first experiment. This is clearly revealed by a simple heatmap of the raw data.

Case Study 6: M. D. Anderson Urine SELDI data

This study was performed at M. D. Anderson Cancer Center, and involved SELDI spectra obtained from urine samples from five groups of individuals: (1) disease-free individuals, (2) patients presenting with low-grade bladder tumors, (3) patients presenting with high-grade bladder tumors, (4) patients with history of low-grade bladder tumors, and (5) patients with history of high-grade bladder tumors. One goal of the study was to find proteins distinguishing the groups. After preprocessing and analysis, we found several peaks that could separate controls from cancers successfully, including the set of three peaks shown in the first three rows of Figure 6 (adapted from Hu, et al. 2005 Briefings in Genomics and Proteomics).

Upon plotting a heat map of the data, however, we discovered that the spectra from the disease-free individuals contained the same three peaks, but that these peaks were shifted to the left relative to many of the peaks from those with cancer. This revealed the data had been inadequately calibrated prior to analysis. After correcting the calibration, there was no difference in protein expression in this region of the spectra.

These three case studies all emphasize the importance of plotting a heat map of the data before conducting any analyses. There are other graphical procedures that can also be routinely used for diagnostic and confirmatory purposes. Dendograms produced by hierarchical clustering of the raw and preprocessed spectra, as demonstrated in the previous section, are useful for diagnosing systematic trends in the data, those we want (between treatment groups) and those we don’t (between nuisance factors). In the next section, we will discuss the issue of preprocessing. It is always a good idea to view plots of individual spectra before and after preprocessing, to ensure that the preprocessing is sufficient, and to ensure that it did not induce any unwanted artifacts. Also, once identifying peaks in mass spectrometry experiments or spots in 2DE experiments that are differentially expressed, it is also advisable to look at these regions in the preprocessed as well as raw data to ensure that you believe those results are real. Statistical summaries and tests of statistical significance are useful, but it is still important to look at the actual data to confirm that the results look believable and practically significant. Don’t just trust the numbers – look at the pictures!

Preprocessing

The first step in the analysis of proteomics data is to extract the meaningful proteomic information from the raw spectra or images. We use the term preprocessing as a collective term referring to the data and image analysis steps that are necessary to accomplish this goal. Given a set of N spectra or images containing information from a total of p proteins or peptides, the goal of preprocessing is to obtain an N×p matrix, whose rows correspond to the individual spectra or images, and the columns contain some quantification of a proteomic unit such as a spectral peak or 2DE spot. From this matrix, we can perform a variety of different types of statistical analyses to find out which proteins are associated with outcomes of interest, as discussed in the next section. The different steps in preprocessing include calibration or alignment, baseline or background correction, normalization, denoising, and feature (peak or spot) detection. It is important to find effective methods for performing these steps, since subsequent analyses condition on these determinations. While other methods are available in existing literature and new methods are constantly being developed, here we briefly describe methods we have developed for one-dimensional mass spectrometry methods such as MALDI-MS and SELDI-MS, and for two- dimensional methods such as 2DE. We have found our methods to be very effective and believe they outperform other existing alternatives.

Preprocessing MALDI-MS and SELDI-MS spectra involves a number of steps that interact in complex ways. Some of these steps are as follows.

• Alignment involves adjusting the time of flight axes of the observed spectra so that the features of the spectra are suitably aligned with one another.

• Calibration involves mapping the observed time-of-flight to the inferred m/z ratio.

• Denoising removes random noise, likely caused by electrical noise from the detector.

• Baseline subtraction removes a systematic artifact typically observed for these data, usually attributed to an abundance of ionized particles striking the detector during early portions of the experiment.

• Normalization corrects for systematic differences in the total amount of protein desorbed and ionized from the sample plate.

• Peak detection involves the identification of locations on the time or m/z scale that correspond to specific proteins or peptides striking the detector. Note that this differs from the process of peak identification, which is the process of determining the species molecule that cause a peak to be manifest in the spectra.

• Peak quantification involves obtaining some quantification for each detected peak for all spectra in a sample, and may involve computing heights or areas.

• Peak matching across samples may be necessary if peak detection is applied to the individual spectra, in order to match and align the peaks detected for different spectra.

We view preprocessing as the decomposition of the observed raw spectra into three components: true signal, baseline, and noise. The basic idea is to estimate and remove the baseline and noise, and then decompose the signal into a list of peaks, whose intensities are then recorded. Our procedure is described below, and follows two basic principles: (1) Keep it simple; we wish to keep processing to a minimum in order to avoid introducing additional bias or variance into the measurements, and (2) Borrow strength; we wish to borrow information across spectra wherever possible in order to make more accurate determinations. This procedure has evolved, with the principles discussed in Baggerly, et al. 2003, Coombes, et al. 2004, Coombes, et al. 2005, Morris, et al. 2005, and Coombes, et al. 2007. Standalone software implementing this process is freely available (PrepMS, Karpevitch, et al. 2006, which implements method described in Morris, et al. 2005).

1. Align the spectra on the time scale by choosing a linear change of variables for each spectrum in order to maximize the correlation between pairs. We have found that alignment can be done much more simply and efficiently on the time scale rather than the clock tick scale.

2. Compute the mean of the aligned raw spectra.

3. Denoise the mean spectrum using the undecimated discrete wavelet transform (UDWT).

4. Locate intervals containing peaks by finding local maxima and minima in the denoised mean spectrum.

5. Quantify peaks in individual raw spectra by recording the maximum height and minimum height in each interval, which should contain a peak, then taking their difference. This quantification method implicitly removes the baseline artifact.

6. Calibrate all spectra using the mean of the full set of calibration experiments.

Assuming that a total of p peaks are detected on the average gel, this leaves us with an N×p matrix of peak intensities for the N spectra in the study that can be surveyed for potential biomarkers. Figure 7 contains an illustration of the preprocessing and peak detection process.

A key component of our approach is that we perform peak detection on the average spectrum, rather than on individual spectra, which has a number of advantages (Morris, et al. 2005). First, it avoids the difficult and error-prone peak-matching step that is necessary when using individual spectra, improving the accuracy of the quantifications and eliminating the problem of missing data. Second, it tends to result in greater sensitivity and specificity for peak detection, since averaging across N spectra reinforces the true signal while weakening the noise by a factor of $\sqrt{N}$. This enables us to do a better job of detecting real peaks down near the noise region of the spectra, and decreases the chance of flagging spurious peaks that are in fact just noise. These points are demonstrated by the simulation study presented in Morris, et al. (2005), which shows that using the average spectrum results in improved peak detection, with the largest improvement being for low abundance peaks of high prevalence. Third, it speeds preprocessing time considerably, since peak matching is by far the most time-consuming preprocessing step.

Following similar principles, we have also proposed an approach for preprocessing 2DE data that we refer to as Pinnacle (Morris, Walla, and Gutstein 2007). The name comes from the fact that, unlike most existing methods, this method performs spot quantification using pixel intensities at pinnacles (peaks in two dimensions) rather than spot volumes. Again, the fundamental principle is to keep the preprocessing as simple as possible, to prevent the extra bias and variance that can result from the propagation of errors, especially when complex methods are used. Following are the steps of the Pinnacle method:

1. Align the 2DE gel images.

2. Compute the average gel, averaging the staining intensities across gels for each pixel in the image.

3. Denoise the average gel using the 2-dimensional undecimated discrete wavelet transform (UDWT).

4. Detect pinnacles on the denoised average gel, which are pixel locations that are local maxima in both the horizontal and vertical directions with intensity above some minimum threshold (e.g. the 75^th percentile for the average gel).

5. Perform spot quantification on the individual gels by taking the maximum intensity within a stated tolerance of each pinnacle location.

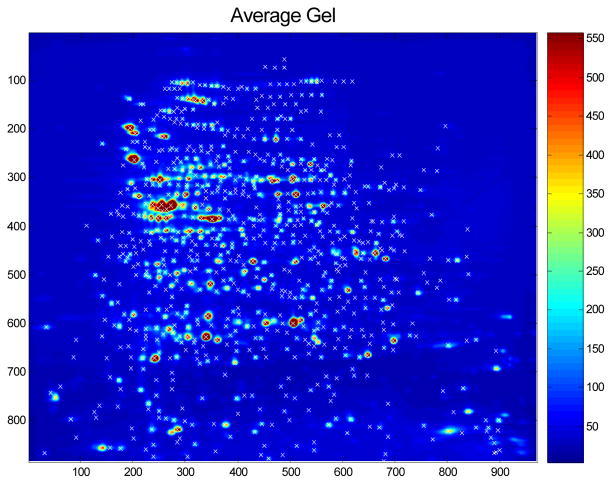
Assuming we detect p pinnacles on the average gel, this leaves us with an N×p matrix of spot intensities that can be surveyed for potential biomarkers. Figure 8 contains the heat map of an average gel, with detected spots marked.

Figure 8.

Average gel from a 2d gel experiment, with detected spots using the Pinnacle method indicated the symbol “x”.

This method is significantly quicker and simpler than the most commonly used algorithms for spot detection in 2DE, which involve performing spot detection on individual gels using complex spot definitions, quantifying using spot volumes, then matching spots across gels. As for mass spectrometry, use of the average gel for spot detection leads to a number of advantages over methods performing detection on individual gels than matching spots across gels. First, the use of the average gel leads to greater sensitivity and specificity for spot detection, and leads to robust results, since it can automatically discount artifacts unique to individual gels. Second, the use of the average gel allows one to avoid the difficult and error-prone step of matching spots across gels. As a result, with our approach the accuracy of spot detection actually increases with larger studies, in contrast with other approaches that match across gels, whose accuracy decreases markedly with larger numbers of gels because of the propagation of spot detection and matching errors. Third, use of the average gel eliminates the missing data problem, since quantifications are well defined for every spot on every gel in the study. Fourth, the method is quick and automatic, not requiring any of the subjective, time-consuming hand editing that is necessary with other approaches to fix their errors in spot detection, matching, and boundary estimation. Two independent dilution series experiments (Morris, Walla and Gutstein 2007) were used to demonstrate that Pinnacle yielded more reliable and precise spot quantifications than two popular commercial packages, PDQuest (Bio-Rad, Hercules, CA) and Progenesis (Nonlinear Dynamics, Newcastle upon Tyne, UK).

Another important feature of Pinnacle is that pinnacle intensities are used in lieu of spot volumes for quantification. We believe that this property explains the dramatically increased precision as demonstrated by lower CVs in the dilution series experiments. Although the physical properties of the technology suggest that spot volumes are a natural choice for protein quantification, they are also problematic since they require estimation of the boundaries of each individual spot, which is a difficult and error-prone exercise, especially when many spots overlap. The spot boundary estimation variability is a major component in the CVs for individual spots across gels. It can be easily shown that pinnacle intensities are highly correlated with spot volumes, yet can be computed without estimating spot boundaries, which leads to more precise quantifications and lower CVs. Pinnacle is currently being developed into a standalone executable.

Biomarker Discovery

The final step of analysis is to discern which protein peaks or spots are associated with the factors of interest, e.g. differentially expressed, and thus may indicate potential biomarkers. This is the analysis step frequently receiving the most attention, but in this chapter, we give it the least. This is because the probability of success in this step depends strongly on the adequacy of the previous steps discussed in lengths in this chapter. If the experimental design and/or the preprocessing have been done poorly, then there is little hope of finding meaningful biomarkers regardless of what methods are used in the biomarker discovery phase. Poor design or preprocessing can mask significant results, making them more difficult to discover, or more ominously can raise many false positive results that can mislead one into thinking they have discovered a potential biomarker, only to be disappointed when subsequent studies fail to replicate or validate the results. That said, we still discuss some statistical principles for guiding the biomarker discovery process.

Given an N×p matrix of features (peak/spot quantifications) from each spectrum/gel, there are a large number of possible methods that can be used to identify which features are significantly associated with the factor of interest, and thus may indicate potential biomarkers. These methods can be divided into two types. The first are univariate methods that look at the features one-at-a-time. One example is to apply a simple statistical test (e.g. a t-test or simple linear regression) to each feature, and then compose a ranked list of the features based on the p-values and/or effect sizes. The second are multivariate methods that seek to build models to predict an outcome of interest using multiple features. In either case, the key statistical challenge is dealing with the multiplicity problem that results from surveying a large number of features. In the univariate context, we expect a certain number of features to have small p-values even if no proteins are truly related to the factor of interest. In the multivariate context, given the large number of potential features that could be used in the model, we expect it is easy to find a model that is nearly perfect in predicting the desired outcome by random chance alone, even when in fact none of the features are truly predictive of the outcome. In their survey of published microarray studies, Dupuy and Simon (2007) found that a large number of them did not adequately control for multiple testing. Methods that adjust for these multiplicities ensure that the reported outcomes of the study are likely to be real, and not simply due to random chance.

In the univariate case, adjusting for multiplicities means finding an appropriate p-value cutoff that has desirable statistical properties. The usual cutoff of .05 is typically not appropriate, since we expect about 5% of the features to have p-values of less than .05 even if none are in fact truly associated with the feature of interest. A classical approach for dealing with multiplicities is Bonferroni, which would use a cutoff of .05/p for determining significance, where recall p is the number of features surveyed. This cutoff would control the experiment-wise error rate at .05, meaning the total expected number of false discoveries in the study is .05. This criterion strongly controls the false positive positive rate, but results in a large number of false negatives, so is widely considered too conservative for exploratory analyses like these. Other methods control the false discovery rate, or FDR (Benjamini and Hochberg 1995). Controlling the false discovery rate at .05 means that of the features declared significant, we expect 5% or fewer of them to be false positives. There are a number of procedures for controlling FDR (Benjamini and Hochberg 1995, Yekutieli and Benjamini 1999, Benjamini and Liu 1999, Storey 2002, Storey 2003, Genovese and Wasserman 2002, Ishwaran and Rao 2003, Pounds and Morris 2003, Efron 2004, Newton 2004, Pounds and Cheng 2004). Many of these methods take advantage of the property that the p-values corresponding to features that are not associated with the factor of interest should follow a uniform distribution, while the distribution of p-values for predictive features should be characterized by an overabundance of small p-values. In most of these methods, one inputs the list of p-values and desired FDR, and receives as output a p-value cutoff that preserves the desired FDR. Typically, this cutoff is smaller than .05, but quite a bit larger than the corresponding Bonferroni bound .05/p.

When building multivariate models, it is important to validate the model in some way to assess how well the model can predict future outcomes. The key principle is that the same data should not be used to both build the model (called training) and assess its predictive accuracy (called testing). Testing a model with the same data used to build it results in an overly optimistic sense of the model’s predictive ability, with the problem much worse in settings like proteomics in which we have such a large number of potential models. We have performed simulation studies (not published) that demonstrate that building a model with just 14 features from a set of 1000 features to distinguish 30 cases from 30 controls, we can obtain 100% predictive accuracy on the training set nearly every time even when none of the features are truly predictive, i.e. all of the data are just random noise. This highlights the notion that over-fitting training data when fitting multivariate models with large numbers of potential features is very easy. It is crucial to perform some type of independent validation when performing multivariate modeling. As discussed by Dupuy and Simon (2007), improper validation is a frequent flaw in published reports from many microarray studies, even those published in very high impact journals.

One commonly used validation approach is to split the data into two sets, using the first in building the model, then using the second to assess its predictive accuracy. While straightforward, this method has its drawbacks. It is inefficient, since it uses only half of the data to build the model, and also it may be difficult to convince skeptical reviewers that you didn’t “cheat”, i.e. look at various training/test splits and only report the one that yielded good results for both! One way to combat this is to repeat the analysis over for many different random splits of the data and average the prediction error results over them. A special case of this is called K-fold cross validation (CV). In K-fold CV, the data is split into K different subsets and K different analyses are performed. For each analysis, a different set of K-1 subsets are used to build a model, with the remaining subset set aside and used to test its predictive accuracy. The reported prediction error is then obtained by averaging over the predictive accuracies obtained for the K different analyses. It is possible to further improve this estimate by averaging over different random splits into K subsets.

One key point about performing model validation in these high dimensional settings is that it is important to perform external, not internal, cross validation. This means that one should repeat the feature selection process on every subset (external CV), as opposed to the common practice of selecting the predictive features using the entire data set then only repeating the model-fitting process for the different subsets (internal CV). Using internal cross-validation does not deal properly with the multiplicity problem of selecting the features, and can result in strongly optimistically biased assessments of predictive accuracy (Lecocke and Hess 2006). This point is not well appreciated in the biological literature, as internal cross-validation is widely employed in practice (Dupuy and Simon, 2007).

Validation methods that involve splitting a given data set are useful, but also have limitations because any systematic biases that may be hardwired into a given data set will be present in both the training and test splits. For example, when sample processing is confounded with group as in case studies 2 and 3 above, classifiers built using a subset of the data will yield impressively low classification errors on the remaining part of the data because of the systematic biases hard-coded into the data by the confounding factor, yet a model based on these data is very likely to have poor predictive accuracy in classifying future data. Thus, it is also beneficial after building a model with one data set to go out and collect some new data in an independent study and see how well the model predicts the outcomes in these data. It may be true that the current proteomic technologies are not consistent enough for this level of validation. If this is the case, then another alternative is to use the high-throughput proteomic technologies to discover proteins that are predictive of outcome, then subsequently validate these results using more quantitative methods for specific proteins of interest, e.g. using antibodies. These types of assays have the chance to be robust enough to develop clinical applications, so may result in improved translation of proteomic discoveries to clinical settings.

Conclusion

In this chapter, we have outlined some statistical principles for clinical proteomics studies. These guidelines span all aspects of the study, from sample collection and experimental design to preprocessing to biomarker discovery. While these principles are well known in the world of statistics, some of them have been underappreciated and underutilized in laboratory science, and specifically in clinical proteomics. The incorporation of these principles into your scientific workflow can ensure that the data collected will be able to answer the questions of interest and can prevent the results from being distorted by external biases. While anyone can follow the principles outlined here, we believe there is a strong benefit for a proteomics research team to involve a fully collaborating statistician or other quantitative scientist in all aspects of the study, and to involve them in all phases of the study design and planning process. Their involvement provides an individual whose role is specifically to think through these issues and concerns and ensure that the study has the best chance of fulfilling its intended purpose.