Simultaneous Nonrigid Registration, Segmentation, and Tumor Detection in MRI Guided Cervical Cancer Radiation Therapy

Abstract

External beam radiation therapy (EBRT) for the treatment of cancer enables accurate placement of radiation dose on the cancerous region. However, the deformation of soft tissue during the course of treatment, such as in cervical cancer, presents significant challenges for the delineation of the target volume and other structures of interest. Furthermore, the presence and regression of pathologies such as tumors may violate registration constraints and cause registration errors. In this paper, automatic segmentation, nonrigid registration and tumor detection in cervical magnetic resonance (MR) data are addressed simultaneously using a unified Bayesian framework. The proposed novel method can generate a tumor probability map while progressively identifying the boundary of an organ of interest based on the achieved nonrigid transformation. The method is able to handle the challenges of significant tumor regression and its effect on surrounding tissues. The new method was compared to various currently existing algorithms on a set of 36 MR data from six patients, each patient has six T2-weighted MR cervical images. The results show that the proposed approach achieves an accuracy comparable to manual segmentation and it significantly outperforms the existing registration algorithms. In addition, the tumor detection result generated by the proposed method has a high agreement with manual delineation by a qualified clinician.

I. Introduction

EACH year in the United States about 12 200 women are diagnosed with invasive cervical cancer [1]. This cancer is a major health threat for women in less developed nations where vaccination programs are likely to have minimal impact, with 529 900 incidences and 275 100 deaths worldwide in 2008 [2]. The traditional treatment for carcinoma of the cervix has been by surgery or external beam radiation therapy (EBRT). However, when the disease is at an advanced stage, EBRT is the primary modality of treatment, in combination with chemotherapy [3]. Radiotherapy is feasible, effective, and is used to treat over 80% of patients [4]. For some patients, a special type of EBRT is employed, known as intensity modulated radiotherapy (IMRT) [5]. In general, but especially in cases requiring IMRT, understanding and accounting for soft tissue change during fracionated treatment is important. Fig. 1 shows an example of a 3-D dose plan created for a patient undergoing IMRT for cervical cancer. The dose plan is overlaid on the planning-day CT image, with the tumor outlined in red, bladder in yellow, and rectum in green.

Fig. 1.

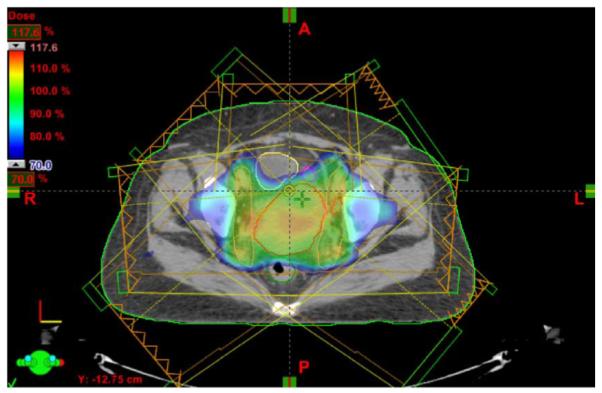
An example of a 3-D IMRT dose plan created for a patient undergoing EBRT for cervical cancer with tumor outlined in red, bladder outlined in yellow, and rectum outlined in green. The dose plan was created using the Varian Eclipse Treatment Planning System [6].

Imaging systems capable of visualizing patient soft-tissue structure in the treatment position have become the dominant method of positioning patients for both conformal and stereotactic radiation therapy. Traditional computed tomography (CT) images suffer from low resolution and low soft tissue contrast, while magnetic resonance (MR) imaging is able to characterize deformable structure with superior visualization and differentiation of normal soft tissue as well as tumor-infiltrated soft tissue. MR imaging also performs better for measuring cervical carcinoma size and uterine extension [7]. Meanwhile, advanced MR imaging with modalities such as diffusion, perfusion and spectroscopic imaging has the potential to better localize and understand the disease and its response to treatment [8]. Therefore, magnetic resonance guided radiation therapy (MRgRT) systems with integrated MR imaging in the treatment room are now being developed as an advanced system in radiation therapy [9].

During radiation therapy treatment, a patient is irradiated multiple times across the whole treatment process that usually lasts for more than several weeks. The main factor controlling the success of treatment is dose targeting, i.e., delivering as much dose as possible to the tumor [gross tumor volume (GTV)], while trying to deliver as little dose as possible to surrounding organs at risk [10]–[12]. Thereafter, accurate localization of the GTV and neighboring normal structures is essential to effectively aim the dose delivery. However, precise delineation of the tumor as well as the soft tissue structure is challenging because of structure adjacency and deformation over treatment. Due to unpredictable inter- and intra-fractional organ motion over the process of the weekly treatments, it is desirable to adapt the original treatment plan to changes in the anatomy, which requires an accurate mapping and precise anatomical correspondence between treatment and planning day. Another important factor in radiation therapy concerns the treatment margins around the GTV that form the clinical target volume (CTV) [13]. The prescribed margin is used to accommodate uncertainties in the position of the target volumes, and the uncertainty can be high due to the large movement of the bladder, uterus and rectum. Therefore, the clinical motivations to shrink the margin, to place accurate dosage and to adapt the treatment plan call for a robust method that can achieve precise organ segmentation, tumor detection, and nonrigid registration.

A. Previous Work

Some previous work has been performed in simultaneously handling registration as well as segmentation, and some interesting results have been reported. Chelikani et al. integrated rigid 2-D portal to 3-D CT registration and pixel classification in an entropy-based formulation [14]. Yezzi et al. integrated segmentation using level sets with rigid and affine registration [15]. A similar method was proposed by Song et al., which could only correct rigid rotation and translation [16]. Unal et al. proposed a PDE-based method without shape priors [17]. Pohl et al. performed voxel-wise classification and registration which could align an atlas to MRI [18]. Chen et al. used a 3-D meshless segmentation framework to retrieve clinically critical objects in CT and cone-beam CT data [19], but no registration result was given. Lu et al. performed an iterative conditional mode (ICM) strategy and integrated constrained nonrigid registration and deformable level set segmentation [12], [20]. On the other hand, the automatic mass detection problem mainly focuses on the application of mammography [21]. Recently, Song et al. proposed a graph-based method to achieve surface segmentation and regional tumor segmentation in one framework for pulmonary CT images [22], no registration incorporated though. Very limited work has been reported to register cervical MR images. [23] investigated the accuracy of rigid, nonrigid, and point-set registrations of MR images for interfractional contour propagation in patients with cervical cancer. Staring et al. presented a multifeature mutual information based method to perform registration of cervical MRI [24].

However, the presence of pathologies such as tumors may violate registration constraints and cause registration errors, because the abnormalities often invalidate gray-level dependency assumptions that are usually made in intensity-based registration. Furthermore, the registration problem is particularly challenging due to the missing correspondences caused by tumor regression. Incorporating knowledge about abnormalities into the framework can improve the registration. All of the above approaches neglect the deformation generated by abnormalities, while such deformation is usually significant during the treatment of cervical cancer. Greene et al. [5] updated the manually created treatment plan of the planning day, to that of the treatment day. Automatic updates are approximated by performing a nonrigid intrasubject registration, and propagating the segmentation of the planning day to the treatment day. However, for cervical cancer radiotherapy cases, propagation of the GTV segmentation is probably not possible with intensity based registration only. Even if anatomical correspondence is found, tumorous tissue may disappear in time due to successful treatment. Staring et al. [24] and Lu et al. [12] mention this challenge but do not give any solution. The tumor regression phenomenon distorts the intensity assumptions and raises questions regarding the applicability of the above approaches.

Limited work has been reported for handling tumor in registration framework. Kyriacou et al. [25] presented a biomechanical model of the brain to capture the soft-tissue deformations induced by the growth of tumors and its application to the registration of anatomical atlases. Mohamed et al. [26] and Zacharaki et al. [27] proposed similar approaches. However, these methods are only applied to brain MRI and can not solve the missing correspondence problem induced by tumor regression in radiotherapy treatment course.

B. Our Contributions

Since a standard approach based on MR image intensity matching only may not be sufficient to overcome these limiting factors, in this paper, we present a novel probability based technique as an extension to our previous work in [28], for the motivations mentioned above. Our model is based on a maximum a posteriori (MAP) framework which can achieve deformable segmentation, nonrigid registration and tumor detection simultaneously. The deformable segmentation extends the previous level set deformable model with shape prior information, and the constrained nonrigid registration part considers organ surface matching and intensity matching together. Different from our previous work [12], in this paper, a tumor probability map is simultaneously generated, which estimates each voxel’s probability of belonging to tumor. A key novelty of this paper is that the intensity matching is defined as a mixture of two distributions which statistically describe image gray-level variations for two pixel classes: tumor and normal tissue. The mixture of the two distributions is weighted using the tumor probability map. The constraint of the transformation is also constructed in a weighted mixture manner, where the probability density functions are well-designed functions of the transformation’s Jacobian map, and the constraint guarantees the transformation to be smooth and simulates the tumor regression process.

In this manner, we can interleave the segmentation, registration and detection processes, and take proper advantage of the dependence among them. Using the proposed approach, it is easy to calculate the location changes of the lesion for diagnosis and assessment; thus we can precisely guide the interventional devices toward the tumor during radiation therapy. Escalated dosages can then be administered while maintaining or lowering normal tissue irradiation. There are a number of clinical treatment sites that will benefit from our MR-guided radiotherapy technology, especially when tumor regression and its effect on surrounding tissue can be significant. Here we focus on the treatment of cervical cancer as the key example application.

The remainder of this paper is organized as follows. In Section II, details about the unified framework are given. Deformable segmentation, nonrigid registration and tumor detection modules are explained in details. In Section III, we provide experimental results using our new approach. We also compare the results with those obtained with existing methods. In Section IV, we provide a discussion of our approach, and conclude this paper.

II. Methods

Fig. 2 illustrates the workflow of our proposed algorithm. First, a preprocedural (planning day) MR image is captured before the treatment. Then, the GTV, bladder, and uterus are manually segmented for therapy planning. During the course of treatment, the weekly intra-procedural MR image is first obtained, and the clinicians perform the preprocessing steps, i.e., image reslicing, etc. Then, our proposed method is performed. The 3-D normal tissue segmentation, tumor detection and nonrigid registration modules are performed iteratively, and the algorithm converges when the difference between two consecutive iterations is smaller than a prescribed threshold.

Fig. 2.

Diagram of the proposed method.

A. A Unified Framework: Bayesian Formulation

Using a probabilistic formulation, various models can be fit to the image data by finding the model parameters that maximize the posterior probability. Let I₀ and I_d be the planning day (day 0) and treatment day (day d) 3-D MR images, respectively, and S0 be the set of segmented planning day organs. A unified framework is developed using Bayesian analysis to calculate the most likely segmentation in the treatment day fractions S_d, the deformation field between the planning day and treatment day data T_0d, and the tumor map M_d at treatment day which associates with each voxel of the image its probability of belonging to a tumor

$$\widehat{S_d},\widehat{T_{0d}},\widehat{M_d}=\arg \underset{S_d,T_{0d},M_d}{\max }\left[p\right(S_d,T_{0d},M_d\mid I_0,I_d,S_0\left)\right].$$ (1)

As in our previous effort [12], this problem is reformulated so that it is solved in two basic iterative computational stages [29]. With k indexing each iterative step, we have

$$\widehat{S_d^k}=\arg \underset{S_d^k}{\max }\left[p\right(S_d^k\mid T_{0d}^k\left(S_0\right),I_d,M_d^k\left)\right]$$ (2)

$$\widehat{T_{0d}^{k+1}},\widehat{M_d^{k+1}}=\arg \underset{T_{0d}^{k+1},M_d}{\max }\left[p\right(T_{0d}^{k+1},M_d^{k+1}\mid S_d^k,S_0,I_d,I_0\left)\right].$$ (3)

These two equations represent the key problems we are addressing. Equation (2) estimates the segmentation of the treatment day structure $\left(S_d^k\right)$. Equation (3) estimates the next iterative step of the mapping $T_{0d}^{k+1}$ between the day 0 and day d spaces, as well as the tumor probability map M^k+1 in treatment day.

B. Segmentation

The segmentation module here is similar to our previous work [12], [28]. In this paper, we use (2) to segment the normal or noncancerous organs (bladder and uterus). For the sake of simplicity, we assume the normal organ segmentations $S_d^k$ here are independent of the abnormal tumor map M. Bayes’ theorem is applied to (2)

$$\begin{array}{cc}\hfill {\widehat{S}}_d^k& =\arg \underset{S_d^k}{\max }\left[p\right(S_d^k\mid T_{0d}^k\left(S_0\right),I_d,M_d^k\left)\right]\hfill \\ \hfill & =\arg \underset{S_d^k}{\max }\left[p\right(S_d^k\mid T_{0d}^k\left(S_0\right),I_d\left)\right]\hfill \\ \hfill & =\arg \underset{S_d^k}{\max }\left[p\right(I_d\mid S_d^k)\cdot p(T_{0d}^k\left(S_0\right)\mid S_d^k)\cdot p(S_d\left)\right].\hfill \end{array}$$ (4)

1) Shape Prior Construction: Nonparametric Kernel Density Estimation Model

Here we assume that the priors are stationary over the iterations, so we can drop the k index for that term only, i.e., $p\left(S_d^k\right)=p\left(S_d\right)$. Instead of using a point model to represent the object, we choose a level set representation of the object to build a model for the shape prior, and then define the probability density function p(S_d) in (4).

The Bayesian formulation of the image segmentation problem allows us to introduce higher-level prior knowledge about the shape of expected objects. The first application of shape priors for level set segmentation was developed by Leventon et al., who proposed to perform principal component analysis (PCA) on a set of signed distance functions embedding a set of sample shapes [30]. This PCA-based approach was widely accepted by researchers and it works well in practical applications ([20], [31]–[34]). However, the use of PCA to model level set based shape distributions has two limitations. Firstly, the space of signed distance functions is not a linear space, i.e., arbitrary linear combinations of signed distance functions will in general not correspond to a valid signed distance function. Secondly, the PCA-based methods typically use the first few principal components in the feature space to capture the most variation on the space of embedding functions. As a consequence, they may need a larger number of eigenmodes to capture certain details of the modeled shape [33].

Instead of using the PCA-based priors, in this paper, we use a nonparametric technique of kernel density estimation (KDE) to model the shape variation, which addresses above limitations and allows the shape prior to approximate arbitrary distributions [35], [36].

Consider a training set of n rigidly aligned images, with L objects or structures in each image. Fig. 3 shows a training set of bladders overlaid on six MR pelvic images. Ideally, the rigid alignment removes the pose variability in the training data, and what remains is just shape variability. The training data were generated from manual segmentations by a qualified clinician. Each object in the training set is embedded as the zero level set of higher dimensional level sets Ψ₁, …, Ψn with negative distances outside and positive distances inside the object. The prior constructing problem then is to estimate p(S_d) = p(Ψ_Sd) from which the training samples Ψ₁, …, Ψn are drawn. This density is a probability density over an infinite dimensional space. We would like to leave the shape of this density unconstrained, therefore we adopt a nonparametric density estimation route. Assuming that we have a distance metric D(·, ·) in the space of implicit surfaces Ψ, we can form a Parzen density estimator as follows:

$$p\left(S_d\right)=p\left({\Psi }_{S_d}\right)=\frac{1}{n}\sum _{i=1}^{n}k\left(D\right({\Psi }_{S_d},{\Psi }_i),\sigma )$$ (5)

where k(·, σ) denotes a Gaussian kernel with kernel size σ, i.e.,

$$k(x,\sigma )=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{x^2}{2{\sigma }^2}\right).$$ (6)

Conceptually, the nonparametric density estimate in (5) can be used with a variety of distance metrics. Kim et al. [36] provide a detailed analysis of different distance metrics including template metric and Euclidean distance, etc.

Fig. 3.

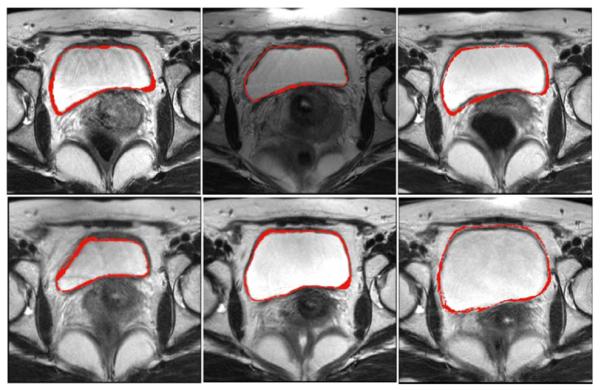
Training set: outlines of bladders on six 3-D MR pelvic images (2-D slices shown).

With the level set representation, the above Parzen density estimator (5) can be rewritten explicity in terms of Ψ as well as the distance metric. Here, we define the distance measure between level set shapes (D_LS) as the area of the symmetric difference, as was previously proposed [35], [37]

$$D_{\mathit{LS}}({\Psi }_{S_d},{\Psi }_i)={\int }_{\Omega }{\left(H\right({\Psi }_{S_d}\left(\mathbf{x}\right))-H({\Psi }_i\left(\mathbf{x}\right)\left)\right)}^{2}d\mathbf{x}$$ (7)

where H is the Heaviside function

$$H\left(x\right)=\{\begin{array}{cc}1,\hfill & x\ge 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (8)

There exist extensive studies on how to optimally choose the kernel width σ, based on asymptotic expansion such as heuristic estimates [38] or maximum likelihood optimization by cross validation [39]. For this work, we simply fix σ² to be the mean squared nearest-neighbor distance

$${\sigma }^2=\frac{1}{n}\sum _{i=1}^n\underset{j\ne k}{\min }{D}_{\mathit{LS}}({\Psi }_j,{\Psi }_k).$$ (9)

The intuition behind this choice is that the width of the Gaussian is chosen such that on average the next training shape is within one standard deviation [35].

When learning a reference level set from training shapes, the PCA-based approaches need to make the statistical assumption that the training shapes are distributed according to a Gaussian distribution. This assumption sometimes does not hold since many real-world objects undergo complex shape variations in different scenarios. On the other hand, the nonparametric technique of KDE model allows the shape prior to approximate arbitrary distributions. Since the level sets are not linear functions, the problem of applying PCA to level sets is that it tries to represent nonlinear distance functions and their variation. In this paper, we do not have this problem since KDE estimates the probability of the surface, not the variations.

2) Segmentation Likelihoods

As we did previously [12], we impose a key assumption here: the segmentation likelihood term is separable into two independent data-related likelihoods, requiring that the estimation of the normal structure at day d be close to: 1) the same structure segmented at day 0, but mapped to a new estimated position at day d by the current iterative mapping estimate $T_{0d}^k$ and 2) the intensity-based feature information derived from the day d image.

In (4), $p\left(T_{0d}^k\right(S_0)\mid S_d)$ constrains the organ segmentation in day to be adherent to the transformed day 0 organs by current mapping estimation $T_{0d}^k$. The segmented object is still embedded as the zero level set of a higher dimensional level set Ψ. Thus, we use the difference between the two level sets to model the probability density of the day 0 segmentation likelihood term

$$p\left(T_{0d}^k\right(S_0)\mid S_d^k)=\frac{1}{Z}\prod _{\mathbf{x}}\exp \left[-{\left({\Psi }_{T_{0d}^k\left(S_0\right)}\right(\mathbf{x})-{\Psi }_{S_d^k}(\mathbf{x}\left)\right)}^2\right]$$ (10)

where x represents all the voxels in the image domain, and Z is a normalizing constant that can be removed once the logarithm is taken.

In (4), $p(I_d\mid S_d^k)$ indicates the probability of producing an image I_d given $S_d^k$. In three-dimensions, considering L organs in the image, assuming gray level homogeneity within each object, we use the imaging model defined by Chan and Vese [40] in (11), where c_1–obj and σ_1–obj are the average and standard deviation of I_d inside $S_{d-\mathrm{obj}}^k,c_{2-\mathrm{obj}}$, and σ_2–obj are the average and standard deviation of I_d outside $S_{d-\mathrm{obj}}^k$ but also inside a certain domain Ω that contains $S_{d-\mathrm{obj}}^k$

$$\begin{array}{cc}\hfill p(I_d\mid S_d^k)& =\prod _{\mathrm{obj}=1}^L[\prod _{\text{inside}\left(S_{d-\mathrm{obj}}^k\right)}\exp \left[-\frac{{\left(I_d\right(\mathbf{x})-c_{1-\mathrm{obj}})}^2}{2{\sigma }_{1-\mathrm{obj}}^2}\right]\phantom{]}\hfill \\ \hfill & \cdot \phantom{[}\prod _{\text{outside}\left(S_{d-\mathrm{obj}}^k\right)}\exp \left[-\frac{{\left(I_d\right(\mathbf{x})-c_{2-\mathrm{obj}})}^2}{2{\sigma }_{2-\mathrm{obj}}^2}\right]].\hfill \end{array}$$ (11)

In practice, MR images often suffer from intensity inhomogeneity due to various factors, such as spatial variations in illumination and imperfections of imaging devices [41]. In our work, the clinicians perform the bias field correction after the acquisition of MR images, in order to eliminate the intensity inhomogeneity. In addition, we also incorporate the constraints from registration to guide the surface evolving [use (10)], which guarantees an accurate segmentation.

3) Energy Function

Combining (5), (10), and (11), we introduce the segmentation energy function E_seg defined by

$$\begin{array}{cc}\hfill E_{\mathrm{seg}}& =-\ln p(S_d^k\mid T_{0d}^k(S_0),I_d)\hfill \\ \hfill & =-\ln p(I_d\mid S_d^k)\cdot p\left(T_{0d}^k\right(S_0)\mid S_d^k)\cdot p\left(S_d^k\right)\hfill \\ \hfill & \propto \sum _{\mathit{obj}=1}^L[{\lambda }_1{\int }_{\text{inside}\left(S_{d-\mathrm{obj}}^k\right)}{\mid I_d\left(\mathbf{x}\right)-c_{1-\mathrm{obj}}\mid }^{2}d\mathbf{x}\phantom{]}\hfill \\ \hfill & +\phantom{[}{\lambda }_2{\int }_{\text{outside}\left(S_{d-\mathrm{obj}}^k\right)}{\mid I_d\left(\mathbf{x}\right)-c_{2-\mathrm{obj}}\mid }^{2}d\mathbf{x}]\hfill \\ \hfill & +\gamma {\int }_{\mathbf{x}}{\mid {\Psi }_{T_{0d}^k\left(S_0\right)}\left(\mathbf{x}\right)-{\Psi }_{S_d^k}\left(\mathbf{x}\right)\mid }^{2}d\mathbf{x}\hfill \\ \hfill & -\mu \ln \sum _{i=1}^{n}k\left(D_{\mathit{LS}}\right({\Psi }_{S_d},{\Psi }_i),\sigma ).\hfill \end{array}$$ (12)

The parameters λ₁, λ₂, γ, μ are used to balance the influence of the registration constraint, KDE prior model and the image information model. Notice that the MAP estimation of the objects in (12), $\widehat{S_d^k}$, is also the minimizer of the above energy functional E_seg. This minimization problem can be formulated and solved using the level set surface evolution method [42].

To simplify the complexity of the segmentation system, we generally choose the parameters in our experiments as follows: λ₁ = λ₂ = λ, μ = 0.5. This leaves us only two free parameters (λ and γ) to balance the influence of two terms, the constraints from registration module and the image data term. The tradeoff between these two terms depends on the strength of the constraints and the image quality.

C. Registration and Tumor Detection

In this section, in order to solve the challenging intrapatient registration problem while taking tumor detection into consideration, we develop a novel module that is different from previous registration approaches [5], [12], [24], [43]–[47]. The goal here is to register the planning day (0) data to the treatment day (d) data and carry the planning information forward, as well as to carry forward segmentation constraints. In the mean time, the tumor detection map M is estimated, which associates each pixel in the image to its probability of belonging to a tumor.

The second stage of the proposed strategy described above in (3) can be further developed using Bayes rule. As indicated in Section II-B, the normal organ segmentations $S_d^k$ are independent of the tumor detection map M_d, and the priors are stationary over the iterations

$$\begin{array}{cc}\hfill \widehat{T_{0d}^{k+1}},\widehat{M^{k+1}}=& \arg \underset{T_{0d}^{k+1},M^{k+1}}{\max }\left[p\right(T_{0d}^{k+1},M^{k+1}\mid S_d^k,S_0,I_d,I_0\left)\right]\hfill \\ \hfill =& \arg \underset{T_{0d}^{k+1},M_d^{k+1}}{\max }\left[p\right(S_d^k,S_0\mid T_{0d}^{k+1},M^{k+1})\hfill \\ \hfill & \cdot p(I_d,I_0\mid T_{0d}^{k+1},M_d^{k+1})\cdot p(T_{0d},M_d)]\hfill \\ \hfill =& \arg \underset{T_{0d}^{k+1},M_d^{k+1}}{\max }\left[p\right(S_d^k,S_0\mid T_{0d}^{k+1})\hfill \\ \hfill & \cdot p(I_d,I_0\mid T_{0d}^{k+1},M_d^{k+1})\hfill \\ \hfill & \cdot p(T_{0d}\mid M_d)\cdot p\left(M_d\right)].\hfill \end{array}$$ (13)

The first term on the right-hand side represents the conditional likelihood related to mapping the segmented soft tissue structures (organs) at days 0 and d, and the second term registers the intensities of the images while simultaneously estimating the probability tumor map. The third term constrains the overall nonrigid transformation, and the fourth term represents prior assumptions for the tumor map.

1) Segmented Organ Matching

To begin breaking down the organ matching term, $p(S_d^k,S_0\mid T_{0d}^{k+1})$, we must make the reasonable assumption that the individual organs can be registered

$$p(S_d^k,S_0\mid T_{0d}^{k+1})=\prod _{\mathrm{obj}=1}^{L}p(S_{d-\mathrm{obj}}^k,S_{0-\mathrm{obj}}\mid T_{0d}^{k+1})$$ (14)

with L represents the number of objects in each image.

As discussed in the segmentation section, each object is represented by the zero level set of a higher dimensional level set Ψ. Assuming the objects vary during the treatment process according to a Gaussian distribution, and given that the different organs can be mapped, respectively, we further simplify the organ matching term to be

$$\begin{array}{cc}\hfill p& (S_d^k,S_0\mid T_{0d}^{k+1})\hfill \\ \hfill =& \prod _{\mathrm{obj}=1}^{L}p(S_{d-\mathrm{obj}}^k,S_{0-\mathrm{obj}}\mid T_{0d}^{k+1})\hfill \\ \hfill =& \prod _{\mathrm{obj}=1}^L\frac{1}{\sqrt{2\pi }{\sigma }_{\mathrm{obj}}}\exp \left[\frac{-{({\Psi }_{T_{0d}^{k+1}\left(S_{0-\mathrm{obj}}\right)}-{\Psi }_{S_{d-\mathrm{obj}}^k})}^2}{2{\sigma }_{\mathrm{obj}}^2}\right]\hfill \\ \hfill =& \frac{1}{{\left(2\pi \right)}^{L∕2}{\sigma }_1\cdots {\sigma }_L}\hfill \\ \hfill & \cdot \exp \left[\sum _{\mathrm{obj}=1}^L-{\omega }_{\mathrm{obj}}{\left[{\Psi }_{T_{0d}^{k+1}\left(S_{0-\mathrm{obj}}\right)}-{\Psi }_{S_{d-\mathrm{obj}}^k}\right]}^2\right]\hfill \\ \hfill =& Z_1\cdot \exp \left[\sum _{\mathrm{obj}=1}^L-{\omega }_{\mathrm{obj}}{\int }_{\mathbf{x}}{\left[{\Psi }_{T_{0d}^{k+1}\left(S_{0-\mathrm{obj}}\right)}\left(\mathbf{x}\right)-{\Psi }_{S_{d-\mathrm{obj}}^k}\left(\mathbf{x}\right)\right]}^{2}d\mathbf{x}\right]\hfill \end{array}$$ (15)

where ${\omega }_{\mathrm{obj}}=1∕2{\sigma }_{\mathrm{obj}}^2$, and ω_obj are used to weight different organs. Z₁ is a constant that can be omitted when the logarithm is taken. When maximized with respect to $T_{0d}^{k+1}$, the organ matching term ensures the transformed day 0 organs and the segmented day d organs align over the regions. We note that ultimately we may use several organs here (rectum, uterus, and bladder) in the future, although in some applications (e.g., biomarker development) only the uterus is the key organ. In this paper, we use the uterus and the bladder as the constraints.

2) Intensity Matching and Tumor Probability Map Estimation

To determine the relationship between a planning day image and a treatment day image, a similarity criterion which determines the degree of match between the two images must be defined. Previous works have made use of various intensity matching similarity metrics, including sum of squared differences (SSD) [5], normalized correlation coefficient (NCC) [20], mutual information (MI) [44], [48], and multifeature mutual information (α-MI) [24]. However, all of the above methods use a single similarity metric, and their intensity dependency assumptions are often invalidated due to the existence and regression of tumor.

For our work, in order to define the likelihood term $p(I_d,I_0\mid T_{0d}^{k+1},M_d^{k+1})$, we assume conditional independence over the voxel locations x. This assumption is reasonable and the image processing/computer vision literature are replete with this correlated random field image models [49]

$$p(I_d,I_0\mid T_{0d}^{k+1},M_d^{k+1})=\prod _{\mathbf{x}}p\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right))\mid M_d^{k+1}(\mathbf{x}\left)\right).$$ (16)

Different from previous work which only use a single similarity metric, here we model the probability of the pair $p\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right))\mid M_d^{k+1}(\mathbf{x}\left)\right)$ to be dependent on the class of each voxel. Each class is characterized by a well-designed probability distribution, denoted by p_N for the normal tissue p_T and for the tumor. Let $M_d^{k+1}\left(\mathbf{x}\right)$ be the tumor map which associates with x its probability of belonging to a tumor, the probability distribution $p\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right))\mid M_d^{k+1}(\mathbf{x}\left)\right)$ can be defined as a mixture of the two class distributions

$$\begin{array}{cc}\hfill p\left(I_d\right(& \mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right))\mid M^{k+1}(\mathbf{x}\left)\right)\hfill \\ \hfill =& (1-M^{k+1}(\mathbf{x}\left)\right)p_N\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right)\left)\right)\hfill \\ \hfill & +M^{k+1}\left(\mathbf{x}\right)p_T\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right)\left)\right).\hfill \end{array}$$ (17)

Normal Tissue Class

Across the treatment procedure, the tumor experiences a regression process if the treatment is successful [13]. The tumor regression is illustrated in Fig. 4, which presents a plot of mean relative tumor volume as measured with weekly MRI during EBRT in five patients with cancer of the uterine cervix.

Fig. 4.

Tumor regression: plot of mean relative tumor volume.

As the tumor shrinks, part of the tumor turns into scar, and returns to the intensity level near normal tissue. Thereafter, normal appearing tissue in treatment day MR has two origins: originally normal tissue (type I), and tumor that returns to a normal intensity level due to treatment (type II). We choose two different probabilities for these two types. The histograms of normal cervical tissue and tumor are plotted in Fig. 5. From current clinical research [50] and Fig. 5, we can see that the intensities of tumor are generally much higher than those of normal cervical tissue in T₂-weighted MR images.

Fig. 5.

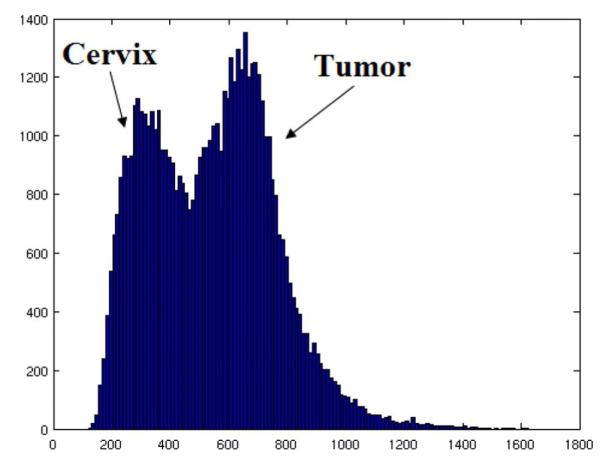
Histograms of normal cervix and tumor.

Therefore, for the sake of simplicity, we characterize normal tissue of type II (tumor that returned to normal intensity) as areas with much lower intensity in treatment day MR [50]. We assume a voxel labeled type II in day d MR can match any tumor voxel in day 0 with equal probability and use a uniform distribution. The remaining normal tissue voxels are labeled as type I normal tissue (always normal since the planning day), which are modeled assuming a discrete Gaussian distribution across the corresponding voxel locations

$$\begin{array}{cc}\hfill & p_N\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right)\left)\right)=\hfill \\ \hfill & \{\begin{array}{cc}\frac{1}{c},\hfill & T_{0d}\left(I_0\right(\mathbf{x}\left)\right)-I_d\left(\mathbf{x}\right)>\Delta \hfill \\ \frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\mid T_{0d}^{k+1}\left(I_0\right(\mathbf{x}\left)\right)-I_d\left(\mathbf{x}\right)\mid }^2}{2{\sigma }^2}\right),\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (18)

where c is the number of voxels in the day 0 tumor, and Δ is the predetermined threshold used to differentiate the intensity of normal and tumor tissue.

Tumor Class

The definition of the tumor distribution is a difficult task. Similar to normal tissue, the tumor tissue in treatment day MR also has two origins. One is the tumor tissue in planning day MR (type I), which represents the remaining tumor after the radiotherapy. We assume a voxel in the residual tumor can match any voxel in the initial tumor (day 0) with equal probability and use a uniform distribution. The other origin of the tumor class in day d (type II) is from normal tissue in planning MR that has become tumor due to disease progression. This type is characterized with a much higher intensity in day d image[50]. We assume that each normal voxel in the day 0 MR can turn into a tumor voxel with equal probability. Thus, this type is also modeled using a uniform distribution, but with lower probability, since the chance of this deterioration process is relatively small across the radiotherapy treatment

$$\begin{array}{cc}\hfill p_T\left(I_d\right(\mathbf{x}),& T_{0d}^{k+1}\left(I_0\right(\mathbf{x}\left)\right))\hfill \\ \hfill & =\{\begin{array}{cc}\frac{1}{(V-c)},\hfill & T_{0d}^{k+1}\left(I_0\right(\mathbf{x}\left)\right)-I_d\left(\mathbf{x}\right)<-\Delta \hfill \\ \frac{1}{c},\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (19)

where V is the total number of voxels in MR image, c is the number of voxels in the day 0 tumor [the same as in (18)].

3) Transformation Smoothness: Weighted Non-Negative Jacobian Constraints

To constrain a transformation to be smooth, a penalty term which regularizes the transformation is required [12]. The penalty term will disfavor impossible or unlikely transformation, promoting a smooth transformation field and local volume conservation or expected volume change. Previously, regularization measures based on the bending energy of a thin-plate of metal have been widely used [12], [43]; this kind of constraint penalizes nonaffine transformations.

A key property of nonrigid transformations is the determinant of the Jacobian of the transformation, often referred to as the Jacobian map. This measure gives the local volume expansion required to map the images. If the determinant of the Jacobian is equal to 1, then there is no volume change; if it is greater than 1, it implies that the fixed image is bigger than the moving image; whereas if it is less than 1, it implies that the moving image has to be shrunk to match the target [51]. If this value goes below zero (or even close to zero), it is a sign of trouble, which implies that the transformation has become singular. In such cases, one can discard the transformation and repeat the registration with higher smoothness settings.

The use of the Jacobian map as a regularization constraint has been introduced into image registration [48], [51], [52]. Here, we extend the previously reported Jacobian penalty methods by designing a novel regularization term to constrain the deformation. The new regularization is based on the weighted sum of two probability density functions computed from the Jacobian map. Similar to the discussion of (16) and (17), here we have

$$\begin{array}{cc}\hfill p(T_{0d}\mid M)& =\prod _{\mathbf{x}}p\left(T_{0d}\right(\mathbf{x})\mid M(\mathbf{x}\left)\right)\hfill \\ \hfill p\left(T_{0d}\right(\mathbf{x})\mid M(\mathbf{x}\left)\right)& =(1-M(\mathbf{x}\left)\right)p_N\left(T_{0d}\right(\mathbf{x}\left)\right)+M\left(\mathbf{x}\right)p_T\left(T_{0d}\right(\mathbf{x}\left)\right).\hfill \end{array}$$ (20)

We expect the transformation to be nonsingular hence we would like to have a large penalty on a negative Jacobian for normal tissues. Meanwhile, we simulate the tumor regression process by constraining the determinant of the transformation’s Jacobian at tumor M(x) to be between 0 and 1. In our approach, p_N and p_T are calculated using the modified continuous logistic functions: (∊ = 0.1)

$$\begin{array}{cc}\hfill p_N\left(T_{0d}\right(\mathbf{x}\left)\right)=& {\left(\frac{1}{1+\exp \left(\frac{-\mid J\left(T_{0d}\right(\mathbf{x}\left)\right)\mid }{∊}\right)}\right)}^2\hfill \end{array}$$ (21)

$$\begin{array}{cc}\hfill p_T\left(T_{0d}\right(\mathbf{x}\left)\right)=& {\left(\frac{1}{1+\exp \left(\frac{-\mid J\left(T_{0d}\right(\mathbf{x}\left)\right)\mid }{∊}\right)}\right)}^2\hfill \\ \hfill & -{\left(\frac{1}{1+\exp \left(\frac{1-\mid J\left(T_{0d}\right(\mathbf{x}\left)\right)\mid }{∊}\right)}\right)}^2\hfill \end{array}$$ (22)

p_Nand p_T are plotted in Fig. 6. These constraints (p_N and p_T) penalize negative Jacobians, thus reduce the probability of folding in the registration maps. p_T encourages the determinant of the transformation’s Jacobian to be less than 1, which simulates the tumor regression process.

Fig. 6.

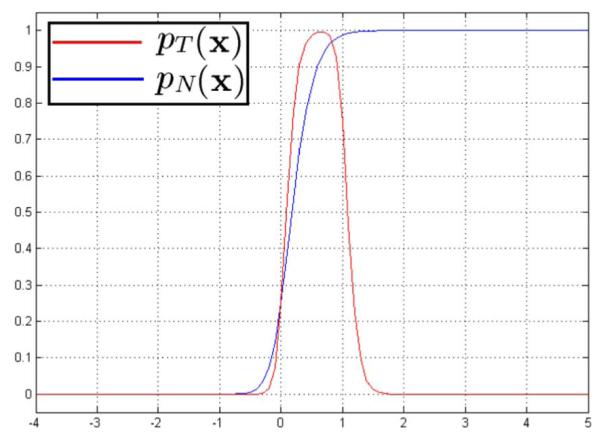
Jacobian constraints: Plot for probability density functions of tumor class and normal tissue class.

We have studied tumor regression [53] using structural MR images from 27 cervical cancer patients receiving EBRT [53]. Tumor regression was estimated from manually-outlined surfaces of any residual tumor during treatment. Regression occurred for all patients, but the shapes of the regression curves and the relative volume reduction varied substantially. Therefore, it is reasonable to make the assumption that the Jacobian constraint for the tumor label lies between 0 and 1; and the underlining assumption of (18), i.e., each tumor voxel might return to normal with equal probability, is also applicable.

4) Tumor Map Prior

We assume that the tumor map arises from a Gibbs distribution

$$p\left(M_d\right)=\frac{1}{Z}{e}^{-U\left(M_d\right)}$$ (23)

where Z is a normalization constant, and U(M_d) is a discrete energy of regularization. Many specific terms can be defined to describe the spatial configurations of different types of lesion. The previous detection approaches applied to mammography have a tendency to over-detect (to find more regions than the real ones) [21], hence in this paper, we use an energy restricting the total amount of abnormal pixels in the image

$$p\left(M_d\right)=\frac{1}{Z}{e}^{-U\left(M_d\right)}=\frac{1}{Z}{e}^{-\sum _{\mathbf{x}}{M}_d\left(\mathbf{x}\right)}.$$ (24)

5) Registration – Detection Energy Function

Combining the above (13), (15), (16), (17), (20), (24), we introduce

$$\begin{array}{cc}\hfill E_{\mathrm{reg}-\det }& (T,M)\hfill \\ \hfill =& -\ln p(T_{0d}^{(k+1)},M^{(k+1)}\mid S_d^k,S_0,I_d,I_0)\hfill \\ \hfill =& -\ln p(S_d^k,S_0\mid T_{0d}^{k+1})-\ln p(I_d,I_0\mid T_{0d}^{k+1},M^{k+1})\hfill \\ \hfill & -\ln p(T_{0d}\mid M)-\ln p\left(M\right)\hfill \\ \hfill =& \sum _{\mathrm{obj}=1}^N{\omega }_{\mathrm{obj}}{\int }_{\mathbf{x}}{\left[{\Psi }_{T_{0d}^{k+1}\left(S_{0-\mathrm{obj}}\right)}\left(\mathbf{x}\right)-{\Psi }_{S_{d-\mathrm{obj}}^k}\left(\mathbf{x}\right)\right]}^{2}d\mathbf{x}\hfill \\ \hfill =& -{\int }_{\mathbf{x}}\ln p\left(I_d\right(\mathbf{x}),T_{0d}^{k+1}(I_0\left(\mathbf{x}\right))\mid M^{k+1}(\mathbf{x}\left)\right)d\mathbf{x}\hfill \\ \hfill =& -{\int }_{\mathbf{x}}\ln p\left(T_{0d}\right(\mathbf{x})\mid M(\mathbf{x}\left)\right)d\mathbf{x}+\sum _{\mathbf{x}}M\left(\mathbf{x}\right).\hfill \end{array}$$ (25)

At each iteration, $T_{0d}^{k+1}$ and $M_d^{k+1}$ are updated by minimizing (25). Equations (12) and (25) run alternatively until convergence. Thereafter, the soft tissue segmentation as well as the nonrigid registration and tumor detection in day d benefit from each other and are estimated simultaneously.

6) Transformation Model

The registration module is implemented using a hierarchical multi-resolution free form deformation (FFD) transformation model based on cubic B-splines. An FFD based transform was chosen because an FFD is locally controllable due to the underlying mesh of control points which are used to manipulate the image [54]. B-splines are locally controlled, which makes them computationally efficient, even for a large number of control points. Local control means that cubic B-splines have limited support, such that changing one control point only affects the transformation in the local neighborhood of the manipulated control point [5], [43], [47], [54].

D. Implementation

The practical implementation of the algorithm described by the solution of (2) and (3) will proceed as follows.

1) Initialization

First, an expert manually segmented the key soft tissue structures (S₀) in the planning 3-D MR images, i.e., the bladder, uterus, cervix, and GTV. Then, the first iterative estimate (k = 1) of a nonrigid mapping from day 0 to day $d\left(T_{0d}^1\right)$ will be formed. This is done by performing a intensity based conventional nonrigid registration. The first iterative estimate (k = 1) of the tumor probability map (M¹) is initiated to be bi-modal. For the pixels within the planning day cervix (including normal cervix tissue and GTV), the probability is set to be the ratio of day 0 GTV volume divided by the day 0 overall cervix tissue volume. For the pixels outside the planning day cervix, the initial probability is set to be cervix tissue volume divided by the whole image volume.

2) Iterative Solution

Here we alternately perform: (a) Segmentation: Using the current transformation estimated, the soft tissue segmentations obtained at day 0 will be mapped into day d, thus forming $T_{0d}^k\left(S_0\right)$. Now using this information as a constraint, as well as the likelihood information and shape prior model defined in Section II-B, the segmentation module (12) is run, producing the soft tissue segmentations at day $d\left(S_d^k\right)$. (b) Registration and Tumor Detection: A full 3-D nonrigid mapping of the 3-D MRI from day 0 to the day d 3-D MRI is estimated in the second stage using (25), producing a newer mapping estimation $\left(T_{0d}^{k+1}\right)$. Meanwhile, the tumor map M^k+1 is also updated. The two steps run alternatively until convergence. Thereafter, the normal tissue segmentation in day d, nonrigid transformation between planning day and treatment day, as well as the tumor probability map at day d are estimated simultaneously. For the optimization, we use the level set surface evolving technique to update the segmentation after each iteration, and the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method [55] is used to solve registration-detection module. Due to the difficulty of obtaining the analytic gradient of the entire energy function, we use a numerical gradient.

III. Results

A. Data and Training

MR data were acquired with a GE EXCITE 1.5T magnet from six different patients undergoing EBRT for cervical cancer at Princess Margaret Hospital, Toronto, ON, Canada. Each patient was scanned six times, one scan at baseline and then every week of treatment, i.e., 36 MR images overall. T₂-weighted, fast spin echo images (echo time/repetition time 100/5000 ms, voxel size 0.36 mm × 0.36 mm × 5 mm, and image dimension 512 × 512 × 38) were acquired in all cases. Bias field correction was performed so that the intensities can be directly compared, and the MR images were resliced to be isotropic with a clinically applicable spatial resolution 2 mm × 2 mm × 2 mm, and image dimension 92 × 92 × 95, using the software BioImage Suite 3.0 [56]. MR data were acquired with a GE EXCITE 1.5T magnet from six different patients undergoing EBRT for cervical cancer at Princess Margaret Hospital, Toronto, ON, Canada. Each patient was scanned six times, one scan at baseline and then every week of treatment, i.e., 36 MR images overall. T₂-weighted, fast spin echo images (echo time/repetition time 100/5000 ms, voxel size 0.36 mm × 0.36 mm × 5 mm, and image dimension 512 × 512 × 38) were acquired in all cases. Bias field correction was performed so that the intensities can be directly compared, and the MR images were resliced to be isotropic with a clinically applicable spatial resolution 2 mm × 2 mm × 2 mm, and image dimension 92 × 92 × 95, using the software BioImage Suite 3.0 [56].

Manual segmentations of the GTV, bladder, and uterus were available for each image. They were created by a radiation oncologist and approved by a radiologist. The manual segmentations of bladder and uterus was used to form the training set. We adopted a “leave-one-patient-out” test that alternately chose one patient out of the 30 sequences to validate our algorithm. The tested images were not included in the corresponding training sets. Fig. 3 shows a training set for bladder overlaid on six MR pelvic images. Using the KDE approach described in Section II-B1, we built a model of the shape profile of the bladder and uterus. The manual segmentations of GTV were not used in the algorithm, but for evaluating the detection results only.

B. Segmentation Results

In this section, we describe and evaluate the segmentation result of normal structures; the delineation result for cancerous tumor tissue will be discussed in Section III-D. Figs. 7 and 8 show example segmentation results for bladder and uterus using the proposed method, respectively. Both figures present the coronal, sagittal, axial, and 3-D views of the segmented surface. The results presented here are achieved with parameters λ = 0.3, γ = 0.7. The algorithm typically converges in 20–30 iterations, and it usually takes around half an hour on a 8 Core 2.83 GHz Intel XEON CPU with 16 G RAM using MATLAB. Implementing using C++ is able to speed it up to achieve a more acceptable performance for usage.

Fig. 7.

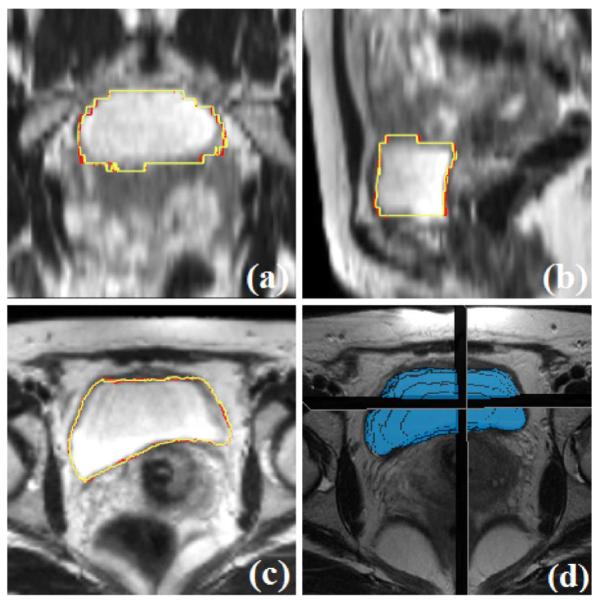
Segmentation results for the bladder, comparing the proposed algorithm (yellow) with manual segmentation (red). Subplots show the (a) coronal, (b) sagittal, (c) axial, and (d) 3-D views.

Fig. 8.

Segmentation results for the uterus, comparing the proposed algorithm (yellow) with manual segmentation (red). Subplots show the (a) coronal, (b) sagittal, (c) axial, and (d) 3-D views.

To validate the segmentation results, we compare the expert’s manual delineations (which are used as ground truth) to the automatic results using three metrics, namely mean absolute distance (MAD), Hausdorff distance (HD), and Dice coefficient. While MAD represents the global disagreement between two contours, HD compares their local similarities [57], and Dice coefficient evaluates their volume overlaps.

We compare the experimental results from our algorithm with those obtained from segmentation using an active contour model (defined by Chan and Vese [40]), level set active shape models with shape priors only (defined by Leventon et al. [30]), and iterative conditional mode (ICM) model we described previously [12]. Tables I and II use MAD, HD and Dice coefficient to quantitatively analyze the segmentation results on bladder and uterus surfaces, respectively.

TABLE I.

Evaluation of Segmentation of the Bladder

	MAD(mm)	HD(mm)	Dice
Chan-Vese model [40]	8.13 ± 2.57	9.22 ± 3.04	0.62 ± 0.04
Leventon model [30]	3.67 ± 1.82	4.49 ± 2.10	0.76 ± 0.05
ICM model [12]	1.09 ± 0.13	1.26 ± 0.38	0.85 ± 0.03
Proposed method	1.03 ± 0.16	1.17 ± 0.32	0.88 ± 0.03

TABLE II.

Evaluation of Segmentation of the Uterus

	MAD(mm)	HD(mm)	Dice
Chan-Vese model [40]	10.93 ± 6.54	13.22 ± 5.81	0.53 ± 0.09
Leventon model [30]	6.42 ± 1.56	7.01 ± 1.36	0.72 ± 0.06
ICM model [12]	1.25 ± 0.31	1.97 ± 0.51	0.81 ± 0.04
Proposed method	1.18 ± 0.24	1.86 ± 0.36	0.83 ± 0.04

From Tables I and II, we see that the Chan–Vese method produces the largest error and lowest Dice coefficients for both bladder and uterus. The key reason is that the Chan–Vese model assumes the image to be bi-modal, which is mostly unrealistic in actual medical images. The Leventon model incorporates a shape prior into the segmentation framework [30], and provides better results than Chan–Vese model. Our previously developed ICM model takes the shape prior as well as the registration constraints into consideration [12], and thus performs much better than both the Chan–Vese model and the Leventon model. However, the ICM model uses a PCA-based prior, and the PCA-based level set method only works well when the shape variation is relatively small, so that the space of signed distance functions can be approximated by a linear space[36]. The proposed algorithm in this paper replaces the PCA prior with a KDE based prior, which allows the shape prior to approximate arbitrary distributions. From Tables I and II, we observe that both MAD and HD decrease with the proposed method, while Dice coefficient increases slightly compared to the ICM model. The quantitative results imply that our newly developed method has a consistent agreement with the manual segmentation, and performs equally with our previous ICM technique, yielding an approach that performs accurated segmentation while now incorporating nonrigid registration as well as tumor estimation.

C. Registration Results

In Fig. 9, a typical example registration result is given; the checkerboard and deformed grid are also presented. The treatment day image (a) and planning day image (b) are quite different largely due to the filling of the bladder, therefore, a large deformation is required at that position. Much less deformation is expected near the bony anatomy; see the bottom and right side of Fig. 9(a) and (b). The example shows accurate registration near both the bladder and the bony area using the proposed approach; see Fig. 9(c) and (d). The deformed grid is presented in Fig. 9(e). Due to the use of Jacobian constraints, Fig. 9(e) shows no folding in the deformation field generated by our method. Fig. 9(f) illustrates the organ matching result using the proposed method; the nonrigid alignment of the bladder is seen here. The parameters in (25) are set to be ω_uterus = ω_bladder = 0.5.

Fig. 9.

Registration results: The (a) treatment day (fixed) MR image and (b) the planning day (moving) image are quite different, and a large deformation is required. (c) The deformed moving image using the proposed method. (d) Checkerboard of the fixed image and the deformed image. (e) The achieved non-rigid transformation visualized by the underlying grids. (f) Matching of bladder surfaces using the proposed method.

The registration performance of the proposed algorithm is also evaluated quantitatively. For comparison, a rigid registration (RR), an intensity-based FFD nonrigid registration (NRR) [43] using sum-of-squared difference (SSD) as the similarity metric, as well as an ICM-based nonrigid registration [12] are performed on the same sets of real patient data. The control point setting is kept to be the same for all the approaches.

Organ overlaps between the ground truth in day d and the transformed organs from day 0 are used as metrics to assess the quality of the registration (Table III). We also track the registration error percentage for both bladder and uterus, shown in Table IV. The organ overlap is represented as percentage of true positives (PTP), while the registration error is represented as percentage of false positives (PFP), which calculates the percentage of a nonmatching voxels being declared as matching. Besides the above two area error metrics, we also use two intensity metrics to evaluate the overall performance of the different approaches: mutual information (MI) and normalized correlation coefficient (NCC).

TABLE III.

Evaluation of Registration: Organ Overlaps/PTP (%)

	Bladder	Uterus
Rigid Registration	61.03 ± 7.41	64.70 ± 6.89
Nonrigid Registration [43]	77.18 ± 2.94	74.01 ± 4.36
ICM Nonrigid Registration [12]	88.07 ± 1.64	86.91 ± 2.50
Proposed Method	91.12 ± 2.10	88.76 ± 2.08

TABLE IV.

Evaluation of Registration Error: PFP (%)

	Bladder	Uterus
Rigid Registration	37.24 ± 7.21	33.90 ± 5.22
Nonrigid Registration [43]	21.56 ± 4.29	26.78 ± 4.32
ICM Nonrigid Registration [12]	10.36 ± 1.52	12.72 ± 1.80
Proposed Method	9.04 ± 1.28	10.62 ± 1.87

From Tables III–V, we find that the RR performs the poorest out of all the registrations algorithms, while NRR performs better than RR. From our prior experience with radiotherapy research ([5], [58]), we know that the best organ registration results occur when the organ is used as the only constraint or one of the main constraints. Thus, it is not a surprise to see the ICM method and the proposed method significantly outperform NRR at aligning segmented organs. We showed [47] that the correct alignment of one organ would help align the adjacent tissues. While the ICM method neglects tumor regression, it can not accurately delineate the GTV, nor can it achieve precise matching at the tumor region, which is adjacent to the bladder and uterus. The inclusion of tumor detection helps the proposed method provide slightly better results than the ICM method. This improvement is also confirmed by Table V.

TABLE V.

Evaluation of Registration: Correlation Coefficient and Mutual Information

	CC	MI
Rigid Registration	0.7704 ± 0.04	0.7608 ± 0.06
Nonrigid Registration [43]	0.8493 ± 0.03	0.8977 ± 0.04
ICM Nonrigid Registration [12]	0.9072 ± 0.03	1.4527 ± 0.04
Proposed Method	0.9127 ± 0.03	1.5052 ± 0.04

Fig. 10 shows a registration result of the GTV neighborhood region. Fig. 10(a) was generated using intensity-based nonrigid registration (described in [43]), from which we can clearly observe the mismatching at the boundary of the bladder. Problems also occur around the GTV area (red rectangle), where the tissue changes due to irradiation and tumor regression. At such locations, the tissue intensity changes violate the gray level dependency assumptions made in [43], which leads to severe distortion in the red rectangle. From Fig. 10(b), we see that the ICM registration performs much better but some distortion still exists around GTV. Our proposed approach defines different matching probability density functions for distinct tissue classes, and there is no distortion observed using the proposed method, as shown in Fig. 10(c).

Fig. 10.

Registration results of image pair from Fig. 9 around the GTV region. (a) Intensity based nonrigid registration method (NRR). Severe distortion is visible. (b) ICM based nonrigid registration. Much better than NRR, but some distortion still exists. (c) Proposed method. No distortion is observed.

In Section II-C3, we describe the Jacobian constraints posed on the transformation; here we present the final Jacobian map of the transformation. Fig. 11 shows the Jacobian map as a percentage of volume expansion/contraction. From the figure, we can see that due to the use of nonnegative Jacobian constraints in (21) and (22), the minimum of the Jacobian map is 0.36, which means that folding does not exist in our transformation field. We also use (22) to simulate the tumor regression process, i.e., the determinant of Jacobian should be less than 1 at GTV. The result is presented in Fig. 11, in which the bladder and GTV contours are depicted as black and white, respectively. As expected, the volume of GTV contracts about 20%–40%.

Fig. 11.

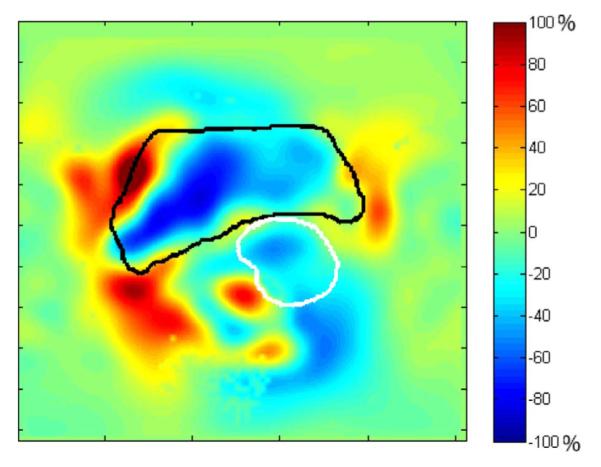
Jacobian map shown as percentage of volume expansion/contraction. Bladder contour (black) and GTV contour (white) are plotted.

D. Detection Results

In this section, we describe and evaluate the performance of our tumor detection module. Fig. 12 shows an example detection result for gross tumor volume (GTV) using the proposed method.

Fig. 12.

Detection results for GTV. Subplots show the (a) coronal, (b) sagittal, (c) axial, and (d) 3-D views.

Accurate propagation of the GTV segmentation or tumor detection is not possible with currently existing registration approaches. Even if anatomical correspondence is found, tumorous tissue may disappear in time, due to successful treatment. Registration problems usually occur at and around the GTV, where the tissue changes due to irradiation. Staring et al. [24] raised this issue but did not propose a solution. Fig. 13 illustrates an example of this problem. The red contour is the original tumor at planning day (day 0), and the yellow contour is the actual remaining tumor after three weeks of radiotherapy. We perform an intensity based nonrigid registration (NRR) [43], and use the transformation to deform the original GTV surface. The derived GTV propagation is depicted as the blue contour. There is obvious disagreement between the NRR derived tumor contour and the actual GTV. Such disagreement happens to all the existing intensity matching registration approaches ([5], [24], [43]) when they are applied to MR guided cervical cancer radiation therapy treatment.

Fig. 13.

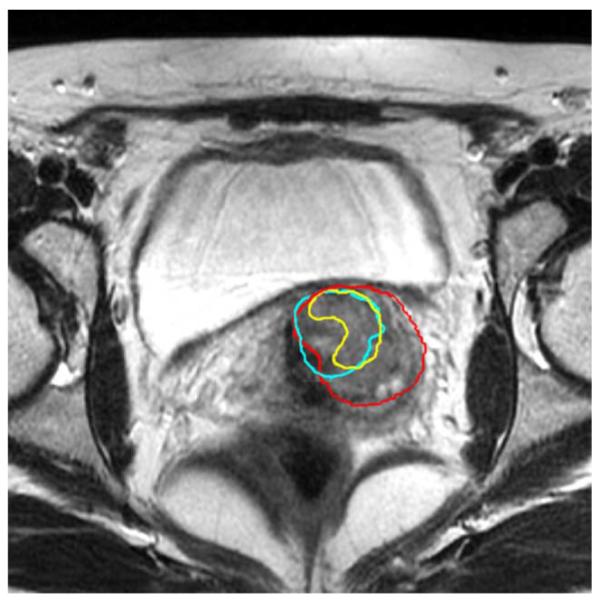
The change of tissue around the GTV leads to the failure of nonrigid registration. Red: initial GTV contour. Yellow: actual tumor contour after three weeks’ treatment. Blue: Propagation of GTV using nonrigid registration.

The proposed method described in this paper defines the matching as a weighted mixture of probability density functions that are carefully designed for different tissue classes, and the new method is able to handle this difficult situation. From Fig. 14, we can see that the detected GTV is consistent with the manual delineation, and only a slight difference exists.

Fig. 14.

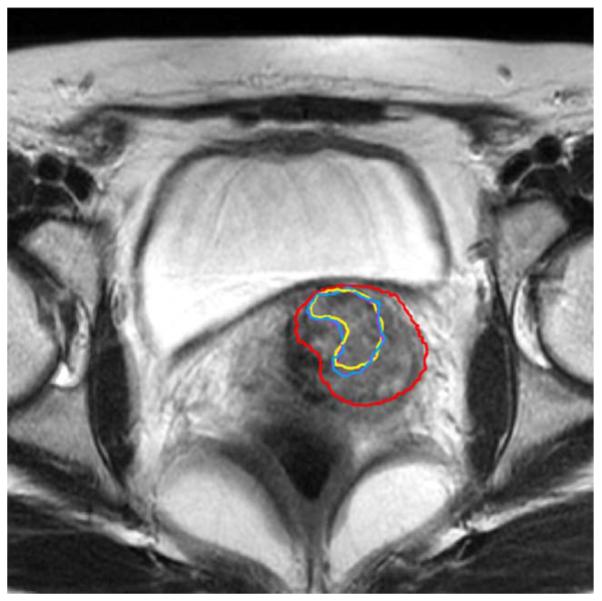
Detection result compared with manual delineation. The change of tissue around the GTV does not affect the proposed method. Red: initial GTV contour. Yellow: actual tumor contour after three weeks of treatment (manual delineation). Purple: Detected GTV contour using the proposed method.

We compare the tumor images obtained using our method with the manual detection performed by a clinician. For the proposed method, we set a threshold for the tumor probability map M. The tumor binary images are obtained with the probability threshold 0.7, which selects all voxels that have an over 70% chance to be in the tumor. From our experiments, we have found that the detection results are not sensitive to the threshold. Thresholds between 0.5 and 0.8 give the same detection results within ±8% (measured using volume size).

Using the expert manual delineations as ground truth, we quantitatively evaluate and compare our detection results in Table VI. Since the NRR and ICM approaches do not take the shrinkage of tumor into account, the volumes of their deformed GTV do not change much. Hence, the Dice coefficients of the NRR and ICM methods decrease for later weeks. On the contrary, a consistent agreement of our detection with the expert’s delineation is shown in Table VI.

TABLE VI.

Evaluation of Detection: Dice Coefficient

	Week 1	Week 2	Week 3	Week 4	Week 5
NRR[43] deformed GTV	0.63 ± 0.02	0.58 ± 0.03	0.48 ± 0.04	0.34 ± 0.02	0.16 ± 0.03
ICM Registration[12] deformed GTV	0.69 ± 0.05	0.63 ± 0.04	0.59 ± 0.03	0.50 ± 0.03	0.45 ± 0.03
Proposed Method detected GTV	0.78 ± 0.03	0.75 ± 0.05	0.82 ± 0.03	0.79 ± 0.03	0.80 ± 0.03

From the experiments, we find that the tumor shape has a strong influence on the performance of the detection results. As a global trend, algorithms show more accurate detection on circumscribed (round or oval shapes) than on ill-defined masses. This is due to the fact that ill-defined masses have irregular and poorly defined borders, which tend to blend into the background. On the other hand, tumor size has a weak influence on the detection performance. From the experiments, we find that there is not a specific size where our algorithm performs poorly, i.e., our algorithm is not sensitive to tumor size, as shown in Table VI.

The tumor volumes detected by the algorithm are considered true positives if they overlap with a ground truth (manual detection), and false positives otherwise. Free-response receiver operating characteristic (FROC) curves [21] are produced as validation of the algorithm. For performing the FROC analysis, a connected component algorithm is run to group neighboring voxels as a single detection. The algorithm achieved 85% sensitivity at six false positives per image. In comparison, the ICM algorithm resulted in only 50% sensitivity and the NRR algorithm gave only 33% sensitivity at the same false positive rate. The corresponding FROC curves are shown in Fig. 15. The proposed method shows better specificity and achieves a higher overall maximum sensitivity.

Fig. 15.

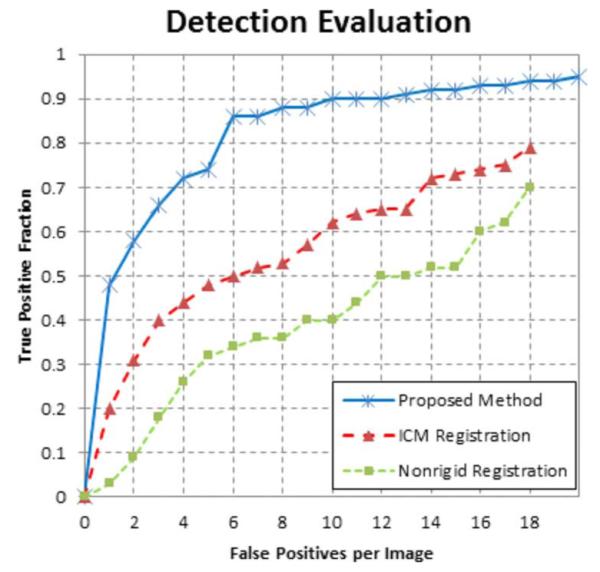
FROC analysis of the proposed algorithm, with comparison to ICM method and NRR method.

Fig. 16 shows a representative slice from the planning day MRI with overlaid five treatment day tumor detection contours. It can be seen that the detected tumor appears in the same slice and the same location in the registered serial treatment images, and the tumor regression process is clearly visible from the contours. Using the proposed technique described in this paper, we can easily segment the organs of interest, estimate the mapping between planning day and treatment day, and calculate the location changes of the tumor for diagnosis and assessment, thus we can precisely guide the interventional devices toward the lesion during image guided therapy.

Fig. 16.

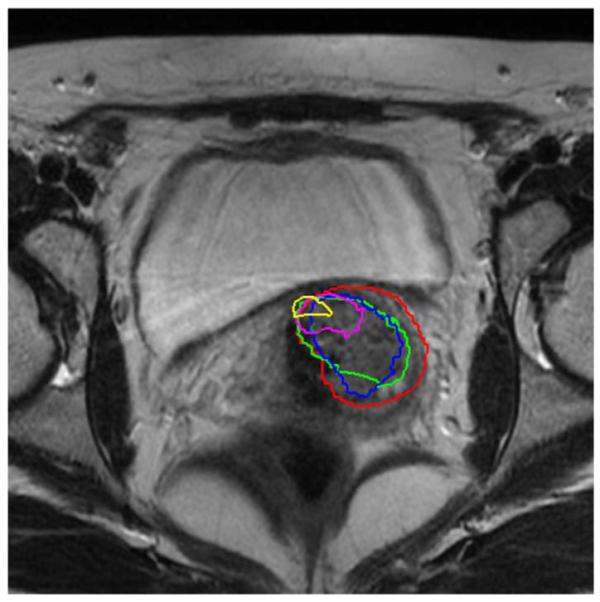
Detected tumor contours mapped to the planning MRI.

IV. Conclusion

In this paper, we have introduced a unified framework for cervical MR image analysis capable of simultaneously solving deformable segmentation, constrained nonrigid registration and automatic tumor detection. We believe that integrating all three modules is a promising direction for solving difficult medical image guided radiotherapy and computer aided diagnosis problems.

The unified framework is derived using Bayesian inference. In the segmentation process, the surfaces evolve according to constraints from deformed contours and image gray level information as well as prior information. The constrained nonrigid registration part matches organs and intensity information together while taking tumor detection into consideration. It has been shown on clinical data of patients with cervical cancer that the proposed method produces results that have an accuracy comparable to that obtained by manual segmentation, and the proposed method outperforms the standard registration approaches based on intensity information only. Most importantly, it has been shown that the proposed method is able to handle the difficult problems induced by the presence and regression of tumor, where all of the existing registration approaches fail.

The novelty of this paper is that we define the intensity matching as a mixture of two distributions which statistically describe image gray-level variations for different pixel classes (i.e., tumor class and normal tissue class). These mixture distributions are weighted by the tumor detection map which assigns to each voxel its probability of abnormality. We also constrain the determinant of the transformation’s Jacobian, which guarantees the transformation to be smooth and simulates the tumor regression process. In addition, the usage of a KDE model to capture the shape variation enables the shape prior to approximate arbitrary distributions.

One possible goal for future research is to incorporate a physical tumor regression model and a shape predicting model into the unified framework, both to enhance the accuracy and to improve the clinical utility of the algorithm. We will also use the dose accumulation metric [12], [59] to extend our current effort to realize dose-guided radiotherapy [60], where the dosimetric considerations are the basis for decisions about whether future treatment fractions should be reoptimized, readjusted, or replanned to compensate for dosimetric errors. The clinician will then be able to make decisions about changing margins based on the difference between the computed and desired treatment. Escalated dosages can then be administered while maintaining or lowering normal tissue irradiation.

In conclusion, compared to the current existing approaches, the proposed method solves the challenging problems in image guided radiotherapy, by combining segmentation, registration, abnormality detection into a unified framework. There are a number of clinical treatment sites that will benefit from our MR-guided radiotherapy technology, especially when tumor regression and its effect on surrounding tissues can be significant.