An illusion predicted by V1 population activity implicates cortical topography in shape perception

Abstract

Mammalian primary visual cortex (V1) is topographically organized such that the pattern of neural activation in V1 reflects the location and spatial extent of visual elements in the retinal image, but it is unclear whether this organization contributes to visual perception. We combined computational modeling, voltage-sensitive dye imaging (VSDI) in behaving monkeys, and behavioral measurements in humans, to investigate whether the large-scale topography of V1 population responses influences shape judgments. Specifically, we used a computational model to design visual stimuli that have the same physical shape, but are predicted to elicit variable V1 response spread. We confirmed these predictions with VSDI. Finally, we designed a behavioral task in which human observers judged the shapes of these stimuli, and found that their judgments were systematically distorted by the spread of V1 activity. This novel illusion suggests that the topographic pattern of neural population responses in visual cortex contributes to visual perception.

Humans are remarkably sensitive to differences in the sizes and shapes of visual objects. For example, we can detect small deviations from circularity and subtle differences in the aspect ratios of different shapes, and we can make these discriminations over a wide range of image sizes, regardless of whether the shapes are defined by texture boundaries, by disparity, or by luminance boundaries^1–3. Researchers have postulated a variety of local^4,5 and global^2,6 mechanisms to explain human ability to perceive particular shape stimuli. An often implicit assumption in these models is that human observers have access to a spatial distribution of filter outputs modeled on the response properties of V1 neurons. The spatial distributions of these neural responses in primate V1 have been measured using various techniques^7–12. At a sub-millimeter scale, V1 population responses are organized into orientation columns, such that the receptive fields of neighboring neurons share similar orientation preferences. At a larger spatial scale, the responses are organized retinotopically, with nearby neurons representing neighboring locations within the visual field. Though this organization is serendipitous for researchers investigating the properties of cortical neurons (e.g., by making it relatively easy to locate neurons that code for similar visual properties), its role in perception is unclear and the functional significance of such topographical maps in general remains an active topic of debate^13–17.

One hypothesis is that these topographical maps may simply be epiphenomena of cortical development, with little functional significance for neural coding and perception¹³. In this view, perceptual judgments might be implemented by flexible decoding mechanisms that combine responses of cortical neurons in a way that is insensitive to their location within the topographic map. Indeed, by ignoring local cortical topography entirely, several prominent models of optimal neural decoding implicitly assume this hypothesis^18–20. The strong version of this ‘labeled line’ hypothesis asserts that the decoding circuits take into account the specific tuning properties of each neuron in the population (e.g., the position and the peaks and bandwidths of orientation and spatial frequency tuning).

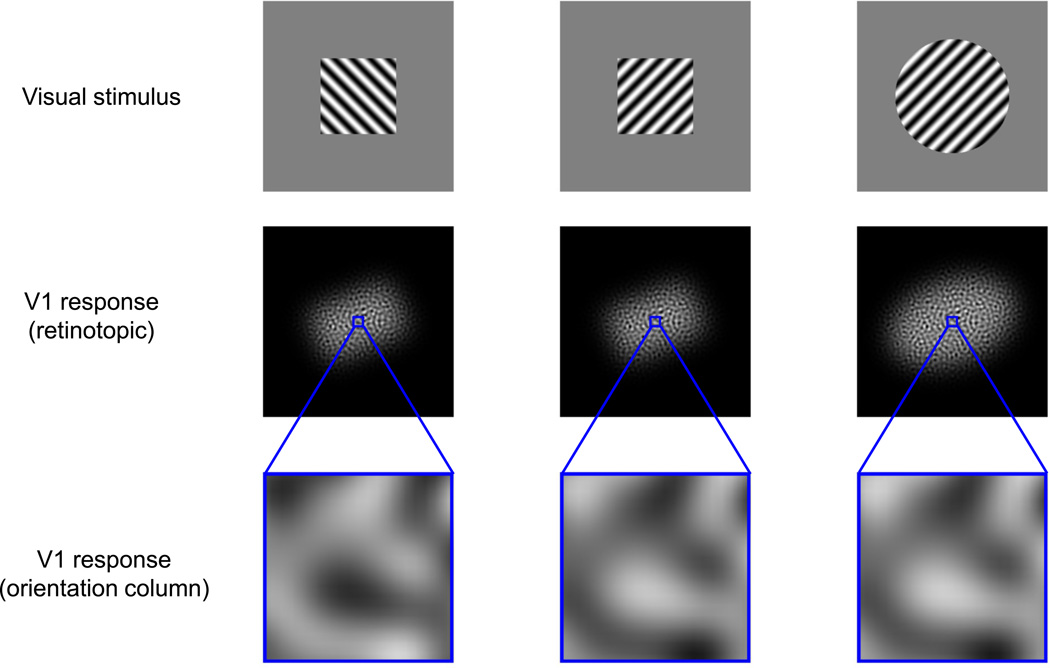
An alternative hypothesis is that the decoding circuits exploit cortical topography^14,21,22. In the strong version of this hypothesis the decoder pools all neurons at the same topographic location while ignoring their specific tuning properties. For example, local pooling of responses at each of the two topographic scales described above might subserve different sets of visual judgments (Fig. 1). Signals at the orientation-column scale pool responses across neurons with similar orientation tuning and reflect the fine-scale orientation content of the visual stimulus, providing information that might be used primarily for discriminating between, or identifying, visual textures. Signals at the retinotopic scale pool responses across neurons with similar location tuning, and might be used primarily for computing the locations, shapes, and sizes of visual objects.

Figure 1.

Schematic illustration of two scales of functional organization in primary visual cortex. The top row shows texture-defined visual shapes that differ either in terms of the textures that define them (left and center columns) or their shape (center and right columns). The middle row schematically illustrates retinotopic-scale V1 population responses to the visual stimuli. The spatial spread or retinotopic extent of activation at this scale can be used to discriminate between the sizes and coarse shapes of visual stimuli, but not to discriminate between their component textures. The bottom row shows schematic responses in orientation columns. Signals at this scale can be used to distinguish between the orientation content of component textures, but not to determine the global shapes of the visual stimuli.

If the visual system is exploiting V1 topography, then stimulus-dependent distortions in the topographic representation may result in concomitant perceptual distortions. On the other hand, if the visual system uses exclusively a ‘labeled line’ decoder, then there is no reason to expect that topographic distortions would affect perception (see discussion). To test the hypothesis that V1 topography plays a role in shape coding, we first used a model of V1 population responses, combined with VSDI, to find stimuli with equal physical shape, but different topographic representations in V1. We then show in psychophysical experiments that these stimuli produce the perceptual distortions expected if the topographic representation in V1 is contributing to shape perception.

Results

Simulating V1 Population Responses

To simulate the expected retinotopic extent of V1 population responses, we created a large population of model V1 neurons representing a 2°×2° patch of the visual field (centered 3° from the fovea) and having realistic distributions of orientation, spatial frequency, and size (see Supplementary Fig. 1). The model predicts that for most visual stimuli, the retinotopic extent of V1 population activity, pooled locally at the retinotopic scale, provides a reliable signal for shape judgment. However, we found that for a small subset of stimuli, the retinotopic extent of V1 activity can be dissociated from the physical shape of the stimulus. Specifically, the model predicts that small sinewave stimuli (Gabors) with a circular contrast envelope and spatial frequency and size similar to the average V1 neuron’s receptive field, should produce a retinotopic pattern of population activity that systematically extended in the direction of grating (the carrier) orientation. This effect results from the tendency of V1 receptive fields to be elongated along the direction of their preferred orientation^23–25.

A consequence of this elongation is that neurons will tend to respond at greater distances to stimuli collinearly aligned with their receptive fields than to stimuli aligned orthogonally, yielding a population response that is retinotopically elongated along the orientation of the carrier (Fig. 2a,b). This orientation-dependent distortion disappears if the spatial frequency or spatial frequency bandwidth of the Gabor stimulus is sufficiently different from the optimal value (Fig. 2c,e) or if the stimulus contains multiple orientation components. Thus, if the predictions of our model are correct and if the extent of the spread of activity in the retinotopic map of V1 influences perceptual estimates of visual shape, the perceived stimulus aspect ratio should be distorted systematically by carrier orientation for stimuli that approximately match the average V1 receptive field.

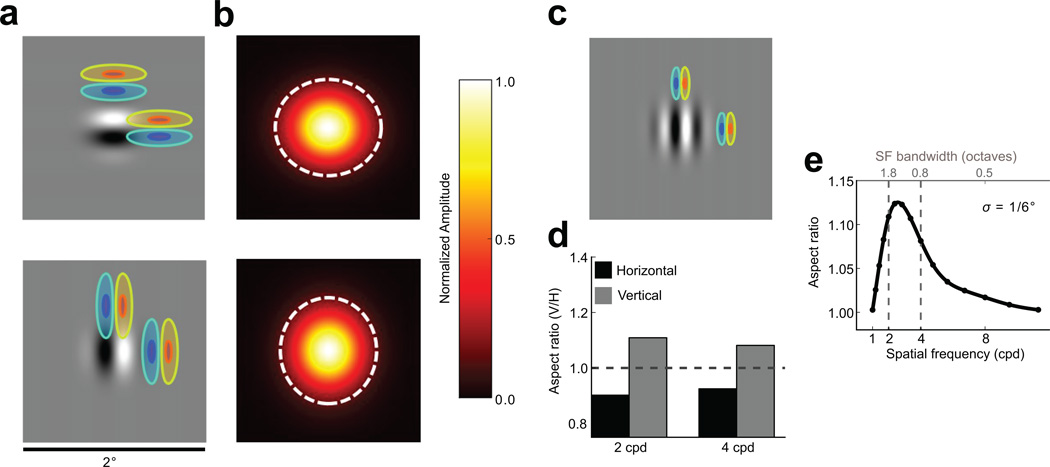
Figure 2.

Predicted effects of elongated receptive fields on the spatial distribution of V1 population responses. a) Receptive fields (overlaid contours) well-tuned to a stimulus (grayscale image) and displaced by equal distances in collinear and orthogonal directions. The stimulus overlaps more with collinearly than orthogonally displaced receptive fields, eliciting cortical population responses elongated along the direction of the Gabor orientation. b) Population responses predicted for the 2 cpd Gabors depicted in (a) using a retinotopic V1 model, shown in visual field coordinates. The dashed white ellipses indicate the 3σ contour of a Gaussian fitted to the population response. For a simulated population of neurons with receptive field parameters based on physiological measurements, the population response is elongated along the direction of carrier orientation. c) Effect of carrier spatial frequency on cortical response elongation. Because receptive field size is inversely correlated with peak spatial frequency³⁸, increasing spatial frequency leads to activation of neurons with smaller receptive fields, reducing the effect of receptive field elongation on the cortical response. d) Response aspect ratios predicted by the V1 model for 2 cpd (left) and 4 cpd (right) Gabor stimuli with vertical and horizontal carriers. e) Predicted response distortion as a function of carrier spatial frequency for a Gabor with a fixed envelope size (σ = 0.167°). The abscissa at the top of the panel indicates the spatial frequency bandwidths of the Gabor stimuli, and the dashed lines represent stimuli used in the physiological experiments.

Imaging orientation-dependent V1 response spread

To confirm that V1 population responses exhibit this orientation-dependent elongation, we measured V1 population responses in awake, fixating macaques using voltage-sensitive-dye imaging (VSDI), which is uniquely well-suited to the investigation of large-scale population activity and cortical topography²⁶. Using VSDI responses from 17 recording sessions in three monkeys, we found that the carrier orientation does systematically alter the retinotopic extent of population responses in V1 as predicted by our model. Note that because the retinotopic map in V1 is locally contiguous, we can express the retinotopy of a small patch of the cortical surface as an isomorphic transformation of a small patch of the visual field. We measured the coarse retinotopy of the cortical surface in our recording chambers (Fig. 3). Note that a circle in the visual field (Fig. 3a) projects to an ellipse on the surface of the cortex (Fig. 3b). This is due to the well-documented anisotropy in cortical magnification parallel versus perpendicular to the V1/V2 border^7,8,10,12,27. Here, we are not interested in this anisotropy, which represents a fixed mapping from the visual field to the cortical surface. Rather, we are interested in determining whether varying the carrier orientation of a fixed-envelope Gabor stimulus results in population responses whose cortical extent varies systematically relative to this fixed mapping. The visual stimuli (Fig. 3c) were small Gabor patches composed of a vertically or horizontally oriented carrier grating windowed by a circularly symmetric Gaussian envelope. To quantify the spatial spread of the response to each stimulus, we computed the standard deviation parameters of an elliptical 2D Gaussian function fit (Fig. 3e) to the average response amplitudes (Fig. 3d).

Figure 3.

Physiological stimuli and spatial distributions of V1 responses measured with VSDI. a) Schematic Fig. of the visual field with 1° × 1° rectangular grid. The colored lines represent the approximate limits of visual space in our imaging window, and the solid blue circle represents the 3σ contour of the stimulus envelope. b) Image of the cortical vasculature in one of our chambers (Monkey 1, left hemisphere) with overlaid scale marker, landmarks, and retinotopy. The blue ellipse represents the approximate retinotopic contours of the circle in (a). The white and black curves represent the vertical and horizontal gridlines in (a). c) The visual stimuli, with solid blue circles overlaid to indicate the 3σ contour of the stimulus envelopes for the horizontal (top) and vertical (bottom) Gabor stimuli. d) Amplitudes of cortical responses in a 10×10 mm² patch of cortex to the horizontal (top) and vertical (bottom) Gabor stimuli, averaged over an experimental session. e) 2D Gaussian fits to the responses in (d). The dashed white line represents a vertical line in the visual field located 2 degrees right of fixation. Relative to the retinotopic shape of the stimulus (blue ellipse in (b)), the vertical Gabor is vertically elongated and the horizontal Gabor is horizontally elongated. f) Normalized aspect ratios (AR_response/AR_retinotopic) of responses to 2 cpd horizontal and vertical Gabors measured in three different monkeys, demonstrating both the robustness of the orientation-dependent elongation effect and the variability of its magnitude across different individuals (n = 5 experiments for Monkey 1, 8 experiments for Monkey 2, and 4 experiments for Monkey 3). g) Normalized population response aspect ratios obtained in one chamber for spatial frequencies of 2 cpd and 4 cpd (Monkey 1, n = 5 experiments). Here and in all subsequent figures, error bars represent 95% confidence intervals.

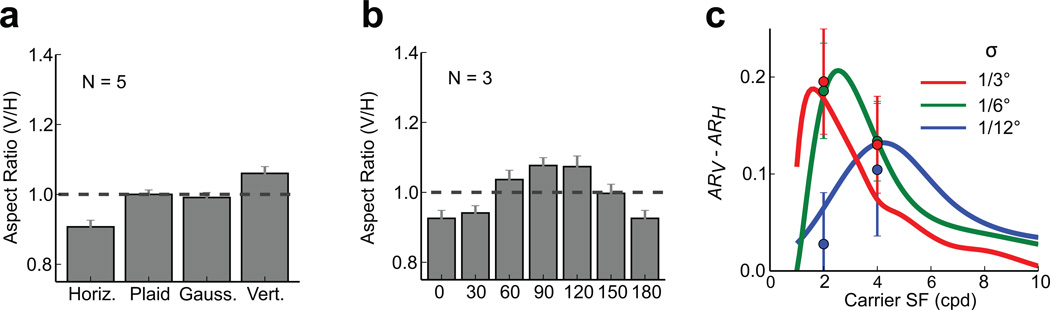
Though the spatial extents of the horizontally and vertically oriented Gabors in the visual field were identical, the spread of the cortical responses varied systematically with the carrier orientation (Fig. 3d–g). Responses to the vertical Gabor were elongated along the cortical direction corresponding to the vertical axis in the visual field (dashed while line in Fig. 3e) and shortened along the orthogonal direction (AR_V / AR̅ = 1.12, one-sample t(16) = 175.73, p = 1.02 × 10⁻²⁷; where AR_V, AR_H, and AR̅ represent the vertical-to-horizontal retinotopic aspect ratios of the horizontal and vertical Gabors and their mean, respectively), while responses to the horizontal Gabor were elongated along the cortical direction corresponding to horizontal and shortened along the vertical direction (AR_H / AR̅ = 0.87, one-sample t(16) = 158.09,p = 5.51 × 10⁻²⁷). Experiments using additional stimuli (Fig. 4) confirmed that these systematic changes in the retinotopic-scale population responses reflect the effect of the carrier orientation. For example, the responses to plaid and Gaussian stimuli, which contain energy at both the vertical and horizontal orientations, exhibited no systematic retinotopic distortion (Fig. 4a); the vertical-to-horizontal aspect ratio of elicited responses varied systematically as a function of carrier orientation, with responses to horizontal orientations exhibiting the smallest aspect ratios and those to vertical orientations exhibiting the largest aspect ratios (Fig. 4b).

Figure 4.

Spatial properties of physiological responses for additional stimuli. a) Normalized vertical-to-horizontal aspect ratio of VSDI response to stimuli with an identical, circular Gaussian contrast envelope with a 2 cpd horizontal, vertical, plaid, or luminance carrier (Gauss.). In contrast to the horizontal and vertical Gabors, population responses to the plaid and Gaussian stimuli do not exhibit retinotopic elongation. b) Normalized vertical-to-horizontal aspect ratio of responses to 2 cpd carriers with orientations spaced at 30° intervals. As expected, the vertical-to-horizontal aspect ratio is largest for vertical stimuli (90°), smallest for horizontal stimuli (0°) and varies smoothly across intermediate orientations. c) Model predictions (curves) and measurements (circles; N = 2 experimental sessions) of the orientation-dependent elongation effect, measured as differences between the aspect ratios of responses to vertically (AR_V) and horizontally (AR_H) oriented Gabor stimuli as a function of spatial frequency for different Gaussian envelope sizes (σ). The observed effects of varying envelope size and spatial frequency are qualitatively consistent with those predicted by the model. Data in all panels are from Monkey 1.

A key prediction of our model was that the orientation-dependent distortions should diminish as the stimulus’ spatial frequency or spatial frequency bandwidth deviate from the optimal values (Fig. 2c,e). To test this prediction, we ran additional conditions with suboptimal Gabor stimuli with identical envelopes but double the spatial frequency. For all stimuli the VSDI response is still elongated in the direction corresponding to the Gabor’s carrier orientation (Fig. 3g). However, as predicted, the difference between the aspect-ratios of the responses to horizontal and vertical Gabors is significantly smaller for the higher spatial frequency stimuli ((AR_V − AR_H) / AR̅= 0.09) than for the lower spatial frequency stimuli ((AR_V − AR_H) / AR̅ = 0.15; paired t(4) = 5.34, p = 0.006).

To further test the predictions of our model, we created several additional stimulus conditions by doubling or halving the size of the Gaussian contrast envelope while keeping the carrier spatial frequencies at 2 and 4 cpd. The model predicted that for Gabor stimuli with envelope sizes (σ) of 1/3° and 1/6°, increasing the carrier spatial frequency from 2 to 4 cpd will attenuate the elongation effect, while for Gabor stimuli with an envelope size of 1/12°, increasing the carrier spatial frequency will enhance the elongation effect. Across these stimulus conditions, the patterns of elicited VSDI response aspect ratios were qualitatively consistent with the predictions of our V1 population response model (Fig. 4c). Overall, our physiological results confirm the hypothesis that, due to receptive field elongation, the retinotopic-scale topography of V1 population responses can be distorted systematically by the orientation of local visual features.

Perceptual consequences: a novel shape illusion

Our primary goal is to test the hypothesis that the retinotopic extent of V1 activation influences shape perception. If this hypothesis is correct, then the circuits that estimate shape based on the V1 activation pattern must take into account the mapping between the retinotopic extent of V1 activation and the shape of the visual stimulus. Thus, our next step is to characterize this mapping. To do this, we first focus on stimuli that do not produce the orientation dependent distortion.

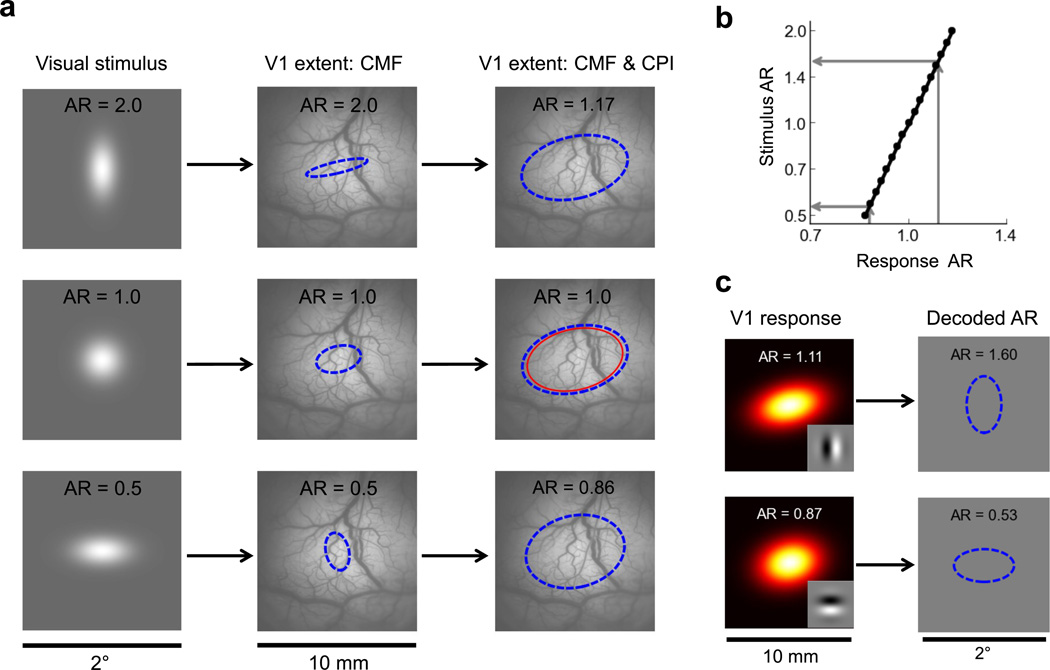
The cortical spread of the response elicited by a visual stimulus depends both on its direct retinotopic mapping (shown in Fig. 3a,b), which can be described in terms of the local cortical magnification factor (CMF), and on the cortical point image (CPI), which describes the shape and size of the cortical surface in V1 that processes information from a single point in visual space^28,29. To determine the expected cortical spread as a function of visual spatial extent, we used our model, together with our VSDI-based estimates of the CMF and CPI, to predict the cortical response spread to Gaussian stimuli with aspect ratios ranging from 0.5 to 2.0 (Fig. 5a). The Gaussian stimuli had an average space constant equal to that of our Gabor stimuli (1/6°). Due to the large size of the CPI relative to the direct retinotopic projection of the stimuli, the aspect ratios of the predicted cortical responses are considerably smaller than the aspect ratios of the visual stimuli (Fig. 5a). In other words, for these small stimuli, large deviations from spatial isotropy in the visual field are associated with considerably smaller deviations from retinotopic isotropy in the cortical response. This systematic cortical aspect ratio “compression” is further illustrated in Fig. 5b, which shows the relationship between the retinotopic aspect ratio of the cortical response and the aspect ratio of the Gaussian visual stimulus.

Figure 5.

Modeling the relationship between the spatial extent of a visual stimulus and the retinotopic extent of its elicited cortical response. a) A schematic representation of the cortical responses to vertical (top row), isotropic (middle row), and horizontal Gaussian stimuli. The first column shows the visual stimulus; the second column illustrates the mapping due to the fixed retinotopic projection to V1 (shown in Fig. 3b), which can be expressed in terms of the local cortical magnification factor (CMF); and the third column illustrates the added effect of the cortical point image (CPI), whose size is indicated by the thin red ellipse in the central row. The dashed blue ellipses represent the 2σ Gaussian envelope contours of the predicted VSDI responses. Retinotopic aspect ratios (AR) are indicated at the top of each subpanel. b) Predicted aspect ratio of a Gaussian stimulus as a function of the retinotopic aspect ratio of its elicited response. Due to the large size of the CPI relative to the retinotopic extent of the visual stimuli, the aspect ratio of the elicited cortical response is retinotopically "compressed", with an envelope that tends to be more isotropic than that of the eliciting stimulus. c) Perceptual orientation-dependent elongation predicted by the V1 model for the 2cpd vertical (top) and horizontal (bottom) circular Gabor stimuli if observers compensate for the effects of the aspect ratio compression shown in (b). The dashed blue ellipses represent the predicted 2σ Gaussian envelope contour of the perceived stimulus.

To accurately estimate the stimulus’ aspect ratio form the cortical response aspect ratio, shape decoding mechanisms must take this relationship in account. Now consider decoding the cortical responses to circular Gabor patches with horizontal and vertical carriers (Fig. 3c–g). If the decoding mechanisms are exploiting the relationship between spatial and retinotopic aspect ratios (Fig. 5b), then the estimated visual aspect ratios (Fig. 5c) should be much larger than the retinotopic aspect ratios that we observed physiologically. Specifically, a circular Gabor with a vertical carrier should have a perceived aspect ratio of 1.6 whereas a circular Gabor with horizontal carrier should have a perceived aspect ratio of 0.57. We therefore hypothesized that such Gabor stimuli might produce a visual illusion, with small circular Gabors appearing stretched in the direction corresponding to the orientation of their carrier gratings.

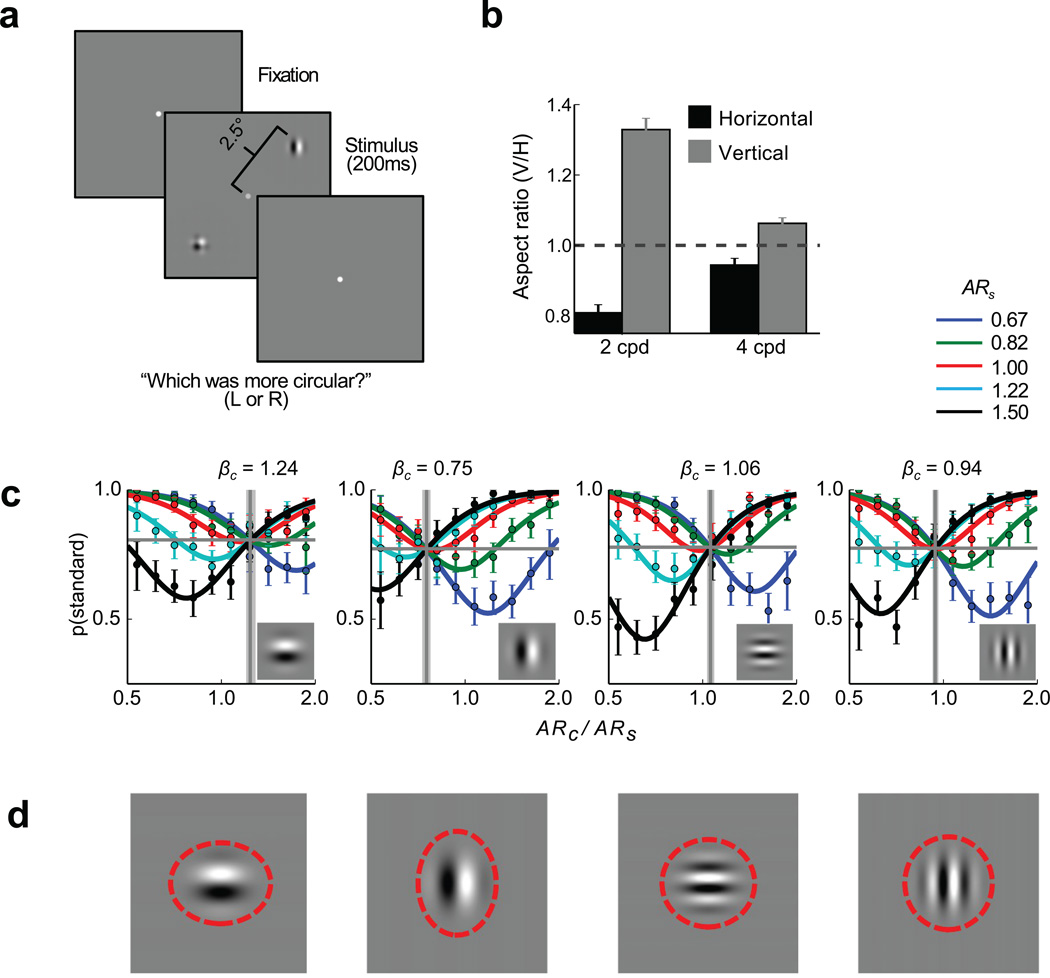
We tested this hypothesis in human observers by designing a suitable psychophysical task (Fig. 6a). Testing this hypothesis in human subjects had two advantages: it allowed us to avoid methodological confounds that can arise when training monkeys to make subjective judgments in visual illusions, and it allowed as to minimize possible learning effects by providing the subjects with no feedback. Observers briefly viewed a display containing two stimulus patches on opposite sides of the screen. One of the patches, the standard, was a composite Gabor stimulus (a plaid) composed of both horizontally and vertically oriented gratings. This plaid patch acted as a neutral stimulus. The other patch, the comparison, was a simple Gabor containing either a vertical or a horizontal grating. In each trial, the vertical-to-horizontal aspect ratio of the Gaussian contrast envelope defining each of the two patches was chosen randomly, and observers were asked to judge which of the patches appeared more circular (see online Methods for details).

Figure 6.

Psychophysical results averaged across 10 subjects. a) Schematic of the visual stimulus. Human observers briefly (200 ms) viewed a display consisting of a plaid standard and an oriented comparison stimulus whose vertical-to-horizontal aspect ratios were selected randomly and were asked to decide which stimulus had a more circular envelope. b) Psychophysically-determined perceptual aspect ratios and 95% confidence intervals for 2 cpd and 4 cpd Gabor stimuli (N = 10 human subjects). c) Psychometric functions obtained for horizontal and vertical 2 cpd and 4 cpd comparison Gabors. The abscissae represent the relative aspect ratio of the comparison stimuli (AR_comparison / AR_standard) and the ordinates represent the probability of selecting the standard as more circular. Each of the solid curves represents the psychometric function for a particular standard aspect ratio. The colored markers represent the corresponding observed response probabilities and 95% confidence intervals averaged across each of 10 aspect ratio bins. In each plot, the horizontal gray line represents γ, the estimated guess rate, while the vertical gray line and shaded region represent the estimated point of subjective equality (PSE), which corresponds to the reciprocal of the perceived aspect ratio, and its 95% confidence interval, respectively. The comparison stimulus is indicated by the inset images d) The Gabor comparison stimuli at an aspect ratio of 1.0. The dashed red ellipses illustrate the perceived shapes of these stimuli as estimated by the PSE’s.

The logic of the experiment is as follows: each trial requires the observer to compare the aspect ratios of a (neutral) plaid stimulus and an oriented Gabor stimulus. If, as hypothesized, the oriented Gabors are perceived as being more elongated along their carrier orientation than the neutral plaids, then for a Gabor’s aspect ratio to appear equal to that of a plaid stimulus, the Gabor has to be stretched in the direction orthogonal to its carrier orientation. For example, to match the perceived shape of a plaid with a vertical-to-horizontal aspect ratio of one, a vertical Gabor would need to have an aspect ratio smaller than one, while a horizontal Gabor would need to have an aspect ratio larger than one.

The results of our psychophysical experiments confirm these predictions and demonstrate a novel shape illusion. Psychometric functions (Fig. 6b) were estimated for each of five different standard aspect ratios (AR_s = {0.67,0.82,1.0,1.22,1.5}). The amount of adjustment required for the comparison to perceptually match the standard is indicated by the vertical gray lines. As predicted, across all values of the standard, human observers perceive the horizontal Gabor to be horizontally stretched (AR_H =0.81, one-sample t(9) = 68.76, p = 1.47 × 10⁻¹³) and the vertical Gabor to be vertically stretched (AR_V =1.33, one-sample t(9) = 81.18, p = 3.31 × 10⁻¹⁴) relative to the plaid stimulus. These perceived shape distortions are consistent with, but somewhat smaller than, predictions based on the physiological data (Fig. 5c). This difference is not unexpected. While we expect qualitative agreement between the monkey physiology and the human psychophysics, multiple factors make it difficult to make precise quantitative predictions about perceptual judgments based on our physiological measurements (see Limitations of the Population Response Model in the Online Methods).

As in the physiological portion of the study, we expected the perceptual distortion to decrease for stimuli that poorly match V1 receptive fields. To test this prediction, we ran additional psychophysical conditions using Gabor stimuli with identical Gaussian envelope sizes but double the spatial frequency. As predicted, the perceived difference in the aspect ratios of vertical and horizontal Gabors was significantly smaller for the higher spatial frequency Gabors (AR_V − AR_H = 0.12) than for the lower spatial frequency Gabors (AR_V − AR_H = 0.49; paired t(9) = 29.42, p = 2.96 × 10⁻¹⁰) (Fig. 6b–d). Overall, our psychophysical results show that, for small stimuli with oriented texture, human observers exhibit shape judgment biases consistent with those predicted by the topographical distortions observed in V1 population responses.

Discussion

Visual stimuli elicit widespread activation in V1 due to their overlap with the receptive fields of many V1 neurons^9,27–29. Generally, the retinotopic extent of this activation is dominated by the spatial extent of the stimulus, and should therefore serve as a reliable signal for size and shape judgments. However, we show that for small visual stimuli dominated by a single texture orientation, this activation extends farther in the direction collinear with the texture orientation than in the orthogonal direction, leading to a distorted pattern of retinotopic activation that varies systematically with texture orientation. We exploited this orientation-dependent distortion in order to test the hypothesis that human observers rely (at least in part) on the retinotopic extent of population activity in V1 when making shape judgments. Our behavioral results support this hypothesis. In addition, our results provide a rare example of a novel perceptual illusion predicted from new physiological observations.

As our modeling results suggest, the orientation-dependent distortion at the population level can be explained by the previously documented elongation of receptive fields in V1. Given this receptive field elongation, one’s first intuition may be that the perceptual illusion reported here would be predicted by any decoder, including ‘labeled line’ decoders. However, this is not the case. It is well known from sampling theory that there are many receptive field encoding schemes (including those with elongated receptive fields) that will preserve all the information in an image, and hence, allow a ‘labeled line’ decoder to extract image properties without loss or distortion. Therefore, there is no a priori reason to expect a ‘labeled line’ decoder to be affected by receptive field elongation. It is possible to postulate post hoc a ‘labeled line’ decoder that ignores this fundamental receptive-field property, but such a decoder is bound to make systematic errors for a wide range of visual stimuli, not just the very specific stimuli that produce a distortion in the retinotopic pattern of activity. This seems unlikely given the veridicality of shape perception under most circumstances. Thus, the most parsimonious explanation of our results is that the retinotopic pattern of activity is contributing to shape perception, at least for the stimuli in our study.

Our results suggest that cortical topography is one factor influencing shape perception, not that it is the only such factor. In fact, it is likely that a variety of mechanisms, including mechanisms that are more consistent with a ‘labeled line’ hypothesis, contribute to shape perception.

Why do human observers not compensate for the retinotopically distorted responses elicited by our Gabor stimuli? After all, the cortical map exhibits many distortions and inhomogeneities, both at a fine scale, where position-based maps give way to orientation and ocular-dominance based maps, and at a coarser scale, where the area of cortex devoted to different regions of visual space varies systematically. For example, near the V1/V2 border, the cortical magnification is considerably smaller in the horizontal direction than in the vertical direction (Fig. 3a,b). Nonetheless, observers do not seem to exhibit a corresponding perceptual bias, perceiving visual space to be compressed in the horizontal direction. Similarly, observers appear to have veridical shape perception for most small visual stimuli despite their aspect ratio “compression” in V1 (Fig. 5a,b). Two important differences separate these distortions from those elicited by our oriented Gabors. First, unlike the fixed spatial distortions in the V1 retinotopic map or the fixed aspect ratio “compression”, the distortions introduced by our stimuli vary as a function of the stimulus’ carrier (i.e., texture) orientation. Second, as with most visual illusions, these distortions only occur for a small, carefully selected, subset of stimuli. Therefore, while the shape distortions elicited by these oriented Gabor stimuli reveal an important feature of the visual mechanisms mediating shape perception, they are unlikely to systematically bias the shape judgments humans make in natural tasks.

In addition to their significance regarding shape perception, the observed orientation-dependent distortions of V1 response spread could have important implications for the representation of multiple contour elements in V1. Physiological^5,30 and psychophysical^31,32 studies have shown that nearby collinear elements tend to have stronger interactions than orthogonal elements at the same distance. Our results suggest that some of these effects could be due to the elongation of V1 population responses along the retinotopic representation of contour orientation. Due to this elongation, V1 representations of two collinear elements will have larger overlap than the representations of two orthogonal elements at the same distance. Additional studies are needed to determine the exact contribution of this elongation to collinear interactions in V1.

Researchers have previously reported relationships between perception and the retinotopic extent of V1 activation^33–36. For example, the surface area of V1 or of a portion of V1 can predict the ability of individual human observers to accurately report the relative positions³³ or relative sizes³⁴ of visual stimuli, suggesting that stimuli encoded using larger neural populations may be perceptually represented with greater fidelity. Other studies^35,36 demonstrated that in the context of a configural size illusion, attention can act to correlate the retinotopic extent of activation in V1 with the (erroneous) perceived size of visual stimuli, suggesting that the extent of activation in V1 may reflect perceived size. Our findings go beyond these previous results by demonstrating that human shape perception can be biased by stimuli that are coextensive in visual space but vary in the retinotopic extent of their elicited activation in V1. More generally, our results suggest that the retinotopic pattern of population responses in V1 might influence, or constrain, shape perception. This finding is consistent with recent reports^37,38 that later visual areas, which have been more directly implicated in shape processing^39–42, seem to sample from an approximately constant extent of the V1 cortical surface, thereby inheriting the retinotopic inhomogeneities of V1. In conclusion, our results suggest that the retinotopic extent of population activity in V1 influences human shape judgments. Thus, our findings support the hypothesis that cortical topography can play an important role in sensory coding and in supporting perceptual judgments.

Online Methods

Imaging Subjects and Stimuli

The results reported here are based on methods that have been described in detail previously^22,44,45. Here we focus on details that are of specific relevance to the current study. All procedures have been approved by the University of Texas Institutional Animal Care and Use Committee and conform to NIH standards.

Three male adult monkeys (macaca mulatta) were trained to maintain fixation while a small stationary Gabor or plaid stimulus was presented on a uniform gray background. Each trial began when the monkey fixated on a small spot of light (0.1deg) on a CRT display. Following an initial fixation, the sine-phase Gabor stimulus (σ = 0.167°, f = 2 cpd or 4 cpd) was flashed at 5 Hz for 1000 ms (60 ms on, 140 ms off) at a visual eccentricity between 2.40 and 3.82 degrees. To minimize the risk that monkeys would shift their gaze towards or away from the stimulus, a second, identical Gabor stimulus was simultaneously presented in the opposite quadrant of the visual field. Throughout the trial, the monkey was required to maintain gaze within a small window (< 2° full width) around the fixation point in order to obtain a reward. The contrast of the stimulus was 100%, at a mean luminance of 30 cd/m². The display had a resolution of 1024 × 768 and a 100 Hz refresh rate. In each session, trials representing different visual stimulus conditions, including blank trials, were randomly interleaved.

Selection of Stimulus Parameters

We used stimulus spatial frequencies of 2 cpd and 4 cpd despite the fact that our V1 model predicted larger reductions in the effect of carrier orientation on cortical aspect ratio, and thus larger experimental effects, for stimuli composed of higher spatial frequency carriers. Our decision to use the 4cpd stimuli for the high spatial frequency condition was motivated primarily by concerns about the quality of signals in the imaging experiments. At the eccentricities represented in our VSDI recording chambers (2–4 degrees), the response is strongest to 2 cpd stimuli and drops rapidly as the spatial frequency increases. Therefore, in addition to changing the aspect ratio of the response, using Gabors composed of higher spatial frequency carriers reduces both the amplitude and the signal-to-noise ratio of the VSDI responses so that fits to the spatial envelope of the response become unreliable. We selected the 4 cpd stimuli as a compromise to simultaneously maximize both the experimental effect size and the signal-to-noise ratio.

Analysis of the Imaging Data

Imaging data were collected at 110Hz at a resolution of 512 × 512 pixels. The size of each pixel was approximately 32 × 32 µm². Our basic analysis is divided into four steps: (i) normalize the responses at each pixel by the average fluorescence at that pixel across all trials and frames, (ii) remove from each pixel a linear trend estimated on the basis of the response in the 100ms interval before stimulus onset for each trial, (iii) remove trials with aberrant VSDI responses (generally fewer than 1% of the trials⁴⁵), and (iv) subtract the average response to the blank condition from the stimulus-present conditions.

After the basic analysis described above, the spatial properties of the responses in each trial were determined. First, we computed the amplitude of the 5 Hz response at each location in the fluorescence image. Then we averaged these response amplitudes across all trials within a particular stimulus condition and experimental session. Finally, for each condition we computed the center, orientation, amplitude, and aspect ratio of the best-fitting (in a least-squares sense) two dimensional Gaussian function of the following form:

$$\begin{array}{c}g(x,y)=A\text{exp}(\raisebox{1ex}{${-x\prime }^2$}\!\left/ \!\raisebox{-1ex}{$2{\sigma }_{x\prime }^2$}\right.-\raisebox{1ex}{${-y\prime }^2$}\!\left/ \!\raisebox{-1ex}{$2{\sigma }_{x\prime }^2$}\right.)\hfill \\ \{\begin{array}{c}x\prime =(x-{\mu }_x)\text{cos}\theta -(y-{\mu }_y)\text{sin}\theta \hfill \\ y\prime =(x-{\mu }_x)\text{sin}\theta -(y-{\mu }_y)\text{cos}\theta \hfill \end{array}\hfill \end{array}$$ (1)

In analyzing each experiment, the Gaussian location (μ_x, μ_y) and orientation (θ) parameters were fit to all conditions and held fixed across conditions. Effectively, this meant that the major axis of the Gaussian was aligned with the direction maximizing the cortical magnification. Results from sessions that included retinotopic-mapping blocks indicated that this direction was generally within 5 degrees of the direction corresponding to the visual vertical axis. Retinotopic maps (such as that in Fig. 3b) were obtained using a previously described method⁹. Normalized physiological aspect ratios were computed by taking the physiological aspect ratio for each carrier condition (σ_y / σ_x) and dividing by the average aspect ratio across conditions. We computed standard errors on the aspect ratio in each condition and session using a jackknife technique. We combined these estimates to compute the maximum-likelihood aspect ratio and the associated standard errors and confidence intervals across sessions. These values (the maximum likelihood aspect ratios and associated standard errors) were used in computing the reported statistical tests.

Effects of Fixational Eye Movements

Small fixational eye movements could potentially give rise to elongated responses such as those reported here if they were systematically correlated with the orientation of the carrier grating. To test for such an effect, we quantified the eye movements within each trial by computing the horizontal (σ_x) and vertical (σ_y) standard deviations of eye position during the stimulus presentation (Supplementary Fig. 3). We then ran two t-tests to determine whether either of these measures varied systematically as a function of the carrier orientation. These tests indicated that Neither the standard deviation along the horizontal direction (t(102) = 0.015, p = 0.99), nor the standard deviation along the vertical direction (t(102) = 0.270, p = 0.79) varied significantly as a function of Gabor carrier orientation.

Relationship between VSDI Signals and Population Spiking Activity

An important question in considering the implications of measured VSDI signals for perception is: what is the relationship between the VSDI signals we observe and the spiking activity that is accessible to the downstream visual and decision areas that contribute more directly to behavior? Recent results⁵² suggest that the VSDI signal is dominated by subthreshold activity and that the spiking activity of the neural population can be represented approximately as a power function of the VSDI responses. Because a Gaussian function raised to a power N is still a Gaussian function (with a space constant σ that is smaller by a factor of $\sqrt{N}$), the spiking responses of a neural population whose VSDI responses are described by a 2D Gaussian with space constants of σ_H in the horizontal direction and σ_V in the vertical direction could be described by a 2D Gaussian with space constants ${\sigma }_H/\sqrt{N}$ and ${\sigma }_V/\sqrt{N}.$. In other words, the population spiking responses should have an aspect ratio similar to that of the VSDI responses, but a reduced overall extent.

Psychophysical Subjects and Stimuli

Ten human subjects (eight naïve undergraduates, 4 male and 4 female, and two experienced psychophysical observers, both males, who were naïve to the aims of the study) with normal or corrected-to-normal vision participated in this study. All human subjects provided informed consent to participate in the procedures decribed below, which were approved by the University of Texas Institutional Review Board. Stimuli were grayscale images presented on a calibrated CRT monitor located 70cm from observers and set to a resolution of 1280 × 1024 pixels (pixel size = 0.27 × 0.27mm). Each stimulus display consisted of a pair of targets, each positioned 2.5 degrees from fixation and centered in opposing quadrants of the display, so that one of the stimuli always appeared on the left and one on the right. The target stimuli were horizontal, vertical, and plaid 2 cycle/degree (cpd) gratings (4 cpd in the high frequency conditions) windowed by a two dimensional Gaussian contrast function whose standard deviations in the vertical and horizontal direction had a geometric average of 0.167 degrees. All stimuli were presented at 80% contrast against a uniform gray background with a mean luminance of 40 cd/m².

Shape Judgment Task

Before each trial, the observer fixated a dot at the center of the display and initiated the trial with a button press. The fixation point dimmed immediately and a random time (150–350 ms) later the two target stimuli appeared for 200 ms. The observer’s task was to determine which of the two targets (left-side or right-side) had the more circular contrast envelope (i.e., the target whose spatial extent was more circular). In each pair of targets, one (the standard) was a plaid stimulus, while the other (the comparison) could be either a plaid, horizontal, or vertical stimulus. The location of the standard (i.e., left or right) was selected randomly, as were the pair of quadrants (i.e., upper left & lower right or upper right and lower left) in which the stimuli were presented and the phases of the carrier gratings. The standard stimulus took on five discrete aspect ratio values (0.67, 0.82, 1.0, 1.22, 1.50) spaced evenly along a log axis. The value of the comparison stimulus on each trial was chosen on a uniform interval ± one log (base 2) unit from the aspect ratio of the standard.

All observers completed five sessions of the experiment. Each session began with a practice block in which the standard and comparison stimuli were both plaids and subjects received auditory feedback on each trial. After the practice block was completed, subjects ran 4 blocks of 300 experimental trials each without feedback. High and low spatial-frequency blocks were interleaved and their order counterbalanced across observers.

Analysis of Psychophysical Data

The purpose of the psychophysical task was to determine whether the perceived shape of the Gabor stimuli varied systematically with the orientation of the carrier grating, as we hypothesized based on the physiological measurements. Our prediction was that, relative to a neutral (plaid) stimulus, a Gabor would appear stretched along the orientation of the bars composing its carrier grating. For example, a vertical Gabor should appear vertically stretched, while a horizontal Gabor should appear horizontally stretched.

To measure this effect, we determined the point of subjective equality—the scaling adjustment required to make the aspect ratio of the Gabor comparison stimulus perceptually equivalent to that of the plaid standard. Note that this adjustment should exactly counter the perceptual effect. For example, if a circular vertical Gabor (AR = 1.0) were perceived as having a vertical-to-horizontal aspect ratio of 1.5, then to appear circular, its aspect ratio would have to be 1/1.5. The point of subjective equality β_c is therefore equal to the reciprocal of the perceptual effect. We estimated the point of subjective equality by determining the maximum likelihood value of β_c, using a psychophysical task.

To determine the value of β_c, we assumed that observers make their decisions based on noisy perceptual estimates of the aspect ratios of the comparison (AR_c) and the standard (AR_s) stimuli. The noise associated with each of these estimates was assumed to be proportional to the aspect ratio and distributed log-normally.

That is,

$${\text{log}}_2(A{R}_s)=X_s~N({\mu }_s,\sigma ){\text{log}}_2(A{R}_c)=X_c~N({\mu }_c-{\text{log}}_2({\beta }_c),\sigma ),$$ (2)

where μ_s is the veridical (log) aspect ratio of the standard stimulus, and μ_c is the veridical (log) aspect ratio of the comparison stimulus. This assumption is equivalent to assuming Weber’s law behavior for aspect ratios, which seems to hold approximately for the relatively small aspect ratios used here⁴⁶. Furthermore, the estimates of the point of subjective equality are not strongly dependent on the assumed form of the noise.

The task is to determine which stimulus is more circular, which is equivalent to determining which of the two log aspect ratios is closer to zero. In other words, the observer selects the standard whenever $X_s^2<X_c^2$ and chooses the comparison otherwise. In the simplest case, we can compute the probability of choosing the standard as

$$p(X_s^2<X_c^2|{\mu }_s,{\mu }_c,\sigma ,{\beta }_c)=\underset{-\infty }{\overset{\infty }{\int }}p(X_s^2<x_c^2|{\mu }_s,\sigma )p(x_c^2|{\mu }_c,\sigma ,{\beta }_c)d{x}_c,$$ (3)

where p(X² | μ,σ) is a non-central chi-squared distribution with one degree of freedom and noncentrality parameter λ = (μ² / σ²). The analytic properties of this distribution, along with approximations of the associated cumulative distribution function p(X² < x | μ,σ) have been characterized elsewhere⁴⁷.

In this simple case, the point of subjective equality (PSE) occurs when the observer is equally likely to choose the standard or the comparison stimulus. PSE’s for two alternative forced-choice tasks are usually determined by finding the value of the comparison for which the probability of choosing the standard is 50%. However, when the standard can be physically distinguished from the comparison using features irrelevant to the task, PSE’s estimated using the 50% point can be confounded with response bias⁴⁸.

In our psychophysical experiment the carrier of the standard target was always a plaid, while the comparison was usually an oriented Gabor. Therefore, the observer could usually determine which of the two stimuli the standard was. Observers exhibited a systematic response bias, favoring the standard when the aspect ratios were perceptually indistinguishable and even when the comparison stimulus was perceived as slightly more round than the comparison.

This bias is evident in the psychometric functions plotted in Fig. 6c. The reversals in individual curves from a decreasing slope to an increasing slope indicate the perceived transition of the comparison from a horizontally oriented to a vertically oriented shape, with points of zero slope indicating perceived circularity. If observers responded in an unbiased way, then at these points of perceived circularity the probability of choosing the standard should be at most 0.5. Instead, in Fig. 6c these points always occur at values greater than 0.5, indicating a response bias.

To account for this response bias we introduced the adjusted guessing rate parameterγ, reflecting the observers overall bias toward choosing the standard as the most circular of the stimuli. Formally,γ represents the observer’s prior probability on the standard stimulus.

Applying this prior using Bayes’ rule and solving for p(standard) = p(μ_s < μ_c − log₂(β_c)) yields

$$p(\text{standard}|{\mu }_s,{\mu }_c,\sigma ,{\beta }_c)=\frac{\gamma p(X_s^2<X_c^2|{\mu }_s,{\mu }_c,\sigma ,{\beta }_c)}{\gamma p(X_s^2<X_c^2|{\mu }_s,{\mu }_c,\sigma ,{\beta }_c)+(1-\gamma )p(X_s^2>X_c^2|{\mu }_s,{\mu }_c,\sigma ,{\beta }_c)}.$$ (4)

For trials in which the comparison and the standard were both plaids (and thus physically indistinguishable), the value of this parameter was 0.5 (γ = 0.5). Generally however, observers were biased toward choosing the standard as more circular (γ > 0.5). Note that because the design of the task allowed more extreme aspect ratios for the comparison stimuli (chosen from a symmetric log-scale interval around the standard) than for the standard stimuli, the empirical probability of the standard being the more circular of the two stimuli in our experiment was actually 0.67 and therefore the response bias exhibited by the observers is sensible.

In fitting the psychometric functions, we used the form in (Eq. 4), except that we assumed a small fixed lapse rate of 1% to keep rare lapse errors from dominating the maximum likelihood fit, and we introduced a fourth parameter β_s to account for any overall tendency to perceive round stimuli as elongated (as might be caused by a small geometric anisotropy in the display). This parameter simultaneously added a fixed offset to the veridical log aspect ratios of the standard (μ_s) and the comparison (μ_c). We estimated the four free psychometric parameters {σ,γ,β_c, β_s} simultaneously by pooling the response data across human observers and finding the maximum likelihood fit across all values of the standard. Separate fits were obtained for each comparison carrier condition (e.g., plaid, horizontal grating, vertical grating), and 95% confidence intervals were estimated via bootstrapping using a case-resampling procedure with 1000 repetitions.

Finally, our results do not depend critically on the details of this psychometric model. For example, though the dot markers in Fig. 6c and Supplementary Fig. 2a, which represent log-space binned averages of the human responses (the raw data at each point was a binary response) show that the data were well fit by the psychometric model (solid lines), the shifts in PSEs shown for the vertical and horizontal carriers in Fig. 6c are evident even in the averaged human responses.

V1 Population Response Model

Simulating Population Responses

We simulated V1 responses within a 2° × 2° patch of the visual field using 10,000 unique receptive field parameters (see Sampling Receptive Field Parameters below). Briefly, each complex cell’s receptive field was represented by the nonlinear combination of a pair of Gabor functions in quadrature phase. Additionally each unique receptive field tiled the simulated visual field patch along a 101 × 101 rectangular array, so that each location in the grid was associated with the responses of 10,000 unique receptive fields centered on that location. The spatial distribution of complex cell responses was convolved with a Gaussian kernel to simulate the effect of receptive field position scatter that occurs at any given location in the visual cortex.

The specific steps of the simulation were as follows:

1. For each cell in the population, we construct two Gabors, one in sine phase (g_s) and one in cosine phase (g_c), from the sampled frequency, height, width, orientation parameters.

2. To simulate the response of a complex cell to a particular stimulus we take the sum of squares of the dot products each of the quadrature pair of Gabors⁴⁹ with the stimulus; i.e., r (x, y)= [g_s (x, y)· I]² + [g_c (x, y)· I]². This is equivalent to computing the sum of the half-squared outputs of four Gabor-shaped simple cell receptive fields each shifted from the next in 90° increments of phase.

3. For each set of cell parameters, we simulate a the stimulus-elicited responses R of a population of cells with identical parameters but different receptive field locations representing a 2×2 degree portion of the visual field, such that R_ij = r(x_j, y_i).

4. To simulate scatter in receptive field positions, we convolve the result with a Gaussian kernel whose variance is set to match the variance of the receptive field center positions at a point in cortex (or, equivalently, the variance of the cortical positions of cells with RFs centered on the same point in visual space).

   B_l = R_l ⊗ K (σ_PS (l)) where σ_PS (l) is the scatter associated with the l^th receptive field.

   Physiological measurements in monkey⁵⁰ and cat⁵¹ suggest that the average scatter in receptive field centers at a particular location in V1 is about 50% of the average receptive field size, which is what we assume in our model. In our simulations:

   1. Preliminary results from our lab (not shown) suggest that the size of the cortical point image (CPI) for Gabor stimuli sharing a common envelope size is approximately constant across carriers of different spatial frequency, suggesting that the population receptive field (pRF) does not change as a function of spatial frequency²⁹. To account for these results, we assume that the scatter of receptive field centers increases as a function of spatial frequency (i.e., that smaller receptive fields have more scatter than larger receptive fields centered on the same cortical location). This is effectively equivalent to assuming a uniform tiling of visual space for each of our receptive field sizes. Relaxing this assumption (e.g., assuming a fixed scatter) does not significantly affect our predictions regarding aspect ratios, but it predicts that response spread should decrease with increasing spatial frequency.
   2. To implement this relationship, we vary the scatter associated with each receptive field such that the sum of the positional scatter variance ${\sigma }_{PS}^2(l)$ and the receptive field envelope variance ${\sigma }_{RF}^2(l)$ remains constant; i.e., ${\sigma }_{PS}^2(l)=\text{max}({\sigma }_{PS}^2+{\sigma }_{RF}^2-{\sigma }_{RF}^2(l),0).$

5. At each location, the final response (across all receptive fields) is simply the average of the responses to the individual receptive fields $\mathbf{E}=\frac{1}{N}\sum _i^N{\mathbf{B}}_i$

Sampling Receptive Field Parameters

Peak spatial frequency tuning parameters were estimated from existing electrophysiological data²³ measured from cells with receptive field centers falling between 3 and 5 degrees in the visual periphery (Fig. 6, parafoveal data). A log Gaussian (μ = 2.34cpd, σ = 2.01octaves) was fitted to the combined histograms.

The distributions of receptive field shape parameters were obtained by combining data from a more recent study²⁴ that provides simple-cell width and length parameters in period-units (i.e., n_x = σ_xf_x, n_y =σ_yf_x), and those from an older study²³ that provides orientation and spatial frequency bandwidth parameters.

To use common parameters, the bandwidth parameters from the older study²³ were transformed as

$$n_x=\frac{\sqrt{\text{ln}(4)}}{2\pi }\frac{2^{w_{SF}}+1}{2^{w_{SF}}-1},n_y=\frac{\sqrt{\text{ln}(4)}}{2\pi \text{tan}(W_0/2)},$$

where W_SF represents the spatial frequency bandwidth in octaves and W_O represents the orientation bandwidth. Additionally, sample RF parameters were excluded if they led to undefined spatial frequency bandwidths or if they had extremely large orientation bandwidths (i.e., W_O > 180°).

Unfortunately, while one study²³ shows that a cell’s spatial frequency bandwidth varies systematically with its peak spatial frequency, the receptive field shape data in both studies cited above was reported in a spatial frequency-independent manner. Mean spatial frequency bandwidth decreases approximately linearly with the log of the peak spatial frequency (slope = −0.246, intercept = 1.779). To account for this trend when sampling receptive field shape for a cell with a particular peak spatial frequency, we

1. Computed a function q(W_SF) representing the distribution of spatial frequency bandwidths in our distribution of sample RFs. This function was obtained as the maximum-likelihood gamma distribution function fit to the octave bandwidths.

2. Computed p(W_SF | f), the (Gaussian) distribution of bandwidths expected for a given frequency from the previously reported empirical relationship²³.

3. Sampled RFs from a multinomial distribution where the probability of choosing each RF was weighted by p(W_SF | f) / q(W_SF) and W_SF represents the RF’s spatial frequency octave bandwidth.

To sample the set of receptive field parameters for a single V1 neuron, we first sampled a spatial frequency from the distribution described in (1), we then sampled a receptive field shape from the distributions described in (2) and (3), and finally we sampled the orientation from a uniform distribution. To obtain a population of receptive field parameters for cells centered at a particular location, we simply repeated this process. A summary of the resulting distribution of receptive field parameters is shown in Fig. S1. The average simulated receptive field had a peak spatial frequency tuning of 2.98 cpd, and bandwidth of 1.6 octaves, and a space constant (σ_RF) of 0.26°. Because the average simulated receptive field position scatter (σ_PS) was half the width of the average receptive field, the resulting population receptive field (pRF), had a space constant of about 0.29°.

Limitations of the Population Response Model

It is important to point out that our estimates of V1 parameters are informed and limited by the measurements available in the literature. Consequently, our simulations are only intended to provide qualitative predictions of the physiological and perceptual responses. The precise perceived and physiological aspect ratios for a particular stimulus, depend on the amount of scatter in receptive field center locations, the exact form of the simple-cell response nonlinearity, and the distribution of receptive field shapes, which have not been measured precisely, and may vary somewhat from one cortical location to another, from an individual animal to another, and certainly from one species to another.

Additional simulations (not shown), in which we varied the receptive field parameter distributions, receptive field scatter, and the exponent of the simple-cell nonlinearity, resulted in small quantitative, but not qualitative differences in our results confirming that our main predictions—that population responses in V1 are systematically elongated for Gabors matching the average spatial frequency and bandwidth parameters of V1 neurons and that this elongation effect is attenuated for more poorly matching stimuli—are robust to minor variations in the specific population parameters used in the simulation.

Statistical Analysis

All error bars represent 95% bootstrap-computed confidence intervals for the mean and statistical significance was determined using two-sided t tests, with conservative estimates of the effective degrees of freedom. For the physiological data, jackknife estimates of standard error were computed across all trials (10 trials/condition/session) and the effective degrees of freedom were determined by the number of experimental sessions. For the psychophysical data, standard error was estimated from the bootstrap-computed 95% confidence intervals and the effective degrees of freedom were determined by the number of individual subjects. No statistical methods were used to pre-determine sample sizes, but our sample sizes were similar to those reported in previous publications in the field^2,12,45,46. Data distribution was assumed to be normal, but this was not formally tested. However, the bootstrap-computed confidence intervals accurately reflect the empirical data distributions and can be used to aid interpretation.