Heat-related mortality risk model for climate change impact projection

Abstract

Objectives

We previously developed a model for projection of heat-related mortality attributable to climate change. The objective of this paper is to improve the fit and precision of and examine the robustness of the model.

Methods

We obtained daily data for number of deaths and maximum temperature from respective governmental organizations of Japan, Korea, Taiwan, the USA, and European countries. For future projection, we used the Bergen climate model 2 (BCM2) general circulation model, the Special Report on Emissions Scenarios (SRES) A1B socioeconomic scenario, and the mortality projection for the 65+-year-old age group developed by the World Health Organization (WHO). The heat-related excess mortality was defined as follows: The temperature–mortality relation forms a V-shaped curve, and the temperature at which mortality becomes lowest is called the optimum temperature (OT). The difference in mortality between the OT and a temperature beyond the OT is the excess mortality. To develop the model for projection, we used Japanese 47-prefecture data from 1972 to 2008. Using a distributed lag nonlinear model (two-dimensional nonparametric regression of temperature and its lag effect), we included the lag effect of temperature up to 15 days, and created a risk function curve on which the projection is based. As an example, we perform a future projection using the above-mentioned risk function. In the projection, we used 1961–1990 temperature as the baseline, and temperatures in the 2030s and 2050s were projected using the BCM2 global circulation model, SRES A1B scenario, and WHO-provided annual mortality. Here, we used the “counterfactual method” to evaluate the climate change impact; For example, baseline temperature and 2030 mortality were used to determine the baseline excess, and compared with the 2030 excess, for which we used 2030 temperature and 2030 mortality. In terms of adaptation to warmer climate, we assumed 0 % adaptation when the OT as of the current climate is used and 100 % adaptation when the OT as of the future climate is used. The midpoint of the OTs of the two types of adaptation was set to be the OT for 50 % adaptation.

Results

We calculated heat-related excess mortality for 2030 and 2050.

Conclusions

Our new model is considered to be better fit, and more precise and robust compared with the previous model.

Introduction

In 2002, the World Health Organization reported for the first time the health impact of climate change [1]. In the report, however, heat-related impact was not included in the final aggregate total number, because it was not easy to model the relationship between ambient temperature and mortality for projecting future impact of climate change.

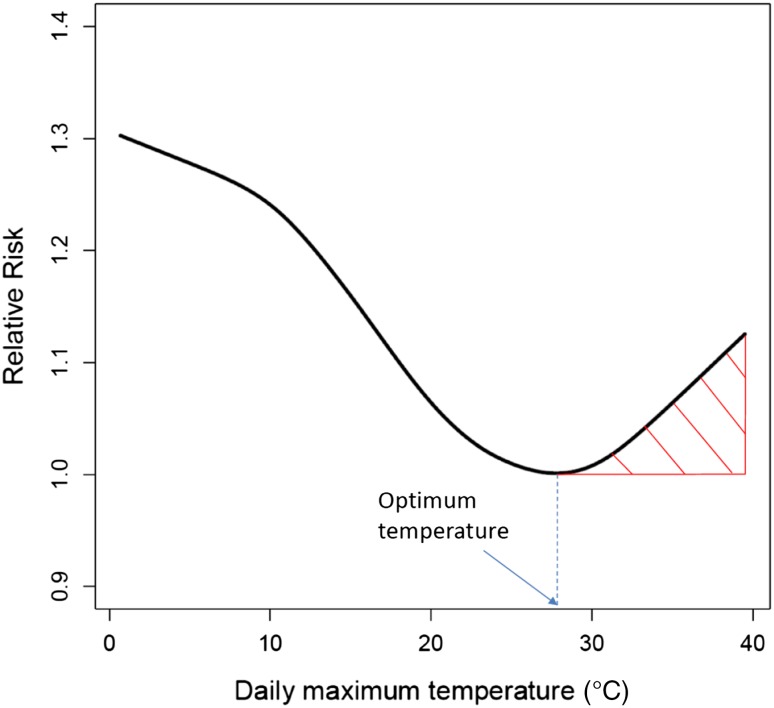
One of the reasons for not being able to construct the model was as follows: In many places of the world, a V-shaped temperature–mortality relation was observed [2, 3]. Using this relation, heat-related excess mortality can be defined as the shaded area in Fig. 1 (where the V-shaped relation was constructed from data for Tokyo from 1972 to 2008). So, if we can identify the optimum temperature (OT), at which the mortality risk becomes smallest, we should be able to estimate the excess mortality with some additional information (as described later). Although the OT level was found to be higher for warmer areas [4, 5], no good index to estimate the OT had been available.

Fig. 1.

Heat-related excess mortality, considered as the shaded area; the figure shows an example using data for Tokyo Prefecture for 1972–2008

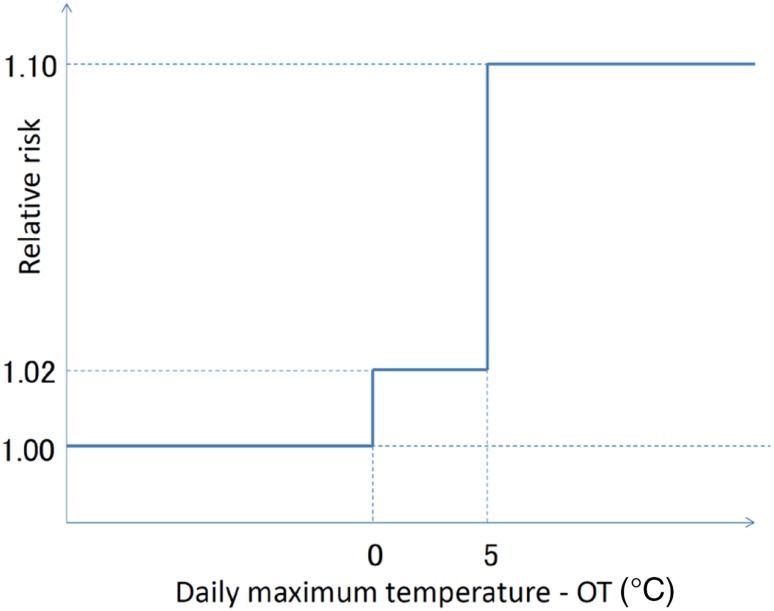
In 2007, we found that the optimum temperature can be estimated using the 80–85th percentile of daily maximum temperature based on 47 prefectures in Japan [6]. Using this estimation method and a risk function model, we projected excess mortality due to heat [7]. The projection method can be summarized as follows: The observation period was 24 years (1972–1995), and we used males and females with all ages combined. The OT was the 85th percentile value of daily maximum temperature. Although the risk function of excess mortality due to heat is nonlinear as shown in Fig. 1, we used the categorical function shown in Fig. 2. In this projection, we do not even show a confidence interval.

Fig. 2.

Risk function of excess mortality due to heat used in the previous projection

Although the above projection was one of the first projections of climate change impact on heat-related mortality, there were some weaknesses to the method, including (1) the applicability of the OT estimation method to other regions of the world, and (2) that the risk function was categorical. In this paper, we solve problem (2) by using a nonparametric risk function. This should be a substantial improvement, because the average of the temperatures in the highest temperature category was actually very close to the lower boundary of the category and huge underestimation was expected for the risk of this category. Regarding problem (1), we examine in this paper the applicability using cities in Korea, Taiwan, Europe, and the USA as well as 47 Japanese prefectures.

Another concern is the temporal pattern of exposure–mortality effects. This can be regarded in two ways [8]. One is the carry-over effect (lag effect), and the other is mortality displacement or harvesting. The former effect has been considered not to last long for heat-related mortality. In the latter case, heat just kills people who would die in a very short period of time anyway, and avoiding heat would extend the lives of people for only a short period of time. In the case of the 2003 heat wave in Europe, however, there was little evidence of mortality displacement [9]. Here, we address this lag effect using a distributed lag nonlinear model developed by Armstrong [8].

Materials and methods

Meteorological data and mortality data were obtained from respective governmental organizations of Japan, Korea, Taiwan, and European countries. For the USA, we downloaded the National Morbidity, Mortality, and Air Pollution Study (NMMAPS) files (which used to be downloadable at http://www.ihapss.jhsph.edu/data/data.htm, but are no longer available) [10]. Some descriptive information for the mortality data is presented in Table 1; because heat-related impact in occupational setting was also included in the new WHO project, we restricted mortality to 65+ years of age.

Table 1.

Description of mortality data by country

Country/region	Observation period	Age category	Note
Japan	1972–2008	65+	47 prefectures, 1973–2008 for Okinawa
Korea	1992–2010	65+	6 cities
Taiwan	1994–2007	65+	3 cities
USA	1987–2000	65+	20 cities
Spain	1992–2000	All ages	Barcelona
France	1991–1998	All ages	Paris
Italy	1992–2000	All ages	Rome

A set of mortality projections for the 2030s and 2050s was developed for this project by the World Health Organization. The approach built upon previous methods developed by Mathers and Loncar [11]. The method uses a series of regression equations that quantify the current and historical relationships between mortality and a set of independent variables. The major independent variables that were shown to be structurally related to mortality were (i) gross domestic product (GDP)/capita, (ii) years of education, and (iii) time, which is assumed to be a proxy for health benefits arising from technological developments. In addition, specific assumptions are made regarding future patterns of human immunodeficiency virus (HIV)/acquired immunodeficiency syndrome (AIDS), tuberculosis, malaria, smoking, and body mass index (BMI).

Development of the new risk function

We developed the risk function based on all 47 prefectures in Japan. Then, we examined the applicability of the assumptions in combining these 47 prefectures described below. For this purpose, we used the data for the selected cities in Korea, Taiwan, the USA, and Europe. We did not include data other than from Japan, because, although these cities somewhat represent large cities in each region, the data are not systematically collected and are not suitable for calculating average values.

Applicability of OT estimation method

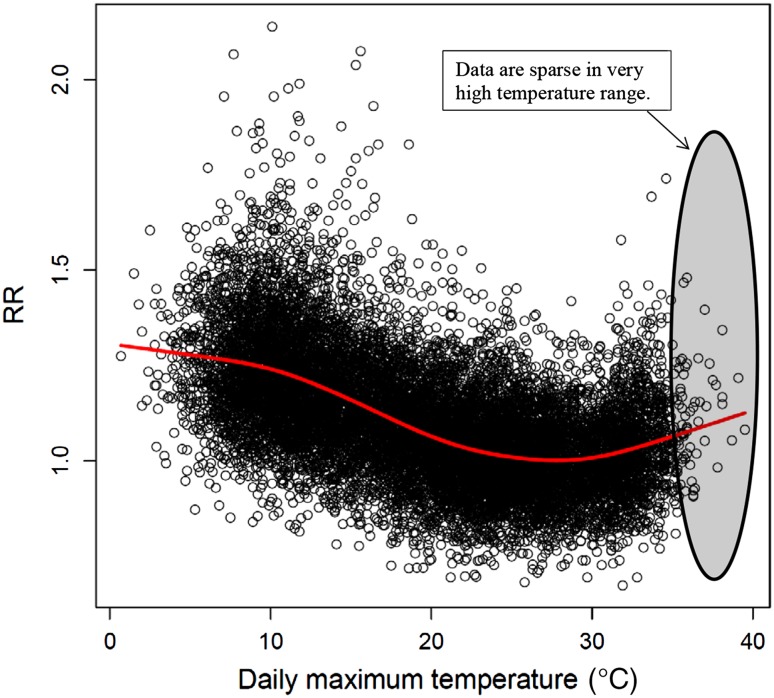
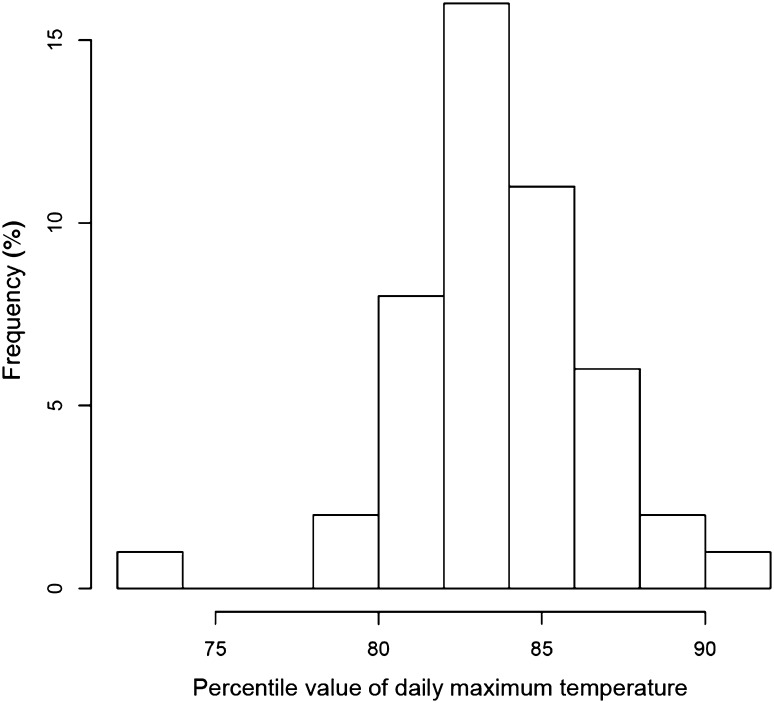
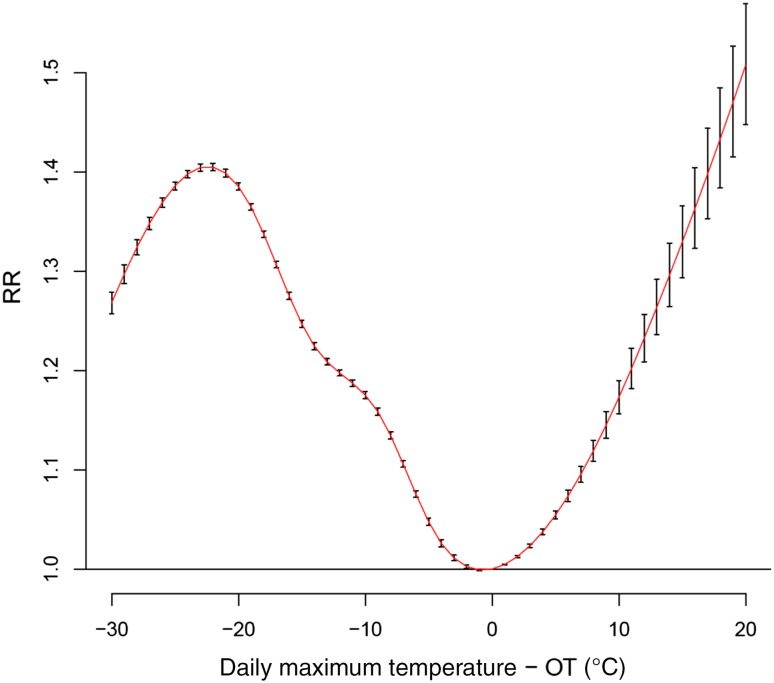
We obtained OT estimates for 47 prefectures in Japan using a smoothing spline with six degrees of freedom. As shown in Fig. 3, data points in the very hot range, especially beyond 35 °C, are sparse. Figure 4 shows the distribution of percentile values that correspond to the OT. In most cases, the value was around the 84th percentile. The mean of all the 47 prefectures was the 83.6th percentile, and we used this value to estimate the OT.

Fig. 3.

Relation between daily maximum temperature and relative risk (RR) in Tokyo, 1972–2008

Fig. 4.

Distribution of optimum temperature (expressed as percentile value of daily maximum temperature) in Japan

Table 2 presents the OT and 84th percentile value of daily maximum temperature in the cities of the other countries examined in this study. The OTs and 84th percentile values were close to each other in a majority of the cities. There were 3 US cities (Dallas/Fort Worth, Houston, and San Diego) that did not show a V-shaped relation. These 3 cities are located in the south, and it is possible to speculate that air-conditioned houses are very popular in these hot cities such that residents of these cities have adapted to heat exposure. However, other southern cities showed a V-shaped relation, even when the OT was higher than 40 °C. Also, in many mid- to southern Japanese prefectures, more than 90 % of households are equipped with air-conditioners (based on the 2009 National Survey of Family Income and Expenditure, for example), but these prefectures still showed V-shaped temperature–mortality relations. Hence, these 3 US cities may be exceptions due to statistical variation. From this multicountry examination, we concluded that OT can be estimated by the 83.6th percentile value of daily maximum temperature.

Table 2.

OT, 84th percentile of T _max, and ratio of RM_OT over RM_av

Country	City	OT	84th percentile of T max	Ratio
Taiwan	Taipei	33.4	33.9	0.95
	Taichung	33.0	33.0	0.94
	Kaohsiung	31.2	32.5	0.96
Korea	Seoul	27.8	28.1	0.93
	Busan	28.7	26.6	0.93
	Daegu	29.9	29.5	0.93
	Incheon	27.5	26.9	0.94
	Gwangju	29.1	28.8	0.92
	Daejeon	29.6	28.4	0.91
USA	Los Angeles	30.0	28.3	0.95
	New York	26.7	28.3	0.92
	Chicago	26.1	27.8	0.94
	Dallas/Fort Worthb	37.2	34.4	0.93
	Houstonb	41.7	33.9	0.93
	Phoenix	41.7	40.0	0.89
	Santa Ana/Anaheim	33.3	31.1	0.94
	San Diegob	41.7	24.4	0.95
	Miami	31.7	32.2	0.96
	Detroit	25.0	27.2	0.93
	Seattle	22.2	23.3	0.93
	San Bernardino	39.4	38.9	0.91
	San Jose	30.6	31.7	0.91
	Minneapolis/St. Paul	26.7	26.7	0.92
	Riverside	44.4	42.8	0.91
	Philadelphia	27.8	29.4	0.92
	Atlanta	31.7	31.1	0.93
	Oakland	32.8	33.9	0.90
	Denver	33.3	32.2	0.92
	Cleveland	26.1	26.7	0.94
Spain	Barcelona	27.9	29.4	0.88a
France	Paris	22.8	23.6	0.92a
Italy	Rome	25.0	26.8	0.89a

^aTarget population is all ages combined

^bOptimum temperature was not observed; the lowest mortality was observed at the highest end of the temperature

Precision improvement

To improve precision, use of long-term data and combining area-specific data are effective, provided that the chronological trend is well controlled and the heterogeneity among areas is reasonably small.

To control for chronological trend and population size, we introduced relative risk. The reference mortality for each year is the average number of deaths during the days with daily maximum temperature from the 75th to 85th percentile for each year. We chose this reference because this reference temperature range usually covers the OT, and because this reference is less affected by influenza epidemic than the annual average daily number of deaths or adding time trend in regression models as a nonparametric term.

Lag effect inclusion

As explained earlier, lag effect should be controlled for to obtain the overall heat-related effect. For this purpose, we used a distributed lag nonlinear model [8]. In the actual calculation, we used the dlnm package developed by Gasparrini [12] in R 2.15.1 [13]. In their paper, they describe dlnm as “a modelling framework that can simultaneously represent non-linear exposure–response dependencies and delayed effects. This methodology is based on the definition of a ‘cross-basis’, a bi-dimensional space of functions that describes simultaneously the shape of the relationship along both the space of the predictor and the lag dimension of its occurrence.” In our model, we used OT-offset daily maximum temperature (expressed as “T_max − OT”) as the temperature index. Another choice would be the percentile value of daily maximum temperature, because most prefectures have OT close to the 84th percentile value. However, the range of daily maximum temperature is very wide in northern prefectures, whereas that in southern prefectures is narrow, so a one-unit increase of the percentile corresponds to a different increase in temperature.

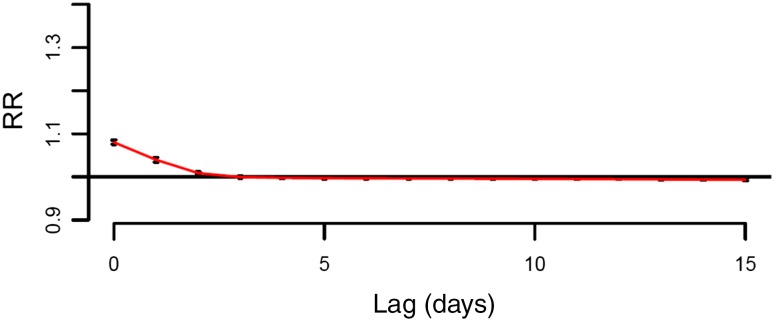
The parameter setting of the dlnm model is as follows: For both OT-offset daily maximum temperature and its lag (from 0 to 15 days), we used natural cubic splines with degree of freedom 6. OT-offset daily maximum temperature = 0, i.e., the mortality level at OT, was used as a reference. Since we used relative mortality, quasi-Poisson distribution was assumed. Figure 5 shows the dlnm result. This curve shows the result of adding up the lag effect. Figure 6 shows the lag pattern for the situation when the daily maximum temperature is 5 °C higher than OT. Lag 0 days had the highest risk, followed by lag 1 day. These risks, including slightly negative risk up to lag 15 days, were added up to construct Fig. 5. As observed, heat-related mortality increases monotonically above OT. On the other hand, below OT there is a complex relationship between mortality and temperature.

Fig. 5.

Risk function of excess mortality due to heat (for 47 prefectures in Japan, 1972–2008). Note: Lag effects up to 15 days were added to construct this curve

Fig. 6.

Lag structure of the heat-related relative risk when the daily maximum temperature is 5 °C higher than OT. Note: Lag structure when T _max − OT was 5

From relative risk to excess number of deaths

The above risk function curve used the relative risk, and we need to estimate the excess number of deaths using this relative risk. Because the reference of the relative risk is the risk at OT, we can convert the relative risks if we can calculate the number of deaths when the temperature is the OT (ND_OT). For this purpose, considering that the available information is the annual number of deaths (NAN), we need the following formula:

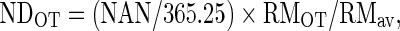where RM_OT is the relative risk at OT and RM_av is the average daily relative risk. (NAN/365.25) yields the daily average number of deaths. We obtained both RM_OT and RM_av using the Japanese dataset. Based on the Japanese dataset, the average and standard deviation of RM_OT/RM_av were 0.88 and 0.014, respectively.

To examine the robustness of the above index, we used selected data from cities in Korea, Taiwan, the USA, and Europe. Table 2 presents the values of this ratio in these countries selected for this manuscript. Although cities in Korea, Taiwan, and the USA showed a higher ratio than Japanese prefectures, two European countries showed a lower ratio. Considering that the European data are for all ages combined, the ratios for the 65+-year-old age group is expected to be even lower, because <65-year-old age groups are usually more resistant to heat; heat-related relative risk is lower for younger age groups. Based on this observation, we decided to use the Japanese ratio, 0.88, for global projection.

Projection of future impact of climate change on heat-related mortality

We need the daily maximum temperature distribution for risk estimation. So, we chose NCC (= NCEP Corrected by CRU, where NCEP stands for National Centers for Environmental Prediction, USA, and CRU stands for Climate Research Unit, University of East Anglia) daily data [14] as the baseline climate data. For the future climates, we used one of the general circulation models provided by the WHO Global Burden of Diseases project, i.e., BCM2. Here, we added the monthly average difference between the current climate and the future climate from models to each of the baseline daily maximum temperatures within the same month. The grid resolution is 1°. As the socioeconomic scenario, we used SRES A1B.

Adaptation is another concern. When the OT is estimated as the 83.6th percentile value of daily maximum temperature as of the current climate, we assume no adaptation (0 % adaptation). If the future climate is used for OT estimation, we assume 100 % adaptation. The midpoint of the 0 and 100 % adaptation OTs is assumed to be the OT for 50 % adaptation. V-shape flattening is another possible type of adaptation, but our preliminary analyses showed no evidence of flattening (this will be published in another paper), and we did not include this type of adaptation in this manuscript.

Because there are excess deaths due to heat even at present, the excess number of deaths attributable to climate change is calculated using the “counterfactual method.” The idea is that, with identical annual mortality rate, what is the difference between the number of excess deaths in the baseline case and that in the altered climate case? The actual procedure for 2030 is as follows: The calculation was done for each 1° × 1° grid of the globe. We used the annual number of deaths (provided by the WHO) in 2030 for both the baseline and altered climate case. Then, for the baseline case, we applied the temperature distribution of the current climate (1961–1990) to the risk functions (based on 47 prefectures of Japan) for 0, 50, and 100 % adaptation; for the altered climate case, we applied the temperature distribution of the projected 2030 climate obtained using BCM2 instead of the current climate. The difference in the number of excess deaths between these two cases is considered to be the climate-attributable excess number of deaths. These grid-specific numbers of deaths were summed up for each WHO region (Table 3). Likewise, the 2050 climate-attributable excess number of deaths was calculated.

Table 3.

WHO regions

WHO_REG_NEW	GBDname
AP_HI	Asia Pacific, High Income
As_C	Asia, Central
As_E	Asia, East
As_S	Asia, South
As_SE	Asia, Southeast
Au	Australasia
Ca	Caribbean
Eu_C	Europe, Central
Eu_E	Europe, Eastern
Eu_W	Europe, Western
LA_A	Latin America, Andean
LA_C	Latin America, Central
LA_S	Latin America, Southern
LA_T	Latin America, Tropical
NA_HI	North America, High Income
NA_ME	North Africa/Middle East
Oc	Oceania
SSA_C	Sub-Saharan Africa, Central
SSA_E	Sub-Saharan Africa, East
SSA_S	Sub-Saharan Africa, Southern
SSA_W	Sub-Saharan Africa, West

Results

Table 4 presents the projected excess heat-related deaths by WHO region. Asian regions are vulnerable to climate change impact.

Table 4.

Projection of heat-related excess deaths

Region	2030					2050
	Populationa	Baseline	0 %b	50 %b	100 %b	Populationa	Baseline	0 %b	50 %b	100 %b
AP_HI	177,053	2,427	4,802	3,635	2,598	162,307	2,528	6,866	4,395	2,588
As_C	9,529	611	1,458	975	598	103,588	947	3,797	2,024	854
As_E	1,428,481	5,343	18,423	11,053	5,837	1,332,115	7,050	36,739	18,612	7,184
As_S	2,033,885	10,692	26,666	18,022	11,296	2,284,943	17,429	65,562	37,524	18,489
As_SE	723,970	1,449	5,718	3,078	1,594	777,181	2,487	19,662	8,371	2,549
Au	32,982	119	370	230	125	37,063	156	837	424	174
Ca	48,633	2	195	75	2	49,792	3	553	261	3
Eu_C	115,732	988	3,123	1,955	1,090	107,099	1,058	5,396	2,998	1,417
Eu_E	195,411	1,708	6,350	3,647	1,860	178,872	1,732	10,471	4,845	1,721
Eu_W	441,260	3,570	6,214	4,722	3,485	446,713	4,425	13,367	8,334	4,677
LA_A	66,776	41	372	160	40	75,150	71	1,760	548	78
LA_C	287,206	700	2,181	1,239	711	318,626	1,226	7,364	3,363	1,249
LA_S	69,901	234	924	537	263	74,285	301	2,069	925	289
LA_T	229,162	364	2,050	1,066	432	233,166	563	6,546	2,545	694
NA_HI	401,536	2,408	7,394	4,704	2,702	446,749	2,953	15,441	7,877	3,235
NA_ME	584,318	1,596	4,780	2,977	1,683	681,137	3,209	15,331	7,940	3,302
Oc	14,113	4	47	14	3	18,172	8	195	68	7
SSA_C	152,539	201	918	482	221	212,327	438	4,007	1,645	485
SSA_E	574,918	858	3,686	1,923	857	848,878	1,679	14,734	6,060	1,776
SSA_S	81,752	156	539	319	165	87,940	246	1,737	798	300
SSA_W	543,556	775	2,491	1,486	785	809,872	1,578	9,468	4,465	1,679

^aIn thousands. Based on United Nations 2010 revision, medium estimates

^b0, 50, and 100 % represent adaptation level

In some regions, the heat-related excess deaths constitute up to 0.6 % of deaths, and some high-income regions also suffer a 0.1–0.4 % excess.

Discussion

Because this manuscript aims at developing a better projection model for heat-related excess deaths, the problems and their solutions were already addressed in “Materials and methods” section. Here, we evaluate how our goal was achieved, i.e., how much the fit, precision, and robustness of the proposed model have been improved from the previous projection [7]. As shown in Figs. 2 and 5, it is obvious that the fit is much better for the present model. To show the improvement of precision, we used the present model and applied it to the observation period of the previous model, i.e., 1972–1995. As an example, when the temperature was 10 °C higher than OT, the risk estimate (95 % confidence interval) of this calculation was 1.241 (1.218–1.265), whereas the present calculation gave 1.173 (1.156–1.189); the range of the confidence interval was 30 % smaller. As for the robustness, Table 2 clearly shows the similarity of the OT and the ratio of RM_OT over RM_av across a wide range of areas, including Asia, the USA, and Europe. Hence, our model that sets OT to be around the 84th percentile value of daily maximum temperature can be generalizable to all over the world. One additional concern may be the applicability of our OT estimation to tropical areas, where the annual temperature difference is very small. Our analyses covered very cold areas to subtropical areas, but did not cover tropical areas or countries in the Southern Hemisphere. In this regard, McMichael and coworkers’ report [15] is worth mentioning, because they observed the heat-related effect for 12 cities including cities in tropical countries and those in the Southern Hemisphere. Their model used a different method from ours; For example, they used daily mean temperature instead of daily maximum temperature, and they averaged out lag effect for lag 0–1 day and for lag 0–13 days. Still, the relation of the 0–1 averaged lag model was V-shaped for the majority of the cities. Considering that the 84th percentile value is roughly equal to the summer mean temperature, we tried to identify summer average temperature and optimum temperature from the graphs they provided. Among the cities with a V-shaped relation, most of the cities, including a tropical city (Bangkok, Thailand), had optimum temperature similar to their respective summer average temperature. Although this procedure is not accurate, at least use of the 84th percentile value in predicting OT cannot be falsified even by observations of cities in tropical zones or in the Southern Hemisphere. Another supporting report is the 4th Assessment Report of the Intergovernmental Panel on Climate Change [16]; temperature rise in tropical areas is expected to be less prominent compared with temperate areas and high-latitude areas. Hence, our projection would not be wide of the mark.

Compared with our previous projection, this new projection has advantages in terms of fit, precision, and robustness. Also, we included lag effect, which addresses mortality displacement. This implies that, although there may be some mortality displacement effect, the overall risk exists and climate change would increase the burden due to heat-related mortality.

Because the purpose of this paper is to show how we have improved the model for the global projection, we showed the projection results using only one global circulation model. However, the model described in this paper was adopted in the new WHO Global Burden of Diseases attributable to climate change, which will appear somewhere soon, and several models will be used and compared.

Compared with the total number of deaths, the proportion of deaths due to heat-related mortality attributable to climate change appears small. However, considering that even huge cyclones do not kill many people nowadays in high-income countries, heat waves are a major environmental hazard. Of course, we need to compare the heat-related impact and cold-related impact to obtain the net impact of global warming. However, new papers have warned that we should not naively apply the V-shaped temperature–mortality relation to projections for future cold-related excess deaths [17, 18]. We will try to develop our model for cold-related excess mortality after taking into account the points these papers raised in the near future.