Abstract
Many constructs are measured using multi-item data collection instruments. Differential item functioning (DIF) occurs when construct-irrelevant covariates interfere with the relationship between construct levels and item responses. DIF assessment is an active area of research, and several techniques are available to identify and account for DIF in cross-sectional settings. Many studies include data collected from individuals over time; yet appropriate methods for identifying and accounting for items with DIF in these settings are not widely available. We present an approach to this problem and apply it to longitudinal Modified Mini-Mental State Examination (3MS) data from English speakers in the Canadian Study of Health and Aging. We analyzed 3MS items for DIF with respect to sex, birth cohort and education. First, we focused on cross-sectional data from a subset of Canadian Study of Health and Aging participants who had complete data at all three data collection periods. We performed cross-sectional DIF analyses at each time point using an iterative hybrid ordinal logistic regression/item response theory (OLR/IRT) framework. We found that item-level findings differed at the three time points. We then developed and applied an approach to detecting and accounting for DIF using longitudinal data in which covariation within individuals over time is accounted for by clustering on person. We applied this approach to data for the “entire” dataset of English speaking participants including people who later dropped out or died. Accounting for longitudinal DIF modestly attenuated differences between groups defined by educational attainment. We conclude with a discussion of further directions for this line of research.
Keywords: item response theory, differential item functioning, ordinal logistic regression
Violations of measurement invariance are a threat to the validity of inference in observational and experimental studies. Assessing items for differential item functioning (DIF) is an important step in the evaluation of test bias. DIF occurs when examinees from different groups have differing probabilities of endorsing an item after controlling for the underlying ability or trait level measured by the test (Camilli & Shepard, 1994). Several techniques exist for identifying and accounting for DIF (Holland & Wainer, 1993; Millsap & Everson, 1993; Mungas & Reed, 2000; Teresi, 2006; Teresi, Kleinman, & Ocepek-Welikson, 2000). Existing algorithms and software for DIF detection presume a cross-sectional data structure, in which independent observations are assumed. Longitudinal data violate this assumption. Our aim was to suggest a new method for testing and accounting for longitudinal DIF, extending an iterative hybrid ordinal logistic regression/ item response theory (OLR/IRT) framework.
Most of the work on measurement invariance in longitudinal data has been in the setting of confirmatory factor analysis and structural equation modeling (SEM) (McDonald, 2000; Meredith & Teresi, 2006; Muthen, 1984). Several of these approaches rely on test-level rather than item-level data (Tisak & Meredith, 1989). However, accounting for item-level and scale-level violations of measurement invariance may provide a different result than limiting focus to scale-level violations. Three papers evaluated violations of measurement invariance for continuous data over time (Pentz & Chou, 1994; Pitts, West, & Tein, 1996; Raykov, 2004). Grimm et al. (Grimm, Pianta, & Konold, 2009) proposed a longitudinal correlated-trait correlated-method model that allows for trait and method variance in observed scores over time. Cai (Cai, 2010) evaluated measurement non-invariance in a longitudinal setting using a variant of a two-stage linking/testing factor analysis model (Baker & Kim, 2004; Canadian study of health and aging working group, 1994; Stocking & Lord, 1983) developed by Langer (Langer) for cross-sectional DIF testing. In the first stage, Cai constrained item parameters to be the same across occasions to estimate factor means and variances over time, essentially using all items to anchor the latent variables over time. In the second stage Cai treated estimated latent variable means and variances as fixed, and freely estimated item intercepts and slopes. Currently, the IRTPRO package implements this technique for exactly two time points. To date, there is no available DIF detection package that facilitates evaluation of uniform and non-uniform DIF for categorical items at more than two time points.
In this paper we address these issues with analyses of a longitudinal dataset from the Canadian Study of Health and Aging. We evaluated cognitive test items for DIF related to sex, birth cohort, and education.
First, we present results of cross-sectional DIF analyses for each covariate at each time point. These analyses permitted us to determine stability over time of item-level DIF presence, individual-level DIF impact, and group-level DIF impact. We then present methods and results for longitudinal DIF analyses.
Study data for all analyses
Participants
The Canadian Study of Health and Aging was planned in 1989 as a national longitudinal study. Representative samples were drawn from each community (the remainder resided in nursing homes), and participants were assessed at 5-yearly intervals: in 1991, 1996, and 2001. Details of study design and sampling procedures have been described (Canadian study of health and aging working group, 1994; McDowell, Aylesworth, Stewart, Hill, & Lindsay, 2001; McDowell, Kristjansson, & Hill, 1997; Tuokko, Kristjansson, & Miller, 1995). At baseline (Canadian Study of Health and Aging -1; 1991), 8,949 community-dwelling participants were interviewed for screening. The Modified Mini-Mental State Examination (3MS) (Teng & Chui, 1987) was administered at each time point. Of the 7,221 community-dwelling English speakers at baseline, 4,619 (64 %) had 3MS data from 1996, and 2,698 (37 %) had 3MS data from 2001; 2,635 (36 %) participants had data from all three time points and comprise the “completers” dataset.
Materials
The Mini-Mental State Examination (MMSE) was introduced as a brief assessment of cognitive functioning (Folstein, Folstein, & McHugh, 1975). The 3MS extends the MMSE. It adds four additional sub-tests (date and place of birth, word fluency, similarities, and delayed recall of words). The 3MS can be considered sufficiently unidimensional for IRT analyses (Crane, Narasimhalu, Gibbons, Mungas, et al., 2008). Brief descriptions of item content are found in most of the tables.
Statistical methods
We analyzed DIF related to three covariates: sex, birth cohort, and education (See Table 1). We dichotomized birth cohort at up to 1919 vs. 1920 and later, roughly the median of the “completers” dataset. DIF related to education has been found in cognitive tests even with very few years of education (Crane, Gibbons, Jolley, van Belle, et al., 2006), so we dichotomized education at 6 years.
Table 1.
Demographic Characteristics of English Speakers from the Canadian Study of Health and Aging
| Covariate | “Completers” dataset | “Entire” dataset | |||
|---|---|---|---|---|---|
| Baseline | 2nd visit | 3rd visit | |||
| Sex | Male | 985 | 2,949 | 1,834 | 993 |
| Female | 1,650 | 4,272 | 2,785 | 1,705 | |
| Total | 2,635 | 7,221 | 4,619 | 2,698 | |
| Birth cohort | ≤ 75 | 1,869 | 3,574 | 2,688 | 1,899 |
| > 75 | 766 | 3,647 | 1,931 | 799 | |
| Total | 2,635 | 7,221 | 4,619 | 2,698 | |
| Education* | ≤ 6 years | 414 | 1,594 | 846 | 419 |
| > 6 years | 2,216 | 5,582 | 3,745 | 2,230 | |
| Total | 2,630 | 7,176 | 4,591 | 2,649 | |
Note: Education level was missing for 5 participants.
We focus our presentation on education. Complete results for sex and birth cohort can be obtained from the authors on request.
Cross-sectional method
DIF detection methodology
We have developed and refined an iterative hybrid OLR/IRT approach to detect and account for DIF (Crane, Gibbons, Jolley, & van Belle, 2006; Crane, Narasimhalu, Gibbons, Pedraza, et al., 2008). We summarize the steps of our algorithm here:
Obtain unadjusted (“naïve”) ability estimates (θ̂) using IRT.
Categorize each item as having or not having DIF using a series of nested OLR models, conditioning on θ̂ from Step 1.
Use IRT to obtain revised ability estimates (θ̂r) that account for items identified with DIF in Step 2.
Categorize each item as having or not having DIF again, conditioning on θ̂r from Step 3.
Compare results of Step 2 and Step 4. If the same items are categorized as having and not having DIF, stop.
If different items are identified, obtain revised ability estimates (θ̂r) that account for items identified with DIF in Step 4.
Repeat steps 4–6 until items categorized as having and not having DIF are the same as seen in a prior run.
Each of these steps is discussed in more detail in Crane, Gibbons, Jolley, & van Belle, 2006 and Crane, Narasimhalu et al., 2008.
Cross-sectional results
Cross-sectional item-level DIF results for the “Completers” dataset (n = 2,635)
Item-level DIF findings related to education are presented in Table 2 for the “completers” dataset (n = 2,635 at each time point). For each of the covariates, too few items remained without DIF to anchor the scale when we used a p-value of 0.05, so we used a more stringent p-value criterion of 0.005.
Model 1: Logit P(Y=1|θ̂,G,T)=β0+β1×θ̂
Model 2: Logit P(Y=1|θ̂,G,T)=β0+β1×θ̂+β2×G
Model 3: Logit P(Y=1|θ̂,G,T)=β0+β1×θ̂+β2×G+β3×θ̂×G
Table 2.
Non-uniform & Uniform Differential Item Functioning with respect to Education (n = 2,635 English speakers) at Baseline, 2nd visit & 3rd visit and (n = 7,221) English Speakers at Baseline of the “Entire” Dataset
| Items | Baseline (p = 0.005) | 2nd visit (p = 0.005) | 3rd visit (p = 0.005) | Baseline entire (p = 5×10−8) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NUDIF | UDIF | NUDIF | UDIF | NUDIF | UDIF | NUDIF | UDIF | |||||||||
| Birth Year | 0.3 | no | 0.05 | no | 0.4 | no | 0.4 | no | 0.6 | no | 0.08 | no | 0.3 | no | 0.01 | no |
| Birth Day | 0.8 | no | 0.07 | no | 0.6 | no | 0.5 | no | 0.6 | no | 0.9 | no | 0.1 | no | 0.6 | no |
| Birth Month | 0.6 | no | 0.7 | no | 0.4 | no | 0.08 | no | 0.9 | no | 0.8 | no | 0.9 | no | 0.4 | no |
| Birth Province | 0.8 | no | 0.9 | no | 0.3 | no | 0.3 | no | 0.3 | no | 0.3 | no | 0.3 | no | 0.2 | no |
| Birth Town | 0.8 | no | 0.5 | no | 0.8 | no | 0.5 | no | 0.5 | no | 0.8 | no | 0.6 | no | 0.8 | no |
| Three Words | 0.7 | no | 0.01 | no | 0.05 | no | 0.02 | no | 0.2 | no | 0.7 | no | 0.5 | no | 0.03 | no |
| Counting | 0.03 | no | < 0.001 | yes | < 0.001 | yes | < 0.001 | yes | 0.9 | no | < 0.001 | yes | 0.4 | no | < 5×10−8 | yes |
| First Recall | < 0.001 | Yes | < 0.001 | yes | < 0.001 | yes | 0.01 | no | 0.7 | no | 0.3 | no | < 5×10−8 | yes | 0.07 | no |
| Today's Date | 0.07 | no | < 0.001 | yes | 0.7 | no | 0.7 | no | 0.7 | no | 0.05 | no | < 0.001 | no | 0.3 | no |
| Spatial Orientation | 0.5 | no | 0.3 | no | 0.06 | no | < 0.001 | yes | 0.08 | no | 0.2 | no | < 0.001 | no | < 0.001 | no |
| Naming | 0.6 | no | 0.05 | no | 0.04 | no | 0.1 | no | 0.4 | no | 0.5 | no | 0.8 | no | 0.04 | no |
| Four-legged Animals | 0.4 | no | < 0.001 | yes | 0.02 | no | 0.3 | no | 0.05 | no | 0.6 | no | < 0.001 | no | 0.7 | no |
| Similarities | 0.3 | no | < 0.001 | yes | 0.4 | no | < 0.001 | yes | 0.01 | no | < 0.001 | yes | < 0.001 | no | < 5×10−8 | yes |
| Repetition | 0.6 | no | < 0.001 | yes | < 0.001 | yes | < 0.001 | yes | 0.5 | no | < 0.001 | yes | < 0.001 | no | < 5×10−8 | yes |
| Read & Obey | 0.5 | no | 0.01 | no | 0.6 | no | < 0.001 | yes | 0.2 | no | 0.03 | no | 0.9 | no | < 0.001 | no |
| Writing | 0.09 | no | < 0.001 | yes | < 0.001 | yes | < 0.001 | yes | 0.04 | no | < 0.001 | yes | < 0.001 | no | < 5×10−8 | yes |
| Copying Pentagons | 0.5 | no | < 0.001 | yes | 0.7 | no | < 0.001 | yes | 0.7 | no | < 0.001 | yes | 0.2 | no | < 5×10−8 | yes |
| Three-stage Command | 0.2 | no | 0.4 | no | 0.03 | no | 0.4 | no | 0.6 | no | 0.9 | no | 0.3 | no | 0.5 | no |
| Second Recall | < 0.001 | yes | < 0.001 | yes | < 0.001 | yes | 0.01 | no | 0.7 | no | 0.3 | no | < 0.001 | no | < 0.001 | no |
Numbers in the columns indicate the p-value associated with the χ2 difference between models 2 and 3 for NUDIF and between models 1 and 2 for UDIF. Five items – counting, similarities, repetition of a phrase, writing a sentence, and copying interlocking pentagons – were identified with DIF in all three datasets. Two items – first recall of 3 words and second recall of 3 words – were identified with DIF at two time points but not the third. Four of the other items were identified with DIF at only one of the three time points.
Table 3 summarizes the cross-sectional DIF findings for all 3 covariates. Across the 3 time points and the 3 covariates, 28/57 item×covariate pairs (49 %) were consistently identified to be free of DIF, 13/57 (23 %) were consistently identified with DIF, and the remaining 16/57 pairs (28 %) were identified with DIF at some time points but not others. Thus in a sizable proportion of cases, we found inconsistent results across time points for item×covariate pairs, though the same individuals were examined at each time point, the covariates did not change, and the same DIF detection algorithm was used with the same p-value threshold for determining whether items were identified with DIF for each covariate.
Table 3.
Summary Table of Cross-sectional DIF Findings for the “Completers” Dataset at 3 Time Points
| Items | Sex | Birth cohort |
Education | Total |
|---|---|---|---|---|
| Not identified with DIF at any time point | 9 | 11 | 8 | 28 |
| Identified with DIF at all 3 time points | 6 | 2 | 5 | 13 |
| Identified with DIF at any 1 or 2 time points | 4 | 6 | 6 | 16 |
| Total | 19 | 19 | 19 | 57 |
Cross-sectional results at baseline for all English speakers (baseline of the "entire" dataset, n = 7,221)
We then turned our attention to the dataset that included baseline data from all participants, including those who subsequently died or dropped out of the study. Item-level DIF findings for education are summarized in the right hand columns of Table 2.
Referring to the left column of Table 2, 9 items – counting, first recall of three words, date, four-legged animals, similarities, repetition of a phrase, writing a sentence, copying interlocking pentagons, and second recall of three words – were identified with DIF with respect to education in the baseline “completers” dataset. The right column of Table 2 shows itemlevel findings for DIF associated with education in the baseline “entire” dataset using the more stringent p-value criterion of 5×10−8. With three exceptions – date, animals and second recall of three words – all of the items identified with DIF in the baseline “completers” dataset were also identified with DIF in the baseline “entire” dataset.
The different p-value thresholds used for these three analyses may explain the differences in item-level findings, as a subset of items identified with DIF using a less stringent p-value criterion applied to the smaller “completers” dataset were also identified with DIF using the more stringent p-value criterion in the larger “entire” dataset. However, differences in power and p-value criterion cannot explain differences in our findings for sex; most (but not all) of the items identified with DIF in the smaller “completers” dataset were also found to have DIF in the larger “entire” dataset, while an additional item was identified with DIF in the larger “entire” dataset but not the smaller “completers” dataset.
Individual-level DIF impact
DIF impact is an expression of the clinical relevance of DIF at the scale level, and can be quantified as the difference between scores that account for DIF and scores that ignore DIF. We analyzed each covariate separately starting with an unadjusted (naïve) ability estimate for item-level DIF presence. It is also useful to determine the cumulative impact of DIF across all of the covariates simultaneously. To do this, we evaluated each demographic category in turn, starting with sex. Next we evaluated age, using the sex-specific items when necessary. Finally, we evaluated education using age and sex-specific items. This resulted in scores that account for DIF with respect to all of the covariates simultaneously. In the absence of any published data on a clinically important difference or minimal important difference (Hays, Farivar, & Liu, 2005; Revicki, Hays, Cella, & Sloan, 2008) for the 3MS, we use the median standard error of measurement from the naïve IRT ability estimates as our comparator for determinations of individual-level impact, and refer to differences larger than that value as indicating salient DIF impact (Crane, Cetin, et al., 2007; Crane, Narasimhalu, Gibbons, Pedraza, et al., 2008). For the 3MS in the Canadian Study of Health and Aging, the median standard error of measurement at the baseline evaluation was 0.42.
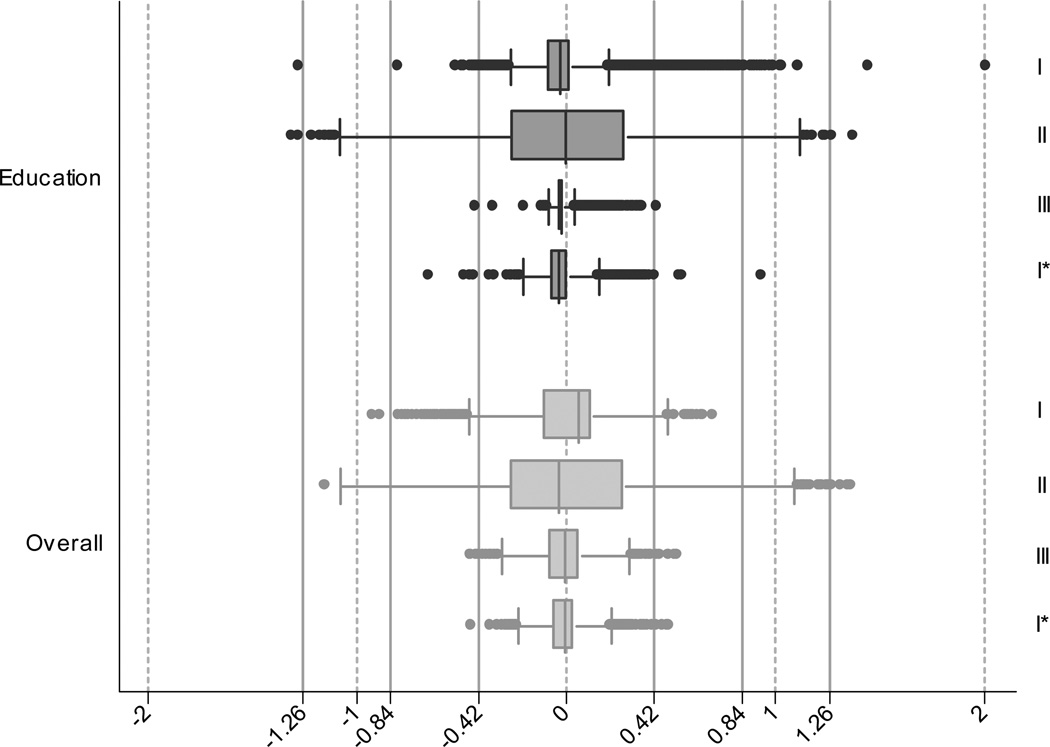
The top group of four plots in Figure 1 shows the individual-level impact of DIF related to education. The top three plots show results from the “completers” dataset (n = 2,635) for the first, second and third study visits, and the last shows results from the baseline of the “entire” dataset (n = 7,221). The first box plot of this group shows results for the baseline time point for the “completers” dataset (n = 2,635). The dots on either side of the box for this top plot extend beyond the median of the standard error of measurement, indicating that for many individuals there was salient DIF impact related to education at this time point. At the second time point, we see a lot more individuals with salient DIF impact related to education. At the third, the impact of DIF appears to be attenuated compared to the second time point, as even the most extremely impacted individuals had differences between scores right around 0.42. Figure 1 demonstrates that not only do the specific items with DIF identified across time points differ, so too does the magnitude of DIF impact. The final box plot in this top group shows results for the baseline time point for the “entire” dataset (n = 7,221). Compared with the top box plot, the larger sample size and smaller p-value criterion appear to result in smaller magnitude of DIF impact. The bottom four plots in Figure 1 show individual-level DIF impact of all three covariates considered simultaneously. We see similar patterns of results across time points as seen for education.
Figure 1.
Cross-sectional DIF impact for English speakers. In this box-whiskers plot, the box indicates the inter quartile range (IQR), while the whiskers indicate the upper and lower adjacent values as defined by Tukey (Tukey, 1977). Outliers (observations more extreme than the upper and lower adjacent values) are represented by dots. The graph shows the difference between ability estimates accounting for DIF for each covariate (and overall) and unadjusted ability estimates. If DIF had no impact for an individual, that observation should lie at zero. The plots are presented in order: I (baseline for “completers”), II (2nd visit for “completers” data), III (3rd visit for “completers”) and I* (baseline for “entire” data). Vertical reference lines are placed at ±0.42 to indicate the presence of ‘salient’ DIF. 0.42 was the median of the standard error for the unadjusted ability estimate at baseline for the “entire” dataset
Group-level DIF impact
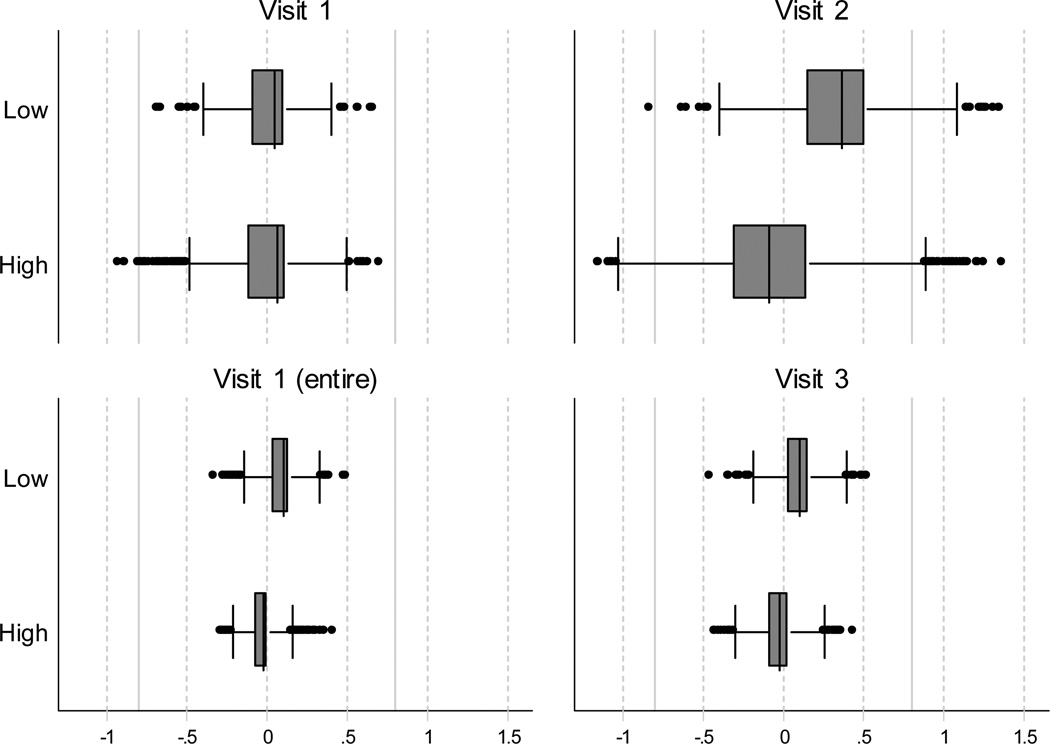
An example of group-level impact is shown in Figure 2, comparing DIF impact between scores that accounted for DIF related to all three covariates and the naïve scores that did not account for any source of DIF. The top left graph shows results for the “completers” dataset (n = 2,635) at the baseline time point. The median effect of accounting for DIF is to shift values for people with low education to the right as depicted in the top box plot, so that values accounting for DIF on average leads to a higher score than scores not accounting for DIF. The top right graph in Figure 2 shows group-level DIF impact for the “completers” dataset at the second time point. Here, the median effect of accounting for DIF for those with higher levels of education is to shift values to the left. The bottom left graph in Figure 2 shows group-level DIF impact for the “entire” dataset at the baseline time point (n = 7,221). While the median effect is the same as for the baseline of the “completers” dataset shown in the top left graph, it is somewhat attenuated here.
Figure 2.
Group-level DIF impact for education
For the baseline of the “completers” dataset, the difference between the means for the lower and higher education group for the naïve scores that do not account for DIF was 0.92 and after accounting for DIF the difference decreased to 0.90 (See Table 4). For the baseline of the “entire” dataset and the second and third visits for the “completers” dataset we see the same pattern; the difference between the means decreased by 0.12, 0.41, and 0.10 after accounting for DIF. Ignoring DIF related to education exaggerates differences between education subgroups.
Table 4.
Mean Differences between Naïve & Adjusted Estimates for Education
| Education | ||||||
|---|---|---|---|---|---|---|
| Low | High | Differences | ||||
| naïve | adjusted | naïve | adjusted | naïve | adjusted | |
| Completers at baseline | −0.77 | −0.76 | 0.15 | 0.14 | 0.92 | 0.90 |
| Entire at baseline | −0.69 | −0.60 | 0.21 | 0.18 | 0.90 | 0.78 |
| Completers at visit 2 | −0.79 | −0.45 | 0.15 | 0.08 | 0.94 | 0.53 |
| Completers at visit 3 | −0.55 | −0.46 | 0.10 | 0.09 | 0.65 | 0.55 |
Summary and implications of cross-sectional findings
Our evaluations of the “completers” dataset enabled us to use data from each time point as an independent assessment of item-level DIF findings. We were impressed with the instability of item-level findings across time points. As shown in Table 3, a large group of items were inconsistently found to have DIF (16 item-covariate pairs, or 28 % of all item-covariate pairs).
The “completers” dataset represented a non-random sample of all data points, so we compared findings from baseline from the “completers” dataset to the “entire” dataset that also included people who subsequently died or dropped out of the study. Here several issues were clarified. One was that analyzing DIF in a larger dataset necessitated more stringent criteria for labeling an item as having DIF to avoid categorizing items with miniscule differences as having DIF. Second was that increased power explained some but not all of the discrepancies in findings between the “completers” and the “entire” datasets at the baseline time point.
Individual-level and group-level DIF impact findings were also very interesting. Figure 1 shows that the magnitude of DIF impact varied across time points for the “completers” dataset, while the magnitude of DIF impact for the “completers” dataset and the “entire” dataset at the baseline time point could be very different.
Taken together, these findings motivated the need to develop an extension of our cross-sectional approach to detecting and accounting for DIF to the case of longitudinal data. Such an approach will be able to use all available data to determine whether items have DIF, overcoming the problem of variability across time points in whether items were found with DIF.
Longitudinal methods
With longitudinal datasets, it is likely more efficient to use all of the data in a single analysis. We thus set out to modify our cross-sectional DIF detection procedures to appropriately handle longitudinal data. In the sections below we delineate the considerations we faced when extending the framework outlined above to the case of longitudinal data.
Obtain unadjusted naïve ability estimates using IRT
Like all confirmatory factor analysis factor scores, the metric of IRT scores is indeterminate. It is common in cross-sectional IRT analyses to fix the mean and standard deviation of the metric to 0 and 1 in some relevant population. In the cross-sectional analyses, this comprised the entire cohort analyzed at each time point. Thus, in the cross-sectional analyses summarized above, the mean (standard deviation) at each time point for the population considered was 0(1).
With longitudinal data, we were interested in tracking changes in cognition over time on a single metric. Recent years have seen the development of models that can incorporate longitudinal item-level data to obtain item parameters using data from all time points (Glas, Geerlings, van de Laar, & Taal, 2009; Liu, 2008; te Marvelde, Glas, van Landeghem, & van Damme, 2006). Existing DIF detection packages do not accommodate these more sophisticated models. We thus focused our item parameter estimation efforts on the baseline dataset from the “entire” sample (n = 7,221), and then used these item parameters to obtain ability estimates at subsequent time points. This strategy has the advantage of estimating item parameters from the largest available cross-sectional dataset, and of obtaining ability estimates at subsequent time points on the same scale.
Categorize items as having or not having DIF using a series of nested ordinal logistic regression models
An important consideration in using the longitudinal data was to account for the fact that observations of the relationship between item responses and covariates while controlling for cognitive ability levels were not from independent analytic units. There are limited options currently available for accomplishing this task for ordinal logistic regression models. We used a simple approach for this relatively straightforward dataset, where we used Stata's default approach to clustering by person. The clustered sandwich estimator specifies that the standard errors allow for intragroup correlation, relaxing the usual requirement that the observations be independent. That is, the observations are independent across groups (clusters) but not necessarily within groups.
It was fairly straightforward to modify the nested logistic regression models shown on Pg. 131 to include a main effect for time and interactions between time and each of the other terms, as seen in the models shown below:
Model 1: Logit P(Y=1|θ̂,G,T)=β0+β,×T+β2×θ̂+β3×θ̂×T
Model 2: Logit P(Y=1|θ̂,G,T)=β0+β,×T+β2×θ̂+β3×θ̂×T+β4×G
Model 3: Logit P(Y=1|θ̂,G,T)=β0+β,×T+β2×θ̂+β3×θ̂×T+β4×G+β5×G×T
Model 4: Logit P(Y=1|θ̂,G,T)=β0+β,×T+β2×θ̂+β3×θ̂×T+β4×G+β5×G×T+β6×θ̂×G
where P(Y = 1) is the probability of endorsing an item, θ̂ represents the IRT estimate of the cognitive ability, G (group) represents a demographic category (sex, birth cohort or education) and T represents time point.
The reader will note that we did not model the 3-way interaction term between time, group, and ability. Such a term would capture differences across time in non-uniform DIF (that is, the interaction between ability and demographic group). Such a term could be of interest to those whose primary interest was in DIF effects over time, but our interest was in capturing the average non-uniform DIF effect across time points, which is captured by the 2-way interaction between group and ability identified by the β6 coefficient in Model 4.
We were similarly interested in the average uniform DIF effect across time points; this is captured by the β4 coefficient in Model 2. This approach ignores changes in the uniform DIF effect over time points, captured by the group by time interaction associated with the β5 coefficient in models 3 and 4.
Account for items identified with DIF in step 2 to obtain revised ability estimates
We used results obtained from the DIF detection with longitudinal data to prepare a new cross-sectional baseline dataset. A limitation of this method is that if the average DIF effect is driven by DIF effects at time points other than the initial time point, accounting for DIF in this way will result in under-adjustment. This approach is appropriate to the extent that time 1 DIF is representative of the overall DIF effect, which is an unexamined assumption and a limitation of this approach. Some extension of the te Marvelde / Glas approach (Glas, et al., 2009; te Marvelde, et al., 2006) which uses data from all the time points to determine item parameters will handle this problem better.
Results with longitudinal data
Table 5 shows DIF findings related to education for the longitudinal dataset. Comparing the results with the right-most columns in Table 2, we see that with one exception – first recall of three words – all items identified with DIF in the cross-sectional dataset were also identified with DIF in the longitudinal dataset.
Table 5.
Longitudinal Non-uniform & Uniform Differential Item Functioning with respect to Education for English Speakers (“Entire” Dataset)
| Items | Education (p = 5×10−16) |
|||
|---|---|---|---|---|
| NUDIF | UDIF | |||
| Birth Year | 0.8 | no | 0.7 | no |
| Birth Day | 0.1 | no | 0.4 | no |
| Birth Month | 0.9 | no | 0.2 | no |
| Birth Province | 0.8 | no | 0.3 | no |
| Birth Town | 0.7 | no | 0.8 | no |
| Three Words | 0.5 | no | 0.03 | no |
| Counting | 0.01 | no | < 5×10−16 | yes |
| First Recall | < 0.001 | no | 0.8 | no |
| Today's Date | < 0.001 | no | 0.01 | no |
| Spatial Orientation | < 0.001 | no | < 5×10−16 | no |
| Naming | 0.8 | no | 0.05 | no |
| Four-legged Animals | < 0.001 | no | 0.7 | no |
| Similarities | < 0.001 | no | < 5×10−16 | yes |
| Repetition | 0.2 | no | < 5×10−16 | yes |
| Read & Obey | 0.8 | no | < 0.001 | no |
| Writing | 0.01 | no | < 5×10−16 | yes |
| Copying Pentagons | 0.9 | no | < 5×10−16 | yes |
| Three-stage Command | 0.9 | no | 0.7 | no |
| Second Recall | < 0.001 | no | 0.04 | no |
Our findings with the entire longitudinal dataset were similar to but slightly different from the cross-sectional analyses of the entire baseline dataset. Because we had substantially more power to detect DIF with the longitudinal dataset, we had to use more stringent criteria to ensure adequate numbers of anchor items for each analysis. We used longitudinal data to categorize DIF, so time point-to-time point variability in findings summarized in Table 4 was attenuated.
Cross-sectional person-level DIF impact from longitudinal DIF analyses
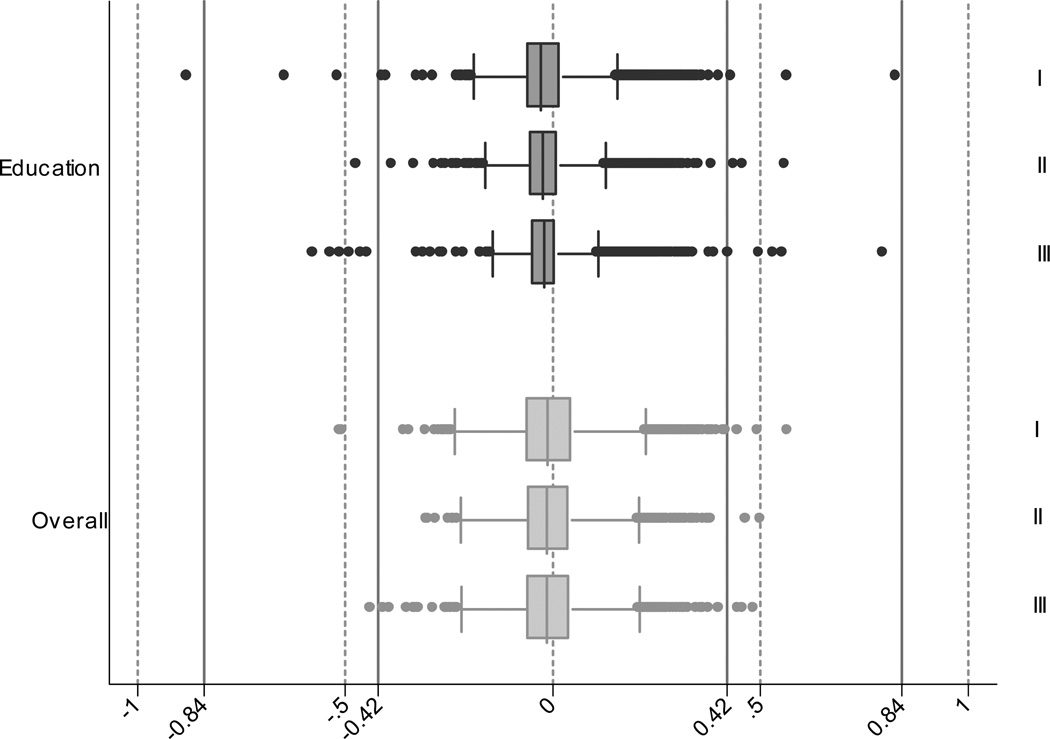
We used ability estimates of each time point from longitudinal DIF detection analyses and used the difference between scores that accounted for DIF and scores that ignored DIF to analyze individual-level DIF impact. The top group of three box plots in Figure 3 shows individual-level DIF impact related to education. Sizable numbers of individuals have salient DIF impact in both positive and negative directions. Nevertheless, the magnitude of DIF impact related to education is rather smaller in the longitudinal “entire” dataset than it was in the cross-sectional “completers” datasets (see Figure 1).
Figure 3.
Cross-sectional DIF impact for English speakers using estimates from longitudinal analysis. In this box-whiskers plot, the box indicates the inter quartile range (IQR), while the whiskers indicate the upper and lower adjacent values as defined by Tukey (Tukey, 1977). Outliers (observations more extreme than the upper and lower adjacent values) are represented by dots. The graph shows the difference between ability estimates accounting for DIF for each covariate (and overall) and unadjusted ability estimates. If DIF had no impact for an individual, that observation should lie at zero. The plots are presented in order: I (baseline for “entire” dataset), II (2nd visit for “entire” dataset) and III (3rd visit for “entire” dataset). Vertical reference lines are placed at ±0.42 to indicate the presence of ‘salient’ DIF. 0.42 was the median of the standard error for the unadjusted ability estimate at baseline for the “entire” dataset.
The bottom group of three box plots in Figure 3 shows individual-level DIF impact of all covariates considered simultaneously. There are a few individuals with salient DIF impact at each time point. Again, compared with the individual-level DIF in the “completers” dataset depicted in Figure 1, individual-level DIF impact appears smaller with the “entire” longitudinal dataset.
Cross-sectional group-level DIF impact
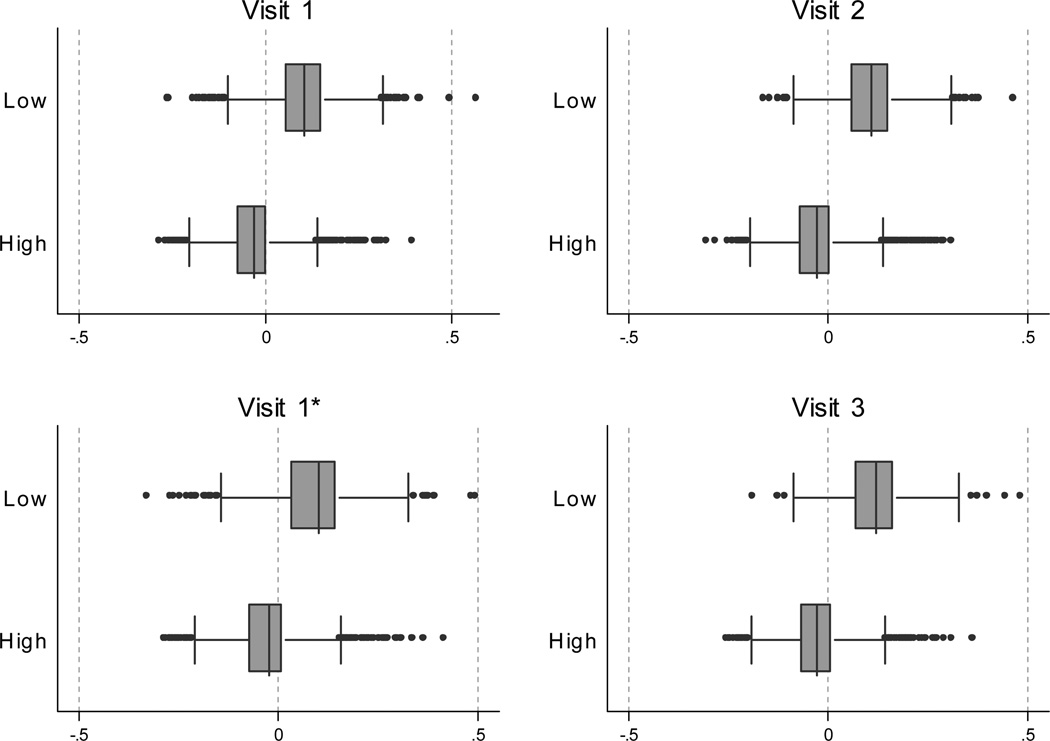
Figure 4 presents group-level DIF impact for education at each time point based on longitudinal DIF findings. Group-level DIF impact for education in the cross-sectional DIF analyses of the completers dataset was depicted in Figure 2, which is characterized by inconsistent DIF effects at different time points, though the same individuals were included in each analysis. In contrast, as shown in Figure 4, when we evaluated grouplevel DIF impact at each time point using longitudinal analyses for the “entire” dataset, a consistent picture of DIF related to education emerges, such that accounting for DIF attenuates differences in scores between individuals with high and those with low education. Accounting for longitudinal DIF smoothed out some of the time point-to-time point variability that characterized cross-sectional DIF findings.
Figure 4.
Group-level DIF impact for education using estimates from longitudinal analysis. The plots are presented in order: Visit 1 (baseline for “entire” dataset using estimates from longitudinal analyses), Visit 2 (2nd visit for “entire” dataset using estimates from longitudinal analyses), Visit 1* (baseline for “entire” dataset using estimates from cross-sectional analyses) and Visit 3 (3rd visit for “entire” dataset using estimates from longitudinal analyses).
Longitudinal group-level DIF impact for education
We developed a way to address longitudinal group-level DIF impact. As a first step, we normalized scores at baseline to have a mean of 0 and a SD of 1. We applied these transformations at the follow-up visits so all scores were on the same metric. We were interested in the effects of education on the intercept and slope terms. We performed mixed effects regressions for naïve scores ignoring DIF and scores accounting for all sources of DIF, including terms for education and the interaction of education and time.
Results from the mixed-effects models are presented in Table 6. The most noticeable difference between the two models is in the difference in cognitive ability at baseline associated with high vs. low education subgroups. In the model with scores that ignore DIF, predicted scores at baseline are 0.47 for the better-educated group and −0.88 for the less-well educated group, a difference of 1.35. In the model with scores that account for DIF, predicted scores at baseline are 0.44 for the better-educated group and −0.74 for the less well-educated group, a difference of 1.18. These results suggest that 14 % of the observed difference in model-predicted intercepts of cognitive functioning is due entirely to DIF.
Table 6.
Effect of Education on the Rate of Cognitive Decline
| Coefficient | S.E. | p-value | C.I. | |
|---|---|---|---|---|
| Coefficients for models using IRT scores that ignore DIF: | ||||
| Constant | 0.47 | 0.02 | < 0.001 | (0.44, 0.50) |
| Time | −0.26 | 0.01 | < 0.001 | (−0.28, −0.24) |
| Group | −0.88 | 0.04 | < 0.001 | (−0.95, −0.80) |
| Time×Group | −0.03 | 0.02 | 0.24 | (−0.07, 0.02) |
| Coefficients for models using overall DIF adjusted IRT scores: | ||||
| Constant | 0.44 | 0.02 | < 0.001 | (0.41, 0.48) |
| Time | −0.27 | 0.01 | < 0.001 | (−0.29, −0.25) |
| Group | −0.74 | 0.04 | < 0.001 | (−0.81, −0.66) |
| Time×Group | −0.03 | 0.02 | 0.20 | (−0.08, 0.02) |
Discussion
We analyzed longitudinal data from the Canadian Study of Health and Aging for DIF related to sex, birth cohort and education. Analyses of the “completers” dataset enabled us to treat the data as three independent opportunities to evaluate cross-sectional DIF. We found considerable differences in which items were identified with DIF, though the sample size and distribution of demographic covariates were fixed. We also evaluated baseline data from the “entire” dataset that included people who subsequently died or dropped out of the study, and again found differences in items identified with DIF compared to the baseline of the “completers” dataset.
The baseline data from the “entire” dataset was roughly 3 times larger than the “completers” subset of the data. With large sample sizes even trivial differences across groups may be statistically significant. We thus reduced the sensitivity of our DIF detection criterion to ensure adequate calibration of the 3MS and found cross-sectional results of the smaller dataset of those with complete data and the larger “entire” dataset were different from each other.
We thus set out to develop an approach to using longitudinal data to evaluate scales for DIF. We extended our cross-sectional OLR/IRT hybrid framework. With the longitudinal dataset, we were able to estimate whether items had DIF when accounting for within-person correlation across time. We were able to account for DIF, and use scores that accounted for DIF to determine whether demographic characteristics were associated with cognition at the intercept and with the rate of cognitive decline. Rates of cognitive decline were negligibly different when accounting for or ignoring DIF. However, modelbased intercepts were quite a bit different when ignoring and accounting for DIF, indicating that some of the differences in scores across education groups are due to DIF.
We had to address several challenges to analyze longitudinal data for DIF. The first challenge we faced was in estimating ability levels using the longitudinal data. We chose to use the baseline dataset for calibration and then to use item parameters derived from the baseline data to generate scores for the other time points. A more elegant solution would have been to use a hierarchical IRT model that places the measurement part (the item parameters and ability estimates) on one level in the hierarchy, and trajectories of ability over time on another level in the hierarchy. Hierarchical IRT models have been developed in the past several years (Fox & Glas, 2001) and more recently have been extended to the case of longitudinal data (Glas, et al., 2009; te Marvelde, et al., 2006). While these are important and exciting developments, they require specialized software and expertise. It will be interesting to develop a framework for DIF detection that incorporates these hierarchical models and to compare them to the approach illustrated here. The two stage approach taken by our algorithm implicitly ignores measurement error by using the scores and ignoring their standard errors. Further refinements to our algorithm could include incorporating the standard errors, following approaches used in the plausible values framework (Mislevy, Beaton, Kaplan & Sheehan, 1992). The structural equation modeling framework and other single step procedures elegantly propagate measurement error through to other stages of the model, while two-stage procedures such as ours would need to incorporate specific attention to measurement error to ensure that it was not driving results. Such a structural equation modeling approach would also need to account for correlations of item residuals across time points.
The second challenge we faced was accounting for the within person covariation of ability estimates across time. Longitudinal extensions of ordinal logistic regression have been less well developed than extensions appropriate for other forms of regression (Feldman, Masyn, & Conger, 2009). We chose a technique that was easily implemented in Stata, which was to cluster on person within Stata's ordinal logistic regression framework. Another choice would have been to use structural equation modeling approaches to these sorts of data (Feldman, et al., 2009), though that approach would require additional modification to account for categorical data (Preacher, Zyphur, & Zhang, 2010). The clustering approach we adopted here is based on specific assumptions related to the equally spaced intervals and limited numbers of time points.
The third challenge we faced was the “problem” of having increased power to identify negligible differences as statistically significant DIF. In previous studies we have found that altering the sensitivity of the threshold used to identify DIF may change the number of items identified with DIF, but tends to have limited effect on DIF impact (Crane, Gibbons, et al., 2007). This somewhat counter-intuitive finding can be explained as follows. With a very stringent DIF detection threshold, only items with the most egregious amounts of DIF will be identified; these items will have the greatest impact on people's scores when we account for DIF. With a more lenient threshold, items with the most egregious amounts of DIF will still be identified, but so too will be items with smaller amounts of DIF. These items with smaller amounts of DIF will not have much impact on people's scores. The need to have sufficient items to anchor the scale when accounting for DIF led us to modify the sensitivity of our DIF detection thresholds quite a bit, especially for DIF related to education, which necessitated a p-value threshold of 5×10−8. When we incorporated longitudinal data, our power to detect DIF increased. In this situation, miniscule and irrelevant differences are increasingly likely to be identified as statistically different from 0. This is not a problem in our algorithm when detecting DIF. However, when accounting for DIF, we use demographic group-specific item parameters, and the scale is anchored by items deemed not to have DIF. Had we used nominal levels for tests of statistical significance to identify items as having DIF, for education in particular, all of the items would have been declared to have DIF, resulting in an unanchored scale when we generated scores that accounted for DIF. The longitudinal DIF detection framework magnified the relevance of this challenge, as we ended up with a DIF threshold of 5×10−16 for education.
We have developed a framework for thinking about cross-sectional DIF impact at the level of individuals and groups. In the present paper, we extended that framework to the case of longitudinal data. Here, we found that DIF had moderate effects on differences in cognitive functioning across groups defined by educational attainment.
In summary, we have extended our OLR/IRT framework to address DIF using longitudinal data, and discussed several of the challenges of these sorts of analyses. Future efforts will further extend this line of research.
Acknowledgments
Drs. Mukherjee, Gibbons, and Crane were supported by R01 AG 029672 (P Crane, PI) and by R01 AG 010220 (D Mungas, PI) from the National Institute on Aging. Dr. Gibbons was also supported by P50 AG 05136 (M Raskind, PI) from the National Institute on Aging.
References
- Baker FB, Kim S-H. Item response theory: parameter estimation techniques. Second edition, revised and expanded ed. NY: Marcel Dekker; 2004. [Google Scholar]
- Cai L. A Two-tier Full-information Item Factor Analysis Model with Applications. Psychometrika. 2010 (in press) [Google Scholar]
- Camilli G, Shepard LA. Methods for identifying biased test items. Thousand Oaks: Sage; 1994. [Google Scholar]
- Canadian study of health and aging working group. Canadian study of health and aging: study methods and prevalence of dementia. Journal of the Canadian Medical Association. 1994;150(6):899–913. [PMC free article] [PubMed] [Google Scholar]
- Crane PK, Cetin K, Cook KF, Johnson K, Deyo R, Amtmann D. Differential item functioning impact in a modified version of the Roland-Morris Disability Questionnaire. Qual Life Res. 2007;16(6):981–990. doi: 10.1007/s11136-007-9200-x. [DOI] [PubMed] [Google Scholar]
- Crane PK, Gibbons LE, Jolley L, van Belle G. Differential item functioning analysis with ordinal logistic regression techniques. DIFdetect and difwithpar. Med Care. 2006;44:S115–S123. doi: 10.1097/01.mlr.0000245183.28384.ed. (11 Suppl 3) [DOI] [PubMed] [Google Scholar]
- Crane PK, Gibbons LE, Jolley L, van Belle G, Selleri R, Dalmonte E, De Ronchi D. Differential item functioning related to education and age in the Italian version of the Mini-mental State Examination. Int Psychogeriatr. 2006;18(3):505–515. doi: 10.1017/S1041610205002978. [DOI] [PubMed] [Google Scholar]
- Crane PK, Gibbons LE, Ocepek-Welikson K, Cook K, Cella D, Narasimhalu K, Teresi JA. A comparison of three sets of criteria for determining the presence of differential item functioning using ordinal logistic regression. Qual Life Res. 2007;16(Suppl 1):69–84. doi: 10.1007/s11136-007-9185-5. [DOI] [PubMed] [Google Scholar]
- Crane PK, Narasimhalu K, Gibbons LE, Mungas DM, Haneuse S, Larson EB, van Belle G. Item response theory facilitated cocalibrating cognitive tests and reduced bias in estimated rates of decline. J Clin Epidemiol. 2008;61(10):1018–1027. doi: 10.1016/j.jclinepi.2007.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane PK, Narasimhalu K, Gibbons LE, Pedraza O, Mehta KM, Tang Y, Mungas DM. Composite scores for executive function items: demographic heterogeneity and relationships with quantitative magnetic resonance imaging. J Int Neuropsychol Soc. 2008;14(5):746–759. doi: 10.1017/S1355617708081162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman BJ, Masyn KE, Conger R. New approaches to studying problem behaviors: a comparison of methods for modeling longitudinal, categorical adolescent drinking data. Developmental Psychology. 2009;45(3):652–676. doi: 10.1037/a0014851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. "Mini-mental state". A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12(3):189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Fox J-P, Glas CAW. Bayesian estimation of a multilevel IRT model using Gibbs sampling. Psychometrika. 2001;66(2):271–288. [Google Scholar]
- Glas CA, Geerlings H, van de Laar MA, Taal E. Analysis of longitudinal randomized clinical trials using item response models. Contemp Clin Trials. 2009;30(2):158–170. doi: 10.1016/j.cct.2008.12.003. [DOI] [PubMed] [Google Scholar]
- Grimm KJ, Pianta RC, Konold T. Longitudinal multitrait-multimethod models for developmental research. Multivariate Behavioral Research. 2009;44:233–258. doi: 10.1080/00273170902794230. [DOI] [PubMed] [Google Scholar]
- Hays RD, Farivar SS, Liu H. Approaches and recommendations for estimating minimally important differences for health-related quality of life measures. Copd. 2005;2(1):63–67. doi: 10.1081/copd-200050663. [DOI] [PubMed] [Google Scholar]
- Holland PW, Wainer H. Differential item functioning. Hillsdale, N.J.: Erlbaum; 1993. [Google Scholar]
- Langer MM. A reexamination of Lords Wald test for differential item functioning using item response theory and modern error estimation. Doctoral Dissertation, Department of Psychology, University of North Carolina at Chapel Hill; [Google Scholar]
- Liu LC. A model for incomplete longitudinal multivariate ordinal data. Stat Med. 2008;27(30):6299–6309. doi: 10.1002/sim.3422. [DOI] [PubMed] [Google Scholar]
- McDonald RP. A basis for multidimensional item response theory. 2000; 24:24-114. Applied Psychological Measurement. 2000;24:24–114. [Google Scholar]
- McDowell I, Aylesworth R, Stewart M, Hill G, Lindsay J. Study sampling in the Canadian Study of Health and Aging. Int Psychogeriatr. 2001;13(Supp 1):19–28. doi: 10.1017/s1041610202007950. [DOI] [PubMed] [Google Scholar]
- McDowell I, Kristjansson E, Hill GB. The Mini-Mental State Exam (MMSE) and Modified Mini-Mental State Exam (3MS) compared. Journal of Clinical Epidemiology. 1997;50:377–383. doi: 10.1016/s0895-4356(97)00060-7. [DOI] [PubMed] [Google Scholar]
- Meredith W, Teresi JA. An essay on measurement and factorial invariance. Med Care. 2006;44:S69–S77. doi: 10.1097/01.mlr.0000245438.73837.89. 11 Suppl 3. [DOI] [PubMed] [Google Scholar]
- Millsap RE, Everson HT. Methodology review: statistical approaches for assessing measurement bias. Applied Psychological Measurement. 1993;17(4):297–334. [Google Scholar]
- Mungas D, Reed BR. Application of item response theory for development of a global functioning measure of dementia with linear measurement properties. Stat Med. 2000;19(11–12):1631–1644. doi: 10.1002/(sici)1097-0258(20000615/30)19:11/12<1631::aid-sim451>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- Muthen BO. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika. 1984;49:115–132. [Google Scholar]
- Pentz MA, Chou CP. Measurement Invariance in Longitudinal Clinical Research Assuming Change from Development and Intervention. Journal of Consulting and Clinical Psychology. 1994;62(3):450–462. doi: 10.1037//0022-006x.62.3.450. [DOI] [PubMed] [Google Scholar]
- Pitts SC, West SG, Tein J-Y. Longitudinal Measurement Models in Evaluation Research: Examining Stability and Change. Evaluation and Program Planning. 1996;19(4):333–350. [Google Scholar]
- Preacher KJ, Zyphur MJ, Zhang Z. A general multilevel SEM framework for assessing multilevel mediation. Psychological Methods. 2010;15(3):209–233. doi: 10.1037/a0020141. [DOI] [PubMed] [Google Scholar]
- Raykov T. Behavioral Scale Reliability and Measurement Invariance Evaluation Using Latent Variable Modeling. Behavior Therapy. 2004;35(2):299–331. [Google Scholar]
- Revicki D, Hays RD, Cella D, Sloan J. Recommended methods for determining responsiveness and minimally important differences for patient-reported outcomes. J Clin Epidemiol. 2008;61(2):102–109. doi: 10.1016/j.jclinepi.2007.03.012. [DOI] [PubMed] [Google Scholar]
- Stocking ML, Lord FM. Developing a Common Metric in Item Response Theory. Applied Psychological Measurement. 1983;7:201–210. [Google Scholar]
- te Marvelde JM, Glas CAW, van Landeghem G, van Damme J. Application of multidimensional IRT models to longitudinal data. Application of multidimensional IRT models to longitudinal data. 2006;66:5–34. [Google Scholar]
- Teng EL, Chui HC. The Modified Mini-Mental State (3MS) examination. J Clin Psychiatry. 1987;48(8):314–318. [PubMed] [Google Scholar]
- Teresi JA. Overview of quantitative measurement methods. Equivalence, invariance, and differential item functioning in health applications. Med Care. 2006;44:S39–S49. doi: 10.1097/01.mlr.0000245452.48613.45. (11 Suppl 3) [DOI] [PubMed] [Google Scholar]
- Teresi JA, Kleinman M, Ocepek-Welikson K. Modern psychometric methods for detection of differential item functioning: application to cognitive assessment measures. Stat Med. 2000;19(11–12):1651–1683. doi: 10.1002/(sici)1097-0258(20000615/30)19:11/12<1651::aid-sim453>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Tisak J, Meredith W. Exploratory longitudinal factor analysis in multiple populations. Psychometrika. 1989;54:261–281. [Google Scholar]
- Tukey JW. Exploratory Data Analysis. Reading, MA: Addison-Wesley; 1977. [Google Scholar]
- Tuokko H, Kristjansson E, Miller J. Neuropsychological detection of dementia: an overview of the neuropsychological component of the Canadian Study of Health and Aging. J Clin Exp Neuropsychol. 1995;17(3):352–373. doi: 10.1080/01688639508405129. [DOI] [PubMed] [Google Scholar]