Individual Differences in Learning and Transfer: Stable Tendencies for Learning Exemplars versus Abstracting Rules

Abstract

We hypothesize that during training some learners may focus on acquiring the particular exemplars and responses associated with the exemplars (termed exemplar learners), whereas other learners attempt to abstract underlying regularities reflected in the particular exemplars linked to an appropriate response (termed rule learners). Supporting this distinction, after training (on a function-learning task), participants either displayed an extrapolation profile reflecting acquisition of the trained cue-criterion associations (exemplar learners) or abstraction of the function rule (rule learners; Studies 1a and 1b). Further, working memory capacity (measured by Ospan) was associated with the tendency to rely on rule versus exemplar processes. Studies 1c and 2 examined the persistence of these learning tendencies on several categorization tasks. Study 1c showed that rule learners were more likely than exemplar learners (indexed a priori by extrapolation profiles) to resist using idiosyncratic features (exemplar similarity) in generalization (transfer) of the trained category. Study 2 showed that the rule learners but not the exemplar learners performed well on a novel categorization task (transfer) after training on an abstract coherent category. These patterns suggest that in complex conceptual tasks, (a) individuals tend to either focus on exemplars during learning or on extracting some abstraction of the concept, (b) this tendency might be a relatively stable characteristic of the individual, and (c) transfer patterns are determined by that tendency.

In the concept learning and problem solving literatures, individual differences, though implicitly assumed, have not received extensive empirical or theoretical attention. In the concept-problem literature, a few researchers have attempted to identify qualitative differences across individuals in what is learned during training. In one seminal study, Medin, Altom, and Murphy (1984) trained participants to learn to categorize instances from an ill-defined category. Based on the training performances and classification of new instances, Medin et al. suggested that some learners had abstracted a prototype during training, whereas others had learned particular exemplar—category associations to represent the ill-defined category. In a more complicated category learning paradigm, Erickson (2008) required subjects to learn to classify stimuli into four categories, with two categories determined by a single dimension and two categories determined by two dimensions. Subjects’ responses indicated that individuals differed in what they had learned, with one group appearing to acquire a single category bound (one overarching representation) to map the four categories, whereas another group had partitioned the space into two bounds (one for one pair of categories and one for the other pair of categories).

In the domain of function concepts—continuous inputs mapped to continuous outputs through an underlying functional relation, DeLosh, Busemeyer, and McDaniel (1997) trained participants on a range of input—output pairings sampled from continuous input and output scales. After training, extrapolation performance was assessed by requiring participants to predict the output values that would be associated with inputs sampled from outside the training range. DeLosh et al. (1997) noted that for a quadratic function, individuals showed dramatically different extrapolation profiles. Some learners predicted outputs that quite closely followed the function from which the training stimuli were derived (see Figure 1, top panel depicting the Delosh et al. finding), thereby suggesting that these learners had abstracted the underlying function rule (in line with this interpretation a formal rule-learning model showed similar extrapolation performance). By contrast, several learners predicted outputs that were similar in value to outputs associated with inputs from the extremes of the training range (Figure 1, bottom panel shows these results). Apparently, these learners had represented their training experience as a set of exemplars reflecting the input—output training instances (supporting this claim, an exemplar-based associative model showed similar extrapolation performance; see Figure 10 in DeLosh et al.).

Figure 1.

Top panel: Two learners demonstrating extrapolation that closely follows the function (Figure 4 reprinted from DeLosh et al., 1997). Bottom panel: Two learners with extrapolation profiles in which their outputs were similar in value to outputs associated with inputs from the training stimuli (Figure 6 reprinted from DeLosh et al., 1997).

DeLosh et al. (1997) speculated that the individual differences just outlined might be accommodated by assuming that during training all participants had focused on learning the individual training instances (exemplars) but had differed in whether they applied a post-hoc extrapolation rule during testing. In this article we propose instead that one important difference across individuals may be in the qualitative characteristics of what they learn from training experiences. In Studies 1a and 1b we describe a method to assess this individual difference in learning tendency, and we explore whether several classic individual difference measures of cognitive ability (Ravens Advanced Progressive Matrices, working memory capacity) correspond to learners’ tendencies toward rule or exemplar learning. In Studies 1c and 2 we then report results that suggest that this individual difference is relatively stable and predicts performance across other concept learning tasks.

Exemplar Learners versus Rule Learners

Our suggestion is that two competing fundamental approaches to concept learning may each characterize particular sub-sets of learners. Rather than assume that all concept learners engage an exemplar-based process (e.g., Kruschke, 1992; Medin & Schaffer, 1978; Nosofsky & Kruschke, 1992) or that all concept learners abstract underlying rules (e.g., Bourne, 1974; Koh & Meyer, 1991; Little, Nosofsky, & Denton, 2011; Nosofsky, Palmeri, & McKinley, 1994) or schemata (Posner & Keele, 1968), we suggest that the prominence of each process differs across individuals. Specifically, drawing on preliminary findings from different kinds of concept problems (ill-defined concepts, function concepts), we suggest, that unless the task strongly favors a particular structural solution (e.g., Ashby, Ell, & Waldron, 2003), during training some learners focus on acquiring the particular exemplars and the appropriate response associated with those exemplars (i.e., a classification response, Medin et al., 1984; a response consisting of a particular value, DeLosh et al., 1997). Other learners attempt to abstract underlying regularities reflected in the particular exemplars that are linked to an appropriate response (i.e., a protoptye in Medin et al; a function rule in DeLosh et al.).

Our approach bears some similarity to recently proposed hybrid models that assume that both an exemplar-based module and a rule-learning module operate to mediate learning (Anderson & Betz, 2001; Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Bott & Heit, 2004; Erickson & Kruschke, 1998). In these models, one module or the other may predominate for learning the appropriate responses to particular stimuli or to particular concept problems. However, as the models currently stand, the contribution of each particular module is determined by the stimuli and the structure of the conceptual tasks that are encountered (see Erickson, 2008, for further discussion, and Juslin, Olsson, & Olsson, 2003, for related findings). The formulation that we develop in this paper is that individual differences, exhibited across different stimuli and problems, also play a key role in the degree to which particular learning processes are evidenced in complex conceptual learning. It is important to note that we are not claiming that extant hybrid models are necessarily incompatible with the findings that we report. We are attempting to provide evidence that individuals (adults; cf. Minda, Desroches, & Church, 2008, for work with children) differ in the degree to which they rely on exemplar learning versus abstraction, an assumption that is not embedded in the current hybrid models (cf. Erickson, 2008).

Our approach also shares correspondences with the classic distinction that Katona (1940) proposed between two kinds of learning: “memorization” of connections established by repetition of examples, and “apprehension of relations” through encounter with examples. One of Katona’s significant insights was that both kinds of learning can be evidenced with the same materials. However, Katona focused on how these two kinds of learning were forged by presentation of the target materials and the instruction that accompanied the materials. Our notion is that even under identical presentation of target materials and instructions, learners will diverge, with some reflecting an orientation toward memorizing particular examples and others reflecting an orientation toward understanding underlying relations.

Further, our second key assumption is that the individual’s tendency to either focus on exemplars during learning versus focusing on extracting some abstraction of the concept or problem solution might be a relatively stable characteristic of the individual, at least for the relatively challenging concept tasks examined in the present study. To date, the few findings noted above that have identified individual differences in exemplar learning versus abstraction have been restricted to investigations within a single conceptual task. From both a theoretical and an empirical perspective, little if any work is available in the experimental literature that addresses whether the individuals who display exemplar-based learning (or rule learning) in one context will be the same individuals who display reliance on exemplars (or rule learning) in a different concept problem domain. The present studies are directed at providing the first evaluation of this novel idea. Following directly from the assumption that a learner’s tendency toward exemplar versus rule-learning is fairly stable, we anticipate that identifying the individuals’ tendencies (e.g., in one conceptual domain) will provide the basis for predicting diverging patterns of transfer across individuals in very different conceptual learning domains (Studies 1c and 2).

Study 1a

To reveal exemplar versus rule-learning tendencies, we used a function-learning paradigm developed by DeLosh et al. (1997). Participants were given multiple training blocks; in each training block continuous cue values were paired with continuous criterion values and the cue-criterion pairings were repeated across blocks. The values were generated from a bi-linear function (a “V”). Participants attempted to learn to produce the appropriate criterion value of each presented cue value (with feedback provided). Critically, following training participants were given an extrapolation task in which cue values outside the training range were presented and learners had to predict its associated output (criterion).

In this initial study, we attempted to demonstrate qualitative differences across learners based on their extrapolation performances, differences that would inform what participants learned during training trials. We assumed that learners who displayed relatively flat extrapolation after having met a strict learning criterion (e.g., see bottom panel of Figure 1) could be considered to have primarily learned the individual cue-criterion pairings for the 20 training points (termed exemplar learners). This assumption is based on simulations showing that a basic exemplar model with no additional extrapolation component generates similar extrapolation profiles (DeLosh et al., 1997; see also Busemeyer, Byun, DeLosh, & McDaniel, 1997). In contrast, learners who generally extrapolated along the slopes of the bi-linear function (the “V”) could be considered to have abstracted the relations among the training points (termed rule learners).

In a previous function-learning study that modeled the extent to which learners relied on exemplar processes (an exemplar module) versus rule-learning processes (a rule module), all learners appeared to rely on exemplar processes initially but by the end of training all were evidencing rule learning (i.e., extrapolation paralleled the trained cyclical function; Bott & Heit, 2004). In that study, however, learning blocks were interleaved with transfer blocks, and so the task arguably demanded attention to underlying function topography. In the present task, all training was completed before extrapolation was tested, thereby allowing learning based on either exemplars or abstraction of the function rule to promote successful performance (during training when feedback was provided). In this case, based on preliminary analyses of individual differences in a similar paradigm (DeLosh et al., 1997), we expected to find salient differences among learners in their extrapolation patterns.

We then explored whether these implied qualitative differences in the tendency to rely on learning the trained exemplars (cue-criterion values) versus abstracting the relation among exemplars (the bi-linear rule) were associated with other established individual differences measures that might reflect or support this distinction. Of primary interest were individual differences in two performance-based cognitive assessments: fluid intelligence as measured by Raven’s Advanced Progressive Matrices (RAPM; Raven, Raven, & Court, 1998) and working memory capacity (WMC), measured with the operation span (Ospan; Turner & Engle, 1989). The RAPM requires individuals to complete a visual pattern that reflects a progression of instances that illustrate a rule or set of relations among the instances. It is accepted as an excellent measure of abstract reasoning (or fluid intelligence)—the ability to construct representations that are only loosely tied to the specific perceptual inputs and afford a high degree of generalization (Carpenter, Just, & Shell, 1990). Accordingly, one clear hypothesis is that RAPM performance will be correlated with whether participants in the function-learning task tend to display rule learning (as indicated in extrapolation) or tend to rely on learning the individual training points.

WMC is typically regarded as reflecting the number of representations that can be maintained in awareness (e.g., see Fukuda, Vogel, Mayr, & Awh, 2010) and simultaneously being able to manipulate that information (Baddeley & Hitch, 1974; Conway et al., 2005). It seems possible that individuals who can readily consider more representations (i.e., learned training points in the present context) and control attention to consider possible relations among these representations are more likely to attempt to abstract the function rule. If so, then we should observe a significant correlation between WMC (as measured by Ospan) and the tendency for participants to display rule abstraction versus an exemplar focus in function learning.

Of secondary interest were several other individual difference measures: the Need for Cognition Scale (Cacioppo & Petty, 1982), the Kolb Learning Style Inventory (Kolb, 2007, free recall, and paired-associate learning. We explored whether these measures might be related to the tendency to display an exemplar-learning or rule-learning approach. Because correlations were not significant, we have reported the description of these measures and the results in Appendix A.

Method

Participants

Sixty-two introductory psychology students from Washington University in St. Louis participated in exchange for course credit. One participant did not complete the interpolation trials and extrapolation trials of the function learning task due to a technical error. Thirteen participants did not exhibit accurate learning of the cue-criterion values during training (mean absolute error between a participant’s predicted criterion and the actual criterion on the final training block ≥ 10) and were excluded from further analysis. The final, analyzable sample consisted of 48 participants. In addition, one participant did not attend Session 2 and thus had missing Ospan and RAPM data. A second participant had RAPM data excluded due to obvious lack of effort (0% accuracy and just over 2 minutes spent on the task).

Procedure

Participants were tested in two sessions, separated by approximately one week. During session 1, participants completed the function learning task, a free recall measure, and the Kolb Learning Style Inventory. In session 2, participants completed a concept learning task (reported in Study 1c for ease of exposition), a paired-associate learning task, an abbreviated version of the RAPM, the need for cognition scale, and the Ospan.

Session 1

Participants were given instructions on a monitor that asked them to pretend they were working for NASA, examining printouts of data collected on a newly discovered Martian organism in order to determine how much of a particular newly discovered element this organism excreted after absorbing a certain amount of another new element. Training was done on a bi-linear function (‘V’-shaped) function centered on 100 with an input range of 80 to 120. For input (cue) values less than 100, output (criterion) values were derived using the equation y = 229.2−2.197x; for inputs greater than 100, output values followed the equation y = 2.197x−210 (participant responses could only be whole numbers, so all output values were rounded to the nearest whole number). There was a total of 200 training trials presented in 10 blocks of 20, with the order of the input values randomized across blocks. Within a block, each odd value between 80 and 120 (i.e. 81, 83, 85 etc.) was presented as an input value.

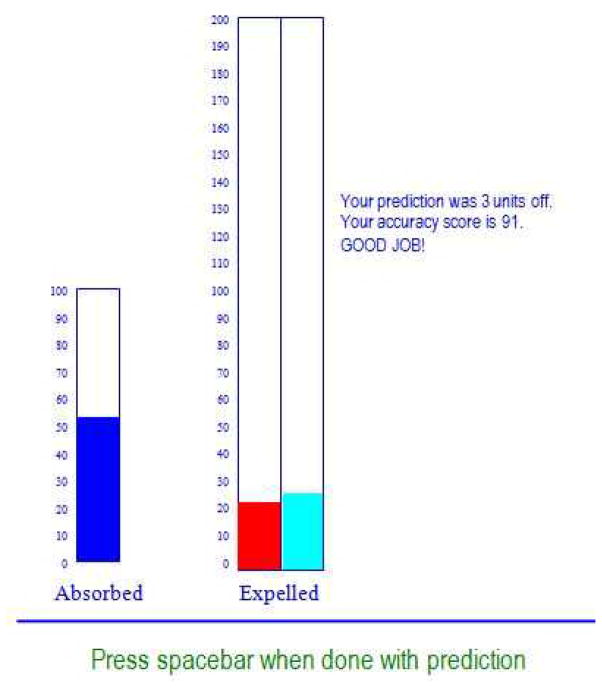
After participants read the cover story, they were presented with the training trials. On each training trial, participants were presented with three vertical bars (see Figure 2). Each bar had tick marks every 5 units ranging from 0 to 200, with value labels every 10 units. The leftmost bar gave the input value and participants made their output predictions by filling up the middle bar using the arrow keys (the up and down arrow keys moved the bar 5 units and the left and right arrow keys moved the bar 1 unit) and submitting their answer by pressing the space bar. They then received three forms of accuracy feedback. First, the rightmost bar was filled to the correct output value so they could visually compare their actual answer with the correct answer. Second, a message displayed the exact number of units of error in numerical form. Third, participants were given an accuracy score out of 100 that was equal to (100 − error squared). At the end of each block of 20 trials, participants were shown their mean error and mean accuracy score for the given block.

Figure 2.

An example of the display screen for the function learning task. The bar on the left is the given input value, the first bar above the label “expelled” is a participant’s output response, the second bar above “expelled” is the correct output, and the verbal feedback is given on the far right of the screen.

Upon completing the 10 training blocks, participants completed a transfer test consisting of 36 novel input values. These transfer trials consisted of 6 even input values within the training range (interpolation) followed by 30 odd values falling outside the training range (extrapolation). The extrapolation values ranged from 51 to 79 on the lower end, and from 121 to 149 on the upper end. Interpolation and extrapolation trials were in a random order and the same for all participants. Participants were not given feedback on their transfer trial responses.

After the function-learning task, participants completed a free recall task and the Kolb Learning Style Inventory (see Appendix A). Participants were then dismissed and scheduled for Session 2 approximately one week later.

Session 2

Participants first completed a concept-learning task developed by Regehr and Brooks (1993) and a paired-associates task (see Appendix A). The method and results of the concept-learning task will be described separately below in Study 1c. Participants then completed an abbreviated version of RAPM. On each trial, participants saw 8 boxes arranged in a 3 × 3 grid with the bottom right block missing. Each grid contained patterns proceeding from left to right and from top to bottom. The participants were to select, from a total of eight options, the box that completed both the horizontal and vertical patterns. In the current study, participants completed a short form version of the RAPM (Bors & Stokes, 1998) that includes a 12-item subset of the original RAPM (Set II). This short form has a correlation of .88 with the full RAPM and demonstrates test-retest reliability of .82, compared to .83 for the full version (Bors & Stokes, 1998).

Next participants completed the need for cognition scale (see Appendix A). After the need for cognition, participants completed the Ospan. The Ospan is a commonly used measure of working memory capacity with demonstrated test-retest reliabilities ranging from .67–.81 (Klein & Fiss, 1999). In this task, participants were presented with sets of 2–5 operation-word strings such as the following:

$$\text{Is}(8/4)-1=1?\text{Bear}$$

They were instructed to read the operation-word string, solve the math problem, and then read the word that follows the math, and they were instructed to do all of this aloud for the experimenter to hear. After the participant completed each string, the experimenter advanced the program by pressing ‘Spacebar’. After 2–5 strings, the set ended, and participants were asked to write down, in order, all of the words they had seen in the set. Participants completed 12 sets (3 of each possible string length). Thus, each participant saw 42 total operation-word strings. After completing the Ospan, participants were debriefed about both sessions and dismissed from the study

Results and Discussion

Function learning classifications

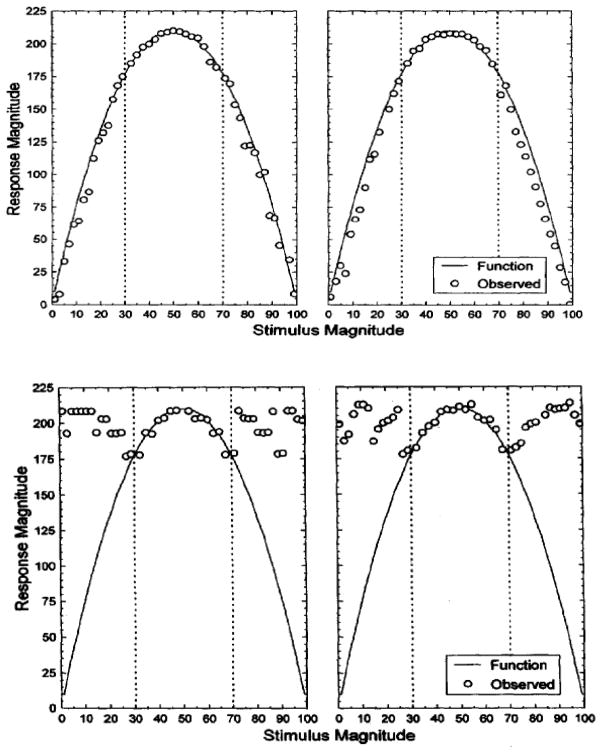
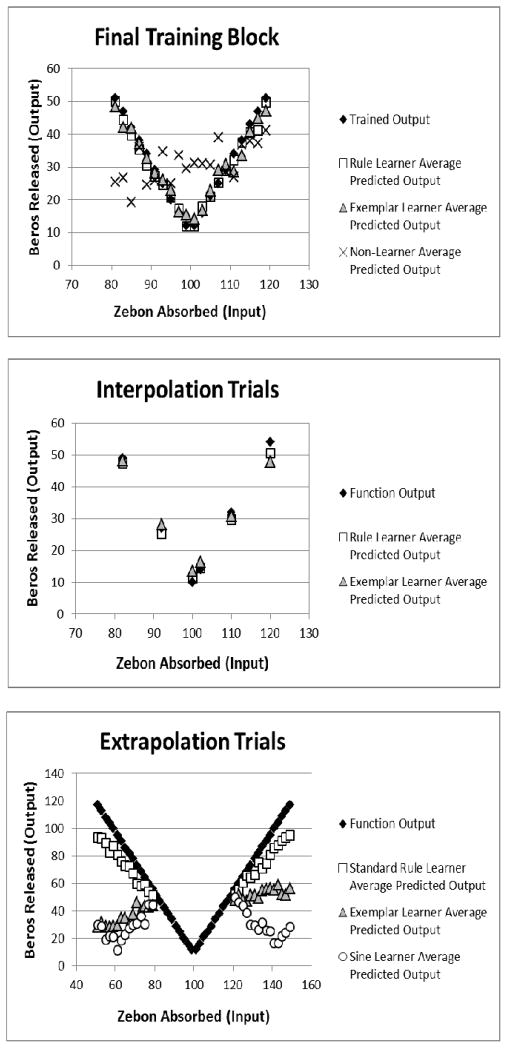
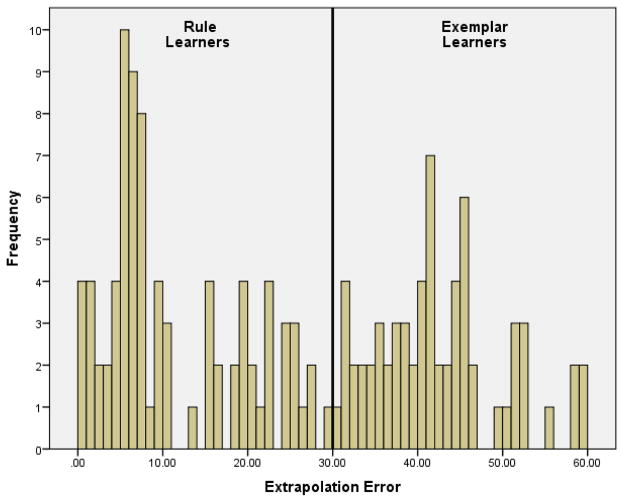
Mean absolute errors (MAE) of prediction were computed for the first and last training blocks, the interpolation trials, and the extrapolation trials for each participant. Participants with MAE ≥ 10 during the final training block were classified as non-learners (N = 13), as their response patterns deviated noticeably from the criterion values (see Figure 3, top panel); these participants were excluded from further analysis. Next, extrapolation performance was used to further classify the remaining individuals into rule learners and exemplar learners. Flat extrapolation, reflective of a simple exemplar model (see DeLosh et al., Figure 10, 1997), produces an MAE of 34.72. Thus, we assumed that participants with extrapolation MAE significantly lower than 34.72 were utilizing rule-based information during extrapolation. For each participant, the extrapolation MAE and a 95% confidence interval (CI) were computed, and participants whose entire CI fell below 34.72 were classified as rule learners; the remaining participants were classified as exemplar learners (with four exceptions as described below). The average predicted output for each extrapolation trial from these two groups can be seen in Figure 3 (bottom panel). The limited extrapolation shown by the exemplar group deviates little from the end of the training range, similar to what would be expected from an associative learning model. On the other hand, rule learners more closely approximated the function in a manner consistent with performance by a model that incorporates a rule learning mechanism (e.g., DeLosh et al., 1997; Kalish, Lewandowsky, & Kruschke, 2004).

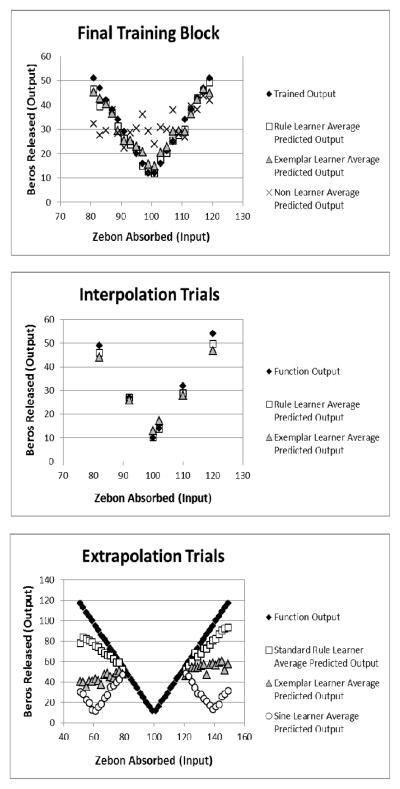
Figure 3.

Top panel: Average predictions on the last training block for the participants classified as rule learners, the participants classified as exemplar learners, and the participants classified as non-learners in Study 1a. Middle panel: Interpolation predictions averaged for rule learners and for exemplar learners. Lower panel: Extrapolation predictions averaged for rule learners and for exemplar learners.

In addition to the above mentioned extrapolation responses, the extrapolation of four participants appeared to be following a sine-like function rather than the V-shaped function that generated the stimuli. Based strictly on MAE calculated from the V shaped function, these participants fell under the exemplar learner classification, but because a sine function potentially could be abstracted from the training points we presented, we considered individuals with a sine-shaped extrapolation to be rule learners (see Bott & Heit, 2004). To confirm that these extrapolations reasonably followed a sine function, extrapolation error was calculated relative to a sine function (rather than the V-shaped function). All four sine learners had MAE < 10 and confidence intervals with an upper limit well below the 24.09 (the MAE reflective of flat extrapolation with respect to this sine function) and were thus considered rule learners (see Figure 3, bottom panel, for average extrapolation predictions from sine learners). Including sine learners, the sample consisted of 25 rule learners and 23 exemplar learners.

The patterns of extrapolation may not index qualitative differences in learning, but instead could reflect poorer learning of the trained cue-criterion values for the learners classified as exemplar learners (i.e., a quantitative difference). Rule learners (M = 3.06) did show significantly lower MAE than exemplar learners (M = 5.65) on the final training block, F(1,46) = 20.69, p < .001, η² = .31. However, an interpretation of the divergent extrapolation patterns based on quantitative differences in learning is disfavored by the fact that, though slightly disadvantaged relative to rule learners, exemplar learners generally displayed relatively high levels of accuracy on the last training block (see Figure 3, top panel). Further, note that these MAE values on the final training block are relatively small, compared to initial training blocks (described after the next paragraph).

Moreover, final block training MAE was strongly associated with extrapolation MAE for rule learners, r(23) = .74, 95% confidence interval (CI) [.48, .88], p < .001, but not exemplar learners, r(21) =.10, 95% CI [−.32, .50], p = .64, and these correlations significantly differed, z = 2.72, p < .01. This dissociation reinforces the conclusion that the differences in learning between participants identified as rule and exemplar learners were qualitative rather than quantitative. Specifically, for rule learners, final block MAE presumably represents, at least in part, how closely the learner’s rule-based representation developed during training matches the bi-linear function governing the training points. The more accurate this rule-based representation, the more accurate extrapolation performance should be (i.e., the extension of the rule to points outside the training range), as confirmed by the significant correlation just reported. In contrast, for exemplar learners, the final block MAE presumably represents the precision with which learners were able to acquire individual cue-criterion pairings during training. Because an exemplar representation alone does not support extrapolation (DeLosh et al., 1997; Busemeyer et al., 1997), the precision of this exemplar representation would have little bearing on accuracy for extrapolation trials (as evidence by a nonsignficant correlation).

Finally, the learners identified as exemplar learners did not appear to be simply slower learners (this issue is further addressed in Study 1b), as rule and exemplar learners exhibited similar learning rates across training. As expected, on the first block neither training group’s predicted values closely approximated the criterion values (mean MAE’s of 17.19 and 18.43 for rule learner and exemplar learners, respectively), but by the end of training both groups were able to generate predicted values that mirrored the actual criterion values. Statistical analyses of the mean MAEs on the first and last training blocks (2 × 2 mixed analysis of variance [ANOVA] with learner type as the between-subjects variable and trial block as the within-subjects variable), confirmed that there was significant improvement in prediction accuracy with training, F (1, 46) = 126.98, MSE = 34.14, p < .001, η² = .73 . Collapsed across blocks, prediction accuracy was nominally better for rule learners (M = 10.12) than exemplar learners (M = 12.04; F (1, 46) = 2.55, MSE = 34.55, p = .12). Importantly there was no hint that learner type interacted with training block (F < 1), suggesting that though rule learners held a small advantage throughout training (that for some reason emerged nominally even in the first block), the two groups improved (i.e., learned) equivalently from the first training block to the end of training. Thus rule learners and exemplar learners are not distinguished by quantitative differences in learning rate during the training phase¹.

Perhaps learners who displayed poor extrapolation (the “exemplar” learners) were learners who were uncertain or confused when confronted with new trials that were not seen during training. If so, then exemplar learners might be expected to be as impaired on interpolation as on extrapolation (both reflect new trials). Rule learners (M = 2.57) did exhibit significantly less error on interpolation trials than did exemplar learners (M = 5.80), F(1,46) = 20.95, p <. 001, η² = .31. However, as seen in Figure 3 (middle panel), interpolation for both groups nicely paralleled the function form. A 2 × 2 mixed ANOVA that included both interpolation and extrapolation test trials revealed that the group differences in prediction accuracy on transfer trials was significantly more substantial on extrapolation (Ms = 13.47 and 41.44, respectively, for rule and exemplar learners) than on interpolation, F(1, 46) = 115.81, MSE = 31.67, p < .001, η² = .20, for the interaction.

In sum, what is striking is that the profiles of the responses for trained and interpolation trials were quite similar for the rule and exemplar learners but diverged substantially on extrapolation trials. Moreover, this pattern across groups is consistent with formal modeling confirming that both exemplar and rule-models perform equally well on interpolation but not on extrapolation (DeLosh et al, 1997).

Correlations

We computed the correlations among the individual differences measures for all participants included in the above analyses. In computing the point-biserial correlations involving learner type, abstractors were assigned a value of 1 and exemplar learners a value of 2. It is important to first note that the correlation we obtained between the Ospan and Ravens Advanced Progressive Matrices assessments (r(44) = .29, 95% CI [.00, .54], p < .05) was nearly identical to the summary value of this correlation (found in previous studies) mentioned in a recent review (“around .30”; Wiley, Jarosz, Cusher, & Colflesh, 2011). Thus, these measures are reflecting expected associations.

A prominent finding was that Ospan (a measure of working memory capacity) was significantly correlated with learning tendency, r(45) = −.39, 95% CI [−.61, −.12], p < .01, such that learners with larger working memory capacity were most likely to display function learning performances (extrapolation) reflective of rule learning (learning the functional relation). In line with received interpretations of working memory (Conway et al., 2005; Engle, 2002), it may be that greater working memory capacity would allow the learner to maintain several cue-criterion trials in mind and concurrently compare critical information across these trials to abstract the function rule (e.g., to notice how the criterion values change with changes in the cue value). Another theoretical process that contributes to a rule-based approach to function learning is partitioning of the function into linear segments (Kalish et al., 2004; Lewandowsky, Kalish, & Ngang, 2002; McDaniel, Dimperio, Griego, & Busemeyer, 2009); such a process might be helpful for learning the current bi-linear function. Importantly, Erickson (2008) has suggested that monitoring training stimuli for particular partitions and switching from one partition to another to guide predictions requires executive control (which overlaps considerably with WMC; McCabe, Roediger, McDaniel, Balota, & Hambrick, 2010, and was also assessed with a working memory measure in Erickson, 2008). The idea here is that learners with higher working memory capacity would more easily be able to support the comparison or partitioning processes, or both, necessary for rule abstraction than those with lower working memory capacity and thus would be more inclined to attempt rule abstraction. Learners with lower working memory capacity could find it easier to focus on learning the individual cue-criterion pairs.

There was no significant association between performance on the RAPM and the differences in learning tendency revealed on the function-learning task (r (45) = −.16, 95% CI [−.43, .13]). One uninteresting interpretation of this finding is that the categorical nature of the learning tendency measure reduces the opportunity to reveal associations with other individual difference measures. This interpretation is disfavored in light of the significant correlation between learning tendency (in the function learning task) and Ospan. Another interpretation is that there is a modest association between the tendency to display rule-like extrapolation on the function learning task (implying abstraction during learning) and general fluid intelligence (as assessed by the RAPM), but that the sample size was not large enough to detect the observed association as statistically significant. Study 1b, reported next, was conducted in part to evaluate this interpretation.

Study 1b

The central conclusion from Study 1a is that some individuals (who we label rule leaners) were attempting to derive the relation among the training stimuli, whereas others (who we label exemplar learners) focused primarily on learning the individual stimuli. What remains unclear is the persistence of these differential foci across extended training. The idea being advanced in this article is that exemplar learners’ focus on learning the individual stimuli is a fundamental orientation that should persist across extensive training on the function-learning task. A different idea is that some individuals may first focus on learning well the individual training stimuli, and then having gained complete knowledge of these stimuli, proceed to extract underlying regularities across the range of training stimuli. According to this idea, many more (maybe all) learners eventually develop an understanding of the abstract relation among the stimuli (i.e., the function rule), with some learners focusing on learning the relation from early on and other learners focusing on learning the relation only after having learned well the training stimuli. This idea dovetails with a previous function-learning study that found that all learners focused on exemplar learning during initial training, but all then eventually demonstrated rule-like learning by the end of training (Bott & Heit, 2004). More generally, the category literature has documented that rule and exemplar strategies can shift as training progresses so that one strategy becomes modal with extensive training (e.g., Craig & Lewandowsky, 2012; Johansen & Palmeri, 2002; Smith & Minda, 1998).

In the present study, we implemented two training conditions to shed light on these competing ideas. In the moderate training condition, after participants first met the learning criterion on a particular training block (MAE < 10), they were given an additional six blocks of training. Previous unpublished studies in our lab had demonstrated that the mean number of training blocks needed to reach this criterion was approximately four, so this condition was designed to provide training that was similar in magnitude (10 blocks) to that in Study 1a. In the extended training condition, after first meeting criterion, participants received an additional 12 blocks of training. If the individual differences in focusing on exemplars versus extracting the underlying function rule remains stable even after extended training on the target stimuli, then the proportion of exemplar and rule learners (as evidenced on the extrapolation task) displayed in the extended training condition should parallel that found in the moderate training condition. Alternatively, if participants indentified as exemplar learners after moderate training (e.g., in Study 1a) are learners who would proceed to discern the underlying function rule with additional training, then the proportion of exemplar learners evidenced in the extended training condition should significantly decline relative to the proportion observed in the moderate training condition.

Another major objective of Study 1b was to further explore the finding of an association between WMC (as assessed by Ospan) and learning tendency. It may be that this association is eliminated when training is sufficient to allow substantial learning of the training stimuli (in the long training condition), thereby perhaps reducing working memory capacity needed to support rule abstraction. However, if we find that the orientation toward rule learning versus exemplar learning is stable across the different degrees of training implemented in this study, then we would expect to replicate the association between Ospan and learning tendency observed in Study 1a. We also continued to investigate whether RAPM might be associated with the learning tendencies identified in Study 1a. Finally, in addition to analyzing Study 1b results alone, we were able to combine the data from Studies 1a and 1b to achieve a more customary sample size of over 100 participants with which to conduct the correlational analyses with Ospan and RAPM.

Method

Participants

Seventy-six introductory psychology students from Washington University in St. Louis participated in exchange for course credit or pay ($5 per half hour of participation), with 40 randomly assigned to the moderate training condition and 36 randomly assigned to the extended training condition. Eleven participants (seven from the moderate condition and 4 from the extended condition) were excluded from analysis, five had previous exposure to the function learning task, four had shown obvious signs of disinterest/distraction (e.g., looking at phone during study), and two failed to follow instructions (they wrote down values during the function learning task). In addition, five participants (three from the moderate condition and two from the extended condition) did not meet the learning criterion (MAE < 10) after the first 10 training blocks, and their data were excluded from analysis. The final, analyzable sample consisted of 60 students (30 in each training condition). From this sample, three participants (one from the moderate training condition and two from the extended training condition) did not complete the Ospan due to technical problems.

Procedure

Participants were tested in a single session. For the function-learning task, the cover story, function, and training points were identical to that used in Study 1a. The procedure deviated from Study 1a in the following ways. First, and most critically, participants’ mean absolute error between their predicted criterion and the actual criterion on the twenty trials in each training block was monitored and used to determine the length of training. After the first training block on which a participant’s MAE was less than 10, 6 additional training blocks were administered for participants assigned to the moderate training condition and 12 additional training blocks were administered for the participants assigned to the extended training condition. If a participant did not meet the learning criterion (MAE < 10) after 10 training blocks, the participant was moved to the additional training blocks but was considered a non-learner regardless of their performance on these training blocks.

Second, participants received 5-minute breaks during which they were allowed to leave the testing room (but were instructed to not use phones or internet). All participants received a break after reaching criterion. The extended condition received a second break after completing the first six blocks of additional training. Third, participants completed a short distractor task (five minutes of Tetris) between the final block of training and the transfer phase. Finally, the transfer phase consisted of 60, rather than 36 trials. This phase contained 30 extrapolation trials (the same points as in Study 1a), 20 interpolation trials, and 10 repeat training trials.

After the function-learning task, participants completed the same short-form version of RAPM that was used in Study 1a. Finally, to facilitate participant testing we used the automated version of the Ospan (Unsworth, Heitz, Schrock, & Engle, 2005). This version of the Ospan is designed to run without oversight by the experimenter. In this version, the experimenter is not in the room during the Ospan, participants read the strings silently, and participants advance themselves through the task by clicking a mouse. During practice, the program computed each participant’s baseline equation-solving time, and participants were allotted a timeframe of their individual baseline + 2.5 SD to solve each equation during the test trials. If a participant failed to advance past an equation within this timeframe, the program counted the trial as an error and automatically advanced to the next trial. Further, in this version participants attempted to remember letters rather than numbers, and the to-be-remembered numbers appeared onscreen only after the equation had been solved. During response collection, participants were presented with a 3 × 4 array of boxes, each labeled with a letter. Participants attempted to click on the boxes in the order that the letters were presented in a given set. The letter sets ranged from 3–7, and participants were presented with three sets of each size. In all, this task included 75 equation-letter strings and had a maximum score of 75. Though this version differs from that used in Study 1a in several ways, Unsworth et al. (2005) demonstrated that the automated Ospan is correlated with both the standard Ospan (r =.45) and RAPM (r =.38) and that it loads highly (.68) onto a working memory factor also containing the original Ospan and reading span. Unsworth et al. also demonstrated test-retest reliability of .83 with this version.

Results and Discussion

Experimental group characteristics

Before turning to the effect of the training manipulation on function learning performance, it is important to establish that there were no pre-existing group differences that could have contributed to any differences in function learning performance (or lack thereof) between the moderate and extended training conditions. Table 1 shows the means and standard deviations for the moderate and extended groups on Ospan, RAPM, Block 1 MAE, Block 8 MAE, and the block at which the learning criterion (MAE < 10) was reached (Criterion block). Overall, there was no evidence that the two conditions had any pre-manipulation differences. The two conditions did not differ on Ospan (F(1,58) = 2.27, p >.10) or RAPM (F < 1). Also, the two groups did not significantly differ on any measures of function learning performance that occurred before the two groups diverged procedurally (F’s < 1 for Block 1 MAE, Block 8 MAE [the latest block that was experienced by all participants], and the block on which the learning criterion was met).

Table 1.

Pre-Manipulation Characteristics of the Moderate Training Condition and Extended Training Condition in Experiment 1b.

	Moderate Training		Extended Training
	M	SD	M	SD
WMC	56.83	17.56	48.77	20.22
RAPM	.61	.22	.65	.19
Block 1 MAE	17.92	4.71	18.05	4.63
Block 8 MAE	4.36	4.03	5.01	2.97
Criterion Block	4.07	2.48	4.03	2.04

Note. WMC, working memory capacity; RAPM, Ravens advanced progressive matrices short form; MAE, mean absolute error; Criterion Block is the earliest training block at which a participant’s MAE < 10.

Function Learning Performance

Rule learners (including sine learners), exemplar learners, and non-learners were classified in the same manner as in Study 1a. The sample contained 5 non-learners (3 from the moderate training condition; 2 from the extended training condition) who were excluded from subsequent analyses and 60 total learners (30 in each condition). In the moderate training condition there were 18 rule learners (4 sine) and 12 exemplar learners, and in the extended training condition there were 17 rule learners (3 sine) and 13 exemplar learners. Thus, extended training did not increase the proportion of learners who oriented toward abstracting the function rule (χ² (1, N = 60) = .07, p =.793).

Parallel to Study 1a, we conducted analyses on the MAE for the training and transfer trials across rule and exemplar learners. Training condition was also included as a factor in the analyses to examine whether training condition had any general effects or interactions with learning tendency that were not reflected in the classification proportions. Figure 4 provides the MAEs for training and transfer performances for rule and exemplar learners in each training condition.

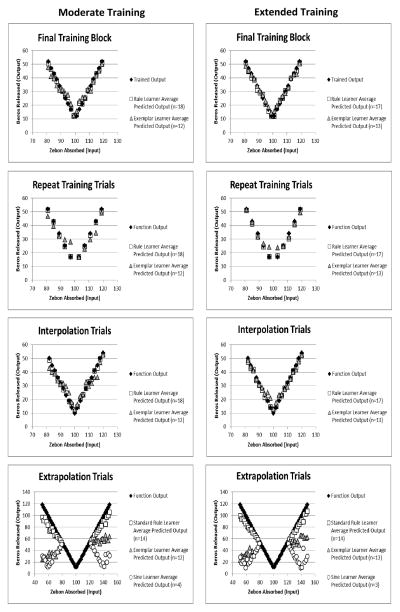
Figure 4.

Top left panel: Average predictions on the last training block for the participants classified as rule learners and participants classified as exemplar learners from the moderate training condition in Study 1b. Top right panel: Average predictions on the last training block for rule learners and for exemplar learners in the extended training condition. Second left panel: Repeat training point predictions for rule learners and for exemplar learners in the moderate training condition. Second right panel: Repeat training point predictions for rule learners and for exemplar learners in the extended training condition. Third left panel: Interpolation predictions averaged for rule learners and for exemplar learners in the moderate training condition. Third right panel: Interpolation predictions averaged for rule learners and for exemplar learners in the extended training condition. Bottom left panel: Extrapolation predictions averaged for rule learners and for exemplar learners in the moderate training condition. Bottom right panel: Extrapolation predictions averaged for rule learners and for exemplar learners in the extended training condition.

A 2 (learner type) × 2 (training condition) between-subjects ANOVA was conducted with final training block MAE as the dependent variable. Consistent with Study 1a, a main effect of learner type emerged, with rule learners (1.98) exhibiting lower MAE than exemplar learners (4.31), F (1,56) = 17.23, p < .001, η² = .23. Though less accurate than rule learners on the final training block, exemplar learners still displayed relatively high accuracy (see Figure 4, top panels). The main effect of training condition (F (1,56) = 1.17, p = .29) and the interaction (F (1,56) = 1.75, p = .19) were not significant, indicating that the additional six blocks of training in the extended training condition did not substantially increase final training-block accuracy. Also, as in Study 1a, final block MAE was highly correlated with extrapolation MAE for rule leaners (r (33) = .67, 95% CI [.44, .82], p <. 001) but not for exemplar learners (r (23) = −.06, 95% CI [−.44, .35], p = .78), and the difference between these correlations was significant (z = 3.16, p < .01). As discussed in Study 1a, these diverging correlations suggest qualitative differences in what was learned across rule and exemplar learners.

Also paralleling Study 1a, we examined the rate of learning. All participants (across the moderate and extended training conditions) received at least eight blocks of training, so the rate of learning was analyzed by comparing error rates for Block 1 and Block 8. A 2 (block: Block 1 vs. Block 8) × 2 (learner type) × 2 (training condition) ANOVA revealed a main effect of block, F (1,56) = 343.23, p < .001, η² = .85, with error lowering from 17.98 at Block 1 to 4.69 at Block 8. Rule learners MAE (10.13) displayed significantly lower MAE than exemplar learners MAE (13.03) in general, F (1,56) = 15.70, p < .001, η² = .22 (for the main effect), but the block x learner type interaction was not significant, F (1,56) = 2.30, p = .135, suggesting that rule and exemplar learners had similar rates of learning across the first eight training blocks. None of the effects involving training condition was significant (all F’s < 1).

As in Study 1a, the interpolation trials were also analyzed. A 2 (learner type) × 2 (training condition) ANOVA showed a main effect of learner type, with lower error rates among rule learners (2.24) than among exemplar learners (5.18), F(1,56) = 36.92, p < .001, η² = .39. The main effect of training condition and the interaction did not approach significance. As in Study 1a, although the rule learners demonstrated an advantage in interpolation, exemplar learners’ interpolation responses followed the function relatively closely (see Figure 4, third panels from the top). Tested training trials showed a pattern similar to interpolation. A 2 (learner type) × 2 (training condition) ANOVA revealed a lower error rate on tested training trials among rule learners (M = 1.64) than among exemplar learners (M = 5.36), F(1,56) = 39.36, p < .001, η² = .40, for the main effect, mimicking performance on the last block of training. Training condition had no main or interactive effects on tested training-trial performance. A 2 (learner type) × 2 (training condition) × 3 (test trial type: training points, interpolation, extrapolation) ANOVA revealed a significant learner type x trial type interaction, F(2,112) = 229.70, MSE = 18.23, p < .001, η² = .29, driven by a pattern in which advantages for rule learners on tested training and interpolation trials were quite minimal relative to divergent MAE’s found in extrapolation (8.83 vs. 41.51 for rule and exemplar learners, respectively).

Overall, the patterns of function learning data from Study 1b replicated those from Study 1a. Rule and exemplar learners were characterized by strikingly different extrapolation profiles even though they displayed relatively similar training and interpolation performances. And again, final training block performance was predictive of extrapolation for rule but not exemplar learners, consistent with the conclusion that the two groups of learners had adopted qualitatively different approaches to the learning task. For present purposes, a critical finding was that the moderate training condition and the extended training condition showed equivalent outcomes in terms of differentiation between rule and exemplar learners and performances displayed by these two learner classifications (as highlighted by Figure 4). This pattern counters the possible interpretation that those classified as exemplar learners in Study 1a were slower learners that would have figured out the rule with more training. On this interpretation, additional training should have led to a higher proportion of rule learners. Yet, the additional 120 training trials enjoyed by the extended training group in the present study did not produce even a slight increase in the proportion of rule learners (relative to the moderate training condition). This pattern suggests that the divergence between rule and exemplar orientations to the function learning task remains stable even with extensive training.

Correlations

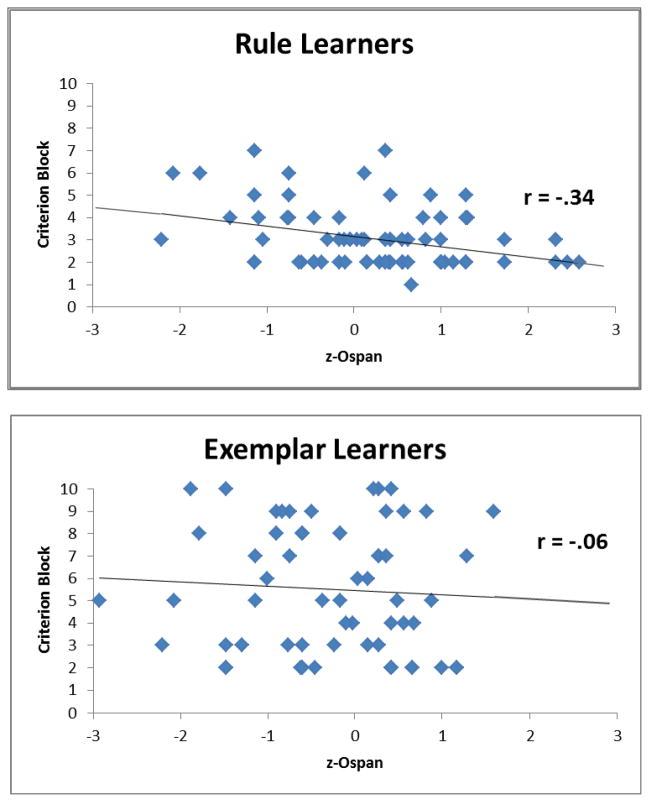
Because the training manipulation produced no effects, we collapsed across the moderate and extended conditions to conduct correlational analyses among function learning tendency Ospan, and RAPM. Again, point-biserial correlations were conducted with rule learner = 1 and exemplar learner = 2. Learner type tended to be correlated with Ospan, (r (55) = −.22, 95% CI [−.46, .04], p = .098), and was significantly correlated with RAPM, (r (58) = −.34, 95% CI [−.55, −.09], p < .01), such that higher working memory and RAPM scores were associated with a tendency toward rule learning. The correlation between Ospan and RAPM did not reach significance in the Study 1b sample, r (55) = .23, 95% CI [−.04, .46], p = .087.

To obtain a larger sample for providing a more reliable analysis of the correlations, we combined the samples from Studies 1a and 1b thereby providing over 100 participants for these analyses. Because the Ospan used in Study 1a differed somewhat from the version used in Study 1b, we first z-transformed each Ospan/automated and Ospan score within each study and then conducted correlations using those z-scores. In the larger sample, both RAPM (r (104) = −.25, 95% CI [−.42, −.07], p < .01) and z-Ospan (r(102) = −.30, 95% CI [−.46, −.11], p < .01) were correlated with learner type. RAPM and z-Ospan were also correlated with each other, (r (101) = .25, 95% CI [.06, .43], p < .01). We will fully address these results in the General Discussion

Study 1c

The novel individual-difference tendencies reported in the function-learning task in Studies 1a and 1b may generally emerge across a range of complex conceptual tasks. To provide an initial test of this hypothesis and provide further currency for the assumption that the individual difference reflects an orientation toward abstracting rules versus learning exemplars, we attempted to show that these tendencies in Study 1a would be associated with the nature of transfer on a non-quantitative categorization task. Regehr and Brooks (1993) argued that in natural category learning, stimuli can provide both a systematic structure that favors rule-based categorization processes and idiosyncratic features that favor learning of individual stimuli as the basis for categorization and generalization (transfer). In their work, they examined how the variations in the stimuli controlled the extent to which rule-based versus exemplar-based processes would contribute to category learning. In the present study, we adopted the Regehr and Brooks paradigm to test whether the individual differences identified in Study 1a persist to influence rule versus exemplar-based processes in this category learning task. Specifically, we examined whether transfer on critical instances diverged for the rule versus exemplar learners indentified in Study 1a.

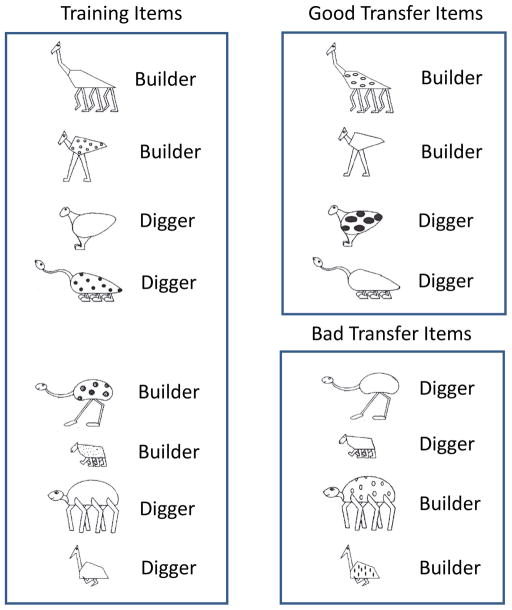
Briefly, the stimuli were animals that differed on five binary-valued dimensions. Animals were divided into two categories (builders and diggers) based on a three-feature additive rule. That is, at least two of three features for the category had to be present for the animal to be classified in that category. The other critical aspect of the stimuli was that the perceptual forms of each dimension varied considerably, so that the animals had idiosyncratic appearances that individuated each animal (see Figure 5 for sample stimuli). Thus, the stimulus set potentially supported either rule-based or exemplar-based processes as the basis for categorization. Critically, transfer items can be presented that have high perceptual similarity to old items in the training set, but do not contain a majority of the categorical features of the old items (following Regehr & Brooks, 1993, we label these the “Bad Transfer” items). Thus, a reliance on exemplars will lead to the (incorrect) decision that the Bad Transfer item is in the category of the old item it resembles, whereas a reliance on rules will oppose that incorrect decision.

Figure 5.

Imaginary animal stimuli for the concept task in Study 1c. Left Panel: A sample training set and category membership. The category membership listed next to each item is based on the rule that builders possess at least two of the three features: long legs, angular body, and spots. Top Right Panel: Good transfer items and their category membership. These items share category membership with their training “twins.” Bottom Right Panel: Bad transfer items and their category membership. These items have category membership that opposes that of their training “twins.”

Using these stimuli, Regehr and Brooks (1993, Experiment 1C) found that after completing several blocks of learning trials, subjects in general were highly likely to make an error on the bad transfer items (77 % of the time). The implication is that in general subjects had relied on memorized exemplars to support their category learning and transfer responses (see Regehr & Brooks, 1993, for amplification). Regehr and Brooks concluded more specifically that with these stimuli, the exemplar-based processes took precedence over tentative rule-like information.

According to our framework, however, we might find predictable individual differences. The exemplar learners identified in the function learning task from Study 1a should be more likely to display extensive reliance on exemplars for learning and transfer in this categorization task (as revealed by high error rates on the bad transfer items) than would the rule learners. We expected that the rule learners (identified as such in the function learning task) would be less influenced by exemplar based processes (as revealed by more modest error rates on the bad transfer items), though we did not expect them to perfectly categorize the bad transfer items. The additive rule is difficult to learn (rule learners might thus acquire a simple rule plus some knowledge about exceptions; Nosofsky et al., 1994), and moreover, effects of similarity for these stimuli persist somewhat even when learners are told the rule prior to training (33% error on bad transfer items in Regehr & Brooks’ 1993 Experiment 1D).

Method

Twenty-four rule learners and twenty-three exemplar learners from Study 1a completed the Regehr and Brooks’ (1993) concept learning task during session 2. In this task, participants saw drawings of fictitious animals that varied on five binary dimensions: body shape (angular or round), leg length (short or long), number of legs (two or six), neck (short or long), and spots (spots or no spots). Each animal was either a digger or a builder, and group membership was determined by an additive rule in which an animal must possess at least two of three critical features to be a builder. Four different category structures were created by varying the critical features, and we attempted to counterbalance these category structures across participants². The following is a listing of the features associated with the builder category for the four structures:

Rule 1: Long legs, angular body, and spots present

Rule 2: Short legs, long neck, and spots present

Rule 3: Six legs, angular body, and spots present

Rule 4: Two legs, long neck and spots present

The training stimuli (from Regehr & Brooks, 1993) maximized perceptual distinctiveness (exemplar salience) by giving each training animal an idiosyncratic form of the five primary features (as shown in Figure 5). For example, although multiple animals had long necks, this feature manifested itself differently in each animal, and such was the case for all features.

During training, stimuli were presented on a computer monitor, and participants tried to classify each one as either a builder or digger by pressing designated keys. Participants were not explicitly presented with the rule. Once they made a response, feedback appeared onscreen in the form of the word ‘correct’ or ‘incorrect’. There were eight training stimuli (four for each category), and participants completed 5 blocks of training, for a total of 40 training trials.

After training, participants completed a test phase consisting of three types of items: Repeat Training Items, Good Transfer Items, and Bad Transfer Items. The transfer items were created simply by changing the spots designation of the eight training items. For training items with spots, a transfer item was created by removing the spots; for training items with no spots, a transfer item was created by adding spots. This resulted in eight transfer items, each identical to one of the training items with the exception of the change in spot designation. The two sets of items were counterbalanced across participants such that a given set was the training set for some participants and the transfer set for others. For four of the transfer items (two each from the builder and the digger categories), the change in spots was not enough to shift categories based on the given rule. Thus, the transfer item was in the same category as its training “twin”. These items are referred to as “Good Transfer” items (following Regehr & Brooks’, 1993, terminology). Conversely, for four of the transfer items (two each from the builder and digger categories), the change in spots led to a shift in category, creating a situation in which the transfer item was in a different category from its training “twin” even though perceptually they were nearly identical. These are referred to as “Bad Transfer” items.

The test phase consisted of the eight repeat training items, the four Good Transfer items, and the four Bad Transfer items. These 16 test stimuli were presented in a random order with the constraint that “twins” had to be separated from each other by at least two items. Participants classified the stimuli as during training, but received no feedback during the test portion.

Results and Discussion

We first compared performance accuracy on the last training block for rule and exemplar learners (identified from their previous extrapolation performance on the function learning task in Study 1a). The two groups performed comparably, with neither group displaying perfect learning (Mean correct performance = 75% and 73% for rule and exemplar learners, respectively; F < 1). Because the anticipated divergence across groups in transfer performance on the Bad Transfer items should be most robust for participants who have learned the categories (with high levels of exemplar learning producing endorsement of the Bad Transfer items in the same category as its twin and rule learning opposing that classification), we stratified the participants based on their classification accuracy for the trained items in the test phase. (We did so because participants were likely continuing to learn on the final training trial, as evidenced by nominally better performance on the trained items in the test phase—81% and 74% for rule and exemplar learners, respectively—than on those identical items on the final training trial.)

Table 2 shows the classification performances on the Good and Bad Transfer items for learners who performed near chance on the trained items (62.5%), for learners who approached perfect learning (75–87.5%), and for learners who correctly classified all training items (these cut-points were used as they corresponded to percentage values derived from the eight-item pool). As can be seen, those participants classified as rule learners (on the function task) had a fairly consistent level of performance on the Bad Transfer items, averaging 40% accuracy, with relatively little change from the less accurate performers (as indexed by the training items) (M = .50) to the perfect performers (M = .45); a similar dynamic emerged for performance on the Good Transfer items, with modest improvement from the less-accurate to the perfect performers (on the training items). A 3 (near chance, almost perfect, perfect accuracy on trained items) × 2 (Bad, Good Transfer items) mixed ANOVA for the rule learners confirmed that classification accuracy on bad and good transfer items did not significantly vary as a function of accuracy on old items (Fs < 1 for the main effect and interaction). Performance was better on good than bad items, F(1, 21) = 5.47, MSE = .14, p < .05, η² = .20.

Table 2.

Classification Accuracy on Good and Bad Transfer Items for Rule and Exemplar Learners as a Function of Trained (Old) Item Accuracy in Study 1c

Trained Item Accuracy	Exemplar Learners				GT-BT
	GT		BT
	M	SD	M	SD
≤62.5% (N=8)	.59	.35	.44	.26	.15
75%–87.5% (N=10)	.85	.21	.38	.32	.47
100% (N= 5)	.95	.12	.00	.00	.95

Trained Item Accuracy	Rule Learners				GT-BT
	GT		BT
	M	SD	M	SD
≤62.5% (N=5)	.65	.14	.50	.18	.15
75%–87.5% (N=14)	.80	.28	.36	.27	.44
100% (N=5)	.70	.33	.45	.41	.25

Note. GT, Good Transfer; BT, Bad Transfer. The entries in the “Trained Item Accuracy” columns exhaust all possible performance levels for the trained items because participants classified eight trained items in total.

In contrast, in the group of participants classified as exemplar learners, higher levels of performance on the training items was associated with decreasing accuracy on the Bad Transfer items and increasing accuracy on the Good Transfer items. This pattern produced a significant interaction between the level of accuracy on old items (near chance, almost perfect, perfect) and the classification accuracy for Bad versus Good items, F (2, 20) = 5.58, MSE = .09, p < .05, η² = .17 (from a 3 × 2 mixed ANOVA)³. In general, Good items were classified much more accurately than Bad items, F(1, 20) = 33.88, MSE = .09, p < .001, η² = .52. Regehr and Brooks (1993) concluded that this kind of pattern—a rise in errors for Bad Transfer items with a corresponding drop in errors for Good Transfer items—implicated a nonanalytic (non-rule) similarity (to memorized training items) approach to classification. Particularly compelling in the present data is that the exemplar learners who classified the training items perfectly (in the test phase) always placed the bad transfer items in the incorrect category with its twin. This demonstrates exclusive reliance on exemplar similarity for classification of new instances, more extreme reliance than has been reported in the literature when individual differences are not considered (Regehr & Brooks, 1993). Such reliance on similarity was not evident in the performance of rule learners (as reported above). However, an omnibus 2 (rule, exemplar learner) × 3 (accuracy on trained items) × 2 (transfer-item type) mixed ANOVA indicated that the 3-way interaction was not statistically significant (F (2, 41) = 1.98, p = .15).

These patterns nevertheless suggest that the participants classified as exemplar learners (at least some of them) were learning the particular examples and the associated category response. As these learners more accurately learned the training examples, their classification decisions on the Bad Transfer item became completely linked to the category of the twinned training example. For exemplar learners, the association between trained-item accuracy (in the test phase) and Bad-Transfer item classification was significant; r(21) = −.46, 95% CI [−.73, −.06], p < .05. Note that it was not the case that improved performance on the trained examples (old items) necessarily led to similarity-based (exemplar-oriented) classification of the Bad Transfer items. For the rule learners there was no association between trained-item accuracy (in the test phase) and Bad Transfer classification (r(22) = −.14, 95% CI [−.51, .28], p > .50), and the rule learners with perfect training item accuracy incorrectly placed the bad training example in the category of its trained twin just over half the time (55%). Thus, it appears that this set of learners was able to oppose salient exemplar similarity with some (perhaps incomplete) abstraction of a classification rule to guide their categorization decisions. Still, these learners (at least some) probably did not learn the underlying additive rule (or possibly just did not apply it well during transfer), as performance of learners who are provided with the rule prior to training display better classification of the bad transfer items than found here (33% incorrect responses reported in Regehr & Brooks, 1993).

In sum, these results are consistent with the idea that the participants identified as exemplar learners on the function learning task also adopted an exemplar approach to the present categorization task, whereas the learners identified as rule learners generally attempted, albeit somewhat unsuccessfully, to discover the rule underlying the category structure of the stimuli. We believe that the persistence of these rule learners’ tendencies to attempt to abstract the underlying rule is underscored by the finding that these learners apparently did not abandon a rule approach (in the face of the difficult additive rule) in favor of exclusive reliance on exemplar learning (as indicated by the absence of an association between training item accuracy and inaccurate classification of bad training items, as found for the exemplar learners). Clearly, however, the evidence for rule use in the categorization task for these learners was not as direct as it could have been. Accordingly, in Study 2 we turned to a different categorization task in which transfer performance more directly implicates abstraction (or its absence) of a classification rule.

Study 2

In this study, we had two major objectives. The first was to replicate the key finding that when given the function learning task, a new set of individual participants would display a tendency to either abstract the functional relation among the cue and criterion values (rule learners) or learn only these values (exemplar learners) Second, we further tested our hypothesis that the rule-learning (abstraction) and exemplar-learning tendencies that participants display in the function learning task will persist across an unrelated, new conceptual task.

Wisniewski (1995) introduced the notion of abstract coherent categories, categories that make sense in light of previous knowledge, and whose members can be determined using only the relationships among features. Building on previous work (e.g., Rehder & Ross, 2001), Erickson et al. (2005) developed a laboratory instantiation of an abstract coherent category in which participants were trained on one coherent category and one incoherent category. For the coherent category, the presented features could be used to create a functional machine; for the incoherent category the presented features could not realize a functional machine. Participants were trained to classify certain feature combinations (which were coherent) as one category and other feature combinations (which were incoherent) as another category. Accordingly, during training, successful performance could be achieved either through abstracting the underlying coherence relationship, or by simply memorizing feature co-occurrences. Those participants who demonstrated learning in the training task (high levels of performance during training), were then transferred to a categorization task with novel items (we label this key task, the novel categorization task). These items all had completely new features, but some features were coherent and some were not. Learners were required to indicate which of the two trained categories the novel items should be placed. As a whole, trained groups did not reach 70% accuracy in any of the three experiments.

One interpretation of the above finding is that there was variation in the kind of representations people formed during training: some participants failed to learn the coherence relation, whereas others had learned the coherence relationship. Paralleling the absence of explanation in the problem solving literature for why some individuals spontaneously transfer and others do not, Erickson et al. (2005) made no mention of why some people would glean the underlying structure to the category, while others would not. In the current experiment we apply our framework to gain leverage on characterizing those learners who successfully glean the underlying structure and those who do not in this task. To reiterate, we suggest that this variation in performance reflects fairly stable tendencies of learners toward either a focus on exemplars or a focus on abstracting underlying relations. If our hypothesis is correct, then identifying such tendencies in the function learning context will significantly predict those learners who will perform well on the novel categorization (transfer) task (rule learning tendency) and those who will not (exemplar learning tendency).

Method

Participants

A total of 72 undergraduates at Washington University in St. Louis participated in at least part of the experiment and received course credit in exchange for either one or two hours of participation (depending on whether they attended one or both sessions). Participants were only included in analyses if they were native English speakers (because of the verbal stimuli), attended both sessions, and demonstrated learning during training on both the abstract coherent categories (ACC) task (final training block accuracy ≥ 75%, following Erickson et al., 2005) and function learning task (final training block mean absolute error < 10). A total of 35 participants were excluded from analyses (10 did not return for session two, 3 were non-native English speakers, 15 were non-learners during ACC training, and 7 were non-learners during function learning training), leaving 37 participants available for analysis.

Procedure

Participants were tested during two sessions, approximately one week apart. During the first session, participants completed the abstract coherent category task and RAPM; during the second session, they completed the Ospan and then the function learning task. These versions of the Ospan and function learning task were identical to those from Study 1a4.

Day 1 session

In the first one-hour experimental session, participants began by completing the abstract coherent categorization task. The procedure for this was the same as that for participants in the classification condition of Erickson et al. (2005, Experiment 3). The categorization materials were presented to participants on 3 × 5 index cards. Each card represented a machine and had four attributes listed on it. These four attributes describing the machine (where it operated, the action in which it engaged, what instrument it used, and its means of locomotion) appeared in the same order on each card. Each morkel was comprised of two sets of coherent features--pairs of features that made sense together—that, when combined, formed a set of four features that were also coherent. Krenshaws were composed of two sets of consistent features that were inconsistent across pairs. In other words, for krenshaws, features 1 and 3 made sense together, as did 2 and 4, but the combination of all the features yielded an implausible machine (See Appendix B for example stimuli).

During training, participants were told that they would be learning about two kinds of imaginary machines called morkels and krenshaws, and that they would see a series of cards representing a particular machine that they would attempt to classify. They were told that two instances of the same kind of machine could differ from each other, and that machines of different types could share common features. Participants were told that at first they would be guessing because they had had no prior experience with the machines, but as they progressed they could use feedback given to them after each trial to improve their performance. For feedback, the experimenter simply indicated whether the classification response was correct or incorrect on every training trial. There was a total of six training blocks, each with a random sequence of eight possible machines (four morkels and four krenshaws) presented once per block, yielding a total of 48 training trials.

After these training trials, participants were told that they would now be tested on what they had learned by seeing cards containing two features of a machine they had previously seen and asked to classify the machine on the card as either a morkel or a krenshaw. This two-feature test was the same as that used in Erickson et al. (2005), with each possible pair of features presented together (except the features that would have appeared together in position 1 and 3 or in position 2 and 4 because these could be accurately classified as either kind of machine). Participants were told that they would not be receiving feedback on these trials, but that they would rate their confidence in each classification on a scale from 1 to 7 (where one is least confident, just guessing and 7 is certain). There was a total of 16 feature pairs presented to the participant in random order.

The final test was the novel classification test. There was a total of 12 novel test items, 6 each of morkels and krenshaws presented to each participant in random order. The novel stimuli fit the template established by the training items, with each one being composed of two pairs of coherent attributes. All four attributes of the morkels were coherent, whereas for krenshaws the location of operation was coherent with instrument used, but not coherent with the location and locomotion. Participants were told they would be seeing some more morkels and krenshaws, but that the four features that these machines would have were ones that they had not previously seen. They were told that they could use the information they had learned thus far in the experiment about the two kinds of machines to help them classify the novel ones. As in the two-feature test, participants were given no feedback and instead, after each item, rated their confidence on a scale of 1 to 7. Next, participants completed the full, 36-item version of RAPM (Raven, Raven, & Court, 1998).

Day 2 session

Participants returned to the lab about 1 week after the first session to complete the function learning task and the Ospan. Both versions were identical to those used in Study 1a.

Results and Discussion

Function learning classifications

The classification scheme was identical to the one used in Study 1a and resulted in 19 participants classified as rule learners (including 4 sine learners) and 18 as exemplar learners. The analyses of the training and interpolation performances (MAE) replicated the patterns reported in Studies 1a and 1b. On the final block of training rule learners (M = 2.67) had significantly less error than exemplar learners (M = 4.69), F(1,35) = 11.24, p < .01, η² = .24. However, both rule and exemplar learners showed similarly high accuracy at the end of training, particularly compared to the drastically different extrapolation profiles exhibited by the two groups (see Figure 6). Also, the rate of learning for rule learners and exemplar learners was similar, as confirmed by a training block (Block 1 vs. Block 10) x learner type ANOVA revealing a nonsignificant interaction (F < 1). Rule learners (M = 2.42) also showed significantly lower MAE’s than did exemplar learners (M = 4.66) on interpolation trials, F(1,35) = 16.84, p < .001, η² = .32. Again, however, these differences were extremely small relative to the dramatic differences in extrapolation MAE between rule learners (M = 11.77) and exemplar learners (M = 43.26), as confirmed by a learner type (rule vs. exemplar) x trial type (interpolation vs. extrapolation) interaction, F (1,35) = 133.50, p < .001, η² = .25. Thus, the divergent patterns of extrapolation for the participants classified as exemplar learners versus those classified as rule-learners cannot be accounted for by differences in learning accuracy of the trained cue-criterion values nor in the ability to transfer to interpolation regions (for which both associative models and rule models transfer well; Busemeyer et al., 1997).

Figure 6.

Top panel: Average predictions on the last training block for the participants classified as rule learners, the participants classified as exemplar learners, and the participants classified as non-learners in Study 2. Middle panel: Interpolation predictions averaged for rule learners and for exemplar learners. Lower panel: Extrapolation predictions averaged for rule learners and for exemplar learners.

The result from Studies 1a and 1b that did not emerge here was that the correlation between final training block MAE and extrapolation MAE was not significant for rule learners (r(17) = .11, 95% CI [−.36, .54], p = .65; for exemplar learners, r(16) = .13, 95% CI [−.36, .56], p = .61).

Correlations

As with Studies 1a and 1b, point-biserial correlations were computed with rule learner = 1 and exemplar learner = 2. Learner type was not significantly correlated with RAPM, r (35) = −.28, 95% CI [−.55, .05], p <. 10, or with Ospan, r (35) = −.13, 95% CI [−.44, .20]. The correlation between RAPM and Ospan was also not significant, r (35) = .21, 95% CI [−.12, .50]. The small sample size likely provided insufficient power to detect these correlations in the present study. To achieve relatively substantial sample sizes for obtaining stable correlational patterns, we conducted a final set of correlations that combined the function learning, Ospan, and RAPM data from Study 2 with those from Studies 1a and 1b.

Correlational Analyses Collapsing across Studies 1a, 1b, and 2

When Studies 1a, 1b, and 2 were collapsed, the correlation between final training block MAE and extrapolation MAE was highly reliable among rule learners (r(77) = .62, 95% CI [.47, .74], p < .001) and nonexistent among exemplar learners (r(64) = .04, 95% CI [−.20, .28], p = .73). This difference in correlations across the two learner types was also significant (z = 4.04, p < .001).

Correlations among RAPM⁴, Ospan, and the function learning task were also computed for the combined sample from Studies 1a, 1b, and 2. Both RAPM (r (141) = −.23, 95% CI [−.38, −.07], p < .01) and Ospan (r (139) = −.25, 95% CI [−.40, −.09], p < .001) were correlated with learner type. As is typical, RAPM and Ospan were also positively and significantly correlated with each other (r (138) = .23, 95% CI [.07, .38], p < .01. Multiple regression analyses revealed that, when entered together as predictors, both RAPM (β = −.18, p < .05) and Ospan (β = −.23, p < .01) uniquely predicted learner type, and together they accounted for 10.4% of the variance in learner type.

In addition, in light of recent reports that working memory capacity is associated with speed of category learning (Craig & Lewandowsky, 2012; Lewandowsky, 2011), we computed correlations between Ospan and the efficiency of learning (and RAPM the efficiency of learning). Learning efficiency was gauged by the block number at which individuals permanently reached the criterion value for classifying individuals as learners (MAE < 10). Extending previous work on category learning, Ospan (but not RAPM, r (141) = −.15, 95% CI [−.31, .02]) was significantly associated with the speed of learning the training points in the function learning task (r (139) = −.26, 95% CI [−.41, −.10], p = .002).

Because working memory capacity might be especially important for rule learning (e.g., to support relational processing among the stimuli, Ashby & O’Brien, 2005, or for partitioning training stimuli into subsets of linear segments, Erickson, 2008; Sewell & Lewandowsky, 2012) but not necessarily for learning of the individual training points (exemplar learning), we computed correlations separately for the rule and exemplar learners. For learners who appeared to rely on function abstraction (rule learners), Ospan (but not RAPM, r (76) = −.11, 95% CI [−.33, .11]) was significantly associated with the speed of learning the training points (r (75) = −.34, 95% CI [−.53, −.13], p =.002). The implication is that for the rule learners, those with higher working memory capacity were able to more effectively support the processing needed to determine the functional relation among the training points, thereby supporting faster learning. By contrast, for the exemplar learners there was no significant association between Ospan (nor RAPM, r (63) = −.01, 95% CI [−.25, .23]) and speed of learning in the function task (r (62) = −.06, 95% CI [−.30, .19], p > .60). Further, the Ospan-criterion block correlation was marginally significantly different between rule and exemplar learners (z = −1.71, p < .09). As shown in the scatterplot (Figure 7), the absence of a significant correlation for exemplar learners was not an artifact of restricted range for either Ospan or the learning criterion measure; exemplar learners scoring at the high end of Ospan were just as likely to reach criterion after many training blocks (e.g., Block 9) as they were to quickly reach the criterion.

Figure 7.

Top panel: Scatterplot of the association between training block at which learning criterion was met in function learning and working memory capacity for rule learners across Studies 1a, 1b, and 2. Bottom panel: Scatterplot of the same variables for exemplar learners across Studies 1a, 1b, and 2.

Abstract Coherent Categories

Rule and exemplar learners (as indexed by the function learning task) showed similar learning trajectories during the training phase of the categorization task, as shown in Figure 8. A 2 (learner type) × 6 (Training Block) mixed-model ANOVA on categorization accuracy confirmed this impression. There was no effect of learner type and no interaction (F’s < 1). A significant block effect emerged, F(1,35) = 41.85, p < .001, η² = .54, indicating that both groups showed significant learning across training blocks, with both groups performing at 97% accuracy on the last block of learning. These results allow two possible interpretations. One is that the differences in function learning were idiosyncratic to the function-learning task, with both groups now engaging similar learning processes on the abstract coherent categories task. The other interpretation is that, akin to the function learning task, learning in the abstract coherent categories task was supported by an exemplar orientation for some learners (the exemplar learners identified in function learning) and a rule orientation by other learners (the rule learners). If this interpretation has merit, then the two groups should diverge in their transfer performances.

Figure 8.

Classification accuracy in Study 2 on each training block for the abstract coherent category task as a function of learner type (rule learners vs. exemplar learners as determined from extrapolation performance on the function learning task).

The two types of function learners did show different patterns of performance during the transfer phase. On the two-feature test, the rule learners were nominally more accurate (M’s = .78 vs. .71, F(1, 35) = 1.23, p > .27) and trended toward higher confidence-adjusted scores as well (M’s = 3.13 vs. 2.09, F(1, 35) = 2.29, MSE = 4.32, p < .14). Most telling, as predicted, the difference between the two groups was most pronounced on the novel test. Rule learners were significantly more accurate in their categorization responses (M = .71) compared to the exemplar learners (M = .57), F(1, 35) = 4.64, MSE = .04, p < .05, η² = .12, and rule learners also averaged a higher confidence-adjusted score (M = 2.21) as opposed to exemplar learners (M = .75), F(1, 35) = 5.07, MSE = 3.89, p < .05, η² = .13).

The results provide continuing support for our hypothesis that the nature of extrapolation on the function learning task indexes a somewhat stable learning tendency. There was a significant association between extrapolation performance on the function learning task and performance on the novel categorization task, indicating that people who extracted a rule-like underlying representation of the function were likely to abstract the underlying coherence in the categorization task. Further, we have provided a purchase on differentiating sub-sets of learners who will be likely to transfer (rule learners) from those who will not be likely to transfer (exemplar learners) on a higher-order concept task that requires acquisition of underlying abstractions. This is not a trivial advance in light of the current literature, which remains virtually silent in terms of differentiating and characterizing learners who are likely to demonstrate transfer and those who are not likely to do so.

General Discussion

The present findings offer initial support for the main tenets of the framework we have sketched to characterize and anticipate individual differences in higher order concept learning. First, the framework refines the longstanding debate in the concept literature concerning whether human conceptual behavior is best characterized by an exemplar model (Choi, McDaniel, & Busemeyer, 1993; Kruschke, 1992; Nosofsky, 1984, 1986) or an abstractionist model (Bourne, 1974; Koh & Meyer, 1991; Nosofsky et al., 1994). We proposed that each approach may reflect the tendencies of different sets of learners. On a number of fronts, the results were consistent with our proposal. For the function learning task, Studies 1a, 1b, and 2 all showed that individuals differed in their extrapolation performances. Some individuals’ extrapolation reflected output values that were generally within the range of outputs learned in training (see Figures 3, 4, and 6), a topography that is captured well by an exemplar model (see DeLosh et al., 1997). Other individuals’ extrapolation was characterized by output values extending beyond the learned outputs that generally followed the slope of the underlying function (Figures 3, 4, and 6), a topography that implicates a rule (Koh & Meyer, 1991) or abstractionist-based approach (some sort of relational abstraction, McDaniel & Busemeyer, 2005). Moreover, the classification of these two groups based on MAE scores does not appear to reflect a partitioning of a uni-modal distribution of extrapolation performances (assessed by MAE). Inspection of Figure 9, which shows the distribution of MAE scores for learners in Studies 1a, 1b, and 2 combined, reveals a substantially bi-modal distribution.

Figure 9.

Distribution of average MAE values in extrapolation in the function-learning task for learners in Studies 1a, 1b, and 2. The bold vertical bar indicates the division between those classified as rule learners and those classified as exemplar learners.

Further supporting the interpretation that one set of learners was attempting to abstract the function rule and the other set was focusing on acquiring the individual input-output pairs (exemplars), were the distinctive patterns of correlations across each set of learners. First consider that the accuracy of output (criterion) responses on the final training block was correlated with the accuracy of responses on extrapolation trials for the learners characterized as rule learners but not those characterized as exemplar learners. As discussed earlier (see Study 1a), for learners focusing on a rule representation, the degree to which the abstracted rule accurately reflected the given functional relation would drive the accuracy of responding to both the final training stimuli and the extrapolation stimuli. In contrast, for learners focusing on an exemplar representation, the precision with which the learners’ acquired the individual cue-criterion pairings in training would have little impact on their extrapolation accuracy. Thus, the significantly higher correlation for the group identified as rule learners (in both Studies 1a and 1b, and when participants were combined from all studies), coupled with the nonsignificant correlation for the group identified as exemplar learners, converges with the idea that one group focused on abstracting the function rule, whereas the other group focused on learning the individual exemplars.

A second suggestive pattern of correlations was that Opsan was significantly associated with the speed of learning during training for the participants characterized as rule learners (when participants from Studies 1a, 1b, and 2 were combined to achieve high sample sizes). This finding lends currency to the interpretation that this set of participants was attempting to learn the function rule during training. Learning the function rule presumably requires maintaining and comparing stimuli across trials (“comparative hypothesizing”, Klayman, 1988) and possibly partitioning the stimuli into subsets for the different slopes and switching back and forth across these partitioned segments during training (Lewandowsky et al., 2002; Sewall & Lewandowsky, 2012), and these processes require working memory capacity (both from a theoretical perspective, Craig & Lewandowsky, 2012; and based on empirical findings, Sewall & Lewandowsky, 2012). Consequently, for participants attempting to abstract the function rule, higher working memory capacity (as indexed by Ospan scores), would facilitate learning. By contrast, working memory capacity would not necessarily speed learning of the individual training points (cf. Ashby & Maddox, 2005), and Ospan was not significantly associated with the speed of learning for the set of participants that appeared (based on extrapolation) to focus on learning the individual training points (exemplars) during training. This pattern must be considered only suggestive, however, as the difference in the correlations for rule-learning versus exemplar participants were only marginally significant.

Additional convergence for the idea that some participants attempted to abstract the function rule and others focused on learning the individual stimuli was the finding that higher RAPM scores were associated with the likelihood that a participant would show rule-like extrapolation (significantly so in Study 1b, in the combined Study 1a and 1b sample, and in the entire combined sample). RAPM assesses an individual’s ability to derive rules that characterize an assembly of stimuli (see Wiley et al., 2011), and it is sensible that the participants with more general ability to abstract rules would be likely to recruit these rule-abstraction skills for a novel learning task. Participants with less general ability to derive rules would instead likely focus on learning the individual training instances (exemplars) to achieve proficiency during training.

Though RAPM did correlate with the individual differences in extrapolation patterns in function learning, the amount of variance accounted for by RAPM was modest (r² = .053 for the combined Studies 1a, 1b, and 2 samples). Thus, the tendency to focus on exemplar versus rule-like representations does not completely overlap with a general ability (or strategies; Hayes, Petrov, & Sederberg, 2011) for abstracting relations. The RAPM task instructs individuals to find the relation among patterns; by contrast, during the training portion of the function learning task, participants are not explicitly instructed to extract a rule. Further, a successful approach to learning during the training phase does not require relational processing among the stimuli; learning of the individual training points supports high levels of performance. Accordingly, differential ability in relational abstraction per se would not necessarily be a sole determinant in an individual’s spontaneous orientation toward exemplar versus rule-like representations in function learning. Indeed, another factor that appeared to play a role in the tendency to rely on rule versus exemplar processing was working memory capacity. We next consider this important result.

Working Memory and Individual Differences in Rule versus Exemplar Learning

As just noted, working memory capacity (as measured by Ospan following Wiley et al., 2011) was a significant and unique predictor of the tendency to rely on rule versus exemplar processes in the function learning task, such that higher working memory capacity was related to reliance on rule learning. For a number of reasons, greater working memory capacity could facilitate abstracting the function rule during learning, including the ability to maintain and compare several stimuli concurrently (Craig & Lewandowsky, 2012), to partition the training stimuli into two linear segments and switch back and forth between them during learning (Erickson, 2008; Sewell & Lewandowsky, 2012), and to reject or ignore initial biases (e.g., a positive linear) in order to discern the given function (cf., Wiley et al., 2011). Thus, learners enjoying greater working memory capacity might be more inclined to engage processes that would support rule learning (relating several training trials, partitioning training trials, ignoring initial biases) than would learners with more limited working memory capacity.

Despite the compelling theoretical reasons for why working memory would be linked to learners’ orientation toward rule versus exemplar representations in conceptual tasks (see Craig & Lewandowsky, 2012, for more extended discussion), the present findings are among the first to document a link between working memory and strategy choice in conceptual tasks. Accordingly, existing related findings warrant close consideration. Craig and Lewandowsky (2012) examined the relation between working memory capacity and learners’ strategies in a correlated cues task (accurate categorization depended on the correlation of values of two of the four stimulus dimensions). Based on learners’ response profiles in transfer trials, two prominent strategies were identified. One strategy reflected a bi-conditional rule (if the values on both dimensions matched, classify the stimulus in one category and if not, classify the stimulus in the other category; see Bourne, 1974), and the other reflected a conditional rule (the value on one dimension determined a particular second dimension on which classification was based). Working memory capacity was not related to which category-learning strategy was adopted. However, both strategies were rule-based, with both rules involving a focus on several dimensions. Accordingly, there would not be a strong expectation that working capacity would particularly favor one of these rule strategies over the other. As discussed above, working memory capacity might be more important in supporting rule strategies in general versus exemplar strategies. (It is also worth noting that the conditional rule was prominent with one particular counterbalanced set of materials but not the other. Thus, affordances of the stimuli impacted the conceptual strategy, thereby perhaps minimizing contributions of working memory.)

Directly related to this possibility, Craig and Lewandowky (2012) examined the emergence of a rule versus an exemplar strategy in a low-structured categorization task, a task in which a logical rule cannot capture the category space (Medin & Schaffer, 1978). Working memory was not significantly related to whether learners displayed use of a rule or exemplar strategy. However, the poorly differentiated categories in this task favor an exemplar approach (see Smith & Minda, 1998, for supporting theoretical and empirical work). In line with this observation, the rule strategy did not lead to levels of accuracy obtained with the exemplar strategy (the rule strategy requires that learners also identify an exception(s) stimulus, and doing so retards learning). Because the category structure favored one strategy (exemplar) over another in terms of performance, this may have biased against the influence of working memory on the learners’ approach (i.e., the working memory influence toward a rule strategy would be opposed by the influence of the category structure toward an exemplar strategy; Smith & Minda). Favoring this interpretation is that variations in the structure of a conceptual task, (see for instance, findings in multiple cue prediction tasks, Juslin et al., 2003; also Smith & Minda) can have strong influences on the degree to which learners adopt a rule or exemplar-based approach. Thus, one integrative interpretation of the present results and the existing literature is that working memory capacity may be associated with the learner’s approach primarily for concept tasks for which rule and exemplar approaches are equally favored by the structure of the conceptual-learning task.

One limitation of the present study is that a single measure (Ospan) was used to index working memory capacity. Such an approach is not as robust as using a latent variable approach (which would use several individual “working memory” tasks) to assess working memory capacity, because relying on one measure introduces task-specific variance that may not be associated with working memory per se. We suggest, however, that the patterns reported herein are likely not restricted to specific Ospan related variance. One prominent reason is that we replicated in the function learning domain the relation between working memory and category learning efficiency reported in studies using a latent variable approach to measure working memory. Specifically, across several types of categorization tasks, Craig and Lewandowsky (2012) and Lewandowsky (2011) reported significant correlations between speed of learning and working memory capacity. In the present study, we found a similar general association between speed of learning in the function task and working memory capacity as indexed by Ospan alone. These parallel findings add to the emergent evidence that working memory capacity influences learning on a range of conceptual learning tasks.

In this regard, a theoretical issue that remains is to delineate the role(s) that working memory plays in conceptual learning. Lewandowsky (2011) used an exemplar based model (ALCOVE) to capture the relation between working memory capacity and individuals’ learning performance across a range of categorization problems, and found that working memory variation was linked predominantly to the learning rate parameter. The process model proposed was that increased working memory capacity supports additional rehearsal, thereby promoting associative learning (learning of exemplar—category label associations). The current finding that working memory capacity (as measured by Ospan) was a significant predictor of the tendency to rely on rule versus exemplar processes in the function learning task, might suggest a modified interpretation of Lewandowsky’s (2011) result. Perhaps, the link between working memory and categorization process obtained in Lewandowsky reflected qualitative, in addition to (or instead of) quantitative, differences in individuals’ learning processes. The idea is that individuals with higher working memory capacity may have been more likely to attempt to learn a categorization rule (than to focus on exemplars), which could have facilitated learning in the classic categorization tasks examined by Lewandowsky. Note that if the underlying processes for some learners were in fact rule-based, the ALCOVE (exemplar) model appears robust enough that it still could have accommodated the categorization performances (which it did; see Choi et al., 1993).

Recently, Sewell and Lewandowsky (2012) provided a more penetrating analysis of the categorization processes linked to working memory. They suggested that in complex categorization tasks, working memory serves to selectively consider particular candidate representations (or strategy) for subsets of stimuli (e.g, a rule for one subset and an exemplar-based representation for another subset; Erickson & Kruschke, 1998) and to control attentional shifts so that these candidate representations are appropriately engaged across the entire set of stimuli. This posited role of working memory in deliberate control of representation selection and representation shifting could bear on learning the bilinear function used herein. The idea, as briefly mentioned earlier, is that higher working capacity could facilitate partitioning the stimuli into more easily learned negative linear and positive linear segments, and shifting appropriately between these representations on a trial by trial basis.

This theoretical approach might thus suggest that the association observed in the current study between working memory capacity and individual differences in rule versus exemplar tendencies might more specifically reflect learners’ ability to engage and control multiple representations to achieve learning in complex conceptual tasks. In this regard, it is worth recalling that participants characterized as exemplar learners displayed a reasonable range of Ospan scores (Figure 7), and for these learners higher capacity was not related to faster learning. Thus, having the capacity to engage and control multiple representations appears not sufficient to spontaneously stimulate partitioning processes (that would support or suggest rule-like representations). Along these lines, Erickson (2008) found that working memory capacity was not related to whether individuals partitioned the category space (according to quadrants in a two-dimensional space) in attempting to learn a complex categorization task (though, learning accuracy for individuals who did partition the category space was positively associated with working memory span). Note that in Sewell and Lewandowsky’s (2012) Experiment 2, participants were instructed to switch back and forth across blocks between two representational strategies (rule-like), so the association between working memory and tendencies to spontaneously display rule versus exemplar representations could not be determined. Still, an intriguing direction for future research (using a latent factor approach to assessing working memory capacity) will be to determine whether working memory’s role in representational flexibility might itself characterize the individual differences delineated in the present study, might contribute to a learner’s preference to adopt a rule (which could require multiple representations) or an exemplar approach (which would require only an exemplar representation), or is possibly not aligned with learners’ preferences for adopting rule versus exemplar approaches in tasks like those examined here.

Additional Considerations of Individual Differences in Extrapolation

Individual differences in extrapolation in function learning could reflect quantitative differences in learning (DeLosh et al., 1997; McDaniel & Busemeyer, 2005). Several findings disfavor this interpretation for the present results. First, for both groups (“exemplar” and “rule” extrapolators) and across studies, by the end of training the deviation (error) between the participants’ responses on the trained values and the actual criterion values was relatively low, with average MAE generally no worse than about 6 (relative to 16 or greater on the first block). These values suggest that both the “exemplar” extrapolators and the “rule-based” extrapolators had accurately learned the criterion values that were associated with the cue values presented for training (see Figures 3, 4, and 6). The exemplar learners did demonstrate slightly (but significantly) higher MAE than the rule learners by the end of training. However, the transfer performances for extrapolation were dramatically different across the two groups. If this difference were simply a consequence of different amounts of learning, then a difference of similar magnitude might have been expected on transfer in interpolation (e.g., DeLosh et al., 1997), which we did not obtain. This suggests that different representations rather than different amounts of learning by the end of training were mediating the striking differences (across groups) in extrapolation.

Second, formal modeling of transfer in function learning tasks similar to the one used here suggests that the range of extrapolation behaviors observed cannot be adequately captured by fitting the parameters (including learning rate parameters) of a rule-like model to individual learners or the parameters of an exemplar-like model to individual learners (see McDaniel et al., 2009, Experiment 1). With regard to formal models, an interesting implication of the present study is that current hybrid models that embrace rule and exemplar learning (e.g., within an ACT-R formalism; Anderson & Betz, 2001; ATRIUM, Erickson & Kruschke, 1998; COVIS, Ashby et al., 1998) might more accurately describe human concept learning by incorporating individual difference parameters to reflect individual tendencies to rely on either the rule system (module) or the exemplar system (module) (see Erickson, 2008, for a similar suggestion).

Stable Tendencies for Learning Exemplars versus Abstracting Rules

With regard to the stability of the learning tendencies illuminated herein, one concern that might be raised is that the appearance of exemplar versus rule tendencies in the function-learning task reflected an intermediate state in training and not a final state. This possibility is suggested by work showing that in some categorization tasks, learners’ tendencies toward a rule or exemplar strategy can switch midway through training (Craig & Lewandowky, 2012). In a function-learning task, Bott and Heit (2004) reported that though learners may have oriented toward exemplar representations during initial training at the conclusion of training all learners evidenced rule learning (note that in this paradigm transfer probes were inserted in the training task). The results in Study 1b strongly suggest that for the present training regimen, the learners’ observed tendencies toward exemplar or rule representations were quite stable. The extended training group, with at least 14 and up to 22 blocks of training, showed nearly identical patterns to the “moderate” training group (receiving training comparable to that in Studies 1a and 2). Quantitative indices of performance indicated that the block at which criterion was reached did not differ across groups, and accuracy levels on the last block of moderate training were not significantly improved with extended training. Most telling, the distributions of rule and exemplar learners did not change with extended training (about 60% rule learners).

The more novel assumption of our framework is that the individual differences discussed above reflect tendencies that may persist across a range of higher-order conceptual tasks. A spate of past work has identified individual differences in forming exemplar representations versus summary (abstract) representations on a single laboratory concept learning (Medin et al., 1984), a single function learning problem (DeLosh et al., 1997), or a single multiple cue prediction task (Juslin et al., 2003). The present work substantially advances these earlier findings by demonstrating that these individual differences may represent fairly stable learning tendencies. Learners who appeared to rely on exemplar-based representations in function learning tended to also do so in entirely different non-numerical categorization tasks. For the categorization task in Study 1c, learners showing exemplar-like extrapolation in function learning tended to base categorization decisions in transfer on similarity of the new examples to the trained examples. Especially telling was the classification behavior of those learners who responded perfectly on the trained items during final testing. For new “bad” transfer examples with close similarity to trained examples, classification performance was in direct opposition (i.e., 100% errors) to the categorization decision specified by an underlying rule. By contrast, learners showing rule-like extrapolation were better at resisting incorrect similarity-based classification decisions to the new (“bad”) examples.

In Study 2, again the exemplar and rule-learning tendencies evidenced in function learning persisted to yet another very different categorization task (different from both the function learning task, as well as from the categorization task in Study 1c). Those learners that displayed rule-like extrapolation in the function learning task appeared to extract an abstract rule (functional coherence or incoherence of the features of the machines), as evidenced by average transfer performance that was substantially above chance, whereas those learners that displayed exemplar-like extrapolation were relatively unable to accurately classify new instances (even though their performance on the final learning trial was nearly perfect). These findings are theoretically important because they reinforce a distinction between exemplar and rule-learning tendencies, and they are novel in establishing that these individual tendencies are relatively persistent across disparate conceptual tasks and are not limited to mathematically oriented domains.

The Study 2 finding just mentioned also helps illuminate an issue not yet mentioned. Recent work with complex category spaces that afford several strategies to differentially partition the category space for categorization responses suggests that common underlying knowledge was gleaned in learning (rules in this case), but across learners different strategic coordination of the rules was applied (Yang & Lewandowsky, 2003; 2004). In a similar vein, in the present study it is theoretically possible that the individual differences observed in extrapolation reflected a common exemplar learning process but that the exemplar information was used differently in extrapolation. Specifically, display of rule-like extrapolation versus exemplar-like extrapolation could indicate that when faced with extrapolation, some learners applied a linear extrapolation computation to their exemplar representations, whereas others did not (e.g., see McDaniel & Busemeyer, 2005). However, this possibility does not readily accommodate the correspondence between those learners’ rule-like performances in extrapolation and the evidence of transfer in the abstract coherent category task. Neither an exemplar representation, nor a linear extrapolation tendency, would support transfer in the abstract-coherent category task. Transfer in this category task relies on abstracting the underlying rule, and accordingly suggests that the individual-difference characteristic that was reflected across both the function learning and category task was a tendency to attempt to abstract the rule that related the training instances (or to focus on learning exemplars).

The above findings provide initial progress toward a principled analysis of learning tendencies that enables prediction of which individuals will likely display transfer and which will not (or the pattern of transfer; cf. Study 1c) on higher-order conceptual tasks. A learner’s tendency to focus on exemplars versus abstraction of a relation among exemplars during function learning predicted performance on the novel transfer items in the abstract coherent category task. Such a finding is not trivial in light of a literature that has attempted with little success to establish an empirical relation between conceptual problem solving performance and a theoretically-relevant individual difference measure (e.g., intelligence). As stated in a recent review, “no convincing empirical evidence exists that would support a relation, let alone a causal relation, between complex explicit or implicit problem solving competence on the one hand, and global intelligence on the other” (Wenke, Frensch, & Funke, 2005, p. 181). The present findings and approach thus represent a potentially significant extension over the standard theoretical and empirical literature in cognitive psychology by (1) focusing on understanding individual differences in conceptual learning and transfer and (2) identifying a theoretically-grounded learning tendency that has predictive utility.

Further favoring the above conclusion are the results of a study that we completed (McDaniel, Frey, Kudelka, & Shields, 2012) that examined whether introductory college chemistry students’ tendencies to display rule learning or exemplar-based learning (as determined by extrapolation in the present bi-linear function learning task) were predictive of their grades in the first and second semester courses. In these chemistry classes, the examinations primarily demanded integration and generalization of the particular problems and examples presented in class and assigned for homework. Accordingly, we thought it possible that students who were identified as rule learners in the function learning task would also tend to attempt to extract the underlying relations in their chemistry classes, thereby supporting better examination performances. Of 179 learners on the function learning task, 96 were classified as rule learners and 83 as exemplar learners. This distinction captured significant variance in the course grades above and beyond that accounted for by Math ACT scores for both the fall course (change in R² = .05, relative to .07 accounted for in the base model with ACT scores) and the spring course (change in R² = .06 relative to .06 for the base model). Those students who displayed rule learning in the function learning task performed better on average than those who displayed a reliance on exemplar-learning in the function task.

We offer the present findings and framework as a potentially fruitful avenue for identifying and characterizing important learning tendencies across individuals and for predicting the nature of transfer based on those tendencies. We also believe that the findings may provide a basis for further development of hybrid categorization models to accommodate individual differences in conceptual tasks (which have not been straightforward to accommodate; see McDaniel et al., 2009). Finally, though the present work is grounded in laboratory conceptual tasks, based on the preliminary findings just mentioned (from the college chemistry class), we speculate that the tendency identified in the present study to focus on exemplars versus underlying abstractions (rules) may bear on learning and transfer in at least some educationally relevant conceptual learning domains.

Appendix A. Description and Results of the Secondary Individual Difference Measures

Need for Cognition Scale

The need for cognition (Cacioppo & Petty, 1982) is a domain-general measure of the degree to which individuals are motivated to expend cognitive effort (e.g., “I would prefer complex to simply problems.”, “I enjoy thinking about an issue even when the results of my thought will have no effect on the outcome of the issue.”). This scale is a 34-item, 9-point Likert Scale with anchors 0 (“Very strong disagreement”) and 8 (“Very strong agreement”).

Kolb Learning Style Inventory

This inventory (Kolb, 2007) is a 12-item scale in which participants are presented with sentence stems (e.g., “I learn best when:”), and they are asked to rank four response options (e.g., “I listen and watch carefully.” or “I rely on logical thinking.”) from 1(least like you) to 4(most like you). Each response option corresponds to one of four “learning modes” (concrete experience, reflective observation, abstract conceptualization, and active experimentation.), and the rankings of each learning mode are summed across the 12 items (as specified by Kolb, 2007). These scores are then used to compute two dimensions of learning: taking in experience and dealing with experience. The dimension of taking in experience is calculated by subtracting the concrete experience score from the abstract conceptualization score. The dimension of dealing with experience is calculated by subtracting the reflective observation score from the active experimentation score.

Free Recall

The English Lexicon Project Database (Balota et al., 2007) was used to generate a pool of words with the following constraints: nouns with 1–2 syllables, 5–7 letters, Kucera-Francis frequency (Kucera & Francis, 1967) ranging from 5–25, concreteness ranging from 318–558, and familiarity ranging from 389–587. From this pool, 24 words were randomly selected and assigned to two recall lists of 12 words each. For each list, words were presented in random order, and each word was presented for 2s with a 1s inter-stimulus interval. After the final word of the list, participants were instructed to type the alphabet backwards for 30s as a delay task, and then they were asked to type out all of the words they could remember from the preceding list. List 2 was presented immediately after the recall phase of List 1

Paired Associates

The pool of words for this task was generated using the same criteria as in the free recall task. Twenty words were randomly selected from the pool, and it was confirmed, using the University of South Florida Free Association Norms (Nelson, McEvoy, & Schreiber, 1998), that no pre-existing associations existed among any of the 20 words (4 of the words--token, flock, segment, and garment-- were not included in the norms, but there were no obvious associations between these words and any others in the list). The words were then divided into 10 cues and 10 targets, and the cues and targets were randomly linked to create 10 cue-target pairs. At encoding, these 10 pairs were randomly presented, one at a time, on a computer monitor. The two paired words were presented together onscreen for 2s, and a 1s inter-stimulus interval separated each pair presentation. After the 10 word pairs were presented, participants completed a test phase in which the first word of a pair was presented, and participants were instructed to type in the word that previously had been paired with it.

Correlation Results

Due to attrition across sessions, time constraints, and technical issues, three participants were missing free recall data, two participants were missing need for cognition data, and one participant was missing paired associates and Kolb Learning Style Inventory data. The primary objective of the correlational analyses was to investigate the extent to which the current distinction between learners’ tendencies to focus on exemplars versus the relations (rule) among the training instances was related to the individual difference measures described above. Neither of the self-report measures, the need for cognition, r(44) = −.07, or the Kolb (2007) learning style dimensions, captured the rule/exemplar learning distinction. At best, the dimension of taking in experience (from Kolb) showed a modest, nonsignificant correlation r(45) = −.24, p < .10) such that rule learners tended to fall more toward the “abstract conceptualization” end of the dimension (the opposite anchor being “concrete experience”). The dimension dealing with experience showed no relationship with rule/exemplar categories, r(45) = .15. Though it remains possible that the current distinction might correspond somewhat with the Kolb learning style dimension of how a learner reports that he or she prefers to “take in experience”, the present results do not compel the conclusion that the Kolb learning style instrument overlaps with the performance-based distinction developed in the present work.

The secondary memory measures (free recall and paired associate learning) also did not correlate with the learners’ tendency to focus on exemplars versus on abstracting the function rule (for free recall, r(43) = −.08; for pair-associate learning, r(45) = −.04).

Appendix B. Sample Stimuli from the Abstract Coherent Categories Task (Study 2)

Training Stimuli	Novel Test Stimuli
Morkels operates on land works to gather harmful solids has a shovel rolls on wheels	Morkels operates in highway tunnels works to remove carbon dioxide has a large intake fan flies with a propeller
operates on the surface of the water works to clean spilled oil has a spongy material slides on skis	operates on the seafloor works to remove lost fishing nets has a hook swims with fins
Krenshaws operates on land works to clean spilled oil has a shovel slides on skis	Krenshaws operates on the seafloor works to remove broken glass has a large intake fan flies with a propeller
operates on the surface of the water works to gather harmful solids has a spongy material rolls on wheels	operates on the beach works to remove carbon dioxide has a hook rolls on a tread

Note. Morkels are machines whose features combine in a coherent manner. Krenshaws are machines whose features do not combine in a coherent manner.