Morphological optimization for access to dual oxidants in biofilms

Significance

Principle questions in the field of biology concern the evolutionary advantages conferred by the multicellular lifestyle and by the formation of specific multicellular structures. In microbial biofilms, many cells cooperate to form distinct macroscopic patterns. Here we develop and apply a mathematical model, which incorporates empirical values, to show that the tall “ridges” produced by Pseudomonas aeruginosa colony biofilms maximize community growth via enhanced access to oxygen. Production of endogenous redox-active compounds, which mediate electron transfer from cells to oxygen, allows the formation of wider ridges. Externally supplied and endogenously produced oxidant availability controls feature geometry in a manner consistent with the model predictions for optimal geometry.

Abstract

A major theme driving research in biology is the relationship between form and function. In particular, a longstanding goal has been to understand how the evolution of multicellularity conferred fitness advantages. Here we show that biofilms of the bacterium Pseudomonas aeruginosa produce structures that maximize cellular reproduction. Specifically, we develop a mathematical model of resource availability and metabolic response within colony features. This analysis accurately predicts the measured distribution of two types of electron acceptors: oxygen, which is available from the atmosphere, and phenazines, redox-active antibiotics produced by the bacterium. Using this model, we demonstrate that the geometry of colony structures is optimal with respect to growth efficiency. Because our model is based on resource dynamics, we also can anticipate shifts in feature geometry based on changes to the availability of electron acceptors, including variations in the external availability of oxygen and genetic manipulation that renders the cells incapable of phenazine production.

A desire to understand the relationship between form and function motivates many lines of inquiry in biology, including the study of multicellular morphologies and the evolution of these features. Cells grow and survive in populations in many types of natural systems. These multicellular populations include bacterial biofilms, such as Pseudomonas aeruginosa microcolonies in the lungs of cystic fibrosis patients (1) and cyanobacterial colonies and mats in marshes, lakes, and oceans (2, 3), and complex eukaryotic macroorganisms, such as plants and animals. In many of these contexts, enhanced survival arises from advantages associated with multicellularity at multiple scales. Recent work demonstrated that simple cooperation within aqueous microbial biofilms allows groups of genetically similar cells to form tall mushroom-like structures that reach beyond local depletion zones into areas of fresh resources (4–12). Other work has shown that basic colonial growth (e.g., that of budding yeast) and the evolution of complex multicellular life are accompanied by enhanced growth efficiency and several energetic advantages (13–15).

The specific organization of and relationship between cells living within a population are important characteristics that determine whether organisms benefit from the multicellular lifestyle. For example, in mammals the metabolic rate of individual cells is regulated by the size of the whole organism, an effect that confers greater efficiency (15). Cells have dramatically elevated metabolic rates when living as individuals in culture compared with when they survive and grow as members of a multicellular organism (15). This regulation is considered a natural consequence of resource supply within hierarchical vascular networks (15–17) and highlights the importance of morphology and structure in dictating cellular physiology for multicellular systems. Variations in gross morphology also may provide information about how different species are adapted to their environments. For example, differences in leaf venation patterns among diverse species of plants are fundamentally related to tradeoffs associated with carbon assimilation and transpiration rates, water supply rates, and overall mass investment (18). This variation in venation network structure is affected by and may influence the mechanisms and efficiency with which resources are supplied to individual cells. Gradients of resources, particularly oxygen, are similarly important in modulating the development of embryos, lungs, hearts, and tumors (19–24).

Thus, one of the dominant effects of multicellularity is to alter the environment experienced by the individual cell. This raises questions such as (i) how are morphology, metabolism, and environmental conditions interconnected and (ii) how do these relationships govern the fundamental benefits and tradeoffs of multicellularity? Understanding these connections may help us understand the general trajectory by which simple and complex multicellular life evolved and allow us to better identify and quantify morphologically complex structures that may represent paleobiological populations (25).

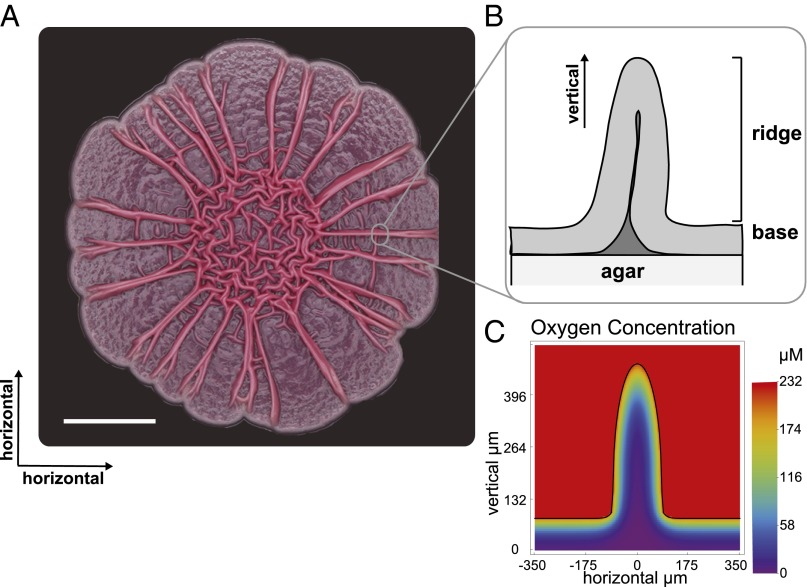
Bacteria form structurally diverse biofilms in different environments and are well-suited for the study of relationships among the morphology, metabolism, and chemical heterogeneity of multicellular populations (26). Most laboratory studies addressing biofilm development are performed in flow-cell systems, in which bacteria are grown on a glass slide and exposed to a continuous flow of a liquid growth medium. In the regime of biofilms submersed in liquid, representative Gram-negative bacteria, including P. aeruginosa, form mushroom-like structures in response to external nutrient gradients (4–12). We grow P. aeruginosa biofilms on agar-solidified growth media in a controlled atmosphere. A standard protocol, the colony morphology assay, is used to generate these biofilms (27). Ten microliters of a cell suspension is pipetted onto an agar plate, and the development of the colony at room temperature and constant humidity is monitored over several days. In this model system, we can modify the environmental and biological conditions and examine the resulting shifts in structure and chemistry. Colony biofilms that form under these conditions exhibit spatial patterning (Fig. 1A) and environmental sensitivity and constitute an ideal model system for exploring morphology as a metabolic adaptation (28).

Fig. 1.

Horizontal (A) and vertical (B) structures of P. aeruginosa colony biofilms. The colony was grown air-exposed on 1% tryptone, 1% agar for 5 d. The scale bar represents 0.5 cm. (C) The simulated concentration of oxygen within a ridge.

Although numerous processes, including extracellular matrix production, osmotic pressure gradients, cellular motility, and spatially heterogeneous cellular death (e.g., refs. 4, 9, 12, 29, 30), have been shown to be involved in the production of biofilm patterning, it is not yet fully understood why or how feature formation has evolved, especially in the context of air-exposed biofilms. We have reported that redox-active signaling molecules called phenazines have dramatic effects on population behavior. Whereas wild-type colonies remain smooth for the first 2 d of growth, phenazine-null mutant (Δphz) colonies undergo a major morphotypic transformation (31). At day 2, Δphz colonies begin to spread over the surface of the agar plate. Two types of wrinkle structures form: those within the area of the original droplet, which appear to be more “disorganized,” at the colony center and those that radiate from the center toward the colony edge (referred to here as “ridges”). Both types of features are vertical structures (Fig. 1). Wild-type colonies also form wrinkles in the center, but only after 3 d of growth, and a mutant that overproduces phenazines remains smooth when monitored for 6 d. These strains therefore demonstrate an inverse correlation between increased colony surface area and phenazine production (31).

More recently, we showed that P. aeruginosa colony wrinkling is a strategy to increase oxygen accessibility (28). We have proposed that phenazines attenuate this mechanism because they act as electron acceptors for cells in anoxic regions of the biofilm and shuttle electrons to the well-aerated regions, allowing cells to balance their internal redox state (28, 32, 33). We proposed that a reduced cellular redox status triggers a morphological change at the population level. Consistent with this model, adding nitrate (an alternate electron acceptor) to the agar, or increasing atmospheric oxygen concentrations (to 40%) prevents spreading of the Δphz colony and discourages wrinkle formation. Decreasing external oxygen availability (to 15%) increases wrinkle formation as well as spreading of the colony (28). Oxygen profiling of the colonies indicates that the Δphz mutant is well oxygenated within wrinkles, suggesting that its morphotype is an adaptation for enhanced oxygen uptake (28). It is noteworthy that wrinkles reach a final, static width while continuing to grow taller. The wrinkle width achieved is correlated with the concentration of oxygen provided in the atmosphere. Additionally, eliminating the ability to wrinkle (by deleting the genes for extracellular matrix production) has been shown to lead to a redox imbalance, as indicated by an elevated NADH/NAD⁺ ratio (28).

The sensitivity of colony morphogenesis to oxygen, nitrate, and phenazines suggests a significant role for oxidative capacity in modulating morphology. Here we develop a simple mathematical model, rooted in established physical laws and physiology, that demonstrates and confirms this significance. Combining this model with experimental verification enables us to make predictions and interpretations that would be infeasible using modeling or experimentation alone. The model incorporates the response of growth rate to oxygen availability and accurately predicts the measured oxygen distribution within colony features. Because it is based on resource dynamics, it also anticipates shifts in feature geometry based on external oxygen availability. Finally, quantitative experiments verify our methodology. We demonstrate that biofilms produce features with geometries optimal for the growth efficiency of the entire colony and sensitive to the redox environment, as determined by factors such as oxygen availability and phenazine production.

Modeling Biofilm Metabolism and Oxygen Dynamics

Several key features of the colony biofilm system inform our understanding of the processes governing morphology and form the foundation for our modeling framework. (i) Wrinkling in the colony system is a basic feature of the wild type that occurs late in development as a response to electron acceptor limitation (28). (ii) Overall colony wrinkling, as well as the geometry of individual features (width of wrinkles), can be modified easily by altering the redox conditions (e.g., increasing oxygen availability or knocking out the ability to produce phenazines) (see ref. 28 for P. aeruginosa and ref. 34 for similar results in Bacillus subtilis). (iii) Colony wrinkles reach a constant width early in development but continue to grow taller at a nearly linear rate. Taking these last two observations together, we assume that electron acceptor rather than nutrient supply is the primary limitation faced during colony development and is responsible for feature geometry. If nutrient supply from the agar below a feature were controlling width, we would expect to see a decrease in the overall growth of a feature as the constant width is reached. We would not expect to observe the linear increase in ridge height; this would only increase nutrient limitation as chemicals are forced to diffuse over a narrow and increasingly long distance.

To study the basic dynamics of resources and geometric feature formation, we first empirically characterize and model colonies of the phenazine-deficient mutant (Δphz) in a context in which oxygen is the only available terminal electron acceptor. We later expand experiments and the model to consider wild-type colonies, which have the sole addition of redox-active phenazines produced by the cells.

We base our mathematical model on the simplest hypothesis for feature regulation: the dynamic feedback between metabolism, resource availability, and physical diffusion (e.g., refs. 6, 8, 35–43). We use the Pirt model, which interprets the linear relationship between population metabolism and growth rate as a metabolic partitioning between growth and maintenance (44) and is consistent with the physiology of a broad range of bacterial and eukaryotic species (see, e.g., refs. 13, 45 for a review). It is combined with the Monod model, which parameterizes population growth rate as a saturating function of the external concentration of a limiting resource (46). This combination of parameterizations has been used widely (e.g., refs. 6, 35, 41, 43) and here provides an equation for the oxygen consumption as a function of available oxygen:

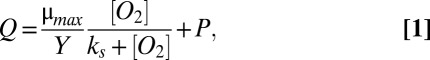where Q is a consumption rate per unit mass of a limiting resource that provides energy and/or structural material to the population of cells (mol resource⋅s⁻¹⋅g cells⁻¹), μ is the specific growth rate (s⁻¹), Y is a yield coefficient (g cells⋅mol resource⁻¹), P is a maintenance term (mol resource⋅s⁻¹⋅g cells⁻¹), μ_max is the maximum growth rate approached as the substrate concentration is taken to infinity, and k_s is the half-saturation constant.

Depletion of oxygen within the biofilm creates a gradient with the atmosphere and drives a diffusive flux of oxygen into the colony. The time-dependent spatial concentration of oxygen may be described by

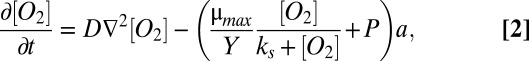where a is the density of cells in the colony (g cells ⋅ m⁻³). Similar models have been used widely in biofilm and broad ecological modeling (e.g., ref. 35). This equation can be conveniently nondimensionalized:

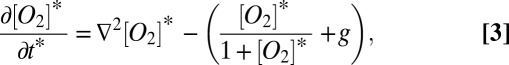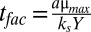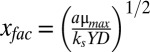where the temporal and spatial scales, respectively, have been normalized by the factors and . Oxygen concentrations have been divided by k_s, and the nondimensional maintenance term is g = YP/μ_max. For steady-state solutions, the model relies only on the concentration of oxygen at the colony surface, which is determined by the atmospheric mixing ratio and pressure, and the two parameters x_fac and k_s. We determined the value for both parameters by first compiling published measurements and then constructing the mean of every combination within this compilation (Table S1). Here we use the Pirt–Monod diffusion model framework to interpret the community benefit of specific geometrical features of the colony and to interpret mechanisms underlying the architectural optimization within biofilms. We also model the dynamics and benefits associated with multiple oxidative resources and show that biogenic redox-active molecules are beneficial to community growth and survival.

Results

Observations of Internal Oxygen Distribution.

To investigate how these mechanisms regulate morphology, we study a single feature of a P. aeruginosa colony biofilm, i.e., the ridge (Fig. 1), and its surrounding geometry.

We take oxygen profiles of the colony “base” (Fig. 1B), where biofilm geometry is simplest, and we use these profiles to examine our literature-based parameter estimates and calibrate our model. First, we measure oxygen availability with increasing depth (Fig. 2). There is some variation in the decay rate and the depth at which oxygen no longer can be detected (Figs. S1 and S2). Most of this observed variation may be accounted for by rescaling the depth axis by a simple factor, after which the profiles share a similar shape. This normalization highlights common overall biological activity and variation in the physiological parameter values.

Fig. 2.

Oxygen profiles of 4-d-old colony biofilms for (A) the base region and (B) the ridge. Measured values are given by points, and simulations are represented by the solid curves. We took measurements for 37 base profiles and 27 ridge profiles over 5 d of growth, and the data in A and B represent the variation within the observed profiles. Arrows indicate the top of the biofilm surface. Data from ref. 28.

We fit the observed variation in vertical 1D profiles by varying x_fac and solving for the steady-state oxygen concentration in our model for an isolated base geometry while keeping k_s fixed. Fig. 2A shows that steady-state solutions of our model in the base capture the range of observed oxygen profiles. The variation in profiles also allows us to calibrate the range of x_fac to be bounded by 7.3 × 10⁴ and 1.6 × 10⁵ with a mean value of 9.1 × 10⁴. This range compares well to our estimate from the literature of 7.7 × 10⁴ μm (Supporting Information). Given our definition of x_fac the observed variation could be due to differences in physiological parameters, such as maximum growth rate or substrate yield, or to differences in the physical parameters, such as density, wetness, and overall oxygen diffusivity of the colony.

Experimentally, we find that oxygen availability decreases with increasing depth into the colony. However, this effect is much more dramatic in the base than in the ridge. This likely is the result of increased surface area for a reduced cellular mass. To interpret this phenomenon, we use the calibrated model to simulate the steady-state distribution of oxygen availability within a ridge and the surrounding base, and we do this for various geometries of the ridge (Fig. S3A).

Our model also captures the general decay rate and shape of these ridge profiles (Fig. 2B). These profiles were created using the mean value of the parameter calibration and the general variation in ridge width because it is experimentally challenging to measure the width and oxygen profile simultaneously.

Our ability to anticipate the general shape and variation of oxygen profiles within the ridge gives us confidence in our calibration and the model’s predictive capacity. It should be noted that once these calibrations have been made, all other results in this paper follow directly as predictions.

The Impact of Colony and Feature Geometry.

The increased depth of oxygen penetration in the ridge region (Fig. 2B) illustrates the importance of geometry in enhancing oxygen availability within the colony. The question then becomes how changes in this geometry affect oxygen availability within the colony. To explore this, we simulate the simplest geometric variation by preserving the overall shape of the ridge but varying the width of the ridge for a fixed height. Fig. S3A (Supporting Information) shows the distribution of oxygen within ridges of different widths. From the internal oxygen distribution and Monod equation (Supporting Information), we can calculate the local growth rate and we find that ridges generally have an enhanced growth rate relative to flatter regions of the colony (Fig. S3B). This is because tall, thin features increase the total surface area for a relatively small amount of biomass, which enhances the oxygen flux per total consumption, resulting in increased oxygen penetration. However, we also see in Fig. S3 (Supporting Information) that as ridges grow wider, the effect of enhanced growth is diminished and the layer of growing cells within the ridge region becomes similar in thickness to that of the base regions.

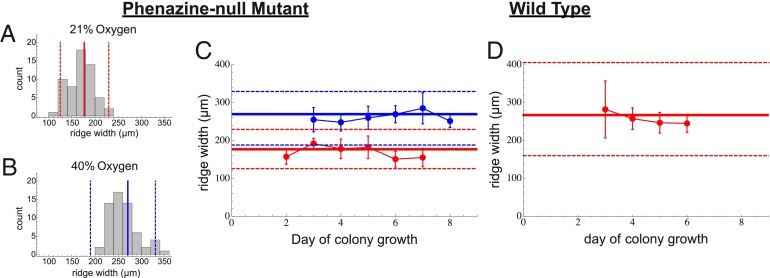
This effect implies a tradeoff for population metabolism: Although thin structures are entirely oxygenated, allowing cells to grow quickly, their relatively small size limits the number of cells they contain. Thick features house many more cells, but the region of enhanced oxygen penetration and growth is smaller. This tradeoff may be summarized using the total reproductive rate, R, of the colony, where the derivative of R with respect to mass describes how much added growth the colony will experience given an investment in additional mass. This derivative gives the growth efficiency of the colony in that it represents the return on mass investment in terms of total reproductive capacity. We calculate R for an ensemble of simulated features at a fixed height but with different widths, and find that R reaches a maximum for ridges with a specific width. This represents the optimal width for efficient cell proliferation within the colony and also corresponds to the width at which all cells within a feature can at least meet their minimum metabolic maintenance requirements. More importantly, the optimal width found in our model accurately predicts the observed average width of colony features along with the observed variation in widths for colonies growing on an agar plate exposed to 21% external oxygen (Fig. 3). This prediction is made by solving for the optimal width using the minimum, maximum, and average parameter values from our calibration to base profiles.

Fig. 3.

The average width of colony ridges as a function of time for Δphz (A–C) and wild-type (D) colonies. (A and B) Histograms for all ridge width measurements at 21% and 40% oxygen. (A–D) The solid red (21% oxygen) and blue (40% oxygen) lines represent our predictions for optimal ridge width, and the dashed lines represent our predictions for the bounds of variation in ridge width.

Similarly, for simulations of the base, we find that R approaches a constant value when the height of the base reaches the maximum depth to which oxygen can penetrate. Thus, any additional base height does not produce additional growth for the colony. Experimentally, we find that the average base thickness corresponds to the average depth at which oxygen no longer is detectable.

The observed colony features are such that if features grow wider (or taller in the case of the base) than this optimal size, the colony has invested a large amount of mass that will not grow quickly. If the features are smaller than this optimum, the colony has invested a small amount of mass, but there will be less overall growth as a consequence. We suggest that natural selection has favored cellular behavior that gives rise to features with emergent geometries that maximally benefit the population, as was proposed previously in similar contexts (e.g., ref. 26).

It should be noted that we observe that during early colony growth, the ridges maintain a constant width while height continues to increase. This implies that nutrients are not limiting, and it then is surprising that in the outermost layer of cells, growth is arrested despite the abundance of oxygen and capacity for further growth. This raises the possibility that cellular growth within the ridges is regulated to optimize the growth efficiency of the population.

Morphological Response to Oxygen Availability.

We have shown evidence of oxygen control driving the optimization of colony form. Feature geometry is important because of the impact it has on the availability of oxygen within the colony. Given this interconnection between geometry and oxygen, we would expect that changes in the external availability of oxygen would result in shifts in colony form. To test this hypothesis, we exposed colonies to elevated concentrations of external oxygen (40% compared with the standard 21%).

To quantify these shifts, we again calibrate the parameters of our model. We do not have the appropriate experimental setup to measure oxygen profiles in colonies grown in our hyperoxia chambers. As an alternative, we use colony base heights as proxies for oxygen penetration distances (base heights correspond to the depth at which oxygen is depleted). These measurements are sufficient for calibrating x_fac to the 40% external oxygen conditions.

The observed widths in 40% external oxygen are wider than in 21%. Running our simulations with 40% external oxygen, and the calibrated range of parameter values, we again successfully predict the mean, upper bound, and lower bound on observed ridge widths (Fig. 3). Through our model, we interpret the wider ridge width as the result of deeper oxygen penetration, which extends the width at which a diminishing return on mass investment occurs. We also predict, in good agreement with data, that in 15% external oxygen, ridge width will be reduced (Fig. S4).

Morphological Response to Other Oxidants.

Our observations and modeling thus far have concerned a P. aeruginosa Δphz mutant, which cannot produce phenazines. We can predict the significant effects of oxygen availability on feature development and the optimal ridge width in this scenario, in which oxygen is the only electron acceptor the bacteria can use to balance the intracellular redox state. However, it is important to test whether our conceptual framework may be used to determine the effects that phenazines, as endogenously produced oxidants, have on feature geometry (28). To address this challenge, we examine aspects of the wild-type colony in which we have developed a model that accounts for the dual use of oxygen and phenazines as electron acceptors. We have developed a mathematical model in which we allow both oxygen and phenazines to diffuse and be reduced within the colony. In this model, oxygen is consumed directly by cells and also is used for reoxidizing phenazines, and cells reduce both substrates to support their metabolic rate (see Supporting Information for a detailed presentation of the model).

This model accurately predicts the decay of oxygen with increasing depth into the base region of the colony. Near the surface, this decay rate is observed to be nearly identical to that of the Δphz colonies. However, deep in wild-type colonies, cells cease to consume oxygen, which in the context of our model, may be interpreted as the point at which phenazines are used as alternate electron acceptors. Experimentally, cells expressing YFP from a constitutive promoter (suggesting metabolic activity) have been observed at a depth of 100 μm in wild-type colonies compared with a depth of only 60 μm in Δphz mutant colonies (28).

It appears that the presence of phenazines allows an oxidative potential to extend deeper into the colony. In our model, we see that this is the consequence of phenazines being oxidized in the surface layer and diffusing into the deep layers, where they are consumed when oxygen reaches a low enough level.

Using this model, we again can evaluate the effect of ridge width on colony growth and predict optimal ridge width when phenazines are present. Our predictions agree well with observations for the wild type growing in 21% oxygen (Fig. 3C). The observed and predicted features are significantly wider than the Δphz ridges grown under the same conditions. The wild type is effectively a Δphz mutant with phenazines added, and the effect of phenazine addition is qualitatively the same as that of increasing oxygen availability for the Δphz mutant. This highlights that the availability of oxidative resources strongly controls feature geometry and that these effects can be modeled predictably, provided that the redox chemistry and physiology of the colony are well defined.

Discussion

The study of biofilms has diverse applications. For example, biofilms may act as model ecological systems to investigate the nature of cooperative and competitive behavior and dynamics (e.g., refs. 4, 12). To understand biofilm physiology in a variety of contexts, it is critical to define the connections between population structure and access to resources. We have developed a mathematical model of substrate availability and cellular metabolism within colonies. The predicted oxygen distribution and its effects on colony morphology have been verified empirically using a standard biofilm assay. We have shown that standard physiological characterizations of biofilms may be combined with an analysis of community growth as a function of geometry to predict optimal biofilm morphology. Furthermore, we have illustrated that these optima are influenced greatly by external redox conditions and the ability of biofilms to produce redox-active molecules.

One of the major findings of this paper is that the shapes of biofilms may allow optimal interaction with the environment for resource availability and therefore optimal total growth and return on mass investment. The ridges of P. aeruginosa colonies maintain fairly uniform width even as they grow taller. Previous studies showed that steady-state biofilm feature shape results from external resource limitation and occurs when the environment no longer can supply substrates for further growth (e.g., refs. 4, 5, 7, 12, 47). In contrast to the model systems used for these studies, our colony biofilm is exposed to the open atmosphere, in which external resource gradients effectively are nonexistent. Thus, cells in the outermost layer of a colony are not resource limited, and they have the capacity for further growth, as evidenced by the oxygen profiles and the observation that they grow taller. The ridges have the capacity for horizontal growth, and the simplest passive model of the dynamics driven solely by growth rate would predict increasing ridge width over time. Therefore, unknown mechanisms must maintain the constant ridge width that apparently is advantageous to the overall colony.

Although wrinkling is a common response of the biofilm system, we have seen that ridge geometry is affected by both environmental (external oxygen availability) and physiological (the inability of the Δphz mutant to produce phenazines) alterations. Furthermore, it has been observed that no wrinkling occurs in a mutant unable to produce the Pel polysaccharide [a critical component of matrix structure (27, 28)], and our experience with a wide variety of single gene knockouts indicates that many physiological changes alter the details of spatial patterning and wrinkle formation. This suggests that wrinkling is the result of many physiological processes, as already highlighted by the variety of single mechanisms shown to be related to pattern formation in biofilms (4, 12, 29). Given the complexity of cellular physiology and response, there are countless systems of cellular behaviors, interactions, and feedbacks that conceivably might evolve to produce diverse biofilm structures. Many of these structures would not be optimal for the average reproductive success of cells within the colony. This suggests that the specific set of mechanisms in our biofilm system may have been selected to produce emergent patterns that we observe to be optimally beneficial to the colony. Studies recently indicated that biofilm structures are underpinned by diverse cell behaviors, including chemotaxis, extracellular matrix production, chemical signaling, and selective cellular death as an induction for mechanical buckling in thin films (4, 12, 29). Whether disruptions in these mechanisms produce suboptimal biofilm structures remains to be investigated. In addition, features may serve multiple roles in different contexts or species, implying a variety of selective pressures. For example, a recent study reported that the channels that form within wrinkles in B. subtilis biofilms facilitate liquid movement through the structure (48).

In considering the possibility that biofilm patterning has been selected for as a stable adaptive trait, it is important to recognize the tradeoffs faced by individual cells, including the potential for “cheaters” to disrupt patterning and the associated benefits to the population. For example, phenazines are a community resource produced at a cost. Once excreted, these compounds may be taken up and participate in repeated redox cycling by both phenazine-producing and nonproducing cells (32). In the biofilm context, strategies may be used to avoid the likely benefit experienced by cheaters that catalyze redox cycling without contributing to the phenazine pool. Recent work has shown that extracellular matrix formation is a strategy that allows only cooperating cells to gain the benefit of the tall structures built by the community, so long as the cooperators exist in high enough local abundance and matrix properties (production rate and density) fall within a predictable range (4, 12).

Characterization of the relationships among metabolism, chemical gradients, and morphogenesis of bacterial biofilms provides information relevant to diverse fields. Bacterial biofilms may exhibit complex spatial patterning at scales comparable to those of putative microbial fossils (25, 47). Our biofilm system has allowed us to test the effects of different atmospheric oxygen concentrations directly and to demonstrate that the width of features changes predictably. These findings may provide a basis for verifying microbial fossils and using them as reporters of the ancient environment. For example, in aquatic environments, the diffusive boundary layer for oxygen that forms around the biofilm is what influences feature geometry (4–12) in contrast to the open-atmosphere biofilms studied here, in which the important oxidative gradients occur inside the biofilm. These differences provide avenues for interpreting which environments are capable of producing an observed morphology.

Biofilm development is a critical component of bacterial colonization of and persistence within human and other eukaryotic hosts. It contributes to the establishment and maintenance of various types of P. aeruginosa infections. Here we find that biofilms produce optimal structures to enhance growth and that the success of the colony depends on the ability to build these structures effectively. As we learn more about the complex set of cellular behaviors responsible for the emergent regulation of these features, we become better equipped to take new approaches toward controlling biofilms in clinical and industrial settings.

Methods

Bacterial Strains and Growth Conditions.

Wild-type P. aeruginosa PA14 and a mutant (Δphz) deficient in phenazine production were used in this study (49). Bacterial cultures were grown routinely at 37 °C in lysogeny broth, shaking at 250 rpm overnight. For all oxygen profiling experiments, colony biofilms were grown on 1% tryptone (Teknova)/1% agar (Teknova) plates amended with 20 μg/mL Coomassie blue (EMD) and 40 μg/mL Congo red (EMD). Colony biofilms were grown at room temperature (22–25 °C) and at high humidity (>90%). Sixty milliliters of the medium was poured per 10-cm² plate (D210-16; Simport) and allowed to dry with closed lids at room temperature for 24 h. Ten microliters of the overnight culture was spotted on these agar plates, and colony biofilms were grown for 6 d. Colonies were grown under hypoxic (15% oxygen) or hyperoxic conditions (40% oxygen) as described earlier (28). Briefly, we incubated agar plates in C-Chambers (C274; BioSpherix). Oxygen concentrations were regulated by mixing pure nitrogen and oxygen (Tech Air), using the gas controller ProOx P110 (BioSpherix).

Colony Geometry Measurements.

Width and height of ridges within colony biofilms were measured with a digital microscope (Keyence VHX-1000).

Oxygen Depth Profiles.

Oxygen profiling was done using a miniaturized Clark-type oxygen sensor (Unisense; 10-μm tip diameter) on a motorized micromanipulator (Unisense) for depth control. The electrode was connected to a picoampere amplifier multimeter (Unisense) and polarized at −800 mV. The sensor was calibrated using a two-point calibration system at atmospheric oxygen and zero oxygen. The atmospheric oxygen reading was obtained by placing the electrode in a calibration chamber (Unisense) containing well-aerated deionized water. Complete aeration was achieved by constantly bubbling the water with air. The zero reading was obtained by bubbling water in the calibration chamber with ultra–high-purity nitrogen gas (Tech Air). All calibration readings and profile measurements were obtained using SensorTrace Pro 2.0 software (Unisense).