Mechanisms underlying subunit independence in pyramidal neuron dendrites

Significance

Historically, neurons were thought to collect synaptic currents from across their dendritic trees and passively conduct them to the soma where action potentials (APs) are generated. More recent studies have shown that dendrites can generate local spikes and thus may function as independent computational subunits. It remains unknown, however, how dendrites can maintain the integrity and separateness of their local computations, which depend on voltage, despite the repeated synchronization of dendritic potentials by back-propagating somatic APs. This modeling study identifies three biophysical specializations that allow dendrites to remain functionally independent in a firing neuron, one of which is the somatic spiking mechanism itself. Our results suggest that a major class of neurons has been optimized for subunitized computation.

Abstract

Pyramidal neuron (PN) dendrites compartmentalize voltage signals and can generate local spikes, which has led to the proposal that their dendrites act as independent computational subunits within a multilayered processing scheme. However, when a PN is strongly activated, back-propagating action potentials (bAPs) sweeping outward from the soma synchronize dendritic membrane potentials many times per second. How PN dendrites maintain the independence of their voltage-dependent computations, despite these repeated voltage resets, remains unknown. Using a detailed compartmental model of a layer 5 PN, and an improved method for quantifying subunit independence that incorporates a more accurate model of dendritic integration, we first established that the output of each dendrite can be almost perfectly predicted by the intensity and spatial configuration of its own synaptic inputs, and is nearly invariant to the rate of bAP-mediated “cross-talk” from other dendrites over a 100-fold range. Then, through an analysis of conductance, voltage, and current waveforms within the model cell, we identify three biophysical mechanisms that together help make independent dendritic computation possible in a firing neuron, suggesting that a major subtype of neocortical neuron has been optimized for layered, compartmentalized processing under in-vivo–like spiking conditions.

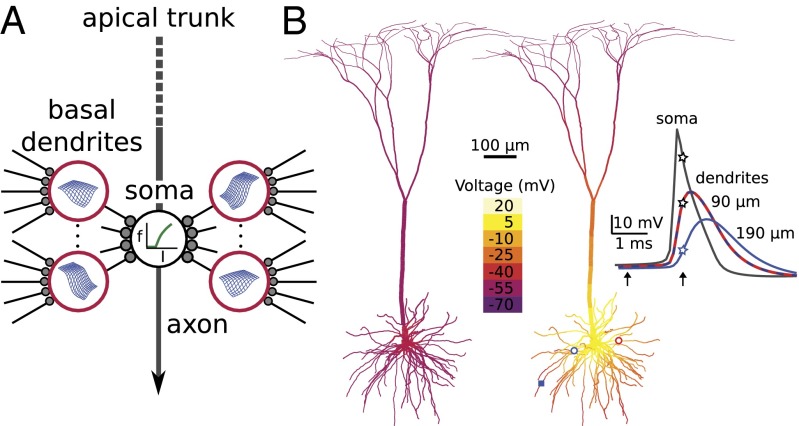
On the path to understanding the diverse information processing functions of the brain, it is essential to develop simplified models of individual neurons. The classical view that a neuron collects excitatory and inhibitory influences from across its dendritic arbor and passively funnels them to a single spike-generating zone near the soma has been challenged by the finding that dendrites generate local spikes (1–15) and can support a variety of compartmentalized computations (16–28). We previously showed that the input–output (i/o) behavior of a dendritic subtree, whose branches emanate from a main trunk or soma, can be described by a two-layer model (2LM), where the first layer consists of multiple independent dendritic “subunits” with stereotyped nonlinear i/o functions. In the second layer, corresponding to the soma, the dendritic outputs are summed and fed through the cell’s somatic firing rate-current (f-I) curve (8, 21, 22, 29) (Fig. 1A). The core assumption of the 2LM is that each dendrite’s output depends only on its synaptic inputs, and is independent of the activity of other dendrites or the cell as a whole. The 2LM was previously tested in both experimental and modeling studies, outperforming passive dendrite (one-layer) models in predicting pyramidal neuron (PN) responses both to brief inputs leading to subthreshold somatic responses (8, 29) and to high-frequency stimulation that produced output trains lasting hundreds of milliseconds (21, 22). Notwithstanding the improved description of PN responses provided by two-layer models, a substantial fraction of the response variance remained unexplained by 2LM predictions in those previous studies (21, 22), leaving unanswered whether the prediction failures arose from (i) inadequately modeled first-layer details, such as location (30) or spatial interaction (31, 32) effects within dendrites, or variation in the sigmoidal input–output functions from dendrite to dendrite, either of which could be incorporated into a two-layer scheme (Fig. 1A), vs. (ii) functional “cross-talk” between dendrites that would signify a breakdown of the 2LM’s core assumption of subunit independence. On its face, the notion that dendrites can independently process their synaptic inputs using local voltage signals in a firing neuron is counterintuitive, given the global synchronizing effects of back-propagating somatic action potentials (bAPs) (33–36) (Fig. 1B). These high-amplitude voltage waves repeatedly sweeping into the dendritic arbor broadcast summary information from the entire cell back to the entire cell and would seem likely to disrupt and/or homogenize the subtle voltage-dependent interactions between synapses occurring at the same time in different dendrites. In particular, bAPs repeatedly invading the dendrites would seem likely to alter the timing, duration, or pattern of synaptically evoked dendritic spikes, which constitute a major readout mechanism of PN thin dendrites (11, 37, 38). On the other hand, PNs might be specialized to minimize the disruptive effects of bAP-mediated cross-talk, allowing multiple dendrites to be simultaneously engaged in distinct voltage-dependent computations. To distinguish these possibilities, we developed an improved method to quantify subunit independence in a firing neuron under multisite, multibranch stimulus conditions. Applying this method to a detailed model of a layer 5 pyramidal neuron, we show that PN dendrites are more functionally independent than previously appreciated, and we identify the biophysical mechanisms that allow a PN to function as a nearly ideal two-layer network even under the highly variable conditions that exist in vivo.

Fig. 1.

Two-layer model of dendritic integration, and the challenge of bAP-induced voltage synchronization. (A) The two-layer model consists of a layer of independent dendritic subunits (red circles) feeding into the soma (the second layer) where the axosomatic spike-generating mechanism converts the total dendritic current (I) into an output firing rate (f). Two-dimensional sigmoidal surfaces (in blue) represent multidimensional dendritic input–output functions, reflecting recent findings that dendritic responses depend both on the absolute and relative locations of activated synapses on the branch (30, 31). (B) Snapshots of the layer 5 PN model’s membrane potential just before (Left) and near the peak (Right) of a spike generated by a somatic current injection. Right frame illustrates the synchronization of membrane potential across the basal arbor as a back-propagating action potential (bAP) sweeps outward from the soma. (Inset) Timing of somatic AP (black trace) relative to bAPs recorded in two dendrites 90 μm from the soma (superimposed red and dashed blue traces, corresponding to red and blue open circles), and at a third site 190 μm from the soma (blue square and solid blue trace). Note that the action potential back propagation is decremental. Arrows indicate times of Left and Right voltage snapshots. Vertically aligned stars mark traces at time of second snapshot.

Results

We quantified subunit independence as follows. A somatic f-I plot was first generated for the model cell. Then, varying numbers of excitatory synapses were activated at one or more sites on one or more dendrites in a large number of simulation experiments, and for each stimulus configuration, the resulting firing rate was recorded, translated back through the somatic f-I curve into a current value, and tabulated. Based on the 2LM assumption that the current a dendrite produces depends only on its synaptic inputs, we used least squares linear regression to determine the best single estimate for the current reaching the soma for every stimulus configuration on every dendrite considered separately (SI Materials and Methods). Roughly speaking, the current estimate for any given stimulus on a single branch was the average increment in the current reaching the soma when that stimulus was applied on top of every other possible stimulus configuration delivered to the other branch(es). Predictions of the 2LM in response to multibranch stimulation could then be generated by summing the current estimates for each stimulated branch and mapping the total current through the somatic f-I curve to arrive at a predicted firing rate (Fig. 1A). This prediction could then be compared with the actual firing rate generated by the compartmental model in response to the multibranch stimulus. To the extent that the predicted and actual rates matched over a wide variety of stimulus configurations, the independent subunit hypothesis would be supported. Prediction failures would signal the presence of cross-talk between dendrites in violation of the core 2LM assumption.

Simple Test of the 2LM: One Stimulus Site on Two Dendrites.

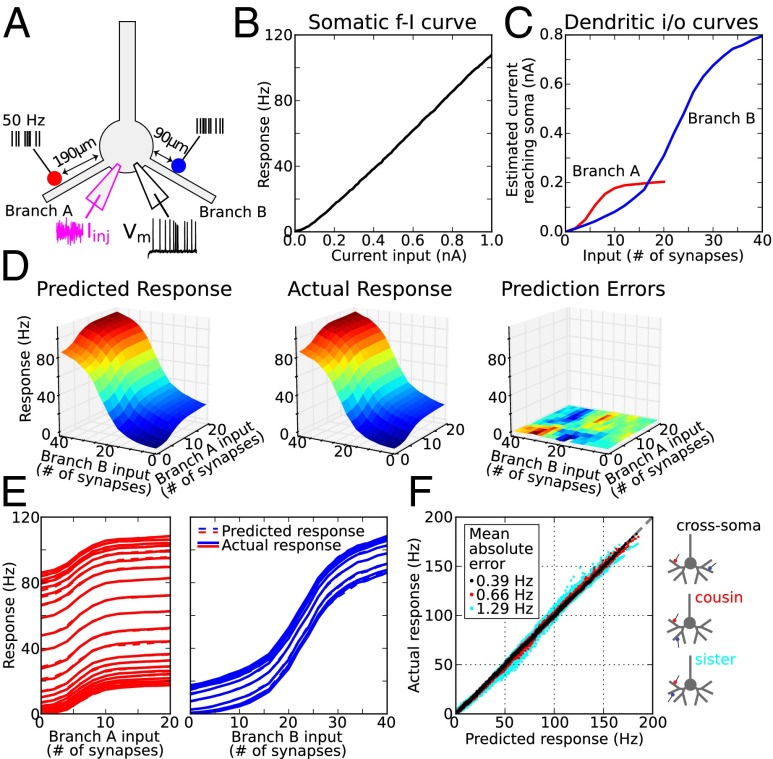
We first considered a simple case involving two dendritic branches, each one stimulated at a single site (Fig. 2A). Random background activity was modeled by a noisy current injection at the soma (Fig. 2A, magenta trace) that produced a very low (∼0.5 Hz) resting firing rate; the resulting somatic f-I curve is shown in Fig. 2B. Against this background, we stimulated 1–20 synapses on branch A in a cluster 190 μm from the soma (Fig. 2A, red marker indicates cluster center), and 1–40 synapses 90 μm from the soma on branch B (Fig. 2A, blue marker), for a total of 800 stimulus configurations. All synapses contained both AMPA- and NMDA-type conductances and were activated by independent 50-Hz Poisson trains for 500 ms. Dendritic i/o curves derived using the least squares method described above (see also SI Materials and Methods) show the somatic current estimates for the two stimulus sites considered separately (Fig. 2C). The sigmoidal form of the two i/o curves was due primarily to the voltage dependence of the NMDA channels (30, 39). The “threshold” stimulus intensity (taken as the inflection points of each sigmoid) was fourfold lower for the more distal site on branch A, given the much higher input resistance near the distal tip of a dendrite. The amplitude of the distal sigmoid was also several-fold lower, given the smaller amount of current injected at the peak of the spike and the greater attenuation of the distally injected current along the path to the soma. By mathematically composing the dendritic and somatic i/o curves representing the first and second layers of the 2LM (Fig. 2 B and C), and using only the information contained in Fig. 2 B and C, we generated predicted firing rates for all 800 stimulus configurations (Fig. 2D, Left). Actual firing rates were then generated by the compartmental model for the same configurations (Fig. 2D, Center). Prediction errors were very small [Fig. 2D, Right; mean absolute error (MAE) = 0.32 Hz; maximum error <2 Hz over the entire stimulus space]. To facilitate comparison of predicted vs. actual responses, slices of the 3D response plots along both main directions are shown in Fig. 2E (predicted rates, dashed lines; actual rates, solid lines). Fits between predicted and actual rates were accurate over the >100-Hz range. The progressive vertical shifts of the input–output curves in the slice plots reflect that in the special case of a nearly linear somatic f-I curve (Fig. 2B), subunit independence means the effect of a given stimulus on a given branch is to increment the firing rate of the cell by a fixed amount. We repeated the analysis shown in Fig. 2 C–E for all 81 (9 × 9) pairs of locations on the same two dendrites from 50 to 210 μm in 20-μm steps. A scatterplot of all 136,000 predicted vs. actual responses is shown in Fig. 2F (black dots; MAE = 0.39 Hz).

Fig. 2.

Quantifying subunit independence in a simple case: one stimulus site on two dendrites. (A) Schematic of the simulation experiment. Red and blue dots show stimulus locations. Every synapse at each site was driven by an independent 50-Hz Poisson train. A noisy current injection at the soma of 0.75 ± 1 nA set the background firing rate to ∼0.5 Hz, modeling the effects of random network input. (B) Somatic f-I plot. (C) Estimated current arriving at the soma from branch A (red) and branch B (blue) based on the regression fit to actual responses (SI Materials and Methods). Sigmoidal i/o curves for this pair of branches and locations had thresholds (i.e., inflection points) at 5 and 20 synapses, respectively. (D, Left) Predicted firing rates based on plots in B and C and assumption of subunit independence (i.e., that dendritic currents add at the soma). (Center) Actual responses are nearly identical. (Right) Prediction errors (actual–predicted) are very small; color indicates firing rate errors from −1.2 Hz to +1.6 Hz. (E) Slices of the 3D plots in D allowing comparison of predicted (dashed) and actual (solid) firing rates from two orthogonal views. Vertical progression of curves in each plot is due to increasing stimulus intensity in the other branch. (F) Scatterplot of actual vs. predicted firing rates for 81 different stimulus location pairs on two branches (9 × 9, 50–210 μm on each branch in 20-μm steps) for inputs to a pair of cross-soma dendrites (black, mean absolute error MAE = 0.39 Hz; same pair of dendrites was used as in A–E), a pair of cousin dendrites in the same subtree (red, MAE = 0.66 Hz), and a pair of sister dendrites with the same parent (cyan, MAE = 1.29 Hz). See Figs. S1–S5 for control experiments and Fig. S6 for illustrations of synaptic locations on the neuron model.

In comparison with the well-isolated cross-soma branch pair used in Fig. 2 C–E, prediction errors worsened when inputs were delivered to two cousin branches (red dots; MAE = 0.66 Hz) and to two sister branches (cyan dots; MAE = 1.29 Hz), whose closer electrical coupling worked against their independence. Nevertheless, the prediction errors remained small on an absolute scale even for these “worst case” branch pairs, so that over all ∼400,000 combinations of stimulus intensities, dendritic locations, and branch pairs tested, and a >150-Hz response range, firing rate predictions of the 2LM were overall very accurate.

Generality of the Findings.

We manipulated several variables in the model known to affect integrative behavior in PNs. First, given that spine neck resistance can influence the degree of nonlinear cooperativity among neighboring synapses (40) (Fig. S1 A and B), a model-based prediction recently validated experimentally (41), we repeated the experiment of Fig. 2 with spines having 200- and 500-MΩ neck resistances. Although dendritic i/o curves varied as spine neck resistance increased (Fig. S1 C–E, first column), firing rate predictions of the 2-layer model remained highly accurate over the entire range tested (Fig. S1 C–E, second through fifth columns). Second, whereas it is clear that fast spiking Na⁺ channels are part and parcel of the spike-generating mechanism in PN dendrites (9, 10, 39), a recent study in CA1 PNs found that the fast sodium component underlying dendritic spiking can inactivate with repeated stimulation (42). To test whether two-layer behavior would be compromised by the suppression of dendritic Na⁺ currents, we reran the simulations of Fig. 2 with dendritic Na⁺ channels blocked (Fig. S2 A and B). Two-layer model prediction errors, already small, were further reduced, consistent with the fact that the loss of dendritic Na⁺ channels suppressed bAPs, which in turn reduced their disruptive effects (Fig. S2 C and D). Third, apical calcium spikes are known to alter the integrative behavior of neocortical PNs (43, 44). Among other effects, the distal calcium spiking mechanism provides a mechanism for gain modulation, wherein an excitatory input to the distal apical tree lowers the threshold and increases the slope of the somatic f-I curve (45). To determine whether this nonlinear apical–basal interaction would interfere with subunit independence and two-layer summation, we ran additional simulations that incorporated voltage-dependent calcium channels in the apical tree. Although the somatic f-I curve was significantly altered by distal apical stimulation (Fig. S3A), we found minimal disruption to the pattern of two-layer synaptic integration in the basal tree (Fig. S3 B and C); mean absolute prediction errors remained under 1 Hz (MAE = 0.48 Hz). Fourth, although previous studies have shown that synaptic integration in apical tuft dendrites and basal dendrites is more similar than it is different (20, 37), to confirm this, we repeated the basal dendrite experiments of Fig. 2 in a pair of perisomatic oblique branches connected directly to the apical trunk (Fig. S4A), as well as cousin and sister branch pairs in the apical tuft (Fig. S4 B and C). Other than the much lower firing rates evoked in the distal apical case, two-layer prediction results for apical branches were very similar to those seen for basal dendrites.

Finally, to determine whether the accuracy of the 2LM predictions in Fig. 2 depended on the activation of only two dendrites, or on the essentially linear somatic f-I curve, we repeated the test in a case where every stimulus was delivered simultaneously to four branches instead of one (Fig. S5A), and the noisy background input at the soma was shifted down to a zero mean (keeping the same variance) to produce a high threshold, nonlinear somatic f-I curve (Fig. S5B). Despite these changes, firing rate predictions assuming independent subunits remained highly accurate (MAE = 1.06 Hz, Fig. S5 C–F).

Challenging the 2LM: Including Within-Branch Interactions.

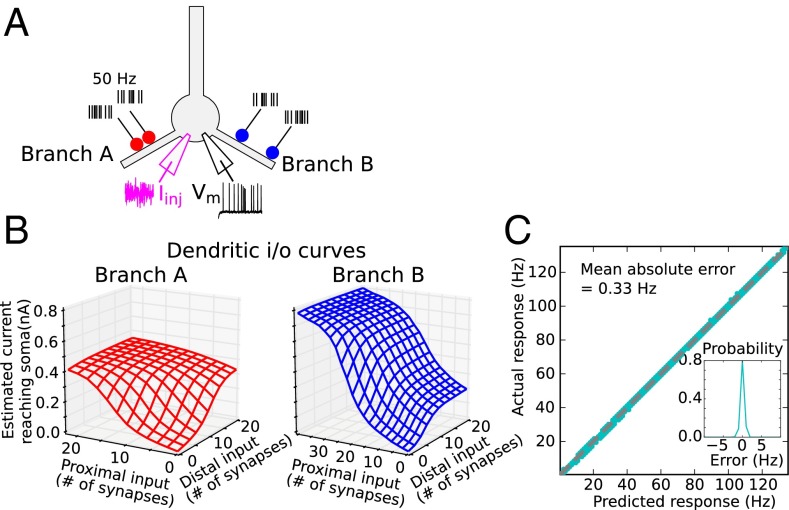
In the tests of Fig. 2 and Figs. S1–S5 only a single site was activated on any given dendrite. Here we asked whether the location-dependent synaptic interactions known to occur within a thin dendrite when two spatially separated inputs are activated (16, 31, 32, 46, 47) (Fig. 1A) can proceed independently in two different dendrites when each is stimulated at a different pair of locations (Fig. 3A). This scenario presents a particularly difficult challenge to subunit independence, because each dendrite must manage a different location and voltage-dependent computation within its confines, all the while both dendrites are repeatedly synchronized by the same train of bAPs that both dendrites are helping to cause. The somatic current estimates for each of the branches considered separately are shown as 3D plots in Fig. 3B (analogous to the line plots in Fig. 2C). The plots differ from each other, reflecting the different locations of the two stimulus sites in the two branches. Given the 4 degrees of freedom in the stimulus configuration in this case (i.e., varying stimulus intensity at two sites on two branches), plots showing predicted and actual responses would be 5D and could not be directly visualized. However, a scatterplot of predicted vs. actual firing rates for all 384,000 stimulus configurations shows the firing rate predictions of the 2LM were again highly accurate (Fig. 3C, MAE = 0.33 Hz), indicating that PNs can maintain cleanly separated voltage and location-dependent synaptic interactions within different dendrites at the same time.

Fig. 3.

Quantifying subunit independence with two stimulus sites on two dendrites. (A) Simulation experiment was as in Fig. 2 but with two stimulus sites on each dendrite (130 and 150 μm on branch A and 90 and 190 μm on branch B). (B) Estimated current reaching the soma for location pairs on branch A and branch B, respectively, computed from regression fits to actual responses. Nonlinear interactions between proximal and distal inputs within each branch lead to asymmetric 2D sigmoidal surfaces, more so in branch B with greater separation of the sites (31). Somatic f-I curve used in generating predictions was the same as in Fig. 2B (over a larger range). (C) Scatterplot of actual vs. predicted firing rates for 384,000 stimulus configurations shows predictions are again close to perfect (MAE = 0.33 Hz). (Inset) Probability density of prediction errors (actual–predicted).

Biophysical Basis for Subunit Independence.

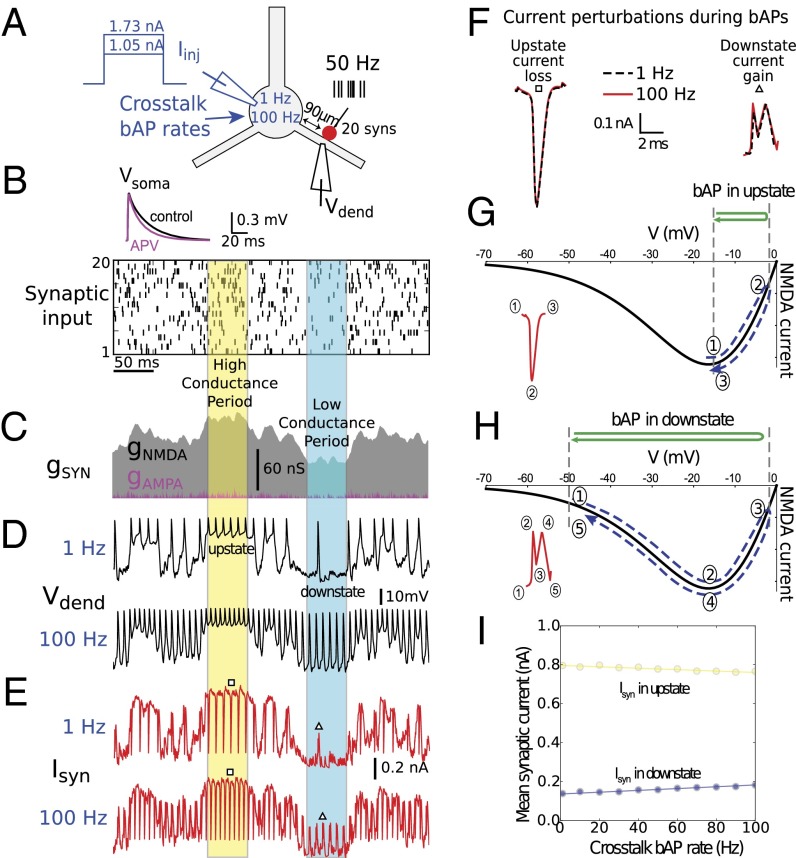
In a firing neuron, every ionic current in a dendrite experiences driving force “whiplash” by each invading bAP in obeyance of Ohm’s law, and every voltage-dependent current will in addition experience conductance changes as the membrane potential cycles up and down. A dendrite’s response cannot therefore depend solely on its own synaptic inputs, and be strictly independent of externally imposed voltage signals, on a moment-by-moment basis. To understand what allows dendritic outputs to be nearly independent of each other over longer time scales, we compared total synaptic current in a dendrite under two conditions in which the synaptic stimulus delivered to the branch was identical, but the rate of bAPs generated at the soma, representing cross-talk from other dendrites, was set to either a low (1 Hz) or a high (100 Hz) rate by a steady somatic current injection (Fig. 4A). In both low and high cross-talk conditions, 20 synapses located 90 μm from the soma on one branch were activated by the same raster of spike trains (Fig. 4B), leading to the same AMPA and NMDA conductance waveforms within the stimulated dendrite (Fig. 4C). Membrane potential and total (NMDA + AMPA) synaptic current for the 1-Hz cross-talk case are shown in Fig. 4 D and E, respectively (Upper traces). Fast spikes riding on top of the voltage and current traces were mostly not due to the 1-Hz cross-talk, but were additional somatic bAPs caused by synaptic stimulation in the branch itself (i.e., “self-talk”).

Fig. 4.

Analysis of synaptic current perturbations by bAPs. (A) Schematic showing simulation experiments for two levels of somatic current injection, producing low (1 Hz) and high (100 Hz) “cross-talk” bAP rates. (Inset) Somatic response to activation of a single synapse at rest, 90 μm from the soma, with NMDA conductance present (control) and blocked by 2-amino-5-phosphonovaleric acid (APV). (B) Twenty mixed AMPA–NMDA synapses (90 μm from the soma, ratio of NMDA to AMPA peak conductance was 2.5) were activated by independent 50-Hz Poisson spike trains, as shown in raster plot. Identical spike raster was used for both cross-talk cases. (C) Total synaptic conductance for all 20 synapses. Periods of relatively high and relatively low NMDA conductance are indicated. (D) Dendritic membrane potential in response to synaptic stimulation at two levels of cross-talk (Upper and Lower traces) with superimposed somatic bAPs. An up state and a down state are indicated, corresponding to the high and low conductance periods. bAPs in excess of the cross-talk bAP rate were due to synaptic stimulation, which causes additional somatic APs. (E) Total synaptic current at two levels of cross-talk. Inward currents are plotted in the positive direction. bAPs caused transient losses of synaptic current during up states (downward blips) and transient boosts during down states (upward blips). (F) bAP-induced synaptic current perturbations during up and down states were stereotyped in shape/size. Examples corresponding to squares and triangles in E are shown superimposed. (G and H) Monotonic form of current loss during up state (G) and double-humped current boost during down state (H) are explained by bAP-induced traversal of NMDA I–V curve from different voltage baselines. (I) Small magnitude of individual current perturbations [roughly 0.5 picocoulombs (pC) per bAP in down state and −0.45 pC per bAP in up state] led to only small changes in mean synaptic current in worst case (pure up or down states) over 1- to 100-Hz range of cross-talk bAP rates. See also Fig. S7.

Results for the 100-Hz cross-talk case are shown in Fig. 4 D and E, Lower traces. In a slight departure from subunit independence, the total synaptic current averaged over the 500-ms stimulus period was 6.5% larger for the 100-Hz vs. 1-Hz cross-talk case (0.49 nA vs. 0.46 nA), indicating that cross-talk bAPs slightly boosted synaptic current within the dendrite. According to the somatic f-I curve in Fig. 2B, a 0.03-nA increase in injected synaptic current, reduced to 0.02 nA by passive current attenuation on the path to the soma, would lead to a roughly 2-Hz maximum cross-talk–level–dependent spread in firing rates at the soma for the 20 synapses at 90 μm case. The maximum firing rate prediction error would be roughly half that; however, by setting the somatic current prediction to an intermediate value [i.e., (0.46 + 0.49)/2 = 0.475 nA], the maximum firing rate prediction error would be cut to ±1 Hz, and the average error magnitude including all intermediate bAP rates would be smaller still. This slight deviation from subunit independence in the example shown in Fig. 4 is thus consistent with the very low average prediction error seen for the stimulus ensembles shown in Figs. 2 and 3.

Why do bAPs have such a small time-averaged effect on synaptic current? Inspection of synaptic current traces shows that the largest bAP-induced perturbations were of two stereotyped forms: simple downward “spikes” in injected current when the membrane potential began in an “up” state, and complex double-peaked boosts in synaptic current when the membrane began in a down state (Fig. 4 E and F). Both cases were explained by the nonmonotonic form of the NMDA channel current–voltage (I–V) curve (Fig. 4 G and H). Worst case cross-talk effects would be expected to occur when a dendrite is in a pure up or down state condition, because bAP-induced synaptic current perturbations would then always be in the same direction (down or up, respectively), and would accumulate with increasing bAP rate, rather than cancel. To quantify this worst-case bAP rate dependence, we plotted the time-averaged synaptic current as a function of bAP rate during pure up (yellow) and pure down (blue) periods. The resulting linear relationships had low negative and positive slopes, respectively (Fig. 4I), indicating that the synaptic current in these pure scenarios can be modeled as a baseline current determined by the level of excitation (y intercept), plus a small stereotyped increment or decrement in synaptic charge per invading bAP. However, even in these two worst-case scenarios, prediction errors caused by bAPs remained very small in terms of somatic firing rate changes (almost always <2 Hz over the >100-Hz range).

Discussion

We found that a PN basal dendritic tree exhibits an almost machine-like adherence to the two-layer model and its core assumption of subunit independence, even under highly variable in-vivo–like firing conditions with different dendrites simultaneously engaged in different synapse-location–dependent computations. Our findings go beyond the demonstrations in previous experimental and modeling studies that PN responses are better predicted by a two-layer than a one-layer “point neuron” model (8, 21, 22). We show here that when the dendritic layer is augmented to take into account (i) nonlinear spatial interactions that occur between synapses within a dendrite (31), and (ii) variability in the input–output functions from dendrite to dendrite (the branch-specific multidimensional sigmoid functions in Fig. 3B illustrate both of these effects), then a 2LM that can be evaluated “by hand” using graphs like those in Figs. 2B and 3C produces highly accurate predictions of PN firing rates over a wide range of stimulus configurations. Thus, our findings provide a more solid mechanistic basis for the 2LM of a PN dendritic subtree, while highlighting the importance of first layer details, including location-dependent synaptic interactions and branch-to-branch variability that were not taken into account in previous work and that would have contributed to the substantial prediction errors reported there (21, 22). We also found that sister and cousin branches are nearly as independent as cross-soma branches in the firing rate regime despite their much closer electrical coupling (Fig. 2F).

Biophysical Mechanisms Underlying Subunit Independence.

The ability of PN thin dendrites to carry out independent voltage-dependent computations in a firing neuron can be attributed to three different kinds of biophysical effects: (i) voltage clamping by the somatic firing mechanism, (ii) fast equilibrium seeking in neural cables, and (iii) various cancellation effects.

First, ironically, we found that the somatic firing mechanism actually promotes dendritic independence. This conclusion is supported by our finding that the independent subunit assumption is most severely violated when the cell remains subthreshold for somatic AP generation. In this deeply polarized in-vitro–like scenario, the slow depolarizing output of one strongly activated dendrite substantially boosts the baseline potential across the entire basal arbor [Fig. S7B; see humps in the unstimulated (purple) branch voltage trace at −60 mV at times when the stimulated branch was in an up state]. The effect of this type of slow, subthreshold (“DC”) cross-talk is to substantially lower the threshold for NMDA channel activation in other branches, as shown by the leftward progression from the dotted to dashed i/o curves in Fig. S7C. DC cross-talk is effectively squelched by the firing mechanism at the cell body: once the soma has been biased up to even a minimal (<1 Hz) background firing rate, further excitation of the soma up to 100 Hz or more has a nearly negligible effect on the time-averaged synaptic currents in branches receiving synaptic stimulation (Fig. S7C, see the nonprogression of blue, green, and red i/o curves; see also ref. 42). Thus, ironically, the axosomatic spiking mechanism, while increasing the biophysical complexity of the cell, and on the surface seeming to promote cross-talk between dendrites, actually maintains the somatic voltage at a relatively constant average baseline (48), which leads to greater subunit independence and a functionally simpler two-layer integrative scheme.

Second, the fast voltage equalization times of dendrites (49) compared with the soma, mean that each bAP perturbs the dendritic membrane potential only very briefly. At the soma, a large potassium conductance is needed to rapidly repolarize the membrane at the end of the AP. In contrast, according to passive cable theory, the response time in mid-dendrite is determined mainly by the low internal resistance of the dendrite, R_i, rather than the much higher membrane resistance, R_m, so that the membrane potential in the dendrite tracks the local equilibrium potential with little delay. This allows the bAP-induced voltage disturbance to be very brief even in the absence of a repolarizing K⁺ conductance: when the voltage-dependent Na⁺ conductance underlying a passing bAP inactivates after a millisecond or two, the dendritic voltage returns rapidly to whatever equilibrium potential was in effect due to the local synaptic conductances and leaks (Fig. 4D). This fast equalization property of dendrites is fortuitous in the sense that, were a large K⁺ conductance required to abruptly terminate the bAP in the dendrite as it is in the soma, then the disturbance to dendritic voltage traces caused by bAPs might be more severe, and subunit independence would be correspondingly degraded. Beyond the natural tendency toward fast equilibrium seeking in dendrites, we noted that bAP-induced perturbations were further shortened during periods of high synaptic conductance in a dendrite: bAP-induced synaptic current losses during high-conductance (up) states were limited to a roughly 2-ms period (Fig. 4F, Left), compared with the ∼3- to 4-ms perturbations seen during lower-conductance down states (Fig. 4F, Right). The small overall effect of bAPs on synaptic currents may also be credited in part to the difference in time scales between the very brief voltage transients caused by bAPs, and the much longer lasting NMDA-dependent spikes/plateaus driven by ongoing synaptic activation. Even at bAP rates in excess of 100 Hz, the overall “duty cycle” of the bAP train remained low in comparison with the much longer duration synaptic currents (Fig. 4D). This time scale mismatch, helpful for subunit independence, would not be expected to hold for dendrites whose local spike generation is dominated by fast Na⁺ channels—possibly including CA1 pyramidal neurons (9, 50)—implying either that strict two-layer processing is not essential in these cells (22), different biophysical mechanisms are used, or dendritic spike generation is so sparse that cross-talk between coactivated dendrites does not normally occur.

Third, subunit independence is enhanced by three types of cancellation effects that reduce the space- and time-averaged perturbations to total synaptic current caused by bAPs. First, in a relatively minor effect, when a bAP arrives in a dendrite when the membrane potential is in an intermediate range between up and down states (in the vicinity of −30 mV), the bAP-induced perturbation to the synaptic current will be to some extent self-cancelling. The effect can be understood as a cross between the pure current gain that results when a bAP arrives during a down state (Fig. 4F, Right), and the pure current loss that results when a bAP arrives during an up state (Fig. 4F, Left). Second, the boosting and suppressive effects of different bAPs in a train tend to cancel over longer time scales under stimulus conditions that produce mixtures of up and down states, as in Fig. 4 C–E. The third effect involves cancellation between different branches: bAPs entering dendrites in down states tend to cancel the effects of the same bAPs entering other dendrites in up states.

In summary, the somatic firing mechanism effectively squelches DC cross-talk between dendrites by converting what would have been large subthreshold voltage swings at the soma into variable-rate trains of bAPs that have relatively little effect on the mean somatic potential. Furthermore, bAPs are surprisingly innocuous from the perspective of ongoing dendritic computations: individual bAPs alter NMDA-type synaptic currents only very briefly, owing to the fast equalization times of dendrites, and trains of bAPs have a low duty cycle even at high firing rates. Finally, bAPs produce offsetting gains and losses in synaptic current at different moments in time in different dendrites within the cell, significantly reducing their overall impact. It may be speculated that dendrites and bAPs have been optimized to allow signals from the soma crucial for the induction of synaptic plasticity (48) to be broadcast throughout the dendritic arbor while minimally disrupting ongoing dendritic computations.

In conclusion, our findings lend further support to the view that dendrites are key integrative subunits in various types of neurons (8, 9, 13–15, 21, 22, 29, 37, 52–55) and may play a variety of computational roles including the representation of different receptive field subunits (20, 21, 56–59), the mediation of attentional and/or contextual modulation effects (60, 61), the encoding of higher-order stimulus features for learning and memory (19, 25, 62–69), the representation of multiple place fields within the same cell (27) (although see ref. 70), and the generation of graded persistent activity in the context of working memory (71, 72) or motor output (73, 74). Future experimental and modeling studies will be needed to establish whether subunit independence and two-layer behavior hold for pyramidal neurons in other layers and areas of the neocortex and hippocampus, which can differ substantially in their morphological and physiological properties, and to determine if, when, and where independent dendritic computations are exploited in the awake behaving brain.

Materials and Methods

See SI Materials and Methods for a detailed description of the biophysical model. Ion channel models and parameters are shown in Table S1. Also see SI Materials and Methods for details of the two-layer model and parameter estimation technique.