Critical slowing down as early warning for the onset and termination of depression

Significance

As complex systems such as the climate or ecosystems approach a tipping point, their dynamics tend to become dominated by a phenomenon known as critical slowing down. Using time series of autorecorded mood, we show that indicators of slowing down are also predictive of future transitions in depression. Specifically, in persons who are more likely to have a future transition, mood dynamics are slower and different aspects of mood are more correlated. This supports the view that the mood system may have tipping points where reinforcing feedbacks among a web of symptoms can propagate a person into a disorder. Our findings suggest the possibility of early warning systems for psychiatric disorders, using smartphone-based mood monitoring.

Abstract

About 17% of humanity goes through an episode of major depression at some point in their lifetime. Despite the enormous societal costs of this incapacitating disorder, it is largely unknown how the likelihood of falling into a depressive episode can be assessed. Here, we show for a large group of healthy individuals and patients that the probability of an upcoming shift between a depressed and a normal state is related to elevated temporal autocorrelation, variance, and correlation between emotions in fluctuations of autorecorded emotions. These are indicators of the general phenomenon of critical slowing down, which is expected to occur when a system approaches a tipping point. Our results support the hypothesis that mood may have alternative stable states separated by tipping points, and suggest an approach for assessing the likelihood of transitions into and out of depression.

Depression is one of the main mental health hazards of our time. It can be viewed as a continuum with an absence of depressive symptoms at the low endpoint and severe and debilitating complaints at the high end (1). (Throughout this manuscript, the term “depression” refers to this continuum of depressive symptoms.) The diagnosis major depressive disorder (MDD) defines individuals at the high end of this continuum. Approximately 10–20% (2) of the general population will experience at least one episode of MDD during their lives, but even subclinical levels of depression may considerably reduce quality of life and work productivity (3). Depressive symptoms are therefore associated with substantial personal and societal costs (4, 5). The onset of MDD in an individual can be quite abrupt, and similarly rapid shifts from depression into a remitted state, so-called sudden gains, are common (6). However, despite the high prevalence and associated societal costs of depression, we have little insight into how such critical transitions from health to depression (and vice versa) in individuals might be foreseen. Traditionally, the broad array of correlated symptoms found in depressed people (e.g., depressed mood, insomnia, fatigue, concentration problems, loss of interest, suicidal ideation, etc.) was thought to stem from some common cause, much as a lung tumor is the common cause of symptoms such as shortness of breath, chest pain, and coughing up blood. Recently, however, this common-cause view has been challenged (7–9). The alternative view is that the correlated symptoms should be regarded as the result of interactions of components of a complex dynamical system (7, 10–12). Consequently, new models of the etiology of depression involve a network of interactions between components, such as emotions, cognitions, and behaviors (8, 9). This implies, for instance, that a person may become depressed through a causal chain of feelings and experiences, such as the following: stress → negative emotions → sleep problems → anhedonia (9, 13–15). However, the network view also implies that there can be positive feedback mechanisms between symptoms, such as the following: worrying → feeling down → more worrying or feeling down → engaging less in social life → feeling more down (16). It is easy to imagine that such vicious circles could cause a person to become trapped in a depressed state.

The plausibility of this theoretical framework with regard to MDD is supported in at least four ways. First, intraindividual analyses of multivariate time series of variables related to MDD symptomatology show clear interactions between these variables (15–17). Second, MDD symptoms display distinct responses to different life events (18, 19) and are differently related to other external variables and disorders (20), which is consistent with a network view of interacting variables related to MDD symptomatology, but not with a classical disease model that postulates the existence of a common cause (21). Third, when asked how MDD symptoms are related, clinical experts report a dense set of causal relations between them (9, 22). Fourth, using recently developed self-report methods, it has been shown that individuals with elevated symptom levels typically report causal interactions between their symptoms, including those of MDD (23, 24).

Thus, there is ample evidence to support the thesis that MDD is characterized by causal interactions between its “symptoms.” From dynamical systems theory, it is known that positive-feedback loops among such causal interactions can cause a system to have alternative stable states (25). This has profound implications for the way a system responds to change. For example, gradually changing external conditions may cause a system to approach a tipping point. Close to such a point, the system typically loses resilience, that is, increasingly small perturbations may suffice to cause a shift to an alternative stable state (25). In the mood system, characterized by the “mood state” of an individual that may range from normal to severe depression, stressful conditions may bring the system to such a fragile state (26). For example, a chronically unpleasant working situation may reduce resilience of the “normal state” by precipitating insomnia and other related symptoms. Then, only a slight additional perturbation (e.g., an unpleasant phone call with mother-in-law) may be enough to trigger a chain of symptoms that causes the system to shift from a stable normal state into an alternative “depressed state.”

In this paper, we analyze time series of four emotions as the observed variables of the mood system in healthy persons and depressed patients providing support for the view that the mood system can have tipping points. Specifically, we show indicators of critical slowing down (27), which have recently been shown to be linked to tipping points in a range of complex systems (28–30). These indicators can be used as early warning signals that can help assess the likelihood that an individual will go through a major transition in mood. Before moving to the empirical evidence, we briefly introduce the generic phenomenon of critical slowing down, using a simple model of the mood system as an illustration.

Results and Discussion

Theory of Critical Slowing Down.

Marked transitions from one dynamical regime to a contrasting one are observed in complex systems ranging from oceans, the climate, and lake ecosystems, to financial markets. Such “regime shifts” (31) can simply be the result of a massive external shock, or stepwise change in the conditions. However, it is also possible that a slight perturbation can invoke a massive shift to a contrasting and lasting state. It is intuitively clear that this can happen to an object such as a chair or a ship when it is close to a tipping point, but complex systems such as the climate or ecosystems can also have tipping points (25). The term tipping point in such systems is informally used to refer to a family of catastrophic bifurcations in mathematical models (32), which in turn are simplifications of what characterizes the stability properties of real complex systems (25).

As tipping points can have large consequences, there is much interest in finding ways to know whether a catastrophic bifurcation is near. In principle, this could be computed if one has a reliable mechanistic model. However, we have little hope of having sufficiently accurate models for complex systems such as lakes or the climate, let alone psychiatric disorders. A recent alternative approach is to look for indicators of the proximity of tipping points that are generic in the sense that they do not depend on the particular mechanism that causes the tipping point. A possibility that has attracted much attention is that, across complex systems, the vicinity of a tipping point may be detected on the basis of a phenomenon known as “critical slowing down” (32, 33). Specifically, critical slowing down happens as the dominant eigenvalue, characterizing the return rate to equilibrium upon small perturbations, goes to zero in tipping points related to zero-eigenvalue bifurcations. On an intuitive level, this can be understood from a ball-in-a-cup diagram (Fig. 1 A and B). As the slope represents the rate of change, close to the tipping point where the basin of attraction becomes shallower, return to equilibrium upon small perturbations will become slower. Although critical slowing down has been known for a long time in mathematics, slowing down at tipping points has only recently been demonstrated experimentally in living systems (34, 35).

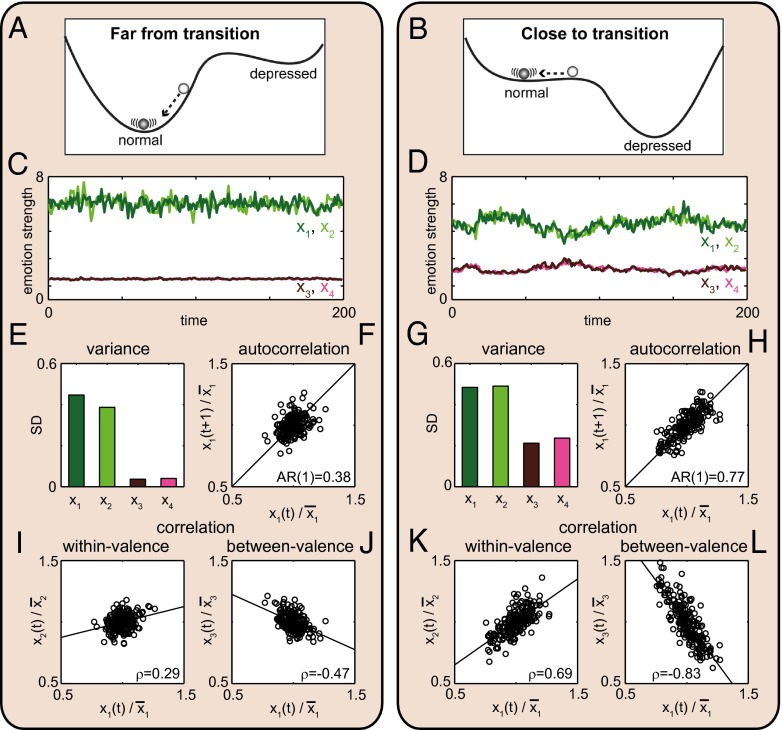
Fig. 1.

Model simulations illustrating generic indicators of proximity to a tipping point from a normal to a depressed state. The stability of a healthy person may become more fragile close to a transition toward depression, which can intuitively be understood from a ball-in-a-cup diagram (B versus A). This fragility would lead to critical slowing down in a system with tipping points between alternative stable states, illustrated by model simulations. Under a permanent regime of stochastic perturbations on the strength of each emotion (C and D), slowing down near the tipping point results in higher variance (SD = standard deviation) in emotion strength (G versus E), higher temporal autocorrelation [AR(1) = lag-1 autoregression coefficient] in emotion strength (H versus F), and stronger correlation (ρ = Pearson correlation coefficient) between emotion strength of emotions with the same valence (K versus I), and between emotions with different valence (L versus J). Positive emotions are represented by x₁ and x₂, and negative emotions by x₃ and x₄. Parameters: (Left) r₃ = r₄ = 0.5, (Right) r₃ = r₄ = 1.18.

For most systems, it is either impractical or unethical to experimentally perturb them to find out if they are close to a tipping point. However, any system, including mood, is continuously subject to small natural perturbations. One can imagine the effect as a combination of direct impacts on the ball (in models this corresponds to so-called additive noise) and fluctuations in the shape of the stability landscape (multiplicative noise). A range of modeling studies, laboratory experiments, and field studies now suggests that, under such stochastic conditions, critical slowing down typically causes an increase in the variance and temporal autocorrelation of fluctuations in the system elements (29, 30, 34–37). Besides, in a network of fluctuating elements, one expects an increase in cross-correlation between elements that will shift together (38). This implies the possibility that elevated variance and correlation may be used as indicators of critical slowing down and therefore as early warning signals that may reveal the loss of resilience in the proximity of a tipping point (27).

Minimal Models of Mood.

Critical slowing down will occur independently of the specific mechanisms involved in bringing about a tipping point. However, to illustrate how indicators of critical slowing down might signal the proximity of a tipping point in mood, we use a simple dynamical model, based on the classical and well-studied Lotka–Volterra equations (Materials and Methods). This is about the simplest way of modeling positive and negative interactions between dynamically varying entities such as populations of organisms. Specifically, we model four emotions as variables of the mood system (reflecting the four quadrants of the affective circumplex: cheerful, content, sad, and anxious; see ref. 39), and assume that emotions with the same “valence” (positive or negative) promote each other, whereas emotions of opposite valence tend to compete (SI Appendix, Fig. S1A). This is of course an overly simple representation of the mood system, but consistent with the empirical observations that same-valenced emotions tend to augment and opposite-valenced emotions tend to blunt each other (16, 40), and that this dynamic interplay has relevance for the course of depression (41). Also on theoretical grounds, it stands to reason that emotions that show large overlap in terms of their underlying components (such as appraisals; see ref. 40) would augment each other, whereas emotions that diverge in these components, would counteract each other (40). Given suitable parameter settings, the model has two alternative stable states over a range of conditions: one state dominated by strong positive emotions, the normal state, and the second dominated by strong negative emotions, the depressed state (SI Appendix, Fig. S1B).

To mimic the stochastic environment, we expose the model to a regime of random perturbations (Fig. 1 C and D). The resulting fluctuations in the strength of the four modeled emotions show signs of critical slowing down as expected from the generic theory (27). Specifically, close to the tipping point toward depression, the fluctuations have a higher variance (Fig. 1 G versus E), and temporal autocorrelation (Fig. 1 H versus F). Also, the cross-correlations between the strength of the modeled emotions become stronger in the vicinity of the tipping point (Fig. 1 K and L versus I and J). Note that positive correlations between emotions within the same valence will tend toward 1 (Fig. 1K), whereas negative correlations between opposed valence emotions will tend toward −1 (Fig. 1L). Similarly, once the model system is in the depressed state, we see elevated variance and correlations close to the critical point of recovery (SI Appendix, Fig. S2).

Although the view of mood as consisting of interactions between its various components (e.g., cheerful and sad) fits well with recent theories regarding the pathology of MDD (7, 8), one could argue that such mood variables (unlike, for instance, populations of animals) are not on equal par with true physical quantities. Rather, emotions such as feeling cheerful or anxious seem to be the result of complex interactions between biology (including genetics), previous life experiences, and current contextual influences. We will probably never be able to assess and understand the full complexity of this system. However, psychologists work with emotions because they are thought to reflect meaningful aspects of the mood system (39, 42). In fact, the subjective experience component of emotions is thought to function as a monitoring tool for organisms to detect important changes in the complex mood system (39). Given that emotions are unitless subjective measures that are not governed by any laws of conservation, one could wonder if they should still be expected to reflect critical slowing down if that underlying system approaches a tipping point. To explore this, we made a model of a complex network of interactions between 20 variables, representing (in principle) objectively measurable components of mood (e.g., elements ranging from neurotransmitter and hormone concentrations to physical activity modes and social interactions). We created the model such that it has tipping points. Then, we mimicked the strength of emotions as indirect indicators of the state of the highly complex network by using principal components [principal component analysis (PCA) axes] (SI Appendix, Text S1). Analyses of this model illustrate that critical slowing down remains clearly reflected in the PCA-based indicators (SI Appendix, Figs. S3–S5 and Text S1).

Clearly, many other dynamical models of the mood system could be conceived. However, the examples we analyzed may serve to illustrate the general phenomenon that indicators of critical slowing down can be found at tipping points independently of the precise underlying complex mechanisms involved, and on the way the variables are measured (27, 28, 43). Thus, even if we cannot attain a complete understanding of the complex array of mechanisms that are involved in regulating mood, we may expect that, if transitions in mood are related to the proximity of tipping points, the likelihood of such shifts to happen should be evident in indicators of critical slowing down.

Patterns in Recorded Mood Dynamics.

To explore whether mood dynamics do indeed display such indications of critical slowing down before tipping points in depression, we analyzed time series of four emotions (cheerful, content, sad, and anxious) as observed variables of the overall mood state obtained through the Experience Sampling Method (ESM) (Materials and Methods), in which subjects have monitored, for each emotion, their position on an emotional scale during 5–6 consecutive days. We refer to this as their “emotion score” at a certain time. We studied a general population sample that varies in the development of depressive symptoms over time (in follow-up measurements). Some subjects shifted upward along the continuum of depression and some downward. A fraction of this group (13.5%) showed a transition from a normal state to a DSM-IV clinical diagnosis of MDD. We investigated in this general population sample whether indicators of critical slowing down are associated with elevated risk of future shifts toward depression. In addition, we analyzed ESM data from a population sample of depressed patients to see whether critical slowing down is related to the probability of upcoming recovery (for sample descriptions, see SI Appendix, Table S1).

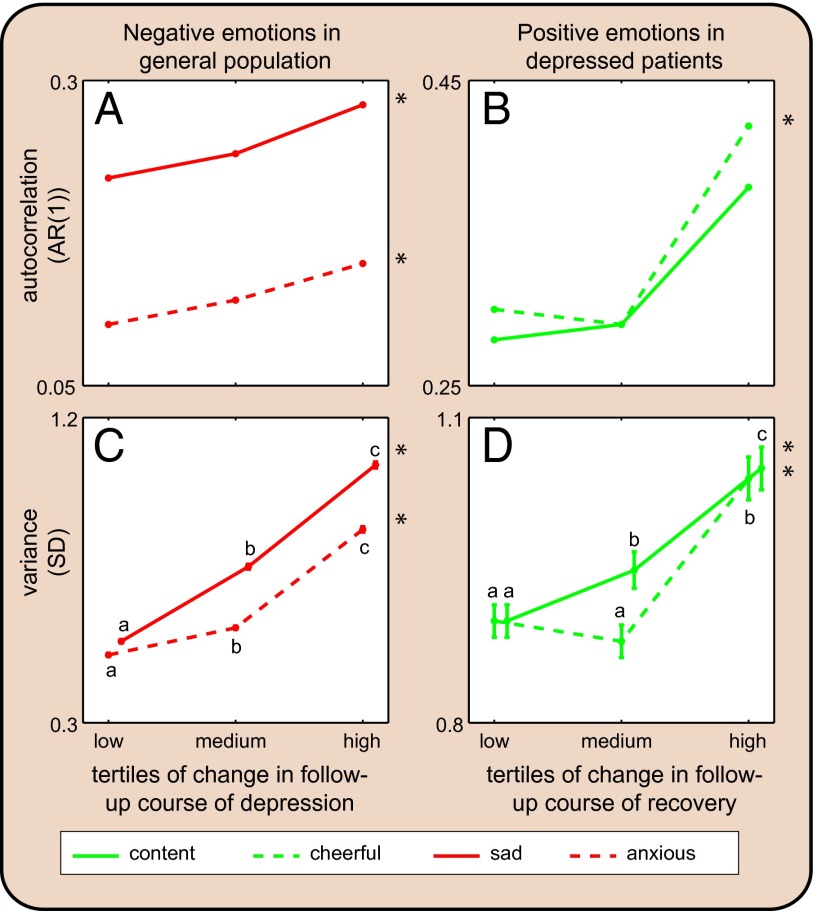
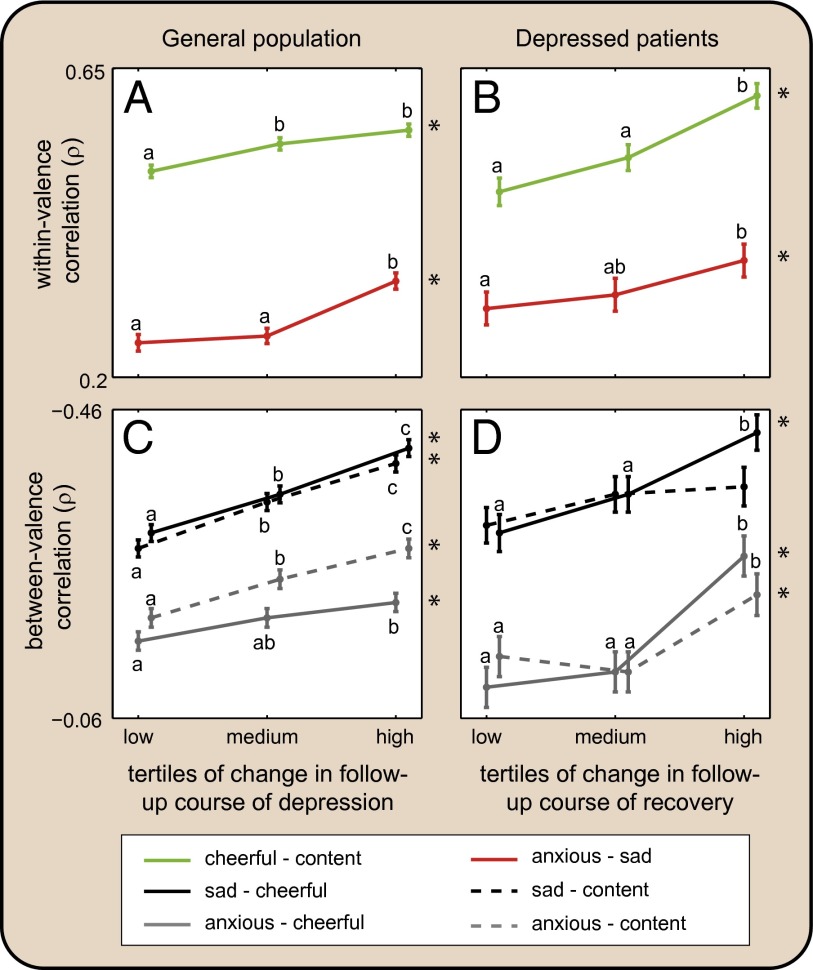
Both temporal autocorrelation (i.e., the autoregression coefficient) and variance of fluctuations in emotion scores were higher in individuals with upcoming transitions (Fig. 2 and SI Appendix, Tables S2 and S3). For an impending worsening of depressive symptoms, these signals are strongest for negative emotions (Fig. 2 A and C), whereas for an upcoming improvement in depressive symptoms in individuals with current MDD, these signals are strongest for positive emotions (Fig. 2 B and D) compared with the other emotions (SI Appendix, Fig. S6). Also, correlations between emotion scores were consistently stronger for individuals who experienced a future transition upward on the continuum of depression (Fig. 3 A and C) as well as in depressed patients who were moving downward on the continuum within the study period (Fig. 3 B and D) (SI Appendix, Table S4). Note that the main structure of our model of positive and negative interactions is consistent with the data: emotions of opposite valence affect each other negatively, whereas emotions with the same valence are positively correlated (Fig. 3).

Fig. 2.

Temporal autocorrelation and variance of emotion scores as a function of future symptoms. Increasing autocorrelation [AR(1) = mean lag-1 autoregression coefficient] (A and B) and variance (SD = mean standard deviation) (C and D) of negative emotions according to tertiles of development of future depressive symptoms in a general population (n = 535) (Left), and of positive emotions according to tertiles of future recovery in depressed patients (n = 93) (Right). For temporal autocorrelation (A and B), we present data according to tertiles of change in follow-up course for illustrative purposes only; however, note that in the statistical analyses continuous variables were used. Asterisks indicate a significant upward trend in temporal autocorrelation (positive interaction effect of future symptoms: P < 0.05). For variance (C and D), error bars represent SEs. Note that the SEs in C are very small. Asterisks indicate an overall significant upward trend in variance (overall tests: P < 0.05). Mean values represented by different letters within emotions are significantly different (post hoc tests: P < 0.05).

Fig. 3.

Correlations between emotion scores as a function of future symptoms. Strengthening correlations between emotions of the same valence (A and B), and between emotions of different valence (C and D) according to tertiles of the development of future depressive symptoms in a general population (n = 535) (Left), and to tertiles of future recovery in depressed patients (n = 93) (Right). Error bars represent SEs. Asterisks indicate an overall significant strengthening trend in correlation (overall tests: P < 0.05). Mean values represented by different letters within emotions are significantly different (post hoc tests: P < 0.05).

The rise in temporal correlations and cross-correlations is likely a more direct indicator than the rise in variance. This is because change in variance can be confounded by several mechanisms (44). For instance, a trend in variance may be related to a trend in the mean. Indeed, such a coupling of variance to mean may partly explain the trends we observe in upcoming emotions (SI Appendix, Fig. S6). However, an analysis of trends in the coefficients of variation illustrates that, especially in the general population, rising variability in all emotions may be an observable indicator of critical slowing down associated with an elevated risk of an impending depression (SI Appendix, Fig. S7). Also, one could argue that the observed effect in variance might be an effect of increased external perturbations (“noise” in the model), and not a result of critical slowing down. As temporal autocorrelation and cross-correlations are independent of the means as well as the amplitude of noise (44), the trends in correlations may be our most robust indicator of critical slowing down.

Taken together, our results suggest that there is an elevated chance of upcoming shifts between a depressed and a normal mood state in persons who show indications of critical slowing down in their emotion scores. This is consistent with the idea that such transitions tend to happen when a subject is close to a tipping point. The relationship between elevated temporal correlations and upcoming transitions we detected is also consistent with independent earlier studies, showing that “emotional inertia” (slower rates of change in emotion scores) is associated with future transition into a more depressed state (45, 46). Moreover, the corresponding view of depression as an alternative stable state is in line with the finding of reinforcing feedbacks between emotions, and with the sudden character of shifts to depression and recovery (6).

Importantly, this body of evidence does not imply that all persons would have such tipping points. It seems more likely that whereas some persons abruptly shift between a normal and a depressed state, for others, certain positive-feedback mechanisms (e.g., feeling down → engaging less in social life → feeling more down) remain too weak to cause alternative stable states. Such persons would be expected to move more gradually between a normal and a depressed state, experiencing intermediate states to be stable as well. Indeed, dynamical systems with tipping points will often respond more smoothly if the positive feedback responsible for this feature becomes weaker (SI Appendix, Fig. S8). Hints of slowing down may still be detected for persons without alternative stable states in case their mood responds relatively strongly to a gradual change in conditions. This is because some slowing down (albeit not full-blown critical slowing down, where recovery rate upon perturbation reaches zero) is expected across a wide range of situations where systems respond relatively sensitively around a threshold (47).

Implications.

Clearly, the effects of stressors may differ widely between persons and contexts depending on a complex set of interacting factors shaped by genes and history (e.g., genetic variants, epigenetic regulation, early life events, and connection strength between neurons that are changed by experience). This makes it unlikely that we would ever be able to obtain accurate individual predictions of risk for relapse or recovery based on a mechanistic insight into the mood regulation system. However, if the mood system, as our results suggest, shows signals of critical slowing down, we may use this generic feature to improve our ability to anticipate clinically relevant mood shifts, even in the absence of a full understanding of the complex underlying system that is responsible for such shifts. Clearly, such mechanistic insight may be important to develop better treatment strategies. However, when it comes to risk stratification, the indicators of critical slowing down may be a powerful and independent addition to our clinical toolkit.

This has important implications for treatment. Mood data suitable for analysis of critical slowing down are now easy to assess and monitor, for instance through an app on a smartphone. Furthermore, web applications are able to provide user-friendly feedback to patients and clinicians on the patient’s critical slowing-down patterns. The ability to anticipate transitions (e.g., a shift upward on the continuum of depression for a person at risk, or a shift downward on the continuum for a patient with current MDD) could prove beneficial in terms of the timing and magnitude of treatment interventions. This information may prove especially valuable in optimizing health care and in reducing mental health care costs. Hence, in terms of understanding and treating psychiatric disorders like depression, the potential gains associated with our approach are considerable. Therefore, our central hypothesis—that symptomatology like depression should be conceptualized as alternative states of complex dynamical systems—is not an endpoint; rather, it should mark the beginning of novel research programs.

Materials and Methods

Samples.

We analyzed data from (i) the general population (females; n = 621) and (ii) depressed patients eligible for treatment (n = 118; for sample descriptions, see SI Appendix, Table S1). The first sample was recruited from a population-based sample of the East-Flanders Prospective Twin Survey (Belgium). The data of depressed patients came from two studies. Both included baseline ESM measurements followed by an intervention (either a combination of pharmacotherapy and supportive counseling or allocation to either imipramine or placebo) and follow-up assessments of depressive symptoms. For details on inclusion criteria and final set of participants, see SI Appendix, Text S2. A total of 535 individuals from the general population and 93 depressed patients were included in the final analyses.

ESM.

To calculate early warning signals for transition, the four emotions were measured repetitively and prospectively using the ESM. This structured diary technique prospectively assesses individual experience in the context of daily life (48, 49). Subjects received a digital wristwatch and a set of ESM self-assessment forms collated in a booklet for each day. The wristwatch was programmed to emit a signal (“beep”) at an unpredictable moment in each of 10 90-min time blocks between 0730 hours and 2230 hours, on 5 or 6 consecutive days, depending on the study. After each beep, subjects were asked to fill out the ESM self-assessment forms, including emotion scores on seven-point Likert scales. This resulted in a maximum of 50 or 60 measurements, depending on the study. The local ethics committees of Maastricht and Leuven University granted permission and all participants had provided their informed consent.

Design.

All participants underwent a baseline period of ESM. In the depressed patients, follow-up course of depression was measured with the Hamilton Depression Rating Scale (HDRS-17) at 6–8 wk following start of treatment. In the general population, the Symptom Checklist 90 (SCL-90-R) was completed at baseline and at four follow-up measurements, ∼3 mo apart from each other. Follow-up depression score was based on the average of the four follow-up measurements.

Analyses.

The aim was to analyze whether the hypothesized early warning signals (autoregression coefficients, variance, and correlation between emotions as derived from the repeated ESM measures) are associated with follow-up course of depression in both samples. Analyses were performed for four emotions that were a priori chosen to represent each quadrant of the affective space defined by valence and arousal (39): feeling cheerful (positive valence, high arousal), content (positive valence, low arousal), anxious (negative valence, high arousal), and sad (negative valence, low arousal). Data on these four emotions were available in both samples. Because the ESM data have a hierarchical structure [in which the four emotions are clustered within measurement moments (about 50–60 “beeps”) and measurement moments are clustered within persons], a statistical model needs to be used that deals appropriately with the hierarchical structure. These models are known as multilevel models. Two different models were used (see Multilevel Model 1: Autocorrelation). All multilevel models included modeling of random intercept and slope. Data were analyzed using STATA 12.1 (50) and most analyses were replicated independently in R (51). See SI Appendix, Text S2 for details on heteroscedasticity and normality, and Dataset S1 for the R code.

Multilevel Model 1: Autocorrelation.

To extract the information on autocorrelation, we analyzed each emotion separately. A multilevel model was set up in which the emotion score at time t (e.g., anxious at time t) is predicted by the emotion score at time t − 1 (e.g., anxious at time t − 1). The regression coefficient of the emotion scores at time t − 1 on emotion scores at time t is the autoregression coefficient. In the model we used, we additionally included an interaction between the emotion scores at time t − 1 and follow-up course of depression. This means that in this model the size of the autoregression coefficient for a person depends on the continuous follow-up course of depression score. Thus, the autoregression coefficient (and henceforth the autocorrelation) may differ between people with a different follow-up course of depression score. In this way, we are able to test whether persons whose depression score shows a large change over time, will have a higher autoregression coefficient, whereas persons whose depression score shows little change, will have a lower autoregression coefficient (this being the phenomenon of critical slowing down). However, the follow-up in course of depression score is probably not the only variable that is related to differences in autoregression coefficients between persons. A multitude of other variables may contribute to the individual differences in the autoregression coefficient. For this reason, a person-specific deviation is added to the regression coefficient of the person, which is drawn from a normal distribution with zero mean and a to-be-estimated variance, which makes the model formally a multilevel regression model. (Note that also the intercept of the regression model is assumed to be random.) In this way, we are able to examine the association between autoregression coefficients of the four emotions and follow-up course of depression. This multilevel approach enables us to assess this so-called interaction effect between emotion scores at time t − 1 and the follow-up course of depression, while respecting the hierarchical structure of the data. Note that for the purpose of visualization tertiles of depression scores were used in Fig. 2 and SI Appendix, Fig. S6 (see Multilevel Model 2: Variance and Correlations for the definition of the tertile groups).

Multilevel Model 2: Variance and Correlations.

In this second multilevel model, we examined the extent to which variance and correlations differ with follow-up course of depression. In contrast to the autocorrelation analysis, we first clustered the individuals into discrete tertile groups according to follow-up course of depression score and used these tertile groups in our analysis (instead of the continuous score). Those individuals in the general population with the lowest level of depressive symptoms (33%) at follow-up were classified as group 1, those in the middle (33%) as group 2, and the highest 33% as group 3. Similarly, patients with the lowest decrease in symptoms over course of treatment were classified as group 1, those in the middle as group 2, and those with the highest decrease as group 3. Ideally, we would have liked to model the variances and correlations in some (non)linear way as a function of the covariate (future depressive symptoms) in the context of a multilevel model directly, but appropriate models for such an analysis have not been fully developed and tested yet. In the analyses, all four emotions were simultaneously considered. This creates a three-level structure: emotions nested in measurement moments nested in persons. For each tertile group, a multilevel regression model was fitted with emotion score as the dependent variable and dummy codes for the four emotions as independent variables. Random effects corresponding to these dummy-coded variables were added at the person and at the measurement level. These random effects were allowed to have different variances for the four items and their correlations were estimated freely. Therefore, no structure was imposed on the model, making this a saturated model [i.e., the model with the most complex covariance structure possible for the data at hand (52)] The estimated variation in these random effects was used to estimate variance in emotion scores at the measurement level. Correlations between these random effects were used to estimate correlations between emotions at the measurement level. Wald-type tests were used to test for overall differences in the variances and correlations between the three groups.

The Dynamical Systems Model.

We analyzed a minimal model, simulating interactions between four modeled emotions in a person as a stochastic differential equation (inspired by the Lotka–Volterra models, as in ref. 53):

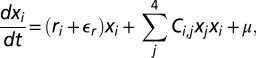where x₁ and x₂ signify the strength of positive emotions (such as cheerful and content), and x₃ and x₄, the strength of negative emotions (such as sad and anxious). The maximum rate of change of the positive emotions, r₁ and r₂, was set to 1, whereas the maximum rate of change of the negative emotions, r₃ and r₄, was assumed to be stress-related, ranging between 0.5 (low stress) and 1.5 (high stress). The matrix C represents the interaction network between the emotions:

Each term of this interaction network describes the strength and direction of the interaction. Negative terms mean that these emotions suppress each other and positive terms imply enhancement. The maximum rate of change (r_i) of each emotion was subjected to a noise term (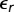) representing short-term fluctuations in the rate of change of each emotion. 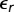is represented by a Gaussian white-noise process of mean zero and intensity σ²/dt (σ = 0.15). Effectively, this means that the system is subject to multiplicative noise. Independent of the strength of the emotions, their value increases by a fixed amount (μ = 1) to prevent emotion levels to be close to zero. The model was solved using a Euler–Maruyama scheme in MATLAB.