Abstract
Task-based assessments of image quality constitute a rigorous, principled approach to the evaluation of imaging system performance. To conduct such assessments, it has been recognized that mathematical model observers are very useful, particularly for purposes of imaging system development and optimization. One type of model observer that has been widely applied in the medical imaging community is the channelized Hotelling observer (CHO). Since estimates of CHO performance typically include statistical variability, it is important to control and limit this variability to maximize the statistical power of image-quality studies. In a previous paper, we demonstrated that by including prior knowledge of the image class means, a large decrease in the bias and variance of CHO performance estimates can be realized. The purpose of the present work is to present refinements and extensions of the estimation theory given in our previous paper, which was limited to point estimation with equal numbers of images from each class. Specifically, we present and characterize minimum-variance unbiased point estimators for observer signal-to-noise ratio (SNR) that allow for unequal numbers of lesion-absent and lesion-present images. Building on this SNR point estimation theory, we then show that confidence intervals with exactly-known coverage probabilities can be constructed for commonly-used CHO performance measures. Moreover, we propose simple, approximate confidence intervals for CHO performance, and we show that they are well-behaved in most scenarios of interest.
Keywords: AUC, image quality assessment, model observer, signal-to-noise ratio (SNR), receiver operating characteristic (ROC)
I. Introduction
Because they can be implemented efficiently using computers, mathematical model observers are a valuable tool for task-based image quality assessments [1], [2], particularly for purposes of imaging system development and optimization [1], [3]. One type of model observer that has been widely utilized in the medical imaging community is the channelized Hotelling observer (CHO) [2]. Due to nice optimality properties and the flexibility afforded through the selection of channel weights, CHOs have been shown to track both human [4]-[9] and ideal linear [10] observer performance. Consequently, CHO methodology has been applied in many areas of medical imaging research, e.g., [3], [5], [6], [11]-[23].
Although CHO performance can be calculated accurately from analytical models in some cases, e.g., [11], [14], [18], [20], this is not usually feasible due to complexities in the image formation process. Instead, most practical evaluations must be carried out by estimating CHO performance from a finite set of images, and the resulting estimates necessarily suffer from statistical variability. Obviously, variability in performance estimates decreases as more images are used, but it is rarely the case that the number of images is so large that statistical variability can be neglected. Furthermore, statistical variability is generally a concern not only for real-data assessments, but also for evaluations with computer-simulated data. Indeed, modern three-dimensional image reconstruction algorithms require considerable computation which limits the number of images that can be reasonably produced (typically around 200). The issue of computational effort becomes particularly striking when there are many parameters for the reconstruction algorithm, since assessments with different parameter values require the reconstruction of new images. Thus, even for simulated data sets, there is a strong need to control and reduce statistical variability in image-quality evaluations with a CHO.
In [2, p. 972], Barrett and Myers suggested that variability in CHO performance estimates could be reduced by utilizing prior knowledge of the channel output means for each class of images, which can be obtained from the image means. This suggestion was associated with the observation that the image means are available in many practical situations. Specifically, when evaluations are performed with simulated tomographic data, which is common for early-stage assessments, the image means can often be accurately estimated by reconstructing the data means. Clearly, this is true for linear reconstruction algorithms, such as those of the filtered backprojection (FBP) type. Moreover, this is frequently a very good approximation for nonlinear iterative reconstruction algorithms such as expectation maximization (EM) [24], [25] and penalized maximum likelihood [26].
When the image class means are difficult to obtain, it might still be that their difference is accessible. For example, in simulated-data experiments with complex anatomical variability, the difference of image class means can be much simpler to obtain than the individual means, since the effects of the background cancel out when the image classes are subtracted; the evaluation in [27] took advantage of this property. Also, for real-data experiments, getting the mean images may be challenging, whereas the difference of the image class means can be accurately produced in some types of real-data experiments; see, e.g., [3], [28].
In a previous paper [29], we proposed and characterized point estimators for CHO performance when either the image class means, or their difference, is known. Our evaluation validated Barrett and Myers’ suggestion and quantitatively demonstrated that a very large statistical advantage can be realized by utilizing prior knowledge of the class means. The estimators in [29] were based on three assumptions: (i) the class means of the channel outputs, or their difference, is known, (ii) the channel outputs follow a multivariate normal distribution for each image class, and (iii) the covariance matrices for the channel outputs are the same for each class. Practically, these assumptions are generally satisfied for CHOs applied to tasks involving small, low-contrast lesions at a known location with a normally-distributed variable back-ground. As discussed earlier, the first assumption is valid in many circumstances. Evidence in favor of the other two assumptions is discussed below.
The second assumption is well-justified since reconstructed tomographic images are often approximately multivariate normal. Furthermore, even for non-normally distributed images, the normality of the channel outputs is supported by the central limit theorem. Khurd and Gindi [30] provided a strong argument in favor of the normality assumption for nuclear medicine applications. In the context of X-ray CT two papers addressed this issue. First, Zeng et al. [31] supported the validity of the normality assumption using various histogram plots. Second, the normality assumption was successfully tested by Wunderlich et al. in [32] using a univariate test and in [27] using the multivariate Henze-Zirkler test.
The third assumption is substantiated by the fact that a small, low-contrast lesion has little influence on the image covariance matrix. Barrett and Myers [2, p. 1209] provided an argument supporting this assumption in the context of nuclear medicine, while Wunderlich and Noo [32] gave a quantitative analysis of the validity of this assumption for X-ray CT. For example, Wunderlich and Noo [32] showed that inclusion of a lesion in a water cylinder cannot change the pixel noise by more than 1% when its diameter and contrast are less than 10 mm and 50 HU, respectively.
The purpose of this article is to present refinements and extensions of the theory in [29] in four useful ways. First, we develop and characterize minimum-variance, unbiased estimators of observer signal-to-noise ratio (SNR), whereas [29] focuses on unbiased estimation of SNR2. This refinement is motivated by the fact that SNR is often preferred over SNR2 as a figure of merit. Second, while the estimators in [29] require equal numbers of images from each class, the theory presented in this work allows for unequal numbers of lesion-absent and lesion-present images, with the possibility that the number of images from one class is zero. This flexibility is especially useful in settings where collection of lesion-present images is difficult, such as in real-data experiments involving anthropomorphic CT phantoms, which are typically not readily modified to include a lesion; see, e.g., [28]. Third, we propose and evaluate exact confidence intervals for commonly used CHO performance measures.1 These confidence intervals enable rigorous statistical analysis of image-quality studies employing CHOs. Fourth, we present robust, approximate confidence intervals that can be used as simple alternatives to the exact confidence intervals. These approximate intervals are found from our SNR point estimators, and they are validated by utilizing our results on exact confidence intervals and the point estimator sampling distributions. Our new findings are presented in Sections 3, 4, and 5, after a brief review of CHOs and associated ROC figures of merit. To aid in readability, all proofs are deferred to the appendices.
In many respects, the present work is closely related to another theory that we have presented for estimation of linear observer performance with known difference of class means [33], [34]. The estimators given in [33], [34] are for general linear observers defined by a fixed, known template, and they operate on scalar-valued ratings. Hence, the estimators in [33], [34] are well-suited for evaluations of non-prewhitening matched filter observers and finitely-trained observers. By contrast, the theory presented here concerns estimation of ideal (perfectly trained) CHO performance, and involves estimators that act directly on samples of the channel output vector. In this setting, the observer’s template is unknown and the approach of [33], [34] does not apply. Thus, the present investigation complements [33], [34], and provides additional flexibility regarding the choice of observer when the difference of class means is known.
II. Channelized Hotelling Observers and ROC Figures of Merit
The present work pertains to estimation of channelized Hotelling observer (CHO) [2] performance for any binary discrimination task at a fixed image location. In this section, we review channelized Hotelling observers and associated figures of merit based on ROC curves.
Consider a binary discrimination task in which an observer attempts to classify each image as belonging to one of two classes, denoted as class 1 and class 2. For medical images, these classes may correspond to normal and diseased conditions, respectively. A CHO generates a rating statistic, t, for each image, and classifies the image by comparing t to a threshold, c. If t > c, then the image is classified as belonging to class 2, otherwise, the image is classified as belonging to class 1.
Before generating the rating statistic for an image, a CHO applies channel weights to reduce the dimensionality of the data. Write the image as a q×1 column vector, g, and let the number of channels be p, where p is typically much SCer than q. The weights for each of the p channels are placed into a column of the q×p channel matrix, U, and the channel outputs are generated as v = UT g, where v is a p× 1 channel output vector. Considerations regarding the choice of channel weights are beyond the scope of this work. For a thorough discussion of this issue, the reader is referred to [2, pp. 936-937] and references cited therein.
Denote the means of the channel output vector, v, for classes 1 and 2 as μ1 and μ2, respectively, and write their difference as Δ μ = μ2μ 1. Also, denote the covariance matrices of v for class 1 and class 2 as Σ1 and Σ2, respectively, and their average as . Once the channel outputs for an image are obtained, a CHO computes the rating statistic as t = wTv, where is the p × 1 CHO template.
Let the channel outputs for classes 1 and 2 be denoted as v(1) and v(2), respectively. Throughout this work, we assume that the channel output vector follows a multivariate normal distribution under each class with equal covariance matrices, i.e., and . (If a p × 1 random vector follows a multivariate normal distribution with mean μ and covariance matrix Σ, we write .) In this setting, the CHO template becomes w = Σ−1Δμ, and the CHO is optimal among all observers that operate on the channel output vector [2, p. 851].
The performance of an observer on a binary classification task is fully characterized by the observer’s receiver operating characteristic (ROC) curve, which plots true positive fraction (TPF) as a function of false positive fraction (FPF) [2], [35]. One figure of merit that is commonly used for ROC evaluations is the area under the ROC curve, denoted as AUC. The AUC can be interpreted as the average TPF, averaged uniformly over all FPF values [35]. Alternatively, if the only pertinent FPF values are in the range [FPFa; FPFb], then the partial area under the ROC curve, defined as
| (1) |
can be a useful figure of merit [35]. The pAUC may be interpreted as the TPF averaged over the FPF values between FPFa and FPFb.
Let Φ(x) and Φ− 1(p) be the cumulative distribution function (cdf) and the inverse cdf, respectively, for the standard normal distribution, . Under our distributional assumptions for the channel outputs, the ROC curve for a CHO takes the special form [35, Result 4.7, p. 82]
| (2) |
where SNR is the observer signal-to-noise ratio, defined as the difference of class means for t divided by the pooled standard deviation [2, p. 819]. In our setting, where the CHO rating statistic, t, is normally distributed for each class, SNR is a meaningful figure of merit for class separability [2, p. 819], and it can be written in the form [2, p. 967]
| (3) |
From (2), observe that the ROC curve is parameterized by only SNR. Hence, TPF at fixed FPF, AUC, and pAUC are functions of SNR. Moreover, these figures of merit are all strictly increasing functions of SNR, i.e., they are related to each other through one-to-one mappings. This fact directly results from (2), which shows that TPF at fixed FPF is a strictly increasing function of SNR. Later, we will utilize this property to construct confidence intervals for TPF, AUC, and pAUC from confidence intervals for SNR.
The functional dependence of AUC and pAUC on SNR that was mentioned above is relatively simple. Namely, under our assumptions, AUC takes the form [2, p. 819] [35, p. 84]
| (4) |
and pAUC can be written as
| (5) |
Note that for a CHO, SNR > 0, and hence, 0.5 < AUC < 1.
III. SNR Point Estimation
Here, we introduce our unbiased SNR point estimators, which are a useful alternative to the unbiased SNR2 estimators given in [29], since SNR, rather than SNR2 is often of interest. Generally, we use the same notation as in [29], with only SC changes that are clear from the text. In order to write general expressions that include the possibility of zero images from one class, we use the notational convention that a summation is zero if its upper limit is zero.
Suppose that we wish to estimate SNR for a CHO with p channels. That is, given m independent, identically distributed (i.i.d.) measurements of the class-1 channel output vector, denoted as , ,…,, and n i.i.d. measurements of the class-2 channel output vector, denoted as , ,…,, we seek to estimate .
A. Estimator Definitions
As in our previous paper [29], we consider two estimation scenarios:
known μ1 and μ2 with unknown Σ
known Δμ with unknown μ1, μ2, and Σ.
Both scenarios have their practical merits. As discussed in the introduction, there are cases where finding Δμ is much easier than finding μ1 and μ2. On the other hand, finding μ1 and μ2 may sometimes be easier than finding Δμ directly, particularly when the imaging process includes strong nonlinearities.
To build our SNR estimator for scenario 1, we start by defining the pooled sample covariance matrix estimator
| (6) |
Next, the SNR point estimator for scenario 1 is defined to be
| (7) |
where
| (8) |
andB(x, y) is the Euler Beta function. The multiplicative constant γ1 is an original contribution of this work; as we will see later, it makes the SNR estimator unbiased.
For scenario 2, in which only Δμ is known, we construct a sample covariance matrix estimator that incorporates our prior knowledge of Δμ. For this task, first define the unbiased sample mean estimators
| (9) |
and
| (10) |
The unbiasedness of and is a direct consequence of and , where E[·] stands for expected value. Using these mean estimators, we introduce a pooled sample covariance matrix estimator as
| (11) |
The SNR point estimator for scenario 2 is then defined as
| (12) |
where
| (13) |
Similar to γ1, the multiplicative constant γ2 is designed to make the estimator unbiased.
B. Sampling Distributions and Optimality
It turns out that the sampling distributions of our SNR estimators are closely related to the inverted gamma distribution, and to prove these relationships, we make use of various facts regarding the inverted Wishart distribution. The inverted gamma, Wishart, and inverted Wishart distributions are reviewed in Appendix A. If a random variable, X, follows an inverted gamma distribution with parameters α and β, we will write X ~ IG(α,β). The following theorem, which is proved in Appendix B, characterizes and .
Theorem 1: Suppose that the conditions of scenario k are satisfied, where either k = 1 or k = 2 and let l = m + n − p − k + 1. If is computed from i.i.d. samples and , where i = 1, 2,…, m, j = 1, 2,…, n with m ≥ 0, n ≥ 0, and l > 0, then
with α = (l + 1)/2 and where
is the uniformly minimum variance unbiased (UMVU) estimator for SNR under scenario k.
From the first part of Theorem 1, observe that the distributions of and differ only through the value of l, which is m + n − p and m + n − p − 1 under scenarios 1 and 2, respectively. Consequently, these distributions are very similar, especially for large values of m + n − p. A way to gain intuitive insight into this similarity is to observe that 2α for an inverted gamma distribution plays a role akin to that of degrees of freedom for a χ2 distribution. Using this analogy together with the observation that 2α = l + 1 in Theorem 1, one can say that scenarios 1 and 2 differ by only one ‘degree of freedom’. Because estimators based on and behave similarly for values of m + n − p that are typical (> 50) in image-quality studies, all evaluations later in this paper focus on scenario 2.
Another useful observation can be gleaned from the expressions in Theorem 1(a). Namely, the distributions of and depend on only two independent parameters: m+n−p SNR; we will rely on this fact later in our confidence interval evaluations. Because the number of images affects the distributions only through the quantity m + n − p, we see that as long as the total number of images, m + n is fixed, having an unequal number of images from each class does not make a difference.
The second part of Theorem 1 clarifies the optimality of our SNR estimators. Specifically, it states that and are UMVU estimators [36], i.e., they are the minimum variance estimators among all unbiased estimators of SNR under scenarios 1 and 2, respectively.
The following corollary to Theorem 1(a) is also proved in Appendix B.
Corollary 1: Suppose that the hypotheses of the previous theorem are satisfied. If l > 1, then
where l = m + n − p − k + 1 and .
Corollary 1 indicates that for both and , the ratio of their mean to their standard deviation only on m + n − p. Thus, Corollary 1 can be used as a basis for quick sample-size estimates when setting up a study. Later, in Section V, we will apply the simple standard deviation expressions implied by Corollary 1 to construct approximate confidence intervals.
IV. Exact Confidence Intervals
In this section, we explain how confidence intervals with exactly-known coverage probabilities can be constructed for the ROC figures of merit from Section II. We start by reviewing the definition of a confidence interval. Let X be a random variable, with a distribution depending on a parameter, θ. A random interval estimate, [θL(X), θU(X)] is said to be a 1 − ω confidence interval for θ if P(θ ∈ [θL(X), θU (X)]) = 1 − ω for any value of θ [37]. The quantity 1 − ω is called the coverage probability for the confidence interval.
Our construction of exact confidence intervals relies on the following lemma for the inverted gamma distribution, the primary role of which is to implicitly define a function, b. This lemma is a direct consequence of Lemma 2(c) in Appendix A.
Lemma 1: Let ρ ∈ (0, 1), suppose that X ~ IG(α, β), and let FX(x ; α, β) denote the cdf of X. For each observation x of X, there exists a unique value b(x α ρ ) satisfying FX(x ; α, β) = ρ for any given α.
Now, let ω1, ω2 ∈ (0, 1) be such that ω1 + ω2 = ω for some ω ∈ (0, 1). For any fixed α, we define functions βL(x) = b(x, α, 1 − ω1) and βU(x) = b(x, α, ω2). Lemma 1 together with our knowledge of the sampling distributions for and yields the next theorem, which is proved in Appendix C.
Theorem 2: Suppose that the hypotheses of scenario k are satisfied, where either k = 1 or k = 2. Let l = m+n−p−k+1, let and let βL(x) and βU(x) be defined as above with α = (l + 1)/2. Further, define , , and . If is computed from i.i.d. samples and , wherei = 1, 2,…, m, j = 1, 2,…, n with m ≥ 0, n ≥ 0, and l > 0, then the random intervals
and
are exact 1 − ω confidence intervals for SNR, TPF(FPF), AUC, and pAUC(FPFa, FPFb), respectively.
Theorem 2 defines an approach to compute exact 1 − ω confidence intervals for CHO figures of merit. Namely, for a given realization x of , βL(x) and βU(x) can be calculated by iteratively solving the inverted gamma cdf equation given in Lemma 1. Next, exact confidence intervals for SNR, TPF, AUC, and pAUC are obtained by inserting β L(x) and βU(x) into the relations in Theorem 2.
Plots of mean confidence interval length (MCIL) for the exact AUC confidence intervals of Theorem 2 under scenario 2 are shown in Figure 1 for different AUC values. MCIL was defined as the expected value of the AUC confidence interval length, i.e.,
| (14) |
where SNR was obtained from AUC according to (4), where ω1, ω2 and m+n−p were fixed, and where fX is the inverted gamma probability density function (pdf) for with parameters given by Theorem 1. This integral was evaluated numerically with the total absolute error constrained to be less than 10−6.
Fig. 1.
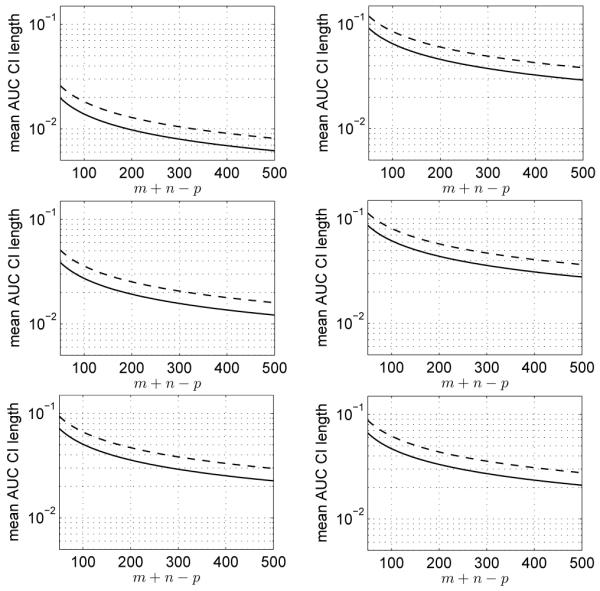
Mean confidence interval length (MCIL) plotted versus m + n − p for the AUC confidence intervals of Theorem 2 under scenario 2. The solid curves are for 95% intervals with ω1 = ω2 = 0.025, and the dashed curves are for 99% intervals with ω1 = ω2 = 0.005. From top to bottom, the plots in the left column are for true AUC values of 0.55, 0.6, and 0.7, and the plots in the right column are for true AUC values of 0.8, 0.9, and 0.95.
Note that the confidence intervals resulting from Theorem 2 can be found graphically by plotting quantile functions versus the true parameter values. (Recall that a quantile function is an inverse cdf.) Namely, under scenario k, we can define a point estimator of AUC as . From Theorem 1 and the appropriate result for a strictly increasing transformation of a random variable [38, Thm. 2.1.3, p. 51], it is straightforward to find an expression for the quantile function, of where q ∈ (0, 1). The AUC confidence interval described by Theorem 2 that corresponds to a specific realization, , can then be equivalently obtained by solving the relations and and AUCL(y) and AUCU(y), respectively. Graphical solution of these relations can be carried out by plotting and as functions of AUC. The desired confidence interval bounds are the intersection points of the quantile curves with the horizontal line of height y. We call the aforementioned plot of quantile curves a coverage diagram. In addition to providing a graphical interpretation of Theorem 2, coverage diagrams also nicely summarize trends in confidence interval length as the distributional parameters vary.
Figure 2 contains 95% coverage diagrams for AUC plotted as solid curves for m + n − p = 50 and m + n − p = 150, as expected. From these diagrams it can be seen that the confidence intervals shrink in size as m + n − p increases. Furthermore, we observe that the confidence interval lengths are SCer for AUC values near 0.5 and 1, with a more rapid decrease near 0.5; this observation is in agreement with the plots of MCIL in Figure 1. The dashed curves in Figure 2 correspond to quantile plots for an AUC estimator that does not utilize knowledge of Δμ that was used for comparisons in our previous paper [29].2 The dashed quantile plots re-emphasize the conclusions of [29] that incorporating knowledge of Δμ yields estimators with more concentrated distributions. They also show that exact confidence intervals similar to those of Theorem 2 are not possible for , since some horizontal lines do not intersect both dashed curves. This observation relates to our earlier footnote in the introduction: building exact confidence intervals for CHO performance in the unknown-Δμ case is challenging.
Fig. 2.
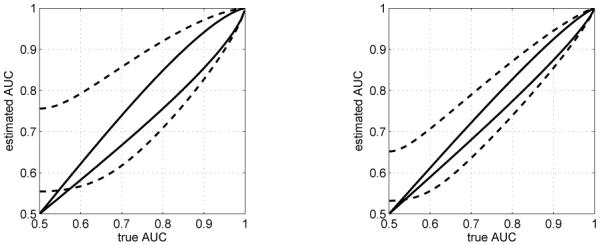
Ninety-five percent AUC coverage diagrams for m + n − p = 50 (Left) and m + n − p = 150 (Right), with ω1 = w2 = 0.025. The solid lines are the 97.5% and 2.5% quantiles of . The dashed lines are the 97.5% and 2.5% quantiles of from [29], with m = n and p = 4.
V. Approximate Confidence Intervals
While being exact, the confidence intervals introduced in the previous section may not be attractive to all readers because they require sophisticated numerical machinery for their computation. In this section, we introduce simpler, but approximate confidence intervals that are straightforward to compute. Moreover, we demonstrate that these approximate intervals are highly robust.
Suppose that the conditions of scenario k are satisfied, where either k = 1 or k = 2. From Corollary 1 and the unbiasedness of our SNR point estimators, it follows that the standard deviation of is
| (15) |
where l = m + n − p − k + 1 and is as given in Theorem 1.We apply this simple expression to construct two types of approximate SNR confidence intervals based on assumptions of asymptotic normality.
The first interval is constructed as a classical Wald interval [38, p. 499]. Namely, we assume that approximately follows a standard normal distribution, and thereby obtain the following interval
| (16) |
where zc = Φ−1(1 − ω/2) is the 1 − ω/2 quantile for the standard normal distribution.
The second interval is motivated by the Wilson interval for a binomial proportion [39], which is known to be better than the corresponding Wald interval for a proportion [38, p. 501] [40]. This Wilson-style interval for SNR is constructed by assuming that approximately follows a standard normal distribution. In other words, the event
| (17) |
occurs with approximate probability 1 − ω. Solving these inequalities for SNR, we obtain the Wilson-style 1 − ω confidence interval
| (18) |
for scenario k, where we assumed that 1 − τkzc > 0.
Interestingly, we see from (17) and (18) that the endpoints for the Wald and Wilson style intervals for SNR are both strictly positive and well-defined if 1 − Tkzc > 0. This condition turns out to be relatively unrestrictive. For example, for 95% and 99% confidence intervals under scenario 2, m + n − p is required to be at least 5 and 6, respectively
Recall from Section II that when our distributional assumptions are satisfied, TPF, AUC, and pAUC are related to SNR through strictly increasing transformations. Thus, Lemma 6 in Appendix C implies that we can obtain approximate 1 − ω intervals for TPF, AUC, and pAUC from the above Wald and Wilson intervals by transforming according to (2), (4), and (5), respectively. Moreover, for a fixed set of parameter values, the coverage probabilities of these intervals are exactly the same.
Because we know the sampling distribution for under scenario k, we can calculate the coverage probabilities for approximate Wald and Wilson-style intervals. Specifically, denote the cdf for as . It is straightforward see that the coverage probabilities for the Wald and Wilson style intervals are
| (19) |
and
| (20) |
respectively. From Theorem 1, (26) in Appendix A, and the strictly increasing transformation property for cdfs [38, Thm. 2.1.3], we find that the cdf of takes the form
| (21) |
where Γ(s) is the Gamma function, Γ(s, t) is the upper incomplete Gamma function, α = (l+1)/2, and SNR2. Using the expression for β, (19) and (20) may be rewritten as
| (22) |
and
| (23) |
respectively. From these relations, we observe that CPWald and CPWilson have the unique property of being independent of SNR, which enables easy evaluation of their coverage probability, as presented next.
The coverage probabilities for the approximate 95% and 99% Wald and Wilson-style SNR confidence intervals are plotted in Figure 3. These plots were computed by evaluating the expressions (22) and (23) with the MATLAB® command gammainc. They indicate that both types of confidence intervals are highly accurate and quickly approach the desired coverage probability. They also show that the Wald-style intervals generally have more accurate coverage probabilities. The same conclusions also apply to TPF, AUC, and pAUC confidence intervals obtained as strictly increasing transformations of the Wald and Wilson SNR intervals (see Lemma 6 in Appendix C for justification).
Fig. 3.
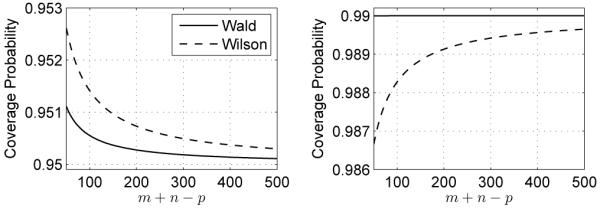
Coverage probabilities of approximate 95% (Left) and 99% (Right) Wald and Wilson confidence intervals for SNR. Note that the coverage probability plot for the exact 95% confidence interval introduced in Section IV would simply be a horizontal line at 0.95. Likewise the plot for the exact 99% confidence interval is a horizontal line at 0.99.
Figures 4 and 5 compare the relative differences in mean confidence interval length (MCIL) of the Wald and Wilson AUC intervals to the exact AUC confidence intervals introduced in Section IV with ω1 = ω2. Specifically, for a fixed set of parameters, the relative difference (in %) between the MCILs of the Wald and exact AUC intervals was calculated as (MCILWald − MCILExact /MCILExact × 100, where the MCILs were calculated by numerically evaluating (14) for the Wald and exact AUC intervals, respectively. The relative difference between the MCILs for the Wilson and exact AUC intervals was computed similarly.
Fig. 4.
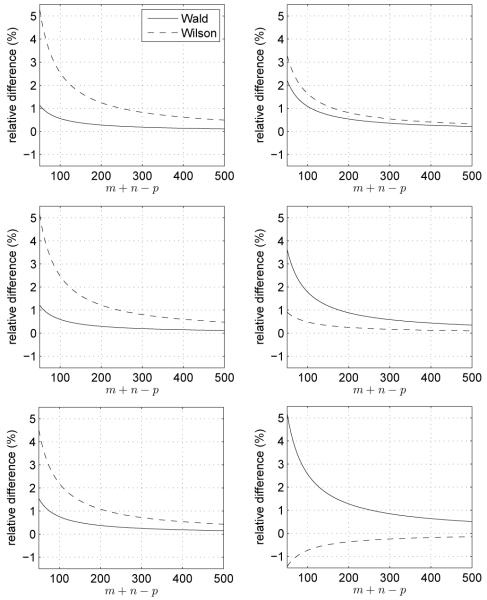
Relative difference in mean confidence interval length for 95% AUC confidence intervals. Left Column: From top to bottom, the plots correspond to true AUC values of 0.55, 0.6, and 0.7. Right Column: From top to bottom, the plots correspond to true AUC values of 0.8, 0.9, and 0.95.
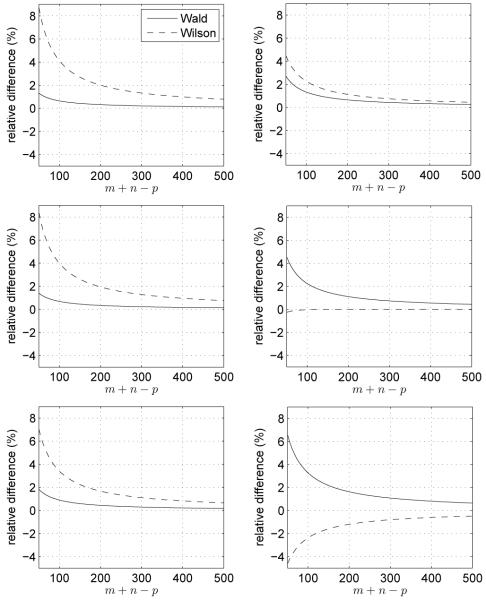
Fig. 5.
Relative difference in mean confidence interval length for 99% AUC confidence intervals. Left Column: From top to bottom, the plots correspond to true AUC values of 0.55, 0.6, and 0.7. Right Column: From top to bottom, the plots correspond to true AUC values of 0.8, 0.9, and 0.95.
The plots for the 95% and 99% Wald intervals indicate that they are always slightly larger than the exact AUC confidence intervals, with the discrepancy increasing with AUC value. For the Wilson intervals, the situation is more complex. Specifically, the Wilson intervals are larger than the exact intervals for SC AUC values, with the difference shrinking until the Wilson intervals become SCer for AUC = 0.95.
The approximate Wald and Wilson AUC confidence intervals are both simple alternatives to the exact AUC intervals of Section IV. From our evaluations, it appears that there is a critical AUC value, slightly above 0.8, where the performance of the two intervals is inverted. Specifically, the Wald AUC intervals are more attractive below the critical value, whereas the Wilson intervals might be preferred for AUC values above the critical value.
VI. Discussion and Conclusions
We have presented refinements and extensions of the results in [29] for CHO performance estimation with known difference of class means. In particular, we have developed unbiased, minimum-variance SNR point estimators, we have extended our theory to unequal numbers of images from each class, and we have proposed both exact and approximate confidence intervals for ROC summary figures of merit. These contributions enable broader utilization of known-Δμ estima-tors in CHO image-quality evaluations. Such estimators are particularly valuable for studies related to imaging system development and optimization, where statistical variability can be a limiting factor.
As outlined in the introduction, there are many practical situations in which the difference of class means, Δμ, can be obtained with good accuracy, and our estimators can be applied. To illustrate the practical utilization of our theory, we have already carried out two investigations in the context of X-ray CT. First, in [28] we used real CT data to evaluate lesion detectability at multiple locations in an anthropomorphic chest phantom with a CHO. In this study, lesions were modeled with plastic rods, and Δμ was obtained by scanning a grid of rods surrounded by air with a high-tube current setting. Subsequently, class-1 images were produced by scanning the chest phantom. Hence, the example in [28] highlights a convenient feature of our estimation theory: class-2 images are not required. In a second investigation [27], we applied our estimation theory to a variable-background discrimination task utilizing simulated abdominal scans of the XCAT phantom [41]. Namely, we evaluated CHO performance for the task of discriminating between two types of kidney stones at a fixed location in the kidney. In addition to Poisson noise, our data simulation included anatomical background variability, modeled by zero-mean, colored Gaussian noise and a variable size fat region in the kidney. Since the CT data was simulated, Δμ was obtained by taking the difference of noiseless reconstructed images. Thus, the example in [27] illustrates how CHO performance for variable-background detection tasks [2] can be evaluated efficiently with our estimators.
In addition to confidence intervals for ROC summary figures of merit, such as AUC, it is sometimes desirable to construct confidence bands for the whole ROC curve. Since our assumptions on the channel output vectors imply that the CHO ratings are normally distributed for each class with equal variances, a theorem we proved in [32, Thm. 3] can be applied to construct a simultaneous confidence band for the ROC curve from a confidence interval for SNR. Specifically, a simultaneous 1 − α confidence band can be constructed as the union over all FPF values of 1 1 − α confidence intervals for TPF; see [32] for more details.
Acknowledgments
This work was partially supported by NIH grants R01 EB007236, R21 EB009168, and by a grant from the Ben B. and Iris M. Margolis Foundation. Its contents are solely the responsibility of the authors.
Appendix A
Properties of Inverted Gamma, Wishart, and Inverted Wishart Distributions
In this appendix, we review the inverted gamma, Wishart, and inverted Wishart distributions, recalling several properties that are needed to prove Theorems 1 and 2. Although this material is covered in [29] and [34], we restate it here for easy reference and completeness.
Inverted Gamma Distribution
The inverted gamma distribution is the distribution of the reciprocal of a gamma random variable. It has two positive parameters, α and β, called the shape and the scale parameters, respectively. A random variable X is said to have an inverted gamma distribution if its probability density function (pdf) takes the form [42]
| (24) |
when x > 0, with fX(x) = 0 otherwise. Above, Γ(x) is the gamma function. If X is an inverted gamma random variable with parameters α and β, we write X ~ IG(α, β).
The mean of an inverted gamma random variable is easily shown to be [42]
| (25) |
An important special case of the inverted gamma distribution is the inverted x2 distribution. Specifically, it can be shown that the reciprocal of a x2 random variable with ν degrees of freedom is an inverted gamma random variable with α ν/2 and β = 1/2.
It is straightforward to show that the cumulative distribution function (cdf) for the inverted gamma distribution is
| (26) |
where Γ(x, y) is the upper incomplete gamma function.
The following lemma states several properties of the inverted gamma distribution that are needed in our proofs of Theorems 1 and 2.
Lemma 2: Suppose that X ~ IG(α, β). Then the following statements hold:
Let c > 0 be an arbitrary constant and let Y = cX. Then Y ~ IG(α, cβ).
Suppose that α > 1/2 and let Then , where B(a, b) is the Euler Beta function.
At arbitrary fixed values of x and α, the cdf of X, FX(x ; α, β), is a continuous, strictly decreasing function of β.
Proof: For part (a), see [29, Lemma 7]. Parts (b) and (c) are proved as Lemmas 2 and 3 in [34], respectively.
Wishart and Inverted Wishart Distributions
The Wishart distribution [43]-[45] is a matrix variate generalization of the χ2 distribution and it arises as the distribution of the sample covariance matrix for multivariate normal measurements [43, p. 82], [44, p. 92-93]. Suppose that z1, z2,…, zn are i.i.d. random vectors distributed as and let . The p × p matrix W has a Wishart distribution, denoted as W ~ Wp(n, Σ), with n degrees of freedom and p × p positive definite scale matrix Σ. When n ≥ p, W is positive definite (and hence, nonsingular) with probability one [43], [44] and the pdf of W is well-defined; see [43]-[45] for expressions of the pdf in this case. When n < p, W is singular, and the pdf does not exist in the conventional sense, but the distribution is nonetheless defined [43, p. 85].
The inverted Wishart distribution emerges as the distribution of the inverse of a Wishart distributed random matrix, and it is the matrix variate generalization of the inverted gamma distribution [44, p. 111]. If a p × p random matrix V follows an inverted Wishart distribution, we write V ~ IWp(m, Ψ), where m is the degrees of freedom and Ψ is a p × p positive definite parameter matrix. The inverted Wishart distribution is defined if m > 2p and is undefined otherwise. An expression for the pdf may be found in [43], [44]. Some properties of Wishart and inverted Wishart matrices that we will use to prove Theorem 1 are collected in the following lemma.
Lemma 3:
If A1 ~ Wp(m, Σ) and A2 ~ Wp(n, Σ) are independent, p × p random matrices, then A1 + A2 ~ Wp(m + n, Σ).
- Let n ≥ p. If S ~ Wp(n, Σ) and A is a nonrandom q × p matrix of rank q ≤ p, then
If X ~ IW1(m, Ψ) and m > 2, then X ~ IG((m−2)/2, Ψ/2).
Proof: See Lemmas 1, 5, and 6 of [29].
Appendix B
Proof of Theorem 1 and Corollary 1
Now, we prove Theorem 1 and Corollary 1. For this task, we need the following lemma.
Lemma 4: Suppose that and are i.i.d. samples from classes 1 and 2, where i = 1, 2,…, m, j = 1, 2,…, n with m ≥ 0, n ≥ 0, and m + n ≥ 1. If and are computed from these sample saccording to (6) and (11), respectively, then (a) and (b)
Proof:
-
From (6), we have
If m = 0, then n ≥ 1 and (27) consists of one summation over class-2 samples. This summation is of the form where Since zj for j = 1, 2,…, n are independently distributed as , the definition of the Wishart distribution [43, p. 82] implies that is distributed as Wp(n, Σ). Similarly, if n = 0, then m ≥ 1 and (27) consists of one summation over class-1 samples that is distributed as Wp(m, Σ). Hence, when either m = 0 or n = 0, we have(27) Now, when m ≥ 1 and n ≥ 1, the same argument as above implies that the first and second summations in (27) are distributed as Wp(m, Σ), and Wp(n, Σ), respectively. Because the first and second summations are independent, Lemma 3(a) implies that
- From (11), we have
If m = 0, then n ≥ 1 and where . In this case, (28) reduces to a summation over class-2 samples that takes the form of the conventional sample covariance matrix. By a standard theorem for the distribution of the sample covariance matrix [44, Thm. 3.3.6(iii), p. 92], this summation is distributed as Wp(n − 1, Σ). Similarly, if n = 0, then m ≥ 1 and where In this case, (28) reduces to a summation over class-1 samples that is distributed as Wp(m − 1, Σ). Hence, when either m = 0 or n = 0(28)
Now, suppose that m ≥ 1 and n ≥ 1. Substituting for and for , and rearranging yields
| (29) |
Using the definitions of and letting and performing some simple algebra, we find that
| (30) |
By a standard result for the conventional sample covariance matrix [44, Thm. 3.3.6(iii), p. 92], the first and second summations in (30) are distributed as Wp(m − 1, Σ), and Wp(n − 1, Σ), respectively. Also, since it follows that Hence, the definition of the Wishart distribu-tion implies that the last term in (30) is distributed as Wp(1, Σ). Since the class-1 samples are independent of the class-2 samples, and because and are indepen-dent of the first and second summations, respectively [44, Thm. 3.3.6(iii), p. 92], it follows that all three terms in (30) are independent. Therefore, Lemma 3(a) allows us to conclude that
Proof of Theorem 1(a):
First, we prove the statement for scenario 1. Lemma 3(b) and Lemma 4(a) together imply that Application of Lemma 3(c) then gives . From the definition of in (7), we see that . Thus, . Finally, Lemma 2(a) yields the stated result for scenario 1.
For scenario 2, the proof is similar. Namely, Lemma 3(b) and Lemma 4(b) together imply that . Lemma 3(c) then yields . From the definition of in (12), it follows that . Thus, . Finally, Lemma 2(a) yields the stated result for scenario 2.
Proof of Theorem 1(b), scenario 1:
From Thereom 1(a), Lemma 2(b), and (8), it follows that , i.e, is an unbiased estimator of SNR.
The joint pdf of the sample is
| (31) |
where
| (32) |
Applying the additive and cyclic properties of the trace, denoted tr, we find that
| (33) |
i.e.,
| (34) |
Hence, the joint pdf has the form
| (35) |
By the Fisher-Neyman factorization theorem [36, Thm. 6.5, p. 35], is a sufficient statistic. Moreover, because the expres-sion in equation (35) has the form of a full rank exponential family [36, p. 23-24], is a complete statistic [36, Thm. 6.22,p. 42]. (Strictly speaking, only the p(p + 1)/2 nonredundant upper triangular entries of comprise a complete statistic. However, following common practice, we say that is complete.) Since (i) is a complete sufficient statistic, (ii) is an unbiased estimator of SNR2 , and (iii) i.e., is a function of only, the Lehmann-Scheffé Theorem [36, Thm. 1.11, p. 88] implies that is the unique UMVU estimator of SNR for scenario 1.
Proof of Theorem 1(b), scenario 2:
From Thereom 1(a), Lemma 2(b), and (13), it follows that , i.e, is an unbiased estimator of SNR.
The joint pdf of the sample is given by (31) and (32). Since Δμ is known, the joint pdf is parameterized by μ1 and Σ After lengthy algebra, λ can be expressed as
| (36) |
where
| (37) |
From the form of the joint sample pdf as given by (31) and (36) and the Fisher-Neyman factorization theorem [36, Thm. 6.5, p. 35], the statistic
| (38) |
is sufficient. In addition, because the joint sample pdf given by (31) and (36) has the form of a full rank exponential family [36, p. 23-24], T is a complete statistic [36, Thm. 6.22, p. 42]. (Strictly speaking, a complete statistic is only comprised of and the p(p + 1)/2 nonredundant upper triangular entries of . However, following common practice, we say that T is complete.) Since (i) T is a complete sufficient statistic, (ii) is an unbiased estimator of SNR2, and (iii) , i.e., is a function of T only, the Lehmann-Scheffé Theorem [36, Thm. 1.11, p. 88] implies that is the unique UMVU estimator of SNR for scenario 2.
Proof of Corollary 1:
From Theorem 1(b), we have . Also, applying Theorem 1(a) and (25), we see that
| (39) |
where l = m + n − p − k + 1. The identity Var then yields
| (40) |
The stated ratio of mean to standard deviation thus follows.
Appendix C
Proof of Theorem 2
In this appendix, we prove Theorem 2, which shows how we can calculate exact confidence intervals for CHO performance. For the proof, we need the following two lemmas.
Lemma 5: Let X be a continuous random variable with cdf, Fx(x ; θ), that is a strictly decreasing function of the parameter θ for each x. Also, let ω1, ω2 ∈ (0, 1) be such that ω1+ω2 = ω for some ω ∈ (0, 1). Suppose that, for each x in the sample space of X, the functions θL(x) and θU(x) can be defined by the relations
then the random interval [θL(X), θU(X)] is an exact 1 −ω confidence interval for θ.
Proof: See [38, Theorem 9.2.12, p. 432] for a proof, and [37, Section 11.4] for a complementary discussion.
Lemma 6: Let g(θ) be a continuous, strictly increasing function of θ. If [θL, θU] is a 1 − ω confidence interval for θ, then [g(θL), g(θU)] is a 1 − ω confidence interval for g(θ).
Proof: See Lemma 3 in [32].
Theorem 2 follows from Theorem 1(a) together with Lemmas 1, 5, and 6. Recall that under our distributional assump-tions, TPF, AUC, and pAUC are strictly increasing functions of SNR.
Footnotes
Note that this construction is a unique property of our theory; in particular, exact confidence intervals for the unknown means case are still not available.
For large m + n, the estimator is essentially equivalent to the maximum likelihood estimator in the unknown-Δμ case. Additional properties of are discussed in [29].
References
- [1].Barrett H, Yao J, Rolland J, Myers K. Model observers for assessment of image quality. Proc. Natl. Acad. Sci. USA. 1993 Nov;90(21):9758–9765. doi: 10.1073/pnas.90.21.9758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Barrett HH, Myers KJ. Foundations of Image Science. Wiley; 2004. [Google Scholar]
- [3].Park S, Jennings R, Liu H, Badano A, Myers K. A statistical, task-based evaluation method for three-dimensional x-ray breast imaging systems using variable-background phantoms. Med. Phys. 2010;37:6253–6270. doi: 10.1118/1.3488910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Myers K, Barrett H. Addition of a channel mechanism to the ideal-observer model. J. Opt. Soc. Am. A. 1987 Dec;4(12):2447–2457. doi: 10.1364/josaa.4.002447. [DOI] [PubMed] [Google Scholar]
- [5].Wollenweber S, Tsui B, Lalush D, Frey E, LaCroix K, Gullberg G. Comparison of Hotelling observer models and human observers in defect detection from myocardial SPECT imaging. IEEE Trans. Nuc. Sci. 1999 Dec;46(6):2098–2103. [Google Scholar]
- [6].Gifford HC, King MA, de Vries DJ, Soares EJ. Channelized Hotelling and human observer correlation for lesion detection in hepatic SPECT imaging. J. Nucl. Med. 2000 Mar;41(3):514–521. [PubMed] [Google Scholar]
- [7].Abbey C, Barrett H. Human-and model-observer performance in ramp-spectrum noise: effects of regularization and object variability. J. Opt. Soc. Am. A. 2001 Mar;18(3):473–488. doi: 10.1364/josaa.18.000473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Zhang Y, Pham B, Eckstein M. The effect of nonlinear human visual system components on performance of a channelized Hotelling observer in structured backgrounds. IEEE Trans. Med. Imag. 2006 Oct;25(10):1348–1362. doi: 10.1109/tmi.2006.880681. [DOI] [PubMed] [Google Scholar]
- [9].Park S, Badano A, Gallas B, Myers K. Incorporating human contrast sensitivity in model observers for detection tasks. IEEE Trans. Med. Imag. 2009 Mar;28(3):339–347. doi: 10.1109/TMI.2008.929096. [DOI] [PubMed] [Google Scholar]
- [10].Gallas B, Barrett H. Validating the use of channels to estimate the ideal linear observer. J. Opt. Soc. Am. A. 2003 Sep;20(9):1725–1738. doi: 10.1364/josaa.20.001725. [DOI] [PubMed] [Google Scholar]
- [11].Bonetto P, Qi J, Leahy R. Covariance approximation for fast and accurate computation of channelized Hotelling observer statistics. IEEE Trans. Nucl. Sci. 2000 Aug;47(4):1567–1572. [Google Scholar]
- [12].Kim J-S, Kinahan PE, Lartizien C, Comtat C, Lewellen TK. A comparison of planar versus volumetric numerical observers for detection task performance in whole-body PET imaging. IEEE Trans. Nucl. Sci. 2004 Feb;51(1):34–40. [Google Scholar]
- [13].Wang J, Li T, Lu H, Liang Z. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose x-ray computed tomography. IEEE Trans. Med. Imag. 2006 Oct;25(10):1272–1283. doi: 10.1109/42.896783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Kulkarni S, Khurd P, Hsiao I, Zhou L, Gindi G. A channelized Hotelling observer study of lesion detection in SPECT MAP reconstruction using anatomical priors. Phys. Med. Biol. 2007;52:3601–3617. doi: 10.1088/0031-9155/52/12/017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].El Fakhri G, Santos P, Badawi R, Holdsworth C, Van Den Abbeele A, Kijewski M. Impact of acquisition geometry, image processing, and patient size on lesion detection in whole-body 18F-FDG PET. J. Nucl. Med. 2007 Dec;48(12):1951–1960. doi: 10.2967/jnumed.108.007369. [DOI] [PubMed] [Google Scholar]
- [16].Hesterman JY, Kupinski MA, Clarkson E, Barrett HH. Harware assessment using the multi-module, multi-resolution system (M3R): A signal-detection study. Med. Phys. 2007 Jul;34(7):3034–3044. doi: 10.1118/1.2745920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Liang H, Park S, Gallas B, Myers K, Badano A. Image browsing in slow medical liquid crystal displays. Acad. Radiol. 2008 Mar;15(3):370–382. doi: 10.1016/j.acra.2007.10.017. [DOI] [PubMed] [Google Scholar]
- [18].Wunderlich A, Noo F. Image covariance and lesion detectability in direct fan-beam x-ray computed tomography. Phys. Med. Biol. 2008 May;53(10):2471–2493. doi: 10.1088/0031-9155/53/10/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Tang J, Rahmim A, Lautam̈aki R, Lodge M, Bengel F, Tsui B. Optimization of Rb-82 PET acquisition and reconstruction protocols for myocardial perfusion defect detection. Phys. Med. Biol. 2009;54:3161–3171. doi: 10.1088/0031-9155/54/10/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Cao N, Huesman R, Moses W, Qi J. Detection performance analysis for time-of-flight PET. Phys. Med. Biol. 2010;55:6931–6950. doi: 10.1088/0031-9155/55/22/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].He X, Links J, Frey E. An investigation of the trade-off between the count level and image quality in myocardial perfusion SPECT using simulated images: the effects of statistical noise and object variability on defect detectability. Physics in medicine and biology. 2010;55:4949–4961. doi: 10.1088/0031-9155/55/17/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].El Fakhri G, Surti S, Trott C, Scheuermann J, Karp J. Improvement in lesion detection with whole-body oncologic time-of-flight PET. J. Nucl. Med. 2011 Mar;52(3):347–353. doi: 10.2967/jnumed.110.080382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Sgouros G, Frey E, Bolch W, Wayson M, Abadia A, Treves S. An approach for balancing diagnostic image quality with cancer risk: Application to pediatric diagnostic imaging of 99mTc-dimercaptosuccinic acid. J. Nucl. Med. 2011 Dec;52(12):1923–1929. doi: 10.2967/jnumed.111.092221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Barrett HH, Wilson DW, Tsui BMW. Noise properties of the EM algorithm: I. Theory. Phys. Med. Biol. 1994;39:833–846. doi: 10.1088/0031-9155/39/5/004. [DOI] [PubMed] [Google Scholar]
- [25].Wilson DW, Tsui BMW, Barrett HH. Noise properties of the EM algorithm: II. Monte Carlo simulations. Phys. Med. Biol. 1994;39:847–871. doi: 10.1088/0031-9155/39/5/005. [DOI] [PubMed] [Google Scholar]
- [26].Fessler JA. Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): applications to tomography. IEEE Trans. Image Processing. 1996 Mar;5(3):493–506. doi: 10.1109/83.491322. [DOI] [PubMed] [Google Scholar]
- [27].Wunderlich A, Noo F, Heilbrun M. New results for efficient estimation of CHO performance; Proc. 2nd Intl. Conf. on Image Formation in X-ray CT; June 2012.pp. 153–156. [Google Scholar]
- [28].Wunderlich A, Noo F. Practical estimation of detectability maps for assessment of CT scanner performance; IEEE Nucl. Sci. Symp. Conf. Record; November 2010.pp. 2801–2804. [Google Scholar]
- [29].Wunderlich A, Noo F. Estimation of channelized Hotelling observer performance with known class means or known difference of class means. IEEE Trans. Med. Imaging. 2009 Aug;28(8):1198–1207. doi: 10.1109/TMI.2009.2012705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Khurd P, Gindi G. Fast LROC analysis of Baysian reconstructed tomotgraphic images using model observers. Phys. Med. Biol. 2005;50:1519–1532. doi: 10.1088/0031-9155/50/7/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zeng R, Petrick N, Gavrielides MA, Myers KJ. Approximations of noise covariance in multi-slice helical CT scans: impact on lung-nodule size estimation. Phys. Med. Biol. 2011;56:6223–6242. doi: 10.1088/0031-9155/56/19/005. [DOI] [PubMed] [Google Scholar]
- [32].Wunderlich A, Noo F. Confidence intervals for performance assessment of linear observers. Med. Phys. 2011 Jul;38(S1):S57–S68. doi: 10.1118/1.3577764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Wunderlich A, Noo F. Estimation of trained-observer performance with known difference of class means; IEEE Nucl. Sci. Symp. Conf. Record; November 2010.pp. 2095–2098. [Google Scholar]
- [34].Wunderlich A, Noo F. On efficient assessment of image-quality metrics based on linear model observers. IEEE Trans. Nucl. Sci. 2012 Jun;59(3):568–578. doi: 10.1109/tns.2012.2190096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Pepe MS. The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford Univ. Press; 2003. [Google Scholar]
- [36].Lehmann E, Casella G. Theory of Point Estimation. 2nd ed Springer; 1998. [Google Scholar]
- [37].Bain LJ, Engelhardt M. Introduction to Probability and Mathematical Statistics. 2nd ed Duxbury; 1992. [Google Scholar]
- [38].Casella G, Berger RL. Statistical Inference. 2nd ed Duxbury; 2001. [Google Scholar]
- [39].Wilson EB. Probable inference, the law of succession, and statistical inference. J. Am. Stat. Assoc. 1927 Jun;22(15):209–212. [Google Scholar]
- [40].Brown L, Cai T, DasGupta A. Interval estimation for a binomial proportion. Stat. Sci. 2001;16(2):101–133. [Google Scholar]
- [41].Segars W, Mahesh M, Beck T, Frey E, Tsui B. Realistic CT simulation using the 4D XCAT phantom. Medical physics. 2008 Aug;35(8):3800–3808. doi: 10.1118/1.2955743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Evans M, Hastings N, Peacock B. Statistical Distributions. 2nd ed Wiley; New York: 1993. [Google Scholar]
- [43].Muirhead RJ. Aspects of Multivariate Statistical Theory. John Wiley & Sons; 1982. [Google Scholar]
- [44].Gupta A, Nagar D. Matrix Variate Distributions. Chapman & Hall/CRC; 2000. [Google Scholar]
- [45].Anderson TW. An Introduction to Multivariate Statistical Analysis. 3rd ed John Wiley & Sons; 2003. [Google Scholar]