Unchanged mitochondrial organization and compartmentation of high-energy phosphates in creatine-deficient GAMT^−/− mouse hearts

Abstract

Disruption of the creatine kinase (CK) system in hearts of CK-deficient mice leads to changes in the ultrastructure and regulation of mitochondrial respiration. We expected to see similar changes in creatine-deficient mice, which lack the enzyme guanidinoacetate methyltransferase (GAMT) to produce creatine. The aim of this study was to characterize the changes in cardiomyocyte mitochondrial organization, regulation of respiration, and intracellular compartmentation associated with GAMT deficiency. Three-dimensional mitochondrial organization was assessed by confocal microscopy. On populations of permeabilized cardiomyocytes, we recorded ADP and ATP kinetics of respiration, competition between mitochondria and pyruvate kinase for ADP produced by ATPases, ADP kinetics of endogenous pyruvate kinase, and ATP kinetics of ATPases. These data were analyzed by mathematical models to estimate intracellular compartmentation. Quantitative analysis of morphological and kinetic data as well as derived model fits showed no difference between GAMT-deficient and wild-type mice. We conclude that inactivation of the CK system by GAMT deficiency does not alter mitochondrial organization and intracellular compartmentation in relaxed cardiomyocytes. Thus, our results suggest that the healthy heart is able to preserve cardiac function at a basal level in the absence of CK-facilitated energy transfer without compromising intracellular organization and the regulation of mitochondrial energy homeostasis. This raises questions on the importance of the CK system as a spatial energy buffer in unstressed cardiomyocytes.

creatine kinase (CK) plays an important role as an energy buffer in several cell types, including heart, skeletal muscle, and brain. It catalyzes the phosphotransfer between creatine (Cr) and ATP. The importance of CK is highlighted by its strong regulation of local ATP concentration as shown by studies of sarcolemmal ATP-sensitive K⁺ channels (1) and rigor formation in permeabilized fibers (55, 57). After induction of ischemia, contraction correlates with the phosphocreatine (PCr) level (14), and, after heart failure, the PCr-to-ATP ratio in the heart is a strong predictor of patient mortality (20). Additionally, a recent study (15) has shown that overexpression of cytosolic CK improves cardiac contractile function and viability after induced heart failure.

Cr deficiency inhibits the CK system. It may occur due to deficiency of the enzymes that synthesize Cr [l-arginine:glycine amidinotransferase (AGAT) and guanidinoacetate methyltransferase (GAMT)] or the Cr transporter (CrT or SLC6A8), which imports Cr across the sarcolemma. All three cases of Cr deficiency have been found in humans (8, 43), and all have been reproduced in mouse models (AGAT^−/−, GAMT^−/−, and CrT^−/− mice). The GAMT^−/− model is the most studied to date.

Considering the presumed importance of CK in the heart, it is remarkable that the baseline cardiac function of GAMT^−/− mice is so little affected by the lack of a functional CK system. For example, ejection fraction is normal and only LV systolic pressure is slightly lower in GAMT^−/− mice (19, 42). Furthermore, when the maximal exercise capacity and response to chronic myocardial infarction was compared in GAMT^−/− and wild-type (WT) mice, no significant difference was observed (30). It is only under acute stress conditions that functional deficits are observed in both GAMT^−/− and CK^−/− hearts, e.g., reduced inotropic reserve and impaired recovery from ischemia-reperfusion injury (10, 19, 47). The near-normal basal cardiac performance in GAMT^−/− mice could be due to extensive compensatory changes not identified in Ref. 30, similar to those described in the hearts of CK^−/− mice, where the CK system is disabled by the lack of both cytosolic and mitochondrial muscle-specific CK isoforms. CK^−/− hearts show only minor changes in performance (35), explained in part by cytoarchitectural changes that facilitate direct cross-talk between mitochondria and ATPases (23). Direct cross-talk between organelles is possible due to intracellular diffusion restrictions (60), as evidenced by a low apparent ADP affinity of mitochondrial respiration in permeabilized cardiomyocytes (27), which leads to the coupling of endogenous ATPases to mitochondria or glycolysis (44, 45) as well as anisotropy in diffusion (21, 51). In CK^−/− mice, in the absence of Cr, the apparent ADP affinity of mitochondrial respiration was higher than in control experiments with WT mice (23). This suggests a reduction of the overall diffusion restriction between mitochondria and the surrounding solution (36). However, diffusion was sufficiently restricted for sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA) and myosin ATPase to preferentially use ATP generated in mitochondria as efficiently as in WT mice (23).

The aim of this study was to determine whether the hearts of GAMT^−/− mice exhibit similar compensatory changes as those observed in the hearts of CK^−/− mice. We used three approaches that we have previously applied to rat cardiomyocytes. Using confocal microscopy, we quantified the three-dimensional (3-D) relative position of mitochondrial centers (as in Ref. 4). This allowed us to detect whether mitochondrial positioning is different in GAMT^−/− mice. On permeabilized cardiomyocytes, we recorded a full set of kinetic data to analyze the intracellular compartmentation of ADP/ATP using mathematical models. In rat cardiomyocytes, we discovered a strong functional coupling between pyruvate kinase (PK) and a fraction of ATPases (45). Because the activity of other phosphotransfer systems increases in CK^−/− mice (34) and because failing hearts experiencing a loss of CK (2), we speculated whether the coupling between PK and ATPases is upregulated in GAMT^−/− mice. Finally, we used fluorescence microscopy to record changes in NADH and flavoprotein (Fp) autofluorescence when permeabilized cardiomyocytes were exposed to increasing doses of ADP (as in Ref. 22). This would test whether the ADP kinetics of respiration, as recorded on a population level, also occurred on the single cell level.

MATERIALS AND METHODS

Animal procedures were approved by the Estonian National Committee for Ethics in Animal Experimentation (Estonian Ministry of Agriculture).

Animals.

We received GAMT^−/− mice and WT littermates, which had been bred at The Wellcome Trust Centre for Human Genetics (Oxford, UK). Mice had been backcrossed on to a C57Bl/6J background for at least eight generations. Animals were kept in our local animal facility in cages with free access to water and food (vegetable-based, Cr-free chow, R70 from Lactamin). Mice of different genotypes were housed separately to prevent GAMT^−/− mice from taking up Cr via coprophagia of feces from WT littermates (41).

Cardiomyocytes were successfully isolated from eight GAMT^−/− mice (4 females and 4 males) and nine WT mice (5 females and 4 males) of similar age (female WT: 46.9 ± 4.9 wk and female GAMT^−/−: 45 ± 4.3 wk; male WT: 45.6 ± 1.5 wk and male GAMT^−/−: 45.9 ± 1.4 wk).

Genotyping.

Knockout and WT mice were genotyped by PCR. Briefly, genomic DNA was extracted from tissue samples by SDS/proteinase K digestion followed by isopropanol precipitation. PCR amplification of the DNA fragments was performed using the following specific primers: 5′-CAGGCTCCCACCCACTTGA-3′, 5′-AGGCCTACCCGCTTCCATTG-3′, 5′-CCTCAGGCTCCCACCCACTTG-3′, and 5′-GGTCTCCCAACGCTCCATCACT-3′. PCRs were carried out in a 25-μl volume containing 1× PCR buffer (Bioline Immobuffer), 0.5 mM dNTP mixture (Fermentas), 2 mM MgCl₂ (Bioline), 0.5–0.7 pmol of each primer (TAG Copenhagen), 5% DMSO (Sigma), 0.6 M betaine (Sigma), 0.06 U/μl IMMOLASE DNA polymerase (Bioline), and 5 μl template DNA. After the initial denaturation step at 94°C for 5 min, nine cycles of PCR were carried out as follows: denaturation at 94°C for 60 s, annealing at 60°C for 60 s, and extension at 72°C for 30 s. In each cycle, the temperature was decreased by 0.5°C in each consequent annealing step. This was followed by 34 cycles of the following PCR: denaturation at 94°C for 60 s, annealing at 55°C for 60 s, and extension at 72°C for 30 s. This was done in a thermal cycler (Bio-Rad DNA Engine Peltier Thermal Cycler). PCR products were electrophoresed on a 1% agarose gel with ethidium bromide in 1× Tris-borate-EDTA. Amplification of a single 265-bp product or a 427-bp PCR product corresponded to WT GAMT (GAMT^+/+) or homozygous GAMT knockout (GAMT^−/−) genotype, respectively. Simultaneous amplification of a 265- and 427-bp fragments corresponded to a heterozygous GAMT (GAMT^+/−) genotype.

Total Cr content.

The total Cr content was measured enzymatically from mouse hindlimb skeletal muscle. The metabolite extraction from tissue samples was done as follows. A 50- to 100-mg piece of tissue was homogenized in 2 ml of 0.6 M perchloric acid with 2 mM EDTA. Water was added to provide a total volume of 10 ml, and the suspension was centrifuged at 10,000 g for 10 min at 4°C. The supernatant was neutralized with KOH, the precipitated salt was removed by centrifugation, and total Cr levels were assayed immediately from the resulting extract (pH 7.0–7.2) via coupled enzymatic reactions using a spectrofluorophotometer. The enzymatic reaction was performed in 500 μl of 100 mmol/l potassium phosphate buffer (pH 7.5) containing 5 mmol/l MgCl₂, 16 kU/l CK, 8 mmol/l ADP, 16 kU/l hexokinase, 4 mM glucose, 40 kU/l creatinase, 20 kU/l sarcosine oxidase, 4 kU/l horseradish peroxidase, 10 μmol/l Amplex red, and 6–40 μl tissue extract. This mixture ensured that Cr and PCr were degraded by creatinase, which led to the production of H₂O₂ (which was later determined fluorescently using Amplex red conversion to resorufin). The blank mixture was identical except for the omission of creatinase. The reaction mixture was incubated for 30 min at room temperature. H₂O₂ was determined spectrofluorometrically in 2 ml of 100 mmol/l phosphate buffer containing 5 mmol/l MgCl₂. Fluorescence measurements were performed using 4-ml plastic cuvettes (four-faced transparent cuvettes, Deltalab, Rubí, Spain) in an RF-5301 PC spectrofluorometer (Shimadzu Scientific Instruments, Kyoto, Japan). The temperature was maintained at 25°C (Julabo F12-ED, JULABO Labortechnik). First, background fluorescence of the buffer without enzymes was measured, and 1 μl of 5 mM Amplex red and 5 μl of 100 U/ml horseradish peroxidase were then added to measure the contribution of Amplex red to fluorescence intensity. Finally, the fluorescence of the diluted reaction mixture was measured. At the end of each experiment, a calibration signal was generated with five additions of 1 μl of 0.1 mM H₂O₂, each leading to a concentration increase of 50 nM. Measured fluorescence intensities (emission/excitation = 585/570 nm) were fitted assuming a linear relationship between fluorescence and the resorufin concentration in the cuvette, with the offset determined by the background fluorescence of the buffer. The fit was performed by minimizing the least-square difference between calculated and measured fluorescence through variation of the gain (fluorescence-to-resorufin concentration ratio), total Cr content, and resorufin contamination of Amplex red solution (proportional to the Amplex red concentration). Cr concentrations were expressed as nanomoles per milligram wet weight tissue. All measurements were repeated with three different dilutions, and a paired t-test between recordings with and without creatinase (sample vs. blank) was used to determine whether the total Cr content was identifiable by the method (a significance level of P < 0.05 was used).

Isolation of cardiomyocytes.

Isolation of cardiomyocytes was carried out as previously described (45). Briefly, the heart was excised and immediately transferred to ice-cold wash solution (see composition below). It was cannulated via the aorta on a Langendorff perfusion system, which was thermostatted to 38.5°C (Julabo ED, JULABO Labortechnik). The heart was first perfused with wash solution at a constant pressure of 80 cmH₂O for at least 5 min. The flow rate under these conditions was 3.68 ± 1.68 ml/min (n = 17). After the heart was washed free of blood, the perfusion was switched to a digestion solution containing an additional 0.25 mg/ml collagenase P (Roche) and 3 mg/ml BSA. Perfusion was also switched to a constant flow of 1 ml/min until the pressure had decreased to 10–15% of the initial pressure at 80 cmH₂O and the heart was soft. After perfusion, the ventricles were isolated. They were cut into four pieces, which were incubated further in the digestion solution at 38.5°C with gentle shaking until the tissue started falling apart. Cells were further dissociated with a 5-ml pipette. Sedimentation solution (5 ml) was added before the cells were filtered into a glass tube. As a result, the cell suspension was a mix of isolated cardiomyocytes from the left and right ventricles. Cells were washed by sedimentation. First, extracellular Ca²⁺ was gradually increased to 1 mM to ensure Ca²⁺ tolerance of the cells (Ca²⁺ from a stock of 1 M CaCl₂ was added to the sedimentation solution). After this, extracellular Ca²⁺ was washed out again by washing the cells three times with 10 ml sedimentation solution.

Mitochondrial imaging.

Freshly isolated cells kept in sedimentation solution were loaded with 1 μM TMRE (T-669, Molecular Probes, Life Technologies) for at least 15 min. A small fraction of the cells was added to 200 μl sedimentation solution in the chamber of a flexiPERM micro 12 reusable silicone cell culture chamber (Greiner Bio-One) attached to a coverslip. Confocal images were acquired on a Zeiss LSM 510 Duo built around an inverted Axio Observer Z1 microscope (Carl Zeiss) with a ×63/1.2 numerical aperture (NA) water-immersion objective. The signal was acquired via a high-voltage single photomultiplier tube using 8-bit mode; the pinhole was set to one Airy disk. TMRE was excited with a 543-nm laser, and emission was recorded through a 575-nm long-pass filter. These experiments were carried out at room temperature.

Estimating the relative positioning of mitochondrial centers.

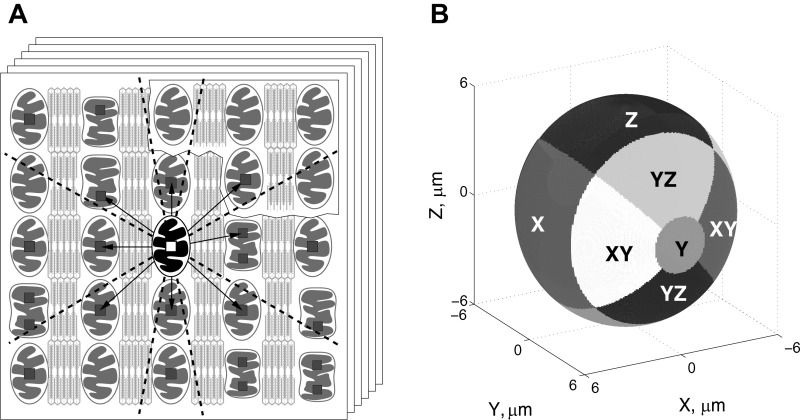
Mitochondrial positioning was quantified by statistical analysis of the relative distances between neighboring mitochondrial centers, as in Ref. 4. In short, the following procedure was used. Each stack of confocal images was blurred by a 3-D Gaussian blur with a SD of 0.3 μm in all directions. The position of all mitochondrial centers was determined by finding local fluorescence maxima of the blurred 3-D stack of images. Subsarcolemmal mitochondria and mitochondria around the nucleus (perinuclear mitochondria) were filtered out as judged by the eye. A space around each mitochondrial center was divided into 14 sectors: 2 sectors in the y-direction along the myofibril, 2 sectors in the x-direction across the myofibril in the image plane, 2 sectors in the z-direction across the myofibril perpendicular to the image plane, 4 diagonal sectors in the xy-direction, and 4 diagonal sectors in the yz-direction (Fig. 1). For each mitochondrial center, we found the closest neighboring mitochondrial center in each of these sectors, as shown in Fig. 1. Finally, the relative position of these neighboring mitochondrial centers was analyzed by finding the probability density function and cumulative probability distribution, as in Ref. 4.

Fig. 1.

Method used to analyze distribution of mitochondria in cardiomyocytes, taken from Ref. 4. A: first, a series of Z-stack confocal images of mitochondria in nonpermeabilized cardiomyocytes was acquired (scheme). Second, the local fluorescence maxima (small squares) were found. As indicated in the scheme, the maxima were not always on the same image in the stack. Note that sometimes two fluorescence maxima seem to be found per mitochondrion (as shown in A). Next, the closest neighbors were found for each mitochondrion, one per sector (the projections of the sector borders in two dimensions are shown by the dashed lines). In this scheme, the mitochondrion, in which neighbors are sought, is highlighted, and the closest neighbors to this mitochondrion are indicated by arrows. Note that the closest mitochondria in some sectors are not always from the same image in the stack. The relative coordinates of the closest neighbors, i.e., the coordinates relative to the highlighted mitochondria, were stored and further analyzed. B: division of three-dimensional space into the sectors, with sectors shown by the different levels of gray. The mitochondrion for which neighbors are sought is positioned at the origin of coordinate system. Here, the coordinate y-axis corresponds to the fiber orientation. The sector names are shown in the scheme.

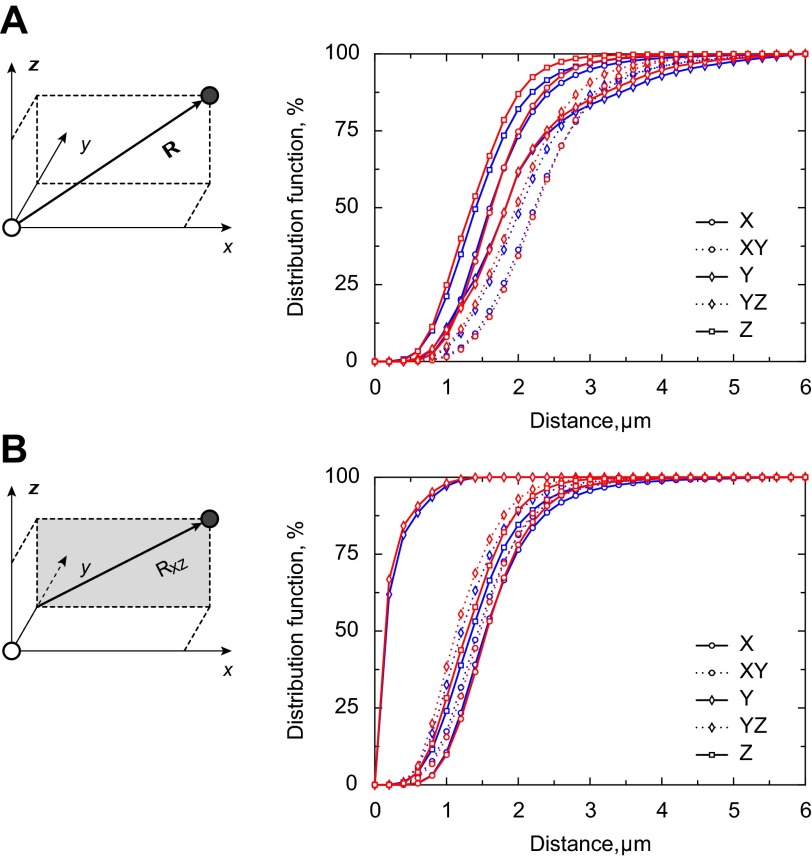
For statistical analysis, we found for each cell separately the cumulative distribution function for the nearest neighboring mitochondria in each direction. The averaged results of the distance at 25%, 50%, and 75% of the distribution function for R and R_XZ (notation from Fig. 5) were compared for WT and GAMT^−/− cardiomyocytes, as detailed in the results.

Fig. 5.

Cumulative distribution function of the distance between centers of neighboring mitochondria in different directions. The distribution functions for the following distances were calculated: distance (R) from the origin to the nearest mitochondrion in each direction (A) and distance (R_XZ) from the y-axis through the origin to the nearest mitochondrion in each direction (B). The differences in the corresponding distances are highlighted on the schemes shown in A and B, left. If the rows of mitochondria were parallel, R_XZ would be the same in the X- and XY-directions and Z- and YZ-directions. Indeed, their distribution functions were very close. For parallel rows, R_XZ in the Y-sector would be 0. Note in both A and B that the distribution functions for the WT (blue) and GAMT^−/− (red) groups were either overlapping or very close to each other.

Respirometer recordings.

Respirometer recordings were used to determine 1) the respiration kinetics of permeabilized cells stimulated by stepwise increases in ADP or ATP and 2) the inhibition of ATP-stimulated respiration by a competitive assay consisting of phosphoenol pyruvate (PEP; 5 mM) and PK (20 IU/ml). For this, we used a Strathkelvin RC 650 respirometer equipped with six 1302 O₂ electrodes connected via a 929 Oxygen System interface (all from Strathkelvin Instruments) to a computer. The respirometer was thermostatted to 25°C (Julabo F12-ED, JULABO Labortechnik). The O₂ tension in each chamber was recorded by the software provided by Strathkelvin and our homemade software, which immediately calculated the rate of O₂ consumption as well. The latter is open-source software and is freely available at http://code.google.com/p/iocbio/wiki/IOCBioStrathKelvin.

For recordings of ADP kinetics, a 15- to 20-μl cell suspension was added to the respiration chamber containing 2 ml Cr and PCr-free respiration solution (see composition below). Cells were allowed at least 5 min to permeabilize before the steady-state basal respiration rate (V₀) was recorded. ADP was added to the respirometer chamber using a Hamilton syringe (801RN, Hamilton Bonaduz). The ADP concentration was increased in steps, and the respiration rate was allowed to reach steady state for at least 2 min before the addition of more ADP. Recordings of ATP kinetics were carried out in a similar way except that a 30- to 50-μl cell suspension was added to the chamber and ATP was added instead of ADP. To record how a competitive ADP-trapping assay consisting of PEP and PK competes with mitochondria for the consumption of ADP from ATPases, a 30- to 60-μl cell suspension was added to the respirometer chamber. After recording V₀, 2 mM ATP was added to stimulate ATPases. Initially, this endogenously produced ADP was exclusively consumed by the mitochondria and stimulated respiration (V_{2 mM ATP}). The addition of 5 mM PEP (no. P-7002, Sigma-Aldrich) activated endogenous PK to compete with mitochondria for the consumption of ADP and the lowered respiration rate (V_PEP). Further addition of 20 U/ml exogenous PK (no. 10109045001, Roche), lowered the respiration rate (V_{PEP + PK}) even more.

Spectrophotometer recordings.

ATP kinetics of ATPases and ADP kinetics of endogenous PK were recorded using an Evolution 600 spectrophotometer (Thermo Fisher Scientific) equipped with a Peltier water-cooled cell changer (SPE 8 W, Thermo Fisher Scientific) to maintain temperature at 25°C. ADP production by ATPases in permeabilized cardiomyocytes was recorded in 2 ml respiration solution using a coupled assay consisting of 5 mM PEP (no. P-7002, Sigma-Aldrich), 0.3 mM NADH (no. 10128015001, Roche), 7.2 U/ml LDH (no. 61311, Sigma-Aldrich), and 20 U/ml PK (no. 10109045001, Roche). To avoid ADP consumption by mitochondria, respiration was inhibited by 5 mM NaCN (no. 205222, Sigma-Aldrich) and 10 μM oligomycin (no. 75351, Sigma-Aldrich). The basal ATPase rate was first recorded in the absence of ATP and then at increasing concentrations of ATP. Rates were recorded for 3 min after each addition, and steady state was verified for each step. NADH was replenished as needed to keep absorbance between 1.7 and 0.7 (the linear range of NADH consumption as verified by preliminary experiments; data not shown). The ADP kinetics of endogenous PK were recorded using the same coupled assay (where only 5 mM NaCN, 10 μM oligomycin, 5 mM PEP, 0.3 mM NADH, and 7.2 U/ml LDH were added), and PK activity was recorded at increasing ADP concentrations.

For normalization, the protein content was measured with a Nanodrop 2000 (Thermo Fisher Scientific).

Mathematical model.

For a detailed description of the model, see Ref. 45. In brief, models of different complexity were considered (Fig. 2). All models included three separate compartments: extracellular solution, cytoplasm, and intermembrane space (IMS). Models 3 and 4 also included a fourth compartment (compartment 4) with PK and ATPase to describe coupling between glycolysis and ATPases, as described in Ref. 45. The processes considered in the models were diffusion between compartments restricted by diffusion barriers, the reactions of ATPases, oxidative phosphorylation, and the reactions of endogenous PK. The models containing two groups of ATPases (2, 3, and 4) were also considered in a simplified form (2s, 3s, and 4s) with both groups of ATPases having the same affinities for ATP and ADP.

Fig. 2.

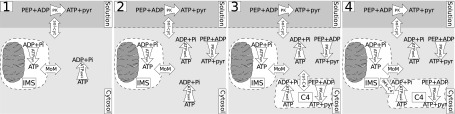
Schematic diagrams of models 1–4. Compartments are indicated by dashed lines, reactions by single-headed curved arrows, and exchange between compartments by double-headed straight arrows. All models have compartments representing the solution, cytosol, and mitochondrial intermembane space (IMS). Models 3 and 4 include a fourth compartment (C4). The reactions considered are mitochondrial ATP synthesis in the mitochondrial matrix leading to the conversion of ADP to ATP in the mitochondrial IMS (ATP_syn), ATP consumption by ATPases (ATPase1 and ATPase2), and ATP synthesis by endogenous pyruvate kinase (PK; PKend1 and PKend2) and exogenous PK. The following exchanges between compartments were calculated: solution and cytosol (sol-cyt), IMS and cytosol through the outer mitochondrial membrane (MoM), cytosol and C4 (cyt-C4), and IMS and C4 (IMS-C4). PEP, phosphoenol pyruvate.

For simplicity, ATP synthesis in mitochondria was described by the simple phenomenological Michaelis-Menten-type equation involving the concentrations of ATP and ADP only in the IMS, as shown in Fig. 2. Note that this approach is possible due to high concentrations of P_i, oxygen, and substrates, as used in our experiments. This simplification allowed us to simulate diffusion and reactions in the intracellular compartments only (cytoplasm, IMS, and compartment 4) and thus allowed us to ignore the details of the reactions involved in the respiratory chain. The same approach has been applied by us earlier and used to estimate the compartmentation of ATPases and intracellular diffusion restrictions in two dimensions (52), three dimensions (36), and simplified multicompartment (45) analysis of the intracellular environment.

To compare the models, the goodness of fit was evaluated using Akaike information criteria (AIC), corrected AIC (AIC_c), and Bayesian information criteria (BIC), which were calculated for each model. For all three criteria, the best-fitting model is the one with the minimum criterion value. Those criteria take into account the goodness of fit and number of parameters in the model. Using AIC_c and BIC, a larger number of parameters is penalized more than in AIC. Multiple goodness criteria were used to ensure that the conclusions would not depend on the selection of one particular criterion.

In addition, models were compared by an F-test for nested models, which allows comparison of models 1 and 2 with model 3 as well as models 1 and 2 with model 4. The F-test takes the number of parameters into account so that statistical significance indicates that the more complicated model fits the data better irrespective of the number of parameters.

Next, the F-test was used to evaluate confidence intervals for each of the fitted model parameters. Confidence intervals were calculated using an F-test and show the range where the fit is worse than an optimal fit but with a P value larger than 0.05 (in terms of extra sum of squares), as in Ref. 45.

Finally, to test whether the data recorded in WT and GAMT^−/− cardiomyocytes were significantly different from each other, the data were fit either separately for different types of cardiomyocytes or by fitting both sets with the same model parameters (pooled data set). The F-test was applied to test whether an increased number of parameters induced by fitting the experiments separately was justified or whether the better fits were due to chance. For this test, a fit of pooled data by a single set of model parameters can be considered as a simplified version of fitting the data separately using two sets of model parameters: one for WT cardiomyocytes and one for GAMT^−/− cardiomyocytes.

For a detailed model description, numeric methods, and statistical analysis, see Ref. 45.

Recordings of NADH and Fp autofluorescence.

Recordings of NADH and Fp autofluoresence were performed as described in Ref. 22. In brief, microscope experiments were performed on an inverted Nikon Eclipse Ti-U microscope (Nikon, Tokyo, Japan; objective CFI Super Plan Fluor ELWD ×20/0.45 NA) equipped with two tiers of motorized filter turrets for simultaneous acquisition of transmission and fluorescence images. For images of NADH and Fp autofluorescence, respectively, light from a Prior Lumen 200 with a 200-W metal halide lamp with extended wavelength (Prior Scientific, Cambridge, UK) was passed via an optical fiber into the upper filter turret. For NADH recordings, the light was passed through a 340/26-nm excitation filter onto a 400-nm long-pass dichroic mirror, which deflected the light onto the specimen. Light emitted from the specimen passed back through the upper filter cube to a 510 XR dichroic in the lower filter cube and reflected through a 460/80-nm emission filter to an Andor Ixon EMCCD camera (Andor Technologies, Belfast, UK). For Fp recordings, the light was passed through a 465/30-nm excitation filter onto a 510-nm dichroic mirror, which deflected the light onto the specimen. Light emitted from the specimen passed back through the upper filter cube to a 560 XR dichroic in the lower filter cube and reflected through a 525/50-nm emission filter. All filters were purchased from AHF Analysentechnik. For each filter, the first number describes the mode wavelength and the second number describes the total bandwidth at half-maximum transparency (half-minimum optical density). This means that a 340/26-nm filter mainly passes light between 327 and 356 nm. Filter specifications, including plots of their optical density at different wavelengths, can be found on the suppliers website (http://www.ahf.de). Transmission images together with images of NADH or Fp autofluorescence were acquired every 30 s. To reduce photobleaching, a Uniblitz shutter (VCM-D1, Vincent Associates, Rochester, NY) timed the light exposure with the acquisition.

Immediately before each experiment, a new batch of cells was permeabilized for 5 min with gentle mixing in an Eppendorf tube with respiration solution containing 25 μg/ml saponin and 50 μM ADP. A fraction of the permeabilized cells was put into a diamond-shaped fast-exchange chamber (15 × 6 mm, RC-24N, Warner Instruments, Harvard Apparatus, March-Hugstetten, Germany) on the microscope. Cells were allowed to sediment for 5–10 min before the superfusion was started with respiration solution containing different concentrations of ADP. Only cells located in the middle of the chamber were used for measurements. According to the manufacturer, the geometry of the chamber provided laminar flow of solutions during experiments at the used flow rate of ≈0.5 ml/min and was laminar in our conditions, as confirmed by mathematical model of the flow (22). The ADP concentration was increased stepwise from 50 to 100, 300, 500, 1,000, and 2,000 μM, and cells were superfused for at least 4.5 min at each step.

Fluorescence signal intensity from microscope single cell experiments was analyzed using ImageJ software. Both regions containing each cell and background regions were selected, and corresponding average fluorescence signal intensities were determined with the ImageJ plug-in “measure stack.” Background fluorescence was then subtracted from cell fluorescence, and the data were plotted on a timescale. From the latter plot, average fluorescence was found for each condition to which the cell was exposed (ADP concentration, uncoupling or block of oxidative phosphorylation). To enable comparison between cells, signals were normalized to maximum and minimum fluorescence recorded under fully reduced (respiration inhibited with oligomycin and cyanide) or oxidized (mitochondria uncoupled with FCCP) conditions.

Solutions.

The wash solution consisted of (in mM) 117 NaCl (no. 71379, Sigma-Aldrich), 5.7 KCl (no. P-5405, Sigma-Aldrich), 1.5 KH₂PO₄ (no. P-0662, Sigma-Aldrich), 4.4 NaHCO₃ (no. S-6014, Sigma-Aldrich), 1.7 MgCl₂ (no. 63068, Sigma-Aldrich), 21 HEPES (no. H-3375, Sigma-Aldrich), 20 taurine (no. 86329, Sigma-Aldrich), and 11.7 glucose (no. 158968, Sigma-Aldrich). pH was adjusted to 7.4 with NaOH.

For the collagenase solution, 0.25 mg/ml collagenase P (no. 11213873001, Roche) and 3 mg/ml BSA (no. 10775835001, Roche) was added to 40 ml of the wash solution.

For the sedimentation solution, 2 mM pyruvate (no. P-2256, Sigma-Aldrich), 10 μM leupeptin (no. 11034626001, Roche), 2 μM soybean trypsin inhibitor (no. 93619, Sigma-Aldrich), and 3 mg/ml BSA (no. 10775835001, Roche) were added to 60 ml of the wash solution.

The respiration solution contained (in mM) 110 sucrose (no. S-1888, Sigma-Aldrich), 60 K-lactobionic acid (no. L-2398, Sigma-Aldrich), 3 KH₂PO₄ (no. P-0662, Sigma-Aldrich), 3 MgCl₂ (no. 63068, Sigma-Aldrich), 20 HEPES (no. H-3375, Sigma-Aldrich), 20 taurine (no. 86329, Sigma-Aldrich), 0.5 EGTA (no. 71379, Sigma-Aldrich), 0.5 DTT (no. D-0632, Sigma-Aldrich), 2 malate (no. M-6413, Sigma-Aldrich), and 5 glutamate (no. 49449, Sigma-Aldrich). pH was adjusted to 7.1 with KOH. Immediately before use, 5 mg/ml BSA (no. 10775835001, Roche) and 20 μg/ml saponin (no. 47036, Sigma-Aldrich) were added.

The ADP stock solution contained 200 mM ADP (no. A-2754, Sigma-Aldrich) and 60 mM MgCl₂ (no. 63068, Sigma-Aldrich). pH was adjusted to 7.1 with KOH.

The ATP stock solution contained (in mM) 200 ATP (no. 10127531001, Roche), 200 Mg-acetate (no. M-5661, Sigma-Aldrich), and 20 HEPES (no. H-3375, Sigma-Aldrich). pH was adjusted to 7.1 with KOH.

Concentrations of the uncoupler and respiration blockers were as follows: FCCP (10 μM, no. Asc-081, Ascent Scientific), oligomycin A (10 μM, no. 579-13-5, Tebu-bio), and sodium cyanide (5 mM, no. 205222, Sigma-Aldrich).

Statistics.

Raw data were analyzed using homemade software. Values are given as means ± SD.

RESULTS

Characteristics of WT and GAMT^−/− mice.

Genotypes of the mice were confirmed by PCR. The results are shown in Fig. 3.

Fig. 3.

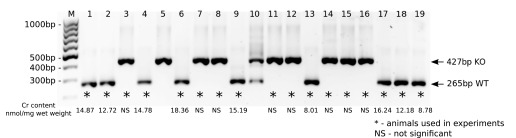
Genotyping of guanidinoacetate methyltransferase (GAMT)-deficient (GAMT^−/−) mice by PCR. After PCR amplification, samples were analyzed on 1% agarose gel stained with ethidium bromide along with a DNA ladder (lane M: GeneRuler 100-bp DNA Ladder). The 265- and 427-bp-long PCR products corresponded to wild-type (WT) GAMT (GAMT^+/+) or homozygous GAMT knockout (GAMT^−/− KO) genotypes, respectively. *Animals that were used in experiments. Total skeletal muscle creatine (Cr) content (expressed as nmol/mg wet wt) is shown under each mouse used in the experiments, respectively. The levels of Cr in GAMT^−/− mice were statistically not significant (NS).

GAMT^−/− mice had a lower body weight than their WT littermates [female WT: 24.2 ± 3.8 g vs. female GAMT^−/−: 17.5 ± 2.6 g (P < 0.05); male WT: 34.5 ± 5.3 g vs. male GAMT^−/−: 23.0 ± 2.7 g (P < 0.01)]. In female mice, tibial length was also shorter in GAMT^−/− than WT mice [female WT: 21.8 ± 0.2 mm vs. female GAMT^−/−: 21.1 ± 0.6 mm (P < 0.05); male WT: 22.6 ± 0.6 mm vs. male GAMT^−/−: 21.7 ± 0.8 mm (P = 0.1330)]. This is in agreement with previous observations (19, 41).

Total Cr content was measured enzymatically in GAMT^−/− and WT mice used in the experiments. Skeletal muscle Cr content was 13.46 ± 3.40 nmol/mg wet wt in WT control mice (n = 9) and undetectable in GAMT^−/− mice (n = 8) (Fig. 3). This was confirmed statistically with a paired t-test showing no significant difference in the Cr content between the GAMT^−/− sample and the corresponding blank (P > 0.05) and a significant difference between the WT sample and the corresponding blank (P < 0.05).

Mitochondrial positioning.

Visual inspection of the confocal images showed similar mitochondrial distribution in GAMT^−/− and WT cardiomyocytes. This was confirmed by quantitative analysis of the relative positioning of the mitochondrial centers (Figs. 4 and 5). Figure 4 shows the probability densities of the closest mitochondrial centers found in the different sectors. There was no difference between GAMT^−/− and WT cardiomyocytes. Figure 5 shows plots of the cumulative distribution functions. The graphs for WT and GAMT^−/− cardiomyocytes were overlapping or were very close in all directions (Fig. 5).

Fig. 4.

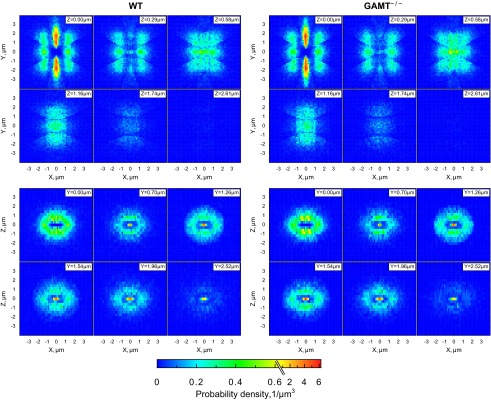
Probability density of the closest mitochondrial centers in each of the directions in WT (left) and GAMT^−/− (right) cardiomyocytes. A total of 24,588 (WT) and 23,405 (GAMT^−/−) mitochondria from 6 cells were analyzed. Each mitochondrial center was considered to be in the origin (0, 0). The space around was divided into 14 sectors, and the distribution of the closest mitochondrial centers in each sector was analyzed. Results from sectors with the same direction were pooled. Here, and in the following analysis, the y-direction was taken along the myofibrills and x- and z-directions were transversal directions at and perpendicular to the image planes, respectively. The xy- and yz-directions were diagonal directions. Two-dimensional probability density is shown at different planes perpendicular to the z-axis (XY-planes; top) or the y-axis (XZ-planes; bottom) at different distances from the origin as indicated at the top right corner of each plane. Note how similar the mitochondrial distributions were in GAMT^−/− and WT cardiomyocytes.

For statistical analysis, we found the averaged distances R and R_XZ (notation from Fig. 5) at 25%, 50%, and 75% of the cumulative distribution function (Table 1). There was no significant difference in the distances between WT and GAMT^−/− cardiomyocytes as analyzed with mixed-design ANOVA. In this statistical test, the between-subject variables were mouse genotypes (2 levels: WT or GAMT^−/−) and the within-subject variables were directions for R and R_XZ (5 directions for each, 10 levels in total) and percentile points (3 levels). On the basis of ANOVA, we concluded that there was no significant main effect of genotype, P = 0.28. No significant differences in the distances were found when we compared the distances obtained at all directions and all percentile points for WT and GAMT^−/− cardiomyocytes using Welch's t-test and correcting for multiple comparisons using the Šidák correction.

Table 1.

Distances at 25%, 50%, and 75% of the distribution function for R_XYZ and R_XZ

Direction	25%		50%		75%
	WT	GAMT−/−	WT	GAMT−/−	WT	GAMT−/−
RXYZ
X	1.28 ± 0.04	1.31 ± 0.08	1.61 ± 0.04	1.64 ± 0.07	2.07 ± 0.09	2.06 ± 0.09
XY	1.81 ± 0.08	1.88 ± 0.12	2.25 ± 0.07	2.29 ± 0.11	2.76 ± 0.10	2.78 ± 0.13
Y	1.35 ± 0.15	1.39 ± 0.18	1.83 ± 0.08	1.82 ± 0.09	2.56 ± 0.29	2.39 ± 0.15
YZ	1.61 ± 0.08	1.57 ± 0.10	2.08 ± 0.11	2.01 ± 0.11	2.65 ± 0.23	2.48 ± 0.11
Z	1.07 ± 0.05	0.99 ± 0.08	1.43 ± 0.08	1.35 ± 0.08	1.89 ± 0.19	1.75 ± 0.08
RXZ
X	1.23 ± 0.03	1.27 ± 0.08	1.55 ± 0.04	1.58 ± 0.07	2.00 ± 0.09	2.00 ± 0.10
XY	1.12 ± 0.03	1.17 ± 0.07	1.45 ± 0.02	1.50 ± 0.08	1.88 ± 0.05	1.90 ± 0.10
Y	0.08 ± 0.01	0.07 ± 0.02	0.16 ± 0.03	0.12 ± 0.04	0.32 ± 0.09	0.24 ± 0.06
YZ	0.92 ± 0.04	0.86 ± 0.07	1.23 ± 0.05	1.14 ± 0.08	1.68 ± 0.15	1.54 ± 0.10
Z	1.03 ± 0.05	0.95 ± 0.08	1.38 ± 0.08	1.29 ± 0.08	1.82 ± 0.20	1.68 ± 0.09

Values (in μm) are means ± SD; n = 6 wild-type (WT) cardiomyocytes and 6 guanidinoacetate methyltransferase (GAMT)-deficient (GAMT^−/−) cardiomyocytes. R_XYZ, distance from the origin to the nearest mitochondrion; R_XZ, distance from the y-axis through the origin to the nearest mitochondrion.

From this analysis, we conclude that the distances between mitochondrial centers in WT and GAMT^−/− cardiomyocytes were not significantly different. Furthermore, we did not observe any compensation in mitochondrial positioning to the lack of a functional CK shuttle in GAMT^−/− cardiomyocytes.

Kinetic recordings.

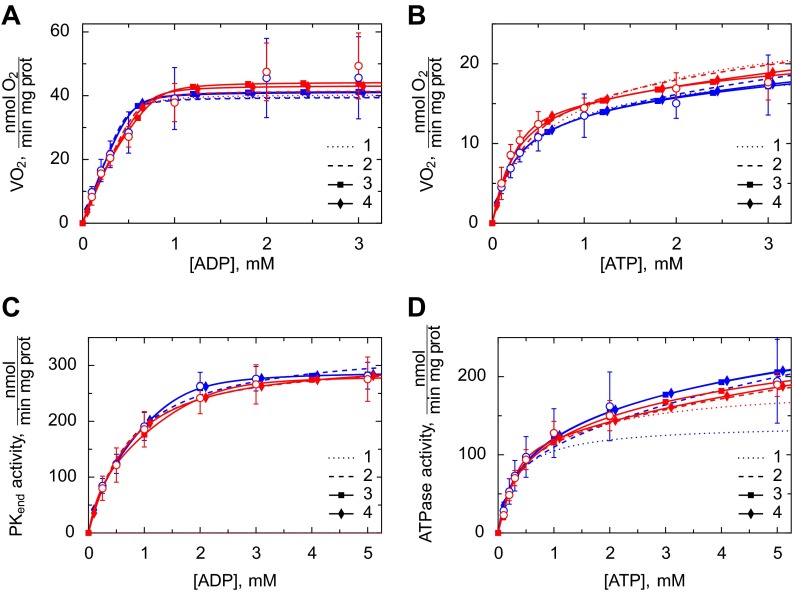
In the respirometer, we recorded the kinetics of ADP- and ATP-stimulated respiration in permeabilized cardiomyocytes. ADP directly stimulates respiration, whereas ATP is first hydrolyzed by ATPases to ADP, which diffuses to the mitochondria and stimulates respiration (Fig. 6, A and B). In addition, we recorded how ATP-stimulated respiration is affected by a competitive ADP-trapping system consisting of PEP activating endogenous PK and PEP activating additional 20 U/ml exogenous PK (Table 2). The respiration data were complemented by spectrophotometric recordings of the kinetics of ATP-stimulated ATPase activity and ADP-stimulated endogenous PK activity using a coupled assay (Fig. 6, C and D).

Fig. 6.

Kinetic analysis of permeabilized cardiomyocytes from WT (blue) and GAMT^−/− (red) mice. Measurements were performed in respiration solution containing 2 mM malate and 5 mM glutamate to support ADP-stimulated respiration. The experimental results are shown as means ± SD (open circles). These were compared with the solutions from models 1–4. Fits from simplified model 2s, 3s, and 4s were excluded for simplicity. A: respiration rate as a function of the ADP concentration added to the respirometer chamber (n = 6 and 5 for WT and GAMT^−/− cardiomyocytes, respectively). B: respiration rate as a function of ATP (n = 7 and 5 for WT and GAMT^−/− cardiomyocytes, respectively). C: endogenous PK activity as a function of ADP in the spectrophotometer cuvette (n = 8 and 7 for WT and GAMT^−/− cardiomyocytes, respectively). D: ATPase activity as a function of ATP in the spectrophotometer cuvette (n = 9 and 7 for WT and GAMT^−/− cardiomyocytes, respectively). Note that the fits from models 3 and 4 were either very close or overlapping in all cases. Vo₂, O₂ consumption.

Table 2.

V_{2 mM ATP}, V_PEP, and V_{PEP + PK} for experimental data and the various models

	Experimental Data	Models
		1	2	2s	3	3s	4	4s
WT
V2 mM ATP	14.48 ± 4.24	15.98	16.14	16.72	15.71	15.33	15.79	15.51
VPEP	11.15 ± 3.73	17.23	11.45	11.73	8.88	11.15	9.1	11.53
VPK + PEP	4.84 ± 2.02	5.53	4.42	5.68	6.5	6.87	6.15	6.43
GAMT−/−
V2 mM ATP	14.07 ± 3.02	18.12	17.97	19.08	17.14	16.58	17.14	17
VPEP	10.86 ± 2.53	19.69	12.36	12.82	9.81	11.29	11.52	13.07
VPK + PEP	5.21 ± 2.18	8.16	7.16	7.62	9.22	9.9	6.46	10.43
Pooled
V2 mM ATP	14.30 ± 3.64	17.66	17.31	18.4	16.6	16.04	16.5	16.55
VPEP	11.02 ± 3.16	19.06	12.06	12.69	9.19	11.07	11.26	12.25
VPK + PEP	5.00 ± 2.03	7.13	6.04	7.07	8.4	8.95	5.61	9.01

Values are in nmol·min⁻¹·mg protein⁻¹; n = 8 WT cardiomyocytes, 7 GAMT^−/− cardiomyocytes, and 15 pooled cardiomyocytes. Experimental data were compared with simulation results obtained by models 1–4 and their simplified versions (models 2s, 3s, and 4s). V_{2 mM ATP}, ATP-stimulated respiration rate; V_PEP, inhibition of ATP-stimulated respiration rate by endogenous pyruvate kinase (PK); V_{PEP + PK}, inhibition of ATP-stimulated respiration rate by endogenous PK; PEP, phosphoenol pyruvate.

Analysis of kinetic data by mathematical models.

The experimental data were fitted by several mathematical models with different levels of compartmentation (Fig. 2). The model fits were compared with the measurements shown in Fig. 6 and Table 2. To analyze the data obtained from WT and GAMT^−/− mouse cardiomyocytes, we first fitted the data separately. The data were then pooled together and fitted (parameters shown in Table 3). As expected, the fit was better when the models were allowed to fit the WT and GAMT^−/− data separately (quantified by sum of squares in least-squares fitting). However, according to the extra sum-of-squares F-test (F-test), the increased number of parameters induced by fitting the experiments separately was not justified, and the better fits were due to chance (depending on the model, P was from 0.37 to 0.99). From this, we concluded that the kinetic recordings in WT and GAMT^−/− mouse cardiomyocytes were not significantly different and that the two cases could be described by a single set of a model parameters.

Table 3.

Model parameters found by fitting the pooled data obtained from WT and GAMT^−/− cardiomyocytes

	Models
	1	2 s	2	3 s	3	4 s	4
VmaxATPsyn, nmol·min−1·mg protein−1
Optimal value	233	248	243	257	262	255	254
Confidence intervals	62–720	174–335	172–330	191–332	193–344	182–338	190–327
Csol-cyt, nmol·mM−1·min−1·mg protein−1
Optimal value	1,461	1,017	1,295	409	299	493	1,234
Confidence intervals	175 to >105	562–2031	606–3,062	249–651	199–426	273–893	635–2,464
CMoM, nmol·mM−1·min−1·mg protein−1
Optimal value	646	676	612	1,132	2,362	950	517
Confidence intervals	222–2,231	530–875	481–791	786–1,788	1,264–7,394	662–1,479	425–635
CIMS-C4, nmol·mM−1·min−1·mg protein−1
Optimal value						8.39	366
Confidence intervals						1.72–16	261–544
Ccyto-C4, nmol·mM−1·min−1·mg protein−1
Optimal value				0.005	156
Confidence intervals				0.003–0.009	81–343
VmaxATPase1, nmol·min−1·mg protein−1
Optimal value	181	177	614	119	89	105	742
Confidence intervals	90–298	156–198	322–954	108–130	79–99	93–117	474–1,045
KmATPase1, Mm
Optimal value	0.21	0.271	10	0.235	0.201	0.201	10
Confidence intervals	0.06–0.834	0.206–0.358	≥10	0.187–0.294	0.147–0.276	0.143–0.279	6.91 to >10
KiATPase1, mM
Optimal value	0.051	0.102	0.05	9.62	10	10	0.051
Confidence intervals	0.05 to >10	0.056–0.228	0.05 to >10	0.208 to >10	≥10	0.229 to >10	0.05–0.09
VmaxATPase2, nmol·min−1·mg protein−1
Optimal value			107	119	278	127	95
Confidence intervals			92–122	75–169	186–391	42–4,500	82–108
KmATPase2, mM
Optimal value			0.194		3.77		0.051
Confidence intervals			0.131–0.286		2.47–6.26		0.05–0.1
KiATPase2, mM
Optimal value			10		0.053		10
Confidence intervals			0.142 to >10		0.05–0.147		0.166 to >10
VmaxPKend1, nmol·min−1·mg protein−1
Optimal value		322	327	235	68	284	327
Confidence intervals		282–362	287–368	204–267	42–94	244–325	293–361
KmPKend1, mM
Optimal value		0.546	0.621	0.33	0.05	0.596	0.616
Confidence intervals		0.366–0.809	0.424–0.904	0.208–0.502	0.05–0.112	0.414–0.852	0.448–0.845
VmaxPKend2, nmol·min−1·mg protein−1
Optimal value				356	217	47	0.118
Confidence intervals				111–7199	180–258	23–72	0.053–29

As previously found for rat cardiomyocytes (45), the fits obtained by models 1, 2, and 2s were considerably worse than the fits with the other models, as shown by statistical analysis using an F-test of the nested models (Table 4). However, when information criteria were used, only model 1 was considerably worse than the other models (AIC_c and BIC). By comparing the results from multiple goodness-of-fit criteria, we can conclude that solutions of all models, except for model 1, can be considered reasonable. The main difference between model 2 and models 3, 3s, 4, and 4s is the introduction of a coupling between a part of endogenous PK and ATPases. Thus, while the F-test strongly suggests that a part of endogenous PK is coupled to ATPases (P < 0.05), the information criteria analysis was not conclusive, and further studies are needed. In addition, considerable diffusion restriction was identified at the level of the mitochondrial outer membrane and at the level of intracellular diffusion restrictions separating mitochondria from the surrounding solution.

Table 4.

Statistical analysis of the fits

	AIC	AICc	BIC	F-Tests
				Model 2s	Model 2	Model 3s	Model 3	Model 4s	Model 4
WT cardiomyocytes
Model 1	98.39	102.2	590.48	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
Model 2s	−23.1	−15.9	34.47		0.124	<0.05	<0.05	<0.05	<0.05
Model 2	−26.13	−10.61	42.56				<0.05		<0.05
Model 3s	−32.68	−17.15	41.44				0.113
Model 3	−36.58	−12.32	47.13
Model 4s	−30.43	−14.9	41.8						<0.05
Model 4	−37.7	−13.44	47.0
GAMT−/− cardiomyocytes
Model 1	77.59	81.41	298.61	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
Model 2s	7.75	14.95	48.76		0.139	<0.01	<0.01	<0.05	<0.001
Model 2	5.14	20.67	53.25				<0.01		<0.001
Model 3s	−11.33	4.2	46.23				0.583
Model 3	−9.28	14.98	52.37
Model 4s	0.55	16.08	50.88						<0.01
Model 4	−16.84	7.43	50.4
Pooled WT and GAMT−/− cardiomyocytes
Model 1	167.94	169.59	877.59	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001
Model 2s	−15.07	−12.13	66.43		<0.01	<0.0001	<0.0001	<0.001	<0.0001
Model 2	−27.04	−21.3	69.56				<0.0001		<0.0001
Model 3s	−47.47	−41.73	62.17				0.052
Model 3	−51.09	−42.82	68.14
Model 4s	−33.13	−27.4	67.08						<0.0001
Model 4	−54.96	−46.68	67.15

Fits were analyzed by calculating Akaike information criteria (AIC), corrected AIC (AIC_c), and Bayesian information criteria (BIC). For all three criteria, the best-fitting model was the one with the minimum criterion value. Note that for AIC_c and BIC, a larger number of parameters is penalized more than in AIC. F-tests of the nested models are shown, with the simpler model (rows) compared with the nested, more complicated model (columns). The analysis was performed for fits of the data recorded from WT and GAMT^−/− mouse cardiomyocytes separately as well as for pooled data.

As explained above, when analyzing the model parameters obtained by fitting the data, we have to consider the pooled case only (Table 3). In the models, all reaction rates were simulated using Michaelis-Menten kinetics with the apparent kinetic constants V_max and K_m. ATPases were considered to be inhibited competitively by ADP (where K_iATPase is the apparent inhibition constant). The diffusion restrictions are described via exchange coefficients between the compartments (where C_{compartment 1-compartment 2} is the exchange coefficient between compartment 1 and compartment 2). Table 3 shows the parameters used for each model. According to our simulation results using the pooled data set, the diffusion restrictions that separate the surrounding solution from mitochondria were similar to the diffusion restrictions induced by mitochondrial outer membrane. This is clear from a comparison of the exchange coefficients C_sol-cyt and C_mom for all the models that provided reasonable fits (Table 3). Namely, while for some models (models 2, 2s, and 4) the diffusion restriction induced by the mitochondrial outer membrane was larger than the one separating the surrounding solution from mitochondria, the opposite was true for the other models (models 3, 3s, and 4s). However, we should note that for all models, with the exception of model 3, those diffusion restrictions were of the same order of magnitude, suggesting that they are similar. Note that the description of ATPases and endogenous PK interaction in compartment 4 is a phenomenological one and that all the model parameters obtained for this compartment, including the exchange coefficient, are phenomenological coefficients and may not represent the interaction between ATPases and PK in a mechanistic way (as discussed in Ref. 45). As such, the obtained low exchange coefficient for compartment 4 is a part of a general description of coupling between PK and ATPases and cannot be compared directly with the other exchange coefficients found by the model.

Autofluorescence of single, permeabilized cardiomyocytes during ADP titration.

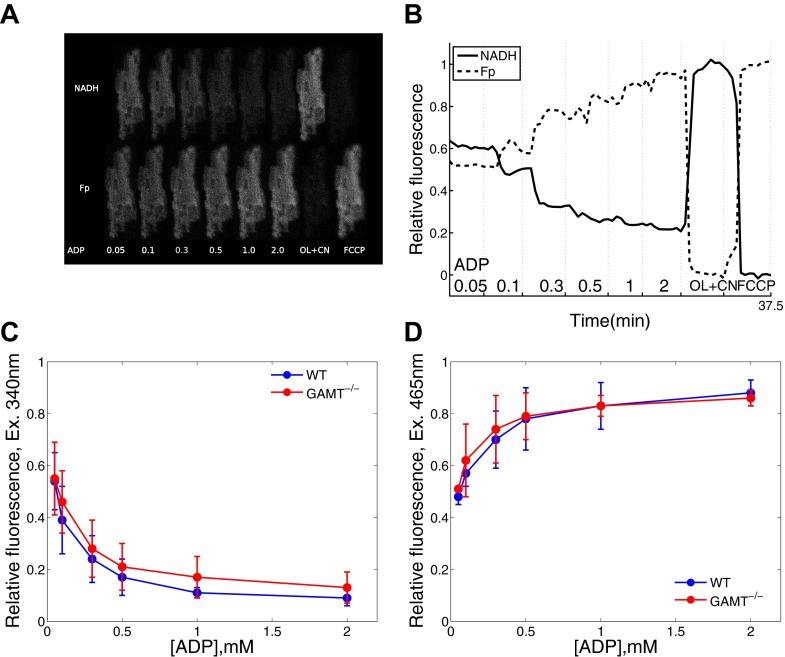
To verify that diffusion restrictions were not due to clumping of the cells, we recorded NADH and Fp autofluorescence responses to the change in ADP at the single cell level (Fig. 7). The mainly mitochondrial origin of NADH and Fp fluorescence signals allowed us to relate fluorescence to the state of oxidative phosphorylation. NADH and Fp signals decreased and increased, respectively, as the concentration of ADP in the surrounding solution was increased (Fig. 7). We compared the normalized NADH and Fp fluorescence at each ADP concentration and found no statistically significant difference between cardiomyocytes from WT and GAMT^−/− mice (P from 0.09 to 0.95 by Welch's t-test; Fig. 7, C and D). Because no statistically significant difference was found when we performed multiple comparisons separately, no additional correction for multiple tests or ANOVA analysis was required to check whether the difference in autofluorescence between cardiomyocytes from WT and GAMT^−/− mice was significant. Thus, on the basis of our results, diffusion from the solution to the mitochondrial inner membrane is restricted to the same extent.

Fig. 7.

Autofluorescence response of a permeabilized cardiomyocytes to changes in solution. A: representative example of NADH and flavoprotein (Fp) fluorescence from a GAMT^−/− cardiomyocyte exposed to different concentrations of ADP, oligomycin and NaCN (OL + CN), and FCCP, as indicated at the bottom. B: normalized integrated fluorescence of the cardiomyocyte shown in A. C and D: comparison of NADH (C) and Fp (D) autofluorescence responses in permeabilized cardiomyocytes from WT (blue; n = 6) and GAMT^−/− (red; n = 6) cardiomyocytes to the changes in exogenous ADP.

DISCUSSION

The present study shows that inactivation of the CK system by GAMT deficiency due to lack of Cr is not associated with any changes in cardiomyocyte mitochondrial organization or stimulated respiration or its regulation by exogenous and endogenous ADP-supply. In addition, according to our modeling results, there was no change in intracellular compartmentation when cells were in a relaxed state. This indicates that inactivation of the CK system by GAMT deficiency does not induce cytoarchitectural changes.

The CK system is considered an important temporal and spatial energy buffer in the heart. In all muscle types, CK is present near sites of ATP consumption and sites of ATP production. In white, glycolytic skeletal muscle, CK is present near the myofibrillar I-band and functionally coupled to glycolytic enzymes (26). In oxidative skeletal muscle and the heart, mitochondrial CK is bound to the outer side of the inner mitochondrial membrane (25) and functionally coupled to respiration (59). Cytosolic CK is localized at the myofibrillar M-band, which is favorable for the regeneration of ATP for myosin ATPase (58). Also, it is bound near and functionally coupled to SERCA (33), sarcolemmal ATP-sensitive K⁺ channels (9), and Na⁺-K⁺-ATPase (13). The “spatial energy buffer” or “energy transport” function of CK has mainly been ascribed to tissues such as the heart, where a relatively large fraction of the CK activity is of mitochondrial origin (56, 59). Mitochondrial CK activity is tissue specific and relates to oxidative capacity (56). This relationship can also be observed during cardiac maturation (12, 16). Facilitation of ADP/ATP transport may seem particularly important in oxidative muscles, where ADP/ATP diffusion is restricted (28, 40, 56) and mitochondrial energy production, although more efficient than glycolysis, is more distant and physically separated from ATPases by the mitochondrial membranes. In terms of energy transport, the CK system provides a parallel energy circuit between sites of production and consumption. PCr and Cr are smaller molecules than ATP and ADP and thus diffuse faster (32). Another advantage is that they are present in higher concentrations, allowing the build up of larger gradients of Cr than ADP. For example, whereas the Cr concentration is in the order of 10 mM, the ADP concentration is ∼50 μM. Since diffusion is driven by the absolute difference in concentration, the same gradient for ADP would require 10 mM/50 μM = 20 × larger relative difference in concentration than for Cr.

The importance of CK has been the subject of debate for a long time, with sometimes vague hypotheses used to define the role of CK, precluding testing of the hypotheses using a strong inference approach (3). An alternative view has been proposed that the high transport via PCr and Cr is simply a consequence of the CK reaction being close to equilibrium (32). After making some assumptions on the relative concentrations of ATP, ADP, PCr, and Cr, it has been shown that CK is expected to facilitate energy transfer, leading to most of the energy transfer to occur through PCr and Cr diffusion. In addition, for small diffusion distances, such as in cardiac muscle, the absence of an active CK system should not have any significant functional consequences (32). The latter was demonstrated assuming that there are no significant diffusion restrictions on the diffusion path of molecules between ATPases and mitochondria. Recently, on the basis of analysis of raster image correlation spectroscopy recordings, we (21) suggested that rat cardiomyocytes are split into smaller compartments with lattice-like barriers. The location of the barriers and the intracellular structures forming them are still unknown and would have different physiological consequences depending on whether the barriers are between ATPases and mitochondria or not. The lack of adaptation to inactive CK reported by us is in agreement with the mechanism of CK operation suggested by Meyer et al. (32) in their analysis.

If we assume the importance of the CK system as an additional energy transport system in the heart, it seems intuitive that disruption of this shuttle by genetic knockout of cytosolic and mitochondrial CK would lead to changes in the ultrastructure and regulation of mitochondrial respiration. In cardiomyocytes from CK^−/− mice, rows of myofilaments were split into thinner myofilaments by mitochondria wedging into the branching points, as if to compensate for a lack of energy transfer by diminishing intracellular diffusion distances (23). In addition, permeabilized fibers from CK^−/− mice have a higher ADP affinity of respiration than WT control mice, indicating smaller intracellular diffusion restrictions imposed on the molecules (23). Such changes in morphology and ADP affinity were consistent with the viewpoint that CK regulates the local ATP-to-ADP ratio and “compensatory mechanisms should be operating in CK^−/− mouse heart to overcome diffusion limitation and to preserve cardiac function at least at moderate levels of activity” (23). It was therefore surprising to find no difference between cardiomyocytes from GAMT^−/− and their WT littermates. Both had parallel rows of mitochondria with the same distances between mitochondrial centers (Figs. 4 and 5 and Table 1). In permeabilized cardiomyocytes, ADP sensitivity was similar at the population level (Fig. 6) as well as at the single cell level (Fig. 7). Finally, intracellular compartmentation, as assessed by kinetic measurements and mathematical modeling, was found to be the same in both WT and GAMT^−/− cardiomyocytes. These findings are in agreement with and extend the observations of a recent study (30) that failed to identify any adaptational changes when left ventricular proteomes, adenylate kinase activity, or mitochondrial respiration were compared.

The difference between our results and those from CK^−/− mice might be explained by differences in the genetic background (CK^−/− mice on a mixed C57BL/6 and S129 background were compared with WT C57BL/6 mice) and genetic drift. This has been shown to play a role in a study (31) of mice deficient in mitochondrial CK (Mt-CK^−/− mice). In the present study, we compared GAMT^−/− mice with their WT littermates. Alternatively, the different outcomes may be the result of different genetic modifications. Indeed, CK is a structural as well as catalytic protein. Muscle-type CK is an integral part of the myofibrillar M-band (17, 18, 49), where it serves as an efficient ATP-regenerating system for myosin ATPase located on both sides of the M-band (58). Mt-CK in the mitochondria seems to play a structural role in addition to ADP regeneration. It has been suggested that the octameric form induces the formation of contact sites between the inner and outer mitochondrial membranes (46), where it is involved in lipid transfer between the two membranes (11). In another study (29), the structural role of Mt-CK has been demonstrated by finding that it stabilizes specific contact sites between inner and outer mitochondrial membranes. It must be noted that these findings are not from cardiac muscle. It remains to be verified whether the lack of Mt-CK in cardiac muscle affects mitochondrial organization. However, an increase citrate synthase activity does suggest an increased mitochondrial volume in cardiac muscle of Mt-CK^−/− mice (31). As CK is expressed to the same extent in GAMT^−/− mice as in WT mice (19), these other roles of (especially) Mt-CK are preserved in GAMT^−/− mice, and our results reflect only the catalytic role of CK.

It is tempting to speculate that guanidinoacetate (GA) may be used by CK in a similar manner as Cr. Indeed, although GAMT^−/− mice have undetectable levels of total Cr, as shown in Fig. 3, they have a considerable amount of phosphorylated (p-)GA. In the heart, the p-GA concentration in a GAMT^−/− mouse is ∼2/3 of the PCr concentration in a WT mouse (19). However, phosphotransfer from ATP to p-GA was undetectable in GAMT^−/− mice (29), and it has been shown that the reactivity of muscle-type CK with GA is ∼100 times smaller than with Cr (5). This reactivity is sufficient to dephosphorylate p-GA at the induction of ischemia (24) or cyanide inhibition of oxidative phosphorylation (5). However, for energy transfer between mitochondria and ATPases, Mt-CK must convert ATP into PCr or its analog. When ATP-stimulated respiration on isolated mitochondria or on permeabilized fibers was analyzed, Mt-CK reactivity in the presence of GA was negligible and ADP synthesis from GA and ATP was not able to stimulate respiration (5). Taking into account the inability of Mt-CK to react with GA as well as undetectable levels of total Cr, the contribution of the CK shuttle to energy transfer is expected to be negligible in GAMT^−/− cardiomyocytes. Thus, in contrast to the suggestion cited above from Ref. 23, the present results suggest that disruption of CK shuttle does not necessarily lead to compensatory changes in mitochondrial arrangement and intracellular compartmentation.

Applied methods and study limitations.

In this study, we used confocal microscopy to estimate the intracellular mitochondrial positioning in WT and GAMT^−/− cardiomyocytes. The analysis was based on a method that we have previously applied on rat and trout cardiomyocytes (4, 50). Compared with traditional electron microscopy, there are several differences that ought to be considered when interpreting the data obtained by our method. Analysis of confocal images allowed us to use live cells. Thus, there are no histological artifacts that may be introduced by the fixation and dehydration of cells during their preparation for electron microscopy (38). In addition, the distances between the centers of mitochondria estimated by our method can be analyzed in three dimensions (Fig. 1) with an estimation based on a large number of mitochondria. In this study, >20,000 mitochondria were analyzed for each of the genotypes. Collecting a similar amount of data using electron microscopy is possible but would probably not be feasible when time and monetary costs are considered. Taking into account that most of the SDs of the percentile points shown in Table 1 are below 100 nm, the method can be considered precise and should be able to identify subtle changes in mitochondrial positioning. Note that those deviations include variability between cells as well. Such precision can be attributed to sub-Airy disk accuracy in finding centers of the objects in optical microscopy. However, in contrast to electron microscopy, confocal microscopy images do not allow us to determine relative distances between the borders of the objects, such as the distance between membranes of neighboring mitochondria, due to the limits induced by diffraction. As a result, in our study, such distances cannot be analyzed accurately and have not been reported. A further consideration is the isolation procedure, which is of great importance in obtaining a high yield of viable cardiomyocytes with unaltered morphological characteristics. The dissociation of a heart into a single cell suspension involves several critical factors such as excision and cannulation for perfusion, collagenase quality and activity, the length of enzyme digestion, and the Ca²⁺ concentration in the perfusion solution. To control for these variables, we used several criteria to check the quality of the isolation procedure, for example, contraction of cardiomyocytes upon electrical field stimulation, indicating that cells are Ca²⁺ tolerant, and checking for the prevalence of rod-shaped cells with clear striations and well-delineated membranes. However, even with those tests, we cannot exclude a possibility that there are some morphological changes introduced during the isolation procedure that may influence the analysis of mitochondrial positioning.

It is important to keep in mind the limitations of this study. For the functional assays, we studied cardiomyocytes with the sarcolemma permeabilized by saponin. Because the surrounding solution contained low free Ca²⁺, cells were kept in a resting state. We stimulated mitochondrial respiration and endogenous PK and ATPases by adding ADP or ATP to the solution outside the cells. Thus, these compounds had to cross an unstirred layer around the cells (22) as well as the intracellular diffusion obstacles, which partition cardiomyocytes into smaller compartments (21, 23, 45), before reaching the mitochondria. In contrast, in intact, working cells, there is a circuit of ADP/ATP between adjacent ATPases and mitochondria significantly reducing the diffusion distances and obstacles that influence the energy transfer if compared with the permeabilized cardiomyocyte experiments. In addition, the level of intracellular compartmentation induced by diffusion restrictions is not known in working heart muscle cells. While an analysis of raster image correlation spectroscopy measurements on relaxed rat cardiomyocytes suggested lattice-like intracellular diffusion barriers separating the cardiomyocytes into smaller compartments (21), it is not clear whether such compartmentation persists in the contracting cell. Mitochondrial respiration was stimulated to the maximal rate by very high concentrations of ADP in the presence of a high concentration of P_i, which is also an important regulator of mitochondrial respiration (7, 39, 61). Thus, the changes induced by GAMT deficiency have not been probed in the same conditions as in vivo experiments. However, on the basis of our analysis, we can conclude that the mitochondrial organization and intracellular compartmentation, as observed in our experiments, are unchanged in GAMT^−/− mice.

Disruption of the CK system may be compensated for by other mechanisms that were not measured in this study. For example, upregulation of alternative phosphotransfer systems, such as adenylate kinase, has been observed in CK^−/− mice (34), and upregulation of other glycolytic enzymes is observed after heart failure (2). Upregulation of these alternative phosphotransfer systems may serve to compensate for both the temporal and spatial buffer functions of the CK system. However, the change after heart failure may also simply reflect a change of phenotype induced by reverting to a fetal gene expression (37). Metabolically, this includes an upregulation of glycolytic enzymes and a downregulation of mitochondrial enzymes (48, 54). Clearly, further studies are needed to determine how disruption of the CK system by GAMT deficiency affects the cardiac phenotype.

Our kinetic recordings, such as mitochondrial respiration and ATPase activities, were performed in the absence of Cr in solution. This was done to determine whether intracellular compartmentation and mitochondrial respiration capacity changed during adaptation of the cells to Cr deficiency in GAMT^−/− mice. As we have previously demonstrated (45), this information can be obtained using kinetic recordings without Cr. Thus, while we know on the basis of earlier studies that the total Cr content is too low to be determined in GAMT^−/− mice leading to inactivation of the CK shuttle system in GAMT^−/− mice, the kinetic properties of CK isoforms, their distribution, and coupling to mitochondrial respiration is not known and cannot be predicted on the basis of our measurements.

Physiological implications.

The lack of compensatory changes in GAMT^−/− mice prompts a careful consideration of the role of the CK system in cardiomyocytes. At the whole heart level, both CK^−/− and GAMT^−/− mice show almost no changes in basal contractile performance (6, 42), but they fail to perform at inotropically stimulated high workload and are more susceptible to ischemia-reperfusion injury (10, 19, 47). Clearly, the CK system is indispensable when the heart is exposed to a severe energetic challenge. But how important is it as an energy transport system? It is well established that a significant fraction of energy transport occurs via the CK system in the heart, and this is severely diminished in the failing heart (20). However, Meyer et al. (32) suggested that CK-facilitated energy transfer is merely a consequence of the existence of the CK system and is not required for cardiac function, if the diffusion distances are taken into account. Its main role is to buffer temporal fluctuations in the ADP-to-ATP ratio during situations, when energy demand is higher than energy production (32). A recent analysis of ³¹P NMR data suggested that the contribution of the CK shuttle to overall energy transfer between mitochondria and ATPases can depend on the workload and could reduce with an increase in workload or in pathological conditions (53). While our results are by no means conclusive, they raise questions regarding the importance of CK as an energy transport system at low and moderate workloads.

In conclusion, our results suggest that the healthy heart is able to preserve cardiac function at a basal level in the absence of CK-facilitated energy transfer without compromising intracellular organization and the regulation of mitochondrial energy homeostasis.

GRANTS

This work was funded by The Wellcome Trust Fellowship WT081755MA, the European Union through the European Regional Development Fund, Estonian Science Foundation Grant ETF8041 (PhD stipends for J. Branovets, N. Jepihhina, and N. Sokolova), and British Heart Foundation Grant RG/10/002/28187.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.B., S.K., N.J., N.S., and D.A. performed experiments; J.B., M.S., S.K., N.J., and M.V. analyzed data; J.B., M.S., M.V., and R.B. interpreted results of experiments; J.B., M.S., and M.V. prepared figures; C.A.L., S.N., M.V., and R.B. conception and design of research; C.A.L., S.N., M.V., and R.B. edited and revised manuscript; C.A.L., S.N., M.V., and R.B. approved final version of manuscript; R.B. drafted manuscript.