Abstract
Lens average and equivalent refractive indices are required for purposes such as lens thickness estimation and optical modeling. We modeled the refractive index gradient as a power function of the normalized distance from lens center. Average index along the lens axis was estimated by integration. Equivalent index was estimated by raytracing through a model eye to establish ocular refraction, and then backward raytracing to determine the constant refractive index yielding the same refraction. Assuming center and edge indices remained constant with age, at 1.415 and 1.37 respectively, average axial refractive index increased (1.408 to 1.411) and equivalent index decreased (1.425 to 1.420) with age increase from 20 to 70 years. These values agree well with experimental estimates based on different techniques, although the latter show considerable scatter. The simple model of index gradient gives reasonable estimates of average and equivalent lens indices, although refinements in modeling and measurements are required.
OCIS codes: (330.4460) Ophthalmic optics and devices; (330.7326) Visual optics, modeling
1. Introduction
With the development of optical coherence tomography (OCT) and related non-contact optical methods for measurement of the axial and other dimensions of the eye, the reliability with which these distances can be determined in vivo has improved considerably. Nevertheless, in reality, with these instruments the axial measurements are made of optical path (strictly of transit time) through the eye, rather than of true distances. Hence the accuracy with which true axial distances can be derived from the optical pathlengths depends upon the assumption of the correct refractive indices for the media concerned. The thickness of the crystalline lens provides a particular problem, since the true lens index increases markedly from the lens surfaces to the center in a way that depends upon age, accommodation and the individual eye. At the present time the exact nature of these changes remains uncertain and it is necessary to use some form of average index. If this index is selected correctly, the measured optical path can be converted to the true thickness of the lens. To illustrate the magnitude of any possible errors, if the lens thickness is 4.00 mm and the correct average refractive index is 1.420, the optical path through the lens is 5.68 mm. If the assumed index is 0.001 in error, the error in the estimated lens thickness will be about 3 μm. While this may seem small, it is of about the magnitude that is found by OCT for the changes in the total axial length of the eye when it accommodates [1–3]. Atchison and Smith [4] have therefore suggested that the results found in such studies are influenced by the values of the average refractive index used in deriving the measurements and their dependence on the accommodation state of the eye.
A similar need for a representative refractive index for the lens arises in the context of models of the eye with the simplification that the lens is homogeneous with a single refractive index. Well-known examples of such model eyes are the Gullstrand-Emsley simplified eye, and those of Le Grand, Lotmar, Kooijman and Navarro (see, e.g. compilation in Atchison and Smith [5]). In this case the equivalent lens index is selected to yield the required refraction (usually emmetropia) in an eye whose other component dimensions, curvatures, separations and refractive indices are already specified and are representative of the adult population. An equivalent index of about 1.420 is commonly chosen. A closely-related situation is where the surface curvatures and separations of an individual eye are measured, refractive indices for cornea, aqueous and vitreous indices are assumed, and an equivalent index for the lens is then derived on the basis of the observed refractive error (e.g [6,7].). This may be useful in comparisons of, for example, the lenses of normal and diabetic patients [8]. A third situation, which arises when in vitro measurements are made on the isolated lens, is where an equivalent index is derived from measurements of the power, curvatures and thickness of the lens, using either the thick lens formula (e.g [9].) or raytracing methods [10].
It is reasonable to ask whether these approaches yield the same results. Are the values of the average and equivalent refractive indices the same? Is an equivalent index derived from measurements of the other ocular parameters the correct one to use when converting lenticular optical path to true lens thickness and are any differences of importance? We present here an analysis which suggests that generally the average and equivalent refractive indices are not the same, and we consider our results in relation to experimental findings.
2. Methods
To illustrate the differences that may arise, we use a paraxial model of the lens and eye as developed by Bahrami and Goncharov [11], which is similar to that of Navarro et al. [12, 13]. In this model, the iso-indicial contours of the lens mimic its external shape, so that the normalized gradient index (GRIN) profile and average refractive index are the same in all directions from the lens center. The authors explain how to calculate optical characteristics of any lens with conicoidal surfaces and assume that the distribution of refractive index in the lens can be represented by a modified version of the Smith et al. [14] equation:
| (1) |
where ξ is normalized distance from the center of the lens, ranging from –1 at the anterior surface to + 1 at the posterior surface, and n s and n c are refractive indices at lens surface and center, respectively. The parameter p describes the index distribution shape: for low p-values the refractive index falls steadily from the lens center, whereas with high p most of the changes occur close to the lens surface. In the absence of shape or thickness changes, the lens power can vary as a result of changes in any one or in any combination of the parameters n s, n c and p. All affect the GRIN contribution to total lens power, but only ns affects surface power.
Kasthurirangan et al. [15] found that their axial index profiles, derived from in vivo magnetic resonance imaging (MRI), were well fitted by Eq. (1). The p-value along the lens axis was about 2.45 for unaccommodated young (ca. 23 years) lenses and 3.35 for old (ca. 64 years) lenses. The young lenses had the p-value of about 2.02 when the subjects accommodated to a target at their near point, implying that the index changes became more gradual as the lens thickness increased with accommodation. Navarro et al. [12], fitting the in vitro MRI data of Jones et al. [16] for lenses aged between 7 and 82 years, suggested that p increased with age in years according to the equation
| (2) |
On this basis the physiologically-interesting range of p-values is about 2.9 to 7.8 for the age range 7 to 82 years. Note that it is usually assumed that lenses examined in vitro, where they are free of all zonular forces, take up a shape which approximates to the fully-accommodated condition. Equation (2) gives a p-value of 2.88 for the “accommodated” 23 year-old lens. For a 62 year-old lens, which presumably ought not to “accommodate” in vitro, Eq. (2) gives a value of nearly 4.5, much higher than the axial value of 3.35 found in vivo by Kasthurirangan et al. [15]. This discrepancy may arise because the latter’s in vivo measurements had poor signal-to-noise ratio and low spatial resolution: this would tend to reduce the steeper gradients of the older lenses, yielding apparently lower p-values. Alternatively it may simply reflect both the limited reliability and the validity of using a single estimate of p for any lens: Kasthurirangan et al. [15] found that p was orientation-dependent and had the higher value of 5.14 for the 62 year-old when the index profile was measured in the equatorial direction (see also Jones et al. [16]).
Equation (1) can be applied to obtaining an average lens index, nav, for axial OCT measurements. The corresponding normalized optical pathlength [t norm] from lens center to posterior surface is
| (3) |
Equation (3) gives the appropriate value of the average index, nav, since the normalised true pathlength is 1.0. The same result is given for the lens anterior section (see Section 4 of Bahrami & Goncharov [11]). Evidently for any chosen values of n s and n c, the value of n av will tend to increase with the p-value, since (n s – n c) is negative. Note that n av is independent of the lens thickness and curvatures. We can substitute the p-value from Eq. (2) into Eq. (3) to estimate the variation of n av with age for the in vitro (assumed fully-accommodated) lens.
When applying the Bahrami and Goncharov eye model [11] we initially used the biometric parameters of the Le Grand schematic eye [5, 17] except for the aqueous and lens which had Bahrami and Goncharov’s default parameters (Table 1 ). Bahrami & Goncharov provide a Mathematica program that gives lens equivalent power, lens back vertex power and gradient index power (http://optics.nuigalway.ie/people/mehdiB/CF.html). We used this program and paraxial raytracing to determine the lens surface and gradient index powers and the eye’s refractive error as a function of p. We then assumed that the same model eye had a homogeneous lens with an initially unknown equivalent refractive index, but the same curvatures and thickness, and that this resulted in the same refractive error as in the gradient-index case. Backwards paraxial raytracing from the retina determined the equivalent index.
Table 1. Parameters of model eye.
| Parameter | Value |
|---|---|
| Corneal anterior radius of curvature (mm) | 7.8 |
| Corneal posterior radius of curvature (mm) | 6.5 |
| Lenticular anterior radius of curvature (mm) | 11.0 |
| Lenticular posterior radius of curvature (mm) | −7.5 |
| Corneal thickness (mm) | 0.55 |
| Anterior chamber depth (mm) | 3.05 |
| Lens anterior semi-thickness (mm) | 2.1 |
| Lens posterior semi-thickness (mm) | 1.4 |
| Vitreous length (mm) | 16.597 |
| Corneal refractive index | 1.3771 |
| Anterior chamber refractive index | 1.336 (1.3374)(1.336) |
| Lens surface refractive index | 1.37 |
| Lens center refractive index | 1.415 |
| Vitreous chamber refractive index | 1.336 |
3. Results
3.1 Average refractive index
We assumed that n s = 1.37 and n c = 1.415, similar to those found by Jones et al. [16] of 1.371 for n s and 1.418 for n c, and to those used by Bahrami & Goncharov [11] of 1.376 and 1.416. Figure 1 (top) shows the variation in n av with the p-value, as calculated from Eq. (3) for a lens with the index gradient of Eq. (1). Evidently, if the surface and central indices remain constant, n av increases with p. Note that, over the physiologically-relevant range of p-values (about 2-8), n av is always less than n c: the average index approaches n c asymptotically as p becomes very large.
Fig. 1.
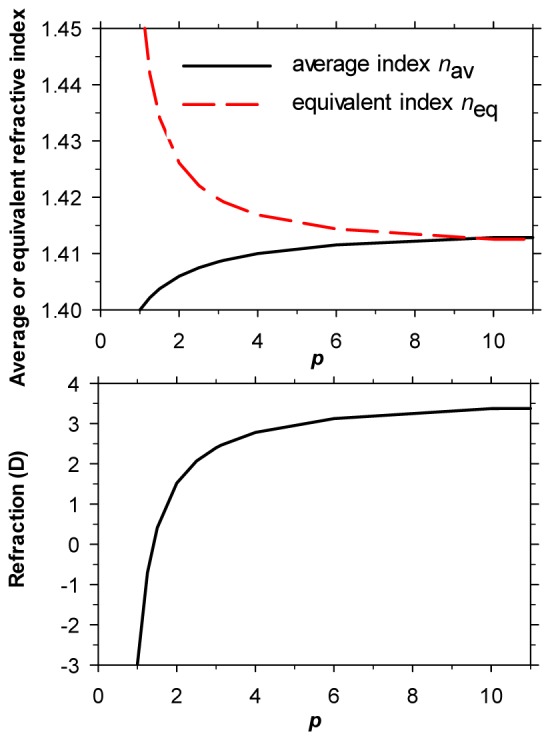
Top - variation in the average and equivalent refractive indices of a lens with the gradient of refractive index given by Eq. (1) as a function of the lens parameter p describing the index gradient: surface and central refractive indices are 1.37 and 1.415, respectively, and other details relevant to equivalent index are as in Table 1. Bottom - variation in the refractive error of the eye model given in Table 1 when the lens parameter p is changed.
3.2 Equivalent refractive index
Figure 1 (top) also shows the corresponding effect produced by changes in p on the equivalent refractive index of the lens in an eye where the lens thickness and surface curvatures, together with n c, n s and all the other biometric parameters, remain constant (as specified in Table 1). As p increases and the index change becomes increasingly concentrated in the outer layers of the lens, the equivalent index falls. This is due to the fall in the GRIN power of the lens, which also results in the refraction of the complete eye moving in the hyperopic direction (Fig. 1, bottom).
It will be noted that the differences between average and equivalent indices may be considerable in the physiologically-interesting range of p-values. If, for example we take the case of a 40 year-old eye, Eq. (2) above suggests that the in vitro p-value is about 3.13, this being the value assumed by Bahrami and Goncharov [11] for their own calculations. Figure 1 shows that this would yield an average index of about 1.41 but an equivalent index of about 1.42, the same as that used in the Le Grand model eye [5, 17]. Note that, unlike n av, for the range of p of physiological interest, n eq is higher than the central index of the lens nc (1.415), as noted by Helmholtz [18].
3.3 Effect of age
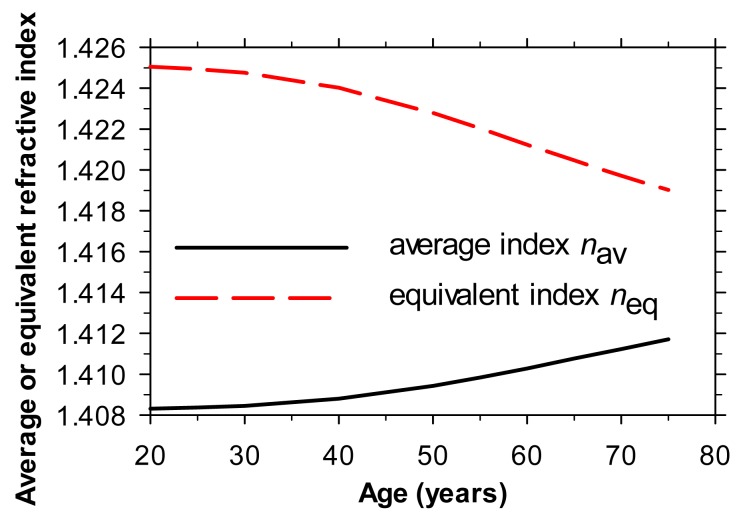
As the adult eye ages, the lens thickens, the surface curvatures change and the anterior chamber depth reduces. As noted earlier, the average lens index depends only on the age-dependent p-value (Eqs. (2) and (3)). However, the equivalent index depends upon both the p-value and the changing geometry of the lens and eye. To explore the effects of age on equivalent index, we combined the p-values of Eq. (2) with the geometric parameters from the emmetropic, 4-surface, model eyes of different ages described by Atchison [19]. At each age we assumed the same values of lens curvatures and thickness as those given by Atchison but that the lens was gradient index with a p-value according to Eq. (2) and a ratio of anterior to posterior thickness of 3:2 [12]. Using Bahrami and Goncharov’s Mathematica program [11] we determined the refractive error of each model eye. Raytracing determined the value of equivalent index that would yield the same refraction for the same eye with a homogeneous lens. The results are shown in Fig. 2 , together with those for the average index (Eq. (2).
Fig. 2.
Average and equivalent refractive indices for the crystalline lens as a function of age, as deduced using eye models based on Atchison [19]. The central and surface indices of the lens are assumed to remain constant at 1.415 and 1.37 respectively. See text for details.
At any age, the difference between the two refractive indices is marked. Whereas average index increases with age, the equivalent index reduces.
4. Discussion
Our modeling indicates that the values of n av and n eq for the same lens are different (Figs. 1 and 2). Within the physiologically-plausible range of p-values, n av is lower than the central index, n c, whereas n eq is higher. Our results suffer from several obvious limitations. For example, they rely on a particular theoretical approximation to the true gradients of index within the lens. As Jones et al. [16] have pointed out, the basic assumption made in the model used for raytracing, that the gradients in all directions from the lens center have the same p value, is of limited validity: the gradients in the axial and equatorial directions differ (see also reference 15). Moreover, our results make use of p-values relating to in vitro conditions when the lens was probably accommodated, rather than in vivo accommodation-relaxed conditions, although the changes in p with accommodation appear to be small [15]. Lastly we have assumed that the central and surface refractive indices remain constant through life [16], which may not be true. Nevertheless, we believe that our results are realistic for typical normal eyes, although not for the eyes of individuals suffering from conditions such as cataract or diabetes [20]. We now consider the results of our modeling in relation to other experimental and theoretical estimates of the indices.
4.1 Average index
Values of n av, as predicted from Eq. (3) on the basis of constant surface and center indices and the p/age relationship of Eq. (2), can be compared directly with those measured experimentally in vitro, since the p/age relationship was obtained under similar conditions. Uhlhorn et al. [21] used OCT to estimate optical thickness of isolated lenses and independently measured their absolute thickness, thus allowing n av to be calculated: a similar approach was adopted by De Castro et al. [22]. The comparison is shown in Fig. 3 , which also includes 3 points based on the in vivo MRI measurements of Kasthurirangan et al. [15].
Fig. 3.
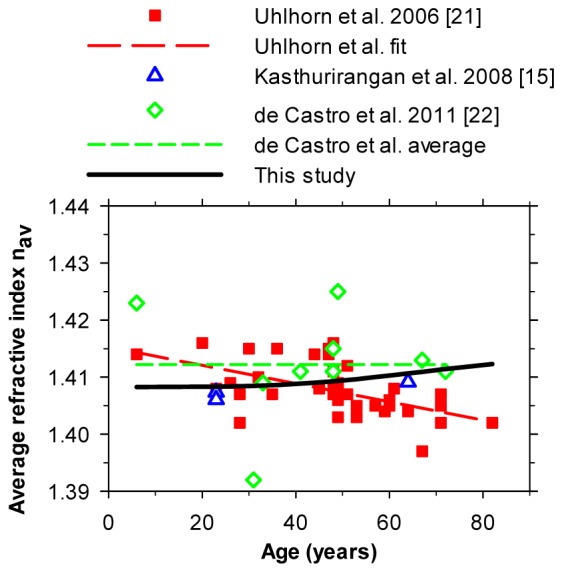
Estimates of n av as a function of age. The thick black solid curve (see also Fig. 2) gives estimates made on the basis of the present model using Eq. (2) for p. For estimates based on the p-values given by Kasthurirangan et al. [15] (triangles), at 23 years the upper symbol is for the unaccommodated case and the lower symbol is for an accommodated case.
The estimates all cluster around a value of about 1.41 but differ in their exact values. The model predictions show a modest increase of about 0.003 in n av through adulthood (20-70 years), as would be expected from the increase in p-values with age. The experimental data show considerable scatter: this may reflect measurement uncertainties and different post mortem lens changes rather than true biological variation [22]. It may be, too, that some cataractous lenses with different properties are included and that these have different distributions of index. Uhlhorn et al.’s regression line fit [21] shows a significant downward trend in n av with age, although this is not supported by the more limited results of De Castro et al. [22]. It is also possible that our model suffers from inadequate representation of the index gradients, and that the assumption that n s and n c are independent of age is incorrect, although MRI studies both in vitro and in vivo suggest that the indices are constant [16,22,23]. Although our results show a slight increase with age, in view of the spread of the current experimental estimates for nav, it may be reasonable to use a constant, age-independent value (perhaps 1.410) for converting optical paths to distances, as in axial OCT measurements. It is of interest that the early biometric study by Hemenger et al. [24], who used their results to estimate the form of the gradients of index within the lens, leads to values of nav of about 1.400. This is lower than the values of Fig. 3, probably because Hemenger et al. assumed that n c = = 1.406 and n s = 1.386, which later work suggests are too low and too high, respectively.
The question of the possible changes in average index with accommodation remains contentious. Atchison and Smith [4] first noted the potential importance of such changes. Navarro et al. [13] assumed in their modeling that p remained constant as the lens accommodated, although the MRI study of Kasthurirangan et al. [15] found that it fell slightly, resulting in a slightly lower value for n av (see Fig. 3). In cynomolgus monkeys, de Castro et al. [25] found that, when isolated lenses were radially stretched in vitro, the average index (like the equivalent index) was independent of the simulated accommodation. De Freitas et al. [26] have recently made use of the assumption that the average index is independent of the accommodation level to deduce the average index from in vivo measurements of the thickness of the lens and aqueous media as a function of accommodation: they find a mean value of about 1.41, but with a rather large standard deviation.
One problem with the concept that accommodation affects only the value of p in Eq. (1) is that Dubbelman et al. [17] observed that, in Scheimpflug images of the accommodating lens, the nucleus becomes thicker but the thickness of the cortex remains constant. This observation cannot easily be reconciled with a simple decrease in p. Jones et al. [23] found by rather indirect arguments that the average index decreased slightly with accommodation. Improved future MRI and other measurements should help to resolve this question.
4.2 Equivalent index
Estimates of the variation of n eq with age are shown in Fig. 4 ; for clarity, only the authors’ regression fits are given.
Fig. 4.
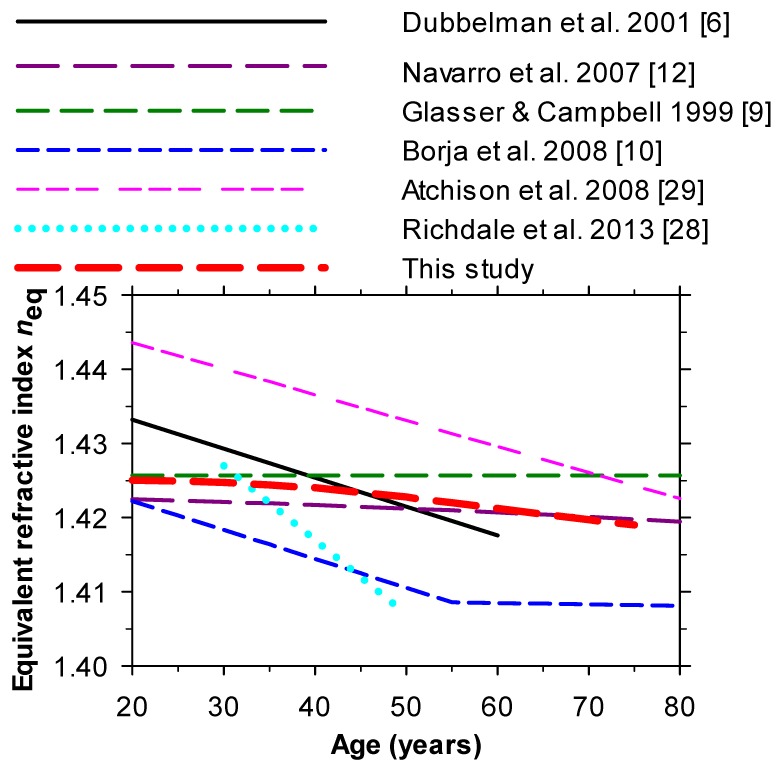
Variation of equivalent refractive index with age from different authors. The thick red dashed curve (see also Fig. 2) gives estimates made on the basis of the present model using Eq. (2) for p.
As can be seen, our own model predictions and those of Navarro et al. [13] who employed an eye model of similar form to that used here combined with the p-values of Eq. (2), suggest that the equivalent index of the lens declines slightly with age.
Experimentally-based estimates of the changes in equivalent index with age have been made by several groups. Dubbelman & van der Heijde [27] and Richdale et al. [28] calculated them from Scheimpflug images and other data for the complete living eye with relaxed accommodation, and found a decline with age: Atchison et al. [29] used a similar technique and found a similar result but with slightly higher values; these values were used by Atchison [19] in his modeling.
Glasser and Campbell [9] made in vitro measurements of the power, curvatures and thickness of isolated lenses and used these to deduce an equivalent index which gave the lens the same power, as also did Borja et al. [10]. Note that in these studies the definition of the equivalent index based on the isolated lens was not exactly the same as that derived by considering the whole eye, since cardinal points may be different for GRIN and homogeneous lenses of the same power and this may affect the overall refractive error of the eye. Moreover, as noted earlier, the isolated lenses were in an accommodated state. Glasser and Campbell [9] found that their equivalent index was independent of age (1.4216) but Borja et al. [10] found that the index fell. It is possible that, in lenses which usually display spherical aberration, some of the differences between investigators arise from measuring lens power at different incidence heights or pupil diameters. Overall, we suggest that the modeling and experimental results favor a slight decrease in equivalent index with age, by around 0.005 between the ages of 20 and 70, although further studies are needed to define the changes more precisely.
Since the equivalent index falls as p gets larger, the refraction for an eye with a lens with constant thickness, curvatures, and central and surface refractive indices changes in the hyperopic direction as p increases (Fig. 1). With aging, the value of p increases (Eq. (2)) but lens thickness and curvatures also increase. The effects of these changes on refraction are in opposition but in practice it appears that, in non-cataractous eyes, a slow drift in the hyperopic direction between the ages of about 30 and 70 years is typically observed [30,31]. Thus the loss in GRIN power associated with the age-dependent increase in p plays an important role in the typical age-dependent changes in refraction [14,16].
Comparison of Figs. 3 and 4 again supports the view that average index is lower than the equivalent index at all ages.
5. Conclusions
Our modeling, supported by experimental studies, shows that the average refractive index of the lens, used in OCT in the conversion of optical paths to physical distances, is lower than the equivalent index which is appropriate for optical modeling of the refractive characteristics of the eye. Both appear to be age-dependent, with the average index increasing and the equivalent index decreasing, throughout adult life. The difference between the two indices reduces from about 0.017 at the age of 20 to 0.009 at 70 years. Further experimental studies are desirable to reduce the uncertainties in absolute values of the two indices and their changes with age and accommodation.
References and links
- 1.Drexler W., Findl O., Schmetterer L., Hitzenberger C. K., Fercher A. F., “Eye elongation during accommodation in humans: differences between emmetropes and myopes,” Invest. Ophthalmol. Vis. Sci. 39(11), 2140–2147 (1998). [PubMed] [Google Scholar]
- 2.Mallen E. A. H., Kashyap P., Hampson K. M., “Transient axial length change during the accommodation response in young adults,” Invest. Ophthalmol. Vis. Sci. 47(3), 1251–1254 (2006). 10.1167/iovs.05-1086 [DOI] [PubMed] [Google Scholar]
- 3.Read S. A., Collins M. J., Woodman E. C., Cheong S. H., “Axial length changes during accommodation in myopes and emmetropes,” Optom. Vis. Sci. 87(9), 656–662 (2010). 10.1097/OPX.0b013e3181e87dd3 [DOI] [PubMed] [Google Scholar]
- 4.Atchison D. A., Smith G., “Possible errors in determining axial length changes during accommodation with the IOLMaster,” Optom. Vis. Sci. 81(4), 283–286 (2004). 10.1097/00006324-200404000-00015 [DOI] [PubMed] [Google Scholar]
- 5.D. A. Atchison and G. Smith, Optics of the Human Eye (Butterworth-Heinemann, Oxford 2000), pp.250–258. [Google Scholar]
- 6.Dubbelman M., van der Heijde G. L., Weeber H. A., “The thickness of the aging human lens obtained from corrected Scheimpflug images,” Optom. Vis. Sci. 78(6), 411–416 (2001). 10.1097/00006324-200106000-00013 [DOI] [PubMed] [Google Scholar]
- 7.Dubbelman M., Van der Heijde G. L., “The shape of the aging human lens: curvature, equivalent refractive index and the lens paradox,” Vision Res. 41(14), 1867–1877 (2001). 10.1016/S0042-6989(01)00057-8 [DOI] [PubMed] [Google Scholar]
- 8.Wiemer N. G. M., Dubbelman M., Kostense P. J., Ringens P. J., Polak B. C. P., “The influence of diabetes mellitus type 1 and 2 on the thickness, shape, and equivalent refractive index of the human crystalline lens,” Ophthalmology 115(10), 1679–1686 (2008). 10.1016/j.ophtha.2008.03.019 [DOI] [PubMed] [Google Scholar]
- 9.Glasser A., Campbell M. C. W., “Biometric, optical and physical changes in the isolated human crystalline lens with age in relation to presbyopia,” Vision Res. 39(11), 1991–2015 (1999). 10.1016/S0042-6989(98)00283-1 [DOI] [PubMed] [Google Scholar]
- 10.Borja D., Manns F., Ho A., Ziebarth N., Rosen A. M., Jain R., Amelinckx A., Arrieta E., Augusteyn R. C., Parel J. M., “Optical power of the isolated human crystalline lens,” Invest. Ophthalmol. Vis. Sci. 49(6), 2541–2548 (2008). 10.1167/iovs.07-1385 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bahrami M., Goncharov A. V., “Geometry-invariant gradient refractive index lens: analytical ray tracing,” J. Biomed. Opt. 17(5), 055001 (2012). 10.1117/1.JBO.17.5.055001 [DOI] [PubMed] [Google Scholar]
- 12.Navarro R., Palos F., González L., “Adaptive model of the gradient index of the human lens. I. Formulation and model of aging ex vivo lenses,” J. Opt. Soc. Am. A 24(8), 2175–2185 (2007). 10.1364/JOSAA.24.002175 [DOI] [PubMed] [Google Scholar]
- 13.Navarro R., Palos F., González L. M., “Adaptive model of the gradient index of the human lens. II. Optics of the accommodating aging lens,” J. Opt. Soc. Am. A 24(9), 2911–2920 (2007). 10.1364/JOSAA.24.002911 [DOI] [PubMed] [Google Scholar]
- 14.Smith G., Atchison D. A., Pierscionek B. K., “Modeling the power of the aging human eye,” J. Opt. Soc. Am. A 9(12), 2111–2117 (1992). 10.1364/JOSAA.9.002111 [DOI] [PubMed] [Google Scholar]
- 15.Kasthurirangan S., Markwell E. L., Atchison D. A., Pope J. M., “In vivo study of changes in refractive index distribution in the human crystalline lens with age and accommodation,” Invest. Ophthalmol. Vis. Sci. 49(6), 2531–2540 (2008). 10.1167/iovs.07-1443 [DOI] [PubMed] [Google Scholar]
- 16.Jones C. E., Atchison D. A., Meder R., Pope J. M., “Refractive index distribution and optical properties of the isolated human lens measured using magnetic resonance imaging (MRI),” Vision Res. 45(18), 2352–2366 (2005). 10.1016/j.visres.2005.03.008 [DOI] [PubMed] [Google Scholar]
- 17.Y. Le Grand and S. G. El Hage, Physiological Optics (Springer Verlag, Berlin, 1980 ) pp. 65–67. [Google Scholar]
- 18.H. von Helmholtz, Treatise on Physiological Optics, Vol. 1, translated from the 3rd German edition by J. P. C. Southall, Optical Society of America, Rochester, p.100. (1924). [Google Scholar]
- 19.Atchison D. A., “Age-related paraxial schematic emmetropic eyes,” Ophthalmic Physiol. Opt. 29(1), 58–64 (2009). 10.1111/j.1475-1313.2008.00598.x [DOI] [PubMed] [Google Scholar]
- 20.Charman W. N., Adnan, Atchison D. A., “Gradients of refractive index in the crystalline lens and transient changes in refraction among patients with diabetes,” Biomed. Opt. Express 3(12), 3033–3042 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Uhlhorn S. R., Borja D., Manns F., Parel J.-M., “Refractive index measurement of the isolated crystalline lens using optical coherence tomography,” Vision Res. 48(27), 2732–2738 (2008). 10.1016/j.visres.2008.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.de Castro A., Siedlecki D., Borja D., Uhlhorn S., Parel J.-M., Manns F., Marcos S., “Age-dependent variation of the gradient index profile in human crystalline lenses,” J. Mod. Opt. 58(19-20), 1781–1787 (2011). 10.1080/09500340.2011.565888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jones C. E., Atchison D. A., Pope J. M., “Changes in lens dimensions and refractive index with age and accommodation,” Optom. Vis. Sci. 84(10), 990–995 (2007). 10.1097/OPX.0b013e318157c6b5 [DOI] [PubMed] [Google Scholar]
- 24.Hemenger R. P., Garner L. F., Ooi C. S., “Change with age of the refractive index gradient of the human ocular lens,” Invest. Ophthalmol. Vis. Sci. 36(3), 703–707 (1995). [PubMed] [Google Scholar]
- 25.de Castro A., Birkenfeld J., Maceo B., Manns F., Arrieta E., Parel J.-M., Marcos S., “Influence of shape and gradient refractive index in the accommodative changes of spherical aberration in nonhuman primate crystalline lenses,” Invest. Ophthalmol. Vis. Sci. 54(9), 6197–6207 (2013). 10.1167/iovs.13-11996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.de Freitas C., Ruggeri M., Manns F., Ho A., Parel J.-M., “In vivo measurement of the average refractive index of the human crystalline lens using optical coherence tomography,” Opt. Lett. 38(2), 85–87 (2013). 10.1364/OL.38.000085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dubbelman M., Van der Heijde G. L., Weeber H. A., Vrensen G. F., “Changes in the internal structure of the human crystalline lens with age and accommodation,” Vision Res. 43(22), 2363–2375 (2003). 10.1016/S0042-6989(03)00428-0 [DOI] [PubMed] [Google Scholar]
- 28.Richdale K., Sinnott L. T., Bullimore M. A., Wassenaar P. A., Schmalbrock P., Kao C. Y., Patz S., Mutti D. O., Glasser A., Zadnik K., “Quantification of age-related and per diopter accommodative changes of the lens and ciliary muscle in the emmetropic human eye,” Invest. Ophthalmol. Vis. Sci. 54(2), 1095–1105 (2013). 10.1167/iovs.12-10619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Atchison D. A., Markwell E. L., Kasthurirangan S., Pope J. M., Smith G., Swann P. G., “Age-related changes in optical and biometric characteristics of emmetropic eyes,” J. Vision 8(4), 29 (2008) [DOI] [PubMed] [Google Scholar]
- 30.Slataper F. J., “Age norms of refraction and vision,” Arch. Ophthalmol. 43(3), 466–481 (1950). 10.1001/archopht.1950.00910010475007 [DOI] [Google Scholar]
- 31.Saunders H., “Age-dependence of human refractive errors,” Ophthalmic Physiol. Opt. 1(3), 159–174 (1981). 10.1111/j.1475-1313.1981.tb00388.x [DOI] [PubMed] [Google Scholar]