Verification of a two-layer inverse Monte Carlo absorption model using multiple source-detector separation diffuse reflectance spectroscopy

Abstract

A two-layer Monte Carlo lookup table-based inverse model is validated with two-layered phantoms across physiologically relevant optical property ranges. Reflectance data for source-detector separations of 370 μm and 740 μm were collected from these two-layered phantoms and top layer thickness, reduced scattering coefficient and the top and bottom layer absorption coefficients were extracted using the inverse model and compared to the known values. The results of the phantom verification show that this method is able to accurately extract top layer thickness and scattering when the top layer thickness ranges from 0 to 550 μm. In this range, top layer thicknesses were measured with an average error of 10% and the reduced scattering coefficient was measured with an average error of 15%. The accuracy of top and bottom layer absorption coefficient measurements was found to be highly dependent on top layer thickness, which agrees with physical expectation; however, within appropriate thickness ranges, the error for absorption properties varies from 12–25%.

1. Introduction

Diffuse reflectance spectroscopy (DRS) has been used to noninvasively measure tissue properties for skin-related disease diagnosis [1–5]. Typically, DRS uses a fiber to deliver light to tissue. The delivered light is both scattered and absorbed by the tissue and is then detected by another fiber, which is at a certain distance, known as the source-detector separation (SDS), from the source fiber. The diffuse reflectance spectra, calculated as the ratio of the collected light intensity to the delivered light intensity, contains quantitative information about tissue structure and composition. While the instrumentation for a DRS system is relatively straight forward, the accurate extraction of optical properties from the measured reflectance is a significant challenge. An accurate model of light transport in tissue is needed to relate the measured reflectance to tissue optical properties. One method for analyzing diffuse reflectance spectra is the diffusion approximation of the radiative transport equation; however, the diffusion approximation is not valid for short source-detector separations or in highly absorbing tissues [6–8].

Because many diseases are located in the epithelial layer at the tissue surface, it is necessary to use probes with a short SDS in order to sample photons that travel through the epithelial layer [9, 10]. Additionally, angiogenesis, an indicator of early cancer, can cause a significant increase in absorption due to blood. Many models of light transport in tissue have been developed to overcome this limitation. These include empirical models [11, 12], experimental models [13, 14], and computational models [15–17]. The majority of these models assume tissue to be a homogeneous semi-infinite turbid medium. However, many tissues have a layered structure and the homogeneity assumption can lead to errors in extracted optical properties [18]. Towards this end, two-layer models of diffuse reflectance have been developed in order to model light transport in two-layer tissues. Despite representing significant advances to the field, these models have several limitations including requiring the top layer thickness to be known a priori [19–21] and utility only for specific tissue types and probe geometries [20–25].

Towards addressing these limitations, we present a two-layer Monte Carlo look-up table (MCLUT) model, extended from a single layer MCLUT model previously developed by our group [16]. Briefly, the advantages of a MCLUT approach are its ability to work for a wide range of probe geometries and tissue types, the ease of implementation, and its speed. Our two-layer MCLUT inverse model is capable of extracting optical properties and top layer thickness from diffuse reflectance spectra. This current work aims to validate our two-layer model by comparing model predictions to experimental measurement for two different SDSs (370 and 740 μm) across a physiologically realistic range of optical properties and top layer thicknesses. Two SDSs were used because the 740 μm SDS will sample deeper than its 370 μm counterpart; it is the difference in reflectance spectra obtained from each SDS - due to the sampling depth variation - that aids in the accurate prediction of top layer thickness over a wider range of thicknesses. The ability of this technique to measure both morphological properties, such as top layer thickness, as well as functional properties, such as hemoglobin concentration, allows us to provide diagnostic information with applications including (1) pigmentary disorder studies, (2) disease (rosacea, lupus, scleroderma, morphea, lymphedema) monitoring, (3) treatment outcome measures, (4) topical medical absorption studies, (5) thickness of psoriasis plaque, and (6) cosmetic studies.

2. Computational methods

2.1. Creation of the Monte Carlo lookup table (MCLUT)

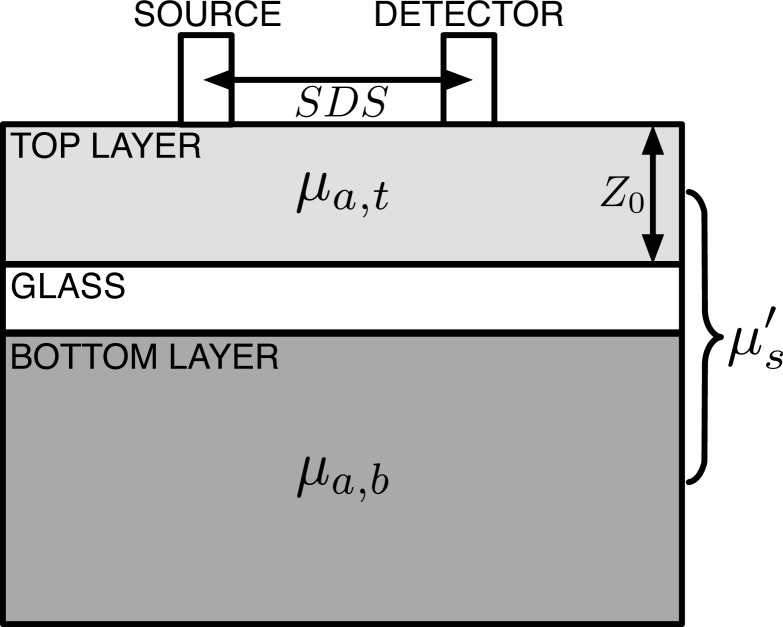
Photon transport in tissue was modeled using Monte Carlo simulation of a two-layer model with four free parameters: top layer thickness (Z ₀), top layer absorption coefficient (μ_a,t), bottom layer absorption coefficient (μ_a,b) and the reduced scattering coefficient (μ′_s), which is assumed to be the same for both layers. In reality, scattering can change from one layer to the next; however our simplifying assumption improves the convergence properties of the inverse model. Additionally, previous two layer models of diffuse reflectance have made this same assumption and shown the ability to accurately measure depth dependent absorption properties in the presence of scattering differences between layers [20,21,26]. Figure 1 shows the two-layer geometry of the model.

Fig. 1.

Two-layer model geometry used in the Monte Carlo simulations. Absorption for the top and bottom layers, scattering for both layers, and the top-layer thickness are used as inputs to generate reflectance values for all SDSs. The coverslip was modeled as a middle layer with constant thickness of .625 mm, no scattering or absorption, and an index of refraction of 1.5.

A two-dimensional Monte Carlo code written in ANSI C implemented on an NVIDIA GTX 560 Ti GPU with NVIDIA’s Compute Unified Device Architecture (CUDA) was used to simulate photon reflectance in the two-layer tissue model on 386 parallel threads [27]. The multiply-with carry random number generator was used. The refractive index above the tissue was set to 1.452 to match the refractive index of an optical fiber, and the refractive index of the medium was set to 1.4 to match the refractive index of tissue. Spatially resolved diffuse reflectance was calculated by convolving the impulse response using a Gaussian shaped beam profile with a diameter of 100 μm [28]. We created two separate MCLUTs: one with an SDS of 370 μm, and one with an SDS of 740 μm, where each was modeled as concentric annuli in order to increase the number of detected photons. The coverslip used in the two layer phantoms was modeled as a middle layer with a constant thickness of .625 mm, no scattering or absorption, and an index of refraction of n = 1.5. Every entry in each MCLUT contains a reflectance value for a given Z ₀, μ_a,t, μ_a,b, and μ′_s. In the MCLUTs, Z ₀ ranges from 0 to 3000 μm, μ_a,t ranges from 0 to 5 mm⁻¹, μ_a,b ranges from 0 to 5 mm⁻¹, and μ′_s ranges from 0 to 7 mm⁻¹. The ranges for the parameters were selected to cover a range larger than the optical properties used to create the phantoms in order to prevent biasing of the results. Twenty evenly spaced increments were used for each of the free parameters listed above, giving a total of 160,000 separate MC simulations. Cubic splines were used to interpolate between values in the MCLUT. A total of 1 × 10⁶ photons were used for each MC simulation and were found to sufficiently reduce stochastic noise below 2% for all values in the MCLUT; however, the error for the values in the MCLUT within the optical property range of the phantoms is below 0.2%. The Henyey-Greenstein phase function was used for sampling scattering angles. Scattering anisotropy, g, was set to 0.85 for all simulations. For the range of g values present in human tissue (g > 0.8), it has been shown [29] that the diffuse reflectance will be the same for any combination of values of μ_s and g that generate the same μ′_s. For light transport near the source location (short SDSs) as employed in this study, previous look-up table studies conducted in our laboratory have shown that extracted absorption and reduced scattering coefficient values have less than 10% error when the anisotropy is greater than 0.7 [14]. Total time to create the MCLUTs was 16.2 hours.

2.2. Forward model of diffuse reflectance

A forward model of diffuse reflectance relates tissue optical and geometric properties to diffuse reflectance as described by the flowchart in Fig. 2. For our two-layer model, the properties of interest are top-layer (μ_a,t) and bottom layer (μ_a,b) absorption coefficients, top-layer thickness (Z ₀), and reduced scattering coefficient (μ′_s), which is assumed to be the same for both layers. Reduced scattering at all wavelengths is calculated using Eq. 1, which is commonly employed for tissue optics:

$${\mu }_s^{\prime }(\lambda )={\mu }_s^{\prime }({\lambda }_0)\times {\left(\frac{\lambda }{{\lambda }_0}\right)}^{-B}$$ (1)

where μ′_s(λ) is the reduced scattering coefficient at wavelength λ, λ ₀ = 630 nm, and B is the scattering exponent. The scattering exponent, B, was fixed to 1.5 and the selection of a value for B was found to have negligible impact on the accuracy of extracted parameters because of the calibration procedure described in section 3.3. Absorption in the top layer at each wavelength is calculated using Eq. 2:

$${\mu }_{a,t}(\lambda )=\sum _{i=1}^{N_t}\text{ln}(10){\epsilon }_{i,t}(\lambda )C_{i,t}$$ (2)

where μ_a,t (λ) is the absorption coefficient at wavelength λ in the top layer, N_t is the number of chromophores in the top layer, ε_i,t (λ) is the extinction coefficient at wavelength λ of chromophore i in the top layer, and C_i,t is the concentration of chromophore i. Similarly, the absorption coefficients at each wavelength for the bottom layer are calculated using Eq. 3:

$${\mu }_{a,b}(\lambda )=\sum _{i=1}^{N_b}\text{ln}(10){\epsilon }_{i,b}(\lambda )C_{i,b}$$ (3)

where μ_a,b(λ) is the absorption coefficient at wavelength λ in the bottom layer, N_b is the number of chromophores in the bottom layer, ε_i,b(λ) is the extinction coefficient at wavelength λ of chromophore i in the bottom layer, and C_i,b is the concentration of chromophore i. Once the optical properties are determined at each wavelength, the MCLUT is used to determine the reflectance at each wavelength and cubic splines used to interpolate between values in the MCLUT.

Fig. 2.

Flowchart for the forward model of diffuse reflectance for a two-layer tissue model. Tissue parameters are inputs into the model and the output is a diffuse reflectance spectrum. The Monte Carlo lookup table is used to determine reflectance based on the set of optical properties and top layer thickness.

2.3. Inverse model of diffuse reflectance

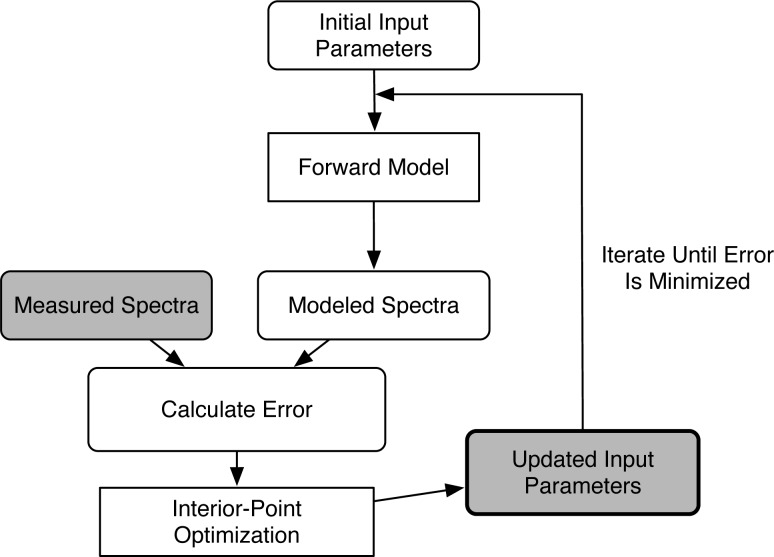
While the forward model provides a useful tool for analyzing the effect of layered tissue geometry on diffuse reflectance, the real utility of the model is realized by inverting the model so that we can extract tissue properties from measured spectra. Figure 3 illustrates the flowchart for the inverse model of diffuse reflectance in a two-layer tissue. This allows one to use the model in conjunction with a DRS system to characterize tissue and aid in disease diagnosis. The two-layer model that relates tissue properties to diffuse reflectance is non-linear and, therefore, cannot be directly inverted. One method is to use an iterative optimization routine. This is achieved by first estimating an initial value for the tissue properties and using the forward model to generate an initial reflectance spectrum. The mean squared percent error between the measured spectrum and model spectrum is then computed using Eq. 4:

$$E=\frac{1}{nS}\sum _S\sum _{\lambda }{\left[\frac{R_{s,\mathit{meas}}(\lambda )-R_{s,\mathit{model}}(\lambda )}{R_{s,\mathit{meas}}(\lambda )}\right]}^2$$ (4)

where E is the error, n is the number of wavelength points, S is the number of source detector separations, R_s,meas(λ) is the reflectance of the measured spectrum at wavelength λ and source detector separation S (370 μm and 740 μm), and R_s,model(λ) is the reflectance of the model spectrum at wavelength λ and source detector separation S. Next, the tissue properties are updated using an interior-point optimization routine [30] from the MATLAB optimization toolbox to work towards minimizing the error. An initial guess of Z ₀ = 300 μm, μ_a,t = 1 mm⁻¹, μ_a,b = 1 mm⁻¹, and μ′_s = 1.5 mm⁻¹ was used for all spectra, and the choice of initial guess was found to have negligible impact on the final results. The average time to convergence is on the order of 1 second on an Intel Core i5 2.7GHz processor.

Fig. 3.

Inverse model of diffuse reflectance. First, an initial guess for the tissue parameters is used to generate a spectrum with the forward model. Next, the error between the measured and modeled spectra is calculated and the parameters are updated using an optimization routine that minimizes the error between the modeled and measured spectra.

3. Experimental methods

3.1. Two-layered phantoms

Experimental data for model verification were obtained by constructing two-layered phantoms. In total, 15 phantoms were constructed to cover the relevant range of optical properties [31,32]. Table 1 summarizes their optical properties.

Table 1.

Summary of the optical properties of the two-layer phantoms used in this study for comparison with MC simulations. The scattering values are given for λ = 630 nm. For the absorbers: g is green dye; r is red dye; b is blue dye; and Hb is dissolved Hemoglobin powder. The largest source of uncertainty for the optical property values is due to errors in the pipette volumes required in order to create the liquid phantoms. The pipettes were calibrated; however, based upon vendor specifications, pipette volume uncertainties were calculated to result in approximately a 4% error in optical property values.

Phantom Number	μ′s(λ 0) (mm−1)	μa,t,max (mm−1)	μa,b,max (mm−1)
1	1.5	0.25 (b)	1.275 (r)
2	1.5	0.25 (r)	1.275 (b)
3	1.5	2.3 (b)	0.25 (g)
4	1.5	2.3 (g)	0.25 (b)
5	1.5	0.25 (b)	2.3 (g)
6	1.5	0.25 (g)	2.3 (b)
7	2.85	0.25 (r)	2.3 (b)
8	2.85	0.25 (b)	2.3 (b)
9	2.85	2.3 (r)	0.25 (b)
10	2.85	1.275 (g)	0.25 (r)
11	2.85	1.275 (g)	2.3 (r)
12	0.75	0.25 (r)	2.3 (g)
13	0.75	0.25 (r)	2.3 (g)
14	1.7	0	1 (Hb)
15	1.54	0	1.5 (Hb)

For Phantoms 1–13, food dyes were used as the absorbers for both the top and bottom layers, while phantoms 14–15 were designed to simulate physiological circumstances with a scattering top layer (epithelial layer) and an absorbing bottom layer containing hemoglobin (stromal layer). Each phantom has the same top and bottom scattering properties, which is presented in terms of the reduced scattering coefficient at 630 nm, μ′_s(λ ₀). The top and the bottom layer absorption properties differ in terms of concentration (maximum absorption co-efficient [μ_a,t,max and μ_a,b,max]) and absorbing molecule. Polystyrene 1.025 μm diameter beads with 2.5% solid by volume (Polysciences, PA) were used as the scattering media; red, green and blue food dyes (Safeway, TX) and lyophilized hemoglobin powder (H0267, Sigma Aldrich, MO) were used as absorbers. The optical density for all absorbers was measured using a spectrophotometer (DU720, Beckman Coulter, CA) and the absorption spectra were calculated using Beer’s law.

Across all these phantoms, μ′_s ranges from 0.81–4.91 mm⁻¹ and the μ_a values range from 0–2.3 mm⁻¹. μ_a,t,max and μ_a,b,max represent the maximum absorption coefficient for top and bottom layers across all wavelengths, respectively. These values correspond to physiologically relevant values of cutaneous optical properties used for skin cancer and other dermatological purposes [5, 31, 32]. The μ′_s(λ ₀) values were chosen and the resultant bead solution (beads + de-ionized water) volumes calculated using a Mie theory algorithm that evaluates the total scattering cross-section across the wavelength range 350–750 nm for each specified bead solution. Both the top and bottom layers were mixed in vials and thoroughly agitated in order to guarantee complete mixing.

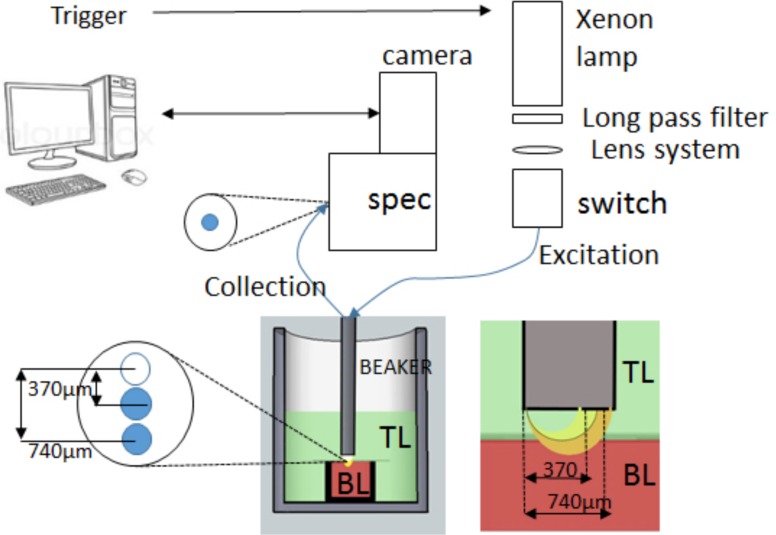
As shown in Fig. 4, each phantom consists of a bottom layer (encapsulated by a small vial cap and a glass coverslip) and a top layer. The vial cap diameter was 19.05 mm; no change in spectra was observed between spectra taken in the center of the vial cap and 5 mm offset from the center, which confirmed that the vial cap was a semi-infinite medium and the vial side-wall was not causing photon attenuation or altering the photon path. The probe is mounted on a fine-scale translation stage with 5 μm resolution (Model 433, Newport, CA) such that it is centered about the vial cap and can be traversed vertically through the volume of the beaker. The bottom layer solution was pipetted into the inside of a small vial lid and capped off by affixing a 0.625 mm thick microscope coverslip to the outside rim of the lid using superglue. Once dry, this lid was then affixed to the internal base of a 30 mL beaker using superglue and care taken to ensure that the vial cap was as flat as possible. The probe was traversed downwards using the translation stage until flush. The top layer solution was then pipetted into the beaker. Small 4–40 screws were placed at the bottom of the beaker (but all below the microscope slide) in order to occupy as much volume as possible and save cost on the polystyrene beads. In each case, the height of the top layer (depth of liquid above microscope slide after top layer volume addition), was measured in order to ensure that the top layer was at least 2 mm deep. Prior to data collection, initial measurements were taken to ensure that no top layer liquid had seeped in between the probe tip and microscope slide.

Fig. 4.

Schematic of the two-layered experiment and the DRS system used to collect the data, including the “photon flow” from: excitation provided by the xenon lamp, whose signal is passed through a long-pass filter and an optical lens system for collimation and focusing into a fiber-optic switch to be delivered to the two-layer phantom, consisting of a top layer (TL) and bottom layer (BL). The bottom layer is housed in a small vial cap with a coverslip placed on top, and the top layer poured on top of it. Collection is at 370 and 740 μm SDSs and passed into a spectrograph and imaged by a cooled CCD camera. Custom software provides the trigger for the light source and detector and also processes and stores the measured spectra for later analysis.

3.2. Detection system

Reflectance measurements were made using a linear probe (FiberTech Optica, Canada), consisting of 15 fibers aligned side-by-side, each at a center-to-center separation of 370 μm. Excitation light was delivered through the central (7) fiber and light collected from fibers 8 and 9, corresponding to SDSs of 370 and 740 μm respectively. As shown in Fig. 4, the 740 μm SDS will sample deeper than the 370 μm and, as discussed previously, it is this difference in sampling depth between the two channels that enables top layer thickness measurements over a wide range. Measurements were taken at flush (0 μm, probe touching microscope slide) and subsequently at 50 μm increments until there was no change in reflectance across all wavelengths.

We used a pulsed Xenon flash lamp as the DRS light source (L7684, Hamamatsu Photonics, NJ), which provided broadband 375–700 nm illumination as identified in Fig. 4. The Xenon lamp provided a pulse of full width half maximum (FWHM) 2.9 μs. In order to prevent second-order dispersion contaminating the reflectance spectra, the Xenon white light was first passed through a 340 nm long-pass filter (Asahi Spectra, Torrance, CA). The light was then collimated and focused using two lenses. Per acquisition, the Xenon lamp was pulsed twice to deliver light for both the 370 and 740 μm SDSs. The two white light pulses are coupled into an optical fiber and guided into a 3× 1 optical switch (FSM-13, Piezosystems Jena, Germany). The switch is a microelectromechanical (MEMS) device, which uses microprisms to control and open different optical ports to ensure that the two broadband Xenon light pulses are separated and coupled sequentially into the linear probe without any overlap. The switch is controlled via transistor-transistor logic (TTL) pulse trains. Light from the switch’s output was then passed to the input of the linear probe via a subminiature version A (SMA) nipple fitting; roughly 30% loss in signal is measured due to the optical switch and SMA fitting. The distal end of the linear probe was aligned with the vertical axis of the spectrograph (SpectraPro 2150i, Princeton Instruments, Trenton, NJ) using software provided by the manufacturer (WinSpec, Princeton Instruments, Trenton, NJ). A 150 grooves/mm grating, blazed at 500 nm, was used in order to capture the entire visible spectrum needed DRS (375–700nm). A slit width of 200 μm was used. All spectra were collected for an exposure time of 50 μs.

The data collection was controlled via custom software written in LabVIEW (National Instrument, Austin, Texas). The software executes two-layer data collection by sequentially capturing the 370 and 740 μm signals. Onboard calculations were performed to convert the raw signals into reflectance spectra (see Section 3.4). The Xenon pulsed lamp was triggered via TTL pulses provided by a timer-counter board (NI 2121, National Instruments, Austin, Texas). The camera was controlled by a PCI card (PCI-6602, National Instruments, Austin, Texas) and operated, in part, by pre-written software (R3 Software, Princeton, NJ). The timing of optical port switching was also controlled by TTL pulses sent by the custom software.

3.3. Calibration measurements

For each phantom, wavelength calibration was performed using a mercury-argon light source (HG-1, Ocean Optics, FL) which provides clear, distinct atomic spectral lines. Because the modeled spectra are in absolute units (photons counted) and the measured spectra are in units relative to a calibration measurement, it was necessary to perform an additional calibration so that the modeled and measured spectra can be compared. Reflectance measurements were taken each day of a stock solution of polystyrene beads (no absorption) where μ′_s(λ ₀) = 1.5 mm⁻¹ and then modeled spectra were calculated using the same optical properties as the stock solution. Next, the ratio of the measured to modeled spectra was calculated and all measured spectra were multiplied by this ratio. Additionally, the calibration corrects for wavelength dependent responses in the experiment that are not accounted for in the forward model, including the wavelength dependent response of the spectrograph, and the wavelength dependance of scattering anisotropy (g) and index of refraction (n).

3.4. Spectral processing

At each height, the final DRS spectrum per SDS is the average across five separate measurements (five pulses per height). To improve the SNR, we bin every three pixels for a final spectral dispersion of 0.77 nm/pixel and a resulting spectral resolution FWHM of 5.3 pixels (4.08 nm). We calculate the reflectance using the following expression (Eq. 5):

$$R(\lambda )=\frac{I_{\mathit{sample}}(\lambda )-I_{\mathit{background}}(\lambda )}{\left[I_{\mathit{standard}}(\lambda )-I_{\mathit{background}}(\lambda )\right]\times 100/R_{\mathit{standard}}}$$ (5)

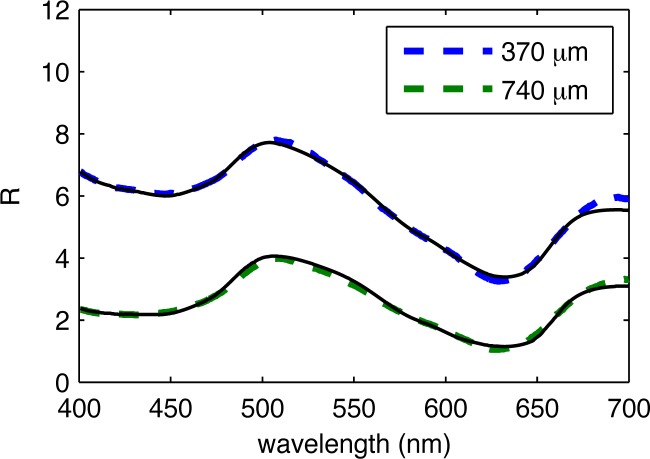
where I_sample(λ) is the raw spectrum from the phantom, I_background(λ) is the background (spectra collected without the white light excitation), I_standard(λ) is the spectralon standard spectra and 100/R_standard is used to account for the calibrated reflectance level of the spectralon standard (throughout this paper all results were obtained with a 20% spectralon reflectance standard). Spectra are presented in terms of wavelength by using the Hg-Ar lines to convert pixels to wavelength. Figure 5 shows the measured spectra and associated MCLUT fits from phantom 3 with a top layer thickness of 300 μm.

Fig. 5.

Measured spectra (colored and dashed) and associated MCLUT fits (solid black) from phantom 3 with a top layer thickness of 300 μm.

4. Results and discussion

Figure 6 is included as a visual demonstration of how the reflectance spectra change with increasing Z ₀ and of the increased sampling depth with increased SDS. Here spectra are shown at selected heights from phantom 8. Scaled absorption spectra of the red and blue dye are shown for reference. We see that at flush (0 μm) only the red dye is sampled. As the depth increases, the blue ink absorption becomes increasingly more pronounced; conversely, the red dye absorption decreases. These are consistent with physical intuition that increasing top layer thickness corresponds to increased top layer absorption and decreased bottom layer absorption. Finally, at 1000 μm, red dye absorption is barely detectable and only the blue ink top layer is being sampled. These trends are more evident for the 740 μm SDS as more dye molecules are sampled. The most dramatic change in the reflectance spectra occurs at reasonably shallow depths (from 250–600 μm).

Fig. 6.

Measured reflectance spectra at selected heights for phantom 8. Top and bottom plots correspond to 370 and 740 μm source-detector separations, respectively. Scaled absorbance profiles of red (dashed red line) and blue (dashed blue line) dyes are also included for reference.

The inverse model was used to extract optical properties (Z ₀, μ′_s(λ ₀), μ_a,t,max, μ_a,b,max) from all spectra across all phantoms. For each of these 4 variables, at each height up to 0.95mm, we computed the normalized root-mean-square-deviation (NRMSD) averaged across all 15 phantoms, which is calculated as shown in Eq. 6:

$$\mathit{NRMSD}=\frac{1}{x_{i,\mathit{max}}-x_{i,\mathit{min}}}\sqrt{\frac{{\sum }_{i=1}^n{\left(x_i(Z_0)-{\widehat{x}}_i(Z_0)\right)}^2}{n}}$$ (6)

where x is the variable of interest, i is the phantom number, n is the total number of phantoms, and x_i(Z ₀) and x̂_i(Z ₀) are the predicted and known values, respectively, at a particular top layer thickness, and x_i,max − x_i,min is the range of known measurements for variable x_i.

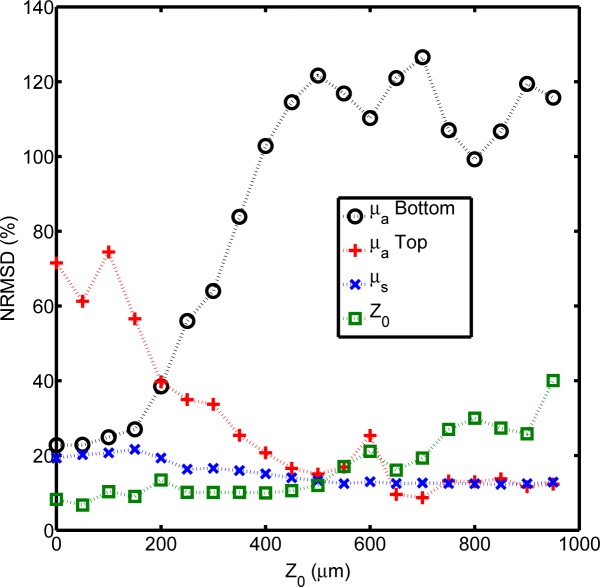
The results from these calculations are plotted in Fig. 7 for the four variables of interest. Overall, amongst the four variables, we see the best agreement in Z ₀ for which the average NRMSD (for all thicknesses) is 17%. However, as the Fig. 7 shows, the prediction of the top layer thickness is considerably better for thicknesses up to 550 μm, with an average error of 10%. We see that the error in both the top and bottom layer absorption is also thickness dependent. With increasing top layer thickness, the top layer absorption error decreases while the bottom layer error increases. Such a result is expected as an increasing top layer thickness corresponds to less photons from the bottom layer being measured (and more top layer photons being measured). Therefore, the accuracy of the model prediction is dependent Z ₀. The top layer absorption value decreases from 72% at flush to 12% for Z ₀ = 950 μm. μ_a,b,max varies from a minimum of 22% at flush up to 118% at maximum thickness. Lastly, the model retains very good accuracy for reduced scattering at 630 nm as the average error (across all thicknesses) is 15%.

Fig. 7.

Average calculated NRMSD values for each top layer thickness..

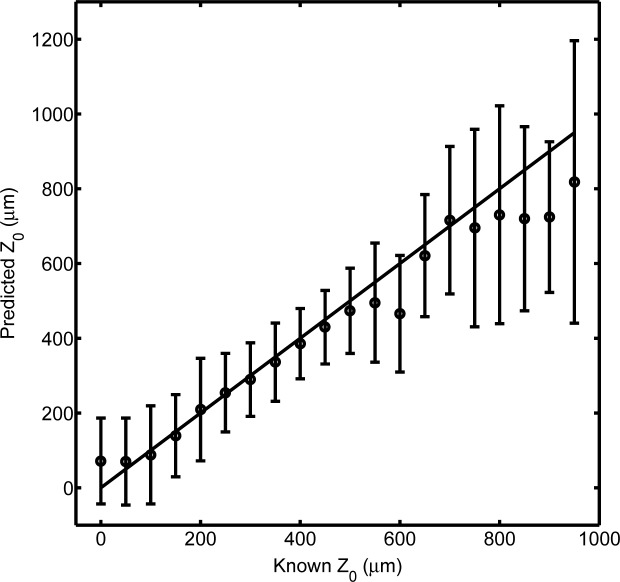
The comparison between the measured and expected top layer thicknesses is plotted in Fig. 8. The solid line represents perfect agreement. For Z ₀ between 100–500 μm the agreement is excellent. As the thickness increases, this agreement decreases and considerable divergence occurs for Z ₀ > 800 μm. Such a trend is physically expected as the model requires a sufficient number of photons originating from the bottom layer for an accurate prediction; however, the probability of a photon arriving from the bottom layer through a thick top layer is very low, and therefore, the prediction significantly suffers.

Fig. 8.

Comparison between measured and predicted top layer thicknesses. The error bars in the figure represent the standard deviation of the thickness prediction at each particular height. The solid line is the line of perfect agreement.

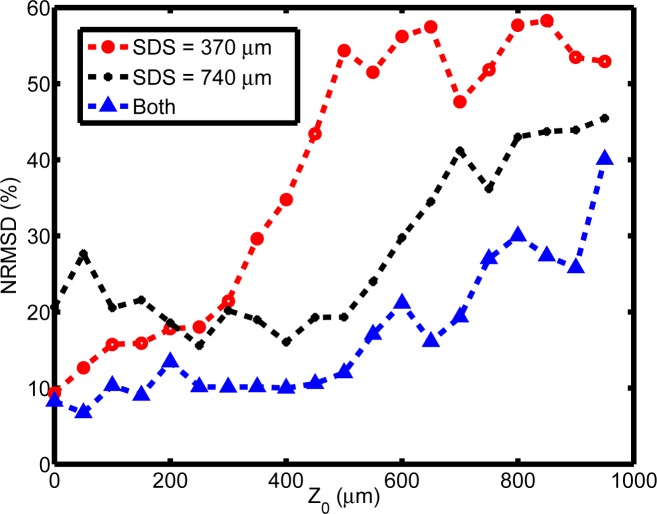
To demonstrate how the use of two SDSs improves results, the top layer thickness was also estimated using only one SDS. For an SDS of 370 μm, the average error across all thicknesses was 38% with the error increasing rapidly when Z ₀ was above 300 μm. For an SDS of 740 μm, the average error across all thicknesses was 28%, with increased error relative to the 370 μm detector when Z ₀ was below 200 μm. The use of multiple SDSs increases the range where Z ₀ can accurately be predicted. Figure 9 shows the NRMSD for predicted Z ₀ vs. known Z ₀ when only one of the SDSs was used. For comparison purposes, the results from using both SDSs are also plotted. Scattering and absorption values were predicted with similar accuracy to using both SDSs.

Fig. 9.

NRMSD for Z ₀ vs. known Z ₀ for when only one of the SDSs is used and for when both are used. This plot shows how using multiple SDSs can expand the range where Z ₀ can accurately be predicted.

5. Conclusions

We present a two-layer Monte Carlo model for skin applications which offers increased utility compared to existing two-layer models as prior knowledge of the top layer thickness is not required. Additionally, our model is sufficiently generalized to be used for a wide variety of probe geometries. The performance of the model has been validated against experimental measurement of reflectance spectra obtained from two-layered liquid phantoms. The phantoms were chosen to span the physiological range of optical properties and three different absorption media (2 food dyes and hemoglobin) were used. In order to construct the depth profiles, spectra were obtained at 50 μm increments until no further changes in spectral profiles occurred. At each height, spectra were measured at two source-detector separations: 370 and 740 μm. We show that the use of multiple SDSs increases the range of values where we can accurately predict top layer thickness. Model predictions of top layer thickness, top and bottom layer absorption coefficient, and reduced scattering coefficient were compared to known experimental values. For thicknesses between 0–550 μm, good agreement was obtained between the numerical and experimental results for top layer thickness and reduced scattering coefficients. The accuracy of top and bottom layer absorption coefficient measurements was found to be highly dependent on top layer thickness, which agrees with physical expectation; however, within appropriate thickness ranges, the error for absorption properties varies from 12–25%. Choosing different source detector separations or including more than two detectors would help to minimize the dependency of the accuracy on top layer thickness. Based upon these results, our two-layered Monte Carlo lookup table based model shows considerable promise for extracting top layer thicknesses using multiple source-detector diffuse reflectance measurements. Our future goal is explore the full potential of our two layer model by performing computational parametric studies to optimize source-detector separation selection for experimental measurement based upon prescribed layer optical properties.